Bifurcation Analysis and Chaos Control of a Discrete Fractional-Order Modified Leslie–Gower Model with Nonlinear Harvesting Effects
Abstract
:1. Introduction
1.1. Motivation and Literature Review
1.2. Discrete Fractional-Order Modified Leslie–Gower Model with Harvesting
1.3. Main Contributions
- –
- Establishing conditions for the existence and stability of nonnegative equilibrium points in model (6);
- –
- Identifying bifurcation sets and conducting a comprehensive analysis of the interior equilibrium point;
- –
- Employing state feedback control and hybrid control methodologies to manage bifurcations and chaos in model (6);
- –
- Validating our theoretical findings through numerical simulations using MATLAB and Mathematica.
1.4. Structure of the Paper
2. Existence and Stability of Nonnegative Equilibrium Points
2.1. Existence of Nonnegative Equilibrium Points
- (1)
- If , , and , two distinct boundary equilibrium points, and , exist;
- (2)
- If and , only one boundary equilibrium point, , exists;
- (3)
- If either or , a single boundary equilibrium point, , exists.
- (1)
- If , , and , then there are two distinct interior equilibrium points, and ;
- (2)
- If and , then there is only one interior equilibrium point, ;
- (3)
- If either or , then there is only one interior equilibrium point, .
2.2. Stability of Nonnegative Equilibrium Points
- (1)
- If and , the equilibrium point exhibits a sink-point behavior and is locally asymptotically stable;
- (2)
- If and , the equilibrium point exhibits a source-point behavior and is locally unstable;
- (3)
- If and (or and ), the equilibrium point exhibits a saddle-point behavior;
- (4)
- If either or , the equilibrium point exhibits a non-hyperbolic-point behavior.
- (1)
- If , then
- (a)
- and if and only if and ;
- (b)
- and (or and ) if and only if ;
- (c)
- and if and only if and ;
- (d)
- and if and only if and ;
- (e)
- and are a pair of conjugate complex roots and if and only if and .
- (2)
- If , then one of the roots satisfies . Furthermore, the other root (or or ) holds if and only if (or or ).
- (3)
- If , then one root satisfies , which implies . Furthermore, the other root
- (a)
- if and only if ;
- (b)
- if and only if ;
- (c)
- if and only if .
- (1)
- The point exhibits the following behaviors:
- (a)
- The equilibrium point exhibits a source-point behavior if ;
- (b)
- The equilibrium point exhibits a saddle-point behavior if ;
- (c)
- The equilibrium point exhibits a non-hyperbolic-point behavior if .
- (2)
- The point exhibits the following behaviors:
- (a)
- The equilibrium point exhibits a sink-point behavior if and ;
- (b)
- The equilibrium point exhibits a source-point behavior if and ;
- (c)
- The equilibrium point exhibits a non-hyperbolic-point behavior if or ;
- (d)
- The equilibrium point exhibits a saddle-point behavior under other conditions.
- (1)
- The point exhibits the following behaviors:
- (a)
- The equilibrium point exhibits a saddle-point behavior if ;
- (b)
- The equilibrium point exhibits a source-point behavior if ;
- (c)
- The equilibrium point exhibits a non-hyperbolic-point behavior if .
- (2)
- The point always exhibits a source-point behavior and is unstable.
- (3)
- The point always exhibits a non-hyperbolic-point behavior.
- (1)
- For , we can obtainwhich impliesAdditionally, since satisfies , we haveTherefore, if holds, then , indicating that is a saddle point. This completes the proof for part (a). The proofs for parts (b) and (c) follow similarly.
- (2)
- For , we find thatConsequently, we deduce that . According to Definition 2, is a source and it is unstable when it exists.
- (3)
- For , from , we can conclude that . Therefore, the eigenvalues of are and , indicating that is always classified as non-hyperbolic according to Definition 2.
- (i)
- , , and ;
- (ii)
- ;
- (iii)
- .
- (1)
- The interior equilibrium point exhibits a sink-point behavior if one of the following conditions holds:
- (a)
- and ;
- (b)
- and .
- (2)
- The interior equilibrium point exhibits a saddle-point behavior if and .
- (3)
- The interior equilibrium point exhibits a source-point behavior if one of the following conditions holds:
- (a)
- and ;
- (b)
- and .
- (4)
- The interior equilibrium point exhibits a non-hyperbolic-point behavior if one of the following conditions holds:
- (a)
- and ;
- (b)
- and .
- (1)
- The interior equilibrium point exhibits a saddle-point behavior if ;
- (2)
- The interior equilibrium point exhibits a source-point behavior if ;
- (3)
- The interior equilibrium point exhibits a non-hyperbolic-point behavior if .
3. Bifurcation Analysis
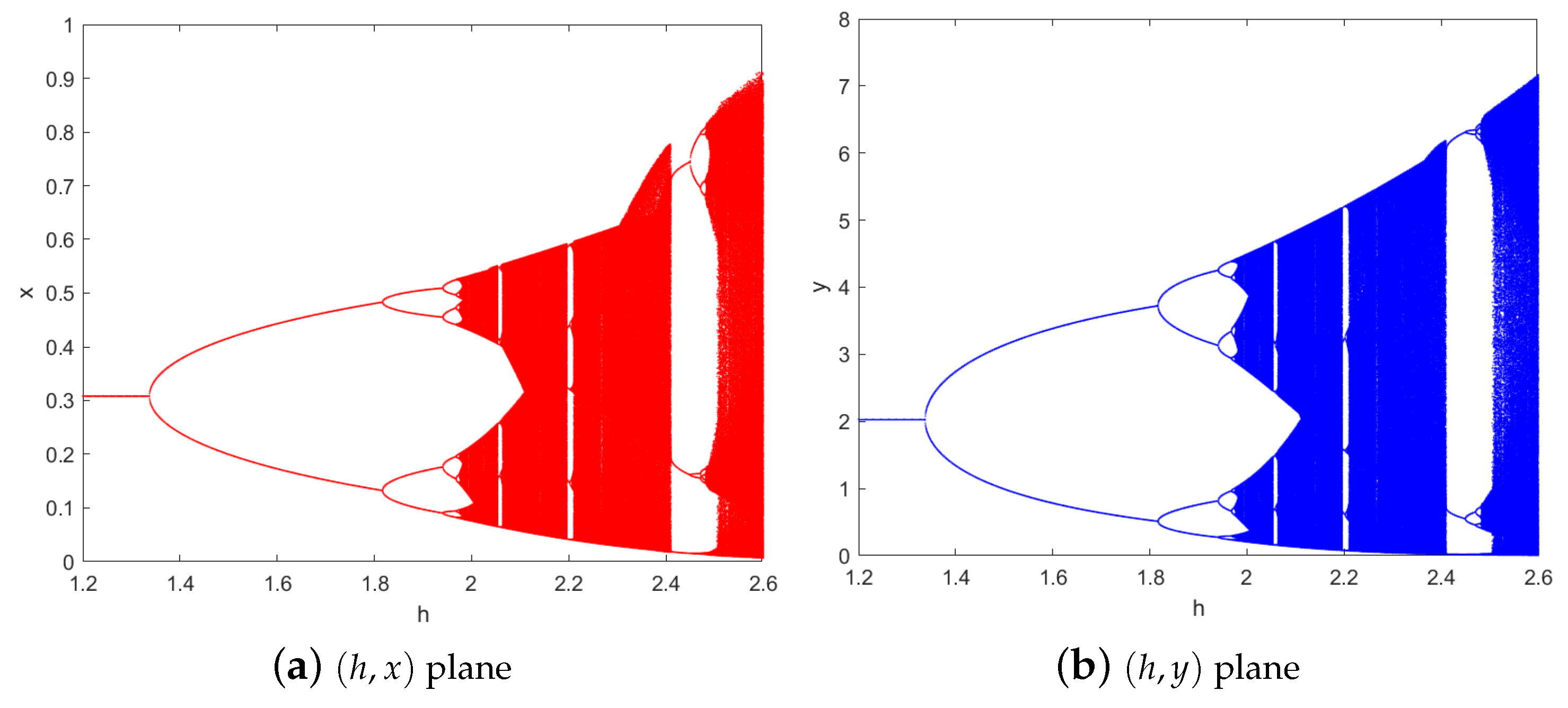
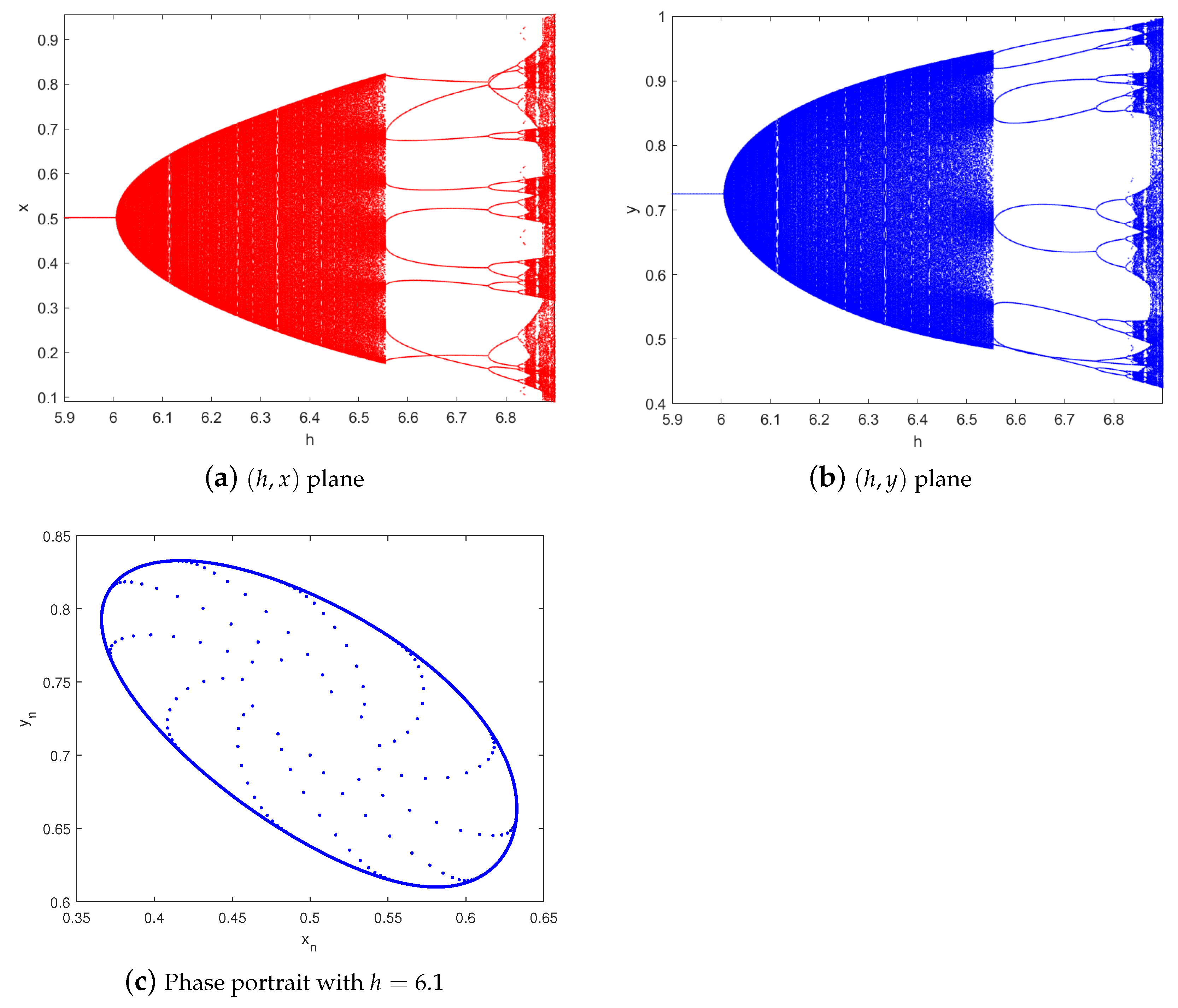
3.1. Period-Doubling Bifurcation
3.2. Neimark–Sacker Bifurcation
4. Strategies for Chaos Control
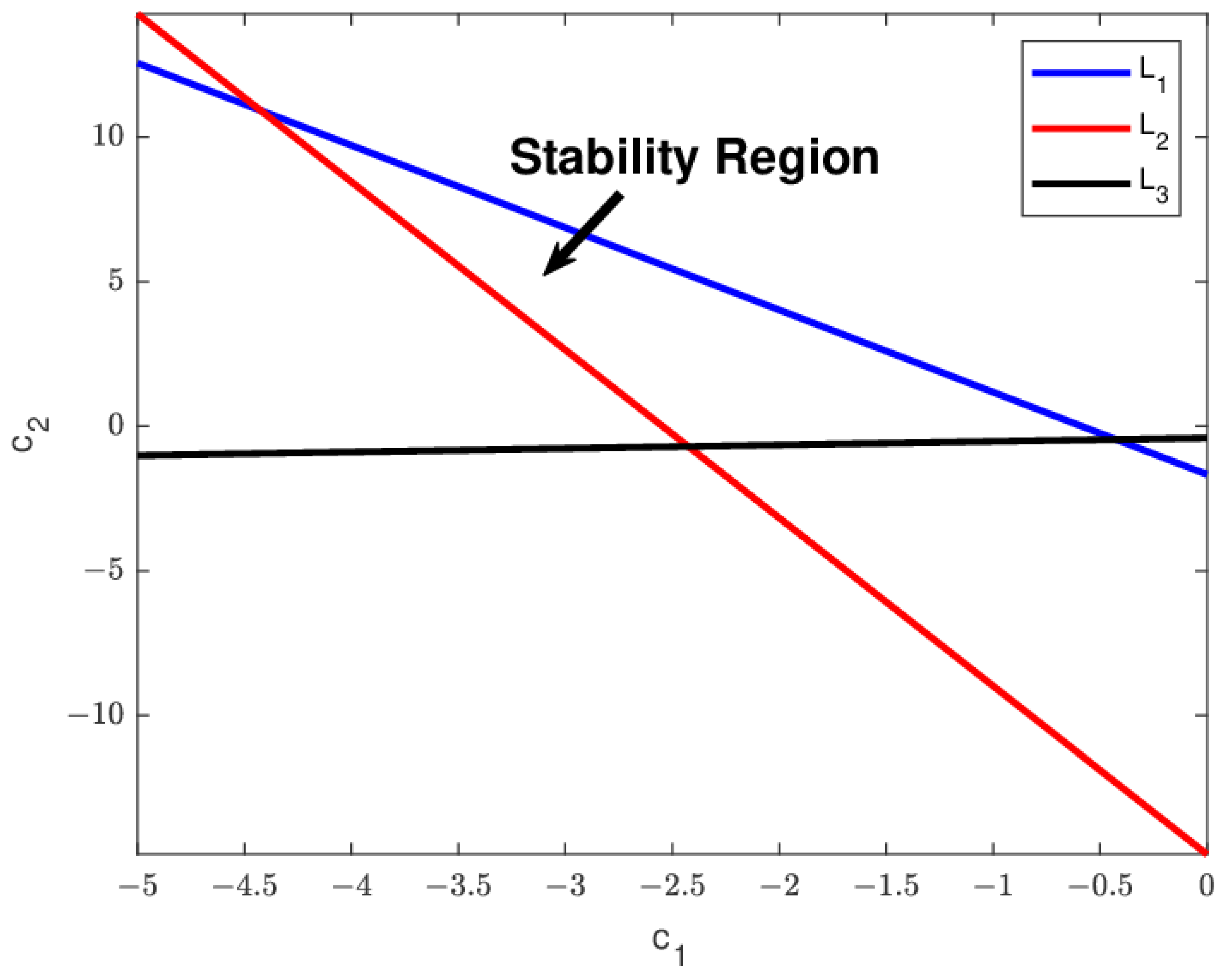
4.1. State Feedback Control Strategy
4.2. Hybrid Control Strategy
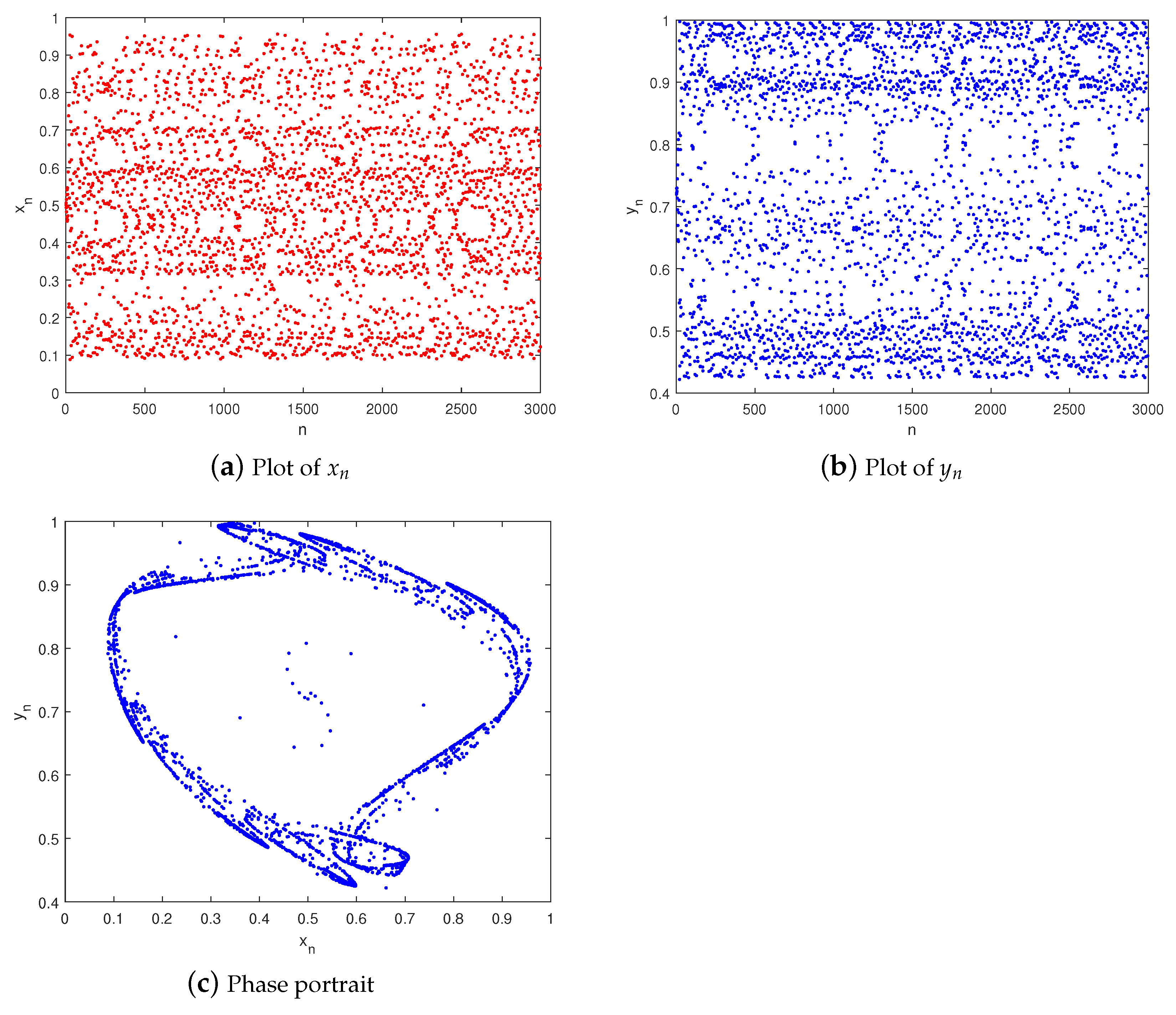
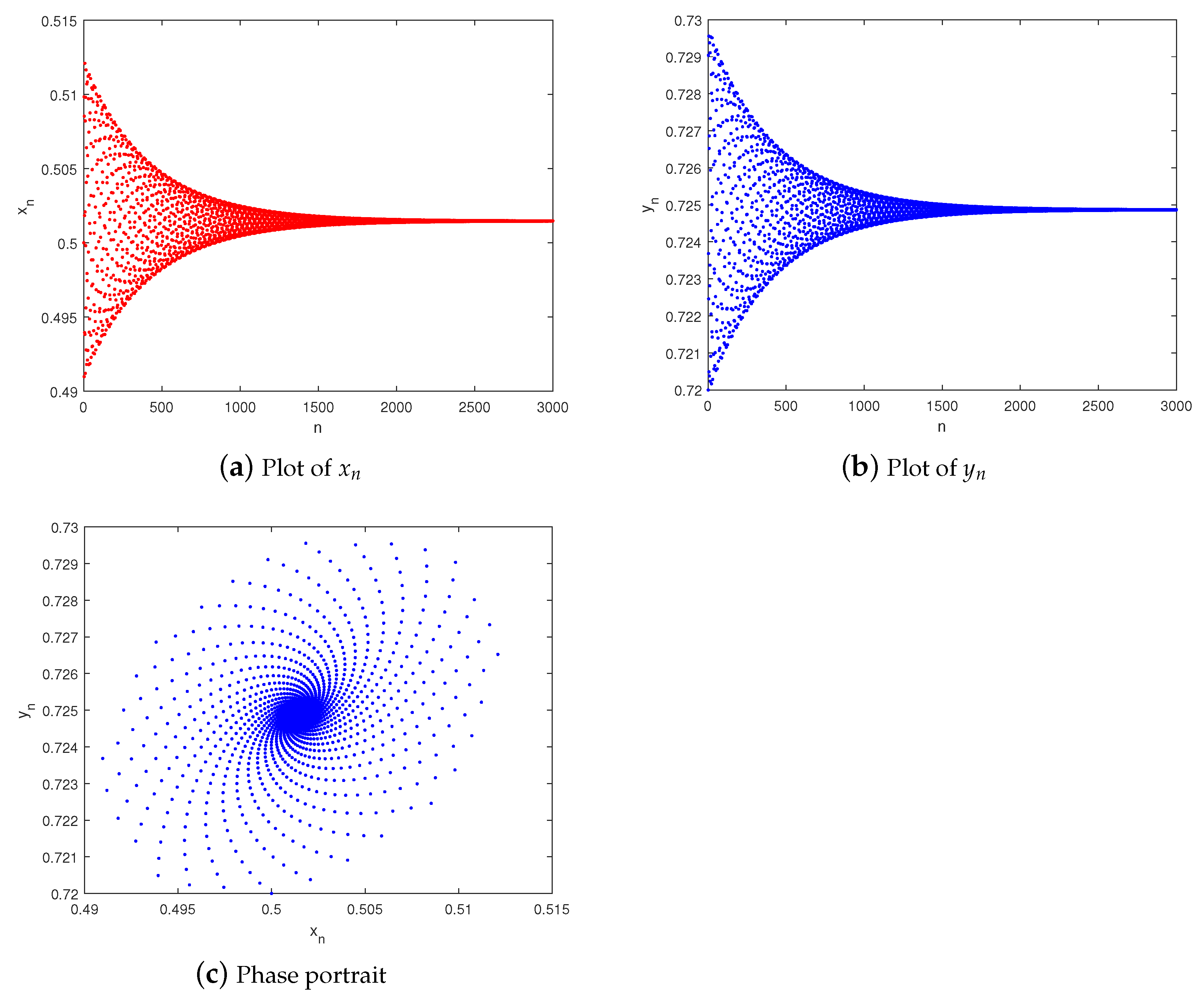
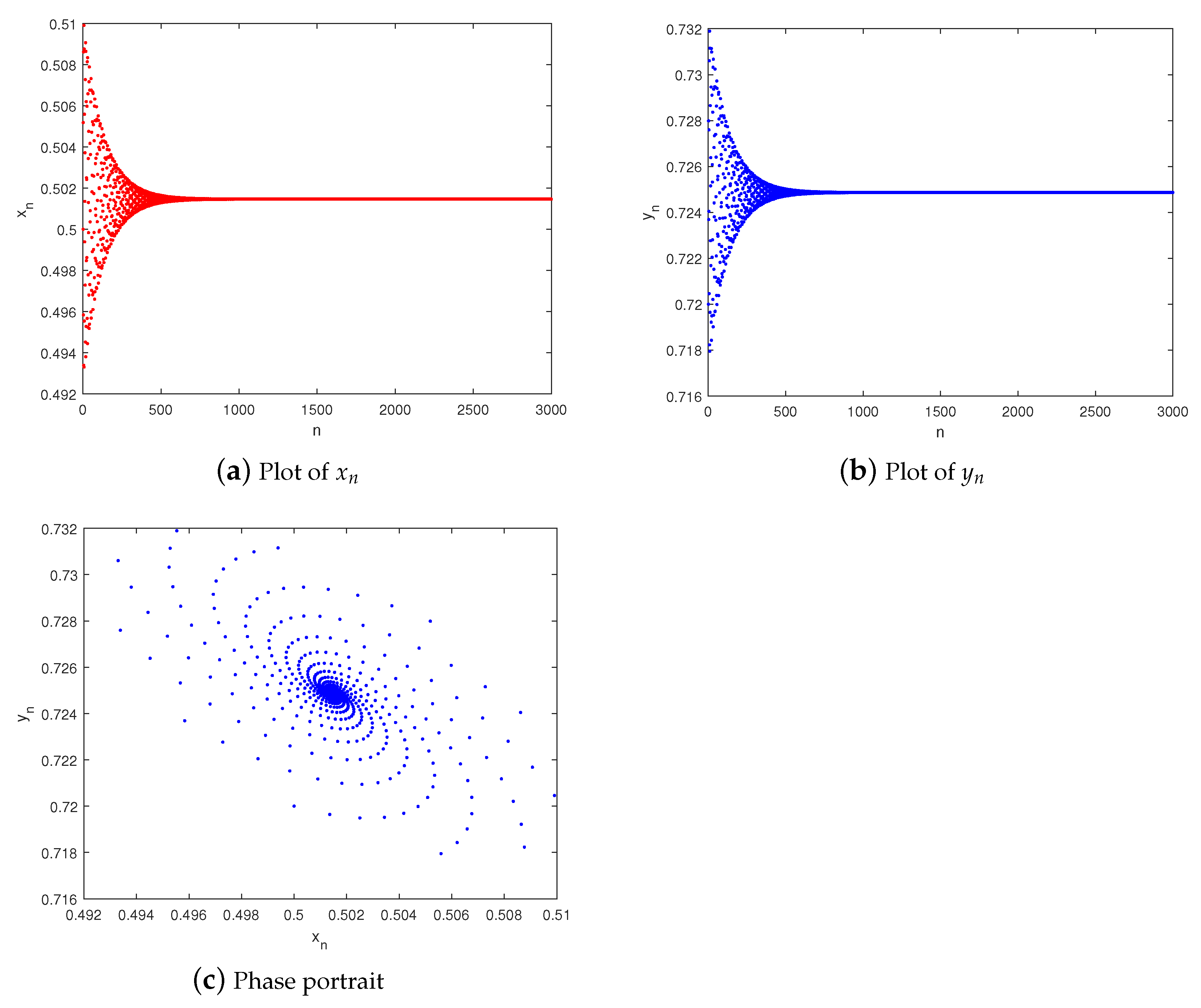
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lotka, A.J. Contribution to the theory of periodic reaction. J. Phys. Chem. 1910, 14, 271–274. [Google Scholar] [CrossRef]
- Volterra, V. Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem. R. Accad. Naz. Lincei. 1926, 2, 31–113. [Google Scholar]
- Volterra, V. Variations and fluctuations of the number of individuals in animal species living together. Anim. Ecol. 1931, 412–433. [Google Scholar] [CrossRef]
- Holling, C.S. The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can. Entomol. 1959, 91, 293–320. [Google Scholar] [CrossRef]
- Holling, C.S. Some characteristics of simple types of predation and parasitism. Can. Entomol. 1959, 91, 385–398. [Google Scholar] [CrossRef]
- Leslie, P.H. Some further notes on the use of matrices in population mathematics. Biometrika 1948, 35, 213–245. [Google Scholar] [CrossRef]
- Leslie, P.H.; Gower, J.C. The properties of a stochastic model for the predator-prey type of interaction between two species. Biometrika 1960, 47, 219–234. [Google Scholar] [CrossRef]
- May, R. Stability and complexity in model ecosystems. In Monographs in Population Biology; Princeton University Press: Princeton, NJ, USA, 1974. [Google Scholar]
- Gupta, R.P.; Chandra, P. Bifurcation analysis of modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting. J. Math. Anal. Appl. 2013, 398, 278–295. [Google Scholar] [CrossRef]
- Hu, D.; Cao, H. Stability and bifurcation analysis in a predator-prey system with Michaelis-Menten type predator harvesting. Nonlinear Anal. Real World Appl. 2017, 33, 58–82. [Google Scholar] [CrossRef]
- Song, Q.; Yang, R.; Zhang, C.; Tang, L. Bifurcation analysis in a diffusive predator-prey system with Michaelis-Menten-type predator harvesting. Adv. Differ. Equ. 2018, 329, 2018. [Google Scholar] [CrossRef]
- Singh, A.; Malik, P. Bifurcations in a modified Leslie-Gower predator-prey discrete model with Michaelis-Menten prey harvesting. J. Appl. Math. Comput. 2021, 67, 143–174. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; He, X.; Chen, F. Bifurcation and chaos in a discrete predator-prey system of Leslie type with Michaelis-Menten prey harvesting. Open Math. 2022, 20, 608–628. [Google Scholar] [CrossRef]
- Khan, M.S.; Abbas, M.; Bonyah, E.; Qi, H. Michaelis-Menten-type prey harvesting in discrete modified Leslie-Gower predator-prey model. J. Funct. Spaces 2022, 2022, 9575638. [Google Scholar] [CrossRef]
- Han, X.; Du, X. Dynamics study of nonlinear discrete predator-prey system with Michaelis-Menten type harvesting. Math. Biosci. Eng. 2023, 20, 16939–16961. [Google Scholar] [CrossRef]
- Shi, Y.; Ma, Q.; Ding, X. Dynamical behaviors in a discrete fractional-order predator-prey system. Filomat 2018, 32, 5857–5874. [Google Scholar] [CrossRef]
- Moustafa, M.; Mohd, M.H.; Ismail, A.I.; Abdullah, F.A. Dynamical analysis of a fractional-order eco-epidemiological model with disease in prey population. Adv. Differ. Equ. 2020, 2020, 1–24. [Google Scholar] [CrossRef]
- Arif, M.S.; Abodayeh, K.; Ejaz, A. Stability analysis of fractional-order predator-prey system with consuming food resource. Axioms 2023, 12, 64. [Google Scholar] [CrossRef]
- Wang, B.; Li, X. Modeling and dynamical analysis of a fractional-order predator-prey system with anti-predator behavior and a Holling type IV functional response. Fractals Fract. 2023, 7, 722. [Google Scholar] [CrossRef]
- Xu, C.; Cui, X.; Li, P.; Yan, J.; Yao, L. Exploration on dynamics in a discrete predatorprey competitive model involving feedback controls. J. Biol. Dyn. 2023, 17, 2220349. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Pan, Y.; Aouiti, C.; Yao, L. Exploring bifurcation in a fractional-order predator-prey system with mixed delays. J. Appl. Anal. Comput. 2023, 13, 1119–1136. [Google Scholar] [CrossRef]
- Xu, C.; Cui, Q.; Liu, Z.; Pan, Y.; Cui, X.; Ou, W.; Rahman, M.U.; Farman, M.; Ahmad, S.; Zeb, A. Extended hybrid controller design of bifurcation in a delayed chemostat model. MATCH Commun. Math. Comput. Chem. 2023, 90, 609–648. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Xu, C.; Peng, X.; Qiao, R. Investigating the effects of a fractional operator on the evolution of the enso model: Bifurcations, stability and numerical analysis. Fractal Fract. 2023, 7, 602. [Google Scholar] [CrossRef]
- Li, B.; Eskandari, Z.; Avazzadeh, Z. Dynamical behaviors of an SIR epidemic model with discrete time. Fractal Fract. 2022, 6, 659. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Shabbir, M.S.; Din, Q.; Naaz, H. Discretization, bifurcation, and control for a class of predator-prey interactions. Fractal Fract. 2020, 6, 31. [Google Scholar] [CrossRef]
- Rahmi, E.; Darti, I.; Suryanto, A.; Trisilowati. A modified Leslie-Gower model incorporating Beddington-DeAngelis functional response, double Allee effect and memory effect. Fractal Fract. 2021, 5, 84. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Kuzenetsov, Y.A. Elements of Applied Bifurcation Theory, 4th ed.; Springer: New York, NY, USA, 2023; pp. 129–173. [Google Scholar]
- Shi, Y.; Wang, Z. Bifurcation analysis and chaos control of a discrete fractional-order Leslie-Gower model with fear factor. AIMS Math. 2024, 9, 30298–30319. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, V.S. Bifurcations and chaos control in a discrete-time prey-predator model with Holling type-II functional response and prey refuge. J. Comput. Appl. Math. 2023, 418, 114666. [Google Scholar] [CrossRef]
- Berkal, M.; Almatrafi, M.B. Bifurcation and stability of two-dimensional activator-inhibitor model with fractional-order derivative. Fractal Fract. 2023, 7, 344. [Google Scholar] [CrossRef]
- Saadeh, R.; Abbes, A.; Al-Husban, A.; Ouannas, A.; Grassi, G. The fractional discrete predator-prey model: Chaos, control and synchronization. Fractal Fract. 2023, 7, 120. [Google Scholar] [CrossRef]
- Din, Q.; Naseem, R.A.; Shabbir, M.S. Predator-prey interaction with fear effects: Stability, bifurcation and two-parameter analysis incorporating complex and fractal behavior. Fractal Fract. 2024, 8, 221. [Google Scholar] [CrossRef]
- Ishaque, W.; Din, Q.; Khan, K.; Mabela, R. Dynamics of predator-prey model based on fear effect with bifurcation analysis and chaos control. Qual. Theory Dyn. Syst. 2024, 23, 26. [Google Scholar] [CrossRef]
- Wiener, J. Differential Equations with Piecewise Constant Delays, Trends in Theory and Practice of Nonlinear Differential Equations: Lecture Notes in Pure and Applied Math; Dekke: New York, NY, USA, 1984. [Google Scholar]
- Luo, A.C.J. Regularity and Complexity in Dynamical Systems; Springer: New York, NY, USA, 2012. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Luo, X.S.; Chen, G.; Wang, B.H.; Fang, J.Q. Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems. Chaos Solitons Fractals 2003, 18, 775–783. [Google Scholar] [CrossRef]
- Din, Q. Compexity and chaos control in a discrete-time prey-predator model. Commun. Nonlinear Sci. Numer. Simul. 2017, 49, 113–134. [Google Scholar] [CrossRef]
| Parameters | Interpretation |
|---|---|
| the prey and predator species densities, respectively | |
| r | the prey species’ intrinsic growth rate |
| K | the environment’s maximum carrying capacity for the prey species |
| the rate at which the prey is consumed | |
| n | the half-saturation constant |
| q | the prey catchability coefficient |
| E | the harvesting effort applied to capture individuals |
| suitable positive constants | |
| s | the predator species’ intrinsic growth rate |
| the maximum per capita reduction rate of the predator |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Liu, X.; Wang, Z. Bifurcation Analysis and Chaos Control of a Discrete Fractional-Order Modified Leslie–Gower Model with Nonlinear Harvesting Effects. Fractal Fract. 2024, 8, 744. https://doi.org/10.3390/fractalfract8120744
Shi Y, Liu X, Wang Z. Bifurcation Analysis and Chaos Control of a Discrete Fractional-Order Modified Leslie–Gower Model with Nonlinear Harvesting Effects. Fractal and Fractional. 2024; 8(12):744. https://doi.org/10.3390/fractalfract8120744
Chicago/Turabian StyleShi, Yao, Xiaozhen Liu, and Zhenyu Wang. 2024. "Bifurcation Analysis and Chaos Control of a Discrete Fractional-Order Modified Leslie–Gower Model with Nonlinear Harvesting Effects" Fractal and Fractional 8, no. 12: 744. https://doi.org/10.3390/fractalfract8120744
APA StyleShi, Y., Liu, X., & Wang, Z. (2024). Bifurcation Analysis and Chaos Control of a Discrete Fractional-Order Modified Leslie–Gower Model with Nonlinear Harvesting Effects. Fractal and Fractional, 8(12), 744. https://doi.org/10.3390/fractalfract8120744






