Analysis and Warning Prediction of Tunnel Deformation Based on Multifractal Theory
Abstract
:1. Introduction
2. Materials and Methods
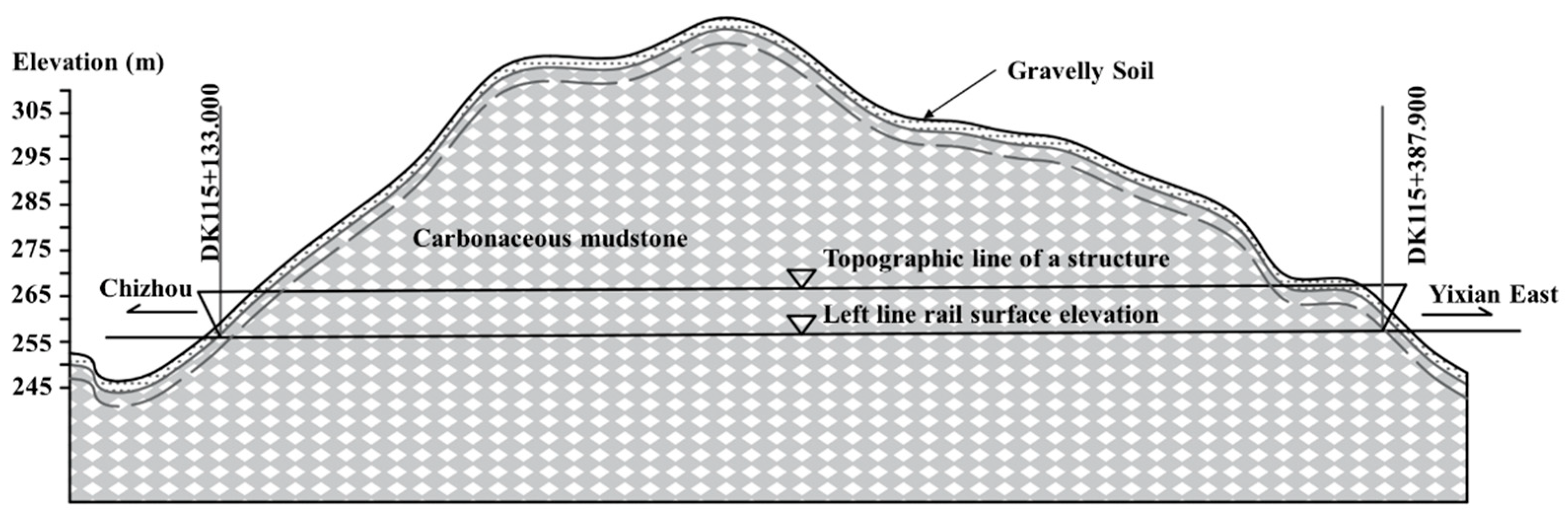
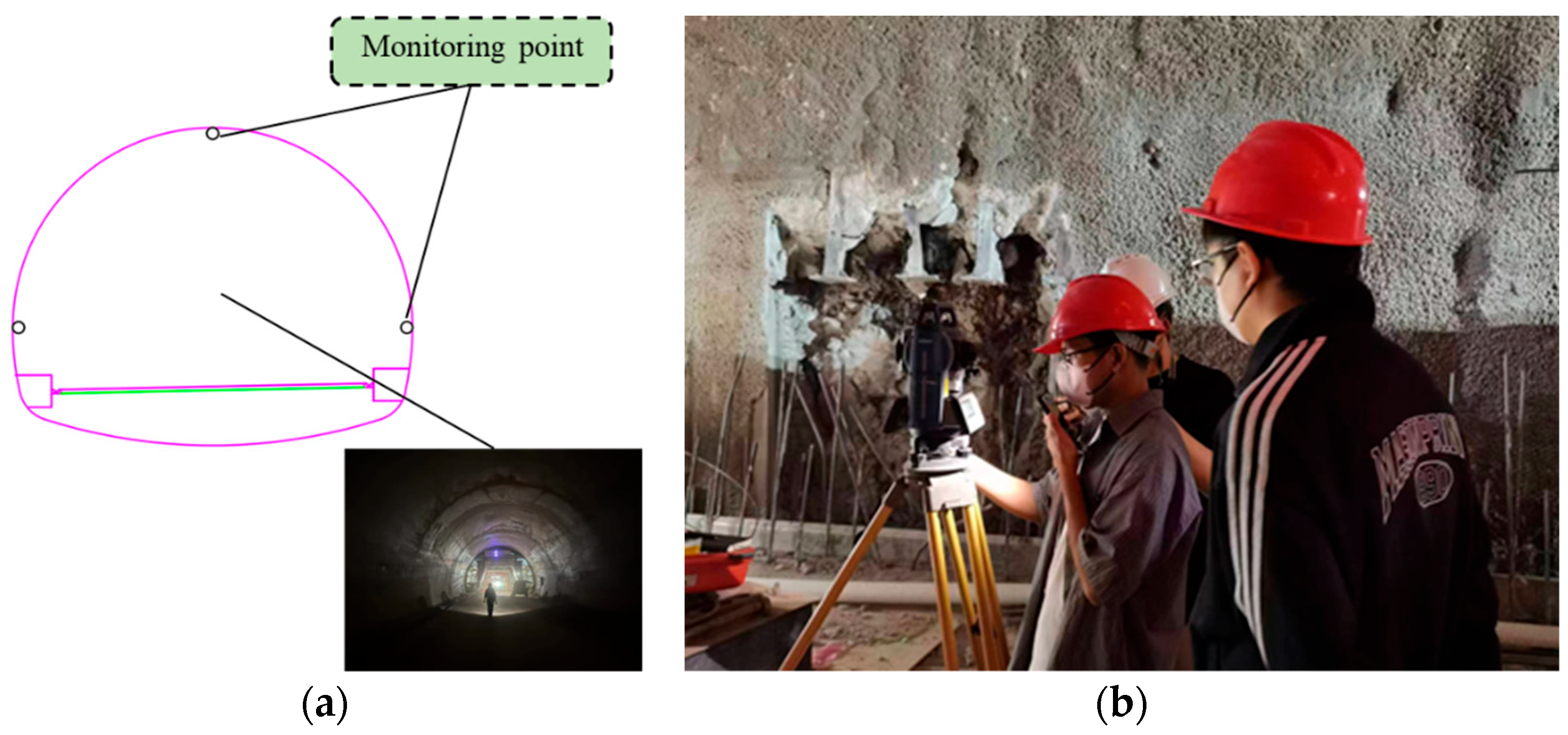
2.1. Project Overview and Monitoring Data
2.2. MF-DFA
2.3. M–K Test Method
2.4. PSO-LSTM Prediction Modeling
2.4.1. LSTM
2.4.2. PSO
2.4.3. PSO-LSTM
3. Results and Discussion
3.1. Multifractal Characterization of Tunnel Deformation Rates
3.1.1. Characterization of Tunnel Deformation Rate Data
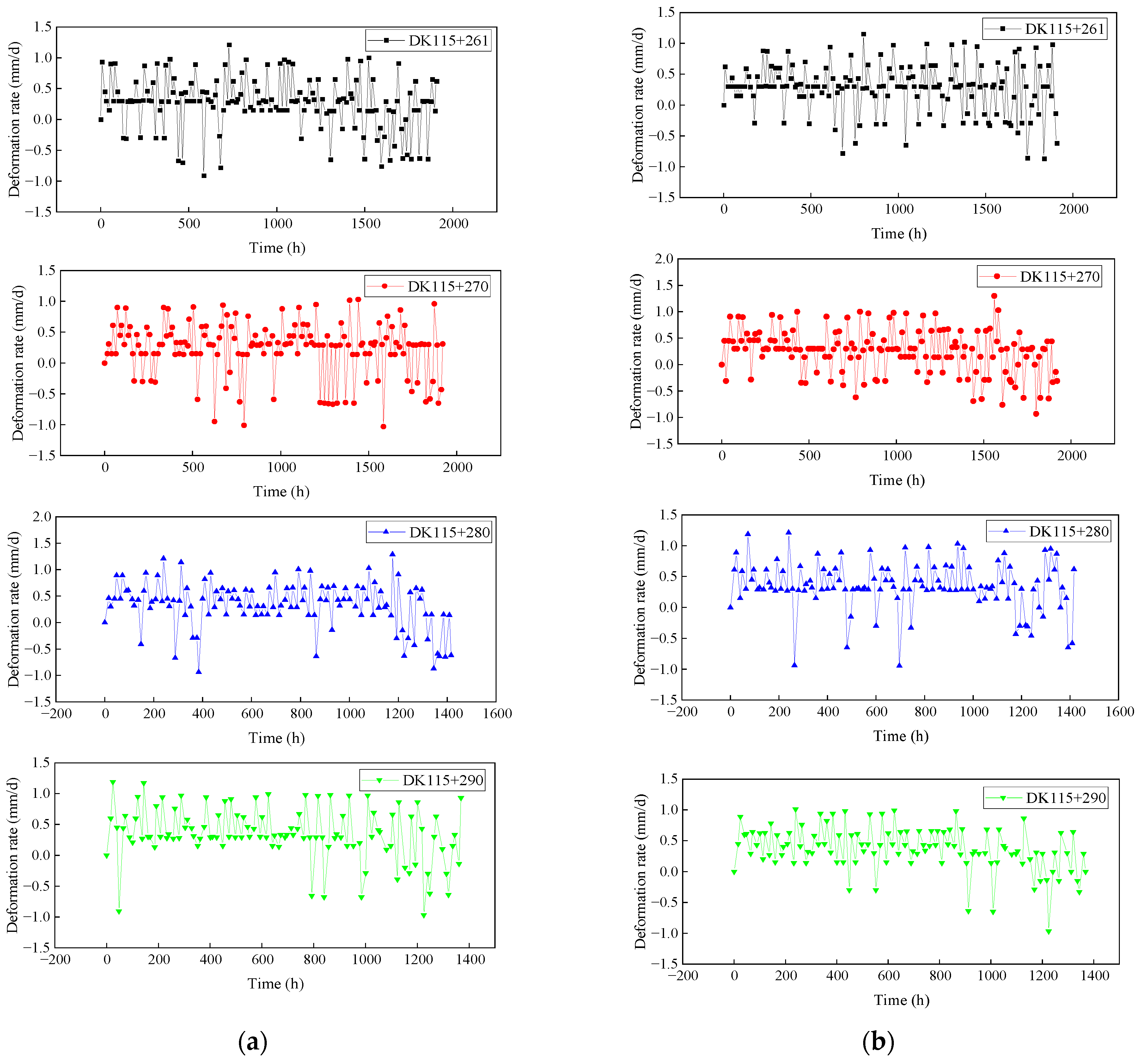
- From the average: the average tunnel deformation rate of each cross-section is greater than 0, which shows positive deformation.
- From the standard deviation: The standard deviation values of the tunnel deformation rate at each cross-section are close. In the deformation rate of tunnel settlement, the standard deviation at DK115 + 280 is the largest, which can be visualized in Figure 2a. In the deformation rate of tunnel convergence, the standard deviation at DK115 + 270 is the largest, which can be visualized in Figure 2b. The standard deviations are all close to or greater than the mean, indicating a greater degree of dispersion in the data.
- From the skewness: The skewness value of each cross-section is greater than 0, indicating that the data distribution is right-skewed. That is, the dispersion on the right side of the mean is stronger than that on the left side, showing a certain degree of long tail on the right side. All skewness values are greater than the mean and standard deviation, indicating a greater degree of skewness in the data distribution.
- From the kurtosis: the kurtosis value for each cross-section is greater than 0, indicating that the peaks of the data are steeper than the peaks of the normal distribution resulting in a spiky state.
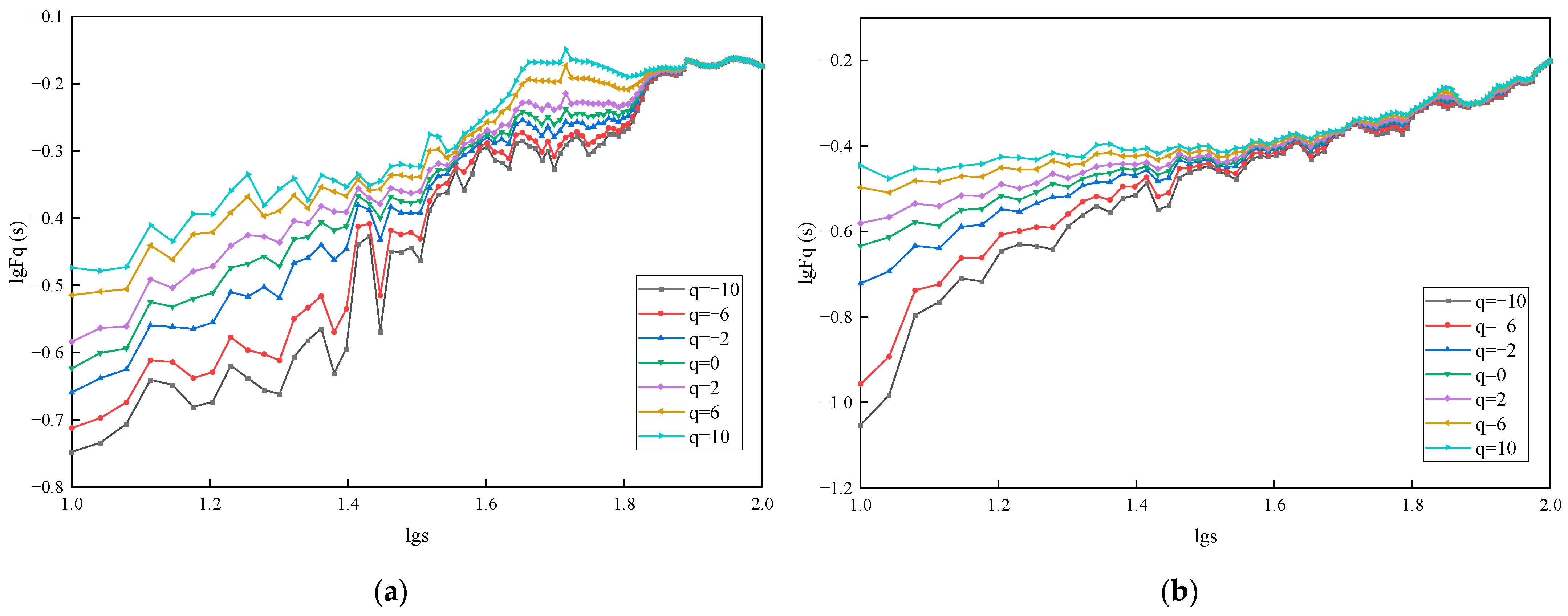
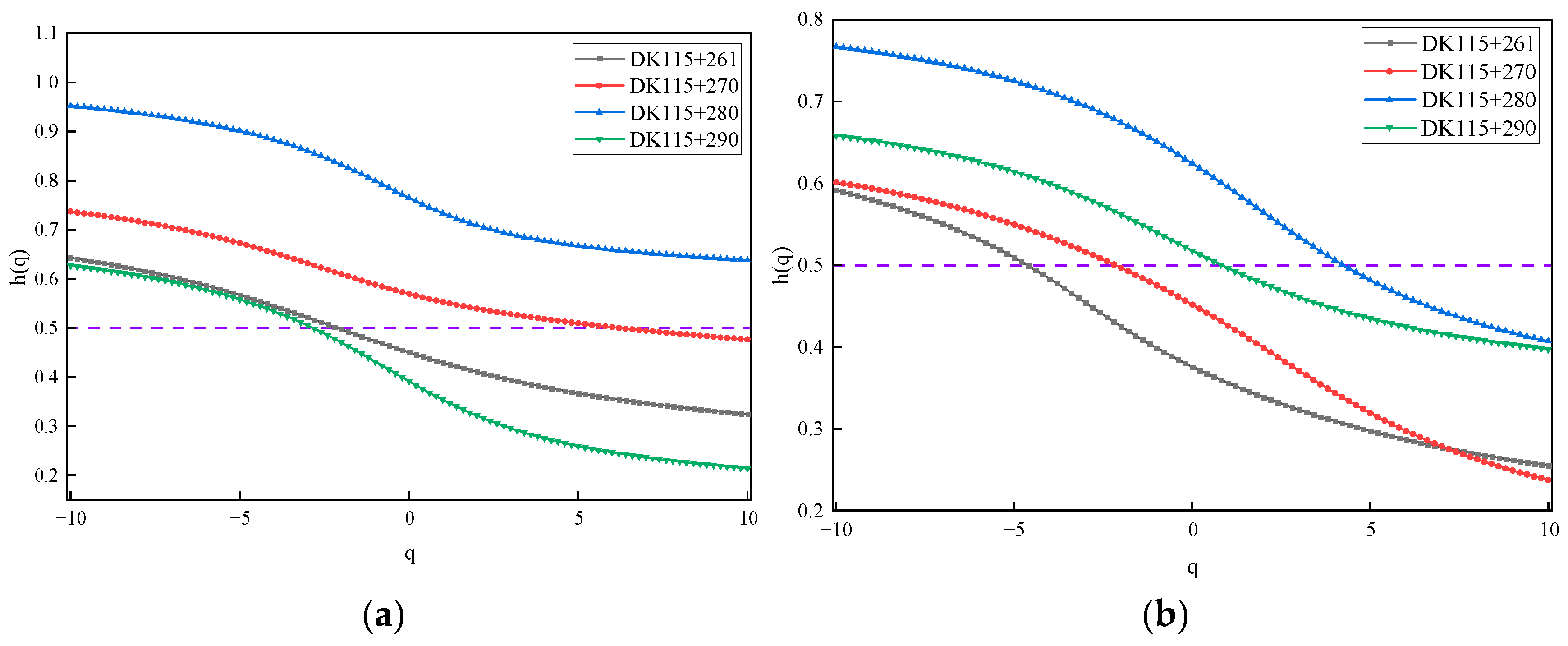
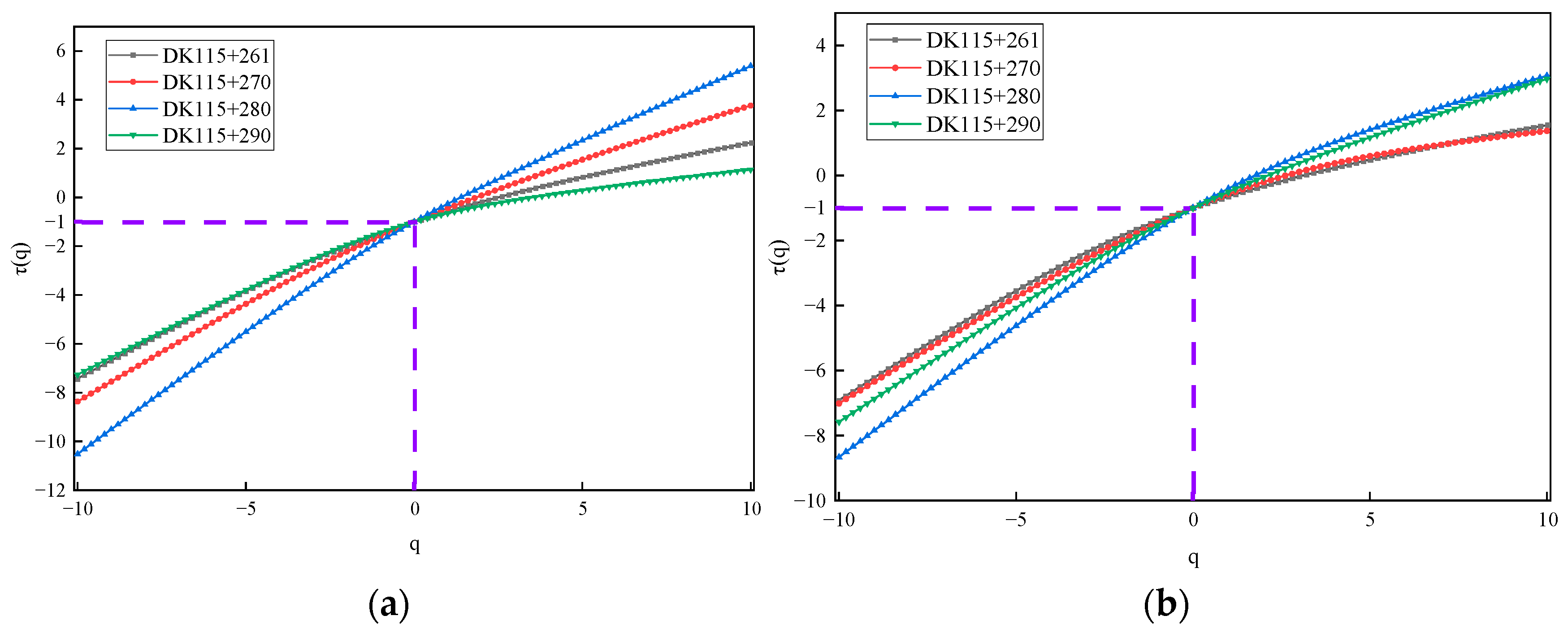
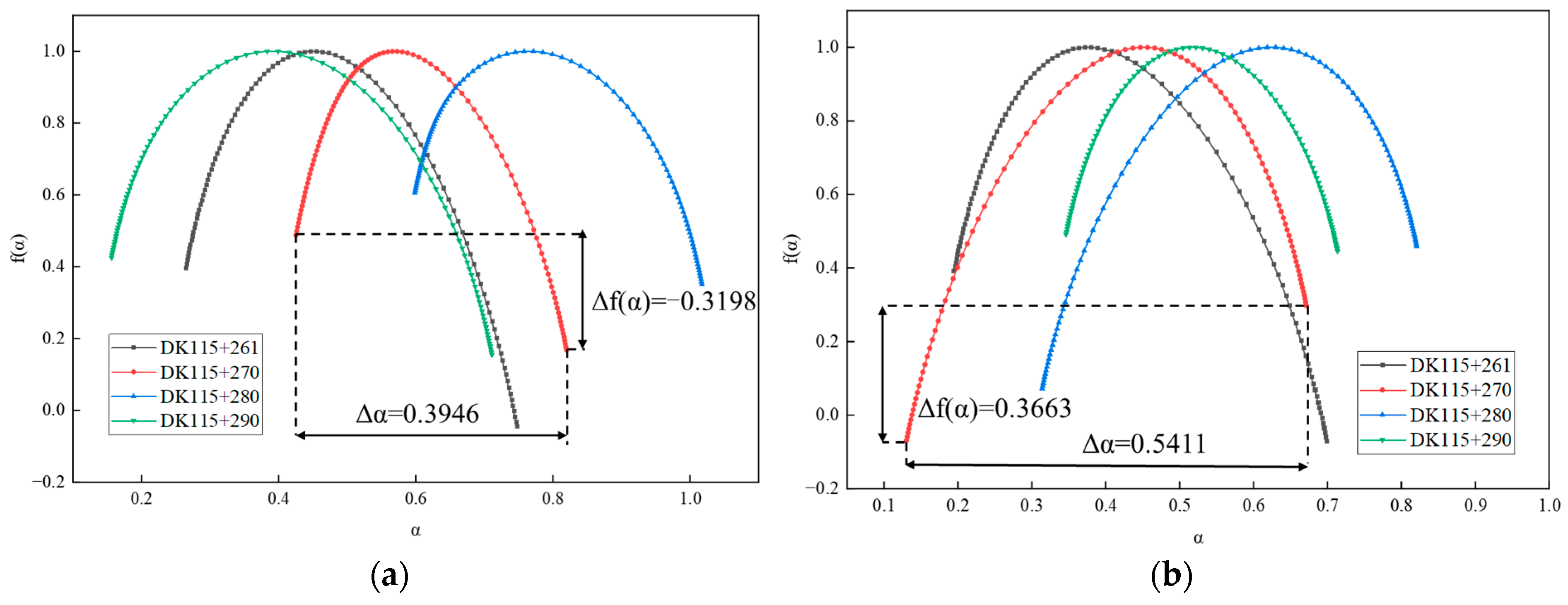
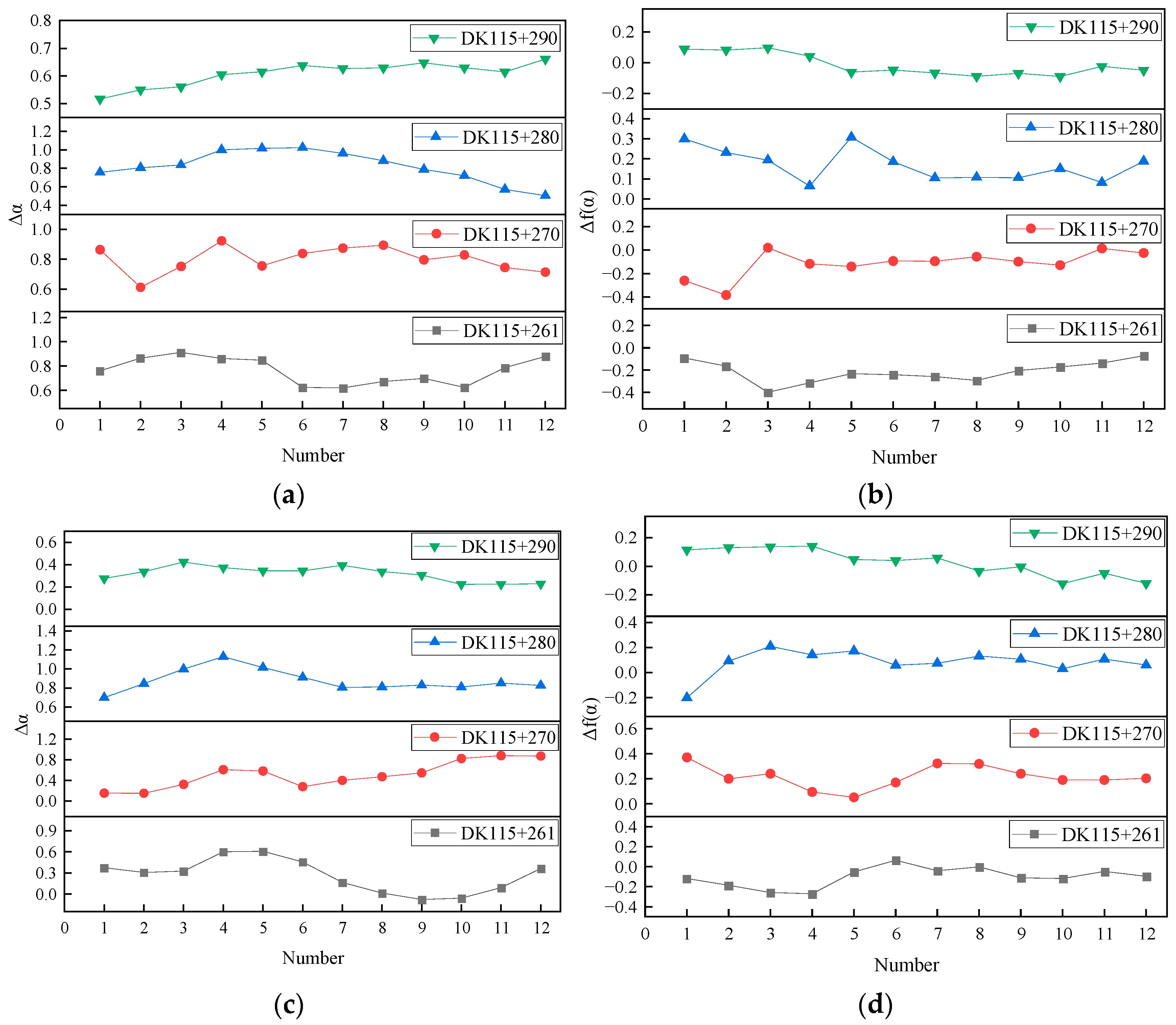
3.1.2. Multifractal Analysis
- 1.
- MF-DFA key parameter settings
- 2.
- Multifractal characterization of tunnel deformation rates
3.2. Tunnel Deformation Warning Classification Study
3.2.1. Tunnel Deformation Warning Level Classification Criteria
3.2.2. Warning Classification of Tunnel Deformation
- The analysis of index criterion results: Through calculations and statistical analysis, the results of the index criterion are obtained (see Table 4). In the cross-section settlement monitoring data, the Z values for DK115 + 261 and DK115 + 270 fall within the range [−2.32, 2.32], which is a steady trend. The Z value for DK115 + 280 is less than −2.32, which is a decreasing trend. The Z value for DK115 + 290 is more than 2.32, which is an increasing trend. In the cross-section convergence monitoring data, the Z value for DK115 + 280 falls within the range [−2.32, 2.32], which is a steady trend. The Z values for DK115 + 261 and DK115 + 290 are less than −2.32, which is a decreasing trend. The Z value for DK115 + 270 is more than 2.32, which is an increasing trend.
- The analysis of index criterion results: Through statistical calculations, the results of index criterion are obtained (see Table 5). In the section settlement monitoring data, the Z value for DK115 + 261 falls between the ranges [−2.32, 2.32], which is a steady trend. The Z value for DK115 + 270 is greater than 2.32, which is an increasing trend. The Z values for DK115 + 280 and DK115 + 290 are less than −2.32, which is a decreasing trend. In the section convergence monitoring data, the Z values for DK115 + 261, DK115 + 270, and DK115 + 280 fall within the range [−2.32, 2.32], which is a steady trend. The Z value for DK115 + 290 is less than −2.32, which is a decreasing trend.
- The analysis of final warning results: On the basis of the results for the indicator criterion and indicator criterion, the final warning results of the four monitoring cross-sections are analyzed (see Table 6). In the section settlement, the warning level for DK115 + 261 is level III, and all other sections are at level II. In section convergence, the warning level of DK115 + 280 is grade III, and all other sections are grade II. Therefore, according to the most unfavorable principle of synthesis, the final warning level of the four sections are all level II. That is, monitoring and measurement should be strengthened, and corresponding engineering countermeasures should be taken if necessary.
3.3. Tunnel Settlement Prediction
3.3.1. Prediction Model Selection
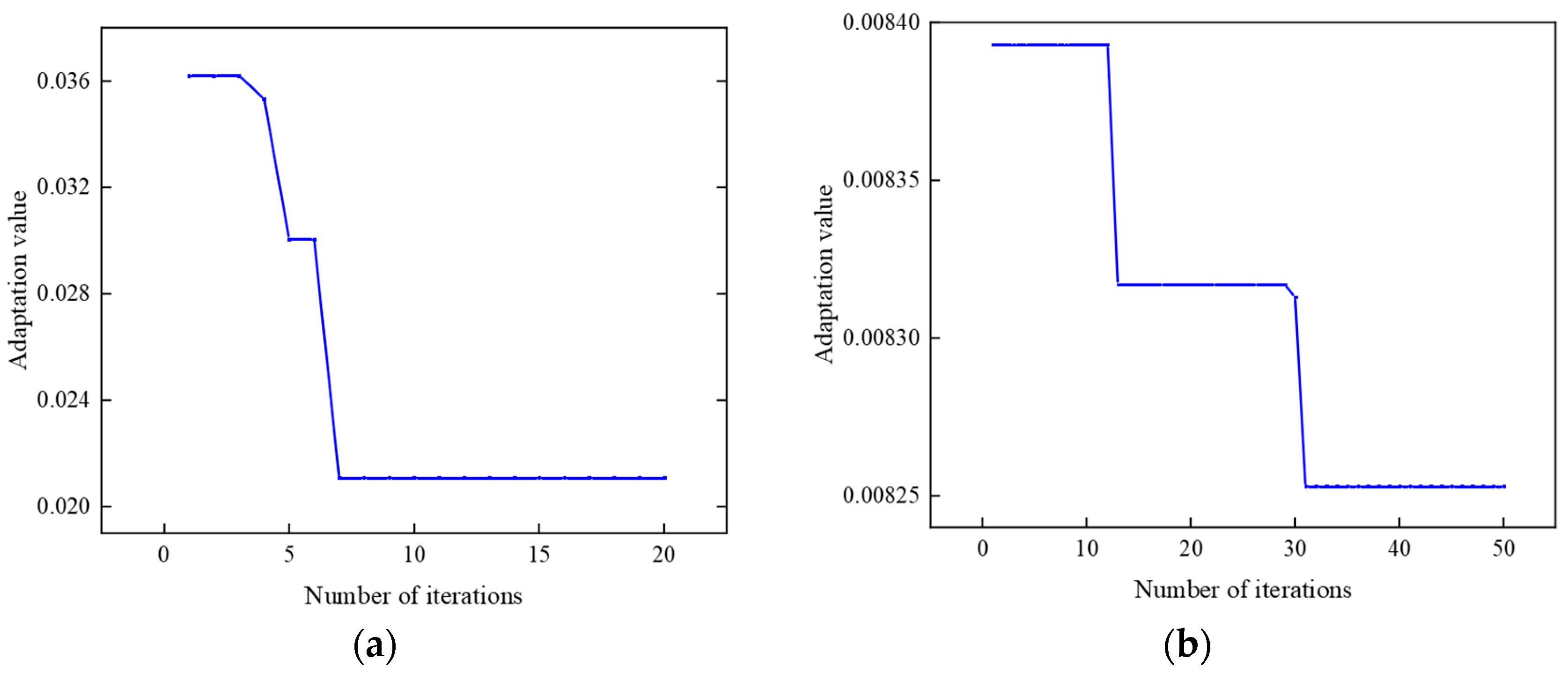
3.3.2. Optimization of PSO-LSTM Parameters
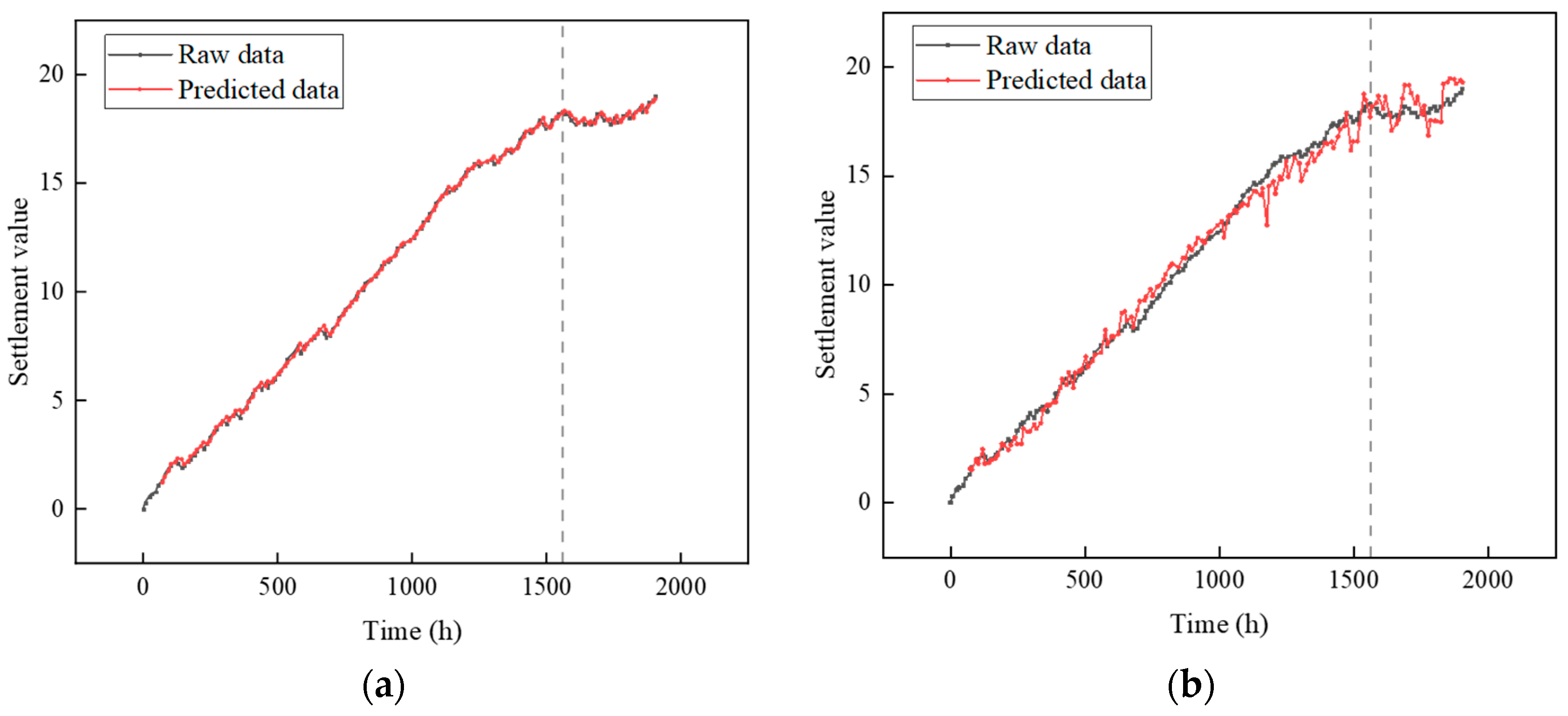
3.3.3. PSO-LSTM Prediction Results
4. Conclusions
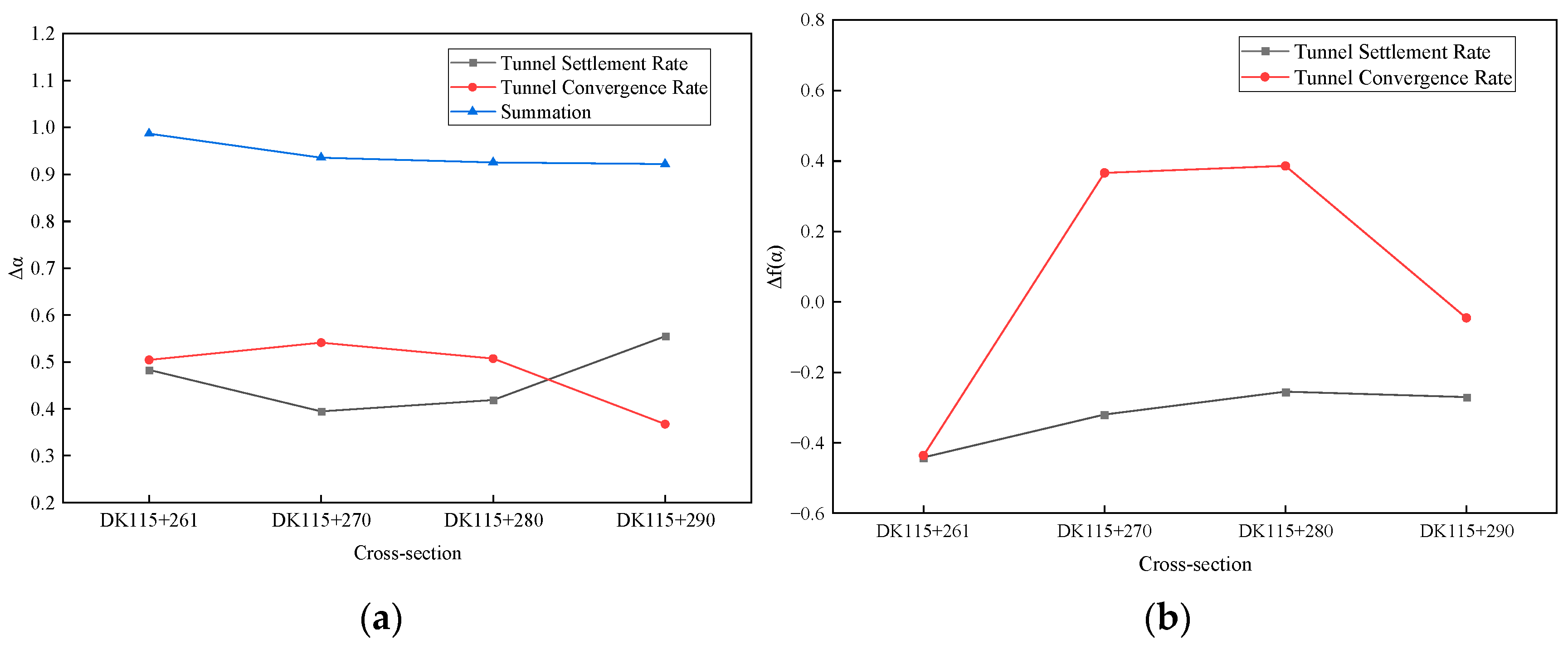
- The tunnel settlement and convergence rates of the four sections exhibit distinct fractal sequence characteristics. The width of the multifractal spectra in the measured data series of tunnel settlement rate and tunnel convergence rate within the same section shows an inverse relationship, with the sum of the two remaining stable between 0.9 and 1. Additionally, the proportion of size fluctuations in the measured data series of the tunnel settlement rate and the tunnel convergence rate within the same section demonstrate a consistent trend.
- The analysis of tunnel settlement prediction indicates that the PSO-LSTM prediction model delivers superior predictive performance and stability in tunnel settlement forecasts.
- A comprehensive analysis of the tunnel warning level and tunnel settlement prediction results reveals a class II tunnel deformation warning level, which aligns with the actual tunnel conditions. This approach, leveraging quantitative data as a reference, enables a more precise determination of the tunnel warning level.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Liu, Y.; Chen, Y.; Zhao, C.; Qiu, J.; Wu, D.; Liu, T.; Fan, H.; Qin, Y.; Tang, K. A State-of-the-Practice Review of Three-Dimensional Laser Scanning Technology for Tunnel Distress Monitoring. J. Perform. Constr. Facil. 2023, 37, 03123001. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Z.; Cheng, F.; Su, S. Trajectory Optimization for High-Speed Trains via a Mixed Integer Linear Programming Approach. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17666–17676. [Google Scholar] [CrossRef]
- Zhao, T. Research on Invert Heave Mechanism and Control Technique of High-speed Railway Tunnel in Mudstone. Ph.D. Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2022. [Google Scholar]
- Chen, H.; Lai, H.; Qiu, Y.; Chen, R. Reinforcing Distressed Lining Structure of Highway Tunnel with Bonded Steel Plates: Case Study. J. Perform. Constr. Facil. 2020, 34, 04019082. [Google Scholar] [CrossRef]
- Li, Z.; Lai, J.; Ren, Z.; Shi, Y.; Kong, X. Failure mechanical behaviors and prevention methods of shaft lining in China. Eng. Fail. Anal. 2023, 143, 106904. [Google Scholar] [CrossRef]
- Weng, X.; Li, H.; Hu, J.; Li, L.; Xu, L. Behavior of Saturated Remolded Loess Subjected to Coupled Change of the Magnitude and Direction of Principal Stress. Int. J. Géoméch. 2023, 23, 04022244. [Google Scholar] [CrossRef]
- Wang, Z.; Cai, Y.; Fang, Y.; Lai, J.; Han, H.; Liu, J.; Lei, H.; Kong, X. Local buckling characteristic of hollow π-type steel-concrete composite support in hilly-gully region of loess tunnel. Eng. Fail. Anal. 2023, 143, 106828. [Google Scholar] [CrossRef]
- Zhou, M.; Fang, Q.; Peng, C. A mortar segment-to-segment contact method for stabilized total-Lagrangian smoothed particle hydrodynamics. Appl. Math. Model. 2022, 107, 20–38. [Google Scholar] [CrossRef]
- Zhen, Y.; Guo, P.; Wang, L.; Chen, X.; Duan, X.; Wang, A. Key Technologies for Treating High Ground Stress and Large Deformation of Soft Rock in Daliangshan Tunnel of Yunlin Expressway. Tunn. Constr. Available online: https://link.cnki.net/urlid/44.1745.U.20231107.1430.003 (accessed on 8 November 2023).
- Zhang, C.; Han, K.; Zhang, D. Face stability analysis of shallow circular tunnels in cohesive-frictional soils. Tunn. Undergr. Space Technol. 2015, 50, 345–357. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Zhang, D.; Ye, Z.; Tan, Z. Face stability of shield tunnels considering a kinematically admissible velocity field of soil arching. J. Rock Mech. Geotech. Eng. 2021, 14, 505–526. [Google Scholar] [CrossRef]
- Li, G.; Hu, Y.; Tian, S.-M.; Weibin, M.; Huang, H.-L. Analysis of deformation control mechanism of prestressed anchor on jointed soft rock in large cross-section tunnel. Bull. Eng. Geol. Environ. 2021, 80, 9089–9103. [Google Scholar] [CrossRef]
- Wu, H.-N.; Shen, S.-L.; Chen, R.-P.; Zhou, A. Three-dimensional numerical modelling on localised leakage in segmental lining of shield tunnels. Comput. Geotech. 2020, 122, 103549. [Google Scholar] [CrossRef]
- Shen, S.-L.; Wu, H.-N.; Cui, Y.-J.; Yin, Z.-Y. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai. Tunn. Undergr. Space Technol. 2014, 40, 309–323. [Google Scholar] [CrossRef]
- Lai, H.; Zhao, X.; Kang, Z.; Chen, R. A new method for predicting ground settlement caused by twin-tunneling under-crossing an existing tunnel. Environ. Earth Sci. 2017, 76, 726. [Google Scholar] [CrossRef]
- Suwansawat, S.; Einstein, H.H. Describing settlement troughs over twin tunnels using a superposition technique. Geotech. Geoenviron. Eng. 2007, 133, 445–468. [Google Scholar] [CrossRef]
- Chou, W.I.; Bobet, A. Predictions of ground deformations in shallow tunnels in clay. Tunn. Undergr. Space Technol. 2002, 17, 3–19. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Huang, H.-W.; Zhang, D.-M.; Phoon, K.K.; Liu, Z.-Q.; Tang, C. Quantitative evaluation of geological uncertainty and its influence on tunnel structural performance using improved coupled Markov chain. Acta Geotech. 2021, 16, 3709–3724. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Zhao, J.; Zhao, T.; Guo, D. Research on a Safety Evaluation System for Railway-Tunnel Structures by Fuzzy Comprehensive Evaluation Theory. Civ. Eng. J.-Staveb. Obz. 2023, 32, 122–136. [Google Scholar] [CrossRef]
- Li, Z.; Meng, X.; Liu, D.; Tang, Y.; Chen, T. Disaster Risk Evaluation of Superlong Highways Tunnel Based on the Cloud and AHP Model. Adv. Civ. Eng. 2022, 2022, 8785030. [Google Scholar] [CrossRef]
- Yan, X.; Li, H.; Liu, F.; Liu, Y. Structural Safety Evaluation of Tunnel Based on the Dynamic Monitoring Data during Construction. Shock Vib. 2021, 2021, 6680675. [Google Scholar] [CrossRef]
- Tan, X.; Chen, W.; Zou, T.; Yang, J.; Du, B. Real-time prediction of mechanical behaviors of underwater shield tunnel structure using machine learning method based on structural health monitoring data. J. Rock Mech. Geotech. Eng. 2023, 15, 886–895. [Google Scholar] [CrossRef]
- Tang, L.; Na, S. Comparison of machine learning methods for ground settlement prediction with different tunneling datasets. J. Rock Mech. Geotech. Eng. 2021, 13, 1274–1289. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Wu, C.; Li, H.; Goh, A.; Liu, H. Prediction of lining response for twin tunnels constructed in anisotropic clay using machine learning techniques. Undergr. Space 2022, 7, 122–133. [Google Scholar] [CrossRef]
- Suwansawat, S.; Einstein, H.H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling. Tunn. Undergr. Space Technol. 2006, 21, 133–150. [Google Scholar] [CrossRef]
- Yang, H.; Song, K.; Zhou, J. Automated Recognition Model of Geomechanical Information Based on Operational Data of Tunneling Boring Machines. Rock Mech. Rock Eng. 2022, 55, 1499–1516. [Google Scholar] [CrossRef]
- Schappacher, N. Mandelbrot, Benoît B. The Fractal Geometry of Nature. In Kindlers Literatur Lexikon (KLL); WH Freeman: New York, NY, USA, 2020; pp. 1–2. [Google Scholar]
- Zuo, C.; Liu, D.; Ding, S.; Li, L. Analysis and Prediction of Tunnel Surface Subsidence Based on Fractal Theory. J. Yangtze River Sci. Res. Inst. 2016, 33, 51–56. [Google Scholar] [CrossRef]
- Ye, D.; Liu, G.; Tian, Y.; Sun, Z.; Yu, B. A Fractal Model for the Micro–Macro Interactions on Tunnel Leakage. Fractals 2022, 30, 2250142. [Google Scholar] [CrossRef]
- Grassberger, P. Generalized dimensions of strange attractors. Phys. Lett. A 1983, 97, 227–230. [Google Scholar] [CrossRef]
- Lei, H.; Zhou, X.; Wang, Y. Research on Landslide Early Warning and Prediction Based on Combined Response of Multifractal Characteristics and Sub Item Prediction. J. Geod. Geodyn. 2022, 42, 885–891. [Google Scholar]
- Mao, H.; Zhang, M.; Jiang, R.; Li, B.; Xu, J.; Xu, N. Study on deformation pre-warning of rock slopes based on multi-fractal characteristics of microseismic signals. Chin. J. Rock Mech. Eng. 2020, 39, 560–571. [Google Scholar]
- Zhou, L.; Liu, Z. Multifractal feature analysis method for measured data of dam deformation. Adv. Sci. Technol. Water Resour. 2021, 41, 18–24. [Google Scholar] [CrossRef]
- Hughes, H.M. The relative cuttability of coal-measures stone. Min. Sci. Technol. 1986, 3, 95–109. [Google Scholar] [CrossRef]
- Hamidi, J.K.; Shahriar, K.; Rezai, B.; Rostami, J. Performance prediction of hard rock TBM using Rock Mass Rating (RMR) system. Tunn. Undergr. Space Technol. 2010, 25, 333–345. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, W.; Zhang, Y.; Xiao, Y.; Xiang, Y. Determination of earth pressure balance tunnel-related maximum surface settlement: A multivariate adaptive regression splines approach. Bull. Eng. Geol. Environ. 2018, 77, 489–500. [Google Scholar] [CrossRef]
- Ozdemir, L. Development of Theoretical Equations for Predicting Tunnel Boreability. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 1977. [Google Scholar]
- Resendiz, D.; Romo, M.P. Settlements upon soft-ground tunneling: Theoretical solution. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 151, 65–74. [Google Scholar]
- Bai, B. Fluctuation responses of saturated porous media subjected to cyclic thermal loading. Comput. Geotech. 2006, 33, 396–403. [Google Scholar] [CrossRef]
- Bai, B.; Nie, Q.; Zhang, Y.; Wang, X.; Hu, W. Cotransport of heavy metals and SiO2 particles at different temperatures by seepage. J. Hydrol. 2020, 597, 125771. [Google Scholar] [CrossRef]
- Rowe, R.K.; Lee, K.M. Subsidence owing to tunnelling. II. Evaluation of a prediction technique. Can. Geotech. J. 1992, 29, 941–954. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Su, Z.; Luo, Q.; Chen, M.; Zhao, Z. Sensitivity of Multistage Fill Slope Based on Finite Element Model. Adv. Civ. Eng. 2021, 2021, 6622936. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Zhao, Z.; Ni, H.; Su, Z.; Li, Z. Experimental study of displacement field of layered soils surrounding laterally loaded pile based on transparent soil. J. Soils Sediments 2021, 21, 3072–3083. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Chen, Y.; Ni, H.; Zhao, Z.; Chen, W.; Zhao, J. Mechanical and microstructural properties of recycling granite residual soil reinforced with glass fiber and liquid-modified polyvinyl alcohol polymer. Chemosphere 2021, 286, 131652. [Google Scholar] [CrossRef]
- Chou, J.; Lin, C. Predicting Disputes in Public-Private Partnership Projects: Classification and Ensemble Models. J. Comput. Civ. Eng. 2013, 27, 51–60. [Google Scholar] [CrossRef]
- Bouayad, D.; Emeriault, F. Modeling the relationship between ground surface settlements induced by shield tunneling and the operational and geological parameters based on the hybrid PCA/ANFIS method. Tunn. Undergr. Space Technol. 2017, 68, 142–152. [Google Scholar] [CrossRef]
- Santos, O.J.; Celestino, T.B. Artificial neural networks analysis of Sao Paulo subway tunnel settlement data. Tunn. Undergr. Space Technol. 2008, 23, 481–491. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Noorian-Bidgoli, M.; Armaghani, D.J.; Khamesi, H. Feasibility of PSO-ANN model for predicting surface settlement caused by tunneling. Eng. Comput. 2016, 32, 705–715. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, B.; Wang, H.; Zheng, J.; Gao, Y. Time-Series InSAR Ground Deformation Prediction Based an LSTM Model. Yangtze River. Available online: https://link.cnki.net/urlid/42.1202.TV.20231117.0949.002 (accessed on 17 November 2023).
- Li, C.; Li, J.; Shi, Z.; Li, L.; Li, M.; Jin, D.; Dong, G. Prediction of Surface Settlement Induced by Large-Diameter Shield Tunneling Based on Machine-Learning Algorithms. Geofluids 2022, 2022, 4174768. [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, X.; Yan, K. Deep Learning Neural Network Model for Tunnel Ground Surface Settlement Prediction Based on Sensor Data. Math. Probl. Eng. 2021, 2021, 9488892. [Google Scholar] [CrossRef]
- Duan, C.; Hu, M.; Zhang, H. Comparison of ARIMA and LSTM in Predicting Structural Deformation of Tunnels during Operation Period. Data 2023, 8, 104. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G.; Gibbons, J.D. Rank Correlation Method. Biometrika. 1990. Available online: http://www.jstor.org/stable/2333282 (accessed on 18 June 2014).
- Wang, L.I.; Gao, X.; Zhou, W. Testing for Intrinsic Multifractality in the Global Grain Spot Market Indices: A Multifractal Detrended Fluctuation Analysis. Fractals 2023, 31, 2350090. [Google Scholar] [CrossRef]
- Wang, F.; Shao, W.; Yu, H.; Kan, G.; He, X.; Zhang, D.; Ren, M.; Wang, G. Re-evaluation of the Power of the Mann-Kendall Test for Detecting Monotonic Trends in Hydrometeorological Time Series. Front. Earth Sci. 2020, 8, 14. [Google Scholar] [CrossRef]
- Hochreiter, S.T.U.M.; Schmidhuber, J. Long short-term memory. Neural Comput. 2010, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Wu, Z. Time-Varying Risk Aversion and Crude Oil Futures Price Volatility. Master’s Thesis, Anhui University of Finance & Economics, Bengbu, China, 2023. [Google Scholar]
- Xie, W. Study on the Interdependence Structure and Risk Spillover Effect between Cryptocurrency and Chinese financial Assets. Ph.D. Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2023. [Google Scholar]
- Guo, Y.; Zheng, J.; Liu, H. An early warning method for tunneling-induced ground surface settlement considering accident precursors and consequences. Tunn. Undergr. Space Technol. 2023, 140, 105214. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X. Early Warning and Prediction of Side Displacement and Deformation of Soft Soil Foundation Pit. J. Yangtze River Sci. Res. Inst. 2021, 38, 91–96. [Google Scholar]


| Typology | Cross-Section | Average (mm) | Standard Deviation (mm) | Skewness | Kurtosis | J–B Statistic |
|---|---|---|---|---|---|---|
| Tunnel settlement deformation rate | DK115 + 261 | 0.2611 | 0.4294 | 0.5138 | 0.2869 | 7.3987 |
| DK115 + 270 | 0.2343 | 0.4292 | 0.8202 | 0.6275 | 20.6918 | |
| DK115 + 280 | 0.3354 | 0.4405 | 0.7564 | 0.7089 | 13.7218 | |
| DK115 + 290 | 0.3454 | 0.4327 | 0.7001 | 0.9317 | 13.0826 | |
| Tunnel convergence deformation rate | DK115 + 261 | 0.2711 | 0.3971 | 0.4901 | 0.3564 | 7.0700 |
| DK115 + 270 | 0.2509 | 0.4171 | 0.3174 | 0.0704 | 2.7189 | |
| DK115 + 280 | 0.3469 | 0.3950 | 0.7898 | 1.5932 | 24.7456 | |
| DK115 + 290 | 0.3686 | 0.3523 | 0.8295 | 1.7593 | 27.0453 |
| Cross-Section | DK115 + 261 | DK115 + 270 | DK115 + 280 | DK115 + 290 | |
|---|---|---|---|---|---|
| Feature | |||||
| Tunnel settlement rate | 0.4829 | 0.3946 | 0.4187 | 0.5547 | |
| −0.4415 | −0.3198 | −0.2551 | −0.2704 | ||
| Tunnel convergence rate | 0.5042 | 0.5411 | 0.5069 | 0.3674 | |
| −0.4360 | 0.3663 | 0.3860 | −0.0455 |
| Warning Level | Indicator Criterion | Indicator Criterion | Treatment Measures |
|---|---|---|---|
| I | Decreasing trend | Increasing trend | Suspend construction. Use additional temporary support, grouting, and other measures to reinforce the deformed section. |
| II | Other trend combinations | Conduct a comprehensive evaluation of design and construction measures, reinforce monitoring and measurement protocols, develop disaster prevention plans, and implement appropriate engineering countermeasures when necessary. | |
| III | Steady trend | Steady trend | Normal construction. |
| Cross-Section | Section Settlement | Section Convergence | ||
|---|---|---|---|---|
| Z-Value | Growing Trend | Z-Value | Growing Trend | |
| DK115 + 261 | −1.3540 | Steady trend | −2.5849 | Decreasing trend |
| DK115 + 270 | −0.8616 | Steady trend | 5.0468 | Increasing trend |
| DK115 + 280 | −2.5849 | Decreasing trend | −0.8616 | Steady trend |
| DK115 + 290 | 5.5391 | Increasing trend | −2.8311 | Decreasing trend |
| Cross-Section | Section Settlement | Section Convergence | ||
|---|---|---|---|---|
| Z-Value | Growing Trend | Z-Value | Growing Trend | |
| DK115 + 261 | 2.0926 | Steady trend | 1.6002 | Steady trend |
| DK115 + 270 | 2.8311 | Increasing trend | −0.3693 | Steady trend |
| DK115 + 280 | −2.5849 | Decreasing trend | −0.8616 | Steady trend |
| DK115 + 290 | −4.3082 | Decreasing trend | −5.2929 | Decreasing trend |
| Cross-Section | DK115 + 261 | DK115 + 270 | DK115 + 280 | DK115 + 290 |
|---|---|---|---|---|
| Section settlement | III | II | II | II |
| Section convergence | II | II | III | II |
| Combined warning levels | II | II | II | II |
| Prediction Model | R2 | MAE | RMSE |
|---|---|---|---|
| PSO-LSTM | 0.98 | 0.05 | 0.06 |
| BP-ANN | 0.71 | 0.16 | 0.18 |
| Optimal Parameter | Number of Neurons | Training Rounds | Batch Size |
|---|---|---|---|
| DK115 + 261 | 77 | 72 | 1 |
| DK115 + 270 | 82 | 72 | 1 |
| DK115 + 280 | 11 | 99 | 6 |
| DK115 + 290 | 20 | 81 | 2 |
| Cross-Section | Test Set Evaluation Metrics | Predicted Results | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | Day 1 | Day 2 | Day 3 | Day 4 | Day 5 | |
| DK115 + 261 | 0.96 | 0.28 | 0.06 | 18.80 | 18.81 | 18.81 | 18.82 | 18.82 |
| DK115 + 270 | 0.97 | 0.10 | 0.01 | 18.31 | 18.32 | 18.34 | 18.35 | 18.36 |
| DK115 + 280 | 0.98 | 0.04 | 0.04 | 17.50 | 17.51 | 17.51 | 17.51 | 17.52 |
| DK115 + 290 | 0.98 | 0.02 | 0.02 | 16.52 | 16.54 | 16.55 | 16.57 | 16.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Huang, R.; Liu, D.; Qiu, W.; Zhang, R.; Tang, Y. Analysis and Warning Prediction of Tunnel Deformation Based on Multifractal Theory. Fractal Fract. 2024, 8, 108. https://doi.org/10.3390/fractalfract8020108
Yang C, Huang R, Liu D, Qiu W, Zhang R, Tang Y. Analysis and Warning Prediction of Tunnel Deformation Based on Multifractal Theory. Fractal and Fractional. 2024; 8(2):108. https://doi.org/10.3390/fractalfract8020108
Chicago/Turabian StyleYang, Chengtao, Rendong Huang, Dunwen Liu, Weichao Qiu, Ruiping Zhang, and Yu Tang. 2024. "Analysis and Warning Prediction of Tunnel Deformation Based on Multifractal Theory" Fractal and Fractional 8, no. 2: 108. https://doi.org/10.3390/fractalfract8020108
APA StyleYang, C., Huang, R., Liu, D., Qiu, W., Zhang, R., & Tang, Y. (2024). Analysis and Warning Prediction of Tunnel Deformation Based on Multifractal Theory. Fractal and Fractional, 8(2), 108. https://doi.org/10.3390/fractalfract8020108






