Ultrafast Diffusion Modeling via the Riemann–Liouville Nonlocal Structural Derivative and Its Application in Porous Media
Abstract
:1. Introduction
2. Theory
2.1. The Riemann–Liouville Nonlocal Structural Derivative
2.2. The Ultrafast Diffusion Model via Riemann–Liouville Nonlocal Structural Derivative
3. Applications and Results
4. Discussion
5. Conclusions
- The Riemann–Liouville nonlocal structural derivative diffusion equation has the advantages of strong application potential, high flexibility, and a mean square displacement that is analogous to the integral form of the corresponding structural function.
- The physical mechanism of the Riemann–Liouville nonlocal structural derivative diffusion model is obvious, and the law of the ultrafast diffusion in cement mortar over a short time scale satisfies the inverse Mittag–Leffler function.
- The verification of the experimental results indicated that the Riemann–Liouville nonlocal structural derivative diffusion model is more effective at depicting ultrafast diffusion behavior in cement mortar, as evidenced by the fitting curves and errors.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abe, S.; Thurner, S. Anomalous diffusion in view of Einstein’s 1905 theory of Brownian motion. Phys. A 2005, 356, 403–407. [Google Scholar] [CrossRef]
- Masuda, A.; Ushida, K.; Okamoto, T. Direct observation of spatiotemporal dependence of anomalous diffusion in inhomogeneous fluid by sampling-volume-controlled fluorescence correlation spectroscopy. Phys. Rev. E 2005, 72, 060101. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Liang, Y. A non-local structural derivative model based on the Caputo fractional derivative for ultrafast diffusion in heterogeneous media. Fractals 2020, 28, 2050122. [Google Scholar] [CrossRef]
- Ghoufi, A.; Szymczyk, A.; Malfreyt, P. Ultrafast diffusion of ionic liquids confined in carbon nanotubes. Sci. Rep. 2016, 6, 28518. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Tian, P.; Wang, S.; Xu, W.; Taylor, T. Non-fickian diffusion in time-space fluctuating diffusivity landscapes: From ultrafast to ultraslow. Fractals 2021, 29, 2150191. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, S.H.; Shi, Y.; Huang, Y.J.; Zhao, F.; Huo, T.T.; Tang, S.W. The influence of fly ash dosages on the permeability, pore structure and fractal features of face slab concrete. Fractal Fract. 2022, 6, 476. [Google Scholar] [CrossRef]
- Zhou, C.J.; Chen, L.L.; Zheng, S.P.; Xu, Y.X.; Feng, D.C. Rheological, mechanical, and abrasion characteristics of polymer-modified cement mortar and concrete. Can. J. Civ. Eng. 2020, 47, 1226–1237. [Google Scholar] [CrossRef]
- Wu, H.X.; Hu, R.H.; Yang, D.Y.; Ma, Z.M. Micro-macro characterizations of mortar containing construction waste fines as replacement of cement and sand: A comparative study. Constr. Build. Mater. 2023, 383, 131328. [Google Scholar] [CrossRef]
- Kueh, A.B.H.; Razali, A.W.; Lee, Y.Y.; Hamdan, S.; Yakub, I.; Suhaili, N. Acoustical and mechanical characteristics of mortars with pineapple leaf fiber and silica aerogel infills-Measurement and modeling. Mater. Today Commun. 2023, 35, 105540. [Google Scholar] [CrossRef]
- Tian, Y.; Jin, X.Y.; Jin, N.G.; Zhao, R.; Li, Z.J.; Ma, H.Y. Research on the microstructure formation of polyacrylate latex modified mortars. Constr. Build. Mater. 2013, 47, 1381–1394. [Google Scholar] [CrossRef]
- Ziehensack, E.; Kessler, S.; Angst, U.; Hilbig, H.; Gehlen, C. Diffusion potentials in saturated hardened cement paste upon chloride exposure. Mater. Struct. 2023, 56, 100. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Z.Y.; Zhang, Y.S. A multi-scale framework for modelling effective gas diffusivity in dry cement paste: Combined effects of surface, knudsen and molecular diffusion. Cem. Concr. Res. 2020, 131, 106035. [Google Scholar] [CrossRef]
- Jiang, J.Y.; Sun, G.W.; Wang, C.H. Numerical calculation on the porosity distribution and diffusion coefficient of interfacial transition zone in cement-based composite materials. Constr. Build. Mater. 2013, 39, 134–138. [Google Scholar] [CrossRef]
- Ying, J.; Jiang, Z.; Xiao, J. Synergistic effects of three-dimensional graphene and silica fume on mechanical and chloride diffusion properties of hardened cement paste. Constr Build. Mater. 2022, 316, 125756. [Google Scholar] [CrossRef]
- Baskin, E.; Iomin, A. Super-diffusion on a comb structure. Phys. Rev. Lett. 2004, 93, 120603. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A.; Kantz, H. Fractional diffusion on a fractal grid comb. Phys. Rev. E 2015, 91, 032108. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Fomin, S.; Chugunov, V.; Hashida, T. Application of fractional differential equations for modeling the anomalous diffusion of contaminant from fracture into porous rock matrix with bordering alteration zone. Transp. Porous Media 2010, 81, 187–205. [Google Scholar] [CrossRef]
- Zhang, Z.; Angst, U. Modeling anomalous moisture transport in cement-based materials with kinetic permeability. Int. J. Mol. Sci. 2020, 21, 837. [Google Scholar] [CrossRef]
- Hou, Y.; Wu, J.; Jiang, J. Time behavior of anomalous solute transport in three-dimensional cemented porous media. Soil Sci. Soc. Am. J. 2019, 83, 1012–1023. [Google Scholar] [CrossRef]
- O’Malley, D.; Cushman, J.H. Fractional Brownian motion run with a nonlinear clock. Phys. Rev. E 2010, 82, 032102. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Liang, Y.; Chen, W.; Cushman, J.H. A spatial structural derivative model for the characterization of ultrafast diffusion/dispersion in porous media. Int. J. Heat Mass Tran. 2019, 139, 39–45. [Google Scholar] [CrossRef]
- Chen, W.; Liang, Y.; Hei, X.D. Local structural derivative and its applications. J. Solid Mech. 2016, 37, 456–460. [Google Scholar]
- Liang, Y.; Chen, W. A non-local structural derivative model for characterization of ultraslow diffusion in dense colloids. Commun. Nonlinear Sci. 2018, 56, 131–137. [Google Scholar] [CrossRef]
- Chen, W.; Liang, Y. New methodologies in fractional and fractal derivatives modeling. Chaos Solitons Fractals 2017, 102, 72–77. [Google Scholar] [CrossRef]
- Su, X.; Chen, W.; Xu, W.; Liang, Y. Non-local structural derivative Maxwell model for characterizing ultra-slow rheology in concrete. Constr. Build. Mater. 2018, 190, 342–348. [Google Scholar] [CrossRef]
- Hou, D.; Yan, H.; Zhang, J.; Wang, P.; Li, Z. Experimental and computational investigation of magnesium phosphate cement mortar. Constr. Build. Mater. 2016, 112, 331–342. [Google Scholar] [CrossRef]
- Jumarie, G. Laplace’s transform of fractional order via the Mittag-Leffler function and modified Riemann-Liouville derivative. Appl. Math. Lett. 2009, 22, 1659–1664. [Google Scholar] [CrossRef]
- Xu, W.; Liang, Y.; Cushman, J.H.; Chen, W. Ultrafast dynamics modeling via fractional Brownian motion run with Mittag-Leffler clock in porous media. Int. J. Heat Mass Tran. 2020, 151, 119402. [Google Scholar] [CrossRef]
- Yu, J.C.; Qian, J.S.; Chen, H.X.; Ou, Y.B.; Kuang, D.L.; Jia, X.W.; Qiu, H.P. The influence of calcium sulphoaluminate on the properties of low-cost magnesium phosphate cement mortars. J. Build. Eng. 2023, 76, 107146. [Google Scholar] [CrossRef]
- Xiao, Y.; Jiang, Y.; Chen, B.; Wang, L.Y. Properties of red mud blended magnesium phosphate cements: Workability and microstructure evolution. Constr. Build. Mater. 2023, 409, 134023. [Google Scholar] [CrossRef]
- Buj, I.; Torras, J.; Casellas, D.; Rovira, M.; de Pablo, J. Effect of heavy metals and water content on the strength of magnesium phosphate cements. J. Hazard. Mater. 2009, 170, 345–350. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Zhang, C.; Li, D. Linearized fast time-stepping schemes for time–space fractional Schrödinger equations. Phys. D 2023, 454, 133865. [Google Scholar] [CrossRef]
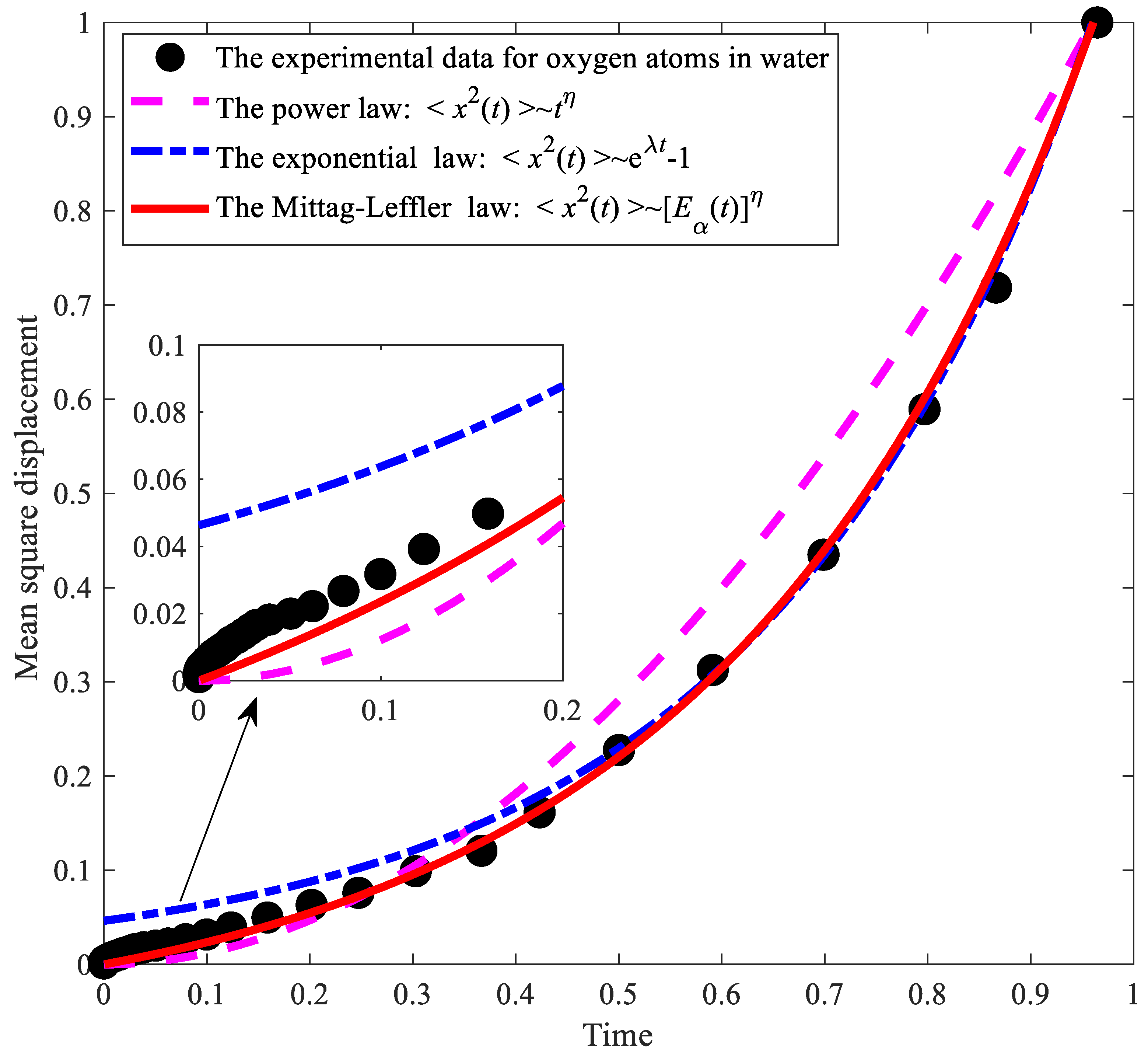
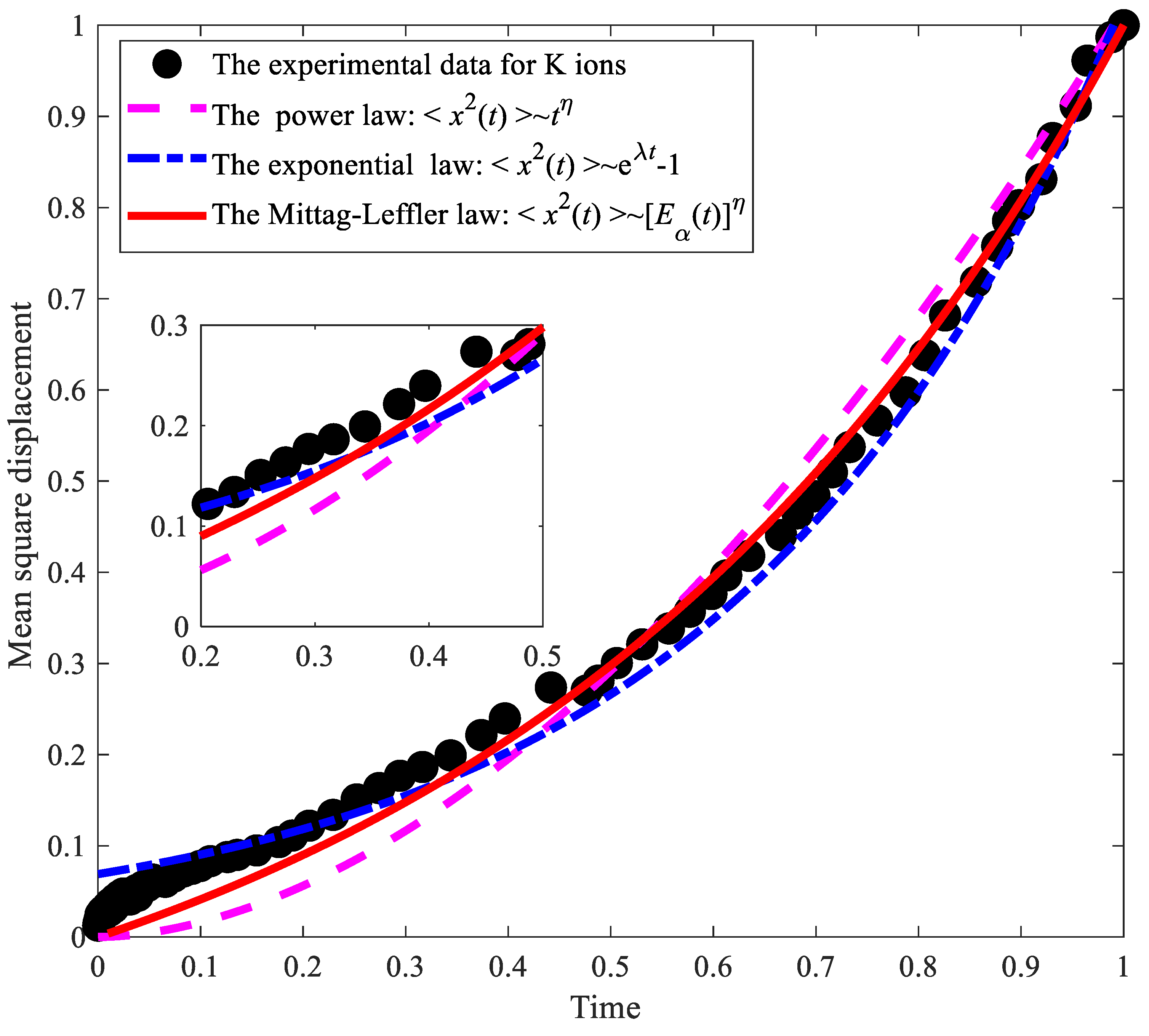
| Models | Power Law Diffusion | Exponential Law Diffusion | Mittag–Leffler Law Diffusion |
|---|---|---|---|
| Maximum absolute error | 0.0995 | 0.0446 | 0.0201 |
| Mean square error | 0.0314 | 0.0341 | 0.0017 |
| Models | Power Law Diffusion | Exponential Law Diffusion | Mittag–Leffler Law Diffusion |
|---|---|---|---|
| Maximum absolute error | 0.0671 | 0.0567 | 0.0418 |
| Mean square error | 0.0390 | 0.0371 | 0.0252 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Liu, H.; Chen, L.; Zhou, Y. Ultrafast Diffusion Modeling via the Riemann–Liouville Nonlocal Structural Derivative and Its Application in Porous Media. Fractal Fract. 2024, 8, 110. https://doi.org/10.3390/fractalfract8020110
Xu W, Liu H, Chen L, Zhou Y. Ultrafast Diffusion Modeling via the Riemann–Liouville Nonlocal Structural Derivative and Its Application in Porous Media. Fractal and Fractional. 2024; 8(2):110. https://doi.org/10.3390/fractalfract8020110
Chicago/Turabian StyleXu, Wei, Hui Liu, Lijuan Chen, and Yongtao Zhou. 2024. "Ultrafast Diffusion Modeling via the Riemann–Liouville Nonlocal Structural Derivative and Its Application in Porous Media" Fractal and Fractional 8, no. 2: 110. https://doi.org/10.3390/fractalfract8020110
APA StyleXu, W., Liu, H., Chen, L., & Zhou, Y. (2024). Ultrafast Diffusion Modeling via the Riemann–Liouville Nonlocal Structural Derivative and Its Application in Porous Media. Fractal and Fractional, 8(2), 110. https://doi.org/10.3390/fractalfract8020110








