A Bearing Fault Diagnosis Method under Small Sample Conditions Based on the Fractional Order Siamese Deep Residual Shrinkage Network
Abstract
:1. Introduction
- (1)
- The one-dimensional vibration signals are converted into two-dimensional time series feature maps, which is convenient for the neural network model to extract the feature of the signal. The combination of the DRSN and Siamese network is conducive to improving the feature extraction ability of fault signals under small sample conditions.
- (2)
- In the parameter updating process of neural network backpropagation, momentum and fractional order calculus are applied to the gradient descent optimizer to make it converge to the optimal solution, thus improving the accuracy of fault diagnosis in the case of limited training data.
- (3)
- In order to simulate the limited data conditions in engineering applications, four sets of small sample training data were selected from the CWRU dataset to analyze and verify the FO-SDRSN method, which provides a possibility for its further application in bearing fault diagnosis with small sample data.
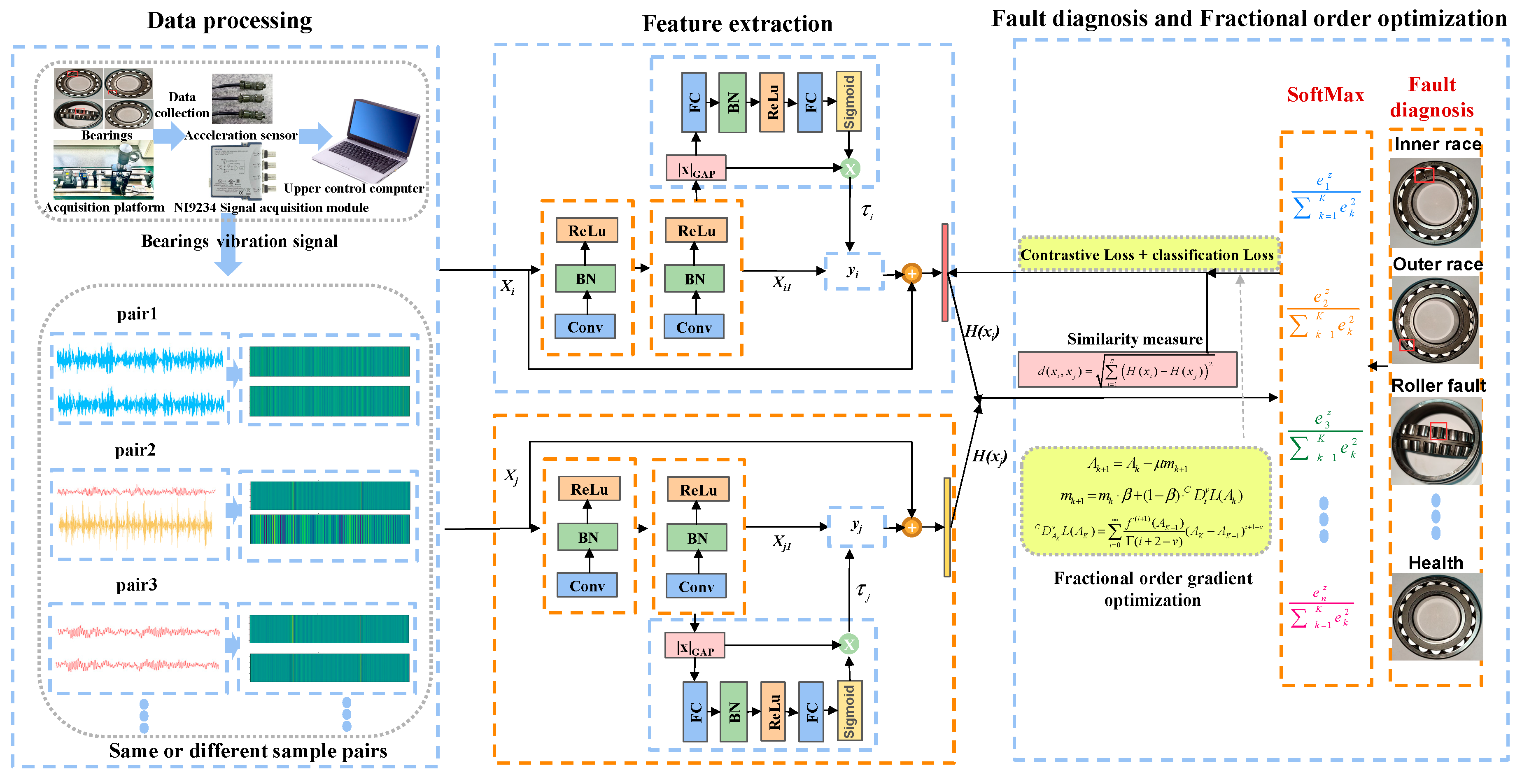
2. Proposed Method
2.1. Data Processing and Feature Extraction
2.2. Fault Diagnosis and Parameter Update
3. Experiments and Evaluations
3.1. Data Acquisition
3.2. Experiments
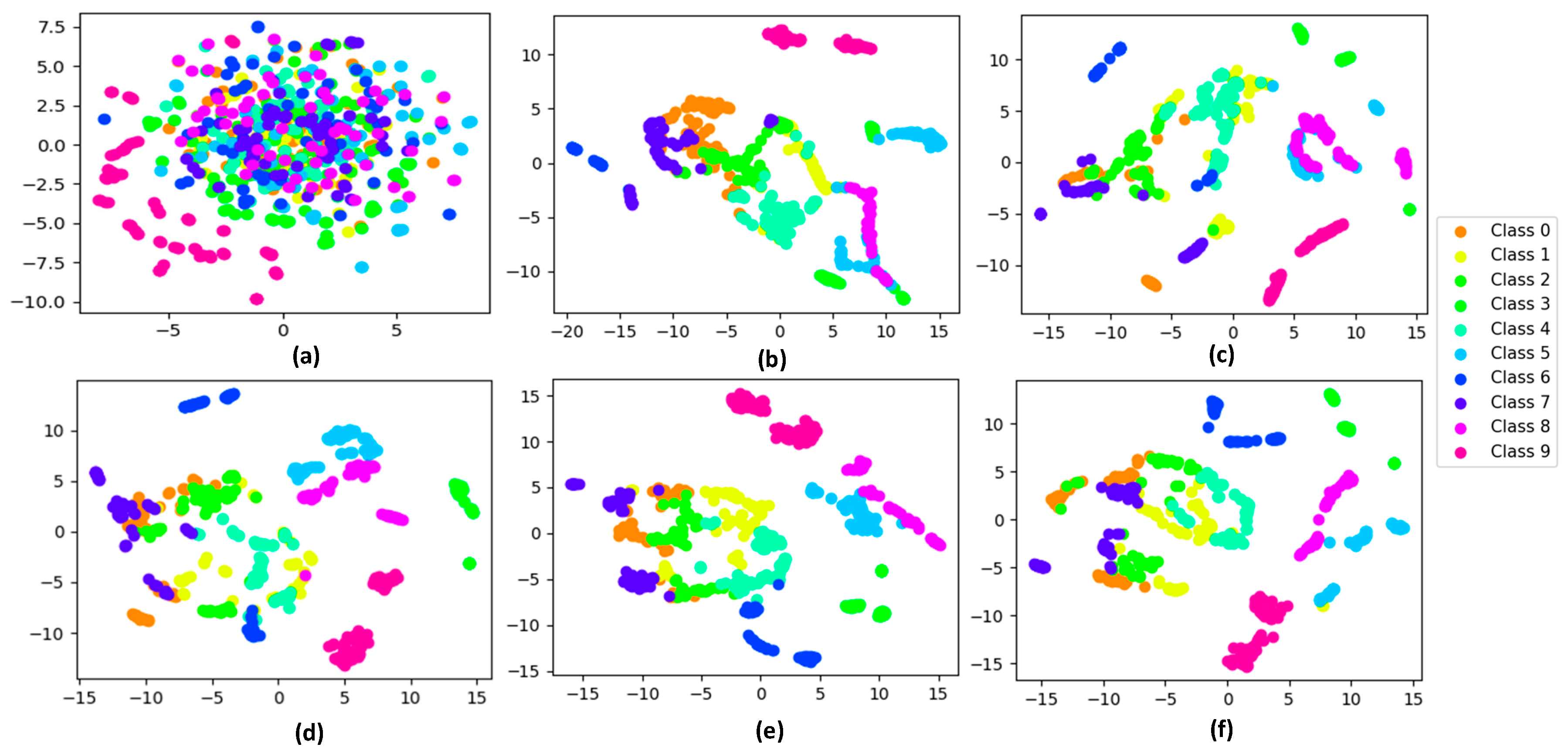
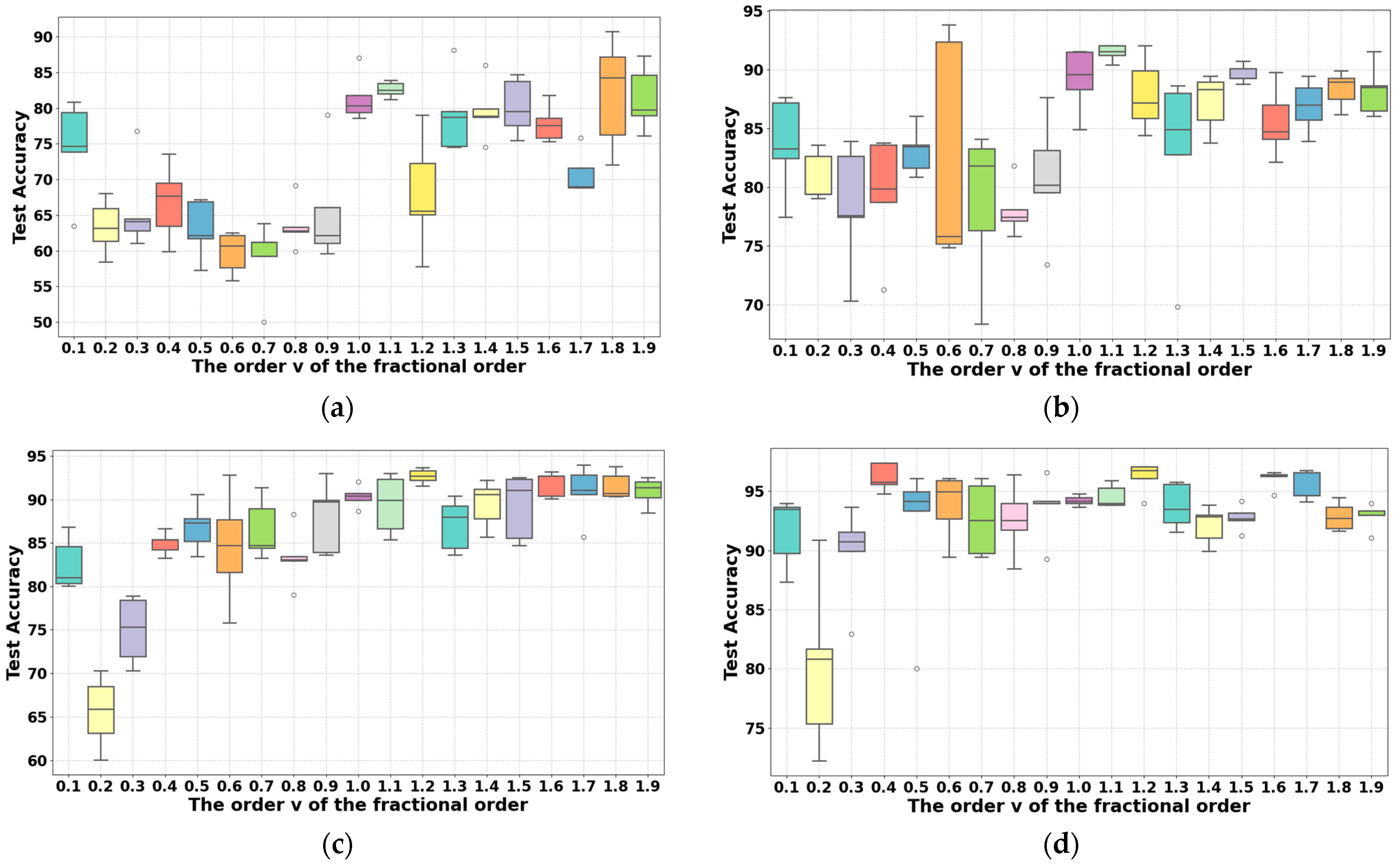
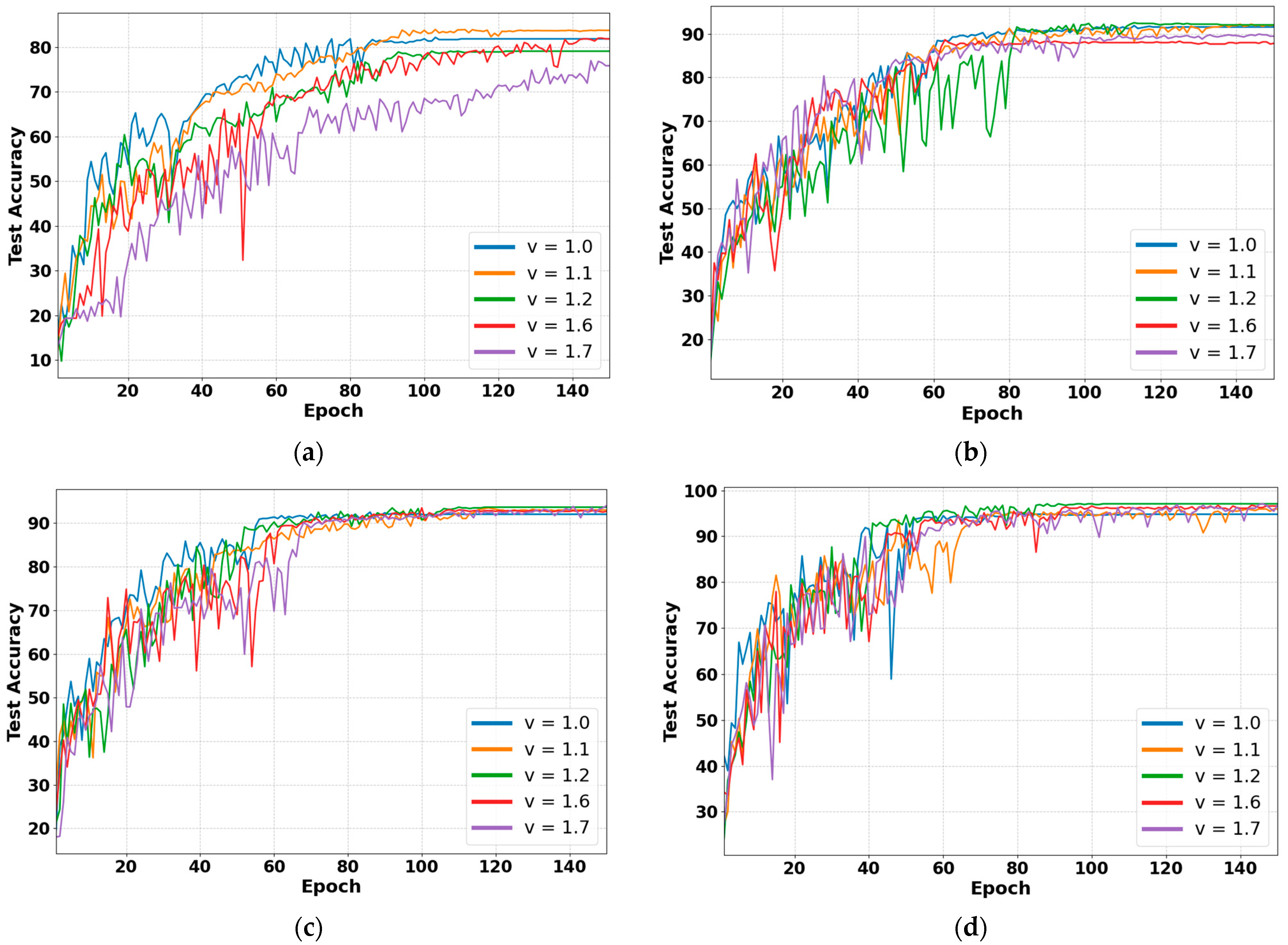
4. Discussion
5. Conclusions
- (1)
- The FO-SDRSN method can be used to diagnose bearing fault types under small sample conditions. This method can further reduce the loss during the repeated iterative updating of the network parameters, and the results are constantly close to the optimal solution, thus improving the accuracy of bearing fault diagnosis under small sample conditions.
- (2)
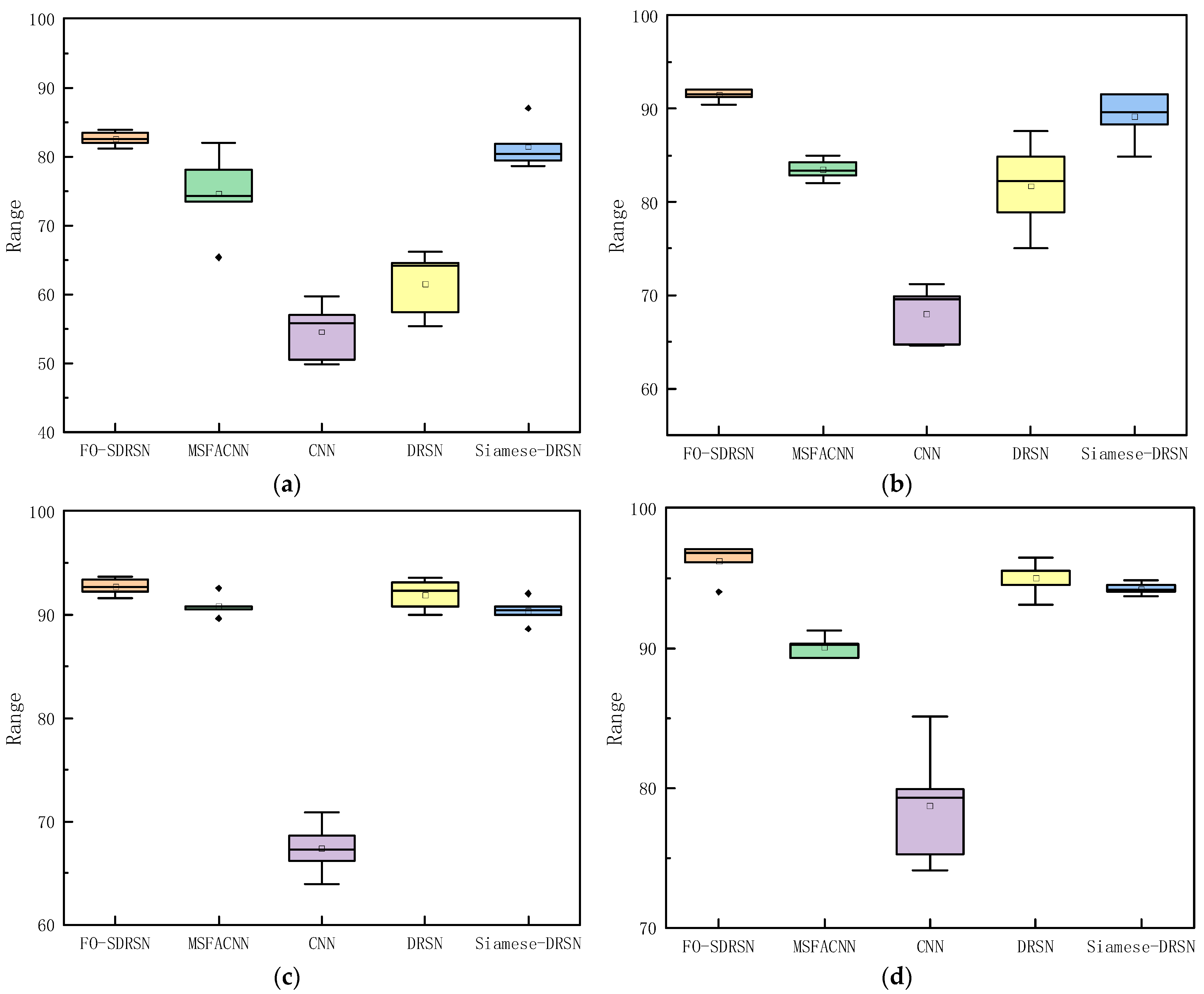
- The experiments indicated that the FO-SDRSN method was more accurate and stable than other progressive methods under the given four small sample datasets. When the number of samples for each fault was 15, the average fault diagnostic accuracy was 2.27% higher than that of the progressive Siamese–DRSN method. The Discussion Section shows that the fault diagnosis performance of the FO-SDRSN method under different orders was associated with the quantity of small sample data.
- (3)
- In cases where there are limited data, the improvement in the accuracy of bearing fault diagnosis is crucial for the subsequent rapid and targeted maintenance and enhancement of the working efficiency of rotating machinery. The improvements demonstrated in this study also provide a new approach for the fault diagnosis of bearings equipment under actual industrial operation and maintenance conditions. This study was validated with publicly available datasets, so the robustness and applicability of the proposed method will be further verified in different engineering scenarios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Niu, G.; Liu, E.; Wang, X.; Ziehl, P.; Zhang, B. Enhanced Discriminate Feature Learning Deep Residual CNN for Multitask Bearing Fault Diagnosis with Information Fusion. IEEE Trans. Ind. Inform. 2022, 19, 762–770. [Google Scholar] [CrossRef]
- Liu, K.; Yang, P.; Wang, R.; Jiao, L.; Li, T.; Zhang, J. Observer-Based Adaptive Fuzzy Finite-Time Attitude Control for Quadrotor UAVs. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8637–8654. [Google Scholar] [CrossRef]
- Liu, K.; Yang, P.; Jiao, L.; Wang, R.; Yuan, Z.; Dong, S. Antisaturation fixed-time attitude tracking control based low-computation learning for uncertain quadrotor UAVs with external disturbances. Aerosp. Sci. Technol. 2023, 142, 108668. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, W.-A.; Guo, F.; Liu, W.; Shi, X. Wavelet Packet Decomposition-Based Multiscale CNN for Fault Diagnosis of Wind Turbine Gearbox. IEEE Trans. Cybern. 2021, 53, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chen, J.; Yang, C.; Yang, J.; Liu, Z.; Davari, P. Convolutional Neural Network-Based Transformer Fault Diagnosis Using Vibration Signals. Sensors 2023, 23, 4781. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Huang, Q.; Yang, K.; Zhang, C. Intelligent Fault Diagnosis Method through ACCC-Based Improved Convolutional Neural Network. Actuators 2023, 12, 154. [Google Scholar] [CrossRef]
- Chen, J.; Huang, R.; Zhao, K.; Wang, W.; Liu, L.; Li, W. Multiscale Convolutional Neural Network With Feature Alignment for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 3077673. [Google Scholar] [CrossRef]
- Ren, H.; Wang, J.; Dai, J.; Zhu, Z.; Liu, J. Dynamic Balanced Domain-Adversarial Networks for Cross-Domain Fault Diagnosis of Train Bearings. IEEE Trans. Instrum. Meas. 2022, 71, 3179468. [Google Scholar] [CrossRef]
- Fu, W.; Jiang, X.; Tan, C.; Li, B.; Chen, B. Rolling Bearing Fault Diagnosis in Limited Data Scenarios Using Feature Enhanced Generative Adversarial Networks. IEEE Sens. J. 2022, 22, 8749–8759. [Google Scholar] [CrossRef]
- Pham, M.T.; Kim, J.-M.; Kim, C.H. Rolling Bearing Fault Diagnosis Based on Improved GAN and 2-D Representation of Acoustic Emission Signals. IEEE Access 2022, 10, 78056–78069. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Xie, J.; Wang, C.; Ding, T. Conditional GAN and 2-D CNN for bearing fault diagnosis with small samples. IEEE Trans. Instrum. Meas. 2021, 70, 3119135. [Google Scholar] [CrossRef]
- Shi, J.; Peng, D.; Peng, Z.; Zhang, Z.; Goebel, K.; Wu, D. Planetary gearbox fault diagnosis using bidirectional-convolutional LSTM networks. Mech. Syst. Signal Process. 2022, 162, 107996. [Google Scholar] [CrossRef]
- Yang, M.; Liu, W.; Zhang, W.; Wang, M.; Fang, X. Bearing Vibration Signal Fault Diagnosis Based on LSTM-Cascade Cat-Boost. J. Internet Technol. 2022, 23, 1155–1161. [Google Scholar] [CrossRef]
- Aljemely, A.H.; Xuan, J.; Al-Azzawi, O.; Jawad, F.K.J. Intelligent fault diagnosis of rolling bearings based on LSTM with large margin nearest neighbor algorithm. Neural Comput. Appl. 2022, 34, 19401–19421. [Google Scholar] [CrossRef]
- Cao, X.; Xu, X.; Duan, Y.; Yang, X. Health Status Recognition of Rotating Machinery Based on Deep Residual Shrinkage Network Under Time-Varying Conditions. IEEE Sens. J. 2022, 22, 18332–18348. [Google Scholar] [CrossRef]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep Residual Shrinkage Networks for Fault Diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 4681–4690. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.; Peng, Y.; Lin, J. Intra-Domain Transfer Learning for Fault Diagnosis with Small Samples. Appl. Sci. 2022, 12, 7032. [Google Scholar] [CrossRef]
- Zhou, X.; Li, A.; Han, G. An Intelligent Multi-Local Model Bearing Fault Diagnosis Method Using Small Sample Fusion. Sensors 2023, 23, 7567. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Li, Y.; Zheng, H.; Wang, R.; Xu, M. A new dynamic model and transfer learning based intelligent fault diagnosis framework for rolling element bearings race faults: Solving the small sample problem. ISA Trans. 2022, 121, 327–348. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, R.; Li, M.; Li, X.; Yang, Z.; Yan, R.; Chen, X. Feature Enhancement Based on Regular Sparse Model for Planetary Gearbox Fault Diagnosis. IEEE Trans. Instrum. Meas. 2022, 71, 3176244. [Google Scholar] [CrossRef]
- Xie, Z.; Tan, X.; Yuan, X.; Yang, G.; Han, Y. Small Sample Signal Modulation Recognition Algorithm Based on Support Vector Machine Enhanced by Generative Adversarial Networks Generated Data. J. Electron. Inf. Technol. 2023, 45, 2071–2080. [Google Scholar] [CrossRef]
- Yang, X.; Liu, B.; Xiang, L.; Hu, A.; Xu, Y. A novel intelligent fault diagnosis method of rolling bearings with small samples. Measurement 2022, 203, 111899. [Google Scholar] [CrossRef]
- Lei, T.; Hu, J.; Riaz, S. An innovative approach based on meta-learning for real-time modal fault diagnosis with small sample learning. Front. Phys. 2023, 11, 1207381. [Google Scholar] [CrossRef]
- Ma, R.; Han, T.; Lei, W. Cross-domain meta learning fault diagnosis based on multi-scale dilated convolution and adaptive relation module. Knowl.-Based Syst. 2023, 261, 110175. [Google Scholar] [CrossRef]
- Su, H.; Xiang, L.; Hu, A.; Xu, Y.; Yang, X. A novel method based on meta-learning for bearing fault diagnosis with small sample learning under different working conditions. Mech. Syst. Signal Process. 2022, 169, 108765. [Google Scholar] [CrossRef]
- Cheng, Q.; He, Z.; Zhang, T.; Li, Y.; Liu, Z.; Zhang, Z. Bearing Fault Diagnosis Based on Small Sample Learning of Maml–Triplet. Appl. Sci. 2022, 12, 10723. [Google Scholar] [CrossRef]
- Zhao, X.; Ma, M.; Shao, F. Bearing fault diagnosis method based on improved Siamese neural network with small sample. J. Cloud Comput. 2022, 11, 79. [Google Scholar] [CrossRef]
- Xing, X.; Guo, W.; Wan, X. An Improved Multidimensional Distance Siamese Network for Bearing Fault Diagnosis with Few Labelled Data. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, X.; Lu, J.; Li, Z. Multiscale Fusion Attention Convolutional Neural Network for Fault Diagnosis of Aero-Engine Rolling Bearing. IEEE Sens. J. 2023, 23, 19918–19934. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Z.; Chen, X.; Feng, Y.; Chen, J. A Novel Multisensor Orthogonal Attention Fusion Network for Multibolt Looseness State Recognition Under Small Sample. IEEE Trans. Instrum. Meas. 2022, 71, 3217855. [Google Scholar] [CrossRef]
- Xue, L.; Lei, C.; Jiao, M.; Shi, J.; Li, J. Rolling Bearing Fault Diagnosis Method Based on Self-Calibrated Coordinate Attention Mechanism and Multi-Scale Convolutional Neural Network Under Small Samples. IEEE Sens. J. 2023, 23, 10206–10214. [Google Scholar] [CrossRef]
- Gungor, O.; Rosing, T.; Aksanli, B. ENFES: ENsemble FEw-Shot Learning For Intelligent Fault Diagnosis with Limited Data. In Proceedings of the 2021 IEEE Sensors, Sydney, Australia, 31 October 2021–3 November 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Li, T.; Wu, X.; He, Y.; Peng, X.; Yang, J.; Ding, R.; He, C. Small samples noise prediction of train electric traction system fan based on a multiple regression-fuzzy neural network. Eng. Appl. Artif. Intell. 2023, 126, 106781. [Google Scholar] [CrossRef]
- Zhao, C.; Dai, L.; Huang, Y. Fractional Order Sequential Minimal Optimization Classification Method. Fractal Fract. 2023, 7, 637. [Google Scholar] [CrossRef]
- Huang, L.; Shen, X. Research on Speech Emotion Recognition Based on the Fractional Fourier Transform. Electronics 2022, 11, 3393. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, D.; Zhao, T.; Chen, Y. Fractional Calculus in Image Processing: A Review. Fract. Calc. Appl. Anal. 2016, 19, 1222–1249. [Google Scholar] [CrossRef]
- Henriques, M.; Valério, D.; Gordo, P.; Melicio, R. Fractional-Order Colour Image Processing. Mathematics 2021, 9, 457. [Google Scholar] [CrossRef]
- Yin, L.; Cao, X.; Chen, L. High-dimensional Multiple Fractional Order Controller for Automatic Generation Control and Automatic Voltage Regulation. Int. J. Control. Autom. Syst. 2022, 20, 3979–3995. [Google Scholar] [CrossRef]
- Marinangeli, L.; Alijani, F.; HosseinNia, S. A Fractional-order Positive Position Feedback Compensator for Active Vibration Control. IFAC-PapersOnLine 2017, 50, 12809–12816. [Google Scholar] [CrossRef]
- Li, T.; Wang, N.; He, Y.; Xiao, G.; Gui, W.; Feng, J. Noise Cancellation of a Train Electric Traction System Fan Based on a Fractional-Order Variable-Step-Size Active Noise Control Algorithm. IEEE Trans. Ind. Appl. 2023, 59, 2081–2090. [Google Scholar] [CrossRef]
- Sheng, D.; Wei, Y.; Chen, Y.; Wang, Y. Convolutional neural networks with fractional order gradient method. Neurocomputing 2020, 408, 42–50. [Google Scholar] [CrossRef]
- Loparo, K.A. Bearings Vibration Data Set Case Western Reserve University. [EB/OL]. Available online: http://www.eecs.cwru.edu/laborato-ry/bearing/download.htm (accessed on 1 September 2020).





| Label | Fault Size (Inch) | Fault Location | Number of Training Samples in Four Small Sample Datasets |
|---|---|---|---|
| 0 | 0.007 | Roller | 10, 15, 20, 30 |
| 1 | 0.014 | Roller | 10, 15, 20, 30 |
| 2 | 0.021 | Roller | 10, 15, 20, 30 |
| 3 | 0.007 | Inner race | 10, 15, 20, 30 |
| 4 | 0.014 | Inner race | 10, 15, 20, 30 |
| 5 | 0.021 | Inner race | 10, 15, 20, 30 |
| 6 | 0.007 | Outer race | 10, 15, 20, 30 |
| 7 | 0.014 | Outer race | 10, 15, 20, 30 |
| 8 | 0.021 | Outer race | 10, 15, 20, 30 |
| 9 | - | Health | 10, 15, 20, 30 |
| Model | Number of Training Samples for Each Type of Fault Is 10 | Number of Training Samples for Each Type of Fault Is 15 | Number of Training Samples for Each Type of Fault Is 20 | Number of Training Samples for Each Type of Fault Is 30 | ||||
|---|---|---|---|---|---|---|---|---|
| Average Accuracy (%) | Standard Deviation | Average Accuracy (%) | Standard Deviation | Average Accuracy (%) | Standard Deviation | Average Accuracy (%) | Standard Deviation | |
| FO-SDRSN | 82.6091 | 0.985746 | 91.46106 | 0.603937 | 92.6948 | 0.761442 | 96.20128 | 1.296661 |
| MSFACNN | 74.62782 | 5.53897 | 83.49514 | 1.033596 | 90.84142 | 0.952347 | 90.08976 | 0.724449 |
| CNN | 54.56308 | 3.814642 | 67.99352 | 2.788438 | 67.37864 | 2.33054 | 78.73786 | 3.899128 |
| DRSN | 61.51612 | 4.303248 | 81.70968 | 4.418985 | 91.93034 | 1.348297 | 95 | 1.145057 |
| Siamese–DRSN | 81.42856 | 2.994431 | 89.18832 | 2.465018 | 90.35718 | 1.108664 | 94.22076 | 0.392317 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Wu, X.; Luo, Z.; Chen, Y.; He, C.; Ding, R.; Zhang, C.; Yang, J. A Bearing Fault Diagnosis Method under Small Sample Conditions Based on the Fractional Order Siamese Deep Residual Shrinkage Network. Fractal Fract. 2024, 8, 134. https://doi.org/10.3390/fractalfract8030134
Li T, Wu X, Luo Z, Chen Y, He C, Ding R, Zhang C, Yang J. A Bearing Fault Diagnosis Method under Small Sample Conditions Based on the Fractional Order Siamese Deep Residual Shrinkage Network. Fractal and Fractional. 2024; 8(3):134. https://doi.org/10.3390/fractalfract8030134
Chicago/Turabian StyleLi, Tao, Xiaoting Wu, Zhuhui Luo, Yanan Chen, Caichun He, Rongjun Ding, Changfan Zhang, and Jun Yang. 2024. "A Bearing Fault Diagnosis Method under Small Sample Conditions Based on the Fractional Order Siamese Deep Residual Shrinkage Network" Fractal and Fractional 8, no. 3: 134. https://doi.org/10.3390/fractalfract8030134
APA StyleLi, T., Wu, X., Luo, Z., Chen, Y., He, C., Ding, R., Zhang, C., & Yang, J. (2024). A Bearing Fault Diagnosis Method under Small Sample Conditions Based on the Fractional Order Siamese Deep Residual Shrinkage Network. Fractal and Fractional, 8(3), 134. https://doi.org/10.3390/fractalfract8030134







