Investigation of the Robust Fractional Order Control Approach Associated with the Online Analytic Unity Magnitude Shaper: The Case of Wind Energy Systems

Abstract

This paper investigates the development of a novel analytic approach for computing Unity Magnitude (UM) shapers that deviates from established numerical methodologies. The experimental validation on a test bench confirms the practicality and benefits of the suggested UM shaper technique. The study extends the use of UM shapers to improve the control of wind conversion systems (WCSs), particularly those including hybrid excitation synchronous generators (HESGs), demonstrating their adaptability and versatility. Experimental validation guarantees real-world application, confirming the suggested UM shapers’ trustworthiness. Strict management is still required to assure the system’s efficiency and dependability. In reality, the dynamic equations of a turbine, as well as those of an HESG, are substantially nonlinear; most system parameters are very uncertain; and, finally, a WCS is always impacted by disturbance sources such as load variations, harmonics, and mechanical vibrations. Robust control measures must be used to overcome these issues. A CRONE controller (Robust Fractional Order Control) of the second generation is created. A comparative study performed on the Simulink platform reveals substantial gains brought about by UM shapers in real-world circumstances. The study demonstrates the effectiveness of UM-shaped inputs in mechanical stabilization and Maximum Power Point Tracking (MPPT), emphasizing both theoretical soundness and practical advantages. The analytic equations for UM shapers in undamped and damped systems, offered together with a real-time algorithm, contribute to the optimization of wind conversion systems.

1. Introduction

Wind turbines experience oscillations caused by changing wind conditions. These oscillations can cause severe problems for the turbine’s structural integrity as well as its power-generating efficiency [1]. Numerous research studies on oscillation control in wind turbines have been conducted [1]. From 2000 to 2016, different control strategies, including both feedforward and feedback control approaches, were suggested [1]. These technologies, which include input shaping methods, command smoothing techniques, linear and nonlinear controls, intelligent controls, and adaptive controls, have successfully suppressed oscillations, resulting in improved wind turbine performance and lifetime [1]. The use of hybrid excitation synchronous generators (HESGs) in wind control systems has been a key area of interest in the sphere of wind energy. Wind control systems based on HESGs are a viable way to handle a variety of issues, including the requirement for effective energy capture and control measures that are adapted to the dynamic nature of wind conditions [2]. A hierarchical control system for HESG-based wind turbines has been introduced, improving their adaptation to varying wind conditions while maximizing power production [2,3]. In addition, improved rotor design and control techniques to increase the overall efficiency of HESG turbines have been investigated. These recent discoveries highlight the potential of HESG-based WCSs to transform wind energy generation. However, it is important to acknowledge that while HESG-based systems offer promising opportunities, there are still challenges and limitations that need to be addressed. These may include issues related to system control, as an HESG is a highly nonlinear machine, variable wind conditions (which can lead to relatively high torsional torque vibration and less mechanical stability), and economic viability.

In our study, we suggest using Unity Magnitude (UM) shaping to capture wind-extracted electricity for the first time in the literature. Input shaping is a method of producing commands in flexible systems that reduce vibrations [4,5]. It is accomplished by combining a series of impulses with the system’s instruction [6]. To achieve oscillation cancellation, the impulses of the shaper must have certain amplitudes and positions [7]. These impulses, such as the Zero Vibration Shaper (ZV) and Zero Vibration Derivative Shaper (ZVD), have traditionally had positive values. These shapers have been enhanced to support fractional derivative systems. The use of UM input shapers is one remarkable illustration of this technical advancement [8]. These shapers have progressively gained significance in a variety of sectors, offering higher control and improved performance [9]. As we dive into the complexities of Unity Magnitude shapers, it is critical to recognize their influence in a variety of fields, notably crane control [10]. In recent advances, Unity Magnitude input shapers have been used to minimize sway in overhead cranes. Advanced UM shapers, particularly built for underactuated 3D overhead cranes [11], have been proposed by researchers, exhibiting the flexibility for variations in cable length and crane dynamics during hoisting [12]. These shapers significantly reduce transient and persistent sways, enhancing their efficacy in crane control. Furthermore, Unity Magnitude shapers have been used in overhead crane swing control, solving the difficulty of simultaneous cargo lifting and external disturbances [13]. The novel technique blends predictive UM shapers with adaptive feedback management, resulting in significant swing reduction even when time-varying parameters and external disturbances are present [14].

The design of robust controllers, capable of smoothly and efficiently tracking the optimal energy extracted from the wind, is, therefore, of real interest to the wind industry. The synthesis of these controllers must meet the following requirements:

• Maximization of power extracted from the wind in zone 2.
• Minimization of mechanical undulations and the forces suffered by the wind turbine during gusts of wind.
• Robustness to parametric variations and disturbances caused by intermittent wind energy.

Among the various methods available, variable gain controllers have been widely used for variable speed wind turbines [15,16] while using Linear Parameter Varying (LPV) models [17]. However, these methods did not maximize performance while limiting mechanical fatigue of the system. Adaptive algorithms [18], predictive control [19], Fuzzy logic approaches [20], and predictive control using linear matrix inequalities (LMI) [21] have also been applied to maximize the power extracted from the wind. Studies have also compared the performance of linear versus nonlinear control methods [22]. The effectiveness of H∞ controllers in the field of WCS control has also been demonstrated in numerous studies [23,24]. For speed control, we considered evaluating the performance of a CRONE corrector (French abbreviation of non-integer order robust control) [25,26]. While this controller is widely used for vehicles (braking system [27], air suspension system [28]), the use of the Robust Fractional Order Control methodology for Maximum Power Point Tracking (MPP Tracking) and the minimization of the torsional torque was not studied to our knowledge. Indeed, few references deal with the Robust Fractional Order Control methodology in the wind energy sector. In addition, the main focus of this work has been on MPP Tracking, as reported in [29,30,31].

To sum up, fractional derivative systems have received increased attention in recent years due to their potential to capture complicated dynamics and enhance controller performance in a variety of engineering applications. However, the actual implementation of fractional-order controllers presents issues such as modeling, analysis, and control design. The absence of established techniques for tuning and constructing fractional-order controllers, as well as the computational complexity associated with their implementation, are key challenges that must be overcome.

To overcome these difficulties, we propose a unique technique for managing HESG-based WCSs using Unity Magnitude (UM) shapers. Our research aims to solve the practical issues associated with HESG-based systems and fractional derivative controllers by developing a robust and effective control technique that may improve the performance and reliability of wind energy conversion systems. We will rewrite the introduction section to include a more in-depth explanation of these concerns and relevant research to back up our statements. Several contributions to the field of UM input shapers and their application to WCSs based on HESG have been made in this work:

• Analytic method for calculating UM shapers: One of the most important achievements of this study is the development of an analytic technique for calculating UM shapers. This technique sets our study apart from the previous literature, which is mostly based on numerical methodologies.
• Experimental validation: The proposed methodology is validated on an experimental test bench with changeable inertia. It turns out that it is robust to parameter uncertainty, which adds credibility and usefulness to our study by proving that theoretical advances are adaptable and successful in real-world circumstances.
• WCS behavior expansion: The research extends the use of UM shapers to harness the behavior of WCS, particularly those using HESG. This development demonstrates the versatility and adaptability of UM shapers, emphasizing their potential to change wind energy system control and optimization.
• Comparative research: We compare the performance of a WCS controlled by a second-generation CRONE controller (Robust Fractional Order Control) with a shaped input to that of an unshaped control input using the Simulink platform. This comparison investigation proves the performance enhancements brought about by UM shapers in the real world.
• Mechanical stabilization and MPP tracking efficiency: The study proves the efficiency of UM-shaped inputs in mechanical stabilization and Maximum Power Point Tracking.

The structure of the paper is as follows: Section 2 provides an overview of the proposed UM shaper approach and presents our real-time algorithm. Section 3 discusses the modeling of wind energy conversion systems (WECSs). Section 4 presents the synthesis of control strategies, including excitation current control and CRONE controller synthesis. Section 5 validates the performance of the UM shaper experimentally on a variable inertia test bench. The simulation methodology and results, followed by a discussion of the findings, are presented in the section. Finally, Section 6 concludes the paper with insights into the robustness and efficacy of the proposed control strategy and avenues for future research.

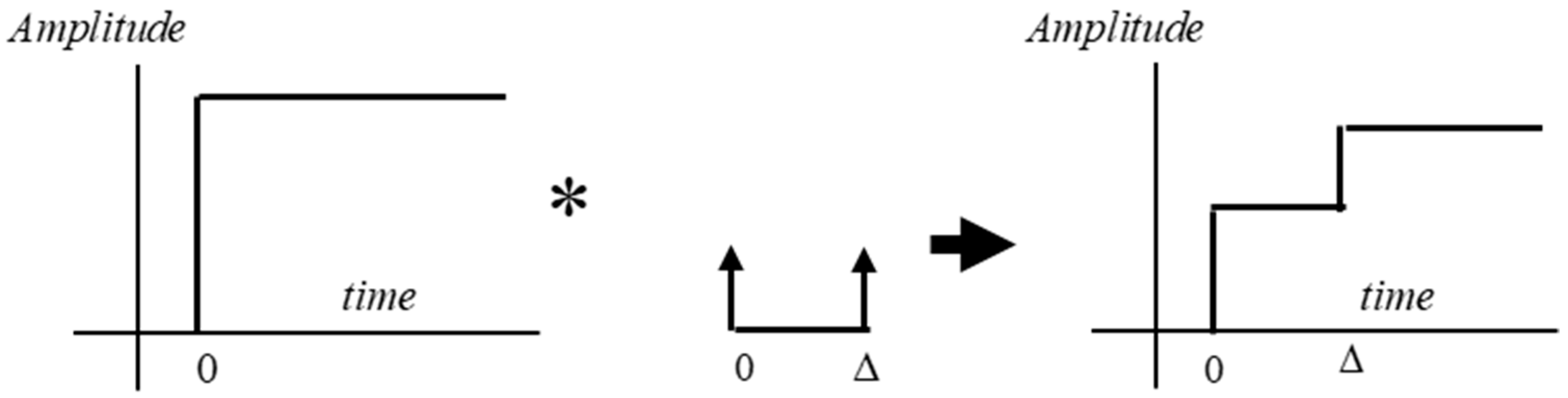
2. Unity Magnitude Shaper: Background and Synthesis Methodology

Since its initial introduction in [5], input shaping has been the subject of numerous explorations. It has proven its effectiveness in optimizing the performance for second-order systems, as outlined in [6], and further adapted to accommodate fractional-order systems, specifically for ZV and ZVD shapers [7,10].

To enhance the rise time and mitigate unwanted oscillations, innovative shapers have been devised by incorporating negative impulses, a strategy aiming to truncate the shaper duration. Nevertheless, this approach can inadvertently activate unaccounted-for higher modes, complicating the system dynamics. Notably, the Unity Magnitude shaper (UM) is a case in point, allowing for the utilization of negative impulses by toggling impulse amplitudes between positive and negative unity [10]. However, finding an analytical solution for the timing of these impulses in damped systems can be a challenging endeavor. In [10], an analytical solution for the timing of impulses in the context of the Unity Magnitude shaper was successfully derived for second-order undamped plants and low-damped systems. Traditional ZV shapers, on the other hand, consist of generating two impulses (positive ones) with a random input signal to effectively counteract output oscillations. This process is illustrated in Figure 1.

In the pursuit of accelerating the rise time, it is possible to reduce the shaper’s duration by incorporating negative impulse amplitudes, necessitating a switch between the values of 1 and −1. This approach results in the shaped command of Figure 2.

2.1. Calculus of UM Shapers for Second-Order Plants

(1)

Proof

Considering a second-order plant characterized by the following:

• ${\omega }_n$, its natural frequency;
• $\xi$, its damping ratio.

The amplitudes and timing of the impulses within an input shaper are established by ensuring compliance with the system (1), which enforces constraints related to residual vibrations.

$$\left\{\begin{array}{l}C\left({\omega }_n,\zeta \right)={\displaystyle \sum _{k=1}^N}{A}_k{e}^{-\zeta {\omega }_n\left(t_N-t_k\right)}\mathrm{c}\mathrm{o}\mathrm{s}\left(t_k{\omega }_n\sqrt{1-{\xi }^2}\right)=0\\ S\left({\omega }_n,\zeta \right)={\displaystyle \sum _{k=1}^N}{A}_k{e}^{-\zeta {\omega }_n\left(t_N-t_k\right)}\mathrm{s}\mathrm{i}\mathrm{n}\left(t_k{\omega }_n\sqrt{1-{\xi }^2}\right)=0\end{array}\right.$$

(1)

$A_i$ stands for the amplitude, while $t_i$ represents the timing of the $i^{\mathrm{th}}$ impulse, with $N$ denoting the total count of impulses within the shaper.

When dealing with the unity magnitude shaper, it involves a total of three impulses. To achieve an optimal shaper duration, the initial impulse is positioned at $t_1=0$ s.

To guarantee that the shaped input replicates the same motions of the rigid body as the unshaped command, it is imperative to consider the following condition:

$$A_1+A_2+A_3=1$$

(2)

The expressions for on–off amplitudes are articulated as follows:

$$\left\{\begin{array}{l}{A}_1=1\\ A_2=-1\\ A_3=1\end{array}\right.$$

(3)

Thus, by employing the relationships defined in (3) and (2), the system of equations in (1) transforms into:

$$\begin{gathered} \left\{\begin{array}{l}{e}^{-\xi {\omega }_n{t}_3}-e^{-\xi {\omega }_n\left(t_3-t_2\right)}\cos \left(t_2{\omega }_n\sqrt{1-{\xi }^2}\right)\\ +\mathrm{c}\mathrm{o}\mathrm{s}\left(t_3{\omega }_n\sqrt{1-{\xi }^2}\right)=0\end{array}\right. \\ \left\{\begin{array}{l}-e^{-\xi {\omega }_n\left(t_3-t_2\right)}\mathrm{s}\mathrm{i}\mathrm{n}\left(t_2{\omega }_n\sqrt{1-{\xi }^2}\right)\\ +\mathrm{s}\mathrm{i}\mathrm{n}\left(t_3{\omega }_n\sqrt{1-{\xi }^2}\right)=0\end{array}\right. \end{gathered}$$

(4)

For the sake of simplification, Equation (4) is expressed as follows:

$$\left\{\begin{array}{l}1-e^{\beta t_2}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha t_2\right)+e^{\beta t_3}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha t_3\right)=0\\ -e^{\beta t_2}\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha t_2\right)+e^{\beta t_3}\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha t_3\right)=0\end{array}\right.$$

(5)

where

$$\left\{\begin{array}{l}\alpha ={\omega }_n\sqrt{1-{\xi }^2}\\ \beta =\xi {\omega }_n\end{array}\right.$$

(6)

The term “damped frequency” is used to refer to $\alpha$.

The distinctive characteristic of the unity magnitude (UM) shaper lies in its utilization of a negative impulse with a value of (−1). By making certain assumptions about an undamped system and applying constraints related to amplitude summation, zero vibration, and a trigonometric identity, it is possible to derive a closed-form expression for the UM shaper. The specific formulation for the undamped UM shaper can be found in references [7,10]:

$$\left[\begin{array}{c}{A}_i\\ t_i\end{array}\right]=\left[\begin{array}{ccc}1& & -1\\ 0& \frac{1}{\omega }{\mathrm{c}\mathrm{o}\mathrm{s}}^{-1}\left(\frac{1}{2}\right)& \frac{1}{\omega }{\mathrm{c}\mathrm{o}\mathrm{s}}^{-1}\left(\frac{-1}{2}\right)\end{array}\right]$$

(7)

In the upcoming section, our attention will shift towards damped systems, with the aim of establishing a universal formula that is applicable to all linear systems.

(2)

Analytic UM shaper synthesis for damped plants

A Unity Magnitude shaper, known for its ease of implementation and efficient control duration, has found favor across numerous application domains. However, when it comes to damped systems, finding an analytical resolution of the time positions of the UM shaper becomes a formidable challenge. Nonetheless, S. S. Gürleyük [14] has introduced an analytical solution, although it should be noted that it does not yield precise results for all values of damping ratios. It is confined to damping ratios within the range of 0 to 0.35 [14].

In this study, we explore graphical approximations as a means to derive analytical expressions for the timing of the second and third impulses, focusing on second-order systems and without limitations on $\xi$, which varies between 0 and 1.

(3)

Unity Magnitude shaper impulses times: graphical resolution

By employing a curve-fitting approach [14], a graphical method is applied to determine the values of $t_2$ and $t_3$. This technique involves initially selecting $t_2$ randomly and then graphically searching for $t_3$ to fulfill the constraints outlined in Equation (4). An example of this approach is illustrated in Figure 3.

In this instance, the damping ratio and natural frequency are set at $\xi =0.5$ and ${\omega }_n=10$ radians per second. As a first step, $t_2$ is arbitrarily chosen as 0.2265 s, and through graphical analysis, an appropriate solution for $t_3$ that satisfies the constraints is deduced as $t_3=0.2564$ s.

The resultant parameters for the Unity Magnitude shaper are as follows:

$$\left[\begin{array}{c}{A}_i\\ t_i\end{array}\right]=\left[\begin{array}{ccc}1& -1& 1\\ 0& 0.2265& 0.25645\end{array}\right]$$

(8)

The UM shaper, synthesized through graphical means, is subsequently implemented on the second-order plant. Here, we considered $\xi =0.5$ and $\omega =10 \mathrm{r}\mathrm{d}/\mathrm{s}$. Figure 4 illustrates the unshaped response versus the shaped one.

The simulation demonstrates the elimination of overshoot and oscillations. This unequivocally attests to the efficacy of the UM shaper synthesized through the curve-fitting technique.

(4)

Advanced observation

The efficacy of the curve fitting technique is evaluated across various sets of parameters for second-order systems. Throughout these simulations, an intriguing feature becomes evident. Specifically, as we modify the damping ratio, we observe that $t_2$ and $t_3$ exhibit a symmetric placement in relation to the rise time $t_r$, as illustrated in Figure 5.

Figure 5 illustrates the temporal placement of UM shaper impulses and the rise time ($t_r$) for both the unshaped response (represented by the dotted line) and the UM-shaped response (represented by the continuous line). This comparison is crucial for understanding how the UM shaper affects the response time of the system under consideration.

Table 1. Time values of $t_2,t_3$, and $t_r$ across varied $\xi$ settings.

$\mathit{\xi }$	$0.2$	$0.3$	$0.5$	$0.6$	$0.7$
${\mathit{t}}_{\mathbf{2}}$	0.1445	0.1675	0.2265	0.2671	0.3235
${\mathit{t}}_{\mathbf{3}}$	0.2156	0.2240	0.2565	0.2861	0.3335
${\mathit{t}}_{\mathit{r}}$	0.1809	0.1967	0.2420	0.2768	0.3287

complements the information provided in Figure 5 by presenting specific time values for $t_2,t_3$ and $t_r$ across varied damping ratio (ξ) settings. These values allow for a quantitative assessment of how changes in damping ratio impact the temporal placement of UM shaper impulses and the rise time. Notably, as the damping ratio varies, $t_2 \mathrm{a}\mathrm{n}\mathrm{d} t_3$ exhibit symmetric placement around the rise time $t_r$, highlighting the consistency of this relationship across different damping ratios.

Equation (9) encapsulates this observed relationship, providing a concise mathematical expression to facilitate analytical derivation and parameter tuning for UM shaper implementation in damped systems. Using this connection, engineers may modify the UM shaper settings to produce the appropriate system response characteristics matched to individual application requirements and damping circumstances.

$$t_3=2t_r-t_2$$

(9)

The feature described by Equation (9) is taken into account to facilitate the analytical derivation aimed at expressing the UM shaper parameters, particularly in the context of damped systems, with a specific focus on the timing of $t_2$ and $t_3$.

(5)

Analytic expression of UM shaper impulse times

The analytical formulation representing the step response of a second-order plant is as follows:

$$y(t)=1-\frac{1}{\sqrt{1-{\xi }^2}}{e}^{-\xi {\omega }_{n}t}\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_n\sqrt{1-{\xi }^2}t-\mathrm{atan}\left(\frac{\sqrt{1-{\xi }^2}}{-\xi }\right)\right)$$

(10)

The analytical derivation of $t_r$ is straightforwardly obtained using the following equation when dealing with a unit step command.

$$t_r=\frac{1}{{\omega }_n\sqrt{1-{\xi }^2}}\left(\mathrm{atan}\left(\frac{\sqrt{1-{\xi }^2}}{-\xi }\right)+\pi \right)$$

(11)

Equations (10) and (11) result in the establishment of a straightforward analytical relationship between $t_2$ and $t_3$ as presented in (12).

$$t_3=\frac{2}{{\omega }_n\sqrt{1-{\xi }^2}}\left(\mathrm{atan}\left(\frac{\sqrt{1-{\xi }^2}}{-\xi }\right)+\pi \right)-t_2$$

(12)

The solution to Equation (6) with the utilization of (12) becomes rather intricate. Therefore, we employ an advanced graphical exploration method in this study. Essentially, we make the assumption that the interval between the second and third impulses is exceedingly brief. Under this assumption, the system’s response during this interval closely aligns with the tangent at the midpoint time $t_r$. Figure 5 illustrates the fundamental concept of our approach with unshaped response (dotted line), UM-shaped response (continuous line), and tangent at $t_r$ (mixed line).

The derivative form of the response at the time $t_r$ is given by

$$y^{\prime }\left(t_r\right)={\omega }_n\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{\xi }{\sqrt{1-{\xi }^2}}\left(\mathrm{atan}\left(\frac{\sqrt{1-{\xi }^2}}{-\xi }\right)+\pi \right)\right)$$

(13)

Through the graphical estimation technique, we express the expression of $y^{\prime }\left(t_r\right)$ as follows:

$$y^{\prime }\left(t_r\right)={\omega }_n^2\left(t_3-t_2\right)$$

(14)

By merging Equations (9) and (14), it becomes possible to represent the time of the second impulse as follows:

$$t_2=t_r-\frac{1}{2{\omega }_n^2}{y}^{\prime }\left(t_r\right)$$

(15)

Furthermore, the position of the third impulse is given by:

$$t_3=t_r+\frac{1}{2{\omega }_n^2}{y}^{\prime }\left(t_r\right)$$

(16)

In summary, the formulations derived from Equations (11), (13), (15), and (16) enable us to provide an analytical representation of the UM shaper as follows:

$$\left[\begin{array}{c}{A}_i\\ t_i\end{array}\right]=\left[\begin{array}{ccc}1& -1& 1\\ 0& t_r-\frac{1}{2{\omega }_n^2}{y}^{\prime }\left(t_r\right)& t_r+\frac{1}{2{\omega }_n^2}{y}^{\prime }\left(t_r\right)\end{array}\right]$$

(17)

Table 2. Time impulses of UM shaper: calculated vs. estimated.

$\mathit{\xi }$	$0.2$	$0.3$	$0.5$	$0.6$	$0.7$
${\mathit{t}}_{\mathbf{2}\mathit{graph}}$	0.14445	0.1675	0.2265	0.26709	0.32346
${\mathit{t}}_{\mathbf{3}\mathit{graph}}$	0.21560	0.2240	0.25645	0.28612	0.33350
${\mathit{t}}_{\mathbf{2}\mathit{anal}}$	0.14597	0.1689	0.2271	0.2673	0.32350
${\mathit{t}}_{\mathbf{3}\mathit{anal}}$	0.21562	0.2244	0.2569	0.2863	0.33350
${\mathit{error} }_{{\mathit{t}}_{\mathbf{2}}}$	0.00152	0.0014	0.0006	0.00021	0.00004
${\mathit{error} }_{{\mathit{t}}_{\mathbf{3}}}$	0.00002	0.0004	0.00045	0.00018	0.00000

is prepared to assess the disparity between impulse times computed analytically and those estimated through graphical methods (curve fitting). It proves that the discrepancy between analytical and graphical time values is negligible, affirming the validity of the analytical approach.

2.2. Robust Design of UM Shaper

To enhance the resilience of the fractional control loop against variations in the system’s natural frequency, real-time synthesis of the UM shaper is carried out. In this section, the parameters of the UM shaper are determined by leveraging characteristics of explicit derivative systems as in (18) [7].

This assumes the following:

$$\left[\begin{array}{c}{A}_i\\ t_i\end{array}\right]=\left[\begin{array}{ccc}1& -1& 1\\ 0& \frac{1}{{\omega }_n}\left(\psi -\frac{e^{-\xi \psi }}{2}\right)& \frac{1}{{\omega }_n}\left(\psi +\frac{e^{-\xi \psi }}{2}\right)\end{array}\right]$$

(18)

$$\left\{\begin{array}{c}\psi =\frac{\theta }{\sqrt{1-{\xi }^2}}\\ \theta =\mathrm{atan}\left(\frac{\sqrt{1-{\xi }^2}}{-\xi }\right)+\pi \end{array}\right.$$

(19)

Figure 6 shows the step responses of a second-order plant with a fixed damping ratio (ξ = 0.5) and varying natural frequencies ${\omega }_n$ (multiplied by a factor of 9), comparing the unshaped and shaped responses. This comparison analysis is useful for understanding how the UM shaper influences the system’s response characteristics under different natural frequency settings.

By examining the step responses, two constant ratios, denoted as α₁ and α₂, emerge. These ratios represent the relationship between specific time points in the response curve, specifically between the inflection time $\left(t_{\mathrm{Inf} }\right)$ and $t_2$, and between $t_{\mathrm{Inf} }$ and $t_3$, respectively.

The constant values of α₁ and α₂ across different natural frequencies indicate that the temporal placement of the UM shaper impulses remains relatively constant, irrespective of variations in the system’s natural frequency. This observation underscores the robustness of the UM shaper design in maintaining constant performance across a range of operating conditions.

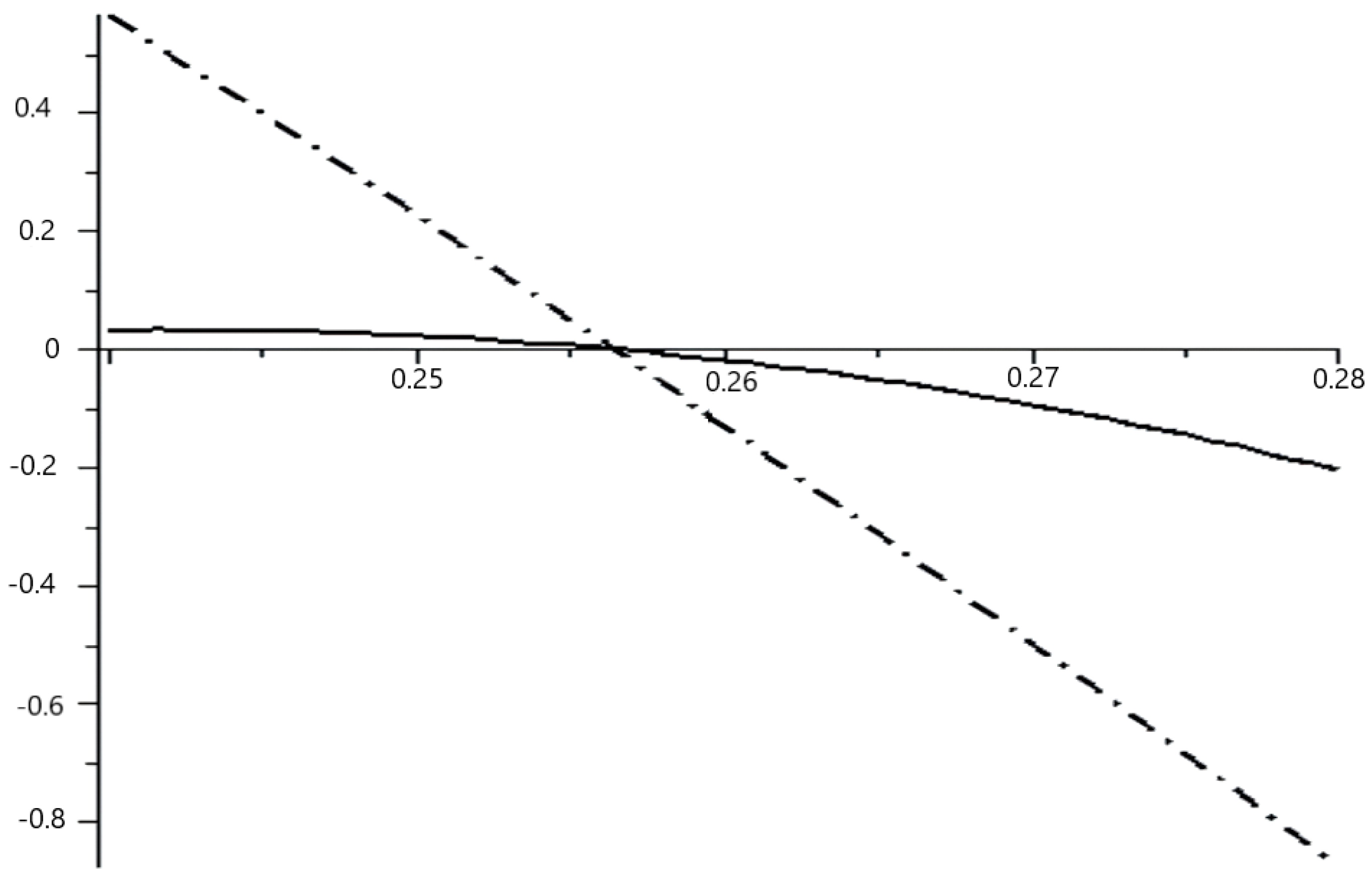
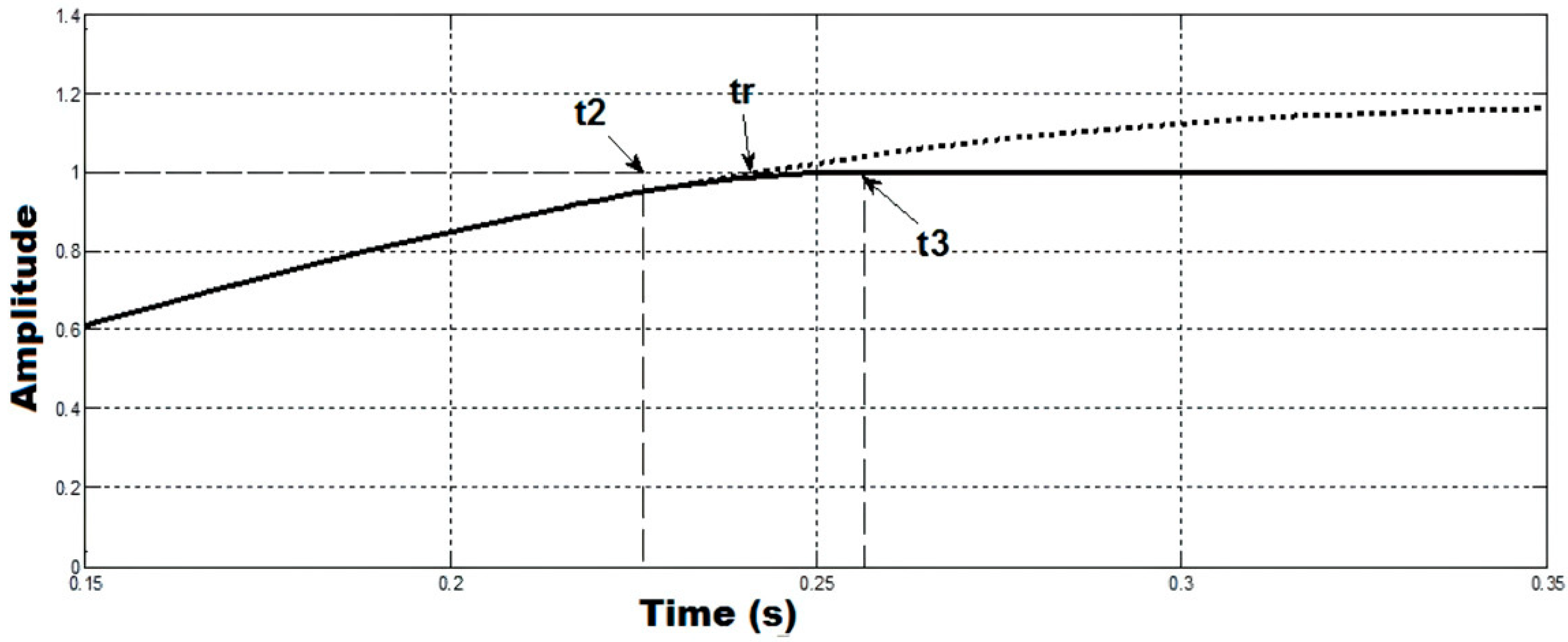
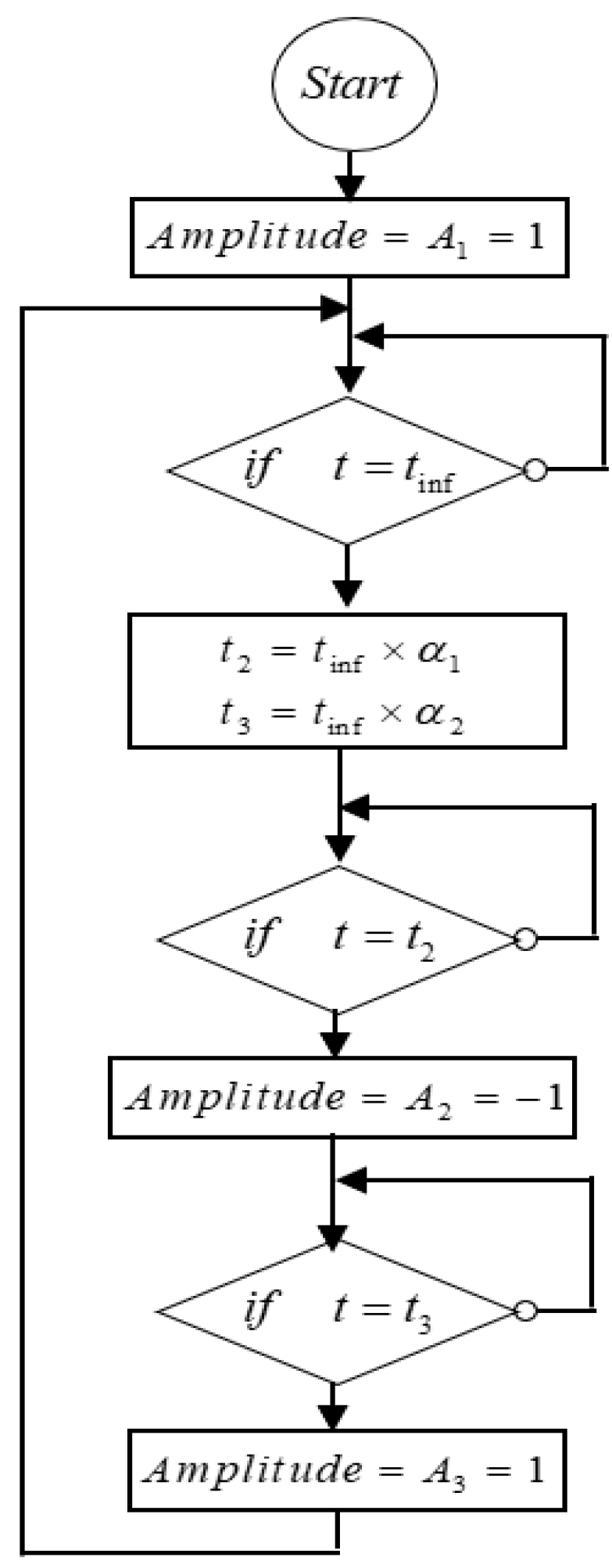
2.3. Real-Time Algorithm

To make the input shaper technique adaptable to real-world systems and improve its durability, it is imperative to calculate the shaper’s parameters in real-time. This real-time calculation process consists of two distinct steps. The initial step is performed offline and encompasses the following computations:

• Determining the inflection point time $\left(t_{\inf ,\mathrm{nom}}\right)$ for the nominal system through computation.
• Calculating $t_{2 \mathrm{nom}}$ and $t_{3 \mathrm{nom}}$ through computation.
• Deriving ${\alpha }_1$ as $\frac{t_{2 \mathrm{nom}}}{t_{\inf ,\mathrm{nom}}}$ and ${\alpha }_2$ as $\frac{t_{3 \mathrm{nom}}}{t_{\inf ,\mathrm{nom}}}$ through computation.

The second phase involves the real-time calculation of $t_2$ and $t_3$, utilizing the inflection time $t_{\mathit{inf}}$ and employing the previously discussed property:

$$\left\{\begin{array}{l}{\mathrm{t}}_2={\alpha }_1\times {\mathrm{t}}_{\inf }\\ {\mathrm{t}}_3={\alpha }_2\times {\mathrm{t}}_{\inf }\end{array}\right.$$

(20)

The subsequent flowchart illustrates the algorithm for designing the UM shaper in real-time in Figure 7.

To confirm the presence of constants ${\alpha }_1$ and ${\alpha }_2$, it is essential that the ratios $\frac{t_2}{t_{\mathrm{Inf}}}$ and $\frac{t_3}{t_{\mathrm{Inf}}}$ depend exclusively on the damping ratio $\xi$.

The times $t_2$ and $t_3$ are expressed as follows:

$$t_2=\frac{1}{{\omega }_n}\left(\psi -\frac{e^{-\xi \psi }}{2}\right)$$

(21)

$$t_3=\frac{1}{{\omega }_n}\left(\psi +\frac{e^{-\xi \psi }}{2}\right)$$

(22)

$\psi$ is introduced and discussed in (19) earlier in the text.

For second-order systems, the time of the inflection point is defined as

$$t_{\mathrm{Inf}}=\frac{\mathrm{atan}\left(\frac{\sqrt{1-{\xi }^2}}{\xi }\right)}{\sqrt{1-{\xi }^2}}\times \frac{1}{{\omega }_n}$$

(23)

We have,

$${\alpha }_1=\frac{t_2}{t_{\mathrm{Inf} }}=\frac{\psi -\frac{e^{-\xi \psi }}{2}}{\mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{\sqrt{1-{\xi }^2}}{\xi }\right)/\frac{\mathrm{a}}{\sqrt{1-{\xi }^2}}}$$

(24)

$${\alpha }_2=\frac{t_3}{t_{\mathrm{Inf} }}=\frac{\psi +\frac{e^{-\xi \psi }}{2}}{\frac{\mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{\sqrt{1-{\xi }^2}}{\xi }\right)}{\sqrt{1-{\xi }^2}}}$$

(25)

These equations reveal an important characteristic: the ratios ${\alpha }_1$ and ${\alpha }_2$ are unaffected by ${\omega }_{\mathrm{n}}$ and remain constant for a specific $\xi$ value.

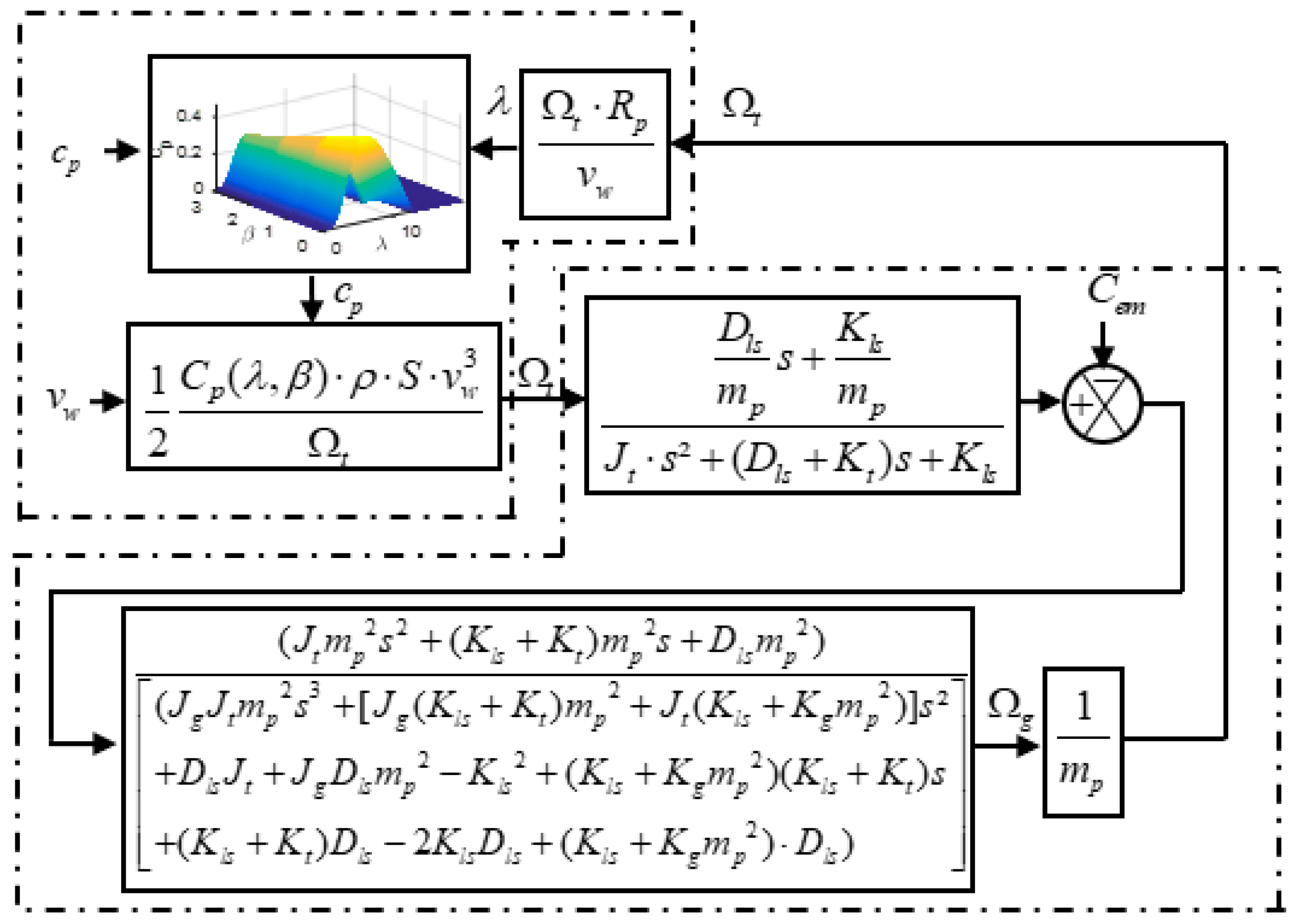
3. WCS Modeling

Formula (26) can be used to represent the aerodynamic torque C_t in a horizontal axis wind turbine (HAWT) [2].

$$C_t=\frac{0.5\cdot C_p(\lambda ,\beta )\cdot \rho \cdot S\cdot V_w^3}{{\mathsf{\Omega }}_t} \mathrm{with} \lambda =\frac{{\mathsf{\Omega }}_t\cdot R_p}{V_w}$$

(26)

In this context, the variables are defined as follows:

• P is the air density;
• V_w represents the wind velocity;
• S is the surface area swept by the blades;
• R_p is the blades radius;
• C_p is the aerodynamic efficiency is dependent on the pitch angle, β, and the tip speed ratio, λ.

Typically, a multiplier, or a gearbox, is employed to connect the hub of the slow shaft of the wind turbine to the fast shaft of the generator, matching the turbine’s rotational speed, Ω_t, to that of the generator, Ω_g.

It is necessary to consider the possibility of mechanical torsion that may affect the turbine shafts. Therefore, a two-mass mechanical model has been utilized in this study. It is critical to consider the dynamics of the drive train when designing velocity regulators for a WECS to ensure system stability and prevent mechanical vibrations. The dynamic equations of the turbine described in the slow shaft reference are given by Equations (27) and (28):

$$J_t\cdot \frac{d{\mathsf{\Omega }}_t}{dt}=C_t-K_{ls}\left({\mathsf{\Omega }}_t-\frac{{\mathsf{\Omega }}_g}{m_p}\right)-D_{ls}\left({\theta }_t-\frac{{\theta }_g}{m_p}\right)-K_t{\mathsf{\Omega }}_t$$

(27)

$$J_g\cdot \frac{d{\mathsf{\Omega }}_{\mathrm{g}}}{dt}=-C_{em}+\frac{K_{ls}}{m_p}\left({\mathsf{\Omega }}_t-\frac{{\mathsf{\Omega }}_{\mathrm{g}}}{m_p}\right)+\frac{D_{ls}}{m_p}\left({\theta }_t-\frac{{\theta }_g}{m_p}\right)-K_g{\mathsf{\Omega }}_{\mathrm{g}}$$

(28)

where θ_g and θ_t are the positions of the generator and the turbine, respectively. Assuming that the transmission via the multiplier is ideal, we then have

$$m_p=\frac{{\theta }_g}{{\theta }_t}=\frac{{\mathsf{\Omega }}_g}{{\mathsf{\Omega }}_t}$$

(29)

The block diagram of the wind turbine for a two-mass model is given in Figure 8.

A hybrid generator, a full-bridge rectifier powering a resistive load, and a shaper controlling the excitation winding are among the WECS’s electrical components. SimPowerSystem tools (Matlab R2016-a) are used to model the load and converters, allowing for realistic controller testing while accounting for commutation effects. Harmonic distortions, on the other hand, can cause torque rippling and poor reference tracking in the HESG model, affecting the waveforms of currents and armature voltages, and ultimately, the power obtained from the wind. As a result, additional research is required to investigate their impact. In the Concordia reference frame, the electrical model of the HESG is expressed using Equation (30) [2].

$$\begin{array}{l}\left[{\phi }_2\right]=\left[L_2\right]\left[I_2\right]+\left[M_{e2}\right]I_e+\left[{\phi }_{e2}\right]\hfill \\ {\phi }_e={\left[M_{e2}\right]}^t\left[I_2\right]+L_e{I}_e+{\phi }_{ae}\\ \left[V_2\right]=R_s\left[I_2\right]+\frac{d\left[{\phi }_2\right]}{dt}\\ V_e=R_e{I}_e+\frac{d{\phi }_e}{dt}\\ \left[C_{em}\right]=\frac{1}{2}{\left[I_2\right]}^t\frac{d\left[L_2\right]}{d\theta }\left[I_2\right]+{\left[I_2\right]}^t\frac{d\left[M_{e2}\right]}{d\theta }{I}_e+{\left[I_2\right]}^t\frac{d\left[{\varphi }_{e2}\right]}{d\theta }\end{array}$$

(30)

where $\left[V_2\right]=\left[\begin{array}{c}{V}_{\alpha }\\ V_{\beta }\end{array}\right]$ $\left[I_2\right]=\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]$ $\left[M_{e2}\right]=\left[\begin{array}{c}{M}_{e\alpha }\\ M_{e\beta }\end{array}\right]\left[{\varphi }_2\right]=\left[\begin{array}{c}{\varphi }_{\alpha }\\ {\varphi }_{\beta }\end{array}\right]$

$$\left[L_2\right]=\left[\begin{array}{cc}{L}_{\alpha }& M_{\alpha \beta }\\ M_{\alpha \beta }& L_{\beta }\end{array}\right]\left[{\varphi }_{e2}\right]=\left[\begin{array}{c}{\varphi }_{e\alpha }\\ {\varphi }_{e\beta }\end{array}\right]$$

4. Control of the WECS

Turbine and HESG dynamic equations are nonlinear, system characteristics are unknown, and disturbance sources including load variations, harmonics, and mechanical vibrations can all have an impact on a WCS. To solve these issues, strong control measures must be implemented. The H_∞ regulator’s efficiency in controlling wind conversion systems has been demonstrated in several studies [24,32,33,34]. A comparison of LQG control with H_∞ control in [24] found equal power generation performance. Another research in [32] confirmed the performance of the H_∞ control approach against a standard PID regulator.

Wind turbine control must ensure precise reference tracking while minimizing dynamic errors. Setting the optimal turbine rotation speed for maximum power extraction is achievable through a HESG by adjusting the generator’s excitation current (Figure 9). In [33], the authors prove the performance of the H_∞ control approach versus adaptive PI controllers in terms of robustness to parameters uncertainty. However, Ref. [34] describes two robust control algorithms for a HESG in a wind conversion system with an isolated load. The article introduces two techniques and compares CRONE and H_∞ controllers. The comparison looks at both performance and resilience in the face of the generator’s inherent uncertainties, as well as space harmonics, electronic commutations, wind severe fluctuations, and mechanical vibrations. The simulation findings reveal that the CRONE regulator performs better in terms of mechanical parameter uncertainty and mechanical stress reduction, demonstrating its resilience. In terms of ideal rotation speed tracking, comparable results were found with a settling time of 6.5 s and an overshoot of 27% for the stepped wind profile. In this work, we will evaluate the effect of associating our novel UM shaper with the CRONE controller.

This section discusses the design of robust controllers that provides stable and reliable closed-loop operation in the face of external disturbances such as the wind’s gusts.

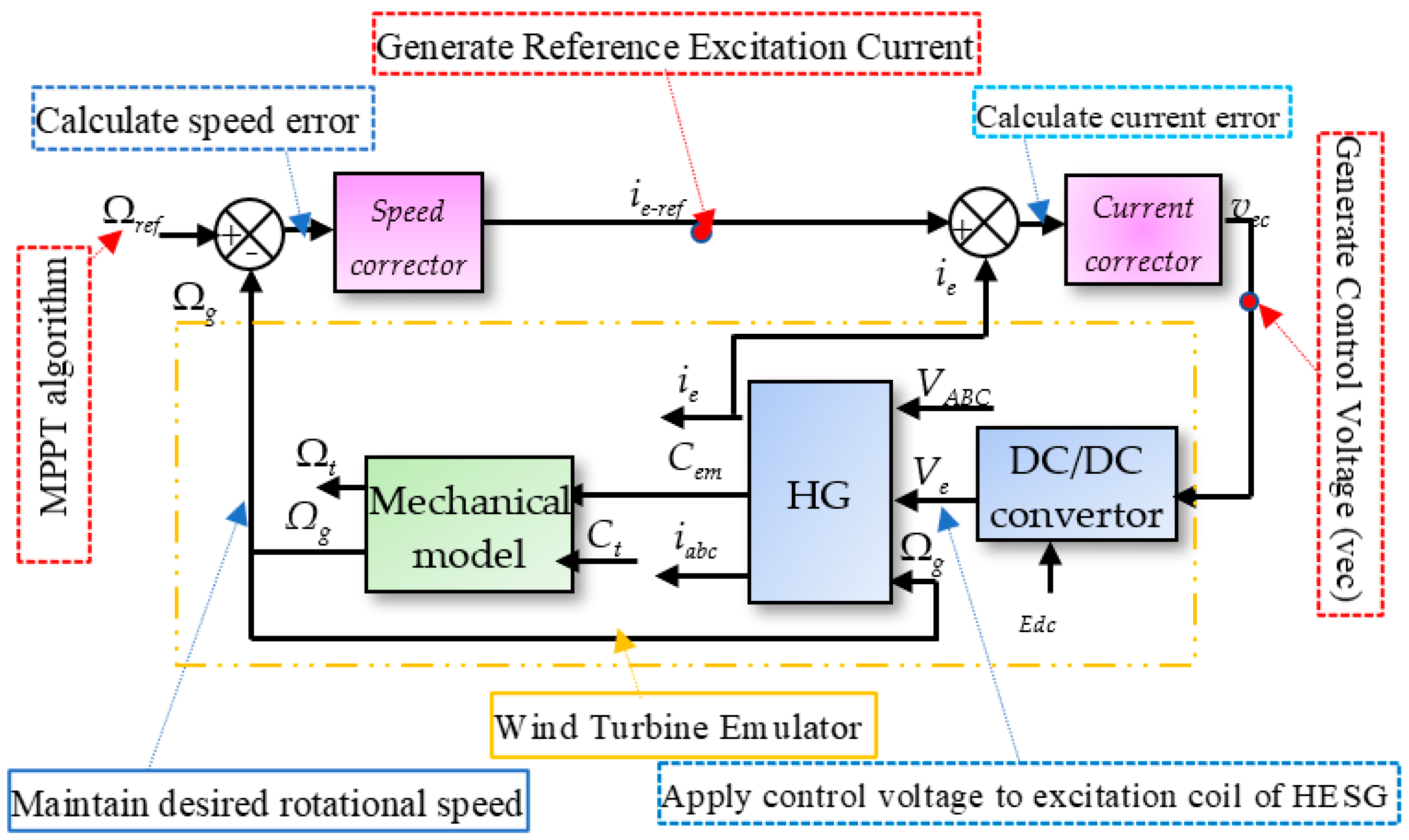
4.1. Excitation Current Control

K_i(s), a proportional integral (PI) controller is designed to ensure that the control voltage v_ec is less than v_ecm, and that the response time is 0.015 s [2]. The value of w₀ is set to approximately 300 rd/s.

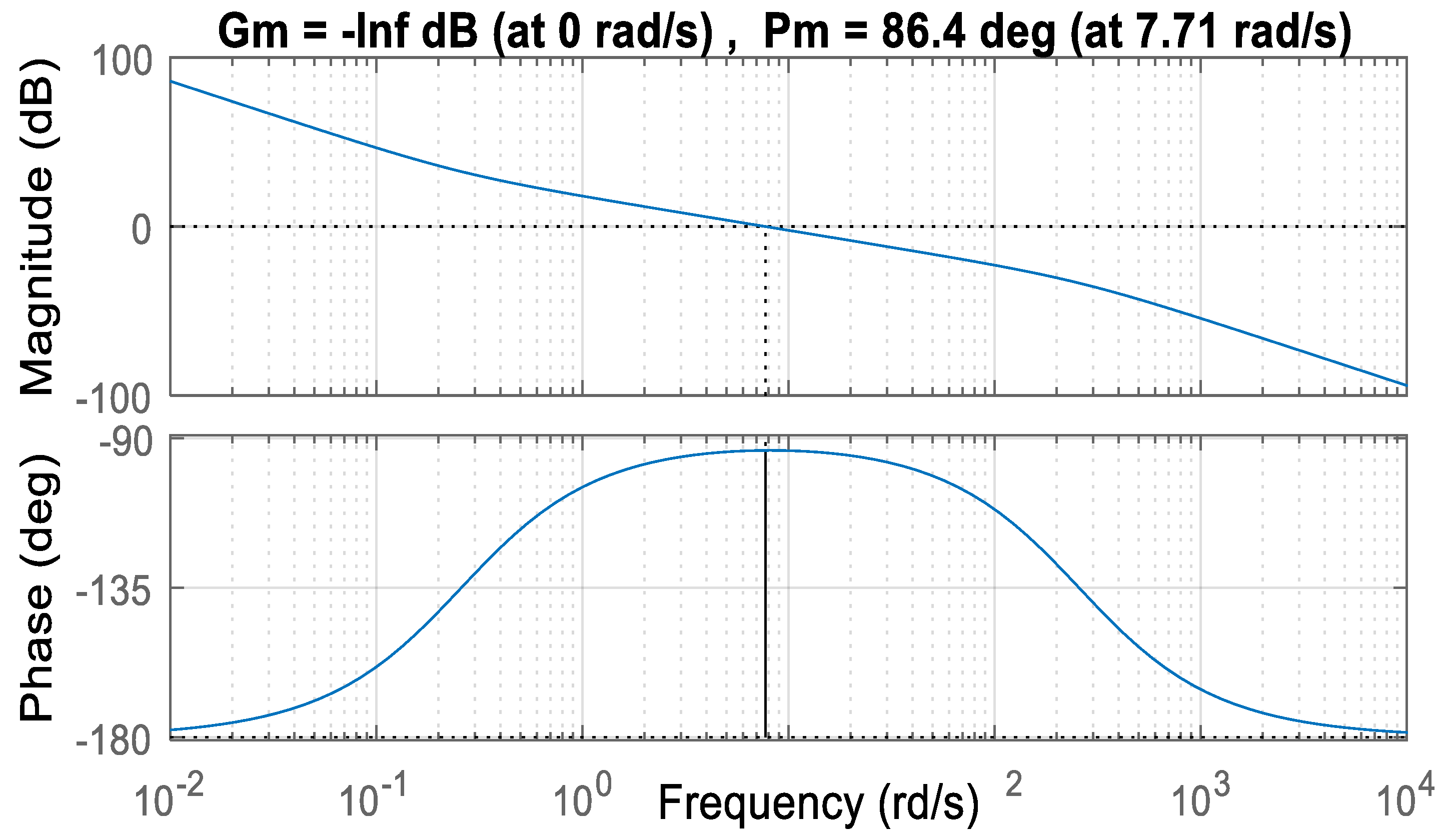
4.2. Crone Controller Synthesis

CRONE control (Robust Fractional Order Control) consists of three generations [25]:

• The first generation is used if there are only nominal model gain variations to be controlled.
• The second one is used when there are nominal models gain changes to be checked as well as phase variations.
• The third generation should be used when the frequency response of the model to be monitored contains uncertainties of various types.

The non-complete order, real or complex, depending on the generation, allows defining the optimal open-loop transfer function in terms of overload, speed, and accuracy with a few parameters. The bode diagram of $G(s)={\Omega }_g(s)/i_{eref}(s)$ identified for several operation points [32,34] are in Figure 10. Given these bode diagrams, the second generation seems to be a good choice [2]. The non-integer order, real or complex, depending on the generation, allows defining the optimal open-loop transfer function in terms of overshoot, speed, and accuracy with a few parameters [25]. The β(s) of the corrected open loop that guarantees the required specifications [26] is defined by (31):

$$\begin{array}{l}\beta (s)=K_{CRONE}(s)\cdot G(s)\\ =K_u{\left((1+\frac{s}{w_l})/(\frac{s}{w_l})\right)}^{n_1}\cdot {\left((1+\frac{s}{w_h})/(\frac{s}{w_l})\right)}^n\cdot \left(1/{\left(1+\frac{s}{w_h}\right)}^{n_h}\right)\end{array}$$

(31)

• G(s) is the uncertain model;
• K_CRONE(s) is the CRONE controller;
• K_u is a constant providing a unit gain at the desired pulsation w₀;
• W_h is the high transition frequency;
• w_l is the low transition frequency;
• n_h is the order in high frequencies;
• n_l is the order in low frequencies;
• n is the order around w₀.

The parameters of the open-loop transfer function β(s) are provided by (32) [27].

$$n=\frac{180-M\varphi }{90} w_l=\frac{w_0}{10\sqrt{a}}{w}_h=w_0\cdot 10\sqrt{a}a=\mathsf{\Delta }{\beta }^{\frac{1}{n}}$$

(32)

Mϕ is the desired phase margin in degrees and Δβ is the gain change in the open loop.

In the process of validating the robustness of the strategies adopted, the first step is to define the objectives of the control. We want to maximize power in the MPPT region and maintain stable closed-loop behavior under all operating conditions while ensuring the following:

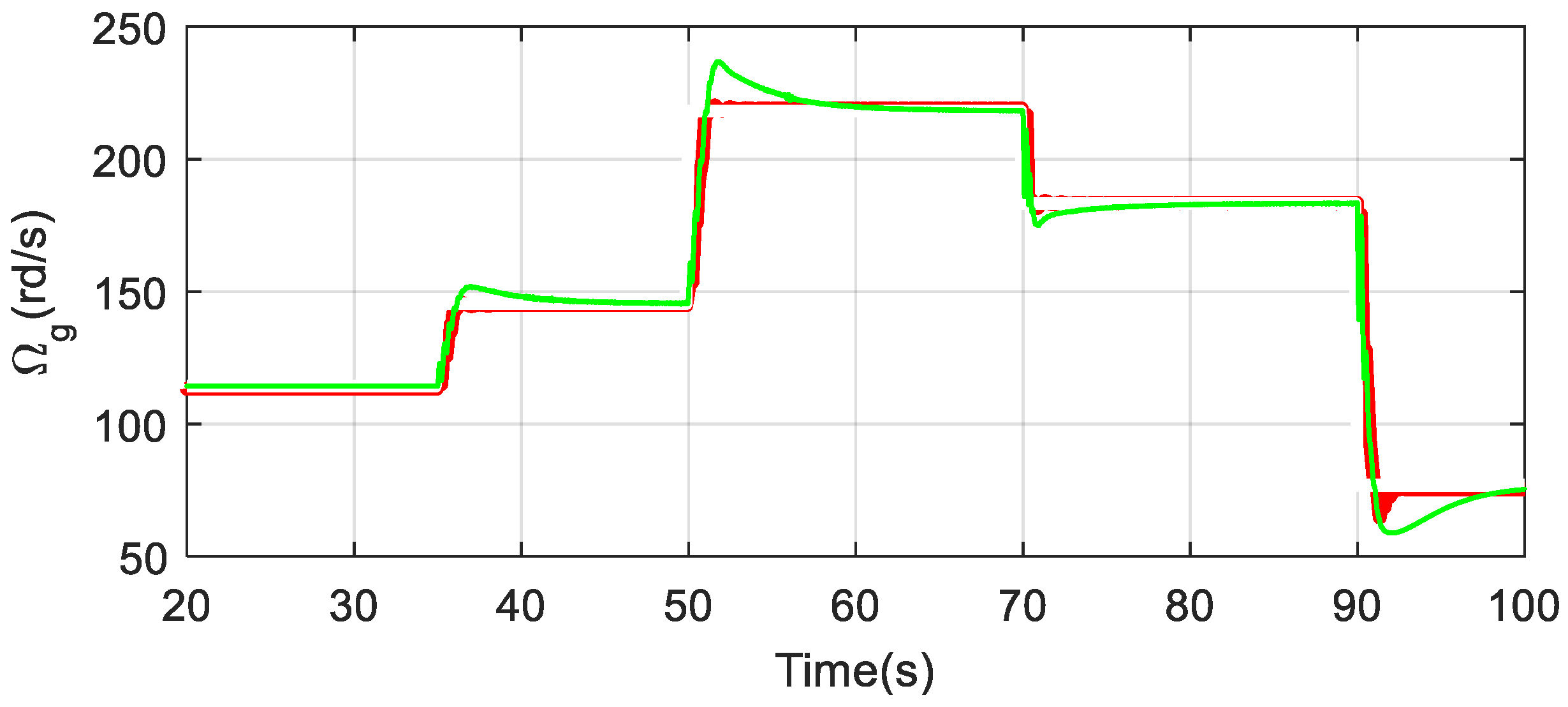
• Good reference speed tracking.
• Good rejection of noise and disturbance.
• No static error in steady state.
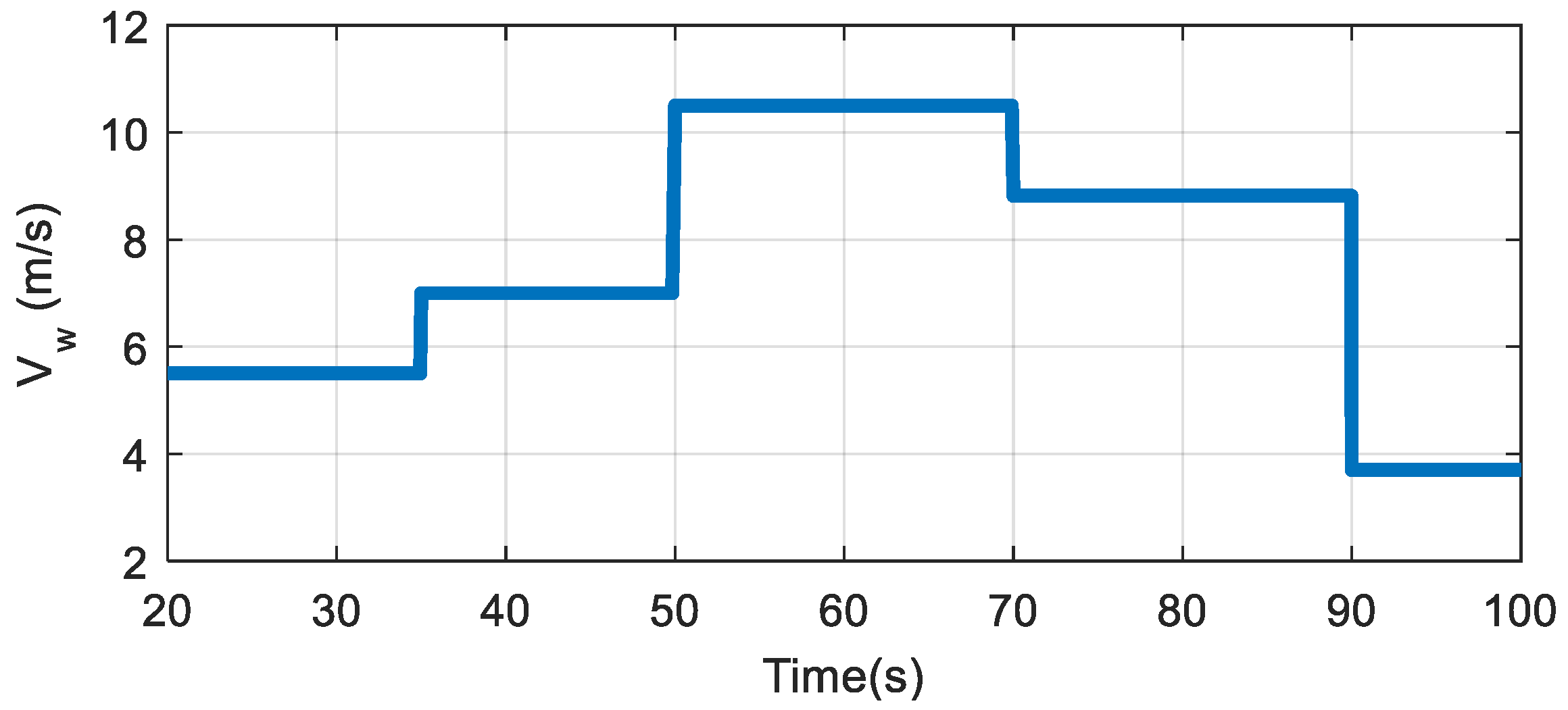
• Non-saturation of the corrector due to a sudden change in wind speed limited to 0.5 m/s. Indeed, for this variation, we are almost around the same point of operation. Because of this, if the regulator is properly sized, it should ensure a smooth response.

These specifications are imposed rather than tuned in the CRONE toolbox [35]. This tool transforms the non-integer controller (31) into rational parallel transmittances by adjusting the curve of its frequency response. This rational controller is equivalent to the fractional controller. The purpose of this approximation is to avoid any numerical simulation problems.

The following parameters have been chosen for the adjustment of the concealer:

• n_h = 1.5 to limit the sensitivity of the input;
• n_l = 2 to cancel the steady-state error;
• Mϕ = 85° to ensure closed-loop robustness.

After tuning, the structure of the controller is given by Figure 11.

A satisfactory phase margin of about 86.4° is reached around w₀ (Figure 12).

4.3. Real-Time UM Shaper Extension on Hybrid Excitation Synchronous Generator Wind Conversion Systems: Online Input Shaping Implementaion

The online computation of shaper synthesis employs a methodology akin to that applied to second-order plants. This is done to enhance resilience against fluctuations in the ${\omega }_{\mathrm{n}}$.

As illustrated in Figure 6, with step and shaped responses of systems having an order (n) but with a varying natural frequency, a visual deduction is made about the correlation between the impulse times of the UM shaper and the moment of the inflection point.

Through experimental verification, it has been established that the relationship between $t_2$ and $t_{\mathrm{Inf}}$ remains constant across different systems sharing the same order $n$ but featuring diverse natural frequencies. Likewise, the constancy of the $t_3$ and $t_{\mathrm{Inf}}$ ratio has been confirmed.

The organizational hierarchy depicted in Figure 6 (step responses of an explicit fractional order system with variable ω_n, scaled by a factor of 9, comparing unshaped and shaped curves) is expanded to encompass explicit fractional derivative systems.

Indeed, we follow the identical procedure as outlined in the preceding section. To confirm the presence of ${\alpha }_1$ and ${\alpha }_2$, it is imperative to demonstrate that the relationships $\frac{t_2}{ t_{\mathrm{Inf} }}$ and $\frac{t_3}{t_{\mathrm{Inf} }}$ are contingent solely on the fractional order $n$.

The instance of the inflection point in explicit fractional derivative systems is denoted as per references [8,9].

$$\begin{array}{ll}{t}_{\mathrm{Inf} }=\frac{1}{{\omega }_n}\times (& -2.34+2.02n+1.89(n-1.5{)}^2+1.62(n-1.5{)}^3+0.95(n-1.5{)}^4\\ & +0.49(n-1.5{)}^5+0.22(n-1.5{)}^6+0.086(n-1.5{)}^7\\ & {\left.+0.028(n-1.5{)}^8\right)}^{1/n}\end{array}$$

(33)

So,

$$\begin{array}{rr} & {\alpha }_1=\frac{t_2}{t_{\mathrm{Inf} }}=\frac{\left(\psi -\frac{e^{-\xi \psi }}{2}\right)}{{\left(\begin{array}{c}-2.34+2.02n+1.89(n-1.5{)}^2+1.62(n-1.5{)}^3+0.95(n-1.5{)}^4+\\ 0.49(n-1.5{)}^5+0.22(n-1.5{)}^6+0.086(n-1.5{)}^7+0.028(n-1.5{)}^8\end{array}\right)}^{1/n}}\\ & {\alpha }_2=\frac{t_3}{t_{\mathrm{Inf} }}=\frac{\left(\psi +\frac{e^{-\xi \psi }}{2}\right)}{{\left(\begin{array}{c}-2.34+2.02n+1.89(n-1.5{)}^2+1.62(n-1.5{)}^3+0.95(n-1.5{)}^4+\\ 0.49(n-1.5{)}^5+0.22(n-1.5{)}^6+0.086(n-1.5{)}^7+0.028(n-1.5{)}^8\end{array}\right)}^{1/n}}\end{array}$$

(34)

Much like with second-order systems, these equations unveil a notable characteristic: the ratios ${\alpha }_1$ and ${\alpha }_2$ remain unaffected by ${\omega }_{\mathrm{n}}$, staying consistent for a specific $n$ value.

5. Validation and Analysis

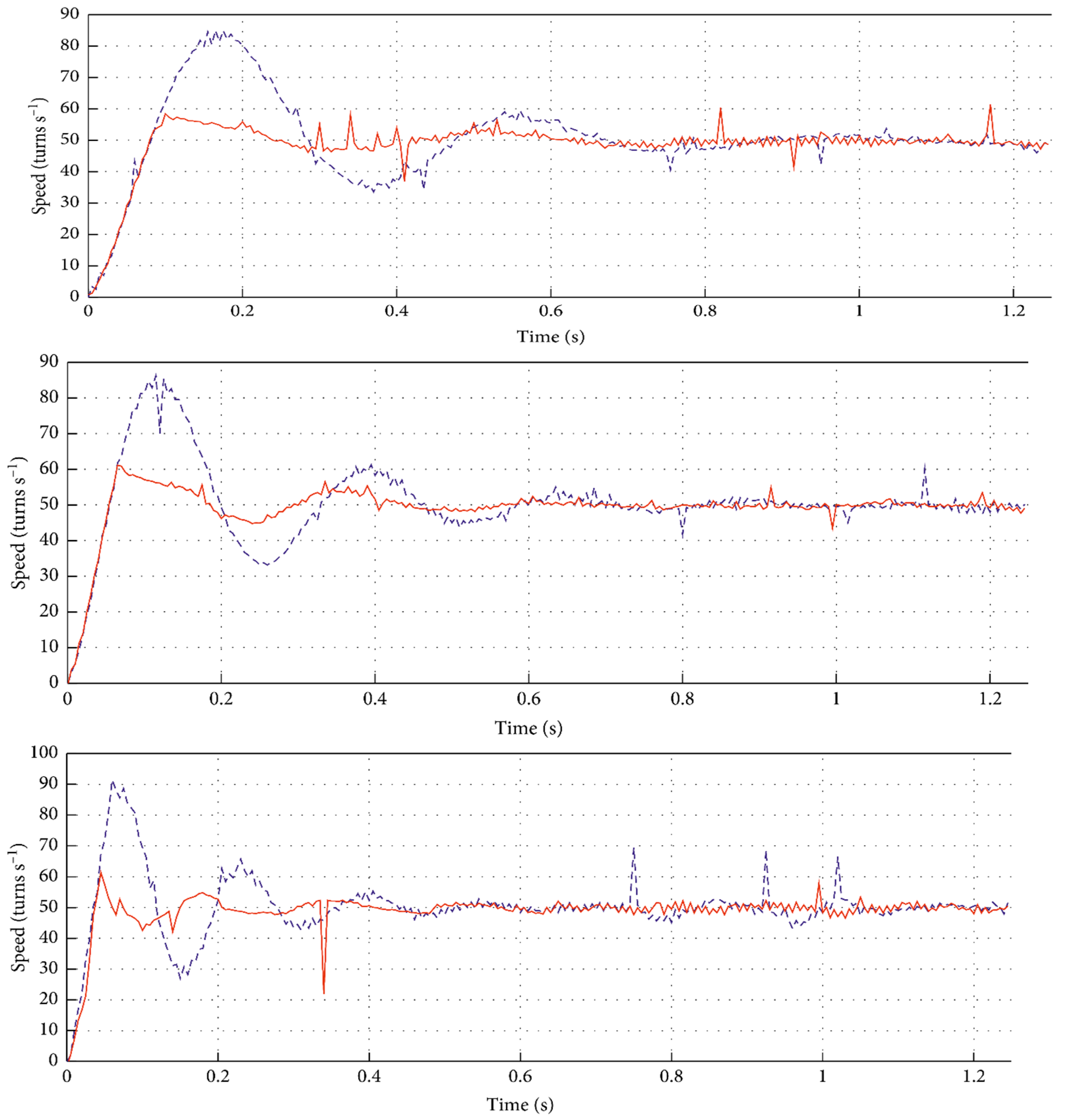
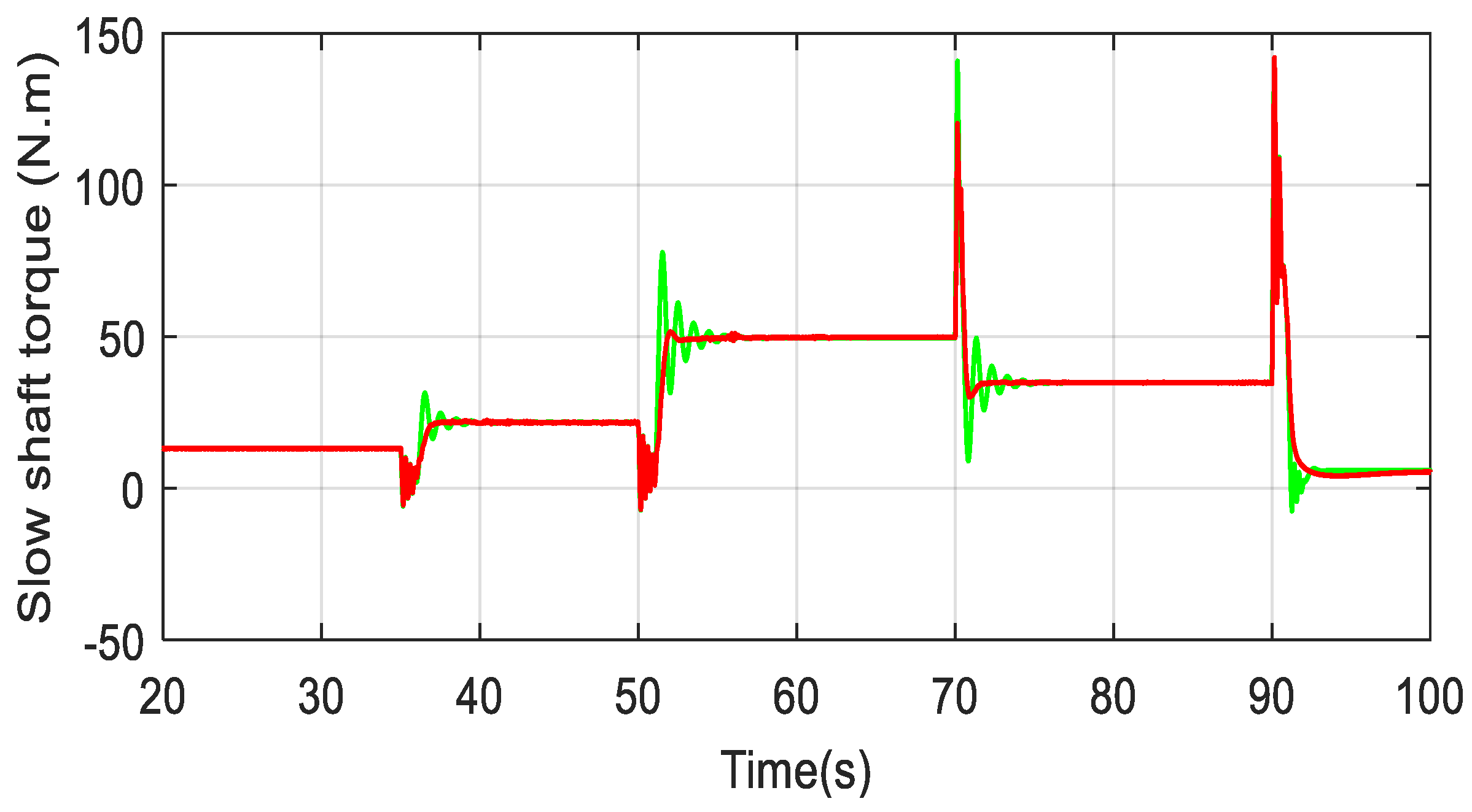
5.1. Experimental Validation of the Performance of the Proposed Algorithm

Figure 13 shows all the equipment used to apply the UM shaper approach in association with the second-generation CRONE controller (Robust Fractional Order Control) on the test bench. It is composed of two identical parts that may be used separately or in combination. Its electromechanical components are branded GEC Alsthom Parvex servo motors. Each part is provided with an actuator of the DC motor type, with a Permanent Magnet (Samarium Cobalt) type T 4C 4B power of about 2 kW. The stator of the motor is integrated with a support able to slide and to be fixed on a bench whose stability is assured by four concrete feet of high masses. The control of the bench is provided by a National Instrument (NI) chassis, connected to a PC, equipped with an analog-to-digital I/O card managed by the LABVIEW software (Version 6).

In order to operate the test bench, a LABVIEW program was developed and connected to the equipment using a chassis called “CompactRIO” (see Figure 14).

CompactRIO has a microprocessor for developing control algorithms and can operate at various clock rates. Controllers are only compatible with National Instrument’s C Series I/O modules. In our case, the I/O modules are NI 9215, NI 9254, and NI 9401. The FPGA module may be used to implement high-performance data processing on reconfigurable fabric. Such data processing may be performed on data streaming in from connected I/O modules.

The chassis includes an Ethernet port, which can connect the CompactRIO controller to a PC. To achieve the application of the UM shaper and to extract the results, the CompactRIO was connected to the PC, executing a LabVIEW program, during the process.

In summary, the I/O modules were connected to the tachometer dynamo fixed on the test bench to receive the velocity value. They were also connected to the chopper commanding the two DC motors of the test bench to apply the calculated and programmed command from LabVIEW.

Experimental identifications were conducted on the test bench, and a transfer function was identified:

$$\mathrm{T}(\mathrm{p})=\frac{2.34}{(1+0.0047p)(0.001+j_{m}p)}$$

(35)

where j_m is the adjustable inertia

Three tests are performed on the experimental bench (Figure 15). The curves correspond to the angular velocity for each case study (minimum weight, 57% of maximum weight, and maximum weight) with and without the UM shaper.

The following can be noted:

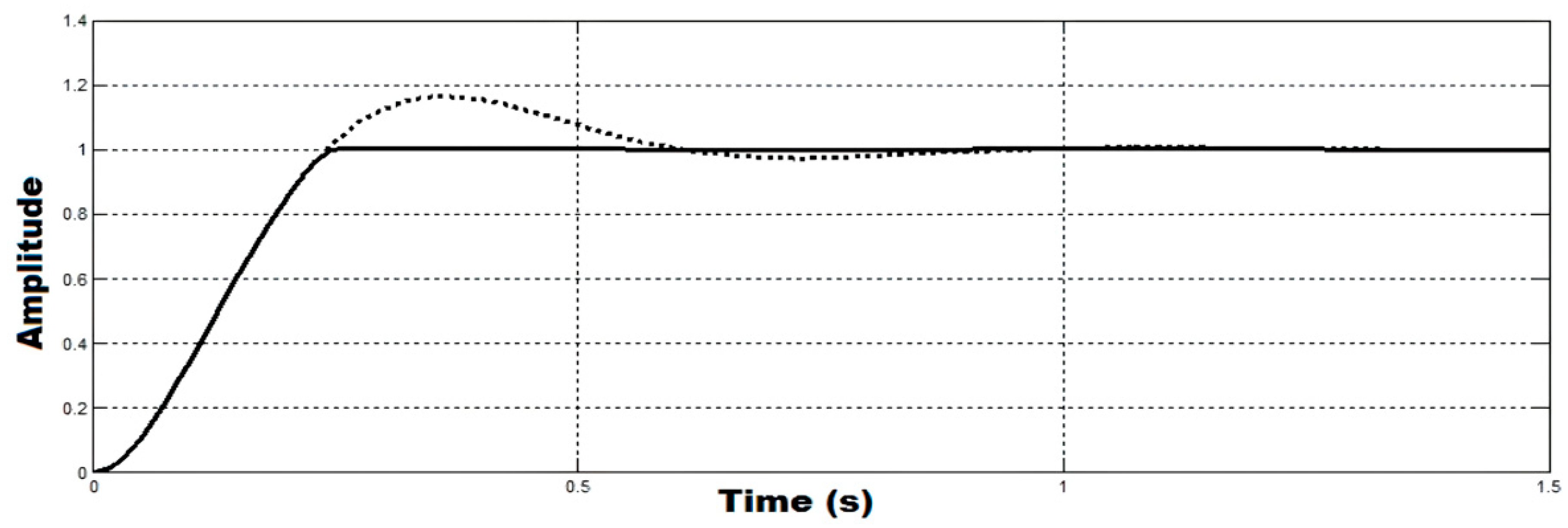
• The overshoot is lowered by 3.5;
• The actuator is less strained, lowering the possibility of saturation;
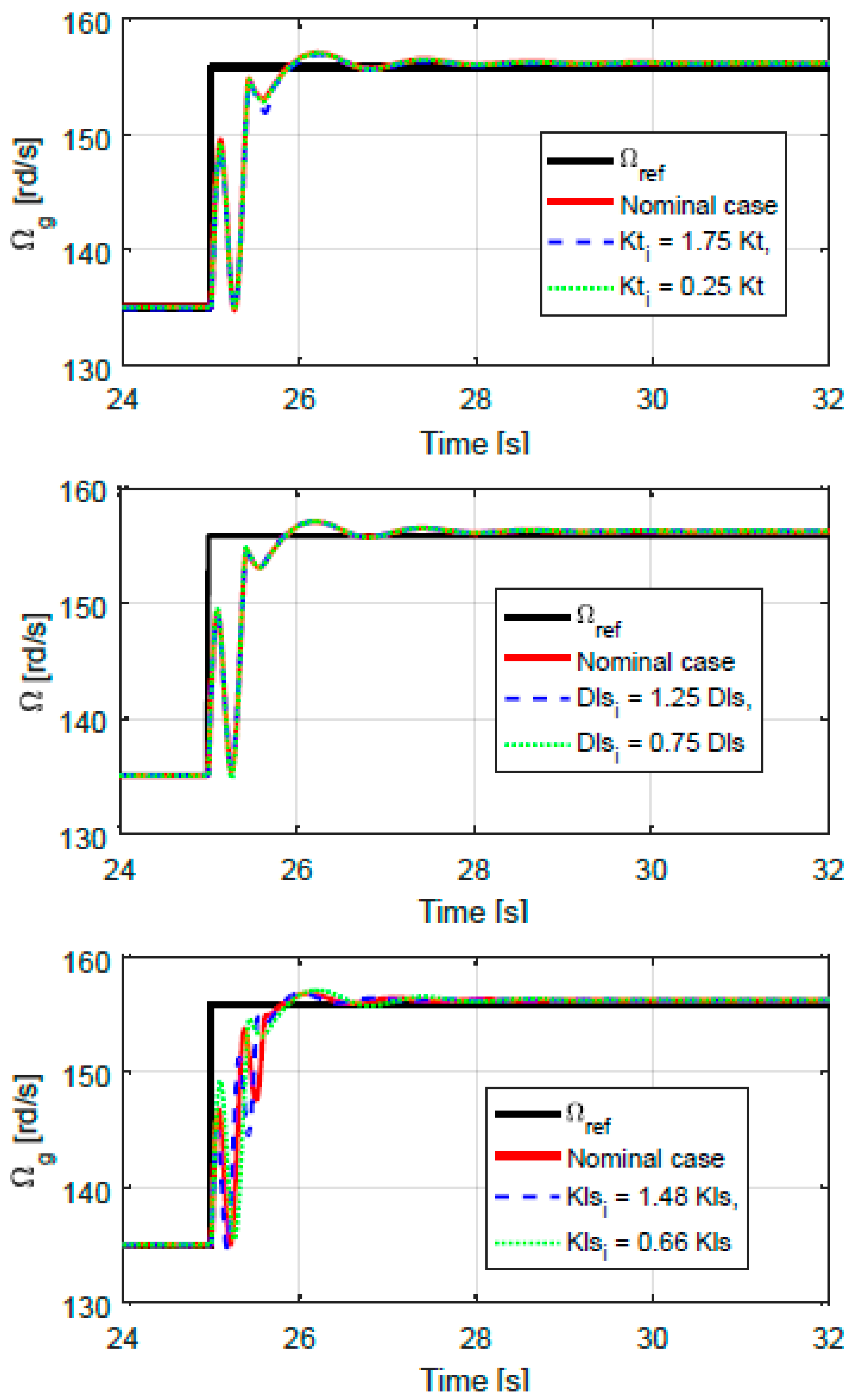
• The overshoots are quite near in all shaped situations, demonstrating its robustness.

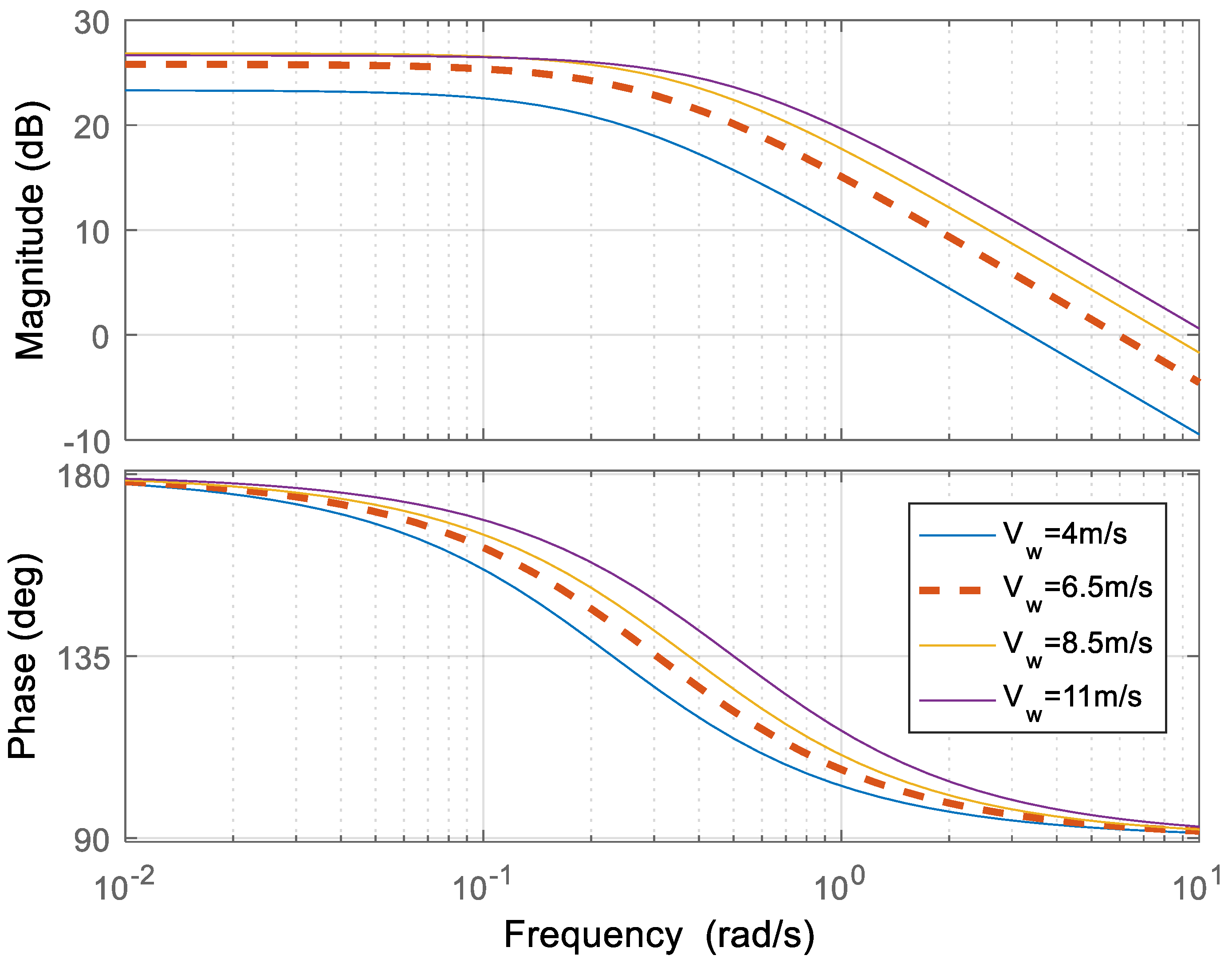
5.2. Simulation Results

The performance of the shaped and unshaped reference in zone 2 is compared in this paragraph based on simulations performed using the Simulink model of our WECS. In this test, a simulated wind of five levels (see Figure 16) fluctuating in zone 2 is injected into the nonlinear model of the WECS to compare the performance of the CRONE controller with a shaped and an unshaped reference to harsh wind fluctuations. The data are examined in terms of settling time and overshoot.

Figure 17 depicts the rotation speeds of the generator achieved using a stepwise method. The static error tends to zero with the UM-shaped reference, and the oscillations during the transient state are well-damped for all of the evaluated operating points. The settling time is equal to 1 s. On the other hand, a maximum overshoot of 20% is obtained with an unshaped reference, indicating poorer stability compared to the UM-shaped control strategy. In terms of settling time, 6.5 s is obtained without shaping the reference.

Mechanical stress is substantially higher when considering a wind gust. Therefore, maintaining a steady rotation speed with minimal rippling is critical. The sluggish shaft torque (C_ls) response indicates the shaft’s twist angle, making it a strong predictor of structural mechanical behavior. The UM-shaped velocity reference results in a superior closed-loop response, substantially reducing torsional torque variations. Torsional torque variations are reduced in Figure 18.

Given that these tests are conducted by simulation, it is highly probable that in the real-world application, the mechanical parameters of the 3 kW WECS subject to the study are not similar to the ones used in our simulation. A robustness test is conducted to evaluate the effect of the variation in the mismatched parameters (Figure 19).

From Figure 20, the robustness of the adopted control strategy is validated. Even with a 75% uncertainty in the parameter value, the speed of the generator tracks its reference properly. The electrical parameters may also change (due to temperature, operation frequency, etc.). In the following test, a decrease down to 20% in the inductance parameters (due to a high rotation speed) and an increase of 50% in the resistance value (due to high-temperature operation conditions) are evaluated. The wind speed is changed from 6.5 to 7.5 m/s (at second 25 of the simulation). It turns out that the proposed control strategy is robust to these variations. The overshoot does not surpass 1.5% in the worst case (M = 0.8 Me, L_d = 0.7L_dnom, L_q = 0.7L_qnom, R_s = 1.5R_snom, R_e = 1.5R_enom, and Φ_a = 0.8Φ_anom).

6. Conclusions

In conclusion, the simulation results underscore the robustness and efficacy of the proposed control strategy, which employs Unity Magnitude (UM)-shaped references in WECSs, particularly under challenging conditions in the MPPT zone. The comparison between shaped and unshaped references reveals substantial improvements in performance metrics such as settling time and overshoot. The UM-shaped reference demonstrates superior performance, minimizing static error and damping oscillations during transient states, resulting in a settling time of 1 s. In contrast, the unshaped reference exhibits poorer stability with a maximum overshoot of 20% and a longer settling time of 6.5 s. Moreover, the examination of mechanical aspects highlights the critical role of maintaining a steady rotation speed, especially under wind gust conditions. The UM-shaped velocity reference significantly reduces mechanical stress and torsional torque variations, showcasing a superior closed-loop response compared to the unshaped reference. Considering the robustness of the proposed strategy, a comprehensive evaluation is conducted to assess the impact of potential variations in mechanical and electrical parameters. The simulation results indicate that the control strategy remains robust, even under significant variations in parameters such as inductances and resistance values, affirming its adaptability to real-world application scenarios. This resilience is particularly evident in the context of changes in wind speed, further supporting the viability and effectiveness of the proposed UM-shaped control strategy for diverse operational conditions in WECSs.