Abstract
Many fundamental physical problems are modeled using differential equations, describing time- and space-dependent variables from conservation laws. Practical problems, such as surface morphology, particle interactions, and memory effects, reveal the limitations of traditional tools. Fractional calculus is a valuable tool for these issues, with applications ranging from membrane diffusion to electrical response of complex fluids, particularly electrolytic cells like liquid crystal cells. This paper presents the main fractional tools to formulate a diffusive model regarding time-fractional derivatives and modify the continuity equations stating the conservation laws. We explore two possible ways to introduce time-fractional derivatives to extend the continuity equations to the field of arbitrary-order derivatives. This investigation is essential, because while the mathematical description of neutral particle diffusion has been extensively covered by various authors, a comprehensive treatment of the problem for electrically charged particles remains in its early stages. For this reason, after presenting the appropriate mathematical tools based on fractional calculus, we demonstrate that generalizing the diffusion equation leads to a generalized definition of the displacement current. This modification has strong implications in defining the electrical impedance of electrolytic cells but, more importantly, in the formulation of the Maxwell equations in material systems.
1. Introduction
Physics is a science devoted to the investigation of natural phenomena. The primary objective is to gather experimental data pertinent to a phenomenon and formulate a mathematical representation. The mathematical descriptions follow from assumptions taken as fundamental laws considered obvious. Among them, conservation laws are fundamental principles in physics. They describe the preservation of certain quantities in isolated systems over time by governing a wide range of phenomena and play a crucial role in our understanding of the universe. For example, the principle of energy conservation demands that energy cannot be generated or annihilated within an isolated system; linear and angular momentum conservation states that the total momentum and the angular momentum of an isolated system remain constant if no external forces act on it; and the conservation of the number of particles or of the electric charge must be conserved in a closed volume whenever annihilation/creation phenomena are absent inside the volume itself.
In a broader sense, by noting that a specific physical quantity must be conserved, we can formulate a mathematical expression for the related conservation law by examining a closed volume through the use of continuity equations. In fact, continuity equations play a fundamental role in several science and engineering contexts, describing the conservation of several quantities like particles, charges, or others within a system. These equations provide valuable insights into the behavior of fluids, electrical currents, and other physical phenomena. At its core, a continuity equation states the rate of change of a quantity within a given volume that must be equal to the net flow of the same quantity into or out of the volume. In fact, if the considered system can exchange a physical quantity with the external world, the rapidity of using the quantity contained in it has to be identical to the rapidity by means of which the same quantity is leaving the bulk across its limiting surface. This is the classical continuity equation in its integral form. Of course, to write it as a mathematical expression, we need to define the concept of rapidity of time variation of the given quantity . A rather simple definition is to consider its time derivative , which is a local-in-time property. In a more general fashion, the local expression of a continuity equation reads
where represents the density of the physical quantity , according to
while
the current density of particles.
In electromagnetism theory, continuity equations are crucial in describing the behavior of electrical currents. For instance, in the case of steady-state direct current (DC) circuits, the continuity equation states that the net flow of charge into or out of a closed system must be zero. This equation ensures that charge is conserved within the circuit, forming the basis for comprehending the operation of electrical devices. It is in this context that in 1860, James Clerk Maxwell, by noticing that Ampère law alone is insufficient to explain certain phenomena, particularly those involving time-varying electric fields, introduced the displacement current as an additional term charge particle current, given by
where is the electric permittivity and the local electric field.
The introduction of the displacement current in the framework of electromagnetism represents one of the most fundamental examples in physics in which the continuity equation played a fundamental role in the comprehension of the underlying physical law, and it was vital in the formulation of Maxwell’s equations, being a cornerstone in the development of the theory.
Often, continuity equations are strictly related to the famous Noether theorem, formulated in 1915, which plays an impressive role as a fundamental result in theoretical physics. It reveals a profound link between the symmetries inherent in a physical system and the conserved quantities that arise from the associated continuity equation. In fact, this theorem shows that if the dynamical evolution of a physical system can be obtained through the principle of minimal action, a variational problem involving the time-integral of the Lagrangian system, then there is a conserved quantity corresponding to each continuous symmetry of the action. Consequently, a corresponding continuity equation can be established. The power of the Noether theorem lies in its generality. It applies to a wide range of symmetries, including time symmetry as well as the translational and rotational symmetries that, according to this theorem, are at the base of the existence of the continuity equation for energy, linear, and angular momentum.
In this sense, the Noether theorem has profoundly impacted the development of modern physics, where symmetries and conservation laws are central concepts. In particular, it has become a powerful tool for understanding the hidden laws of nature, including the gauge symmetries, whose first example in physics arises exactly in the framework of the electromagnetic theory, these symmetries being the heart of local conservation of the electric charge.
However, there are several anomalous phenomena for which the rapidity of variation of a given quantity at time t depends on the previous story, i.e., these phenomena have a memory of the past and a nonlocal spatial dependence. In this case, identifying the rapidity of variation of a physical quantity using may not adequately describe the phenomenon under investigation. This is the case in many phenomena observed in complex fluids, predominantly liquid crystal materials. Because of molecular anisometry, these materials form anisotropic mesophases that present long-range orientational order and, in some cases, positional order. Furthermore, they are highly responsive to many stimuli, including applied field, confinement (and geometry), and several others. Therefore, it is not uncommon for reports of anomalous behavior of some sort to be received in liquid crystals. For example, anomalous diffusion [1,2] and transport in liquid crystals [3], anomalous variation of elastic constants near interfaces [4], anomalous behavior of ferroelectric pitch upon a change in dopant concentration [5], anomalous phase behavior [6], anomalous relaxation time [7], and many others. Hence, liquid crystals are one of several examples of complex fluids in which physical quantities do not obey a simple behavior. For this reason, a few generalizations of the derivative have been proposed from the beginning of differential calculus, which has become a powerful tool to investigate such anomalous behavior in recent decades. Among the several mathematical generalizations proposed, the one based on fractional calculus has caught the interest of several people working in this field. Indeed, the foundation of fractional calculus lies in the concept of fractional operators, which accommodates various non-equivalent definitions. Among these, well-established expressions of fractional operators include Riemann–Liouville [8,9], Caputo [10], Caputo–Fabrizio [11], Riesz [12], Grünwald–Letnikov [13,14], Weil [15], Hadamard [16], Marchaud [17], and others [18].
Fractional calculus can be seen as an extension of standard differentiation and integration to noninteger orders [19]. The inquiry regarding the potential significance of a derivative of any order was posed by Guillaume François Antoine, Marquis de L’Hôpital, in a letter sent to Gottfried Wilhelm Leibniz, who gave a positive and correct answer to the instigating question. Since then fractional calculus has been the object of analysis by great mathematicians, including Jean-Baptiste Joseph Fourier, Georg Friedrich Bernhard Riemann, Pierre Simon Laplace, Leonhard Euler, Paul Mathieu Hermann Laurent, Niels Henrik Abel, Joseph Liouville, Nikolay Yakovlevich Sonin, and Aleksey Vasilievich Letnikov, among many others [9,20,21,22,23,24,25,26,27,28,29]. A derivative of arbitrary order was first referenced in 1819 by Sylvestre François Lacroix (1765–1843), who provided an explicit formula for a fractional derivative [20]. These fractional-order operators are formulated through integrals, making the fractional derivative reliant on the system’s past behavior, thereby enabling the description of memory effects. In a sense, it captures the function’s behavior over a fractional number of steps, allowing for a more nuanced understanding of complex systems.
One of the crucial applications of fractional calculus is the study of anomalous diffusion processes. In classical diffusion, particles follow a random walk described by the standard second-order differential equation. Nevertheless, diffusion manifests non-Gaussian characteristics and non-Markovian dynamics in numerous empirical contexts. Hence, fractional calculus provides a mathematical framework for modeling and analyzing these processes. Fractional calculus also finds applications in signal processing, where signals with fractional derivatives, known as fractional signals, have been shown to be helpful in analyzing and processing nonstationary and nonlinear responses. Fractional calculus can be used to characterize the scaling properties and long-term memory of signals, such as the electrical impedance of an electrical device, providing valuable tools for time-series analysis and filtering.
Over recent decades, fractional calculus has found applications in variational problems within physics and engineering. As demonstrated in [30] (and further discussed in [31]), the fractional Euler–Lagrange equations were formulated by employing the principle of minimal action on a Lagrangian functional that incorporates the field and its fractional derivatives. Remarkably, the resulting equations bear striking similarities to those obtained from ordinary variational problems involving integer-order derivatives. Consequently, it has been natural to explore the generalization of Noether theorem within the framework of fractional calculus [32]. In this way, new conserved quantities associated with specific symmetries of the system and related to corresponding fractional continuity equations may be obtained, mirroring the remarkable result obtained within the realm of standard calculus. We aim to provide a general framework for analyzing systems where anomalous behavior may occur, which is the case in many complex fluids. Liquid crystals, for example, are especially prone to present anomalous behavior. However, it is surprising how only a few works employ fractional calculus to study liquid crystal materials. Hence, here we provide a general toolkit for this purpose, which may be extended as necessary and, being very general, always applicable, recovering the usual parameters (without fractional derivatives) if the system does not present anomalous behaviors.
This paper seeks to acquaint the nonspecialist reader with the topic of fractional calculus and to demonstrate several applications to physical problems involving time-fractional derivatives, especially in relation to anomalous diffusion and adsorption phenomena in an electrolytic cell, with a special emphasis on complex fluids like liquid crystals. Of course, spatial fractional derivatives could also be of some importance. In this respect, several papers are devoted to generalizing vectorial differential calculus concerning Stokes, Gauss, and Green formulae, and to the fractional form of Maxwell equations (see, for instance, [33]). Our analysis mainly focuses on diffusion or adsorption problems involving just fractional time derivatives, and we propose a generalization of their phenomenological description.
The structure of our manuscript is delineated as follows. In Section 2, we provide a comprehensive review of fractional calculus, with a primary focus on the Riemann–Liouville and Caputo methodologies. In Section 3, we revisit briefly its application to the study of anomalous diffusion and its possible solution within the fractional calculus formalism. Section 4 presents the diffusion and adsorption phenomena in the fractional kinetic approach by discussing the case of an electrolytic cell with adsorbing electrodes. The model is then detailed in Section 5, where the fractional Poisson–Nernst–Planck model is proposed, including our new proposal for the fractional displacement current, and the impedance response is analyzed for the anomalous system proposed. Section 6 contains our concluding comments.
2. Elements of Fractional Calculus
Nowadays, the Riemann–Liouville operator is a well-established fractional derivative, although it is the result of several contributions (mainly by Liouville), which is defined as
for , where is the gamma function [34], c is the left-hand point and t is the terminal point, and is the order of the derivative. We notice that n is the smallest integer greater than , with being the usual derivative of . In Equation (5), we utilize a notation pioneered by the mathematician Harold Thayer Davis (1892–1974) [35], which is particularly useful for making the left subscript c explicit. This subscript is not immediately apparent in a derivative and has led to extensive discussions on the complementary function [24]. We consider simple cases to illustrate the fractional time derivative for and . One of them is the function which yields
Figure 1 shows vs. t for for several values of and .
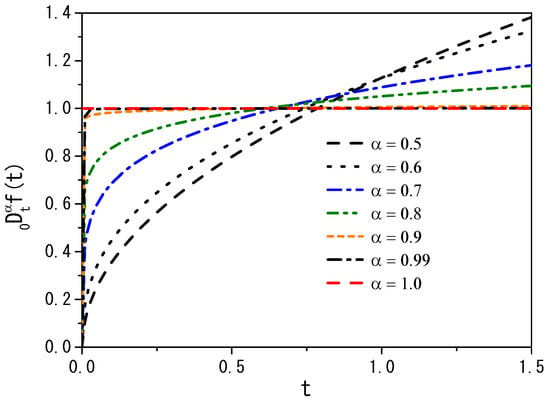
For the exponential function, i.e., , we have
where is the generalized Mittag–Leffler function [19]. Another function is . In this case, the fractional time derivative gives
It is worth mentioning the if in Equation (8), we have that .
One can reinterpret the Riemann–Liouville fractional derivative by using the concept of an integral of arbitrary order, as detailed in the subsequent method [19]. The Riemann–Liouville integral of arbitrary order may be defined from the Cauchy integral formula:
In Equation (9), the parameter is allowed to be complex provided that its real part is strictly positive, i.e., . For the sake of simplicity, let us temporarily assume that . The definition provided in Equation (9) exhibits the following properties:
Now, let us define the fractional derivative as
But this identification inspired by the usual calculus has some problems. A problem arises because the gamma function is undefined for zero or negative integer values. Therefore, we should proceed with caution when using this approach. It is important to remember that for , we are permitted to write
In other words, applying the derivative operator n times to a function after integrating it n times results in the identity operator. Similarly, we anticipate discovering a fractional derivative operator such that
that is, according to the Riemann–Liouville framework, as indicated by Equation (11), the operator denotes the fractional derivative of order , acting as the left-inverse of the Riemann–Liouville integral of order , analogous to the relationship between the standard derivative and its integral.
where is the identity operator.
One possible operator to accomplish this task could be constructed as
where represents the ceiling function, which determines the smallest integer that is not less than (i.e., the subsequent integer must be considered). Some illustrative examples are as follows:
Thus, the Riemann–Liouville fractional derivative [29] can be more rigorously defined as
that coincides with the operator (5) with the assumption .
Now, it should be clear that for , such that when , the following holds:
In fact, by using this last relation and (10), we have
Therefore, we can rewrite relation (17) in
that coincides with (5) and establishes the arbitrary-order Riemann–Liouville derivative operator.
If not differently specified, let us assume from now on the left subscript and denote, for the sake of simplicity, the corresponding operator in , that is, [risp. ].
By recalling the Laplace transform definition of a function
applied to the Riemann–Liouville fractional derivative of gives
Furthermore, represents the Riemann–Liouville integral operator of order . It is well-known that the Laplace transform of the n-th derivative of a function , for , is expressed as
where denotes the n-th derivative of .
Then, from Equation (21) and using Equation (17), we obtain the Laplace transform of the Riemann–Liouville fractional derivative of :
An important remark is in order here if we want to apply this formalism to solve initial and boundary-value problems in mathematical physics. We observe that the initial conditions will be expressed using fractional derivatives, specifically,
This is not a usual way to establish initial conditions and, in some sense, may be an additional problem in practical applications of this powerful formalism.
In 1967, Caputo presented a novel idea for a fractional derivative. This idea is linked to the fractional Riemann–Liouville integral and differential operators. It is now referred to as the Caputo fractional derivative [10]. In terms of this operator, the initial conditions can be formulated in the usual way, i.e., by stating them in terms of integer-order operators. The Caputo operator is defined as
allowing us to view it as equivalent to the Riemann–Liouville integral of the derivative of the function . Observe that, similar to how the Riemann–Liouville derivative operator is defined in Equation (17), the fractional derivative of order in the Caputo sense can be defined as
where, with respect to Equation (17), the roles of operators and have been interchanged. This relation clarifies the difference between the Riemann–Liouville and the Caputo derivative operators [36] and, in a very direct way, gives the definition above:
which matches (25) and characterizes the Caputo derivative operator of any order. For noninteger orders, fractional derivatives generally differ because usual derivatives of order k do not commute with integral fractional operators. The Caputo differential operator uses regular conditions on compared to the Riemann–Liouville differential operator. According to the Cauchy integral formula, we can express
Thus, as already stated [Cfr. Equation (14)], we expect that if is the left derivative, then
Nevertheless, if and its first derivatives do not vanish at , generally, we obtain
In fact, consider now
By performing integration by parts, we have that
Alternatively, it can be demonstrated that the Caputo operator satisfies
Thus, a relationship between the previous differential operators can be expressed as follows [37]:
which, when , i.e., , yields
Based on the equation above, we can infer that these operators are equivalent when .
The paramount advantage of employing the Caputo approach lies in its initial conditions for fractional differential equations. Unlike other methods, the Caputo derivative ensures that these initial conditions mirror those of integer-order differential equations. This means they encapsulate the limit values of integer-order derivatives of the unknown functions precisely when , namely:
meaning conditions (initial or boundary) can be represented as integer-order derivatives. This idea becomes more understandable when we look at the Laplace transform of the Caputo operator:
Upon deriving the Laplace transform of the convolution and noting that , one can determine the Caputo derivative of order in the Laplace domain as follows:
Notice that the initial condition is expressed using the integer derivatives.
For physical applications, it is useful to put in the Riemann–Liouville derivative; then, we obtain that
In this scenario, both definitions coincide if and its derivatives exhibit appropriate behavior as , meaning for , where . This property is important from a physical perspective because it allows for the consideration of stationary processes. For example, it can be applicable to fractional-order dynamical systems with periodic signals, which is necessary for impedance problems [38], wave propagation in continuous media, and other similar scenarios.
One way to generalize these operators is by introducing the distributed-order fractional operator [39]. This operator is essentially a linear combination of fractional operators with various arbitrary orders. A simple example is obtained if we consider the Caputo operator in the following way:
for and . Some special regularity and boundary behavior conditions are required for the weight function , also called order density [39]. For instance, when , the operator (40) reduces to
As we discuss in Section 3, this formalism is shown to be very useful in handling diffusion problems involving time-fractional derivatives.
3. Fractional Diffusion Equations
Fractional diffusion equations can be derived, for instance, from continuous-time random walk (CTRW) formalisms by appropriately selecting the waiting-time and jump probability distributions [40,41] and from the master Equation [42] or comb models [43]; they can also be expressed using time-fractional derivatives of distributed order [44]. In this latter case, the main novelty is the presence of different diffusion regimes in the theoretical approach [45]. To investigate the capabilities of fractional calculus in modeling the diffusion process, we revisit, for demonstration purposes, the task of finding the fundamental solution to the Cauchy problem for a time- and space-fractional diffusion equation, closely following the methodology of Mainardi et al. [46]. The fractional diffusion equation is
for . To comprehend the fractional indices, we can employ the continuous-time random walk method to link these indices with the waiting-time and jumping distributions. For simplicity, we limit our discussion to the diffusive scenario, where , to explain the significance of and . When , we need to use the approach presented in Refs. [47,48]. In the first case, the process is governed by the probability density function from which it is possible to obtain the waiting-time distribution and the jumping distributions, respectively, as follows:
By using , the distribution related to the diffusion process is found by combining the equations
and
where denotes the survival probability at the initial location. By applying the Fourier–Laplace transforms ( = and ), it is feasible to derive
By considering and with a long-tailed behavior, i.e., in the limit of and , we have
with , we obtain
with a direct connection with Equation (42) for and . This feature implies that the fractional derivative in time and space appear connected with the behavior of the particles in the bulk, i.e., the waiting-time and jumping distributions, which determine the system’s behavior. Notice that Equation (46) is formally equivalent to the generalized master equation:
with
Let us assume to work out the fractional diffusion in space and time with
where is a specified function. In Equation (42), the fractional operator with respect to the spatial variable is known as the Riesz–Feller operator [40], which is defined here such that its Fourier transform is straightforward:
where represents the Fourier transform of . For , the initial condition on the first derivative must also be taken into account:
The form of the solution to Equation (42) will be
where represents the Green’s function of the given problem, meaning it solves Equation (42) when . By utilizing the Fourier transform on the Riesz–Feller operator and the Laplace transform on the Caputo time-fractional derivative, Equation (42) can be reformulated as
where
represents the Green’s function of the problem in the Fourier–Laplace domain, i.e., = and . We need to invert both transforms to find the desired solution . This is not straightforward, but it can be achieved using the Mellin transform along with some scaling properties of the Fourier and Laplace transforms (refer to refs. [19,46] for more details). The fundamental solution of the problem, specifically for , is given by
where the function is the Fourier transform of the Mittag–Leffler function:
Notably, an important result can be derived without the exact form of . By setting , we can construct the quantity
where
Based on Equation (59), with the assumption that if exists, it can be generally inferred that subdiffusion occurs when because ; superdiffusion occurs when , i.e., ; and normal diffusion occurs when , i.e., . A similar analysis for a broad range of diffusion-like equations can be found in ref. [49].
In what follows, we consider some particular cases. For , , the solution becomes
where is the Lévy distribution given in
For and , the solution is
i.e., it is expressed in terms of the -Wright function, , often called the Mainardi function, which is significant in the analysis of stochastic processes [50].
Furthermore, for and , it yields the classical diffusion equation, and the solution to the Cauchy problem is given by
which is the expected result for normal diffusion.
In the broader context, it is necessary to address the space-time fractional diffusion equation formulated as [46,51,52]
with the real parameters constrained by the following conditions:
Here, denotes the most general Riesz–Feller fractional derivative such that for , it reduces to the case discussed in Equation (42). The Green’s function can be represented using the -function of Fox, beginning with its general Mellin–Barnes integral form for [51]:
Table 1 shows some cases of the aforementioned solution.

Table 1.
This table shows representative results for some choice of the fractional parameters. Note that depending on the relation between each parameter, we may have different diffusion regimes.
An approach similar to the one outlined above can be modified to address time-fractional diffusion equations of distributed order. Here, the fundamental solution can be represented as an integral involving a Mellin–Barnes integral representation with two parameters that are functionals of the order density, (refer to ref. [46] for more details). In the following sections, we apply the formalism presented above to two general challenging physical problems, dealing with adsorption phenomena and impedance spectroscopy response of materials to the external fields.
4. Diffusion and Adsorption Phenomena
Particles diffusing in confined spaces can undergo adsorption (desorption) onto solid substrates. The kinetics of this process are crucial for a range of problems from fundamental science to industrial separation processes [53,54,55,56,57,58,59]. The most straightforward method to model adsorption–desorption phenomena is the Langmuir adsorption model [60], commonly known as Langmuir kinetics [61,62]. Regarding particles in the bulk, their diffusion process is typically described by Fick’s law [63], as adsorption–desorption is expected to happen in practical scenarios involving transport [64,65]. The adsorption behavior at this boundary is governed by a phenomenological kinetic equation that includes appropriate adsorption–desorption rates [66].
Adsorption–desorption phenomena are particularly important when dealing with complex fluids. Because liquids generally need some sort of confinement, the solid substrate often plays an important role because of adsorption. This process may be due to the adsorption of molecules in the fluid itself, of added dopants, or of any impurities from molecular dissociation or the synthesis process, since removing all impurities in a liquid sample is almost impossible [67]. For example, polymers in solution are often adsorbed by confining solid surfaces, having tremendous consequences that are important in pharmaceutical applications [57], biophysics [58], and nanocomposite materials [68]. Liquid crystals, known for their high sensitivity to surface modifications, have demonstrated significant effects due to adsorption phenomena. These include alterations in anchoring energy [55], surface transitions triggered by light-controlled adsorbed dyes [69], and degradation of display performance linked to ion adsorption [56]. In fact, liquid crystals, one of the best representative materials of complex fluids, are mainly applied in electro-optical devices such as displays. In most devices, the liquid crystal material is in direct contact with an electrode (which may be coated with an alignment layer), and thus, the confining walls present adsorption–desorption phenomena. As will be discussed later, the dielectric response of many liquid crystal cells requires the use of constant phase elements (CPEs) when the data are analyzed by equivalent circuits, and the need for CPEs is directly related to interfacial heterogeneity [70], which in turn may be associated with the fractal nature of the electrodes. We thus now describe how fractional calculus can be introduced to formulate anomalous processes in the adsorption–desorption process, aiming to model the phenomena in heterogeneous interfaces with complex fluid materials.
4.1. Fractional Kinetic Equation
Within the Langmuir framework for adsorption–desorption processes occurring at the boundary between two distinct media (consider, for instance, an isotropic fluid with suspended particles interacting with a solid surface), the kinetic equation states that time variation in the density of adsorbed particles, , is influenced by the bulk density of particles in the vicinity of the surface, . Additionally, it is affected by the surface density of particles already adsorbed. We can thus use the following straightforward equation:
where denotes the adsorption rate constant and signifies the characteristic desorption time, both of which are phenomenological parameters.
The solution of Equation (68) in the Laplace domain is given by
where and , assuming . Equation (69) provides the density of adsorbed particles. The time-domain solution can be found via the inverse Laplace transform of Equation (69) or by directly integrating Equation (68).
By performing integration by parts, Equation (70) can be reformulated as
highlighting that two terms contribute to the effective density of particles near the surface. The first term represents particle adsorption in the first surface layer; the second term describes desorption with exponential relaxation times. Note that the second term is essentially the Caputo–Fabrizio fractional time derivative [71], which has a nonsingular kernel.
An alternative method to tackle the intricacy of these relaxation phenomena, which considers potential frequency-dependent changes in effective adsorption parameters, involves extending the kinetic equation through fractional calculus [66]. This approach assumes the adsorption–desorption process is governed by a generalized kinetic equation formulated using a fractional derivative of order , as outlined below:
where represents an intrinsic timescale associated with internal dynamics. In the case where , Equation (72) clearly simplifies to Equation (68).
As mentioned in Section 3, the generalized kinetic equation (Equation (72)) can be solved using either the Fox -function or the two-parameter Mittag–Leffler function [72,73]. For demonstration purposes, we rewrite Equation (72) with as follows:
It is noted that Saxena et al. [72,73] examine an alternative fractional integral kinetic equation of order :
with , , and being an integrable function over the interval , where . In Equation (74), the Riemann–Liouville fractional integral of order u is specified as in Equation (9), specifically,
Equation (74) has as solution:
specifically, it is expressed using the H-function of Fox [19]. For the scenario we are examining, . Consequently, the integral
remains finite if the initial conditions ensure that . Consequently, the solution to the fractional differential kinetic Equation (72) can be derived from Equation (76), specifically
Moreover, this specific Fox H-function can be related to the two- or three-parameter Mittag–Leffler function, thereby providing a formal solution to the problem. It is important to mention that other different fractional operators may be used to extend the kinetic equation (or diffusion equation), such as the ones characterized by nonsingular kernels [74], implying different relaxation processes. One of them is the Atangana–Baleanu fractional operator given by
where is a normalization constant. Equation (72) can be written, in terms of the Atangana–Baleanu fractional time operator, as follows:
The solution to this equation can be determined and is expressed as
with , , and . It is worth mentioning that the relaxation process present in Equation (81) is different from the previous one as a consequence of the kernel expressed in terms of a Mittag–Leffler function. Figure 2 illustrates the adsorption process for the different kinetic equations considered above. It shows that the differential operator is important in the relaxation process.
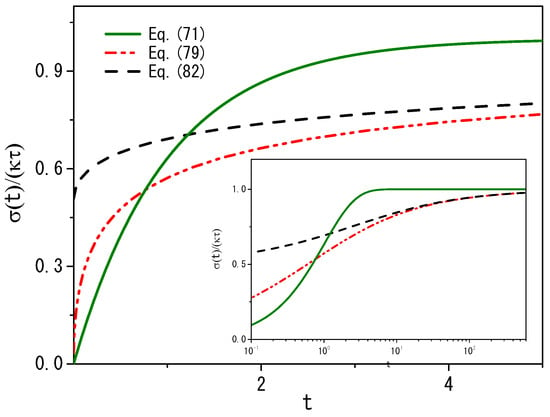
Figure 2.
Behavior predicted by kinetic equations for when different differential operators are considered for . The standard case corresponds to the green line. We consider, for simplicity, , , and .
Thus, we observe that different fractional operators can extend the standard approach and be powerful tools for capturing experimental behavior when the standard formalism is unsuitable. In the next sections, we consider the Riemann–Liouville and Caputo fractional operators, which can capture the experimental behavior of the scenarios discussed here.
4.2. The Poisson–Nernst–Planck Model
We provide a concise review of the main equations of the Poisson–Nernst–Planck (PNP) model in three dimensions as a preliminary step towards exploring its fractional extension [75]. We examine a system consisting of neutral particles that can, through dissociation, become positive and negative charges with varying mobilities [76,77]. When an external electric field is applied, these charges move, leading to currents of neutral, positive, and negative charges within the sample. In three dimensions, the bulk density of these particles will be denoted by , , and and, likewise, the current density as , , and . The following continuity equations may assure the conservation of particles:
where is connected to the processes (dissociation and recombination) in bulk. For total dissociation, neutral particle terms vanish. The Poisson equation completes the PNP model.
where denotes the dielectric permittivity of the ion-free insulating medium, assumed to be nondispersive over the relevant frequency spectrum. This equation connects the bulk densities of positive and negative ions, with an absolute charge of q, to the resulting electric field distribution within the sample.
The total electric current is composed of the conduction and the displacement currents as follows:
If we now combine the last two formulae of Equation (82) with Equation (84), we obtain
and accounting for the Poisson Equation (83), we conclude that . Thus, the model requires that the total current has to be solenoidal, i.e.,
In a one-dimensional scenario, the current density J does not vary with position. This requirement is essential for the concept of electrical impedance, which is the ratio of the voltage difference to the overall current, to be valid [78].
4.3. Bulk Diffusion and Surface Adsorption
Before moving on to the fractional generalization of the PNP model discussed here, let us consider the question of determining the equilibrium distribution of charges and neutral particles in an insulating medium containing ionic impurities that are diffusing in a bulk in contact with adsorbing surfaces. We consider a system confined within a slab of thickness d, with adsorbing surfaces (which are electrodes) located at . Here, x is the coordinate perpendicular to the surfaces in a Cartesian reference frame, making the mathematical problem one-dimensional. The system consists of neutral and charged particles, and the generation–recombination process is taken into account. The goal is to incorporate a general kinetic equation similar to Equation (68), which includes a time-fractional derivative and a memory kernel for the adsorption–desorption phenomena [79].
Thus, we rewrite the continuity Equation (82) as
in which the bulk current densities of particles are given by
and the source term reads
In Equations (87) and (88), is the electrical potential profile across the sample, is the thermal energy, and , , and are the diffusion coefficients for positive, negative, and neutral particles, respectively. In addition, the coefficients and are the constants of association and dissociation, respectively, for a first-order chemical reaction assumed in the bulk.
The next step to construct the continuous PNP model is to impose the Poisson equation relating the net bulk density of charge to the actual electric potential, which may be written as
The equations of the model are thus Equations (90) and (91), which have to be solved for chosen boundary conditions. To proceed, we assume that the limiting surfaces are blocking for neutral particles, i.e.,
and adsorbing for charged particles:
Finally, the electric potential has to be such that, at the boundaries,
where is the amplitude of the potential applied to the system by means of an external power supply. The mathematical problem is thus well posed in the sense that the number of coupled equations to be solved are the four partial differential Equations (90) and (91), necessitating eight integration constants, which are to be found using the eight boundary conditions given by Equations (92)–(94).
Before proceeding, let us focus our attention, for a moment, on a possible meaning of Equation (93). In the present approach, we assume that these equations are stated for the first and last bulk layers of an insulating liquid sample containing ions. They are stated for the last bulk layer of the sample at , i.e., on the left of the right surface (placed at ), and are also stated on the first layer of the bulk of the sample at , i.e., on the right of the left surface (placed at ). These are the bulk positions at which the rates of change in the density of charges in the surface layer (first and last) are represented by and are equal to the bulk density of current arriving at the same layers of the liquid sample.
When solid surfaces (electrodes or solid phase) are put in contact with the liquid sample (liquid phase) at these points, we have in practice a contact between two different systems, forming a liquid–solid interface. Eventually, due to electrochemical forces, the charged particles present in the bulk can be adsorbed and, after a while, desorbed by the solid surfaces. This usually happens because the liquid phase delivers charges to the solid phase at a certain rate, which combines the particles arriving from the bulk, as a result of the diffusion process, and the particles coming back to that position, as a result of the desorption process occurring at the surface. This process yields a net density ( and −) of charges per unit surface which become again available to the solid surface. Once these charges are supplied again to the solid surface, usually they are assumed to undergo a dynamical adsorption–desorption process governed by an equation of the type of Equation (68).
Here, to implement a possible extension of the Langmuir approximation to the field of fractional calculus, we assume that the adsorption–desorption phenomenon occurring for charged particles, which have been delivered to the surface by the bulk and received back from the surface, is governed by the following general kinetic equation:
To generalize further the approach, a memory kernel has been inserted in the desorption term to account in a phenomenological way for the presence of roughness on the surface and its effect on the process. The roughness on the surface (electrodes in the case of impedance spectroscopy focused here) plays an important role in determining the anomalous character of the impedance [80]. Indeed, this effect may lead to a nonusual, i.e., non-Debye, relaxation and, consistently, to an anomalous diffusion behavior.
From the perspective we adopt here, we solve Equations (90) and (91) to obtain , , and . Then, we use to obtain to be inserted into Equation (95), accordingly. Once this is performed, Equation (95) is solved to obtain the profiles of . Finally, we impose the boundary conditions, Equation (93), together with the other ones, Equations (92) and (95), to fix the values of the integration constants. At this point, the problem is again formally solved, and an analysis of the electrical response of the material to an external difference of potential, in the presence of the adsorption–desorption phenomenon, can be carried out.
Proceeding in this way is equivalent to assuming that the sources (the reservoir) of the charged particles, which are supplied to the surface, are represented by the densities , which are bulk quantities (liquid phase), if only adsorption is concerned. However, when desorption from the surface is also invoked, a net density of charged particles is present in the last (or the first) layer of the bulk. These net quantities are in turn supplied to the surface (solid phase) at the rate , and once they are adsorbed on the surface, these charged particles will be subjected to the dynamics imposed by that specific surface on the particles, which is now governed by Equation (95). Thus, imposing the boundary conditions Equation (93) is a way to put the liquid phase (the bulk) and solid phase (the surface) in physical contact. The charged particles of the system will follow dynamical processes that are different when they are in the bulk (drift diffusion) or when they are on the surface (fractional adsorption kinetics in the present case). In this way as well, the extension of the kinetic equation to the fractional calculus does not require any change in the continuity equations that guarantee the conservation of the number of charges in the whole system. The details of a partial analysis of this complex phenomenon in the linear approximation, i.e., in the small AC voltage limit, can be found in Ref. [79].
5. Fractional Extensions of the PNP Model and Electrical Impedance
Let us briefly revisit a recent discussion on two distinct methods for extending the PNP model into the realm of fractional calculus by altering the time derivative. These methods will be examined within the CTRW framework, which affects the probability density function, . In the context of time-fractional diffusion equations, the waiting-time distributions show long-tailed properties characterized by power-law behavior (see refs. [38,40,81] for a detailed discussion). These diffusion equations are generally represented as follows:
or
where
where represents an external field influencing the system. We emphasize that Equations (96) and (97) are identical for the range . Equations (96) and (97) propose two alternative methods for modifying the conventional PNP model to include time-fractional derivatives.
According to ref. [75], in the initial scenario, the continuity equation remains intact, with the time-fractional operators applied solely to the conduction current term. In the subsequent scenario, the continuity equation is modified, altering the current density, with the time-fractional derivative applied exclusively to the displacement current term. As we show below, in the latter case, the implications of this extension are severe because one has to consider also changing the Maxwell equations. Now, we consider for both cases to study the system’s response to the periodic applied potential, as required by impedance spectroscopy experiments.
5.1. The Conduction Current
We turn our attention to the initial scenario, focusing on the alteration of the PNP model. First, it is necessary to incorporate the Riemann–Liouville fractional time derivative into the particle density. This requires considering , indicating that the continuity equations of the PNP model can be
where is the intrinsic time of the problem. Combining Equations (99) and (83) of the extended model, as performed previously for the usual case, we conclude that , with
This extension of the PNP model with fractional derivatives alters the total current. With the Riemann–Liouville derivative of arbitrary order, the conduction current is expressed, as introduced in Equation (84), along with a parameter related to intrinsic relaxation time. In practice, we have to promote the replacement:
The term for the displacement current keeps its original definition, which is represented as a first-order partial derivative with respect to the time of the electric field. This is a crucial point because no modifications in the Maxwell equations are required, while Fick’s law should now be replaced with another version of the gradient of the particles in which the fractional operator is present.
5.2. The Displacement Current
We explore an alternative methodology for extending the approach to fractional calculus by scrutinizing an extension of the PNP model through the formulation of the continuity equation with the Caputo fractional time derivative. To achieve this, it is imperative to consider the following foundational equations:
The temporal derivative in Equation (82) is substituted with the Caputo fractional time derivative. An analogous modification employing the Riemann–Liouville fractional operator was suggested in [82]. This modification was applied in the diffusion-like equation to investigate the stationary state within the linear response regime to an external stimulus. By merging the new set of fundamental equations of the extended model, Equations (102) and (83), using the previously employed method, one can deduce that , where
This suggests that incorporating fractional derivatives into the PNP model requires an updated formula for the total current density, in which the displacement current is redefined using a derivative of arbitrary order, namely:
In this case, the conduction current keeps its usual definition. The suggested expression for the modified displacement current, Equation (104), aligns with the form recently utilized in certain generalizations of Maxwell’s equations [83,84] for material media that incorporate fractional-order operators. To avoid this work going down the road that involves analyzing problems related to the covariance of Maxwell’s equations, from now on, we restrict ourselves to analyzing the extensions of the PNP model to the fractional field that implies a change in the conduction current. As we will now show, the problem can also be formulated in more general terms using the distributed-order derivative operator. Undoubtedly, it is possible to show that the new model, which we call PNPA—PNP anomalous model—is a very useful tool for analyzing a wide class of experimental impedance data in complex systems and fluids.
5.3. PNPA: The Time-Fractional Derivative of Distributed Order
Let us generalize the PNP model by considering Equation (99) with a time-fractional derivative of distributed order [39,44], namely,
where represents a distribution of , satisfying , rather than employing a solitary fractional operator . In this context, we find that
and, consequently, , with
Equation (107), which is now more general than Equation (100), shows that this extension of the PNP model implies a modification of the conduction current in terms of the time-fractional distributed order derivative, while the displacement current remains unchanged. Alternative modifications of the current density may produce various operators for the conduction current term [85,86]. Furthermore, the continuity equation can also be expanded in conjunction with the current density as shown:
and, consequently, , with
This is a significant accomplishment of the PNPA model, as incorporating the distributed-order operator might allow for the consideration of various diffusion regimes within the theoretical framework. This aspect of the issue can be clarified further through the lens of the CTRW approach. Based on the work in Ref. [87], it becomes feasible to link a fractional diffusion equation of distributed order to a random walk by employing an appropriate probability density function.
In the context of the current discussion, the probability density function can be written in a separable form, i.e., , where represents the jump length probability, such that signifies the probability that the walker’s jump length is within the interval from x to . Likewise, denotes the probability that the waiting time for the walker is within the interval from t to . Note that the separable form for the probability density function allows us to obtain the fractional diffusion equations as discussed in refs. [19,38,40], which are used in our developments. A nonseparable form for the probability density function has been considered in turbulence [88] and transport in disordered media [89]. In ref. [90], a discussion about different forms of nonseparable probability density functions can be found. The waiting-time distribution relevant to the problem we are treating here is essentially given by
where , the diffusion coefficient is constant, , the forces are absent (free diffusion), and (see Figure 3). This outcome is distinct from that observed in standard diffusion and basic fractional scenarios. The interaction between the various operators significantly influences the overall system behavior, especially its electrical impedance response to an external field. Such a characteristic will be notably evident, for instance, in the electrical conductivity behavior, which is related to the mean square displacement, as elaborated subsequently.
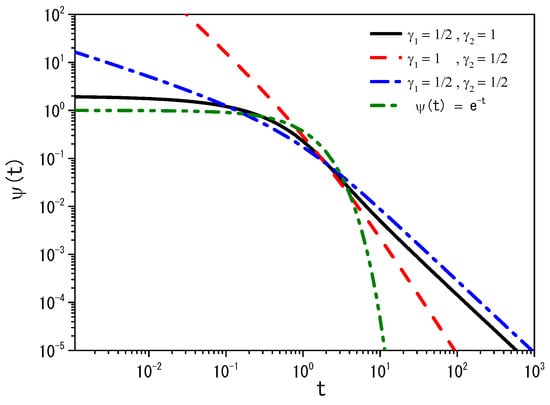
Figure 3.
Behavior predicted by Equation (109) for different values of and . The standard case, i.e., usual diffusion, is also illustrated.
5.4. PNPA Anomalous Model: Impedance Response
The PNP model is valuable for analyzing impedance spectroscopy data for different systems and electrolytic cells [91,92,93]. At frequencies where it accurately represents ion response to an external field, the electric current used to determine cell impedance must account for the displacement current caused by the time variation of the electric field. For normal diffusion, the displacement current is expressed as . In the case of anomalous diffusion, the overall current density is described by Equation (107) when accounting for time-fractional derivatives of distributed order. A crucial aspect to note is that within the context of anomalous diffusion, the conventional, nonfractional form of the total electric current is not applicable [94].
An illustrative example demonstrates the PNP model extended by incorporating noninteger (fractional) operators. The electrolytic cell is described as a slab with a thickness d in a Cartesian coordinate system, with electrodes at and having an area A. This simplifies the problem to one dimension. Assuming full dissociation, in Equation (106), and , and the ions have identical diffusion coefficients.
Now, the two resulting equations to be solved are obtained from Equation (106), rewritten as
together with the Poisson Equation (83). The cell experiences a time-varying electric potential given by , and our analysis is limited to the periodic state. For (perfect blocking electrodes), the impedance can be analyzed for small alternating current signals. This situation permits the investigation of solutions to Equations (110) and (83) as follows:
where and , with N denoting the equilibrium ion density, and (refer to Ref. [38] for more information). We derive the following analytical formula for the electrical impedance:
where
as the Debye length,
(see Figure 4, Figure 5 and Figure 6).
Figure 4.
Nyquist diagram for and . The black (solid), red (dashed), and blue (dashed-dotted) lines correspond to the different values of and , respectively. The green (dashed-dotted-dotted) line corresponds to the standard case. We consider, for illustrative purposes, /s, , ( F/m), m, s, , and m.
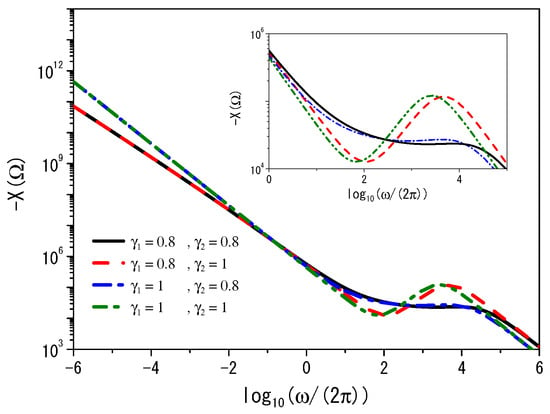
Figure 5.
The imaginary part of the impedance, , for and . The black (solid), red (dashed), and blue (dashed-dotted) lines correspond to the different values of and , respectively. The green (dashed-dotted-dotted) line corresponds to the standard case. We consider, for illustrative purposes, /s, , ( F/m), m, s, , and m.
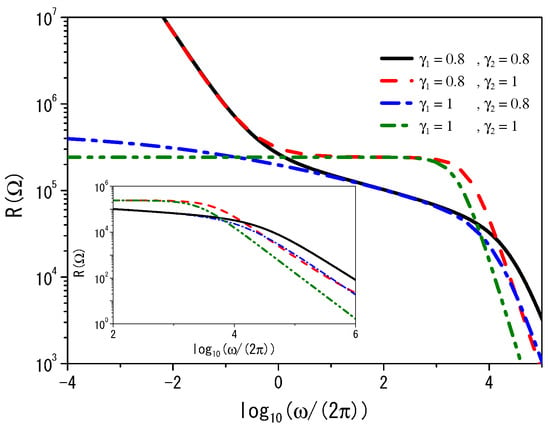
Figure 6.
The real part of the impedance, , for and . The black (solid), red (dashed), and blue (dashed-dotted) lines correspond to the different values of and , respectively. The green (dashed-dotted-dotted) line corresponds to the standard case. We consider, for illustrative purposes, /s, , ( F/m), m, s, , and m.
In the low-frequency limit, the imaginary part of the impedance behaves as when , leading to . For the other part of the impedance, we have . These findings can be confirmed by examining the asymptotic limit described by
Electrical conductivity examines the impact of fractional operators on the behavior of the electrolytic cells through the measurement of ionic movement and diffusion. It is defined as (see Figure 7). In the high-frequency limit, its behavior differs and is given by for and . According to refs. [95,96], we have the relation
demonstrating a relation between the mean square displacement and electrical conductivity. This leads to , meaning a subdiffusive process. As discussed earlier, this can be related to a random walk with a long-tailed behavior for the waiting-time distribution. Importantly, when is constant, it results in (indicating normal diffusion). This result, connected to the usual diffusion, implies that the waiting-time distribution can be associated with a Poisson distribution.
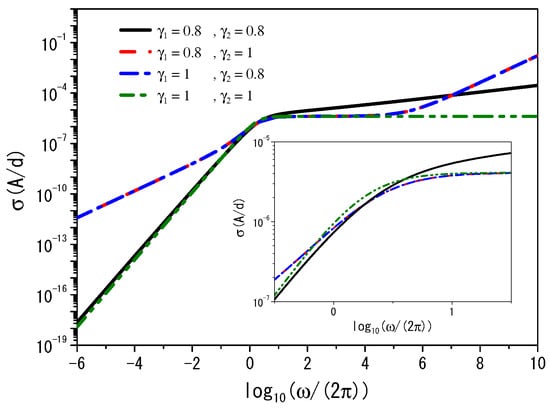
Figure 7.
Electrical conductivity, , for and . The black (solid), red (dashed), and blue (dashed-dotted) lines correspond to the different values of and , respectively. The green (dashed-dotted-dotted) line corresponds to the standard case. We consider, for illustrative purposes, /s, , ( F/m), m, s, , and m.
We now discuss some recent results involving PNPA and its variants that are used to better understand impedance spectroscopy measurements in liquid crystal samples. Our goal is to provide the reader with some examples of applications of fractional calculus in complex fluids and thus pave the way for broader use of the equations presented here since they correspond to a very general framework, which can be applied in any situation even if the system is not anomalous, in which case the fractional parameters are chosen to recover the usual equations. As discussed previously, anomalous behavior may occur due to several factors, from the morphology structure (such as modulation) to molecular crowding and the electrode/electrolyte connection heterogeneity.
The first example of fractional calculus applied to anomalous behavior in liquid crystals was published in the reference [79]. A nematic material (5CB) was filled into a cell of thickness ∼30 μm, whose substrates were made active by evaporated gold and whose alignment was produced by spin coating the substrates with 10 wt. % solution of LQ1800 in methyl pyrrolidinone. The complex impedance of the sample was then measured with a impedantiometer under low applied voltage (25 mV) [79]. Due to the complex processes occurring at the electrodes, the relaxation process at the substrates is essentially non-Debye-like in the low-frequency regime (where ionic motion and adsorption effects play major roles), which is clear from the real and imaginary parts of the impedance, both of which show a behavior that is not explainable by using the PNP model with the kinetic equation given by Equation (68). To overcome this problem, Equation (68) was written by replacing the time derivative with the Caputo fractional derivative (25). Figure 8 shows the real (R) and imaginary (X) parts of the impedance as a function of frequency. The open circles represent the measured data, while the solid line gives the data adjusted with the fractional kinetic equation. The dashed line represents the same model but with the conventional kinetic Equation (68). For adjustment, all the parameters concerning the system (such as diffusion coefficient, thickness, dielectric constants, etc.) are from the experiment, leaving the rate of adsorption and desorption and the fractional coefficient as fit parameters.
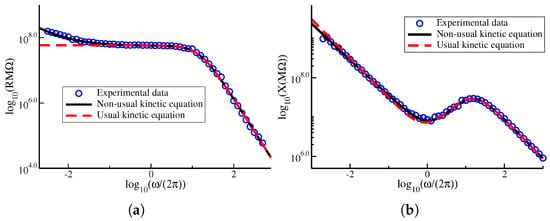
Figure 8.
(a) Real (R) and (b) imaginary (X) part of the impedance vs. frequency for a nematic liquid crystal (5 CB) slab confined by gold, electrodes, and the alignment produced by spin coating the substrates with 10 wt.% solution of LQ1800 in methyl pyrrolidinone (open circles). The dashed curve corresponds to the PNP model with Equation (68) representing the adsorption process, while the solid curve replaces the usual kinetic equation with a fractional kinetic equation. All the bulk parameters come from the experiment or the literature, and the kinetic equation parameters are used as fitting parameters, with m3/s, s, and . Adapted from ref. [79] with permission from APS.
An even more pronounced effect in the low-frequency region is observed if the LQ1800 solution is raised to 20 wt.%, when still considering gold-evaporated electrodes [97]. In this case, the alignment layer is much thicker, roughly 50 nm compared to the previous case (∼20 nm). This thicker layer induces a more complex interaction between the electrode and the nematic medium so that the anomalous behavior in the low frequency (characterized by the inclination of the real part of the impedance for low frequencies) is much more pronounced. It turns out that, in this case, a fractional kinetic equation alone is not enough to describe the results. The complex interaction between the thick covered layer and the complex fluid induces non-Debye dynamics, which results in an anomalous time diffusion in bulk, characterized by more than one diffusion regime (hence the distributed order). As a result, the experimental data are confronted by assuming a fractional operator of distributed order for the diffusion equation, as in Equation (40). Figure 9 shows the real and imaginary parts of the impedance. The black squares give the experimental data, while the red solid line gives the model a distributed order. If only anomalous diffusion is considered (no distributed-order diffusion in bulk), the result is the “fractional” curve given by the green diamonds. The classical model, without any fractional operator, is represented by the blue triangles, and it is clearly the worst adjustment to the experimental data [97]. A further step to demonstrate the need to use fractional calculus to model diffusive processes in liquid crystal was demonstrated in reference [98], where the explicit dependence of the electrical conductivity with the mean square displacement was established. It was shown that in the low-frequency limit, the conductivity dependence on the frequency can be written as (), whereas the mean square displacement dependence on time, which characterizes anomalous diffusion, follows the rule . Therefore, a normal diffusive process produces horizontal conductivity for low frequencies. With this result, in reference [98] the conductivities measured for 5CB and confronted with fractional calculus, shown in references [79,97], were shown to be anomalous in the low-frequency regime. More recent results have shown that the nematic phases of the thermotropic material E7 [99] and on lyotropic chromonic material [100] also present anomalous diffusion during dielectric measurements in the low-frequency regime, in both cases, with .
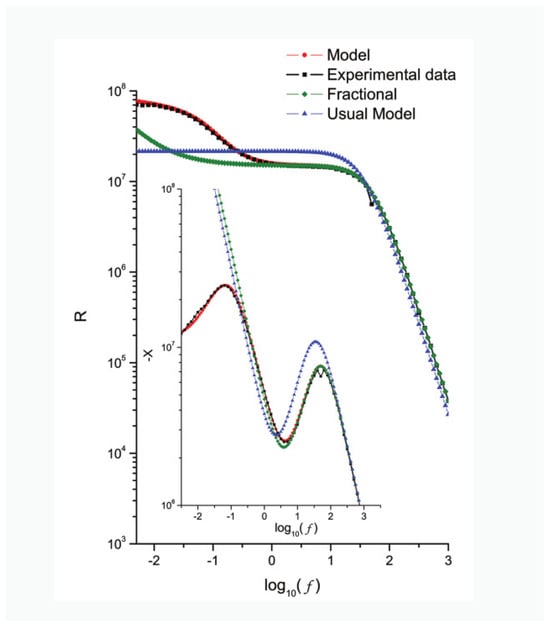
Figure 9.
Real (R) and imaginary (X) parts of the impedance for a nematic liquid crystal cell with gold electrodes and LQ1800 solution 20 wt.% in methyl pyrrolidinone. The black squares give experimental data, the red solid line shows the fractional model with diffusion of distributed order, the green diamonds show the case of the simple fractional model, and the blue triangles are the usual model, without fractional calculus. Reproduced from ref [97] with permission from ACS.
A recent work looked more closely into the anomalous diffusion that occurs in several kinds of liquid crystal materials [101]. Samples of nematic, cholesteric, and smectic A phases [102] were analyzed in different orientations. Although the nematic phase does not have any bulk modulation, and hence the anomalous process is likely due to the complex processes occurring near the electrodes, the cholesteric and smectic phases are modulated, meaning that the cholesteric phase has a pseudolayered structure, while the smectic A is a layered phase. As expected, the impedance spectra of all samples require fractional calculus, but the diffusive regimes heavily depend on the morphology of the medium. The mean square displacement time exponent for low frequencies is very similar for nematics and for the cases where diffusion occurs within the layers, with , as previously reported. However, diffusion across modulation, both in cholesterics and smectics, is more subdiffusive, with , indicating that permeation and cagelike diffusion play an important role in the dielectric response of modulated materials [101].
6. Conclusions
Our analysis examined the electrical response through the lens of the PNP model, exploring various potential extensions using a fractional approach. As outlined in Section 2, fractional derivatives offer a simple way to extend differential operators, enabling the capture of behaviors that are not possible with standard operators. In the context of diffusion, where diverse stochastic processes occur, this approach has proven to be a promising tool, particularly for investigating anomalous diffusion. We incorporated these points in Section 4.3 and Section 5, where we used the fractional approach to extend the key operators used to describe the electrical response. This allowed us to extend the kinetic equation to encompass non-Debye relaxations and achieve the behavior in the low-frequency limit. This behavior is also observed in some extensions discussed in Section 5. This paper facilitates the connection between the PNP model and constant phase elements (CPEs) exhibiting frequency dispersion.
Furthermore, we explored the electrical conductivity to analyze diffusion behavior in several of these extensions. This analysis revealed that anomalous diffusion could be described in the low-frequency limit, high-frequency limit, or both, depending on the specific extension used. This translates to the presence of the behavior in these scenarios. We believe this review can serve as a valuable resource, opening up new avenues for connecting experimental findings with theoretical approaches that utilize electrical and physicochemical parameters.
Author Contributions
Conceptualization, G.B., L.R.E., R.S.Z., E.K.L. and A.M.S.; methodology, G.B., L.R.E., R.S.Z., E.K.L. and A.M.S.; formal analysis, G.B., L.R.E., R.S.Z., E.K.L. and A.M.S.; investigation, G.B., L.R.E., R.S.Z., E.K.L. and A.M.S.; writing—original draft preparation, G.B., L.R.E., R.S.Z., E.K.L. and A.M.S.; writing—review and editing, G.B., L.R.E., R.S.Z., E.K.L. and A.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the MEPhI Academic Excellence Project (G.B.) and by the Program of Visiting Professor of Università della Calabria (L.R.E.). E.K.L. thanks the partial financial support of the CNPq under Grant No. 301715/2022-0. R.S.Z. thanks the National Council for Scientific and Technological Development, CNPq, process number 304634/2020-4 and 465259/2014-6, the National Institute of Science and Technology Complex Fluids (INCT-FCx), and the São Paulo Research Foundation (FAPESP—2014/50983-3).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pagès, J.M.; Ignés-Mullol, J.; Sagués, F. Anomalous Diffusion of Motile Colloids Dispersed in Liquid Crystals. Phys. Rev. Lett. 2019, 122, 198001. [Google Scholar] [CrossRef] [PubMed]
- Ferreiro-Córdova, C.; Toner, J.; Löwen, H.; Wensink, H.H. Long-time anomalous swimmer diffusion in smectic liquid crystals. Phys. Rev. E 2018, 97, 062606. [Google Scholar] [CrossRef] [PubMed]
- Shrivastav, G.P.; Klapp, S.H.L. Anomalous transport of magnetic colloids in a liquid crystal–magnetic colloid mixture. Soft Matter 2019, 15, 973–982. [Google Scholar] [CrossRef] [PubMed]
- Sandro, F.; Aurizio, N. Elastic anomalies at the interface between a nematic liquid crystal and its vapour: A microscopic approach. J. Phys. II France 1994, 4, 1617–1630. [Google Scholar] [CrossRef]
- Mikami, N.; Higuchi, R.I.; Sakurai, T. Anomalous behaviour in helical pitch of ferroelectric liquid crystal mixtures. J. Chem. Soc. Chem. Commun. 1990, 22, 1561–1562. [Google Scholar] [CrossRef]
- Zhuang, B.; Wang, Z.G. Anomalous Concentration Effects on Phase Behavior and Nematic Order in Mixtures of Side-Chain Liquid Crystal Polymers and Low-Molecular-Weight Liquid Crystals. Macromolecules 2012, 45, 6220–6229. [Google Scholar] [CrossRef]
- Yang, D.K.; Cui, Y.; Nemati, H.; Zhou, X.; Moheghi, A. Modeling aligning effect of polymer network in polymer stabilized nematic liquid crystals. J. Appl. Phys. 2013, 114, 243515. [Google Scholar] [CrossRef]
- Riemann, B. Versuch einer allgemeinen Auffassung der Integration und Differentiation. Gesammelte Werke 1876, 62, 331–344. [Google Scholar]
- Liouville, J. Mémoire sur le calcul des différentielles à indices quelconques. J. l’École Polytech. 1832, 13, 1–69. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Riesz, M.; Lars, G.; Hörmander, L. Potentiels de divers ordres et leurs fonctions de Green. In Collected Papers; Springer: Berlin/Heidelberg, Germany, 1988; p. 480. [Google Scholar]
- Grunwald, A.K. Uber “begrente” Derivationen und deren Anwedung. Zangew Math Phys. 1867, 12, 441–480. [Google Scholar]
- Letnikov, A. Theory of differentiation with an arbitrary index (Russian). Math. Sb. 1868, 3, 1–66. [Google Scholar]
- Weyl, H. Bemerkungen zum begriff des differentialquotienten gebrochener ordnung. Vierteljschr. Naturforsch. Gesellsch. 1917, 62, 296–302. [Google Scholar]
- Hadamard, J. Essai sur l’étude des fonctions données par leur développement de Taylor. J. MathéMatiques Pures Appliquées 1892, 8, 101–186. [Google Scholar]
- Marchaud, A. Sur les dérivées et sur les différences des fonctions de variables réelles. J. MathéMatiques Pures Appliquées 1927, 6, 337–425. [Google Scholar]
- De Oliveira, E.C.; Tenreiro Machado, J.A. A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. An Introduction to Anomalous Diffusion and Relaxation; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Lacroix, S.F. Traité du Calcul Différentiel et du Calcul Intégral; JBM Duprat: Paris, France, 1797; Volume 1. [Google Scholar]
- Abel, N.H. Solution de quelques problèmes à l’aide d’integrales définies. Mag. Naturvidenskabenerne Mag. Naturvidenskabenerne 1881, 1, 16–18. [Google Scholar]
- Abel, N.H. Résolution d’un problème de mécanique. Journal Für Die Reine Angewandte Mathematik Crelle 1826, 42, 153–157. [Google Scholar]
- Liouville, J. Mémoire sur Quelques Questions de Géométrie et de Mécanique, et sur un Nouveau Genre de Calcul Pour Résoudre ces Questions; SCIRP: Wuhan, China, 1832; Volume 13, pp. 1–69. [Google Scholar]
- Liouville, J. Mémoire sur le théorème des fonctions complémentaires. J. Die Reine Angew. Math. 1834, 11, 1–19. [Google Scholar]
- Sonin, N.Y.S. On differentiation with arbitrary index. J. Die Reine Angew. Math. 1869, 6, 1–38. [Google Scholar]
- Letnikov, A. An explanation of the concepts of the theory of differentiation of arbitrary index. Moscow Matem. Sbornik 1872, 6, 413–445. [Google Scholar]
- Laurent, H. Sur le calcul des dérivées à indices quelconques. Nouv. Ann. Math. J. Des Candidats Aux ÉColes Polytech. Norm. 1884, 3, 240–252. [Google Scholar]
- Letnikov, A. An investigation related to the theory of integrals of the form (x − u)p−1f(u)du. Moscow Matem. Sbornik 1874, 7, 5–205. [Google Scholar]
- Ross, B. The Development of fractional calculus 1695–1900. Hist. Math. 1900, 4, 75. [Google Scholar] [CrossRef]
- Agrawal, O.P. Formulation of Euler—Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 2002, 272, 368–379. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Frederico, G.S.; Torres, D.F. A formulation of Noether’s theorem for fractional problems of the calculus of variations. J. Math. Anal. Appl. 2007, 334, 834–846. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional vector calculus and fractional Maxwell’s equations. Ann. Phys. 2008, 323, 2756–2778. [Google Scholar] [CrossRef]
- Godefroy, M. La Fonction Gamma: Théorie, Histoire, Bibliographie; Gauthier-Villars: Paris, France, 1901. [Google Scholar]
- Davis, H.T. The application of fractional operators to functional equations Amer. J. Math. 1927, 49, 1936. [Google Scholar] [CrossRef]
- Mainardi, F.; Gorenflo, R. Time-fractional derivatives in relaxation processes: A tutorial survey. arXiv 2008, arXiv:0801.4914. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Some aspects of fractional diffusion equations of single and distributed order. Appl. Math. Comput. 2007, 187, 295–305. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks: From Tools to Applications; OUP: Oxford, UK, 2011. [Google Scholar]
- Metzler, R.; Barkai, E.; Klafter, J. Deriving fractional Fokker-Planck equations from a generalised master equation. Europhys. Lett. 1999, 46, 431. [Google Scholar] [CrossRef]
- Zahran, M. On the derivation of fractional diffusion equation with an absorbent term and a linear external force. Appl. Math. Model. 2009, 33, 3088–3092. [Google Scholar] [CrossRef]
- Chechkin, A.; Gorenflo, R.; Sokolov, I. Retarding subdiffusion and accelerating superdiffusion governed by distributed-order fractional diffusion equations. Phys. Rev. E 2002, 66, 046129. [Google Scholar] [CrossRef]
- Lenzi, E.; Mendes, R.; Tsallis, C. Crossover in diffusion equation: Anomalous and normal behaviors. Phys. Rev. E 2003, 67, 031104. [Google Scholar] [CrossRef]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. arXiv 2007, arXiv:10.0702419. [Google Scholar]
- Masoliver, J.; Lindenberg, K. Continuous time persistent random walk: A review and some generalizations. Eur. Phys. J. B 2017, 90, 1–13. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A.; Lenzi, E.; Pagnini, G.; Sandev, T. Generalized Cattaneo (telegrapher’s) equations in modeling anomalous diffusion phenomena. Phys. Rev. E 2020, 102, 022128. [Google Scholar] [CrossRef]
- Magin, R.L.; Lenzi, E.K. Slices of the anomalous phase cube depict regions of sub-and super-diffusion in the fractional diffusion equation. Mathematics 2021, 9, 1481. [Google Scholar] [CrossRef]
- Pagninia, G.; Scalas, E. Historical notes on the M-Wright/Mainardi function. Commun. Appl. Ind. Math. 2015, 6, e496. [Google Scholar] [CrossRef]
- Mainardi, F.; Pagnini, G.; Saxena, R. Fox H functions in fractional diffusion. J. Comput. Appl. Math. 2005, 178, 321–331. [Google Scholar] [CrossRef]
- Scalas, E.; Gorenflo, R.; Mainardi, F.; Raberto, M. Revisiting the derivation of the fractional diffusion equation. Fractals 2003, 11, 281–289. [Google Scholar] [CrossRef]
- Li, J.R.; Kuppler, R.J.; Zhou, H.C. Selective gas adsorption and separation in metal–organic frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. [Google Scholar] [CrossRef] [PubMed]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces; Interscience Publishers: New York, NY, USA, 1967; Volume 150. [Google Scholar]
- Barbero, G.; Evangelista, L.R. Adsorption Phenomena and Anchoring Energy in Nematic Liquid Crystals; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Perlmutter, S.; Doroski, D.; Moddel, G. Degradation of liquid crystal device performance due to selective adsorption of ions. Appl. Phys. Lett. 1996, 69, 1182–1184. [Google Scholar] [CrossRef]
- Zhang, M.; Soto-Rodríguez, J.; Chen, I.C.; Akbulut, M. Adsorption and removal dynamics of polymeric micellar nanocarriers loaded with a therapeutic agent on silica surfaces. Soft Matter 2013, 9, 10155–10164. [Google Scholar] [CrossRef]
- Yaseen, M.; Salacinski, H.; Seifalian, A.; Lu, J. Dynamic protein adsorption at the polyurethane copolymer/water interface. Biomed. Mater. 2008, 3, 034123. [Google Scholar] [CrossRef] [PubMed]
- Nugent, P.; Belmabkhout, Y.; Burd, S.D.; Cairns, A.J.; Luebke, R.; Forrest, K.; Pham, T.; Ma, S.; Space, B.; Wojtas, L.; et al. Porous materials with optimal adsorption thermodynamics and kinetics for CO2 separation. Nature 2013, 495, 80–84. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Kuan, W.H.; Lo, S.L.; Chang, C.M.; Wang, M.K. A geometric approach to determine adsorption and desorption kinetic constants. Chemosphere 2000, 41, 1741–1747. [Google Scholar] [CrossRef]
- Swenson, H.; Stadie, N.P. Langmuir’s theory of adsorption: A centennial review. Langmuir 2019, 35, 5409–5426. [Google Scholar] [CrossRef] [PubMed]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists: A Comprehensive Guide; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Bénichou, O.; Grebenkov, D.; Levitz, P.; Loverdo, C.; Voituriez, R. Optimal reaction time for surface-mediated diffusion. Phys. Rev. Lett. 2010, 105, 150606. [Google Scholar] [CrossRef] [PubMed]
- Levesque, M.; Bénichou, O.; Voituriez, R.; Rotenberg, B. Taylor dispersion with adsorption and desorption. Phys. Rev. E 2012, 86, 036316. [Google Scholar] [CrossRef] [PubMed]
- Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Frequency dispersion in the fractional Langmuir approximation for the adsorption–desorption phenomena. Proc. R. Soc. A 2020, 476, 20190570. [Google Scholar] [CrossRef]
- Jakli, A.; Saupe, A. One- and Two-Dimensional Fluids: Properties of Smectic, Lamellar and Columnar Liquid Crystals; Condensed Matter Physics; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Ramanathan, T.; Abdala, A.A.; Stankovich, S.; Dikin, D.A.; Herrera-Alonso, M.; Piner, R.D.; Adamson, D.H.; Schniepp, H.C.; Chen, X.; Ruoff, R.S.; et al. Functionalized graphene sheets for polymer nanocomposites. Nat. Nanotechnol. 2008, 3, 327–331. [Google Scholar] [CrossRef] [PubMed]
- Jánossy, I. Molecular interpretation of the absorption-induced optical reorientation of nematic liquid crystals. Phys. Rev. E 1994, 49, 2957–2963. [Google Scholar] [CrossRef] [PubMed]
- Jorcin, J.B.; Orazem, M.E.; Pébère, N.; Tribollet, B. CPE analysis by local electrochemical impedance spectroscopy. Electrochim. Acta 2006, 51, 1473–1479. [Google Scholar] [CrossRef]
- Al-Refai, M.; Pal, K. New aspects of Caputo—Fabrizio fractional derivative. Prog. Fract. Differ. Appl. 2019, 5, 157–166. [Google Scholar] [CrossRef]
- Saxena, R.; Mathai, A.; Haubold, H. On fractional kinetic equations. Astrophys. Space Sci. 2002, 282, 281–287. [Google Scholar] [CrossRef]
- Saxena, R.; Mathai, A.; Haubold, H. Unified fractional kinetic equation and a fractional diffusion equation. Astrophys. Space Sci. 2004, 290, 299–310. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernandez, A. On fractional operators and their classifications. Mathematics 2019, 7, 830. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Time-fractional approach to the electrochemical impedance: The Displacement current. J. Electroanal. Chem. 2022, 920, 116588. [Google Scholar] [CrossRef]
- Macdonald, J.R. Theory of ac space-charge polarization effects in photoconductors, semiconductors, and electrolytes. Phys. Rev. 1953, 92, 4. [Google Scholar] [CrossRef]
- Trukhan, E. Dispersion of the dielectric constant of heterogeneous systems. Sov. Phys. Solid State 1963, 4, 2560–2570. [Google Scholar]
- Lelidis, I.; Barbero, G. Role of the displacement current on Warburg-type behavior. Phys. Rev. E 2017, 95, 052604. [Google Scholar] [CrossRef] [PubMed]
- De Paula, J.; Santoro, P.; Zola, R.; Lenzi, E.; Evangelista, L.; Ciuchi, F.; Mazzulla, A.; Scaramuzza, N. Non-Debye relaxation in the dielectric response of nematic liquid crystals: Surface and memory effects in the adsorption-desorption process of ionic impurities. Phys. Rev. E 2012, 86, 051705. [Google Scholar] [CrossRef] [PubMed]
- Halsey, T.C.; Leibig, M. The double layer impedance at a rough surface: Theoretical results. Ann. Phys. 1992, 219, 109–147. [Google Scholar] [CrossRef]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 2000, 61, 132. [Google Scholar] [CrossRef] [PubMed]
- Lenzi, E.; Evangelista, L.; Barbero, G. Fractional diffusion equation and impedance spectroscopy of electrolytic cells. J. Phys. Chem. B 2009, 113, 11371–11374. [Google Scholar] [CrossRef]
- Bogolyubov, A.; Potapov, A.; Rehviashvili, S.S. An approach to introducing fractional integro-differentiation in classical electrodynamics. Mosc. Univ. Phys. Bull. 2009, 64, 365–368. [Google Scholar] [CrossRef]
- Stefański, T.P.; Gulgowski, J. Formulation of time-fractional electrodynamics based on Riemann-Silberstein vector. Entropy 2021, 23, 987. [Google Scholar] [CrossRef]
- Nonnenmacher, T.F.; Metzler, R. Applications of fractional calculus techniques to problems in biophysics. Appl. Fract. Calc. Phys. 2000, 377–427. [Google Scholar] [CrossRef]
- Brady, J.F.; Koch, D.L. Dispersion in porous media. In Disorder and Mixing: Convection, Diffusion and Reaction in Random Materials and Processes; Springer: Berlin/Heidelberg, Germany, 1988; pp. 107–122. [Google Scholar]
- Sandev, T.; Metzler, R.; Chechkin, A. From continuous time random walks to the generalized diffusion equation. Fract. Calc. Appl. Anal. 2018, 21, 10–28. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; West, B.; Klafter, J. Lévy dynamics of enhanced diffusion: Application to turbulence. Phys. Rev. Lett. 1987, 58, 1100. [Google Scholar] [CrossRef]
- Dentz, M.; Scher, H.; Holder, D.; Berkowitz, B. Transport behavior of coupled continuous-time random walks. Phys. Rev. E 2008, 78, 041110. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; Klafter, J.; Wong, Y. Random walks with infinite spatial and temporal moments. J. Stat. Phys. 1982, 27, 499–512. [Google Scholar] [CrossRef]
- L’vov, P.E.; Sibatov, R.T.; Yavtushenko, I.O.; Kitsyuk, E.P. Time-fractional phase field model of electrochemical impedance. Fractal Fract. 2021, 5, 191. [Google Scholar] [CrossRef]
- Golovnev, A.; Trimper, S. Analytical solution of the Poisson–Nernst–Planck equations in the linear regime at an applied dc-voltage. J. Chem. Phys. 2011, 134, 154902. [Google Scholar] [CrossRef] [PubMed]
- Pabst, M. Analytical solution of the Poisson-Nernst-Planck equations for an electrochemical system close to electroneutrality. J. Chem. Phys. 2014, 140, 224113. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J. From diffusion to anomalous diffusion: A century after Einstein’s Brownian motion. Chaos Interdiscip. J. Nonlinear Sci. 2005, 15, 026103. [Google Scholar] [CrossRef] [PubMed]
- Scher, H.; Lax, M. Stochastic transport in a disordered solid. I. Theory. Phys. Rev. B 1973, 7, 4491. [Google Scholar] [CrossRef]
- Scher, H.; Lax, M. Stochastic transport in a disordered solid: Part II. Impurity conduction. Phys. Rev. B Solid State 1973, 7, 4502. [Google Scholar] [CrossRef]
- Ciuchi, F.; Mazzulla, A.; Scaramuzza, N.; Lenzi, E.K.; Evangelista, L.R. Fractional Diffusion Equation and the Electrical Impedance: Experimental Evidence in Liquid-Crystalline Cells. J. Phys. Chem. C 2012, 116, 8773–8777. [Google Scholar] [CrossRef]
- Lenzi, E.; Zola, R.; Ribeiro, H.; Vieira, D.S.; Ciuchi, F.; Mazzulla, A.; Scaramuzza, N.; Evangelista, L. Ion motion in electrolytic cells: Anomalous diffusion evidences. J. Phys. Chem. B 2017, 121, 2882–2886. [Google Scholar] [CrossRef]
- Rosseto, M.P.; de Almeida, R.R.R.; Zola, R.S.; Lenzi, E.K.; Evangelista, L.R. Electrical Impedance Response of Liquid Crystals and Anomalous Diffusion: A Fractional Approach. J. Electrochem. Soc. 2023, 170, 096504. [Google Scholar] [CrossRef]
- Ciuchi, F.; de Santo, M.P.; Tone, C.M.; Evangelista, L.R.; Lenzi, E.K.; de Almeida, R.R.R.; Rosseto, M.P.; Zola, R.S. Modelling dielectric behaviour and anomalous relaxation in chromonic liquid crystals. Liq. Cryst. 2024, 51, 1–10. [Google Scholar] [CrossRef]
- Rosseto, M.; Ribeiro de Almeida, R.; Lenzi, E.; Evangelista, L.; Zola, R. Probing modulated liquid crystal media with dielectric spectroscopy. J. Mol. Liq. 2023, 390, 122943. [Google Scholar] [CrossRef]
- De Gennes, P.; Prost, J. The Physics of Liquid Crystals; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).