Novel Admissibility Criteria and Multiple Simulations for Descriptor Fractional Order Systems with Minimal LMI Variables
Abstract
:1. Introduction
- (1)
- The simulation of the anti-symmetric matrix within the stability criteria based on LMIs for FOSs has consistently presented challenges. This paper addresses these challenges by utilizing MATLAB, offering a range of simulation methods employing both the LMI toolbox and the YALMIP toolbox.
- (2)
- There are a large number of results for the admissibility criteria for DFOSs with eigenvalues not on the boundary axes, but none of them deal with them directly using LMIs. This paper advances this area by converting this hypothetical condition into LMI-based admissibility criteria, thus making it easy to use MATLAB to determine feasible solutions.
- (3)
- Previously proposed admissibility criteria for DFOSs include several decision variables and even involve complex variables, making it difficult to determine feasible solutions using MATLAB. The admissibility criteria proposed in this paper involve the minimal LMIs variable, which makes it easy to determine feasible solutions.
- (4)
- Diverging from the methodologies of existing algorithms, which segregate the interval into two distinct ranges: and , this research constructs an LMI structure, which is applicable to DFOSs with .
- (5)
- The admissibility criteria derived in this paper, through the application of methodologies including contract transformation, are contingent solely upon factors such as fractional order, the pseudo state matrix, and the direction of control.
2. Problem Statements and Preliminaries
3. Main Results
3.1. Multiple Simulations of Anti Symmetric Matrices in Stability Criteria of FOSs
3.2. Admissibility Criteria Based on LMIs for DFOSs with Eigenvalues Not on Boundary Axes
3.3. Admissibility Criteria for DOFS Involving Minimal LMIs Variable
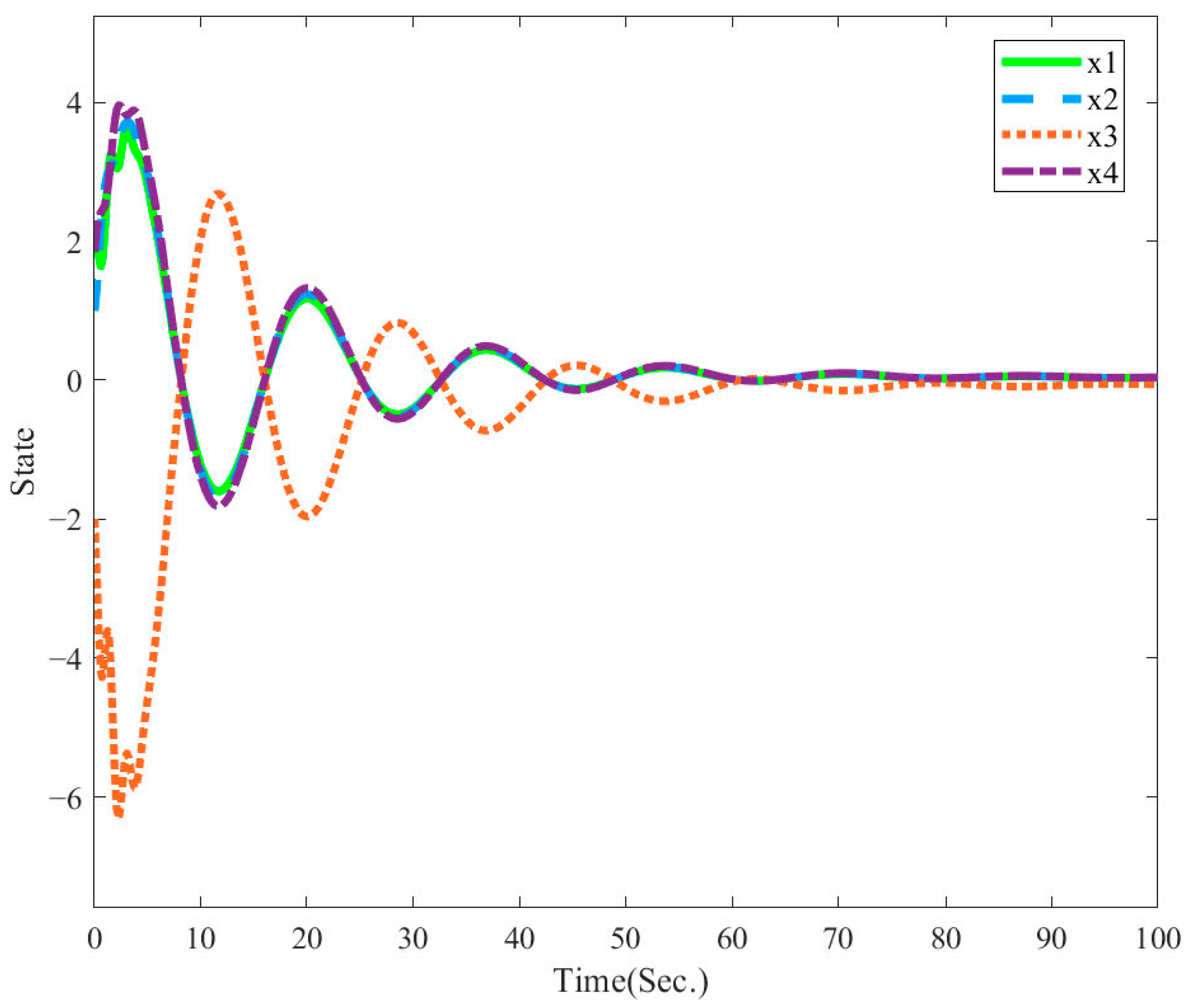
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Appendix A
Appendix A.1

Appendix A.2

Appendix A.3

Appendix A.4

Appendix A.5

Appendix A.6

Appendix A.7

References
- Marir, S.; Chadli, M.; Basin, M.V. Bounded real lemma for singular linear continuous-time fractional-order systems. Automatica 2022, 135, 109962. [Google Scholar] [CrossRef]
- Li, R.C.; Zhang, Q.L. Robust H∞ sliding mode observer design for a class of Takagi-Sugeno fuzzy descriptor systems with time-varying delay. Appl. Math. Comput. 2018, 337, 158–178. [Google Scholar] [CrossRef]
- Li, R.C.; Zhang, Q.L. Robust H∞ observer-based sliding mode control for uncertain Takagi-Sugeno fuzzy descriptor systems with unmeasurable premise variables and time-varying delay. Inf. Sci. 2021, 566, 239–261. [Google Scholar]
- Zhang, X.F.; Wang, Z. Stability and robust stabilization of uncertain switched fractional order systems. ISA Trans. 2020, 103, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xue, D.Y.; Pan, F. Observer-based robust control for singular switched fractional order systems subject to actuator saturation. Appl. Math. Comput. 2021, 411, 126538. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Mousavi, Y.; Kucukdemiral, I.B.; Fekih, A. Guaranteed cost robust output feedback control design for fractional-order uncertain neutral delay systems. Chaos Solitons Fractals 2022, 163, 112523. [Google Scholar] [CrossRef]
- Gong, P.; Lan, W.; Han, Q.L. Robust adaptive fault-tolerant consensus control for uncertain nonlinear fractional-order multi-agent systems with directed topologies. Automatica 2020, 117, 109011. [Google Scholar] [CrossRef]
- Angel, L.; Viola, J. Fractional order PID for tracking control of a parallel robotic manipulator type delta. ISA Trans. 2018, 79, 172–188. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.F.; Huang, W.K.; Wang, Q.G. Robust H∞ adaptive sliding mode fault tolerant control for T-S fuzzy fractional order systems with mismatched disturbances. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 1297–1307. [Google Scholar] [CrossRef]
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simulat. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, W. A fractional-order model on new experiments oflinear viscoelastic creep of Hami Melon. Comput. Math. Appl. 2013, 66, 677–681. [Google Scholar] [CrossRef]
- Duan, G.R.; Patton, R.J. A note on hurwitz stability of matrices. Automatica 1998, 34, 509–511. [Google Scholar] [CrossRef]
- Zhang, J.X.; Chai, T.Y. Proportional-integral funnel control of unknown lower-triangular nonlinear systems. IEEE Trans. Autom. Control 2024, 69, 1921–1927. [Google Scholar] [CrossRef]
- Zhang, J.X.; Ding, J.L.; Chai, T.Y. Fault-tolerant prescribed performance control of wheeled mobile robots: A mixed-gain adaption approach. IEEE Trans. Autom. Control 2024, 1–8. [Google Scholar] [CrossRef]
- Matignon, D. Stability result on fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Oustaloup, A.; Mathieu, B.; Lanusse, P. The CRONE control of resonant plants: Application to a flexible transmission. Eur. J. Control 1995, 1, 113–121. [Google Scholar] [CrossRef]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo-state feedback stabilization of commensurate fractional order systems. Automatica 2010, 46, 1730–1734. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.Q. D-stability based LMI criteria of stability and stabilization for fractional order systems. In Proceedings of the International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (DETC/CIE), Boston, MA, USA, 2–5 August 2015. DETC2015-46692. [Google Scholar]
- Chilali, M.; Gahinet, P. H∞ design with pole placement constraints: An LMI approach. IEEE Trans. Autom. Control 1996, 41, 358–367. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional-order interval systems with the fractional order α: The 0 < α < 1 case. Automatica 2008, 44, 2985–2988. [Google Scholar]
- Ahn, H.S.; Chen, Y.Q. Necessary and sufficient stability condition of fractional-order interval linear systems. Automatica 2008, 44, 2985–2988. [Google Scholar] [CrossRef]
- Wei, Y.H.; Chen, Y.Q.; Cheng, S.S.; Wang, Y. Completeness on the stability criterion of fractional order LTI systems. Fract. Calc. Appl. Anal. 2017, 20, 159–172. [Google Scholar] [CrossRef]
- Aguila-Gamacho, N.; Duarte-Mermound, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Reyad, E.K.; Shaher, M. Stability analysis of composite fractional systems. Int. J. Appl. Math. 2003, 12, 73–85. [Google Scholar]
- Wei, Y.H.; Tse, P.W.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Trans. 2017, 69, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.F.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0 < α < 2. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3237–3241. [Google Scholar]
- Di, Y.; Zhang, J.X.; Zhang, X.F. Robust stabilization of descriptor fractional-order interval systems with uncertain derivative matrices. Appl. Math. Comput. 2023, 453, 128076. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.; Basin, M.V. Necessary and sufficient admissibility conditions of dynamic output feedback for singular linear fractional-order systems. Asian J. Control 2023, 25, 2439–2450. [Google Scholar] [CrossRef]
- Lin, C.; Chen, B.; Shi, P.; Yu, J.P. Necessary and sufficient conditions of observer-based stabilization for a class of fractional-order descriptor systems. Syst. Control Lett. 2018, 112, 31–35. [Google Scholar] [CrossRef]
- Zhang, X.F.; Yan, Y.Q. Admissibility of fractional order descriptor systems based on complex variables: An LMI approach. Fractal Fract. 2020, 4, 8. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhao, Z.L.; Li, L. An alternative admissibility theorem for singular fractional order systems. IEEE Access 2019, 7, 126005–126013. [Google Scholar] [CrossRef]
- Sabatier, J.; Moze, M.; Farges, C. LMI stability conditions for fractional order systems. Comput. Math. Appl. 2010, 59, 1594–1609. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.Q. Improvement of strict LMI admissibility criteria of singular systems: Continuous and discrete. In Proceedings of the International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (DETC/CIE), Boston, MA, USA, 2–5 August 2015. V009T07A028. [Google Scholar]
- Shen, J.; Lam, J. State feedback H∞ control of commensurate fractional-order systems. Int. J. Syst. Sci. 2014, 45, 363–372. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M. Robust admissibility and stabilization of uncertain singular fractional-order linear time-invariant systems. IEEE/CAA J. Autom. Sin. 2019, 6, 685–692. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.; Bouagada, D. New admissibility conditions for singular linear continuous-time fractional-order systems. J. Frankl. Inst. 2019, 7, 126005–126013. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhao, Z.L.; Wang, Q.G. Static and dynamic output feedback stabilisation of descriptor fractional order systems. IET Control Theory Appl. 2020, 14, 324–333. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α < 1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [PubMed]
- N’Doye, I.; Darouach, M.; Zasadzinski, M.; Radhy, N.E. Robust stabilization of uncertain descriptor fractional-order systems. Automatica 2013, 49, 1907–1913. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Zhang, X.F.; Boutat, D.; Shi, P. Quadratic admissibility for a class of LTI uncertain singular fractional-order systems with 0 < α < 2. Fractal Fract. 2022, 7, 1. [Google Scholar]
- Di, Y.; Zhang, L.X.; Zhang, X.F. Alternate admissibility LMI criteria for descriptor fractional order systems with 0 < α < 2. Fractal Fract. 2023, 7, 577. [Google Scholar]


| LMIs in Stability Criterion | Matlab Toolbox | Matlab Commands | Feasible Solutions |
|---|---|---|---|
| LMIs of Theorem 2.1 in [18] | LMI Toolbox | Appendix A.1 | |
| Appendix A.2 | |||
| Yalmip | Appendix A.3 | ||
| Appendix A.4 | |||
| LMIs (14) and (15) of Theorem 1 | LMI Toolbox | Appendix A.5 | |
| Yalmip | Appendix A.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, J.-X. Novel Admissibility Criteria and Multiple Simulations for Descriptor Fractional Order Systems with Minimal LMI Variables. Fractal Fract. 2024, 8, 373. https://doi.org/10.3390/fractalfract8070373
Wang X, Zhang J-X. Novel Admissibility Criteria and Multiple Simulations for Descriptor Fractional Order Systems with Minimal LMI Variables. Fractal and Fractional. 2024; 8(7):373. https://doi.org/10.3390/fractalfract8070373
Chicago/Turabian StyleWang, Xinhai, and Jin-Xi Zhang. 2024. "Novel Admissibility Criteria and Multiple Simulations for Descriptor Fractional Order Systems with Minimal LMI Variables" Fractal and Fractional 8, no. 7: 373. https://doi.org/10.3390/fractalfract8070373
APA StyleWang, X., & Zhang, J.-X. (2024). Novel Admissibility Criteria and Multiple Simulations for Descriptor Fractional Order Systems with Minimal LMI Variables. Fractal and Fractional, 8(7), 373. https://doi.org/10.3390/fractalfract8070373







