Damage Law and Reasonable Width of Coal Pillar under Gully Area: Linking Fractal Characteristics of Coal Pillar Fractures to Their Stability
Abstract
1. Introduction
2. Engineering Geological Conditions
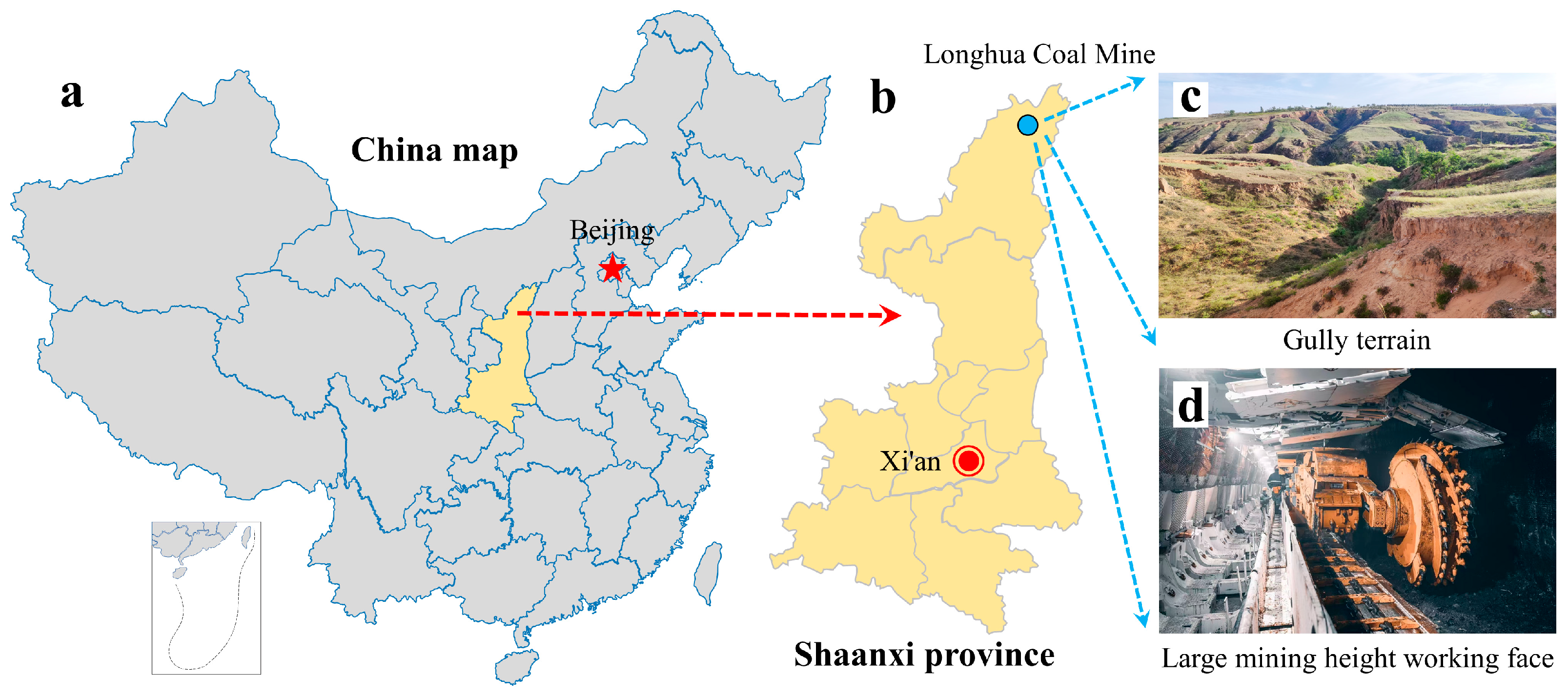
2.1. Study Area and Mining Settings
2.2. UAV Observation of the Topography of the Study Area
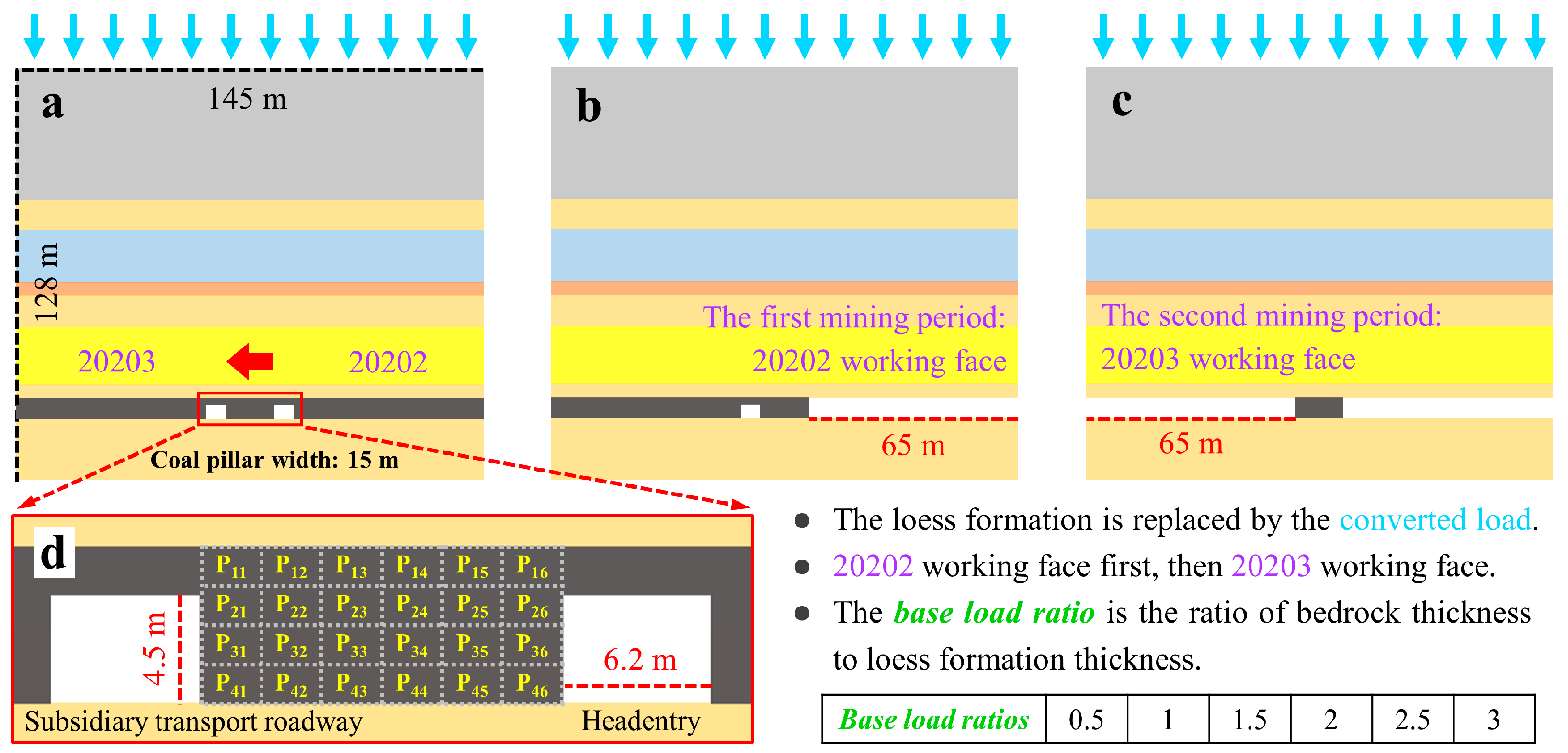
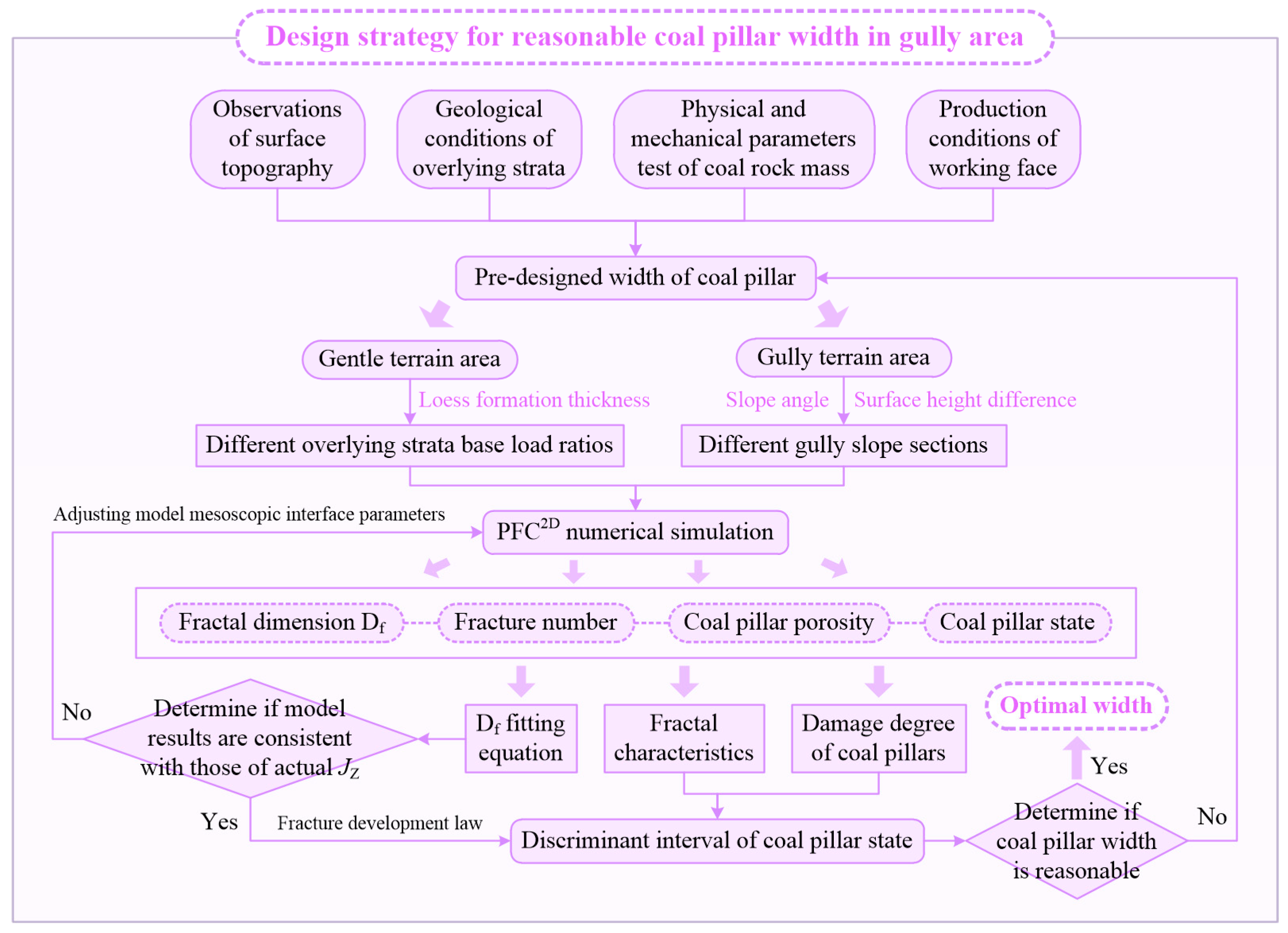
2.3. Coal Pillar Stabilization Conditions and Design Principles
- (1)
- Consider the effect of the repeated mining at the working face on the damage degree to the coal pillar. Ensure that the coal pillar can be in a semi-steady state during the first mining period, and the coal pillar can still be in critical yield state during the second mining period.
- (2)
- Consider the influence of the overlying strata base load ratio on the damage degree of the coal pillar. Determine the width of the coal pillar according to the actual overlying strata base load ratio of the working face to ensure that the coal pillar can still be in a critical yield state during the second mining period.
- (3)
- Consider the influence of gully topography on the damage degree of the coal pillar. The thickness of the loess formation on the surface of the working face at different locations is different because of the topography of the gully. For the case of different base load ratio of the overlying strata caused by the topography of the gully, the actual maximum loess formation thickness should be used to convert the load under the fixed thickness of bedrock to ensure that the coal pillar can still be in the critical yield state during the second mining period.
- (4)
- Consider the influence of the relative spatial position of the coal pillar and the gully slope sections on the damage degree of the coal pillar. If the coal pillar is below the gully topography, due to the fixed sequence of the first and the second mining periods of the coal pillar, it is necessary to discuss the damage degree and stability of the coal pillar when it is directly below different gully slope sections. On the one hand, the analysis results can be used as a reference basis for the determination of the coal pillar setting position and working face length in other working faces in the panel area, and on the other hand, they can be used to ensure that the relative position of the coal pillar below the gully slope section can still be in the critical yield state during the second mining period.
3. Fractal Characteristics of Coal Pillars with Different Overlying Strata Base Load Ratios in the Gentle Terrain Area
3.1. Numerical Model and Model Parameters
3.2. Fractal Characteristics of Coal Pillar Fractures
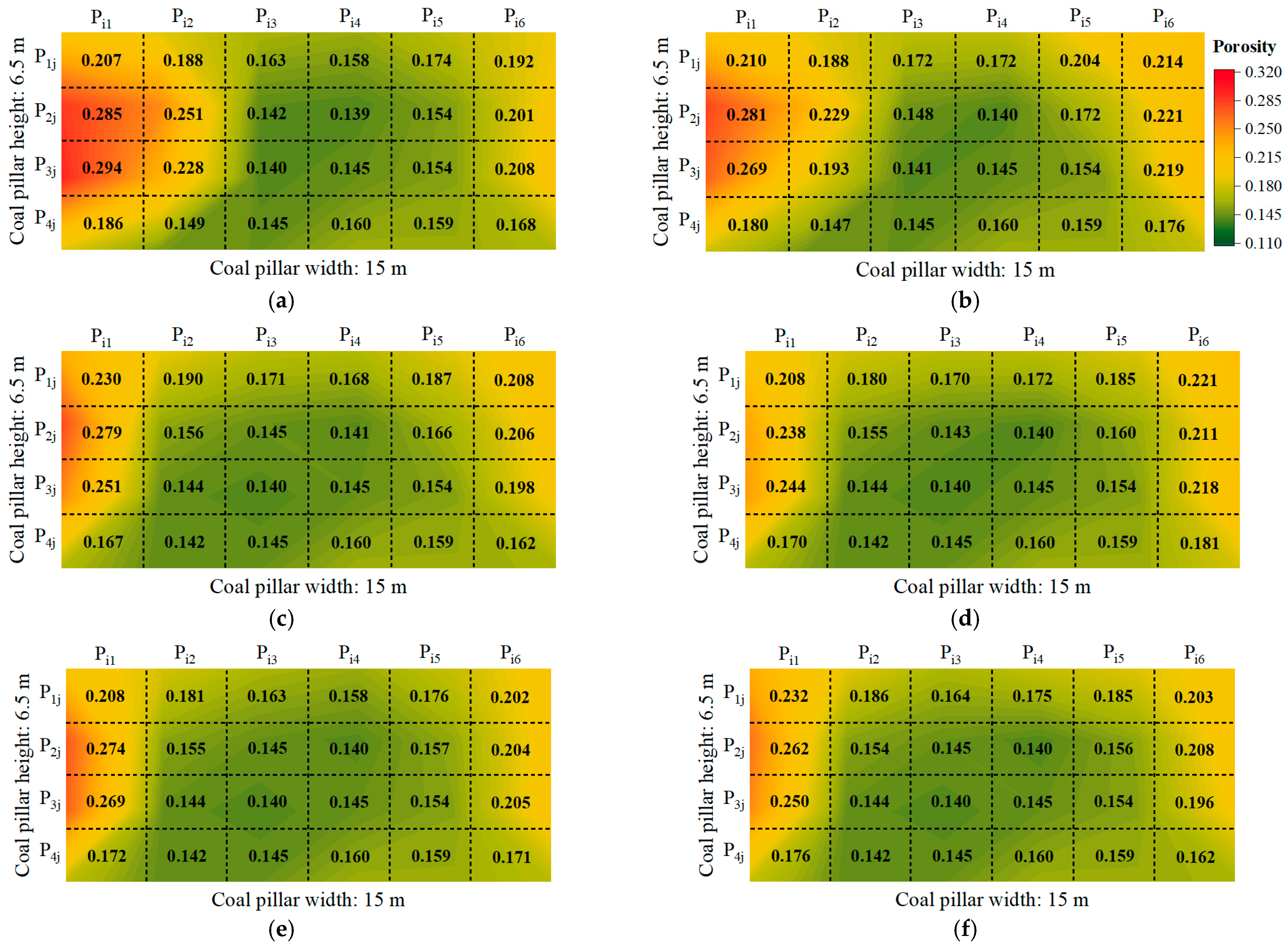
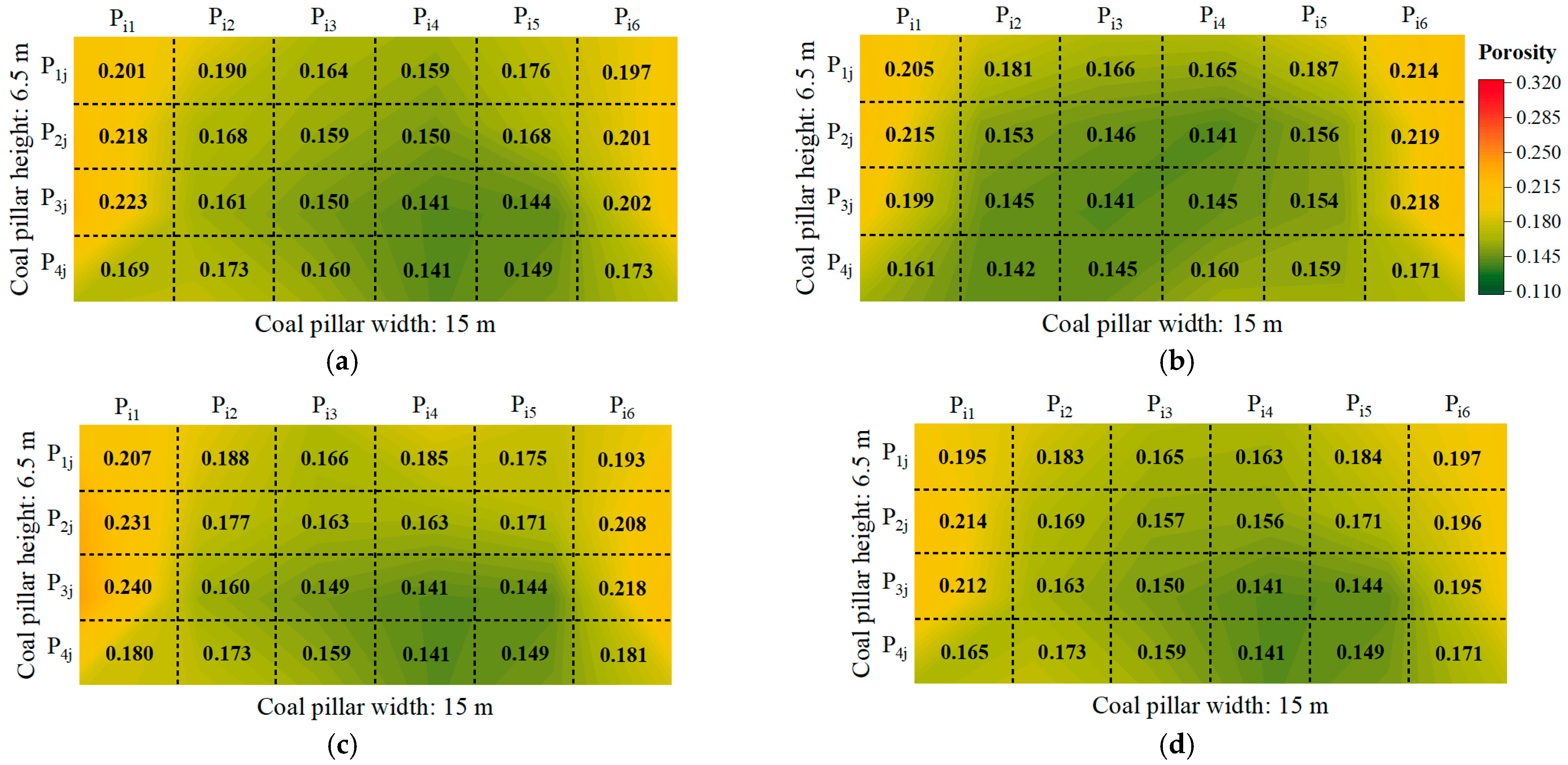
3.3. The Number of Fractures and Characteristics of Porosity Evolution within the Coal Pillar
3.4. Discussion
4. Damage Law of Coal Pillars under Different Gully Slope Sections in the Gully Terrain Area
4.1. Numerical Model
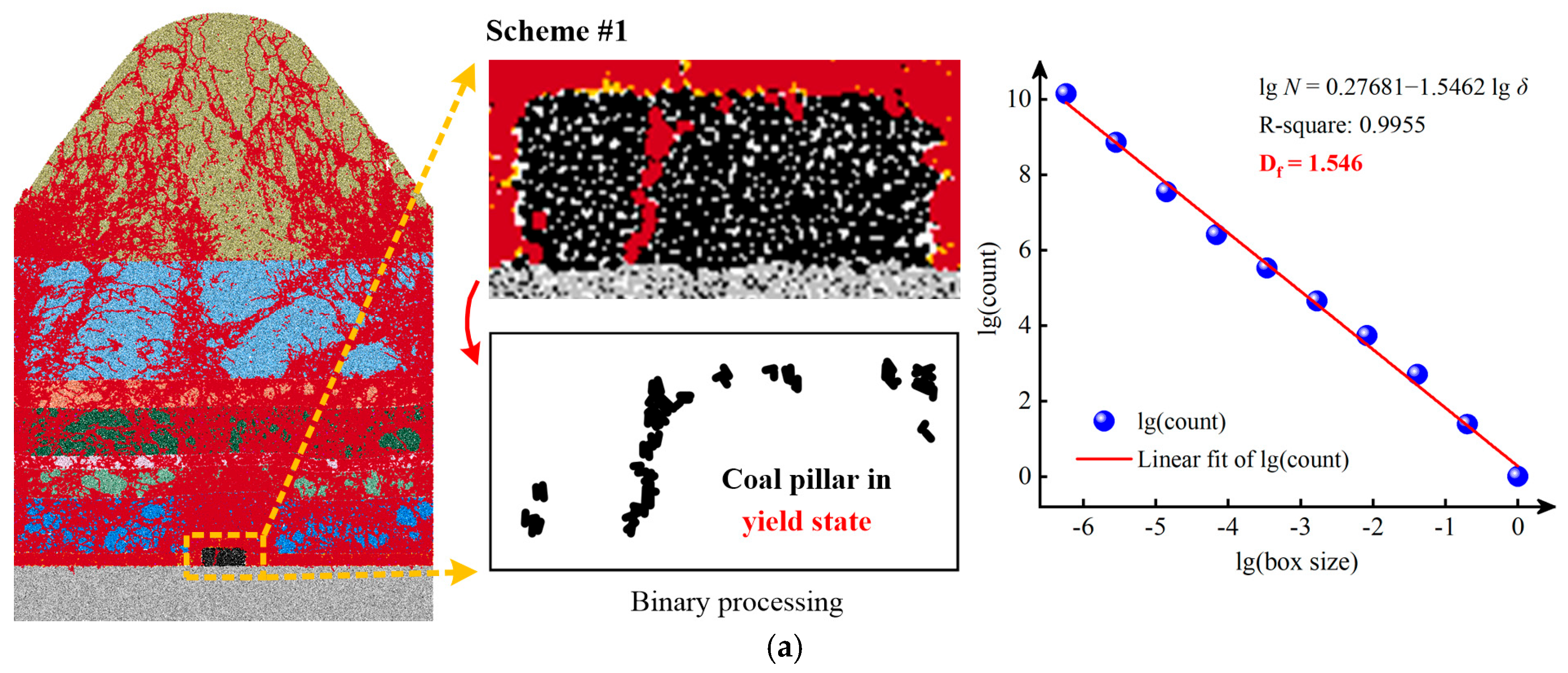
4.2. Fractal Characteristics of Coal Pillar Fractures
4.3. The Number of Fractures and Characteristics of Porosity Evolution within the Coal Pillar
4.4. Discussion
5. Coal Pillar Design Strategy Based on the Fractal Characteristics of Fractures
6. Conclusions
- (1)
- Through UAV observation of the topography of the study area, the surface topographic features of the 20202 working face were determined. On this basis, the stability conditions and design principles of coal pillars were proposed, and the coal pillars were classified into four states, namely steady state, semi-steady state, critical yield state, and yield state, according to the damage degree of the coal pillars. The effects of repeated mining in the working face, the overlying strata base load ratio, the topography of the gully, and the relative spatial position of the gully slope section on the damage degree and stability of the coal pillars were considered to ensure that the coal pillars would be stable during the second mining period.
- (2)
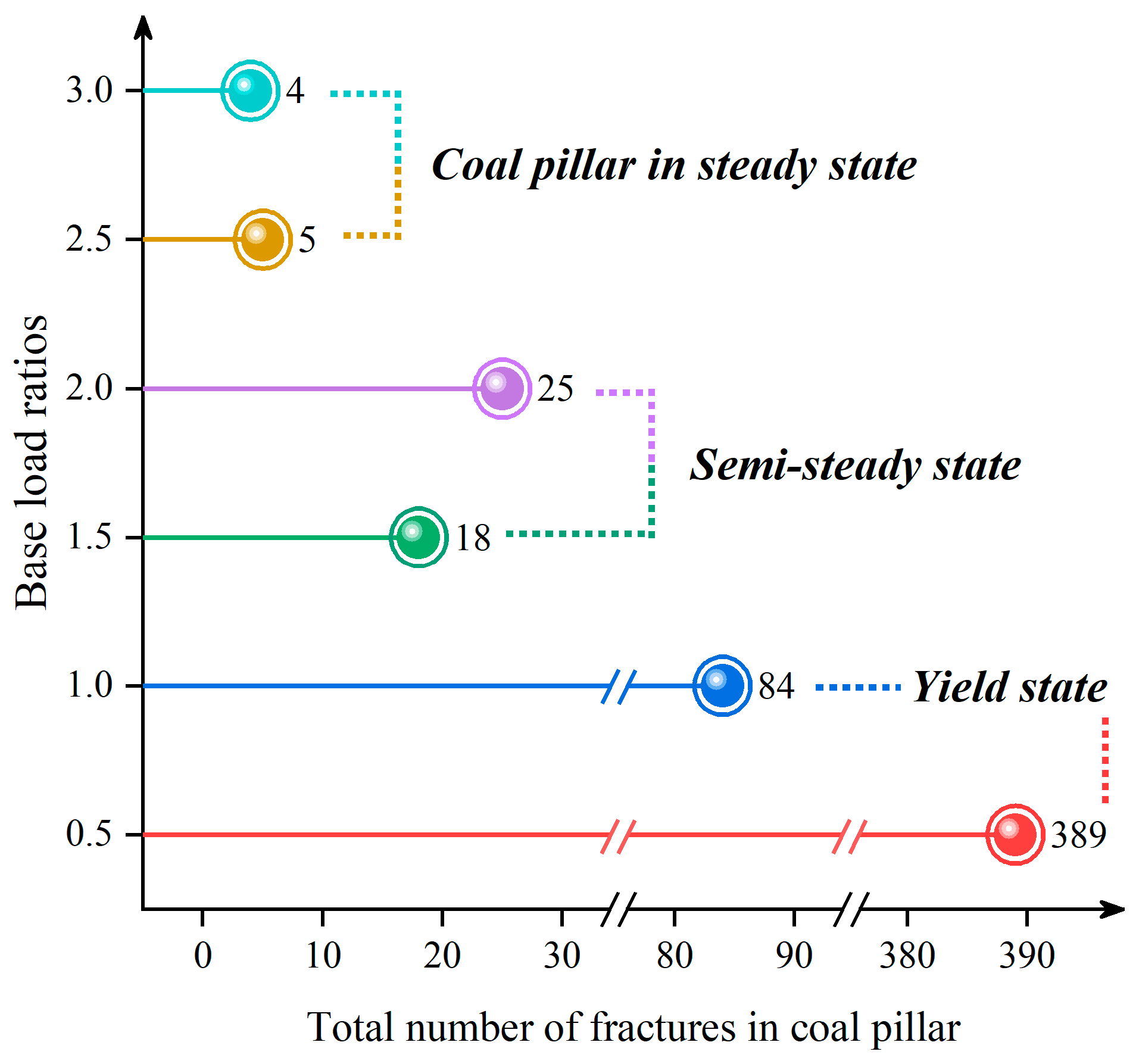
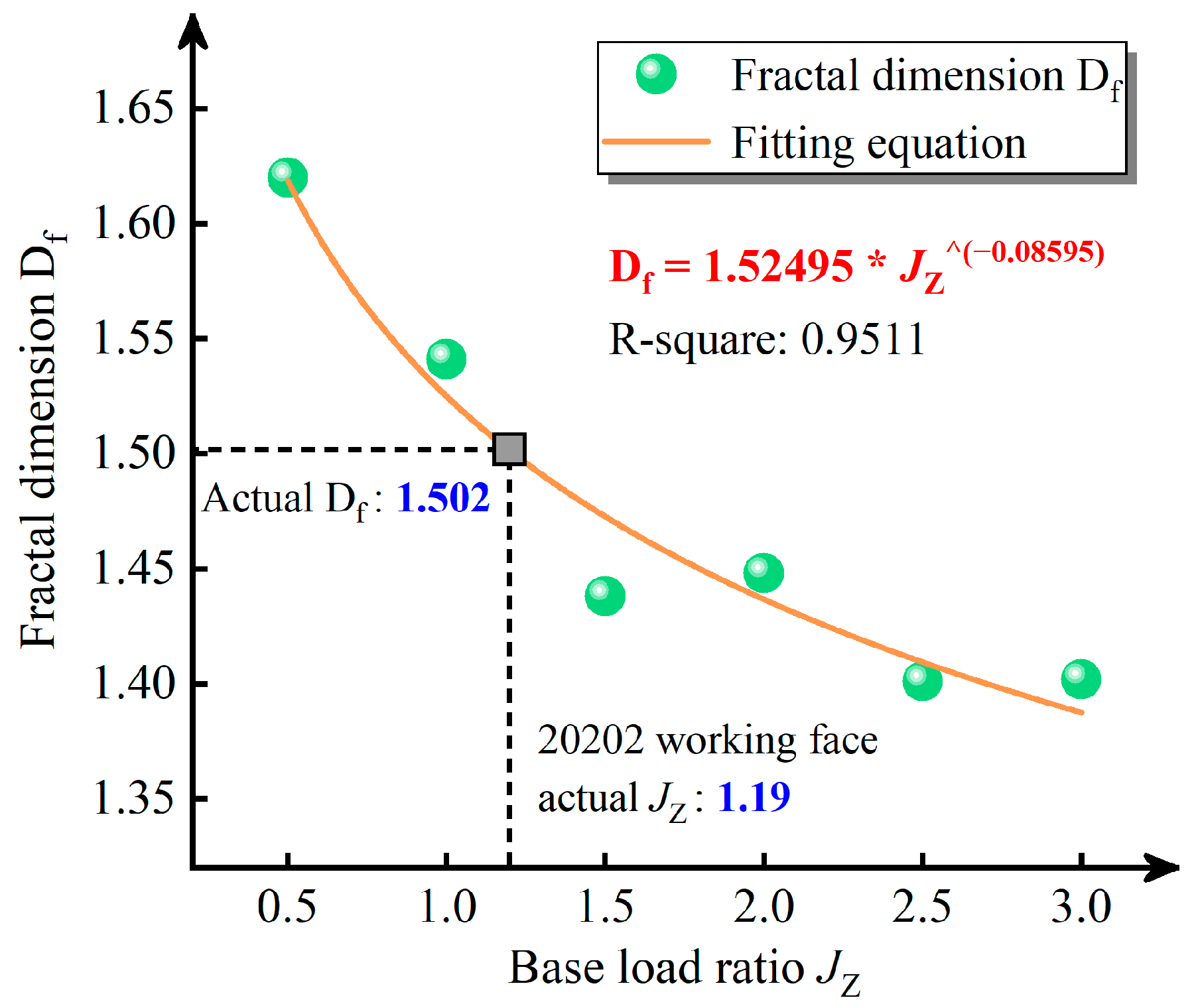
- The PFC2D numerical model was established under the conditions of different overlying strata base load ratios in the gentle terrain area, and the mathematical relationship between the overlying strata base load ratios and the fractal dimensions of the fractures in the coal pillars was obtained, and the corresponding fitting equation was established, which basically conformed to the results of the fractal dimension of the fractures in the coal pillar in the numerical simulation of the actual base load ratio of the 20202 working face, and proved the reliability of the fitting equation. The simulation results show that the damage degree of the coal pillar near the side of the 20203 working face is greater after the second mining period, and the coal pillar is basically in the critical yield state under the condition of the actual overlying strata base load ratio (1.19), which indicates that the width of 15 m for the coal pillar is more reasonable.
- (3)
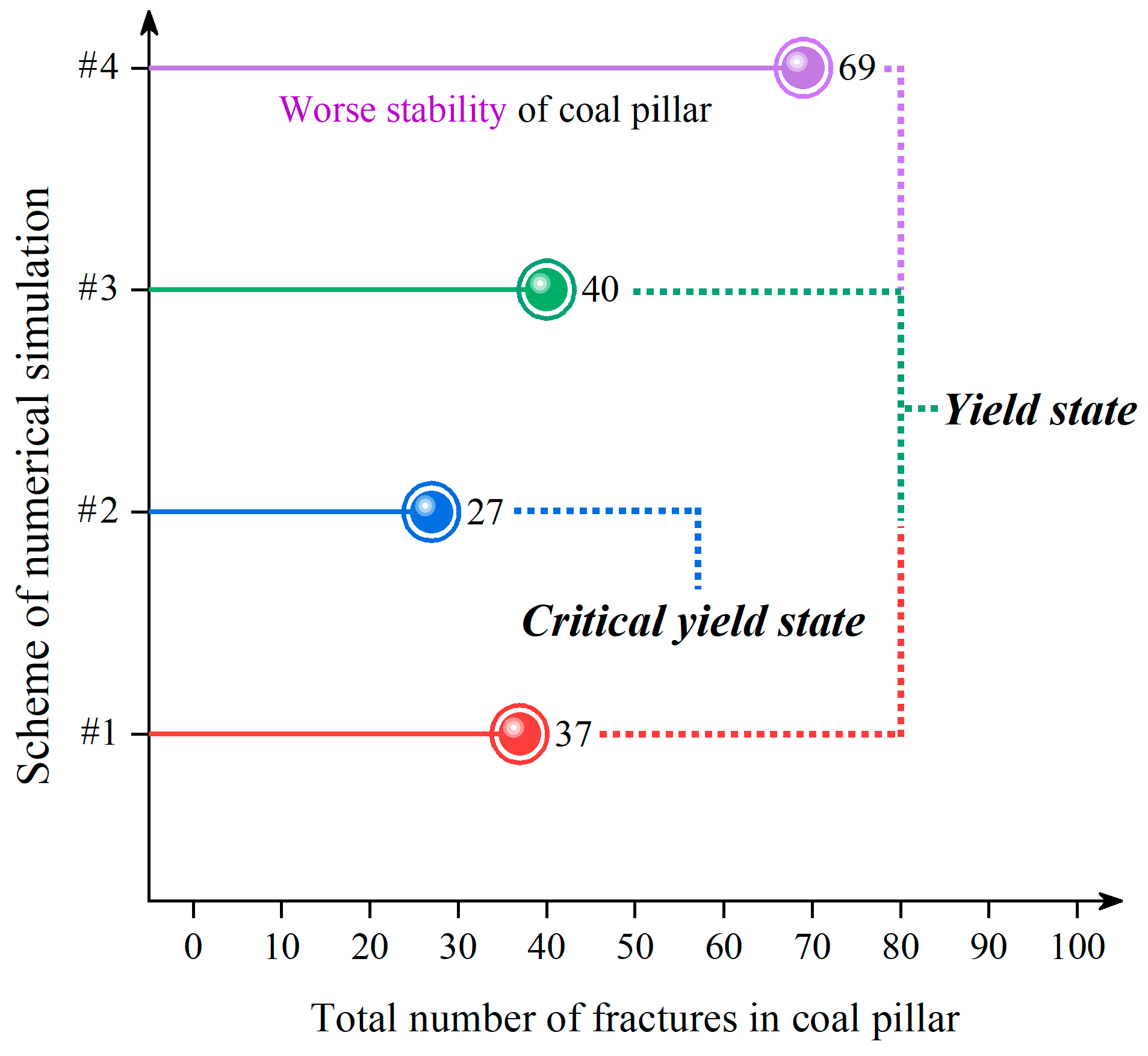
- The numerical simulation results for different gully slope sections in the gully terrain area show that the damage degree of the coal pillar in the gully terrain area is larger than that in the gentle terrain area, and the laws of coal pillar bearing and fracture development are more complicated. Among them, the fractal dimension of the fractures in the coal pillar located below the downslope section of the gully is the largest, and the fractal dimension of the fractures in the coal pillar located below the gully bottom is the smallest, so the coal pillar can be kept below the gully bottom as much as possible by changing the length of the working face, so as to ensure the stability of the coal pillar.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, G.; Liu, Y.; Liang, X.Y.; Huang, H. Hydrogeological characteristics and mechanism of a water-rich coal seam in the Jurassic coalfield, northern Shaanxi Province, China. Arab. J. Geosci. 2020, 13, 1088. [Google Scholar] [CrossRef]
- Wei, J.B.; Wang, S.M.; Song, S.J.; Sun, Q.; Yang, T. Experiment and numerical simulation of overburden and surface damage law in shallow coal seam mining under the gully. Bull. Eng. Geol. Environ. 2022, 81, 207. [Google Scholar] [CrossRef]
- Wang, M.; Xu, Y.L.; Xu, Q.Y.; Shan, C.F.; Li, Z.H.; Nan, H.; Li, Y.F.; Liu, H.L.; Chu, T.X. Stability control of overburden and coal pillars in the gob-side entry under dynamic pressure. Int. J. Rock Mech. Min. Sci. 2023, 170, 105490. [Google Scholar] [CrossRef]
- Xu, X.H.; He, F.L.; Li, X.B.; He, W.R. Research on mechanism and control of asymmetric deformation of gob side coal roadway with fully mechanized caving mining. Eng. Fail. Anal. 2021, 120, 105097. [Google Scholar] [CrossRef]
- Luo, P.; Zhang, Z.Y.; Zhang, L.; Liu, X.Q.; Liu, X.B. Influence of different CO2 phase states on fluid flow pathways in coal: Insights from image reconstruction and fractal study. Bull. Eng. Geol. Environ. 2023, 82, 266. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Xu, G.; Gao, X.J.; Liu, Q.J.; Li, Z.J.; Liu, J.C. Lateral abutment pressure distribution and evolution in wide pillars under the first mining effect. Int. J. Min. Sci. Technol. 2023, 33, 309–322. [Google Scholar] [CrossRef]
- Yang, T.; Yang, Y.R.; Zhang, J.; Gao, S.S.; Li, T. Study on Development Law of Mining-Induced Slope Fracture in Gully Mining Area. Adv. Civ. Eng. 2021, 3, 1–9. [Google Scholar] [CrossRef]
- Ran, Q.C.; Liang, Y.P.; Zou, Q.L.; Hong, Y.; Zhang, B.C.; Liu, H.; Kong, F.J. Experimental investigation on mechanical characteristics of red sandstone under graded cyclic loading and its inspirations for stability of overlying strata. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 11. [Google Scholar] [CrossRef]
- Li, Z.; Xu, J.L.; Ju, J.F.; Zhu, W.B.; Xu, J.M. The effects of the rotational speed of voussoir beam structures formed by key strata on the ground pressure of stopes. Int. J. Rock Mech. Min. Sci. 2018, 108, 67–79. [Google Scholar] [CrossRef]
- Xu, J.L.; Zhu, W.B.; Wang, X.Z.; Zhang, Z.Q. Influencing mechanism of gully terrain on ground pressure behaviors in shallow seam longwall mining. J. China Coal Soc. 2012, 37, 179–185. [Google Scholar]
- Liu, S.F.; Wan, Z.J.; Zhang, Y.; Lu, S.F.; Ta, X.P.; Wu, Z.P. Research on Evaluation and Control Technology of Coal Pillar Stability Based on the Fracture Digitization Method. Measurement 2020, 158, 107713. [Google Scholar] [CrossRef]
- Wang, B.N.; Dang, F.N.; Gu, S.C.; Huang, R.B.; Miao, Y.P.; Chao, W. Method for determining the width of protective coal pillar in the pre-driven longwall recovery room considering main roof failure form. Int. J. Rock Mech. Min. Sci. 2020, 130, 104340. [Google Scholar] [CrossRef]
- Song, C.H.; Lu, C.P.; Zhang, X.F.; Wang, C.; Xie, H.D.; Yan, X.Y.; Yang, H.W. Moment Tensor Inversion and Stress Evolution of Coal Pillar Failure Mechanism. Rock Mech. Rock Eng. 2022, 55, 2371–2383. [Google Scholar] [CrossRef]
- Ran, Q.C.; Liang, Y.P.; Zou, Q.L.; Zhang, B.C.; Li, R.F.; Chen, Z.H.; Ma, T.F.; Kong, F.J.; Liu, H. Characteristics of Mining-Induced Fractures Under Inclined Coal Seam Group Multiple Mining and Implications for Gas Migration. Nat. Resour. Res. 2023, 32, 1481–1501. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, H.K.; Jiang, B.; Li, S.C.; He, M.C.; Wang, D.C.; Lu, W.; Qin, Q.; Gao, S.; Yu, H.C. Research on reasonable coal pillar width of roadway driven along goaf in deep mine. Arab. J. Geosci. 2017, 10, 466. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, C.Y.; Li, J.W.; Wang, W.C. Three-dimensional geological modeling and surface damage in gully area due to shallow coal seam mining. J. Min. Saf. Eng. 2018, 35, 969–977. [Google Scholar]
- Wang, Q.W.; Feng, H.; Tang, P.; Peng, Y.T.; Li, C.A.; Jiang, L.S.; Mitri, H.S. Influence of Yield Pillar Width on Coal Mine Roadway Stability in Western China: A Case Study. Processes 2022, 10, 251. [Google Scholar] [CrossRef]
- Shan, C.H.; Cao, S.G.; Zhang, Z.Y.; Lin, K.W.; Sun, J.L. Numerical Investigation on the Yield Pillar Bearing Capacity under the Two-End-Type Cable Reinforcement. Energies 2023, 16, 6418. [Google Scholar] [CrossRef]
- Liang, T.; Liu, X.L.; Wang, S.J.; Wang, E.Z.; Li, Q.S. Study on the Fractal Characteristics of Fracture Network Evolution Induced by Mining. Adv. Civ. Eng. 2018, 1, 9589364. [Google Scholar] [CrossRef]
- Miao, K.J.; Tu, S.H.; Tu, H.S.; Liu, X.; Li, W.L.; Zhao, H.B.; Tang, L.; Ma, J.Y.; Li, Y. Research on Fractal Evolution Characteristics and Safe Mining Technology of Overburden Fissures under Gully Water Body. Fractal Fract. 2022, 6, 486. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Guo, J.Z.; Xu, B.; Xu, L.L.; Dai, Z.X.; Yin, S.X.; Soltanian, M.R. Quantitative analysis and evaluation of coal mine geological structures based on fractal theory. Energies 2021, 14, 1925. [Google Scholar] [CrossRef]
- Liu, C.; Xue, J.H.; Yu, G.F.; Cheng, X.Y. Fractal characterization for the mining crack evolution process of overlying strata based on microseismic monitoring technology. Int. J. Min. Sci. Technol. 2016, 26, 295–299. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Zhang, Y.B.; Xu, Y.X.; Zheng, Q.; Wang, Z.L.; Guo, L.L. Fracture development and fractal characteristics of overburden rock under repeated mining. Arab. J. Geosci. 2021, 14, 225. [Google Scholar] [CrossRef]
- Han, P.H.; Zhang, C.; Wang, W. Failure analysis of coal pillars and gateroads in longwall faces under the mining-water invasion coupling effect. Eng. Fail. Anal. 2022, 131, 105912. [Google Scholar] [CrossRef]
- Wang, P.; Luan, H.J. Size effect analysis of remaining coal pillar on rock burst caused by fault. Bull. Eng. Geol. Environ. 2022, 81, 1. [Google Scholar] [CrossRef]
- Li, W.L.; Tu, S.H.; Tu, H.S.; Li, Y.; Liu, X.; Miao, K.J. Failure characteristics and control techniques for mining roadway affected by stress accumulation of residual pillars in contiguous coal seams. Eng. Fail. Anal. 2022, 141, 106646. [Google Scholar] [CrossRef]
- Yang, P.J.; Zhang, S.R.; Wang, X.F. Numerical Study on the Characteristics and Control Method of Coal Leakage between Supports in Integrated Mining of Extremely Loose and Soft Coal Seams. Energies 2024, 17, 1013. [Google Scholar] [CrossRef]
- Fan, N.; Wang, J.R.; Zhang, B.; Liu, D.; Wang, R.D. Reasonable Width of Segment Pillar of Fully-Mechanized Caving Face in Inclined Extra-Thick Coal Seam. Geotech. Geol. Eng. 2020, 38, 4189–4200. [Google Scholar] [CrossRef]
- Ran, Q.C.; Chen, P.; Liang, Y.P.; Ye, C.F.; Zhang, B.C.; Wu, Z.P.; Ma, T.F.; Chen, Z.H. Hardening-damage evolutionary mechanism of sandstone under multi-level cyclic loading. Eng. Fract. Mech. 2024, 307, 110291. [Google Scholar]
- Zhu, D.F.; Yu, B.B.; Wang, D.Y.; Zhang, Y.J. Fusion of finite element and machine learning methods to predict rock shear strength parameters. J. Geophys. Eng. 2024, gxae064. [Google Scholar] [CrossRef]
- Hu, J.H.; Ren, Q.F.; Yang, D.J.; Ma, S.W.; Shang, J.L.; Ding, X.T.; Luo, Z.Q. Cross-scale characteristics of backfill material using NMR and fractal theory. Trans. Nonferrous Met. Soc. China 2020, 30, 1347–1363. [Google Scholar] [CrossRef]
- Hou, S.S.; He, X.; Meng, X.S.; Cheng, L.; Feng, Z.; Liu, M.X.; Li, A.; Guo, C.B.; Ji, F. Mesostructure and strength characteristics of granite under freeze-thaw cycles based on CT scanning. J. Geomech. 2024, 30, 462–472. [Google Scholar]
- Zhang, G.C.; He, F.L.; Jia, H.G.; Lai, Y.H. Analysis of Gateroad Stability in Relation to Yield Pillar Size: A Case Study. Rock Mech. Rock Eng. 2017, 50, 1263–1278. [Google Scholar] [CrossRef]
- Yang, P.J.; Zhang, S.R.; Liu, C.Y. Study on Shear Failure Process and Zonal Disintegration Mechanism of Roadway under High Ground Stress: A Numerical Simulation via a Strain-Softening Plastic Model and the Discrete Element Method. Appl. Sci. 2024, 14, 4106. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, Z.Y.; Kuang, T.J.; Liu, J.R. Stress Changes and Deformation Monitoring of Longwall Coal Pillars Located in Weak Ground. Rock Mech. Rock Eng. 2016, 49, 3293–3305. [Google Scholar] [CrossRef]



| Lithology | Elastic Modulus (Gpa) | Shear Modulus (Gpa) | Friction Angle (°) | Cohesion (Mpa) | Tensile Strength (Mpa) |
|---|---|---|---|---|---|
| loess formation | 0.15 | 0.13 | 9.00 | 0.26 | 0.04 |
| fine grained sandstone | 8.56 | 7.42 | 38.89 | 3.08 | 1.09 |
| siltstone | 4.86 | 4.17 | 42.03 | 4.23 | 1.87 |
| fine-siltstone interbedding | 13.54 | 12.03 | 41.22 | 4.85 | 3.31 |
| medium grained sandstone | 18.77 | 15.12 | 43.54 | 5.21 | 4.13 |
| siltstone | 8.44 | 6.93 | 42.08 | 4.31 | 2.12 |
| compound main roof | 12.04 | 10.23 | 33.47 | 4.29 | 3.13 |
| siltstone | 7.92 | 6.42 | 41.87 | 4.28 | 2.07 |
| 2-2 coal seam | 4.57 | 3.43 | 35.46 | 4.91 | 0.42 |
| siltstone | 9.94 | 8.13 | 42.07 | 4.59 | 2.08 |
| Base Load Ratio | Loess Formation Thickness (m) | Fractal Dimension Df | Correlation Coefficient | Fracture Number | Coal Pillar State |
|---|---|---|---|---|---|
| 0.5 | 205 | 1.620 | 0.9974 | 389 | yield state |
| 1 | 102.5 | 1.541 | 0.9959 | 84 | yield state |
| 1.5 | 68.33 | 1.438 | 0.9929 | 18 | semi-steady state |
| 2 | 51.25 | 1.448 | 0.9936 | 25 | semi-steady state |
| 2.5 | 41 | 1.401 | 0.9909 | 5 | steady state |
| 3 | 34.17 | 1.402 | 0.9908 | 4 | steady state |
| Scheme Order | Gully Slope Section | Fractal Dimension Df | Correlation Coefficient | Fracture Number | Coal Pillar State |
|---|---|---|---|---|---|
| #1 | peak of the gully | 1.546 | 0.9955 | 37 | yield state |
| #2 | gully bottom | 1.512 | 0.9942 | 27 | critical yield state |
| #3 | upslope section of the gully | 1.547 | 0.9956 | 40 | yield state |
| #4 | downslope section of the gully | 1.594 | 0.9963 | 69 | yield state |
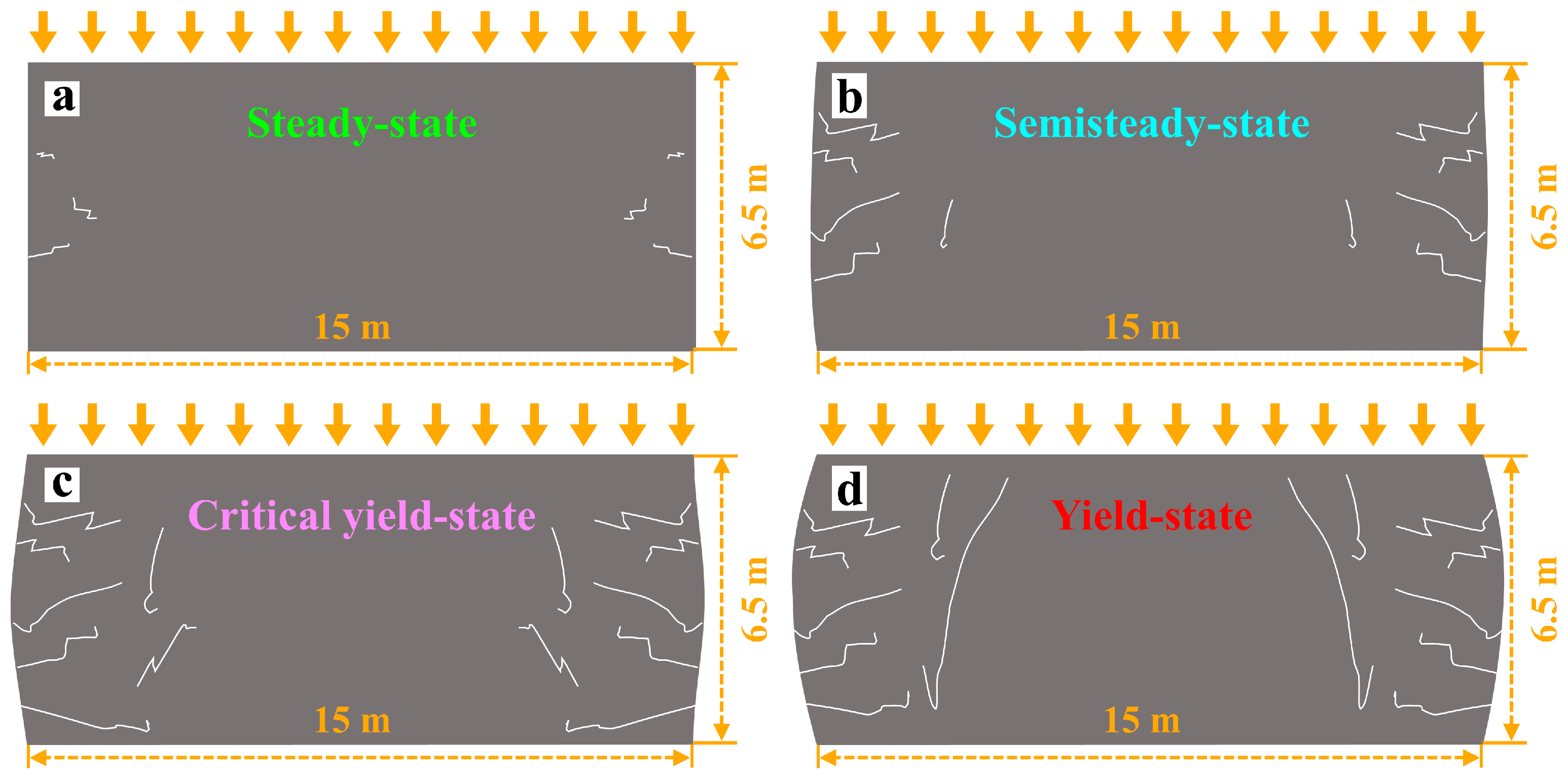
| Type | Steady State | Semi-steady State | Critical Yield State | Yield State |
|---|---|---|---|---|
| fracture number | <10 | 10~25 | 26~35 | >35 |
| fractal dimension Df | <1.420 | 1.420~1.499 | 1.500~1.535 | >1.535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Liang, Y.; Miao, K.; Li, Q.; Liu, S.; Ran, Q.; Sun, W.; Yin, H.; Ma, Y. Damage Law and Reasonable Width of Coal Pillar under Gully Area: Linking Fractal Characteristics of Coal Pillar Fractures to Their Stability. Fractal Fract. 2024, 8, 407. https://doi.org/10.3390/fractalfract8070407
Wu Z, Liang Y, Miao K, Li Q, Liu S, Ran Q, Sun W, Yin H, Ma Y. Damage Law and Reasonable Width of Coal Pillar under Gully Area: Linking Fractal Characteristics of Coal Pillar Fractures to Their Stability. Fractal and Fractional. 2024; 8(7):407. https://doi.org/10.3390/fractalfract8070407
Chicago/Turabian StyleWu, Zhaopeng, Yunpei Liang, Kaijun Miao, Qigang Li, Sichen Liu, Qican Ran, Wanjie Sun, Hualong Yin, and Yun Ma. 2024. "Damage Law and Reasonable Width of Coal Pillar under Gully Area: Linking Fractal Characteristics of Coal Pillar Fractures to Their Stability" Fractal and Fractional 8, no. 7: 407. https://doi.org/10.3390/fractalfract8070407
APA StyleWu, Z., Liang, Y., Miao, K., Li, Q., Liu, S., Ran, Q., Sun, W., Yin, H., & Ma, Y. (2024). Damage Law and Reasonable Width of Coal Pillar under Gully Area: Linking Fractal Characteristics of Coal Pillar Fractures to Their Stability. Fractal and Fractional, 8(7), 407. https://doi.org/10.3390/fractalfract8070407






