Comparative Analysis of the Chaotic Behavior of a Five-Dimensional Fractional Hyperchaotic System with Constant and Variable Order
Abstract
1. Introduction
- 5D constant-order fractional Caputo hyperchaotic system:
- 5D variable-order fractional Caputo hyperchaotic system:
- 5D constant-order fractional Caputo–Fabrizio hyperchaotic system:
- 5D variable-order fractional Caputo–Fabrizio hyperchaotic system:
2. Preliminaries
3. Computational Techniques for Solving a 5D Constant- and Variable-Order Fractional Caputo Hyperchaotic System
3.1. Computational Techniques for Solving a 5D Constant-Order Caputo Hyperchaotic System
3.2. Computational Techniques for Solving a 5D Variable-Order Fractional Caputo Hyperchaotic System
4. Computational Techniques for Solving the 5D Constant- and Variable-Order Fractional CF Hyperchaotic Systems
4.1. Numerical Solutions for Solving the 5D Constant-Order Fractional CF Hyperchaotic System
4.2. A Computational Method for Solving the 5D Variable-Order Fractional CF Hyperchaotic System
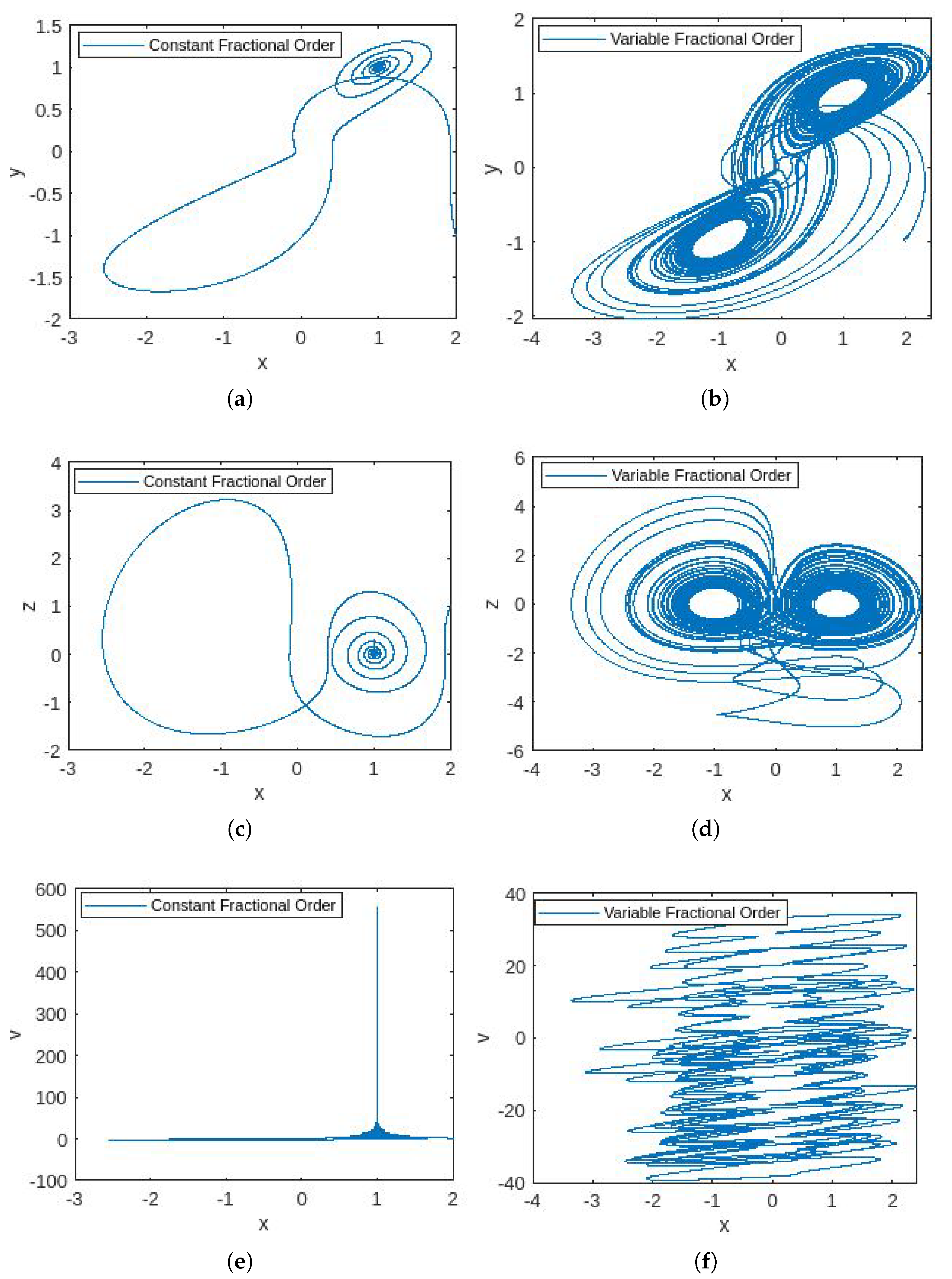
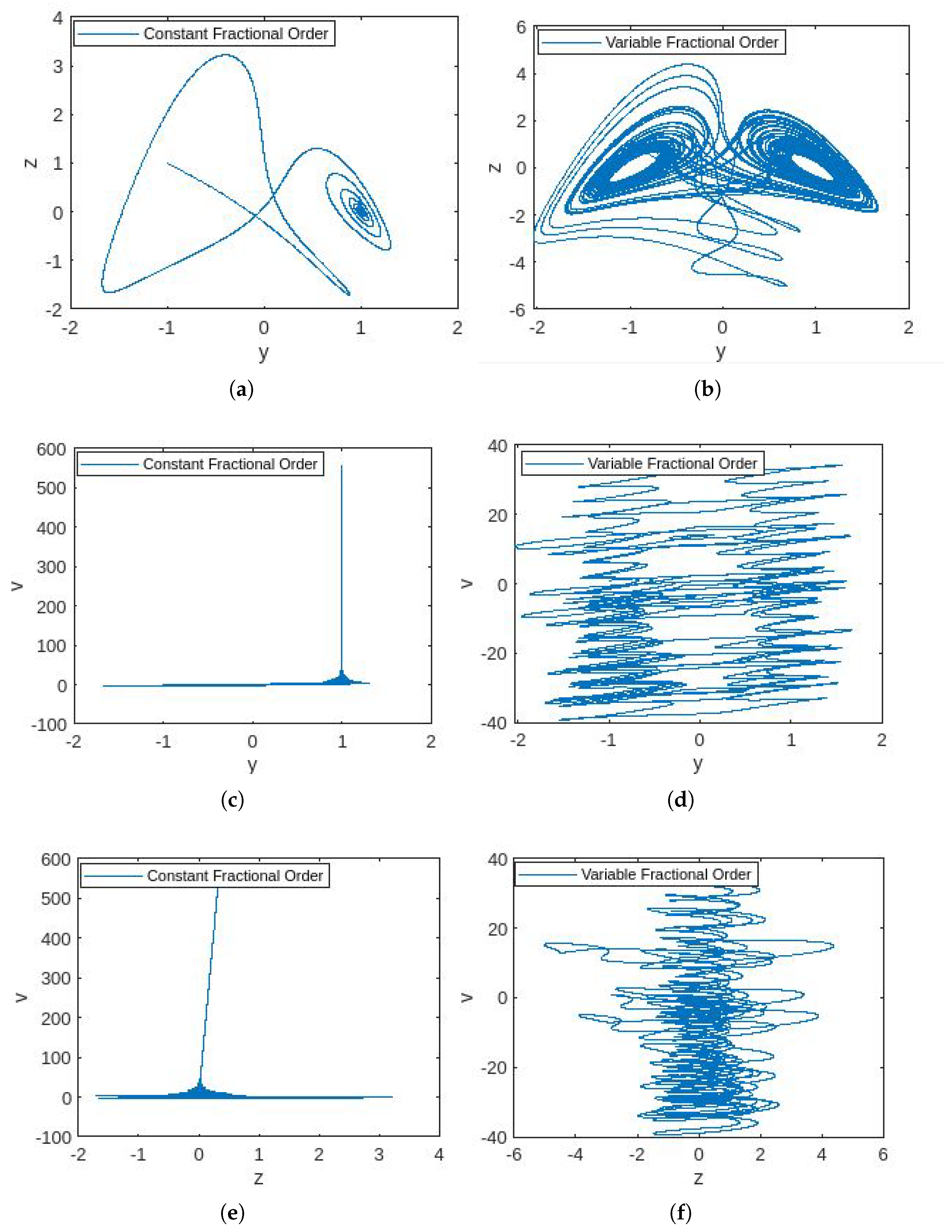
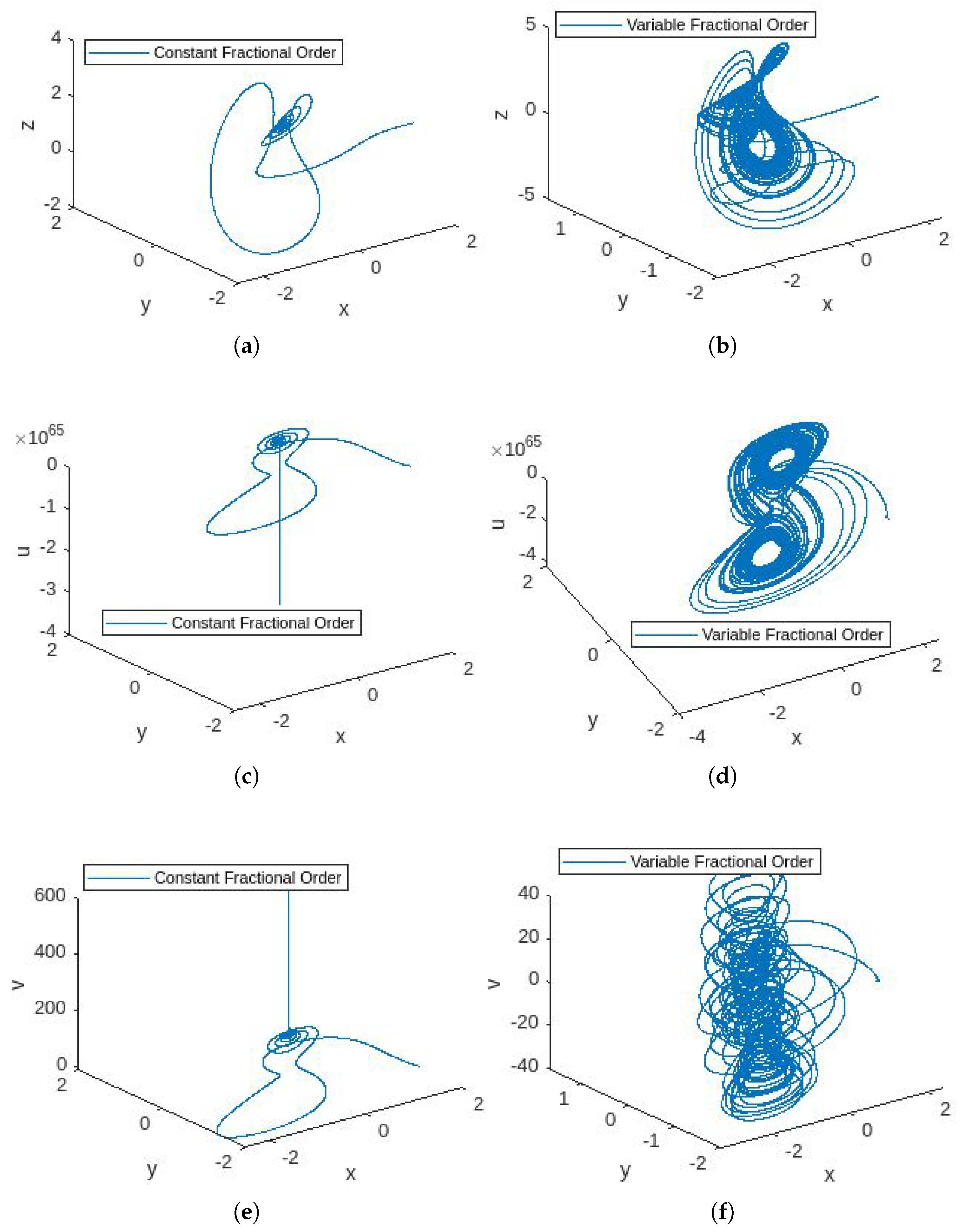
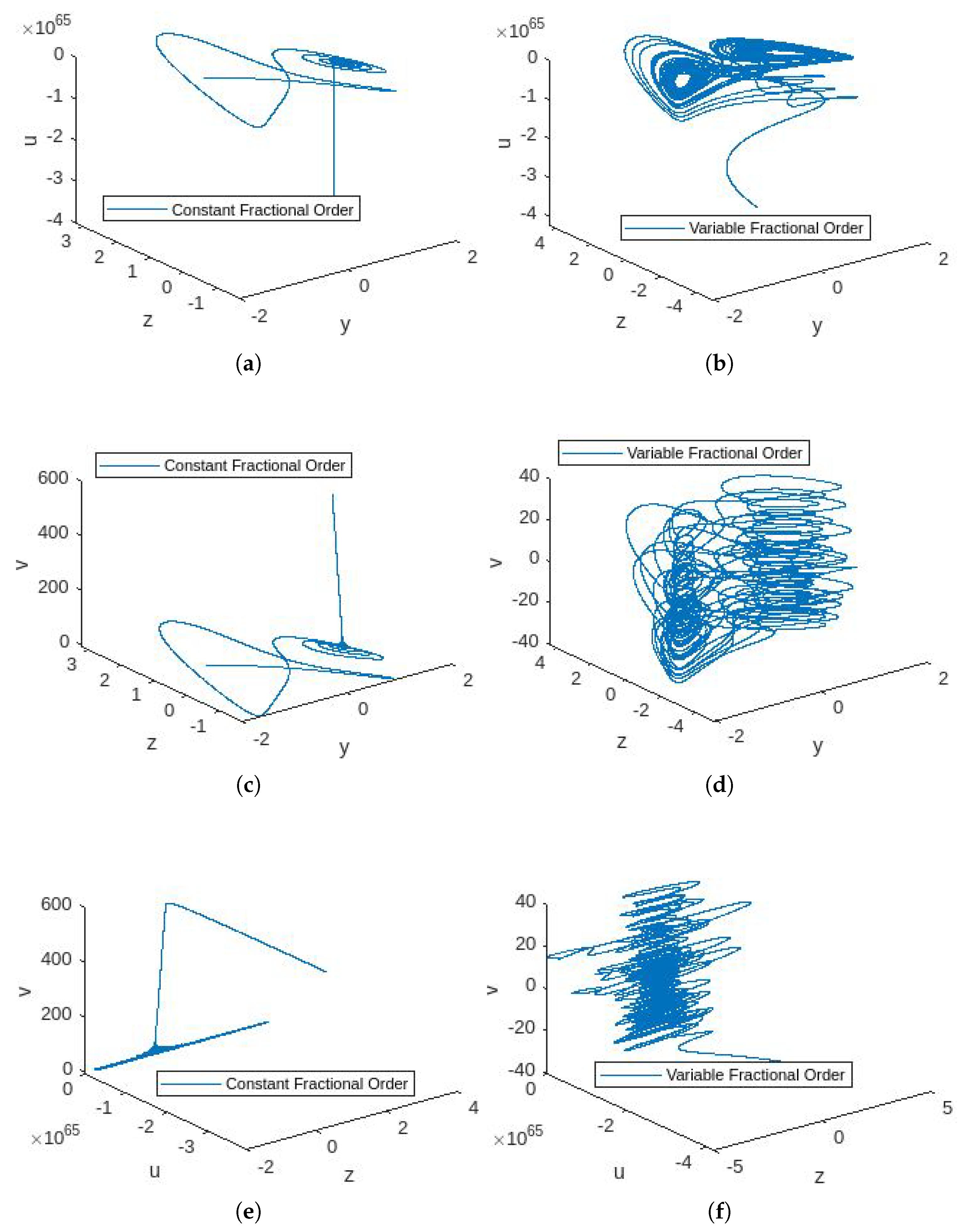
4.3. Simulations
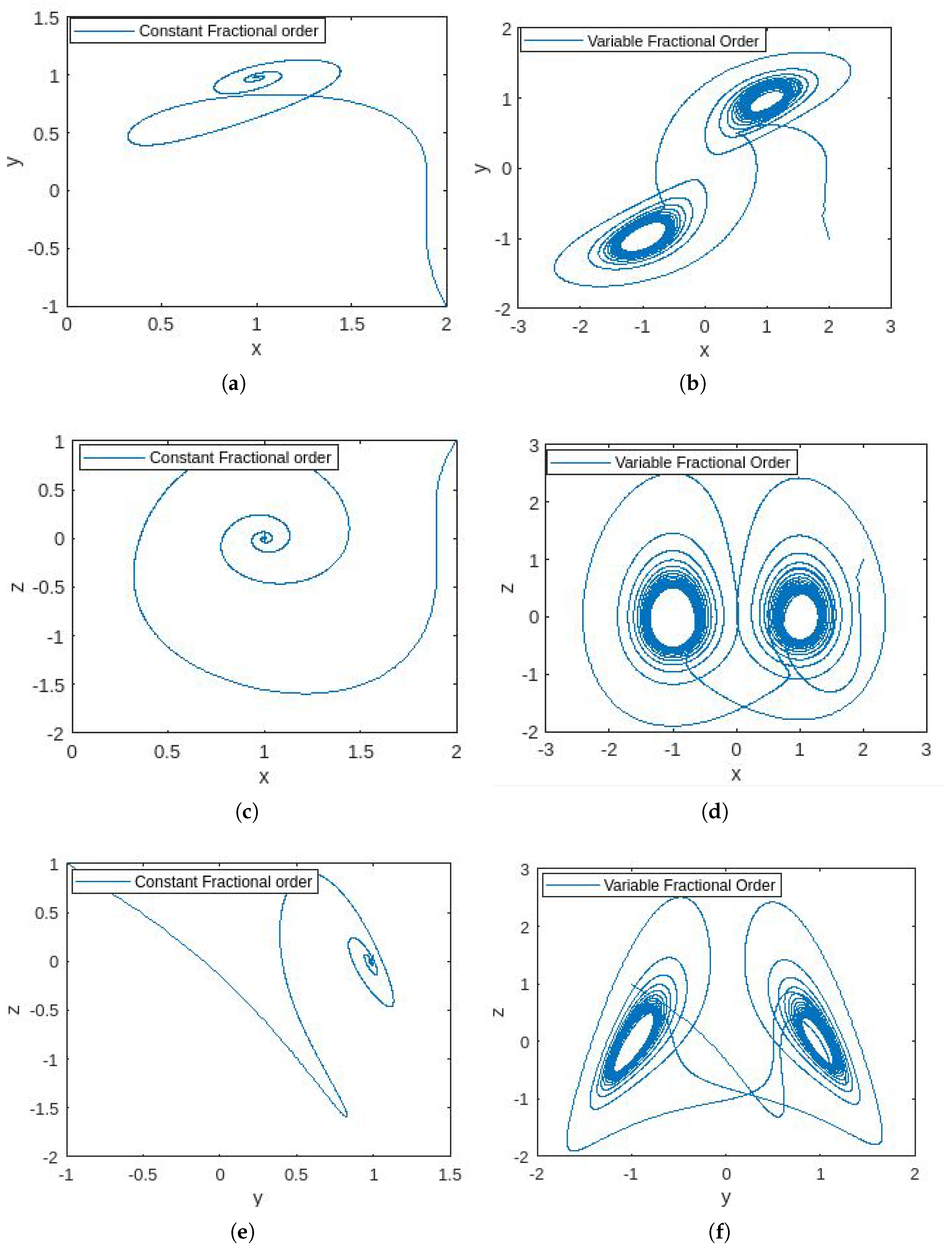
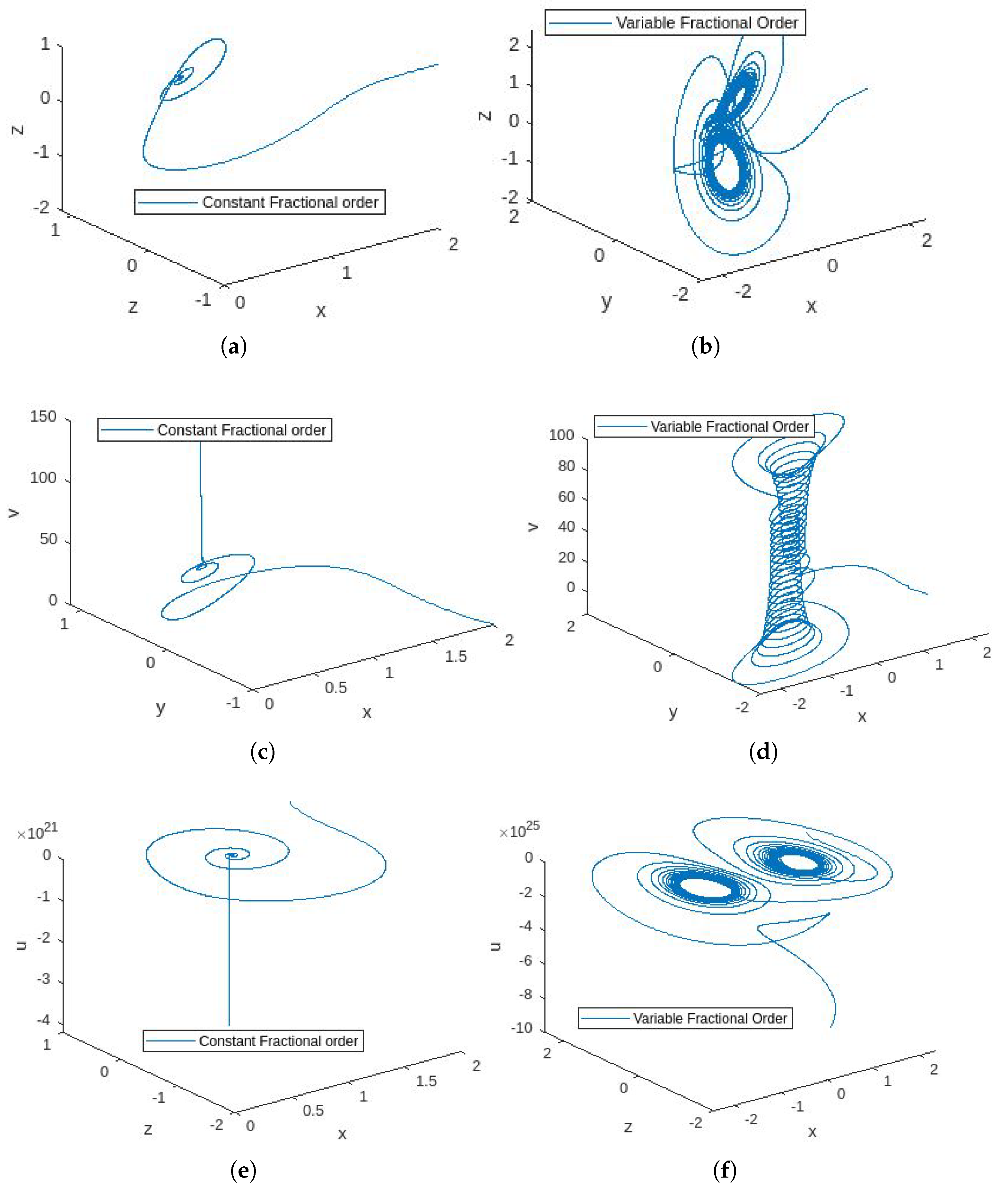
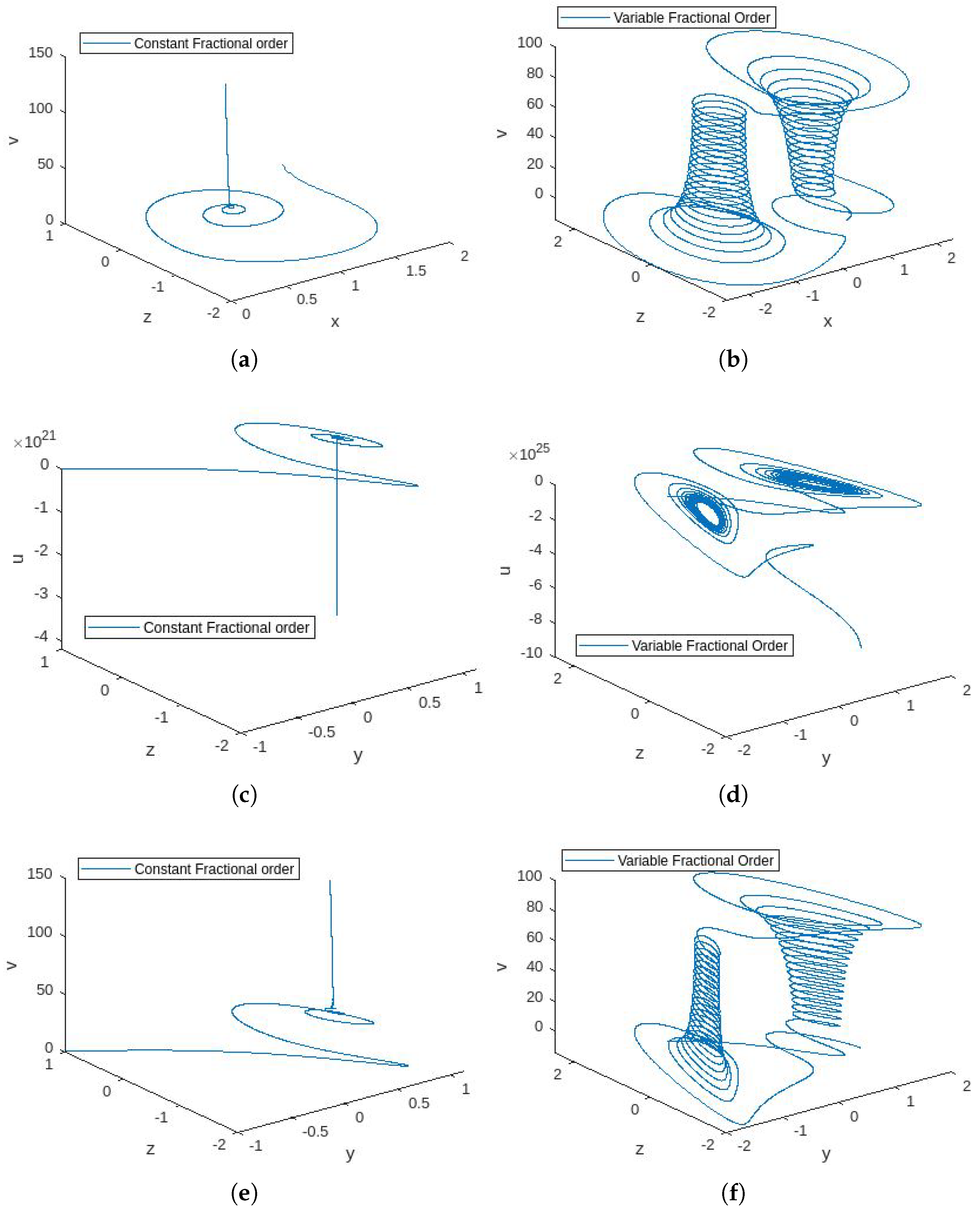
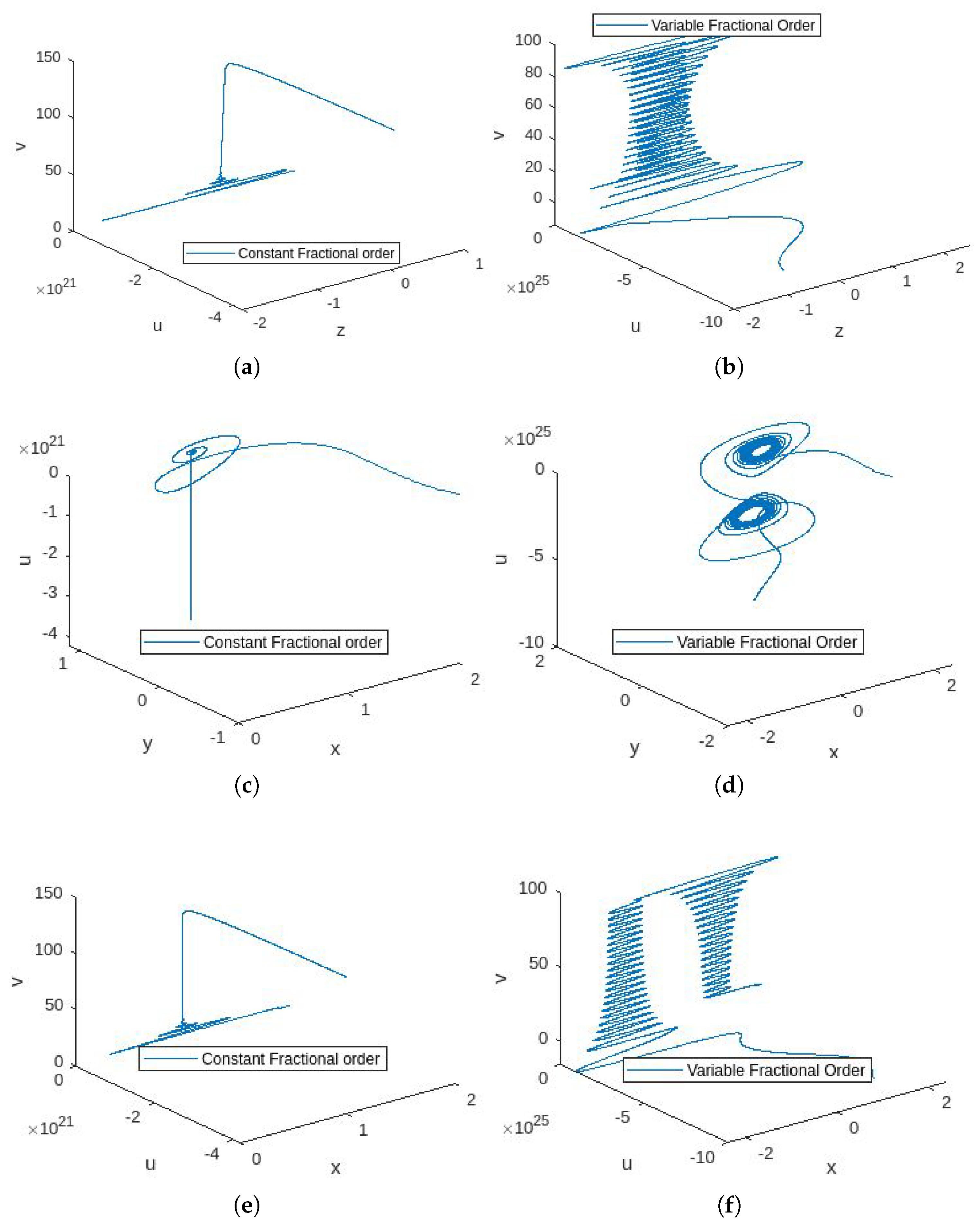
4.4. Discussion
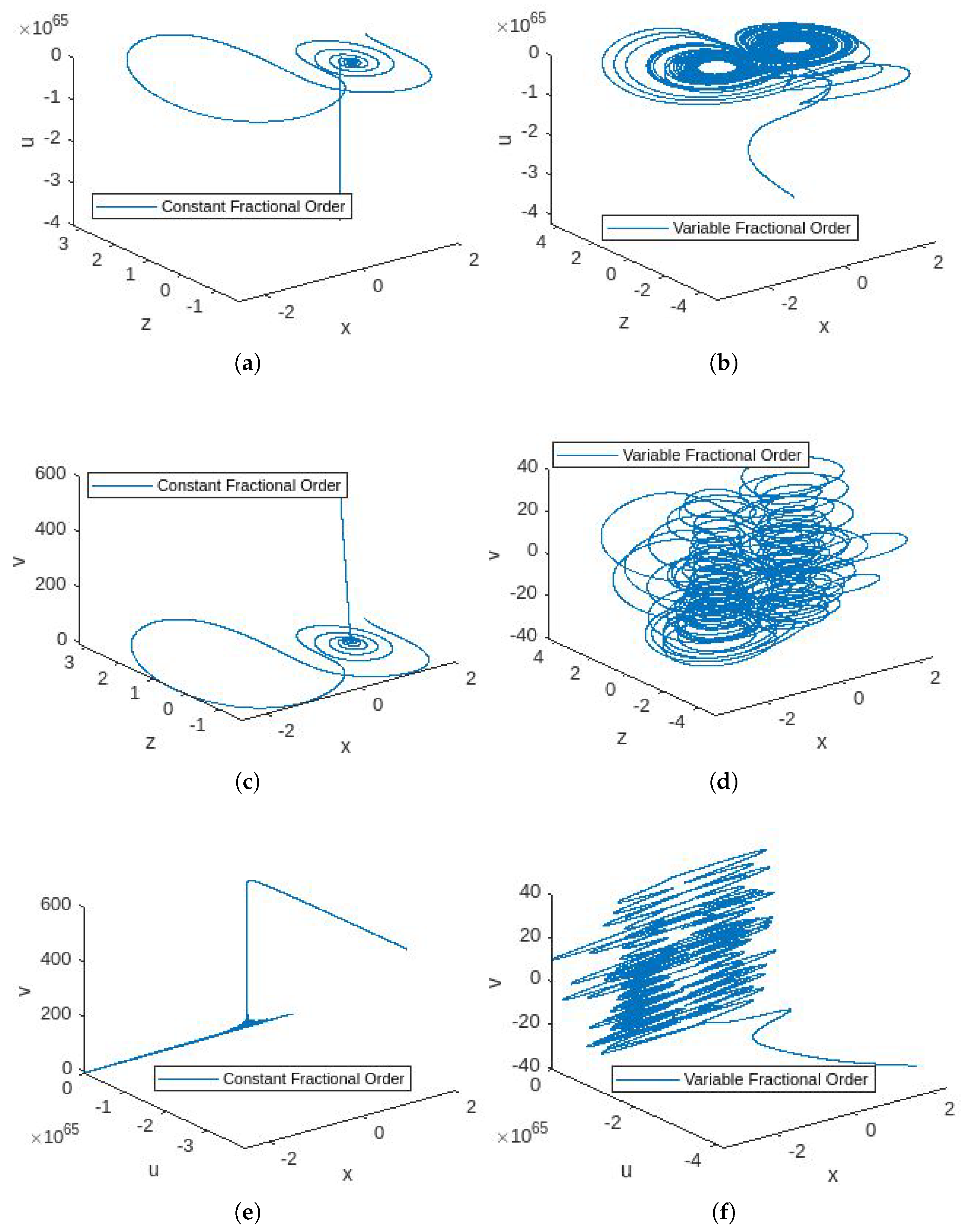
- In Figure 1, the phase portraits illustrating the behavior of the 5D constant- and variable-order fractional hyperchaotic systems with the Caputo derivative are presented.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rossler, O.E. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Lai, Q. 2D hyperchaotic system based on Schaffer function for image encryption. Expert Syst. Appl. 2023, 213, 119076. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Lai, Q. Design of two dimensional hyperchaotic system through optimization benchmark function. Chaos Solitons Fractals 2023, 167, 113032. [Google Scholar] [CrossRef]
- Zhu, S.; Deng, X.; Zhang, W.; Zhu, C. Construction of a new 2D hyperchaotic map with application in efficient pseudo-random number generator design and color image encryption. Mathematics 2023, 11, 3171. [Google Scholar] [CrossRef]
- Gao, X. Image encryption algorithm based on 2D hyperchaotic map. Opt. Laser Technol. 2021, 142, 107252. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, Z.; Huang, T. Two-dimensional cosine–sine interleaved chaotic system for secure communication. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2479–2483. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, Z.; Chen, P.; Huang, Z.; Huang, T. A simple chaotic model with complex chaotic behaviors and its hardware implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 3676–3688. [Google Scholar] [CrossRef]
- Li, W.; Yan, W.; Zhang, R.; Wang, C.; Ding, Q. A new 3D discrete hyperchaotic system and its application in secure transmission. Int. J. Bifurc. Chaos 2019, 29, 1950206. [Google Scholar] [CrossRef]
- Huang, L.; Li, C.; Liu, J.; Zhong, Y.; Zhang, H. A novel 3D non-degenerate hyperchaotic map with ultra-wide parameter range and coexisting attractors periodic switching. Nonlinear Dyn. 2024, 112, 2289–2304. [Google Scholar] [CrossRef]
- Cui, N.; Li, J. A new 4D hyperchaotic system and its control. AIMS Math. 2023, 8, 905–923. [Google Scholar] [CrossRef]
- Leutcho, G.D.; Wang, H.; Fozin, T.F.; Sun, K.; Njitacke, Z.T.; Kengne, J. Dynamics of a new multistable 4D hyperchaotic Lorenz system and its applications. Int. J. Birfurc. Chaos 2022, 32, 2250001. [Google Scholar] [CrossRef]
- Ojoniyi, O.S.; Njah, N.A. A 5D hyperchaotic Sprott B system with coexisting hidden attractors. Chaos Solitons Fractals 2016, 87, 172–181. [Google Scholar] [CrossRef]
- Yu, F.; Liu, L.; Qian, S.; Li, L.; Huang, Y.; Shi, C.; Cai, S.; Wu, X.; Du, S.; Wan, Q. Chaos based application of a novel multistable 5D memristive hyperchaotic system with coexisting multiple attractors. Complexity 2020, 2020, 8034196. [Google Scholar] [CrossRef]
- Li, J.; Cui, N. Dynamical analysis of a new 5D hyperchaotic system. Phys. Scr. 2023, 98, 105205. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Zhang, M.; Wang, Z. A highly secure image encryption algorithm based on conservative hyperchaotic system and dynamic biogenetic gene algorithms. Chaos Solitons Fractals 2023, 171, 113450. [Google Scholar] [CrossRef]
- Kocak, O.; Erkan, U.; Toktas, A.; Gao, S. PSO-based image encryption scheme using modular integrated logistic exponential map. Expert Syst. Appl. 2024, 237, 121452. [Google Scholar] [CrossRef]
- Li, H.; Yu, S.; Feng, W.; Chen, Y.; Zhang, J.; Qin, Z.; Zhu, Z.; Wozniak, M. Exploiting dynamic vector-level operations and a 2D-enhanced logistic modular map for efficient chaotic image encryption. Entropy 2023, 25, 1147. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Zhao, X.; Zhang, J.; Qin, Z.; Zhang, J.; He, Y. Image encryption algorithm based on plane-level image filtering and discrete logarithmic transform. Mathematics 2022, 10, 2751. [Google Scholar] [CrossRef]
- Wen, H.; Lin, Y. Cryptanalysis of an image encryption algorithm using quantum chaotic map and DNA coding. Expert Syst. Appl. 2024, 237, 121514. [Google Scholar] [CrossRef]
- Nestor, T.; Belazi, A.; Abd-El-Atty, B.; Aslam, M.N.; Volos, C.; Dieu, N.J.D.; Abd-El-Latif, A.A. A new 4D hyperchaotic system with dynamics analysis, synchronization, and application to image encryption. Symmetry 2022, 14, 424. [Google Scholar] [CrossRef]
- Wen, H.; Huang, Y.; Lin, Y. High-quality color image compression-encryption using chaos and block permutation. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101660. [Google Scholar] [CrossRef]
- Hui, Y.; Liu, H.; Fang, P. A DNA image encryption based on a new hyperchaotic system. Multimed. Tools Appl. 2023, 82, 21983–22007. [Google Scholar] [CrossRef]
- Benkouider, K.; Sambas, A.; Bonny, T.; Nassan, W.A.; Moghrabi, I.A.R.; Sulaiman, I.M.; Hassan, B.A.; Mamat, M. A comprehensive study of the novel 4D hyperchaotic system with self-exited multistability and application in the voice encryption. Sci. Rep. 2024, 14, 12993. [Google Scholar] [CrossRef] [PubMed]
- Bonny, T.; Nassan, W.A.; Baba, A. Voice encryption using a unified hyper-chaotic system. Multimed. Tools Appl. 2023, 82, 1067–1085. [Google Scholar] [CrossRef]
- Wen, H.; Lin, Y.; Xie, Z.; Liu, T. Chaos-based block permutation and dynamic sequence multiplexing for video encryption. Sci. Rep. 2023, 13, 14721. [Google Scholar] [CrossRef] [PubMed]
- Naik, R.B.; Singh, U. A review on applications of chaotic maps in psuedo-random number generators and encryption. Ann. Data Sci. 2022, 11, 25–50. [Google Scholar] [CrossRef]
- Bonny, T.; Debsi, R.A.; Majzoub, S.; Elwakil, A.S. Hardware optimized FPGA implementations of high-speed true random bit generators based on switching-type chaotic oscillators. Circuits Sys. Signal Process. 2019, 38, 1342–1359. [Google Scholar] [CrossRef]
- Wong, K.-W.; Lin, Q.; Chen, J. Simultaneous arithmetic coding and encryption using chaotic maps. IEEE Trans. Circuits Sys. II Express Briefs 2010, 57, 146–150. [Google Scholar] [CrossRef]
- Al-Kateeb, Z.N.; Mohammed, S.J. Encrypting an audio file based on integer wavelet transform and hand geometry. Telecommun. Comput. Electron. Control 2020, 18, 2012–2017. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus. Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA, 1974; p. 9780125255509. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel, Prog. Fract.Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Iskakova, K.; Alam, M.M.; Ahmad, S.; Saifullah, S.; Akgul, A.; Yılmaz, G. Dynamical study of a novel 4D hyperchaotic system: An integer and fractional order analysis. Math. Comput. Simul. 2023, 208, 219–245. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting newly designed fractional-order 3D lorenz chaotic system and 2D discrete polynomial hyper-chaotic map for high-performance multi-image encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A.; Alomari, Q.M.M.; Afef, K.; Inc, M. Dynamics of generalized time-fractional viscous-capillarity compressible fluid model. Opt. Quantum Electron. 2024, 56, 629. [Google Scholar] [CrossRef]
- Sene, N. Theory and applications of new fractional-order chaotic system under Caputo operator. Int. J. Optim. Control Theor. Appl. 2022, 12, 20–38. [Google Scholar] [CrossRef]
- Deng, H.; Li, T.; Wang, Q.; Li, H. A fractional-order hyperchaotic system and its synchronization. Chaos Solitons Fractals 2009, 41, 962–969. [Google Scholar] [CrossRef]
- Balootaki, M.A.; Rahmani, H.; Moeinkhah, H.; Mohammadzadeh, A. On the synchronization and stabilization of fractional-order chaotic systems: Recent advances and future perspectives. Phys. A Stat. Mech. Appl. 2020, 551, 124203. [Google Scholar] [CrossRef]
- Rahman, Z.A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Hu, Y.F.; Alhameed, R.A.A.; Alhasnawi, B.N. A New Fractional-Order Chaotic System with Its Analysis, Synchronization, and Circuit Realization for Secure Communication Applications. Mathematics 2021, 20, 2593. [Google Scholar] [CrossRef]
- Fuentes, O.M.; Garcia, J.J.M.; Aguilar, J.F.G. Generalized synchronization of commensurate fractional-order chaotic systems: Applications in secure information transmission. Digit. Signal Process. 2022, 126, 103494. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Ma, C.; Cao, Y. Dynamic analysis of an improper fractional-order laser chaotic system and its image encryption application. Opt. Lasers Eng. 2020, 129, 106031. [Google Scholar] [CrossRef]
- Mohamed, S.M.; Sayed, W.S.; Madian, A.H.; Radwan, A.G.; Said, L.A. An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System. Electronics 2023, 12, 1219. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Ye, X. A new fractional-order chaos system of Hopfield neural network and its application in image processing. Chaos Solitons Fractals 2022, 157, 111889. [Google Scholar] [CrossRef]
- Chen, L.; Yin, H.; Huang, T.; Yuan, L.; Zheng, S.; Yin, L. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 2020, 125, 174–184. [Google Scholar] [CrossRef] [PubMed]
- Azzawi, S.F.A.; Hasan, A.M. New 5D Hyperchaotic system derived from the Sprott C system: Properties and Anti Synchronization. J. Intell. Syst. Control 2023, 2, 110–122. [Google Scholar] [CrossRef]
- Samko, S. Fractional integration and differentiation of variable order: An overview. Nonlinear Dyn. 2013, 71, 653–662. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Castillo, O. Application of variable-order fractional calculus in neural networks: Where do we stand? Eur. Phys. J. Spec. Top. 2022, 231, 1753–1756. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Dabiri, A.; Machado, J.A.T. Application of variable-order fractional calculus in solid mechanics. Appl. Eng. Life Soc. Sci. Part A 2019, 7, 207–224. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Application of variable- and distributed-order fractional operators to the dynamic analysis of nonlinear oscillators. Nonlinear Dyn. 2020, 100, 561–580. [Google Scholar] [CrossRef]
- Perez, J.E.S.; Aguilar, J.F.G.; Atangana, A. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals 2018, 114, 175–185. [Google Scholar] [CrossRef]
- Butt, A.I.K.; Ahmad, W.; Rafiq, M.; Baleanu, D. Numerical analysis of Atangana-Baleanu fractional model to understand the propagation of a novel corona virus pandemic. Alex. Eng. J. 2022, 61, 7007–7027. [Google Scholar] [CrossRef]
- Toufik, M.; Atangana, A. Correction to: New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus. 2022, 137, 191. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqahtani, A.M.; Chaudhary, A.; Dubey, R.S.; Sharma, S. Comparative Analysis of the Chaotic Behavior of a Five-Dimensional Fractional Hyperchaotic System with Constant and Variable Order. Fractal Fract. 2024, 8, 421. https://doi.org/10.3390/fractalfract8070421
Alqahtani AM, Chaudhary A, Dubey RS, Sharma S. Comparative Analysis of the Chaotic Behavior of a Five-Dimensional Fractional Hyperchaotic System with Constant and Variable Order. Fractal and Fractional. 2024; 8(7):421. https://doi.org/10.3390/fractalfract8070421
Chicago/Turabian StyleAlqahtani, Awatif Muflih, Arun Chaudhary, Ravi Shanker Dubey, and Shivani Sharma. 2024. "Comparative Analysis of the Chaotic Behavior of a Five-Dimensional Fractional Hyperchaotic System with Constant and Variable Order" Fractal and Fractional 8, no. 7: 421. https://doi.org/10.3390/fractalfract8070421
APA StyleAlqahtani, A. M., Chaudhary, A., Dubey, R. S., & Sharma, S. (2024). Comparative Analysis of the Chaotic Behavior of a Five-Dimensional Fractional Hyperchaotic System with Constant and Variable Order. Fractal and Fractional, 8(7), 421. https://doi.org/10.3390/fractalfract8070421







