Analytic Solution of the Time-Fractional Partial Differential Equation Using a Multi-G-Laplace Transform Method

Abstract

In several recent studies, many researchers have shown the advantage of fractional calculus in the production of particular solutions of a huge number of linear and nonlinear partial differential equations. In this research work, different theorems related to the G-double Laplace transform (DGLT) are proved. The solution of the system of time-fractional partial differential equations is addressed using a new analytical method. This technique is a combination of the multi-G-Laplace transform and decomposition methods (MGLTDM). Moreover, we discuss the convergence of this method. Two examples are provided to check the applicability and efficiency of our technique.

1. Introduction

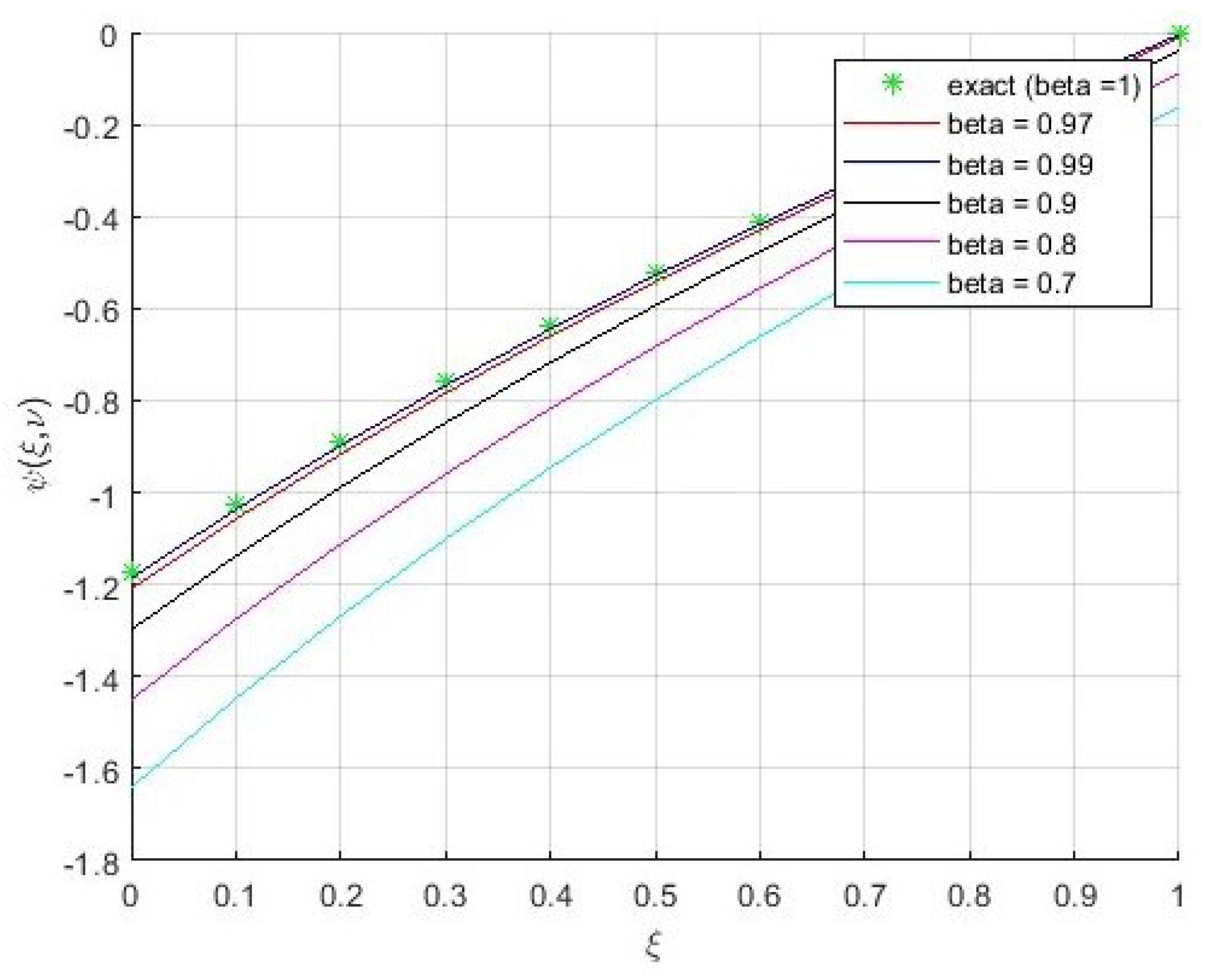
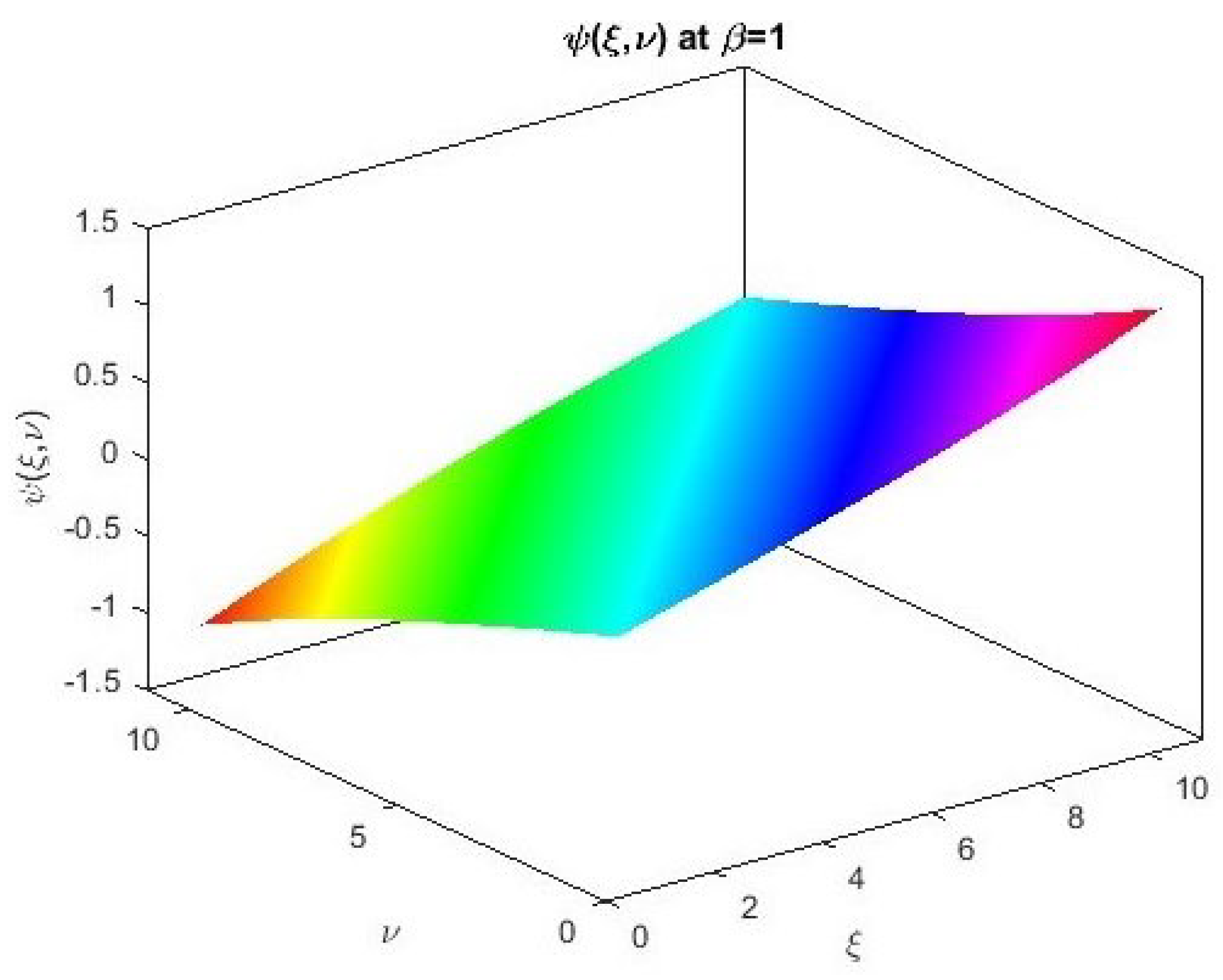
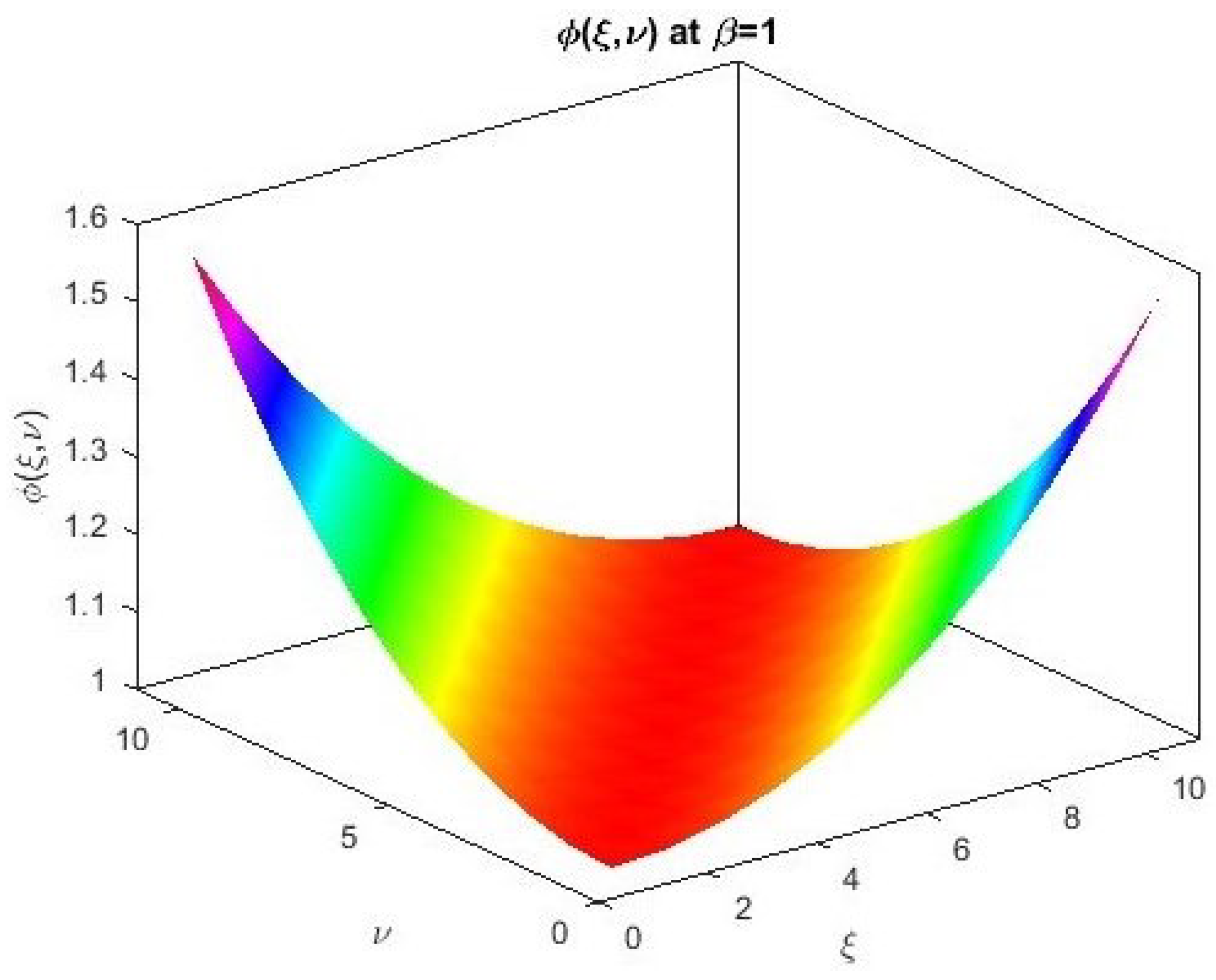
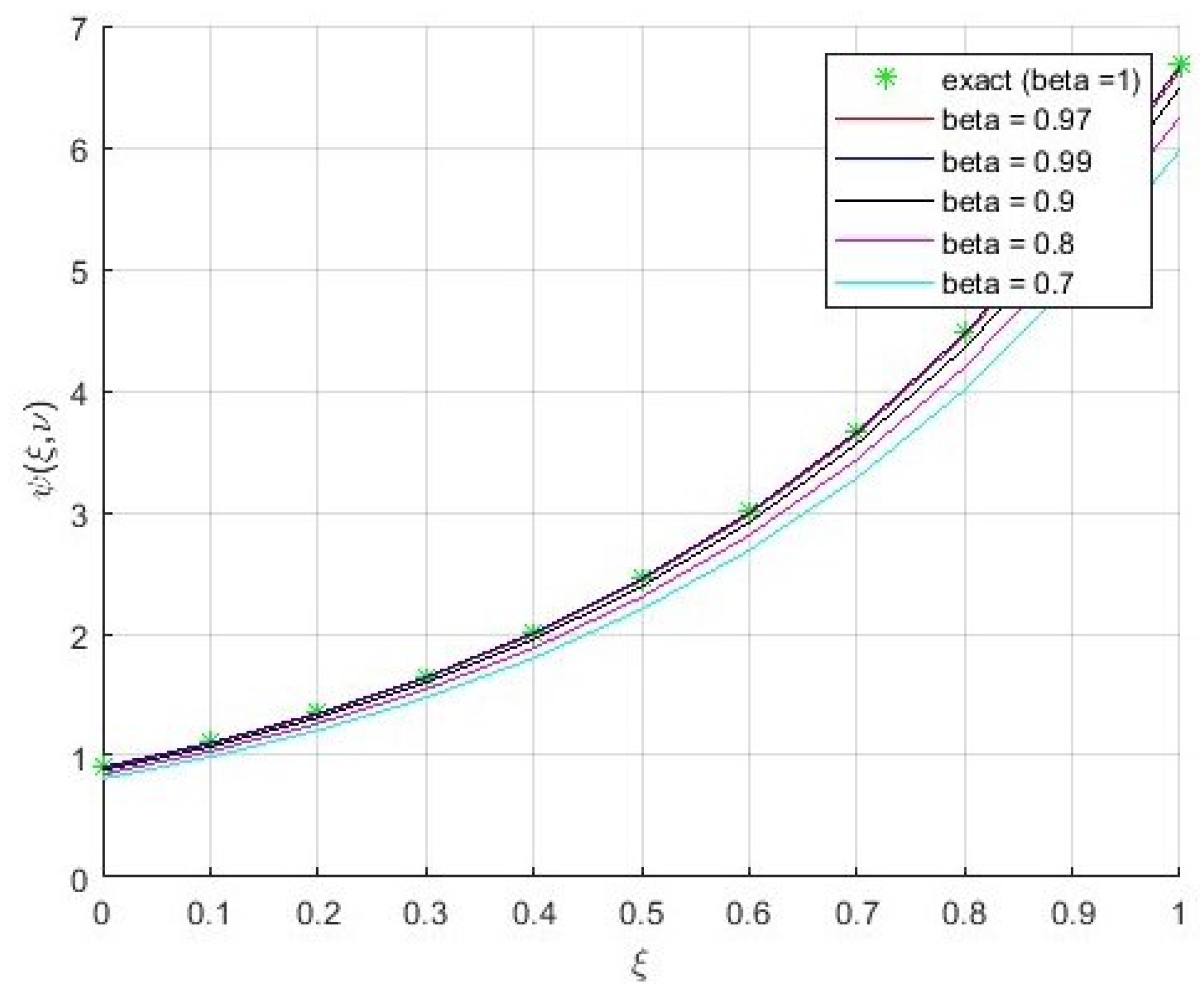
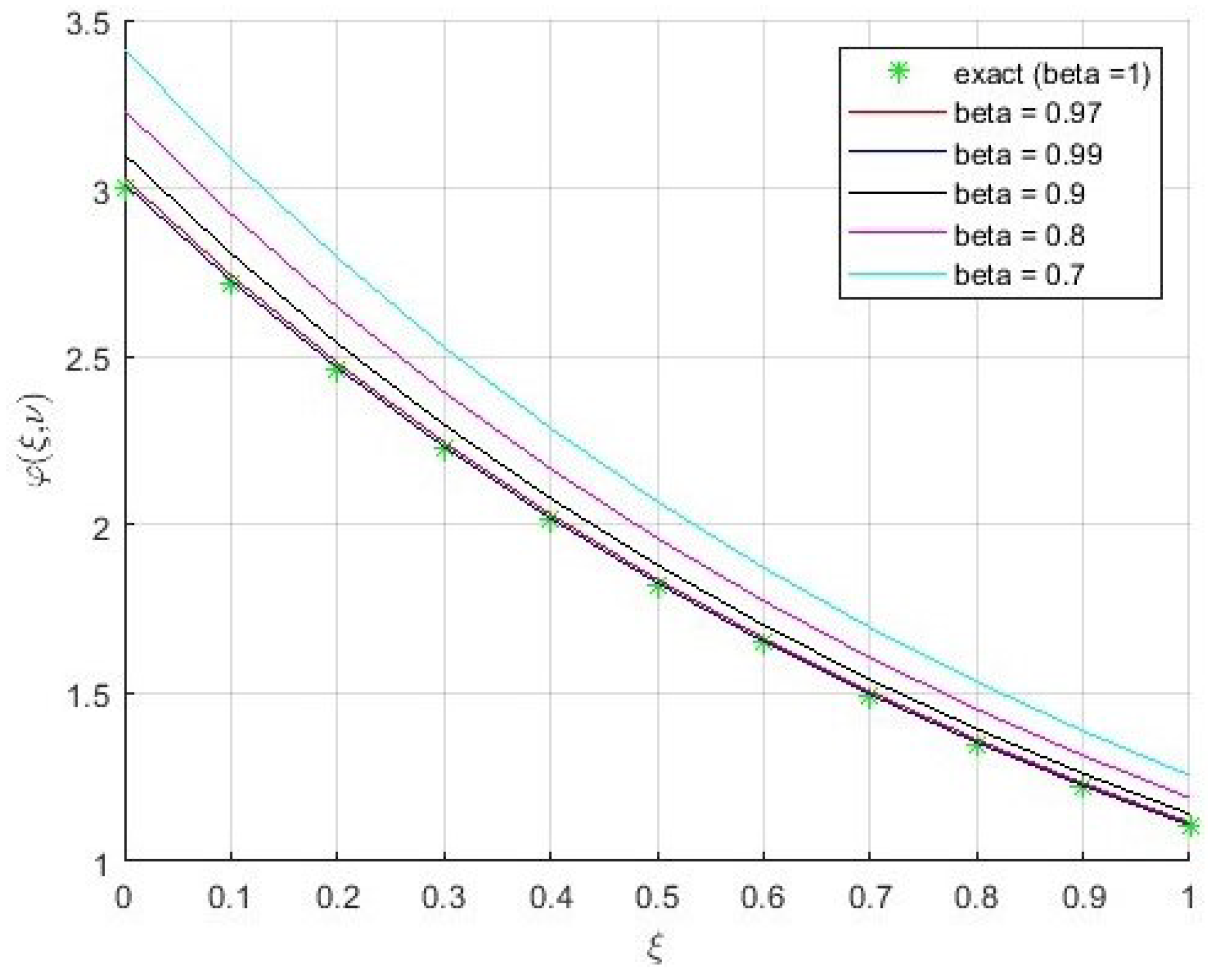
The recently widely explored topic of fractional calculus has gained significance and popularity through its implementation in various fields of science and engineering based on mathematical analysis. Recent applications of fractional calculus in diverse fields have attracted the interest of a wide range of scientists, with several results completed. Numerous problems related to mathematical physics and science, for instance, in polymer physics, viscoelastic materials, viscous damping, and seismic analysis have been successfully addressed in recent years by fractional differential equations [1]. In the literature, many analytical and numerical methods for solving FPDEs have been reported, such as fractional complex transformation [2], the homotopy perturbation method [3,4], the variational iteration method [5], the Yang transform decomposition method for fractional-order diffusion equations [6], the natural transform decomposition method for solving fractional Caudrey–Dodd–Gibbon equations [7], the shifted Jacobi collocation method for solving space-time fractional PDEs with variable coefficients [8], the solution of the system of nonlinear fractional partial differential equations by the Laplace–Adomian decomposition method [9,10], and the solution of the system of fractional-order partial differential equations by applying a new analytical technique [11]. The authors of [12] acquired the solution of the time-fractional coupled (KdV) equation by fusing the new Yang transform, the homotopy perturbation approach, and the Adomian decomposition method. The natural transform related to the Adomian decomposition method (NADM) is used to solve nonlinear fractional Burgers equations in [13]. The authors of [14] applied the decomposition method, accompanied by natural transform, to solve the system of fractional-order partial differential equations. The solution of two-dimensional fractional partial differential equations was achieved by utilizing a hybrid of the (ADM) and the Sumudu transform method [15]. The G-Laplace transform was first utilized in [16]; furthermore, features of this transform are obtained in [17]. The Laplace-type integral transform coupled with the Adomian was used to acquire the solution to nonlinear evolution equations endowed with non-integer derivatives [18]. The nonlinear sine-Gordon and coupled sine-Gordon equations were studied by a new technique called the G-double-Laplace transform [19]. This work aims to apply double and triple G-transform decomposition methods to solve the time-fractional system partial differential equation and evaluate the approximation solution. The rest of the paper is arranged as follows: In Section 2, we present essential definitions. Section 3 provides the definitions of the triple G-Laplace transform, which are needed in this paper. Also, the existing condition is proven. In Section 4, we apply our technique for solving time-fractional system partial differential equations. Section 5 provides two examples to support our methodology. In Section 6, we provide a summary of our paper.

2. Preliminaries

We retrieve some fundamental definitions:

Definition 1.

The left-side Caputo fractional derivative of f, $f\in C_{-1}^m,$ $m\in \mathbb{N}\cup \left\{0\right\}$ is defined in [10,20]

$$D_{*}^{\mu }f\left(\eta \right)={\displaystyle \frac{{\partial }^{\mu }f\left(\nu \right)}{\partial {\nu }^{\mu }}}=\left\{\begin{array}{l}{I}^{n-\mu }\left[{\displaystyle \frac{{\partial }^{n}f\left(\nu \right)}{\partial {\nu }^n}}\right],n-1<\mu <n,n\in \mathbb{N}\\ {\displaystyle \frac{{\partial }^{n}f\left(\nu \right)}{\partial {\nu }^n}},\mu =n\end{array},\right.$$

Definition 2

([21]). The partial fractional integrals and Caputo derivatives of a function $f\left(\zeta ,\nu \right)$, where $\left(\zeta ,\nu \right)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}$ are given by

$$D_{\nu }^{\mu }f\left(\zeta ,\nu \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(n-\mu \right)}}{\int }_0^{\nu }{\left(\nu -\lambda \right)}^{n-\mu -1}{\displaystyle \frac{{\partial }^n}{\partial {\lambda }^n}}f\left(\zeta ,\lambda \right)d\lambda ,$$

(1)

where $n-1<\mu \le n,$ $0<$ $\mu .$

Definition 3

([16]). Let $f\left(\nu \right)$ be integrable for $\forall \nu \ge 0$. The generalized integral transform $G_{\alpha }$ of the function $f\left(\nu \right)$ is denoted by

$$F\left(s\right)=G_{\alpha }\left(f\right)=s^{\alpha }\underset{0}{\overset{\infty }{\int }}f\left(\nu \right)e^{-{\displaystyle \frac{\nu }{s}}}d\nu ,$$

(2)

for, $s\in \mathbb{C}$ and $\alpha \in Z$.

Definition 4

([19]). The (DGLT) of the function $f(\zeta ,\nu )$ is defined as

$$G_{\zeta }{G}_{\nu }\left[f(\zeta ,\nu )\right]=F(\rho ,s)={\rho }^{\alpha }{s}^{\alpha }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\displaystyle \frac{\zeta }{\rho }}-{\displaystyle \frac{\nu }{s}}}f(\zeta ,\nu )d\nu d\zeta ,$$

(3)

where $\alpha \in \mathbb{Z}$, $\rho ,s\in \mathbb{C}$ and the symbol $G_{\zeta }{G}_{\nu }$ indicate the transform of ζ and ν, respectively, and the function $F\left(\rho ,s\right)$ is denoted as the (DGLT) of the $f\left(\zeta ,\nu \right).$

Definition 5

([19]). The inverse double G-Laplace transform (IDGLT)

$$G_{\rho }^{-1}{G}_s^{-1}\left(F\left(\rho ,s\right)\right)=f\left(\zeta ,\nu \right)={\displaystyle \frac{1}{{\left(2\pi i\right)}^2}}{\int }_{\tau -i\infty }^{\tau +i\infty }{\int }_{\xi -i\infty }^{\xi +i\infty }{e}^{{\displaystyle \frac{1}{\rho }}\zeta +{\displaystyle \frac{1}{s}}\nu }F\left(\rho ,s\right)dsd\rho ,$$

where $G_{\rho }^{-1}{G}_s^{-1}$ indicates the (IDGLT).

Definition 6.

The (TGLT) of the function $f(\zeta ,\eta ,\nu )$ is defined as

$$G_{\zeta }{G}_{\eta }{G}_{\nu }\left[f(\zeta ,\eta ,\nu )\right]=F(\rho ,\sigma ,s)={\rho }^{\alpha }{\sigma }^{\alpha }{s}^{\alpha }{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\displaystyle \frac{\zeta }{\rho }}-{\displaystyle \frac{\eta }{\sigma }}-{\displaystyle \frac{\nu }{s}}}f(\zeta ,\eta ,\nu )d\nu d\eta d\zeta ,$$

(4)

where $\alpha \in \mathbb{Z}$, $\rho ,\sigma ,s\in \mathbb{C}$ and the symbol $G_{\zeta }{G}_{\eta }{G}_{\nu }$ indicates the transform of $\zeta ,\eta$ and ν, respectively, and the function $F\left(\rho ,\sigma ,s\right)$ is denoted as the (TGLT) of the $f\left(\zeta ,\eta ,\nu \right).$

Definition 7.

The inverse triple G-Laplace transform (ITGLT) is defined by

$$\begin{array}{ccc}& & G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left(F\left(\rho ,\sigma ,s\right)\right)=f\left(\zeta ,\eta ,\nu \right)\hfill \\ & =& {\displaystyle \frac{1}{{\left(2\pi i\right)}^3}}{\int }_{\tau -i\infty }^{\tau +i\infty }{\int }_{\vartheta -i\infty }^{\vartheta +i\infty }{\int }_{\epsilon -i\infty }^{\epsilon +i\infty }{e}^{{\displaystyle \frac{1}{\rho }}\zeta +{\displaystyle \frac{1}{\sigma }}\eta +{\displaystyle \frac{1}{s}}\nu }F\left(\rho ,\sigma ,s\right)dsd\sigma d\rho ,\hfill \end{array}$$

where $G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}$ indicates (ITGLT).

The following example is useful in this work:

Example 1.

The (DGLT) of functions $f\left(\zeta ,\eta \right)=e^{\zeta +\eta }$ and $g\left(\zeta ,\eta \right)=e^{\zeta -\eta }$ is given by

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\eta }\left[f\left(\zeta ,\eta \right)\right]& =& {\displaystyle \frac{{\rho }^{\alpha +1}{\sigma }^{\alpha +1}}{\left(1-\rho \right)\left(1-\sigma \right)}},\hfill \\ \hfill G_{\zeta }{G}_{\eta }\left[g\left(\zeta ,\eta \right)\right]& =& {\displaystyle \frac{{\rho }^{\alpha +1}{\sigma }^{\alpha +1}}{\left(1-\rho \right)\left(1+\sigma \right)}},\hfill \end{array}$$

The primary benefit of the (DGLT) is that it is easy to generate some transformations from Definition 4 as follows:

1. 

If we set $\alpha =0$, $s={\displaystyle \frac{1}{s}}$ and $\rho ={\displaystyle \frac{1}{\rho }}$, we obtain the double Laplace transform

$$L_{\zeta }{L}_{\nu }\left(f\left(\zeta ,\nu \right)\right)=F\left(\rho ,s\right)=\underset{0}{\stackrel{\infty }{\int }}\underset{0}{\stackrel{\infty }{\int }}f\left(\zeta ,\nu \right)e^{-\left(\rho \zeta +s\nu \right)}d\nu d\zeta ,$$

(5)

2. 

If we set $\alpha =0,$ $\sigma ={\displaystyle \frac{1}{\rho }}$ and substituting s by ϖ, we obtain the Laplace–Yang transform

$$L_{\zeta }\eta \left(f\left(\zeta ,\nu \right)\right)=F\left(\rho ,\varpi \right)=\underset{0}{\stackrel{\infty }{\int }}\underset{0}{\stackrel{\infty }{\int }}f\left(\zeta ,\nu \right)e^{-\left(\sigma \zeta +{\displaystyle \frac{\nu }{\varpi }}\right)}d\nu d\zeta ,$$

(6)

3. 

At $\alpha =-1$ and substituting $\rho ,s$ by $u,$v, respectively, we obtain thw double Sumudu transform

$$S_{\zeta }{S}_{\nu }\left(f\left(\zeta ,\nu \right)\right)=F\left(u,v\right)={\displaystyle \frac{1}{uv}}\underset{0}{\stackrel{\infty }{\int }}\underset{0}{\stackrel{\infty }{\int }}f\left(\zeta ,\nu \right)e^{-\left({\displaystyle \frac{\zeta }{u}}+{\displaystyle \frac{\nu }{v}}\right)}d\nu d\zeta .$$

(7)

3. Main Results

This unit covers the theorem of existence condition and the fractional partial derivatives $D_{\nu }^{\beta }\psi \left(\zeta ,\nu \right)$ are also proved using (DGLT).

The existence conditions of the (TGLT) of the function $f\left(\zeta ,\eta ,\nu \right)$ are defined as follows: Suppose that $f\left(\zeta ,\eta ,\nu \right)$ is piecewise continuous on $[0,\infty )\times [0,\infty )\times [0,\infty )$ and with exponential order at infinity

$$\left|f\left(\zeta ,\eta ,\nu \right)\right|\le K{e}^{m_1\zeta +m_2\eta +m_3\nu },$$

(8)

for $\zeta >\zeta$, $\eta >\eta ,$ $\nu >\nu$, where $K\ge 0,$ and $m_1,m_2,m_3,\zeta ,\eta ,\nu$ are constants.

and we write

$$f\left(\zeta ,\eta ,\nu \right)=O\left(e^{m_1\zeta +m_2\eta +m_3\nu }\right)\mathrm{as}\zeta \to \infty ,\eta \to \infty ,\nu \to \infty$$

or similarly,

$$\underset{\begin{array}{c}\zeta \to \infty \\ \eta \to \infty \\ \nu \to \infty \end{array}}{lim}{e}^{-{\displaystyle \frac{1}{\mu }}\zeta -{\displaystyle \frac{1}{\tau }}\eta -{\displaystyle \frac{1}{\lambda }}\nu }\left|f\left(\zeta ,\eta ,\nu \right)\right|=K\underset{\begin{array}{c}\zeta \to \infty \\ \eta \to \infty \\ \nu \to \infty \end{array}}{lim}{e}^{-\left({\displaystyle \frac{1}{\mu }}-m_1\right)\zeta -\left({\displaystyle \frac{1}{\tau }}-m_2\right)\eta -\left({\displaystyle \frac{1}{\lambda }}-m_3\right)\nu }=0,$$

(9)

whenever ${\displaystyle \frac{1}{\mu }}>m_1$, ${\displaystyle \frac{1}{\tau }}>m_2$ and ${\displaystyle \frac{1}{\lambda }}>m_3$. The function $f\left(\zeta ,\eta ,\nu \right)$ does not grow quicker than $K{e}^{m_1\zeta +m_2\eta +m_3\nu }$ as $\zeta \to \infty$, $\eta \to \infty ,$ $\nu \to \infty$.

Theorem 1.

If the function $f\left(\zeta ,\eta ,\nu \right)$ is a continuous function defined on $(0,\zeta ),(0,\eta )$ and $(0,\nu )$ with exponential order $e^{m_1\zeta +m_2\eta +m_3\nu }$, then the (TGLT) of $f\left(\zeta ,\eta ,\nu \right)$ exists $\forall \mathrm{Re}\left({\displaystyle \frac{1}{\rho }}\right)>$ ${\displaystyle \frac{1}{\mu }},$ $\forall \mathrm{Re}\left({\displaystyle \frac{1}{\sigma }}\right)>$ ${\displaystyle \frac{1}{\tau }}$ and $\forall \mathrm{Re}\left({\displaystyle \frac{1}{\mathrm{s}}}\right)>$ ${\displaystyle \frac{1}{\lambda }}$.

Proof. 

By placing Equation (4) into Equation (8), we obtain

$$\begin{array}{ccc}\hfill \left|F\left(\rho ,\sigma ,s\right)\right|& =& \left|{\rho }^{\alpha }{\sigma }^{\alpha }{s}^{\alpha }\underset{0}{\stackrel{\infty }{\int }}\underset{0}{\stackrel{\infty }{\int }\stackrel{\infty }{\int }}{e}^{-({\displaystyle \frac{\zeta }{\rho }}+{\displaystyle \frac{\eta }{\sigma }}+{\displaystyle \frac{\nu }{s}})}f(\zeta ,\nu )d\zeta d\eta d\nu \right|\le K\left|e^{\left(m_1-{\displaystyle \frac{1}{\rho }}\right)\zeta +\left(m_2-{\displaystyle \frac{1}{\sigma }}\right)\eta +\left(m_3-{\displaystyle \frac{1}{s}}\right)\nu }\right|\hfill \\ & =& {\displaystyle \frac{R{\rho }^{\alpha +1}{\sigma }^{\alpha +1}{s}^{\alpha +1}}{\left(1-m_1\rho \right)\left(1-m_2\sigma \right)\left(1-m_{3}s\right)}}.\hfill \end{array}$$

Utilizing the condition $\mathrm{Re}\left({\displaystyle \frac{1}{\rho }}\right)>$ ${\displaystyle \frac{1}{\mu }},$ $\mathrm{Re}\left({\displaystyle \frac{1}{\sigma }}\right)>$ ${\displaystyle \frac{1}{\tau }}$ and $\mathrm{Re}\left({\displaystyle \frac{1}{\mathrm{s}}}\right)>$ ${\displaystyle \frac{1}{\lambda }}$, we obtain

$$\underset{\begin{array}{c}\rho \to \infty \\ \sigma \to \infty \\ s\to \infty \end{array}}{lim}\left|F\left(\rho ,\sigma ,s\right)\right|=0\mathrm{or}\underset{\begin{array}{c}\rho \to \infty \\ s\to \infty \end{array}}{lim}F\left(\rho ,\sigma ,s\right)=0,$$

□

Definition 8.

The (DGLT) of the partial derivative $D_{\nu }^n\psi \left(\zeta ,\nu \right)$ is denoted by

$$G_{\zeta }{G}_{\nu }\left[D_{\nu }^n\psi \left(\zeta ,\nu \right)\right]={\displaystyle \frac{\mathsf{\Psi }\left(\rho ,s\right)}{s^n}}-s^{\alpha }\sum _{k=1}^n{\displaystyle \frac{1}{s^{n-k}}}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{k-1}\psi \left(\zeta ,0\right)}{\partial {\nu }^{k-1}}}\right],$$

(10)

and the (TGLT) of the partial derivative $D_{\nu }^n\psi \left(\zeta ,\eta ,\nu \right)$ is denoted by

$$G_{\zeta }{G}_{\eta }{G}_{\nu }\left[D_{\nu }^n\psi \left(\zeta ,\eta ,\nu \right)\right]={\displaystyle \frac{\mathsf{\Psi }\left(\rho ,\sigma ,s\right)}{s^n}}-s^{\alpha }\sum _{k=1}^n{\displaystyle \frac{1}{s^{n-k}}}{G}_{\zeta }{G}_{\eta }\left[{\displaystyle \frac{{\partial }^{k-1}\psi \left(\zeta ,\eta ,0\right)}{\partial {\nu }^{k-1}}}\right].$$

Theorem 2.

The (DGLT) of th Caputo fractional derivative $D_{\nu }^{\beta }\psi \left(\zeta ,\nu \right)$ is given by

$$G_{\zeta }{G}_{\nu }\left[D_{\nu }^{\mu }\psi \left(\zeta ,\nu \right)\right]={\displaystyle \frac{\mathsf{\Psi }\left(\rho ,s\right)}{s^{\mu }}}-s^{\alpha }\sum _{k=1}^n{\displaystyle \frac{1}{s^{\mu -k}}}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{k-1}\psi \left(\zeta ,0\right)}{\partial {\nu }^{k-1}}}\right]$$

(11)

where $n-1<\mu \le n,$ $0<$ $\mu .$

Proof. 

Using Equations (1) and (3), we have

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\nu }\left[D_{\nu }^{\mu }\psi \left(\zeta ,\nu \right)\right]& =& {\rho }^{\alpha }{s}^{\alpha }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\displaystyle \frac{\zeta }{\rho }}-{\displaystyle \frac{\nu }{s}}}{D}_{\nu }^{\mu }\psi \left(\zeta ,\nu \right)d\nu d\zeta \hfill \\ & =& {\rho }^{\alpha }{s}^{\alpha }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\displaystyle \frac{\zeta }{\rho }}-{\displaystyle \frac{\nu }{s}}}{\displaystyle \frac{1}{\mathsf{\Gamma }\left(n-\mu \right)}}{\int }_0^{\nu }{\left(\nu -\lambda \right)}^{n-\mu -1}{\displaystyle \frac{{\partial }^n\psi \left(\zeta ,\lambda \right)}{\partial {\lambda }^n}}d\lambda d\nu d\zeta \hfill \\ & =& {\displaystyle \frac{{\rho }^{\alpha }{s}^{\alpha }}{\mathsf{\Gamma }\left(n-\mu \right)}}{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\displaystyle \frac{\zeta }{\rho }}-{\displaystyle \frac{\nu }{s}}}{\int }_{\lambda }^{\infty }{\left(\nu -\lambda \right)}^{n-\mu -1}{\displaystyle \frac{{\partial }^n\psi \left(\zeta ,\lambda \right)}{\partial {\lambda }^n}}d\nu d\zeta d\lambda .\hfill \end{array}$$

(12)

By putting $r=\nu -\lambda$ into Equation (12), we obtain

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\nu }\left[D_{\nu }^{\mu }\psi \left(\zeta ,\nu \right)\right]& =& {\displaystyle \frac{{\rho }^{\alpha }{s}^{\alpha }}{\mathsf{\Gamma }\left(n-\mu \right)}}{\int }_0^{\infty }{e}^{-{\displaystyle \frac{\zeta }{\rho }}}{\int }_0^{\infty }{\displaystyle \frac{{\partial }^n\psi \left(\zeta ,\lambda \right)}{\partial {\lambda }^n}}{e}^{-{\displaystyle \frac{\lambda }{s}}}\left[{\int }_0^{\infty }{r}^{n-\mu -1}{e}^{-{\displaystyle \frac{r}{s}}}dr\right]d\lambda d\zeta .\hfill \end{array}$$

(13)

The integral inside the bracket is defined by the gamma function as

$${\int }_0^{\infty }{r}^{n-\mu -1}{e}^{-{\displaystyle \frac{r}{s}}}dr={\displaystyle \frac{\mathsf{\Gamma }\left(n-\mu \right)}{{\left(\frac{1}{s}\right)}^{n-\mu }}},$$

Therefore, Equation (13) becomes

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\nu }\left[D_{\nu }^{\mu }\psi \left(\zeta ,\nu \right)\right]& =& {\displaystyle \frac{{\rho }^{\alpha }{s}^{\alpha }}{\mathsf{\Gamma }\left(n-\mu \right)}}{\int }_0^{\infty }{e}^{-{\displaystyle \frac{\zeta }{\rho }}}{\int }_0^{\infty }{\displaystyle \frac{{\partial }^n\psi \left(\zeta ,\lambda \right)}{\partial {\lambda }^n}}{e}^{-{\displaystyle \frac{\lambda }{s}}}\left[{\displaystyle \frac{\mathsf{\Gamma }\left(n-\mu \right)}{{\left(\frac{1}{s}\right)}^{n-\mu }}}\right]d\lambda d\zeta .\hfill \end{array}$$

(14)

By rewriting Equation (14), we obtain

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\nu }\left[D_{\nu }^{\mu }\psi \left(\zeta ,\nu \right)\right]& =& s^{n-\mu }\left[{\rho }^{\alpha }{s}^{\alpha }{\int }_0^{\infty }{\int }_0^{\infty }{\displaystyle \frac{{\partial }^n\psi \left(\zeta ,\lambda \right)}{\partial {\lambda }^n}}{e}^{-{\displaystyle \frac{\zeta }{\rho }}-{\displaystyle \frac{\lambda }{s}}}d\lambda d\zeta \right].\hfill \end{array}$$

(15)

The integral inside the bracket is defined by

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\nu }\left[D_{\nu }^n\psi \left(\zeta ,\nu \right)\right]& =& {\rho }^{\alpha }{s}^{\alpha }{\int }_0^{\infty }{\int }_0^{\infty }{\displaystyle \frac{{\partial }^n\psi \left(\zeta ,\lambda \right)}{\partial {\lambda }^n}}{e}^{-{\displaystyle \frac{\zeta }{\rho }}-{\displaystyle \frac{\lambda }{s}}}d\lambda d\zeta \hfill \\ & =& {\displaystyle \frac{\mathsf{\Psi }\left(\rho ,s\right)}{s^n}}-s^{\alpha }\sum _{k=1}^n{\displaystyle \frac{1}{s^{n-k}}}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{k-1}\psi \left(\zeta ,0\right)}{\partial {\nu }^{k-1}}}\right].\hfill \end{array}$$

(16)

By replacing Equation (16) into Equation (15), we have

$$G_{\zeta }{G}_{\nu }\left[D_{\nu }^{\mu }\psi \left(\zeta ,\nu \right)\right]={\displaystyle \frac{\mathsf{\Psi }\left(\rho ,s\right)}{s^{\mu }}}-s^{\alpha }\sum _{k=1}^n{\displaystyle \frac{1}{s^{\mu -k}}}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{k-1}\psi \left(\zeta ,0\right)}{\partial {\nu }^{k-1}}}\right].$$

The proof is complete. □

4. Formulation of (DGLT) for System of Fractional Partial Differential Equations

To solve time-fractional system partial differential equations in the Caputo meaning, this unit expands the basic concept of the multi-G-Laplace transform decomposition method (MGLTDM) for the suggested problem. For this purpose, we investigate the system of fractional partial differential equations having initial conditions in the following form:

$$\begin{array}{ccc}\hfill D_{\nu }^{{\beta }_i}{\psi }_i\left(\stackrel{*}{\zeta },\nu \right)& =& f\left(\stackrel{*}{\zeta },\nu \right)+L_i\stackrel{*}{\psi }+N\stackrel{*}{\psi },n_i-1<{\beta }_i<n_i,i=1,2,\cdots \hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{\left(m_i-1\right)}{\psi }_i\left(\stackrel{*}{\zeta },0\right)}{\partial {\nu }^{m_i-1}}}& =& f_{i{m}_i}\left(\stackrel{*}{\zeta }\right),m_i=1,2,\cdots ,n_i-1,n_i\in \mathbb{N},\hfill \end{array}$$

(18)

where $L_i$ and $N_i$ are linear and nonlinear operators, respectively, $\stackrel{*}{\psi }=$ $\psi \left(\stackrel{*}{\zeta },\nu \right)$, $f\left(\stackrel{*}{\zeta },\nu \right)$ is a given function and $D_{\nu }^{{\beta }_i}$ are the Caputo partial derivatives of fractional orders ${\beta }_i.$ We define $\psi \left(\stackrel{*}{\zeta },\nu \right)=\left({\psi }_1\left(\stackrel{*}{\zeta },\nu \right),{\psi }_2\left(\stackrel{*}{\zeta },\nu \right),\cdots ,{\psi }_n\left(\stackrel{*}{\zeta },\nu \right)\right),$ $\stackrel{*}{\zeta }=\left({\zeta }_1,{\zeta }_2,\cdots .{\zeta }_n\right)\in {\mathbb{R}}^n.$ To solve Equation (17), by (MGLTDM), the following steps are used:

Step 1: Applying (DGLT) for Equation (17) and the single G-Laplace transform for Equation (18), and using Theorem 2, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{G_{\zeta }{G}_{\nu }\left[{\psi }_i\left(\stackrel{*}{\zeta },\nu \right)\right]}{s^{{\beta }_i}}}& =& s^{\alpha }\sum _{m_i=1}^{n_i-1}{\displaystyle \frac{1}{s^{{\beta }_i-k}}}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{m_i-1}\psi \left(\stackrel{*}{\zeta },0\right)}{\partial {\nu }^{m_i-1}}}\right]\hfill \\ & & +G_{\zeta }{G}_{\nu }\left[f\left(\stackrel{*}{\zeta },\nu \right)+L_i\stackrel{*}{\psi }+N\stackrel{*}{\psi }\right],\hfill \end{array}$$

(19)

where $i=1,2,3,\cdots ,n$, by arranging the above equation

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\nu }\left[{\psi }_i\left(\stackrel{*}{\zeta },\nu \right)\right]& =& \sum _{m_i=1}^{n_i-1}{s}^{\alpha +m_i}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{m_i-1}\psi \left(\stackrel{*}{\zeta },0\right)}{\partial {\nu }^{m_i-1}}}\right]\hfill \\ & & +s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[f\left(\stackrel{*}{\zeta },\nu \right)+L_i\stackrel{*}{\psi }+N\stackrel{*}{\psi }\right].\hfill \end{array}$$

(20)

Step 2: On using (IDGLT) for both sides of the Equation (20), we obtain

$$\begin{array}{ccc}\hfill {\psi }_i\left(\stackrel{*}{\zeta },\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[\sum _{m_i=1}^{n_i-1}{s}^{\alpha +m_i}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{m_i-1}\psi \left(\stackrel{*}{\zeta },0\right)}{\partial {\nu }^{m_i-1}}}\right]\right]\hfill \\ & & +G_{\rho }^{-1}{G}_s^{-1}\left[s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[f\left(\stackrel{*}{\zeta },\nu \right)\right]\right]\hfill \\ & & +G_{\rho }^{-1}{G}_s^{-1}\left[s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[f\left(\stackrel{*}{\zeta },\nu \right)+L_i\stackrel{*}{\psi }+N\stackrel{*}{\psi }\right]\right].\hfill \end{array}$$

(21)

Step 3: The solution to the Equation (17) is given by the following series:

$${\psi }_i\left(\stackrel{*}{\zeta },\nu \right)=\sum _{j=0}^{\infty }{\psi }_{ij}\left(\stackrel{*}{\zeta },\nu \right).i=1,2,\cdots ,n.$$

(22)

Therefore, Equation (21) becomes

$$\begin{array}{ccc}\hfill \sum _{j=0}^{\infty }{\psi }_{ij}\left(\stackrel{*}{\zeta },\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[\sum _{m_i=1}^{n_i-1}{s}^{\alpha +m_i}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{m_i-1}\psi \left(\stackrel{*}{\zeta },0\right)}{\partial {\nu }^{m_i-1}}}\right]\right]\hfill \\ & & +G_{\rho }^{-1}{G}_s^{-1}\left[s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[f\left(\stackrel{*}{\zeta },\nu \right)\right]\right]\hfill \\ & & +G_{\rho }^{-1}{G}_s^{-1}\left[s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[\sum _{j=0}^{\infty }{L}_i\stackrel{*}{{\psi }_j}+\sum _{j=0}^{\infty }N{\stackrel{*}{\psi }}_j\right]\right].\hfill \end{array}$$

(23)

Step 4: We define the iteration relation by

$${\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)=G_{\rho }^{-1}{G}_s^{-1}\left[\sum _{m_i=1}^{n_i-1}{s}^{\alpha +m_i}{G}_{\zeta }\left[{\displaystyle \frac{{\partial }^{m_i-1}\psi \left(\stackrel{*}{\zeta },0\right)}{\partial {\nu }^{m_i-1}}}\right]+s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[f\left(\stackrel{*}{\zeta },\nu \right)\right]\right],$$

and

$$\begin{array}{ccc}\hfill {\psi }_{i1}\left(\stackrel{*}{\zeta },\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[L_i\stackrel{*}{{\psi }_0}+N\stackrel{*}{{\psi }_0}\right]\right]\hfill \\ \hfill {\psi }_{i2}\left(\stackrel{*}{\zeta },\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[L_i\stackrel{*}{{\psi }_1}+N{\stackrel{*}{\psi }}_1\right]\right]\hfill \\ \hfill {\psi }_{i3}\left(\stackrel{*}{\zeta },\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[L_i\stackrel{*}{{\psi }_2}+N{\stackrel{*}{\psi }}_2\right]\right]\hfill \\ & & \begin{array}{c}.\\ .\\ .\end{array}\hfill \\ \hfill {\psi }_{ij}\left(\stackrel{*}{\zeta },\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{{\beta }_i}{G}_{\zeta }{G}_{\nu }\left[L_i\stackrel{*}{{\psi }_{j-1}}+N{\stackrel{*}{\psi }}_{j-1}\right]\right].\hfill \end{array}$$

(24)

The solution of Equation (17) is given by substituting Equation (24) into Equation (22) as follows:

$${\psi }_i\left(\stackrel{*}{\zeta },\nu \right)=\underset{j\to 1}{lim}{\psi }_{ij}\left(\stackrel{*}{\zeta },\nu \right)={\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)+{\psi }_{i1}\left(\stackrel{*}{\zeta },\nu \right)+{\psi }_{i2}\left(\stackrel{*}{\zeta },\nu \right)+\cdots +{\psi }_{in}\left(\stackrel{*}{\zeta },\nu \right),i=1,2,\cdots ,n$$

Convergence:

Theorem 3.

Let A be a Banach space. The series solution of Equation (24) converges to $S_i\in A$ for $i=1,2,..n,$ if there exists ${\lambda }_i,$ $0\le {\lambda }_i<1,$ such that, $∥{\psi }_{in}\left(\stackrel{*}{\zeta },\nu \right)∥\le {\lambda }_i∥{\psi }_{in-1}\left(\stackrel{*}{\zeta },\nu \right)∥$ for all $n\in \mathbb{N}.$

Proof. 

By defining sequence $S_{in}$ of the partial sums of the series of Equation (24) as follows:

$$\begin{array}{ccc}\hfill S_{i0}& =& {\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)\hfill \\ \hfill S_{i1}& =& {\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)+{\psi }_{i1}\left(\stackrel{*}{\zeta },\nu \right)\hfill \\ \hfill S_{i2}& =& {\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)+{\psi }_{i1}\left(\stackrel{*}{\zeta },\nu \right)+{\psi }_{i2}\left(\stackrel{*}{\zeta },\nu \right)\hfill \\ & & \begin{array}{c}.\\ .\\ .\end{array}\hfill \\ \hfill S_{in}& =& {\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)+{\psi }_{i1}\left(\stackrel{*}{\zeta },\nu \right)+{\psi }_{i2}\left(\stackrel{*}{\zeta },\nu \right)+\cdots +{\psi }_{in}\left(\stackrel{*}{\zeta },\nu \right),\hfill \end{array}$$

to show that $\left\{S_{in}\right\}$ is a Cauchy sequence in Banach space A. Therefore, we consider

$$\begin{array}{ccc}\hfill ∥S_{i\left(n+1\right)}-S_{in}∥& =& ∥{\psi }_{i\left(n+1\right)}\left(\stackrel{*}{\zeta },\nu \right)∥\le {\lambda }_i∥{\psi }_{in}\left(\stackrel{*}{\zeta },\nu \right)∥\le {\lambda }_i^2∥{\psi }_{i\left(n-1\right)}\left(\stackrel{*}{\zeta },\nu \right)∥\le \cdots \hfill \\ & \le & {\lambda }_i^{n+1}∥{\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)∥,i=1,2,\cdots ,n.\hfill \end{array}$$

By using the above triangle inequality for $n\ge m,$ we have

$$\begin{array}{ccc}\hfill ∥S_{in}-S_{im}∥& =& ∥S_{i\left(m+1\right)}-S_{im}+S_{i\left(m+1\right)}-S_{i\left(m+1\right)}+\cdots +S_{in}-S_{i\left(n-1\right)}∥\hfill \\ & \le & ∥S_{i\left(m+1\right)}-S_{im}∥+∥S_{i\left(m+1\right)}-S_{i\left(m+1\right)}∥+\cdots +∥S_{in}-S_{i\left(n-1\right)}∥\hfill \\ & \le & {\lambda }_i^{m+1}∥{\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)∥+{\lambda }_i^{m+2}∥{\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)∥+\cdots +{\lambda }_i^n∥{\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)∥\hfill \\ & =& {\lambda }_i^{m+1}\left(1+{\lambda }_i+\cdots +{\lambda }_i^{n-m-1}\right)∥{\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)∥\hfill \\ & \le & {\lambda }_i^{m+1}\left({\displaystyle \frac{1-{\lambda }_i^{n-m}}{1-{\lambda }_i}}\right)∥{\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)∥.\hfill \end{array}$$

From $0\le {\lambda }_i<1$, we see that $1-{\lambda }_i^{n-m}\le 1.$ Therefore,

$$∥S_{in}-S_{im}∥\le {\displaystyle \frac{{\lambda }_i^{m+1}}{1-{\lambda }_i}}∥{\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)∥$$

since ${\psi }_{i0}\left(\stackrel{*}{\zeta },\nu \right)$ is bounded, hence, $∥S_{in}-S_{im}∥\to 0$ at $n,m\to \infty$. Therefore, the sequence $\left\{S_{in}\right\}$ is a Cauchy sequence in the Banach space A; then, the series solution of Equation (24) is convergent. □

5. Applications

This section contains two parts:

In the first part, we solve the homogeneous telegraphic equation using a double-generalized Laplace transform with initial and boundary conditions.

In the second part, we offer examples of some systems of time-fractional partial differential equations and solve them by the double G-Laplace decomposition method (DGLDM). Before we start to solve the following examples some notes are needed.

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_v\left[{\psi }_v\right]& =& {\displaystyle \frac{1}{s}}\mathsf{\Psi }\left(\rho ,s\right)-s^{\alpha }{G}_{\zeta }\left[\psi \left(\zeta ,0\right)\right]\hfill \\ \hfill G_{\zeta }{G}_v\left[{\psi }_{\zeta \zeta }\right]& =& {\displaystyle \frac{1}{{\rho }^2}}\mathsf{\Psi }\left(\rho ,s\right)-{\rho }^{\alpha -1}{G}_v\left[\psi \left(0,v\right)\right]-{\rho }^{\alpha }{G}_v\left[{\psi }_{\zeta }\left(0,v\right)\right]\hfill \\ \hfill G_{\zeta }{G}_v\left[{\psi }_{vv}\right]& =& {\displaystyle \frac{1}{s^2}}\mathsf{\Psi }\left(\rho ,s\right)-s^{\alpha -1}{G}_{\zeta }\left[\psi \left(\zeta ,0\right)\right]-s^{\alpha }{G}_{\zeta }\left[{\psi }_v\left(\zeta ,0\right)\right].\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill sinh\left(\zeta \right)& =& \zeta +{\displaystyle \frac{{\zeta }^3}{3!}}+{\displaystyle \frac{{\zeta }^5}{5!}}+{\displaystyle \frac{{\zeta }^7}{7!}}+\cdots .\hfill \\ \hfill cosh\left(\zeta \right)& =& 1+{\displaystyle \frac{{\zeta }^2}{2!}}+{\displaystyle \frac{{\zeta }^4}{4!}}+{\displaystyle \frac{{\zeta }^6}{6!}}+\cdots .\hfill \end{array}$$

(26)

In the next example, we apply (DGLT).

Example 2.

Consider the homogeneous telegraphic equation denoted by

$${\psi }_{\zeta \zeta }-{\psi }_{\nu \nu }-{\psi }_{\nu }-\psi =0,$$

(27)

with boundary conditions

$$\psi \left(0,\nu \right)=e^{-\nu },{\psi }_{\zeta }\left(0,\nu \right)=e^{-\nu },$$

(28)

and initial conditions

$$\psi \left(\zeta ,0\right)=e^{\zeta },{\psi }_{\nu }\left(\zeta ,0\right)=-e^{\zeta }.$$

(29)

Using (DGLT) on the Equation (27), we have

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{{\rho }^2}}\mathsf{\Psi }\left(\rho ,s\right)-{\rho }^{\alpha -1}{G}_v\left[\psi \left(0,v\right)\right]-{\rho }^{\alpha }{G}_v\left[{\psi }_{\zeta }\left(0,v\right)\right]\hfill \\ & & -{\displaystyle \frac{1}{s^2}}\mathsf{\Psi }\left(\rho ,s\right)-s^{\alpha -1}{G}_{\zeta }\left[\psi \left(\zeta ,0\right)\right]-s^{\alpha }{G}_{\zeta }\left[{\psi }_v\left(\zeta ,0\right)\right]\hfill \\ & & -{\displaystyle \frac{1}{s}}\mathsf{\Psi }\left(\rho ,s\right)-s^{\alpha }{G}_{\zeta }\left[\psi \left(\zeta ,0\right)\right]-\mathsf{\Psi }\left(\rho ,s\right)\hfill \\ & =& 0.\hfill \end{array}$$

(30)

Taking the G-Laplace transform for Equations (28) and (29), we obtain

$$\begin{array}{ccc}\hfill G_v\left[\psi \left(0,v\right)\right]& =& {\displaystyle \frac{s^{\alpha +1}}{\left(1+s\right)}},G_v\left[{\psi }_{\zeta }\left(0,v\right)\right]={\displaystyle \frac{s^{\alpha +1}}{\left(1+s\right)}}\hfill \\ \hfill G_{\zeta }\left[\psi \left(\zeta ,0\right)\right]& =& {\displaystyle \frac{{\rho }^{\alpha +1}}{\left(1-\rho \right)}},G_{\zeta }\left[{\psi }_v\left(\zeta ,0\right)\right]=-{\displaystyle \frac{{\rho }^{\alpha +1}}{\left(1-\rho \right)}}.\hfill \end{array}$$

(31)

Substituting Equation (31) into Equation (30), we obtain

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{{\rho }^2}}\mathsf{\Psi }\left(\rho ,s\right)-{\rho }^{\alpha -1}{\displaystyle \frac{s^{\alpha +1}}{\left(1+s\right)}}-{\rho }^{\alpha }{\displaystyle \frac{s^{\alpha +1}}{\left(1+s\right)}}\hfill \\ & & -\left[{\displaystyle \frac{1}{s^2}}\mathsf{\Psi }\left(\rho ,s\right)-s^{\alpha -1}{\displaystyle \frac{{\rho }^{\alpha +1}}{\left(1-\rho \right)}}+s^{\alpha }{\displaystyle \frac{{\rho }^{\alpha +1}}{\left(1-\rho \right)}}\right]\hfill \\ & & -\left[{\displaystyle \frac{1}{s}}\mathsf{\Psi }\left(\rho ,s\right)-s^{\alpha }{\displaystyle \frac{{\rho }^{\alpha +1}}{\left(1-\rho \right)}}\right]-\mathsf{\Psi }\left(\rho ,s\right)\hfill \\ & =& 0.\hfill \end{array}$$

(32)

Rearranging Equation (32), we obtain

$$\begin{array}{ccc}& & \left[{\displaystyle \frac{1}{{\rho }^2}}-{\displaystyle \frac{1}{s^2}}-{\displaystyle \frac{1}{s}}-1\right]\mathsf{\Psi }\left(\rho ,s\right)\hfill \\ & =& {\rho }^{\alpha -1}{\displaystyle \frac{s^{\alpha +1}}{\left(1+s\right)}}+{\rho }^{\alpha }{\displaystyle \frac{s^{\alpha +1}}{\left(1+s\right)}}-s^{\alpha -1}{\displaystyle \frac{{\rho }^{\alpha +1}}{\left(1-\rho \right)}}\hfill \end{array}$$

(33)

By simplifying Equation (33), we have

$$\mathsf{\Psi }\left(\rho ,s\right)={\displaystyle \frac{s^{\alpha +1}{\rho }^{\alpha +1}}{\left(1+s\right)\left(1-\rho \right)}}.$$

(34)

Taking (IDGLT) for the Equation (34), we obtain the solution of Equation (27) as follows:

$$\psi \left(\zeta ,v\right)=e^{\zeta -v}.$$

The solution we obtained is in agreement with the result obtained in [22].

In the following examples, we apply (DGLDM).

Example 3.

Consider the linear time-fractional partial differential equation with the initial conditions of the form:

$$\begin{array}{ccc}\hfill D_{\nu }^{\beta }\psi -{\varphi }_{\zeta }+\psi +\varphi & =& 0\hfill \\ \hfill D_{\nu }^{\beta }\varphi -{\psi }_{\zeta }+\psi +\varphi & =& 0,0<\beta \le 1\hfill \end{array}$$

(35)

subject to initial conditions

$$\psi \left(\zeta ,0\right)=sinh\left(\zeta \right),\varphi \left(\zeta ,0\right)=cosh\left(\zeta \right).$$

(36)

To solve Equation (35) utilizing the (DGLDM). First, applying (DGLT) for Equation (35), we have

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\nu }\left[D_{\nu }^{\beta }\psi \right]& =& G_{\zeta }{G}_{\nu }\left[{\varphi }_{\zeta }-\psi -\varphi \right]\hfill \\ \hfill G_{\zeta }{G}_{\nu }\left[D_{\nu }^{\beta }\varphi \right]& =& G_{\zeta }{G}_{\nu }\left[{\psi }_{\zeta }-\psi -\varphi \right],\hfill \end{array}$$

(37)

on using Theorem 2, the left-hand side of Equation (37) becomes

$$\begin{array}{ccc}\hfill {\displaystyle \frac{G_{\zeta }{G}_{\nu }\left[\psi \left(\zeta ,\nu \right)\right]}{s^{\beta }}}-s^{\alpha -\beta +1}{G}_{\zeta }\left[\psi \left(\zeta ,0\right)\right]& =& G_{\zeta }{G}_{\nu }\left[{\varphi }_{\zeta }-\psi -\varphi \right]\hfill \\ \hfill {\displaystyle \frac{G_{\zeta }{G}_{\nu }\left[\varphi \left(\zeta ,\nu \right)\right]}{s^{\beta }}}-s^{\alpha -\beta +1}{G}_{\zeta }\left[\varphi \left(\zeta ,0\right)\right]& =& G_{\zeta }{G}_{\nu }\left[{\psi }_{\zeta }-\psi -\varphi \right].\hfill \end{array}$$

(38)

Second, employing the G-Laplace transform for Equation (35) using Equation (26) and rearranging the results, we obtain

$$\begin{array}{ccc}\hfill \mathsf{\Psi }\left(\rho ,s\right)& =& s^{\alpha +1}\left[{\rho }^{\alpha +2}+{\rho }^{\alpha +4}+{\rho }^{\alpha +6}+{\rho }^{\alpha +8}+\cdots \right]\hfill \\ & & +s^{\beta }{G}_{\zeta }{G}_{\nu }\left[{\varphi }_{\zeta }-\psi -\varphi \right]\hfill \\ \hfill \mathsf{\Phi }\left(\rho ,s\right)& =& s^{\alpha +1}\left[{\rho }^{\alpha +1}+{\rho }^{\alpha +3}+{\rho }^{\alpha +5}+{\rho }^{\alpha +7}+\cdots \right]\hfill \\ & & +s^{\beta }{G}_{\zeta }{G}_{\nu }\left[{\psi }_{\zeta }-\psi -\varphi \right].\hfill \end{array}$$

(39)

Third, taking (IDGLT) for Equation (39), we obtain

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\nu \right)& =& \zeta +{\displaystyle \frac{{\zeta }^3}{3!}}+{\displaystyle \frac{{\zeta }^5}{5!}}+{\displaystyle \frac{{\zeta }^7}{7!}}+\cdots .\hfill \\ & & +G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[{\varphi }_{\zeta }-\psi -\varphi \right]\right]\hfill \\ \hfill \varphi \left(\zeta ,\nu \right)& =& 1+{\displaystyle \frac{{\zeta }^2}{2!}}+{\displaystyle \frac{{\zeta }^4}{4!}}+{\displaystyle \frac{{\zeta }^6}{6!}}+\cdots .\hfill \\ & & +G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[{\psi }_{\zeta }-\psi -\varphi \right]\right].\hfill \end{array}$$

(40)

The series solutions of Equation (35) are defined as follows:

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\nu \right)& =& \sum _{n=0}^{\infty }{\psi }_n\left(\zeta ,\nu \right),n=1,2,\cdots \hfill \\ \hfill \varphi \left(\zeta ,\nu \right)& =& \sum _{n=0}^{\infty }{\varphi }_n\left(\zeta ,\nu \right),n=1,2,\cdots .\hfill \end{array}$$

(41)

Fourth, by replacing Equation (41) into Equation (40), we obtain

$$\begin{array}{ccc}\hfill \sum _{n=0}^{\infty }{\psi }_n\left(\zeta ,\nu \right)& =& \zeta +{\displaystyle \frac{{\zeta }^3}{3!}}+{\displaystyle \frac{{\zeta }^5}{5!}}+{\displaystyle \frac{{\zeta }^7}{7!}}+\cdots .\hfill \\ & & +G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\sum _{n=0}^{\infty }\left({\varphi }_{n\zeta }-{\psi }_n-{\varphi }_n\right)\right]\right]\hfill \\ \hfill \sum _{n=0}^{\infty }{\varphi }_n\left(\zeta ,\nu \right)& =& 1+{\displaystyle \frac{{\zeta }^2}{2!}}+{\displaystyle \frac{{\zeta }^4}{4!}}+{\displaystyle \frac{{\zeta }^6}{6!}}+\cdots .\hfill \\ & & +G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\sum _{n=0}^{\infty }\left({\psi }_{n\zeta }-{\psi }_n-{\varphi }_n\right)\right]\right].\hfill \end{array}$$

(42)

Fifth, from Equation (42), we introduce the iteration relation as follows:

$$\begin{array}{ccc}\hfill {\psi }_0\left(\zeta ,\nu \right)& =& \zeta +{\displaystyle \frac{{\zeta }^3}{3!}}+{\displaystyle \frac{{\zeta }^5}{5!}}+{\displaystyle \frac{{\zeta }^7}{7!}}+\cdots =sinh\zeta \hfill \\ \hfill {\varphi }_0\left(\zeta ,\nu \right)& =& 1+{\displaystyle \frac{{\zeta }^2}{2!}}+{\displaystyle \frac{{\zeta }^4}{4!}}+{\displaystyle \frac{{\zeta }^6}{6!}}+\cdots =cosh\zeta \hfill \end{array}$$

(43)

and

$$\begin{array}{ccc}\hfill {\psi }_{n+1}\left(\zeta ,\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left({\varphi }_{n\zeta }-{\psi }_n-{\varphi }_n\right)\right]\right]\hfill \\ \hfill {\varphi }_{n+1}\left(\zeta ,\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left({\psi }_{n\zeta }-{\psi }_n-{\varphi }_n\right)\right]\right].\hfill \end{array}$$

(44)

At $n=0,$ Equation (44) becomes

$$\begin{array}{ccc}\hfill {\psi }_1\left(\zeta ,\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left({\varphi }_{0\zeta }-{\psi }_0-{\varphi }_0\right)\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left(-{\varphi }_0\right)\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left(1+{\displaystyle \frac{{\zeta }^2}{2!}}+{\displaystyle \frac{{\zeta }^4}{4!}}+{\displaystyle \frac{{\zeta }^6}{6!}}+\cdots .\right)\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_s^{-1}\left[s^{\alpha +\beta +1}\left({\rho }^{\alpha +1}+{\rho }^{\alpha +3}+{\rho }^{\alpha +5}+{\rho }^{\alpha +7}+\cdots .\right)\right]\hfill \\ & =& -\left(1+{\displaystyle \frac{{\zeta }^2}{2!}}+{\displaystyle \frac{{\zeta }^4}{4!}}+{\displaystyle \frac{{\zeta }^6}{6!}}+\cdots .\right){\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}\hfill \\ & =& -{\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}cosh\zeta ,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\varphi }_1\left(\zeta ,\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left({\psi }_{0\zeta }-{\psi }_0-{\varphi }_0\right)\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left({\psi }_0\right)\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left(\zeta +{\displaystyle \frac{{\zeta }^3}{3!}}+{\displaystyle \frac{{\zeta }^5}{5!}}+{\displaystyle \frac{{\zeta }^7}{7!}}+\cdots \right)\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_s^{-1}\left[s^{\alpha +\beta +1}\left[{\rho }^{\alpha +2}+{\rho }^{\alpha +4}+{\rho }^{\alpha +6}+{\rho }^{\alpha +8}+\cdots \right]\right]\hfill \\ & =& -\left(\zeta +{\displaystyle \frac{{\zeta }^3}{3!}}+{\displaystyle \frac{{\zeta }^5}{5!}}+{\displaystyle \frac{{\zeta }^7}{7!}}+\cdots \right){\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}\hfill \\ & =& -{\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}sinh\zeta \hfill \end{array}$$

By substituting $n=1,$ in Equation (44), we obtain

$$\begin{array}{ccc}\hfill {\psi }_2\left(\zeta ,\nu \right)& =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left({\varphi }_{1\zeta }-{\psi }_1-{\varphi }_1\right)\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left({\varphi }_1\right)\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\nu }\left[\left(\zeta +{\displaystyle \frac{{\zeta }^3}{3!}}+{\displaystyle \frac{{\zeta }^5}{5!}}+{\displaystyle \frac{{\zeta }^7}{7!}}+\cdots \right)\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_s^{-1}\left[s^{\alpha +2\beta +1}\left[{\rho }^{\alpha +2}+{\rho }^{\alpha +4}+{\rho }^{\alpha +6}+{\rho }^{\alpha +8}+\cdots \right]\right]\hfill \\ & =& {\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}sinh\zeta .\hfill \end{array}$$

In a similar manner

$${\varphi }_2\left(\zeta ,\nu \right)={\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}cosh\zeta$$

at $n=2,$ we have

$$\begin{array}{ccc}\hfill {\psi }_3\left(\zeta ,\nu \right)& =& -{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}cosh\zeta \hfill \\ \hfill {\varphi }_3\left(\zeta ,\nu \right)& =& -{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}sinh\zeta .\hfill \end{array}$$

Finally, the series solution of Equation (35) is given by

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\nu \right)& =& {\psi }_0+{\psi }_1+{\psi }_2+\cdots \hfill \\ \hfill \varphi \left(\zeta ,\nu \right)& =& {\varphi }_0+{\varphi }_1+{\varphi }_2+\cdots .\hfill \end{array}$$

Hence,

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\nu \right)& =& sinh\zeta -{\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}cosh\zeta +{\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}sinh\zeta -{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}cosh\zeta +\cdots \hfill \\ \hfill \psi \left(\zeta ,\nu \right)& =& \left(1+{\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}+{\displaystyle \frac{{\nu }^{4\beta }}{\mathsf{\Gamma }\left(4\beta +1\right)}}+\cdots \right)sinh\zeta \hfill \\ & & -\left({\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}+{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}+{\displaystyle \frac{{\nu }^{5\beta }}{\mathsf{\Gamma }\left(5\beta +1\right)}}+\cdots \right)cosh\zeta \hfill \\ \hfill \varphi \left(\zeta ,\nu \right)& =& cosh\zeta -{\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}sinh\zeta +{\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}cosh\zeta -{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}sinh\zeta +\cdots \hfill \\ \hfill \varphi \left(\zeta ,\nu \right)& =& \left(1+{\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}+{\displaystyle \frac{{\nu }^{4\beta }}{\mathsf{\Gamma }\left(4\beta +1\right)}}+\cdots \right)cosh\zeta \hfill \\ & & -\left({\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}+{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}+{\displaystyle \frac{{\nu }^{5\beta }}{\mathsf{\Gamma }\left(5\beta +1\right)}}+\cdots \right)sinh\zeta .\hfill \end{array}$$

By putting $\beta =1$, the precise solution of Equation (35) is given by:

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\nu \right)& =& \left(1+{\displaystyle \frac{{\nu }^2}{2!}}+{\displaystyle \frac{{\nu }^4}{4!}}+{\displaystyle \frac{{\nu }^6}{6!}}+\cdots \right)sinh\zeta \hfill \\ & & -\left(\nu +{\displaystyle \frac{{\nu }^3}{3!}}+{\displaystyle \frac{{\nu }^5}{5!}}+\cdots \right)cosh\zeta \hfill \\ \hfill \psi \left(\zeta ,\nu \right)& =& sinh\left(\zeta -\nu \right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \varphi \left(\zeta ,\nu \right)& =& \left(1+{\displaystyle \frac{{\nu }^2}{2!}}+{\displaystyle \frac{{\nu }^4}{4!}}+{\displaystyle \frac{{\nu }^6}{6!}}+\cdots \right)cosh\zeta \hfill \\ & & -\left(\nu +{\displaystyle \frac{{\nu }^3}{3!}}+{\displaystyle \frac{{\nu }^5}{5!}}+\cdots \right)sinh\zeta \hfill \\ \hfill \varphi \left(\zeta ,\nu \right)& =& cosh\left(\zeta -\nu \right).\hfill \end{array}$$

The results we achieved agree with [23].

Figure 1 and Figure 2 indicate the contrast between the exact solution and the achieved numerical solution for Equation (35); at t = 1 and $\beta =1$, we receive the precise solution by taking various values of $\beta$, for example, ($\beta =0.97$, $\beta =0.99$, $\beta =0.9$, $\beta =0.8$ and $\beta =0.7$), and we obtain the approximate solutions.

In Figure 3 and Figure 4, we indicate the result of the functions $\psi (\zeta ,\nu )$, $\varphi (\zeta ,\nu )$, respectively, in three-dimensions.

In the next example, we solve the nonlinear time-fractional partial differential equation.

Example 4.

Consider the nonlinear time-fractional partial differential equation with the initial conditions of the form:

$$\begin{array}{ccc}\hfill D_{\nu }^{\beta }\psi +{\varphi }_{\zeta }{\phi }_{\eta }-{\varphi }_{\eta }{\phi }_{\zeta }& =& -\psi \hfill \\ \hfill D_{\nu }^{\beta }\varphi +{\psi }_{\zeta }{\phi }_{\eta }+{\psi }_{\eta }{\phi }_{\zeta }& =& \varphi \hfill \\ \hfill D_{\nu }^{\beta }\phi +{\psi }_{\zeta }{\varphi }_{\eta }+{\psi }_{\eta }{\varphi }_{\zeta }& =& \phi ,0<\beta \le 1\hfill \end{array}$$

(45)

subject to initial conditions

$$\psi \left(\zeta ,\eta ,0\right)=e^{\zeta +\eta },\varphi \left(\zeta ,\eta ,0\right)=e^{\zeta +\eta },\phi \left(\zeta ,\eta ,0\right)=e^{-\zeta +\eta }.$$

(46)

To solve Equation (45) by employing the triple G-Laplace transform decomposition method (TGLTDM). First, taking (TGLT) for Equation (45), we have

$$\begin{array}{ccc}\hfill G_{\zeta }{G}_{\eta }{G}_{\nu }\left[D_{\nu }^{\beta }\psi \right]& =& -G_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\varphi }_{\zeta }{\phi }_{\eta }-{\varphi }_{\eta }{\phi }_{\zeta }+\psi \right]\hfill \\ \hfill G_{\zeta }{G}_{\eta }{G}_{\nu }\left[D_{\nu }^{\beta }\varphi \right]& =& -G_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_{\zeta }{\phi }_{\eta }+{\psi }_{\eta }{\phi }_{\zeta }-\varphi \right]\hfill \\ \hfill G_{\zeta }{G}_{\eta }{G}_{\nu }\left[D_{\nu }^{\beta }\phi \right]& =& -G_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_{\zeta }{\varphi }_{\eta }+{\psi }_{\eta }{\varphi }_{\zeta }-\phi \right],\hfill \end{array}$$

(47)

on using Theorem 2, the left-hand side of Equation (47) becomes

$$\begin{array}{ccc}\hfill {\displaystyle \frac{G_{\zeta }{G}_{\nu }\left[\psi \left(\zeta ,\eta ,\nu \right)\right]}{s^{\beta }}}-s^{\alpha -\beta +1}{G}_{\zeta }\left[\psi \left(\zeta ,\eta ,0\right)\right]& =& -G_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\varphi }_{\zeta }{\phi }_{\eta }-{\varphi }_{\eta }{\phi }_{\zeta }+\psi \right]\hfill \\ \hfill {\displaystyle \frac{G_{\zeta }{G}_{\nu }\left[\varphi \left(\zeta ,\eta ,\nu \right)\right]}{s^{\beta }}}-s^{\alpha -\beta +1}{G}_{\zeta }\left[\varphi \left(\zeta ,\eta ,0\right)\right]& =& -G_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_{\zeta }{\phi }_{\eta }+{\psi }_{\eta }{\phi }_{\zeta }-\varphi \right]\hfill \\ \hfill {\displaystyle \frac{G_{\zeta }{G}_{\nu }\left[\phi \left(\zeta ,\eta ,\nu \right)\right]}{s^{\beta }}}-s^{\alpha -\beta +1}{G}_{\zeta }\left[\phi \left(\zeta ,\eta ,0\right)\right]& =& -G_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_{\zeta }{\varphi }_{\eta }+{\psi }_{\eta }{\varphi }_{\zeta }-\phi \right].\hfill \end{array}$$

(48)

Second, applying the (DGLT) for Equation (46) and simplifying the results, we obtain

$$\begin{array}{ccc}\hfill \mathsf{\Psi }\left(\rho ,\sigma ,s\right)& =& {\displaystyle \frac{{\rho }^{\alpha +1}{\sigma }^{\alpha +1}{s}^{\alpha +1}}{\left(1-\rho \right)\left(1-\sigma \right)}}\hfill \\ & & -s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\varphi }_{\zeta }{\phi }_{\eta }-{\varphi }_{\eta }{\phi }_{\zeta }+\psi \right]\hfill \\ \hfill \mathsf{\Phi }\left(\rho ,\sigma ,s\right)& =& {\displaystyle \frac{{\rho }^{\alpha +1}{\sigma }^{\alpha +1}{s}^{\alpha +1}}{\left(1-\rho \right)\left(1+\sigma \right)}}\hfill \\ & & -s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_{\zeta }{\phi }_{\eta }+{\psi }_{\eta }{\phi }_{\zeta }-\varphi \right]\hfill \\ \hfill \mathsf{{\rm Y}}\left(\rho ,\sigma ,s\right)& =& {\displaystyle \frac{{\rho }^{\alpha +1}{\sigma }^{\alpha +1}{s}^{\alpha +1}}{\left(1+\rho \right)\left(1-\sigma \right)}}\hfill \\ & & -s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_{\zeta }{\varphi }_{\eta }+{\psi }_{\eta }{\varphi }_{\zeta }-\phi \right].\hfill \end{array}$$

(49)

Third, employing (ITGLT) for Equation (49), we obtain

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\eta ,\nu \right)& =& e^{\zeta +\eta }\hfill \\ & & -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\varphi }_{\zeta }{\phi }_{\eta }-{\varphi }_{\eta }{\phi }_{\zeta }+\psi \right]\right]\hfill \\ \hfill \varphi \left(\zeta ,\eta ,\nu \right)& =& e^{\zeta -\eta }\hfill \\ & & -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_{\zeta }{\phi }_{\eta }+{\psi }_{\eta }{\phi }_{\zeta }-\varphi \right]\right]\hfill \\ \hfill \phi \left(\zeta ,\eta ,\nu \right)& =& e^{-\zeta +\eta }\hfill \\ & & -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_{\zeta }{\varphi }_{\eta }+{\psi }_{\eta }{\varphi }_{\zeta }-\phi \right]\right].\hfill \end{array}$$

(50)

The (TGLTDM) assumes the series solution of Equation (45) as follows:

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\eta ,\nu \right)& =& \sum _{n=0}^{\infty }{\psi }_n\left(\zeta ,\eta ,\nu \right),n=1,2,\cdots \hfill \\ \hfill \varphi \left(\zeta ,\eta ,\nu \right)& =& \sum _{n=0}^{\infty }{\varphi }_n\left(\zeta ,\eta ,\nu \right),n=1,2,\cdots \hfill \\ \hfill \phi \left(\zeta ,\eta ,\nu \right)& =& \sum _{n=0}^{\infty }{\phi }_n\left(\zeta ,\eta ,\nu \right),n=1,2,\cdots .\hfill \end{array}$$

(51)

Furthermore, we assume that the nonlinear terms ${\varphi }_{\zeta }{\phi }_{\eta },$ ${\varphi }_{\eta }{\phi }_{\zeta },$ ${\psi }_{\zeta }{\phi }_{\eta },$ ${\psi }_{\eta }{\phi }_{\zeta },$ ${\psi }_{\zeta }{\varphi }_{\eta },$ ${\psi }_{\eta }{\varphi }_{\zeta }$ are denoted by

$$\begin{array}{ccc}\hfill {\varphi }_{\zeta }{\phi }_{\eta }& =& \sum _{n=0}^{\infty }{A}_n,{\varphi }_{\eta }{\phi }_{\zeta }=\sum _{n=0}^{\infty }{B}_n,{\psi }_{\zeta }{\phi }_{\eta }=\sum _{n=0}^{\infty }{C}_n\hfill \\ \hfill {\psi }_{\eta }{\phi }_{\zeta }& =& \sum _{n=0}^{\infty }{D}_n,{\psi }_{\zeta }{\varphi }_{\eta }=\sum _{n=0}^{\infty }{E}_n,{\psi }_{\eta }{\varphi }_{\zeta }=\sum _{n=0}^{\infty }{F}_n,\hfill \end{array}$$

(52)

where

$$\begin{array}{ccc}\hfill A_0& =& {\varphi }_{0\zeta }{\phi }_{0\eta },A_1={\varphi }_{0\zeta }{\phi }_{1\eta }+{\varphi }_{1\zeta }{\phi }_{0\eta }\hfill \\ \hfill A_2& =& {\varphi }_{0\zeta }{\phi }_{2\eta }+{\varphi }_{1\zeta }{\phi }_{1\eta }+{\varphi }_{2\zeta }{\phi }_{0\eta }\hfill \\ \hfill A_3& =& {\varphi }_{0\zeta }{\phi }_{3\eta }+{\varphi }_{1\zeta }{\phi }_{2\eta }+{\varphi }_{2\zeta }{\phi }_{1\eta }+{\varphi }_{3\zeta }{\phi }_{0\eta }.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill B_0& =& {\varphi }_{0\eta }{\phi }_{0\zeta },B_1={\varphi }_{0\eta }{\phi }_{1\zeta }+{\varphi }_{1\eta }{\phi }_{0\zeta }\hfill \\ \hfill B_2& =& {\varphi }_{0\eta }{\phi }_{2\zeta }+{\varphi }_{1\eta }{\phi }_{1\zeta }+{\varphi }_{2\eta }{\phi }_{0\zeta }\hfill \\ \hfill B_3& =& {\varphi }_{0\eta }{\phi }_{3\zeta }+{\varphi }_{1\eta }{\phi }_{2\zeta }+{\varphi }_{2\eta }{\phi }_{1\zeta }+{\varphi }_{3\eta }{\phi }_{0\zeta }.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill C_0& =& {\psi }_{0\zeta }{\phi }_{0\eta },B_1={\psi }_{0\zeta }{\phi }_{1\eta }+{\psi }_{1\zeta }{\phi }_{0\eta }\hfill \\ \hfill C_2& =& {\psi }_{0\zeta }{\phi }_{2\eta }+{\psi }_{1\zeta }{\phi }_{1\eta }+{\psi }_{2\zeta }{\phi }_{0\eta }\hfill \\ \hfill C_3& =& {\psi }_{0\zeta }{\phi }_{3\eta }+{\psi }_{1\zeta }{\phi }_{2\eta }+{\psi }_{2\zeta }{\phi }_{1\eta }+{\psi }_{3\zeta }{\phi }_{0\eta }.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill D_0& =& {\psi }_{0\eta }{\phi }_{0\zeta },D_1={\psi }_{0\eta }{\phi }_{1\zeta }+{\psi }_{1\eta }{\phi }_{0\zeta }\hfill \\ \hfill D_2& =& {\psi }_{0\eta }{\phi }_{2\zeta }+{\psi }_{1\eta }{\phi }_{1\zeta }+{\psi }_{2\eta }{\phi }_{0\zeta }\hfill \\ \hfill D_3& =& {\psi }_{0\eta }{\phi }_{3\zeta }+{\psi }_{1\eta }{\phi }_{2\zeta }+{\psi }_{2\eta }{\phi }_{1\zeta }+{\psi }_{3\eta }{\phi }_{0\zeta }.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill E_0& =& {\psi }_{0\zeta }{\varphi }_{0\eta },E_1={\psi }_{0\zeta }{\varphi }_{1\eta }+{\psi }_{1\zeta }{\varphi }_{0\eta }\hfill \\ \hfill E_2& =& {\psi }_{0\zeta }{\varphi }_{2\eta }+{\psi }_{1\zeta }{\varphi }_{1\eta }+{\psi }_{2\zeta }{\varphi }_{0\eta }\hfill \\ \hfill E_3& =& {\psi }_{0\zeta }{\varphi }_{3\eta }+{\psi }_{1\zeta }{\varphi }_{2\eta }+{\psi }_{2\zeta }{\varphi }_{1\eta }+{\psi }_{3\zeta }{\varphi }_{0\eta }.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill F_0& =& {\psi }_{0\eta }{\varphi }_{0\zeta },F_1={\psi }_{0\eta }{\varphi }_{1\zeta }+{\psi }_{1\eta }{\varphi }_{0\zeta }\hfill \\ \hfill F_2& =& {\psi }_{0\eta }{\varphi }_{2\zeta }+{\psi }_{1\eta }{\varphi }_{1\zeta }+{\psi }_{2\eta }{\varphi }_{0\zeta }\hfill \\ \hfill F_3& =& {\psi }_{0\eta }{\varphi }_{3\zeta }+{\psi }_{1\eta }{\varphi }_{2\zeta }+{\psi }_{2\eta }{\varphi }_{1\zeta }+{\psi }_{3\eta }{\varphi }_{0\zeta }.\hfill \end{array}$$

Fourth, by substituting Equations (52) and (51) into Equation (50), we obtain

$$\begin{array}{ccc}\hfill \sum _{n=0}^{\infty }{\psi }_n\left(\zeta ,\eta ,\nu \right)& =& e^{\zeta +\eta }\hfill \\ & & -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[\sum _{n=0}^{\infty }\left(A_n-B_n\right)+{\psi }_n\right]\right],\hfill \\ \hfill \sum _{n=0}^{\infty }{\varphi }_n\left(\zeta ,\eta ,\nu \right)& =& e^{\zeta -\eta }\hfill \\ & & -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[\sum _{n=0}^{\infty }\left(C_n+D_n\right)-{\varphi }_n\right]\right],\hfill \\ \hfill \sum _{n=0}^{\infty }{\phi }_n\left(\zeta ,\eta ,\nu \right)& =& e^{-\zeta +\eta }\hfill \\ & & -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[\sum _{n=0}^{\infty }\left(E_n+F_n\right)-{\phi }_n\right]\right].\hfill \end{array}$$

(53)

Fifth, from the Equation (53), we introduce the iteration relation as follows:

$${\psi }_0\left(\zeta ,\eta ,\nu \right)=e^{\zeta +\eta },{\varphi }_0\left(\zeta ,\eta ,\nu \right)=e^{\zeta -\eta },{\phi }_0\left(\zeta ,\eta ,\nu \right)=e^{-\zeta +\eta }$$

and

$$\begin{array}{ccc}\hfill {\psi }_{n+1}\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[A_n-B_n+{\psi }_n\right]\right],\hfill \\ \hfill {\varphi }_{n+1}\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[C_n+D_n-{\varphi }_n\right]\right],\hfill \\ \hfill {\phi }_{n+1}\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[E_n+F_n-{\phi }_n\right]\right],\hfill \end{array}$$

(54)

at $n=0,$ Equation (53) becomes

$$\begin{array}{ccc}\hfill {\psi }_1\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[A_0-B_0+{\psi }_0\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_0\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[e^{\zeta +\eta }\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[{\displaystyle \frac{s^{\alpha +\beta +1}{\rho }^{\alpha +1}{\sigma }^{\alpha +1}}{\left(1-\rho \right)\left(1-\sigma \right)}}\right]\hfill \\ & =& -{\displaystyle \frac{e^{\zeta +\eta }{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\varphi }_1\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[C_0+D_0-{\varphi }_0\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[-{\varphi }_0\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[-e^{\zeta -\eta }\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[{\displaystyle \frac{s^{\alpha +\beta +1}{\rho }^{\alpha +1}{\sigma }^{\alpha +1}}{\left(1-\rho \right)\left(1+\sigma \right)}}\right]\hfill \\ & =& {\displaystyle \frac{e^{\zeta -\eta }{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\phi }_1\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[E_0+F_0-{\phi }_0\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[-{\phi }_0\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[{\displaystyle \frac{s^{\alpha +\beta +1}{\rho }^{\alpha +1}{\sigma }^{\alpha +1}}{\left(1+\rho \right)\left(1-\sigma \right)}}\right]\hfill \\ & =& {\displaystyle \frac{e^{-\zeta +\eta }{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}},\hfill \end{array}$$

at $n=1,$

$$\begin{array}{ccc}\hfill {\psi }_2\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[A_1-B_1+{\psi }_1\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[{\psi }_1\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[-{\displaystyle \frac{e^{\zeta +\eta }{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[{\displaystyle \frac{s^{\alpha +2\beta +1}{\rho }^{\alpha +1}{\sigma }^{\alpha +1}}{\left(1-\rho \right)\left(1-\sigma \right)}}\right]\hfill \\ & =& {\displaystyle \frac{e^{\zeta +\eta }{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\varphi }_2\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[C_1+D_1-{\varphi }_1\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[-{\varphi }_1\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[-e^{\zeta -\eta }\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[{\displaystyle \frac{s^{\alpha +\beta +1}{\rho }^{\alpha +1}{\sigma }^{\alpha +1}}{\left(1-\rho \right)\left(1+\sigma \right)}}\right]\hfill \\ & =& {\displaystyle \frac{e^{\zeta -\eta }{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\phi }_2\left(\zeta ,\eta ,\nu \right)& =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[E_1+F_1-{\phi }_1\right]\right]\hfill \\ & =& -G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[s^{\beta }{G}_{\zeta }{G}_{\eta }{G}_{\nu }\left[-{\phi }_1\right]\right]\hfill \\ & =& G_{\rho }^{-1}{G}_{\sigma }^{-1}{G}_s^{-1}\left[{\displaystyle \frac{s^{\alpha +2\beta +1}{\rho }^{\alpha +1}{\sigma }^{\alpha +1}}{\left(1+\rho \right)\left(1-\sigma \right)}}\right]\hfill \\ & =& {\displaystyle \frac{e^{-\zeta +\eta }{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}.\hfill \end{array}$$

In the same manner at $n=2,$ we have

$${\psi }_3=-{\displaystyle \frac{e^{\zeta +\eta }{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}},{\varphi }_3={\displaystyle \frac{e^{\zeta -\eta }{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}},{\phi }_3={\displaystyle \frac{e^{-\zeta +\eta }{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}$$

Finally, the series solution of Equation (45) is given by

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\eta ,\nu \right)& =& {\psi }_0+{\psi }_1+{\psi }_2+\cdots \hfill \\ \hfill \varphi \left(\zeta ,\eta ,\nu \right)& =& {\varphi }_0+{\varphi }_1+{\varphi }_2+\cdots \hfill \\ \hfill \phi \left(\zeta ,\eta ,\nu \right)& =& {\phi }_0+{\phi }_1+{\phi }_2+\cdots .\hfill \end{array}$$

Hence,

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\eta ,\nu \right)& =& \left(1-{\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}+{\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}-{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}+\cdots \right)e^{\zeta +\eta }\hfill \\ \hfill \varphi \left(\zeta ,\eta ,\nu \right)& =& \left(1+{\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}+{\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}+{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}+\cdots \right)e^{\zeta -\eta }\hfill \\ \hfill \phi \left(\zeta ,\eta ,\nu \right)& =& \left(1+{\displaystyle \frac{{\nu }^{\beta }}{\mathsf{\Gamma }\left(\beta +1\right)}}+{\displaystyle \frac{{\nu }^{2\beta }}{\mathsf{\Gamma }\left(2\beta +1\right)}}+{\displaystyle \frac{{\nu }^{3\beta }}{\mathsf{\Gamma }\left(3\beta +1\right)}}+\cdots \right)e^{-\zeta +\eta },\hfill \end{array}$$

By putting $\beta =1$, the exact solution of Equation (45) is given by:

$$\begin{array}{ccc}\hfill \psi \left(\zeta ,\eta ,\nu \right)& =& \left(1-\nu +{\displaystyle \frac{{\nu }^2}{2!}}-{\displaystyle \frac{{\nu }^3}{3!}}+\cdots \right)e^{\zeta +\eta }\hfill \\ & =& e^{\zeta +\eta -\nu }\hfill \\ \hfill \varphi \left(\zeta ,\eta ,\nu \right)& =& \left(1+\nu +{\displaystyle \frac{{\nu }^2}{2!}}+{\displaystyle \frac{{\nu }^3}{3!}}+\cdots \right)e^{\zeta -\eta }\hfill \\ & =& e^{\zeta -\eta +\nu }\hfill \\ \hfill \phi \left(\zeta ,\eta ,\nu \right)& =& \left(1+\nu +{\displaystyle \frac{{\nu }^2}{2!}}+{\displaystyle \frac{{\nu }^3}{3!}}+\cdots \right)e^{-\zeta +\eta }\hfill \\ & =& e^{\zeta -\eta +\nu }\hfill \end{array}$$

The results we obtained agree with [23].

The contrast between exact and numerical solutions for Equation (46) was presented in Figure 5, Figure 6 and Figure 7. For this, we used $\nu =1$ and $\beta =1$ to achieve the exact solution, and $\beta$, for instance, ($\beta =0.97$, $\beta =0.99$, $\beta =0.9$, $\beta =0.8$ and $\beta =0.7$) to obtain the approximate solutions. Figure 8, Figure 9 and Figure 10 demonstrates the graph of functions $\psi (\zeta ,\eta ,\nu )$, $\varphi (\zeta ,\eta ,\nu )$ and $\phi (\zeta ,\eta ,\nu )$ of the Equation (46), respectively, in three-dimensions.

6. Conclusions

In this work, we introduced a hybrid of the decomposition method and the multi-G-Laplace transform method for solving time FPDEs. This combination creates a powerful method called the MGLTDM method. This method has been successfully utilized in time-fractional systems of linear and nonlinear partial differential equations. The MGLTDM is an analytical method that works by using the initial conditions. Thus, it can be applied to solve equations with fractional and integer order concerning time. An important advantage of the new approach is its very fast computation. Two examples were offered to check the relevance of our method. Furthermore, the existing conditions and the convergence of this technique were discussed. Matlab software was utilized to graph the results. We observed that these results showed the effectiveness of this approach and how it may be implemented in other nonlinear problems. In the future, we aim to apply our technique to solve several novel and scientific problems related to our research area.