Semi-Regular Continued Fractions with Fast-Growing Partial Quotients

Abstract

In number theory, continued fractions are essential tools because they provide distinct representations of real numbers and provide information about their characteristics. Regular continued fractions have been examined in great detail, but less research has been carried out on their semi-regular counterparts, which are produced from the sequences of alternating plus and minus ones. In this study, we investigate the structure and features of semi-regular continuous fractions through the lens of dimension theory. We prove a primary result about the Hausdorff dimension of number sets whose partial quotients increase more quickly than a given pace. Furthermore, we conduct numerical analyses to illustrate the differences between regular and semi-regular continued fractions, shedding light on potential future directions in this field.

1. Introduction

In number theory, continued fractions serve as a fundamental tool for representing real numbers. Notably, continued fraction theory finds applications in diverse fields, such as cryptography [1], number theory [2], dynamical systems [3], and approximation theory [4,5], where its elegant properties offer valuable insights and solutions to complex problems. On the other hand, regular continued fractions have been extensively studied (see, e.g., [6,7,8,9,10] and the references therein); however, their semi-regular counterparts have received comparatively less attention in the literature. Derived from the sequences of alternating plus and minus ones, semi-regular continued fractions (SRCFs) offer a unique approach to representing real numbers within the interval [0, 1), providing insights into the underlying patterns of these numbers. In this paper, we plan to delve into the dimension theory of SRCFs, exploring their structure and properties in depth. Recent review articles [11,12] provide a comprehensive survey of different fractal dimensions, a key concept in this theory. In particular, they offer valuable insights into the topological perspective of fractals. These articles shed light on the interconnectedness and dimensional complexity of fractals.

For any given sequence $\sigma ={\left({\sigma }_n\right)}_{n=1}^{\infty }\in {\{-1,1\}}^{\mathbb{N}}$ of plus and minus ones, the semi-regular continued fraction (SRCF) representation of a number $x\in (0,1)$ is expressed as follows:

$$x=a_{\sigma ,0}\left(x\right)+{\displaystyle \frac{{\sigma }_1}{a_{\sigma ,1}\left(x\right)+\frac{{\sigma }_2}{a_{\sigma ,2}\left(x\right)+\frac{{\sigma }_3}{a_{\sigma ,3}\left(x\right)+\ddots }}}}$$

where $a_{\sigma ,0}\left(x\right)\in \mathbb{Z}$ and $a_{\sigma ,1}\left(x\right),a_{\sigma ,2}\left(x\right),a_{\sigma ,3}\left(x\right),\cdots$ are positive integers dependent on x and $\sigma$, satisfying the following condition:

$$a_{\sigma ,n}\left(x\right)+{\sigma }_{n+1}\ge 1\mathrm{for}\mathrm{any}n\ge 1.$$

(1)

Moreover, when the SRCF is infinite, we additionally require that

$$a_{\sigma ,n}\left(x\right)+{\sigma }_{n+1}\ge 2\mathrm{infinitely}\mathrm{often}.$$

(2)

We note that when ${\sigma }_n=1$ for all $n\ge 1$, we obtain a regular continued fraction representation of x. We observe that by confining our attention to the interval $(0,1)$, the initial term $a_{\sigma ,0}$ takes the value of either 0 or 2. This determination depends on whether ${\sigma }_1$ equals 1 or −1, respectively. It is well known (see, e.g., [13]) that this representation is unique. For the given $x,\sigma$ and its SRCF, the sequence $(p_n\left(x\right)/q_n\left(x\right))$ of convergents encompasses rational numbers defined as

$${\displaystyle \frac{p_n}{q_n}}=a_{\sigma ,0}\left(x\right)+{\displaystyle \frac{{\sigma }_1}{a_{\sigma ,1}\left(x\right)+\frac{{\sigma }_2}{a_{\sigma ,2}\left(x\right)+\frac{{\sigma }_3}{a_{\sigma ,3}\left(x\right)+\ddots +\frac{{\sigma }_n}{a_{\sigma ,n}}}}}}.$$

Then, the convergence of the SRCF is understood as $x={lim}_{n\to \infty }{\displaystyle \frac{p_n\left(x\right)}{q_n\left(x\right)}}.$

In this work, we would like to study the exceptional sets of numbers whose partial quotients grow faster than the exponential function. More specifically, our main result is the following.

Theorem 1. 

Let $b>1$ be given. Then, for any sequence $\sigma \in {\{-1,1\}}^{\mathbb{N}}$ and number $\beta >0$, the Hausdorff dimension of the set $F_b(\sigma ,\beta )$ is given by

$$F_b(\sigma ,\beta )=\left\{x\in (0,1)\mid \underset{n\to \infty }{lim}{\displaystyle \frac{log{a}_{\sigma ,n}\left(x\right)}{b^n}}=\beta \right\}$$

(3)

satisfies

$$dim{F}_b(\sigma ,\beta )={\displaystyle \frac{1}{b+1}}.$$

We note that if x belongs to $F_b(\sigma ,\beta )$, then asymptotically, the partial quotients $a_{\sigma ,n}\left(x\right)$ satisfy

$$a_{\sigma ,n}\left(x\right)\approx exp\left(\beta b^n\right),$$

which results in fast-growing partial quotients.

Similar results and their generalizations have been studied for regular continued fractions when all ${\sigma }_i=1$; for instance, see [14] and the references therein. In particular, the same dimension of $1/(b+1)$ holds true for regular continued fractions.

A few remarks are worth mentioning. It is noteworthy that the sequence of convergents $q_n$ for regular continued fractions is monotonically increasing; in fact, they increase exponentially fast [3]. On the other hand, for semi-regular cases, it often happens that $q_n>q_{n+1}$ (see Lemma 1). For example, if we take $\sigma =\{-1,1,-1,-1,1,1,-1,-1,1,1,-1,-1,1,1,\cdots \}$ and $x=\pi$, then we see that the convergents $\left\{q_n\right\}=\{1,8,15,7,106,219,332,113,33102,\cdots \}$ for the semi-regular continued fraction are non-increasing, while for the regular continued fraction case, they are increasing $\{7,106,113,33102,33215,66317,\cdots \}.$ This makes many straightforward assumptions from regular continued fractions hard to implement for semi-regular continued fractions.

Another interesting point to note is that there are many studies [15,16,17] where methods such as inversion and singularization were developed to convert a regular continued fraction into a semi-regular one and vice versa. The complexity of algorithms for converting finite semi-regular continued fractions to regular, even, or odd continued fractions has been discussed in [18], but further research is needed in this area. Despite the complexity, one may hope that the problem studied in this work can be somehow transferred into a problem in a regular case. Unfortunately, this does not work for the following reason: if all $a_n>1$ for the regular continued fraction, then when converted into a semi-regular one, there will be many partial quotients equal to 2. Hence, divergent partial quotients in one type become non-divergent in another type. For instance, as illustrated in [15] (Proposition 2), when transforming a regular continued fraction into a backward continued fraction with all $\sigma$ entries being negative ones using inversion and singularization, one must include 2 as many times as $a_1-1$. To illustrate further, consider a real number $x=1.43312742\cdots$ with increasing regular partial quotients $1,2,3,4,5,6,7,8,9,10,\cdots$. Then, for the backward continued fraction, the partial quotients $a_{\sigma ,n}\left(x\right)$ are given by $2,2,5,2,2,2,7,2,2,2,2,2,9,2,2,2,2,2,2,2,11,\cdots$ which clearly does not diverge.

In the next section, we provide background and auxiliary results. Section 3 and Section 4 present the proofs of the lower and upper bound estimates of Theorem 1, respectively. In Section 5, we provide some numerical results to illustrate the differences between regular and semi-regular continued fractions. Furthermore, we discuss potential future directions. This article concludes with a section on conclusions.

2. Background and Auxiliary Results

In this section, we review some background information regarding semi-regular continued fraction theory.

Let us assume that we are given $\sigma \in {\{-1,1\}}^{\mathbb{N}}$ and sequence $\left(a_{\sigma ,n}\right)$. When there is no confusion, we let $a_n=a_{\sigma ,n}$ for the simplicity of notation throughout this section. Then, we know (see, e.g., [16]) that the convergents satisfy the following difference equations for any $n\ge 1$:

$$\begin{array}{cc}\hfill p_n& =a_n{p}_{n-1}+{\sigma }_n{p}_{n-2},p_{-1}=1,p_0=a_0,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill q_n& =a_n{q}_{n-1}+{\sigma }_n{q}_{n-2},q_{-1}=0,q_0=1.\hfill \end{array}$$

(5)

One important difference between regular continued fractions and semi-regular continued fractions is the growth of partial convergents $q_n$. As illustrated in the introduction, in contrast to regular continued fractions, $q_n$ may not be increasing for semi-regular continued fractions. The following lemma follows from (5) and the defining property $a_n+{\sigma }_n\ge 1$ (see, e.g., [19]).

Lemma 1. 

For any n, we have $q_n>0$. Moreover, for $n\ge 2$, if $q_n\le q_{n-1}$, then

• $a_n=1$, ${\sigma }_n=-1$, $a_{n-1}>1$, and ${\sigma }_{n+1}=1$,
• $q_{n-2}<q_{n-1}<q_{n+1}$,
• $q_n=q_{n-1}-q_{n-2}$.

Proof. 

We note that the first and second statements of Lemma 5 trivially follow from Lemmas 2.1 and 2.2 in [19] by a change in notation and are left to the reader for verification. Then, using (5) together with the facts that $a_n=1$ and ${\sigma }_n=-1$, we get

$$q_n=a_n{q}_{n-1}+{\sigma }_n{q}_{n-2}=q_{n-1}-q_{n-2},$$

proving the last assertion. □

While this is discouraging, we can still show the growth in certain cases. From Lemma 1, since $q_n\le q_{n-1}$ implies $a_n=1$, by contrapositive, $q_n>q_{n-1}$ whenever $a_n\ge 2$. In particular, when $a_n$’s are at least 2, we have increasing convergents:

Lemma 2. 

If $a_1,a_2,\cdots ,a_n\ge 2$, then $0<q_1<q_2<\cdots <q_n.$

The following lemma is given in [16]:

Lemma 3. 

For any integer $n\ge 0$, we have

• $q_n{p}_{n-1}-p_n{q}_{n-1}={\delta }_n,$
• $q_{n+1}{p}_{n-1}-p_{n+1}{q}_{n-1}=a_{n+1}{\delta }_n,$

where ${\delta }_n:={(-1)}^n{\sigma }_1{\sigma }_2\cdots {\sigma }_n$.

In the next lemma, we estimate how fast the denominators $\left(q_n\right)$ of convergents grow with $a_n$.

Lemma 4. 

Let N be a natural number. For any sequence $\sigma \in {\{-1,1\}}^{\mathbb{N}}$ and any $x\in (0,1)$, let $\left(q_n\right)$ be the associated sequence of convergents. If $q_n\ge q_{n-1}$, then we have

$$(a_n-1)q_{n-1}\le q_n\le (a_n+1)q_{n-1}.$$

(6)

In particular, if there exists a natural number N such that $q_N\le q_{N+1}\le \cdots \le q_n$ for some $n>N$, then

$$q_N\prod _{k=N+1}^n(a_k-1)\le q_n\le q_N\prod _{k=N+1}^n(a_k+1).$$

(7)

Proof. 

Since we assumed $q_n\ge q_{n-1}$, it follows from the difference Equation (5) that

$$q_n=a_n{q}_{n-1}+{\sigma }_n{q}_{n-2}\ge a_n{q}_{n-1}-q_{n-2}\ge (a_n-1)q_{n-1}$$

and

$$q_n=a_n{q}_{n-1}+{\sigma }_n{q}_{n-2}\le a_n{q}_{n-1}+q_{n-2}\le (a_n+1)q_{n-1}.$$

Inductively, we obtain the second assertion. □

Lemma 5. 

For any real numbers $a,b,c,d$, consider the associated linear fractional transformation given by

$$f\left(x\right)={\displaystyle \frac{a+bx}{c+dx}}.$$

Then, the function f is monotone.

Proof. 

This immediately follows from the fact that the derivative of f does not change the sign:

$$f^{\prime }\left(x\right)={\displaystyle \frac{bc-ad}{{(c+bx)}^2}}.$$

□

For any sequence $\sigma \in {\{-1,1\}}^{\mathbb{N}}$ and positive integers n and $a_1,a_2,\cdots ,a_n$, we examine the following nth order cylinder sets.

$$I_n^{\sigma }(a_1,a_2,\cdots ,a_n)=\{x\in (0,1)\mid a_{\sigma ,1}\left(x\right)=a_1,a_{\sigma ,2}\left(x\right)=a_2,\cdots ,a_{\sigma ,n}\left(x\right)=a_n\},$$

(8)

Thus, we have the following.

Lemma 6. 

Let $(p_n/q_n)$ be the convergents for the SRCF with some σ. Then, the nth order cylinder set $I_n^{\sigma }(a_1,a_2,\cdots ,a_n)$ has end points.

$$\begin{array}{c}\hfill {\displaystyle \frac{p_n}{q_n}}\mathit{and}{\displaystyle \frac{p_n+{\sigma }_{n+1}{p}_{n-1}}{q_n+{\sigma }_{n+1}{q}_{n-1}}}.\end{array}$$

In particular, the lengths of the cylinder sets satisfy

$$\begin{array}{c}\hfill |I_n^{\sigma }(a_1,a_2,\cdots ,a_n)|={\displaystyle \frac{1}{q_n(q_n+{\sigma }_{n+1}{q}_{n-1})}}.\end{array}$$

Proof. 

We note that the recurrence relations (4) and (5) hold for real sequences $\left(a_k\right)$. When the $a_k$ values are not integers, $p_k$ and $q_k$ are not necessarily integers. Moreover, if we fix $a_1,a_2,\cdots ,a_{n-1}$ and only replace $a_n$ with a new value $a_n^{\prime }$, then for $k=1,2,\cdots ,n$, the recurrence relations still hold, and all $p_k$ and $q_k$ will remain unchanged except for $p_n$ and $q_n$, which need to be replaced by the new values $a_n^{\prime }{p}_{n-1}+{\sigma }_n{p}_{n-2}$ and $a_n^{\prime }{q}_{n-1}+{\sigma }_n{q}_{n-2}$, respectively.

For any positive integer n, denoting the tail of the continued fraction with $ϵ$, we may write

$$x=a_0+{\displaystyle \frac{{\sigma }_1}{a_1+\frac{{\sigma }_2}{a_2+\frac{{\sigma }_3}{\ddots a_{n-1}+\frac{{\sigma }_n}{a_n+ϵ}}}}}.$$

By replacing $a_n$ in the recurrence relations (4) and (5) with $a_n+ϵ$, we get

$$x={\displaystyle \frac{p_n^{\prime }}{q_n^{\prime }}}={\displaystyle \frac{a_n^{\prime }{p}_{n-1}+{\sigma }_n{p}_{n-2}}{a_n^{\prime }{q}_{n-1}+{\sigma }_n{q}_{n-2}}}={\displaystyle \frac{(a_n+ϵ)p_{n-1}+{\sigma }_n{p}_{n-2}}{(a_n+ϵ)q_{n-1}+{\sigma }_n{q}_{n-2}}}={\displaystyle \frac{p_n+ϵp_{n-1}}{q_n+ϵq_{n-1}}},$$

where

$$ϵ={\displaystyle \frac{{\sigma }_{n+1}}{a_{\sigma ,n+1}\left(x\right)+\frac{{\sigma }_{n+2}}{a_{\sigma ,n+2}\left(x\right)+\ddots }}}.$$

We note that similar ideas have been used before; see, for example, ref. [3]—Equation (3.20). It follows from Lemma 5 that ${\displaystyle \frac{p_n+ϵp_{n-1}}{q_n+ϵq_{n-1}}}$ is monotone w.r.t. $ϵ$. This means the quantity is either an increasing function of $ϵ$ or a decreasing function of $ϵ$, but not both. Therefore, $I_n=I_n^{\sigma }(a_1,a_2,\cdots ,a_n)$ is an interval and its endpoints are determined according to the endpoints for the range of $ϵ$.

Let us assume that ${\sigma }_{n+1}=1$. In this case, $ϵ$ is positive and can be made close to zero by taking $a_{\sigma ,n+1}\left(x\right)$ as a large value. Thus, one of the endpoints of $I_n$ is $p_n/q_n.$ On the other hand, $a_{\sigma ,n+1}\left(x\right)+{\displaystyle \frac{{\sigma }_{n+2}}{a_{\sigma ,n+2}\left(x\right)+\ddots }}\ge 1$, which in turn makes $ϵ$ close to 1. Thus, the other end point of $I_n$ is $(p_n+p_{n-1})/(q_n+q_{n-1})$. So, for ${\sigma }_{n+1}=1$, we have

$$I_n^{\sigma }(a_1,a_2,\cdots ,a_n)=\left({\displaystyle \frac{p_n}{q_n}},{\displaystyle \frac{p_n+p_{n-1}}{q_n+q_{n-1}}}\right)\mathrm{or}\left({\displaystyle \frac{p_n+p_{n-1}}{q_n+q_{n-1}}},{\displaystyle \frac{p_n}{q_n}}\right).$$

Now, let us assume that ${\sigma }_{n+1}=-1.$ Arguing as above, we can see that $ϵ$ ranges from $-1$ to 0, leading to

$$I_n^{\sigma }(a_1,a_2,\cdots ,a_n)=\left({\displaystyle \frac{p_n-p_{n-1}}{q_n-q_{n-1}}},{\displaystyle \frac{p_n}{q_n}}\right)\mathrm{or}\left({\displaystyle \frac{p_n}{q_n}},{\displaystyle \frac{p_n-p_{n-1}}{q_n-q_{n-1}}}\right).$$

This proves the first part; moreover, for the last part, it follows from Lemma 3 that

$$|I_n^{\sigma }(a_1,a_2,\cdots ,a_n)|=\left|{\displaystyle \frac{p_n}{q_n}}-{\displaystyle \frac{p_n+{\sigma }_{n+1}{p}_{n-1}}{q_n+{\sigma }_{n+1}{q}_{n-1}}}\right|={\displaystyle \frac{1}{q_n(q_n+{\sigma }_{n+1}{q}_{n-1})}}.$$

□

Lemma 7. 

For any natural number n and the sequence $\sigma \in {\{-1,1\}}^{\mathbb{N}}$, we let the nth order cylinder sets $I_n^{\sigma }(a_1,a_2,\cdots ,a_n)$ be defined as in (8). Then, the lengths of the cylinder sets satisfy

$$|I_n^{\sigma }(a_1,a_2,\cdots ,a_n)| \le \frac{1}{{\displaystyle \prod _{k=1}^n}(a_k-2){\displaystyle \prod _{k=1}^n}(a_k-1)}.$$

(9)

Proof. 

From Lemma 6, it follows that the cylinder set satisfies

$$|I_n^{\sigma }(a_1,a_2,\cdots ,a_n)| ={\displaystyle \frac{1}{q_n(q_n+{\sigma }_{n+1}{q}_{n-1})}}\le {\displaystyle \frac{1}{q_n(q_n-q_{n-1})}}.$$

From Lemma 4, we have $q_n\ge (a_n-1)q_{n-1}$, which gives

$$q_n-q_{n-1}\ge (a_n-1)q_{n-1}-q_{n-1}=(a_n-2)q_{n-1}.$$

Thus,

$$|I_n^{\sigma }(a_1,a_2,\cdots ,a_n)|\le {\displaystyle \frac{1}{(a_n-2)(a_n-1)q_{n-1}^2}}.$$

Arguing inductively, we obtain the desired result. □

3. Lower Bound for Hausdorff Dimension

We implement the following classical method described in ref. [20] (Example 4.6) to obtain a lower estimate, as follows:

Theorem 2. 

Suppose we have a sequence of sets, starting with the interval $[0,1]$ and denoted as $E_0\supset E_1\supset \dots$, where each set $E_k$ is formed by combining a finite number of non-overlapping closed intervals. Moreover, at each level, the $(k-1)$th set contains at least $m_k\ge 2$ disjoint intervals of the kth level, with each interval separated by gaps of at least ${\delta }_k$. It is also given that these gap sizes decrease as the level increases, meaning that ${\delta }_{k+1}<{\delta }_k$ for each k. Then, the Hausdorff dimension of the resulting set F, which is the intersection of all $E_k$, satisfies the following inequality:

$$dim\left(F\right)\ge \underset{k\to \infty }{lim\; inf}{\displaystyle \frac{log(m_1{m}_2\dots m_{k-1})}{-log\left(m_k{\delta }_k\right)}}.$$

(10)

Proposition 1. 

For any $\beta >0$, the Hausdorff dimension of $F_b(\sigma ,\beta )$ satisfies

$$dim{F}_b(\sigma ,\beta )\ge {\displaystyle \frac{1}{b+1}}.$$

We note that the results of Proposition 1 and Theorem 1 are independent of the choice of the sequence $\sigma$.

Proof. 

Let $ϵ\in (0,1)$ be given. To establish the lower bound, we aim to construct a subset of $F_b(\sigma ,\beta )$ and demonstrate that it meets the desired lower estimation for dimension. For this purpose, we define

$$F=F\left(ϵ\right)=\{x\in (0,1)|e^{b^n\beta (1-{ϵ}_n)}<a_n\le M{e}^{b^n\beta (1+{ϵ}_n)}\mathrm{for}\mathrm{all}n\ge 1\},$$

where ${ϵ}_n=ϵ/n$ and $M\ge 3$ is chosen so that $M{e}^{b\beta }>2.$ Next, observe that for any $x\in F$, we have

$$\beta (1-{ϵ}_n)<{\displaystyle \frac{log{a}_n\left(x\right)}{b^n}}\le \beta (1+{ϵ}_n)+b^{-n}logM.$$

For n tending to infinity, it follows that ${lim}_{n\to \infty }{\displaystyle \frac{log{a}_n\left(x\right)}{b^n}}=\beta$. Consequently, $x\in F_b(\sigma ,\beta )$ implies $F\subset F_b(\sigma ,\beta ).$ Therefore, to establish the lower bound for $F_b(\sigma ,\beta )$, it is sufficient to establish the lower bound for $F.$ We now let $E_0=[0,1]$, and for $k\ge 1$, we define

$$E_k:=\bigcup I_k^{\sigma }(a_1,a_2,\cdots ,a_k),$$

where union is taken over all $e^{b^n\beta (1-{ϵ}_n)}<a_n\le M{e}^{b^n\beta (1+{ϵ}_n)}$ for $1\le n\le k$. We note that each $I_{k-1}^{\sigma }$ in $E_{k-1}$ contains exactly $m_k$ subintervals $I_k^{\sigma }$ in $E_k$, where $m_k$ is the number of integers in the interval $(e^{b^k\beta (1-{ϵ}_k)},M{e}^{b^k\beta (1+{ϵ}_k)}]$, with M determining that it contains at least 2 integers. Hence, we conclude that $E_K$’s satisfy the conditions of Theorem 2 and that

$$m_k=\lfloor M{e}^{b^k\beta (1+{ϵ}_k)}\rfloor -\lceil e^{b^k\beta (1-{ϵ}_k)}\rceil \ge {\displaystyle \frac{M{e}^{b^k\beta (1+{ϵ}_k)}-e^{b^k\beta (1-{ϵ}_k)}}{2}}\ge e^{b^k\beta (1+{ϵ}_k)}>e^{b^k\beta }.$$

One can easily see that $E_{k-1}$ contains $m_k$ intervals of $E_k$ and that these intervals are separated by the sets $I_{k+1}(a_1,a_2,\dots ,a_k,1),$ with endpoints

$${\displaystyle \frac{p_k+{\sigma }_{k+1}{p}_{k-1}}{q_k+{\sigma }_{k+1}{q}_{k-1}}} \text{and} {\displaystyle \frac{(1+{\sigma }_{k+2})p_k+{\sigma }_{k+1}{p}_{k-1}}{(1+{\sigma }_{k+2})q_k+{\sigma }_{k+1}{q}_{k-1}}},$$

where the latter follows from a similar argument as in Lemma 6. Therefore, the lengths of the gaps are given by the following inequality:

$${\displaystyle \frac{1}{(q_k+{\sigma }_{k+1}{q}_{k-1})((1+{\sigma }_{k+2})q_k+{\sigma }_{k+1}{q}_{k-1})}}\ge {\displaystyle \frac{1}{6q_k^2}}.$$

It is worth noting that since $e^{b^n\beta (1-{ϵ}_n)}\ge 1$, all $a_n$ in both sets F and $E_k$ are at least 2. This, coupled with Lemma 2, implies that the sequence of convergents $\left(q_n\right)$ is increasing. Thus, Lemma 4 gives

$${\delta }_k={\displaystyle \frac{1}{6q_k^2}}\ge {\displaystyle \frac{1}{6}}{\left(\prod _{n=1}^k(a_k+1)\right)}^{-2}>{\displaystyle \frac{1}{6}}{\left(\prod _{n=1}^k(M+1)e^{b^n\beta (1+{ϵ}_n)}\right)}^{-2}.$$

Since ${\sum }_{n=1}^k{b}^n\beta (1+{ϵ}_n)\le b\beta (1+ϵ){\displaystyle \frac{b^k-1}{b-1}}$, we get

$${\delta }_k>{\displaystyle \frac{1}{6}}{(M+1)}^{-2k}{e}^{-2b\beta (1+ϵ){\displaystyle \frac{b^k-1}{b-1}}}.$$

Applying Theorem 2, we arrive at

$$\begin{array}{cc}\hfill dimF& \ge \underset{k\to \infty }{lim\; inf}{\displaystyle \frac{log(m_1{m}_2\cdots m_{k-1})}{-log\left(m_k{\delta }_k\right)}}\hfill \\ \hfill & \ge \underset{k\to \infty }{lim\; inf}{\displaystyle \frac{log{\prod }_{n=1}^{k-1}{e}^{b^n\beta }}{-log\left(e^{b^k\beta }\frac{1}{6}{(M+1)}^{-2k}{e}^{-2b\beta (1+ϵ)\frac{b^k-1}{b-1}}\right)}}\hfill \\ \hfill & =\underset{k\to \infty }{lim\; inf}{\displaystyle \frac{b\beta \frac{b^{k-1}-1}{b-1}}{-b^k\beta +2b\beta (1+ϵ)\frac{b^k-1}{b-1}}}\hfill \\ \hfill & =\underset{k\to \infty }{lim\; inf}{\displaystyle \frac{b^{k-1}-1}{-b^{k-1}(b-1)+2(1+ϵ)(b^k-1)}}\hfill \\ \hfill & ={\displaystyle \frac{1}{b+1+2ϵb}}.\hfill \end{array}$$

Thus, we get $dim{F}_b(\sigma ,\beta )\ge {\displaystyle \frac{1}{b+1+2ϵb}}.$ Since $ϵ>0$ is arbitrary, by letting $ϵ\to 0$, we obtain $dim{F}_b(\sigma ,\beta )\ge {\displaystyle \frac{1}{b+1}}.$ □

4. Upper Bound for the Hausdorff Dimension

Let $x\in F_b(\sigma ,\beta )$ for some $\beta >0$. Then, for any $ϵ>0$, there exists $N>0$ such that

$$\beta (1-ϵ)b^n<log{a}_n\left(x\right)<\beta (1+ϵ)b^n$$

for any $n\ge N.$ In other words, for any $n\ge N$, we have

$$e^{b^n\beta (1-ϵ)}<a_n\left(x\right)<e^{b^n\beta (1+ϵ)}$$

Let $E(N,ϵ)$ denote a set given by

$$E(N,ϵ)=\{x\in (0,1)\mid e^{b^n\beta (1-ϵ)}<a_n\left(x\right)<e^{b^n\beta (1+ϵ)}\mathrm{for}n\ge N\}.$$

(11)

It follows that

$$F_b(\sigma ,\beta )=\bigcap _{ϵ>0}\bigcup _{N=1}^{\infty }E(N,ϵ).$$

(12)

Proposition 2. 

For any $\beta >0$, the Hausdorff dimension of $F_b(\sigma ,\beta )$ satisfies

$$dim{F}_b(\sigma ,\beta )\le {\displaystyle \frac{1}{b+1}}.$$

Proof. 

For any $n>N$, we consider covering of $E(N,ϵ)$ with the sets J defines by

$$J(a_1,a_2,\dots ,a_n)=\overline{\bigcup I_{n+1}^{\sigma }(a_1,a_2,\dots ,a_n,a_{n+1})},$$

where $e^{b^k\beta (1-ϵ)}<a_k\left(x\right)<e^{b^k\beta (1+ϵ)}$ for $k=N,N+1,\cdots ,n$ and $a_{n+1}>e^{b^{n+1}\beta (1-ϵ)}$.

We observe that analogous intervals were previously examined by Fan et al. to substantiate their study [21] (Lemma 3.2) concerning regular continued fractions. This analysis proved pivotal in studying the Khintchine spectrum and contributed significantly to establishing fundamental properties of level sets.

Arguing as in Lemma 6, we understand that $J(a_1,a_2,\dots ,a_n)$ is an interval with endpoints

$${\displaystyle \frac{p_n}{q_n}}\mathrm{and}{\displaystyle \frac{e^{b^{n+1}\beta (1-ϵ)}{p}_n+{\sigma }_{n+1}{p}_{n-1}}{e^{b^{n+1}\beta (1-ϵ)}{q}_n+{\sigma }_{n+1}{q}_{n-1}}}.$$

Then,

$$\begin{array}{c}|J(a_1,a_2,\dots ,a_n)|=\left|{\displaystyle \frac{p_n}{q_n}}-{\displaystyle \frac{e^{b^{n+1}\beta (1-ϵ)}{p}_n+{\sigma }_{n+1}{p}_{n-1}}{e^{b^{n+1}\beta (1-ϵ)}{q}_n+{\sigma }_{n+1}{q}_{n-1}}}\right|\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left|{\displaystyle \frac{1}{q_n(e^{b^{n+1}\beta (1-ϵ)}{q}_n+{\sigma }_{n+1}{q}_{n-1})}}\right|.\end{array}$$

(13)

Given that $a_n\ge 2$ for $n\ge N$, Lemma 1 establishes that $q_n>q_{n-1}$. Consequently, according to Lemma 4, we deduce that $q_n\ge (a_n-1)q_{n-1}\ge {\displaystyle \frac{a_n}{2}}{q}_{n-1}$ for $n>N$, yielding the following inequality:

$$e^{b^{n+1}\beta (1-ϵ)}{q}_n+{\sigma }_{n+1}{q}_{n-1}>{\displaystyle \frac{e^{b^{n+1}\beta (1-ϵ)}{a}_n}{4}}{q}_{n-1}.$$

Then, (13) gives

$$|J(a_1,a_2,\dots ,a_n)| <2e^{-b^{n+1}\beta (1-ϵ)}{\left({\displaystyle \frac{a_n}{2}}{q}_{n-1}\right)}^{-2},$$

and using $a_n>e^{b^n\beta (1-ϵ)}$ for $n\ge N$ inductively we obtain

$$|J(a_1,a_2,\dots ,a_n)| <2e^{-b^{n+1}\beta (1-ϵ)}{\left(q_{N-1}\prod _{k=N}^n{\displaystyle \frac{e^{b^k\beta (1-ϵ)}}{2}}\right)}^{-2}.$$

Using $q_{N-1}\ge 1$ and simplifying, we get

$$|J(a_1,a_2,\dots ,a_n)| <2^{2(n-N+1)+1}{e}^{-b^{n+1}\beta (1-ϵ)-2b^N\beta (1-ϵ){\displaystyle \frac{b^{n-N+1}-1}{b-1}}}.$$

(14)

For any given $a_1,a_2\cdots ,a_{N-1}$, we define

$$\begin{array}{c}E(N,ϵ,a_1,a_2,\cdots ,a_{N-1}):=\{x\in (0,1)\mid a_n\left(x\right)=a_n\mathrm{for}n\in [1,N-1]\mathrm{and}\hfill \\ \hfill e^{b^n\beta (1-ϵ)}<a_n\left(x\right)<e^{b^n\beta (1+ϵ)}\mathrm{for}n\ge N\}.\end{array}$$

Then, $E(N,ϵ)=\bigcup E(N,ϵ,a_1,a_2,\cdots ,a_{N-1})$ where the union runs all possible values for $a_1,a_2,\cdots ,a_{N-1}$. To upper estimate the Hausdorff dimension of $E(N,ϵ)$, we first estimate the box dimension of the sets $E(N,ϵ,a_1,a_2,\cdots ,a_{N-1}).$ To this end, let us fix some $a_1,a_2,\cdots ,a_{N-1}$; moreover, for any $n>N$, let us consider the covering $E(N,ϵ,a_1,a_2,\cdots ,a_{N-1})$ with intervals $J(a_1,a_2,\cdots ,a_n)$ such that $e^{b^k\beta (1-ϵ)}<a_k\left(x\right)<e^{b^k\beta (1+ϵ)}$ for $k=N,N+1,\cdots ,n$. Then, there are

$$\begin{array}{c}\stackrel{n}{\prod _{k=N}}(\lfloor e^{b^k\beta (1+ϵ)}\rfloor -\lceil e^{b^k\beta (1-ϵ)}\rceil )\le \stackrel{n}{\prod _{k=N}}\left(e^{b^k\beta (1+ϵ)}-e^{b^k\beta (1-ϵ)}\right)\le \prod _{k=N}^n{e}^{b^k\beta (1+ϵ)}\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=e^{b^N\beta (1+ϵ){\displaystyle \frac{b^{n-N+1}-1}{b-1}}}\end{array}$$

intervals $J(a_1,a_2,\dots ,a_N,\dots ,a_n)$ that cover $E(N,ϵ,a_1,a_2,\cdots ,a_{N-1})$. Using (14) and the definition of the box dimension, we get

$${\underline{dim}}_{B}E(N,ϵ,a_1,a_2,\cdots ,a_{N-1})\le \underset{n\to \infty }{lim\; inf}{\displaystyle \frac{log{e}^{b^N\beta (1+ϵ)\frac{b^{n-N+1}-1}{b-1}}}{-log{2}^{2(n-N+1)+1}{e}^{-b^{n+1}\beta (1-ϵ)-2b^N\beta (1-ϵ)\frac{b^{n-N+1}-1}{b-1}}}}.$$

Since $log{2}^{2(n-N+1)+1}$ is negligible, we get

$$\begin{array}{cc}\hfill {\underline{dim}}_{B}E(N,ϵ,a_1,a_2,\cdots ,a_{N-1})& \le \underset{n\to \infty }{lim\; inf}{\displaystyle \frac{b^N\beta (1+ϵ)\frac{b^{n-N+1}-1}{b-1}}{b^{n+1}\beta (1-ϵ)+2b^N\beta (1-ϵ)\frac{b^{n-N+1}-1}{b-1}}}\hfill \\ \hfill & =\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{(1+ϵ)(b^{n-N+1}-1)}{(b-1)b^{n-N+1}(1-ϵ)+2(1-ϵ)(b^{n-N+1}-1)}}\hfill \\ \hfill & ={\displaystyle \frac{1+ϵ}{(1-ϵ)(b+1)}}.\hfill \end{array}$$

Since the box dimension offers an upper estimate for the Hausdorff dimension (see, for instance [20]), it follows that the Hausdorff dimension of $E(N,ϵ,a_1,a_2,\cdots ,a_{N-1})$ is at most ${\displaystyle \frac{1+ϵ}{(1-ϵ)(b+1)}}$. Utilizing the countable stability property of the Hausdorff dimension, we infer that $E(N,ϵ)$ also possesses a Hausdorff dimension that is at most ${\displaystyle \frac{1+ϵ}{(1-ϵ)(b+1)}}$, as we represent $E(N,ϵ)$ as a countable union of sets of the form $E(N,ϵ,a_1,a_2,\cdots ,a_{N-1})$. Finally, utilizing (12), we establish that the set $F_b(\sigma ,\beta )$ is contained within ${\bigcup }_{N=1}^{\infty }$. As the latter is a countable union, it follows that $dim{F}_b(\sigma ,\beta )\le {\displaystyle \frac{1+ϵ}{(1-ϵ)(b+1)}}$. Since $ϵ$ is arbitrary, we conclude that $dim{F}_b(\sigma ,\beta )\le {\displaystyle \frac{1}{b+1}}$. □

Proof of Theorem 1. 

For $b>1$, $\sigma \in {\{-1,1\}}^{\mathbb{N}}$, and $\beta >0$, let $F_b(\sigma ,\beta )$ be the set defined in (3). Proposition 1 provides the lower estimate for the Hausdorff dimension of $F_b(\sigma ,\beta )$, while Proposition 2 provides the upper estimate. Together, these propositions establish the proof of Theorem 1. □

5. Numerical Analysis

The main result of this paper, Theorem 1, determines the Hausdorff dimension of sets based on the growth of partial quotients in semi-regular continued fractions. In this section, our goal is to present numerical results on the distribution of partial quotients in semi-regular continued fractions and highlight the differences from regular continued fractions. Additionally, we aim to suggest potential research directions based on these numerical estimates.

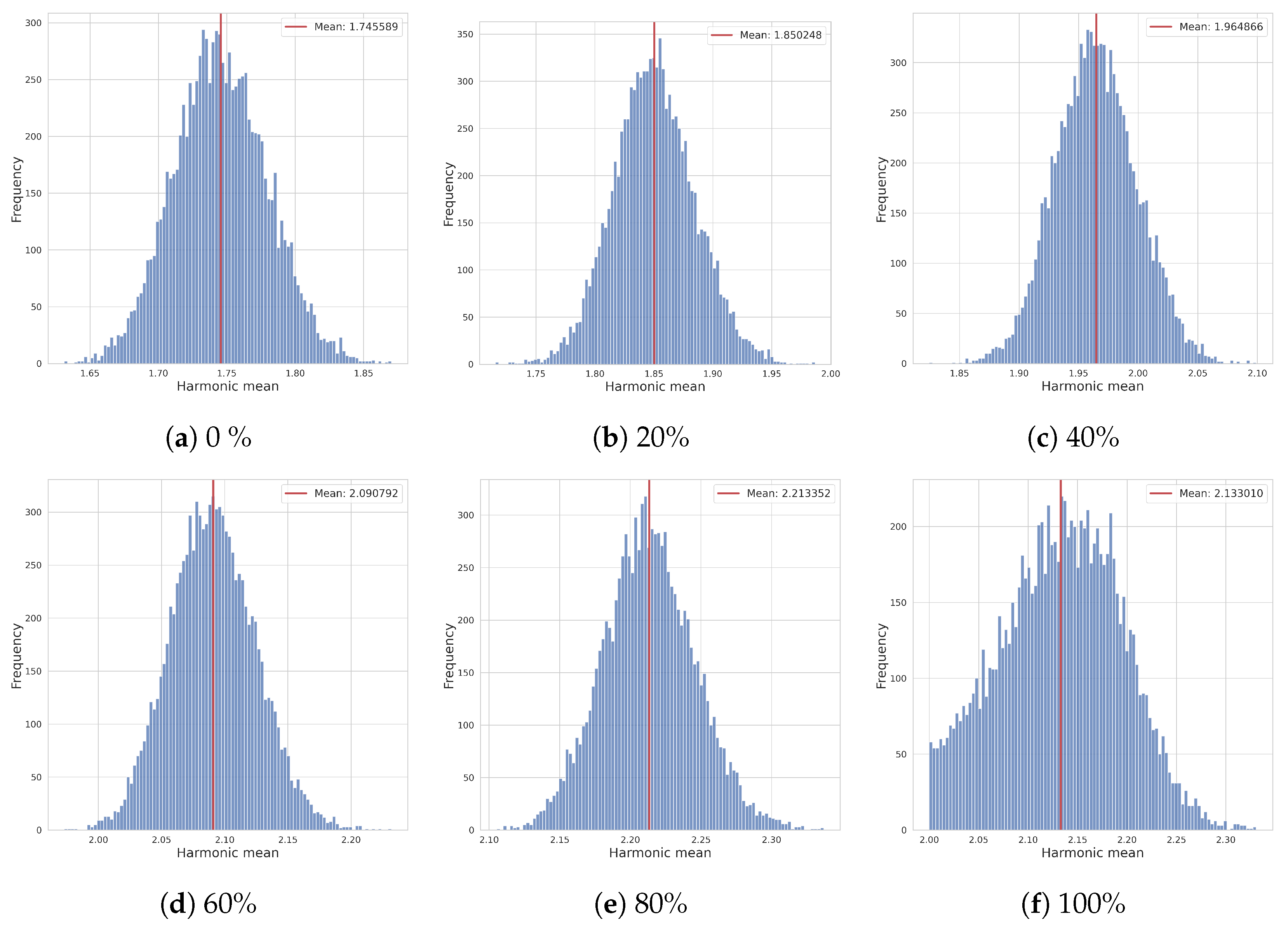
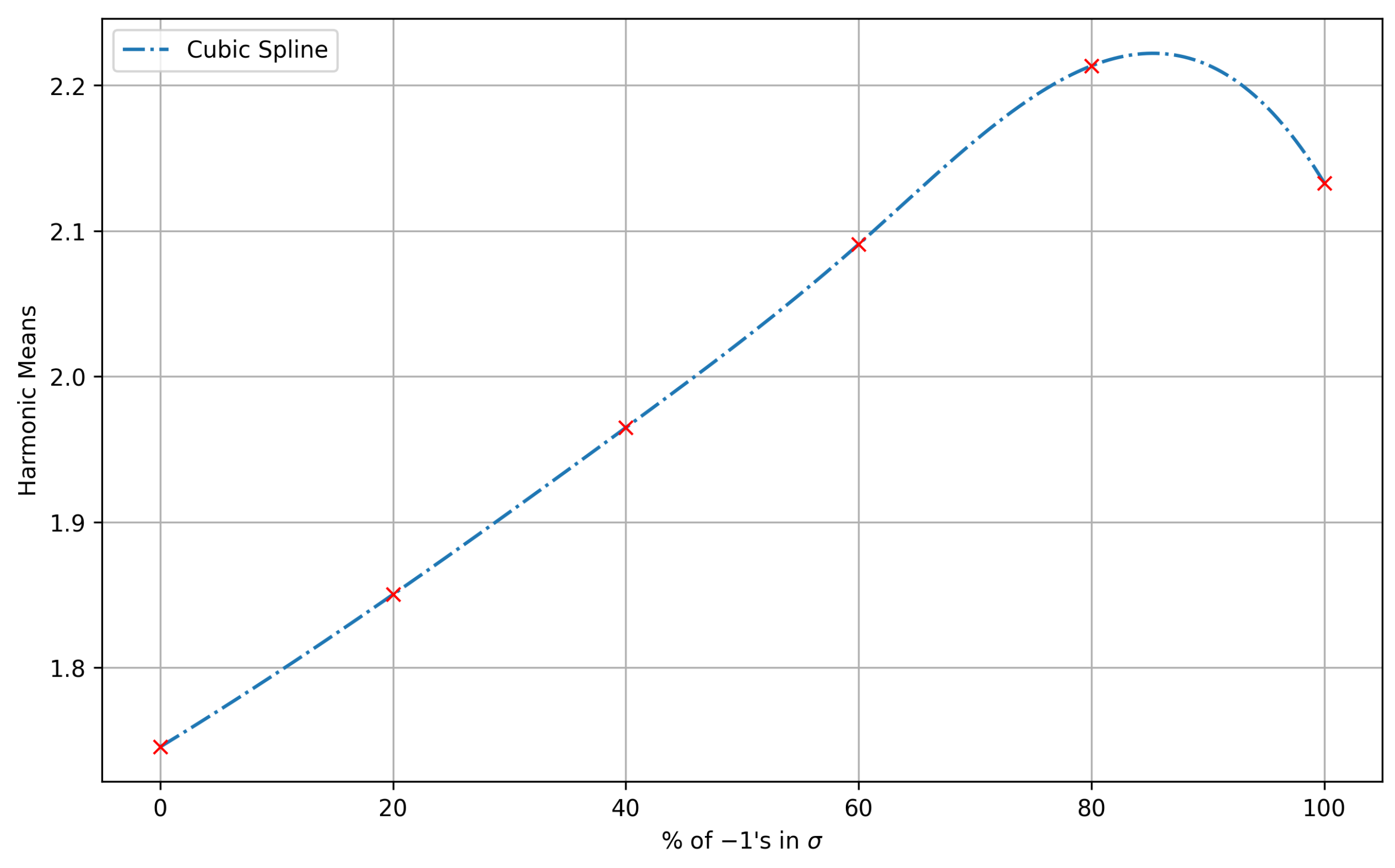
5.1. Harmonic Means of Partial Quotients

It is well known (see, e.g., [22,23]) that for almost every real number x, the harmonic mean of the regular continued fraction convergents satisfies

$$\underset{n\to \infty }{lim}{\displaystyle \frac{n}{\frac{1}{a_1\left(x\right)}+\frac{1}{a_2\left(x\right)}+\dots +\frac{1}{a_n\left(x\right)}}}=K_{-1},$$

(15)

where the constant $K_{-1}=1.74540566\cdots$ is called the Khinchine Harmonic Mean [24], A087491. We would like to study how harmonic means depend on $\sigma$ for the SRCF. To this end, we define the generalized harmonic mean

$$\begin{array}{c}\hfill K_{-1}\left(\sigma \right)=\underset{n\to \infty }{lim}{\displaystyle \frac{n}{\frac{1}{a_{\sigma ,1}\left(x\right)}+\frac{1}{a_{\sigma ,2}\left(x\right)}+\dots +\frac{1}{a_{\sigma ,n}\left(x\right)}}}\end{array}$$

In this experiment, we employed a sample size of 1000 (n = 1000), with 10,000 random observations (x). Figure 1 presents the frequency distributions of harmonic means. We explored six scenarios where the sequence $\sigma \in {\{-1,1\}}^{1000}$ was selected, varying the density of $-1$s at $0\%,20\%,40\%,60\%,80\%$, and $100\%$.

Figure 1a illustrates the regular continued fraction, with a sample mean of 1.745589, closely resembling $K_{-1}$ as anticipated. As the density of $-1$s in $\sigma$ increases, so does the harmonic mean, except for the backward continued fraction shown in Figure 1f, where the mean is 2.133010. Figure 2 depicts the relationship between the percentage of $-1$s in $\sigma$ and their corresponding harmonic means. The curve, derived using cubic spline interpolation, provides a smooth representation of the data.

An interesting research area lies in computing $K_{-1}\left(\sigma \right)$ for any given $\sigma$ and exploring its correlation with the density of $-1$s. Another avenue for investigation involves understanding the decline in the mean for the backward continued fraction. Notably, the distribution for the backward continued fraction displays right skewness. This phenomenon stems from the requirement in semi-regular continued fractions, stated in (1), necessitating $a_n+{\sigma }_{n+1}\ge 1$ for all n. When all ${\sigma }_n=-1$, this compels $a_n$ to be at least 2, ensuring the harmonic mean remains at or above 2.

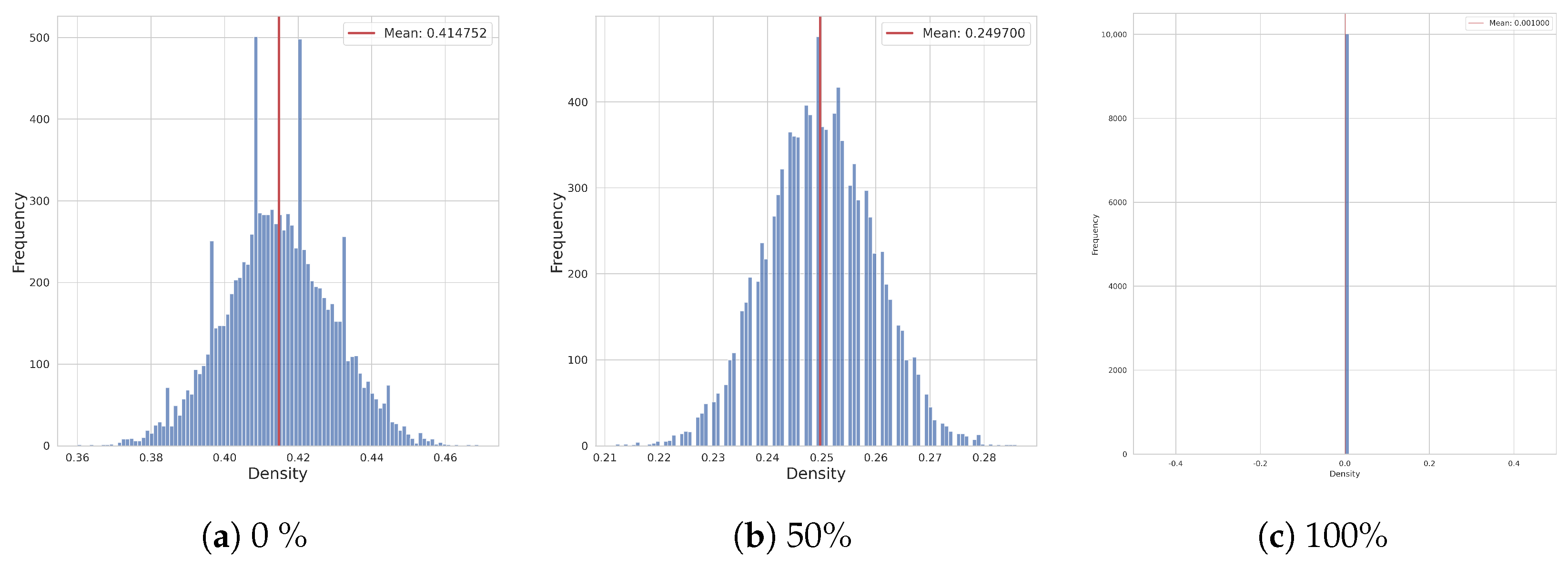
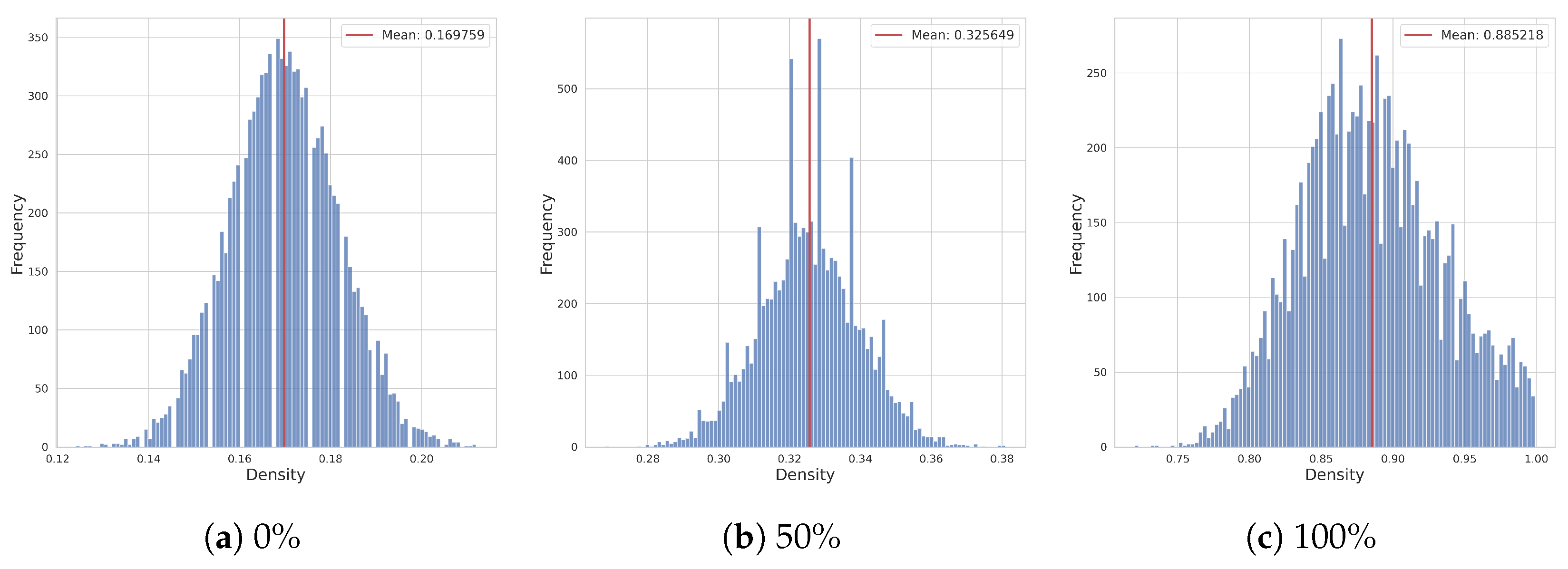
5.2. Proportion of the Number 1 and 2 in Partial Quotients

Figure 3 presents the frequency distribution of the digit 1 in a generic partial fraction for three distinct scenarios. Specifically, we consider three different values for $\sigma$: a regular case where ${\sigma }_n=1$, a random case, and a backward continued fraction scenario where all ${\sigma }_n=-1$. Subsequently, for any arbitrarily chosen $x\in (0,1)$, we calculate the density using the following expression:

$${\displaystyle \frac{1}{1000}}\#\left\{n\in [1,1000]|a_{\sigma ,n}\left(x\right)=1\right\}.$$

It is well established, as documented in [3] (Corollary 3.8), that for regular continued fractions, the density of a natural number j for a generic point can be derived from the ergodicity of the Gauss map with respect to the Gauss measure. The formula is provided as follows:

$${\displaystyle \frac{2log(1+j)-logj-log(2+j)}{log2}}.$$

(16)

For $j=1$, this yields a density of $0.415\cdots$, a value consistent with the mean of the distribution depicted in Figure 3a. For a random $\sigma$, the estimated density of ones is approximately $0.2497$, as illustrated in Figure 3b. Notably, the distribution exhibits ‘gaps’, indicating that certain intervals do not realize densities, warranting further analytical investigation. Finally, it is evident from (1) that the digit 1 does not appear in backward continued fractions, as depicted in Figure 3c.

Continuing in a similar manner, we can analyze the density distribution of the digit 2 for various values of $\sigma$. In a regular case, applying Formula (16) yields a density of approximately $0.17\cdots$, consistent with the prediction in Figure 4a.

Notably, in Figure 4c, we observe that the density of digit 2 for backward continued fractions is estimated to be around $88.52\%$. This observation raises an intriguing research question: is it possible to derive formulas akin to (16) for generic values of $\sigma$? Exploring such formulas could provide deeper insights into the distribution of digits in continued fractions under varying conditions.

6. Conclusions

In conclusion, our investigation into the dimension theory of semi-regular continued fractions (SRCFs) has uncovered intriguing insights into their fractal properties and structure. We have established a main result regarding the Hausdorff dimension of sets defined by the growth of partial quotients. This contributes to the understanding of SRCFs and their relationship with classical methods in fractal geometry. In [14], authors study exceptional sets in regular continued fractions where elements x satisfy $lim\; sup{\displaystyle \frac{log{a}_n\left(x\right)}{\psi \left(n\right)}}=1,$ for a $\psi$ function increasing to infinity in various speeds. In our work, we explored one specific case when $\psi \left(n\right)=\beta b^n$. Thus, an interesting future direction would be to study general $\psi$ for semi-regular continued fractions.

We have demonstrated the unique properties of SRCFs over regular continuous fractions using numerical analyses, opening up new avenues for investigation and potential uses in number theory and related fields. Our findings not only enrich the theoretical understanding of SRCFs but also offer practical implications for their applications in diverse mathematical contexts.