Multifractal Characteristics of Gain Structures: A Universal Law of Polycrystalline Strain-Hardening Behaviors
Abstract
:1. Introduction
2. Method and Experiment
2.1. Correlation Dimension of Polycrystalline Materials
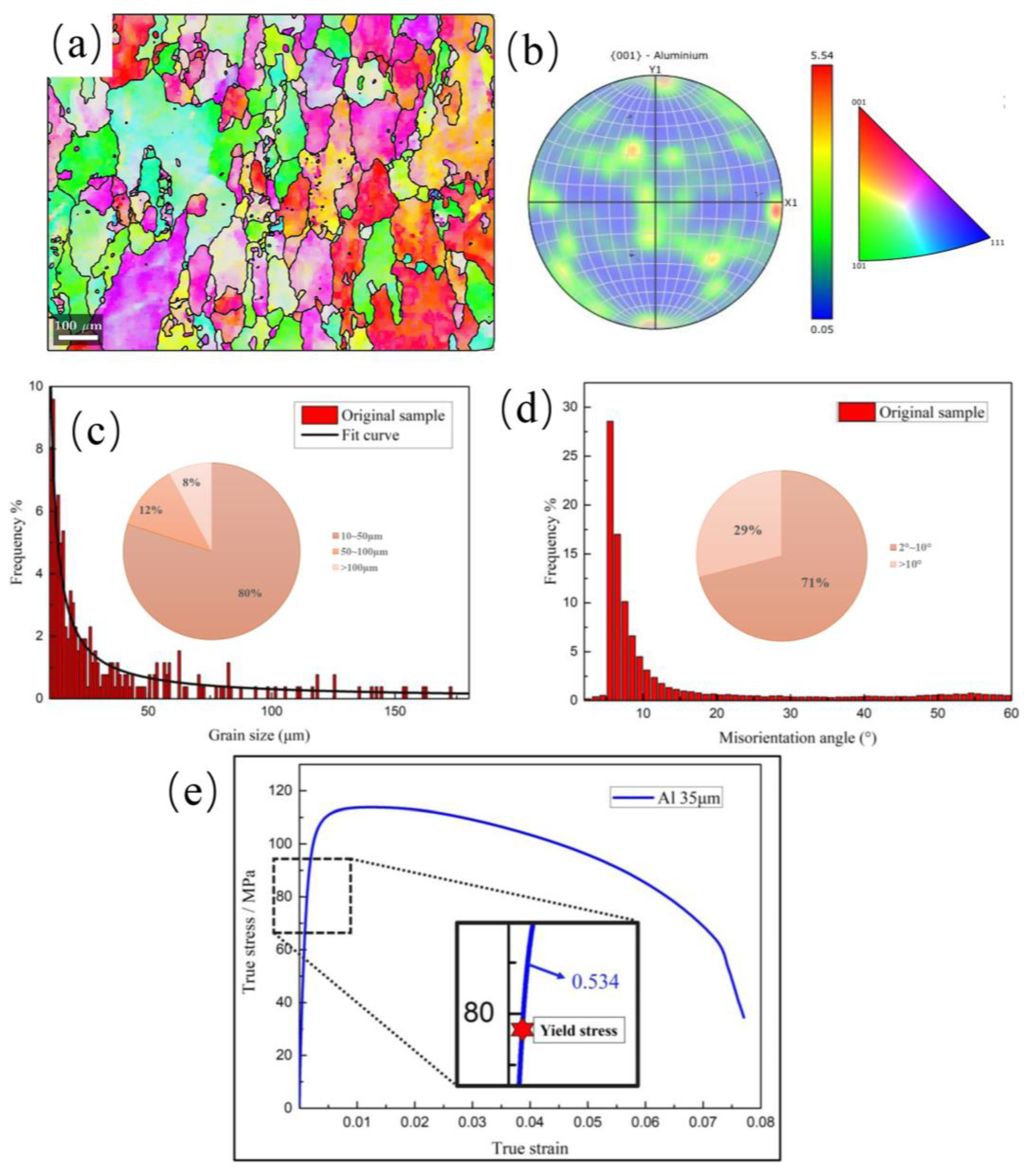
2.2. Results of Al Tensile Experiment
- (1)
- def load_and_preprocess_image (image_path): Load the EBSD image and convert it to a binary image using Otsu’s binarization method;
- (2)
- def find_grain_centers (binary_image): Identify the geometric centers of the grains using the skimage.measure library;
- (3)
- def count_grains_within_radius (centers, scan_points, radius): Use KDTree to calculate the mean number of grain geometric centers within a specified radius r for each scan point;
- (4)
- def plot_grains_and_scan (centers, scan_points, radius, counts, image): Plot the geometric centers of the grains and the scan results on the EBSD image using matplotlib;
- (5)
- Calculate the grain correlation dimension D using Equation (3).
3. Verification
4. Discussion
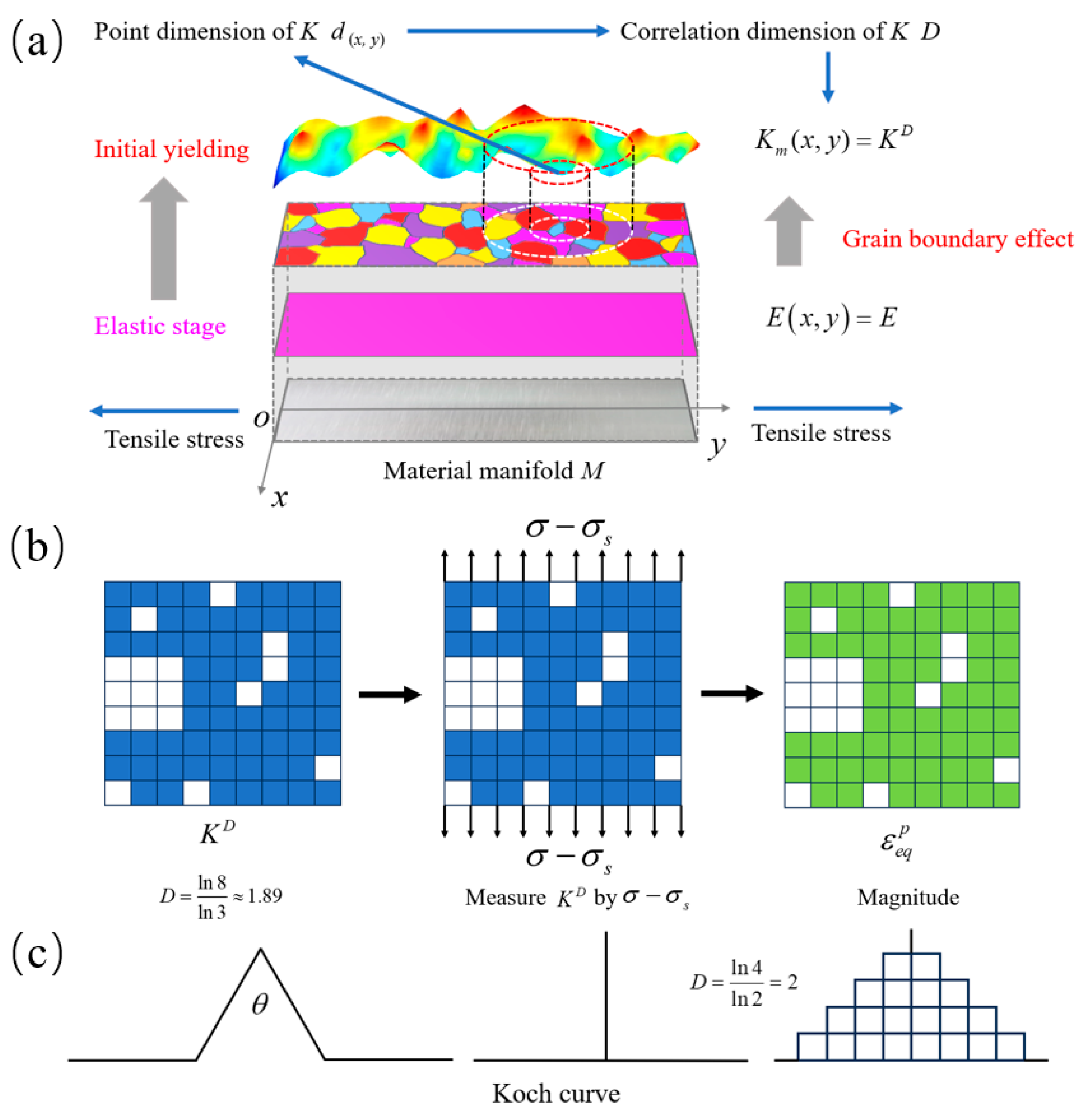
4.1. Relationship between the Pointwise Dimension and Material Manifold
4.2. The Equivalence Relationship between the Correlation Dimension of the Strength Coefficient Field and Grains
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Newnham, R.E. Preface. In Structure-Property Relations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hayat, S.; Khan, A.; Ali, K.; Liu, J.B. Structure-property modeling for thermodynamic properties of benzenoid hydrocarbons by temperature-based topological indices. Ain Shams Eng. J. 2024, 15, 102586. [Google Scholar] [CrossRef]
- Mahboob, A.; Rasheed, M.W.; Hanif, I.; Amin, L.; Alameri, A. Role of molecular descriptors in quantitative structure-property relationship analysis of kidney cancer therapeutics. Int. J. Quantum Chem. 2024, 124, e27241. [Google Scholar] [CrossRef]
- Hasani, M.; Ghods, M. Topological indices and QSPR analysis of some chemical structures applied for the treatment of heart patients. Int. J. Quantum Chem. 2024, 124, e27234. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile deformation. Aime Trans. 1945, 12, 1–22. [Google Scholar]
- Liu, R.; Chen, D.; Ou, M.; Liang, Y. The effect of initial grain size on the strength property of copper with gradient microstructure. J. Mater. Res. Technol. 2023, 24, 407–417. [Google Scholar] [CrossRef]
- Huang, C.X.; Hu, W.; Yang, G.; Zhang, Z.F.; Wu, S.D.; Wang, Q.Y.; Gottstein, G. The effect of stacking fault energy on equilibrium grain size and tensile properties of nanostructured copper and copper–aluminum alloys processed by equal channel angular pressing. Mater. Sci. Eng. A 2012, 556, 638–647. [Google Scholar] [CrossRef]
- Li, W.T.; Li, H.; Fu, M.W. Interactive effect of stress state and grain size on fracture behaviours of copper in micro-scaled plastic deformation. Int. J. Plast. 2019, 114, 126–143. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Cheng, W.L.; Wang, H.X.; Yu, H.; Niu, X.F.; Wang, L.F.; Li, H.; Hou, H. Insight on the correlation between bimodal-sized grain structure and tensile properties of extruded low-alloyed Mg–Sn–Bi–Mn alloy. Mater. Sci. Eng. A 2022, 843, 143128. [Google Scholar] [CrossRef]
- Zhang, Z.; Orlov, D.; Vajpai, S.K.; Tong, B.; Ameyama, K. Importance of bimodal structure topology in the control of mechanical properties of a stainless steel. Adv. Eng. Mater. 2015, 17, 791–795. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Dislocations and Strengthening Mechanisms. In Materials Science and Engineering: An Introduction; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Kadić, A.; Edelen, D.G. The Gauge Theory of Defects. In A Gauge Theory of Dislocations and Disclinations; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Carpinteri, A.; Chiaia, B. Power scaling laws and dimensional transitions in solid mechanics. Chaos Solitons Fractals 1996, 7, 1343–1364. [Google Scholar] [CrossRef]
- Kröger, H. Fractal geometry in quantum mechanics, field theory and spin systems. Phys. Rep. 2000, 323, 81–181. [Google Scholar] [CrossRef]
- Suzuki, M. Phase transition and fractals. Prog. Theor. Phys. 1983, 69, 65–76. [Google Scholar] [CrossRef]
- Morales, I.O.; Landa, E.; Fossion, R.; Frank, A. Scale invariance, self similarity and critical behavior in classical and quantum systems. J. Phys. Conf. Ser. 2012, 380, 012020. [Google Scholar] [CrossRef]
- Zborovský, I. A conservation law, entropy principle and quantization of fractal dimensions in hadron interactions. Int. J. Mod. Phys. A 2018, 33, 1850057. [Google Scholar] [CrossRef]
- Vinogradov, A.; Yasnikov, I.S.; Estrin, Y. Evolution of fractal structures in dislocation ensembles during plastic deformation. Phys. Rev. Lett. 2012, 108, 205504. [Google Scholar] [CrossRef]
- Yasnikov, I.S.; Vinogradov, A.; Estrin, Y. Dislocation model for the behavior of fractal dimension of the microstructure of a strained solid. Phys. Solid State 2013, 55, 346–352. [Google Scholar] [CrossRef]
- Strogatz, S.H. Pointwise and Corrlelation Dimensions. In Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: New York, NY, USA, 2018. [Google Scholar]
- Nie, C. Applying correlation dimension to the analysis of the evolution of network structure. Chaos Solitons Fractals 2019, 123, 294–303. [Google Scholar] [CrossRef]
- Nie, C. Generalized correlation dimension and heterogeneity of network spaces. Chaos Solitons Fractals 2022, 162, 112507. [Google Scholar] [CrossRef]
- Perinelli, A.; Iuppa, R.; Ricci, L. Estimating the correlation dimension of a fractal on a sphere. Chaos Solitons Fractals 2023, 173, 113632. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Tang, A.; Liu, H.; Liu, G.; Zhong, Y.; Wang, L.; Lu, Q.; Wang, J.; Shen, Y. Lognormal distribution of local strain: A universal law of plastic deformation in material. Phys. Rev. Lett. 2020, 124, 155501. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.W.; Yong, P.L.; Zhou, H.; Li, Y.S. Grain size effect on deformation mechanisms and mechanical properties of titanium. Mater. Sci. Eng. A 2020, 773, 138721. [Google Scholar] [CrossRef]
- Ibrahim, J.S.; Mathew, R.T.; Prasad, M.J.N.V.; Narasimhan, K. Processing and specimen thickness to grain size (t/d) ratio effects on tensile behaviour and microformability of copper foils. Met. Mater. Int. 2022, 28, 2340–2355. [Google Scholar] [CrossRef]
- Chong, Y.; Deng, G.; Gao, S.; Yi, J.; Shibata, A.; Tsuji, N. Yielding nature and Hall-Petch relationships in Ti-6Al-4V alloy with fully equiaxed and bimodal microstructures. Scr. Mater. 2019, 172, 77–82. [Google Scholar] [CrossRef]
- ASTM E8/E8M-21; Standard Test Methods for Tension Testing of Metallic Materials. ANSI: New York, NY, USA, 2021.
- Bilby, B.A.; Bullough, R.; Smith, E. Continuous distributions of dislocations: A new application of the methods of non-Riemannian geometry. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 1185, 263–273. [Google Scholar]
- Yavari, A.; Goriely, A. Riemann–Cartan geometry of nonlinear dislocation mechanics. Arch. Ration. Mech. Anal. 2012, 205, 59–118. [Google Scholar] [CrossRef]
- Sozio, F.; Yavari, A. A Geometric Field Theory of Dislocation Mechanics. J. Nonlinear Sci. 2023, 33, 83. [Google Scholar] [CrossRef]
- Li, J.; Ostoja-Starzewski, M. Fractals in elastic-hardening plastic materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 2114, 603–621. [Google Scholar] [CrossRef]
- Falconer, K. Products of fractals. In Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, M.; Chen, J.; Huang, Z.; Chen, B.; Hu, Y.; Wang, B. Multifractal Characteristics of Gain Structures: A Universal Law of Polycrystalline Strain-Hardening Behaviors. Fractal Fract. 2024, 8, 504. https://doi.org/10.3390/fractalfract8090504
Fu M, Chen J, Huang Z, Chen B, Hu Y, Wang B. Multifractal Characteristics of Gain Structures: A Universal Law of Polycrystalline Strain-Hardening Behaviors. Fractal and Fractional. 2024; 8(9):504. https://doi.org/10.3390/fractalfract8090504
Chicago/Turabian StyleFu, Maoqing, Jiapeng Chen, Zhaowen Huang, Bin Chen, Yangfan Hu, and Biao Wang. 2024. "Multifractal Characteristics of Gain Structures: A Universal Law of Polycrystalline Strain-Hardening Behaviors" Fractal and Fractional 8, no. 9: 504. https://doi.org/10.3390/fractalfract8090504
APA StyleFu, M., Chen, J., Huang, Z., Chen, B., Hu, Y., & Wang, B. (2024). Multifractal Characteristics of Gain Structures: A Universal Law of Polycrystalline Strain-Hardening Behaviors. Fractal and Fractional, 8(9), 504. https://doi.org/10.3390/fractalfract8090504






