Abstract
For fractals on Riemannian manifolds, the theory of iterated function systems often does not apply well directly, as these fractal sets are often defined by relations that are multivalued or non-contractive. To overcome this difficulty, we introduce the novel notion of iterated relation systems. We study the attractor of an iterated relation system and formulate a condition under which such an attractor can be identified with that of an associated graph-directed iterated function system. Using this method, we obtain dimension formulas for the attractor of an iterated relation system on locally Euclidean Riemannian manifolds, under the graph open set condition or the graph finite type condition. This method improves the one by Ngai and Xu, which relies on knowing the specific structure of the attractor. We also study fractals generated by iterated relation systems on Riemannian manifolds that are not locally Euclidean.
1. Introduction
Fractals in Riemannian manifolds, especially in Lie groups, Heisenberg groups, and projective spaces, have been studied extensively by many authors (see Strichartz [], Balogh and Tyson [], Barnsley and Vince [], Hossain et al. [,], etc.). A basic theory of iterated function systems (IFSs) on Riemannian manifolds, including Hausdorff dimension, the weak separation condition (WSC), and the finite type condition (FTC), was established by Xu and the second author []. In [], a method for computing the Hausdorff dimension of a certain fractal set in a flat torus is obtained; the fractal set can be identified with the attractor of some IFS on . However, this method is too cumbersome and is not easy to generalize. The purpose of this paper is to establish a new method that can be used to calculate the Hausdorff dimensions of more general fractal sets in Riemannian manifolds. Unlike fractal sets in , many interesting fractals in Riemannian manifolds cannot be described by an IFS. For example, the relations generating a Sierpinski gasket on a cylinder can be multivalued (see Example 4). Thangaraj et al. [] studied fractals generated by multivalued functions in a metric space. Cui et al. [] studied measures generated by nonautonomous iterated function systems consisting of expansive maps. Unlike mappings in these papers, relations that generate fractals considered in the present paper can be multivalued and expansive at the same time. To deal with the problem that the maps (or more precisely, relations) generating a fractal are multivalued and non-contractive, we introduce the notion of iterated relation systems (IRSs) (see Definition 1). We show that many interesting fractals can be described naturally by IRSs.
Let be an IRS on a nonempty compact subset of a topological space, and let K be the attractor of (see Definition 2). Then
(see Proposition 2). However, in general, a nonempty compact set K satisfying (1) need not be unique and, therefore, need not be the attractor of ; Example A2 illustrates this. To study the uniqueness of K, we introduce the notion of a graph-directed iterated function system (GIFS) associated with an IRS (see Definition 4), and prove the uniqueness of K under the assumption that such a GIFS exists.
Since relations need not be single-valued or contractive, it might not be possible to construct a GIFS associated with an IRS (see Examples A3 and A4). Our first goal is to study, under suitable conditions, the existence of a GIFS associated with an IRS (see Theorem 1).
In Section 5, we study IRS attractors under the assumption that an associated GIFS satisfies (GOSC). Our second goal is to describe a method for computing the Hausdorff dimension of an IRS attractor in a Riemannian manifold under the assumption that an associated GIFS G exists and G satisfies (GOSC).
It is worth pointing out that Balogh and Rohner [] extended the Moran–Hutchinson theorem (see []) to the more general setting of doubling metric spaces. Wu and Yamaguchi [] generalized the results of Balogh and Rohner.
For IFSs on , the finite type was first introduced by Wang and the second author [], and was extended to the general finite type condition independently by Jin and Yau [], and Lau and the second author []. The graph finite type condition (GFTC) was extended to Riemannian manifolds by Xu and the second author []. In Section 6, we study IRS attractors under the assumption that a GIFS associated with an IRS satisfies (GFTC). Our third goal is to obtain a method for computing the Hausdorff dimension of the attractor that improves the one in [].
Fractals on spheres have, in fact, been studied quite extensively, especially in connection with the stereographic metric and comparison of dimensions (see []), construction of fractal functions on the sphere (see [,]), and IFSs consisting of Möbius transformations (see []). In Section 7, we study fractals generated by IRSs on spheres. Computing the dimension of an attractor becomes substantially harder, as the sphere is not locally Euclidean. Nevertheless, we show in Example 6 how to obtain the box dimension.
This paper is organized as follows. In Section 2, we state our main theorems. In Section 3, we give the definition of an IRS and study the properties of its attractor. Section 4 is devoted to the proof of Theorem 1. In Section 5, we prove Theorems 2–3. We also construct an IRS satisfying the conditions of Theorem 3, and compute the Hausdorff dimension of the associated attractors. In Section 6, we prove Theorems 4–5 and provide examples to illustrate Theorem 5. In Section 7, we study fractals generated by iterated relation systems on , which is not locally Euclidean. Finally, a conclusion is given in Section 8.
2. Statement of Main Results
This section contains the statements of our main theorems. The proofs of these theorems are presented later in the paper, as we need to first establish some basic theory.
Let be the cardinality of a set F. The definition of a finite family of contractions decomposed from and the definition of a good partition that appear in our first main theorem below are given in Definition 5.
Theorem 1.
Let X be a complete metric space, and let be a nonempty compact set. Let () be an IRS on . For any integer , let . Assume that satisfies the following conditions:
- (a)
- There exists an integer such that for any and any ,
- (b)
- For any , if , we require that the following conditions are satisfied:
- (i)
- can be decomposed as a finite family of contractions , where , and can be decomposed as a finite family of contractions , where .
- (ii)
- There exists a good partition on with respect to some finite family of contractions decomposed from (not necessarily the one in ).
Then there exists a GIFS associated to on .
We give examples (see Examples A3–A6) to investigate the conditions in Theorem 1. Under the assumption that satisfies conditions (a) and (b) (i) in Theorem 1, we give a sufficient condition for the hypothesis (b) (ii) to be satisfied (see Theorem 6).
The construction of the incidence matrices that appear in Theorems 2–3 will be given in Section 5 (see (22)).
Theorem 2.
Let M be a complete n-dimensional smooth orientable Riemannian manifold that is locally Euclidean. Let be an IRS on a nonempty compact subset of M, and K be the associated attractor. Assume that there exists a GIFS associated with , and assume that G consists of contractive similitudes. Suppose that G satisfies (GOSC). Let be the spectral radius of the incidence matrix associated with G. Then
where α is the unique number such that .
The definitions of a simplified GIFS and a minimal simplified GIFS are given in Definitions 6 and 7, respectively.
Theorem 3.
Let M, , K, and be as in Theorem 2. Let be a minimal simplified GIFS associated with G. Assume that satisfies (GOSC). Let be the spectral radius of the incidence matrix associated with .
- (a)
- , where α is the unique real number such that .
- (b)
- In particular, let be a minimal simplified GIFS associated with G and assume that consists of contractive similitudes . Suppose that . If satisfies (OSC), then is the unique number α satisfyingwhere is the contraction ratio of .
The construction of the weighted incidence matrices that appear in the following theorems is given in Section 6.
Theorem 4.
Let M, , K, and be as in Theorem 2. Assume that G satisfies (GFTC). Let be the spectral radius of the weighted incidence matrix associated with G. Then
where α is the unique real number such that .
Theorem 5.
Let M, , K, and be as in Theorem 2. Let be a minimal simplified GIFS associated with G. Assume that satisfies (GFTC). Let be the spectral radius of the weighted incidence matrix associated with . Then
where α is the unique real number such that .
3. Iterated Relation Systems
Throughout this paper, we let , where . We first introduce the definition of an IRS.
Definition 1.
Let T be a topological space and let be a nonempty compact set. Let be a family of relations defined on . For any integer , let
We call an iterated relation system (IRS) if it satisfies the following conditions:
- (a)
- for any nonempty compact set and , is a nonempty compact set;
- (b)
- for any , .
Examples 1, 2–4, and 5–6 illustrate IRSs with various properties.
Proposition 1.
Let T be a topological space, and let be a nonempty compact set. Let be an IRS on . For any integer , let be defined as in (2). Then is a nonempty compact set.
Proof.
By Definition 1 (b), we have . Assume that for some . Then
Hence, for any , . We know that is a nonempty compact set. Assume that is a nonempty compact set for some . By Definition 1 (a), is a nonempty compact set for any . Hence, is a nonempty compact set. Therefore, is a decreasing sequence of nonempty compact subsets of T. This proves the proposition. □
Definition 2.
Let T, , and be as in Proposition 1. For any integer , let be defined as in (2). We call the invariant set or attractor of .
Next, we introduce the following condition, which we call Condition (C).
Definition 3.
Let T, , and be as in Proposition 1. For any integer , let be defined as in (2). We say that satisfies Condition (C) if it has the following property.
- (C)
- For any , if there exist some , a subsequence of , and satisfying for all , then there exists a subsequence of converging to some satisfying .
Condition (C) ensures that the inclusion holds.
Proposition 2.
Let T, , and be defined as in Proposition 1. Let K be the attractor of .
- (a)
- .
- (b)
- If Condition (C) holds, then , and thus (1) holds.
Proof.
(a) By the definition of K, for any , we have . Hence, for any ,
Thus,
(b) We prove the following claims.
Claim 1. . Let . Then for any , there exists such that . Hence there exist some and a subsequence of such that for all . Let such that . By Condition (C), there exists a subsequence converging to some
Therefore, .
Claim 2. . Let . Then there exists such that for any , . Let such that . By Condition (C), there exists a subsequence converging to some
Therefore, . By Claims 1 and 2, we have
Using the result of (a), we have . This proves (b). □
If condition (C) is not assumed, Proposition 2 (b) may fail. We provide a counterexample in Appendix A (see Example A1). Also, for a general IRS, there could be more than one nonempty compact set K satisfying (1) (see Example A2).
In the next section, we study the uniqueness of a nonempty compact set K satisfying equality (1).
4. Associated Graph-Directed Iterated Function Systems
In this section, we let X be a complete metric space, be a nonempty compact set and be an IRS on . We introduce the notion of a graph-directed iterated function system (GIFS) associated with , and prove Theorem 1.
A graph-directed iterated function system (GIFS) of contractions on X is an ordered pair , where is the set of vertices and E is the set of all directed edges. We allow more than one edge between two vertices. A directed path in G is a finite string of edges in E such that the terminal vertex of each is the initial vertex of the edge . For such a path, denote the length of by . For any two vertices and any positive integer q, let be the set of all directed edges from i to j, be the set of all directed paths of length q from i to j, be the set of all directed paths of length q, and be the set of all directed paths, i.e.,
Then there exists a unique collection of nonempty compact sets satisfying
(see, e.g., [,]). Let be the invariant set or attractor of the GIFS. Recall that a GIFS is said to be strongly connected provided that for all , there exists a directed path from i to j.
Definition 4.
Let X be a complete metric space and let be a nonempty compact set. Let be an IRS on . For any integer , let be defined as in (2). We assume that there exists a finite integer such that , where each is compact. Suppose that there exists a GIFS of contractions , where , such that for any ,
Then G is called a graph-directed iterated function system (GIFS) associated with on . We call
the attractor generated by the GIFS G associated with .
We have the following proposition.
Proposition 3.
Let X, , and be as in Definition 4. Let K be the attractor of . Assume that there exists a GIFS associated with and assume that G consists of contractions . Let be the attractor of G. Then .
Proof.
□
Proposition 4.
Let X, , , and K be defined as in Definition 4. Assume that there exists a GIFS associated with , and assume that G consists of contractions . Then there exists a unique nonempty compact set K satisfying (1).
Proof.
Assume that there exists another nonempty compact set satisfying (1). Note that
Hence
Next, we show that . We know that
For any , let be a contraction ratio of . Then for any and for any integer m, n, where , we have
Hence, exists. Thus, for any , there exists satisfying
Therefore, . This proves the proposition. □
Let be a GIFS of contractions . We say that is an invariant family under G if
Definition 5.
Let X, , , and be defined as in Definition 4.
- (a)
- Assume that conditions (i) and (ii) below hold.
- (i)
- For any and ,
- (ii)
- For any , there exists such that for each and , there exists a contraction , and the following holds
Then we say that is a finite family of contractions decomposed from and that each is a branch of . - (b)
- Let be a collection of compact subsets of satisfyingLet be a finite family of contractions decomposed from and composed of all the branches of . Fix . Assume that for any and , is invariant under for all . Then we call a good partition of with respect to .
Let , , and . We are now ready to prove Theorem 1, which is stated in Section 2.
Proof of Theorem 1.
To prove this theorem, we consider the following two cases.
Case 1. For any , . In this case, is an IFS. Hence, there exists a GIFS associated with on , where .
Case 2. For some , . In this case, in order to prove the existence of a GIFS associated with , we first prove the following five claims.
Claim 1. For any , . By (b) (i), we have
Since is compact, we have This proves Claim 1.
Claim 3. For any and , let be a convergent sequence in . Then for any , the sequence converges. If is an open set, then we can extend from to and let be defined as
where for any , (). Moreover, is a surjection. In fact, by (b) (i), is uniformly continuous on . Hence, the sequence converges, and thus we can define if . Note that for any , is independent of the choice of the sequence . Therefore, we can extend from to and let be defined as in (6). To show that is a surjection, we let . Then there exists a sequence such that
We know that is bounded, and hence there exists a convergent subsequence such that
Note that
Combining (b) (i) and the definition of , we have for all , there exists such that for all ,
By (7) and (8), we have , and thus for any , there exists such that for all ,
Let . Then for any , (10) and (11) hold. By (9),
It follows that . This proves the Claim 3.
Claim 4. For any and , let be a convergent sequence in . Then the sequence converges. If is an open set, then we can extend from to , and let be defined as
where for any , when . Moreover, is a surjection. The proof of Claim 4 is similar to that of Claim 3; we omit the details.
Claim 5. For any ,
In fact, by using a method similar to that for Claim 1, we have, for any ,
As in the proof for Claim 3, for any , and , we have
By Claim 3, for any ,
If , then . We know that there exists a sequence , converging to x, such that
Hence, for any , and ,
Combining (15) and (16), we have, for any , and ,
By using a similar argument, we have, for any and ,
Combining (14), (17), and (18) proves (13).
Next, fix . By (b) (ii) and Claim 2, we can rename the nonempty elements in and as , where s and i satisfy the following conditions.
- (1)
- , where and .
- (2)
- , where and .
- (3)
- is invariant under , and is invariant under , where .
Note that
By (13), for any , we have
By the definitions of and , for fixed t, l, s, i, and , , we have
where and . Let be a set of vertices, be the set of all edges from k to j, and be the set of all edges. Let
Then for any , is contractive. Hence, is a GIFS of contractions .
Finally, we show that G is a GIFS associated with on . By (13) and the definition of , we have
Now we show by induction that for ,
For , (19) implies that (20) holds. Assume that (20) holds when . For ,
Hence, (20) holds. By definition, G is a GIFS associated with on , where . This proves Case 2. Combining Cases 1 and 2 completes the proof. □
If condition (a) in Definition 5 is not satisfied, Theorem 1 may fail. We provide a counterexample in Appendix A (see Example A3). We show in Examples A4 and A5 that the conditions in Theorem 1 (b) (i) need not be satisfied. We also show in Example A6 that condition (b) (ii) in Theorem 1 may fail.
Theorem 6.
Let X be a complete metric space and let be a nonempty compact set. Let be an IRS on . For any integer , let be defined as in (2). Assume satisfies the following conditions.
- (a)
- There exists an integer such that for any and any ,
- (b)
- For any , if , we require that the following conditions are satisfied.
- (i)
- can be decomposed as a finite family of contractions , where , and can be decomposed as a finite family of contractions , where .
- (ii)
- There exist or such that for any and any ,and for any ,
Then there exists a GIFS associated with on .
Proof.
For any , let
Fix . By (b) (ii), we can rename the nonempty elements in and as , where s and i satisfy the following conditions:
- (a)
- , where and ;
- (b)
- , where and .
Note that
For , , , and , let . For and , let . Here, and are defined as in (6) and (12), respectively. Then for any , where , , and , there exists some , where and , such that
Similarly, for any , where , , and , there exists some , where and , such that
Hence, is a good partition of with respect to . By Theorem 1, there exists a GIFS associated with on . □
Definition 6.
Let X be a complete metric space, and let be a GIFS of contractions on X, where and E is the set of all directed edges. Let be an invariant family under G. We call a simplified graph-directed iterated function system associated with G, if satisfies the following conditions.
- (a)
- and , where .
- (b)
- Let be contractions associated with , and let be an invariant family under . Then for any ,
By Definition 6, we know that the attractor of G is equal to the attractor of . Note that the simplified GIFS is not unique.
Definition 7.
We say that a simplified GIFS composed of is a minimal simplified graph-directed iterated function system if among all simplified GIFSs composed of , we have , and among all those simplified GIFSs with , we have
Proposition 5.
Assume that satisfies the conditions of Theorem 1 and is a GIFS associated with guaranteed by Theorem 1, where and G consists of contractions . Then there exists a minimal simplified GIFS associated with G.
Proof.
Let and be defined as in the proof of Theorem 1. For fixed t, s, i, we write . Then
Fix . For any , where and , if there exists with such that , then we remove . In particular, if , then we remove one of them. If there are multiple elements in that are equal, then we keep one of them and remove the others. We rename the remaining as , where and . We use a similar method to keep the elements in the set , and thus we rename the remaining as , where and . Note that
For any , we note that the number of elements removed from and is equal to the number of elements removed from . We rename the remaining as , where . Note that
Let be a GIFS of contractions , where , , and is an invariant family under . For any , Note that there exist and such that and Hence, . Therefore, we have and
By induction, for all , we have
Therefore, is a simplified GIFS associated with G.
Among all simplified GIFSs that have been constructed by the above process, we first select the subcollection with the smallest number of vertices. Then, among members of this subcollection, we further select the subfamily with the smallest number of contractions. Members of this subfamily are minimal simplified GIFSs associated with G, denoted . □
5. Hausdorff Dimension of Graph Self-Similar Sets Without Overlaps
In this section, we give the definition of the graph open set condition (GOSC) and prove Theorems 2 and 3. Moreover, we give an example of an IRS that satisfies the conditions of Theorem 3 and compute the Hausdorff dimension of the corresponding attractor.
Definition 8.
Let X be a complete metric space. Let be an IFS of contractions on X. We say that satisfies the open set condition (OSC) if there exists a nonempty bounded open set U on X such that
Definition 9.
Let X be a complete metric space. Let be a GIFS of contractions on X. We say that G satisfies the graph open set condition (GOSC) if there exists a family of nonempty bounded open sets on X such that for all ,
- (a)
- ;
- (b)
- , for all distinct and .
Definition 10.
Let X be a complete metric space, and let be an IRS on a nonempty compact subset of X. Assume that there exists a GIFS G associated with , and assume that G consists of contractions. If G satisfies (GOSC), then we say that satisfies (GOSC) with respect to G. If G does not satisfy (GOSC), then we say that has overlaps with respect to G.
Let be a GIFS of contractions on X. For any , let be the contraction ratio of . Recall that an incidence matrix associated with G is an matrix defined by
where for and , .
We can now use the results in Section 4 to prove Theorem 2.
Proof of Theorem 2.
By Proposition 3, we know that G and have the same attractor. If G satisfies (GOSC), then G satisfies (GFTC). The proof follows by using the results of Theorem 1.6 in []; we omit the details. □
For a connected Riemannian n-manifold, we denote the Riemannian distance by . For , let
Definition 11.
Let M be a Riemannian n-manifold. A measure μ on M is said to satisfy a general doubling condition if there exist constants and such that for any and any satisfying , one has
C is called a general doubling constant. If , we get the standard doubling condition.
Theorem 7.
(Bishop–Gromov volume comparison theorem, see, e.g., [,].) Let M be a complete n-dimensional Riemannian manifold whose Ricci curvature satisfies for some . Then
is a non-increasing function whose limit is 1 as , where denotes the volume of a ball of radius r in the constant curvature space form .
By using Theorem 7, we have the following corollary.
Corollary 1.
Let M be a complete n-dimensional Riemannian manifold whose Ricci curvature satisfies for some . Then the Riemannian volume measure in M satisfies a general doubling condition.
Proof.
The proof of Corollary 1 is similar to that of the Remark on p. 7 in [] and is omitted. □
Lemma 1.
Let M be a complete n-dimensional Riemannian manifold whose Ricci curvature satisfies for some . Let be a bounded open set. Let be a collection of disjoint open subsets of Ω such that each contains a ball of radius and is contained in a ball of radius . Then there exists a constant such that any ball B of radius intersects at most of the .
Proof.
We first claim that . Suppose . Note that for any i,
Since the are disjoint, is compact with being an open cover. By compactness, there exists a finite subcover . This is clearly a contradiction, and the claim is proved. Now let
where . Suppose . Then is contained in a ball concentric with . Let q be the number of such that and denote these ’s by . By summing volumes and using (24), we get
Hence,
Let denote the sectional curvature on . Then there exist constants such that . It is well-known that if the sectional curvatures of M are less than or equal to k, then for every , we have
for all , where is the injectivity radius of M at p (see, e.g., Theorem III.4.2 in []). Hence,
Combining (25) and the Bishop–Gromov volume comparison theorem, we have
Using the Maclaurin series of and , we have
i.e., for any , there exists such that for ,
Hence, there exists a constant such that for , , and thus for ,
Next, we consider the following cases.
Case 1. and . Note that
(see, e.g., p. 128 of []). Let
Then and are continuous functions of t on . Since are continuous functions of r, and
we see that is a continuous function of r on . Hence, there exists a constant such that , and thus for ,
Combining (26) and (27), for , we have
where . Combining Corollary 1 and (28), we have
where is a constant. The following cases can be proved using similar methods:
Combining the above eight cases, we have for some constant . □
We can now use the results in Section 4 and Lemma 1 to prove Theorem 3.
Proof of Theorem 3.
Combining Proposition 3 and Definition 6, we know that G and have the same attractor. If satisfies (GOSC), then satisfies (GFTC). By using the results of Theorem 1.6 in [], we can prove (a). As M is locally Euclidean, the sectional curvature and the Ricci curvature of M are everywhere zero. By using the results of Lemma 1 and a similar method as in [], we can prove (b); we omit the details. □
In the rest of this section, we construct an example of an IRS satisfying Theorem 3 and compute the Hausdorff dimension of the associated attractor.
Example 1.
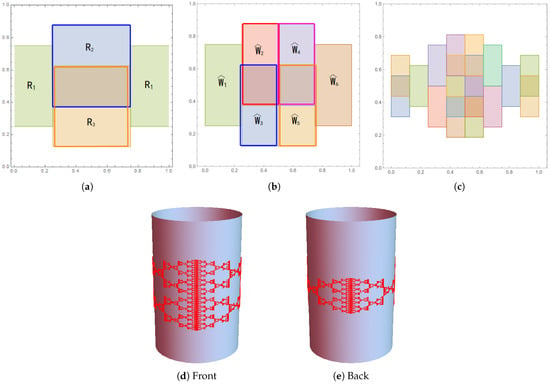
Let be a cylindrical surface. Let . For , let , , and be an IRS on defined as
Let K be the associated attractor (see Figure 1). Then

Figure 1.
Figures for Example 1 with . (a–c) are drawn on and shrunk by . (a) The first iteration of under , where consists of the left and right rectangles, is the top square, and is the bottom square. (b) Vertices of the GIFS associated with . (c) The first iteration of the vertices under the GIFS. (d,e) The attractor of .
Proof of Example 1.
For any , by the definition of , we have . Let and . Then for any ,
For any , let
Then . Let and . Then for any , where ,
Hence, for any , are contractions, where , and are contractions, where . Moreover, for , we have
for any , we have
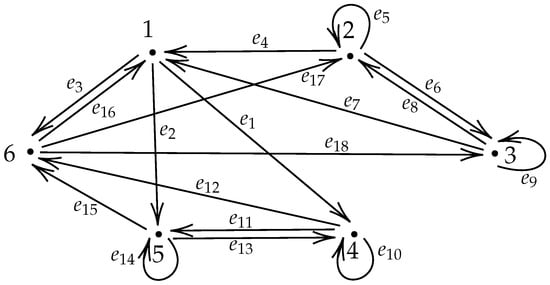
Hence, satisfies the conditions of Theorem 6. By Theorem 6 and Proposition 5, we can find a minimal simplified GIFS with and (see Figure 2).

Figure 2.
The GIFS associated with in Example 1.
The invariant family is defined as
while , , and the associated similitudes are defined as
and
where and are defined as in (6) and (12), respectively.
Note that is strongly connected. Let
Let
Then for , is an open set. For all , satisfies
Hence, satisfies (GOSC). The weighted incidence matrix associated with is
The spectral radius of is . Therefore,
□
6. Hausdorff Dimension of Graph Self-Similar Sets with Overlaps
In this section, we study IRSs with overlaps (see Definition 10). We give the definition of the graph finite type condition (GFTC) and prove Theorems 4–5. Moreover, we illustrate our method for computing the Hausdorff dimension of the associated attractors using several examples.
6.1. Graph Finite Type Condition
For detailed definitions of the notation in this section, especially the definition of a sequence of nested index sets, the reduced graph, and the neighborhood of a vertex in the reduced graph, we refer the reader to [,]. Here we only give a very brief summary. Let be a GIFS as described in Section 4. Let be a sequence of nested index sets (see []), where and is defined as in Section 4. For , let
Then . For , let , where each is a contraction on G. Define
For , we call a vertex and the vertex set. Define a graph , where is the set of all directed edges of . Let be the reduced graph of (see, e.g., [] for the construction of ). Let be a minimal simplified GIFS associated with . We can use a similar method to construct a corresponding reduced GIFS . Two vertices and are equivalent, denoted , if , where is a neighborhood of (see, e.g., []), and induces a bijection , which is defined as
and satisfies the following conditions:
- (a)
- In (29), .
- (b)
- For and satisfying , and for any integer , a directed path satisfies if and only if it satisfies .
Let denote the equivalence class of . We call the neighborhood type of (with respect to ), where is an invariant family under G.
Definition 12.
Let X be a complete metric space. Let be a GIFS of contractions on X, where . If there exists an invariant family of nonempty bounded open sets with respect to some sequence of nested index sets such that is a finite set, where ∼ is an equivalence relation on , then we say that satisfies the graph finite type condition (GFTC). We say that is a finite type condition family.
Definition 13.
Let X be a complete metric space. Let be an IRS on a nonempty compact subset of X. Assume that there exists a GIFS G associated with , and assume that G consists of contractions. If G satisfies (GFTC), then we say thatsatisfies (GFTC) with respect to G.
The following theorem is a direct generalization of Theorem 2.7 in []; it provides a sufficient condition for a GIFS to satisfy the finite type condition. Recall that an algebraic integer is called a Pisot number if all of its algebraic conjugates are in modulus strictly less than one.
Theorem 8.
Let M be a complete smooth n-dimensional Riemannian manifold that is locally Euclidean. Let be a GIFS of contractive similitudes on M. Let be an invariant family of nonempty compact sets, and let be an invariant family of nonempty bounded open sets with , . For each similitude , , assume that there exists an isometry
such that for any , is contractive similitude of the form
where is a set of directed edges, is a Pisot number, is a positive integer, is an orthogonal transformation, and . Assume that generates a finite group H and
for some . Then G is of finite type, and is a finite type condition family of G.
Proof.
By the assumptions, we let be a set of vertices. Then is a GIFS of contractive similitudes on , and is an invariant family of nonempty bounded open sets for . By the results of Theorem 2.7 in [], we have is of finite type and is a finite type condition family for . Let be a vertex, , , , and is a sequence of nested index sets. Then is a finite set. Let , where , , and is a sequence of nested index sets. It follows from the definition of that is a finite set. This proves the proposition. □
We let denote the collection of all distinct neighborhood types, with , , being the neighborhood types of the root vertices. As in [], for each , we define a weighted incidence matrix as follows. Fix i () and a vertex such that , let be the offspring of in , and let , , be the unique edge in connecting to . Then we define
Now we are ready to prove Theorems 4 and 5, which are stated in Section 2.
Proof f Theorem 4.
By Proposition 3, we know that G and have the same attractor. The proof follows by using the results of Theorem 1.6 in []; we omit the details. □
Proof of Theorem 5.
Combining Proposition 3 and Definition 6, we know that the attractor of G is equal to that of . The proof follows by using the results of Theorem 4. □
6.2. Examples
In this subsection, we give three examples of IRSs with overlaps that satisfy (GFTC).
Example 2.
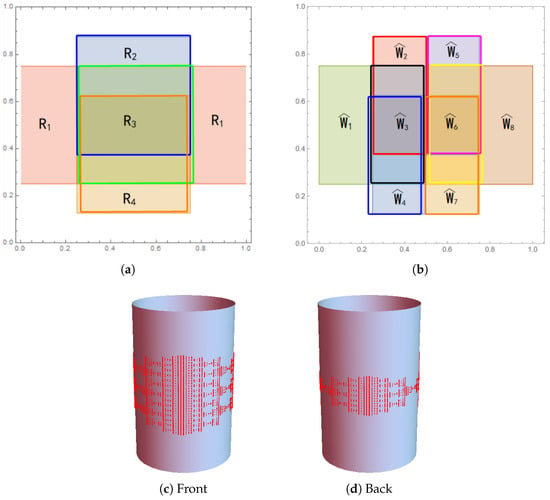
Let be a cylindrical surface. Let . For , we let and let be an IRS on defined as
Let K be the associated attractor (see Figure 3). Then

Figure 3.
Figures for Example 2 with . (a,b) are drawn on and shrunk by . (a) The first iteration of under , where consists of the left and right rectangles, is the top square, is the middle square, and is the bottom square. (b) Vertices of the GIFS associated with . (c,d) The attractor of .
Proof of Example 2.
For any , by the definition of , we have . Let and . Then for any ,
For any , by the definition of , we have
Hence, . Let and . Then for any , where ,
Hence, for any and , are contractions, and for any , are contractions. Moreover, for , we have
for any ,
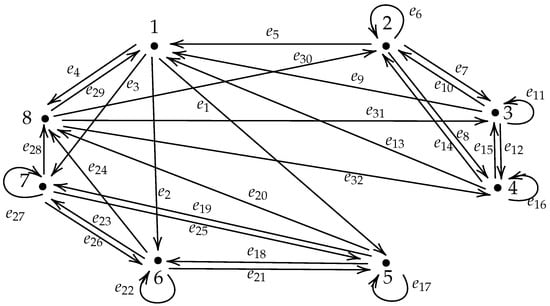
Hence, satisfies the conditions of Theorem 6. By Theorem 6 and Proposition 5, we can find a minimal simplified GIFS with and (see Figure 4).

Figure 4.
The GIFS associated with in Example 2.
The invariant family , the set of edges and the associated similitudes are defined as
and
where and are defined as in (6) and (12), respectively. Let be an invariant family of nonempty bounded open sets with for . By Theorem 8, is of finite type.
For convenience, we let , . Let for . Let be the neighborhood types of the root neighborhoods , respectively. All neighborhood types are generated after two iterations. To construct the weighted incidence matrix in the minimal simplified reduced GIFS . We note that
Denote by the vertices in according to the above order. Then
Let
Then
Since , the edge is removed in . generates three offspring
where , and . Hence,
As , the edge is removed in . generates three offspring
with , and . Thus
generates four offspring
where , , and . Therefore,
Using the same argument, we have
Since no new neighborhood types are generated, we conclude that the is of finite type. The weighted incidence matrix is
The spectral radius of is , and by Theorem 5,
where is the unique solution of the equation □
The following remark explains why the computation of Example 2 is nontrivial, even thought the cylinder is locally Euclidean.
Remark 1.
Let , , and K be defined as in Example 2.
- (1)
- There does not exist a global bi-Lipschitz map such that .
- (2)
- Let . One may try to construct a bi-Lipschitz map , where . As might not be a self-similar set, it is not clear how to compute the Hausdorff dimension of .
- (3)
- If K is has a neighborhood on which there exists a local isometry mapping U to , then the problem is much easier; however, this is not the case for Example 2. In fact, although K can be covered by finitely or countably many coordinate charts and then pulled into the Euclidean space by isometries, the image of K in lacks a well-defined structure, and it is not clear how to find an IFS that generates it.
The following example is from Example 7.6 in []. Here, we use the method in the present paper to compute the Hausdorff dimension of the same fractal. The method here is more systematic.
Example 3.
Let be a flat 2-torus, viewed as with opposite sides identified, and be endowed with the Riemannian metric induced from . We consider the following IFS with overlaps on :
Let . Iterations of induce an IRS on , defined as
Let K be the associated attractor. Then
Proof of Example 3.
The proof of this example is similar to that of Example 2; we only give an outline.
First, for any , by the definition of , we let , , and . Then . Let . Then . For any , let
Hence, . Let . Then . We can show that for any , are contractions, where , and that for , are contractions. Moreover, there exist or such that for any and any ,
and for any ,
Hence, satisfies the conditions of Theorem 6. By Theorem 6 and Proposition 5, we can obtain a minimal simplified GIFS where and , along with the invariant family and the associated similitudes . Let be an invariant family of nonempty bounded open sets with , . It follows from Theorem 8 that the system is of finite type.
Next, let be the neighborhood types of the root neighborhoods , respectively. All neighborhood types are generated after two iterations. The weighted incidence matrix happens to be the same as that in (31). Thus, the spectral radius of is , and by Theorem 5, we have
where is the unique solution of the equation □
Example 4.
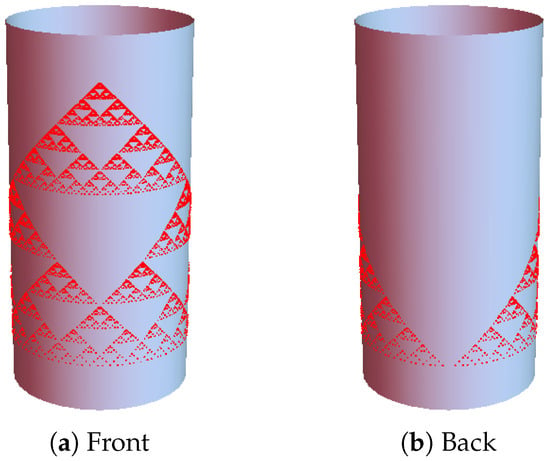
Let be a cylindrical surface. Let
and . Let , , and be an IRS on , defined as
Let K be the associated attractor (see Figure 5). Then

Figure 5.
The attractor of in Example 4.
The proof of this example is similar to that of Example 2 and is omitted.
7. IRSs on Riemannian Manifolds That Are Not Locally Euclidean
In this section, we give two examples of IRSs on , which is not locally Euclidean.
Definition 14.
Let X be a complete metric space and let be a nonempty compact set. Let be an IRS on . Let K be the associated attractor. We say that satisfies the strong separation condition (SSC) if for all .
Definition 15.
Let M be a complete n-dimensional Riemannian manifold, and let K be a non-empty bounded subset in M. Let
The upper and lower box dimensions of K are defined respectively as
If the two are equal, the common value, denoted by , is called the box dimension of K.
Example 5.
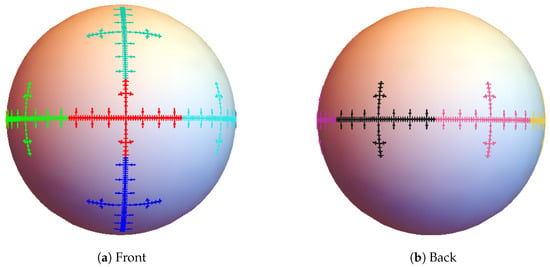
Let be a 2-sphere, where θ is the azimuthal angle and ϕ is the polar angle. For points on , we compress their polar angles by 1/4 and their azimuthal angles by 1/7. Denote the resulting map by . We rotate the image of about the z-axis by , , , , , and to obtain , , , , , and , respectively. We rotate the image of about the y-axis by and to get and , respectively. Then is an IRS on and is post critically finite (see, e.g., []). The attractor is shown in Figure 6.

Figure 6.
The attractor of in Example 5.
The following example illustrates how to obtain the box dimension of an IRS attractor.
Example 6.
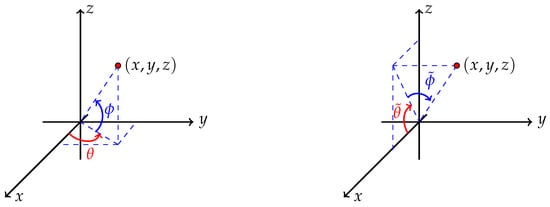
Let and let . We use the following two different parameterizations for and :
Here, we continue to call θ, azimuthal angles, and ϕ, polar angles (see Figure 7). Let be a relation obtained as follows. First, compress the azimuthal angle θ by 1/6 using a relation which we denote by . Next, we compose with a compression of the azimuthal angle by 1/6 to obtain . We compose with rotations about the z-axis by and to obtain and , respectively. We compose with rotations about the y-axis by and to get and , respectively. is an IRS on and satisfies (SSC) (see Figure 8). The images of under the iterations of are closed regions enclosed by the red curves in Figure 8. Let K be the associated attractor. Then
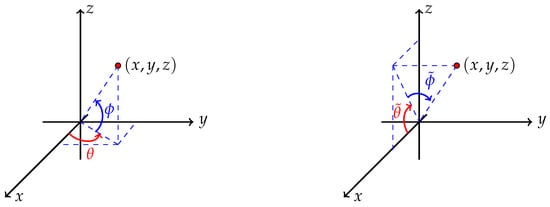
Figure 7.
The polar and azimuthal angles in the two parameterizations in Example 6.

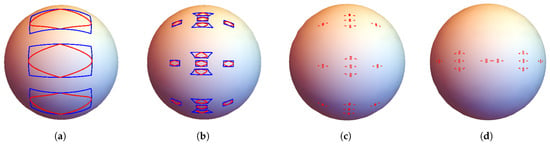
Figure 8.
The IRS in Example 6. Regions enclosed by the red curves are images of under the iterations of . (a) The first iteration. , , and denote the middle, top, and bottom blue regions enclosed by the blue curves, respectively ( and not shown). (b) The second iteration. Figures (c,d) show rough approximations to the front and back of the attractor.
Proof of Example 6.
Let be the region in the middle of Figure 8a enclosed by the blue curves, where the two curves on the left and right are, respectively,
and the two curves on the top and bottom are
respectively. We rotate about the z-axis by and to obtain and , respectively. We rotate about the y-axis by and to get and , respectively. Note that for each t, and the boundary of intersects that of at exactly four points (see Figure 8a). To compute the box dimension of K, we define a sequence of covers of K as follows. Let . For all , define
We need to compute the maximum diameter of the sets in each cover.
First, we find the maximum horizontal compression ratio. Let and be two points in , where . Then and . Let and denote the Euclidean and Riemannian distances, respectively. Then . Hence
Now let and vary while fixing the Euclidean distance between and . Note that the larger the value of (the absolute value of the latitude of A and B), the larger the value of . To prove that as increases, the ratio also increases, define , where . Note that
Hence, is increasing. Therefore, as the latitude increases while keeping the distance between and fixed, the value of increases, and thus the ratio increases. Let
A direct calculation shows that the right boundary curve of is
We can prove that for , is increasing. Thus the maximum value of and for the points in are, respectively,
Hence the maximum value of is , where
Let , where . Then . Thus,
If , similar arguments show that the maximum horizontal compression ratio is .
Next, we find the maximum vertical compression ratio. Let and be two points in , where . When the azimuthal angle is compressed by 1/6 in the vertical direction, the images of and are and , respectively. Hence, . For points in , as one varies while keeping constant so that remains within , the maximum possible values of and are, respectively,
Thus the maximum value of is
Let , where . Then . Thus,
For , similar arguments show that the maximum vertical compression ratio is . Let and be the horizontal and vertical compression ratios of the iteration, respectively. Using a similar proof as that for , we have for any .
Finally, fix . For any two points and in , where or , let be a Euclidean right triangle with . Then . Let , , and . Then is also a Euclidean right triangle. Hence
Let and denote the iterates, under , of the points and , respectively. Then
In view of (33), is monotone decreasing and tends to as n tends to infinity. Let and denote the diameters of in the Euclidean and Riemannian metrics, respectively. Define
By (34), there exist constants such that
where the first inequality can be obtained easily. Let O be the the center of . For any , let . Then
Let and . Combining (35) and (36), we have
Note that as n, the level of iteration, tends to infinity. Thus,
By the definition of , K can be covered by a minimum of sets (say, the ’s), each with Riemannian diameter no more than . Hence . Using the fact that the sequence is slowly decreasing, we have
Similarly, we have . On the other hand, for any , we let
Then, in view of (34) and (37), for all n sufficiently large,
and hence . Thus,
Letting yields . Similarly, we have . This completes the proof. □
8. Conclusions
Fractals on Riemannian manifolds generated by non-contractive or multivalued relations cannot be described by iterated function systems. We introduce the notion of an iterated relation system to describe these fractals. To compute the Hausdorff dimension of an IRS attractor, we introduce the notion of a graph-directed iterated function system associated with an IRS and prove that the IRS attractor can be identified with the attractor of the associated GIFS. In addition, we formulate conditions under which a GIFS associated with an IRS exists. This allows us to obtain a formula for the Hausdorff dimension of an IRS attractor on a locally Euclidean Riemannian manifold, under either the graph open set condition or the graph finite type condition. Finally, we illustrate how to obtain the box dimension of an IRS attractor on .
Author Contributions
Conceptualization, J.L., S.-M.N. and L.O.; methodology, J.L., S.-M.N. and L.O.; software, S.-M.N. and L.O.; validation, S.-M.N. and L.O.; formal analysis, S.-M.N. and L.O.; investigation, J.L., S.-M.N. and L.O.; writing—original draft preparation, J.L. and L.O.; writing—review and editing, S.-M.N. and L.O.; supervision, S.-M.N.; project administration, S.-M.N.; funding acquisition, S.-M.N. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are supported in part by the National Natural Science Foundation of China, grant 12271156, and the Construct Program of the Key Discipline in Hunan Province.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
Part of this work was carried out while the third author was visiting Beijing Institute of Mathematical Sciences and Applications (BIMSA). She thanks the institute for its hospitality and support. The authors are grateful to the anonymous reviewers for some helpful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Some Examples
Examples in this section are designed to illustrate some definitions and conditions in Section 2, Section 3 and Section 4.
The following counterexample shows that Proposition 2 (b) fails if Condition (C) is not assumed.
Example A1.
Let , and let be an IRS on defined as
Then , where . Let , , and , where and . Then converges to , but . Hence, does not satisfy Condition (C). Moreover, we have and . Hence, .
For a general IRS, there could be more than one nonempty compact set K satisfying (1). The following example illustrates this.
Example A2.
Let , and let be an IRS on defined as
Then there exist at least two nonempty compact sets K satisfying Equation (1).
Proof of Example A2.
We know that , …, . Hence, . By Proposition 2, we have . Now let . Note that
Then , which completes the proof. □
We give a counterexample to show that Theorem 1 fails if condition (a) in Definition 5 is not satisfied.
Example A3.
Let , and let be an IRS on defined as
Then Thus, there does not exist any (finite) GIFS associated with .
Examples A4 and A5 show that the condition (b) (i) in Theorem 1 need not be satisfied.
Example A4.
Let . Let be an IRS on defined as
Then , and thus for any ,
Therefore, and are not contractions.
Example A5.
Let . For any , let , and define
Note that
where (see Figure A1). Let be an IRS on defined as
Then , and cannot be decomposed as a finite family of contractions.
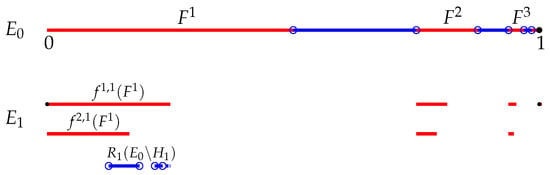
Figure A1.
The sets and in Example A5.
Proof of Example A5.
By the definition of , we have . We prove the following claim.
Claim 1. For any , let be a function decomposed from . Then f is not contractive. To prove this claim, we let and . Then
Note that
Thus, f is not a contraction. Next, suppose that can be decomposed as a finite family of contractions . Then there would exist at least one such that
This contradicts Claim 1 and proves that cannot be decomposed as a finite family of contractions. □
The following example shows that condition (b) (ii) in Theorem 1 need not be satisfied.
Example A6.
Let . For any , let
and let
Note that
(see Figure A2). Let be an IRS on defined as
Let . Then there does not exist a good partition of .
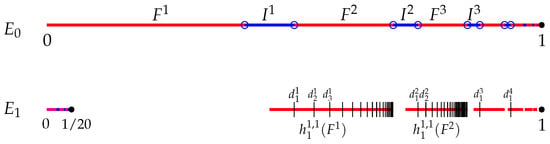
Figure A2.
The sets and in Example A6. represents the set of division points in . Note that for all , .
Proof of Example A6.
By the definition of , we have , and Thus, for any ,
Hence, for l, , and are contractions. For any , let
be a family of division points in . Then for any ,
Hence, for any , Next, we show that for any , is an increasing function of j. By the definition of , we have , where , and is an increasing function on . Assume that for any and , we have . Then
We let and let
Then by (A1), . By induction, for any , is an increasing function of j. Hence, for any , . It follows that for any ,
Note that for any and , we have and
Claim 1. For any and any , let
Then is not contractive. In fact, for any and any , we have , while . This proves Claim 1.
Claim 2. Fix . For any with , let
Then it is not possible for to be contractive and to be invariant under . In fact, suppose that is contractive and is invariant under . By the definitions of and , we have
Hence, is contractive, and is invariant under . Since
Hence, is contractive, and is invariant under . Continue this process. We see that is contractive, and is invariant under . This contradicts Claim 1. This proves Claim 2. Let
Therefore, we can extend from to and let be defined as . Hence,
We assume that is a good partition of with respect to
Then there exists at least one , where and , such that for any ,
This contradicts Claim 2 and proves that there does not exist a good partition of . □
References
- Strichartz, R.S. Self-similarity on nilpotent Lie groups. Contemp. Math. 1992, 140, 123–157. [Google Scholar]
- Balogh, Z.M.; Tyson, J.T. Hausdorff dimensions of self-similar and self-affine fractals in the Heisenberg group. Proc. Lond. Math. Soc. 2005, 91, 153–183. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Vince, A. Real projective iterated function systems. J. Geom. Anal. 2012, 22, 1137–1172. [Google Scholar] [CrossRef]
- Hossain, A.; Akhtar, M.N.; Navascués, M.A. Fractal dimension of fractal functions on the real projective plane. Fractal Fract. 2023, 7, 510. [Google Scholar] [CrossRef]
- Hossain, A.; Akhtar, M.N.; Navascués, M.A. Fractal interpolation on the real projective plane. Numer. Algorithms 2024, 96, 557–582. [Google Scholar] [CrossRef]
- Ngai, S.-M.; Xu, Y.Y. Separation conditions for iterated function systems with overlaps on Riemannian manifolds. J. Geom. Anal. 2023, 33, 262. [Google Scholar] [CrossRef]
- Thangaraj, C.; Easwaramoorthy, D.; Selmi, B.; Chamola, B.P. Generation of fractals via iterated function system of Kannan contractions in controlled metric space. Math. Comput. Simul. 2024, 222, 188–198. [Google Scholar] [CrossRef]
- Cui, M.; Selmi, B.; Li, Z. Expansive measures of nonautonomous iterated function systems. Qual. Theory Dyn. Syst. 2025, 24, 60. [Google Scholar] [CrossRef]
- Balogh, Z.M.; Rohner, H. Self-similar sets in doubling spaces. Ill. J. Math. 2007, 51, 1275–1297. [Google Scholar] [CrossRef]
- Hutchinson, J.E. Fractals and self-similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Wu, D.; Yamaguchi, T. Hausdorff dimension of asymptotic self-similar sets. J. Geom. Anal. 2017, 4, 339–368. [Google Scholar] [CrossRef]
- Ngai, S.-M.; Wang, Y. Hausdorff dimension of self-similar sets with overlaps. J. Lond. Math. Soc. 2001, 2, 655–672. [Google Scholar] [CrossRef]
- Jin, N.; Yau, S.S.T. General finite type IFS and M-matrix. Commun. Anal. Geom. 2005, 13, 821–843. [Google Scholar]
- Lau, K.-S.; Ngai, S.-M. A generalized finite type condition for iterated function systems. Adv. Math. 2007, 208, 647–671. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Hossain, A. Stereographic metric and dimensions of fractals on the sphere. Results Math. 2022, 77, 213. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Prasad, M.G.P.; Navascués, M.A. More general fractal functions on the sphere. Mediterr. J. Math. 2019, 16, 134. [Google Scholar] [CrossRef]
- Navascués, M.A. Fractal functions on the sphere. J. Comput. Anal. Appl. 2007, 9, 257–270. [Google Scholar]
- Vince, A. Möbius iterated function systems. Trans. Amer. Math. Soc. 2013, 365, 491–509. [Google Scholar] [CrossRef]
- Mauldin, R.D.; Williams, S.C. Hausdorff dimension in graph directed constructions. Trans. Amer. Math. Soc. 1988, 309, 811–829. [Google Scholar] [CrossRef]
- Edgar, G.A. Measure, Topology, and Fractal Geometry; Springer: New York, NY, USA, 2008. [Google Scholar]
- Petersen, P. Riemannian Geometry; Graduate Texts in Mathematics; Springer: Cham, Switzerland, 2006; Volume 171. [Google Scholar]
- Jost, J. Riemannian Geometry and Geometric Analysis; Universitext; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Hebey, E. Sobolev Spaces on Riemannian Manifolds; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Chavel, I. Riemannian Geometry: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Falconer, K.J. Fractal Geometry: Mathematical Foundations and Applications, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Das, M.; Ngai, S.-M. Graph-directed iterated function systems with overlaps. Indiana Univ. Math. J. 2004, 53, 109–134. [Google Scholar] [CrossRef]
- Kigami, J. Analysis on Fractals; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).