Donsker-Type Construction for the Self-Stabilizing and Self-Scaling Process

Abstract

Using a Donsker-type construction, we prove the existence of a new class of processes, which we call the self-stabilizing processes. These processes have a particular property: the “local intensities of jumps” vary with the values. Moreover, we also show that the self-stabilizing processes have many other good properties, such as stochastic Hölder continuity and strong localizability. Such a self-stabilizing process is simultaneously a Markov process, a martingale (when the local index of stability is greater than 1), a self-scaling process and a self-regulating process.

1. Introduction

Stable Lévy motions owe their importance in both theory and practice to, among other factors, price fluctuations. The seeming departure from normality, along with the demand for a self-similar model for financial data (i.e., one in which the shape of the distribution for yearly asset price changes resembles that of the constituent daily or monthly price changes), led Benoît Mandelbrot to propose that cotton prices follow an $\alpha$-stable Lévy motion with $\alpha$ equal to $1.7$. The high variability of the stable Lévy motions means that they are much more likely to take values far away from the median, and this is one of the reasons why they play an important role in modeling. Stable Lévy motions have been frequently used to model such diverse phenomena as gravitational fields of stars, temperature distributions in nuclear reactors and stresses in crystalline lattices, as well as stock market prices, gold prices and other financial data.

Recall that a stochastic process $\left\{L\right(t),t\ge 0\}$ is called a (standard) $\alpha$–stable Lévy motion if the following three conditions hold:

(C1)

$L\left(0\right)=0$ almost surely;

(C2)

L has independent increments;

(C3)

$L\left(t\right)-L\left(s\right)\sim S_{\alpha }({(t-s)}^{1/\alpha },\beta ,0)$ for any $0\le s<t$ and for some $0<\alpha \le 2,-1\le \beta \le 1$.

• Here, $S_{\alpha }(\sigma ,\beta ,0)$ stands for a stable random variable with index of stability $\alpha$, scale parameter $\sigma$, skewness parameter $\beta$ and a shift parameter equal to $0.$ When $\beta =0,$ we denote L as $L_{\alpha }$ for clarity. Such processes have stationary increments, and they are $1/\alpha$–self-similar (unless $\alpha =1,\beta \ne 0$); that is, for all $c>0,$ the processes $\{L_{\alpha }\left(ct\right),t\ge 0\}$ and $\{c^{1/\alpha }{L}_{\alpha }\left(t\right),t\ge 0\}$ have the same finite-dimensional distributions. An $\alpha$–stable Lévy motion is symmetric when $\beta =0$. Recall that $\alpha$ governs the intensity of jumps. When $\alpha$ is small, the intensity of jumps is large. Contrarily, when $\alpha$ is large, the intensity of jumps is small; see Figure 1.
  

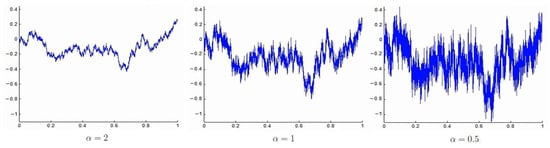  Figure 1. The figure exhibits how $\alpha$ governs the intensity of jumps. When $\alpha$ is small, the intensity of jumps is large. Contrarily, when $\alpha$ is large, the intensity of jumps is small.

However, the stationary property of their increments restricts the uses of stable Lévy motions in some situations, and generalizations are needed for instance to model real-world phenomena such as annual temperature (rainfall, wind speed), epileptic episodes in EEG, stock market prices over long periods and daily internet traffic. A significant feature of these cases is that the “local intensity of jumps” varies with time t; that is, $\alpha =\alpha \left(t\right)$ varies with time t.

One way to deal with such a variation is to set up a class of processes whose stability index $\alpha$ is a function of t. More precisely, one aims at defining non-stationary increments processes that are, at each time t, “tangent” (in a certain sense explained below) to a stable process with stability index $\alpha \left(t\right)$. Such processes are called multistable Lévy motions (MsLM); these are non-stationary increments extensions of stable Lévy motions.

Formally, one says that a stochastic process $\left\{X\right(t),t\in [0,1\left]\right\}$ is multistable if, for almost all $t\in [0,1)$, X is localizable at t with tangent process $X_t^{\prime }$ an $\alpha \left(t\right)$–stable process, $\alpha \left(t\right)\in (0,2)$. Recall that $\left\{X\right(t),t\in [0,1\left]\right\}$ is said to be $h$–localizable at t (cf. Falconer [1,2]), with $h>0$, if there exists a non-trivial process $X_t^{\prime }$, called the tangent process of X at t, such that

$$\begin{array}{c}\hfill \underset{r\searrow 0}{lim}{\displaystyle \frac{X(t+ru)-X\left(t\right)}{r^h}}=X_t^{\prime }\left(u\right),\end{array}$$

(1)

where convergence is in finite dimensional distributions. By (1), a multistable process is also a multifractional process (cf. [3,4] for such processes). Two such extensions exist [5]:

1.

The field-based MsLM admit the following series representation:

$$L_F\left(t\right)=C_{\alpha \left(t\right)}^{1/\alpha \left(t\right)}\sum _{(\mathsf{X},\mathsf{Y})\in \Pi }{\mathbf{1}}_{[0,t]}\left(\mathsf{X}\right){\mathsf{Y}}^{<-1/\alpha \left(t\right)>}(t\in [0,T]),$$

(2)

where $\Pi$ is a Poisson point process on $[0,1]\times \mathbb{R}$ with the Lebesgue measure as a mean measure $\mathcal{L}$, $a^{<b>}:=\mathrm{sign}\left(a\right){\left|a\right|}^b$ and

$$C_u=\Gamma (1-u)cos\left({\displaystyle \frac{u\pi }{2}}\right),u\in (0,2).$$

(3)

Their joint characteristic function is as follows:

$$\begin{array}{ccc}\hfill & & \mathbb{E}\left[exp\left\{i\sum _{j=1}^m{\theta }_j{L}_F\left(t_j\right)\right\}\right]\hfill \\ & & =exp\left\{-2{\int }_{[0,T]}{\int }_0^{+\infty }{sin}^2\left(\sum _{j=1}^m{\theta }_j{\displaystyle \frac{C_{\alpha \left(t_j\right)}^{1/\alpha \left(t_j\right)}}{2y^{1/\alpha \left(t_j\right)}}}{\mathbf{1}}_{[0,t_j]}\left(x\right)\right)dydx\right\}\hfill \end{array}$$

(4)

for $d\in \mathbb{N},({\theta }_1,\dots ,{\theta }_d)\in {\mathbb{R}}^d$ and $(t_1,\dots ,t_d)\in {\mathbb{R}}^d.$ These processes have correlated increments, and they are localizable as soon as the function $\alpha \left(t\right)$ is Hölder-continuous.

2.

The independent-increments MsLM admit the following series representation:

$$L_I\left(t\right)=\sum _{(\mathsf{X},\mathsf{Y})\in \Pi }{C}_{\alpha \left(\mathsf{X}\right)}^{1/\alpha \left(\mathsf{X}\right)}{\mathbf{1}}_{[0,t]}\left(\mathsf{X}\right){\mathsf{Y}}^{<-1/\alpha \left(\mathsf{X}\right)>}(t\in [0,T]).$$

(5)

As their name indicates, they have independent increments, and their joint characteristic function is as follows:

$$\begin{array}{c}\hfill \mathbb{E}\left[exp\left\{i\sum _{j=1}^d{\theta }_j{L}_I\left(t_j\right)\right\}\right]=exp\left\{-\int |\sum _{j=1}^d{\theta }_j{\mathbf{1}}_{[0,t_j]}\left(s\right){|}^{\alpha \left(s\right)}ds\right\},\end{array}$$

(6)

for $d\in \mathbb{N},({\theta }_1,\dots ,{\theta }_d)\in {\mathbb{R}}^d$ and $(t_1,\dots ,t_d)\in {\mathbb{R}}^d.$ These processes are localizable as soon as the function $\alpha$ satisfies the following condition uniformly for all x in finite interval as $t\searrow 0$; see [5]:

$$\begin{array}{c}\hfill \left(\alpha \left(x\right)-\alpha (x+t)\right)lnt\to 0\end{array}$$

(7)

In particular, independent-increments MsLM are, at each time t, “tangent ” to a stable Lévy process with stability index $\alpha \left(t\right)$.

• Of course, when $\alpha \left(t\right)$ is a constant $\alpha$ for all t, both $L_F$ and $L_I$ are simply the Poisson representation of $\alpha$–stable Lévy motion $L_{\alpha }.$ In general, $L_F$ and $L_I$ are semi-martingales. For more properties of $L_F$ and $L_I,$ such as Ferguson-Klass-LePage series representations, Hölder exponents, stochastic Hölder continuity, strong localizability, functional central limit theorem and the Hausdorff dimension of the range, we refer to [6,7,8]. See also [9,10] for wavelet series representation of the multifractional multistable processes.

Similar to the MsLM, we find that some stochastic processes have the property that the “local intensity of jumps” varies with the values of the processes. For instance, when one analysis certain records such as the stock market prices (see Figure 2), the exchange rates (see Figure 3) or annual temperature (see Figure 4), it seems that there exits a relation between the local value of the records, denoted by $S\left(t\right)$, and the local intensity of jumps, measured by the index of stability $\alpha \left(t\right)$.

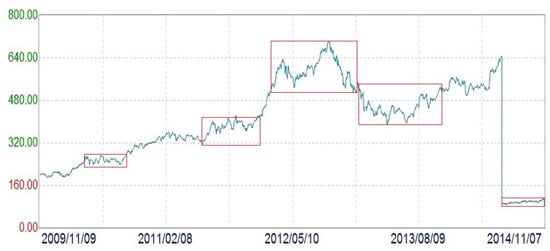
Figure 2. The figure exhibits the fluctuations in stock market prices $S\left(t\right)$ of Apple; see the blue curve. We can see that the “local intensities of jumps” (which means decrements or increments) vary in prices. When the prices are low, the corresponding “local intensities of jumps” are small. Contrarily, when the prices are high, the corresponding local intensities of jumps are large.

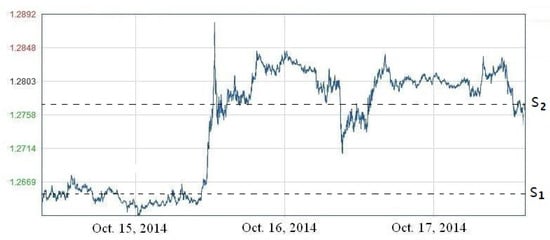
Figure 3. The figure exhibits the fluctuations in exchange rates $S\left(t\right)$ of Euro against US dollar. We can see that the local intensities of jumps vary in values. When the exchange rate is small $S_1$, the corresponding local intensity of jumps is small. Contrarily, when the exchange rate is large $S_2$, the corresponding local intensity of jumps is large. The local intensities of jumps varies with the level of values.

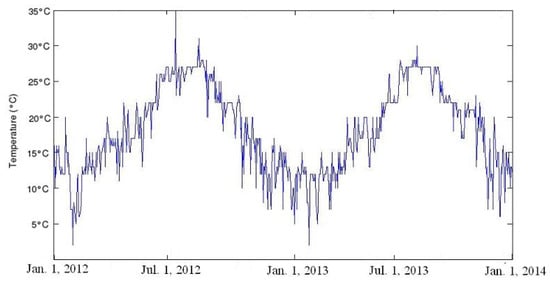
Figure 4. Here is a graph of daytime temperatures $S\left(t\right)$ in Nice, France. We find that the local intensities of jumps vary in values. When the temperature is low, the corresponding local intensity of jumps is large. Contrarily, when the temperature is high, the corresponding local intensity of jumps is small. When the temperatures are at the same level, the local intensities of jumps coincide.

This calls for the development of the self-stabilizing models, i.e., a class of stochastic processes S satisfying a functional equation of the form: $\alpha \left(t\right)=g\left(S\right(t\left)\right)$ almost surely for all t, where g is a smooth deterministic function. All the information concerning the future evolution of $\alpha$ is then incorporated in $g,$ which may be estimated from historical data under the assumption that the relation between S and $\alpha$ does not vary in time. This class of models is in a sense analogous to local volatility models: instead of having the local volatility depending on S, it is the local intensity of jumps that does so. This class of models is also in a sense analogous to MsLM: instead of the “local intensity of jumps” depending on time t, the “local intensity of jumps” depending on the values of $S.$

The main aim of this paper is to establish the self-stabilizing models, called the self-stabilizing processes (cf. Falconer and Lévy Véhel [11]), via a Donsker-type construction. Formally, one says that a stochastic process $\left\{S\right(t),t\in [0,1\left]\right\}$ is a self-stabilizing process if, for almost surely all $t\in [0,1)$, S is localizable at t with tangent process $S_t^{\prime }$ a $g\left(S\right(t\left)\right)$–stable process, with respect to the conditional probability measure ${\mathbb{P}}_{S\left(t\right)}.$ In formula, it holds

$$\begin{array}{c}\hfill \underset{r\searrow 0}{lim}{\displaystyle \frac{S(t+ru)-S\left(t\right)}{r^{1/g\left(S\right(t\left)\right)}}}=S_t^{\prime }\left(u\right),\end{array}$$

(8)

where convergence is in finite dimensional distributions with respect to ${\mathbb{P}}_{S\left(t\right)}.$ Formula (8) states that “local intensity of jumps” varies with the values of $S\left(t\right)$, instead of time t. In particular, if $S_t^{\prime }\left(u\right)=L_{g\left(S\right(t\left)\right)}\left(u\right),$ equality (8) implies that

$$S(t+ru)-S\left(t\right)\approx r^{1/g\left(S\right(t\left)\right)}{L}_{g\left(S\right(t\left)\right)}\left(u\right)=r^{1/g\left(S\right(t\left)\right)}u{L}_{g\left(S\right(t\left)\right)}\left(1\right),$$

provided that r is small. Thus, it is natural to define $S\left(t\right)={lim}_{n\to \infty }{S}_n\left({\displaystyle \frac{\lfloor nt\rfloor }{n}}\right),$ where

$$S_n\left({\displaystyle \frac{k+1}{n}}\right)-S_n\left({\displaystyle \frac{k}{n}}\right)=n^{-1/g\left(S_n(k/n)\right)}{L}_{g\left(S_n(k/n)\right)}\left(1\right),$$

which illustrates the use of our method to prove the existence of these self-stabilizing processes. The main difficulty associated with using this method involves proving the weak convergence of $S_n\left({\displaystyle \frac{\lfloor nt\rfloor }{n}}\right).$ To this end, we make use of the Arzelà–Ascoli theorem and its generalization.

The paper is organized as follows. In Section 2, we establish a self-stabilizing and self-scaling process. In Section 3, we show that it has many good properties, such as stochastic Hölder continuity and strong localizability. In particular, it is simultaneously a Markov process, a martingale (when $g(·)>1$), and a self-regulating process. Conclusions are presented in Section 4. In Appendix A, we give the Arzelà–Ascoli theorem and its generalization.

2. Existence of Self-Stabilizing and Self-Scaling Process

In this section, we make use of the general version of the Arzelà–Ascoli theorem to prove the existence of this self-stabilizing process. Moreover, our self-stabilizing process is also a self-scaling process. We call a random process self-scaling if the scale parameter $\sigma$ is also a function of the value of the process.

Definition 1. 

We call the sequence ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ subequicontinuous on $I\subset {\mathbb{R}}^d,$ if for any $\epsilon >0,$ there exist $\delta >0$ and a sequence of nonnegative numbers ${\left({\epsilon }_n\right)}_{n\ge 1},$${\epsilon }_n\to 0$ as $n\to \infty ,$ such that, for all functions $f_n$ in the sequence,

$$\begin{array}{c}\hfill |f_n\left({\theta }_1\right)-f_n\left({\theta }_2\right)|\le \epsilon +{\epsilon }_n,{\theta }_1,{\theta }_2\in I,\end{array}$$

(9)

whenever $\left|\right|{\theta }_1-{\theta }_2\left|\right|<\delta .$ In particular, if ${\epsilon }_n=0$ for all $n$, then ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is equicontinuous.

The following lemma gives a general version of the Arzelà–Ascoli theorem, whose proof is given in Appendix A.

Lemma 1. 

Assume that ${\left(f_n\right)}_{n\ge 1}$ is a sequence of real-valued continuous functions defined on a closed and bounded set ${\Pi }_{i=1}^d[a_i,b_i]\subset {\mathbb{R}}^d.$ If this sequence is uniformly bounded and subequicontinuous, then there exists a subsequence ${\left(f_{n_k}\right)}_{k\ge 1}$ that converges uniformly.

We give an approximation for a self-stabilizing and self-scaling process via Markov processes. The main idea behind this method is that the unknown stability index and scale parameter of the process at point $t+{\displaystyle \frac{1}{n}}$ are replaced by the predictable values $g\left(S\right(t\left)\right)$ and $\sigma \left(S\right(t\left)\right)$, respectively. When $n\to \infty ,$ it is obvious that $g(S(t+{\displaystyle \frac{1}{n}}))\to g\left(S\left(t\right)\right)$ in distribution, provided that g is a Hölder function and that $S(t+{\displaystyle \frac{1}{n}})-S\left(t\right)\to 0$ almost surely. The same argument holds for $\sigma \left(S\right(t\left)\right).$

Theorem 1. 

Let $g(·)$ be a Hölder function defined on $\mathbb{R}$ with values in the range $[a,b]\subset (0,2]$.

Let $\sigma (·)$ be a positive Hölder function defined on $\mathbb{R}$ and assume that $\sigma \left(x\right)$ lies within the range $[c,d],c>0.$ There exists a self-stabilizing and self-scaling process $S\left(t\right),t\in [0,1],$ such that it is tangent at u to a stable Lévy process $\sigma \left(S\left(u\right)\right)L_{g\left(S\right(u\left)\right)}$ under the conditional expectation given as $S\left(u\right)$.

Proof. 

The theorem can be proved in four steps.

Step 1. Donsker’s construction: For all $n\in \mathbb{N}$ and all $k=0,1,\dots ,n,$ set

$$\begin{array}{ccc}& {\xi }_1\backsim \sigma \left(0\right){\left({\displaystyle \frac{1}{n}}\right)}^{1/g\left(0\right)}{L}_{g\left(0\right)},& S_1^{\prime }={\xi }_1,\hfill \\ & {\xi }_2\backsim \sigma \left(S_1^{\prime }\right){\left({\displaystyle \frac{1}{n}}\right)}^{1/g\left(S_1^{\prime }\right)}{L}_{g\left(S_1^{\prime }\right)},& S_2^{\prime }=S_1^{\prime }+{\xi }_2,\hfill \\ & {\xi }_3\backsim \sigma \left(S_2^{\prime }\right){\left({\displaystyle \frac{1}{n}}\right)}^{1/g\left(S_2^{\prime }\right)}{L}_{g\left(S_2^{\prime }\right)},& S_3^{\prime }=S_2^{\prime }+{\xi }_3,\hfill \\ & \hspace{1em}\hspace{1em} \dots \dots & \dots \dots \hfill \end{array}$$

where $L_{g\left(S_k^{\prime }\right)}$ is a symmetric $g\left(S_k^{\prime }\right)$–stable random variable $Sg\left(S_k^{\prime }\right)S$ with unit-scale parameters and is independent of the random variables $\left\{L_{g\left(S_j^{\prime }\right)},j<k\right\}$ for a given $S_k^{\prime }$. Then, we define a sequence of partial sums ${\left(S_k^{\prime }\right)}_{1\le k\le n}.$ In particular, when $g\left(x\right)\equiv 2$ and $\sigma \left(x\right)\equiv 1$, this method is known as Donsker’s construction (cf. Theorem 16.1 of Billingsley [12] for instance). Define the processes ${\left(S_n\right)}_{n\in \mathbb{N}}$, where

$$\begin{array}{ccc}\hfill S_n\left(t\right)& =& S_{\lfloor nt\rfloor }^{\prime },t\in [0,1].\hfill \end{array}$$

Then, for given n, $S_n\left(t\right),t\in [0,1],$ is a Markov process. For simplicity of notation, denote this as

$${\mathbb{E}}_{S_n\left(t_1\right),\dots ,S_n\left(t_d\right)}\left[·\right]=\mathbb{E}\left[·|S_n\left(t_1\right),\dots ,S_n\left(t_d\right)\right].$$

According to the construction of $S_n\left(t\right),$ we have $S_n(k/n)=S_k^{\prime }$, and, for all $\theta \in \mathbb{R},$

$$\begin{array}{ccc}& & {\mathbb{E}}_{S_n(k/n)}\left[exp\left\{i\theta \left(S_n\left({\displaystyle \frac{k+1}{n}}\right)-S_n\left({\displaystyle \frac{k}{n}}\right)\right)\right\}\right]={\mathbb{E}}_{S_n(k/n)}\left[exp\left\{i\theta {\xi }_k\right\}\right]\hfill \\ & & =exp\left\{-|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}\right\}.\hfill \end{array}$$

(10)

It is easy to see that, for all $t_1,t_2\in [0,1]$ satisfying $t_1<t_2$,

$$\begin{array}{ccc}& & {\mathbb{E}}_{S_n\left(t_1\right)}\left[exp\left\{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & ={\mathbb{E}}_{S_n\left(t_1\right)}\left[{\mathbb{E}}_{S_n\left({\displaystyle \frac{\lfloor n{t}_2\rfloor -1}{n}}\right),\dots ,S_n\left(t_1\right)}\left[exp\left\{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}\right\}\right]\right]\hfill \\ & & ={\mathbb{E}}_{S_n\left(t_1\right)}\left[exp\left\{i\theta \left(S_n\left({\displaystyle \frac{\lfloor n{t}_2\rfloor -1}{n}}\right)-S_n\left(t_1\right)\right)+\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -2}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & =\dots \hfill \\ & & ={\mathbb{E}}_{S_n\left(t_1\right)}\left[exp\left\{i\theta \left(S_n\left({\displaystyle \frac{\lfloor n{t}_1\rfloor +1}{n}}\right)-S_n\left(t_1\right)\right)+|\sigma \left(S_n(\lfloor n{t}_1\rfloor /n)\right)\theta {|}^{g\left(S_n(\lfloor n{t}_1\rfloor /n)\right)}{\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & =1,\hfill \end{array}$$

(11)

where the last line follows from (10). In particular, it can be rewritten in the following form:

$$\begin{array}{ccc}& & {\mathbb{E}}_{S_n\left(t_1\right)}\left[exp\left\{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+{\int }_{t_1^{\left(n\right)}}^{t_2^{\left(n\right)}}|\sigma \left(S_n\left(z^{\left(n\right)}\right)\right)\theta {|}^{g\left(S_n\left(z\right)\right)}dz\right\}\right]=1,\hfill \end{array}$$

(12)

where $z^{\left(n\right)}={\displaystyle \frac{\lfloor nz\rfloor }{n}}$ as before. More generally, we have, for all ${\theta }_j\in \mathbb{R},$$t_j\in [0,1]$ and $t_j\ge t_{j-1}$, $j=1,2,\dots ,d,$

$$\begin{array}{c}{\mathbb{E}}_{S_n\left(t_1\right)}\left[exp\left\{i\sum _{j=2}^d{\theta }_j\left(S_n\left(t_j\right)-S_n\left(t_1\right)\right)+\int |\sum _{j=2}^d{\theta }_j\sigma \left(S_n\left(z^{\left(n\right)}\right)\right){\mathbf{1}}_{[t_1^{\left(n\right)},t_j^{\left(n\right)}]}\left(z\right){|}^{g\left(S_n\left(z\right)\right)}dz\right\}\right]\hfill \\ ={\mathbb{E}}_{S_n\left(t_1\right)}[exp\{i\sum _{j=2}^d\left(\left(\sum _{k=j}^d{\theta }_k\right)\left(S_n\left(t_j\right)-S_n\left(t_{j-1}\right)\right)\right)\hfill \\ +\sum _{j=2}^d\int \left|\left(\sum _{k=j}^d{\theta }_k\right)\sigma \left(S_n\left(z^{\left(n\right)}\right)\right){\mathbf{1}}_{[t_{j-1}^{\left(n\right)},t_j^{\left(n\right)}]}\left(z\right){|}^{g\left(S_n\left(z\right)\right)}dz\right\}]\hfill \\ ={\mathbb{E}}_{S_n\left(t_1\right)}\left[{\mathbb{E}}_{S_n\left(t_1\right),\dots ,S_n\left(t_{d-1}\right)}[exp\{i\sum _{j=2}^d\left(\left(\sum _{k=j}^d{\theta }_k\right)\left(S_n\left(t_j\right)-S_n\left(t_{j-1}\right)\right)\right)\right.\hfill \\ \left.+\sum _{j=2}^d\int \left|\left(\sum _{k=j}^d{\theta }_k\right)\sigma \left(S_n\left(z^{\left(n\right)}\right)\right){\mathbf{1}}_{[t_{j-1}^{\left(n\right)},t_j^{\left(n\right)}]}\left(z\right){|}^{g\left(S_n\left(z\right)\right)}dz\right\}]\right]\hfill \\ ={\mathbb{E}}_{S_n\left(t_1\right)}[exp\{i\sum _{j=2}^{d-1}\left(\left(\sum _{k=j}^d{\theta }_k\right)\left(S_n\left(t_j\right)-S_n\left(t_{j-1}\right)\right)\right)\hfill \\ +\sum _{j=2}^{d-1}\int \left|\left(\sum _{k=j}^d{\theta }_k\right)\sigma \left(S_n\left(z^{\left(n\right)}\right)\right){\mathbf{1}}_{[t_{j-1}^{\left(n\right)},t_j^{\left(n\right)}]}\left(z\right){|}^{g\left(S_n\left(z\right)\right)}dz\right\}]\hfill \\ =\dots \hfill \\ ={\mathbb{E}}_{S_n\left(t_1\right)}\left[exp\left\{i\left(\sum _{k=2}^d{\theta }_k\right)\left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+\int |\left(\sum _{k=2}^d{\theta }_k\right)\sigma \left(S_n\left(z^{\left(n\right)}\right)\right){\mathbf{1}}_{[t_1^{\left(n\right)},t_2^{\left(n\right)}]}\left(z\right){|}^{g\left(S_n\left(z\right)\right)}dz\right\}\right]\hfill \\ =1,\hfill \end{array}$$

(13)

where the last line follows from (12). Since $S_n\left(t\right),t\in [0,1],$ is a Markov process. Equality (13) also holds if ${\mathbb{E}}_{S_n\left(t_1\right)}$ is replaced by ${\mathbb{E}}_{S_n\left(t_{-l}\right),\dots ,S_n\left(t_0\right),S_n\left(t_1\right)},$ where $t_{-l},\dots ,t_0\in [0,1]$ and $t_{-l},\dots ,t_0\le t_1.$

Set

$$f_n(\theta ,t_1,t_2)=\mathbb{E}\left[e^{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)}\right]$$

and set

$${\Delta }_n(t_1,t_2)=|t_2^{\left(n\right)}-t_1^{\left(n\right)}|$$

for all $t_1,t_2\in [0,1]$ and $\theta \in \mathbb{R}.$ It is worth noting that the following estimation holds:

$${\Delta }_n(t_1,t_2)\le |t_1-t_2|+{\displaystyle \frac{1}{n}}.$$

Recall $\sigma (·)\in [c,d],c>0,$ and $g(·)\in [a,b]\subset (0,2].$ Then, we may assume that $\sigma {\left(x\right)}^{g\left(x\right)}$ lies in the range $[m,M],m>0.$ By (11), it is easy to see that the following inequalities hold for all $\left|\theta \right|\le 1,$

$$\begin{array}{ccc}& & exp\left\{-m\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}{\left|\theta \right|}^b{\displaystyle \frac{1}{n}}\right\}\hfill \\ & & =exp\left\{-m\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}{\left|\theta \right|}^b{\displaystyle \frac{1}{n}}\right\}\mathbb{E}\left[exp\left\{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & \ge \mathbb{E}\left[exp\left\{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}-\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & =f_n(\theta ,t_1,t_2)\hfill \end{array}$$

and

$$\begin{array}{ccc}& & exp\left\{-M\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}{\left|\theta \right|}^a{\displaystyle \frac{1}{n}}\right\}\hfill \\ & & =exp\left\{-M\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}{\left|\theta \right|}^a{\displaystyle \frac{1}{n}}\right\}\mathbb{E}\left[exp\left\{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & \le \mathbb{E}\left[exp\left\{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}-\sum _{k=\lfloor n{t}_1\rfloor }^{\lfloor n{t}_2\rfloor -1}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}{\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & =f_n(\theta ,t_1,t_2).\hfill \end{array}$$

Thus, for all $\left|\theta \right|\le 1,$

$$\begin{array}{c}\hfill exp\left\{-M{\Delta }_n(t_1,t_2){\left|\theta \right|}^a\right\}\le f_n(\theta ,t_1,t_2)\le exp\left\{-m{\Delta }_n(t_1,t_2){\left|\theta \right|}^b\right\}.\end{array}$$

(14)

By a similar argument, we have, for all $\left|\theta \right|>1,$

$$\begin{array}{c}\hfill exp\left\{-M{\Delta }_n(t_1,t_2){\left|\theta \right|}^b\right\}\le f_n(\theta ,t_1,t_2)\le exp\left\{-m{\Delta }_n(t_1,t_2){\left|\theta \right|}^a\right\}.\end{array}$$

(15)

The inequalities (14) and (15) can be rewritten in the following form: for all $\theta \in \mathbb{R},$

$$\begin{array}{ccc}& & exp\left\{-M{\Delta }_n(t_1,t_2)max\left\{{\left|\theta \right|}^a,{\left|\theta \right|}^b\right\}\right\}\le f_n(\theta ,t_1,t_2)\hfill \\ & & \le exp\left\{-m{\Delta }_n(t_1,t_2)min\left\{{\left|\theta \right|}^a,{\left|\theta \right|}^b\right\}\right\}.\hfill \end{array}$$

(16)

Step 2. Sub-equicontinuous for $f_n(\theta ,0,t)$: Denote $f_n(\theta ,0,t)$ by $f_n(\theta ,t).$ Next, we prove that for given $N,$ the sequence ${\left(f_n(\theta ,t)\right)}_{n\ge 1}$ is subequicontinuous on $(\theta ,t)\in [-N,N]\times [0,1].$ By Theorems A2 and (14), it is easy to see that ${\left(f_n(\theta ,t)\right)}_{n\ge 1}$ is equicontinuous with respect to $\theta \in [-N,N].$ However, we can even prove a better result, that is ${\left(f_n(\theta ,t)\right)}_{n\ge 1}$ is Hölder equicontinuous of order $a/(1+a)$ with respect to $\theta \in [-N,N].$ By (14) and the Billingsley inequality (cf. p. 47 of [12]), it is easy to see that, for all $t,v\in [0,1]$ with $t,v\ge t_1$ and all $x>2,$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(|S_n\left(t\right)-S_n\left(v\right)|\ge x\right)& \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}\left(1-\mathbb{E}\left[e^{i\theta \left(S_n\left(t\right)-S_n\left(v\right)\right)}\right]\right)d\theta \hfill \\ & \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}\left(1-exp\left\{-{M\left|\theta \right|}^a{\Delta }_n(t,v)\right\}\right)d\theta \hfill \\ & \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}M{\left|\theta \right|}^a{\Delta }_n(t,v)d\theta \hfill \\ & =& {\displaystyle \frac{2^{a+1}}{a+1}}{\displaystyle \frac{M}{x^a}}{\Delta }_n(t,v).\hfill \end{array}$$

(17)

Similarly, by (15), for all $t,v\in [0,1]$ with $t,v\ge t_1$ and all $0<x\le 2,$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(|S_n\left(t\right)-S_n\left(v\right)|\ge x\right)& \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}\left(1-\mathbb{E}\left[e^{i\theta \left(S_n\left(t\right)-S_n\left(v\right)\right)}\right]\right)d\theta \hfill \\ & \le & {\displaystyle \frac{x}{2}}\left[{\int }_{\left|\theta \right|<1}M|\theta {|}^{a}d\theta +{\int }_{1\le \left|\theta \right|\le 2/x}M|\theta {|}^{b}d\theta \right]{\Delta }_n(t,v)\hfill \\ & =& M\left({\displaystyle \frac{x}{a+1}}+{\displaystyle \frac{2^{b+1}}{b+1}}{\displaystyle \frac{1}{x^b}}\right){\Delta }_n(t,v).\hfill \end{array}$$

(18)

For all $({\theta }_i,t_i)\in \mathbb{R}\times [0,1],i=1,2,$ we have

$$\begin{array}{ccc}\hfill |f_n({\theta }_1,t_1)-f_n({\theta }_2,t_1)|& =& \left|\mathbb{E}\left[e^{i{\theta }_1{S}_n\left(t_1\right)}\left(1-e^{i({\theta }_2-{\theta }_1)S_n\left(t_1\right)}\right)\right]\right|\hfill \\ & \le & \mathbb{E}\left[|1-e^{i({\theta }_2-{\theta }_1)S_n\left(t_1\right)}|\right]\hfill \end{array}$$

(19)

and

$$\begin{array}{ccc}\hfill |f_n({\theta }_2,t_1)-f_n({\theta }_2,t_2)|& =& \left|\mathbb{E}\left[e^{i{\theta }_2{S}_n\left(t_1\right)}\left(1-e^{i{\theta }_2(S_n\left(t_2\right)-S_n\left(t_1\right))}\right)\right]\right|\hfill \\ & \le & \mathbb{E}\left[|1-e^{i{\theta }_2(S_n\left(t_2\right)-S_n\left(t_1\right))}|\right].\hfill \end{array}$$

(20)

The random variable $|1-e^{i({\theta }_2-{\theta }_1)S_n\left(t_1\right)}|$ is dominated by the constant 2. Therefore, (19) and (17) imply that

$$\begin{array}{ccc}\hfill |f_n({\theta }_1,t_1)-f_n({\theta }_2,t_1)|& \le & \mathbb{E}\left[|1-e^{i({\theta }_2-{\theta }_1)S_n\left(t_1\right)}|{\mathbf{1}}_{\left\{\right|S_n\left(t_1\right)|\le |{\theta }_2-{\theta }_1{|}^{-1/(1+a)}\}}\right]\hfill \\ & & +\mathbb{E}\left[|1-e^{i({\theta }_2-{\theta }_1)S_n\left(t_1\right)}|{\mathbf{1}}_{\left\{\right|S_n\left(t_1\right)|>|{\theta }_2-{\theta }_1{|}^{-1/(1+a)}\}}\right]\hfill \\ & \le & \mathbb{E}\left[\left|({\theta }_2-{\theta }_1)S_n\left(t_1\right)\right|{\mathbf{1}}_{\left\{\right|S_n\left(t_1\right)|\le |{\theta }_2-{\theta }_1{|}^{-1/(1+a)}\}}\right]\hfill \\ & & +2\mathbb{E}\left[{\mathbf{1}}_{\left\{\right|S_n\left(t_1\right)|>|{\theta }_2-{\theta }_1{|}^{-1/(1+a)}\}}\right]\hfill \\ & \le & C|{\theta }_2-{\theta }_1{|}^{a/(1+a)},\hfill \end{array}$$

where C is a constant only depending on M and $a.$ Thus, ${\left(f_n(\theta ,t)\right)}_{n\ge 1}$ is Hölder equicontinuous of order $a/(1+a)$ with respect to $\theta .$ Similarly, the inequalities (20) and (18) imply that

$$\begin{array}{ccc}\hfill |f_n({\theta }_2,t_1)-f_n({\theta }_2,t_2)|& \le & \mathbb{E}\left[|1-e^{i{\theta }_2(S_n\left(t_2\right)-S_n\left(t_1\right))}|{\mathbf{1}}_{\left\{\right|S_n\left(t_2\right)-S_n\left(t_1\right)|\le {\Delta }_n{(t_1,t_2)}^{1/(1+b)}\}}\right]\hfill \\ & & +\mathbb{E}\left[|1-e^{i{\theta }_2(S_n\left(t_2\right)-S_n\left(t_1\right))}|{\mathbf{1}}_{\left\{\right|S_n\left(t_2\right)-S_n\left(t_1\right)|\ge {\Delta }_n{(t_1,t_2)}^{1/(1+b)}\}}\right]\hfill \\ & \le & \mathbb{E}\left[\left|{\theta }_2(S_n\left(t_2\right)-S_n\left(t_1\right))\right|{\mathbf{1}}_{\left\{\right|S_n\left(t_2\right)-S_n\left(t_1\right)|\le {\Delta }_n{(t_1,t_2)}^{1/(1+b)}\}}\right]\hfill \\ & & +2\mathbb{E}\left[{\mathbf{1}}_{\left\{\right|S_n\left(t_2\right)-S_n\left(t_1\right)|\ge {\Delta }_n{(t_1,t_2)}^{1/(1+b)}\}}\right]\hfill \\ & \le & |{\theta }_2|{\Delta }_n{(t_1,t_2)}^{1/(1+b)}+C{\Delta }_n{(t_1,t_2)}^{1/(1+b)}\hfill \\ & \le & \left(|{\theta }_2|+C\right)\left(|t_2-t_1{|}^{1/(1+b)}+n^{-1/(1+b)}\right),\hfill \end{array}$$

where C is a constant depending on $M,a$ and $b.$ The last inequality implies that for all $\theta \in [-N,N],$${\left(f_n(\theta ,t)\right)}_{n\ge 1}$ is Hölder subequicontinuous of order $1/(1+b)$ with respect to $t.$ Notice that

$$\begin{array}{ccc}\hfill |f_n({\theta }_1,t_1)-f_n({\theta }_2,t_2)|& \le & |f_n({\theta }_1,t_1)-f_n({\theta }_2,t_1)|+|f_n({\theta }_2,t_1)-f_n({\theta }_2,t_2)|.\hfill \end{array}$$

Thus, the sequence ${\left(f_n(\theta ,t)\right)}_{n\ge 1}$ is subequicontinuous on $(\theta ,t)\in [-N,N]\times [0,1].$

Step 3. Convergence for a subsequence: Denote by $f_{{\sigma }_0\left(n\right)}(\theta ,t)=f_n(\theta ,t).$ For every given $N\in \mathbb{N}$ and $N\ge 1$, by Lemma 1, there exists a subsequence ${\left(f_{{\sigma }_N\left(n\right)}(\theta ,t)\right)}_{n\ge 1}$ of ${\left(f_{{\sigma }_{N-1}\left(n\right)}(\theta ,t)\right)}_{n\ge 1}$ and a function $f(\theta ,t)$ defined on $(\theta ,t)\in \mathbb{R}\times [0,1]$ such that ${lim}_{n\to \infty }{f}_{{\sigma }_N\left(n\right)}(\theta ,t)=f(\theta ,t)$ uniformly on $(\theta ,t)\in [-N,N]\times [0,1].$ By induction, the following relation holds:

$${\left(f_n(\theta ,t)\right)}_{n\ge 1}\supseteq {\left(f_{{\sigma }_1\left(n\right)}(\theta ,t)\right)}_{n\ge 1}\supseteq \dots \supseteq {\left(f_{{\sigma }_{N-1}\left(n\right)}(\theta ,t)\right)}_{n\ge 1}\supseteq {\left(f_{{\sigma }_N\left(n\right)}(\theta ,t)\right)}_{n\ge 1}\supseteq \dots$$

Hence, the diagonal subsequence ${\left(f_{{\sigma }_N\left(N\right)}(\theta ,t)\right)}_{N\ge 1}$ converges to $f(\theta ,t)$ on $(\theta ,t)\in \mathbb{R}\times [0,1].$ Moreover, by (14) and (15), the following inequalities hold for all $\left|\theta \right|\le 1,$:

$$\begin{array}{c}\hfill e^{-{tM\left|\theta \right|}^a}\le f(\theta ,t)\le e^{-{tm\left|\theta \right|}^b}\end{array}$$

(21)

and, for all $\left|\theta \right|>1,$

$$\begin{array}{c}\hfill e^{-{tM\left|\theta \right|}^b}\le f(\theta ,t)\le e^{-{tm\left|\theta \right|}^a}.\end{array}$$

(22)

By the Lévy continuous theorem, these exists a random process $S\left(t\right)$ such that $S_{{\sigma }_N\left(N\right)}\left(t\right)$ converges to $S\left(t\right)$ in distribution for any $t\in [0,1]$ as $N\to \infty .$

Similarly, by (13) instead of by (11), we can prove that for all $t_j\in [0,1],$$j=1,\dots ,d,$ there exists a random process $S\left(t\right)$ such that $S_{n_k}\left(t\right)$ converges to $S\left(t\right)$ in finite dimensional distribution, where $S_{n_k}\left(t\right)$ is a subsequence of $S_{{\sigma }_N\left(N\right)}\left(t\right).$ Letting $k\to \infty ,$ by (13) and the dominated convergence theorem, we have, for all $({\theta }_j,t_j)\in \mathbb{R}\times [0,1],j=1,2,\dots ,d,$

$$\begin{array}{c}\hfill {\mathbb{E}}_{S\left(t_1\right)}\left[exp\left\{i\sum _{j=2}^d{\theta }_j\left(S\left(t_j\right)-S\left(t_1\right)\right)+\int |\sum _{j=2}^d{\theta }_j\sigma \left(S\left(z\right)\right){\mathbf{1}}_{[t_1,t_j]}\left(z\right){|}^{g\left(S\right(z\left)\right)}dz\right\}\right]=1.\end{array}$$

(23)

Equality (23) also holds if ${\mathbb{E}}_{S\left(t_1\right)}$ is replaced by ${\mathbb{E}}_{S\left(t_{-l}\right),\dots ,S\left(t_0\right),S\left(t_1\right)},$ where $t_{-l},\dots ,t_0\in [0,1]$ and $t_{-l},\dots ,t_0\le t_1.$

Step 4. Self-stabilizing for the limiting process: Next, we prove that S is a self-stabilizing process, that is, S is localizable at u to a $g\left(S\right(u\left)\right)$–stable Lévy motion $L_{g\left(S\right(u\left)\right)}\left(t\right)$ under the conditional expectation given as $S\left(u\right)$. For any $(t_1,\dots ,t_d)\in {[0,1]}^d$ and $r>0$, from equality (23), it is easy to see that

$$\begin{array}{ccc}& & {\mathbb{E}}_{S\left(u\right)}[exp\{i\sum _{j=1}^d{\theta }_j\left({\displaystyle \frac{S(u+r{t}_j)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}\right)\hfill \\ & & +\int \left|\sum _{j=1}^d{\theta }_j{r}^{-1/g\left(S\right(u\left)\right)}\sigma \left(S\left(z\right)\right){\mathbf{1}}_{[u,u+r{t}_j]}\left(z\right){|}^{g\left(S\right(z\left)\right)}dz\right\}]=1.\hfill \end{array}$$

Setting $z=u+rt$, we find that

$$\begin{array}{ccc}& & {\mathbb{E}}_{S\left(u\right)}[exp\{i\sum _{j=1}^d{\theta }_j\left({\displaystyle \frac{S(u+r{t}_j)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}\right)\hfill \\ & & +\int \left|\sum _{j=1}^d{\theta }_j\sigma \left(S(u+rt)\right){\mathbf{1}}_{[0,t_j]}\left(t\right){|}^{g\left(S\right(u+rt\left)\right)}{r}^{\left(g\left(S\right(u\left)\right)-g\left(S\right(u+rt\left)\right)\right)/g\left(S\left(u\right)\right)}dt\right\}]=1.\hfill \end{array}$$

From equality (23), by an argument similar to (14), we obtain, for all $\theta \in \mathbb{R}$ and all $t,v\in [0,1]$ with $t,v\ge u$,

$$\begin{array}{ccc}\hfill exp\left\{-M|t-v|max\left\{{\left|\theta \right|}^a,{\left|\theta \right|}^b\right\}\right\}& \le & {\mathbb{E}}_{S\left(u\right)}\left[e^{i\theta \left(S\left(t\right)-S\left(v\right)\right)}\right]\hfill \\ & \le & exp\left\{-m|t-v|min\left\{{\left|\theta \right|}^a,{\left|\theta \right|}^b\right\}\right\}.\hfill \end{array}$$

(24)

By an argument similar to that of (18), it follows that, for $t,v\in [0,1]$ and $t,v\ge u$,

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S\left(t\right)-S\left(v\right)|\ge {|t-v|}^{\beta }\right)& \le & {C|t-v|}^{1-b\beta },\hfill \end{array}$$

(25)

where C is a constant depending on $M,a$ and $b.$ Since g and $\sigma$ are both Hölder functions, by (25), we get

$$\begin{array}{c}\hfill \underset{r\searrow 0}{lim}{r}^{\left(g\left(S\right(u\left)\right)-g\left(S\right(u+rt\left)\right)\right)/g\left(S\left(u\right)\right)}=1,\underset{r\searrow 0}{lim}g\left(S(u+rt)\right)=g\left(S\left(u\right)\right)\end{array}$$

(26)

and

$$\begin{array}{c}\hfill \underset{r\searrow 0}{lim}\sigma \left(S(u+rt)\right)=\sigma \left(S\left(u\right)\right)\end{array}$$

(27)

in probability with respect to ${\mathbb{P}}_{S\left(u\right)}.$ Hence, using the dominated convergence theorem, we have

$$\begin{array}{ccc}& & \underset{r\searrow 0}{lim}{\mathbb{E}}_{S\left(u\right)}\left[exp\left\{i\sum _{j=1}^d{\theta }_j\left({\displaystyle \frac{S(u+r{t}_j)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}\right)\right\}\right]\hfill \\ & & =exp\left\{-\int |\sum _{j=1}^d{\theta }_j\sigma \left(S\left(u\right)\right){\mathbf{1}}_{[0,t_j]}\left(t\right){|}^{g\left(S\right(u\left)\right)}dt\right\}\hfill \\ & & ={\mathbb{E}}_{S\left(u\right)}\left[exp\left\{i\sum _{j=1}^d{\theta }_j\left(\sigma \left(S\left(u\right)\right)L_{g\left(S\right(u\left)\right)}\left(t_j\right)\right)\right\}\right],\hfill \end{array}$$

which means that S is localizable at u to a $g\left(S\right(u\left)\right)$–stable Lévy motion $\sigma \left(S\left(u\right)\right)L_{g\left(S\right(u\left)\right)}\left(t\right)$ under the conditional expectation given as $S\left(u\right)$, where $L_{\alpha }\left(t\right)$ is the standard symmetric $\alpha$–stable Lévy motion. This completes the proof of the theorem. □

Remark 1. 

Let us comment on Theorem 1.

1. 

A slightly different method by which to approximate the self-stabilizing and self-scaling process S can be described as follows. Define

$$\begin{array}{ccc}\hfill S_n\left(0\right)& \equiv & 0,\hfill \\ \hfill S_n\left({\displaystyle \frac{1}{n}}\right)& =& \sigma \left(0\right){\left({\displaystyle \frac{1}{n}}\right)}^{1/g\left(0\right)}{L}_{g\left(0\right)},\hfill \\ \hfill \dots & & \dots \hfill \\ \hfill S_n\left({\displaystyle \frac{k+1}{n}}\right)& =& S_n\left({\displaystyle \frac{k}{n}}\right)+\sigma \left(S_n(k/n)\right){\left({\displaystyle \frac{1}{n}}\right)}^{1/g\left(S_n(k/n)\right)}{L}_{g\left(S_n(k/n)\right)},\hfill \\ \hfill \dots & & \dots .\hfill \end{array}$$

Now, let

$$S_n\left(t\right)=S_{\lfloor nt\rfloor }.$$

By an argument similar to the proof of Theorem 1, there exists a subsequence $S_{n_k}$ of $S_n$ such that $S_{n_k}$ converges to the process S in finite dimensional distribution. Notice that with this method, all of the random variables ${\left(L_{g\left(S_n(k/n)\right)}\right)}_{k\in [1,n]}$ are changed from $S_n$ to $S_{n+1},$ even $g\left(x\right)$ is a constant. However, in the proof of Theorem 1, we only add one random variable from $S_n$ to $S_{n+1}$ when $g(·)\equiv c$ a constant.

2. 

Notice that if we define $S_n(k/n)$ for all $k=0,1,2,\dots ,$ then, by a similar argument of Theorem 1, we can define the self-stabilizing and self-scaling process $\{S\left(x\right):x\in {\mathbb{R}}^{+}\}$ on the positive whole line via the limit of

$$\begin{array}{ccc}\hfill S_n\left(x\right)& =& S_n\left({\displaystyle \frac{\lfloor nx\rfloor }{n}}\right),x\in [0,N].\hfill \end{array}$$

(28)

3. 

An interesting question is whether $S_n\left(t\right)$ converges to $S\left(t\right)$ in finite dimensional distribution. To answer this question, we need a judgment that if every subsequence of $\left(x_n\right)$ has a further subsequence that converges to x, then $\left(x_n\right)$ converges to $x.$ According to the proof of the theorem, it is known that every subsequence of $S_n\left(t\right)$ has a further subsequence that converges to S in finite dimensional distribution, where S is defined by (23). Thus, the question reduces to proving that (23) defines a unique process S.

3. Properties of the Self-Stabilizing and Self-Scaling Process

In this section, we consider the properties of the self-stabilizing and self-scaling process S established in the proof of Theorem 1. It seems that the process S shares many properties with the multistable Lévy motions (cf. Falconer and Liu [5]). Assume that $\sigma {\left(x\right)}^{g\left(x\right)}$ lies in the range $[m,M],m>0.$

3.1. Tail Probabilities

Notice that the estimation for the characteristic function of $S\left(t_1\right)-S\left(t_2\right)$ under the probability measure ${\mathbb{P}}_{S\left(u\right)}$ is given by (24). By an argument similar to that of (17) and (18), for all $t_1,t_2,u\in [0,1]$ such that $t_1,t_2\ge u,$ the following two inequalities hold for all $x>2$:

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S\left(t_1\right)-S\left(t_2\right)|\ge x\right)& \le & {\displaystyle \frac{2^{a+1}}{a+1}}{\displaystyle \frac{M}{x^a}}|t_1-t_2|\hfill \end{array}$$

(29)

and, for all $0<x\le 2,$

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S\left(t_1\right)-S\left(t_2\right)|\ge x\right)& \le & M\left({\displaystyle \frac{x}{a+1}}+{\displaystyle \frac{2^{b+1}}{b+1}}{\displaystyle \frac{1}{x^b}}\right)|t_1-t_2|.\hfill \end{array}$$

(30)

Thus, the following inequalities are obvious:

Property 1. 

For $t_1,t_2,u\in [0,1]$ with $t_1,t_2\ge u$ and all $x>2,$ it holds

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S\left(t_1\right)-S\left(t_2\right)|\ge x\right)& \le & C{\displaystyle \frac{1}{x^a}}|t_1-t_2|,\hfill \end{array}$$

where C is a constant depending on M and $a.$ In particular, it implies that, for all $x>2,$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(|S\left(t_1\right)-S\left(t_2\right)|\ge x\right)& \le & C{\displaystyle \frac{1}{x^a}}|t_1-t_2|.\hfill \end{array}$$

For more precise bounds on tail probabilities, we have the following inequalities:

Property 2. 

For $t_1,t_2,u\in [0,1]$ with $t_2\ge t_1\ge u$ and all $x>0,$ it holds

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S\left(t_2\right)-S\left(t_1\right)|\ge x\right)& \le & {\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\displaystyle \frac{2^{g\left(S\right(t\left)\right)+1}}{g\left(S\right(t\left)\right)+1}}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]\hfill \\ & \le & C{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right],\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill C& =& max\left\{{\displaystyle \frac{2^{a+1}}{a+1}},{\displaystyle \frac{2^{b+1}}{b+1}}\right\}.\hfill \end{array}$$

In particular, it implies that, for all $x>0,$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(|S\left(t_2\right)-S\left(t_1\right)|\ge x\right)& \le & C\mathbb{E}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right].\hfill \end{array}$$

Proof. 

Equality (10) and Jensen’s inequality imply that, for $u\le k/n$ and all $\theta \in \mathbb{R},$

$$\begin{array}{ccc}\hfill {\mathbb{E}}_{S_n\left(u\right)}\left[exp\left\{i\theta \left(S_n\left({\displaystyle \frac{k+1}{n}}\right)-S_n\left({\displaystyle \frac{k}{n}}\right)\right)\right\}\right]& =& {\mathbb{E}}_{S_n\left(u\right)}\left[exp\left\{-{\displaystyle \frac{1}{n}}|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}\right\}\right]\hfill \\ & \ge & exp\left\{-{\displaystyle \frac{1}{n}}{\mathbb{E}}_{S_n\left(u\right)}\left[|\sigma \left(S_n(k/n)\right)\theta {|}^{g\left(S_n(k/n)\right)}\right]\right\}.\hfill \end{array}$$

By the last inequality and an argument similar to that of (11), we have, for all $t_1,t_2,u\in [0,1]$ with $t_2\ge t_1\ge u,$

$$\begin{array}{c}\hfill {\mathbb{E}}_{S_n\left(u\right)}\left[exp\left\{i\theta \left(S_n\left(t_2\right)-S_n\left(t_1\right)\right)+{\mathbb{E}}_{S_n\left(u\right)}\left[{\int }_{t_1^{\left(n\right)}}^{t_2^{\left(n\right)}}|\sigma \left(S_n\left(t\right)\right)\theta {|}^{g\left(S_n\left(t\right)\right)}dt\right]\right\}\right]\ge 1.\end{array}$$

Thus, we have

$$\begin{array}{ccc}\hfill {\mathbb{E}}_{S\left(u\right)}\left[e^{i\theta (S\left(t_2\right)-S\left(t_1\right))}\right]& \ge & exp\left\{-{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}|\sigma \left(S\left(t\right)\right)\theta {|}^{g\left(S\right(t\left)\right)}dt\right]\right\}.\hfill \end{array}$$

(31)

By the Billingsley inequality and (31), it is easy to see that, for all $x>0,$

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S\left(t_2\right)-S\left(t_1\right)|\ge x\right)& \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}\left(1-{\mathbb{E}}_{S\left(u\right)}\left[e^{i\theta \left(S\left(t_2\right)-S\left(t_1\right)\right)}\right]\right)d\theta \hfill \\ & \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}\left(1-exp\left\{-{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}|\sigma \left(S\left(t\right)\right)\theta {|}^{g\left(S\right(t\left)\right)}dt\right]\right\}\right)d\theta \hfill \\ & \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}|\sigma \left(S\left(t\right)\right)\theta {|}^{g\left(S\right(t\left)\right)}dt\right]d\theta \hfill \\ & =& {\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}|\sigma \left(S\left(t\right)\right)\theta {|}^{g\left(S\right(t\left)\right)}d\theta dt\right]\hfill \\ & =& {\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\displaystyle \frac{2^{g\left(S\right(t\left)\right)+1}}{g\left(S\right(t\left)\right)+1}}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]\hfill \\ & \le & max\left\{{\displaystyle \frac{2^{a+1}}{a+1}},{\displaystyle \frac{2^{b+1}}{b+1}}\right\}{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right].\hfill \end{array}$$

The last two inequalities represent the desired outcome. □

Remark 2. 

Let us comment on Property 2.

1. 

The order $\mathbb{E}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right],x\to \infty ,$ of Property 2 is the best possible. Indeed, assume $[a,b]\in (0,2)$ and set

$$T\left(x\right)=\mathbb{E}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{x}}\right)}^{g\left(S\right(t\left)\right)}{C}_{\alpha \left(g\right(S\left(t\right)\left)\right)}dt\right],t_2>t_1,$$

where $C_u$ is defined by (3). By an argument similar to that of Ayache [13], we can prove that

$$\begin{array}{c}\hfill \underset{x\to \infty }{lim}\mathbb{P}\left(|S\left(t_2\right)-S\left(t_1\right)|\ge x\right)/T\left(x\right)=1.\end{array}$$

(32)

Since the two functions $\sigma {\left(x\right)}^{g\left(x\right)},x\in \mathbb{R},$ and $C_u,u\in [a,b],$ are bounded, $T\left(x\right)$ is of the order $\mathbb{E}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]$ as $x\to \infty ,$ which represents the best possible order of convergence.

2. 

Property 2 demonstrates that if the stock-market prices are self-stabilizing processes, then investments originating from points with larger stability indices are safer than those originating from points with smaller stability indices.

In mathematical terms, if $g\left(S\left(t_1\right)\right)\ge g\left(S\left(t_2\right)\right),$ then we have

$$\mathbb{E}\left[{\int }_{t_1}^{t_1+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]\le \mathbb{E}\left[{\int }_{t_2}^{t_2+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]$$

for any $z\ge 0$ and any $x\ge 1.$ Indeed, if $g\left(S(t_1+s)\right)>g\left(S(t_2+s)\right),s\in [0,z],$ then it is obvious that

$$\mathbb{E}\left[{\int }_{t_1}^{t_1+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]<\mathbb{E}\left[{\int }_{t_2}^{t_2+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]$$

for any $x\ge 1.$ Otherwise, since S is stochastic continuous (cf. Property 5) and $g(·)$ is a Hölder function, there almost surely exists a point $s_0\in [0,z]$ such that $g\left(S(t_1+s_0)\right)=g\left(S(t_2+s_0)\right)$ and $g\left(S(t_1+s)\right)>g\left(S(t_2+s)\right)$ for any $s\in [0,s_0).$ Hence, it holds for all $x\ge 1,$

$$\begin{array}{c}\hfill \mathbb{E}\left[{\int }_{t_1}^{t_1+s_0}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]\le \mathbb{E}\left[{\int }_{t_2}^{t_2+s_0}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right].\end{array}$$

(33)

By the construction of $S,$ it is obvious that

$$\mathbb{P}\left(S\left(t\right)\le x\right)=\mathbb{P}\left(S(t_0+t)-S\left(t_0\right)\le x|S\left(t_0\right)=g\left(0\right)\right),x\in \mathbb{R}.$$

Hence, for $x\ge 1,$

$$\begin{array}{c}\hfill \mathbb{E}\left[{\int }_{t_1+s_0}^{t_1+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]=\mathbb{E}\left[{\int }_{t_2+s_0}^{t_2+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right].\end{array}$$

(34)

Thus, (33) and (34) imply that

$$\begin{array}{ccc}\hfill \mathbb{E}\left[{\int }_{t_1}^{t_1+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]& =& \mathbb{E}\left[{\int }_{t_1}^{t_1+s_0}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]+\mathbb{E}\left[{\int }_{t_1+s_0}^{t_1+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]\hfill \\ & \le & \mathbb{E}\left[{\int }_{t_2}^{t_2+s_0}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]+\mathbb{E}\left[{\int }_{t_2+s_0}^{t_2+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]\hfill \\ & =& \mathbb{E}\left[{\int }_{t_2}^{t_2+z}{\left({\displaystyle \frac{1}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right].\hfill \end{array}$$

3.2. Absolute Moments

The following property gives some sharp estimations for the absolute moments of the self-stabilizing and self-scaling process.

Property 3. 

Let ${\lambda }_0$ be the positive value such that

$${\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{{\lambda }_0}}\right)}^{g\left(S\right(t\left)\right)}dt\right]=1.$$

For all $\gamma \in (0,a)$ and all $t_1,t_2,u\in [0,1]$ such that $t_2\ge t_1\ge u,$ it holds

$$\begin{array}{ccc}\hfill {\mathbb{E}}_{S\left(u\right)}\left[|S\left(t_2\right)-S\left(t_1\right){|}^{\gamma }\right]& \le & C{\displaystyle \frac{1}{a-\gamma }}{\lambda }_0^{\gamma },\hfill \end{array}$$

(35)

where C is a constant depending on a and $b.$ In particular, it implies that

$$\begin{array}{ccc}\hfill \mathbb{E}\left[|S\left(t_2\right)-S\left(t_1\right){|}^{\gamma }\right]& \le & C{\displaystyle \frac{1}{a-\gamma }}{\lambda }_0^{\gamma }\hfill \end{array}$$

(36)

and

$$\begin{array}{ccc}\hfill \underset{\gamma \to a-}{lim}(a-\gamma )\mathbb{E}\left[|S\left(t_2\right)-S\left(t_1\right){|}^{\gamma }\right]\le C{\lambda }_0^a& <& \infty .\hfill \end{array}$$

(37)

Proof. 

By Property 2, it is easy to see that, for all $\gamma \in (0,a)$ and all $t_1,t_2,u\in [0,1]$ such that $t_2\ge t_1\ge u,$

$$\begin{array}{ccc}& & {\mathbb{E}}_{S\left(u\right)}\left[|S\left(t_2\right)-S\left(t_1\right){|}^{\gamma }\right]\hfill \\ & & =\gamma {\int }_0^{\infty }{x}^{\gamma -1}{\mathbb{P}}_{S\left(u\right)}\left(|S\left(t_2\right)-S\left(t_1\right)|\ge x\right)dx\hfill \\ & & \le \gamma \left({\int }_0^{{\lambda }_0}{x}^{\gamma -1}dx+{\int }_{{\lambda }_0}^{\infty }{x}^{\gamma -1}C{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{x}}\right)}^{g\left(S\right(t\left)\right)}dt\right]dx\right)\hfill \\ & & ={\lambda }_0^{\gamma }+C{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\int }_{{\lambda }_0}^{\infty }{x}^{\gamma -1-g\left(S\right(t\left)\right)}{\left(\sigma \left(S\right(t\left)\right)\right)}^{g\left(S\right(t\left)\right)}dxdt\right]\hfill \\ & & ={\lambda }_0^{\gamma }+C{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\displaystyle \frac{{\lambda }_0^{\gamma -g\left(S\right(t\left)\right)}}{g\left(S\right(t\left)\right)-\gamma }}{\left(\sigma \left(S\right(t\left)\right)\right)}^{g\left(S\right(t\left)\right)}dt\right]\hfill \\ & & \le {\lambda }_0^{\gamma }+C{\displaystyle \frac{{\lambda }_0^{\gamma }}{a-\gamma }}{\mathbb{E}}_{S\left(u\right)}\left[{\int }_{t_1}^{t_2}{\left({\displaystyle \frac{\sigma \left(S\right(t\left)\right)}{{\lambda }_0}}\right)}^{g\left(S\right(t\left)\right)}dt\right]\hfill \\ & & \le C_1{\displaystyle \frac{1}{a-\gamma }}{\lambda }_0^{\gamma },\hfill \end{array}$$

(38)

where C and $C_1$ are constants depending on a and $b.$ □

When $g\equiv a$ and $\sigma$ is a constant, without loss of generality, let $\sigma \equiv 1$. Then, $S\left(t\right)$ is a standard symmetric $a$–stable Lévy motion. Thus, we have

$$S\left(t_1\right)-S\left(t_2\right)\sim S_a\left(\right|t_1-t_2{|}^{1/a},0,0)$$

and

$$\begin{array}{ccc}\hfill \underset{\gamma \to a-}{lim}(a-\gamma )\mathbb{E}\left[{\left|X\right|}^{\gamma }\right]& =& a{C}_a|t_1-t_2|,\hfill \end{array}$$

(39)

where $C_a$ is defined by (3) and is a constant depending only on a (cf. Property 1.2.18 of Samorodnitsky and Taqqu [14]). Thus, the $\gamma$ in inequality (35) cannot equal or larger than $a.$

Property 4. 

For all $\gamma \in (0,a)$ and all $u\in [0,1),$ it holds

$$\begin{array}{ccc}\hfill {\mathbb{E}}_{S\left(u\right)}\left[{|S(u+r)-S\left(u\right)|}^{\gamma }\right]& \sim & {\displaystyle \frac{2^{\gamma -1}\Gamma \left(1-\frac{\gamma }{g\left(S\right(u\left)\right)}\right)}{\gamma {\int }_0^{\infty }{u}^{-\gamma -1}{sin}^2\left(u\right)du}}|\sigma \left(S\left(u\right)\right){|}^{\gamma }{r}^{{\displaystyle \frac{\gamma }{g\left(S\right(u\left)\right)}}},r\to 0+.\hfill \end{array}$$

where $\Gamma \left(t\right)={\int }_0^{\infty }{x}^{t-1}{e}^{-x}dx$ is the gamma function. In particular, it implies that

$$\begin{array}{ccc}& & \mathbb{E}\left[{|S(u+r)-S\left(u\right)|}^{\gamma }\right]\hfill \\ & & \sim {\displaystyle \frac{2^{\gamma -1}}{\gamma {\int }_0^{\infty }{u}^{-\gamma -1}{sin}^2\left(u\right)du}}\mathbb{E}\left[\Gamma \left(1-{\displaystyle \frac{\gamma }{g\left(S\right(u\left)\right)}}\right)|\sigma \left(S\left(u\right)\right){|}^{\gamma }{r}^{{\displaystyle \frac{\gamma }{g\left(S\right(u\left)\right)}}}\right],r\to 0+.\hfill \end{array}$$

Proof. 

Notice that, for all $\gamma \in (0,a)$ and all $u\in [0,1),$

$$\begin{array}{c}\hfill {\mathbb{E}}_{S\left(u\right)}\left[|{\displaystyle \frac{S(u+r)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}{|}^{\gamma }\right]=\gamma {\int }_0^{\infty }{x}^{\gamma -1}{\mathbb{P}}_{S\left(u\right)}\left(\left|{\displaystyle \frac{S(u+r)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}\right|\ge x\right)dx.\end{array}$$

Recall that S is localizable at u to a $g\left(S\right(u\left)\right)$–stable Lévy motion $\sigma \left(S\left(u\right)\right)L_{g\left(S\right(u\left)\right)}\left(t\right)$ under the conditional expectation given $S\left(u\right)$. Thus

$${\mathbb{P}}_{S\left(u\right)}\left(\left|{\displaystyle \frac{S(u+r)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}\right|\ge x\right)\to {\mathbb{P}}_{S\left(u\right)}\left(\left|\sigma \left(S\left(u\right)\right)L_{g\left(S\right(u\left)\right)}\left(1\right)\right|\ge x\right).$$

By Property 1, for x large enough,

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{S\left(u\right)}\left(\left|{\displaystyle \frac{S(u+r)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}\right|\ge x\right)& \le & C{\displaystyle \frac{1}{x^a{r}^{a/g\left(S\right(u\left)\right)}}}.\hfill \end{array}$$

Hence, by Lebesgue dominated convergence theorem, we have

$$\begin{array}{ccc}\hfill \underset{r\to 0+}{lim}{\mathbb{E}}_{S\left(u\right)}\left[|{\displaystyle \frac{S(u+r)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}{|}^{\gamma }\right]& =& \gamma {\int }_0^{\infty }{x}^{\gamma -1}{\mathbb{P}}_{S\left(u\right)}\left(\left|\sigma \left(S\left(u\right)\right)L_{g\left(S\right(u\left)\right)}\left(1\right)\right|\ge x\right)dx\hfill \\ & =& {\mathbb{E}}_{S\left(u\right)}\left[|\sigma \left(S\left(u\right)\right)L_{g\left(S\right(u\left)\right)}\left(1\right){|}^{\gamma }\right]\hfill \\ & =& |\sigma \left(S\left(u\right)\right){|}^{\gamma }{\displaystyle \frac{2^{\gamma -1}\Gamma \left(1-\frac{\gamma }{g\left(S\right(u\left)\right)}\right)}{\gamma {\int }_0^{\infty }{u}^{-\gamma -1}{sin}^2\left(u\right)du}}.\hfill \end{array}$$

We refer to page 18 of Samorodnitsky and Taqqu [14] for the last line. □

3.3. Stochastic Hölder Continuity

We call a random process $S\left(u\right)$, u in an interval $I\subset \mathbb{R}$, is stochastic Hölder continuous of exponent $\beta \in (0,1],$ if it holds

$$\underset{|u-r|\to 0,u\ne r}{lim\; sup}\mathbb{P}\left(|S\left(u\right)-S\left(r\right)|\ge {C|u-r|}^{\beta }\right)=0$$

for a positive constant $C.$ It is obvious that if $S\left(u\right)$ is stochastic Hölder continuous of exponent ${\beta }_1\in (0,1],$ then $S\left(u\right)$ is stochastic Hölder continuous of exponent ${\beta }_2\in (0,{\beta }_1].$ Stochastic Hölder continuity implies continuity in probability, that is, for any $ϵ>0$ and $r\in I$ it holds that ${lim}_{h\to 0}\mathbb{P}\left(\left|S\right(r+h)-S(r\left)\right|>ϵ\right)=0.$

Example 1. 

Assume that a random process $S\left(u\right),u\in I,$ satisfies the following condition: there exists three strictly positive constants $\gamma ,c,\rho$ such that

$$\mathbb{E}\left[{|S\left(u\right)-S\left(r\right)|}^{\gamma }\right]\le c{|u-r|}^{\rho },u,r\in I.$$

Then, $S\left(u\right),u\in I,$ is stochastic Hölder continuous of exponent $\beta \in (0,min\{1,\rho /\gamma \left\}\right).$ Indeed, it is easy to see that, for $u,r\in I,$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(|S\left(u\right)-S\left(r\right)|\ge {C|u-r|}^{\beta }\right)& \le & {\displaystyle \frac{\mathbb{E}\left[{|S\left(u\right)-S\left(r\right)|}^{\gamma }\right]}{C^{\gamma }{|u-r|}^{\beta \gamma }}}\hfill \\ & \le & {\displaystyle \frac{c}{C^{\gamma }}}{|u-r|}^{\rho -\beta \gamma },\hfill \end{array}$$

which implies our claim.

The following theorem shows that the process S is stochastic Hölder continuous.

Property 5. 

For all $t_1,t_2,u\in [0,1]$ and all $t_1,t_2\ge u$, it holds

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S\left(t_1\right)-S\left(t_2\right)|\ge |t_1-t_2{|}^{\beta }\right)& \le & C|t_1-t_2{|}^{1-b\beta },\hfill \end{array}$$

(40)

where C is a constant depending on $M,a$ and $b.$ In particular, it implies that

$$\begin{array}{ccc}\hfill \mathbb{P}\left(|S\left(t_1\right)-S\left(t_2\right)|\ge |t_1-t_2{|}^{\beta }\right)& \le & C|t_1-t_2{|}^{1-b\beta },\hfill \end{array}$$

(41)

which means S is stochastic Hölder continuous of exponent $\beta \in (0,min\{1,1/b\left\}\right)$.

Proof. 

Taking $x=|t_1-t_2{|}^{\beta }$ in (30), we obtain the required inequality (40). □

3.4. Markov Process

It is easy to see that $S_n$ in the proof of Theorem 1 is a Markov process. Thus, it is natural to guess that the self-stabilizing and self-scaling process is also a Markov process. To determine whether this is the case, we need the following theorem:

Theorem 2. 

Assume that ${\left(S_n\left(t\right)\right)}_{n\ge 1},t\in [0,1],$ is a sequence of Markov processes. If $S_n\left(t\right)$ converges to a process $S\left(t\right),t\in [0,1],$ in finite dimensional distributions, then S is a Markov process.

Proof. 

We only need show that for any $d\in \mathbb{N},$$t_1,t_2,\dots ,t_d\in [0,1]$ and $t_1<t_2<\dots <t_d,$ it holds for any Borel set $B\subset \mathbb{R},$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(S\left(t_d\right)\in B|S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_{d-1}\right)\right)& =& \mathbb{P}\left(S\left(t_d\right)\in B|S\left(t_{d-1}\right)\right),\hfill \end{array}$$

(42)

or $\mathbb{E}\left[{\mathbf{1}}_{\{S\left(t_d\right)\in B\}}\right|S\left(t_{d-1}\right)]=\mathbb{E}\left[{\mathbf{1}}_{\{S\left(t_d\right)\in B\}}\right|S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_{d-1}\right)].$ Notice that $S_n\left(t\right),t\in [0,1],$ is a Markov process. Thus

$$\begin{array}{ccc}\hfill \mathbb{P}\left(S_n\left(t_d\right)\in B|S_n\left(t_1\right),S_n\left(t_2\right),\dots ,S_n\left(t_{d-1}\right)\right)& =& \mathbb{P}\left(S_n\left(t_d\right)\in B|S_n\left(t_{d-1}\right)\right).\hfill \end{array}$$

(43)

For any two Borel sets $A_1\subset {\mathbb{R}}^{d-2}$ and $A_2\subset \mathbb{R}$ such that

$$\mathbb{P}\left(\left(S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_{d-1}\right),S\left(t_d\right)\right)\in A_1\times A_2\times B\right)>0,$$

by (43), it is easy to see that

$$\begin{array}{ccc}\hfill \mathbb{E}\left[{\mathbf{1}}_{\{S\left(t_d\right)\in B\}}{\mathbf{1}}_{\{S\left(t_{d-1}\right)\in A_2\}}\right]& =& \underset{n\to \infty }{lim}\mathbb{E}\left[{\mathbf{1}}_{\{S_n\left(t_d\right)\in B\}}{\mathbf{1}}_{\{S_n\left(t_{d-1}\right)\in A_2\}}\right]\hfill \\ & =& \underset{n\to \infty }{lim}\mathbb{E}\left[{\mathbf{1}}_{\{S_n\left(t_d\right)\in B\}}{\mathbf{1}}_{\{(S_n\left(t_1\right),S_n\left(t_2\right),\dots ,S_n\left(t_{d-1}\right))\in A_1\times A_2\}}\right]\hfill \\ & =& \mathbb{E}\left[{\mathbf{1}}_{\{S\left(t_d\right)\in B\}}{\mathbf{1}}_{\{(S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_{d-1}\right))\in A_1\times A_2\}}\right],\hfill \end{array}$$

which means $\mathbb{E}\left[{\mathbf{1}}_{\{S\left(t_d\right)\in B\}}\right|S\left(t_{d-1}\right)]=\mathbb{E}\left[{\mathbf{1}}_{\{S\left(t_d\right)\in B\}}\right|S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_{d-1}\right)].$ □

Since that there exists a subsequence ${\left(n_k\right)}_{k\ge 1}$ of $\mathbb{N}$ such that

$$\left(S_{n_k}\left(t_1\right),S_{n_k}\left(t_2\right),\dots ,S_{n_k}\left(t_d\right)\right)\to \left(S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_d\right)\right)$$

in distribution. Thus, by Theorem 2, we have the following property.

Property 6. 

The process $S\left(t\right),t\in [0,1],$ is a Markov process.

3.5. Strongly Localizability

We have proven that S is localizable under certain conditional expectations in the proof of Theorem 1. In the following theorem, we prove that S is strongly localizable under the conditional expectation given as $S\left(u\right).$

Let $D[0,1]$ be the set of càdlàg functions on $[0,1]$—that is, functions which are continuous on the right and have left limits at all $t\in [0,1],$ and are endowed with the Skorohod metric $d_S$ [12]. If X and $X_t^{\prime }$ have versions in $D[0,1]$ and convergence in (1) is in distribution with respect to $d_S$, then X is said to be $h–$strongly localizable at t with strong local form $X_t^{\prime }$.

Property 7. 

The process $S\left(t\right),t\in [0,1],$ is strongly localizable at u to a $g\left(S\right(u\left)\right)$–stable Lévy motion $L_{g\left(S\right(u\left)\right)}(·)$ under the conditional expectation given as $S\left(u\right)$.

Proof. 

For any $u\in [0,1),$ define

$$S_r\left(x\right)={\displaystyle \frac{S(u+rx)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}},r,u\in (0,1].$$

We only need to prove the tightness. By Theorem 15.6 of Billingsley [12], it suffices to show that, for some $\beta >1$ and $\tau \ge 0$,

$$\begin{array}{c}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S_r\left(x\right)-S_r\left(x_1\right)|\ge \lambda ,|S_r\left(x_2\right)-S_r\left(x\right)|\ge \lambda \right)\le {\displaystyle \frac{C}{{\lambda }^{\tau }}}{\left[x_2-x_1\right]}^{\beta }\end{array}$$

(44)

for $x_1\le x\le x_2,\lambda >0$ and $r\in (0,1]$, where C is a positive constant. Since $S\left(x\right)$ is a Markov process with respect to x, then $S_r\left(x\right)$ is a Markov process with respect to x. Hence, it follows that

$$\begin{array}{ccc}& & {\mathbb{P}}_{S\left(u\right)}\left(|S_r\left(x\right)-S_r\left(x_1\right)|\ge \lambda ,|S_r\left(x_2\right)-S_r\left(x\right)|\ge \lambda \right)\hfill \\ & & ={\mathbb{P}}_{S\left(u\right)}\left(|S_r\left(x\right)-S_r\left(x_1\right)|\ge \lambda \right){\mathbb{P}}_{S\left(u\right)}\left(|S_r\left(x_2\right)-S_r\left(x\right)|\ge \lambda \left|\right|S_r\left(x\right)-S_r\left(x_1\right)|\ge \lambda \right).\hfill \end{array}$$

By the Billingsley inequality (cf. p. 47 of [12]), (29) and (30), we have

$$\begin{array}{c}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S_r\left(x\right)-S_r\left(x_1\right)|\ge \lambda \right)\le {\displaystyle \frac{C_1}{{\lambda }^{\gamma }}}\left[x-x_1\right],\end{array}$$

(45)

where $\gamma =a{\mathbf{1}}_{[1,\infty )}\left(\lambda \right)+b{\mathbf{1}}_{(0,1)}\left(\lambda \right)$ and $C_1$ is a positive constant depending only on $M,a$ and $b.$ By a similar argument, we have

$$\begin{array}{c}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S_r\left(x_2\right)-S_r\left(x\right)|\ge \lambda |S_r\left(x\right),S_r\left(x_1\right)\right)\le {\displaystyle \frac{C_2}{{\lambda }^{\gamma }}}\left[x_2-x\right].\end{array}$$

(46)

Thus

$$\begin{array}{c}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S_r\left(x_2\right)-S_r\left(x\right)|\ge \lambda \left|\right|S_r\left(x\right)-S_r\left(x_1\right)|\ge \lambda \right)\le {\displaystyle \frac{C_2}{{\lambda }^{\gamma }}}\left[x_2-x\right].\end{array}$$

Using the inequality $xy\le {(x+y)}^2/4,$$x,y\ge 0,$ we have

$$\begin{array}{c}\hfill {\mathbb{P}}_{S\left(u\right)}\left(|S_r\left(x\right)-S_r\left(x_1\right)|\ge \lambda ,|S_r\left(x_2\right)-S_r\left(x\right)|\ge \lambda \right)\le {\displaystyle \frac{C_1{C}_2}{4{\lambda }^{2\gamma }}}{\left[x_2-x_1\right]}^2,\end{array}$$

(47)

which gives inequality (44). □

3.6. Self-Regulating Process

The pointwise Hölder exponent at t of a stochastic process (or continuous function) $S:\mathbb{R}\to \mathbb{R}$ is the number ${\alpha }_S\left(t\right)$ such that

$$\begin{array}{c}\hfill {\alpha }_S\left(t\right)=sup\left\{\beta :\underset{h\to 0}{lim\; sup}{\displaystyle \frac{\left|S\right(t+h)-S(t\left)\right|}{{\left|h\right|}^{\beta }}}=0\mathrm{almost}\mathrm{surely}\right\}.\end{array}$$

(48)

A random process $S=S\left(t\right)$ is called a self-regulating process if there exists a function $g\left(x\right):\mathbb{R}\to [\alpha ,\beta ]\subset \mathbb{R}$ such that, at each point t, almost surely,

$$\begin{array}{c}\hfill {\alpha }_S\left(t\right)=g\left(S\left(t\right)\right).\end{array}$$

(49)

The self-regulating processes were introduced by Barrière, Echelard and Lévy Véhel [15], in work in which the authors established two self-regulating multi-fractional Brownian motions (srmBm) via methods of fixed-point theory and random midpoint displacement, respectively.

From Property 7, we see that, for $u\in (0,1],$

$${\displaystyle \frac{S(u+rx)-S\left(u\right)}{r^{1/g\left(S\right(u\left)\right)}}}\to \sigma \left(S\left(u\right)\right)L_{g\left(S\right(u\left)\right)}\left(x\right),r\to 0,$$

in distribution ${\mathbb{P}}_{S\left(u\right)}$ with respect to $d_S$; thus, the following property is obvious.

Property 8. 

The process $S\left(t\right),t\in [0,1],$ is a self-regulating process.

3.7. Martingale

Since $S_n$ is a martingale when $a>1$, we guess that process S is also a martingale when $a>1$. We prove this claim in the following theorem.

Property 9. 

If $a>1$, then the process $S\left(t\right),t\in [0,1],$ is a martingale.

Proof. 

By Property 3, it follows that, for any $t\in [0,1],$

$$\begin{array}{c}\hfill \mathbb{E}\left[\left|S\right(t\left)\right|\right]<\infty ,\end{array}$$

(50)

where C is a constant depending on $M,a$ and $b.$ We only need to verify that for any $d\in \mathbb{N},$$t_1,t_2,\dots ,t_d\in [0,1]$ and $t_1<t_2<\dots <t_d,$ it holds

$$\begin{array}{ccc}\hfill \mathbb{E}\left[S\left(t_d\right)|S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_{d-1}\right)\right]& =& S\left(t_{d-1}\right).\hfill \end{array}$$

(51)

By an argument similar to that of (23), we have, for all $({\theta }_j,t_j)\in \mathbb{R}\times [0,1],j=1,2,\dots ,d,$

$$\begin{array}{ccc}\hfill {\mathbb{E}}_{S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_{d-1}\right)}\left[exp\left\{i\theta \left(S\left(t_d\right)-S\left(t_{d-1}\right)\right)+\int |\theta \sigma \left(S\left(z\right)\right){\mathbf{1}}_{[t_{j-1},t_j]}\left(z\right){|}^{g\left(S\right(z\left)\right)}dz\right\}\right]& =& 1.\hfill \end{array}$$

Taking the derivative with respect to $\theta$ on both sides of the last equality, it follows that

$$\begin{array}{c}\hfill {\mathbb{E}}_{S\left(t_1\right),S\left(t_2\right),\dots ,S\left(t_{d-1}\right)}[exp\left\{i\theta \left(S\left(t_d\right)-S\left(t_{d-1}\right)\right)+\int |\theta \sigma \left(S\left(z\right)\right){\mathbf{1}}_{[t_{j-1},t_j]}\left(z\right){|}^{g\left(S\right(z\left)\right)}dz\right\}\\ \hfill \times \left(i\left(S\left(t_d\right)-S\left(t_{d-1}\right)\right)+\int g\left(S\left(z\right)\right)\sigma {\left(S\left(z\right)\right)}^{g\left(S\right(z\left)\right)}|\theta {\mathbf{1}}_{[t_{j-1},t_j]}\left(z\right){|}^{g\left(S\right(z\left)\right)-1}dz\right)]=0.\end{array}$$

(52)

Notice that $g\left(S\right(z\left)\right)-1\ge a-1>0.$ Taking $\theta =0$ in equality (52), we obtain (51). □

4. Conclusions

Using a general version of the Arzelà–Ascoli theorem and a Donsker-type construction, we prove the existence of the self-stabilizing and self-scaling process. This type of process is localizable at t, with a $g\left(S\right(t\left)\right)$–stable tangent process. Thus, the “local intensities of jumps” vary with the values of the process. Moreover, we also show that the self-stabilizing processes have many other good properties, such as stochastic Hölder continuity and strong localizability. In particular, this type of self-stabilizing process is simultaneously a Markov process, a martingale (when the local index of stability is greater than 1), a self-scaling process and a self-regulating process.

Appendix A.1. Weak Convergence Theorems for Random Vectors

Using the Arzelà–Ascoli theorem and the Lévy continuous theorem, we obtain the following two sufficient conditions for a sequence of random vectors to have a subsequence that converges in distribution.

Denote by $⟨x,y⟩$ the scalar product of two vectors $x=\left(x^{\left(i\right)}\right),y=\left(y^{\left(i\right)}\right)\in {\mathbb{R}}^d,$ i.e.,

$$⟨x,y⟩=\sum _{i=1}^d{x}^{\left(i\right)}{y}^{\left(i\right)},$$

and by $\left|\right|x\left|\right|$ the magnitude of a vector $x,$ i.e., ${\left|\right|x\left|\right|}^2=⟨x,x⟩.$

Theorem A1. 

Let ${\left(X_n\right)}_{n\ge 1}$ be a sequence of real-valued random vectors with values in ${\mathbb{R}}^d$. Assume that

$$\begin{array}{c}\hfill \underset{\left|\right|\theta \left|\right|\to 0}{lim}\mathbb{E}\left[|e^{i⟨\theta ,X_n⟩}-1|\right]=0,\theta \in {\mathbb{R}}^d,\end{array}$$

(A1)

uniformly for all $n\ge 1.$ Denote by

$$\begin{array}{c}\hfill f_n\left(\theta \right)=\mathbb{E}\left[e^{i⟨\theta ,X_n⟩}\right],\theta \in {\mathbb{R}}^d,\end{array}$$

(A2)

the characteristic function of $X_n.$ Then, ${\left(f_n\right)}_{n\ge 1}$ is equicontinuous. Therefore, there exist a subsequence ${\left(X_{n_k}\right)}_{k\ge 1}$ and a random vector X such that $X_{n_k}\to X$ in distribution.

Proof. 

We first give a proof for the case of $d=1.$ For all ${\theta }_1,{\theta }_2\in \mathbb{R},$ it is easy to see that

$$\begin{array}{ccc}\hfill |\mathbb{E}\left[e^{i{\theta }_1{X}_n}\right]-\mathbb{E}\left[e^{i{\theta }_2{X}_n}\right]|& =& \left|\mathbb{E}\left[e^{i{\theta }_1{X}_n}\left(1-e^{i({\theta }_2-{\theta }_1)X_n}\right)\right]\right|\hfill \\ & \le & \mathbb{E}\left[|1-e^{i({\theta }_2-{\theta }_1)X_n}|\right].\hfill \end{array}$$

Since

$$|1-e^{i({\theta }_2-{\theta }_1)X_n}|\le 2\mathrm{and}\underset{\theta \to 0}{lim}\mathbb{E}\left[|e^{i\theta X_n}-1|\right]=0,$$

by Lebesgue’s dominated convergence theorem and (A1), we find that ${\left(f_n\right)}_{n\ge 1}$ is equicontinuous. Let $f_{{\sigma }_0\left(n\right)}\left(\theta \right)=f_n\left(\theta \right)$ for all $n\ge 1.$ For all $N\ge 1,$ by the Arzelà–Ascoli theorem, there exists a subsequence of ${\left(f_{{\sigma }_{N-1}\left(n\right)}\left(\theta \right)\right)}_{n\ge 1},$ denoted as ${\left(f_{{\sigma }_N\left(n\right)}\left(\theta \right)\right)}_{n\ge 1},$ and a function $f\left(\theta \right)$ defined on $\theta \in \mathbb{R}$ such that ${lim}_{n\to \infty }{f}_{{\sigma }_N\left(n\right)}\left(\theta \right)=f\left(\theta \right)$ uniformly on $\theta \in [-N,N].$ By induction, the following relation holds:

$${\left(f_n\left(\theta \right)\right)}_{n\ge 1}\supseteq {\left(f_{{\sigma }_1\left(n\right)}\left(\theta \right)\right)}_{n\ge 1}\supseteq \dots \supseteq {\left(f_{{\sigma }_{N-1}\left(n\right)}\left(\theta \right)\right)}_{n\ge 1}\supseteq {\left(f_{{\sigma }_N\left(n\right)}\left(\theta \right)\right)}_{n\ge 1}\supseteq \dots$$

Define the diagonal subsequence ${\left(f_{{\sigma }_N\left(N\right)}\left(\theta \right)\right)}_{N\ge 1}$ whose Nth term is the Nth term in the Nth subsequence $\left(f_{{\sigma }_N\left(n\right)}\left(\theta \right)\right)$. Then, the diagonal subsequence ${\left(f_{{\sigma }_N\left(N\right)}\left(\theta \right)\right)}_{N\ge 1}$ converges to $f\left(\theta \right)$ on $\theta \in \mathbb{R}.$ Condition (A1) implies that for any $\epsilon >0,$ there exists a $\delta >0$ such that

$$\begin{array}{c}\hfill \mathbb{E}\left[|e^{i\theta X_n}-1|\right]\le \epsilon \end{array}$$

(A3)

uniformly for all n and all $\left|\theta \right|\le \delta .$ In particular, since $\epsilon$ can be any small, inequality (A3) implies that

$$\begin{array}{c}\hfill \underset{\theta \to 0}{lim}\underset{n\to \infty }{lim\; sup}\mathbb{E}\left[|e^{i\theta X_n}-1|\right]=0.\end{array}$$

(A4)

Moreover, by (A4),

$$\begin{array}{ccc}\hfill \underset{\theta \to 0}{lim}|f\left(\theta \right)-1|& =& \underset{\theta \to 0}{lim}|\underset{N\to \infty }{lim}{f}_{{\sigma }_N\left(N\right)}\left(\theta \right)-1|\hfill \\ & \le & \underset{\theta \to 0}{lim}\underset{N\to \infty }{lim\; sup}\mathbb{E}\left[|e^{i\theta X_{{\sigma }_N\left(N\right)}}-1|\right]\hfill \\ & =& 0,\hfill \end{array}$$

(A5)

which means $f\left(\theta \right)$ is continuous at $0.$ By the Lévy continuous theorem, these exists a random variable X such that $X_{{\sigma }_N\left(N\right)}$ converges to X in distribution as $N\to \infty .$

The proof for the case of $d>1$ is very simple. Note the fact that, for all ${\theta }_1,{\theta }_2\in {\mathbb{R}}^d,$

$$\begin{array}{ccc}\hfill |\mathbb{E}\left[e^{i⟨{\theta }_1,X_n⟩}\right]-\mathbb{E}\left[e^{i⟨{\theta }_2,X_n⟩}\right]|& =& \left|\sum _{j=1}^d\mathbb{E}\left[e^{i\left({\sum }_{k=1}^j{\theta }_1^{\left(k\right)}{X}_n^{\left(k\right)}+{\sum }_{k=j+1}^d{\theta }_2^{\left(k\right)}{X}_n^{\left(k\right)}\right)}\left(1-e^{i({\theta }_2^{\left(j\right)}-{\theta }_1^{\left(j\right)})X_n^{\left(j\right)}}\right)\right]\right|\hfill \\ & \le & \sum _{j=1}^d\mathbb{E}\left[|1-e^{i({\theta }_2^{\left(j\right)}-{\theta }_1^{\left(j\right)})X_n^{\left(j\right)}}|\right].\hfill \end{array}$$

Recall that ${\left(f_n\right)}_{k\ge 1}$ is equicontinuous if and only if ${\left(f_n\right)}_{k\ge 1}$ is equicontinuous with respect to every coordinate. Hence ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is equicontinuous on $\theta \in {\mathbb{R}}^d.$ By an argument similar to the case of $d=1,$ there exists a subsequence ${\left(f_{{\sigma }_N\left(N\right)}\left(\theta \right)\right)}_{N\ge 1}$ converges to $f\left(\theta \right)$ on $\theta \in {\mathbb{R}}^d.$ By condition (A1),

$$\begin{array}{ccc}\hfill \underset{\left|\right|\theta \left|\right|\to 0}{lim}|f\left(\theta \right)-1|& =& \underset{\left|\right|\theta \left|\right|\to 0}{lim}|\underset{N\to \infty }{lim}\mathbb{E}\left[e^{i⟨\theta ,X_{{\sigma }_N\left(N\right)}⟩}\right]-1|\hfill \\ & \le & \underset{\left|\right|\theta \left|\right|\to 0}{lim}\underset{N\to \infty }{lim\; sup}\mathbb{E}\left[|e^{i⟨\theta ,X_{{\sigma }_N\left(N\right)}⟩}-1|\right]\hfill \\ & =& 0,\hfill \end{array}$$

which means $f\left(\theta \right)$ is continuous at $0.$ By the Lévy continuous theorem again, these exists a random vector X such that $X_{{\sigma }_N\left(N\right)}$ converges to X in distribution as $N\to \infty .$ This completes the proof of the theorem. □

As an application of Theorem A1, consider the following example, which illustrates that a sequence of uniformly bounded random variables exists a subsequence that converges in distribution.

Example A3. 

Let ${\left(X_n\right)}_{n\ge 1}$ be a sequence of real-valued random vectors with values in ${\mathbb{R}}^d$. If $\left|\right|X_n\left|\right|\le C,$ for a constant C and uniformly for all $n,$ then there exist a subsequence ${\left(X_{n_k}\right)}_{k\ge 1}$ and a random vector X such that $X_{n_k}\to X$ in distribution. Indeed, it is easy to see that

$$\begin{array}{c}\hfill \underset{\left|\right|\theta \left|\right|\to 0}{lim}\mathbb{E}\left[|e^{i⟨\theta ,X_n⟩}-1|\right]\le \underset{\left|\right|\theta \left|\right|\to 0}{lim}\mathbb{E}\left[|⟨\theta ,X_n⟩|\right]\le \underset{\left|\right|\theta \left|\right|\to 0}{lim}\left|\right|\theta \left|\right|C=0,\theta \in {\mathbb{R}}^d,\end{array}$$

(A6)

uniformly for all $n\ge 1.$ Our conclusion follows from Theorem A1.

Since condition (A1) may not easy to verify, we introduce the second sufficient condition. This sufficient condition could be easier to check.

Theorem A2. 

Let ${\left(X_n\right)}_{n\ge 1}$ be a sequence of real-valued random vectors with values in ${\mathbb{R}}^d$. Denote the characteristic function of $X_n$ by $f_n\left(\theta \right),\theta \in {\mathbb{R}}^d.$ Assume that

$$\begin{array}{c}\hfill \underset{\left|\right|\theta \left|\right|\to 0}{lim}{f}_n\left(\theta \right)=1\end{array}$$

(A7)

uniformly for all $n\ge 1.$ Then, ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is equicontinuous. Therefore, there exist a subsequence ${\left(X_{n_k}\right)}_{k\ge 1}$ and a random vector X such that $X_{n_k}\to X$ in distribution.

Proof. 

We first give a proof for the case of $d=1.$ By the Billingsley inequality (cf. page 47 of [12]), it is easy to see that, for all $x>2,$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(\right|X_n|\ge x)& \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}\left(1-f_n\left(\theta \right)\right)d\theta .\hfill \end{array}$$

(A8)

Given any $\epsilon >0,$ by (A7), there is a constant $M=M\left(\epsilon \right)\ge 2$ such that for all $\left|\theta \right|\le 2/M,$

$$|1-f_n\left(\theta \right)|\le {\displaystyle \frac{\epsilon }{8}}.$$

Thus, for all $x\ge M,$

$$\begin{array}{ccc}\hfill \mathbb{P}\left(\right|X_n|\ge x)& \le & {\displaystyle \frac{x}{2}}{\int }_{-2/x}^{2/x}{\displaystyle \frac{\epsilon }{8}}d\theta \le {\displaystyle \frac{\epsilon }{4}}.\hfill \end{array}$$

(A9)

For all ${\theta }_1,{\theta }_2\in \mathbb{R},$ we have

$$\begin{array}{ccc}\hfill |f_n\left({\theta }_1\right)-f_n\left({\theta }_2\right)|& =& \left|\mathbb{E}\left[e^{i{\theta }_1{X}_n}\left(1-e^{i({\theta }_2-{\theta }_1)X_n}\right)\right]\right|\hfill \\ & \le & \mathbb{E}\left[|1-e^{i({\theta }_2-{\theta }_1)X_n}|\right].\hfill \end{array}$$

(A10)

The random variable $|1-e^{i({\theta }_2-{\theta }_1)X_n}|$ is dominated by the constant 2. Therefore, by the inequalities (A9) and (A10), it follows that, for all $x\ge 2,$

$$\begin{array}{ccc}\hfill |f_n\left({\theta }_1\right)-f_n\left({\theta }_2\right)|& \le & \mathbb{E}\left[|1-e^{i({\theta }_2-{\theta }_1)X_n}|{\mathbf{1}}_{\left\{\right|X_n|\le x\}}\right]+\mathbb{E}\left[|1-e^{i({\theta }_2-{\theta }_1)X_n}|{\mathbf{1}}_{\left\{\right|X_n|>x\}}\right]\hfill \\ & \le & \mathbb{E}\left[\left|({\theta }_2-{\theta }_1)X_n\right|{\mathbf{1}}_{\left\{\right|X_n|\le x\}}\right]+2\mathbb{E}\left[{\mathbf{1}}_{\left\{\right|X_n|>x\}}\right]\hfill \\ & \le & x|{\theta }_2-{\theta }_1|+2\mathbb{P}\left(\right|X_n|\ge x).\hfill \end{array}$$

(A11)

For this fixed $\epsilon ,$ from (A11), it is easy to see that

$$\begin{array}{ccc}\hfill |f_n\left({\theta }_1\right)-f_n\left({\theta }_2\right)|& \le & M|{\theta }_2-{\theta }_1|+2\mathbb{P}\left(\right|X_n|\ge M)\hfill \\ & \le & {\displaystyle \frac{\epsilon }{2}}+2{\displaystyle \frac{\epsilon }{4}}=\epsilon \hfill \end{array}$$

(A12)

uniformly for all n, whenever $|{\theta }_2-{\theta }_1|\le \epsilon /\left(2M\right).$ Hence, the family ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is equicontinuous. By the Arzelà–Ascoli theorem, with an argument similar to the proof of Theorem A1, there exist a subsequence ${\left(f_{{\sigma }_N\left(N\right)}\left(\theta \right)\right)}_{k\ge 1}$ and a continuous function $f\left(\theta \right)$ such that $f_{{\sigma }_N\left(N\right)}\left(\theta \right)\to f\left(\theta \right).$ Since $f_n\left(0\right)=1$ for all n, inequality (A12) implies that $\left|f\right(\theta )-1|\le \epsilon$ whenever $\left|\theta \right|\le \epsilon /\left(2M\right).$ Thus $f\left(\theta \right)$ is continuous at $0.$ By the Lévy continuous theorem, these exists a random variable X such that $X_{{\sigma }_N\left(N\right)}$ converges to X in distribution as $N\to \infty .$

For the case where $d>1,$ the proof is similar to that of Theorem A1. This completes the proof of the theorem. □

To illustrate Theorem A2, consider the following two examples.

Example A4. 

Let ${\left(X_n\right)}_{n\ge 1}$ be a sequence of real-valued random vectors with values in ${\mathbb{R}}^d$. Assume

$$\underset{x\to \infty }{lim}\underset{n}{sup}\mathbb{P}\left(\right||X_n\left|\right|\ge x)=0.$$

Then, there exist a subsequence ${\left(X_{n_k}\right)}_{k\ge 1}$ and a random vector X such that $X_{n_k}\to X$ in distribution. Indeed, it is easy to see that

$$\begin{array}{ccc}\hfill \underset{\left|\right|\theta \left|\right|\to 0}{lim}|\mathbb{E}\left[e^{i⟨\theta ,X_n⟩}\right]-1|& \le & \underset{\left|\right|\theta \left|\right|\to 0}{lim}\left(\mathbb{E}\left[|e^{i⟨\theta ,X_n⟩}-1|{\mathbf{1}}_{\left\{\right|\left|X_n\right||\le |\left|\theta \right|{|}^{-1/2}\}}\right]+\mathbb{E}\left[|e^{i⟨\theta ,X_n⟩}-1|{\mathbf{1}}_{\left\{\right|\left|X_n\right||\ge |\left|\theta \right|{|}^{-1/2}\}}\right]\right)\hfill \\ & \le & \underset{\left|\right|\theta \left|\right|\to 0}{lim}\left(\mathbb{E}\left[\left|\right|\theta \left|\right|\left|\right|X_n\left|\right|{\mathbf{1}}_{\left\{\right|\left|X_n\right||\le |\left|\theta \right|{|}^{-1/2}\}}\right]+2\mathbb{P}\left(\right||X_n\left|\right|\ge {\left|\right|\theta \left|\right|}^{-1/2})\right)\hfill \\ & \le & \underset{\left|\right|\theta \left|\right|\to 0}{lim}\left({\left|\right|\theta \left|\right|}^{1/2}+2\mathbb{P}\left(\right||X_n\left|\right|\ge {\left|\right|\theta \left|\right|}^{-1/2})\right)\hfill \\ & =& 0\hfill \end{array}$$

(A13)

uniformly for all $n\ge 1.$ Our conclusion follows from Theorem A2.

Example A5. 

Assume that ${\left(X_n\right)}_{n\ge 1}$ is a sequence of ${\alpha }_n$–stable symmetric random variables with an unite scale parameter, i.e., $X_n\sim S_{{\alpha }_n}(1,0,0).$ If ${\alpha }_n\in [a,b]\subset (0,2],$ then there exists a subsequence ${\left(X_{n_k}\right)}_{k\ge 1}$ and a random variable X such that $X_{n_k}\to X$ in distribution. Indeed, it is obvious that

$$\underset{\theta \to 0}{lim}\mathbb{E}\left[e^{i\theta X_n}\right]=\underset{\theta \to 0}{lim}{e}^{-{\left|\theta \right|}^{{\alpha }_n}}=1$$

uniformly for all $n.$ Thus, the conclusion follows immediately from Theorem A2.

Another route to this conclusion can be obtained from the Bolzano–Weierstrass theorem. In fact, by the Bolzano–Weierstrass theorem, there exists a subsequence ${\alpha }_{n_k}$ such that ${\alpha }_{n_k}\to \alpha \in [a,b].$ It follows that

$$\underset{k\to \infty }{lim}\mathbb{E}\left[e^{i\theta X_{n_k}}\right]=\underset{k\to \infty }{lim}{e}^{-{\left|\theta \right|}^{{\alpha }_{n_k}}}=e^{-{\left|\theta \right|}^{\alpha }},$$

which means $X_{n_k}\to S_{\alpha }(1,0,0),k\to \infty ,$ in distribution.

Remark A1. 

It is easy to see that

$$\begin{array}{c}\hfill |f_n\left(\theta \right)-1|\le \mathbb{E}\left[|e^{i⟨\theta ,X_n⟩}-1|\right].\end{array}$$

(A14)

Thus, condition (A1) implies condition (A7). Hence, Theorem A1 can be regarded as a corollary of Theorem A2.

Appendix A.2. Weak Convergence Theorems for Random Processes

In the previous subsection, we consider the case of random vectors. Now, we consider the case of random processes.

Theorem A3. 

Let ${\left(X_n\left(x\right)\right)}_{n\ge 1},x\in [0,1],$ be a sequence of random processes with values in $\mathbb{R}$. Assume that

$$\begin{array}{c}\hfill \underset{\theta \to 0}{lim}\mathbb{E}\left[|e^{i\theta (X_n\left(x_2\right)-X_n\left(x_1\right))}-1|\right]=0\end{array}$$

(A15)

uniformly for all $n\ge 1$ and all $x_1,x_2\in [0,1],$ and that for any $M>0,$

$$\begin{array}{c}\hfill \underset{|x_2-x_1|\to 0}{lim}\mathbb{E}\left[|e^{i\theta (X_n\left(x_2\right)-X_n\left(x_1\right))}-1|\right]=0\end{array}$$

(A16)

uniformly for all $n\ge 1$ and all $\left|\theta \right|\le M.$ Denote by

$$\begin{array}{c}\hfill f_n(\theta ,x_1,x_2)=\mathbb{E}\left[e^{i\theta (X_n\left(x_2\right)-X_n\left(x_1\right))}\right],x_1,x_2\in [0,1]\mathit{and}\theta \in \mathbb{R}.\end{array}$$

(A17)

Then, $f_n(\theta ,x,y)$ is equicontinuous with respect to $(\theta ,x,y)\in [-M,M]\times {[0,1]}^2$ and therefore, there exist a subsequence ${\left(X_{n_k}\left(x\right)\right)}_{k\ge 1}$ and a random process $X\left(x\right)$ such that, for any $x_1,x_2\in [0,1],$

$$\begin{array}{c}\hfill X_{n_k}\left(x_2\right)-X_{n_k}\left(x_1\right)\to X\left(x_2\right)-X\left(x_1\right)\end{array}$$

(A18)

in distribution.

Moreover, if $X_n\left(0\right)=0$ and all the processes $X\left(x\right)$ and $X_n\left(x\right),n\ge 1,$ have independent increments, then $X_{n_k}\left(x\right)\to X\left(x\right)$ in finite dimensional distribution.

By Theorem A1, condition (A15) is sufficient to prove (A18). However, with this method, the subsequence $n_k$ vary in $x_1$ and $x_2.$ The use of condition (A16) is to make sure that the sequence $n_k$ is common when $x_1$ and $x_2$ vary in the range $[0,1].$

Proof. 

By Theorem A1, condition (A15) implies that $f_n(\theta ,x,x_1)$ is equicontinuous with respect to $\theta \in \mathbb{R}.$ Hence we need only to prove that $f_n(\theta ,x,y)$ is equicontinuous with respect to $(x,y)\in {[0,1]}^2.$ For any $x_2,x_3\in [0,1],$ one has

$$\begin{array}{ccc}\hfill |f_n(\theta ,x_2,y)-f_n(\theta ,x_3,y)|& =& \left|\mathbb{E}\left[e^{i\theta (X_n\left(y\right)-X_n\left(x_2\right))}\left(1-e^{i\theta (X\left(x_2\right)-X\left(x_3\right))}\right)\right]\right|\hfill \\ & \le & \mathbb{E}\left[|1-e^{i\theta (X\left(x_2\right)-X\left(x_3\right))}|\right].\hfill \end{array}$$

(A19)

By (A16), we find that for any $M>0,$$f_n(\theta ,x,y)$ is equicontinuous with respect to $(\theta ,x)\in [-M,M]\times [0,1].$ Similarly, $f_n(\theta ,x,y)$ is equicontinuous with respect to $(\theta ,y)\in [-M,M]\times [0,1].$ Thus, $f_n(\theta ,x,y)$ is equicontinuous with respect to $(\theta ,x,y)\in [-M,M]\times {[0,1]}^2.$ With an argument similar to the proof of Theorem A1, by the Arzelà–Ascoli theorem and the Lévy continuous theorem, there exist a subsequence ${\left(X_{n_k}\left(x\right)\right)}_{k\ge 1}$ and a random process $X\left(x\right)$ such that for any given $x_1,x_2\in [0,1],$

$$X_{n_k}\left(x_2\right)-X_{n_k}\left(x_1\right)\to X\left(x_2\right)-X\left(x_1\right)$$

in distribution.

Assume that $X_n\left(x\right),x\in [0,1],$ has independent increments. For any $(x_1,x_2,\dots ,x_d)\in {[0,1]}^d$ satisfying $0=x_0\le x_1\le x_2\le \dots \le x_d,$ it is easy to see that, for any $({\theta }_1,{\theta }_2,\dots ,{\theta }_d)\in {\mathbb{R}}^d,$

$$\begin{array}{ccc}\hfill \mathbb{E}\left[exp\left\{i\sum _{j=1}^d{\theta }_j{X}_{n_k}\left(x_j\right)\right\}\right]& =& \mathbb{E}\left[exp\left\{i\sum _{j=1}^d\left(\left(\sum _{k=j}^d{\theta }_k\right)\left(X_{n_k}\left(x_j\right)-X_{n_k}\left(x_{j-1}\right)\right)\right)\right\}\right]\hfill \\ & =& \prod _{j=1}^d\mathbb{E}\left[exp\left\{i\left(\left(\sum _{k=j}^d{\theta }_k\right)\left(X_{n_k}\left(x_j\right)-X_{n_k}\left(x_{j-1}\right)\right)\right)\right\}\right].\hfill \end{array}$$

Letting $k\to \infty ,$ by the hypothesis that $X\left(x\right)$ has independent increments, we find that

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim}\mathbb{E}\left[exp\left\{i\sum _{j=1}^d{\theta }_j{X}_{n_k}\left(x_j\right)\right\}\right]& =& \prod _{j=1}^d\mathbb{E}\left[exp\left\{i\left(\left(\sum _{k=j}^d{\theta }_k\right)\left(X\left(x_j\right)-X\left(x_{j-1}\right)\right)\right)\right\}\right]\hfill \\ & =& \mathbb{E}\left[exp\left\{i\sum _{j=1}^d\left(\left(\sum _{k=j}^d{\theta }_k\right)\left(X\left(x_j\right)-X\left(x_{j-1}\right)\right)\right)\right\}\right]\hfill \\ & =& \mathbb{E}\left[exp\left\{i\sum _{j=1}^d{\theta }_{j}X\left(x_j\right)\right\}\right],\hfill \end{array}$$

which means $X_{n_k}\left(x\right)\to X\left(x\right),x\in [0,1],$ in finite dimensional distribution. □

Example A6. 

Let ${\left(X_n\left(x\right)\right)}_{n\ge 1},x\in [0,1],$ be a sequence of random processes with values in $\mathbb{R}$. Assume that $|X_n\left(x\right)|\le C$ for a constant C and uniformly for all x and all $n.$ If

$$\underset{|x_1-x_2|\to 0}{lim}{X}_n\left(x_1\right)-X_n\left(x_2\right)=0$$

in distribution uniformly for all $x_1,x_2\in [0,1]$ and all $n,$ Then, the conclusion of Theorem A3 holds.

Indeed, by (A13), condition (A15) holds. Since ${lim}_{|x_1-x_2|\to 0}{X}_n\left(x_1\right)-X_n\left(x_2\right)=0$ in distribution is equal to ${lim}_{|x_1-x_2|\to 0}{X}_n\left(x_1\right)-X_n\left(x_2\right)=0$ almost surely. Notice that $|X_n\left(x_2\right)-X_n\left(x_1\right)|\le 2C.$ By Lebesgue’s dominated convergence theorem, it follows that for any $M>0,$

$$\begin{array}{ccc}\hfill \underset{|x_2-x_1|\to 0}{lim}\mathbb{E}\left[|e^{i\theta (X_n\left(x_2\right)-X_n\left(x_1\right))}-1|\right]& \le & \underset{|x_2-x_1|\to 0}{lim}\mathbb{E}\left[\left|\theta \right(X_n\left(x_2\right)-X_n\left(x_1\right)\left)\right|\right]\hfill \\ & \le & M\underset{|x_2-x_1|\to 0}{lim}\mathbb{E}\left[|X_n\left(x_2\right)-X_n\left(x_1\right)|\right]\hfill \\ & =& 0\hfill \end{array}$$

uniformly for all $n\ge 1$ and all $\left|\theta \right|\le M.$ Thus, condition (A16) also holds.

The following sufficient condition could be easier to check than that of Theorem A3.

Theorem A4. 

Let ${\left(X_n\left(x\right)\right)}_{n\ge 1},x\in [0,1],$ be a sequence of processes with values in $\mathbb{R}$. Denote by

$$\begin{array}{c}\hfill f_n(\theta ,x_1,x_2)=\mathbb{E}\left[e^{i\theta (X_n\left(x_2\right)-X_n\left(x_1\right))}\right],x_1,x_2\in [0,1]\mathit{and}\theta \in \mathbb{R}.\end{array}$$

(A20)

Assume that

$$\begin{array}{c}\hfill \underset{\theta \to 0}{lim}{f}_n(\theta ,x_1,x_2)=1\end{array}$$

(A21)

uniformly for all $n\ge 1$ and all $x_1,x_2\in [0,1],$ and that for any $M>0$,

$$\begin{array}{c}\hfill \underset{|x_2-x_1|\to 0}{lim}{f}_n(\theta ,x_1,x_2)=1\end{array}$$

(A22)

uniformly for all $n\ge 1$ and all $\left|\theta \right|\le M.$ Then, the conclusion of Theorem A3 holds.

Proof. 

By Theorem A2, condition (A21) implies that $f_n(\theta ,x,y)$ is equicontinuous with respect to $\theta \in \mathbb{R}.$ Next, we prove that $f_n(\theta ,x,y)$ is equicontinuous with respect to $(x,y)\in {[0,1]}^2.$ For any $x_2,x_3\in [0,1],$ one has

$$\begin{array}{ccc}\hfill |f_n(\theta ,x_2,x_1)-f_n(\theta ,x_3,x_1)|& =& \left|\mathbb{E}\left[e^{i\theta (X_n\left(x_1\right)-X_n\left(x_2\right))}\left(1-e^{i\theta (X_n\left(x_2\right)-X_n\left(x_3\right))}\right)\right]\right|\hfill \\ & \le & \mathbb{E}\left[|1-e^{i\theta (X_n\left(x_2\right)-X_n\left(x_3\right))}|\right].\hfill \end{array}$$

(A23)

The random variable $|1-e^{i\theta (X_n\left(x_2\right)-X_n\left(x_3\right))}|$ is dominated by the constant 2. Hence, for all $x>0,$

$$\begin{array}{ccc}\hfill |f_n(\theta ,x_2,x_1)-f_n(\theta ,x_3,x_1)|& \le & \mathbb{E}\left[|1-e^{i\theta (X_n\left(x_2\right)-X_n\left(x_3\right))}|{\mathbf{1}}_{\left\{\right|X_n\left(x_2\right)-X_n\left(x_3\right)|\le x\}}\right]\hfill \\ & & +\mathbb{E}\left[|1-e^{i\theta (X_n\left(x_2\right)-X_n\left(x_3\right))}|{\mathbf{1}}_{\left\{\right|X_n\left(x_2\right)-X_n\left(x_3\right)|>x\}}\right]\hfill \\ & \le & \mathbb{E}\left[\left|\theta (X_n\left(x_2\right)-X_n\left(x_3\right))\right|{\mathbf{1}}_{\left\{\right|X_n\left(x_2\right)-X_n\left(x_3\right)|\le x\}}\right]\hfill \\ & & +2\mathbb{E}\left[{\mathbf{1}}_{\left\{\right|X_n\left(x_2\right)-X_n\left(x_3\right)|>x\}}\right]\hfill \\ & \le & x\left|\theta \right|+2\mathbb{P}\left(\right|X_n\left(x_2\right)-X_n\left(x_3\right)|\ge x).\hfill \end{array}$$

(A24)

Given any $\epsilon >0$ and any $M>0,$ it holds, for all $\left|\theta \right|\le M$ and all $0<x\le \epsilon /\left(2M\right)$,

$$x\left|\theta \right|\le xM\le {\displaystyle \frac{\epsilon }{2}}.$$

By (A22), for the given $4M/\epsilon >0,$ there exists a $\delta >0$ such that if $|x_1-x_2|\le \delta ,$ then

$$\begin{array}{c}\hfill |f_n(\theta ,x_1,x_2)-1|\le {\displaystyle \frac{\epsilon }{8}}\end{array}$$

(A25)

uniformly for all n and all $\left|\theta \right|\le 4M/\epsilon .$ By the Billingsley inequality, it is easy to see that if $|x_2-x_3|\le \delta ,$ then

$$\begin{array}{ccc}\hfill \mathbb{P}\left(|X_n\left(x_3\right)-X_n\left(x_2\right)|\ge {\displaystyle \frac{\epsilon }{2M}}\right)& \le & {\displaystyle \frac{\epsilon }{4M}}{\int }_{-4M/\epsilon }^{4M/\epsilon }\left(1-f_n(\theta ,x_2,x_3)\right)d\theta \hfill \\ & \le & {\displaystyle \frac{\epsilon }{4M}}{\int }_{-4M/\epsilon }^{4M/\epsilon }{\displaystyle \frac{\epsilon }{8}}d\theta ={\displaystyle \frac{\epsilon }{4}}.\hfill \end{array}$$

From (A24), for all $\left|\theta \right|\le M$ and all $x_2,x_3\in [0,1]$ such that $|x_2-x_3|\le \delta ,$

$$\begin{array}{ccc}\hfill |f_n(\theta ,x_2,x_1)-f_n(\theta ,x_3,x_1)|& \le & {\displaystyle \frac{\epsilon }{2M}}M+2\mathbb{P}\left(|X_n\left(x_2\right)-X_n\left(x_3\right)|\ge {\displaystyle \frac{\epsilon }{2M}}\right)\hfill \\ & \le & {\displaystyle \frac{\epsilon }{2}}+2{\displaystyle \frac{\epsilon }{4}}=\epsilon .\hfill \end{array}$$

Thus, for any $M>0,$$f_n(\theta ,x,x_1)$ is equicontinuous with respect to $(\theta ,x)\in [-M,M]\times [0,1].$ Similarly, $f_n(\theta ,x,y)$ is equicontinuous with respect to $(\theta ,y)\in [-M,M]\times [0,1].$ Thus, $f_n(\theta ,x,y)$ is equicontinuous with respect to $(\theta ,x,y)\in [-M,M]\times {[0,1]}^2.$ The rest of the proof is similar to the proof of Theorem A3. □

Example A7. 

Assume that the functions ${\alpha }_n\left(x\right)\in [a,b]\subset (0,2],$ and that ${\left(X_n\left(x\right)\right)}_{n\ge 1}$ is a sequence of (localizable) independent-increments ${\alpha }_n\left(x\right)$–multistable Lévy motions (cf. Falconer and Liu [5]). Then, there exists a subsequence ${\left(X_{n_k}\left(x\right)\right)}_{k\ge 1}$ and a random process $X\left(x\right)$ such that $X_{n_k}\left(x\right)\to X\left(x\right)$ in distribution for any $x\in [0,1].$ In particular, if $X\left(x\right)$ has independent increments, then $X_{n_k}\left(x\right)$ converges to $X\left(x\right)$ in finite dimensional distribution.

Indeed, in work by Falconer and Liu [5], the joint characteristic functions of ${\left(X_n\left(x\right)\right)}_{n\ge 1}$ read as follows:

$$\begin{array}{c}\hfill \mathbb{E}\left[exp\left\{i\sum _{j=1}^d{\theta }_j{X}_n\left(x_j\right)\right\}\right]=exp\left\{-\int |\sum _{j=1}^d{\theta }_j{\mathbf{1}}_{[0,x_j]}\left(s\right){|}^{{\alpha }_n\left(s\right)}ds\right\},\end{array}$$

for $d\in \mathbb{N},({\theta }_1,\dots ,{\theta }_d)\in {\mathbb{R}}^d$ and $(x_1,\dots ,x_d)\in {[0,1]}^d.$ It is obvious that

$$\begin{array}{c}\hfill \underset{\theta \to 0}{lim}{f}_n(\theta ,x_1,x_2)=\underset{\theta \to 0}{lim}exp\left\{-\int |\theta {\mathbf{1}}_{[x_1,x_2]}\left(s\right){|}^{{\alpha }_n\left(s\right)}ds\right\}=1\end{array}$$

(A26)

uniformly for all $n\ge 1$ and all $x_1,x_2\in [0,1],$ and that for any $M>0,$

$$\begin{array}{c}\hfill \underset{|x_2-x_1|\to 0}{lim}{f}_n(\theta ,x_1,x_2)=\underset{|x_2-x_1|\to 0}{lim}exp\left\{-\int |\theta {\mathbf{1}}_{[x_1,x_2]}\left(s\right){|}^{{\alpha }_n\left(s\right)}ds\right\}=1\end{array}$$

(A27)

uniformly for all $n\ge 1$ and all $\left|\theta \right|\le M.$ Hence, the conclusion follows immediately from Theorem A4.

This conclusion can also be obtained from the Arzelà–Ascoli theorem. Since ${\left(X_n\left(x\right)\right)}_{n\ge 1}$ are localizable, by (7), the functions ${\left({\alpha }_n\left(x\right)\right)}_{n\ge 1}$ are equicontinuous. Thus, there exist a subsequence ${\left({\alpha }_{n_k}\right)}_{k\ge 1}$ and a continuous function $\alpha \left(x\right),$ satisfying condition (7) such that $\left|\right|{\alpha }_{n_k}\left(x\right)-\alpha \left(x\right){\left|\right|}_{\infty }\to 0$ as $k\to \infty .$ It is obvious that

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim}\mathbb{E}\left[exp\left\{i\sum _{j=1}^d{\theta }_j{X}_{n_k}\left(x_j\right)\right\}\right]& =& \underset{k\to \infty }{lim}exp\left\{-\int |\sum _{j=1}^d{\theta }_j{\mathbf{1}}_{[0,x_j]}\left(s\right){|}^{{\alpha }_{n_k}\left(s\right)}ds\right\}\hfill \\ & =& exp\left\{-\int |\sum _{j=1}^d{\theta }_j{\mathbf{1}}_{[0,x_j]}\left(s\right){|}^{\alpha \left(s\right)}ds\right\},\hfill \end{array}$$

for $d\in \mathbb{N},({\theta }_1,\dots ,{\theta }_d)\in {\mathbb{R}}^d$ and $(x_1,\dots ,x_d)\in {[0,1]}^d,$ which means $X_{n_k}\left(x\right)$ converges to $X\left(x\right),$ an independent-increments $\alpha \left(x\right)$–multistable Lévy motion, in finite dimensional distribution.

The condition that the sequence ${\left(f_n\right)}_{n\ge 1}$ is equicontinuous cannot be satisfied in some particular cases, for instance, in the construction of self-stabilizing process. Fortunately, in the Arzelà–Ascoli theorem, we find that this condition can be replaced by a more general one.

Definition A1. 

We call the sequence ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ subequicontinuous on $I\subset {\mathbb{R}}^d,$ if for any $\epsilon >0,$ there exist $\delta >0$ and a sequence of nonnegative numbers ${\left({\epsilon }_n\right)}_{n\ge 1},$${\epsilon }_n\to 0$ as $n\to \infty ,$ such that, for all functions $f_n$ in the sequence,

$$\begin{array}{c}\hfill |f_n\left({\theta }_1\right)-f_n\left({\theta }_2\right)|\le \epsilon +{\epsilon }_n,{\theta }_1,{\theta }_2\in I,\end{array}$$

(A28)

whenever $\left|\right|{\theta }_1-{\theta }_2\left|\right|<\delta .$ In particular, if ${\epsilon }_n=0$ for all $n,$ then ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is equicontinuous.

Notice that the definition ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is subequicontinuous on $I\subset {\mathbb{R}}^d$ implies that for any $\epsilon >0,$ there exists $\delta$ and N such that for all ${\theta }_1,{\theta }_2\in I$ and all $n>N,$

$$|f_n\left({\theta }_1\right)-f_n\left({\theta }_2\right)|\le \epsilon ,$$

whenever $\left|\right|{\theta }_1-{\theta }_2\left|\right|<\delta .$

Example A8. 

Assume that ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is a sequence of equicontinuous functions. Set $g_n\left(\theta \right)=f_n\left(\theta \right)+{\displaystyle \frac{1}{n}}{h}_n\left(\theta \right),$ where ${\left(h_n\left(\theta \right)\right)}_{n\ge 1}$ is a sequence of functions that satisfies $\left|\right|h_n\left(\theta \right){\left|\right|}_{\infty }\le C$ for a constant C. Then, it is easy to see that ${\left(g_n\left(\theta \right)\right)}_{n\ge 1}$ is a sequence of subequicontinuous functions. In particular, if $h_n\left(\theta \right)$ is the Dirichlet function, then ${\left(g_n\left(\theta \right)\right)}_{n\ge 1}$ is a sequence of subequicontinuous, but not equicontinuous, functions.

Similarly, we can define Hölder subequicontinuous. A sequence ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is called Hölder subequicontinuous of order $\alpha \in (0,1]$ on $I\subset {\mathbb{R}}^d,$ if there exist a constant $C>0$ and a sequence of nonnegative numbers ${\left({\epsilon }_n\right)}_{n\ge 1},$${\epsilon }_n\to 0$ as $n\to \infty ,$ such that, for all functions $f_n$ in the sequence,

$$\begin{array}{c}\hfill |f_n\left({\theta }_1\right)-f_n\left({\theta }_2\right)|\le C\left|\right|{\theta }_1-{\theta }_2|{|}^{\alpha }+{\epsilon }_n,{\theta }_1,{\theta }_2\in I,\end{array}$$

(A29)

whenever $\left|\right|{\theta }_1-{\theta }_2\left|\right|\le 1.$ In particular, if ${\epsilon }_n=0$ for all $n,$ then ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is Hölder equicontinuous of order $\alpha \in (0,1].$ It is obvious that if ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is Hölder subequicontinuous, then ${\left(f_n\left(\theta \right)\right)}_{n\ge 1}$ is subequicontinuous.

Appendix A.3. Generalization of The Arzel à–Ascoli Theorem

Next, we give a general version of the Arzelà–Ascoli theorem.

Lemma A2. 

Assume that ${\left(f_n\right)}_{n\ge 1}$ is a sequence of real-valued continuous functions defined on a closed and bounded set ${\Pi }_{i=1}^d[a_i,b_i]\subset {\mathbb{R}}^d.$ If this sequence is uniformly bounded and subequicontinuous, then there exists a subsequence ${\left(f_{n_k}\right)}_{k\ge 1}$ that converges uniformly.

Proof. 

The proof is essentially based on a diagonalization argument and is similar to the proof of the Arzelà–Ascoli theorem. We give a proof for the case of $d=1.$ For $d>1,$ the argument follows by applying the $1$–dimensional version of our theorem d times.

Let $[a,b]\subset \mathbb{R}$ be a closed and bounded interval. If ${\left(f_n\right)}_{n\ge 1}$ is a finite set of functions, then there is a subsequence ${\left(f_{n_k}\right)}_{k\ge 1}$ such that $f_{n_k}\equiv f_{n_1}$ for all $k\ge 1.$ Thus, without loss of generality, we may assume that ${\left(f_n\right)}_{n\ge 1}$ is an infinite set of functions. Fix an enumeration ${\left(x_i\right)}_{i\ge 1}$ of all rational numbers in $[a,b].$ Since ${\left(f_n\right)}_{n\ge 1}$ is uniformly bounded, the set of points ${\left(f_n\left(x_1\right)\right)}_{n\ge 1}$ is bounded. By the Bolzano–Weierstrass theorem, there is a sequence ${\left(f_{{\sigma }_1\left(n\right)}\left(x_1\right)\right)}_{n\ge 1}$ of the functions in ${\left(f_n\left(x_1\right)\right)}_{n\ge 1}$ such that ${\left(f_{{\sigma }_1\left(n\right)}\left(x_1\right)\right)}_{n\ge 1}$ converges. Repeating the same argument for the sequence of points ${\left(f_{{\sigma }_1\left(n\right)}\left(x_2\right)\right)}_{n\ge 1}$, there is a subsequence ${\left(f_{{\sigma }_2\left(n\right)}\left(x_2\right)\right)}_{n\ge 1}$ of ${\left(f_{{\sigma }_1\left(n\right)}\left(x_2\right)\right)}_{n\ge 1}$ such that ${\left(f_{{\sigma }_2\left(n\right)}\left(x_2\right)\right)}_{n\ge 1}$ converges. By induction, this process can be continued forever, and so there is a chain of subsequences such that, for each $k\ge 1,$ the subsequence ${\left(f_{{\sigma }_k\left(n\right)}\right)}_{n\ge 1}$ converges at $x_1,\dots ,x_k.$ Moreover, the following relation holds:

$${\left(f_n\right)}_{n\ge 1}\supseteq {\left(f_{{\sigma }_1\left(n\right)}\right)}_{n\ge 1}\supseteq \dots \supseteq {\left(f_{{\sigma }_{N-1}\left(n\right)}\right)}_{n\ge 1}\supseteq {\left(f_{{\sigma }_N\left(n\right)}\right)}_{n\ge 1}\supseteq \dots$$

Define the diagonal subsequence ${\left(f_{{\sigma }_m\left(m\right)}\right)}_{m\ge 1}$ whose mth term is the mth term in the mth subsequence ${\left(f_{{\sigma }_m\left(n\right)}\right)}_{n\ge 1}$. By construction, ${\left(f_{{\sigma }_m\left(m\right)}\right)}_{m\ge 1}$ converges at every rational point of $[a,b].$

Therefore, given any $\epsilon >0$ and rational ${\left(x_i\right)}_{i\ge 1}$ in $[a,b]$, there is an integer $N=N(\epsilon ,x_k)$ such that

$$|f_{{\sigma }_m\left(m\right)}\left(x_i\right)-f_{{\sigma }_m\left(m\right)}\left(x_i\right)|\le {\displaystyle \frac{\epsilon }{3}}.$$

Since the family ${\left(f_n\right)}_{n\ge 1}$ is subequicontinuous, for this fixed $\epsilon$ and for every x in $[a,b]$, there is an open interval $U_x$ containing x and $N_x=N_x\left(\epsilon \right)$ such that

$$|f_n\left(s\right)-f_n\left(t\right)|\le {\displaystyle \frac{\epsilon }{3}}$$

for all ${\left(f_n\right)}_{n\ge N_x}$ and all $s,t\in U_x.$ The collection of intervals $U_x,x\in [a,b],$ forms an open cover of $[a,b]$. Since $[a,b]$ is compact, this covering admits a finite subcover $U_1,\dots ,U_l.$ There exists an integer K such that each open interval $U_j,1\le j\le l,$ contains a rational ${\tilde{x}}_k$ with $1\le k\le K.$ Finally, for any $t\in [a,b],$ there are j and k so that t and ${\tilde{x}}_k$ belong to the same interval $U_j.$ Set $N=max\{N(\epsilon ,x_1),\dots ,N(\epsilon ,x_K),N_{x_1},\dots ,N_{x_K}\},$ then for all $m,n\ge N$ and $t\in [a,b],$

$$\begin{array}{ccc}\hfill |f_{{\sigma }_m\left(m\right)}\left(t\right)-f_{{\sigma }_n\left(n\right)}\left(t\right)|& \le & |f_{{\sigma }_m\left(m\right)}\left(t\right)-f_{{\sigma }_m\left(m\right)}\left({\tilde{x}}_k\right)|+|f_{{\sigma }_m\left(m\right)}\left({\tilde{x}}_k\right)-f_{{\sigma }_n\left(n\right)}\left({\tilde{x}}_k\right)|\hfill \\ & & +|f_{{\sigma }_n\left(n\right)}\left({\tilde{x}}_k\right)-f_{{\sigma }_n\left(n\right)}\left(t\right)|\hfill \\ & \le & {\displaystyle \frac{\epsilon }{3}}+{\displaystyle \frac{\epsilon }{3}}+{\displaystyle \frac{\epsilon }{3}}=\epsilon .\hfill \end{array}$$

Hence, the sequence ${\left(f_{{\sigma }_m\left(m\right)}\right)}_{m\ge 1}$ is an uniform Cauchy sequence, and it therefore uniformly converges to a continuous function, as claimed. This completes the proof. □

Appendix A.4. Some Applications

With this general version of the Arzelà–Ascoli theorem, we can easily obtain the generalizations of Theorems A1–A4. For instance, we have the following generalization of Theorem A4.

Theorem A5. 

Let ${\left(X_n\left(x\right)\right)}_{n\ge 1},x\in [0,1],$ be a sequence of random processes with values in $\mathbb{R}$. Denote by

$$\begin{array}{c}\hfill f_n(\theta ,x_1,x_2)=\mathbb{E}\left[e^{i\theta (X_n\left(x_2\right)-X_n\left(x_1\right))}\right],x_1,x_2\in [0,1]\mathit{and}\theta \in \mathbb{R}.\end{array}$$

Assume that for any $M>0,$ there exists a sequence of nonnegative numbers ${\left({\epsilon }_n\left(M\right)\right)}_{n\ge 1}$, depending only on M, such that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\epsilon }_n\left(M\right)=0,\\ \\ \hfill \underset{\theta \to 0}{lim}|f_n(\theta ,x_1,x_2)-1|\le {\epsilon }_n\left(M\right)\end{array}$$

uniformly for all $x_1,x_2\in [0,1],$ and that

$$\begin{array}{c}\hfill \underset{|x_2-x_1|\to 0}{lim}|f_n(\theta ,x_1,x_2)-1|\le {\epsilon }_n\left(M\right)\end{array}$$

uniformly for all $\left|\theta \right|\le M.$ Denote by

$$\begin{array}{c}\hfill f_n(\theta ,x_1,x_2)=\mathbb{E}\left[e^{i\theta (X_n\left(x_2\right)-X_n\left(x_1\right))}\right],x_1,x_2\in [0,1]\mathit{and}\theta \in \mathbb{R}.\end{array}$$

Then, $f_n(\theta ,x,y)$ is subequicontinuous with respect to $(\theta ,x,y)\in [-M,M]\times {[0,1]}^2$ and therefore, there exist a subsequence ${\left(X_{n_k}\left(x\right)\right)}_{k\ge 1}$ and a random process $X\left(x\right)$ such that, for any $x_1,x_2\in [0,1],$

$$\begin{array}{c}\hfill X_{n_k}\left(x_2\right)-X_{n_k}\left(x_1\right)\to X\left(x_2\right)-X\left(x_1\right)\end{array}$$

in distribution.

Moreover, if $X_n\left(0\right)=0$ and all the processes $X\left(x\right)$ and $X_n\left(x\right),n\ge 1,$ have independent increments, then $X_{n_k}\left(x\right)\to X\left(x\right)$ in finite dimensional distribution.

The proof of Theorem A5 is omitted, since it is similar to that of Theorem A4. Using Theorem A5, we obtain the following corollary.

Denote by $\lfloor x\rfloor$ the greatest integer less than $x.$

Corollary A1. 

Let ${\{S_n(k/n):0\le k\le n\}}_{n\ge 1}$ be a sequence of Markov processes with values in $\mathbb{R}$. Assume that there exists a sequence of Lesbegue measurable functions ${\left(F_n(\theta ,y)\right)}_{n\ge 1},(\theta ,y)\in \mathbb{R}\times [0,1],$ such that, for all k and all $\theta \in \mathbb{R},$

$$\begin{array}{c}\hfill \mathbb{E}\left[\exp \left\{i\theta \left(S_n\left({\displaystyle \frac{k+1}{n}}\right)-S_n\left({\displaystyle \frac{k}{n}}\right)\right)\right\}|S_n\left({\displaystyle \frac{k}{n}}\right)\right]=exp\left\{-{\displaystyle \frac{1}{n}}{F}_n\left(\theta ,{\displaystyle \frac{k}{n}}\right)\right\}.\end{array}$$

(A30)

Assume that ${\left(F_n\right)}_{n\ge 1}$ satisfies the following two conditions:

(A) 

The limit ${lim}_{\theta \to 0}{F}_n(\theta ,·)=0$ holds uniformly for all $n.$

(B) 

There exists a function $F\left(z\right),z\in \mathbb{R},$ such that for any $M,$$0\le F_n(\theta ,·)\le F\left(M\right)$ holds uniformly for all $\left|\theta \right|\le M$ and all $n.$

• Define $S_n\left(x\right)=S_n(\lfloor nx\rfloor /n),x\in [0,1].$ There exist a subsequence ${\left(S_{n_k}\left(x\right)\right)}_{k\ge 1}$ and a random process $S\left(x\right)$ such that, for any $x_1,x_2\in [0,1],$ it converges

$$\begin{array}{c}\hfill S_{n_k}\left(x_2\right)-S_{n_k}\left(x_1\right)\to S\left(x_2\right)-S\left(x_1\right)\end{array}$$

in distribution.

Proof. 

For simplicity of notations, denote by

$${\mathbb{E}}_{S_n\left(t_1\right),\dots ,S_n\left(t_d\right)}\left[·\right]=\mathbb{E}\left[·|S_n\left(t_1\right),\dots ,S_n\left(t_d\right)\right].$$

It is easy to see that, for all $x_1,x_2\in [0,1]$ satisfying $x_1<x_2$,

$$\begin{array}{ccc}& & \mathbb{E}[exp\left\{i\theta \left(S_n\left(x_2\right)-S_n\left(x_1\right)\right)+\sum _{k=\lfloor n{x}_1\rfloor }^{\lfloor n{x}_2\rfloor -1}{F}_n\left(\theta ,{\displaystyle \frac{k}{n}}\right){\displaystyle \frac{1}{n}}\right]\hfill \\ & & =\mathbb{E}\left[{\mathbb{E}}_{S_n\left({\displaystyle \frac{\lfloor n{x}_2\rfloor -1}{n}}\right),\dots ,S_n\left(x_1\right)}\left[exp\left\{i\theta \left(S_n\left(x_2\right)-S_n\left(x_1\right)\right)+\sum _{k=\lfloor n{x}_1\rfloor }^{\lfloor n{x}_2\rfloor -1}{F}_n\left(\theta ,{\displaystyle \frac{k}{n}}\right){\displaystyle \frac{1}{n}}\right\}\right]\right]\hfill \\ & & =\mathbb{E}\left[exp\left\{i\theta \left(S_n\left({\displaystyle \frac{\lfloor n{x}_2\rfloor -1}{n}}\right)-S_n\left(x_1\right)\right)+\sum _{k=\lfloor n{x}_1\rfloor }^{\lfloor n{x}_2\rfloor -2}{F}_n\left(\theta ,{\displaystyle \frac{k}{n}}\right){\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & =\dots \hfill \\ & & =\mathbb{E}\left[exp\left\{i\theta \left(S_n\left({\displaystyle \frac{\lfloor n{x}_1\rfloor +1}{n}}\right)-S_n\left(x_1\right)\right)+F_n\left(\theta ,{\displaystyle \frac{\lfloor n{x}_1\rfloor }{n}}\right){\displaystyle \frac{1}{n}}\right\}\right]\hfill \\ & & =1.\hfill \end{array}$$

(A31)

In particular, it can be rewritten in the following form:

$$\begin{array}{ccc}& & \mathbb{E}\left[exp\left\{i\theta \left(S_n\left(x_2\right)-S_n\left(x_1\right)\right)\right\}\right]=exp\left\{-{\int }_{x_1^{\left(n\right)}}^{x_2^{\left(n\right)}}{F}_n\left(\theta ,t\right)dt\right\},\hfill \end{array}$$

(A32)

where, here and after, we denote

$$x^{\left(n\right)}={\displaystyle \frac{\lfloor nx\rfloor }{n}},$$

which no longer represents the coordinate of $x.$ Set

$$f_n(\theta ,x_1,x_2)=\mathbb{E}\left[e^{i\theta \left(S_n\left(x_2\right)-S_n\left(x_1\right)\right)}\right].$$

Notice that $|e^{-x}-1|\le x,x\ge 0.$ By the conditions (A) and (B), it is easy to verify that

$$\begin{array}{c}\hfill \underset{\theta \to 0}{lim}|f_n(\theta ,x_1,x_2)-1|\le \underset{\theta \to 0}{lim}{\int }_{x_1^{\left(n\right)}}^{x_2^{\left(n\right)}}{F}_n\left(\theta ,t\right)dt=0\end{array}$$

uniformly for all $n\ge 1$ and all $x_1,x_2\in [0,1],$ and that

$$\begin{array}{ccc}\hfill \underset{|x_2-x_1|\to 0}{lim}|f_n(\theta ,x_1,x_2)-1|& \le & \underset{|x_2-x_1|\to 0}{lim}{\int }_{x_1^{\left(n\right)}}^{x_2^{\left(n\right)}}{F}_n\left(\theta ,t\right)dt\hfill \\ & \le & F\left(M\right)\underset{|x_2-x_1|\to 0}{lim}|x_2^{\left(n\right)}-x_1^{\left(n\right)}|\hfill \\ & \le & F\left(M\right){\displaystyle \frac{1}{n}}\hfill \end{array}$$

uniformly for all $\left|\theta \right|\le M.$ Notice that ${lim}_{n\to \infty }F\left(M\right){\displaystyle \frac{1}{n}}=0.$ Thus, by Theorem A5, we obtain the conclusion of Corollary A1. □

We give an example to show that how to apply Corollary A1.

Example A9. 

Assume that the function $\alpha \left(x\right)\in [a,b]\subset (0,2]$ satisfies condition (7). Let $g\left(x\right)$ be a nonnegative integrable function such that $g\left(x\right)\le C$ for a constant $C.$ Let ${\{S_n(k/n):0\le k\le n\}}_{n\ge 1}$ be a sequence of real-value processes with independent increments. Assume that, for all k and $\theta \in \mathbb{R},$

$$\begin{array}{c}\hfill \mathbb{E}\left[exp\left\{i\theta \left(S_n\left({\displaystyle \frac{k+1}{n}}\right)-S_n\left({\displaystyle \frac{k}{n}}\right)\right)\right\}\right]=exp\left\{-{\displaystyle \frac{1}{n}}|\theta {|}^{\alpha (k/n)}g\left({\displaystyle \frac{k}{n}}\right)\right\},\end{array}$$

(A33)

i.e., $S_n\left({\displaystyle \frac{k+1}{n}}\right)-S_n\left({\displaystyle \frac{k}{n}}\right)\sim S_{\alpha (k/n)}\left({\left(g\left({\displaystyle \frac{k}{n}}\right)/n\right)}^{1/\alpha (k/n)},0,0\right).$ Then, the conditions (A) and (B) of Corollary A1 are satisfied with $F_n(\theta ,y)=|\theta {|}^{\alpha \left(y\right)}g\left(y\right)$ and $F\left(z\right)=C\left(\right|z{|}^a+\left|z{|}^b\right).$ Define $S_n\left(x\right)=S_n(\lfloor nx\rfloor /n),x\in [0,1].$ There exist a subsequence ${\left(S_{n_k}\left(x\right)\right)}_{k\ge 1}$ and a random process $S\left(x\right)$ such that, for any $x_1,x_2\in [0,1],$ it converges

$$\begin{array}{c}\hfill S_{n_k}\left(x_2\right)-S_{n_k}\left(x_1\right)\to S\left(x_2\right)-S\left(x_1\right)\end{array}$$

in distribution.

In fact, when $S_n\left(0\right)=0$, this example gives the integral of $g{\left(x\right)}^{1/\alpha \left(x\right)}$ with respect to a multistable Lévy measure. In particular, when $g\equiv 1,$ this example gives a functional central limit theorem for the independent-increments MsLM, that is, $S\left(x\right)$ tends in distribution to $L_I\left(x\right)$ in $(D[0,1],d_S),$ where $d_S$ is the Skorohod metric.

Using Theorem A5 again, we still have the following corollary. An application of this corollary is given in the next section.

Corollary A2. 

Let ${\{S_n(k/n):0\le k\le n\}}_{n\ge 1}$ be a sequence of Markov processes with values in $\mathbb{R}$. Assume that there exists a sequence of Lesbegue measurable functions ${\left(F_n(\theta ,y)\right)}_{n\ge 1},(\theta ,y)\in \mathbb{R}\times [0,1],$ such that, for all k and all $\theta \in \mathbb{R},$

$$\begin{array}{c}\hfill \mathbb{E}\left[exp\left\{i\theta \left(S_n\left({\displaystyle \frac{k+1}{n}}\right)-S_n\left({\displaystyle \frac{k}{n}}\right)\right)\right\}|S_n\left({\displaystyle \frac{k}{n}}\right)\right]=exp\left\{-{\displaystyle \frac{1}{n}}{F}_n\left(\theta ,S_n\left({\displaystyle \frac{k}{n}}\right)\right)\right\}.\end{array}$$

(A34)

Assume that ${\left(F_n\right)}_{n\ge 1}$ satisfies the conditions (A) and (B) of Corollary A1. Define $S_n\left(x\right)=S_n(\lfloor nx\rfloor /n),$$x\in [0,1].$ Then, there exist a subsequence ${\left(S_{n_k}\left(x\right)\right)}_{k\ge 1}$ and a random process $S\left(x\right)$ such that, for any $x_1,x_2\in [0,1],$ it converges

$$\begin{array}{c}\hfill S_{n_k}\left(x_2\right)-S_{n_k}\left(x_1\right)\to S\left(x_2\right)-S\left(x_1\right)\end{array}$$

in distribution.

Proof. 

By an argument similar to that of Corollary A1, it holds, for all $x_1,x_2\in [0,1]$ satisfying $x_1<x_2$,

$$\begin{array}{c}\hfill \mathbb{E}\left[exp\left\{i\theta \left(S_n\left(x_2\right)-S_n\left(x_1\right)\right)+\sum _{k=\lfloor n{x}_1\rfloor }^{\lfloor n{x}_2\rfloor -1}{F}_n\left(\theta ,S_n\left({\displaystyle \frac{k}{n}}\right)\right){\displaystyle \frac{1}{n}}\right\}\right]=1.\end{array}$$

(A35)

Set

$$f_n(\theta ,x_1,x_2)=\mathbb{E}\left[e^{i\theta \left(S_n\left(x_2\right)-S_n\left(x_1\right)\right)}\right].$$

Then, (A35) implies that

$$\begin{array}{c}\hfill exp\left\{-F\left(M\right)(x_2^{\left(n\right)}-x_1^{\left(n\right)})\right\}\le f_n(\theta ,x_1,x_2)\le 1\end{array}$$

(A36)

uniformly for all $\left|\theta \right|\le M.$ Thus, it is easy to verify that

$$\begin{array}{c}\hfill \underset{\theta \to 0}{lim}{f}_n(\theta ,x_1,x_2)=\underset{\theta \to 0}{lim}\mathbb{E}\left[exp\left\{i\theta \left(S_n\left(x_2\right)-S_n\left(x_1\right)\right)+\sum _{k=\lfloor n{x}_1\rfloor }^{\lfloor n{x}_2\rfloor -1}{F}_n\left(\theta ,S_n\left({\displaystyle \frac{k}{n}}\right)\right){\displaystyle \frac{1}{n}}\right\}\right]=1\end{array}$$

uniformly for all $n\ge 1$ and all $x_1,x_2\in [0,1],$ and that, from (A36),

$$\begin{array}{c}\hfill \underset{|x_2-x_1|\to 0}{lim}|f_n(\theta ,x_1,x_2)-1|\le \underset{|x_2-x_1|\to 0}{lim}F\left(M\right)|x_2^{\left(n\right)}-x_1^{\left(n\right)}|\le F\left(M\right){\displaystyle \frac{1}{n}}\end{array}$$

uniformly for all $\left|\theta \right|\le M.$ Notice that ${lim}_{n\to \infty }F\left(M\right){\displaystyle \frac{1}{n}}=0.$ Thus, by Theorem A5, we obtain the conclusion of Corollary A2. □