Mechanical Response of Mudstone Based on Acoustic Emission Fractal Features

Abstract

In this study, the effect of the stress amplitude on the mechanical behavior of mudstone was systematically investigated by cyclic loading and unloading experiments and acoustic emission (AE) monitoring. The results show that at low-stress amplitudes, mudstone specimens show better elastic recovery ability, lower damage accumulation and higher structural stability. At high-stress amplitudes, the irreversible damage of the mudstone increases significantly, the internal fractures gradually expand and penetrate through, and the risk of instability increases significantly. This is manifested by the gradual increase in cumulative irreversible strain of mudstone at different stress amplitudes, up to 0.144%. In addition, different stress amplitudes have significant effects on energy evolution characteristics, with low-stress amplitudes mainly showing elastic deformation and a high percentage of recoverable energy, while high-stress amplitudes show a high percentage of dissipated energy. Under the condition of high-stress amplitude, such as the mudstone specimen #4, the percentage of tensile failure is 81.15%. Tensile failure dominates at all stress amplitudes, where the failure mechanism within mudstone is mainly characterized by the extension of tensile-type fractures. Through the multifractal analysis of AE signals, this study reveals the effect of the stress amplitude on the fracture extension mode and failure mechanism of mudstone. As the stress amplitude increases, Δα and Δf show an increasing trend. This indicates that the fracture extension process transforms from a relatively homogeneous and simple mode to a more inhomogeneous and complex mode. This transformation reflects the nonlinear and multiscale fracture characteristics of mudstone under high-stress conditions. The results of this study help to understand the mechanical behavior of mudstone under cyclic loading during coal mining and provide theoretical support for safe coal production.

1. Introduction

As the main energy resource in China, coal occupies an irreplaceable position in the development of the national economy [1,2,3]. With the large-scale development of coal resources, mining activities have gradually advanced to deep and complex geological conditions [4,5,6,7]. In the mining process, the stability of the overlying rock layer is crucial to the safe production of the mine and the efficient utilization of resources [8]. As an important part of the overlying rock formation, the mechanical properties of mudstone directly affect the stability of the formation and the safety of the mine. However, stress changes caused by mining disturbances have a significant impact on the mechanical behavior of mudstone, which can easily lead to deformation and failure of the rock formation and increase the risk of coal mine safety [9,10]. In the process of coal mining, the change in the stress amplitude under cyclic loading can cause the emergence, expansion and penetration of internal fractures in mudstone, which, in turn, affects the stability of the whole rock formation. At present, insufficient attention has been paid to the failure mechanism of mudstone under cyclic loading, making it difficult to prevent geologic disasters caused by mudstone failure in a timely manner. Mudstone is frequently encountered in mining and construction projects [11,12,13]. The stability of mudstone is essential to ensure the safety and longevity of infrastructure such as railroads, roads and tunnels. Whether from transportation, mining-induced vibrations or cyclic loading conditions from natural processes, the mechanical properties of mudstone can be significantly affected. This study aims to fill this gap by providing new experimental data and insights.

The problem of rock failure has been an important topic in the field of rock mechanics [14,15,16,17]. Regarding the study of mudstone, more cyclic loading and unloading experiments have been conducted [18,19]. Li et al. [20] investigated the mechanical properties and expansive characteristics of deeply buried mudstone under different stress loading rates, and concluded that the mudstone strength parameters, deformation and expansion parameters have a significant stress loading rate dependence. Zhang et al. [21] found that the side-limiting effect of the perimeter pressure increased the specimen bearing capacity, and the total energy density, elastic strain energy density, and dissipated energy density increased with an increase in the perimeter pressure. And in the pre-peak stage, the difference between the elastic strain energy density of the mudstone and the dissipated energy density increased with an increase in the number of cyclic loadings and unloadings. Wang et al. [22] carried out variable amplitude-graded cyclic loading tests on saturated mudstone and found that the damping ratio tends to stabilize with an increase in the number of cycles when the stress amplitude is constant. And the larger the stress amplitude, the larger the damping ratio. Xu et al. [23] defined damage variables from the energy point of view and predicted the fatigue life of specimens in fatigue tests with different load ceilings. The fatigue life of mudstone specimens was predicted to have a power function relationship with the load level. In summary, many researchers have studied the mechanical characteristics of mudstone [24]. However, the complex mechanical behaviors exhibited by mudstones when subjected to mining disturbances, especially the failure mechanism under cyclic loading considering the stress amplitude effect, have not been fully investigated.

Acoustic emission (AE) technology, as a sensitive and non-destructive detection method, is able to capture the microscopic fracture activities of mudstone in real-time during the stressing process [25,26,27,28,29]. By analyzing the AE signals, the pattern of fracture expansion and failure mode within the mudstone can be deeply revealed. Yu et al. [30] used the AE technique to systematically analyze the effects of stress ceiling and loading frequency on the damage and crack extension patterns of red-bedded mudstone. It was found that the cracks produced under cyclic loading of red-bedded mudstone were generally dominated by tension cracks. Li et al. [31] used the AE technique to study water-bearing mudstone under low strain rate dynamic loading, and the results showed that the AE characteristic parameter law indicated that the mudstone went through four fracture evolution stages during the loading process, namely, the initial damage, damage aggravation, damage quiescence (aggravation) and damage development. And the Kaiser effect was more obvious at the lower level of the factors in the dynamic loading perturbation stage, and the Felicity effect was more significant at the higher level of the factors. However, due to the nonlinear and multiscale characteristics of the AE signals of mudstone under cyclic loading, it is difficult for traditional analytical methods to comprehensively describe its complex dynamic behavior [32,33,34]. Multifractal theory can effectively describe the nonlinear characteristics of complex systems and has been gradually introduced into the study of the rock fracturing process in recent years [35,36,37]. Some scholars have analyzed the AE signals using multifractal spectra to reveal the multiscale characteristics of the rock rupture process [38,39,40]. However, there is still a gap in the study of the multifractal characterization of AE signals for mudstone under cyclic loading.

In summary, there are obvious research gaps in existing studies on the stress amplitude effect and multifractal characteristics of AE signals in mudstone. Therefore, this study intends to focus on the mechanical response of mudstone under cyclic loading, considering stress amplitude effects by means of cyclic loading and unloading experiments and AE monitoring. First, the deformation and energy characteristics of mudstone under different stress amplitudes are obtained. Second, the AE counting characteristics are analyzed; then, the failure modes of mudstone under different stress amplitudes are elucidated; finally, the relationship between AE counting multifractal characteristics and fracture extension is revealed. The results of this study have important implications for the stability and mechanical behavior of mudstone in mining and infrastructure applications.

2. Methods

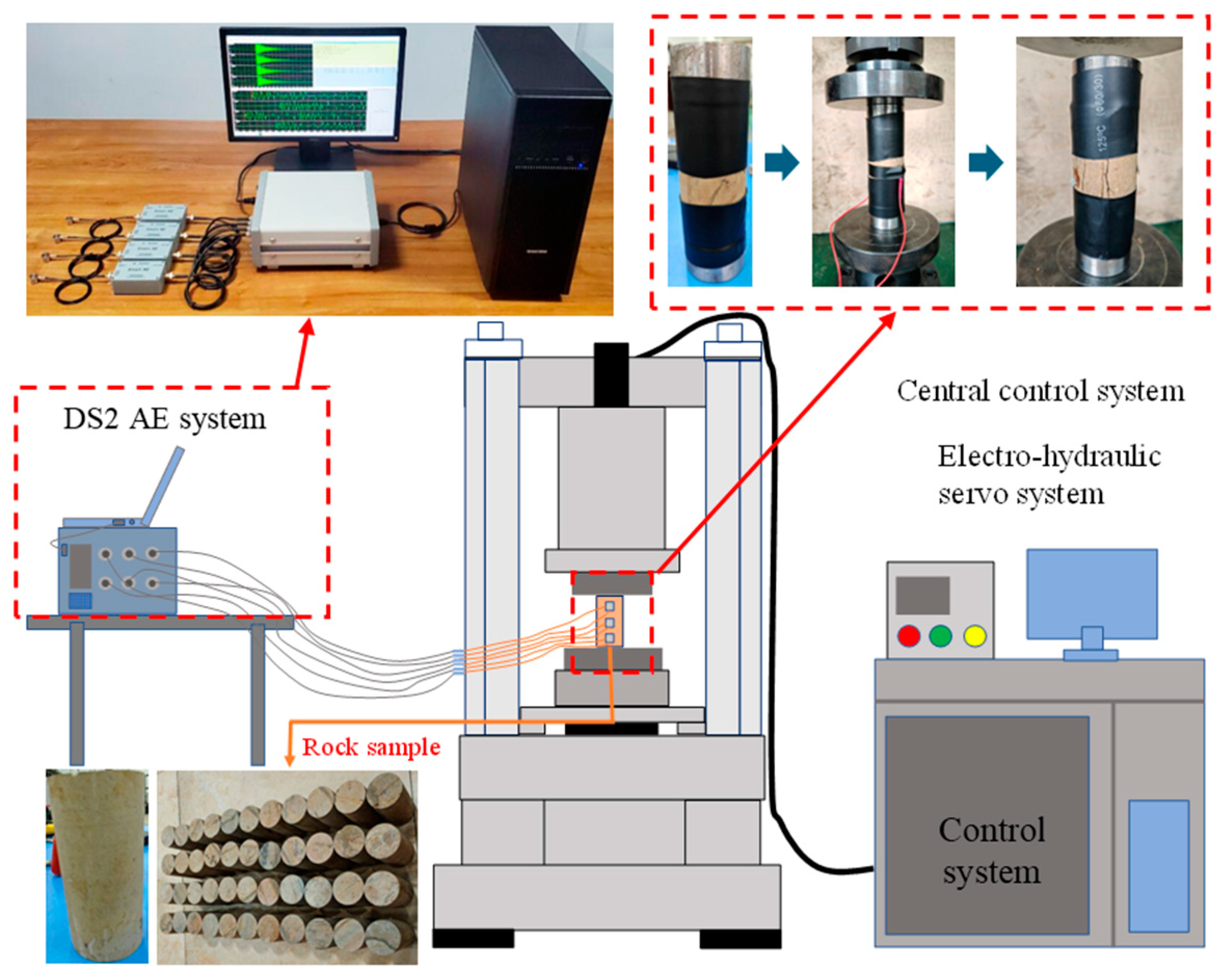
2.1. Specimens and Experimental System

The mudstone specimens used in this study were collected from a coal mine in Shaanxi, China. The overlying strata of the production working face of the mine are dominated by mudstone. The mudstone specimens used in the experiments were cylindrical in shape. The surface of the specimen was meticulously polished to ensure flatness so as to minimize the effect of uneven forces on the results during the experiment. In addition, the weight and p-wave velocity of the mudstone specimens were selected. Mudstone specimens with weights ranging from 390 to 400 g and wave velocities ranging from 3.85 to 3.95 km/s were selected for the experiments. The weight range was selected to ensure uniformity in specimen density and minimize variability in mechanical properties caused by differences in mineral composition or porosity. Similarly, the p-wave velocity range was chosen to exclude specimens with significant pre-existing microcracks or defects, as p-wave velocity is a sensitive indicator of material integrity. By standardizing these parameters, we ensured that the starting conditions for all specimens were comparable, thereby enhancing the reproducibility of the experiments and the reliability of the observed results. The basic parameters of the mudstone specimens are shown in

Table 1. Basic parameters of the specimen.

Number	Diameter (mm)	Height (mm)
#1	49.37	100.71
#2	49.62	100.79
#3	49.57	100.79
#4	49.55	100.62

, and the pictures of the samples are shown in Figure 1. After previous tests, the uniaxial compressive strength (UCS) of the mudstone specimen was 23 MPa.

As shown in Figure 1, the experimental system included the DS2 AE system, electro-hydraulic servo testing machine and control system. The DS2 AE system was used to monitor the AE signals of the mudstone specimen during the loading process and to capture and analyze the process of fracture germination and expansion with the sensor close to the surface of the mudstone specimen. The AE activity during loading was recorded in real-time. To ensure that a complete AE signal was captured, the sampling frequency of the AE system was established at 1.0 MHz. An electro-hydraulic servo system was used to apply uniaxial cyclic loading to the specimen, which is capable of providing precise force and displacement control to simulate the cyclic stress environment to which the subsurface rock mass is subjected and to ensure the stability and repeatability of the loading. The control system consisted of a computer and supporting software, which monitored and adjusted the parameters of the loading procedure in real-time and realized the synchronous data acquisition and processing with the AE equipment. During the experiment, mudstone specimens were fixed to ensure that no deflection occurred during loading, followed by cyclic loading, and the stress–strain data and the AE signals were recorded in real-time, which were used to analyze the mechanical properties and fracture extension behavior of mudstone under cyclic stress.

2.2. Experimental Methods

In this study, the uniaxial cyclic loading method was used to investigate the mechanical properties of mudstone specimens, and the loading path is shown in Figure 2. The experimental variables were stress amplitudes of 8%, 16%, 24% and 32% UCS. Two cyclic phases were set up to simulate the stress perturbations suffered by the rock in actual working conditions. The cyclic stress fluctuated at 64% UCS, i.e., the upper cyclic limit of the first cyclic stage and the lower cyclic limit of the second cyclic stage was 64% UCS. The stress paths were described by taking the path of an 8% UCS stress amplitude as an example. First, loading was performed to the lower limit of the first cyclic stage, 56% UCS, and then cyclic loading and unloading with a stress amplitude of 8% UCS was started with a cyclic upper limit of 64% UCS. Twenty cycles are performed. Then, the loading of the second cyclic stage was started. First, load to the lower cyclic limit of 64% UCS, then start cyclic loading and unloading with a stress amplitude of 8% UCS, with a cyclic upper limit of 72% UCS. The number of cycles was 20. Loading was then continued until specimen failure. The loading rate throughout the experiment was 400 N/s. Through the two-stage cyclic loading and unloading, the experiment was designed to simulate the response of the subsurface rock under multiple stress perturbations and to reveal the deformation and failure mechanisms of mudstone under different stress amplitude conditions. In conjunction with previous research [41,42,43], the 8%, 16%, 24% and 32% UCS stress amplitudes were selected to simulate a range of stress conditions associated with the actual mining environment. The low-stress amplitudes (8% and 16% UCS) simulated conditions subjected to lower levels of disturbance, while higher amplitudes (24% and 32% UCS) reflected conditions subjected to higher levels of disturbance. These stress levels provided a comprehensive framework for studying the progressive damage and fracture evolution of mudstone under cyclic loading.

3. Results and Discussion

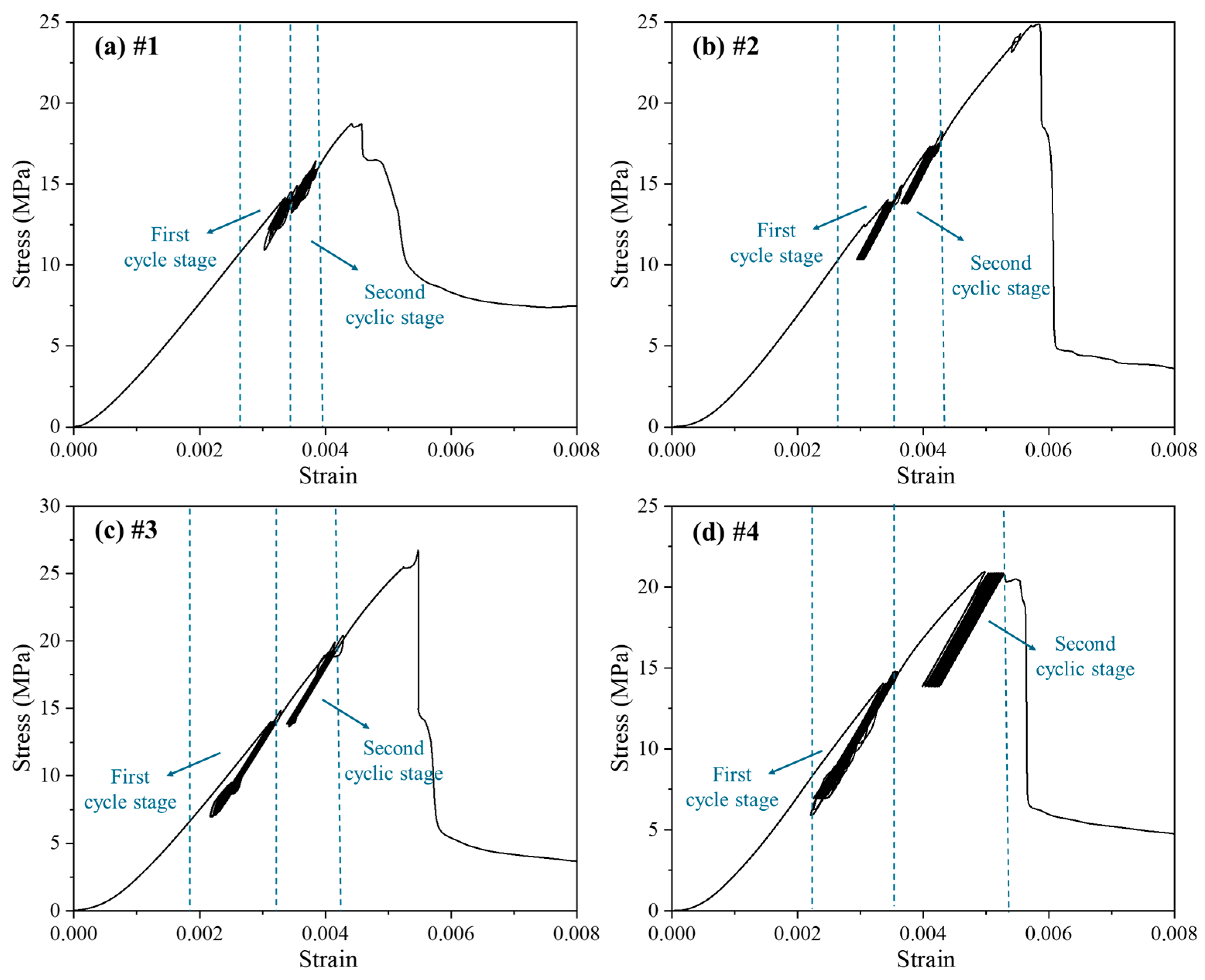
3.1. Stress–Strain Characteristics

Stress–strain curves are important data reflecting the mechanical behavior of mudstone specimens, which can reveal the relationship between stress and strain in mudstone specimens during the loading process [44,45]. Studying the stress–strain curves of mudstone specimens under different stress amplitudes can provide an in-depth understanding of the deformation characteristics of mudstone under cyclic loading conditions [46,47].

Figure 3 shows the stress–strain curves of mudstone specimens at different stress amplitudes. It can be seen that with an increase in the stress amplitude, the stress–strain curves showed obvious changes. In the first cycle stage, mudstone specimens showed relatively linear elastic deformation characteristics at lower stress amplitudes, the slope of the curve was larger, and the loading and unloading paths were almost coincident, which indicated that the deformation of mudstone at this stage is very reversible and the energy loss is small. With an increase in the stress amplitude, especially in the second cycle stage, the curve started to show an obvious hysteresis loop. This indicated that the degree of plastic deformation of mudstone specimens is greater at higher stress amplitudes. At this time, mudstone specimens began to show plastic deformation and localized damage, and the loading and unloading paths were gradually separated, and the hysteresis effect was obviously aggravated. In addition, the peak strains of mudstone specimens at different stress amplitudes were 0.457%, 0.584%, 0.541% and 0.551%, respectively. This showed the overall trend of increasing peak strain in mudstone with increasing stress amplitudes. The mudstone specimen #1, with a low-stress amplitude, had the lowest peak strain, which indicated that the mudstone specimen had less plastic deformation and less damage accumulation at low-stress amplitudes.

3.2. Deformation Evolution

Figure 4 demonstrates the evolution of deformation parameters of mudstone specimens under different stress amplitudes, including loading elastic modulus, unloading elastic modulus, load–unload response ratio (LURR) and cumulative irreversible strain (CIS). By analyzing the evolution characteristics of these key parameters under different stress amplitudes, the deformation behavior and damage evolution mechanism of mudstone during cyclic loading can be deeply understood [48,49].

The loading elastic modulus and unloading elastic modulus reflected the stiffness characteristics of mudstone during loading and unloading, which is an important parameter to measure the ability of material to resist deformation. As can be seen from Figure 4, the loading elastic modulus of mudstone remained relatively stable and high at lower stress amplitudes, indicating that the mudstone had a strong resistance to deformation. The unloading elastic modulus was usually higher than the loading elastic modulus and decreased gradually during the cyclic loading process. This phenomenon indicated that the damage inside the mudstone from deformation was not fully recovered during unloading, and the loss of stiffness gradually increased with an obvious hysteresis effect. It was not difficult to find that the difference between the loading and unloading elastic modulus of mudstone was small under the condition of low-stress amplitudes, which indicated that the elastic deformation characteristics of mudstone are strong, the damage degree is low, and the failure of cyclic loading on mudstone structure is relatively limited. In addition, the average elastic modulus of mudstone specimen #4 was 6.587 GPa, which was lower than that of specimens #1, #2 and #3, which indicated that under high-stress amplitudes, the degree of accumulation of plastic damage in mudstone was large, the structural stiffness decreased, and the specimen showed significant irreversible deformation characteristics, which led to a decrease in the modulus of elasticity.

The LURR reflects the response ratio of mudstone during loading and unloading, which is an important parameter for measuring damage accumulation and rock stability. At lower stress amplitudes, the LURR was at a lower level, and the fluctuation was not obvious, which indicated that the mudstone deformed less under low-stress conditions, the damage was limited, the difference between loading and unloading was not large, and the mudstone had high stability. With an increase in the stress amplitude, the LURR started to increase significantly with fluctuations. This indicated that at higher stress amplitudes, the damage inside the mudstone gradually accumulated, and the difference in response between the loading and unloading processes increased, indicating that the stability of the specimen gradually weakened and the hysteresis effect intensified. The LURR decreased sharply at the initial stage of the cycling, which may be attributed to the local fracture expansion and stress release, leading to stress reorganization and local energy release inside the mudstone. In addition, at low-stress amplitudes, the CIS increased more slowly, indicating that the mudstone had less plastic deformation under this condition and mainly exhibited elastic deformation. With an increase in the stress amplitude, the CIS increased rapidly, especially in the late stage of cyclic loading under high-stress amplitudes. The CIS showed an accelerated rising trend, indicating that the damage to the mudstone was intensified, and the internal fracture expanded gradually, which led to a significant increase in plastic deformation. It can also be seen in Figure 4 that the growth of CIS sometimes stagnated temporarily, forming a plateau stage, which indicated that the fracture expansion of mudstone tended to be temporarily stabilized in a specific stage and expansion tended to be temporarily stabilized. However, with further loading, this equilibrium was broken, and the CIS increased significantly again, reflecting the aggravation of damage and structural instability. In addition, the CIS of mudstone specimens at different stress amplitudes was 0.078%, 0.062%, 0.139% and 0.144%, respectively. The CIS of mudstone specimens showed an increasing trend with increasing stress amplitudes. This indicated that the larger the stress amplitude, the more significant the plastic deformation of mudstone and the greater the damage accumulation.

LURR is a dimensionless parameter. A higher LURR indicates greater inelastic deformation and energy dissipation, which is usually associated with microfracture extension within mudstone. This parameter is sensitive to damage evolution and can be used as an early indicator of mudstone instability. On the other hand, CIS quantifies the total irreversible strain accumulated during cyclic loading. CIS reflects the progressive damage inside the specimen, and larger values indicate more severe degradation of the bearing structure of specimens. Corresponding to Figure 5, when the CIS was larger, it indicated that the dissipative energy accumulated in the specimen at this time was larger, and the elastic energy accounted for less.

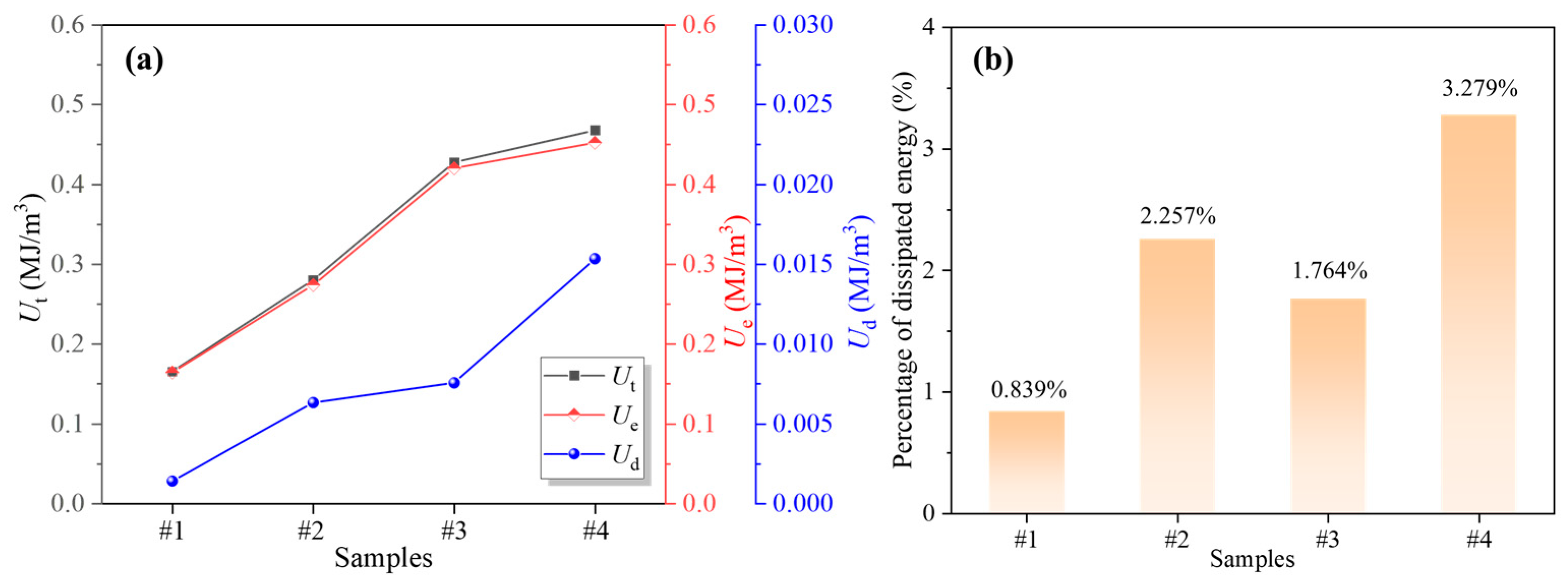
3.3. Energy Characteristics

In rock mechanics research, understanding the energy evolution characteristics of mudstone during cyclic loading under different stress amplitude conditions is important for revealing the deformation and failure mechanisms of mudstone [50,51]. A completely closed system can be viewed as a system that has no heat, light or other forms of energy exchange with the outside world [52]. Therefore, as shown in Figure 5, the strain energy was calculated, as shown in Equation (1) [53,54].

$$\left\{\begin{array}{l}{U}_{\mathrm{t}}={\displaystyle {\int }_0^{{\epsilon }^{\prime }}{f}_1}(\epsilon )\mathrm{d}\epsilon \\ U_{\mathrm{e}}={\displaystyle {\int }_{{\epsilon }^{″}}^{{\epsilon }^{\prime }}{f}_2}(\epsilon )\mathrm{d}\epsilon \\ U_{\mathrm{d}}=U_{\mathrm{t}}-U_{\mathrm{e}}={\displaystyle {\int }_0^{{\epsilon }^{\prime }}{f}_1}(\epsilon )\mathrm{d}\epsilon -{\displaystyle {\int }_{{\epsilon }^{″}}^{{\epsilon }^{\prime }}{f}_2}(\epsilon )\mathrm{d}\epsilon \end{array}\right.$$

(1)

where U_t is the total strain energy, MJ/m³; U_e is the elastic strain energy, MJ/m³; and U_d is the dissipated strain energy, MJ/m³.

Figure 5. The energy calculation [53].

Figure 5. The energy calculation [53].

Figure 6 shows the characterization of the evolution of the strain energy with the dissipated energy share during cyclic loading of mudstone specimens under different stress amplitude conditions. From Figure 6a, it can be found that the input energy, elastic energy and dissipated energy all increased with an increase in stress amplitudes during cyclic loading. This is because an increase in the stress amplitude increases the energy applied by the system to the sample during each cyclic loading, which directly leads to an increase in the input energy. At the same time, as the stress amplitude increased, the deformation within the rock increased, resulting in an increase in the elastic energy stored in the mudstone. This indicated that the mudstone still had the ability to partially recover from deformation under high-stress amplitude conditions. However, high-stress amplitudes accelerated the crack initiation and extension, which intensified the accumulation of irreversible damage and led to an increase in dissipated energy. This also reflects that the brittle damage effect of mudstone is more significant at high-stress amplitudes, and the energy is consumed in a non-recovery manner. Figure 6b shows the evolutionary trend of the dissipated energy share during cyclic loading. The overall trend of dissipated energy percentage increased with increasing stress amplitudes. The mudstone specimen #1 had the lowest dissipated energy percentage of 0.839%. This indicates that under the condition of low-stress amplitudes, the deformation of rocks is mainly elastic; most of the energy is recovered in the unloading process, and only a small portion of the energy is dissipated through the generation of small fractures or friction loss. At high-stress amplitudes, the proportion of dissipated energy increased significantly. This reflects the continuous development of internal fractures in the rock and a gradual increase in the accumulation of irreversible damage to the material, leading to an increase in the loss of system energy. And this can be matched with the CIS results.

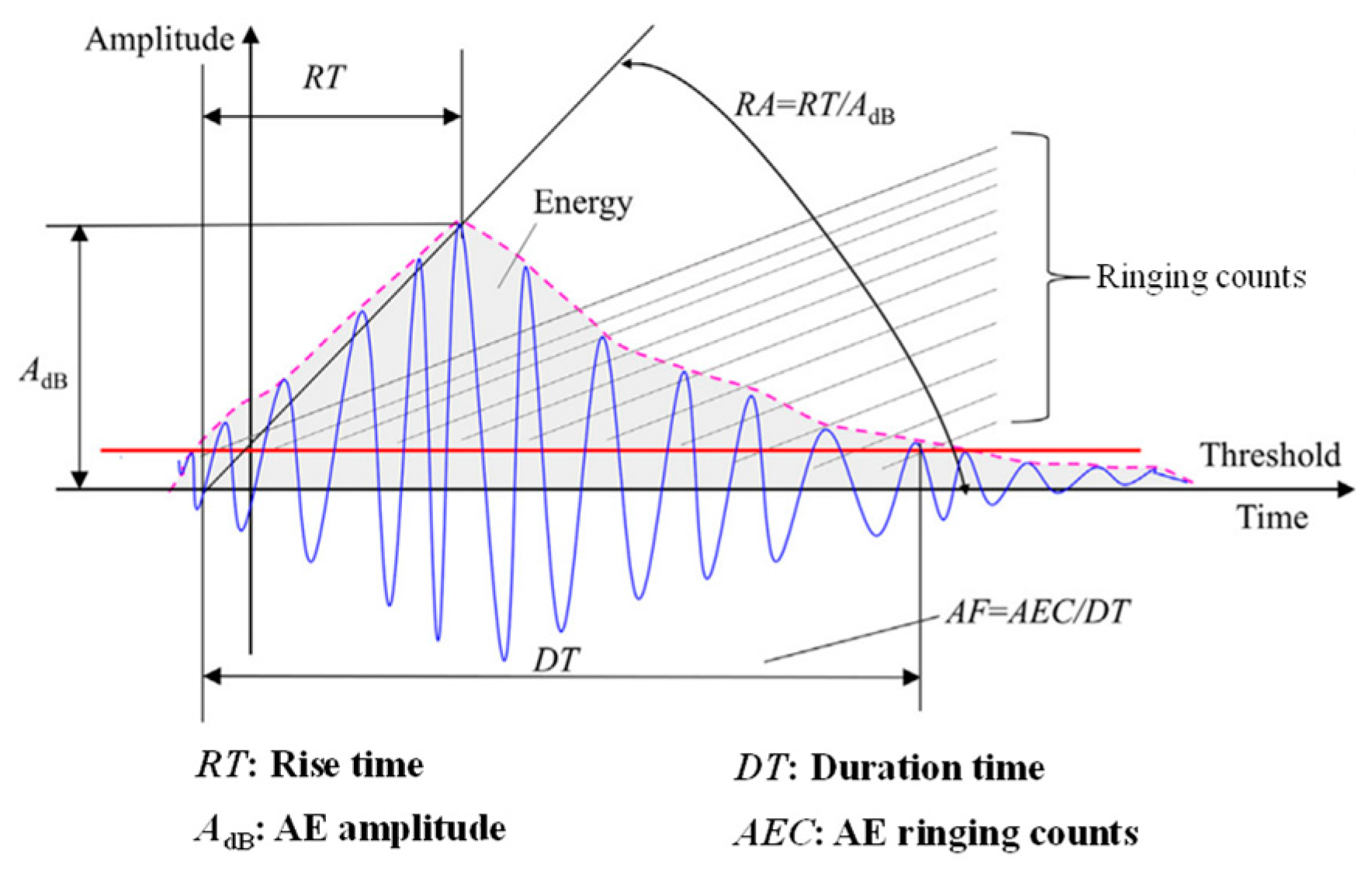
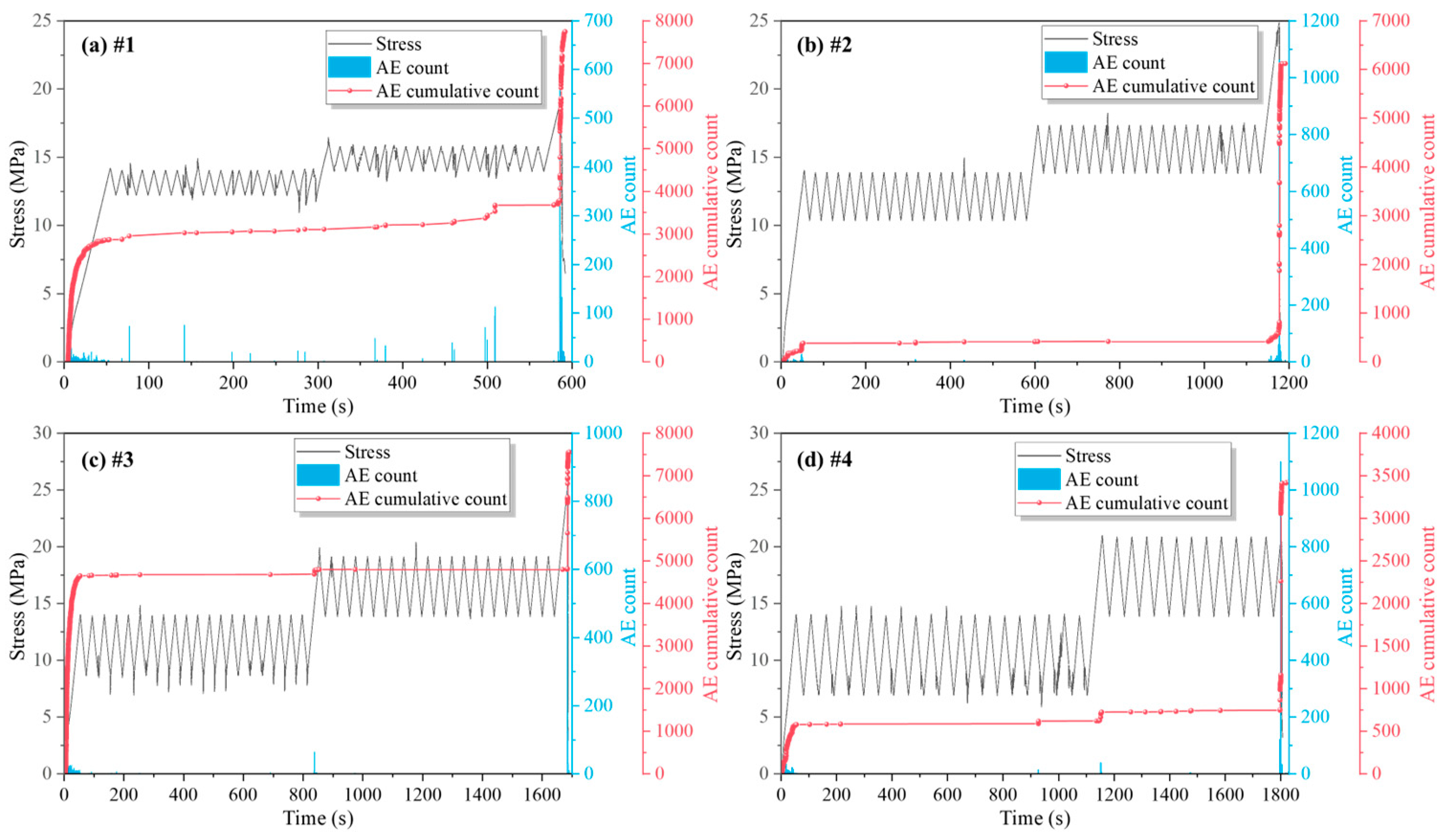
3.4. AE Count Characteristics

AE technology, as an important tool in rock mechanics research, can effectively capture the dynamic evolution characteristics of fractures within rocks and reveal the deformation and failure behavior of mudstone under different stress amplitude conditions [55,56]. As shown in Figure 7, the evolution of AE parameters, such as AE ringing counts and peak frequency, helps to better elucidate the fracture development and damage characteristics [57].

AE signals can reflect the emergence, expansion and interaction of internal fractures in materials, and the evolution characteristics of AE counts and AE cumulative counts can reveal the damage evolution and failure mechanism of mudstone during cyclic loading [58,59]. Figure 8 shows the evolution characteristics of AE counts and cumulative counts of mudstone specimens during cyclic loading under different stress amplitude conditions. At the early stage of loading, the AE ringing and AE cumulative counts of each specimen increased rapidly with high peaks. This phenomenon can be attributed to the role of the compaction stage. In this stage, due to the closure of the original fracture and the friction between the particles, a large amount of energy is released in the form of AE, resulting in a significant sudden increase in the AE counts. An increase in AE counts was found in the first of the two cyclic loading phases. Thereafter, as the number of cycles increased, the AE signal occurred less frequently, and the AE counts were lower. This phenomenon is consistent with the Kaiser effect. When the mudstone was loaded again after loading and unloading, the AE signal rarely occurred when the load did not exceed the maximum load of the previous loading. When coming to the late stage of loading and approaching failure, especially under high-stress amplitude conditions, the AE counts showed frequent peaks near the peak of each cycle of loading. This indicated that the fracture sprouting and expansion became more intense, the rock gradually tended to the destabilized state, and the damage of mudstone reached the critical point. In addition, at low-stress amplitudes, the growth of AE accumulation counts was slower and more stable, indicating that the process of rock damage accumulation was more gradual and gentler. At high-stress amplitudes, the AE accumulated counts showed a rapid growth trend, especially at the late-loading stage, and this growth showed a significant acceleration. This reflected that the fracturing activity inside the rock increased, and the damage accumulation was rapid under high-stress amplitudes.

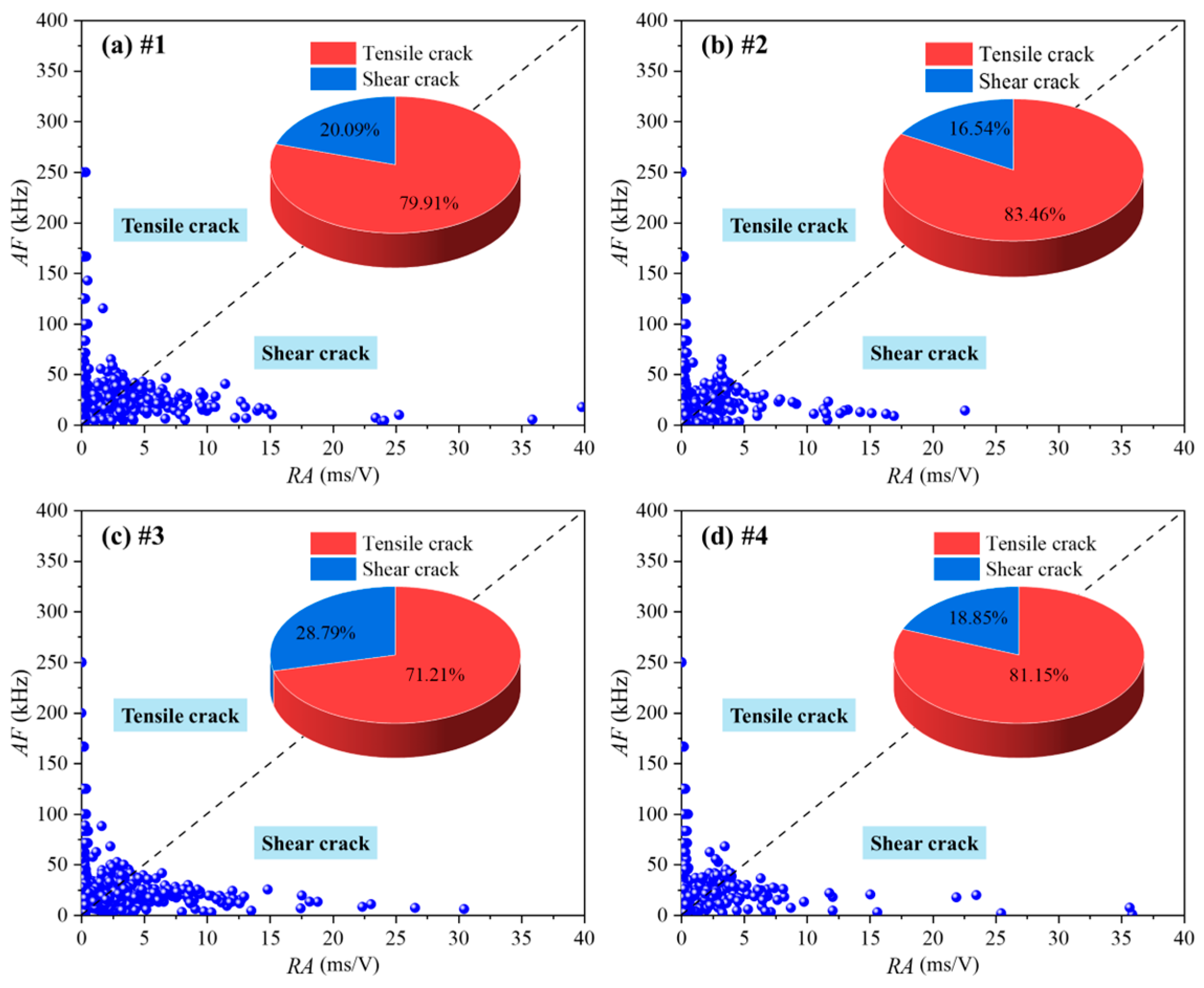
3.5. Failure Modes of Mudstone at Different Stress Amplitudes

In rock mechanics tests, the characteristic AE parameters RA (rise time/amplitude) and AF (average frequency) were used to determine the rupture mode of a material. Generally, tensile rupture produces an AE event characterized by a large AF and a small RA, and conversely, shear rupture produces an AE event characterized by a large RA and a small AF. This distinction is supported by several studies that correlate AE signal characteristics with specific fracture mechanisms in rocks and other brittle materials [60,61,62]. These studies were based on theoretical and experimental research that has shown that tensile cracks tend to release high-frequency signals with a sharp onset (low RA). In contrast, shear cracks produce signals with a long rise and lower frequency (high RA). The use of AF-RA plots to identify microfracture types is widely employed in rock mechanics studies. This approach is particularly advantageous in cyclic loading experiments where mixed-mode cracking may occur, providing more insight into the progressive damage evolution of mudstone specimens. In this study, diagonal lines were used to divide them, as shown in Figure 9.

Figure 10 illustrates the AE RA-AF distribution of mudstone at different stress amplitudes. It can be seen that tensile failure dominated in all mudstone specimens. And this is similar to the results of the previous study [31]. Under low-stress amplitude conditions, such as the mudstone specimen #1, the mudstone was mainly dominated by tensile failure, accounting for 79.91%. Under low-stress amplitudes, the stress concentration area inside the rock was prone to induce tensile cracks, and the percentage of shear failure was relatively low. Under the condition of high-stress amplitudes, such as mudstone specimen #4, the percentage of tensile failure was 81.15%, and the percentage of shear failure was 18.85%. This result indicated that tensile damage was still the main failure mode even under high-stress amplitude conditions, but the proportion of shear damage increased relative to low-stress amplitudes. Thus, as the stress amplitude increased, tensile failure still dominated, but the proportion of shear failure gradually increased. This is due to an increased interaction between fractures and frictional slip caused by an increase in stress levels.

3.6. Relationship Between Multifractal Features and Fracture Extension

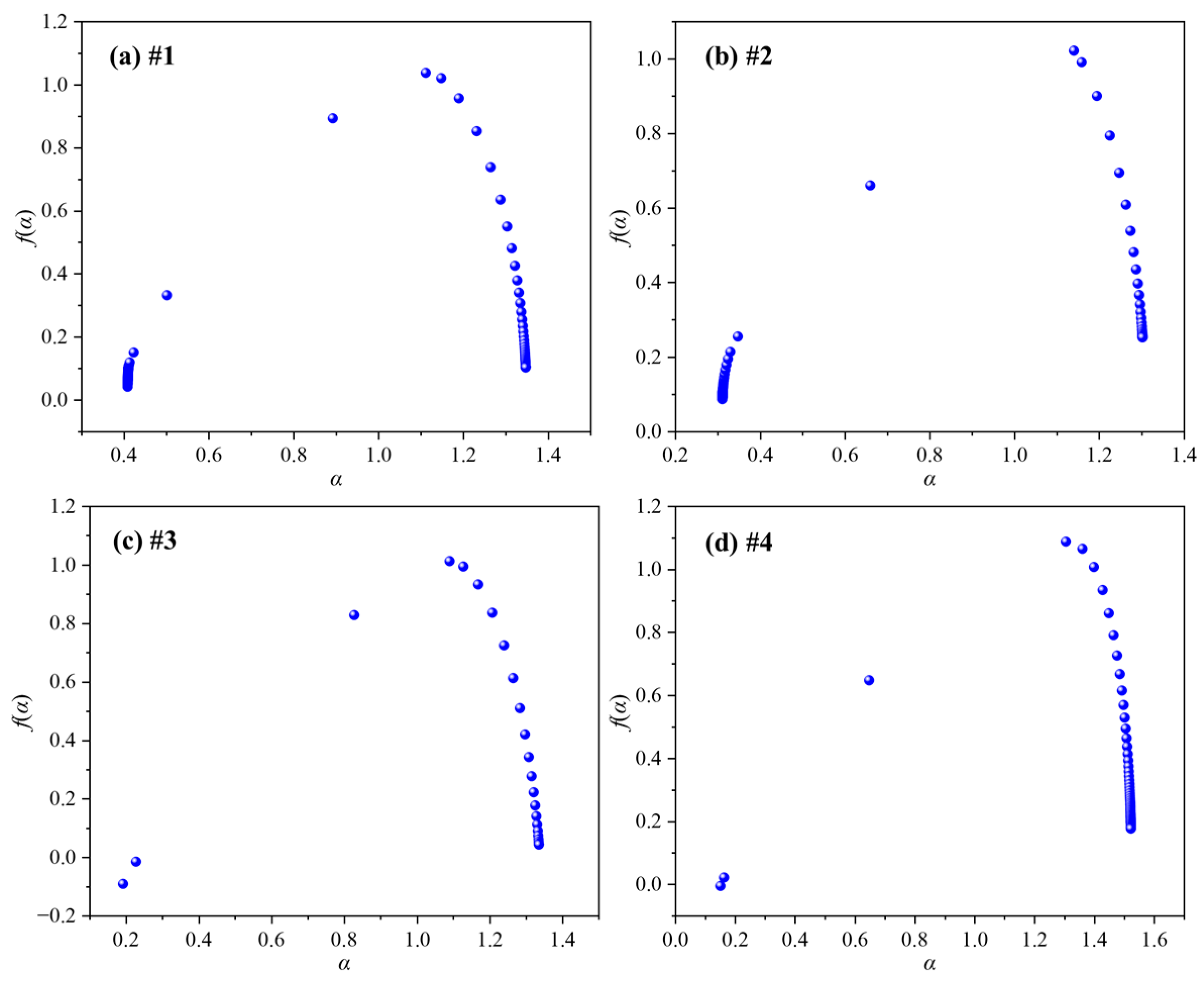
3.6.1. Multifractal Calculations

The AE signal can better reflect the extension of microfracture, but the AE data are also characterized by nonlinearity and discrete nature. Therefore, in order to further explore the deep information of AE time series, some scholars began to adopt multiple fractal theory to describe the instability and inhomogeneity of AE. The box dimension method is more widely used in it [63,64,65]. Therefore, in this study, the box dimension method was used to calculate the multifractal dimension spectra (referred to as multifractal spectra) of the AE time series of mudstone samples.

Defining the AE signal as a time series $\{x(t);t=1,2,\dots ,N\}$ with each subsequence of length $\epsilon$, the probability measure $\{P_t(k)\}$ for each subsequence, is shown in Equation (2).

$$P_t(\epsilon )={\displaystyle \frac{N_t}{{\displaystyle \sum N_t}}}$$

(2)

where $N_t$ is the sum of corresponding subsequence samples under different sample length divisions; t is the total number of subsequences; and ${\displaystyle \sum N_t}$ is the total number of samples.

According to fractal theory, the following relationship exists between the probability measure $\{P_t(\epsilon )\}$ and the measurement scale in the scale-free self-similar region:

$$\left\{P_t(\epsilon )\right\}\propto k^{\alpha }$$

(3)

where α is the singularity scaling index.

Denote the number of subsequences with the same index α as $N_{\alpha }(\epsilon )$, and the following relationship between $N_{\alpha }(\epsilon )$ and $\epsilon$ also exists:

$$N_{\alpha }(\epsilon )\propto {\epsilon }^{-f(\alpha )}$$

(4)

where f (α) is the dimension of the fractal subset of index α, which reflects the frequency of the subset represented by α appearing in the whole set of divisions. Since α can take infinitely many values in the range [α_min, α_max], f (α) is generally a smooth single-peaked function, and f (α) corresponding to different α constitutes a multifractal spectrum.

Physical statistics were used to obtain the fractional dimension values of the multifractal and the collocation function ${\chi }_q(\epsilon )$ was defined to describe the contribution of the probability measure $\{P_t(\epsilon )\}$, as shown in the following Equation (5).

$${\chi }_q(\epsilon )\equiv {\displaystyle \sum P_t}{(\epsilon )}^q-{\epsilon }^{\kappa (q)}$$

(5)

where q is the order of the statistical moments, $-\infty <q<+\infty$, and the magnitude of the q value characterizes the degree of inhomogeneity of the multiple fractal dimensions and q takes the value of [−60, 60] in this study. And, $\kappa (q)$ is the quality index, which is the characteristic function of the fractal behavior.

In turn, the power-exponential weighting process was used to divide the multifractal dimension into multiple regions of varying degrees, and the quality exponential function of the AE signal was determined to be:

$$\kappa (q)=\underset{\epsilon \to \infty }{\lim }{\displaystyle \frac{\ln {\chi }_q(\epsilon )}{\ln \epsilon }}$$

(6)

Further, using Legendre transformations

$$\left\{\begin{array}{l}\alpha ={\displaystyle \frac{\partial (\kappa (q))}{\partial q}}\\ f(\alpha )=\alpha (q)q-\kappa (q)\end{array}\right.$$

(7)

the multifractal spectrum of the AE signal was obtained by calculating the values of α and f (α) according to Equation (7).

In the multifractal spectrum α-f (α), the width Δα of the multifractal spectrum is defined as Equation (8) [66,67,68].

$$\Delta \alpha ={\alpha }_{\max }-{\alpha }_{\min }$$

(8)

where α_min and α_max denote the minimum and maximum singularity scaling indices, respectively; Δα can be a quantitative indicator for assessing the variability of the AE signals. Larger Δα indicates that the distribution between the subsets of the large and small probability measures is more uneven, resulting in a more uneven distribution of the AE signals and more drastic fluctuations in the indicators.

There is another important parameter in the multifractal spectrum, the fractal dimension difference Δf, which is defined as follows:

$$\Delta f=f\left({\alpha }_{\max }\right)-f\left({\alpha }_{\min }\right)$$

(9)

where Δf is the difference between the corresponding fractal dimensions of the large and small probability subsets in the AE time series, which can be interpreted as the ratio of the number of smooth subsets to the number of fluctuating subsets in the AE signals. The larger Δf is, the larger the probability of the small probability measure subset is, which indicates that the probability of occurrence of large-energy events in the AE signals is higher.

3.6.2. AE Counts Multifractal Features

Figure 11 shows the multifractal spectra of AE counts for mudstone samples with different stress amplitudes. It can be seen that the overall shapes of the multifractal spectra of mudstone specimens with different stress amplitudes were the same, and f (α) changed with an increase in α, indicating that the rupture process of mudstone specimens was similar, but the widths of the multifractal spectra were different, indicating that there were differences in the microscopic rupture characteristics of mudstone specimens with different stress amplitudes. The spectral width reflected the inhomogeneous distribution of AE signal frequencies, with larger values indicating greater variability and stronger multifractal features. At low-stress amplitudes, narrower spectral widths indicated relatively uniform energy release dominated by simple fracture extension modes. At high-stress amplitudes, the spectral width increased, reflecting more complex fracture patterns. Wider spectral widths corresponded to more energy release, complex fracture interactions and multiscale fracture processes.

Specifically, Figure 12 shows the evolution characteristics of Δα and Δf for mudstone samples at different stress amplitudes. The Δα of mudstone samples at different stress amplitudes was 0.938, 0.992, 1.144 and 1.373, respectively, and the Δα tended to increase with an increase in the stress amplitude. In addition, the Δf of mudstone specimens at different stress amplitudes was 0.061, 0.166, 0.134 and 0.182, respectively, and the Δf also showed a similar increasing trend with increasing stress amplitudes. This indicated that the specimen underwent failure with a small probability of large-scale fracture, which led to a more complex failure mode.

3.6.3. Fracture Expansion Mechanism Based on AE Multifractal Features

The multifractal parameters Δα and Δf are able to quantitatively characterize the fracture extension of mudstone specimens to some extent [69,70]. However, only the complexity of fracture extension can be characterized, while the specific degree of fracture extension cannot be quantified.

The failure behavior of mudstone under different stress amplitudes can be explored in depth from the perspective of the fracture expansion mechanism. First, an increase in stress amplitudes makes the stress inside the mudstone specimen change, leading to an increase in the stress concentration area, and the microcracks are more likely to sprout and expand. In the pre-peak stage, the ringing counts of AE signals are unevenly distributed, and small signals contribute more to the AE time series, which implies that the microfracture events show a high degree of complexity and inhomogeneity in time and space. Second, an increase in Δf indicates that during the failure process, the large-scale rupture events have a more significant effect on the overall damage pattern, although they have a smaller probability of occurrence. Under high-stress amplitudes, the energy accumulation inside the mudstone specimen reaches a critical point, and the energy release mode is more inclined to form large-scale fractures. Although the number of these large-scale fracture events is small, their energy release is huge and plays a dominant role in the failure of the specimens, leading to an increase in the complexity of the failure mode.

An increase in Δf in the multifractal spectrum reflects an increased change in the extremes of the probability distribution, which implies the existence of low-probability but high-impact large-scale events in the AE signal. The occurrence of these large-scale fracture events significantly increases the connectivity and complexity of the fracture network, which further affects the mechanical behavior and stability of the rock.

Therefore, with an increase in the stress amplitude, the fracture extension process transforms from a relatively homogeneous and simple pattern to a more inhomogeneous and complex pattern. This transformation reflects the nonlinear and multiscale fracture characteristics of mudstone under high-stress conditions, which reflects the advantage of multiple fractal theory in describing the behavior of complex systems.

From a practical point of view, the results of this study have important implications for the design and maintenance of infrastructure in mudstone-dominated areas. The progressive weakening of mudstone mechanical properties observed under cyclic loading highlights the importance of incorporating cyclic stress effects into stability assessment. Future research will focus on expanding mudstone specimen numbers and types and exploring the mechanical behavior of mudstone under different cyclic loading conditions. In addition, quantitative analysis of mudstone fracture distributions, such as computed tomography scanning, was used to correspond with AE multifractal characterization.

4. Conclusions

In this study, mechanical experiments of mudstone under cyclic loading considering the effects of the stress amplitude were carried out. This study fills the insufficiency of the existing research on the mechanical properties of mudstone under the stress amplitude effect and provides important theoretical and practical support for the safe production of coal. Several conclusions can be outlined:

(1)

Under low-stress amplitudes, mudstone shows better elastic recovery ability and less damage accumulation, and each deformation parameter is kept at a relatively stable level, indicating that the stability of the specimen is better. Under high-stress amplitudes and cyclic loadings, the LURR fluctuation of mudstone increases, the CIS rises rapidly, and the loading and unloading elastic modulus decreases significantly, indicating that the internal fracture of the specimen gradually expands and penetrates through, the plastic deformation accumulates, the stiffness decreases and the stability of the structure is gradually lost;

(2)

Different stress amplitudes significantly affect the energy evolution characteristics of mudstone specimens during cyclic loading. At low-stress amplitudes, the mudstone mainly experiences elastic deformation, and most of the energy can be recovered with less damage. At high-stress amplitudes, the mudstone experiences significant irreversible damage and shows a high percentage of dissipated energy;

(3)

With an increase in the stress amplitude, the accumulated AE counts show an accelerated growth trend. This rapid increase in cumulative AE reflects the irreversible damage accumulation characteristic of mudstone under high-stress amplitudes and indicates that the risk of material destabilization under high-stress conditions increases significantly. Tensile failure dominates at all stress amplitudes, where the failure mechanism within mudstone is mainly characterized by the extension of tensile-type fractures;

(4)

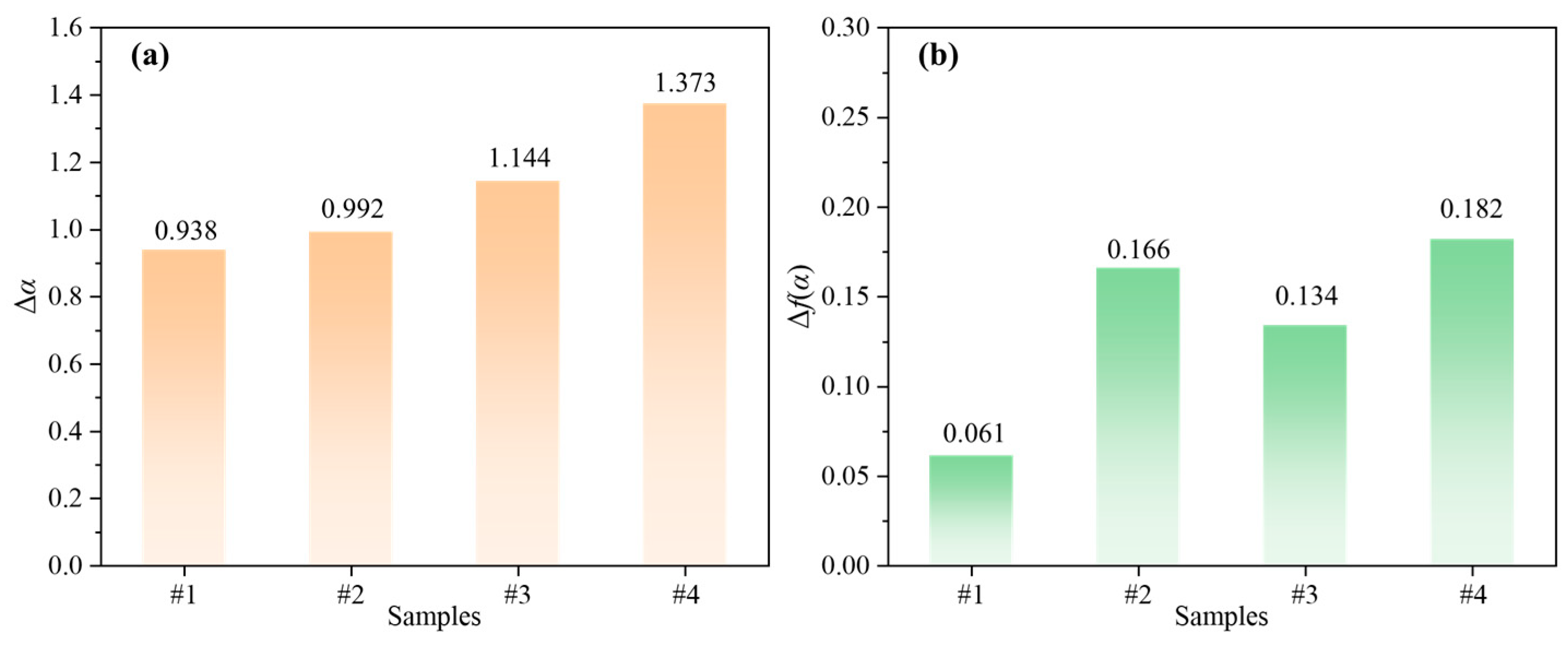
As the stress amplitude increased, Δα and Δf show an increasing trend. This indicates that the fracture extension process shifts from a relatively uniform and simple pattern to a more heterogeneous and complex pattern. This transformation reflects the nonlinear and multiscale fracture characteristics of mudstone under high-stress conditions.