Generalized Fractional Integral Inequalities Derived from Convexity Properties of Twice-Differentiable Functions

Abstract

This study presents novel formulations of fractional integral inequalities, formulated using generalized fractional integral operators and the exploration of convexity properties. A key identity is established for twice-differentiable functions with the absolute value of their second derivative being convex. Using this identity, several generalized fractional Hermite–Hadamard-type inequalities are developed. These inequalities extend the classical midpoint and trapezoidal-type inequalities, while offering new perspectives through convexity properties. Also, some special cases align with known results, and an illustrative example, accompanied by a graphical representation, is provided to demonstrate the practical relevance of the results. Moreover, the findings may offer potential applications in numerical integration, optimization, and fractional differential equations, illustrating their relevance to various areas of mathematical analysis.

1. Introduction and Preliminaries

Inequality theory plays an indispensable role in mathematics due to its broad range of applications across scientific and engineering disciplines [1]. Among the significant results in this field is the Hermite–Hadamard (H–H) inequality, which is substantial for studying convex functions (CFs) [2]. This result has inspired extensive research on its extensions and generalizations, leading to the trapezoidal, midpoint, and Simpson-type inequalities [3,4,5]. These advancements have enhanced the applicability of inequalities in analytical and numerical approaches.

The H–H inequality, attributed to C. Hermite and J. Hadamard [6], characterizes important properties of CFs. Let $Y:I\to \mathbb{R}$ be a CF defined on a real interval I. For any $\lambda ,\sigma \in I$ such that $\lambda <\sigma$, the following inequality is satisfied:

$$\begin{array}{c}\hfill Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\le {\displaystyle \frac{1}{\sigma -\lambda }}\underset{\lambda }{\overset{\sigma }{\int }}Y\left(\varpi \right)d\varpi \le {\displaystyle \frac{Y\left(\lambda \right)+Y\left(\sigma \right)}{2}}.\end{array}$$

(1)

For a concave function Y, the inequalities in (1) hold in reverse order.

Recent studies have emphasized deriving inequalities like trapezoid and midpoint-type inequalities to estimate the two extremities of inequality (1). For instance, ref. [7] explored trapezoid inequalities for CFs, while midpoint-type inequalities were initially discussed in [8]. Fractional extensions of midpoint-type inequalities were analyzed by Iqbal et al. in [9]. Sarikaya et al. generalized inequality (1) to fractional versions, and proposed corresponding trapezoid-type inequalities [10]. H–H inequalities for coordinated CFs were developed in [11], with further extensions in [12,13]. Using generalized fractional integrals, Sarikaya and Ertuğral examined related H–H, trapezoid, and midpoint inequalities in [14]. Additional insights into these inequalities are available in [15,16,17,18] and related works.

The mathematicians have also explored twice-differentiable CFs, resulting in numerous inequalities. For instance, Barani et al. [19] derived inequalities associated with H–H formulations. Mohamad et al. [20] extended fractional integral inequalities of midpoint and trapezoid types to these functions. Sarikaya and Aktan [21] developed Simpson and H–H-type inequalities for functions with the absolute value of their derivatives being convex. Budak et al. [22] investigated the midpoint and trapezoid inequalities for functions characterized by the convexity of their absolute second derivatives. Further details can be found in [23,24,25,26].

We begin by presenting essential definitions and concepts needed for the discussion. The concept of generalized fractional integrals was introduced by Sarikaya and Ertuğral [14] as follows:

Definition 1

([14]). Let $\Theta :[0,\infty )\to [0,\infty )$ be a function satisfying ${\int }_0^1{\displaystyle \frac{\Theta \left(\nu \right)}{\nu }}d\nu <\infty$. The generalized fractional left and right integral operators are given as follows:

$$\begin{array}{c}\hfill {}_{\lambda +}{I}_{\Theta }Y\left(\varpi \right)={\int }_{\lambda }^{\varpi }{\displaystyle \frac{\Theta \left(\varpi -\nu \right)}{\varpi -\nu }}Y\left(\nu \right)d\nu ,\varpi >\lambda ,\end{array}$$

(2)

and

$$\begin{array}{c}\hfill {}_{\sigma -}{I}_{\Theta }Y\left(\varpi \right)={\int }_{\varpi }^{\sigma }{\displaystyle \frac{\Theta \left(\nu -\varpi \right)}{\nu -\varpi }}Y\left(\nu \right)d\nu ,\varpi <\sigma ,\end{array}$$

(3)

respectively.

Generalized fractional integrals are notable for encompassing several well-known fractional integrals, including the fractional Riemann–Liouville, k-Riemann–Liouville, and Hadamard integrals, etc. Specific cases of the integral operators in (2) and (3) are as follows:

• For $\Theta \left(\nu \right)=\nu$, the operators reduce to the classical Riemann integral.
• For $\Theta \left(\nu \right)={\displaystyle \frac{{\nu }^{\gamma }}{\Gamma \left(\gamma \right)}}$ with $\gamma >0$, the operators correspond to Riemann–Liouville fractional integrals $J_{\lambda +}^{\gamma }Y\left(\varpi \right)$ and $J_{\sigma -}^{\gamma }Y\left(\varpi \right)$[27], where $\Gamma$ is defined as

  $$\begin{array}{c}\hfill \Gamma \left(\varpi \right):=\underset{0}{\overset{\infty }{\int }}{\nu }^{\varpi -1}{e}^{-\nu }d\nu ,0<\varpi <\infty .\end{array}$$
• For $\Theta \left(\nu \right)={\displaystyle \frac{1}{k{\Gamma }_k\left(\gamma \right)}}{\nu }^{{\displaystyle \frac{\gamma }{k}}}$, the operators become k-Riemann–Liouville fractional integrals $J_{\lambda +,k}^{\gamma }Y\left(\varpi \right)$ and $J_{\sigma -,k}^{\gamma }Y\left(\varpi \right)$, where ${\Gamma }_k$ is the k-Gamma function, defined as

  $$\begin{array}{c}\hfill {\Gamma }_k\left(\gamma \right)={\int }_0^{\infty }{\nu }^{\gamma -1}{e}^{-{\displaystyle \frac{{\nu }^k}{k}}}d\nu =k^{{\displaystyle \frac{\gamma }{k}}-1}\Gamma \left({\displaystyle \frac{\gamma }{k}}\right),\gamma ,k>0.\end{array}$$

Fractional integral inequalities have been extensively studied using Riemann–Liouville fractional integrals, as in [28]. More information on these integrals and their properties can be found in [27,29,30] and the references therein. H–H inequalities for other fractional integrals have also been examined, including k-fractional, Hadamard, and conformable integrals [31,32].

This work introduces a new identity for twice-differentiable functions with the absolute value of their second derivatives being convex. This identity forms the basis for deriving H–H-type inequalities involving generalized fractional integrals. These findings generalize some established results and provide new corollaries derived from specific cases. A detailed example with a graphical representation illustrates the derived inequalities’ behavior and validity. This work aims to deepen the understanding of fractional integral inequalities and foster further research in this area. Unlike previous studies, this approach provides a unified framework for deriving Hermite–Hadamard-type inequalities and their fractional generalizations, offering sharper bounds and broader applicability. These contributions address gaps in existing literature by introducing novel corollaries and examples, paving the way for future advancements in fractional calculus and its applications. The findings of this study have the potential to enhance numerical methods by offering improved bounds for integration processes. They might also have applications in addressing optimization challenges where convexity is a key factor, with relevance to fields such as economics, engineering, and data analysis. Moreover, these results could provide useful perspectives for studying fractional differential equations, which are widely employed in modeling phenomena in physical and biological systems. The generalizations introduced here may act as a starting point for investigating related topics in higher-dimensional frameworks and other analytical approaches. The paper is organized as follows: Section 1 provides basic definitions and preliminaries on generalized fractional integrals. Section 2 derives an identity for twice-differentiable functions, and establishes midpoint-type inequalities with relevant remarks and corollaries. Finally, Section 3 summarizes the findings and offers concluding remarks.

2. Main Results

This section introduces the primary findings of the study, focusing on inequalities for twice-differentiable functions for twice-differentiable functions with the absolute value of their second derivatives being convex. A central identity is established, leading to Hermite–Hadamard-type inequalities involving generalized fractional integral operators.

Lemma 1.

Assume that $Y:[\lambda ,\sigma ]\to \mathbb{R}$ is an absolutely continuous function on $(\lambda ,\sigma )$ with $Y^{″}\in L_1\left([\lambda ,\sigma ]\right)$. Under these conditions, the following identity is valid:

$${\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)={\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\underset{i=1}{\sum ^4}{I}_i,$$

where

$$\left\{\begin{array}{cc}{I}_1=\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\Xi \left(\nu \right)Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)d\nu ,\hfill & I_3=\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left(\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right)Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)d\nu ,\hfill \\ I_2=\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\Xi \left(\nu \right)Y^{″}\left(ta+\left(1-\nu \right)\sigma \right)d\nu ,\hfill & I_4=\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left(\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right)Y^{″}\left(ta+\left(1-\nu \right)\sigma \right)d\nu ,\hfill \end{array}\right.$$

and

$$\left\{\begin{array}{c}\Xi \left(\nu \right)=\underset{0}{\overset{\nu }{\int }}\Sigma \left(s\right)ds,\hfill \\ \Sigma \left(s\right)=\underset{0}{\overset{s}{\int }}{\displaystyle \frac{\Theta \left(\left(\sigma -\lambda \right)u\right)}{u}}du.\hfill \end{array}\right.$$

Proof. 

We apply integration by parts to simplify the generalized fractional integral and isolate terms involving the function’s derivative. The symmetry of the convex function and the kernel’s properties are then used to restructure the integral, leading to the desired identity. Hence, the resulting expression is obtained as follows:

$$\begin{array}{cc}\hfill I_1& =\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\Xi \left(\nu \right)Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)d\nu \hfill \\ \hfill & ={\left.{\displaystyle \frac{\Xi \left(\nu \right)}{\sigma -\lambda }}{Y}^{\prime }\left(\nu \sigma +\left(1-\nu \right)\lambda \right)\right|}_0^{{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{1}{\sigma -\lambda }}\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\Sigma \left(\nu \right)Y^{\prime }\left(\nu \sigma +\left(1-\nu \right)\lambda \right)d\nu \hfill \\ \hfill & ={\displaystyle \frac{\Xi \left(\frac{1}{2}\right)}{\sigma -\lambda }}{Y}^{\prime }\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)-{\displaystyle \frac{1}{\sigma -\lambda }}[{\left.{\displaystyle \frac{\Sigma \left(\nu \right)}{\sigma -\lambda }}Y\left(\nu \sigma +\left(1-\nu \right)\lambda \right)\right|}_0^{{\displaystyle \frac{1}{2}}}\hfill \\ \hfill & -{\displaystyle \frac{1}{\sigma -\lambda }}\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\displaystyle \frac{\Theta \left(\left(\sigma -\lambda \right)\nu \right)}{\nu }}Y\left(\nu \sigma +\left(1-\nu \right)\lambda \right)d\nu ]\hfill \\ \hfill & ={\displaystyle \frac{\Xi \left(\frac{1}{2}\right)}{\sigma -\lambda }}{Y}^{\prime }\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)-{\displaystyle \frac{\Sigma \left(\frac{1}{2}\right)}{{\left(\sigma -\lambda \right)}^2}}Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\left(\sigma -\lambda \right)}^2}}\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\displaystyle \frac{\Theta \left(\left(\sigma -\lambda \right)\nu \right)}{\nu }}Y\left(\nu \sigma +\left(1-\nu \right)\lambda \right)d\nu .\hfill \end{array}$$

(4)

Following a similar procedure as above, we can derive

$$\begin{array}{cc}\hfill I_2& =-{\displaystyle \frac{\Xi \left(\frac{1}{2}\right)}{\sigma -\lambda }}{Y}^{\prime }\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)-{\displaystyle \frac{\Sigma \left(\frac{1}{2}\right)}{{\left(\sigma -\lambda \right)}^2}}Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\left(\sigma -\lambda \right)}^2}}\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\displaystyle \frac{\Theta \left(\left(\sigma -\lambda \right)\nu \right)}{\nu }}Y\left(\nu \lambda +\left(1-\nu \right)\sigma \right)d\nu ,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill I_3& =-{\displaystyle \frac{\Xi \left(\frac{1}{2}\right)+\frac{\Sigma \left(1\right)}{2}-\Xi \left(1\right)}{\sigma -\lambda }}{Y}^{\prime }\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)+{\displaystyle \frac{\Sigma \left(\frac{1}{2}\right)-\Sigma \left(1\right)}{{\left(\sigma -\lambda \right)}^2}}Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\left(\sigma -\lambda \right)}^2}}\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\displaystyle \frac{\Theta \left(\left(\sigma -\lambda \right)\nu \right)}{\nu }}Y\left(\nu \sigma +\left(1-\nu \right)\lambda \right)d\nu ,\hfill \end{array}$$

(6)

and

$$\begin{array}{cc}\hfill I_4& ={\displaystyle \frac{\Xi \left(\frac{1}{2}\right)+\frac{\Sigma \left(1\right)}{2}-\Xi \left(1\right)}{\sigma -\lambda }}{Y}^{\prime }\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)+{\displaystyle \frac{\Sigma \left(\frac{1}{2}\right)-\Sigma \left(1\right)}{{\left(\sigma -\lambda \right)}^2}}Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\left(\sigma -\lambda \right)}^2}}\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\displaystyle \frac{\Theta \left(\left(\sigma -\lambda \right)\nu \right)}{\nu }}Y\left(\nu \lambda +\left(1-\nu \right)\sigma \right)d\nu .\hfill \end{array}$$

(7)

By summing the equalities from (4) to (7), we obtain the following results:

$$\begin{array}{cc}\hfill \underset{k=1}{\sum ^4}{I}_k& ={\displaystyle \frac{1}{{\left(\sigma -\lambda \right)}^2}}\left[\underset{0}{\overset{1}{\int }}{\displaystyle \frac{\Theta \left(\left(\sigma -\lambda \right)\nu \right)}{t}}Y\left(\nu \sigma +\left(1-\nu \right)\lambda \right)d\nu \right.\hfill \\ \hfill & \left.+\underset{0}{\overset{1}{\int }}{\displaystyle \frac{\Theta \left(\left(\sigma -\lambda \right)\nu \right)}{\nu }}Y\left(\nu \lambda +\left(1-\nu \right)\sigma \right)d\nu \right]-{\displaystyle \frac{2\Sigma \left(1\right)}{{\left(\sigma -\lambda \right)}^2}}Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{{\left(\sigma -\lambda \right)}^2}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right){+}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-{\displaystyle \frac{2\Sigma \left(1\right)}{{\left(\sigma -\lambda \right)}^2}}Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right).\hfill \end{array}$$

(8)

As a result, multiplying both sides of (8) by ${\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}$ completes the proof of Lemma 1.  □

Theorem 1.

Suppose that the requirements of Lemma 1 are satisfied. Additionally, if $\left|Y^{″}\right|$ is convex on $\left[\lambda ,\sigma \right]$, then the following inequality is valid:

$$\left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\Psi }_1+{\Psi }_2\right]\left[\left|Y^{″}\left(\lambda \right)\right|+\left|Y^{″}\left(\sigma \right)\right|\right].$$

Here,

$$\left\{\begin{array}{c}{\Psi }_1=\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\Xi \left(\nu \right)d\nu ,\hfill \\ {\Psi }_2=\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|d\nu .\hfill \end{array}\right.$$

Proof. 

First, we take the modulus of the expression in Lemma 1. Consequently, we have:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|\left|Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)\right|d\nu +\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|\left|Y^{″}\left(\nu \lambda +\left(1-\nu \right)\sigma \right)\right|d\nu \right.\hfill \\ \hfill & +\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|\left|Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)\right|d\nu \hfill \\ \hfill & \left.+\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|\left|Y^{″}\left(\nu \lambda +\left(1-\nu \right)\sigma \right)\right|d\nu \right].\hfill \end{array}$$

(9)

Since $\left|Y^{″}\right|$ is known to be convex, utilizing this property yields

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|\left[\nu \left|Y^{″}\left(\sigma \right)\right|+\left(1-\nu \right)\left|Y^{″}\left(\lambda \right)\right|\right]d\nu +\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|\left[\nu \left|Y^{″}\left(\lambda \right)\right|+\left(1-\nu \right)\left|Y^{″}\left(\sigma \right)\right|\right]d\nu \right.\hfill \\ \hfill & +\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|\left[\nu \left|Y^{″}\left(\sigma \right)\right|+\left(1-\nu \right)\left|Y^{″}\left(\lambda \right)\right|\right]d\nu \hfill \\ \hfill & \left.+\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|\left[\nu \left|Y^{″}\left(\lambda \right)\right|+\left(1-\nu \right)\left|Y^{″}\left(\sigma \right)\right|\right]d\nu \right]\hfill \\ \hfill & ={\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\Xi \left(\nu \right)d\nu +\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|d\nu \right]\left[\left|Y^{″}\left(\lambda \right)\right|+\left|Y^{″}\left(\sigma \right)\right|\right].\hfill \end{array}$$

Hence, the proof of Theorem 1 is finalized.  □

Remark 1.

By setting $\Theta \left(\nu \right)=\nu$ in Theorem 1, we obtain:

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{1}{\sigma -\lambda }}\underset{\lambda }{\overset{\sigma }{\int }}Y\left(\nu \right)d\nu -Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{48}}\left[\left|Y^{″}\left(\lambda \right)\right|+\left|Y^{″}\left(\sigma \right)\right|\right].\end{array}$$

This was proven by Sarikaya et al. in [25].

Corollary 1.

By choosing $\Theta \left(\nu \right)={\displaystyle \frac{{\nu }^{\gamma }}{\Gamma \left(\gamma \right)}}$ with $\gamma >0$ in Theorem 1, the upcoming inequality of midpoint-type is obtained:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\Gamma \left(\gamma +1\right)}{2{\left(\sigma -\lambda \right)}^{\gamma }}}\left[J_{\lambda +}^{\gamma }Y\left(\sigma \right)+J_{\sigma -}^{\gamma }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\left(\gamma +1\right)}}\left[{\displaystyle \frac{1}{\gamma +2}}+{\displaystyle \frac{\gamma -3}{8}}\right]\left[\left|Y^{″}\left(\lambda \right)\right|+\left|Y^{″}\left(\sigma \right)\right|\right].\hfill \end{array}$$

(10)

Example 1.

Consider the function $Y:[\lambda ,\sigma ]=[0,1]\to \mathbb{R}$ defined by $Y\left(\varpi \right)={\varpi }^4$. In this case, the left-hand side of inequality (10) simplifies to

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\Gamma \left(\gamma +1\right)}{2}}\left[J_{0+}^{\gamma }Y\left(1\right)+J_{1-}^{\gamma }Y\left(0\right)\right]-Y\left({\displaystyle \frac{1}{2}}\right)\right|\hfill \\ \hfill & =\left|{\displaystyle \frac{\Gamma \left(\gamma +1\right)}{2}}\left[{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{1}{\int }}{\left(1-\nu \right)}^{\gamma -1}{\nu }^{4}d\nu +{\displaystyle \frac{1}{\Gamma \left(\gamma \right)}}\underset{0}{\overset{1}{\int }}{\nu }^{\gamma -1}{\nu }^{4}d\nu \right]-{\displaystyle \frac{1}{16}}\right|\hfill \\ \hfill & =\left|{\displaystyle \frac{\gamma }{2}}\left[\beta \left(\gamma ,5\right)+{\displaystyle \frac{1}{\gamma +4}}\right]-{\displaystyle \frac{1}{16}}\right|=\left|{\displaystyle \frac{\gamma }{2}}\left[{\displaystyle \frac{\Gamma \left(\gamma \right)\Gamma \left(5\right)}{\Gamma \left(\gamma +5\right)}}+{\displaystyle \frac{1}{\gamma +4}}\right]-{\displaystyle \frac{1}{16}}\right|\hfill \\ \hfill & =\left|{\displaystyle \frac{12}{\left(\gamma +1\right)\left(\gamma +2\right)\left(\gamma +3\right)\left(\gamma +4\right)}}+{\displaystyle \frac{\gamma }{2\left(\gamma +4\right)}}-{\displaystyle \frac{1}{16}}\right|.\hfill \end{array}$$

The right-hand side of inequality (10) simplifies to

$$\begin{array}{c}\hfill {\displaystyle \frac{6}{\left(\gamma +1\right)}}\left[{\displaystyle \frac{1}{\gamma +2}}+{\displaystyle \frac{\gamma -3}{8}}\right].\end{array}$$

As a result, we obtain the following inequality:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{8}}\left|{\displaystyle \frac{24}{\left(\gamma +1\right)\left(\gamma +2\right)\left(\gamma +3\right)\left(\gamma +4\right)}}+{\displaystyle \frac{\gamma }{\gamma +4}}-{\displaystyle \frac{1}{8}}\right|\le {\displaystyle \frac{6}{\left(\gamma +1\right)}}\left[{\displaystyle \frac{1}{\gamma +2}}+{\displaystyle \frac{\gamma -3}{8}}\right].\end{array}$$

(11)

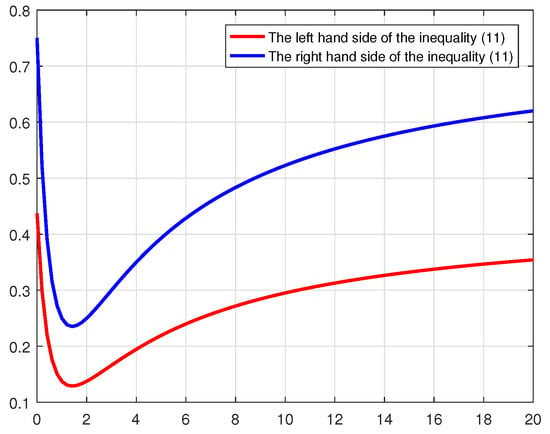
Figure 1 shows the relationship between the left-hand and right-hand sides of inequality (11) for the selected parameters. The difference between the two sides represents the bounds established by the inequality, confirming their agreement and consistency over the range $\gamma \in [0,20]$. This validates the correctness of the theoretical findings under the specified conditions.

Figure 1. The graphs corresponding to the outcome of Example 1 were computed and visualized by using MATLAB (R2024b).

Corollary 2.

By selecting $\Theta \left(\nu \right)={\displaystyle \frac{{\nu }^{\frac{\gamma }{k}}}{k{\Gamma }_k\left(a\right)}}$ for $\gamma ,k>0$ in Theorem 1, we derive the following midpoint-type inequality:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{{\Gamma }_k\left(\gamma +k\right)}{2{\left(\sigma -\lambda \right)}^{\frac{\gamma }{k}}}}\left[J_{\lambda +,k}^{\gamma }Y\left(\sigma \right)+J_{\sigma -,k}^{\gamma }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\left(\frac{\gamma }{k}+1\right)}}\left[{\displaystyle \frac{k}{\gamma +2k}}+{\displaystyle \frac{\gamma -3k}{8k}}\right]\left[\left|Y^{″}\left(\lambda \right)\right|+\left|Y^{″}\left(\sigma \right)\right|\right].\hfill \end{array}$$

Theorem 2.

Assume that the conditions of Lemma 1 are satisfied, and that ${\left|Y^{″}\right|}^{{ϵ}_2}$, with ${ϵ}_2>1$, is convex on $[\lambda ,\sigma ]$. In this case, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|\Xi \left(\nu \right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}+{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right]\hfill \\ \hfill & \times \left[{\left({\displaystyle \frac{3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}+{\left({\displaystyle \frac{3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left(4\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|\Xi \left(\nu \right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}+{\left(4\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right]\hfill \\ \hfill & \times \left[\left|Y^{″}\left(\sigma \right)\right|+\left|Y^{″}\left(\lambda \right)\right|\right],\hfill \end{array}$$

where ${\displaystyle \frac{1}{{ϵ}_1}}+{\displaystyle \frac{1}{{ϵ}_2}}=1$.

Proof. 

By utilizing Hölder’s inequality on (9), we obtain

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|\Xi \left(\nu \right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)\right|}^{{ϵ}_2}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right.\hfill \\ \hfill & +{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|\Xi \left(\nu \right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|Y^{″}\left(\nu \lambda +\left(1-\nu \right)\sigma \right)\right|}^{{ϵ}_2}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & +{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)\right|}^{{ϵ}_2}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \left.+{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|Y^{″}\left(\nu \lambda +\left(1-\nu \right)\sigma \right)\right|}^{{ϵ}_2}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right].\hfill \end{array}$$

Utilizing the convexity of ${\left|Y^{″}\right|}^{{ϵ}_2}$, we derive

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|\Xi \left(\nu \right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left[\nu {\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+\left(1-\nu \right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right.\hfill \\ \hfill & +{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|\Xi \left(\nu \right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left[\nu {\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left(1-\nu \right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & +{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left[\nu {\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+\left(1-\nu \right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \left.+{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left[\nu {\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left(1-\nu \right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}{\left|\Xi \left(\nu \right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}+{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right]\hfill \\ \hfill & \times \left[{\left({\displaystyle \frac{3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}+{\left({\displaystyle \frac{3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right].\hfill \end{array}$$

To prove the second inequality, let us define $c_1={\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}$, $d_1=3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}$, $c_2=3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}$, and $d_2={\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}$. Using the following properties:

$$\sum _{k=1}^n{\left(c_k+d_k\right)}^r\le \sum _{k=1}^n{c}_k^r+\sum _{k=1}^n{d}_k^r,0\le r<1$$

and $3^{{\displaystyle \frac{1}{{ϵ}_2}}}+1\le 4$, the required result follows immediately. This concludes the proof of Theorem 2.  □

Remark 2.

By assigning $\Theta \left(\nu \right)=\nu$ in Theorem 2, we obtain

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{\sigma -\lambda }}\underset{\lambda }{\overset{\sigma }{\int }}Y\left(\nu \right)d\nu -Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{16}}{\left[{\displaystyle \frac{1}{2{ϵ}_1+1}}\right]}^{{\displaystyle \frac{1}{p}}}\left[{\left({\displaystyle \frac{3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}}{4}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}+{\left({\displaystyle \frac{3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}}{4}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{16}}{\left[{\displaystyle \frac{4}{2{ϵ}_1+1}}\right]}^{{\displaystyle \frac{1}{p}}}\left[\left|Y^{″}\left(\sigma \right)\right|+\left|Y^{″}\left(\lambda \right)\right|\right],\hfill \end{array}$$

This result was established by Budak et al. in Corollary 4.8 of [22].

Corollary 3.

Let $\Theta \left(\nu \right)={\displaystyle \frac{{\nu }^{\gamma }}{\Gamma \left(\gamma \right)}}$ with $\gamma >0$ in Theorem 2. In this case, the following midpoint-type inequalities are derived:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\Gamma \left(\gamma +1\right)}{2{\left(\sigma -\lambda \right)}^{\gamma }}}\left[J_{\lambda +}^{\gamma }Y\left(\sigma \right)+J_{\sigma -}^{\gamma }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\left(\gamma +1\right)}}\left[{\left({\displaystyle \frac{1}{\left(\left(\gamma +1\right)p+1\right)2^{\left(\gamma +1\right)p+1}}}\right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}+{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|{\nu }^{\gamma +1}+\left(\gamma +1\right)\left(1-\nu \right)-1\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right]\hfill \\ \hfill & \times \left[{\left({\displaystyle \frac{3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}+{\left({\displaystyle \frac{3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\left(\gamma +1\right)}}\left[{\left({\displaystyle \frac{4}{\left(\left(\gamma +1\right)p+1\right)2^{\left(\gamma +1\right)p+1}}}\right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right.\hfill \\ \hfill & \left.+{\left(4\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|{\nu }^{\gamma +1}+\left(\gamma +1\right)\left(1-\nu \right)-1\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right]\left[\left|Y^{″}\left(\sigma \right)\right|+\left|Y^{″}\left(\lambda \right)\right|\right].\hfill \end{array}$$

Corollary 4.

By choosing $\Theta \left(\nu \right)={\displaystyle \frac{{\nu }^{\frac{\gamma }{k}}}{k{\Gamma }_k\left(a\right)}}$ for $\gamma ,k>0$ in Theorem 2, the following midpoint-type inequalities are true:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{{\Gamma }_k\left(\gamma +k\right)}{2{\left(\sigma -\lambda \right)}^{\frac{\gamma }{k}}}}\left[J_{\lambda +,k}^{\gamma }Y\left(\sigma \right)+J_{\sigma -,k}^{\gamma }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\left(\frac{\gamma }{k}+1\right)}}\left[{\left({\displaystyle \frac{1}{\left(\left(\frac{\gamma }{k}+1\right)p+1\right)2^{\left(\frac{\gamma }{k}+1\right)p+1}}}\right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}+{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|{\nu }^{{\displaystyle \frac{\gamma }{k}}+1}+\left({\displaystyle \frac{\gamma }{k}}+1\right)\left(1-\nu \right)-1\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right]\hfill \\ \hfill & \times \left[{\left({\displaystyle \frac{3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}+{\left({\displaystyle \frac{3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\left(\frac{\gamma }{k}+1\right)}}\left[{\left({\displaystyle \frac{4}{\left(\left(\frac{\gamma }{k}+1\right)p+1\right)2^{\left(\frac{\gamma }{k}+1\right)p+1}}}\right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right.\hfill \\ \hfill & \left.+{\left(4\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}{\left|{\nu }^{{\displaystyle \frac{\gamma }{k}}+1}+\left({\displaystyle \frac{\gamma }{k}}+1\right)\left(1-\nu \right)-1\right|}^{{ϵ}_1}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_1}}}\right]\left[\left|Y^{″}\left(\sigma \right)\right|+\left|Y^{″}\left(\lambda \right)\right|\right].\hfill \end{array}$$

Theorem 3.

If the requirements of Lemma 1 are satisfied and ${\left|Y^{″}\right|}^{{ϵ}_2}$, with ${ϵ}_2\ge 1$, is convex on $[\lambda ,\sigma ]$, then the following inequality holds:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left({\Psi }_1\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left[{\Psi }_3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+\left({\Psi }_1-{\Psi }_3\right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right.\hfill \\ \hfill & +{\left({\Psi }_1\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left[{\Psi }_3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left({\Psi }_1-{\Psi }_3\right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & +{\left({\Psi }_2\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left[{\Psi }_4{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+\left({\Psi }_2-{\Psi }_4\right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \left.+{\left({\Psi }_2\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left[{\Psi }_4{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left({\Psi }_2-{\Psi }_4\right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \end{array}$$

and is valid. Here,

$$\left\{\begin{array}{c}{\Psi }_3=\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\Xi \left(\nu \right)\nu d\nu ,\hfill \\ {\Psi }_4=\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|\nu d\nu .\hfill \end{array}\right.$$

Proof. 

Using the power-mean inequality on (9), we obtain

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|{\left|Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)\right|}^{{ϵ}_2}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right.\hfill \\ \hfill & +{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|{\left|Y^{″}\left(ta+\left(1-\nu \right)\sigma \right)\right|}^{{ϵ}_2}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & +{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \times {\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|{\left|Y^{″}\left(\nu \sigma +\left(1-\nu \right)\lambda \right)\right|}^{{ϵ}_2}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & +{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \left.\times {\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|{\left|Y^{″}\left(ta+\left(1-\nu \right)\sigma \right)\right|}^{{ϵ}_2}d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right].\hfill \end{array}$$

As ${\left|Y^{″}\right|}^{{ϵ}_2}$ is convex, we conclude that

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2\Sigma \left(1\right)}}\left[{}_{\lambda +}{I}_{\Theta }Y\left(\sigma \right)+{}_{\sigma -}{I}_{\Theta }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|\left[\nu {\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+\left(1-\nu \right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right.\hfill \\ \hfill & +{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left(\underset{0}{\overset{{\displaystyle \frac{1}{2}}}{\int }}\left|\Xi \left(\nu \right)\right|\left[\nu {\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left(1-\nu \right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & +{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \times {\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|\left[\nu {\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+\left(1-\nu \right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & +{\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \left.\times {\left(\underset{{\displaystyle \frac{1}{2}}}{\overset{1}{\int }}\left|\Xi \left(\nu \right)+\Sigma \left(1\right)\left(1-\nu \right)-\Xi \left(1\right)\right|\left[\nu {\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left(1-\nu \right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]d\nu \right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\Sigma \left(1\right)}}\left[{\left({\Psi }_1\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left[{\Psi }_3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+\left({\Psi }_1-{\Psi }_3\right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right.\hfill \\ \hfill & +{\left({\Psi }_1\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left[{\Psi }_3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left({\Psi }_1-{\Psi }_3\right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & +{\left({\Psi }_2\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left[{\Psi }_4{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+\left({\Psi }_2-{\Psi }_4\right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \left.+{\left({\Psi }_2\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}{\left[{\Psi }_4{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left({\Psi }_2-{\Psi }_4\right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right].\hfill \end{array}$$

Thus, Theorem 3 is proved.  □

Remark 3.

Let $\Theta \left(\nu \right)=\nu$ in Theorem 3. In this case, we obtain

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{\sigma -\lambda }}\underset{\lambda }{\overset{\sigma }{\int }}Y\left(\nu \right)d\nu -Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{48}}\left[{\left({\displaystyle \frac{3{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+5{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}+{\left({\displaystyle \frac{5{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+3{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}}{8}}\right)}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right].\hfill \end{array}$$

This can be found in Proposition 5 of [21].

Corollary 5.

By setting $\Theta \left(\nu \right)={\displaystyle \frac{{\nu }^{\gamma }}{\Gamma \left(\gamma \right)}}$ with $\gamma >0$ in Theorem 1, the following inequality of midpoint-type is derived:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\Gamma \left(\gamma +1\right)}{2{\left(\sigma -\lambda \right)}^{\gamma }}}\left[J_{\lambda +}^{\gamma }Y\left(\sigma \right)+J_{\sigma -}^{\gamma }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\left(\gamma +1\right)}}\left\{{\left({\displaystyle \frac{1}{\left(\gamma +2\right)2^{\gamma +2}}}\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}\left[{\left[{\displaystyle \frac{1}{\left(\gamma +3\right)2^{\gamma +3}}}{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+{\displaystyle \frac{\gamma +4}{\left(\gamma +2\right)\left(\gamma +3\right)2^{\gamma +3}}}{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right.\right.\hfill \\ \hfill & \left.+{\left[{\displaystyle \frac{1}{\left(\gamma +3\right)2^{\gamma +3}}}{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+{\displaystyle \frac{\gamma +4}{\left(\gamma +2\right)\left(\gamma +3\right)2^{\gamma +3}}}{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \\ \hfill & +{\left({\displaystyle \frac{2^{\gamma +2}-1}{\left(\gamma +2\right)2^{\gamma +2}}}+{\displaystyle \frac{\gamma -3}{8}}\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}\left[\left[\left({\displaystyle \frac{2^{\gamma +3}-1}{\left(\gamma +3\right)2^{\gamma +3}}}+{\displaystyle \frac{2\gamma -7}{24}}\right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right.\right.\hfill \\ \hfill & {\left.+\left({\displaystyle \frac{2^{\gamma +3}-\gamma -4}{\left(\gamma +2\right)\left(\gamma +3\right)2^{\gamma +3}}}+{\displaystyle \frac{\gamma -2}{24}}\right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \left.\left.+{\left[\left({\displaystyle \frac{2^{\gamma +3}-1}{\left(\gamma +3\right)2^{\gamma +3}}}+{\displaystyle \frac{2\gamma -7}{24}}\right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left({\displaystyle \frac{2^{\gamma +3}-\gamma -4}{\left(\gamma +2\right)\left(\gamma +3\right)2^{\gamma +3}}}+{\displaystyle \frac{\gamma -2}{24}}\right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\right\}.\hfill \end{array}$$

Corollary 6.

Consider $\Theta \left(\nu \right)={\displaystyle \frac{{\nu }^{\frac{\gamma }{k}}}{k{\Gamma }_k\left(a\right)}}$ with $\gamma ,k>0$ in Theorem 3. In this case, the following midpoint-type inequality is obtained:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{{\Gamma }_k\left(\gamma +k\right)}{2{\left(\sigma -\lambda \right)}^{\frac{\gamma }{k}}}}\left[J_{\lambda +,k}^{\gamma }Y\left(\sigma \right)+J_{\sigma -,k}^{\gamma }Y\left(\lambda \right)\right]-Y\left({\displaystyle \frac{\lambda +\sigma }{2}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left(\sigma -\lambda \right)}^2}{2\left(\frac{\gamma }{k}+1\right)}}\left\{{\left({\displaystyle \frac{1}{\left(\frac{\gamma }{k}+2\right)2^{\frac{\gamma }{k}+2}}}\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}\left[{\left[{\displaystyle \frac{1}{\left(\frac{\gamma }{k}+3\right)2^{\frac{\gamma }{k}+3}}}{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}+{\displaystyle \frac{\frac{\gamma }{k}+4}{\left(\frac{\gamma }{k}+2\right)\left(\frac{\gamma }{k}+3\right)2^{\frac{\gamma }{k}+3}}}{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right.\right.\hfill \\ \hfill & \left.+{\left[{\displaystyle \frac{1}{\left(\frac{\gamma }{k}+3\right)2^{\gamma +3}}}{\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+{\displaystyle \frac{\frac{\gamma }{k}+4}{\left(\frac{\gamma }{k}+2\right)\left(\frac{\gamma }{k}+3\right)2^{\frac{\gamma }{k}+3}}}{\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\hfill \\ \hfill & +{\left({\displaystyle \frac{2^{\frac{\gamma }{k}+2}-1}{\left(\frac{\gamma }{k}+2\right)2^{\frac{\gamma }{k}+2}}}+{\displaystyle \frac{\frac{\gamma }{k}-3}{8}}\right)}^{1-{\displaystyle \frac{1}{{ϵ}_2}}}\left[\left[\left({\displaystyle \frac{2^{\frac{\gamma }{k}+3}-1}{\left(\frac{\gamma }{k}+3\right)2^{\frac{\gamma }{k}+3}}}+{\displaystyle \frac{\frac{2\gamma }{k}-7}{24}}\right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right.\right.\hfill \\ \hfill & {\left.+\left({\displaystyle \frac{2^{\frac{\gamma }{k}+3}-\frac{\gamma }{k}-4}{\left(\frac{\gamma }{k}+2\right)\left(\frac{\gamma }{k}+3\right)2^{\frac{\gamma }{k}+3}}}+{\displaystyle \frac{\frac{\gamma }{k}-2}{24}}\right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\hfill \\ \hfill & \left.\left.+{\left[\left({\displaystyle \frac{2^{\frac{\gamma }{k}+3}-1}{\left(\frac{\gamma }{k}+3\right)2^{\frac{\gamma }{k}+3}}}+{\displaystyle \frac{\frac{2\gamma }{k}-7}{24}}\right){\left|Y^{″}\left(\lambda \right)\right|}^{{ϵ}_2}+\left({\displaystyle \frac{2^{\frac{\gamma }{k}+3}-\frac{\gamma }{k}-4}{\left(\frac{\gamma }{k}+2\right)\left(\frac{\gamma }{k}+3\right)2^{\frac{\gamma }{k}+3}}}+{\displaystyle \frac{\frac{\gamma }{k}-2}{24}}\right){\left|Y^{″}\left(\sigma \right)\right|}^{{ϵ}_2}\right]}^{{\displaystyle \frac{1}{{ϵ}_2}}}\right]\right\}.\hfill \end{array}$$

3. Conclusions

This work develops a systematic approach to derive inequalities for twice-differentiable functions with convex second derivatives in absolute terms. This study extends classical inequalities, such as Hermite–Hadamard type, to a broader framework. This is achieved by integrating generalized fractional integrals. These results encompass special cases of known fractional integrals, such as the Riemann–Louville and k-fractional integrals, providing a unifying perspective. Examples and corollaries are included to validate the theoretical contributions and demonstrate their relevance to earlier findings. The methods used open avenues for further research into multidimensional inequalities, higher-order convexity, and applications in numerical and analytical methods. Additionally, the results may also be applicable in fields such as fractional differential equations, where precise bounds are essential for estimating solutions, and in optimization theory, where convexity is central to many practical problems. Future research could explore extensions to multidimensional convex functions, inequalities involving higher-order derivatives, and more generalized integral operators to broaden the scope of the presented framework. By linking classical approaches with modern tools in fractional calculus, this study offers a foundational step toward advancing both the theory and application of inequalities.