Shifted Bernstein Polynomial-Based Dynamic Analysis for Variable Fractional Order Nonlinear Viscoelastic Bar
Abstract
1. Introduction
2. Preliminaries
2.1. Caputo Variable Fractional-Order Derivative Operator
2.2. Definition as Well as Related Characteristics of Bernstein Polynomials
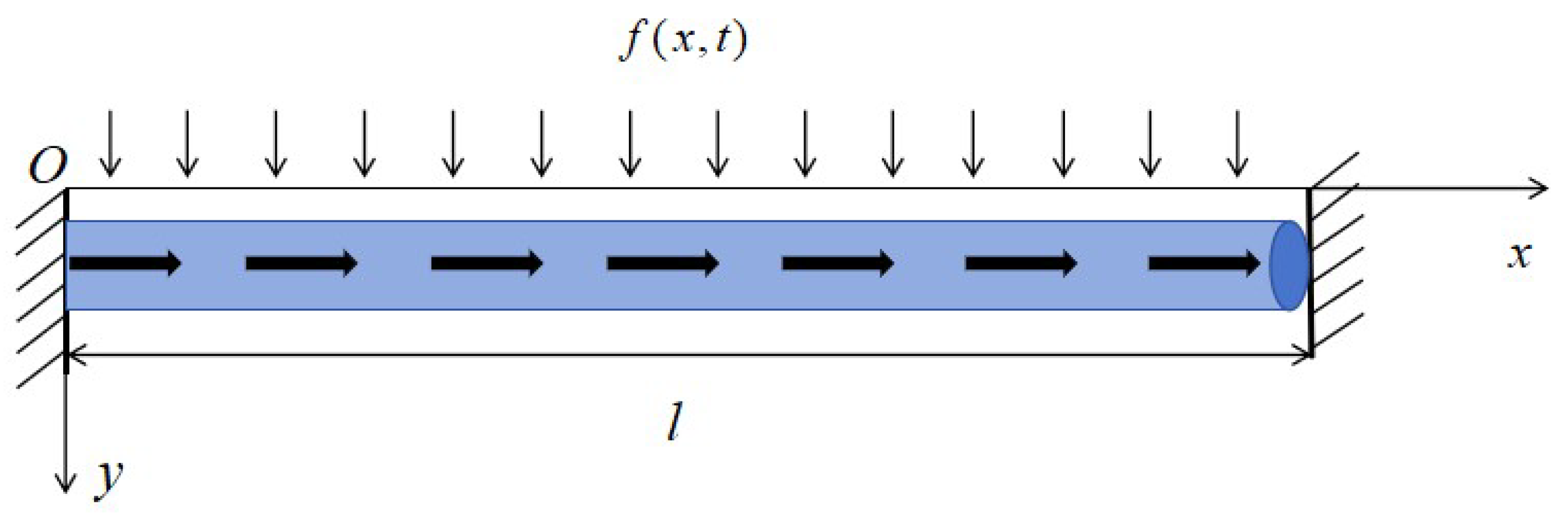
3. Control Equation of the Viscoelastic Bar
4. Numerical Algorithms
4.1. Approximation of Functions
4.2. Bernstein Polynomial Operational Matrices of Integer Order
5. Convergence
6. Numerical Example
6.1. Dimensionless Equation
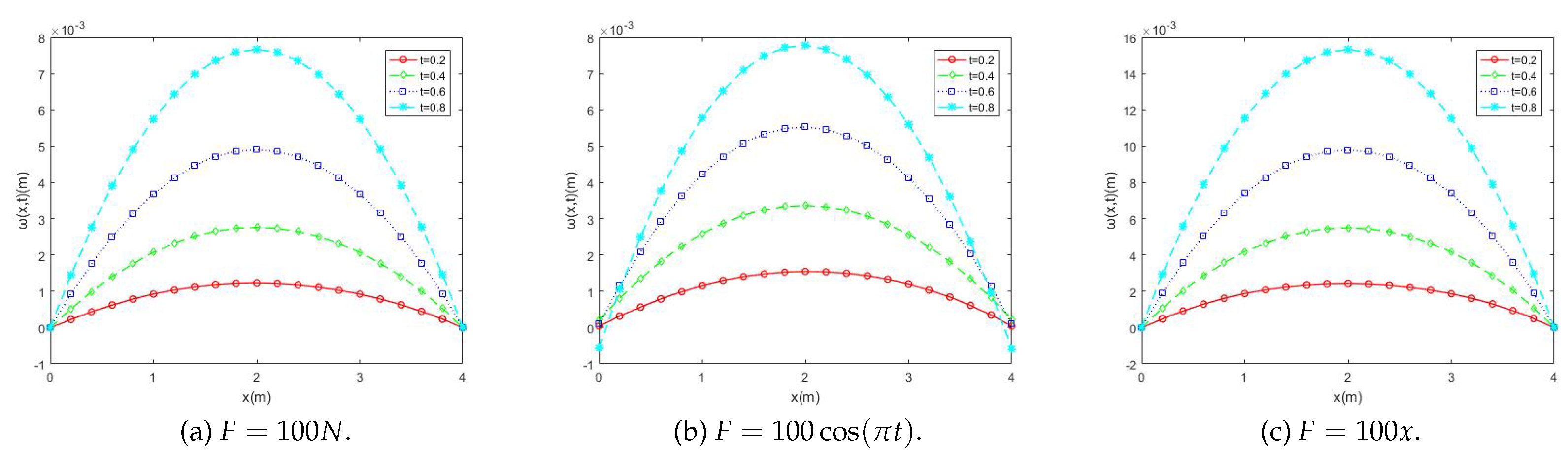
6.2. Displacement Numerical Solution of Viscoelastic Bar
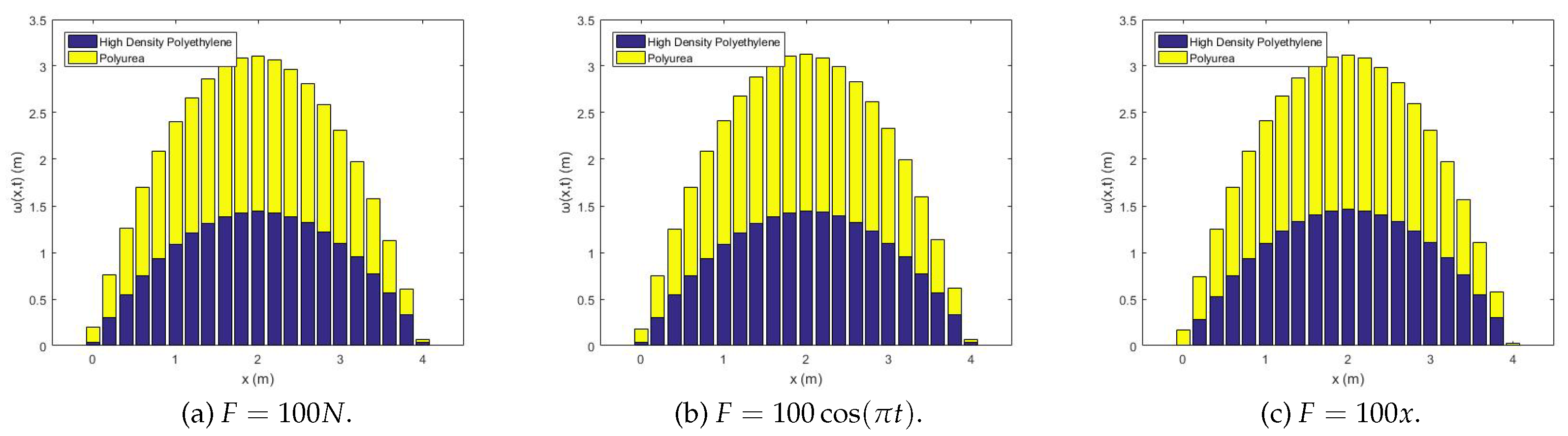
6.3. Displacement Numerical Solutions of HDPE Bar and Polyurea Bar
7. Conclusions
- Through the introduction of dimensionless equations and a thorough kinetic analysis, it is demonstrated that this approach is highly effective in tackling variable fractional-order differential equations that describe viscoelastic bars.
- When the bar is subjected to different axial loads, uniformly distributed, simple harmonic, and linearly distributed, the displacement increases with both load intensity and time.
- Numerical results illustrate the displacement and stress variations for HDPE and polyurea materials under different loading conditions. Additionally, a comparative analysis of materials with different viscoelastic properties provides theoretical insights into their mechanical behavior.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, L.; Zhang, J.; Li, J.; Tian, H.; Zheng, C.; Guo, S. Design of a lightweight broadband vibration reduction structure with embedded acoustic black holes in viscoelastic damping materials. Mater. Des. 2024, 248, 113450. [Google Scholar] [CrossRef]
- Li, F. Incorporating fractional operators into interaction dynamics of a chaotic biological model. Results Phys. 2023, 54, 107052. [Google Scholar] [CrossRef]
- Chen, J.; Du, C.; Wang, Q.; Peng, X. A 3D finite strain constitutive model for shape memory polymers combined viscoelasticity and storage strain. Mech. Mater. 2024, 197, 105103. [Google Scholar] [CrossRef]
- Ribeiro, E.A.; de Oliveira Lopes, E.M.; Bavastri, C.A. A numerical and experimental study on optimal design of multi-DOF viscoelastic supports for passive vibration control in rotating machinery. J. Sound Vib. 2017, 411, 346–361. [Google Scholar] [CrossRef]
- Simoes, R.; Cunha, A.M.; Brostow, W. Computer simulations of true stress development and viscoelastic behavior in amorphous polymeric materials. Comput. Mater. Sci. 2006, 36, 319–328. [Google Scholar] [CrossRef]
- Carrera, Y.; Avila-de La Rosa, G.; Vernon-Carter, E.; Alvarez-Ramirez, J. A fractional-order Maxwell model for non-Newtonian fluids. Phys. A Stat. Mech. Its Appl. 2017, 482, 276–285. [Google Scholar] [CrossRef]
- Ren, D.; Shen, X.; Li, C.; Cao, X. The fractional Kelvin-Voigt model for Rayleigh surface waves in viscoelastic FGM infinite half space. Mech. Res. Commun. 2018, 87, 53–58. [Google Scholar] [CrossRef]
- Lewandowski, R.; Wielentejczyk, P. Nonlinear vibration of viscoelastic beams described using fractional order derivatives. J. Sound Vib. 2017, 399, 228–243. [Google Scholar] [CrossRef]
- Xu, H.; Jiang, X. Creep constitutive models for viscoelastic materials based on fractional derivatives. Comput. Math. Appl. 2017, 73, 1377–1384. [Google Scholar] [CrossRef]
- Tarasov, V.E. Generalized memory: Fractional calculus approach. Fractal Fract. 2018, 2, 23. [Google Scholar] [CrossRef]
- Almeida, R. Functional differential equations involving the ψ-Caputo fractional derivative. Fractal Fract. 2020, 4, 29. [Google Scholar] [CrossRef]
- Guo, S.; Pu, H.; Yang, M.; Sha, Z.; Liu, D.; Xie, J.; Feng, Y. New perspective on the creep characteristic of fiber–dependent shape memory polymers: Variable–order fractional constitutive model. J. Mater. Res. Technol. 2023, 24, 5177–5185. [Google Scholar]
- Han, C.; Chen, Y.; Cheng, G.; Serra, R.; Wang, L.; Feng, J. Numerical analysis of axially non-linear viscoelastic string with the variable fractional order model by using Bernstein polynomials algorithm. Int. J. Comput. Math. 2022, 99, 537–552. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P. Rate-dependent fractional constitutive model for nonlinear behaviors of rubber polymers. Eur. J. Mech.-A/Solids 2024, 103, 105186. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Y.M. Shifted-Chebyshev-polynomial-based numerical algorithm for fractional order polymer visco-elastic rotating beam. Chaos Solitons Fractals 2020, 132, 109585. [Google Scholar] [CrossRef]
- Saeed, U.; ur Rehman, M. Haar wavelet Picard method for fractional nonlinear partial differential equations. Appl. Math. Comput. 2015, 264, 310–322. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y. Shifted Legendre Polynomials algorithm used for the dynamic analysis of viscoelastic pipes conveying fluid with variable fractional order model. Appl. Math. Model. 2020, 81, 159–176. [Google Scholar] [CrossRef]
- Soradi-Zeid, S.; Jahanshahi, H.; Yousefpour, A.; Bekiros, S. King algorithm: A novel optimization approach based on variable-order fractional calculus with application in chaotic financial systems. Chaos Solitons Fractals 2020, 132, 109569. [Google Scholar] [CrossRef]
- Pezza, L.; Pitolli, F. A multiscale collocation method for fractional differential problems. Math. Comput. Simul. 2018, 147, 210–219. [Google Scholar] [CrossRef]
- Wang, Y.; Mei, L.; Li, Q.; Bu, L. Split-step spectral Galerkin method for the two-dimensional nonlinear space-fractional Schrödinger equation. Appl. Numer. Math. 2019, 136, 257–278. [Google Scholar] [CrossRef]
- Yang, Z.; Yuan, Z.; Nie, Y.; Wang, J.; Zhu, X.; Liu, F. Finite element method for nonlinear Riesz space fractional diffusion equations on irregular domains. J. Comput. Phys. 2017, 330, 863–883. [Google Scholar] [CrossRef]
- Wang, Q. Homotopy perturbation method for fractional KdV-Burgers equation. Chaos Solitons Fractals 2008, 35, 843–850. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. Application of variational iteration method to nonlinear differential equations of fractional order. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 27–34. [Google Scholar] [CrossRef]
- Ray, S.S.; Bera, R. An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl. Math. Comput. 2005, 167, 561–571. [Google Scholar]
- Li, J.; Ahmad, I.; Ahmad, H.; Shah, D.; Chu, Y.-M.; Thounthong, P.; Ayaz, M. Numerical solution of two-term time-fractional PDE models arising in mathematical physics using local meshless method. Open Phys. 2020, 18, 1063–1072. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K. Exact solution of two-dimensional fractional partial differential equations. Fractal Fract. 2020, 4, 21. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Y.; Cheng, G.; Barrière, T. Numerical analysis of fractional partial differential equations applied to polymeric visco-elastic Euler-Bernoulli beam under quasi-static loads. Chaos Solitons Fractals 2020, 140, 110255. [Google Scholar] [CrossRef]
- Mei, L.; Wu, B.; Lin, Y. Shifted-Legendre orthonormal method for delay heat conduction equation. Appl. Math. Lett. 2022, 130, 107996. [Google Scholar] [CrossRef]
- Chouhan, D.; Mishra, V.; Srivastava, H. Bernoulli wavelet method for numerical solution of anomalous infiltration and diffusion modeling by nonlinear fractional differential equations of variable order. Results Appl. Math. 2021, 10, 100146. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, L.; Chen, Y. Numerical analysis of fractional-order variable section cantilever beams. ICIC Express Lett. 2019, 13, 547–555. [Google Scholar]
- Kadkhoda, N. A numerical approach for solving variable order differential equations using Bernstein polynomials. Alex. Eng. J. 2020, 59, 3041–3047. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Y.; Han, X.; Cheng, S. The blackbody radiation inversion problem: A numerical perspective utilizing Bernstein polynomials. Int. Commun. Heat Mass Transf. 2019, 107, 114–120. [Google Scholar] [CrossRef]
- Khataybeh, S.N.; Hashim, I.; Alshbool, M. Solving directly third-order ODEs using operational matrices of Bernstein polynomials method with applications to fluid flow equations. J. King Saud Univ. Sci. 2019, 31, 822–826. [Google Scholar] [CrossRef]
- Ahmad, I.; Alshammari, A.O.; Jan, R.; Razak, N.N.A.; Idris, S.A. An Efficient Numerical Solution of a Multi-Dimensional Two-Term Fractional Order PDE via a Hybrid Methodology: The Caputo–Lucas–Fibonacci Approach with Strang Splitting. Fractal Fract. 2024, 8, 364. [Google Scholar] [CrossRef]
- Rostamy, D.; Jafari, H.; Alipour, M.; Khalique, C.M. Computational method based on Bernstein operational matrices for multi-order fractional differential equations. Filomat 2014, 28, 591–601. [Google Scholar] [CrossRef]
- Maleknejad, K.; Hashemizadeh, E.; Basirat, B. Computational method based on Bernstein operational matrices for nonlinear Volterra–Fredholm–Hammerstein integral equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 52–61. [Google Scholar] [CrossRef]
- Bataineh, A.; Isik, O.; Aloushoush, N.; Shawagfeh, N. Bernstein operational matrix with error analysis for solving high order delay differential equations. Int. J. Appl. Comput. Math. 2017, 3, 1749–1762. [Google Scholar] [CrossRef]
- Cui, Y.; Qu, J.; Han, C.; Cheng, G.; Zhang, W.; Chen, Y. Shifted Bernstein–Legendre polynomial collocation algorithm for numerical analysis of viscoelastic Euler–Bernoulli beam with variable order fractional model. Math. Comput. Simul. 2022, 200, 361–376. [Google Scholar] [CrossRef]
- Malara, G.; Pomaro, B.; Spanos, P.D. Nonlinear stochastic vibration of a variable cross-section rod with a fractional derivative element. Int. J. Non-Linear Mech. 2021, 135, 103770. [Google Scholar] [CrossRef]
- Khan, R.A.; Khalil, H. A new method based on legendre polynomials for solution of system of fractional order partial differential equations. Int. J. Comput. Math. 2014, 91, 2554–2567. [Google Scholar] [CrossRef]
- Nemati, S.; Ordokhani, Y. Legendre expansion methods for the numerical solution of nonlinear 2D Fredholm integral equations of the second kind. J. Appl. Math. Inform. 2013, 31, 609–621. [Google Scholar] [CrossRef]

| e(x,t) | |||||||
|---|---|---|---|---|---|---|---|
| x = 0.3 | 4.12 × 10−5 | 7.07 × 10−6 | 1.77 × 10−6 | 1.47 × 10−5 | 3.49 × 10−7 | 1.79 × 10−6 | 4.60 × 10−6 |
| x = 0.5 | 1.06 × 10−4 | 1.72 × 10−5 | 6.13 × 10−6 | 5.04 × 10−5 | 3.48 × 10−7 | 1.80 × 10−6 | 4.59 × 10−6 |
| x = 0.7 | 2.68 × 10−7 | 4.36 × 10−7 | 4.24 × 10−7 | 2.42 × 10−7 | 3.49 × 10−7 | 1.79 × 10−6 | 4.60 × 10−6 |
| e(x,t) | |||||||
|---|---|---|---|---|---|---|---|
| x = 0.3 | 7.26 × 10−4 | 2.94 × 10−4 | 1.27 × 10−4 | 5.75 × 10−4 | 9.41 × 10−6 | 7.75 × 10−6 | 7.74 × 10−6 |
| x = 0.5 | 4.29 × 10−4 | 1.74 × 10−4 | 7.53 × 10−6 | 2.42 × 10−5 | 5.58 × 10−6 | 4.60 × 10−6 | 4.59 × 10−6 |
| x = 0.7 | 1.96 × 10−4 | 3.08 × 10−5 | 1.39 × 10−5 | 1.11 × 10−4 | 9.41 × 10−6 | 7.75 × 10−6 | 7.74 × 10−6 |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Length | l | 4 | m |
| Density | 7500 | kg/m3 | |
| Instant elasticity modulus | 2.5 × 105 | Pa | |
| Prolonged elasticity modulus | 2.5 × 105 | Pa |
| Material | |||
|---|---|---|---|
| HDPE | 960 kg/m3 | 8.5 × 106 Pa | 8.5 × 106 Pa |
| Polyurea | 1060 kg/m3 | 1.2 × 107 Pa | 1.2 × 107 Pa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Ma, L.; Chen, Y.; Qu, J.; Cui, Y.; Wang, L. Shifted Bernstein Polynomial-Based Dynamic Analysis for Variable Fractional Order Nonlinear Viscoelastic Bar. Fractal Fract. 2025, 9, 192. https://doi.org/10.3390/fractalfract9030192
Li Z, Ma L, Chen Y, Qu J, Cui Y, Wang L. Shifted Bernstein Polynomial-Based Dynamic Analysis for Variable Fractional Order Nonlinear Viscoelastic Bar. Fractal and Fractional. 2025; 9(3):192. https://doi.org/10.3390/fractalfract9030192
Chicago/Turabian StyleLi, Zhongze, Lixing Ma, Yiming Chen, Jingguo Qu, Yuhuan Cui, and Lei Wang. 2025. "Shifted Bernstein Polynomial-Based Dynamic Analysis for Variable Fractional Order Nonlinear Viscoelastic Bar" Fractal and Fractional 9, no. 3: 192. https://doi.org/10.3390/fractalfract9030192
APA StyleLi, Z., Ma, L., Chen, Y., Qu, J., Cui, Y., & Wang, L. (2025). Shifted Bernstein Polynomial-Based Dynamic Analysis for Variable Fractional Order Nonlinear Viscoelastic Bar. Fractal and Fractional, 9(3), 192. https://doi.org/10.3390/fractalfract9030192






