Homotopy Analysis Transform Method for Solving Systems of Fractional-Order Partial Differential Equations
Abstract
:1. Introduction
2. Preliminaries
2.1. Basic Definitions Fractional-Calculus Operators
2.2. Basic Definitions and Properties of Jafrai Transform
- The Jafari transform of the Riemann–Liouville fractional derivative is represented as
- The Jafari transform of the Caputo fractional derivative is represented as
- The Jafari transform of certain partial derivatives is represented as
- The Jafari transform of certain functions is provided
2.3. The Definition and Procedure of Homotopy Analysis
3. Homotopy Analysis Transform Method to Solve the System of Equations
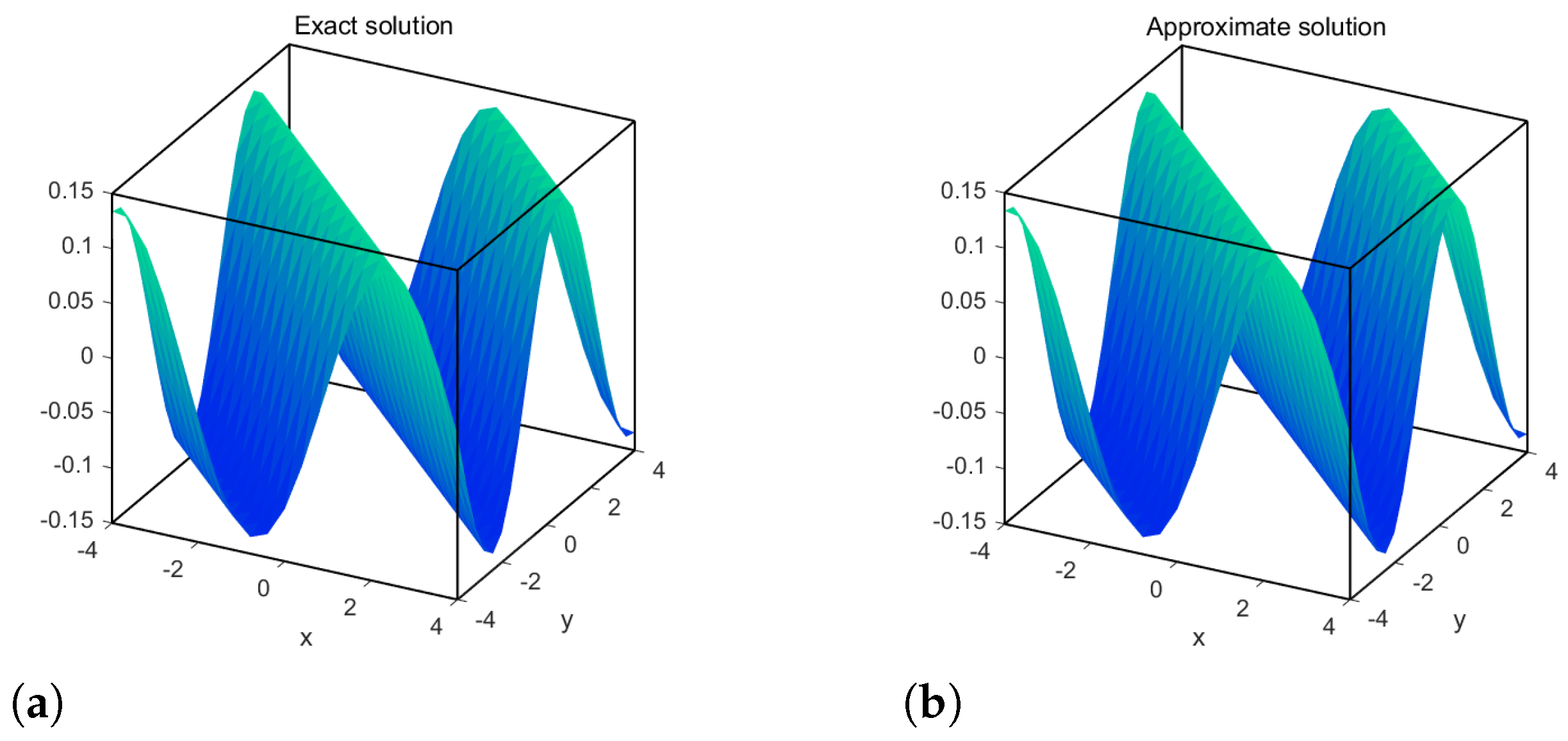
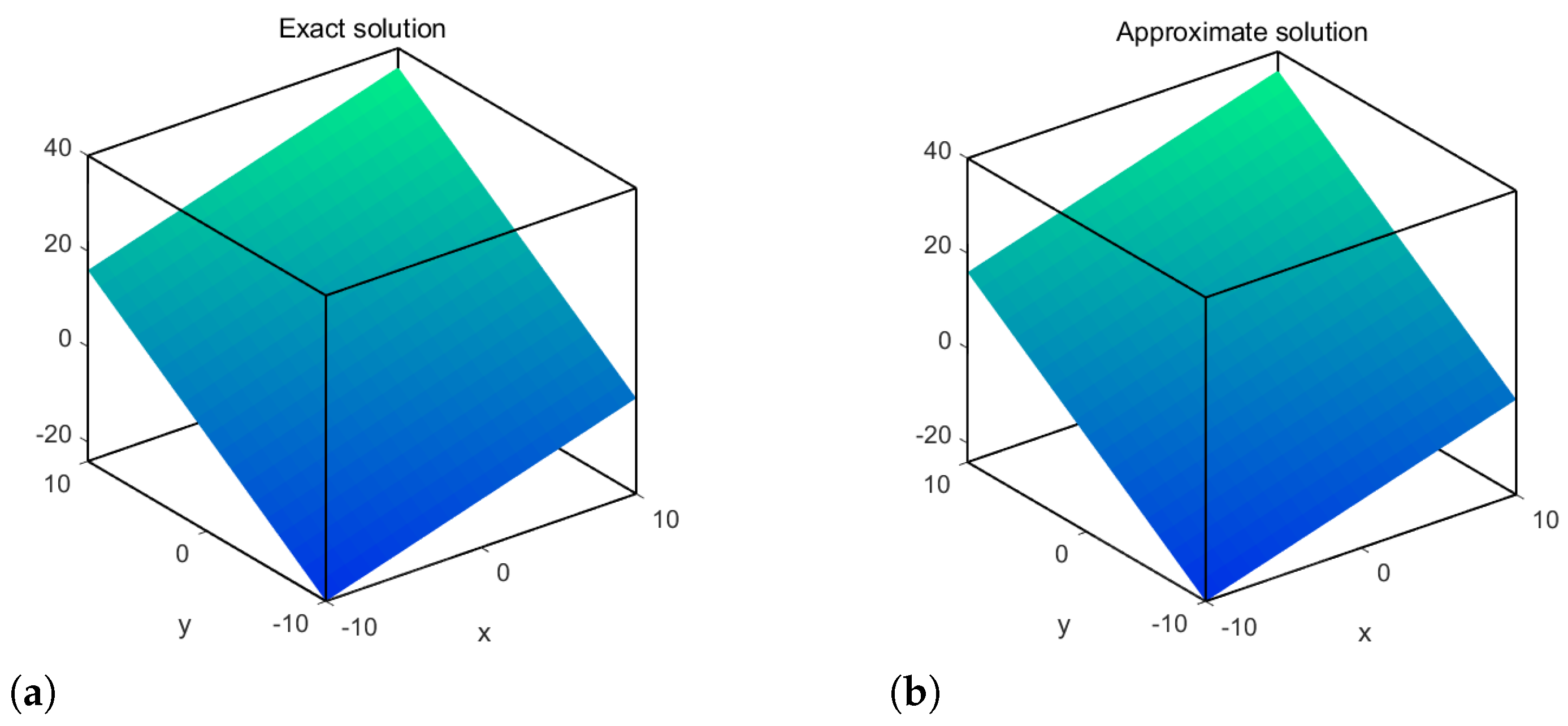
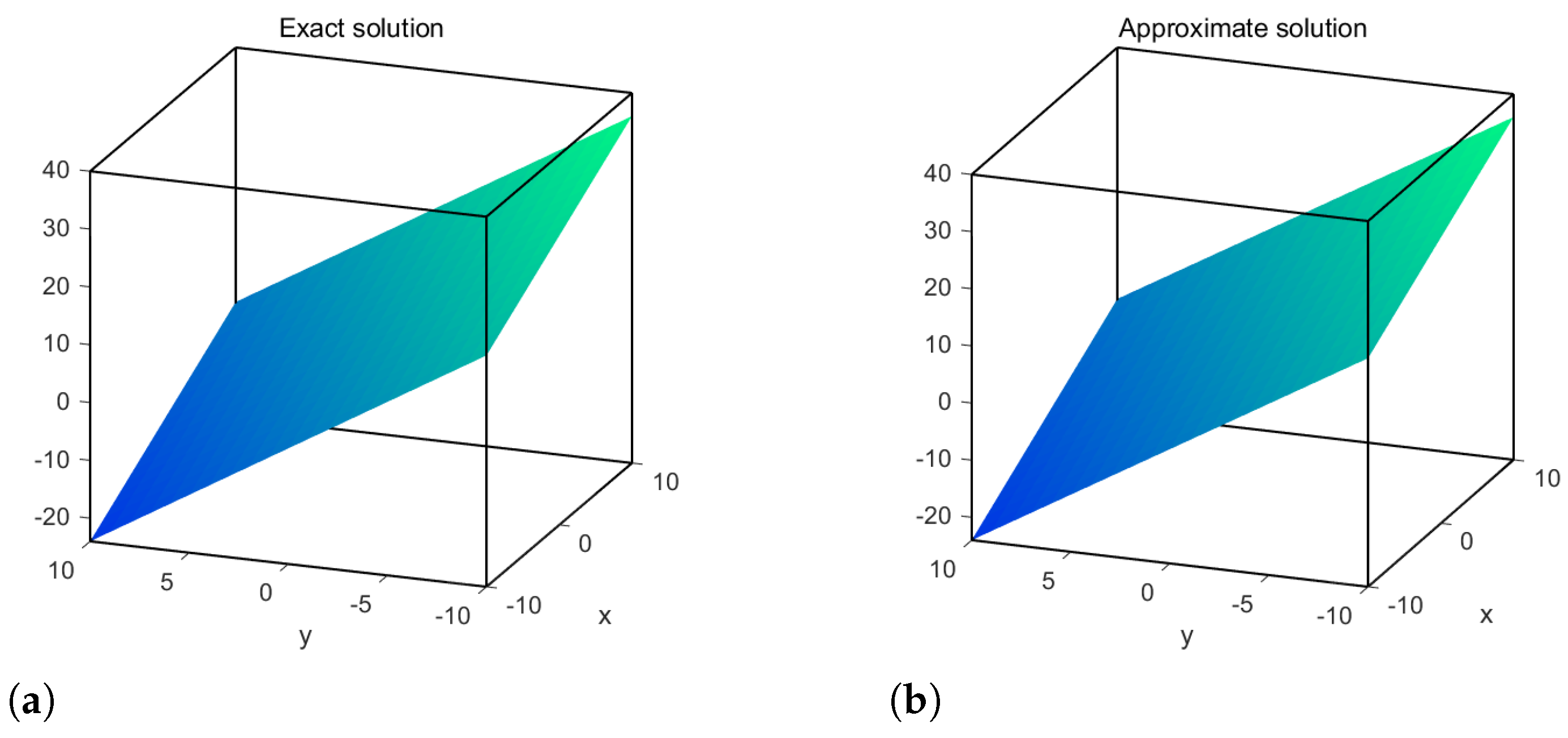
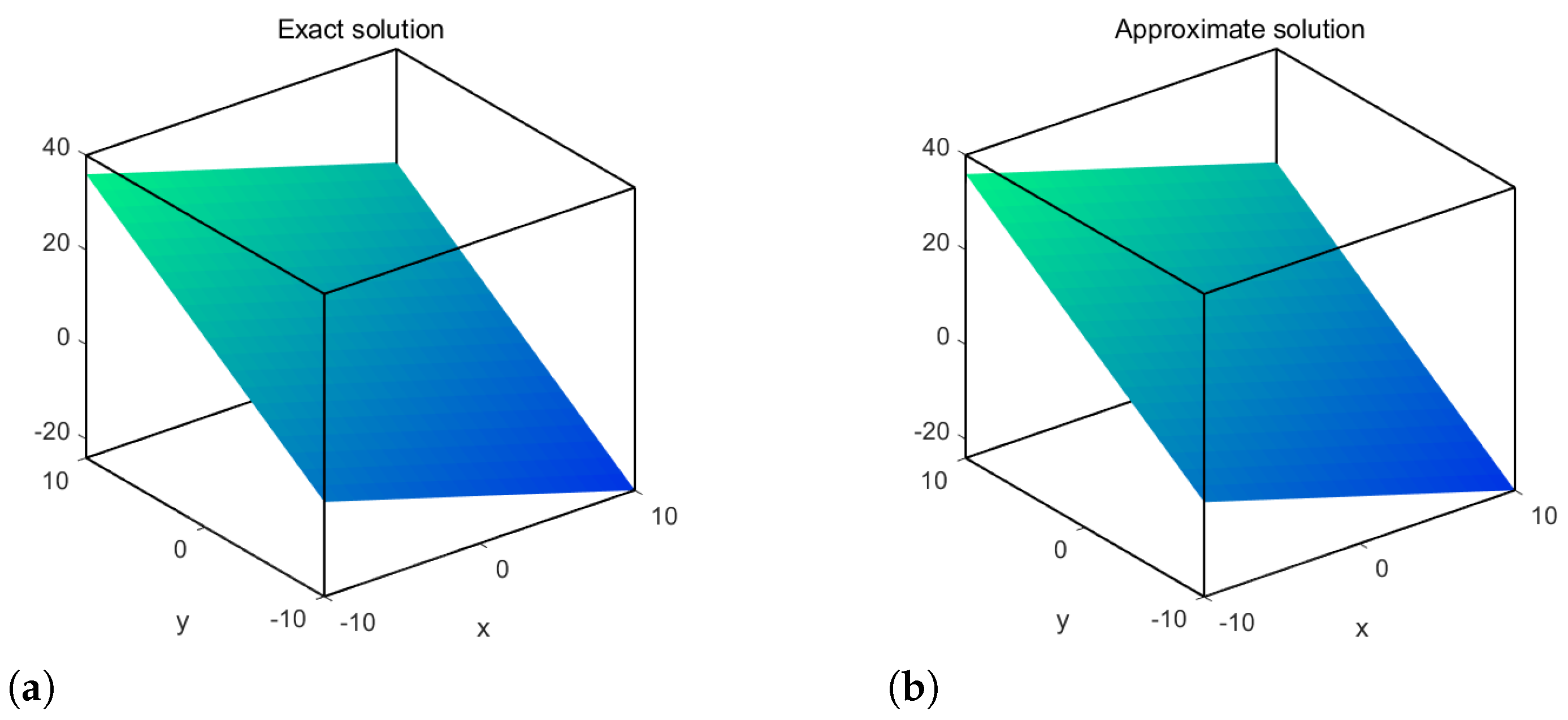
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ait Touchent, K.; Hammouch, Z.; Mekkaoui, T.; Belgacem, F.B. Implementation and convergence analysis of homotopy perturbation coupled with Sumudu transform to construct solutions of local-fractional PDEs. Fractal Fract. 2018, 2, 22. [Google Scholar] [CrossRef]
- Jothimani, K.; Kaliraj, K.; Hammouch, Z.; Ravichandran, C. New results on controllability in the framework of fractional integrodifferential equations with nondense domain. Eur. Phys. J. Plus 2019, 134, 441. [Google Scholar] [CrossRef]
- Zhang, Y. A finite difference method for fractional partial differential equation. Appl. Math. Comput. 2009, 215, 524–529. [Google Scholar] [CrossRef]
- Wang, F.; Xue, L.; Zhao, K.; Zheng, X. Global stabilization and boundary control of generalized Fisher/KPP equation and application to diffusive SIS model. J. Differ. Equ. 2021, 275, 391–417. [Google Scholar] [CrossRef]
- Mendoza, J.; Muriel, C. New exact solutions for a generalised Burgers-Fisher equation. Chaos Solitons Fractals 2021, 152, 111360. [Google Scholar] [CrossRef]
- Nadeem, M.; Iambor, L.F. Prospective analysis of time-fractional Emden–Fowler model using Elzaki transform homotopy perturbation method. Fractal Fract. 2024, 8, 363. [Google Scholar] [CrossRef]
- Inan, B. The Generalized Fractional-Order Fisher Equation: Stability and Numerical Simulation. Symmetry 2024, 16, 393. [Google Scholar] [CrossRef]
- Butera, S.; Di Paola, M. Fractional differential equations solved by using Mellin transform. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2220–2227. [Google Scholar] [CrossRef]
- Rashid, S.; Hammouch, Z.; Aydi, H.; Ahmad, A.G.; Alsharif, A.M. Novel computations of the time-fractional Fisher’s model via generalized fractional integral operators by means of the Elzaki transform. Fractal Fract. 2021, 5, 94. [Google Scholar] [CrossRef]
- Lal, D.; Vir, K. Elzaki transform method for solving the Fokker–Planck equation. NeuroQuantology 2022, 20, 729–739. Available online: https://www.neuroquantology.com/media/article_pdfs/729-739.pdf (accessed on 13 April 2025).
- Wazwaz, A.M.; Gorguis, A. An analytic study of Fisher’s equation by using Adomian decomposition method. Appl. Math. Comput. 2004, 154, 609–620. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical approach to differential equations of fractional order. J. Comput. Appl. Math. 2007, 207, 96–110. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Analytical approach to linear fractional partial differential equations arising in fluid mechanics. Phys. Lett. A 2006, 355, 271–279. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Loyinmi, A.C.; Akinfe, T.K. Exact solutions to the family of Fisher’s reaction-diffusion equation using Elzaki homotopy transformation perturbation method. Eng. Rep. 2020, 2, e12084. [Google Scholar] [CrossRef]
- Liao, S.J. Comparison between the homotopy analysis method and homotopy perturbation method. Appl. Math. Comput. 2005, 169, 1186–1194. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Arafa, A.A.M.; Rida, S.Z.; Mohamed, H. Approximate analytical solutions of Schnakenberg systems by homotopy analysis method. Appl. Math. Model. 2012, 36, 4789–4796. [Google Scholar] [CrossRef]
- Khan, M.; Gondal, M.A.; Hussain, I.; Vanani, S.K. A new comparative study between homotopy analysis transform method and homotopy perturbation transform method on a semi infinite domain. Math. Comput. Model. 2012, 55, 1143–1150. [Google Scholar] [CrossRef]
- Kumar, S. A new analytical modelling for fractional telegraph equation via Laplace transform. Appl. Math. Model. 2014, 38, 3154–3163. [Google Scholar] [CrossRef]
- Sartanpara, P.P.; Meher, R. Analytical study of time fractional Fisher equation using homotopy approach with a generalized transform. In Proceedings of the 2023 International Conference on Fractional Differentiation and Its Applications (ICFDA), Ajman, United Arab Emirates, 14–16 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Sunitha, M.; Gamaoun, F.; Abdulrahman, A.; Malagi, N.S.; Singh, S.; Gowda, R.J.; Gowda, R.P. An efficient analytical approach with novel integral transform to study the two-dimensional solute transport problem. Ain Shams Eng. J. 2023, 14, 101878. [Google Scholar] [CrossRef]
- Sharma, S.; Singh, I. Elzaki transform homotopy analysis techniques for solving fractional (2+1)-D and (3+1)-D nonlinear schrodinger equations. Commun. Appl. Nonlinear Anal. 2024, 31, 305–317. Available online: https://internationalpubls.com (accessed on 13 April 2025). [CrossRef]
- Arshad, M.S.; Afzal, Z.; Almutairi, B.; Macías-Díaz, J.E.; Rafiq, S. Homotopy analysis with shehu transform method for time-fractional modified KdV equation in dusty plasma. Int. J. Theor. Phys. 2024, 63, 94. [Google Scholar] [CrossRef]
- Zurigat, M.; Momani, S.; Odibat, Z.; Alawneh, A. The homotopy analysis method for handling systems of fractional differential equations. Appl. Math. Model. 2010, 34, 24–35. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S. Solving time-fractional Navier–Stokes equations using homotopy perturbation Elzaki transform. SN Appl. Sci. 2019, 1, 16. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Farooq, U.; Baleanu, D.; Kumam, P.; Arif, M. A new analytical technique to solve system of fractional-order partial differential equations. IEEE Access 2019, 7, 150037–150050. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Baleanu, D.; Arif, M. Laplace decomposition for solving nonlinear system of fractional order partial differential equations. Adv. Differ. Equ. 2020, 2020, 375. [Google Scholar] [CrossRef]
- Liao, S.J. A kind of approximate solution technique which does not depend upon small parameters—II. An application in fluid mechanics. Int. J. Non-Linear Mech. 1997, 32, 815–822. [Google Scholar] [CrossRef]
- Liang, S.X.; Jeffrey, D.J. Comparison of homotopy analysis method and homotopy perturbation method through an evolution equation. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 4057–4064. [Google Scholar] [CrossRef]
- Liao, S.J. An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2003–2016. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Kumam, P.; Arif, M. An analytical technique to solve the system of nonlinear fractional partial differential equations. Mathematics 2019, 7, 505. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel simulations to the time-fractional Fisher’s equation. Math. Sci. 2019, 13, 33–42. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Li, C.P.; Qian, D.L.; Chen, Y.Q. On Riemann-Liouville and caputo derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Li, C.P.; Deng, W.H. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Jafari, H. A new general integral transform for solving integral equations. J. Adv. Res. 2021, 32, 133–138. [Google Scholar] [CrossRef]
- Singh, B.K.; Kumar, P. FRDTM for numerical simulation of multi-dimensional, time-fractional model of Navier–Stokes equation. Ain Shams Eng. J. 2018, 9, 827–834. [Google Scholar] [CrossRef]
- Eltayeb, H.; Bachar, I.; Kilicman, A. On Conformable Double Laplace Transform and One Dimensional Fractional Coupled Burgers’ Equation. Symmetry 2019, 11, 417. [Google Scholar] [CrossRef]
- Kothari, K.; Mehta, U.; Vanualailai, J. A novel approach of fractional-order time delay system modeling based on Haar wavelet. ISA Trans. 2018, 80, 371–380. [Google Scholar] [CrossRef]



| Homotopy Analysis Method with Integral Transform | Nonlinear Operator |
|---|---|
| Jafari transform | |
| Laplace transform | |
| Elzaki transform | |
| Aboodh transform | |
| Pourreza transform | |
| Sumudu transform | |
| Sawi transform | |
| Kamal transform | |
| G transform | |
| Mohand transform |
| x | y | ||
|---|---|---|---|
| −4.0 | −4.0 | ||
| −2.0 | −2.0 | ||
| 2.0 | 2.0 | ||
| 4.0 | 4.0 |
| x | ||||
|---|---|---|---|---|
| −4 | 0.019096199070450 | 0.019096199070450 | 0.019096199070450 | 0.019098516261135 |
| 0 | −0.113866897109886 | −0.113866897109886 | −0.113866897109886 | −0.113880714064368 |
| 1 | −0.123045094141044 | −0.123045094141044 | −0.123045094141044 | −0.123060024805777 |
| x | y | ||
|---|---|---|---|
| 0.0 | 0.0 | ||
| 0.2 | 0.2 | ||
| 0.4 | 0.4 | ||
| 0.6 | 0.6 | ||
| 0.8 | 0.8 | ||
| 1.0 | 1.0 |
| First Term | ||||
|---|---|---|---|---|
| 2.1038845625 | 2.104850390625 | 2.10517096666667 | 2.104846140625 | |
| 0.1038845625 | 0.104850390625 | 0.10517096666667 | 0.104846140625 | |
| 2.0538845625 | 2.092350390625 | 2.10517096666667 | 2.092346140625 | |
| 0.0538845625 | 0.092350390625 | 0.10517096666667 | 0.092346140625 |
| First Term | ||||
|---|---|---|---|---|
| 0.3375 | 0.3046875 | 0.3 | 0.2953125 | |
| −1.6625 | −1.6953125 | −1.7 | −1.7046875 | |
| 2.3375 | 2.3046875 | 2.3 | 2.2953125 | |
| 1.075 | 0.6 | 0.3 | 0.1375 | |
| 2.025 | −0.21875 | −1.7 | −2.49325 | |
| 6.025 | 3.78125 | 2.3 | 1.50625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Fang, Q.; Hu, Y. Homotopy Analysis Transform Method for Solving Systems of Fractional-Order Partial Differential Equations. Fractal Fract. 2025, 9, 253. https://doi.org/10.3390/fractalfract9040253
Wang F, Fang Q, Hu Y. Homotopy Analysis Transform Method for Solving Systems of Fractional-Order Partial Differential Equations. Fractal and Fractional. 2025; 9(4):253. https://doi.org/10.3390/fractalfract9040253
Chicago/Turabian StyleWang, Fang, Qing Fang, and Yanyan Hu. 2025. "Homotopy Analysis Transform Method for Solving Systems of Fractional-Order Partial Differential Equations" Fractal and Fractional 9, no. 4: 253. https://doi.org/10.3390/fractalfract9040253
APA StyleWang, F., Fang, Q., & Hu, Y. (2025). Homotopy Analysis Transform Method for Solving Systems of Fractional-Order Partial Differential Equations. Fractal and Fractional, 9(4), 253. https://doi.org/10.3390/fractalfract9040253