Putting an End to the Physical Initial Conditions of the Caputo Derivative: The Infinite State Solution
Abstract
1. Introduction
2. A Counter-Example to the Usual Caputo Approach
2.1. A Realistic Initial Value Problem
2.2. The Usual Caputo Solution
3. The Infinite State Representation
3.1. Introduction
3.2. Riemann–Liouville Integration
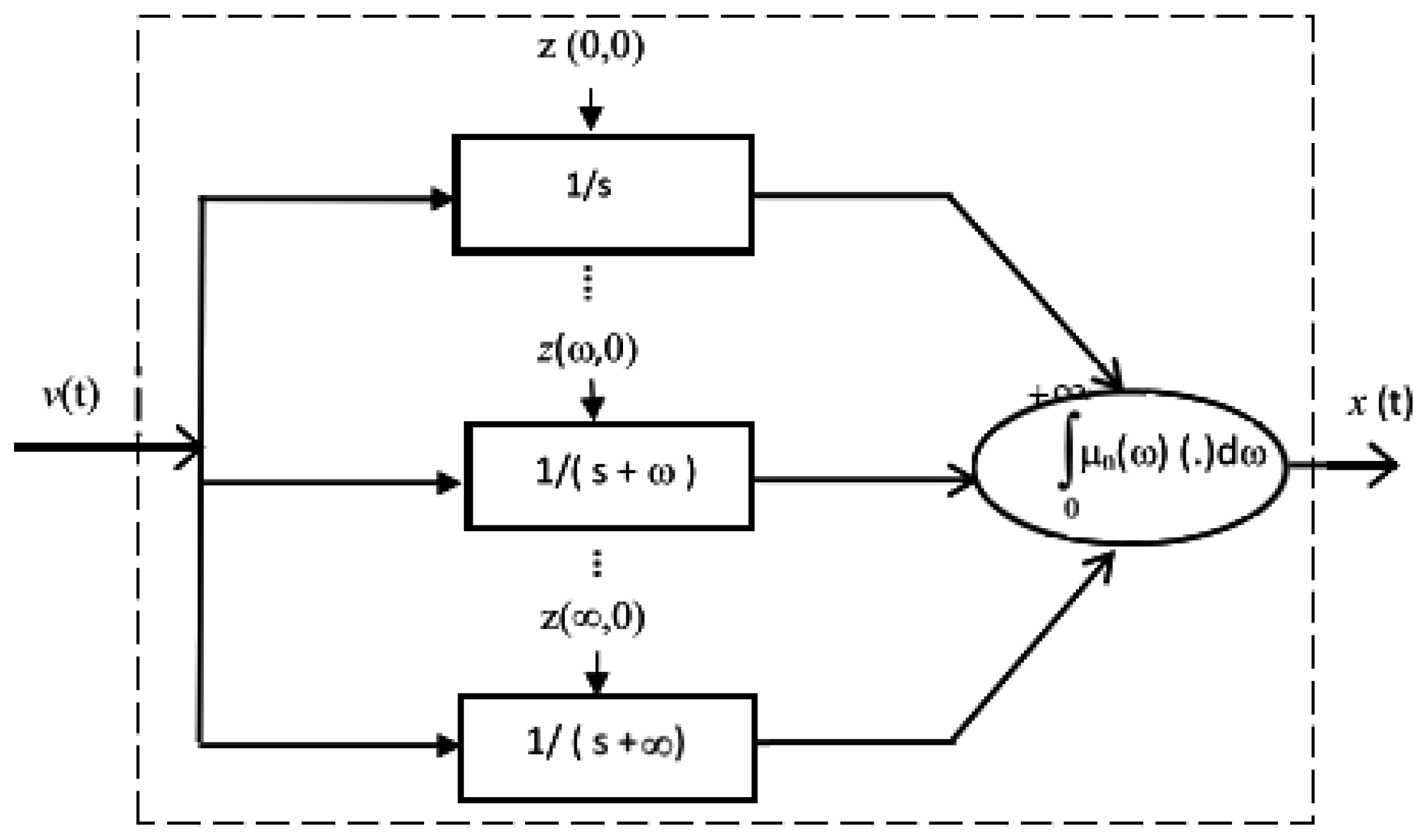
3.3. The Distributed Model of the Fractional Integrator
3.4. Transients of the Frequency-Distributed Integrator
4. Initial Conditions of the Caputo Derivative
4.1. Introduction
4.2. Initial Conditions
5. Counter-Example: The Infinite State Solution
5.1. Introduction
5.2. The Mittag–LefflerApproach
5.2.1. The Mittag–Leffler Free Response
5.2.2. Principle of the Numerical Computation of the Mittag–Lefler Free Response
5.2.3. Numerical Example of the Computation of the Mittag–Leffler Free Response
5.3. The Infinite State Approach
5.3.1. Introduction
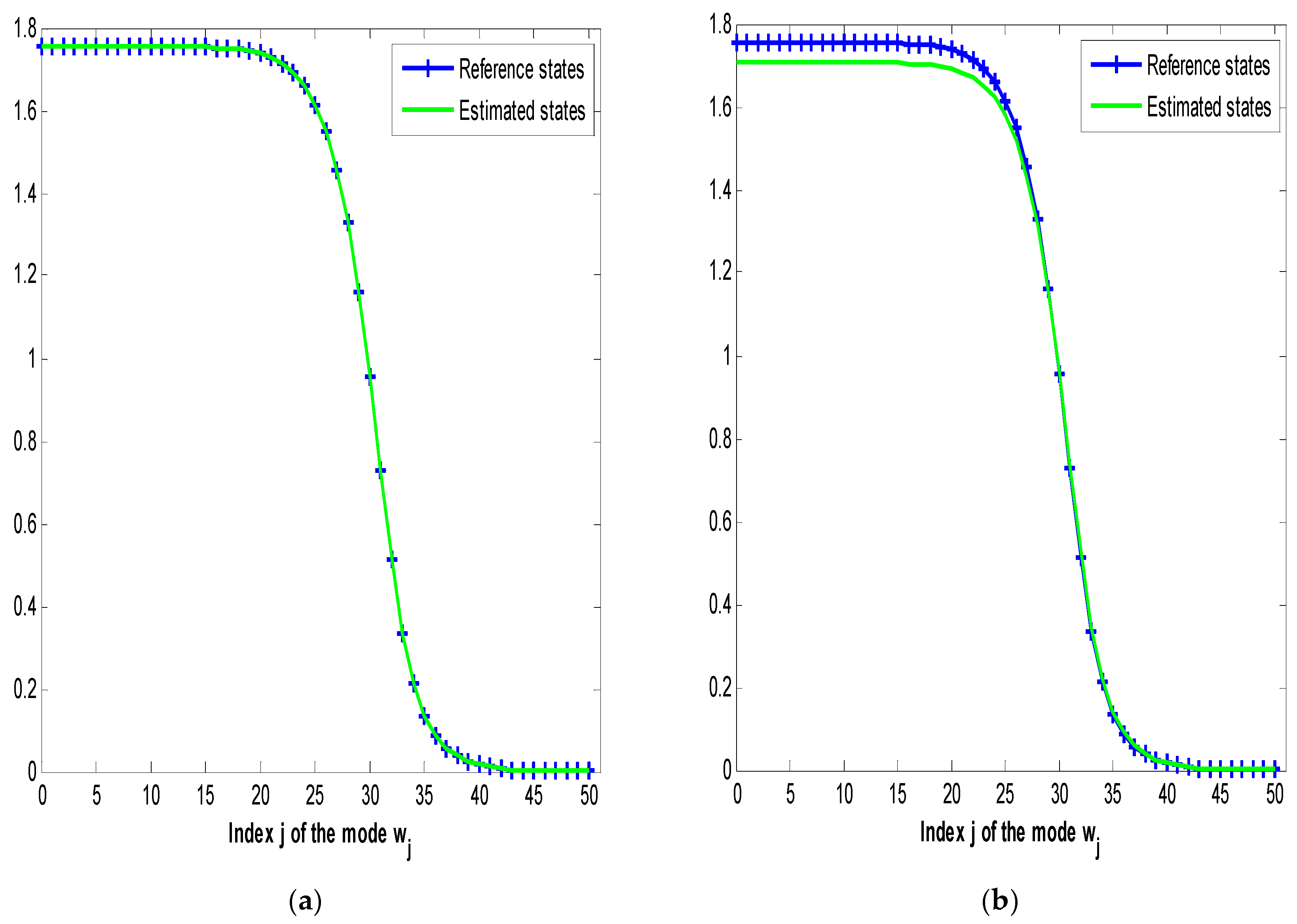
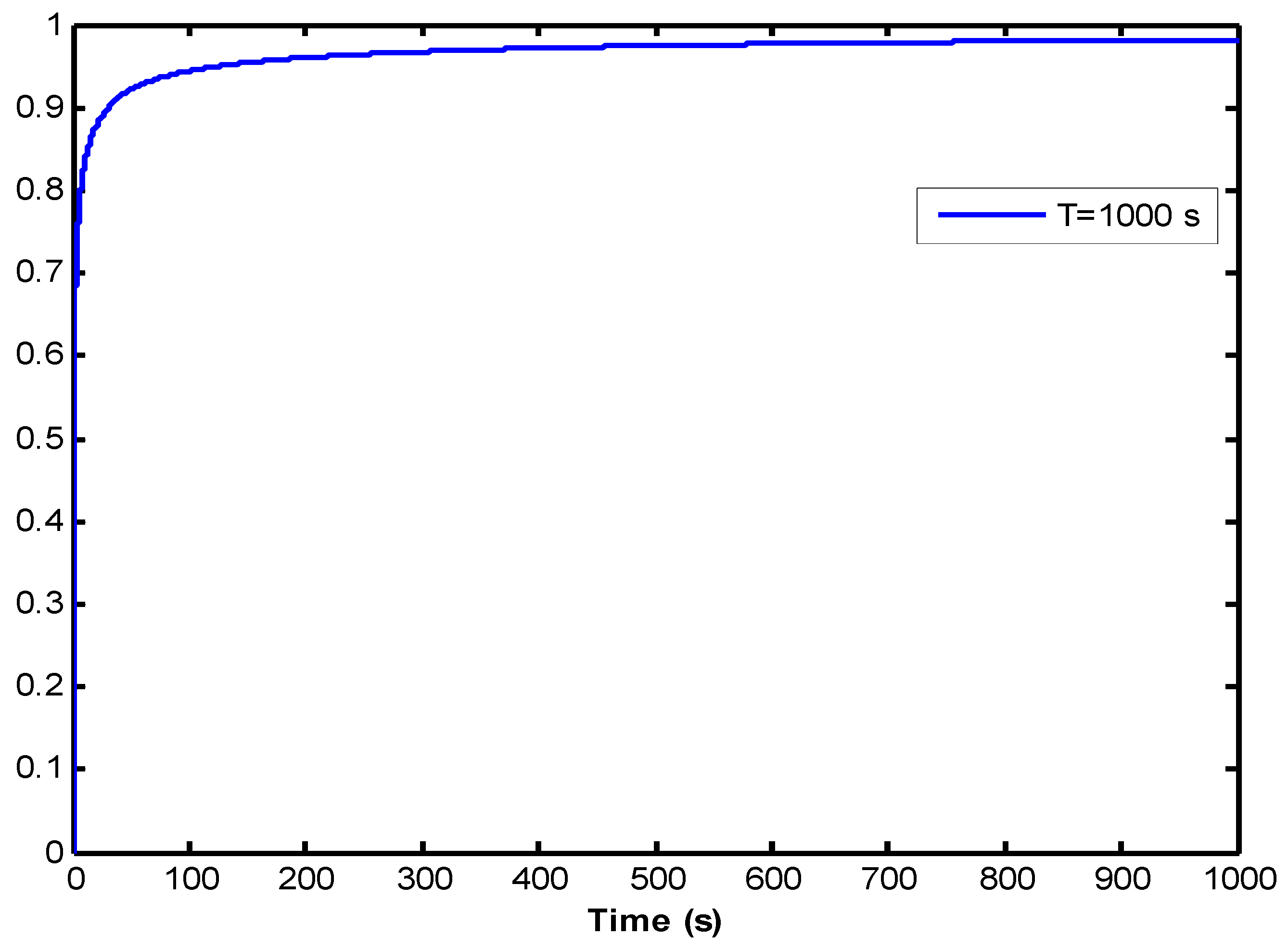
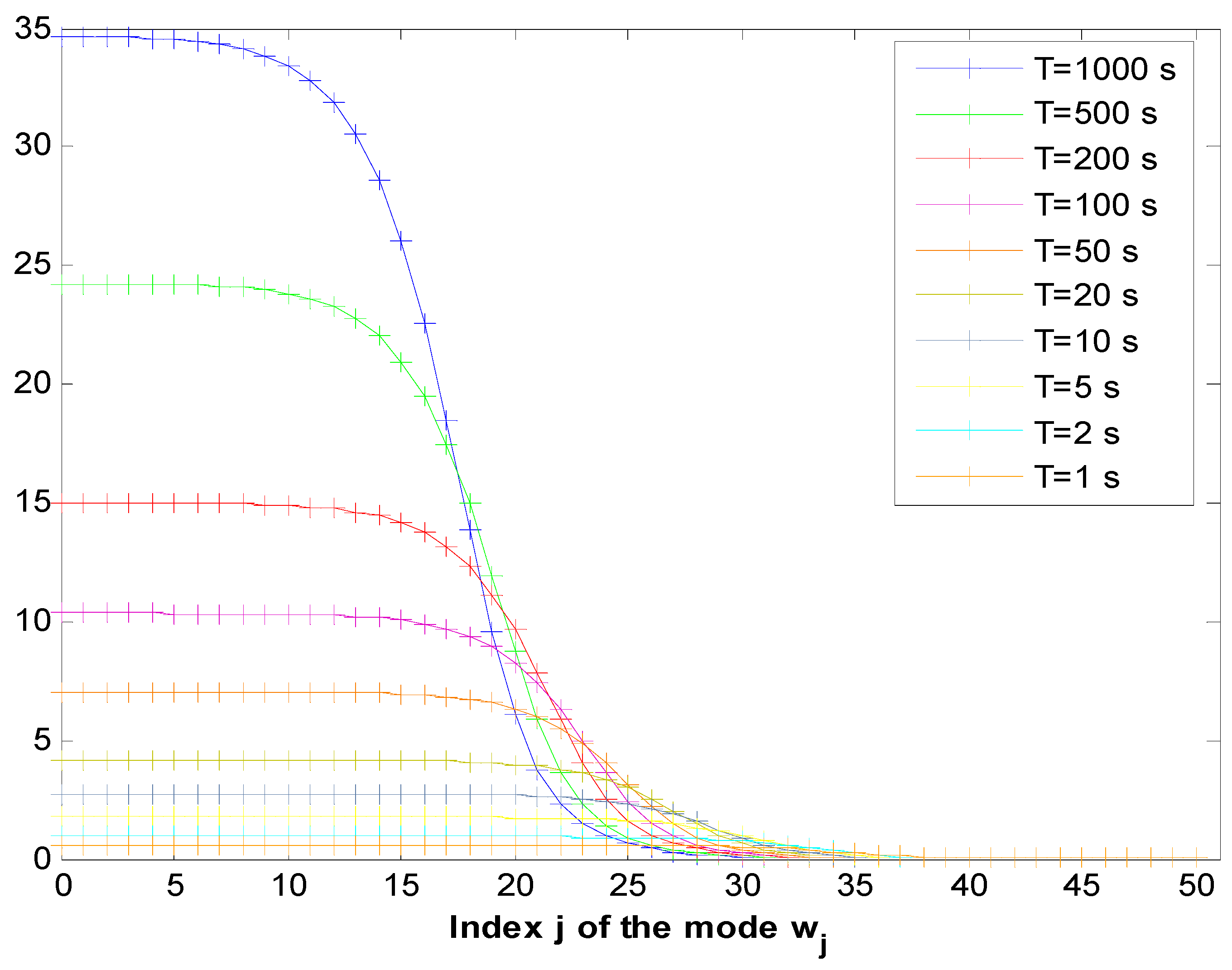
5.3.2. Direct Numerical Solution
5.3.3. The Matrix Exponential Solution
6. Why Is the Usual Caputo Solution Unrealistic?
6.1. Introduction
6.2. Necessary Condition for Rest Based on the History Interval
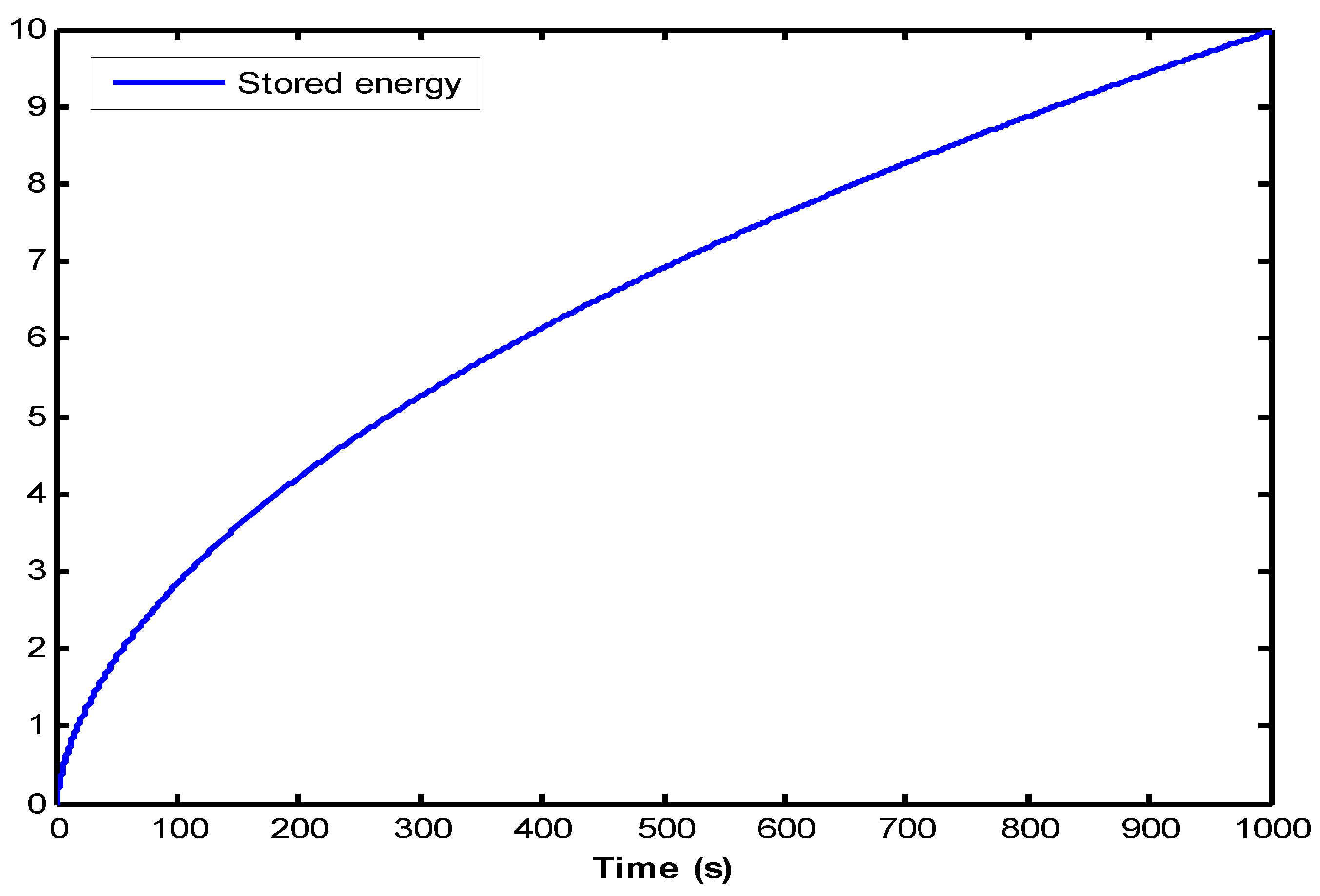
6.3. Stored Energy in the Fractional Integrator
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
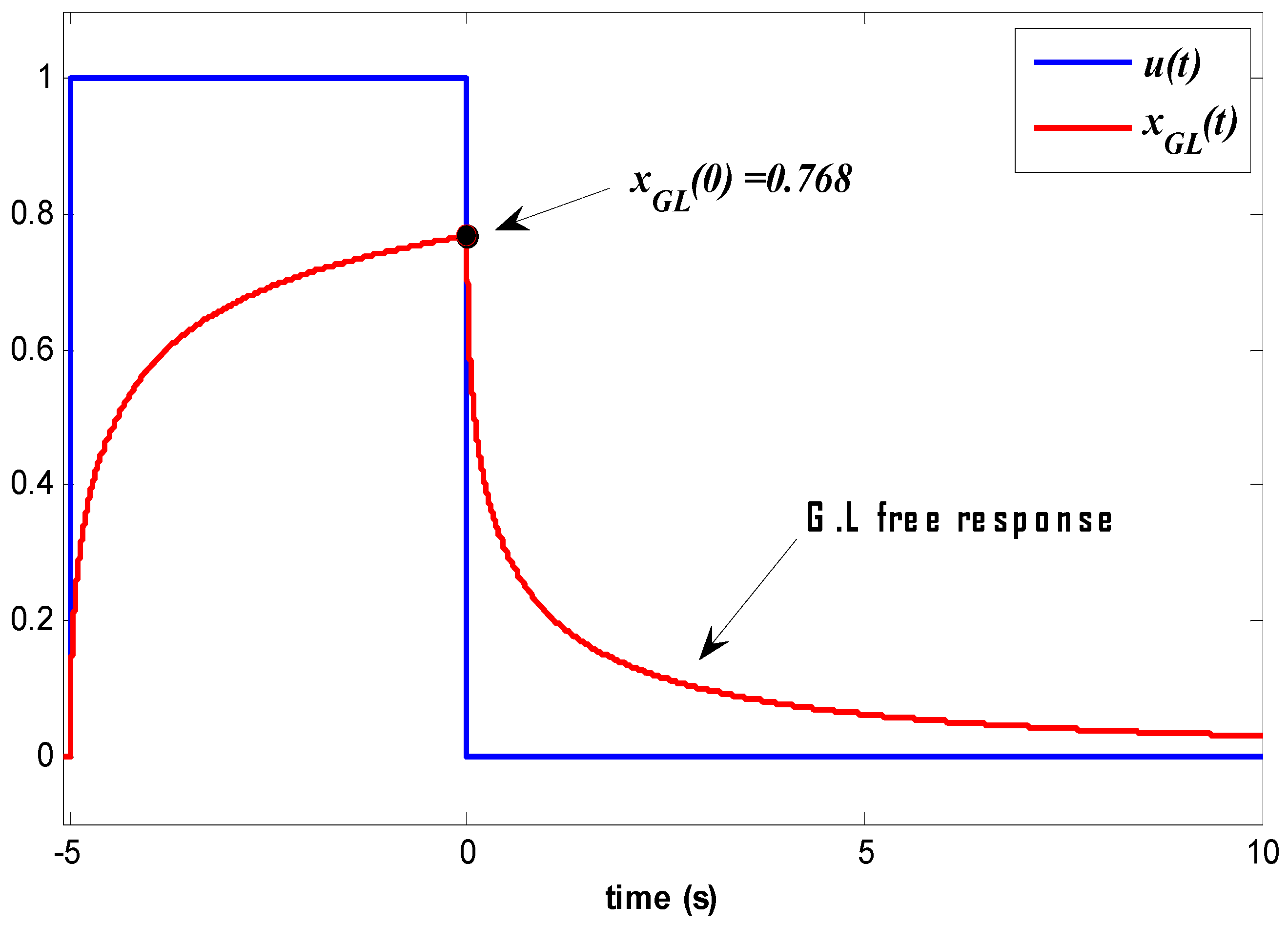
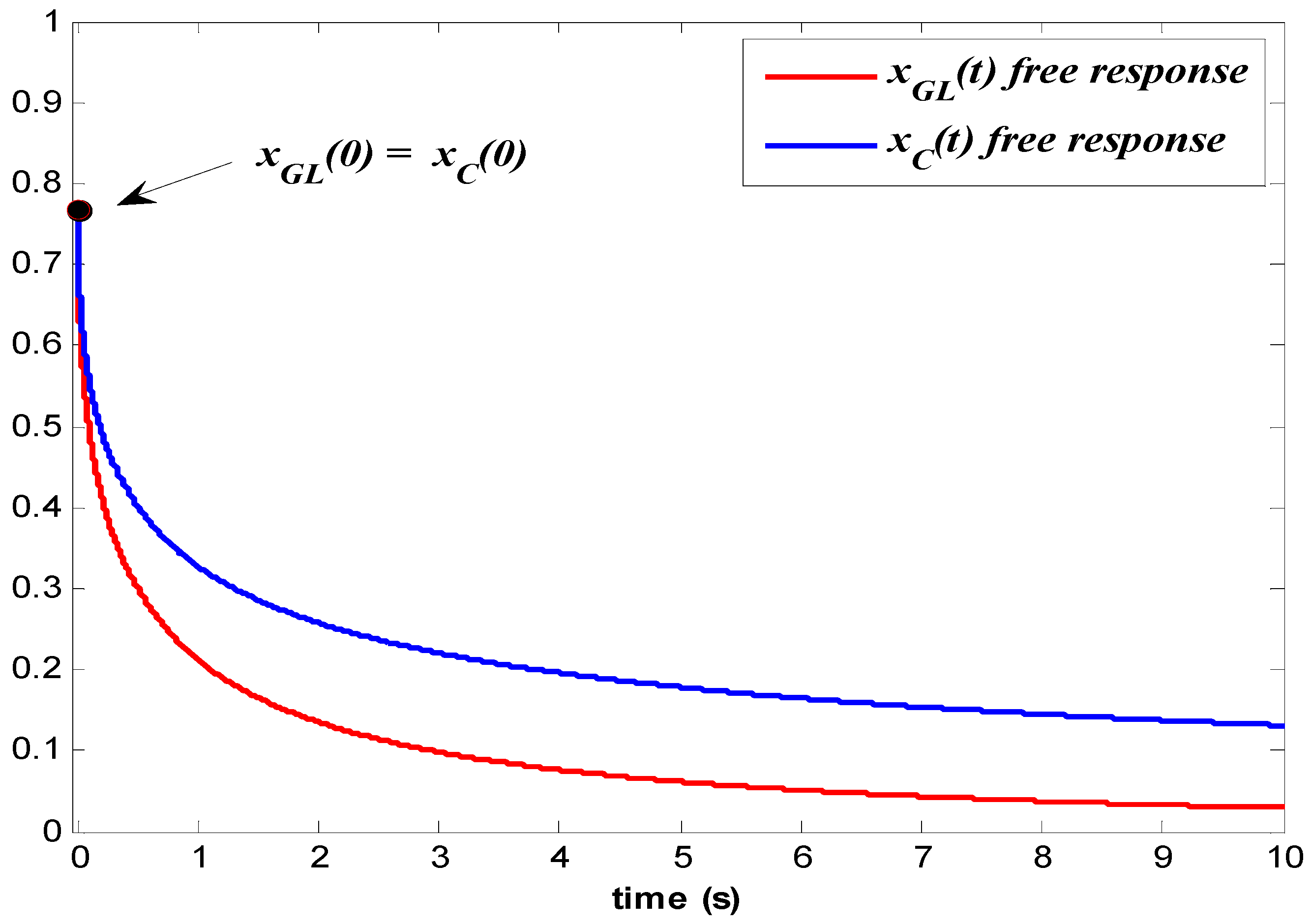
Appendix A. The Grünwald–Letnikov Integrator
Appendix B. Finite-Dimensional Approximation of the Fractional Integrator
Appendix B.1. Direct Approach
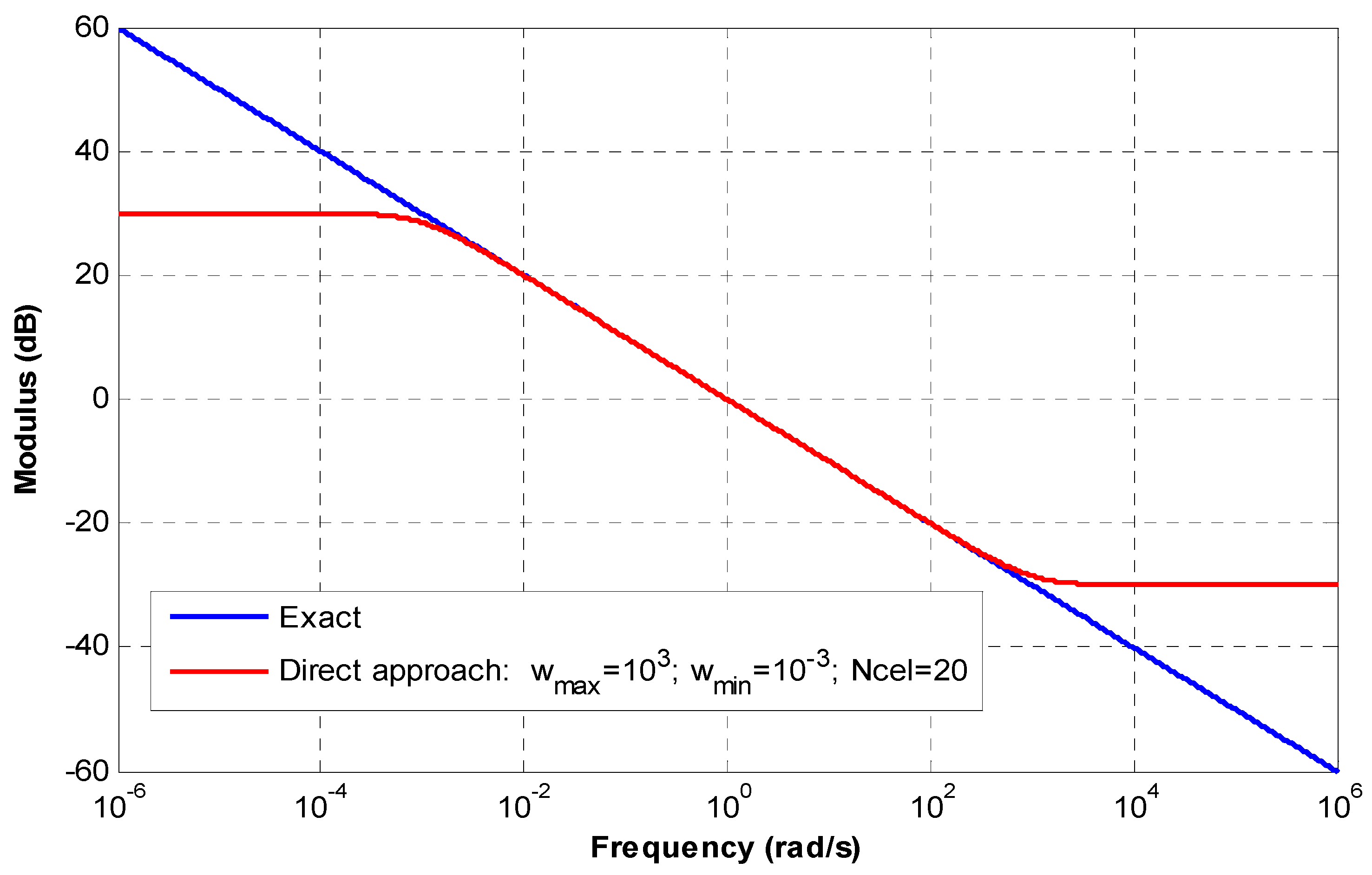
Appendix B.2. Indirect Approach
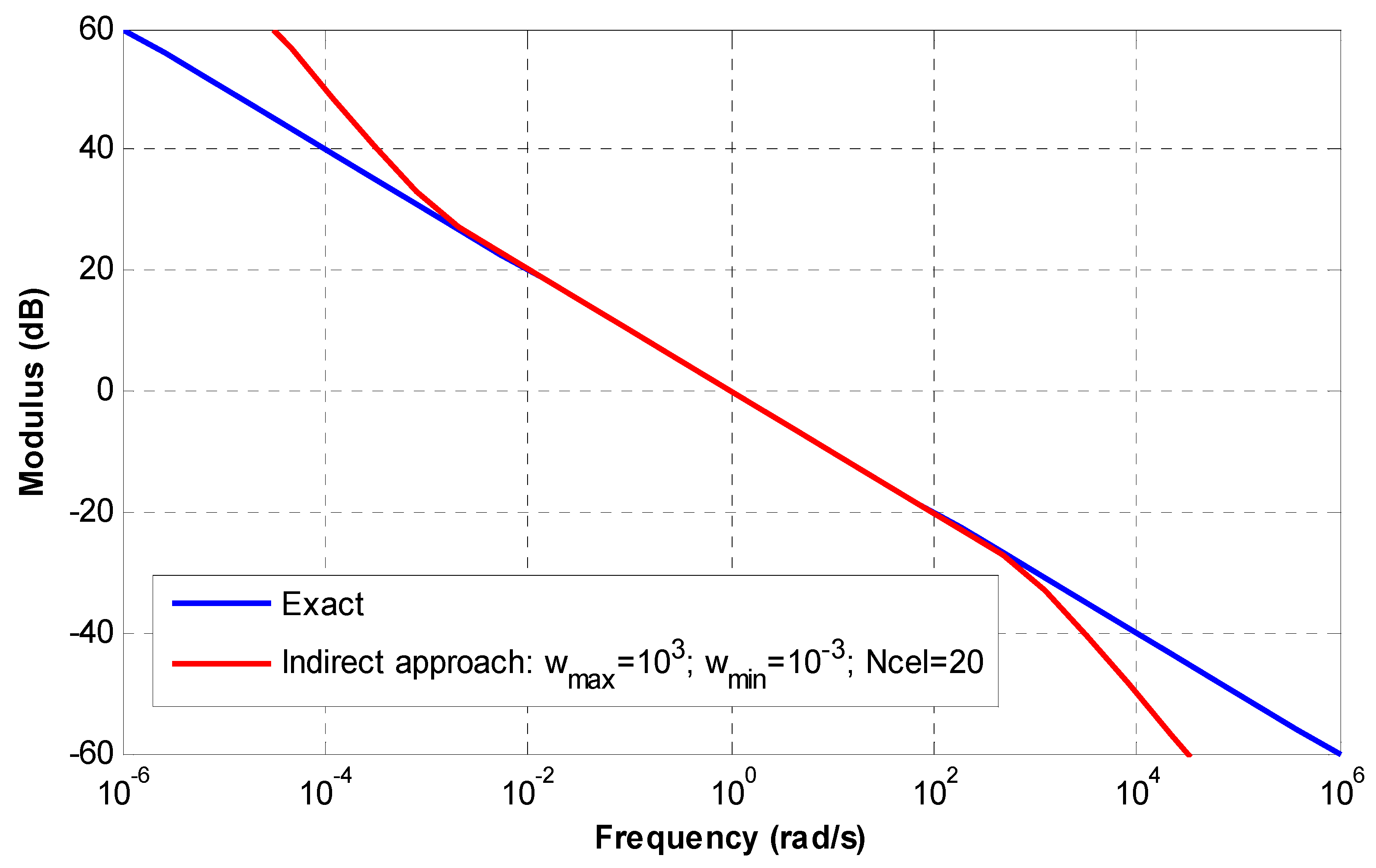
Appendix B.3. Frequency-Discretized Approximation
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. Fract. Calc. Appl. Anal. 2002, 5, 367–386. [Google Scholar]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional Order Systems and Control; Springer: London, UK, 2010. [Google Scholar]
- Fukunaga, M.; Shimizu, N. Role of prehistories in the initial value problems of fractional viscoelastic equations. Nonlinear Dyn. 2004, 38, 207–220. [Google Scholar] [CrossRef]
- Hartley, T.T.; Lorenzo, C.F. The error incurred in using the Caputo derivative Laplace transform. In Proceedings of the ASME IDET-CIE Conferences, San Diego, CA, USA, 30 August–2 September 2009. [Google Scholar]
- Sabatier, J.; Merveillaut, M.; Malti, R.; Oustaloup, A. How to impose physically coherent initial conditions to a fractional system? Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1318–1326. [Google Scholar] [CrossRef]
- Du, M.; Wang, Z. Correcting the initialization of models with fractional derivatives via history dependent conditions. Acta Mech. Sin. 2015, 37, 320–325. [Google Scholar] [CrossRef]
- Du, B.; Wei, Y.; Liang, S.; Wang, Y. Estimation of exact initial states of fractional order systems. Nonlinear Dyn. 2016, 86, 2061–2070. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, Y.; Chen, Y.; Wang, Y. A new look at the fractional initial value problem: The aberration phenomenon. ASME J. Comput. Nonlinear Dyn. 2018, 13, 121004. [Google Scholar] [CrossRef]
- Balin, A.M.; Balint, S. Mathematical description of the groundwater flow and that of the impurity spread, which use temporal Caputo or Riemann–Liouville fractional partial derivatives, is non-objective. Fractal Fract. 2020, 4, 36. [Google Scholar] [CrossRef]
- Khalil, A.; Yousef, M.S. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 2, 73–85. [Google Scholar]
- Atanackovic, T.M.; Pilipovic, S.; Zorica, D. Properties of the Caputo-Fabrizio fractional derivative and its distributional setting. Fract. Calc. Appl. Anal. 2018, 21, 29–44. [Google Scholar] [CrossRef]
- Martinez, F.; Mohammed, P.O.; Valdes, J.N. Non-conformable fractional Laplace transform. Kragujev. J. Math. 2022, 46, 341–354. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. A critical analysis of the Caputo-Fabrizio operator. Commun. Nonlinear Sci. Numer. Simulat. 2018, 59, 608–611. [Google Scholar] [CrossRef]
- Tarasov, V.E. No nonlocality, no fractional derivative. Commun. Nonlinear Sci. Numer. Simulat. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- Hartley, T.T.; Lorenzo, C.F. The initialization response of linear fractional order system with constant History function. In Proceedings of the 2009 ASME/IDETC, San Diego, CA, USA, 30 August–2 September 2009. [Google Scholar]
- Hartley, T.T.; Lorenzo, C.F. The initialization response of linear fractional order system with ramp History function. In Proceedings of the 2009 ASME/IDETC, San Diego, CA, USA, 30 August–2 September 2009. [Google Scholar]
- Maamri, T.J.C.N.; Oustaloup, A. The infinite state approach: Origin and necessity. Comput. Math. Appl. 2013, 66, 892–907. [Google Scholar]
- Hartley, T.T.; Lorenzo, C.F.; Trigeassou, J.C.; Maamri, N. Equivalence of history function based and infinite dimensional state initializations for fractional order operators. ASME J. Comput. Nonlinear Dyn. 2013, 8, 041014. [Google Scholar] [CrossRef]
- Trigeassou, J.C.; Maamri, N. Analysis, Modeling and Stability of Fractional Order Differential Systems 1: The Infinite State Approach; John Wiley and Sons: Hoboken, NJ, USA, 2019; Volume 1–2. [Google Scholar]
- Trigeassou, J.C.; Maamri, N. The Infinite State representation of fractional order differential systems: A survey, parts I and II. IFAC-PapersOnLine 2024, 58, 265–275. [Google Scholar] [CrossRef]
- Wang, B.; Ding, J.; Wu, F.; Zhu, D. Robust finite time control of fractional order nonlinear systems via frequency distributed model. Nonlinear Dyn. 2016, 85, 2133–2142. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, Y.; Liu, J.; Shi, B. Equivalence of initialized fractional integrals and the diffusive model. ASME J. Comput. Nonlinear Dyn. 2018, 13, 034501. [Google Scholar] [CrossRef]
- Yuan, J.; Shi, B.; Ji, W. Adaptive sliding mode control of a novel class of fractional chaotic systems. Adv. Math. Phys. 2013, 2013, 576709. [Google Scholar] [CrossRef]
- Wang, B.; Yin, L.; Wang, S.; Mia, S.; Du, T. Finite time control for fractional order nonlinear hydroturbine governing system via frequency distributed model. Hindawi Math. Phys. 2016, 2016, 7345325. [Google Scholar] [CrossRef]
- Montseny, G. Diffusive representation of pseudo differential time operators. ESAIM Proc. 1998, 5, 159–175. [Google Scholar] [CrossRef]
- Heleschewitz, D.; Matignon, D. Diffusive realizations of fractional integro-differential operators: Structural analysis under approximation. In Proceedings of the IFAC, System, Structure and Control, Nantes, France, 8–10 July 1998; Volume 31, pp. 227–232. [Google Scholar]
- Diethelm, K. Fast solution methods for fractional differential equations in the modeling of viscoelastic materials. In Proceedings of the 9th ICSC Conference, Caen, France, 24–26 November 2021. [Google Scholar]
- Diethelm, K. A new diffusive representation for fractional derivatives, part I: Construction, implementation and numerical examples. In Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Diethelm, K. A new diffusive representation for fractional derivatives, part II: Convergence analysis of the numerical scheme. Mathematics 2022, 10, 1245. [Google Scholar] [CrossRef]
- Hinze, M.; Schmidt, A.; Leine, R.I. Lyapunov stability of a fractionally damped oscillator with linear (anti-)damping. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 425–442. [Google Scholar] [CrossRef]
- Hinze, M.; Schmidt, A.; Leine, R.I. Numerical solution of fractional ordinary differential equations using the reformulated infinite state representation. Fract. Calc. Appl. Anal. 2019, 22, 1321–1350. [Google Scholar] [CrossRef]
- Arumugam, V.; Ferrante, A.; Ntogramatzidis, L.; Padula, F. A geometric framework for distributed frequency models. Commun. Nonlinear Sci. Numer. Simul. 2024, 136, 108088. [Google Scholar] [CrossRef]
- Maamri, N.; Trigeassou, J.C. A plea for the integration of fractional differential systems: The initial value problem. Fractal Fract. 2022, 6, 550. [Google Scholar] [CrossRef]
- Maamri, N.; Tari, M.; Trigeassou, J.C. Improved initialization of fractional order systems. IFAC-PapersOnLine 2017, 50, 8567–8573. [Google Scholar] [CrossRef]
- Curtain, R.F.; Zwart, H.J. An Introduction to Infinite Dimensional Linear Systems Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Hartley, T.T.; Trigeassou, J.C.; Lorenzo, C.F.; Maamri, N. Initialization energy in fractional order systems. In Proceedings of the ASME Conference IDETC/CIE, Boston, MA, USA, 2–5 August 2015. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Limitations of frequency domain approximation for detecting chaos in fractional order systems. Nonlinear Anal. 2008, 69, 1299–1320. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trigeassou, J.-C.; Maamri, N. Putting an End to the Physical Initial Conditions of the Caputo Derivative: The Infinite State Solution. Fractal Fract. 2025, 9, 252. https://doi.org/10.3390/fractalfract9040252
Trigeassou J-C, Maamri N. Putting an End to the Physical Initial Conditions of the Caputo Derivative: The Infinite State Solution. Fractal and Fractional. 2025; 9(4):252. https://doi.org/10.3390/fractalfract9040252
Chicago/Turabian StyleTrigeassou, Jean-Claude, and Nezha Maamri. 2025. "Putting an End to the Physical Initial Conditions of the Caputo Derivative: The Infinite State Solution" Fractal and Fractional 9, no. 4: 252. https://doi.org/10.3390/fractalfract9040252
APA StyleTrigeassou, J.-C., & Maamri, N. (2025). Putting an End to the Physical Initial Conditions of the Caputo Derivative: The Infinite State Solution. Fractal and Fractional, 9(4), 252. https://doi.org/10.3390/fractalfract9040252





