A Simple Fractional Model with Unusual Dynamics in the Derivative Order
Abstract
1. Introduction
- (1)
- In the first case, we proposed a novel dynamics for described by a first-order differential equation that incorporates the state variable and its first derivative . To our knowledge, this approach is unprecedented, as previous works have defined the dynamics of solely as a function of the state variables [19] or in terms of a differential equation (ordinary or fractional) with and t as dependent and independent variables, respectively [17].
- (2)
- In the second case, we proposed second-order dynamics for , which combines an ordinary derivative, a fractional derivative, and the state variable . This example highlights the possibility of using combinations of different types of derivatives to define the dynamics of the variable order.
- (3)
- The third case presents a recursive system based on Scarpi derivatives of variable orders , , and , which interact and influence each other. This approach, still unexplored in the literature, proposes a novel dynamic model that exhibits significant differences compared to the classical case.
2. Preliminaries
- (1)
- exists and its analytical expression is known;
- (2)
- exists and belongs to ;
- (3)
- is locally integrable on for some known T.
3. Examples with Various Dynamics for (t)
3.1. Case 1
3.2. Case 2
3.3. Case 3
4. Conclusions
- (1)
- The first case introduces a new dynamic for , described by a first-order differential equation that includes the state variable and its derivative , which, to our knowledge, has not been previously explored.
- (2)
- The second case proposes a second-order dynamic for , combining ordinary and fractional derivatives with the state variable , illustrating the use of different types of derivatives in defining variable order dynamics.
- (3)
- The third case presents a recursive system involving variable orders , , and , which interact and influence each other. This novel approach has not yet been addressed in the literature and contrasts significantly with traditional models. In addition, a Lemma generalizing the third case is presented.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Feng, X.; Sutton, M. A new theory of fractional differential calculus. Anal. Appl. 2021, 19, 715–750. [Google Scholar] [CrossRef]
- Ostalczyk, P.; Sankowski, D.; Nowakowski, J. Non-Integer Order Calculus and its Applications: 9th International Conference on Non-Integer Order Calculus and its Applications, Łódź, Poland; Springer: Cham, Switerland, 2018. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A review on variable-order fractional differential equations: Mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Polo-Labarrios, M.; Godínez, F.; Quezada-García, S. Numerical-analytical solutions of the fractional point kinetic model with Caputo derivatives. Ann. Nucl. Energy 2022, 166, 108745. [Google Scholar] [CrossRef]
- García-Aspeitia, M.A.; Fernandez-Anaya, G.; Hernández-Almada, A.; Leon, G.; Magaña, J. Cosmology under the fractional calculus approach. Mon. Not. R. Astron. Soc. 2022, 517, 4813–4826. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Zhang, L. Basic Theory of Fractional Differential Equations, 2nd ed.; World Scientific: Singapore, 2016. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Ye, X. A new fractional-order chaos system of Hopfield neural network and its application in image encryption. Chaos Solitons Fractals 2022, 157, 111889. [Google Scholar] [CrossRef]
- Ding, W.; Patnaik, S.; Sidhardh, S.; Semperlotti, F. Applications of Distributed-Order Fractional Operators: A Review. Entropy 2021, 23, 110. [Google Scholar] [CrossRef]
- Ayazi, N.; Mokhtary, P.; Moghaddam, B.P. Efficiently solving fractional delay differential equations of variable order via an adjusted spectral element approach. Chaos Solitons Fractals 2024, 181, 114635. [Google Scholar] [CrossRef]
- Almeida, R.; Martins, N.; da C. Sousa, J.V. Fractional tempered differential equations depending on arbitrary kernels. AIMS Math. 2024, 9, 9107–9127. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Eduardo Carvajal-Rubio, J.; Fernández-Anaya, G.; Sánchez-Torres, J.D. Output feedback robust stabilization of distributed-order systems. Asian J. Control. 2025. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; Machado, J.T.; De Oliveira, E.C. The ψ-Hilfer fractional calculus of variable order and its applications. Comput. Appl. Math. 2020, 39, 296. [Google Scholar] [CrossRef]
- Scarpi, G. Sulla possibilità di un modello reologico intermedio di tipo evolutivo. Atti Accad. Naz. Lincei. Cl. Sci. Fis. Mat. E Naturali. Rend. 1972, 52, 912–917. [Google Scholar]
- Garrappa, R.; Giusti, A.; Mainardi, F. Variable-order fractional calculus: A change of perspective. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105904. [Google Scholar] [CrossRef]
- Garrappa, R.; Giusti, A. A Computational Approach to Exponential-Type Variable-Order Fractional Differential Equations. J. Sci. Comput. 2023, 96, 63. [Google Scholar] [CrossRef]
- Giusti, A.; Colombaro, I.; Garra, R.; Garrappa, R.; Mentrelli, A. On variable-order fractional linear viscoelasticity. Fract. Calc. Appl. Anal. 2024, 27, 1578. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable Order and Distributed Order Fractional Operators. Nonlinear Dyn. 2002, 29, 98. [Google Scholar] [CrossRef]
- Sun, H.-G.; Sheng, H.; Chen, Y.-Q.; Chen, W.; Yu, Z.-B. A Dynamic-Order Fractional Dynamic System. Chin. Phys. Lett. 2013, 30, 046601. [Google Scholar] [CrossRef]
- Horvat, M.A.; Sarajlija, N. On the fractional relaxation equation with Scarpi derivative. arXiv 2024, arXiv:2411.03317. [Google Scholar]
- Han, B.; Yin, D.; Gao, Y. The application of a novel variable-order fractional calculus on rheological model for viscoelastic materials. Mech. Adv. Mater. Struct. 2024, 31, 9951–9963. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Dabiri, A.; Machado, J.A.T. Application of variable-order fractional calculus in solid mechanics. Appl. Eng. Life Soc. Sci. Part A 2019, 7, 207–224. [Google Scholar]
- Cuesta, E.; Kirane, M.; Alsaedi, A.; Ahmad, B. On the sub–diffusion fractional initial value problem with time variable order. Adv. Nonlinear Anal. 2021, 10, 1301–1315. [Google Scholar] [CrossRef]
- Coimbra, C. Mechanics with variable-order differential operators. Ann. Der Phys. 2003, 515, 692–703. [Google Scholar] [CrossRef]
- Godinez, F.A.; Quezada-Garcia, S.; Fernandez-Anaya, G.; Quezada-Tellez, L.A.; Polo-Labarrios, M.A. Variable-Order Fractional Neutron Point Kinetics Model to Nuclear Reactor. Fractals 2024. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Zorica, D. On the Bagley–Torvik Equation. J. Appl. Mech. 2013, 80, 041013. [Google Scholar] [CrossRef]
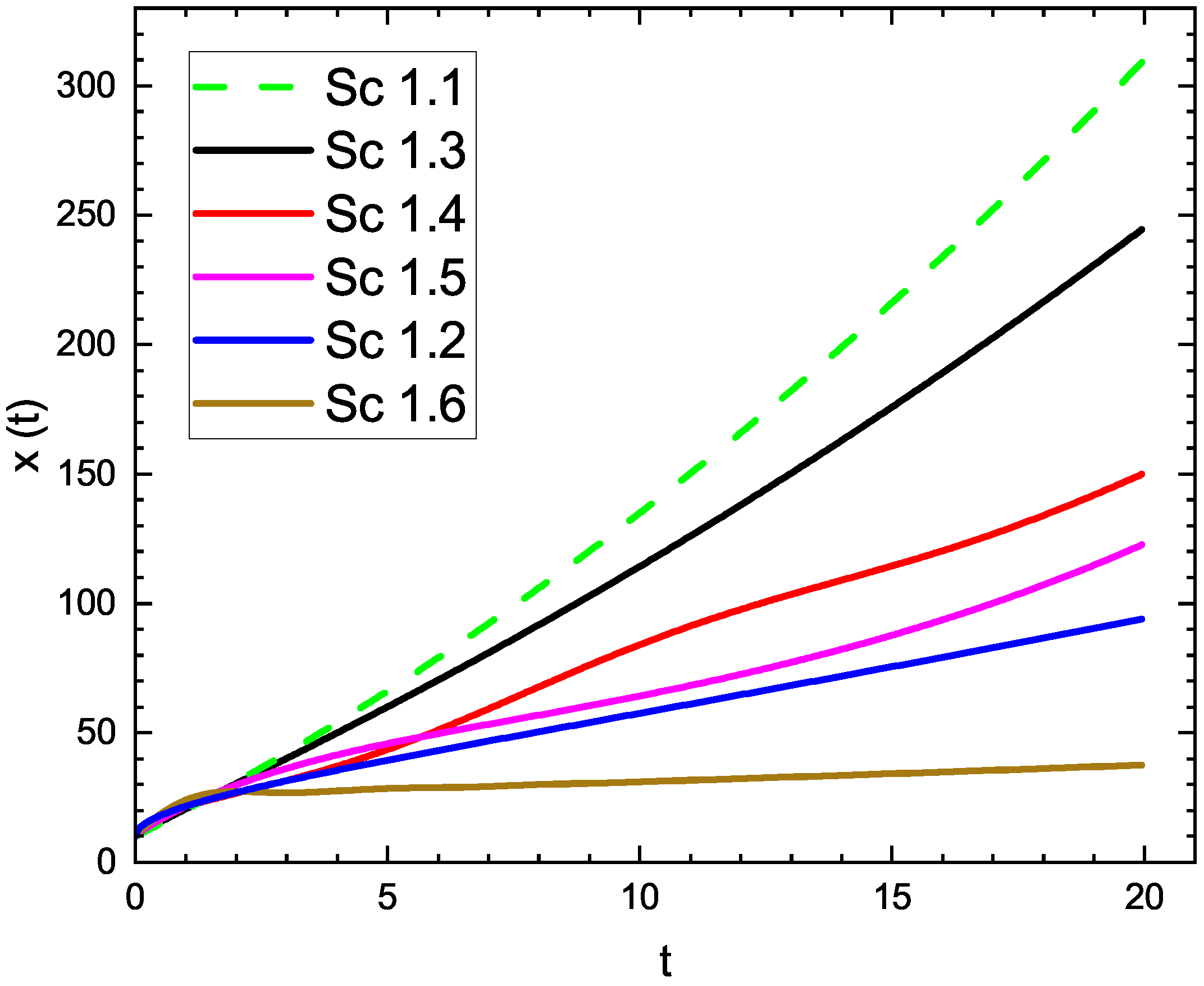
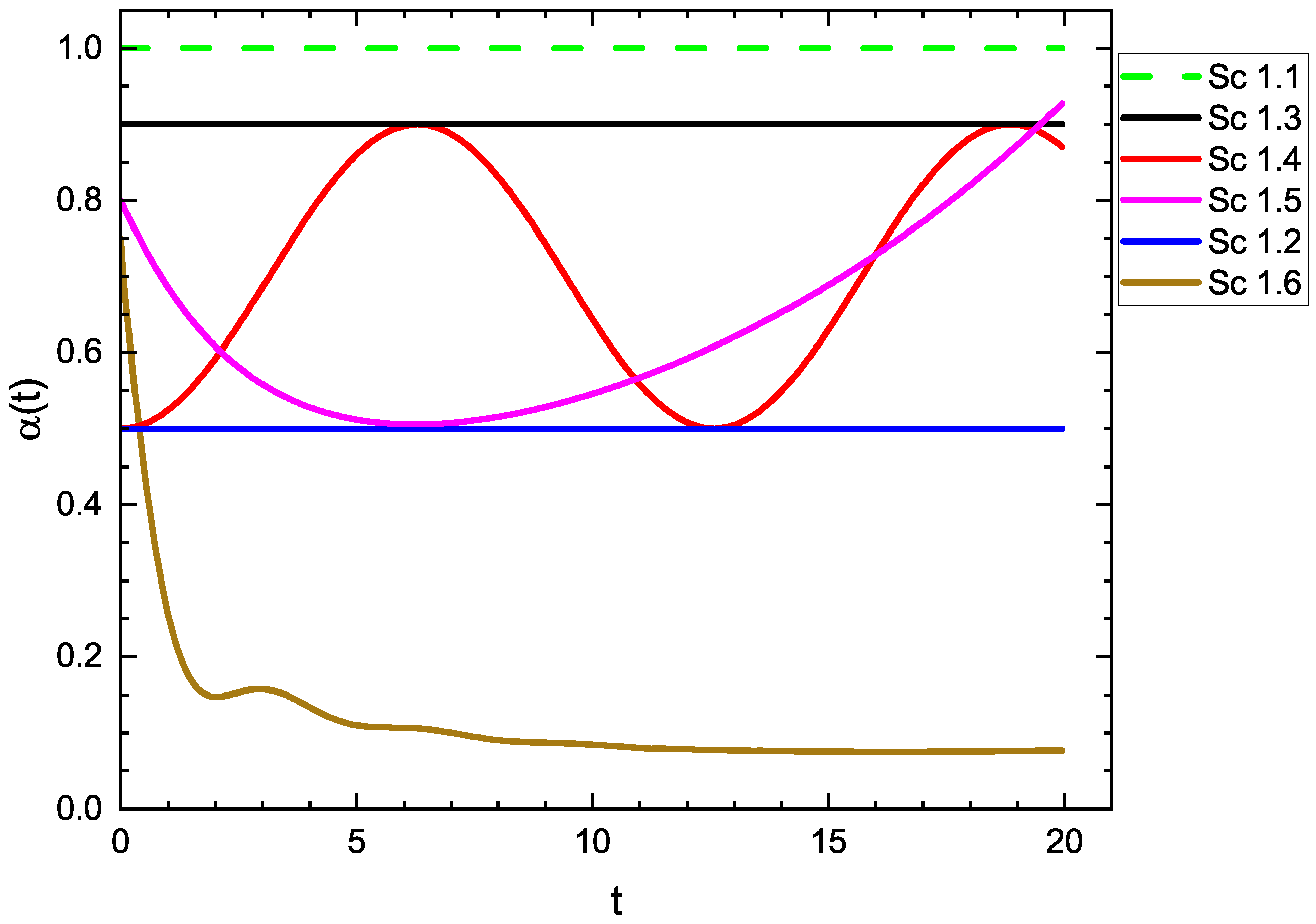
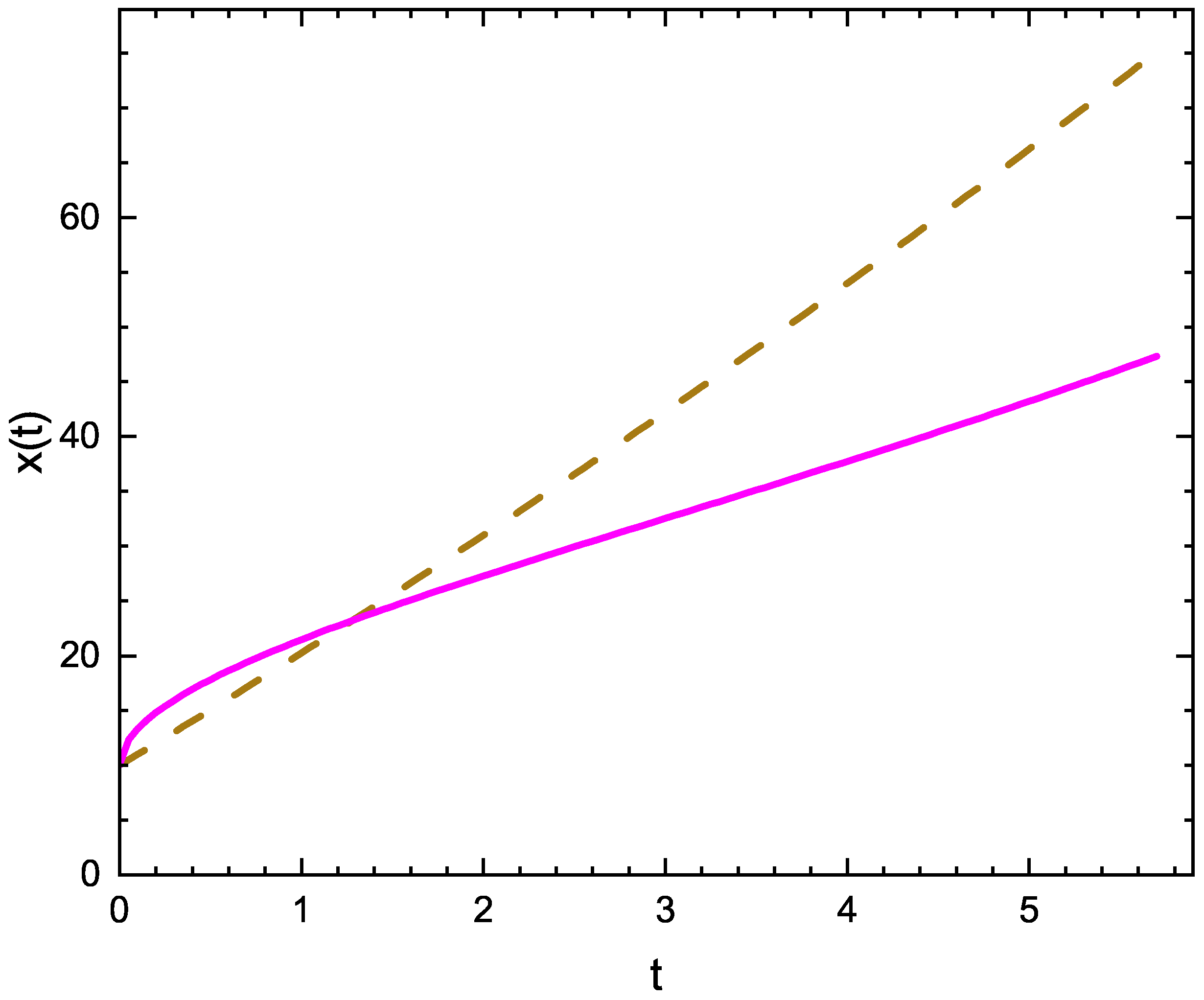
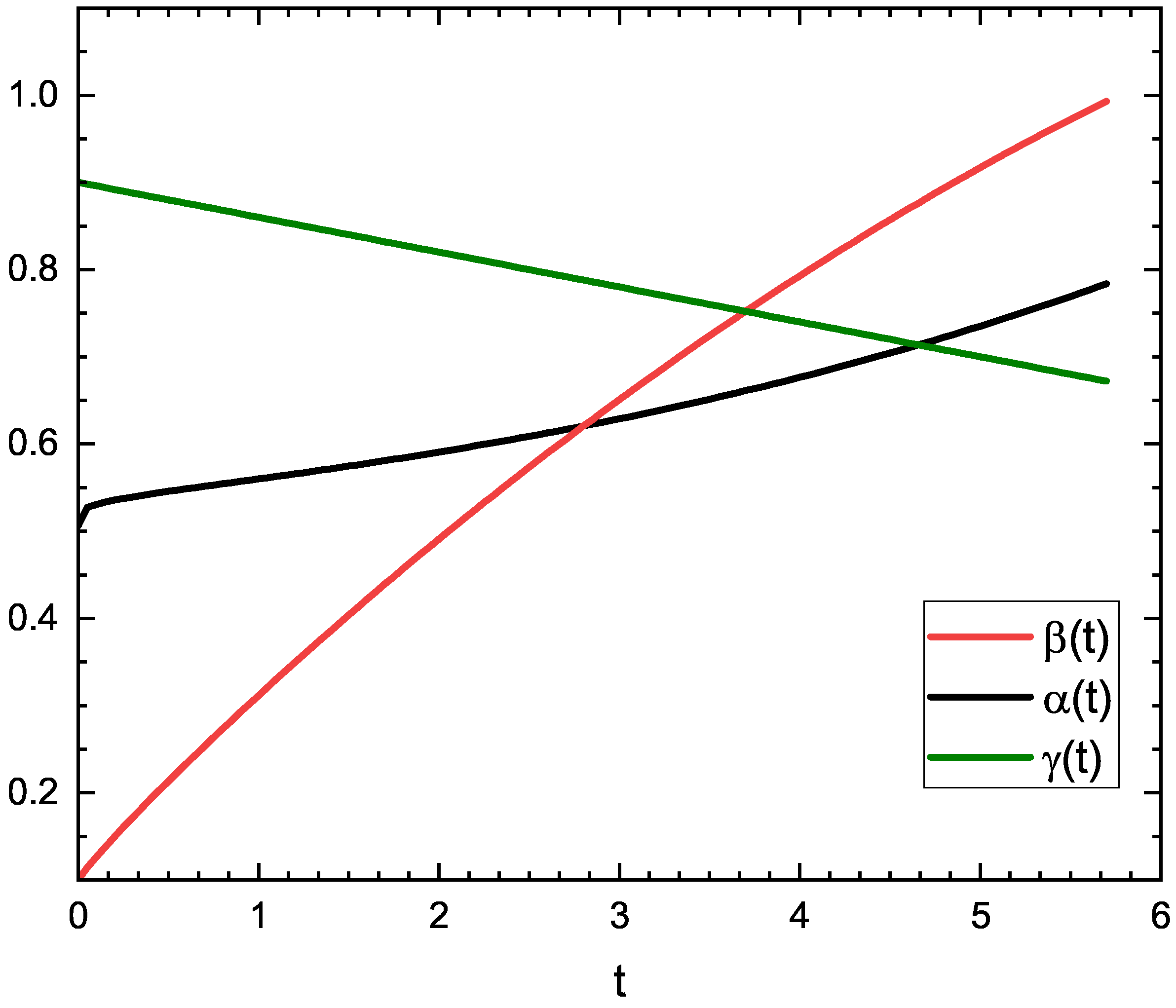
| Subcase | b | c | d | e | ||
|---|---|---|---|---|---|---|
| Sc 1.1 | 0 | 1 | 0 | 0 | −1 | 1 |
| Sc 1.2 | 0 | 1 | 0 | 0 | −1 | 0.5 |
| Sc 1.3 | 0 | 1 | 0 | 0 | −1 | 0.9 |
| Sc 1.4 | 0 | 1 | 0 | 0 | −1 | |
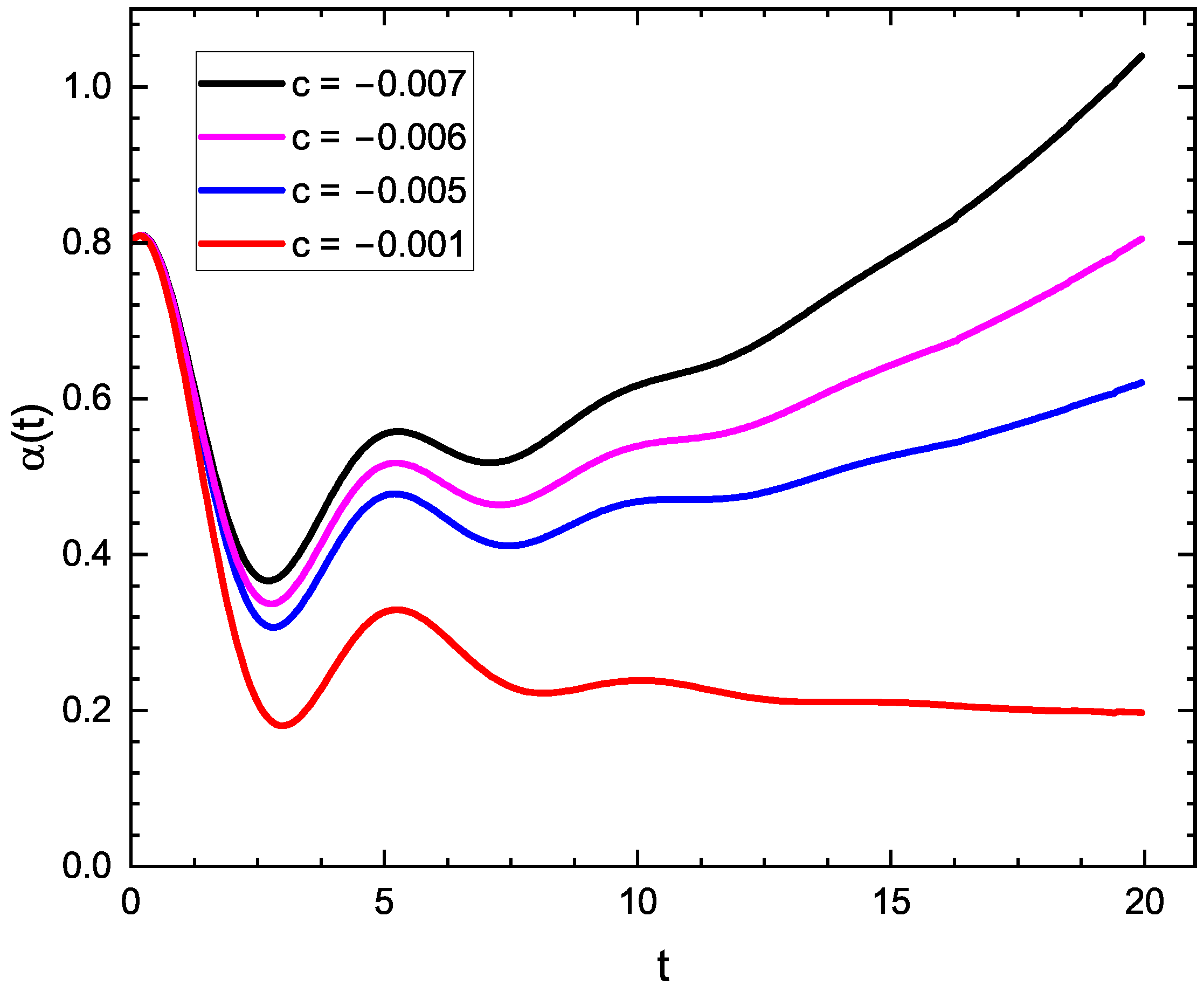
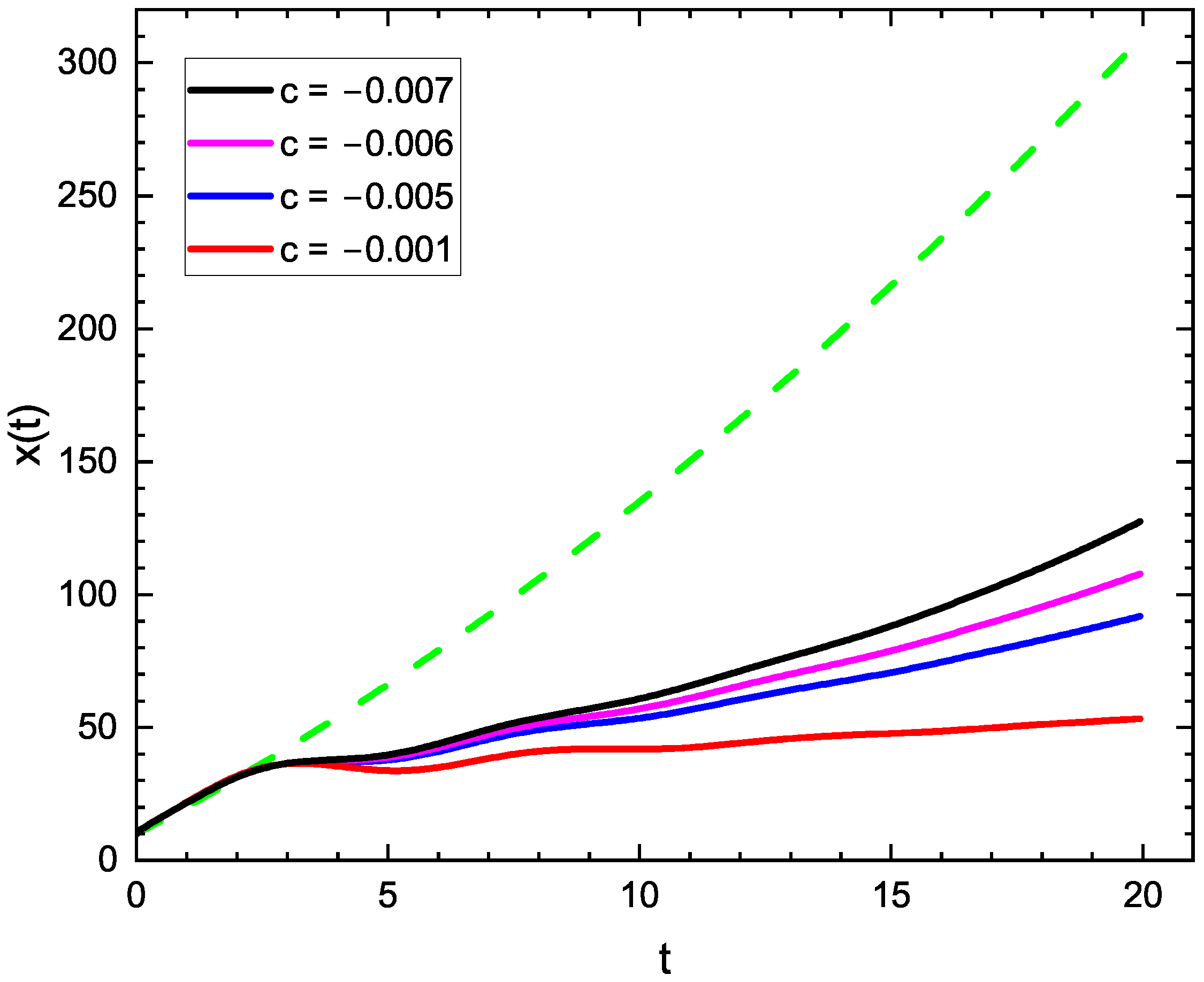
| Sc 1.5 | 1 | 0.2 | −0.002 | 0 | 0 | 0 |
| Sc 1.6 | 1 | 0.2 | −0.001 | 0.03 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Anaya, G.; Godínez, F.A.; Valdés, R.; Quezada-Téllez, L.A.; Polo-Labarrios, M.A. A Simple Fractional Model with Unusual Dynamics in the Derivative Order. Fractal Fract. 2025, 9, 264. https://doi.org/10.3390/fractalfract9040264
Fernández-Anaya G, Godínez FA, Valdés R, Quezada-Téllez LA, Polo-Labarrios MA. A Simple Fractional Model with Unusual Dynamics in the Derivative Order. Fractal and Fractional. 2025; 9(4):264. https://doi.org/10.3390/fractalfract9040264
Chicago/Turabian StyleFernández-Anaya, Guillermo, Francisco A. Godínez, Rogelio Valdés, Luis Alberto Quezada-Téllez, and M. A. Polo-Labarrios. 2025. "A Simple Fractional Model with Unusual Dynamics in the Derivative Order" Fractal and Fractional 9, no. 4: 264. https://doi.org/10.3390/fractalfract9040264
APA StyleFernández-Anaya, G., Godínez, F. A., Valdés, R., Quezada-Téllez, L. A., & Polo-Labarrios, M. A. (2025). A Simple Fractional Model with Unusual Dynamics in the Derivative Order. Fractal and Fractional, 9(4), 264. https://doi.org/10.3390/fractalfract9040264









