Variable-Fractional-Order Nosé–Hoover System: Chaotic Dynamics and Numerical Simulations
Abstract
:1. Introduction
2. Mathematical Preliminaries
3. Numerical Schemes for Variable-Order Fractional System
Variable Order
4. System Dynamical Analysis
4.1. Phase Portrait of the System
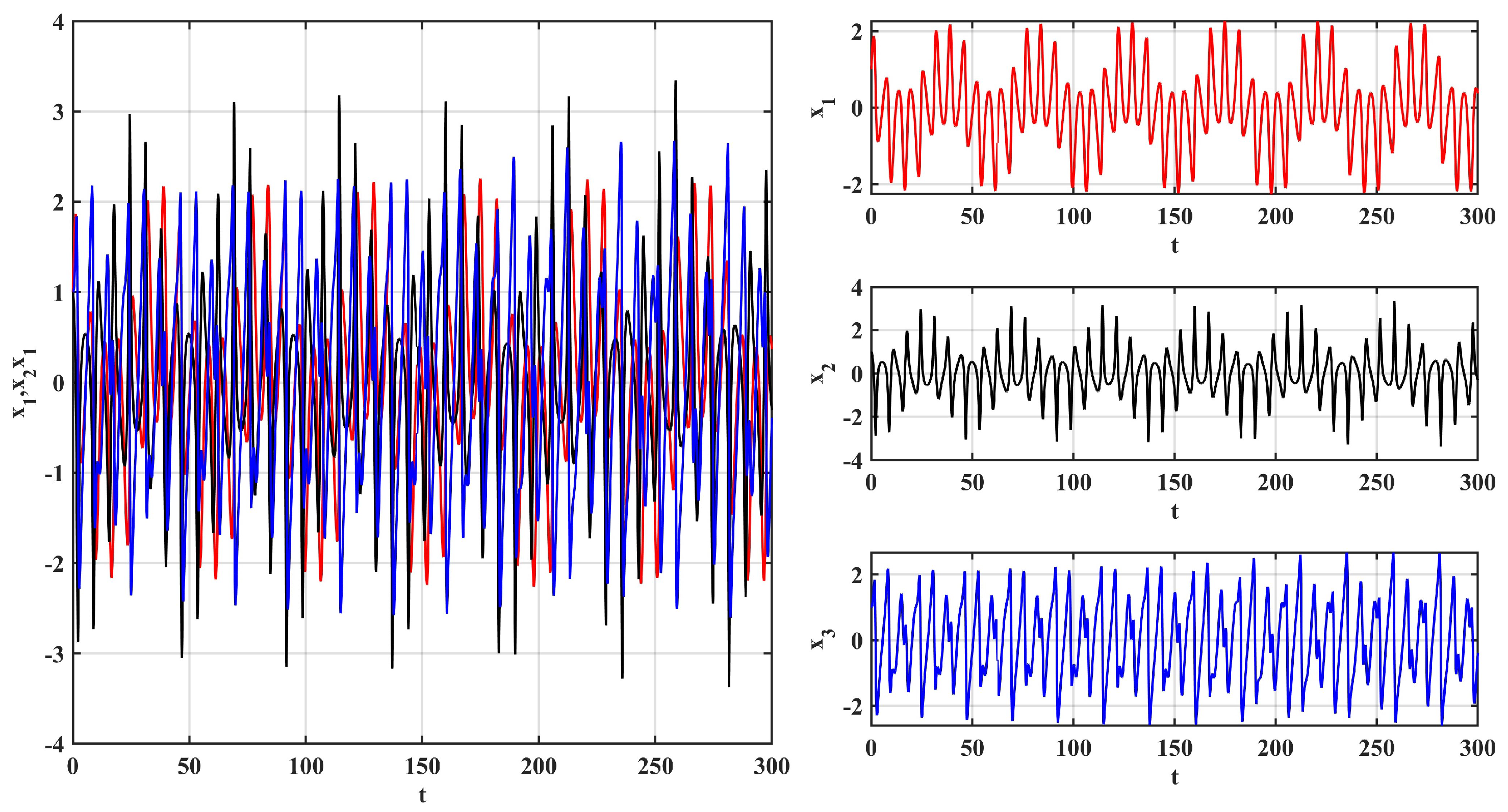
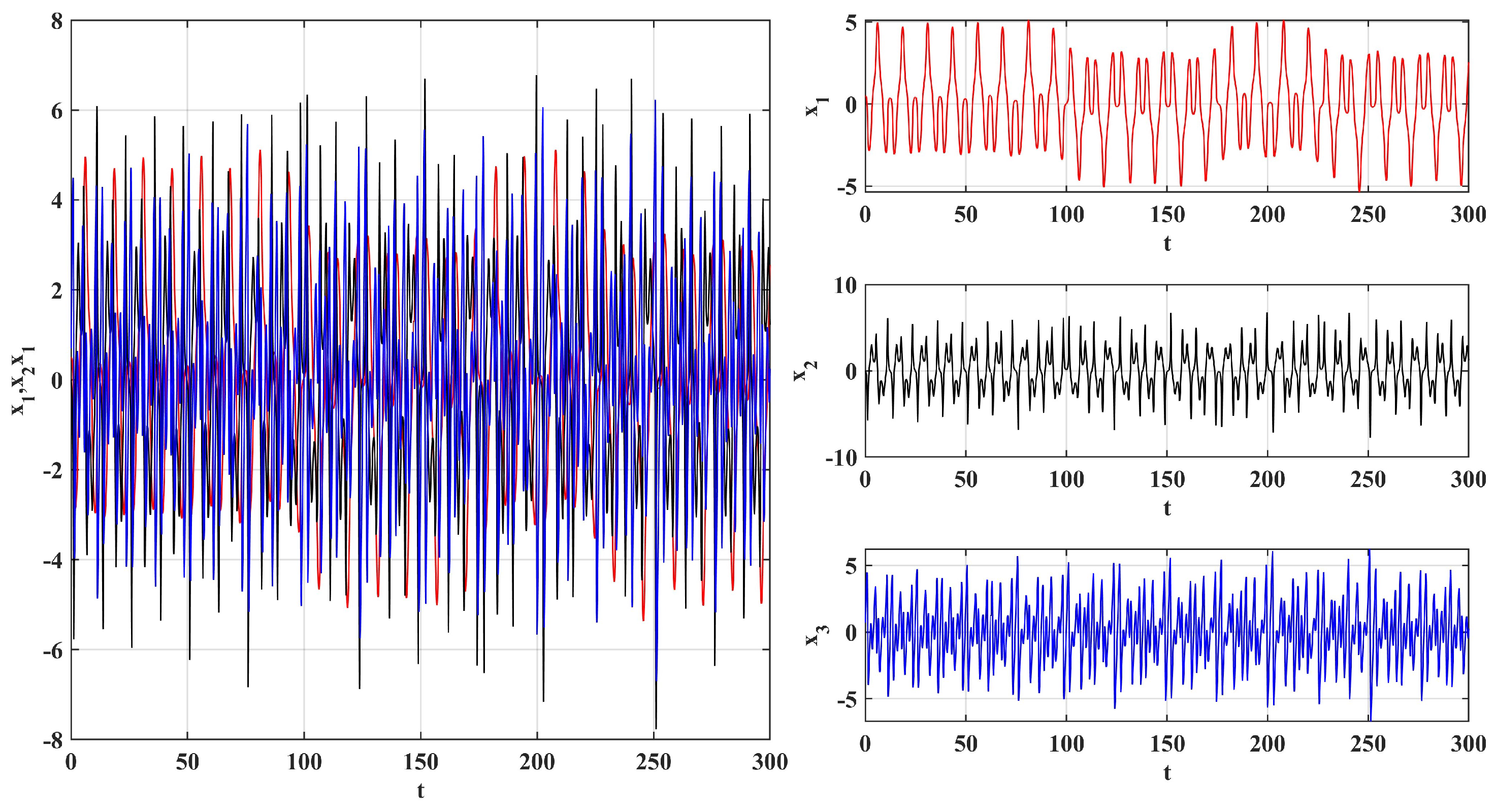
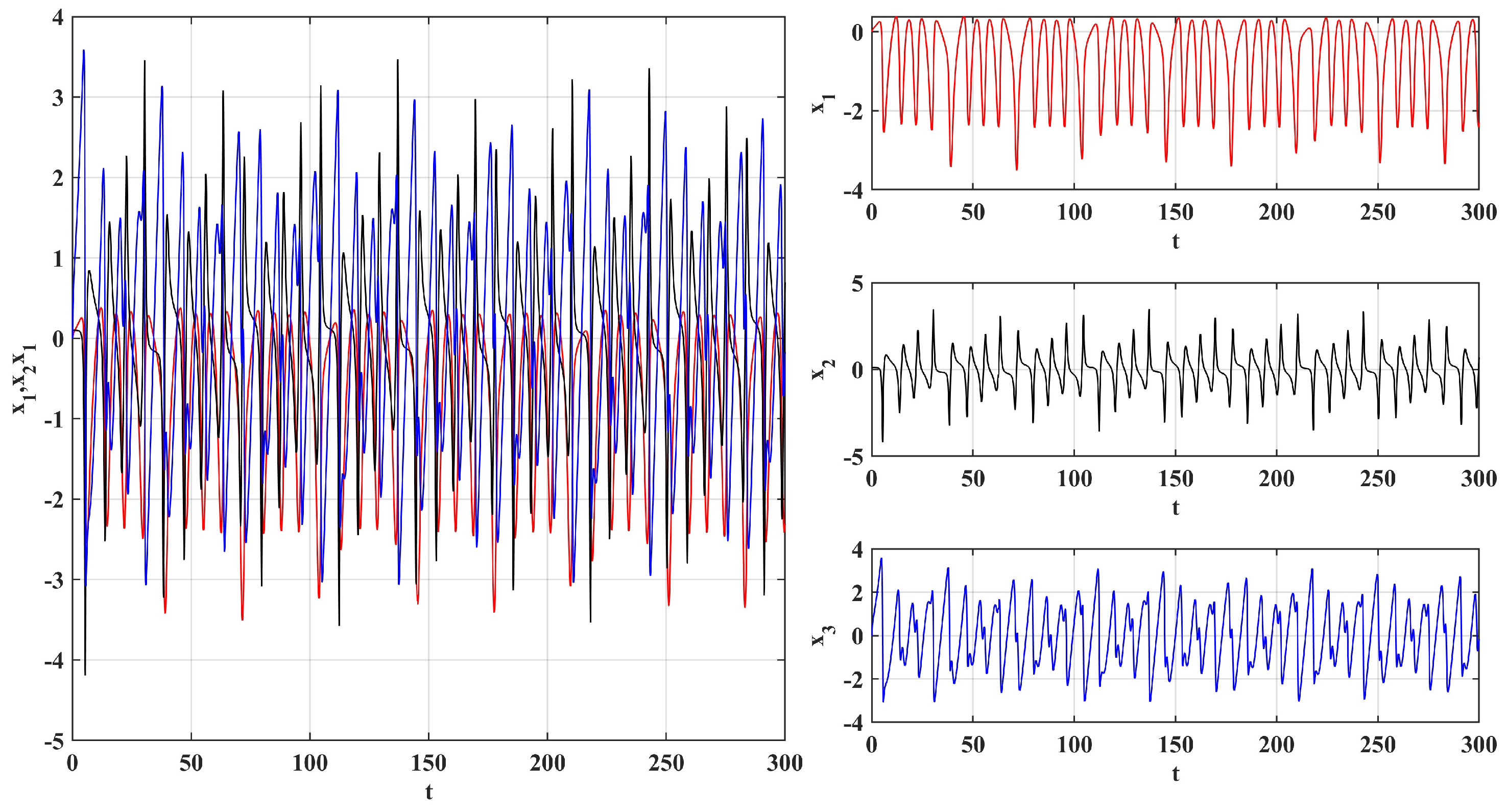
4.2. Time Series
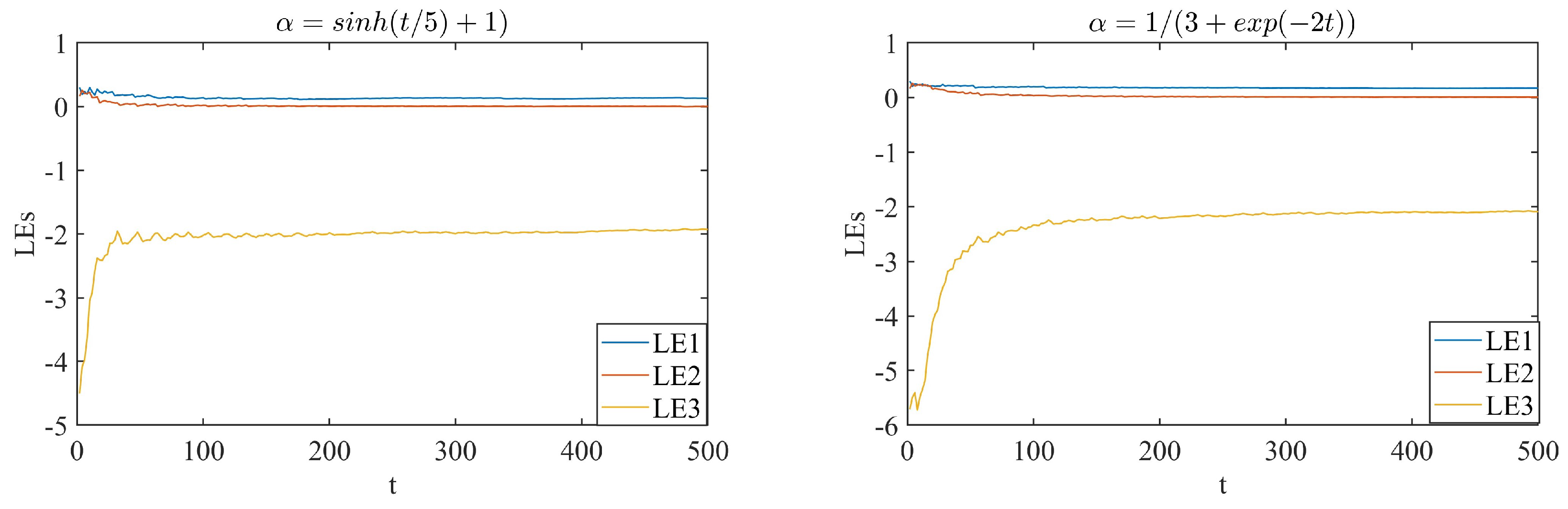
4.3. Lyapunov Exponents
- : The system demonstrates sensitivity to initial conditions, indicating chaotic behavior.
- : The system displays neutral stability, where trajectories neither show exponential divergence nor convergence.
- : Nearby trajectories converge, suggesting that the system is stable and periodic.
5. Numerical Simulation
6. Numerical Solutions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alsubaie, N.E.; EL Guma, F.; Boulehmi, K.; Al-kuleab, N.; Abdoon, M.A. Improving influenza epidemiological models under Caputo fractional-order calculus. Symmetry 2024, 16, 929. [Google Scholar] [CrossRef]
- Alharbi, S.A.; Abdoon, M.A.; Degoot, A.M.; Alsemiry, R.D.; Allogmany, R.; ELGuma, F.; Berir, M. Mathematical modeling of influenza dynamics: A novel approach with SVEIHR and fractional calculus. Int. J. Biomath. 2025, 2025, 2450147. [Google Scholar] [CrossRef]
- Abdoon, M.A.; Alzahrani, A.B.M. Comparative analysis of influenza modeling using novel fractional operators with real data. Symmetry 2024, 16, 1126. [Google Scholar] [CrossRef]
- Abdoon, M.A.; Elgezouli, D.E.; Halouani, B.; Abdelaty, A.M.Y.; Elshazly, I.S.; Ailawalia, P.; El-Qadeem, A.H. Novel dynamic behaviors in fractional chaotic systems: Numerical simulations with Caputo derivatives. Axioms 2024, 13, 791. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Zaslavsky, G.M. Fractional dynamics of systems with long-range space interaction and temporal memory. Phys. A Stat. Mech. Appl. 2007, 383, 291–308. [Google Scholar] [CrossRef]
- Picozzi, S.; West, B.J. Fractional Langevin model of memory in financial markets. Phys. Rev. E 2002, 66, 046118. [Google Scholar] [CrossRef]
- Daoui, A.; Yamni, M.; Karmouni, H.; Sayyouri, M.; Qjidaa, H.; Ahmad, M.; Abd El-Latif, A.A. Biomedical multimedia encryption by fractional-order Meixner polynomials map and quaternion fractional-order Meixner moments. IEEE Access 2022, 10, 102599–102617. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Wu, Q.M.J.; Raman, B. Discrete fractional wavelet transform and its application to multiple encryption. Inf. Sci. 2013, 223, 297–316. [Google Scholar] [CrossRef]
- Kiani-B., A.; Fallahi, K.; Pariz, N.; Leung, H. A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 863–879. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Hu, Y.-F.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A new fractional-order chaotic system with its analysis, synchronization, and circuit realization for secure communication applications. Mathematics 2021, 9, 2593. [Google Scholar] [CrossRef]
- Alqahtani, F.; Amoon, M.; El-Shafai, W. A fractional Fourier based medical image authentication approach. CMC-Comput. Mater. Contin. 2022, 70, 3133–3150. [Google Scholar] [CrossRef]
- Denis, R.; Madhubala, P. Hybrid data encryption model integrating multi-objective adaptive genetic algorithm for secure medical data communication over cloud-based healthcare systems. Multimed. Tools Appl. 2021, 80, 21165–21202. [Google Scholar] [CrossRef]
- Martínez-Guerra, R.; Pérez-Pinacho, C.A. Advances in Synchronization of Coupled Fractional Order Systems: Fundamentals and Methods; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Martínez-Guerra, R.; Gómez-Cortés, G.C.; Pérez-Pinacho, C.A. Synchronization of integral and fractional order chaotic systems. In A Differential Algebraic and Differential Geometric Approach; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Luo, C.; Wang, X. Chaos in the fractional-order complex Lorenz system and its synchronization. Nonlinear Dyn. 2013, 71, 241–257. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.Q.; Qiu, T. Fractional Processes and Fractional-Order Signal Processing: Techniques and Applications; Springer Science & Business Media: London, UK, 2011. [Google Scholar]
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Beyene, G.A.; Rahma, F.; Rajagopal, K.; Al-Hussein, A.-B.A.; Boulaaras, S. Dynamical analysis of a 3D fractional-order chaotic system for high-security communication and its electronic circuit implementation. J. Nonlinear Math. Phys. 2023, 30, 1375–1391. [Google Scholar] [CrossRef]
- Iqbal, S.; Wang, J. A novel fractional-order 3-D chaotic system and its application to secure communication based on chaos synchronization. Phys. Scr. 2025, 100, 025243. [Google Scholar] [CrossRef]
- Zhang, J.-X.; Zhang, X.; Boutat, D.; Liu, D.-Y. Fractional-Order Complex Systems: Advanced Control, Intelligent Estimation and Reinforcement Learning Image-Processing Algorithms. Fractal Fract. 2025, 9, 67. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef]
- Vellappandi, M.; Lee, S. Neural fractional differential networks for modeling complex dynamical systems. Nonlinear Dyn. 2024, 113, 12117–12130. [Google Scholar] [CrossRef]
- Erdinc, U.; Bilgil, H.; Ozturk, Z. A novel fractional forecasting model for time dependent real world cases. REVSTAT-Stat. J. 2024, 22, 169–188. [Google Scholar]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef]
- Mekkaoui, T.; Hammouch, Z.; Belgacem, F.; El Abbassi, A. Fractional-order nonlinear systems: Chaotic dynamics, numerical simulation and circuits design. In Fractional Dynamics; De Gruyter Brill: Berlin, Germany, 2015; pp. 343–356. [Google Scholar]
- Khan, M.A.; Atangana, A.; Muhammad, T.; Alzahrani, E. Numerical solution of a fractal-fractional order chaotic circuit system. Rev. Mex. FíSica 2021, 67, 051401. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Solís-Pérez, J.E.; Gómez-Aguilar, J.F.; Atangana, A. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals 2018, 114, 175–185. [Google Scholar] [CrossRef]
- Kshirsagar, K.; Nikam, V.; Gaikwad, S.; Tarate, S. Fuzzy Laplace-Adomian Decomposition Method for Solving Fuzzy Klein-Gordan Equations. Q. J. R. Meteorol. Soc. 2017, 1–6. [Google Scholar] [CrossRef]
- Bildik, N. Implementation to the Different Differential Equations of Homotopy Analysis, Differential Transformed and Adomian Decomposition Method. Int. J. Model. Optim. 2013, 3, 529–534. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H. On the numerical solutions of some fractional ordinary differential equations by fractional Adams-Bashforth-Moulton method. Open Math. 2015, 13, 000010151520150052. [Google Scholar] [CrossRef]
- Pu, Y.-F. Fractional-order Euler-Lagrange equation for fractional-order variational method: A necessary condition for fractional-order fixed boundary optimization problems in signal processing and image processing. IEEE Access 2016, 4, 10110–10135. [Google Scholar] [CrossRef]
- Ramalakshmi, K.; Sundaravadivoo, B. Necessary conditions for Ψ-Hilfer fractional optimal control problems and Ψ-Hilfer two-step Lagrange interpolation polynomial. Int. J. Dyn. Control 2024, 12, 42–55. [Google Scholar] [CrossRef]
- Buhader, A.A.; Abbas, M.; Imran, M.; Omame, A. Comparative analysis of a fractional co-infection model using nonstandard finite difference and two-step Lagrange polynomial methods. Partial Differ. Equ. Appl. Math. 2024, 10, 100702. [Google Scholar] [CrossRef]
- Alqahtani, A.M.; Chaudhary, A.; Dubey, R.S.; Sharma, S. Comparative analysis of the chaotic behavior of a five-dimensional fractional hyperchaotic system with constant and variable order. Fractal Fract. 2024, 8, 421. [Google Scholar] [CrossRef]
- Butt, A.I.K.; Ahmad, W.; Rafiq, M.; Baleanu, D. Numerical analysis of Atangana-Baleanu fractional model to understand the propagation of a novel corona virus pandemic. Alex. Eng. J. 2022, 61, 7007–7027. [Google Scholar] [CrossRef]
- Elbadri, M.; Abdoon, M.A.; Alzahrani, A.B.M.; Saadeh, R.; Berir, M. A comparative study and numerical solutions for the fractional modified Lorenz–Stenflo system using two methods. Axioms 2024, 14, 20. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Chaos in a new fractional-order system without equilibrium points. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2919–2927. [Google Scholar] [CrossRef]
- Pham, V.-T.; Volos, C.; Jafari, S.; Wang, X.; Vaidyanathan, S. Hidden Hyperchaotic Attractor in a Novel Simple Memristive Neural Network. Optoelectronics Adv. Mater. Commun. 2014, 8, 1157–1163. [Google Scholar]
- Hartley, T.T.; Lorenzo, C.F.; Qammer, H.K. Chaos in a fractional order Chua’s system. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1995, 42, 485–490. [Google Scholar] [CrossRef]
- Lu, J.-G. Chaotic dynamics and synchronization of fractional-order Genesio–Tesi systems. Chin. Phys. 2005, 14, 1517. [Google Scholar]
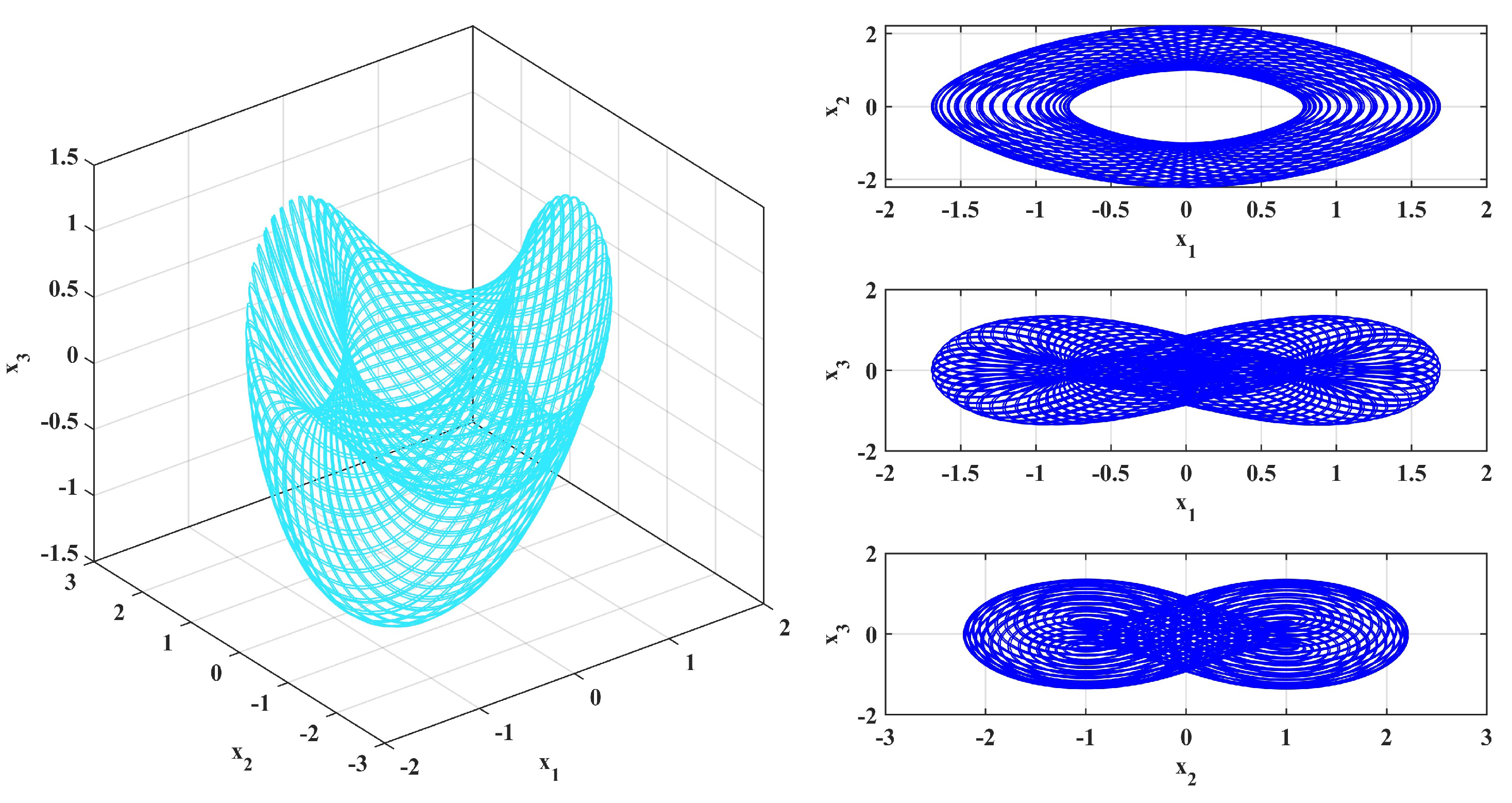

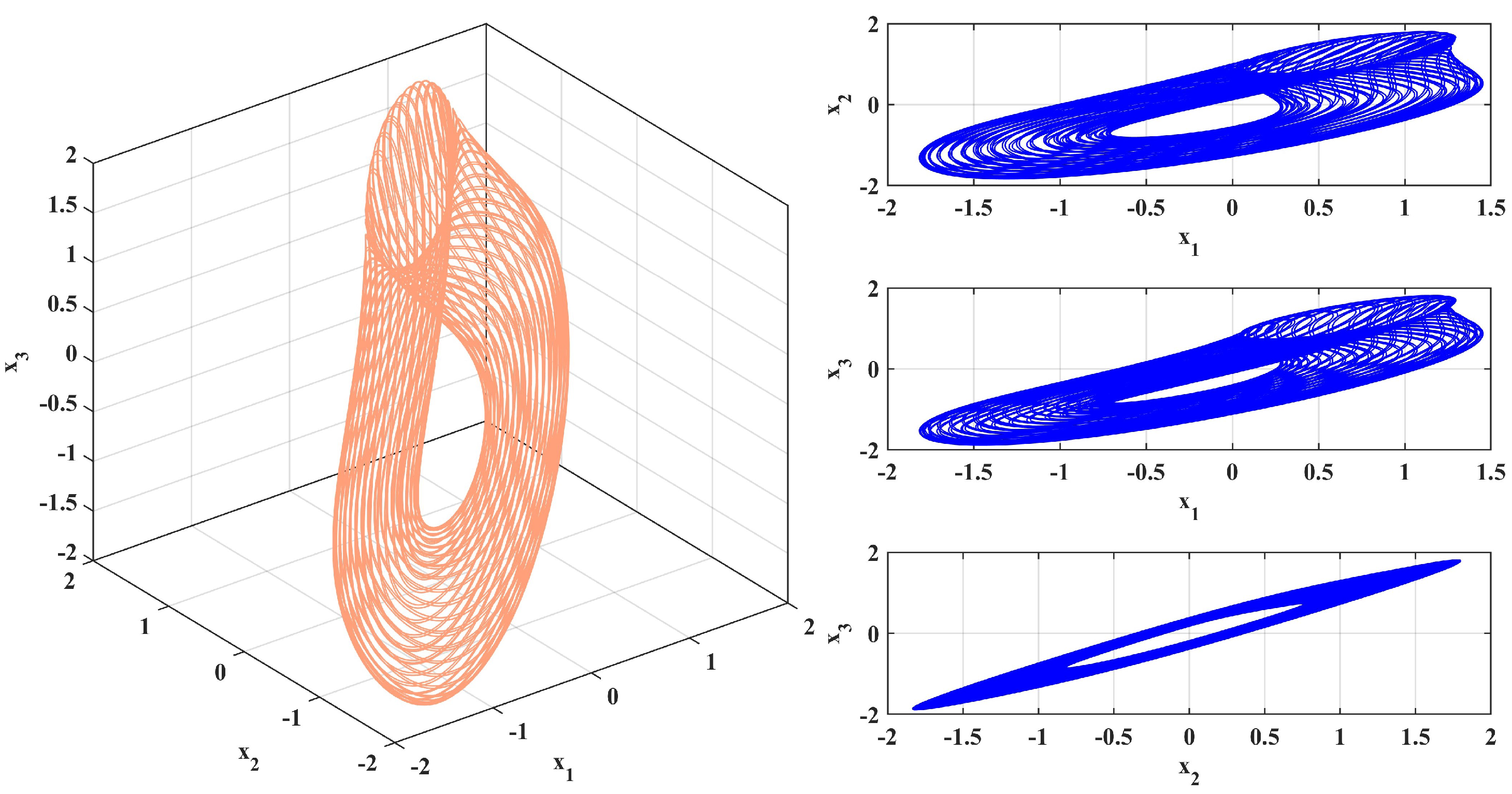

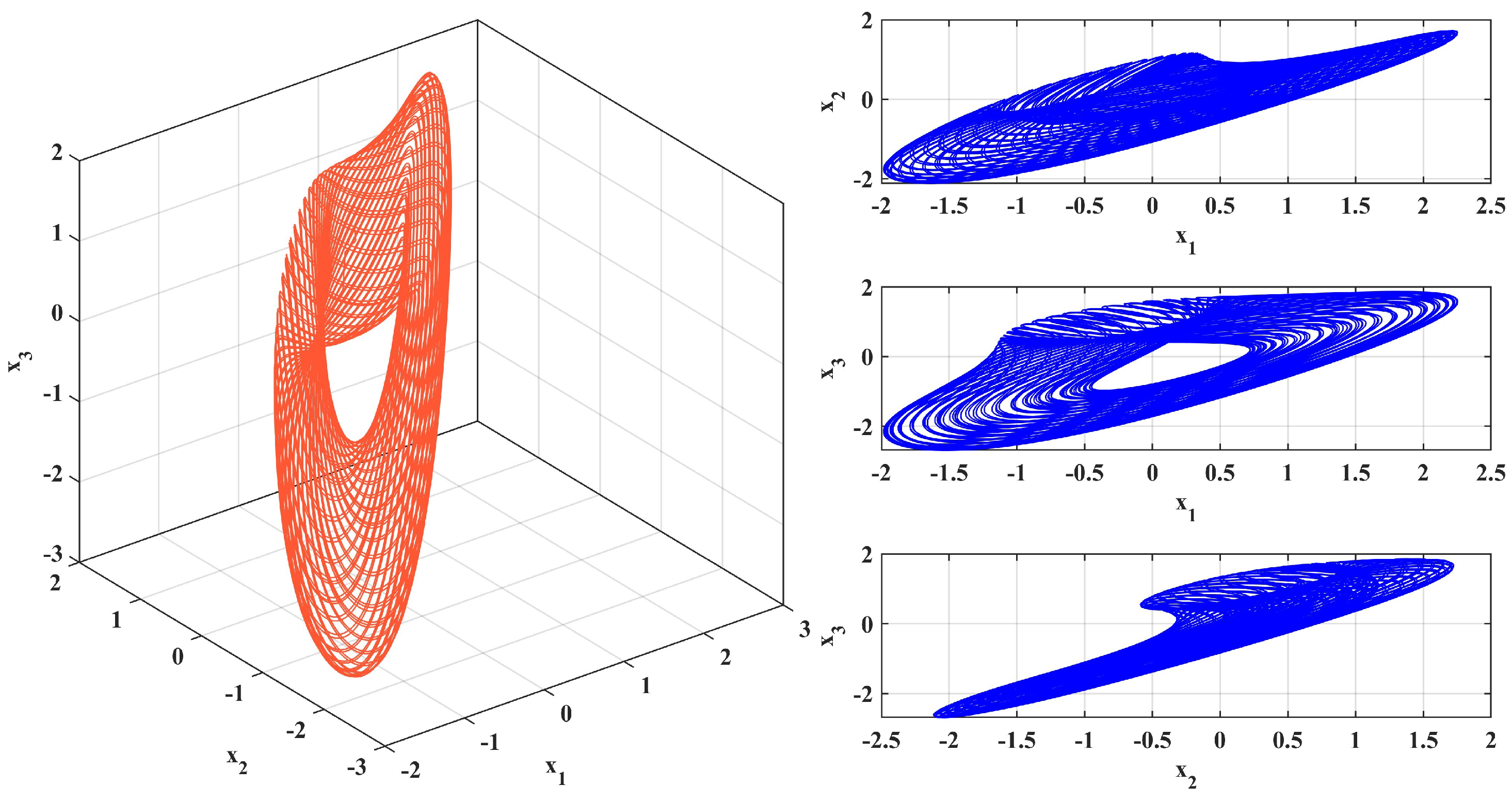
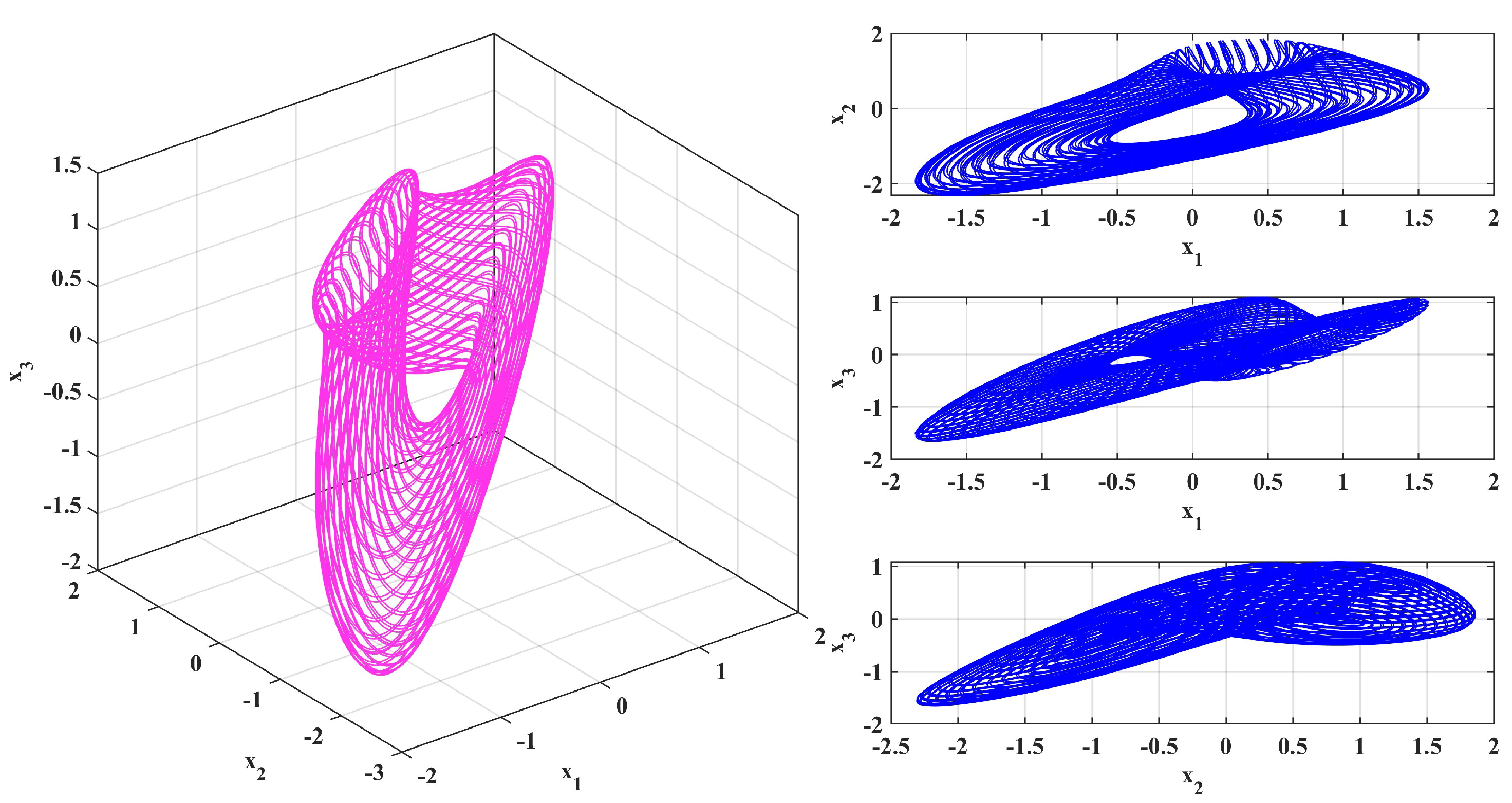
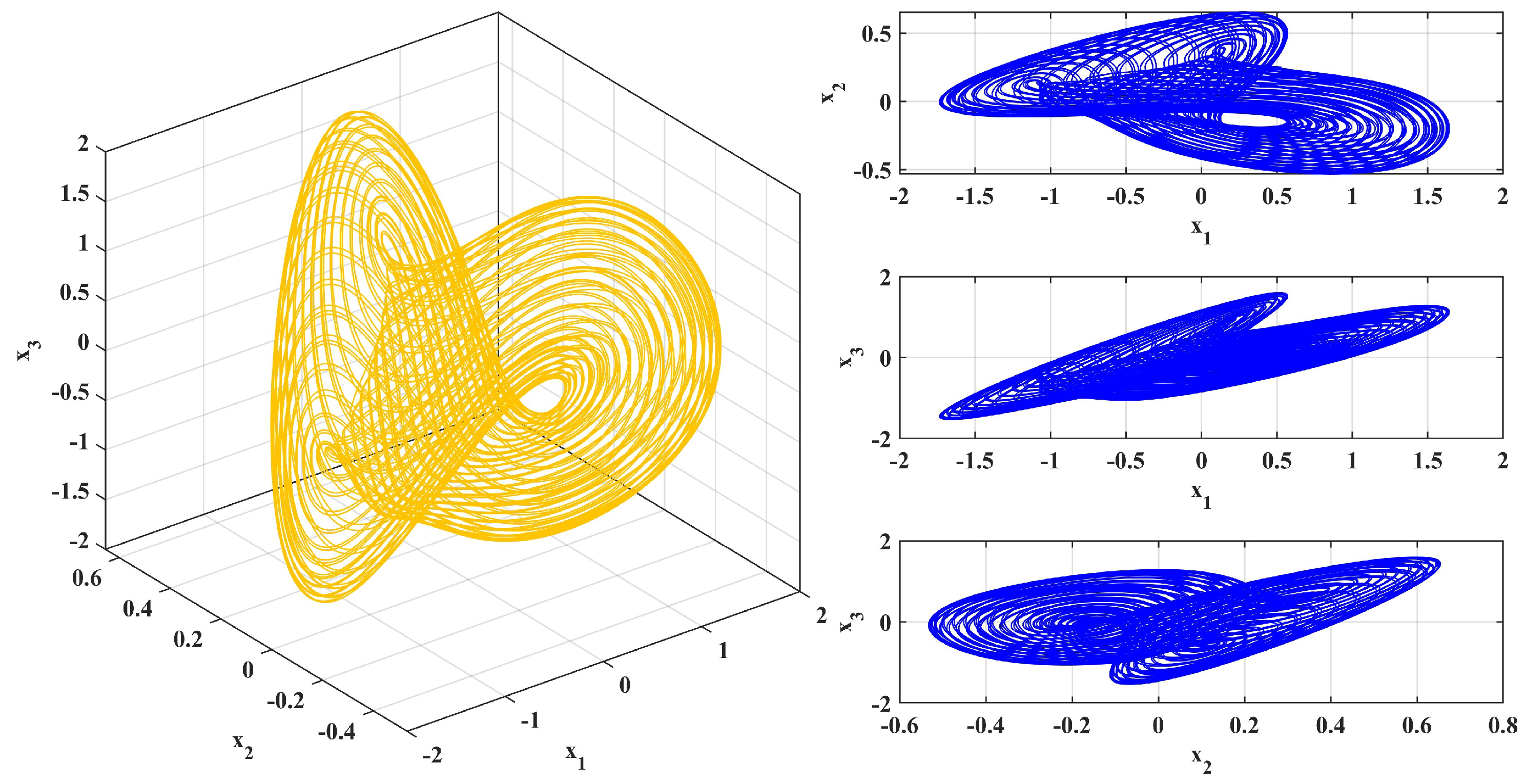
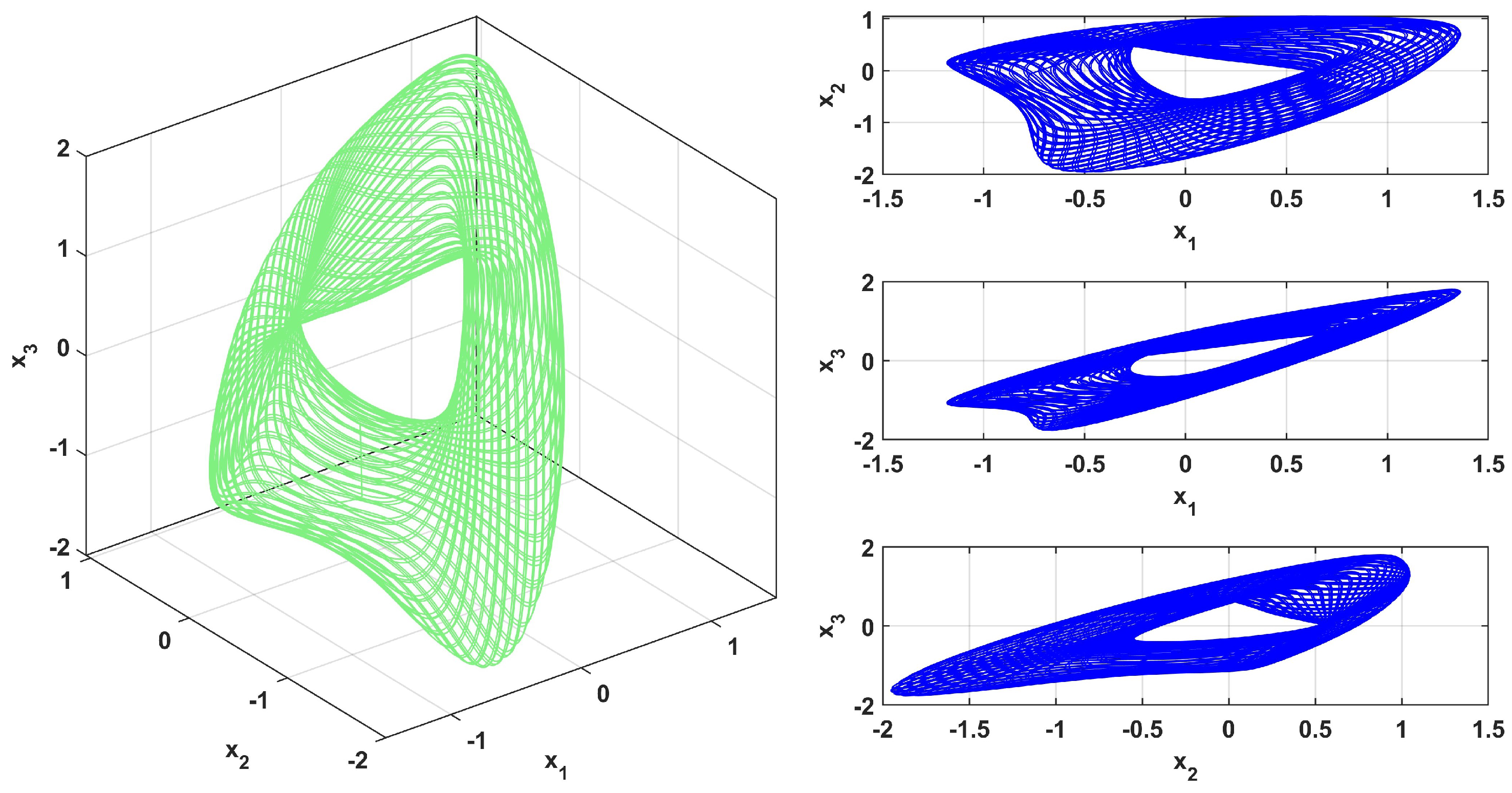

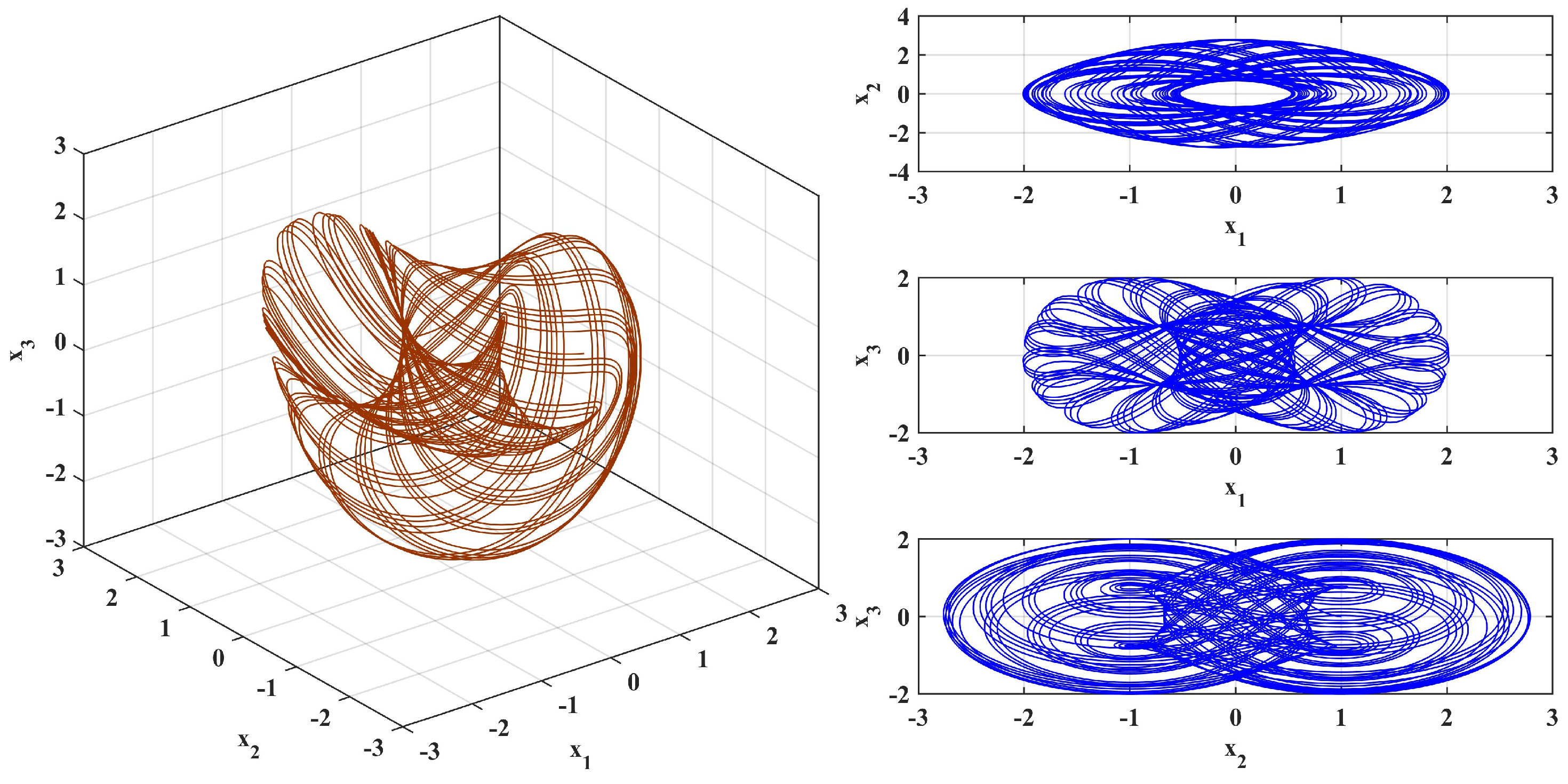
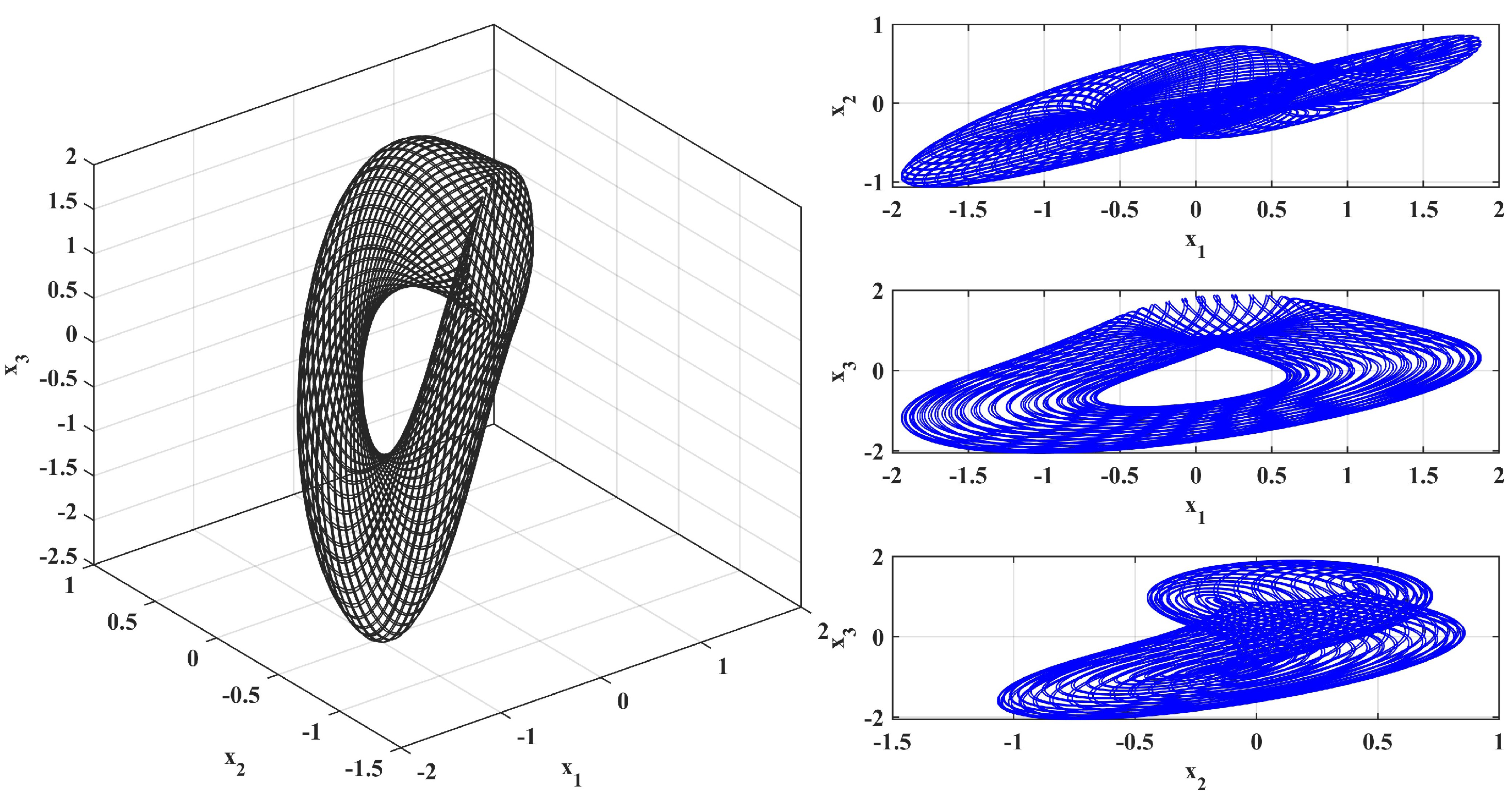
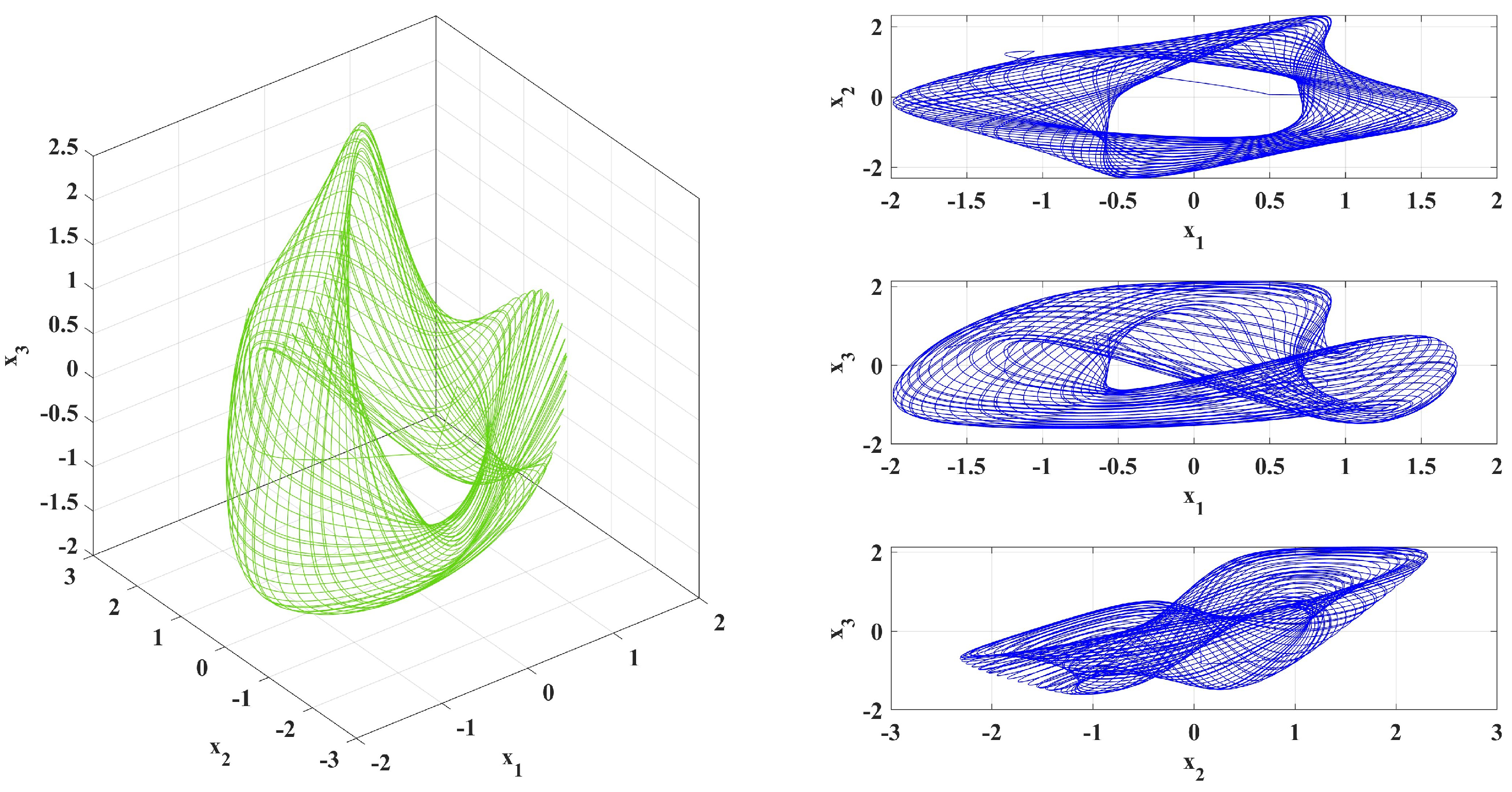

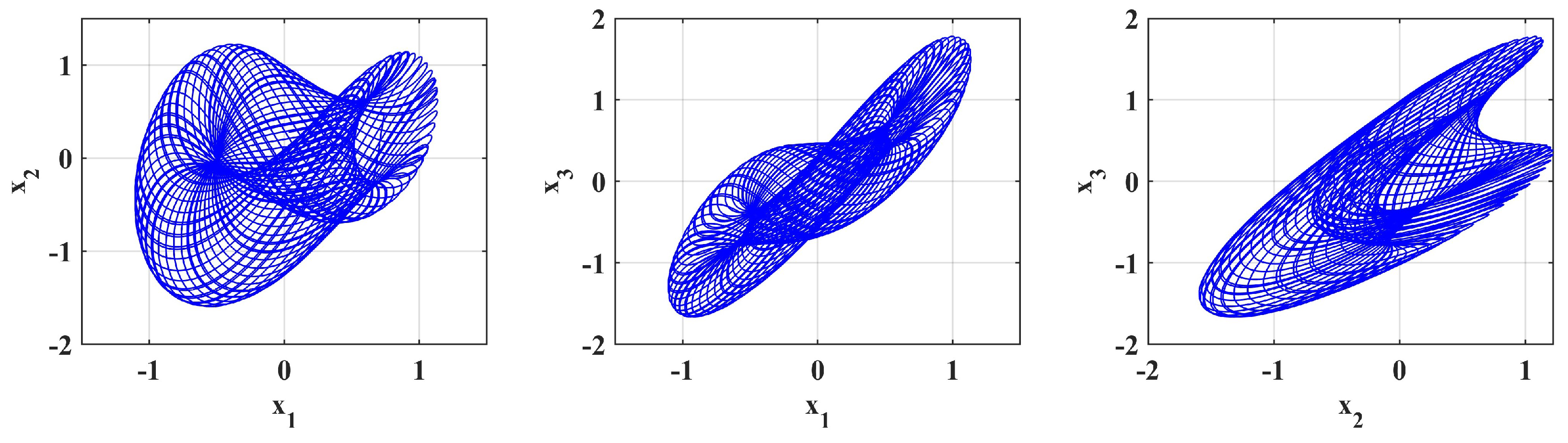
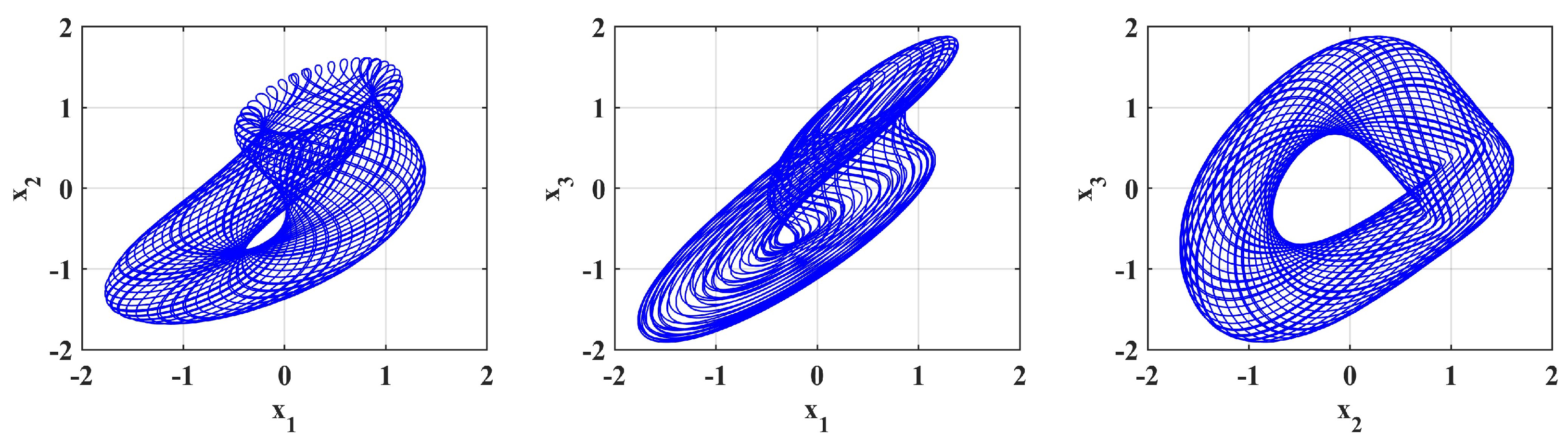
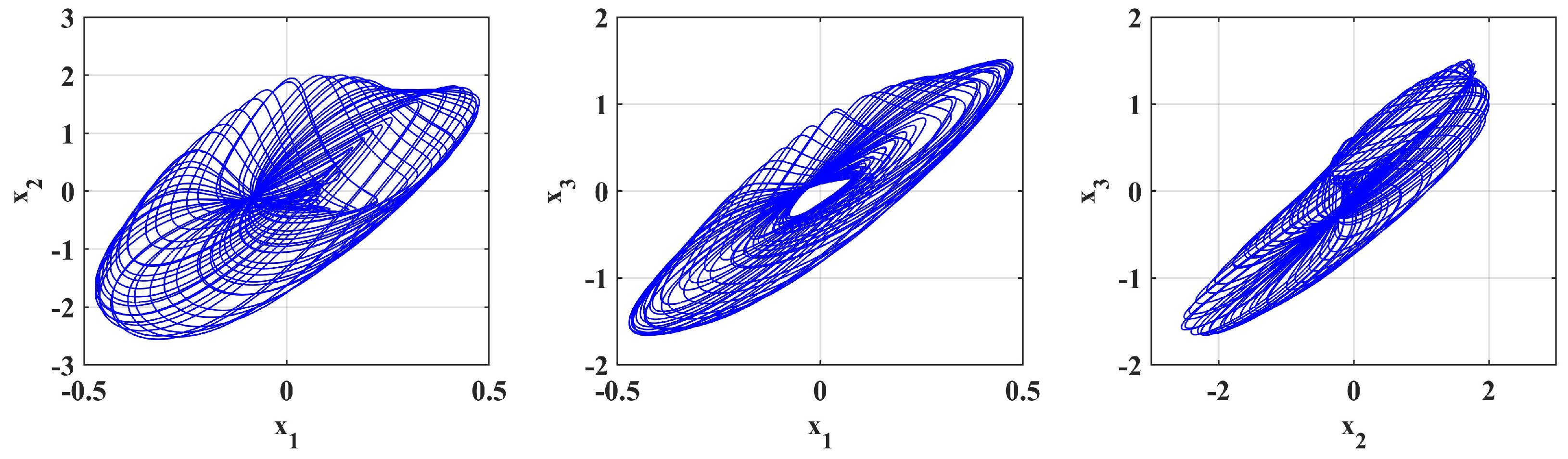

| t | |||
|---|---|---|---|
| 0.1 | 0.160618369311393 | 0.983999926989801 | 0.002324696443139 |
| 0.2 | 0.271271913153119 | 0.954369221336363 | 0.011443865830139 |
| 0.3 | 0.362212867141758 | 0.918908471316148 | 0.027225924704286 |
| 0.4 | 0.442152773808205 | 0.879371780280785 | 0.049515965151088 |
| 0.5 | 0.514540768830809 | 0.836527856150666 | 0.078274324053713 |
| 0.6 | 0.581018359884543 | 0.790801895468594 | 0.113511568066676 |
| 0.7 | 0.642399935904049 | 0.742462013806616 | 0.155237562733242 |
| t | |||
|---|---|---|---|
| 0.1 | 0.319679618427423 | 0.920719063255373 | 0.035343702874417 |
| 0.2 | 0.422676269071848 | 0.862630499078330 | 0.083581018263259 |
| 0.3 | 0.490850043028715 | 0.815895079674831 | 0.133293059665953 |
| 0.4 | 0.542646170337882 | 0.775920823500659 | 0.182911887184131 |
| 0.5 | 0.584928279692839 | 0.740249450751355 | 0.232307866573166 |
| 0.6 | 0.621015049995438 | 0.707399030963379 | 0.281700335765962 |
| 0.7 | 0.652737697455643 | 0.676399787022939 | 0.331386860115778 |
| t | |||
|---|---|---|---|
| 0.1 | 0.129253322964099 | 0.990770704789030 | 0.000924568232129 |
| 0.2 | 0.240126615822257 | 0.968031069379841 | 0.005992097825715 |
| 0.3 | 0.341787791177007 | 0.934858280605783 | 0.017554947037803 |
| 0.4 | 0.435525899311576 | 0.893351536370992 | 0.037089876307740 |
| 0.5 | 0.521666320880403 | 0.845277281367284 | 0.065412627621342 |
| 0.6 | 0.600295728515390 | 0.792120482521920 | 0.102813647581629 |
| 0.7 | 0.671446014982371 | 0.735077009819927 | 0.149182051061457 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almutairi, D.K.; AlMutairi, D.M.; Taha, N.E.; Dafaalla, M.E.; Abdoon, M.A. Variable-Fractional-Order Nosé–Hoover System: Chaotic Dynamics and Numerical Simulations. Fractal Fract. 2025, 9, 277. https://doi.org/10.3390/fractalfract9050277
Almutairi DK, AlMutairi DM, Taha NE, Dafaalla ME, Abdoon MA. Variable-Fractional-Order Nosé–Hoover System: Chaotic Dynamics and Numerical Simulations. Fractal and Fractional. 2025; 9(5):277. https://doi.org/10.3390/fractalfract9050277
Chicago/Turabian StyleAlmutairi, D. K., Dalal M. AlMutairi, Nidal E. Taha, Mohammed E. Dafaalla, and Mohamed A. Abdoon. 2025. "Variable-Fractional-Order Nosé–Hoover System: Chaotic Dynamics and Numerical Simulations" Fractal and Fractional 9, no. 5: 277. https://doi.org/10.3390/fractalfract9050277
APA StyleAlmutairi, D. K., AlMutairi, D. M., Taha, N. E., Dafaalla, M. E., & Abdoon, M. A. (2025). Variable-Fractional-Order Nosé–Hoover System: Chaotic Dynamics and Numerical Simulations. Fractal and Fractional, 9(5), 277. https://doi.org/10.3390/fractalfract9050277







