Hermite–Hadamard-Type Inequalities for h-Godunova–Levin Convex Fuzzy Interval-Valued Functions via Riemann–Liouville Fractional q-Integrals

Abstract

In this study, we develop new Hermite–Hadamard and Hermite–Hadamard–Fejér type inequalities for fuzzy interval-valued functions (FIVFs) that exhibit h-Godunova–Levin convexity, using the framework of the Riemann–Liouville fractional (RLF) q-integral. We introduce novel fuzzy extensions of classical inequalities and establish corresponding inclusion relations by utilizing the properties of fuzzy RLF q-integrals. Furthermore, we validate the theoretical results through illustrative numerical examples and graphical representations, demonstrating the applicability and effectiveness of the derived inequalities in the context of fuzzy and interval analysis.

1. Introduction

The concept of convexity has long played a central role in various branches of mathematical analysis, particularly in optimization, functional analysis, and inequality theory. In recent years, significant advancements have been made in the study of functions exhibiting different types of convexity, including log-convexity [1], F-convexity [2], harmonically convexity [3], h-convexity [4] and h-Godunova–Levin convexity [5]. These developments have provided powerful tools for advancing many fields within mathematical analysis. Among the classical results, the Hermite–Hadamard inequality, first introduced by Hadamard in 1893 [6], plays a central role in inequality theory. This fundamental result provides an elegant estimate of the integral mean of a convex function and has served as the foundation for countless generalizations.

Over the years, researchers have developed several extensions of the Hermite–Hadamard inequality in different frameworks. Steinerberger [7] studied the Hermite–Hadamard inequality in higher dimensions, highlighting its importance in the geometry of convex bodies. Alongside these advancements, considerable attention has also been devoted to inequalities associated with convex functions, particularly the classical Hermite–Hadamard (HH) inequality.

Theorem 1

([8]). Suppose ${\varsigma }_1<{\varsigma }_2$ and $f:[{\varsigma }_1,{\varsigma }_2]⟶\mathbb{R}$ be a convex function, then

$$f\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)\le {\displaystyle \frac{1}{{\varsigma }_2-{\varsigma }_1}}{\int }_{{\varsigma }_1}^{{\varsigma }_2}f\left(x\right)dx\le {\displaystyle \frac{f\left({\varsigma }_1\right)+f\left({\varsigma }_2\right)}{2}},$$

holds.

Fractional calculus has also seen widespread application across a broad range of fields, including mathematics, physics, and engineering. Fractional versions of these inequalities have also been established, for example, in the monograph by Wang and Fečkan [9], where fractional Hermite–Hadamard inequalities were systematically investigated. Furthermore, generalizations involving preinvexity and other convexity concepts were obtained by Awan et al. [10], who derived fractional Hermite–Hadamard–Noor type inequalities via n-polynomial preinvex functions. Recently, Du et al. [11] extended the study of Hermite–Hadamard-type inequalities to the multiplicative fractional setting by employing multiplicative Atangana–Baleanu fractional integral operators. Their results further broaden the scope of HH-type inequalities within fractional calculus, highlighting the versatility of such inequalities across different fractional frameworks. In a related work, Lakhdari et al. [12] derived new fractal–fractional Hermite–Hadamard- and Milne-type inequalities, further broadening the scope of fractional analysis. Moreover, Du and Xu [13] obtained Hermite–Hadamard- and Pachpatte-type inequalities for generalized subadditive functions in the fractal setting. These contributions highlight the richness of Hermite–Hadamard-type inequalities and their adaptability to different settings in mathematical analysis.

In particular, fractional q-calculus has emerged as a powerful tool for solving differential and difference equations, as well as in combinatorics and signal processing [14,15,16,17]. Similarly, Xu et al. [18] explored new estimates for Hermite–Hadamard inequalities in the framework of quantum calculus through $(\alpha ,m)$-convexity. RLF q-integral operator, introduced in [19], has served as a foundation for numerous advancements. Building upon this, Tariboon [20], introduced a modified definition of the RLF q-integral and established existence and uniqueness results for impulsive fractional q-difference equations. Further extending these ideas, the work in [21], introduced the notion of the interval-valued RLF q-integral and explored unique solutions to interval q-Abel integral equations, thereby expanding fractional q-calculus into the framework of interval analysis. Growing interest in fractional q-calculus and its applications to convexity-based inequalities. These contemporary contributions further emphasize the timeliness and wide applicability of Hermite–Hadamard-type results across multiple branches of mathematical analysis.

Interval analysis has rapidly gained attention due to its effectiveness in handling uncertain data, error analysis, nulti-attribute decision-making, inequality theory, optimization, and related fields [22,23,24,25,26,27,28,29,30]. Particularly in the last five years, several extensions of classical inequalities involving fractional integrals have been proposed within interval and fuzzy spaces. For instance, Budak [31] established new interval-valued RLF integrals and associated inequalities. Du and Zhou [32] proved HH-, HH–Fejér-, and Pachpatte-type inclusion relations and Khan [33], derived new fuzzy variants of HH- and HH–Fejér-type inequalities by utilizing fuzzy RLF integrals with up and down convex fuzzy interval-valued functions. Additional fuzzy HH- and HH-Fejér-type inequalities have also been investigated using fuzzy RLF integral operators with exponential kernels [34].

Motivated by the above developments, this paper aims to establish new Hermite–Hadamard- and Hermite–Hadamard–Fejér type inequalities for fuzzy interval-valued functions exhibiting h-Godunova–Levin convexity, utilizing the Riemann–Liouville fractional q-integral framework. The paper is organized as follows: Section 2 introduces preliminary concepts and fundamental results necessary for the development of the main results. Section 3 presents new inclusion relations and the main inequalities. In Section 4, we provide illustrative numerical examples to support the theoretical findings. Finally, Section 5 concludes the paper and discusses potential directions for future research.

2. Preliminaries

In this section, we provide the essential definitions and mathematical background that form the basis of our study. These include concepts from fuzzy set theory, interval analysis, generalized convexity, and fractional q-calculus. The notations and operators introduced here will be used throughout the paper.

Definition 1

([35]). Let ${\mathbb{R}}_I=\{[{\varsigma }_1,{\varsigma }_2]:{\varsigma }_1\le {\varsigma }_2,{\varsigma }_1,{\varsigma }_2\in \mathbb{R}\}.$ If ${\varsigma }_1>0,$ then $[{\varsigma }_1,{\varsigma }_2]\in {\mathbb{R}}_I^{+}$, where ${\mathbb{R}}_I^{+}$ is the set of all real positive intervals. Given $[{\varsigma }_1,{\varsigma }_2],[{\upsilon }_1,{\upsilon }_2]\in {\mathbb{R}}_I$ and $\theta \in \mathbb{R}$, then $\theta [{\varsigma }_1,{\varsigma }_2]$ is defined by

$$\theta [{\varsigma }_1,{\varsigma }_2]=\{[\theta {\varsigma }_1,\theta {\varsigma }_2]if\theta \ge 0,[\theta {\varsigma }_2,\theta {\varsigma }_1]if\theta <0\}.$$

and the addition is given by

$$[{\varsigma }_1,{\varsigma }_2]+[{\upsilon }_1,{\upsilon }_2]=[{\varsigma }_1+{\upsilon }_1,{\varsigma }_2+{\upsilon }_2].$$

For $[{\varsigma }_1,{\varsigma }_2],[{\upsilon }_1,{\upsilon }_2]\in {\mathbb{R}}_I,$ the inclusion relation “${\supseteq }_I^{\prime \prime }$, also called the “up and down" (“UD”) order, is defined by

$$[{\varsigma }_1,{\varsigma }_2]{\supseteq }_I[{\upsilon }_1,{\upsilon }_2]\iff {\varsigma }_1\le {\upsilon }_1,{\upsilon }_2\le {\varsigma }_2.$$

Let $\underline{f}\left(x\right),\overline{f}\left(x\right):[{\varsigma }_1,{\varsigma }_2]\to \mathbb{R}$ be two real functions and satisfy $\underline{f}\left(x\right)\le \overline{f}\left(x\right)$ for every $x\in [{\varsigma }_1,{\varsigma }_2].$ Then $F:[{\varsigma }_1,{\varsigma }_2]\to {\mathbb{R}}_I$ with $F\left(x\right)=[\underline{f}\left(x\right),\overline{f}\left(x\right)]$ is called an interval-valued function.

• We employ the notation $\mathbf{C}([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}_I)$ to represent the set of all continuous interval-valued functions on $[{\varsigma }_1,{\varsigma }_2]$. Again, the notation $\mathbf{C}([{\varsigma }_1,{\varsigma }_2],\mathbb{R})$ characterizes the set of continuous real-valued functions.

Definition 2

([36]). Let $F\in \mathbf{C}([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}_I).$ Then the Aumann integral(AI) of F over $[{\varsigma }_1,{\varsigma }_2]$ is defined by

$$\left(AI\right){\int }_{{\varsigma }_1}^{{\varsigma }_2}F\left(x\right)dx=\left\{{\int }_{{\varsigma }_1}^{{\varsigma }_2}f\left(x\right)dx:f\in S\left(F\right)\right\},$$

where $S\left(F\right)=\{f\in L^1\left([{\varsigma }_1,{\varsigma }_2]\right):f\left(x\right)\in F\left(x\right)$ for almost all $x\in [{\varsigma }_1,{\varsigma }_2]\}$ and $L^1\left([{\varsigma }_1,{\varsigma }_2]\right)$ is called the set of all mappings that are Lebesgue-integrable over $[{\varsigma }_1,{\varsigma }_2]$.

Theorem 2

([37]). Let $F\in \mathbf{C}([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}_I).$ Then F is AI-integrable over $[{\varsigma }_1,{\varsigma }_2]$ if and only if $\underline{f},\overline{f}\in L^1\left([{\varsigma }_1,{\varsigma }_2]\right).$ Furthermore, suppose F is AI-integrable over $[{\varsigma }_1,{\varsigma }_2]$, then

$$\left(IA\right){\int }_{{\varsigma }_1}^{{\varsigma }_2}F\left(x\right)dx=\left[{\int }_{{\varsigma }_1}^{{\varsigma }_2}\underline{f}\left(x\right)dx,{\int }_{{\varsigma }_1}^{{\varsigma }_2}\overline{f}\left(x\right)dx\right].$$

Definition 3

([38]). A fuzzy subset of $\mathbb{R}$ is a function $\tilde{l}:\mathbb{R}\to [0,1]$. The notation $\mathcal{F}\left(\mathbb{R}\right)$ denotes the set of all fuzzy subsets of $\mathbb{R}$. A fuzzy subset $\tilde{l}$ of $\mathbb{R}$ is regarded as a real fuzzy interval providing it satisfies the following properties:

(i) 

$\tilde{l}$ is normal.

(ii) 

$\tilde{l}$ is fuzzy convex.

(iii) 

$\tilde{l}$ is upper semi continuous on $\mathbb{R}$.

(iv) 

$\tilde{l}$ is compactly supported.

• We denote by ${\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right)$ the space of fuzzy intervals.

Definition 4

([38]). Let $\tilde{l}\in {\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right),$ the level sets of $\tilde{l}$ are defined by ${\left[\tilde{l}\right]}^{\xi }=\{x\in \mathbb{R}|\tilde{l}\left(x\right)\ge \xi \}$ for every $\xi \in [0,1]$. These sets are $\xi$-level sets of $\tilde{l}$. In particular, ${\left[\tilde{l}\right]}^0$ is the support of ${\left[\tilde{l}\right]}^1$, which is the core of $\tilde{l}$.

• For $\tilde{l},\tilde{h}\in {\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right),$ the UD order relation ${\supseteq }_{\mathbb{F}}$ is given by

$$\tilde{l}{\supseteq }_{\mathbb{F}}\tilde{h}\iff {\left[\tilde{l}\right]}^{\xi }{\supseteq }_I{\left[\tilde{l}\right]}^{\xi },\xi \in [0,1].$$

Let $\tilde{l},\tilde{h}\in {\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right),$ and $\theta \in [0,1]$. Then the arithmetic operations are given by

$${[\theta \odot \tilde{l}]}^{\xi }=\theta {\left[\tilde{l}\right]}^{\xi },$$

$${[\tilde{l}\oplus \tilde{h}]}^{\xi }={\left[\tilde{l}\right]}^{\xi }+{\left[\tilde{h}\right]}^{\xi },$$

$${[\tilde{l}\otimes \tilde{h}]}^{\xi }={\left[\tilde{l}\right]}^{\xi }\times {\left[\tilde{h}\right]}^{\xi }.$$

A fuzzy interval-valued map $\tilde{F}:[{\varsigma }_1,{\varsigma }_2]\to {\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right)$ is called an fuzzy interval-valued function (FIVF). For notational simplicity, we appoint $\mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$ and $\mathbf{SC}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$ to denote the set of all FIVFs and continuous FIVFs in $[{\varsigma }_1,{\varsigma }_2]$, respectively.

Definition 5

([39]). Let $\tilde{F}\in \mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$. Then the IVF $F_{\xi }:[{\varsigma }_1,{\varsigma }_2]\to {\mathbb{R}}_I$ given by $F_{\xi }\left(x\right)={\left[\tilde{F}\left(x\right)\right]}^{\xi }=[{\underline{f}}_{\xi }\left(x\right),{\overline{f}}_{\xi }\left(x\right)]$ for every $x\in [{\varsigma }_1,{\varsigma }_2]$ is said to be ξ-levels of $\tilde{F}$ for every $\xi \in [0,1]$, where ${\underline{f}}_{\xi }\left(x\right) and {\overline{f}}_{\xi }\left(x\right)$ are two real-valued functions for every $\xi \in [0,1]$.

Definition 6

([39]). Let $\tilde{F}\in \mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$. Then $\tilde{F}$ is continuous at $x\in [{\varsigma }_1,{\varsigma }_2]$ if and only if $F_{\xi }\in \mathbf{C}([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}_I)$ for all $\xi \in [0,1]$, i-e. ${\underline{f}}_{\xi }\left(x\right),{\overline{f}}_{\xi }\left(x\right)\in C([{\varsigma }_1,{\varsigma }_2],\mathbb{R})$ for all $\xi \in [0,1]$.

Definition 7

([37]). Let $\tilde{F}\in \mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$. The fuzzy Aumann integral of $\tilde{F}$ (FA-integral) over $[{\varsigma }_1,{\varsigma }_2]$, denoted by $\left(FA\right){\int }_{{\varsigma }_1}^{{\varsigma }_2}\tilde{F}\left(x\right)dx$, is defined level-wise by

$${\left[\left(FA\right){\int }_{{\varsigma }_1}^{{\varsigma }_2}\tilde{F}\left(x\right)dx\right]}^{\xi }=\left(AI\right){\int }_{{\varsigma }_1}^{{\varsigma }_2}{F}_{\xi }\left(x\right)dx=\left\{{\int }_{{\varsigma }_1}^{{\varsigma }_2}{f}_{\xi }\left(x\right)dx:f_{\xi }\in S\left(F_{\xi }\right)\right\},$$

for all $\xi \in [0,1]$. If ${\int }_{{\varsigma }_1}^{{\varsigma }_2}\tilde{F}\left(x\right)dx\in {\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right),$ then $\tilde{F}$ is integrable over $[{\varsigma }_1,{\varsigma }_2]$.

Theorem 3

([40]). Let $\tilde{F}\in \mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$ and $\xi$-levels of $\tilde{F}$ be given by $F_{\xi }\left(x\right)=[{\underline{f}}_{\xi }\left(x\right),{\overline{f}}_{\xi }\left(x\right)]$ for every $\xi \in [0,1]$ and for all $x\in [{\varsigma }_1,{\varsigma }_2]$. Then $\tilde{F}$ is integrable over $[{\varsigma }_1,{\varsigma }_2]$ if and only if ${\underline{f}}_{\xi }\left(x\right),{\overline{f}}_{\xi }\left(x\right)\in L^1\left([{\varsigma }_1,{\varsigma }_2]\right)$ for all $\xi \in [0,1]$. Moreover, suppose $\tilde{F}$ is integrable over $[{\varsigma }_1,{\varsigma }_2]$, then

$$\begin{array}{ccc}\hfill {\left[{\int }_{{\varsigma }_1}^{{\varsigma }_2}\tilde{F}\left(x\right)dx\right]}^{\xi }& =& \left[{\int }_{{\varsigma }_1}^{{\varsigma }_2}{\underline{f}}_{\xi }\left(x\right),{\int }_{{\varsigma }_1}^{{\varsigma }_2}{\overline{f}}_{\xi }\left(x\right)\right]\hfill \\ & =& {\int }_{{\varsigma }_1}^{{\varsigma }_2}{F}_{\xi }\left(x\right)dx.\hfill \end{array}$$

Definition 8

([41]). Let $\tilde{F}\in \mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$. Then the fuzzy left and right RLF integrals of $\tilde{F}$ with order $\gamma >0$ are defined by

$$I_{{\varsigma }_1^{+}}^{\gamma }\tilde{F}\left(x\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_{{\varsigma }_1}^x{(x-t)}^{\gamma -1}\tilde{F}\left(t\right)dt(x>{\varsigma }_1),$$

and

$$I_{{\varsigma }_2^{-}}^{\gamma }\tilde{F}\left(x\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\gamma \right)}}{\int }_x^{{\varsigma }_2}{(x-t)}^{\gamma -1}\tilde{F}\left(t\right)dt({\varsigma }_2<x),$$

where Γ is Euler gamma function.

Now we shall discuss the notion of convexity.

Definition 9

([42]). A non-negative function $f:K\to \mathbb{R}$ is known as a Godunova–Levin convex function if for all $s,t\in K$ and $\nu \in (0,1)$, we have

$$f(\nu s+(1-\nu )t)\le {\displaystyle \frac{f\left(s\right)}{\nu }}+{\displaystyle \frac{f\left(t\right)}{1-\nu }}.$$

Definition 10

([42]). Let $h:(0,1)\subseteq W\to \mathbb{R}$ be non-negative function. We say $f:W\to \mathbb{R}$ is known as h-Godunova–Levin convex function $f\in SGX(\left({\displaystyle \frac{1}{h}}\right),W)$ if for all $s,t\in W$ and $\nu \in (0,1)$, we have

$$f(\nu s+(1-\nu )t)\le {\displaystyle \frac{f\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{f\left(t\right)}{h(1-\nu )}}.$$

Definition 11

([42]). Let $h:(0,1)\subseteq W\to \mathbb{R}$ be non-negative function. We say $f:W\to {\mathbb{R}}_I^{+}$ is the interval valued h-Godunova–Levin convex function, or $f\in SGX(\left({\displaystyle \frac{1}{h}}\right),W,{\mathbb{R}}_I^{+})$ if for all $s,t\in W$ and $\nu \in (0,1)$, we have

$$f(\nu s+(1-\nu )t)\supseteq {\displaystyle \frac{f\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{f\left(t\right)}{h(1-\nu )}}.$$

Proposition 1

([42]). Let $f:[s,t]\to {\mathbb{R}}_I^{+}$ be h-Godunova–Levin convex interval valued function such that $f\left(\nu \right)=[\underline{f}\left(\nu \right),\overline{f}\left(\nu \right)]$. Then $f\in SGX(\left({\displaystyle \frac{1}{h}}\right),[s,t],{\mathbb{R}}_I^{+})$ if and only if $\underline{f}\in SGX(\left({\displaystyle \frac{1}{h}}\right),[s,t],{\mathbb{R}}_I^{+})$, $\overline{f}\in SGV(\left({\displaystyle \frac{1}{h}}\right),[s,t],{\mathbb{R}}_I^{+}).$

Proposition 2

([42]). Let $f:[s,t]\to {\mathbb{R}}_I^{+}$ be h-Godunova–Levin concave interval valued function such that $f\left(\nu \right)=[\underline{f}\left(\nu \right),\overline{f}\left(\nu \right)]$. Then $f\in SGV(\left({\displaystyle \frac{1}{h}}\right),[s,t],{\mathbb{R}}_I^{+})$ if and only if $\underline{f}\in SGV(\left({\displaystyle \frac{1}{h}}\right),[s,t],{\mathbb{R}}_I^{+})$, $\overline{f}\in SGX(\left({\displaystyle \frac{1}{h}}\right),[s,t],{\mathbb{R}}_I^{+}).$

Now we shall give details of basic concept of q-calculus.

Definition 12

([20]). Suppose $q\in [0,1]$ and ${\varsigma }_1,t,v\in \mathbb{R}$. Then the q-integral number is defined by

$${\left[n\right]}_q=1+q+q^2+...+q^{n-1}={\displaystyle \frac{1-q^n}{1-q}},n\in \mathbb{R}.$$

A q-shift operator is defined by

$${}_{{\varsigma }_1}\mathsf{\Omega }_q\left(t\right)=qt+(1-q){\varsigma }_1.$$

Let $m>0$ be an integer, then we obtain

$${}_{{\varsigma }_1}\mathsf{\Omega }_q^m\left(t\right)=q^m(t-{\varsigma }_1)+{\varsigma }_1.$$

Particularly,

$${}_{{\varsigma }_1}\mathsf{\Omega }_q^0\left(t\right)=t.$$

Proposition 3

([43]). Assuming $\gamma ,t,v\in \mathbb{R}$ with $v\ne {\varsigma }_1$, then

(i) 

${}_{{\varsigma }_1}(v-t)_q^{\gamma }={(v-{\varsigma }_1)}^{\gamma }{\displaystyle \prod _{i=0}^{\infty }}{\displaystyle \frac{1-\frac{t-{\varsigma }_1}{v-{\varsigma }_1}{q}^i}{1-\frac{t-{\varsigma }_1}{v-{\varsigma }_1}{q}^{\gamma +i}}}={(v-{\varsigma }_1)}^{\gamma }{\displaystyle \frac{{(\frac{t-{\varsigma }_1}{v-{\varsigma }_1};q)}_{\infty }}{{(\frac{t-{\varsigma }_1}{v-{\varsigma }_1}{q}^{\gamma };q)}_{\infty }}}.$

(ii) 

${}_{{\varsigma }_1}\left(v{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^m\left(t\right)\right)_q^{\gamma }={(v-{\varsigma }_1)}^{\gamma }{\displaystyle \frac{{(q^m;q)}_{\infty }}{{(q^{\gamma +m};q)}_{\infty }}}.$

• Choosing $\gamma \in \mathbb{R}/\{0,-1,-2,...\}$, then q-gamma function is given as

$${\mathsf{\Gamma }}_q\left(\gamma \right)={\displaystyle \frac{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(1\right)\right)_q^{(\gamma -1)}}{{(1-q)}^{\gamma -1}}}.$$

Moreover, ${\left[\gamma \right]}_q{\mathsf{\Gamma }}_q\left(\gamma \right)={\mathsf{\Gamma }}_q(\gamma +1).$

Lemma 1

([43]). let $\gamma ,\chi >0,$ then we get the following relations for $x\in [{\varsigma }_1,{\varsigma }_2]$:

$$\left({}_{{\varsigma }_1}I_q^{\gamma }{(t-{\varsigma }_1)}^{\chi }\right)\left(x\right)={\displaystyle \frac{{\mathsf{\Gamma }}_q(\chi +1)}{{\mathsf{\Gamma }}_q(\chi +\gamma +1)}}{(x-{\varsigma }_1)}^{\chi +\gamma }.$$

Definition 13

([43]). Let $f\in C([{\varsigma }_1,{\varsigma }_2],\mathbb{R})$ and $\gamma \ge 0$. The RLF q-integral on $[{\varsigma }_1,{\varsigma }_2]$ is defined by $\left({}_{{\varsigma }_1}I_q^{0}f\left(t\right)\right)\left(x\right)=f\left(x\right)$ and

$$\begin{array}{ccc}\hfill \left({}_{{\varsigma }_1}I_q^{\gamma }f\left(t\right)\right)\left(x\right)& =& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_{{\varsigma }_1}^x{}_{{\varsigma }_1}\left(x{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q\left(t\right)\right)_q^{(\gamma -1)}f\left(t\right){}_{{\varsigma }_1}d_{q}t\hfill \\ & =& {\displaystyle \frac{(1-q)(x-{\varsigma }_1)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}\sum _{i=0}^{\infty }{q}^i{}_{{\varsigma }_1}\left(x{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^{i+1}\left(x\right)\right)_q^{(\gamma -1)}f{(}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i\left(x\right)).\hfill \end{array}$$

Definition 14

([44]). Let $F\in \mathbf{C}([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}_I)$ and $\gamma \ge 0$. The RLF Iq-integral on $[{\varsigma }_1,{\varsigma }_2]$ is defined by $\left({}_{{\varsigma }_1}I_q^{0}F\left(t\right)\right)\left(x\right)=F\left(x\right)$ and by

$$\left({}_{{\varsigma }_1}I_q^{\gamma }F\left(t\right)\right)\left(x\right)={\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_{{\varsigma }_1}^x{}_{{\varsigma }_1}\left(x{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q\left(t\right)\right)_q^{(\gamma -1)}F\left(t\right){}_{{\varsigma }_1}d_{q}t.$$

Definition 15

([8]). Let $\tilde{F}\in \mathbf{SC}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$. The fuzzy interval valued RLF q-integral on $[{\varsigma }_1,{\varsigma }_2]$ is defined as

$$\begin{array}{ccc}\hfill \left({}_{{\varsigma }_1}I_q^{\gamma }\tilde{F}\left(t\right)\right)\left(x\right)& =& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_{{\varsigma }_1}^x{}_{{\varsigma }_1}\left(x{-}_{{\mathsf{\varsigma }}_1}{\mathsf{\Omega }}_q\left(t\right)\right)_q^{(\gamma -1)}\tilde{F}\left(t\right){}_{{\varsigma }_1}d_{q}t\hfill \\ & =& {\displaystyle \frac{(1-q)(x-{\varsigma }_1)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}\sum _{i=0}^{\infty }{q}^i{}_{{\varsigma }_1}\left(x{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^{i+1}\left(x\right)\right)_q^{(\gamma -1)}\tilde{F}{(}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i\left(x\right)),\hfill \end{array}$$

for all $\gamma >0,x\in [{\varsigma }_1,{\varsigma }_2]$.

• Moreover, it is defined level-wise by

$$\begin{array}{ccc}\hfill {\left[\left({}_{{\varsigma }_1}I_q^{\gamma }\tilde{F}\left(t\right)\right)\left(x\right)\right]}^{\xi }& =& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_{{\varsigma }_1}^x{}_{{\varsigma }_1}\left(x{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q\left(t\right)\right)_q^{(\gamma -1)}{F}_{\xi }\left(t\right){}_{{\varsigma }_1}d_{q}t\hfill \\ & =& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_{{\varsigma }_1}^x{}_{{\varsigma }_1}\left(x{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q\left(t\right)\right)_q^{(\gamma -1)}\times [{\underline{f}}_{\xi }\left(t\right),{\overline{f}}_{\xi }\left(t\right)]{}_{{\varsigma }_1}d_{q}t,\hfill \end{array}$$

for all $\xi \in [0,1]$. If $\left({}_{{\varsigma }_1}I_q^{\gamma }\tilde{F}\left(t\right)\right)\left(x\right)\in {\mathcal{F}}_{\mathcal{C}}\left(R\right)$, then $\tilde{F}$ is RLF q-integrable over $[{\varsigma }_1,{\varsigma }_2].$

Theorem 4

([8]). Let $\tilde{F}\in \mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$. Then $\tilde{F}$ is RLF q-integrable if and only if ${\underline{f}}_{\xi }\left(x\right)$ and ${\overline{f}}_{\xi }\left(x\right)$ are RLF q-integrable over $[{\varsigma }_1,{\varsigma }_2].$ Moreover, $\tilde{F}$ is RLF q-integrable, then

$${\left[\left({}_{{\varsigma }_1}I_q^{\gamma }\tilde{F}\left(t\right)\right)\left(x\right)\right]}^{\xi }=\left({}_{{\varsigma }_1}I_q^{\gamma }{F}_{\xi }\left(t\right)\right)\left(x\right)=[\left({}_{{\varsigma }_1}I_q^{\gamma }{\underline{f}}_{\xi }\left(t\right)\right)\left(x\right),\left({}_{{\varsigma }_1}I_q^{\gamma }{\overline{f}}_{\xi }\left(t\right)\right)\left(x\right)].$$

3. The Main Results

To lay the foundation of our core results, we introduce a precise framework of notation relevant to the study of UD-h-Godunova–Levin convex or concave fuzzy interval-valued functions.

Definition 16.

Let $\tilde{F}\in \mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$. Then $\tilde{F}$ is a UD-h-Godunova–Levin convex function if and only if

$$\tilde{F}(\nu s+(1-\nu )t){\supseteq }_F{\displaystyle \frac{\tilde{F}\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{\tilde{F}\left(t\right)}{h(1-\nu )}},$$

for every $\nu \in (0,1)$ and for all $s,t\in [{\varsigma }_1,{\varsigma }_2]$, where $h:(0,1)\subseteq M\to {\mathbb{R}}^{+}$ and $h\ne 0$. If is reversed, one obtains that $\tilde{F}$ is a UD-h-Godunova–Levin concave function. The family of all UD-h-Godunova–Levin convex (UD-h-Godunova–Levin concave) FIVFs on $[{\varsigma }_1,{\varsigma }_2]$ is given by $UDSGX([{\varsigma }_1,{\varsigma }_2],F_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h}})\left(UDSGV([{\varsigma }_1,{\varsigma }_2],F_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h}})\right)$.

Remark 1.

The UD-h-Godunova–Levin convex FIVFs have some very nice properties, similar to convex FIVFs.

1. 

If $\tilde{F}$ is a UD-h-Godunova–Levin convex FIVF, then $\mathrm{{\rm Y}}\tilde{F}$ is also a UD-h-Godunova–Levin convex FIVF for $\mathrm{{\rm Y}}\ge 0.$

2. 

If $\tilde{F}$ and $\tilde{G}$ are UD-h-Godunova–Levin convex FIVFs, then max$(\tilde{F},\tilde{G})$ is also a UD-h-Godunova–Levin convex FIVF.

Next, we analyze some distinctive exceptional cases of UD-h-Godunova–Levin convex FIVFs.

• If $h\left(\nu \right)={\nu }^s$, then UD-h-Godunova–Levin convex FIVFs become UD-s-Godunova–Levin convex FIVFs, that is,

  $$\tilde{F}(\nu s+(1-\nu )t){\supseteq }_F{\displaystyle \frac{\tilde{F}\left(s\right)}{{\nu }^s}}+{\displaystyle \frac{\tilde{F}\left(t\right)}{{(1-\nu )}^s}}\mathrm{for} \mathrm{all}s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1).$$
• If $h\left(\nu \right)=1$, then UD-h-Godunova–Levin convex FIVFs become UD-P-Godunova–Levin convex FIVFs, that is,

  $$\tilde{F}(\nu s+(1-\nu )t){\supseteq }_F\tilde{F}\left(s\right)+\tilde{F}\left(t\right)\mathrm{for} \mathrm{all}s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1).$$
• If $h\left(\nu \right)=\nu$, then UD-h-Godunova–Levin convex FIVFs become UD-Godunova–Levin convex FIVFs, that is,

  $$\tilde{F}(\nu s+(1-\nu )t){\supseteq }_F{\displaystyle \frac{\tilde{F}\left(s\right)}{\nu }}+{\displaystyle \frac{\tilde{F}\left(t\right)}{1-\nu }}\mathrm{for} \mathrm{all}s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1).$$

Theorem 5.

Let $\tilde{F}\in \mathbf{S}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$. Then

$$\tilde{F}\in UDSGX\left([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h}}\right),$$

if and only if for all $\xi \in [0,1],$

$${\underline{f}}_{\xi }\left(x\right)\in SGX\left([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}^{+},{\displaystyle \frac{1}{h}}\right),$$

and

$${\overline{f}}_{\xi }\left(x\right)\in SGV\left([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}^{+},{\displaystyle \frac{1}{h}}\right).$$

Proof. 

Assume $\xi \in [0,1],$${\underline{f}}_{\xi }\left(x\right)$ and ${\overline{f}}_{\xi }\left(x\right)$ for each h-Godunova–Levin convex and concave FIVF on $[{\varsigma }_1,{\varsigma }_2].$ Then we have

$${\underline{f}}_{\xi }(\nu s+(1-\nu )t)\le {\displaystyle \frac{{\underline{f}}_{\xi }\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left(t\right)}{h(1-\nu )}}\mathrm{for}\mathrm{all}s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1),$$

and

$${\overline{f}}_{\xi }(\nu s+(1-\nu )t)\ge {\displaystyle \frac{{\overline{f}}_{\xi }\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{{\overline{f}}_{\xi }\left(t\right)}{h(1-\nu )}}\mathrm{for}\mathrm{all}s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1).$$

Then

$$F_{\xi }(\nu s+(1-\nu )t)=[{\underline{f}}_{\xi }(\nu s+(1-\nu )t),{\overline{f}}_{\xi }(\nu s+(1-\nu )t)]$$

$${\supseteq }_I\left[{\displaystyle \frac{{\underline{f}}_{\xi }\left(s\right)}{h\left(\nu \right)}},{\displaystyle \frac{{\overline{f}}_{\xi }\left(s\right)}{h\left(\nu \right)}}\right]+\left[{\displaystyle \frac{{\underline{f}}_{\xi }\left(t\right)}{h(1-\nu )}},{\displaystyle \frac{{\overline{f}}_{\xi }\left(t\right)}{h(1-\nu )}}\right]\mathrm{for}\mathrm{all}s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1).$$

That is,

$$\tilde{F}(\nu s+(1-\nu )t){\supseteq }_F{\displaystyle \frac{\tilde{F}\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{\tilde{F}\left(t\right)}{h(1-\nu )}}.$$

Hence,

$$\tilde{F}\in UDSGX\left([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(R\right),{\displaystyle \frac{1}{h}}\right)\mathrm{for} \mathrm{all} s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1).$$

Conversely, let $\tilde{F}$ is UD-h-Godunova–Levin convex function on $[{\varsigma }_1,{\varsigma }_2]$. Then, for all $s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1)$, we have

$$\tilde{F}(\nu s+(1-\nu )t){\supseteq }_F{\displaystyle \frac{\tilde{F}\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{\tilde{F}\left(t\right)}{h(1-\nu )}}.$$

Therefore,

$$F_{\xi }(\nu s+(1-\nu )t)=[{\underline{f}}_{\xi }(\nu s+(1-\nu )t),{\overline{f}}_{\xi }(\nu s+(1-\nu )t)].$$

This implies that

$${\displaystyle \frac{F_{\xi }\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{F_{\xi }\left(t\right)}{h(1-\nu )}}=\left[{\displaystyle \frac{{\underline{f}}_{\xi }\left(s\right)}{h\left(\nu \right)}},{\displaystyle \frac{{\overline{f}}_{\xi }\left(s\right)}{h\left(\nu \right)}}\right]+\left[{\displaystyle \frac{{\underline{f}}_{\xi }\left(t\right)}{h(1-\nu )}},{\displaystyle \frac{{\overline{f}}_{\xi }\left(t\right)}{h(1-\nu )}}\right],$$

for all $s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1)$. Then, by the UD-h-Godunova–Levin convexity of $\tilde{F}$, we have for all $s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1)$, such that

$${\underline{f}}_{\xi }(\nu s+(1-\nu )t)\le {\displaystyle \frac{{\underline{f}}_{\xi }\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left(t\right)}{h(1-\nu )}}\mathrm{for}\mathrm{all}s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1),$$

and

$${\overline{f}}_{\xi }(\nu s+(1-\nu )t)\ge {\displaystyle \frac{{\overline{f}}_{\xi }\left(s\right)}{h\left(\nu \right)}}+{\displaystyle \frac{{\overline{f}}_{\xi }\left(t\right)}{h(1-\nu )}}\mathrm{for}\mathrm{all}s,t\in [{\varsigma }_1,{\varsigma }_2],\nu \in (0,1),$$

for each $\xi \in [0,1]$. □

The next result will be established by utilizing the UD-h-Godunova–Levin convex FIVFs to derive the RLF q-HH inequalities.

Theorem 6.

Let $\tilde{F}\in \mathbf{SC}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))\bigcap UDSGX([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathcal{R}\right),{\displaystyle \frac{1}{h}})$ and $h\left({\displaystyle \frac{1}{2}}\right)\ne 0$. If $\tilde{F}$ is RLF q-integrable on $[{\varsigma }_1,{\varsigma }_2]$, then

$$\begin{array}{ccc}\hfill {\displaystyle \frac{h\left(\frac{1}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}\circ \tilde{F}\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)& {\supseteq }_F& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}\circ [{(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}\left(x\right))\left({\varsigma }_2\right)\oplus {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)]\hfill \\ & {\supseteq }_F& [\tilde{F}\left({\varsigma }_1\right)\oplus \tilde{F}\left({\varsigma }_2\right)]\circ \left({}_{0}I_q^{\gamma }\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]\right)\left(1\right).\hfill \end{array}$$

Proof. 

By Theorem 5, it follows that

$$h\left({\displaystyle \frac{1}{2}}\right){\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)=h\left({\displaystyle \frac{1}{2}}\right){\underline{f}}_{\xi }\left({\displaystyle \frac{(1-\nu ){\varsigma }_1+\nu {\varsigma }_2+\nu {\varsigma }_1+(1-\nu ){\varsigma }_2}{2}}\right)$$

$$\begin{array}{c}\hfill \le {\underline{f}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)+{\underline{f}}_{\xi }((1-\nu ){\varsigma }_2+\nu {\varsigma }_1).\end{array}$$

(1)

Multiply (1) by ${\displaystyle \frac{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}$ and q-integrating over $[0,1]$. We have

$$\begin{array}{ccc}& & {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}\times {\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}}_{0}d\nu \hfill \\ & \le & {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }{((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)}_{0}d\nu \hfill \\ & +& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }{((1-\nu ){\varsigma }_2+\nu {\varsigma }_1)}_{0}d\nu .\hfill \end{array}$$

Let us say

$$\begin{array}{c}\hfill I\le I_1+I_2.\end{array}$$

(2)

First, we calculate $I_1$ by using Proposition 3, Lemma 1, Definition 12, and Definition 13; we have

$$\begin{array}{ccc}\hfill I_1& =& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q(\gamma )}}{\int }_0^1{{}_0(1{-}_0{\mathsf{\Omega }}_q(\nu ))}_q^{(\gamma -1)}{\underline{f}}_{\xi }{((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)}_{0}d\nu \hfill \\ & =& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q(\gamma )}}{\int }_0^1{}_0(1{-}_0{\mathsf{\Omega }}_q(\nu ))_q^{(\gamma -1)}{\underline{f}}_{\xi }{(}_{{\varsigma }_1}{\mathsf{\Omega }}_q{({\varsigma }_2)}_{0}d\nu \hfill \\ & =& {\displaystyle \frac{(1-q)(1-0)}{{\mathsf{\Gamma }}_q(\gamma )}}\sum _{i=0}^{\infty }{q}^i{}_0(1{-}_0{\mathsf{\Omega }}_q^{i+1}(1))_q^{(\gamma -1)}{\underline{f}}_{\xi }{(}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i({\varsigma }_2))\hfill \\ & =& {\displaystyle \frac{(1-q)}{{\mathsf{\Gamma }}_q(\gamma )}}\sum _{i=0}^{\infty }{q}^i{\displaystyle \frac{{(q^{i+1};q)}_{\infty }}{{(q^{\gamma +i};q)}_{\infty }}}{\underline{f}}_{\xi }{(}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i({\varsigma }_2))\hfill \\ & =& {\displaystyle \frac{(1-q)}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma -1}{\mathsf{\Gamma }}_q(\gamma )}}\sum _{i=0}^{\infty }{q}^i{({\varsigma }_2-{\varsigma }_1)}^{\gamma -1}{\displaystyle \frac{{(q^{i+1};q)}_{\infty }}{{(q^{\gamma +i};q)}_{\infty }}}{\underline{f}}_{\xi }{(}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i({\varsigma }_2))\hfill \\ & =& {\displaystyle \frac{(1-q)({\varsigma }_2-{\varsigma }_1)}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }{\mathsf{\Gamma }}_q(\gamma )}}\sum _{i=0}^{\infty }{q}^i{({\varsigma }_2-{\varsigma }_1)}^{\gamma -1}{\displaystyle \frac{{(q^{i+1};q)}_{\infty }}{{(q^{\gamma +i};q)}_{\infty }}}{\underline{f}}_{\xi }{(}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i({\varsigma }_2))\hfill \\ & =& {\displaystyle \frac{(1-q)({\varsigma }_2-{\varsigma }_1)}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }{\mathsf{\Gamma }}_q(\gamma )}}\sum _{i=0}^{\infty }{q}^i{}_{{\varsigma }_1}({\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^{i+1}(x))_q^{(\gamma -1)}{\underline{f}}_{\xi }{(}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i({\varsigma }_2)\hfill \\ & =& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }{\mathsf{\Gamma }}_q(\gamma )}}{\int }_{{\varsigma }_1}^{{\varsigma }_2}{}_{{\varsigma }_1}({\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q(x))_q^{(\gamma -1)}{\underline{f}}_{\xi }{(x)}_{{\varsigma }_1}dx\hfill \\ & =& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }(x))({\varsigma }_2).\hfill \end{array}$$

Now, similarly, we can calculate $I_2,$ and get

$$\begin{array}{ccc}\hfill I_2& =& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}{\underline{f}}_{\xi }{((1-\nu ){\varsigma }_2+\nu {\varsigma }_1)}_{0}d\nu \hfill \\ & =& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }{({\varsigma }_1+{\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q\left({\varsigma }_2\right))}_{0}d\nu \hfill \\ & =& {\displaystyle \frac{(1-q)(1-0)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}\sum _{i=0}^{\infty }{q}^i{}_0\left(1{-}_0{\mathsf{\Omega }}_q^{i+1}\left(1\right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i\left({\varsigma }_2\right))\hfill \\ & =& {\displaystyle \frac{(1-q)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}\sum _{i=0}^{\infty }{q}^i{\displaystyle \frac{{(q^{i+1};q)}_{\infty }}{{(q^{\gamma +i};q)}_{\infty }}}{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i\left({\varsigma }_2\right))\hfill \\ & =& {\displaystyle \frac{(1-q)}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma -1}{\mathsf{\Gamma }}_q\left(\gamma \right)}}\sum _{i=0}^{\infty }{q}^i{({\varsigma }_2-{\varsigma }_1)}^{\gamma -1}{\displaystyle \frac{{(q^{i+1};q)}_{\infty }}{{(q^{\gamma +i};q)}_{\infty }}}{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i\left({\varsigma }_2\right))\hfill \\ & =& {\displaystyle \frac{(1-q)({\varsigma }_2-{\varsigma }_1)}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }{\mathsf{\Gamma }}_q\left(\gamma \right)}}\sum _{i=0}^{\infty }{q}^i{({\varsigma }_2-{\varsigma }_1)}^{\gamma -1}{\displaystyle \frac{{(q^{i+1};q)}_{\infty }}{{(q^{\gamma +i};q)}_{\infty }}}{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i\left({\varsigma }_2\right))\hfill \\ & =& {\displaystyle \frac{(1-q)({\varsigma }_2-{\varsigma }_1)}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }{\mathsf{\Gamma }}_q\left(\gamma \right)}}\sum _{i=0}^{\infty }{q}^i{}_{{\varsigma }_1}\left({\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^{i+1}\left(x\right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q^i\left({\varsigma }_2\right))\hfill \\ & =& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_{{\varsigma }_1}^{{\varsigma }_2}{}_{{\varsigma }_1}\left({\varsigma }_2{-}_{{\varsigma }_1}{\mathsf{\Omega }}_q\left(x\right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }{({\varsigma }_1+{\varsigma }_2-x)}_{{\varsigma }_1}dx\hfill \\ & =& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right).\hfill \end{array}$$

Similarly, we can calculate I as

$$\begin{array}{ccc}\hfill I& =& {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}{}_{0}d\nu =h\left({\displaystyle \frac{1}{2}}\right){\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)\left({}_{0}I_q^{\gamma }1\right)\left(1\right)\hfill \\ & =& {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}.\hfill \end{array}$$

Putting the values of $I,I_1$ and $I_2$ in (2), we get

$$\begin{array}{c}\hfill {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}\le {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+{\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right).\end{array}$$

(3)

Now, by the definition of the h-Godunova–Levin convex function, we have

$$\begin{array}{ccc}\hfill & & {\underline{f}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)+{\underline{f}}_{\xi }((1-\nu ){\varsigma }_2+\nu {\varsigma }_1)\hfill \\ & \le & {\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_2\right)}{h\left(\nu \right)}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_1\right)}{h(1-\nu )}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_1\right)}{h\left(\nu \right)}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_2\right)}{h(1-\nu )}}\hfill \\ & =& [{\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right)]\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right].\hfill \end{array}$$

(4)

Multiply (4) by ${\displaystyle \frac{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}$ and q-integrating over $[0,1]$. We have

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }{((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)}_{0}d\nu \hfill \\ & +& {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }{((1-\nu ){\varsigma }_2+\nu {\varsigma }_1)}_{0}d\nu \hfill \\ & \le & {\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}({\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right)){\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]{}_{0}d\nu .\hfill \end{array}$$

Let us say

$$\begin{array}{c}\hfill J_1+J_2\le J_3,\end{array}$$

(5)

where

$$J_1={\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }{((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)}_{0}d\nu ,$$

$$J_2={\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}{\underline{f}}_{\xi }{((1-\nu ){\varsigma }_2+\nu {\varsigma }_1)}_{0}d\nu ,$$

and

$$J_3={\displaystyle \frac{1}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}({\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right)){\int }_0^1{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]{}_{0}d\nu .$$

Now we calculate, similarly, $J_1,J_2,$ and $J_3,$ and we get

$$\begin{array}{ccc}\hfill J_1& =& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right)\hfill \\ \hfill J_2& =& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)\hfill \\ \hfill J_3& =& {\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]{}_{0}d\nu \hfill \\ & =& ({\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right))\left({}_{0}I_q^{\gamma }\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]\right)\left(1\right).\hfill \end{array}$$

Putting the values of $J_1,J_2$ and $J_3$ in (5), we get

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+{\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)\end{array}$$

$$\begin{array}{c}\hfill \le ({\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right))\left({}_{0}I_q^{\gamma }\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]\right)\left(1\right).\end{array}$$

(6)

From (3) and (6), we can written as

$$\begin{array}{ccc}\hfill {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}& \le & {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+{\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill & \le & [\underline{f}\left({\varsigma }_1\right)+\underline{f}\left({\varsigma }_2\right)]\left({}_{0}I_q^{\gamma }\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]\right)\left(1\right).\hfill \end{array}$$

(7)

Similarly,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{h\left(\frac{1}{2}\right){\overline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}& \ge & {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right))+{\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)\hfill \\ & \ge & [\overline{f}\left({\varsigma }_1\right)+\overline{f}\left({\varsigma }_2\right)]\left({}_{0}I_q^{\gamma }\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]\right)\left(1\right).\hfill \end{array}$$

(8)

So, from (7) and (8), we have

$$\begin{array}{ccc}& & {\displaystyle \frac{h\left(\frac{1}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}[{\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right),{\overline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)]\hfill \\ & {\supseteq }_I& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}\times \hfill \\ & & [{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right),{(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)]\hfill \\ & {\supseteq }_I& [\underline{f}\left({\varsigma }_1\right)+\underline{f}\left({\varsigma }_2\right),\overline{f}\left({\varsigma }_1\right)+\overline{f}\left({\varsigma }_2\right)]\left({}_{0}I_q^{\gamma }\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]\right)\left(1\right)\hfill \end{array}$$

Hence,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{h\left(\frac{1}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}\circ \tilde{F}\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)& {\supseteq }_F& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}\circ [{(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}\left(x\right))\left({\varsigma }_2\right)\oplus {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)\hfill \\ & {\supseteq }_F& [\tilde{F}\left({\varsigma }_1\right)\oplus \tilde{F}\left({\varsigma }_2\right)]\circ \left({}_{0}I_q^{\gamma }\left[{\displaystyle \frac{1}{h\left(\nu \right)}}+{\displaystyle \frac{1}{h(1-\nu )}}\right]\right)\left(1\right).\hfill \end{array}$$

□

Remark 2.

1.

If we replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{h\left(\nu \right)}}$ in Theorem 2, we obtain the results of in ([8], [Theorem 23]), i-e.,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{h\left(\frac{1}{2}\right){\mathsf{\Gamma }}_q(\gamma +1)}}\circ \tilde{F}\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)& {\supseteq }_F& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}\circ [{(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}\left(x\right))\left({\varsigma }_2\right)\oplus {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)\hfill \\ & {\supseteq }_F& [\tilde{F}\left({\varsigma }_1\right)\oplus \tilde{F}\left({\varsigma }_2\right)]\circ \left({}_{0}I_q^{\gamma }[h\left(\nu \right)+h(1-\nu )]\right)\left(1\right).\hfill \end{array}$$

2.

If we let $q\to 1^{-}$ and replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{h\left(\nu \right)}}$ in Theorem 2, then we get ([45], [Theorem 5]).

3.

If we replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{\nu }}$ and $q\to 1^{-}$ in Theorem 2, then we get ([33], [Theorem 3.1]).

4.

If we let $q\to 1^{-},\xi =1$ and replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{h\left(\nu \right)}}$ in Theorem 2, then we get ([31], [Theorem 3.4]).

5.

If we let $q\to 1^{-},\gamma =\xi =1$ and replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{h\left(\nu \right)}}$ in Theorem 2, then we get ([46], [Theorem 4.1]).

Theorem 7.

Let $\tilde{F},\tilde{G}\in \mathbf{SC}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right)).$ If $\tilde{F}\otimes \tilde{G}$ is RLF q-integrable on $[{\varsigma }_1,{\varsigma }_2],\tilde{F}\in UDSGX([{\varsigma }_1,{\varsigma }_2],F_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h_1}})$ and $\tilde{G}\in UDSGX([{\varsigma }_1,{\varsigma }_2],F_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h_2}})$, then

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}\circ ({(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}(x)\oplus \tilde{G}(x))({\varsigma }_2)\oplus {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}({\varsigma }_1+{\varsigma }_2-x)\otimes \tilde{G}({\varsigma }_1+{\varsigma }_2-x)({\varsigma }_2))\hfill \\ & {\supseteq }_F& T(\nu )\odot [\tilde{F}({\varsigma }_1)\otimes \tilde{G}({\varsigma }_1)\oplus \tilde{F}({\varsigma }_2)\otimes \tilde{G}({\varsigma }_2)]\oplus R(\nu )[\tilde{F}({\varsigma }_1)\otimes \tilde{G}({\varsigma }_2)\oplus \tilde{F}({\varsigma }_2)\otimes \tilde{G}({\varsigma }_1)],\hfill \end{array}$$

where

$$\begin{array}{c}\hfill T\left(\nu \right)=\left({}_{0}I_q^{\gamma }{\displaystyle \frac{1}{h_1\left(\nu \right)}}{\displaystyle \frac{1}{h_2\left(\nu \right)}}\right)\left(1\right)+\left({}_{0}I_q^{\gamma }{\displaystyle \frac{1}{h_1(1-\nu )}}{\displaystyle \frac{1}{h_2(1-\nu )}}\right)\left(1\right),\end{array}$$

(9)

and

$$\begin{array}{c}\hfill R\left(\nu \right)=\left({}_{0}I_q^{\gamma }{\displaystyle \frac{1}{h_1\left(\nu \right)}}{\displaystyle \frac{1}{h_2(1-\nu )}}\right)\left(1\right)+\left({}_{0}I_q^{\gamma }{\displaystyle \frac{1}{h_1(1-\nu )}}{\displaystyle \frac{1}{h_2\left(\nu \right)}}\right)\left(1\right).\end{array}$$

(10)

Proof. 

Derived from the stipulated conditions, one can deduce

$$\begin{array}{ccc}& & {\underline{f}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2){\underline{g}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)\hfill \\ & \le & \left({\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_1\right)}{h_1(1-\nu )}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_2\right)}{h_1\left(\nu \right)}}\right).\left({\displaystyle \frac{{\underline{g}}_{\xi }\left({\varsigma }_1\right)}{h_2(1-\nu )}}+{\displaystyle \frac{{\underline{g}}_{\xi }\left({\varsigma }_2\right)}{h_2\left(\nu \right)}}\right)\hfill \\ & =& {\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_1\right){\underline{g}}_{\xi }\left({\varsigma }_1\right)}{h_1(1-\nu )h_2(1-\nu )}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_2\right){\underline{g}}_{\xi }\left({\varsigma }_2\right)}{h_1\left(\nu \right)h_2\left(\nu \right)}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_1\right){\underline{g}}_{\xi }\left({\varsigma }_2\right)}{h_1(1-\nu )h_2\left(\nu \right)}}+{\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_2\right){\underline{g}}_{\xi }\left({\varsigma }_1\right)}{h_1\left(\nu \right)h_2(1-\nu )}}.\hfill \end{array}$$

The remaining proof follows from Theorem 6. □

Theorem 8.

Let $\tilde{F},\tilde{G}\in \mathbf{SC}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$ and $h_1\left({\displaystyle \frac{1}{2}}\right)h_2\left({\displaystyle \frac{1}{2}}\right)\ne 0.$ If $\tilde{F}\otimes \tilde{G}$ is RLF q-integrable on $[{\varsigma }_1,{\varsigma }_2],\tilde{F}\in UDSGX([{\varsigma }_1,{\varsigma }_2],F_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h_1}})$ and $\tilde{G}\in UDSGX([{\varsigma }_1,{\varsigma }_2],F_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h_2}})$, then

$$\begin{array}{ccc}& & {\displaystyle \frac{h_1(\frac{1}{2})h_2(\frac{1}{2})\tilde{F}(\frac{{\varsigma }_1+{\varsigma }_2}{2})\otimes \tilde{G}(\frac{{\varsigma }_1+{\varsigma }_2}{2})}{{\mathsf{\Gamma }}_q(\gamma +1)}}\hfill \\ & {\supseteq }_F& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}\circ ({(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}(x)\otimes \tilde{G}(x))({\varsigma }_2)\oplus {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}({\varsigma }_1+{\varsigma }_2-x)\otimes \tilde{G}({\varsigma }_1+{\varsigma }_2-x)({\varsigma }_2))\hfill \\ & \oplus & T(\nu )\odot [\tilde{F}({\varsigma }_1)\otimes \tilde{G}({\varsigma }_2)\oplus \tilde{F}({\varsigma }_2)\otimes \tilde{G}({\varsigma }_1)]\oplus R(\nu )[\tilde{F}({\varsigma }_1)\otimes \tilde{G}({\varsigma }_1)\oplus \tilde{F}({\varsigma }_2)\otimes \tilde{G}({\varsigma }_2)],\hfill \end{array}$$

where $T\left(\nu \right)$ and $R\left(\nu \right)$ defined as in (9) and (10), respectively.

Proof. 

By hypothesis, we have

$$h_1\left({\displaystyle \frac{1}{2}}\right)F_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right){\supseteq }_I{F}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)+F_{\xi }(\nu {\varsigma }_1+(1-\nu ){\varsigma }_2),$$

and

$$h_2\left({\displaystyle \frac{1}{2}}\right)G_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right){\supseteq }_I{G}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)+G_{\xi }(\nu {\varsigma }_1+(1-\nu ){\varsigma }_2).$$

Hence,

$$\begin{array}{ccc}& & h_1\left({\displaystyle \frac{1}{2}}\right)h_2\left({\displaystyle \frac{1}{2}}\right)F_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)G_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)\hfill \\ & {\supseteq }_I& F_{\xi }(\left(\nu \right){\varsigma }_1+(1-\nu ){\varsigma }_2)G_{\xi }(\left(\nu \right){\varsigma }_1+(1-\nu ){\varsigma }_2)+F_{\xi }(\left(\nu \right){\varsigma }_1+(1-\nu ){\varsigma }_2)G_{\xi }((1-\nu ){\varsigma }_1+\left(\nu \right){\varsigma }_2)\hfill \\ & +& F_{\xi }((1-\nu ){\varsigma }_1+\left(\nu \right){\varsigma }_2)G_{\xi }(\left(\nu \right){\varsigma }_1+(1-\nu ){\varsigma }_2)+F_{\xi }((1-\nu ){\varsigma }_1+\left(\nu \right){\varsigma }_2)G_{\xi }((1-\nu ){\varsigma }_1+\left(\nu \right){\varsigma }_2)\hfill \\ & {\supseteq }_I& F_{\xi }(\left(\nu \right){\varsigma }_1+(1-\nu ){\varsigma }_2)G_{\xi }(\left(\nu \right){\varsigma }_1+(1-\nu ){\varsigma }_2)+F_{\xi }((1-\nu ){\varsigma }_1+\left(\nu \right){\varsigma }_2)G_{\xi }((1-\nu ){\varsigma }_1+\left(\nu \right){\varsigma }_2)\hfill \\ & +& [F_{\xi }\left({\varsigma }_1\right)G_{\xi }\left({\varsigma }_2\right)+F_{\xi }\left({\varsigma }_2\right)G_{\xi }\left({\varsigma }_1\right)].\left[{\displaystyle \frac{1}{h_1\left(\nu \right)h_2\left(\nu \right)}}+{\displaystyle \frac{1}{h_1(1-\nu )h_2(1-\nu )}}\right]\hfill \\ & +& [F_{\xi }\left({\varsigma }_1\right)G_{\xi }\left({\varsigma }_1\right)+F_{\xi }\left({\varsigma }_2\right)G_{\xi }\left({\varsigma }_2\right)].\left[{\displaystyle \frac{1}{h_1\left(\nu \right)h_2(1-\nu )}}+{\displaystyle \frac{1}{h_1(1-\nu )h_2\left(\nu \right)}}\right].\hfill \end{array}$$

Using the technique in Theorem 6 and the theorem holds true. □

Now we shall derive some known results from our general result.

Remark 3.

1.

If we replace $h_1\left(\nu \right)$ by ${\displaystyle \frac{1}{h_1\left(\nu \right)}}$ and $h_2\left(\nu \right)$ by ${\displaystyle \frac{1}{h_2\left(\nu \right)}}$, and letting $q\to 1^{-}$ in Theorem 3 and Theorem 4, we obtain the results of ([45], [Theorem 6 and Theorem 7]), respectively.

2.

If we replace $h_1\left(\nu \right)$ by ${\displaystyle \frac{1}{h_1\left(\nu \right)}}$ and $h_2\left(\nu \right)$ by ${\displaystyle \frac{1}{h_2\left(\nu \right)}}$ in Theorem 3 and Theorem 4, we obtain the results of ([8], [Theorem 27 and Theorem 28]), respectively.

3.

If we replace $h_1\left(\nu \right)$ and $h_2\left(\nu \right)$ by ${\displaystyle \frac{1}{\nu }}$ in Theorem 3 and Theorem 4, we obtain ([33], [Theorems 3.4 and Theorem 3.6]), respectively.

4.

If we replace $h_1\left(\nu \right)$ and $h_2\left(\nu \right)$ by ${\displaystyle \frac{1}{\nu }}$, and letting $\xi =1$ in Theorem 3 and Theorem 4, we obtain ([31], [Theorems 3.5 and Theorem 3.6]), respectively.

5.

If we replace $h_1\left(\nu \right)$ by ${\displaystyle \frac{1}{h_1\left(\nu \right)}}$ and $h_2\left(\nu \right)$ by ${\displaystyle \frac{1}{h_2\left(\nu \right)}}$, and letting $\gamma =\xi =1$ and $q\to 1^{-}$ in Theorem 3 and Theorem 4, we obtain ([46], [Theorem 4.5 and Theorem 4.6]), respectively.

Theorem 9.

Let $\tilde{F}\in \mathbf{SC}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))\bigcap UDSGX([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h}})$ and $\varpi \in C([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}_0^{+})$ be symmetric with respect to ${\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}$ with ${}_{{\varsigma }_1}I_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)>0.$ If $\tilde{F}\left(x\right)\varpi \left(x\right)$ is RLF q-integrable on $[{\varsigma }_1,{\varsigma }_2]$, then

$$\begin{array}{ccc}\hfill \tilde{F}\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right){\supseteq }_{\mathbb{F}}{\displaystyle \frac{1}{h{\left(\frac{1}{2}\right)}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)}}& & \odot {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}\left(x\right)\odot \varpi \left(x\right))\left({\varsigma }_2\right)\hfill \\ & & \oplus {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}({\varsigma }_1+{\varsigma }_2+x)\odot \varpi ({\varsigma }_1+{\varsigma }_2+x))\left({\varsigma }_2\right).\hfill \end{array}$$

Proof. 

Since ${\underline{f}}_{\xi }\left(x\right)\in SGX([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}_0^{+},{\displaystyle \frac{1}{h}})$, we have

$$h\left({\displaystyle \frac{1}{2}}\right){\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)\le {\underline{f}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)+{\underline{f}}_{\xi }((1-\nu ){\varsigma }_2+\nu {\varsigma }_1).$$

Multiply both sides by ${\displaystyle \frac{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}\varpi ((1-\nu ){\varsigma }_1+{\varsigma }_2)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}$ and q-integrating over $[0,1]$. We have

$$\begin{array}{ccc}& & {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}\varpi {((1-\nu ){\varsigma }_1+{\varsigma }_2)}_0{d}_q\nu \hfill \\ & \le & {\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}{\underline{f}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)\varpi {((1-\nu ){\varsigma }_1+{\varsigma }_2)}_0{d}_q\nu \hfill \\ & +& {\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}{\underline{f}}_{\xi }((1-\nu ){\varsigma }_2+\nu {\varsigma }_1)\varpi {((1-\nu ){\varsigma }_1+{\varsigma }_2)}_0{d}_q\nu .\hfill \end{array}$$

Let us say

$$\begin{array}{c}\hfill K_1\le K_2+K_3.\end{array}$$

(11)

First, we solve $K_1$ by using Proposition 3, Lemma 1, Definition 12, and Definition 13. We have

$$\begin{array}{ccc}\hfill K_1& =& {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}{\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}\varpi {((1-\nu ){\varsigma }_1+{\varsigma }_2)}_0{d}_q\nu \hfill \\ & =& {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right).\hfill \end{array}$$

Similarly,

$$\begin{array}{ccc}\hfill K_2& =& {\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}{\underline{f}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)\varpi {((1-\nu ){\varsigma }_1+{\varsigma }_2)}_0{d}_q\nu \hfill \\ & =& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill K_3& =& {\int }_0^1{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)}_q^{(\gamma -1)}{\underline{f}}_{\xi }((1-\nu ){\varsigma }_2+\nu {\varsigma }_1)\varpi {((1-\nu ){\varsigma }_1+{\varsigma }_2)}_0{d}_q\nu \hfill \\ & =& {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right).\hfill \end{array}$$

Putting the values of $K_1,K_2$, and $K_3$ in (11), we get

$$\begin{array}{ccc}& & {\displaystyle \frac{h\left(\frac{1}{2}\right){\underline{f}}_{\xi }\left(\frac{{\varsigma }_1+{\varsigma }_2}{2}\right)}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)\hfill \\ & \le & {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right).\hfill \end{array}$$

$$h\left({\displaystyle \frac{1}{2}}\right){\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right){(}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)\le {(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right).$$

Similarly,

$$h\left({\displaystyle \frac{1}{2}}\right){\overline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right){(}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)\le {(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right).$$

So, we have

$$\begin{array}{ccc}& & [{\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right),{\overline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)]\hfill \\ & {\supseteq }_I& {\displaystyle \frac{1}{h\left(\frac{1}{2}\right){(}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)}}[{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right),\hfill \\ & & {(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)].\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \tilde{F}\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right){\supseteq }_{\mathbb{F}}{\displaystyle \frac{1}{h{\left(\frac{1}{2}\right)}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)}}& & \odot {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}\left(x\right)\odot \varpi \left(x\right))\left({\varsigma }_2\right)\hfill \\ & & \oplus {(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}({\varsigma }_1+{\varsigma }_2+x)\odot \varpi ({\varsigma }_1+{\varsigma }_2+x))\left({\varsigma }_2\right).\hfill \end{array}$$

□

Theorem 10.

Let $\tilde{F}\in \mathbf{SC}([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))\bigcap UDSGX([{\varsigma }_1,{\varsigma }_2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right),{\displaystyle \frac{1}{h}})$ and $\varpi \in C([{\varsigma }_1,{\varsigma }_2],{\mathbb{R}}_0^{+})$ be symmetric with respect to ${\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}$ with ${}_{{\varsigma }_1}I_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)>0.$ If $\tilde{F}\left(x\right)\varpi \left(x\right)$ is RLF q-integrable on $[{\varsigma }_1,{\varsigma }_2]$, then

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}\odot ({(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}\left(x\right)\odot \varpi \left(x\right))\left({\varsigma }_2\right)& & \oplus ({(}_{{\varsigma }_1}{I}_q^{\gamma }\tilde{F}({\varsigma }_1+{\varsigma }_2-x)\odot \varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right)\hfill \\ & & {\supseteq }_{\mathbb{F}}[\tilde{F}\left({\varsigma }_1\right)\oplus \tilde{F}\left({\varsigma }_2\right)]\odot M\left(\nu \right),\hfill \end{array}$$

where $M\left(\nu \right)={(}_0{I}_q^{\gamma }\varpi (\nu {\varsigma }_1+(1-\nu ){\varsigma }_2)[{\displaystyle \frac{1}{h(1-\nu )}}+{\displaystyle \frac{1}{h\left(\nu \right)}}])\left(1\right).$

Proof. 

According to the given condition, we have

$$\begin{array}{ccc}& & {\underline{f}}_{\xi }(\nu {\varsigma }_1+(1-\nu ){\varsigma }_2)\varpi (\nu {\varsigma }_1+(1-\nu ){\varsigma }_2)\hfill \\ & \le & [{\displaystyle \frac{1}{h\left(\nu \right)}}{\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\displaystyle \frac{1}{h(1-\nu )}}{\underline{f}}_{\xi }\left({\varsigma }_2\right)]\varpi (\nu {\varsigma }_1+(1-\nu ){\varsigma }_2),\hfill \end{array}$$

(12)

and

$$\begin{array}{ccc}& & {\underline{f}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)\varpi ((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)\hfill \\ & \le & [{\displaystyle \frac{1}{h\left(\nu \right)}}{\underline{f}}_{\xi }\left({\varsigma }_2\right)+{\displaystyle \frac{1}{h(1-\nu )}}{\underline{f}}_{\xi }\left({\varsigma }_1\right)]\varpi ((1-\nu ){\varsigma }_1+\nu {\varsigma }_2).\hfill \end{array}$$

(13)

Adding (12) and (13),

$$\begin{array}{ccc}& & {\underline{f}}_{\xi }(\nu {\varsigma }_1+(1-\nu ){\varsigma }_2)\varpi (\nu {\varsigma }_1+(1-\nu ){\varsigma }_2)+{\underline{f}}_{\xi }((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)\varpi ((1-\nu ){\varsigma }_1+\nu {\varsigma }_2)\hfill \\ & \le & [{\displaystyle \frac{1}{h\left(\nu \right)}}{\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\displaystyle \frac{1}{h(1-\nu )}}{\underline{f}}_{\xi }\left({\varsigma }_2\right)]\varpi (\nu {\varsigma }_1+(1-\nu ){\varsigma }_2)\hfill \\ & +& [{\displaystyle \frac{1}{h\left(\nu \right)}}{\underline{f}}_{\xi }\left({\varsigma }_2\right)+{\displaystyle \frac{1}{h(1-\nu )}}{\underline{f}}_{\xi }\left({\varsigma }_1\right)]\varpi ((1-\nu ){\varsigma }_1+\nu {\varsigma }_2).\hfill \end{array}$$

Multiply both sides by ${\displaystyle \frac{{}_0\left(1{-}_0{\mathsf{\Omega }}_q\left(\nu \right)\right)_q^{(\gamma -1)}}{{\mathsf{\Gamma }}_q\left(\gamma \right)}}$; the remaining proof is similar to Theorem 5, making the result self-evident. □

Remark 4.

1.

If we replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{h\left(\nu \right)}}$ in Theorem 5 and Theorem 6, then we have ([8], [Theorem 30 and Theorem 31]), respectively.

2.

If we replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{h\left(\nu \right)}}$, and letting $q\to 1^{-}$ in Theorem 5 and Theorem 6, then we have ([45], [Theorem 9 and Theorem 8]), respectively

3.

If we replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{\nu }}$, and letting $q\to 1^{-}$ in Theorem 5 and Theorem 6, we have ([33], [Theorem 3.8 and Theorem 3.7]), respectively.

4.

If we let $\xi =1$ and replace $h\left(\nu \right)$ by ${\displaystyle \frac{1}{h\left(\nu \right)}}$ in Theorem 5 and Theorem 6, we obtain ([44], [Theorems 3.14 and Theorem 3.15]), respectively.

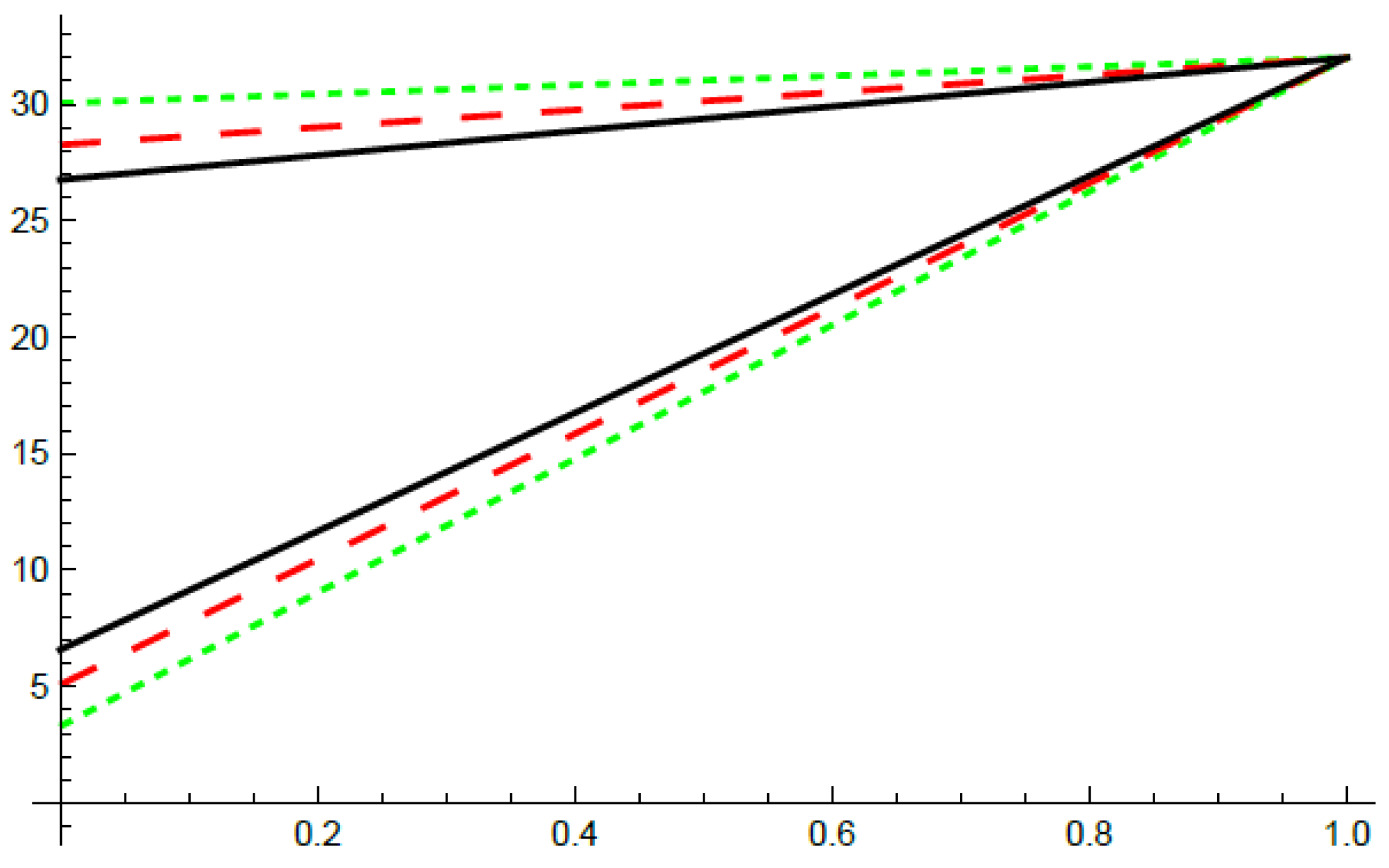
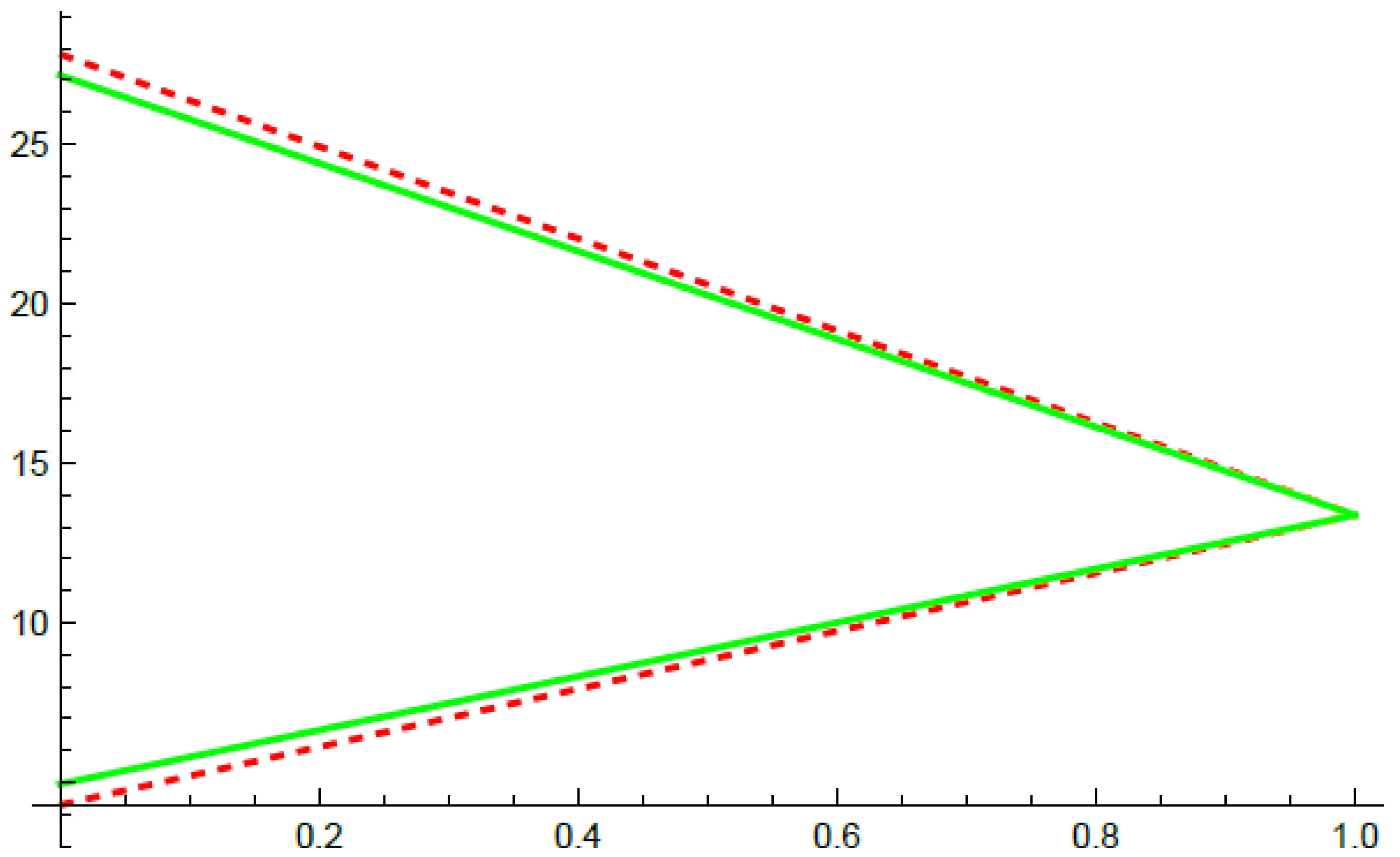
4. Numerical Examples

Example 1.

Let $\tilde{F}\in \mathbf{SC}([0,\pi ],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$ and ξ-levels of $\tilde{F}$ be given by $F_{\xi }\left(x\right)=[(1-\xi )x^2+24\xi ,(1-\xi )(25-x^2)+24\xi ]$ for all $\xi \in [0,1]$ and for all $x\in [{\varsigma }_1,{\varsigma }_2],h\left(\nu \right)={\displaystyle \frac{1}{\nu }},$ for $\nu \in (0,1)$. Obviously, $\tilde{F}\left(x\right)$ satisfies the assumptions in Theorem 2. If we let $q={\displaystyle \frac{1}{2}}$ and $\gamma =2$, then

$$\begin{array}{ccc}\hfill {\displaystyle \frac{h\left(\frac{1}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}{\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)& =& {\displaystyle \frac{2}{{\mathsf{\Gamma }}_{\frac{1}{2}}\left(3\right)}}{\underline{f}}_{\xi }\left({\displaystyle \frac{0+\pi }{2}}\right)\hfill \\ & =& {\displaystyle \frac{(1-\xi ){\pi }^2}{3}}+32\xi .\hfill \end{array}$$

Secondly,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{h\left(\frac{1}{2}\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}{\overline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)& =& {\displaystyle \frac{2}{{\mathsf{\Gamma }}_{\frac{1}{2}\left(3\right)}}}{\overline{f}}_{\xi }\left({\displaystyle \frac{0+\pi }{2}}\right)\hfill \\ & =& (1-\xi ){\displaystyle \frac{100-{\pi }^2}{3}}+32\xi ,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}& =& {\displaystyle \frac{{\underline{f}}_{\xi }\left(0\right)+{\underline{f}}_{\xi }\left(\pi \right)}{{\mathsf{\Gamma }}_{\frac{1}{2}}\left(3\right)}}\hfill \\ & =& {\displaystyle \frac{24\xi +(1-\xi ){\pi }^2+24\xi }{\frac{3}{2}}}\hfill \\ & =& {\displaystyle \frac{2(1-\xi ){\pi }^2}{3}}+32\xi .\hfill \end{array}$$

Next,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\overline{f}}_{\xi }\left({\varsigma }_1\right)+{\overline{f}}_{\xi }\left({\varsigma }_2\right)}{{\mathsf{\Gamma }}_q(\gamma +1)}}& =& {\displaystyle \frac{{\overline{f}}_{\xi }\left(0\right)+{\overline{f}}_{\xi }\left(\pi \right)}{{\mathsf{\Gamma }}_{\frac{1}{2}}\left(3\right)}}\hfill \\ & =& {\displaystyle \frac{(1-\xi )25+24\xi +(1-\xi )(25-{\pi }^2)+24\xi }{\frac{3}{2}}}\hfill \\ & =& {\displaystyle \frac{2(1-\xi )(50-{\pi }^2)}{3}}+32\xi ,\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}({(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+\left({(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1-{\varsigma }_2-x))\left({\varsigma }_2\right)\right)\hfill \\ & =& {\displaystyle \frac{{(}_1{I}_{\frac{1}{2}}^2{\underline{f}}_{\xi }\left(x\right))\left(\pi \right)+{(}_1{I}_{\frac{1}{2}}^2{\underline{f}}_{\xi }(0-\pi -x))\left(\pi \right)}{{(\pi -0)}^2}}\hfill \\ & =& {\displaystyle \frac{54{\pi }^2}{105}}(1-\xi )+32\xi .\hfill \end{array}$$

Also,

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}({(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+\left({(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }({\varsigma }_1-{\varsigma }_2-x))\left({\varsigma }_2\right)\right)\hfill \\ & =& {\displaystyle \frac{{(}_1{I}_{\frac{1}{2}}^2{\overline{f}}_{\xi }\left(x\right))\left(\pi \right)+{(}_1{I}_{\frac{1}{2}}^2{\overline{f}}_{\xi }(0-\pi -x))\left(\pi \right)}{{(\pi -0)}^2}}\hfill \\ & =& {\displaystyle \frac{-54{\pi }^2+3500}{105}}(1-\xi )+32\xi .\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill [{\displaystyle \frac{(1-\xi ){\pi }^2}{3}}+32\xi ,(1-\xi ){\displaystyle \frac{100-{\pi }^2}{3}}+32\xi ]{\supseteq }_I[{\displaystyle \frac{54{\pi }^2}{105}}(1-\xi )+32\xi ,{\displaystyle \frac{-54{\pi }^2+3500}{105}}(1-\xi )+32\xi ]\end{array}$$

$$\begin{array}{c}\hfill {\supseteq }_I[{\displaystyle \frac{2(1-\xi ){\pi }^2}{3}}+32\xi ,{\displaystyle \frac{2(1-\xi )(50-{\pi }^2)}{3}}+32\xi ].\end{array}$$

(14)

As shown in Figure 1, the green chain line represents $F\left(\xi \right)$, where $\underline{f}\left(\xi \right)={\displaystyle \frac{(1-\xi ){\pi }^2}{3}}+32\xi ,$ and $\overline{f}\left(\xi \right)=(1-\xi ){\displaystyle \frac{100-{\pi }^2}{3}}+32\xi ,\xi \in [0,1]$. The dashed red line represents $G\left(\xi \right)$, where $\underline{g}\left(\xi \right)={\displaystyle \frac{54{\pi }^2}{105}}(1-\xi )+32\xi ,$ and $\overline{g}\left(\xi \right)={\displaystyle \frac{-54{\pi }^2+3500}{105}}(1-\xi )+32\xi ,\xi \in [0,1].$ The solid black line represents $H\left(\xi \right)$, where $\underline{h}\left(\xi \right)={\displaystyle \frac{2(1-\xi ){\pi }^2}{3}}+32\xi ,$ and $\overline{f}\left(\xi \right)={\displaystyle \frac{2(1-\xi )(50-{\pi }^2)}{3}}+32\xi ,\xi \in [0,1].$

Example 2.

Choose $h_1\left(\nu \right)=h_2\left(\nu \right)={\displaystyle \frac{1}{\nu }}$ for $\nu \in (0,1).$ Let $\tilde{F},\tilde{G}\in \mathbf{SC}([0,2],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$ and ξ-levels of $\tilde{F},\tilde{G}$ be given by $F_{\xi }\left(x\right)=[(1-\xi )x^2+5\xi ,(1-\xi )(10-x^2)+5\xi ]$ and $G_{\xi }\left(x\right)=[(1-\xi )x^2+5\xi ,(1-\xi )(12-x^2)+5\xi ]$ for all $\xi \in [0,1]$ and for all $x\in [{\varsigma }_1,{\varsigma }_2]$, respectively, since $\tilde{F}\left(x\right)$ and $\tilde{G}\left(x\right)$ satisfy the assumptions of Theorems 3 and 4. Choose $q={\displaystyle \frac{1}{2}}$ and $\gamma =2$. Then we have $T\left(\nu \right)={\displaystyle \frac{18}{35}}$ and $R\left(\nu \right)={\displaystyle \frac{16}{105}}.$

$${\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right){\underline{g}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)={(1-\xi )}^2+10\xi (1-\xi )+25{\xi }^2,$$

$${\overline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right){\overline{g}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)=99{(1-\xi )}^2+100\xi (1-\xi )+25{\xi }^2,$$

$${\underline{f}}_{\xi }\left({\varsigma }_1\right){\underline{g}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right){\underline{g}}_{\xi }\left({\varsigma }_2\right)=16{(1-\xi )}^2+40\xi (1-\xi )+50{\xi }^2,$$

$${\underline{f}}_{\xi }\left({\varsigma }_1\right){\underline{g}}_{\xi }\left({\varsigma }_2\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right){\underline{g}}_{\xi }\left({\varsigma }_1\right)=40\xi (1-\xi )+50{\xi }^2,$$

$${\overline{f}}_{\xi }\left({\varsigma }_1\right){\overline{g}}_{\xi }\left({\varsigma }_1\right)+{\overline{f}}_{\xi }\left({\varsigma }_2\right){\overline{g}}_{\xi }\left({\varsigma }_2\right)=168{(1-\xi )}^2+180\xi (1-\xi )+50{\xi }^2,$$

$${\overline{f}}_{\xi }\left({\varsigma }_1\right){\overline{g}}_{\xi }\left({\varsigma }_2\right)+{\overline{f}}_{\xi }\left({\varsigma }_2\right){\overline{g}}_{\xi }\left({\varsigma }_1\right)=152{(1-\xi )}^2+180\xi (1-\xi )+50{\xi }^2.$$

Since

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}({(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right){\underline{g}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+\left({(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1-{\varsigma }_2-x){\underline{g}}_{\xi }({\varsigma }_1-{\varsigma }_2-x))\left({\varsigma }_2\right)\right)\hfill \\ & =& {\displaystyle \frac{61664}{9765}}{(1-\xi )}^2+{\displaystyle \frac{144}{7}}\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2,\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{{({\varsigma }_2-{\varsigma }_1)}^{\gamma }}}({(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }\left(x\right){\overline{g}}_{\xi }\left(x\right))\left({\varsigma }_2\right)+\left({(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }({\varsigma }_1-{\varsigma }_2-x){\overline{g}}_{\xi }({\varsigma }_1-{\varsigma }_2-x))\left({\varsigma }_2\right)\right)\hfill \\ & =& {\displaystyle \frac{1182128}{9765}}{(1-\xi )}^2+{\displaystyle \frac{2648}{21}}\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2.\hfill \end{array}$$

So, we get

$$\begin{array}{c}\hfill [{\displaystyle \frac{61664}{9765}}{(1-\xi )}^2+{\displaystyle \frac{144}{7}}\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2,{\displaystyle \frac{1182128}{9765}}{(1-\xi )}^2+{\displaystyle \frac{2648}{21}}\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2]\end{array}$$

$$\begin{array}{c}\hfill {\supseteq }_I[{\displaystyle \frac{288}{35}}{(1-\xi )}^2+{\displaystyle \frac{80}{3}}\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2,{\displaystyle \frac{11504}{105}}{(1-\xi )}^2+120\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2].\end{array}$$

(15)

As shown in Figure 2, the dashed red line represents $F\left(\xi \right)$, where $\underline{f}\left(\xi \right)={\displaystyle \frac{61664}{9765}}{(1-\xi )}^2+{\displaystyle \frac{144}{7}}\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2$ and $\overline{f}\left(\xi \right)={\displaystyle \frac{1182128}{9765}}{(1-\xi )}^2+{\displaystyle \frac{2648}{21}}\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2.$ The solid blue line represents $G\left(\xi \right)$, where $\underline{g}\left(\xi \right)={\displaystyle \frac{288}{35}}{(1-\xi )}^2+{\displaystyle \frac{80}{3}}\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2$ and $\overline{g}\left(\xi \right)={\displaystyle \frac{11504}{105}}{(1-\xi )}^2+120\xi (1-\xi )+{\displaystyle \frac{100}{3}}{\xi }^2.$

Also,

$$\begin{array}{c}\hfill [{\displaystyle \frac{8}{3}}{(1-\xi )}^2+{\displaystyle \frac{80}{3}}\xi (1-\xi )+{\displaystyle \frac{200}{3}}{\xi }^2,264{(1-\xi )}^2+{\displaystyle \frac{800}{3}}\xi (1-\xi )+{\displaystyle \frac{200}{3}}{\xi }^2]\end{array}$$

$$\begin{array}{c}\hfill {\supseteq }_I[{\displaystyle \frac{85472}{9765}}{(1-\xi )}^2+{\displaystyle \frac{992}{21}}\xi (1-\xi )+{\displaystyle \frac{200}{3}}{\xi }^2,{\displaystyle \frac{2195456}{9765}}{(1-\xi )}^2+{\displaystyle \frac{5168}{21}}\xi (1-\xi )+{\displaystyle \frac{200}{3}}{\xi }^2].\end{array}$$

(16)

As shown in Figure 3, the dashed red line represents $F\left(\xi \right)$, where $\underline{f}\left(\xi \right)={\displaystyle \frac{8}{3}}{(1-\xi )}^2+{\displaystyle \frac{80}{3}}\xi (1-\xi )+{\displaystyle \frac{200}{3}}{\xi }^2$ and $\overline{f}\left(\xi \right)=264{(1-\xi )}^2+{\displaystyle \frac{800}{3}}\xi (1-\xi )+{\displaystyle \frac{200}{3}}{\xi }^2.$ The solid black line represents $G\left(\xi \right)$, where $\underline{g}\left(\xi \right)={\displaystyle \frac{85472}{9765}}{(1-\xi )}^2+{\displaystyle \frac{992}{21}}\xi (1-\xi )+{\displaystyle \frac{200}{3}}{\xi }^2$ and $\overline{g}\left(\xi \right)={\displaystyle \frac{2195456}{9765}}{(1-\xi )}^2+{\displaystyle \frac{5168}{21}}\xi (1-\xi )+{\displaystyle \frac{200}{3}}{\xi }^2.$

Example 3.

Let $\tilde{F}\in \mathbf{SC}([0,e],{\mathcal{F}}_{\mathcal{C}}\left(\mathbb{R}\right))$ and ξ-levels of $\tilde{F}$ be given by $F_{\xi }\left(x\right)=[(1-\xi )x^2+10\xi ,(1-\xi )(24-x^2)+10\xi ]$ for all $\xi \in [0,1]$ and for all $x\in [{\varsigma }_1,{\varsigma }_2],h\left(\nu \right)={\displaystyle \frac{1}{\nu }},$ for $\nu \in (0,1)$. Obviously, $\tilde{F}\left(x\right)$ satisfies the assumptions in Theorems 5 and 6. If we choose $q={\displaystyle \frac{1}{2}}$, $\gamma =2$ and $\varpi \left(x\right)={(x-{\displaystyle \frac{e}{2}})}^2,$ we have

$${\underline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)={\displaystyle \frac{e^2}{4}}(1-\xi )+10\xi ,$$

$${\overline{f}}_{\xi }\left({\displaystyle \frac{{\varsigma }_1+{\varsigma }_2}{2}}\right)={\displaystyle \frac{96-e^2}{4}}(1-\xi )+10\xi ,$$

$${(}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)={(}_0{I}_q^{\gamma }{(x-{\displaystyle \frac{e}{2}})}^2)\left(e\right)={\displaystyle \frac{19e^4}{210}},$$

$${\displaystyle \frac{1}{h\left(\frac{1}{2}\right){(}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)}}({(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right))$$

$$={\displaystyle \frac{1232e^2-2568e+3534}{1767}}(1-\xi )+10\xi ,$$

$${\displaystyle \frac{1}{h\left(\frac{1}{2}\right){(}_{{\varsigma }_1}{I}_q^{\gamma }\varpi \left(x\right))\left({\varsigma }_2\right)}}({(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right))$$

$$={\displaystyle \frac{38874-1232e^2+2568e}{1767}}(1-\xi )+10\xi ,$$

$$\begin{array}{c}\hfill [{\displaystyle \frac{e^2}{4}}(1-\xi )+10\xi ,{\displaystyle \frac{96-e^2}{4}}(1-\xi )+10\xi ]\end{array}$$

$$\begin{array}{c}\hfill {\supseteq }_I[{\displaystyle \frac{1232e^2-2568e+3534}{1767}}(1-\xi )+10\xi ,{\displaystyle \frac{38874-1232e^2+2568e}{1767}}(1-\xi )+10\xi ]\end{array}$$

(17)

As shown in Figure 4, the dashed green line represents $F\left(\xi \right)$, where $\underline{f}\left(\xi \right)={\displaystyle \frac{e^2}{4}}(1-\xi )+10\xi$ and $\overline{f}\left(\xi \right)={\displaystyle \frac{96-e^2}{4}}(1-\xi )+10\xi ,\xi \in [0,1].$ The solid blue line represents $G\left(\xi \right)$, where $\underline{g}\left(\xi \right)={\displaystyle \frac{1232e^2-2568e+3534}{1767}}(1-\xi )+10\xi$ and $\overline{g}\left(\xi \right)={\displaystyle \frac{38874-1232e^2+2568e}{1767}}(1-\xi )+10\xi ,\xi \in [0,1].$

Also,

$${\displaystyle \frac{1}{{({\varsigma }_1-{\varsigma }_2)}^2}}({(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\underline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right))$$

$$={\displaystyle \frac{1232e^4-2568e^3+3534e^2}{9765}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ,$$

$${\displaystyle \frac{1}{{({\varsigma }_1-{\varsigma }_2)}^2}}({(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }\left(x\right)\varpi \left(x\right))\left({\varsigma }_2\right)+{(}_{{\varsigma }_1}{I}_q^{\gamma }{\overline{f}}_{\xi }({\varsigma }_1+{\varsigma }_2-x)\varpi ({\varsigma }_1+{\varsigma }_2-x))\left({\varsigma }_2\right))$$

$$={\displaystyle \frac{38874e^2-1232e^4+2568e^3}{9765}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ,$$

$$[{\underline{f}}_{\xi }\left({\varsigma }_1\right)+{\underline{f}}_{\xi }\left({\varsigma }_2\right)]M\left(\nu \right)={\displaystyle \frac{19e^4}{210}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ,$$

$$[{\overline{f}}_{\xi }\left({\varsigma }_1\right)+{\overline{f}}_{\xi }\left({\varsigma }_2\right)]M\left(\nu \right)={\displaystyle \frac{912e^2-19e^4}{210}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ,$$

$$\begin{array}{c}\hfill [{\displaystyle \frac{1232e^4-2568e^3+3534e^2}{9765}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ,{\displaystyle \frac{38874e^2-1232e^4+2568e^3}{9765}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ]\end{array}$$

$$\begin{array}{c}\hfill {\supseteq }_I[{\displaystyle \frac{19e^4}{210}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ,{\displaystyle \frac{912e^2-19e^4}{210}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ].\end{array}$$

(18)

As shown in Figure 5, the dashed red line represents $F\left(\xi \right)$, where $\underline{f}\left(\xi \right)={\displaystyle \frac{1232e^4-2568e^3+3534e^2}{9765}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi$ and $\overline{f}\left(\xi \right)={\displaystyle \frac{38874e^2-1232e^4+2568e^3}{9765}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ,\xi \in [0,1].$ The solid green line represents $G\left(\xi \right)$, where $\underline{g}\left(\xi \right)={\displaystyle \frac{19e^4}{210}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi$ and $\overline{g}\left(\xi \right)={\displaystyle \frac{912e^2-19e^4}{210}}(1-\xi )+{\displaystyle \frac{38e^2}{21}}\xi ,\xi \in [0,1].$

5. Conclusions

In this paper, we successfully extended Hermite–Hadamard and Hermite–Hadamard–Fejér inequalities to the setting of fuzzy interval-valued functions possessing h-Godunova–Levin convexity by employing the Riemann–Liouville fractional q-integral operator. Through rigorous analysis, we derived new inclusion relations and demonstrated that the proposed inequalities generalize several existing results. Numerical examples and visual graphs were provided to illustrate the validity and sharpness of the obtained results. This work not only broadens the scope of convexity and integral inequalities into the fuzzy setting but also highlights the potential of fractional q-calculus in addressing problems involving uncertainty and imprecision. Future research may focus on exploring related inequalities under different fractional operators or extending these results to more generalized convex structures.