Fractal Properties of the Cosmic Web
Abstract
1. Introduction
2. Basics of the Concordant CDM Universe
3. A Short History of the Fractal Studies of the Cosmic Web
3.1. Angular Distribution of Galaxies
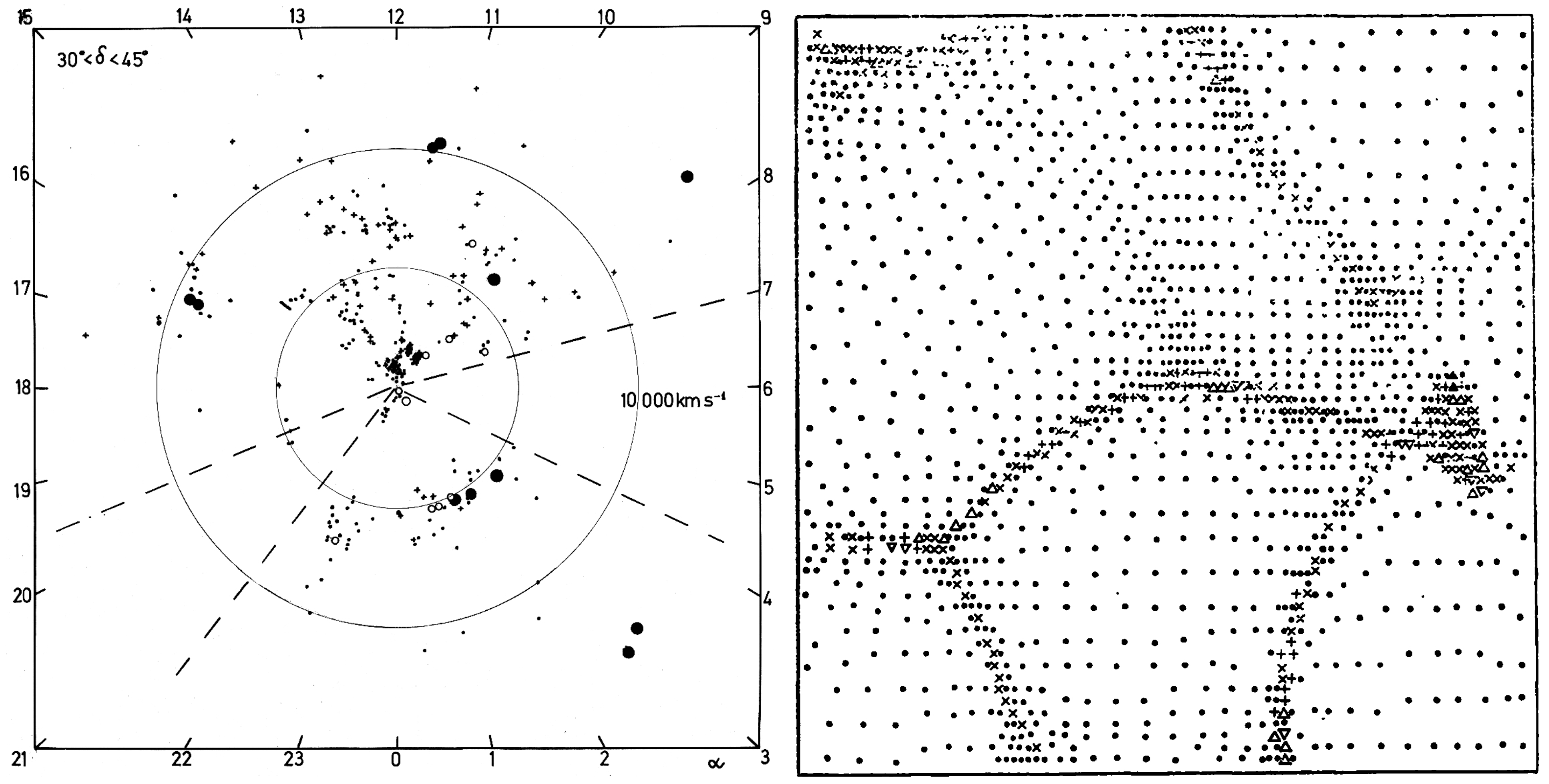
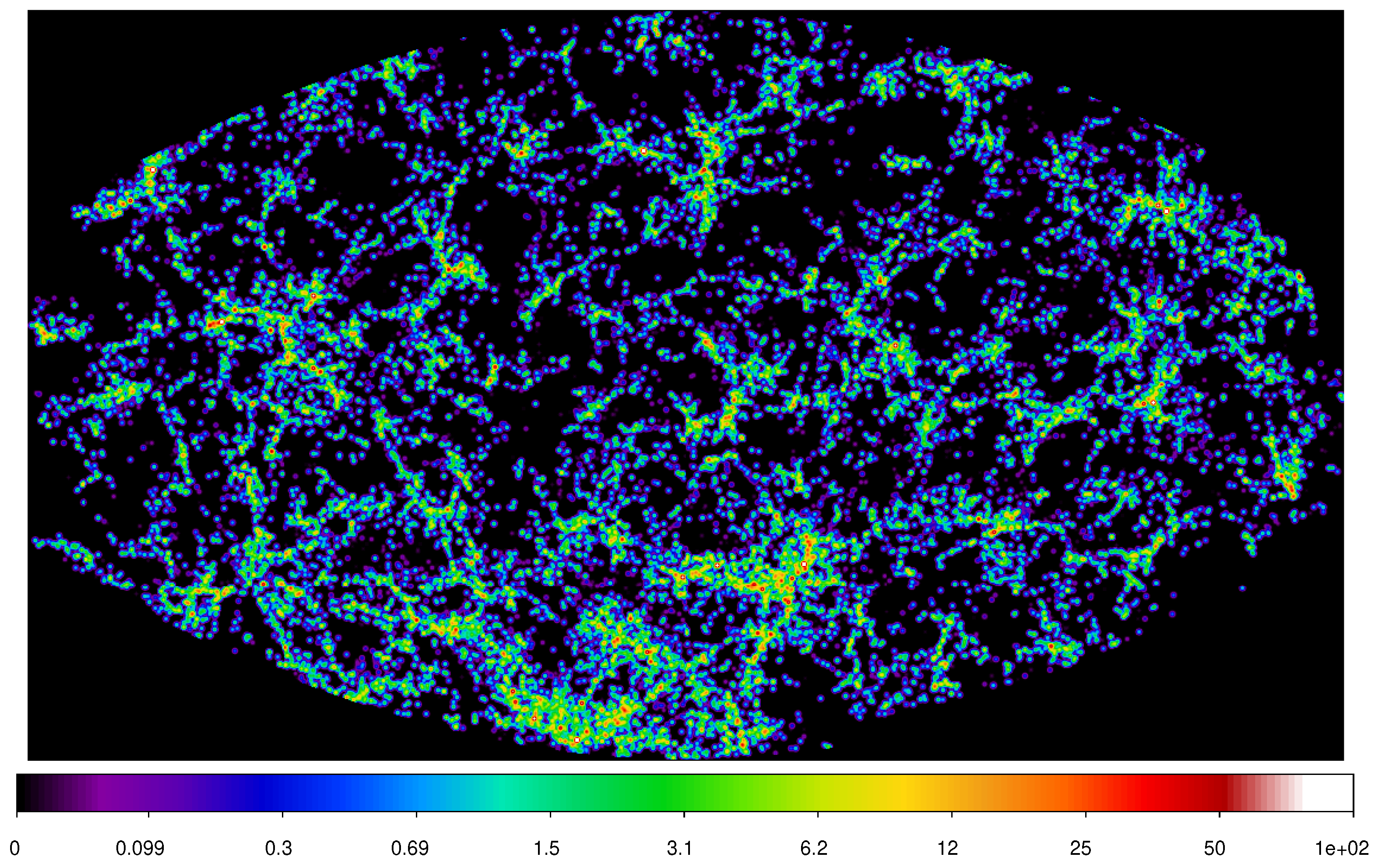
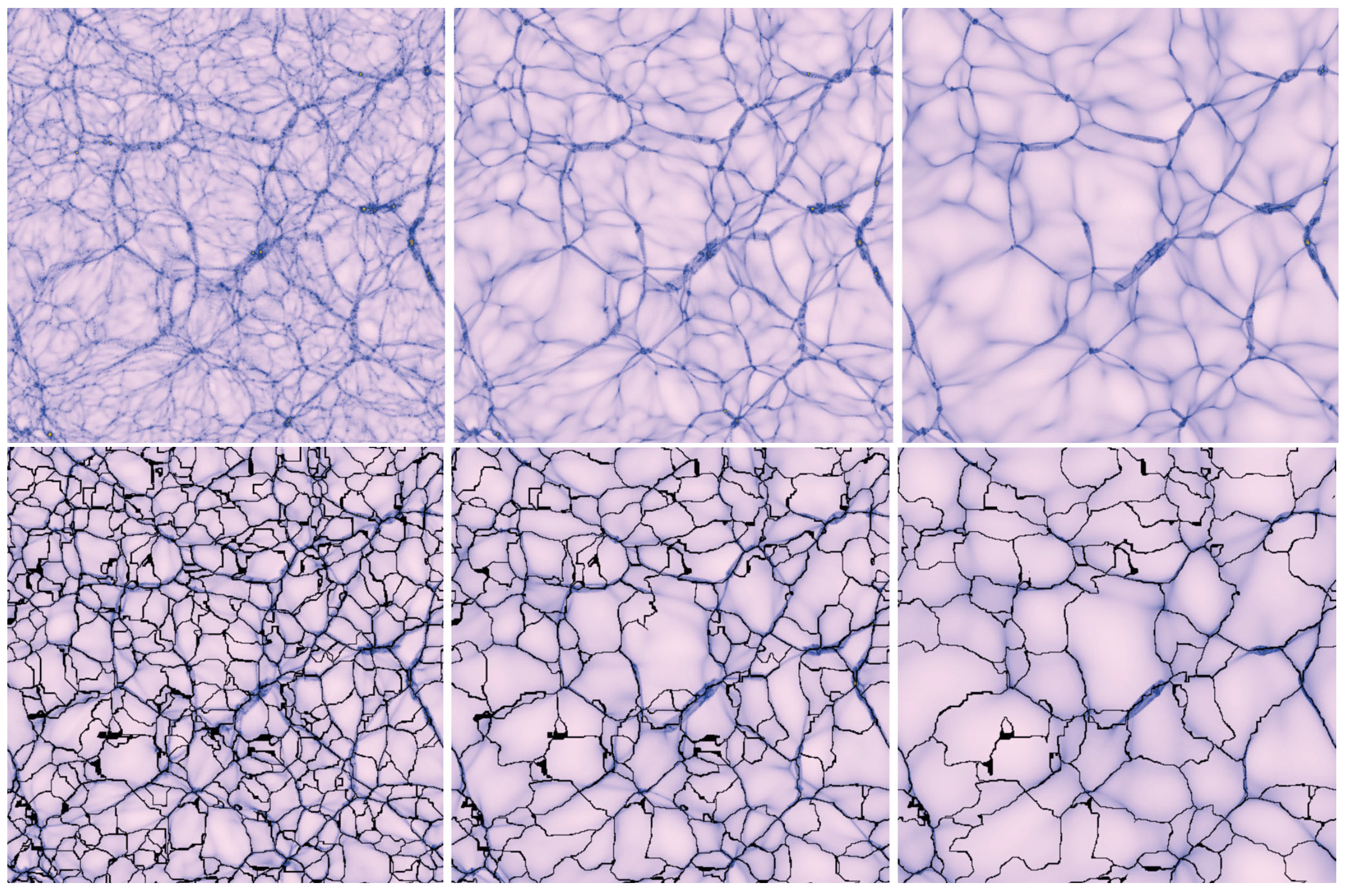
3.2. Discovery of the Cosmic Web
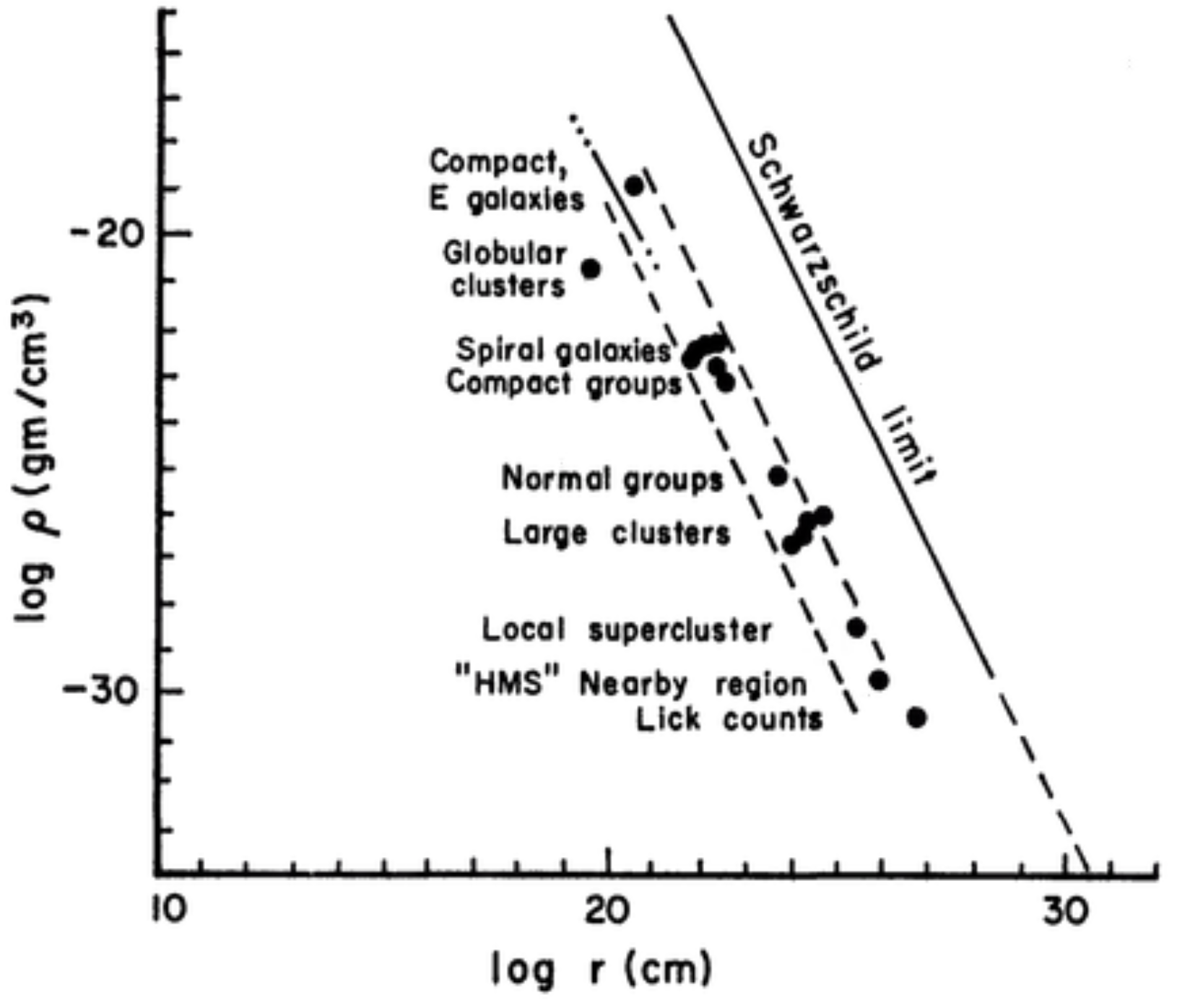
3.3. Discussion of the Fractal Character of the Cosmic Web
4. Statistics of Galaxy Clustering
4.1. Measuring Spatial Distribution of Galaxies
4.2. Measuring the Correlation Function
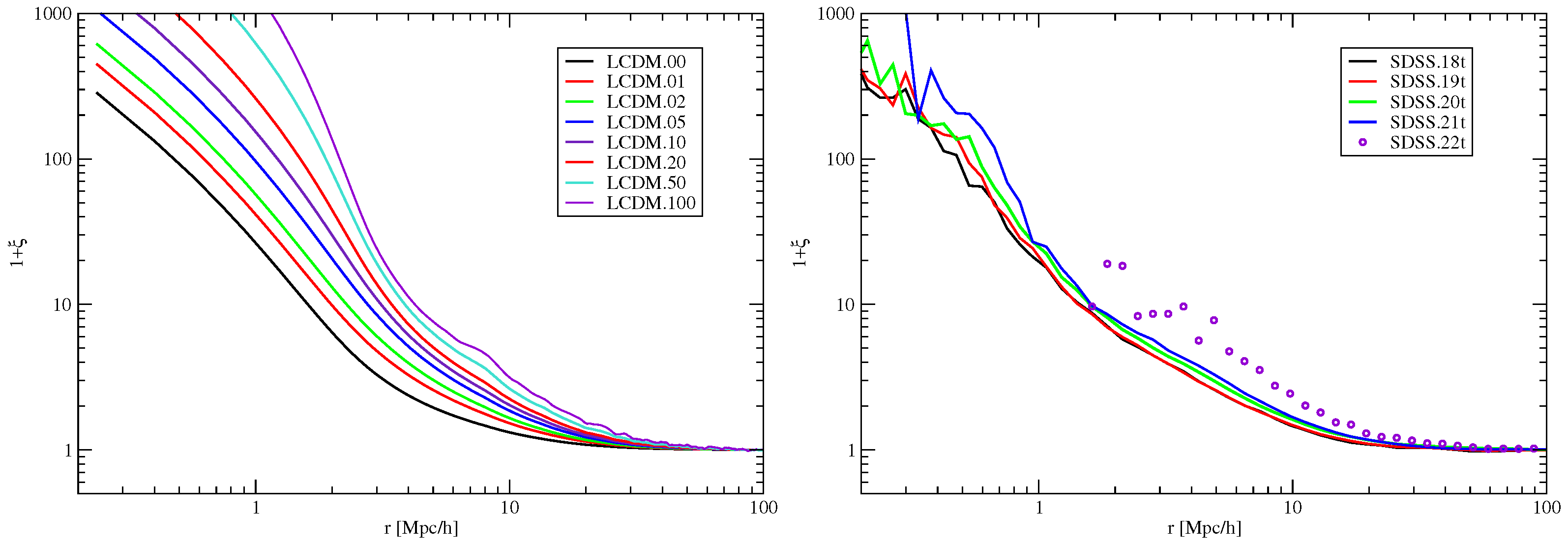
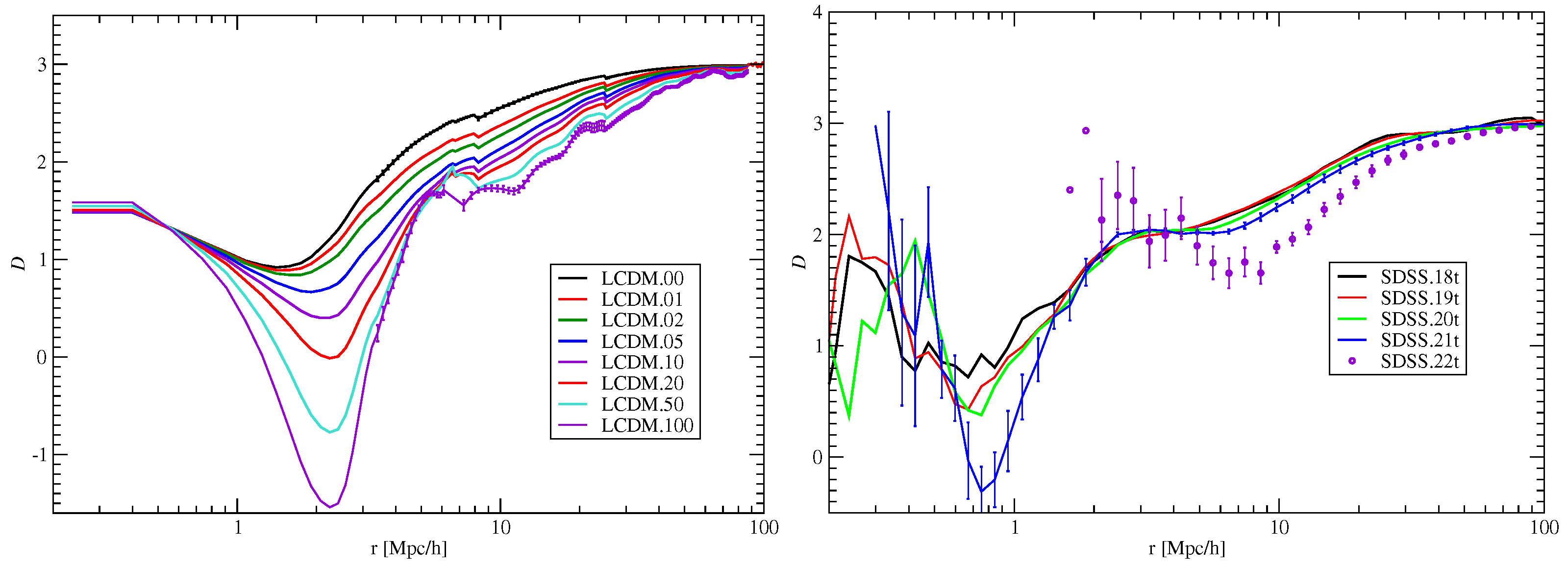
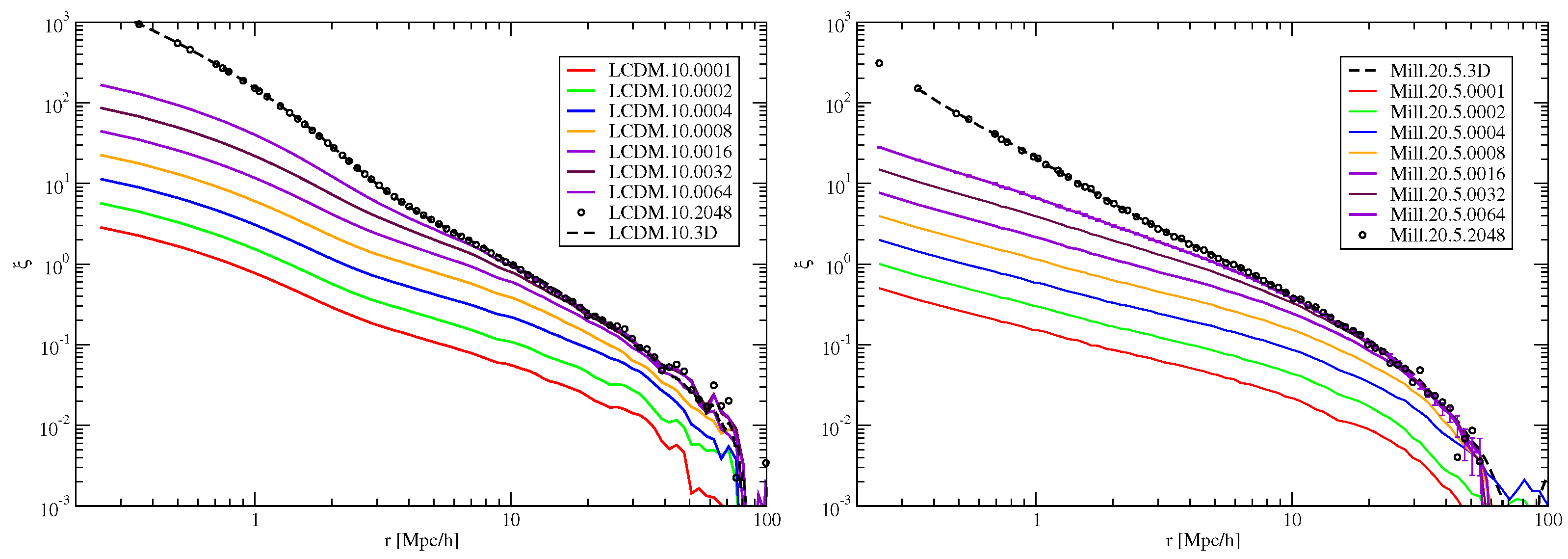
4.3. Measuring the Fractal Dimension
5. Correlation Analysis of the Cosmic Web
5.1. Formation of Galaxies in the Cosmic Web
5.2. Correlation Functions of Galaxies and Matter
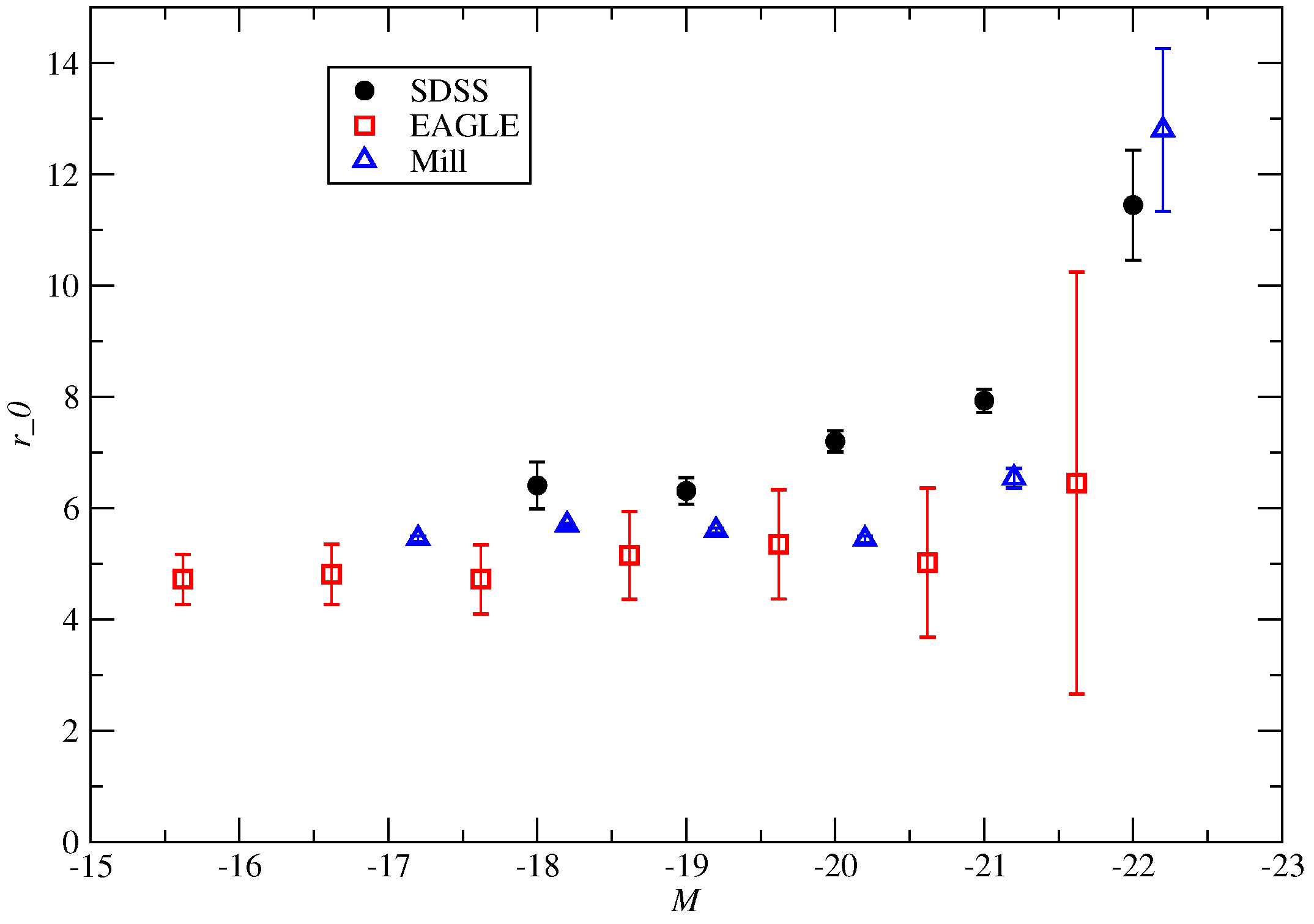
5.3. Luminosity Dependence of the Correlation Length
6. Fractal Analysis of the Cosmic Web
7. Comparing Angular and Spatial Distributions of Galaxies
7.1. Relation Between 2D and 3D Correlation Functions
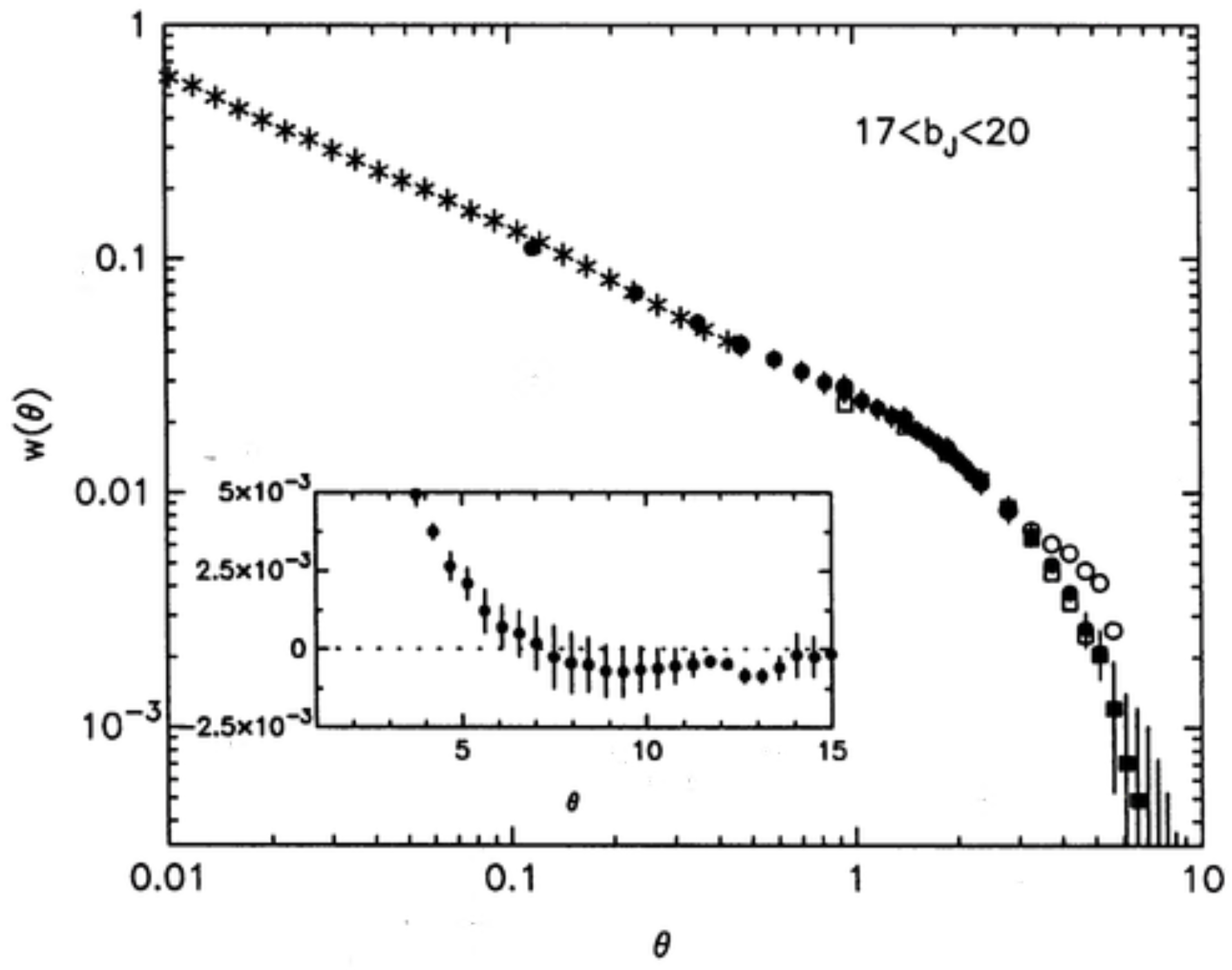
7.2. Fractal Analysis of the 2D Cosmic Web
8. Structure and Evolution of Cosmic Web from Combined Spatial and Velocity Data
8.1. Void Hierarchy
8.2. Evolution of Galaxies in the Void Hierarchy
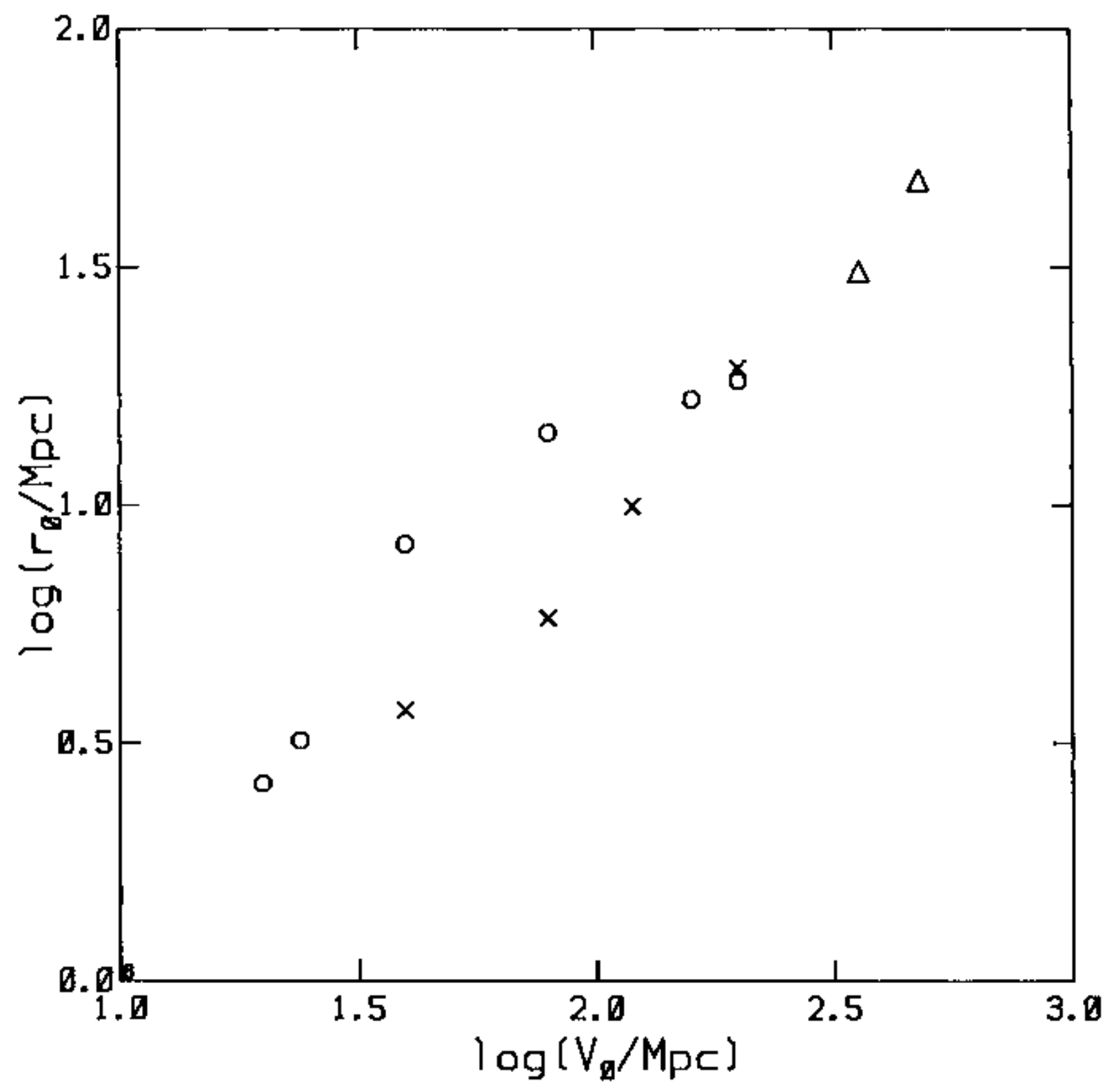
9. Scale of Homogeneity
10. Summary and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; Echo Point Books & Media, LLC: Brattleboro, VT, USA, 1977. [Google Scholar]
- Charlier, C.V.L. How an infinite world may be built up. Medd. Fran Lunds Astron. Obs. Ser. I 1922, 98, 1–37. [Google Scholar]
- Carpenter, E.F. Some Characteristics of Associated Galaxies. I. a. Density Restriction in the Metagalaxy. Astrophys. J. 1938, 88, 344. [Google Scholar] [CrossRef]
- Kiang, T. On the clustering of rich clusters of galaxies. Mon. Not. R. Astron. Soc. 1967, 135, 1–22. [Google Scholar] [CrossRef]
- Wertz, J.R. Newtonian Hierarchical Cosmology. Ph.D. Thesis, University of Texas, Austin, TX, USA, 1970. [Google Scholar]
- Wertz, J.R. A Newtonian Big-Bang Hierarchical Cosmological Model. Astrophys. J. 1971, 164, 227. [Google Scholar] [CrossRef]
- Haggerty, M.J.; Wertz, J.R. On the redshift-magnituderelation in hierarchical cosmologies. Mon. Not. R. Astron. Soc. 1972, 155, 495. [Google Scholar] [CrossRef]
- de Vaucouleurs, G. The Case for a Hierarchical Cosmology. Science 1970, 167, 1203–1213. [Google Scholar] [CrossRef]
- de Vaucouleurs, G. The Large-Scale Distribution of Galaxies and Clusters of Galaxies. Publ. Astron. Soc. Pacif. 1971, 83, 113. [Google Scholar] [CrossRef]
- Pietronero, L. The fractal structure of the universe: Correlations of galaxies and clusters and the average mass density. Phys. A Stat. Mech. Its Appl. 1987, 144, 257–284. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Cosmology’s Century: An Inside History of our Modern Understanding of the Universe; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Whole Truth. A Cosmologist’s Reflections on the Search for Objective Reality; Princeton University Press: Princeton, NJ, USA, 2022. [Google Scholar]
- Einasto, J. Dark Matter and Cosmic Web Story, 2nd ed.; World Scientific: Singapore, 2024. [Google Scholar]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Linde, A. Hybrid inflation. Phys. Rev. D 1994, 49, 748–754. [Google Scholar] [CrossRef]
- Linde, A.; Riotto, A. Hybrid inflation in supergravity. Phys. Rev. D 1997, 56, R1841–R1844. [Google Scholar] [CrossRef]
- Linde, A. Particle Physics and Inflationary Cosmology. arXiv 2005, arXiv:hep-th/0503203. [Google Scholar] [CrossRef]
- Nambu, Y.; Sasaki, M. Stochastic approach to chaotic inflation and the distribution of universes. Phys. Lett. B 1989, 219, 240–246. [Google Scholar] [CrossRef]
- Ambjørn, J.; Jurkiewicz, J.; Loll, R. Reconstructing the Universe. Phys. Rev. D 2005, 72, 064014. [Google Scholar] [CrossRef]
- Calcagni, G. Quantum field theory, gravity and cosmology in a fractal universe. J. High Energy Phys. 2010, 2010, 120. [Google Scholar] [CrossRef]
- Calcagni, G. Fractal Universe and Quantum Gravity. Phys. Rev. Lett. 2010, 104, 251301. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Ann. Der Phys. 1916, 354, 769–822. [Google Scholar] [CrossRef]
- Friedmann, A. Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes. Z. Phys. 1924, 21, 326–332. [Google Scholar] [CrossRef]
- Lemaître, G. Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Ann. Soc. Scietifique Brux. 1927, 47, 49–59. [Google Scholar]
- Hoyle, F. A New Model for the Expanding Universe. Mon. Not. R. Astron. Soc. 1948, 108, 372–382. [Google Scholar] [CrossRef]
- Hoyle, F. The synthesis of the elements from hydrogen. Mon. Not. R. Astron. Soc. 1946, 106, 343. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A. Primordial nucleosynthesis in light of WMAP. Phys. Lett. B 2003, 567, 227–234. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef]
- Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI 2024 VI: Cosmological constraints from the measurements of baryon acoustic oscillations. J. Cosmol. Astropart. Phys. 2025, 2025, 021. [Google Scholar] [CrossRef]
- Einasto, J.; Hütsi, G.; Szapudi, I.; Tenjes, P. Spinning the Cosmic Web; World Scientific: Singapore, 2025. [Google Scholar]
- Sunyaev, R.A.; Chluba, J. Signals from the epoch of cosmological recombination (Karl Schwarzschild Award Lecture 2008). Astron. Nachrichten 2009, 330, 657. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Einasto, J.; Kaasik, A.; Saar, E. Dynamic Evidence on Massive coronas of galaxies. Nature 1974, 250, 309–310. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Peebles, P.J.E.; Yahil, A. The size and mass of galaxies, and the mass of the universe. Astrophys. J. Lett. 1974, 193, L1–L4. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Di Valentino, E.; Levi Said, J.; Riess, A.; Pollo, A.; Poulin, V.; Gómez-Valent, A.; Weltman, A.; Palmese, A.; Huang, C.D.; van de Bruck, C.; et al. The CosmoVerse White Paper: Addressing observational tensions in cosmology with systematics and fundamental physics. arXiv 2025, arXiv:2504.01669. [Google Scholar] [CrossRef]
- Sankhyayan, S.; Bagchi, J.; Tempel, E.; More, S.; Einasto, M.; Dabhade, P.; Raychaudhury, S.; Athreya, R.; Heinämäki, P. Identification of Superclusters and Their Properties in the Sloan Digital Sky Survey Using the WHL Cluster Catalog. Astrophys. J. 2023, 958, 62. [Google Scholar] [CrossRef]
- York, D.G.; Adelman, J.; Anderson, J.E., Jr.; Anderson, S.F.; Annis, J.; Bahcall, N.A.; Bakken, J.A.; Barkhouser, R.; Bastian, S.; Berman, E.; et al. The Sloan Digital Sky Survey: Technical Summary. Astron. J. 2000, 120, 1579–1587. [Google Scholar] [CrossRef]
- Shane, C.; Wirtanen, C. The distribution of galaxies. Publ. Lick Obs. 1967, 22. [Google Scholar] [CrossRef]
- Seldner, M.; Siebers, B.; Groth, E.J.; Peebles, P.J.E. New reduction of the Lick catalog of galaxies. Astron. J. 1977, 82, 249–256. [Google Scholar] [CrossRef]
- Soneira, R.M.; Peebles, P.J.E. A computer model universe—Simulation of the nature of the galaxy distribution in the Lick catalog. Astron. J. 1978, 83, 845–849. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Statistical Analysis of Catalogs of Extragalactic Objects. I. Theory. Astrophys. J. 1973, 185, 413–440. [Google Scholar] [CrossRef]
- Hauser, M.G.; Peebles, P.J.E. Statistical Analysis of Catalogs of Extragalactic Objects. II. the Abell Catalog of Rich Clusters. Astrophys. J. 1973, 185, 757–786. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Hauser, M.G. Statistical Analysis of Catalogs of Extragalactic Objects. III. The Shane-Wirtanen and Zwicky Catalogs. Astrophys. J. Suppl. 1974, 28, 19. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Statistical Analysis of Catalogs of Extragalactic Objects. IV. Cross-Correlation of the Abell and Shane-Wirtanen Catalogs. Astrophys. J. Suppl. 1974, 28, 37. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Groth, E.J. Statistical analysis of catalogs of extragalactic objects. V—Three-point correlation function for the galaxy distribution in the Zwicky catalog. Astrophys. J. 1975, 196, 1–11. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Statistical analysis of catalogs of extragalactic objects. VI—The galaxy distribution in the Jagellonian field. Astrophys. J. 1975, 196, 647–651. [Google Scholar] [CrossRef]
- Groth, E.J.; Peebles, P.J.E. Statistical analysis of catalogs of extragalactic objects. VII. Two- and three-point correlation functions for the high-resolution Shane-Wirtanen catalog of galaxies. Astrophys. J. 1977, 217, 385–405. [Google Scholar] [CrossRef]
- Maddox, S.J.; Efstathiou, G.; Sutherland, W.J.; Loveday, J. Galaxy correlations on large scales. Mon. Not. R. Astron. Soc. 1990, 242, 43. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Galaxy and Mass N-Point Correlation Functions: A Blast from the Past. Astron. Soc. Pac. Conf. Ser. 2001, 252, 201. [Google Scholar]
- Longair, M.S.; Einasto, J. (Eds.) The Large Scale Structure of the Universe; Proceedings of the Symposium, Tallin, Estonian, USSR, September 12–16, 1977; IAU Symposium. 1978, Volume 79. Available online: https://link.springer.com/book/10.1007/978-94-009-9843-8 (accessed on 21 August 2025).
- Jõeveer, M.; Einasto, J.; Tago, E. The cell structure of the Universe. Tartu Astr. Obs. Preprint 1977, 79, 241. [Google Scholar]
- Tully, R.B.; Fisher, J.R. A Tour of the Local Supercluster. In Large Scale Structures in the Universe; Longair, M.S., Einasto, J., Eds.; Symposium—International Astronomical Union; Cambridge University Press: Cambridge, UK, 1978; Volume 79, pp. 214–216. Available online: https://ui.adsabs.harvard.edu/abs/1978IAUS...79..214T/abstract (accessed on 21 August 2025).
- Gregory, S.A.; Thompson, L.A. The Coma/A1367 supercluster and its environs. Astrophys. J. 1978, 222, 784–799. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. Gravitational instability: An approximate theory for large density perturbations. Astron. Astrophys. 1970, 5, 84–89. [Google Scholar]
- Jõeveer, M.; Einasto, J. Has the universe the cell structure. In Large Scale Structures in the Universe; Longair, M.S., Einasto, J., Eds.; IAU Symposium; Cambridge University Press: Cambridge, UK, 1978; Volume 79, pp. 241–250. Available online: https://link.springer.com/chapter/10.1007/978-94-009-9843-8_25 (accessed on 21 August 2025).
- Doroshkevich, A.G.; Kotok, E.V.; Poliudov, A.N.; Shandarin, S.F.; Sigov, I.S.; Novikov, I.D. Two-dimensional simulation of the gravitational system dynamics and formation of the large-scale structure of the universe. Mon. Not. R. Astron. Soc. 1980, 192, 321–337. [Google Scholar]
- Bond, J.R.; Kofman, L.; Pogosyan, D. How filaments of galaxies are woven into the cosmic web. Nature 1996, 380, 603–606. [Google Scholar] [CrossRef]
- Bahcall, N.A.; Soneira, R.M. The spatial correlation function of rich clusters of galaxies. Astrophys. J. 1983, 270, 20–38. [Google Scholar] [CrossRef]
- Klypin, A.A.; Kopylov, A.I. The Spatial Covariance Function for Rich Clusters of Galaxies. Sov. Astron. Lett. 1983, 9, 41. [Google Scholar]
- Kaiser, N. On the spatial correlations of Abell clusters. Astrophys. J. Lett. 1984, 284, L9–L12. [Google Scholar] [CrossRef]
- Szalay, A.S.; Schramm, D.N. Are galaxies more strongly correlated than clusters? Nature 1985, 314, 718–719. [Google Scholar] [CrossRef]
- Einasto, J.; Saar, E.; Klypin, A.A. Structure of superclusters and supercluster formation. V—Spatial correlation and voids. Mon. Not. R. Astron. Soc. 1986, 219, 457–478. [Google Scholar] [CrossRef]
- Jones, B.J.T.; Martinez, V.J.; Saar, E.; Einasto, J. Multifractal description of the large-scale structure of the universe. Astrophys. J. Lett. 1988, 332, L1–L5. [Google Scholar] [CrossRef]
- Gramann, M. Formation of the structure in an axion Universe with a cosmological constant. Tartu Astr. Obs. Publ. 1987, 52, 216–255. [Google Scholar]
- Gramann, M. Structure and formation of superclusters. VIII—Evolution of structure in a model with cold dark matter and cosmological constant. Mon. Not. R. Astron. Soc. 1988, 234, 569–582. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Discussion Panel: Fractal Large Scale Structures and Crossover to Homogeneity: The Mass-Radius Function versus the Correlations, and the Measurement of the Corrrelation Range. In Large Scale Structures of the Universe; Audouze, J., Pelletan, M.C., Szalay, A., Zel’dovich, Y.B., Peebles, P.J.E., Eds.; IAU Symposium. 1988, Volume 130, pp. 482–484. Available online: https://www.cambridge.org/core/journals/symposium-international-astronomical-union/article/discussion-panel/617AC4E14DDB6690A89E56AD0334A35A (accessed on 21 August 2025).
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Abell, G.O.; Chincarini, G. (Eds.) Early Evolution of the Universe and Its Present Structure; IAU Symposium; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1983; Volume 104. [Google Scholar]
- Audouze, J.; Pelletan, M.C.; Szalay, A.; Zel’dovich, Y.B.; Peebles, P.J.E. (Eds.) Large-Scale Structures in the Universe. Observational and Analytical Methods. Proceedings of the 130th Symposium of the International Astronomical Union, Dedicated to the Memory of Marc A. Aaronson (1950–1987), Held in Balatonfured, Hungary, 15–20 June 1987; IAU Symposium; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; Volume 130. [Google Scholar]
- van de Weygaert, R.; Shandarin, S.; Saar, E.; Einasto, J. (Eds.) The Zeldovich Universe: Genesis and Growth of the Cosmic Web; IAU Symposium; Cambridge University Press: Cambridge, UK, 2016; Volume 308. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Yu, J.T. Primeval Adiabatic Perturbation in an Expanding Universe. Astrophys. J. 1970, 162, 815–836. [Google Scholar] [CrossRef]
- Arnold, V.I.; Shandarin, S.F.; Zeldovich, I.B. The large scale structure of the universe I. General properties. One-and two-dimensional models. Geophys. Astrophys. Fluid Dyn. 1982, 20, 111–130. [Google Scholar] [CrossRef]
- Martinez, V.J.; Jones, B.J.T. Why the universe is not a fractal. Mon. Not. R. Astron. Soc. 1990, 242, 517–521. [Google Scholar] [CrossRef]
- Martínez, V.J.; Saar, E. Statistics of the Galaxy Distribution; Chapman & Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Balian, R.; Schaeffer, R. Galaxies: Fractal Dimensions, Counts in Cells, and Correlations. Astrophys. J. Lett. 1988, 335, L43. [Google Scholar] [CrossRef]
- Balian, R.; Schaeffer, R. Scale-invariant matter distribution in the universe. II—Bifractal behaviour. Astron. Astrophys. 1989, 226, 373–414. [Google Scholar]
- Song, D.J.; Ruffini, R. Determination of “inos” Masses Composing Galactic Halos. In Observational Cosmology; Hewitt, A., Burbidge, G., Fang, L.Z., Eds.; IAU Symposium; Cambridge University Press: Cambridge, UK, 1987; Volume 124, p. 723. [Google Scholar]
- Ruffini, R.; Song, D.J.; Taraglio, S. The ’ino’ mass and the cellular large-scale structure of the universe. Astron. Astrophys. 1988, 190, 1–9. [Google Scholar]
- Calzetti, D.; Einasto, J.; Giavalisco, M.; Ruffini, R.; Saar, E. The Correlation Function of Galaxies in the Direction of the Coma Cluster. Astrophys. Space Sci. 1987, 137, 101–106. [Google Scholar] [CrossRef]
- Calzetti, D.; Giavalisco, M.; Ruffini, R. The normalization of the correlation functions for extragalactic structures. Astron. Astrophys. 1988, 198, 1–15. [Google Scholar]
- Gaite, J.; Domínguez, A.; Pérez-Mercader, J. The Fractal Distribution of Galaxies and the Transition to Homogeneity. Astrophys. J. Lett. 1999, 522, L5–L8. [Google Scholar] [CrossRef]
- Gaite, J. Smooth halos in the cosmic web. J. Cosmol. Astropart. Phys. 2015, 2015, 020. [Google Scholar] [CrossRef]
- Gaite, J. The Fractal Geometry of the Cosmic Web and Its Formation. Adv. Astron. 2019, 2019, 6587138. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The fractal galaxy distribution. Phys. D Nonlinear Phenom. 1989, 38, 273–278. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Principles of Physical Cosmology; Prinseton University Press: Prinseton, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Pietronero, L.; Montuori, M.; Sylos Labini, F. On the Fractal Structure of the Visible Universe. arXiv 1997, arXiv:astro-ph/9611197. [Google Scholar] [CrossRef]
- Pietronero, L.; Sylos Labini, F. Fractal Structures and the Large Scale Distribution of Galaxies. In Current Topics in Astrofundamental Physics: The Cosmic Microwave Background; Sánchez, N.G., Ed.; Springer: Dordrecht, The Netherlands, 2001; p. 391. [Google Scholar] [CrossRef][Green Version]
- Sylos Labini, F.; Gabrielli, A.; Montuori, M.; Pietronero, L. Finite size effects on the galaxy number counts: Evidence for fractal behavior up to the deepest scale. Phys. A Stat. Mech. Its Appl. 1996, 226, 195–242. [Google Scholar] [CrossRef]
- Borgani, S. Scaling in the Universe. Phys. Rep. 1995, 251, 1–152. [Google Scholar] [CrossRef]
- Turok, N. (Ed.) Critical Dialogues in Cosmology; World Scientific: Singapore, 1997. [Google Scholar][Green Version]
- Davis, M. Is the Universe Homogeneous on Large Scales? arXiv 1997, arXiv:astro-ph/9610149. [Google Scholar] [CrossRef]
- de Swart, J.G. Five decades of missing matter. Phys. Today 2024, 77, 24–43. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Einasto, J.; Shandarin, S.F. Giant voids in the universe. Nature 1982, 300, 407–413. [Google Scholar] [CrossRef]
- Klypin, A.A.; Shandarin, S.F. Three-dimensional numerical model of the formation of large-scale structure in the Universe. Mon. Not. R. Astron. Soc. 1983, 204, 891–907. [Google Scholar] [CrossRef]
- van den Bergh, S. Are Clusters of Galaxies Stable? Astron. J. 1962, 67, 285. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Large-scale background temperature and mass fluctuations due to scale-invariant primeval perturbations. Astrophys. J. Lett. 1982, 263, L1–L5. [Google Scholar] [CrossRef]
- Melott, A.L.; Einasto, J.; Saar, E.; Suisalu, I.; Klypin, A.A.; Shandarin, S.F. Cluster analysis of the nonlinear evolution of large-scale structure in an axion/gravitino/photino-dominated universe. Phys. Rev. Lett. 1983, 51, 935–938. [Google Scholar] [CrossRef]
- Centrella, J.; Melott, A.L. Three-dimensional simulation of large-scale structure in the universe. Nature 1983, 305, 196–198. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Large-Scale Structure of the Universe; Princeton Series in Physics; Prinseton University Press: Prinseton, NJ, USA, 1980. [Google Scholar]
- Kaiser, N. Clustering in real space and in redshift space. Mon. Not. R. Astron. Soc. 1987, 227, 1–21. [Google Scholar] [CrossRef]
- Davis, M.; Peebles, P.J.E. A survey of galaxy redshifts. V. The two-point position and velocity correlations. Astrophys. J. 1983, 267, 465–482. [Google Scholar] [CrossRef]
- Norberg, P.; Baugh, C.M.; Hawkins, E.; Maddox, S.; Peacock, J.A.; Cole, S.; Frenk, C.S.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; et al. The 2dF Galaxy Redshift Survey: Luminosity dependence of galaxy clustering. Mon. Not. R. Astron. Soc. 2001, 328, 64–70. [Google Scholar] [CrossRef]
- Zehavi, I.; Zheng, Z.; Weinberg, D.H.; Frieman, J.A.; Berlind, A.A.; Blanton, M.R.; Scoccimarro, R.; Sheth, R.K.; Strauss, M.A.; Kayo, I.; et al. The Luminosity and Color Dependence of the Galaxy Correlation Function. Astrophys. J. 2005, 630, 1–27. [Google Scholar] [CrossRef]
- Zehavi, I.; Zheng, Z.; Weinberg, D.H.; Blanton, M.R.; Bahcall, N.A.; Berlind, A.A.; Brinkmann, J.; Frieman, J.A.; Gunn, J.E.; Lupton, R.H.; et al. Galaxy Clustering in the Completed SDSS Redshift Survey: The Dependence on Color and Luminosity. Astrophys. J. 2011, 736, 59. [Google Scholar] [CrossRef]
- Coleman, P.H.; Pietronero, L. The fractal structure of the universe. Phys. Rep. 1992, 213, 311–389. [Google Scholar] [CrossRef]
- Coleman, P.H.; Pietronero, L.; Sanders, R.H. Absence of any characteristic correlation length in the CfA galaxy catalogue. Astron. Astrophys. 1988, 200, L32–L34. [Google Scholar]
- Coles, P.; Chiang, L. Characterizing the nonlinear growth of large-scale structure in the Universe. Nature 2000, 406, 376–378. [Google Scholar] [CrossRef]
- Colless, M.; Peterson, B.A.; Jackson, C.; Peacock, J.A.; Cole, S.; Norberg, P.; Baldry, I.K.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; et al. The 2dF Galaxy Redshift Survey: Final Data Release. arXiv 2003, arXiv:astro–ph/0306581. [Google Scholar] [CrossRef]
- Aihara, H.; Allende Prieto, C.; An, D.; Anderson, S.F.; Aubourg, É.; Balbinot, E.; Beers, T.C.; Berlind, A.A.; Bickerton, S.J.; Bizyaev, D.; et al. The Eighth Data Release of the Sloan Digital Sky Survey: First Data from SDSS-III. Astrophys. J. Suppl. 2011, 193, 29. [Google Scholar] [CrossRef]
- Alam, S.; Albareti, F.D.; Allende Prieto, C.; Anders, F.; Anderson, S.F.; Anderton, T.; Andrews, B.H.; Armengaud, E.; Aubourg, É.; Bailey, S.; et al. The Eleventh and Twelfth Data Releases of the Sloan Digital Sky Survey: Final Data from SDSS-III. Astrophys. J. Suppl. 2015, 219, 12. [Google Scholar] [CrossRef]
- Tegmark, M.; Blanton, M.R.; Strauss, M.A.; Hoyle, F.; Schlegel, D.; Scoccimarro, R.; Vogeley, M.S.; Weinberg, D.H.; Zehavi, I.; Berlind, A.; et al. The Three-Dimensional Power Spectrum of Galaxies from the Sloan Digital Sky Survey. Astrophys. J. 2004, 606, 702–740. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef] [PubMed]
- Springel, V.; Pakmor, R.; Pillepich, A.; Weinberger, R.; Nelson, D.; Hernquist, L.; Vogelsberger, M.; Genel, S.; Torrey, P.; Marinacci, F.; et al. First results from the IllustrisTNG simulations: Matter and galaxy clustering. Mon. Not. R. Astron. Soc. 2018, 475, 676–698. [Google Scholar] [CrossRef]
- Einasto, J.; Hütsi, G.; Kuutma, T.; Einasto, M. Correlation function: Biasing and fractal properties of the cosmic web. Astron. Astrophys. 2020, 640, A47. [Google Scholar] [CrossRef]
- Einasto, J.; Hütsi, G.; Einasto, M. Correlation functions in 2D and 3D as descriptors of the cosmic web. Astron. Astrophys. 2021, 652, A152. [Google Scholar] [CrossRef]
- White, S.D.M.; Rees, M.J. Core condensation in heavy halos—A two-stage theory for galaxy formation and clustering. Mon. Not. R. Astron. Soc. 1978, 183, 341–358. [Google Scholar] [CrossRef]
- Cen, R.; Ostriker, J.P. A three-dimensional hydrodynamic treatment of the hot dark matter cosmological scenario. Astrophys. J. 1992, 399, 331–344. [Google Scholar] [CrossRef]
- Repp, A.; Szapudi, I. A Gravitational Ising Model for the Statistical Bias of Galaxies. arXiv 2019, arXiv:1904.05048. [Google Scholar] [CrossRef]
- Tempel, E.; Tamm, A.; Gramann, M.; Tuvikene, T.; Liivamägi, L.J.; Suhhonenko, I.; Kipper, R.; Einasto, M.; Saar, E. Flux- and volume-limited groups/clusters for the SDSS galaxies: Catalogues and mass estimation. Astron. Astrophys. 2014, 566, A1. [Google Scholar] [CrossRef]
- Ahn, C.P.; Alexandroff, R.; Allende Prieto, C.; Anders, F.; Anderson, S.F.; Anderton, T.; Andrews, B.H.; Aubourg, É.; Bailey, S.; Bastien, F.A.; et al. The Tenth Data Release of the Sloan Digital Sky Survey: First Spectroscopic Data from the SDSS-III Apache Point Observatory Galactic Evolution Experiment. Astrophys. J. Suppl. 2014, 211, 17. [Google Scholar] [CrossRef]
- Liivamägi, L.J.; Tempel, E.; Saar, E. SDSS DR7 superclusters. The catalogues. Astron. Astrophys. 2012, 539, A80. [Google Scholar] [CrossRef]
- Croton, D.J.; Springel, V.; White, S.D.M.; De Lucia, G.; Frenk, C.S.; Gao, L.; Jenkins, A.; Kauffmann, G.; Navarro, J.F.; Yoshida, N. The many lives of active galactic nuclei: Cooling flows, black holes and the luminosities and colours of galaxies. Mon. Not. R. Astron. Soc. 2006, 365, 11–28. [Google Scholar] [CrossRef]
- McAlpine, S.; Helly, J.C.; Schaller, M.; Trayford, J.W.; Qu, Y.; Furlong, M.; Bower, R.G.; Crain, R.A.; Schaye, J.; Theuns, T.; et al. The EAGLE simulations of galaxy formation: Public release of halo and galaxy catalogues. Astron. Comput. 2016, 15, 72–89. [Google Scholar] [CrossRef]
- Zehavi, I.; Weinberg, D.H.; Zheng, Z.; Berlind, A.A.; Frieman, J.A.; Scoccimarro, R.; Sheth, R.K.; Blanton, M.R.; Tegmark, M.; Mo, H.J.; et al. On Departures from a Power Law in the Galaxy Correlation Function. Astrophys. J. 2004, 608, 16–24. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- Wang, J.; Bose, S.; Frenk, C.S.; Gao, L.; Jenkins, A.; Springel, V.; White, S.D.M. Universal structure of dark matter haloes over a mass range of 20 orders of magnitude. Nature 2020, 585, 39–42. [Google Scholar] [CrossRef] [PubMed]
- Kirshner, R.P.; Oemler, A., Jr.; Schechter, P.L.; Shectman, S.A. A million cubic megaparsec void in Bootes. Astrophys. J. Lett. 1981, 248, L57–L60. [Google Scholar] [CrossRef]
- Pan, D.C.; Vogeley, M.S.; Hoyle, F.; Choi, Y.Y.; Park, C. Cosmic voids in Sloan Digital Sky Survey Data Release 7. Mon. Not. R. Astron. Soc. 2012, 421, 926–934. [Google Scholar] [CrossRef]
- Sutter, P.M.; Lavaux, G.; Wandelt, B.D.; Weinberg, D.H. A Public Void Catalog from the SDSS DR7 Galaxy Redshift Surveys Based on the Watershed Transform. Astrophys. J. 2012, 761, 44. [Google Scholar] [CrossRef]
- Nadathur, S.; Hotchkiss, S. A robust public catalogue of voids and superclusters in the SDSS Data Release 7 galaxy surveys. Mon. Not. R. Astron. Soc. 2014, 440, 1248–1262. [Google Scholar] [CrossRef]
- Sheth, R.K.; van de Weygaert, R. A hierarchy of voids: Much ado about nothing. Mon. Not. R. Astron. Soc. 2004, 350, 517–538. [Google Scholar] [CrossRef]
- Aragon-Calvo, M.A.; Szalay, A.S. The Hierarchical Structure and Dynamics of Voids. Mon. Not. R. Astron. Soc. 2013, 428, 3409–3424. [Google Scholar] [CrossRef]
- Aragon Calvo, M.A.; Neyrinck, M.C.; Silk, J. Galaxy Quenching from Cosmic Web Detachment. Open J. Astrophys. 2019, 2, 7. [Google Scholar] [CrossRef]
- Pan, J.; Coles, P. Large-scale cosmic homogeneity from a multifractal analysis of the PSCz catalogue. Mon. Not. R. Astron. Soc. 2000, 318, L51–L54. [Google Scholar] [CrossRef]
- Sarkar, P.; Yadav, J.; Pandey, B.; Bharadwaj, S. The scale of homogeneity of the galaxy distribution in SDSS DR6. Mon. Not. R. Astron. Soc. 2009, 399, L128–L131. [Google Scholar] [CrossRef]
- Scrimgeour, M.I.; Davis, T.; Blake, C.; James, J.B.; Poole, G.B.; Staveley-Smith, L.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; et al. The WiggleZ Dark Energy Survey: The transition to large-scale cosmic homogeneity. Mon. Not. R. Astron. Soc. 2012, 425, 116–134. [Google Scholar] [CrossRef]
- Courtois, H.M.; Mould, J.; Hollinger, A.M.; Dupuy, A.; Zhang, C.P. In search for the Local Universe dynamical homogeneity scale with CF4++ peculiar velocities. arXiv 2025, arXiv:2502.01308. [Google Scholar] [CrossRef]
- Park, C.; Song, H.; Einasto, M.; Lietzen, H.; Heinamaki, P. Large SDSS Quasar Groups and Their Statistical Significance. J. Korean Astron. Soc. 2015, 48, 75–82. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Einasto, J. Fractal Properties of the Cosmic Web. Fractal Fract. 2025, 9, 579. https://doi.org/10.3390/fractalfract9090579
Einasto J. Fractal Properties of the Cosmic Web. Fractal and Fractional. 2025; 9(9):579. https://doi.org/10.3390/fractalfract9090579
Chicago/Turabian StyleEinasto, Jaan. 2025. "Fractal Properties of the Cosmic Web" Fractal and Fractional 9, no. 9: 579. https://doi.org/10.3390/fractalfract9090579
APA StyleEinasto, J. (2025). Fractal Properties of the Cosmic Web. Fractal and Fractional, 9(9), 579. https://doi.org/10.3390/fractalfract9090579




