Abstract
Unmanned aerial vehicle (UAV) formation flying is an efficient and economical operation mode for air transportation systems. To improve the effectiveness of synergetic formation control for UAVs, this paper proposes a pairwise conflict resolution approach for UAV formation through mathematical analysis and designs a dynamic pairing and deep reinforcement learning framework (P-DRL formation control framework). Firstly, a new pairwise UAV formation control theorem is proposed, which breaks down the multi-UAVs formation control problem into multiple sequential control problems involving UAV pairs through a dynamic pairing algorithm. The training difficulty of Agents that only control each pair (two UAVs) is lower compared to controlling all UAVs directly, resulting in better and more stable formation control performance. Then, a deep reinforcement learning model for a UAV pair based on the Environment–Agent interaction is built, where segmented reward functions are designed to reduce the collision possibility of UAVs. Finally, P-DRL completes the formation control task of the UAV fleet through continuous pairing and Agent-based pairwise formation control. The simulations used the dynamic pairing algorithm combined with the DRL architectures of asynchronous advantage actor–critic (P-A3C), actor–critic (P-AC), and double deep q-value network (P-DDQN) to achieve synergetic formation control. This approach yielded effective control results with a strong generalization ability. The success rate of controlling dense, fast, and multi-UAV (10–20) formations reached 96.3%, with good real-time performance (17.14 Hz).
1. Introduction
The formation of UAVs refers to the process of multi-UAVs arranging or maintaining a specific spatial configuration in the airspace while performing flight tasks [1,2]. In transportation systems, UAV formation aims to make the fleet more efficient by receiving better navigation/position signals, improving communication stability and reducing conflicts during transportation tasks. It is also widely used in stunt performance, geographic exploration, and joint positioning in other fields. In recent years, with the continuous growth of logistics demand in urban air transportation systems, UAV formation flying has become increasingly widespread due to its efficient and flexible transportation advantages.
The primary task of UAV formation is to arrange or maintain a spatial configuration, which is different from the primary task of trajectory planning to arrive at a destination [3,4]. Therefore, UAV formation focuses on “trajectory control”, while UAV trajectory planning focuses on “trajectory determination”. Synergetic formation control is the basic technology behind the formatting process, which generally has high requirements for surfaces, obstacles, and other environments. Therefore, UAV formatting usually chooses an open and flat site, which is helpful for the operation and implementation of the formation control algorithm [5]. However, when it is difficult to meet the operating requirements of no obstacles and no interference, the UAV synergetic formation control algorithm emerges for complex operating environments [6,7]. At the same time, some complex tasks such as terrain exploration and multi-resource fusion positioning require the synergetic operation of multi-UAVs, which makes controlling multiple UAVs simultaneously a new research direction [8,9].
Generally, due to advanced information transmission systems such as 5G and sensors, as well as continuous improvements in low complexity control algorithms, the real-time performance and accuracy of UAV controls are superior [10]. However, compared to the real-time performance and control accuracy of the UAV formation control method, the synergetic control capability for simultaneous control of multi-UAV and the environmental adaptability of multi-UAVs, such as the formation control ability under operational uncertainty and unknown environment, are drawbacks of the current research in the field of UAV formation control [11]. Fortunately, as theories of deep reinforcement learning and systems control become more complete, there are new opportunities for improvements in the synergetic control scale of UAVs as well as their adaptability to various complex scenarios.
This paper proposes a P-DRL multi-UAV synergetic formation control framework, which combines mathematical analysis, heuristic algorithms, and deep reinforcement learning theory to achieve formation control of multi-UAVs with high safety and real-time performance in unknown environments. The paper’s main contributions are listed as follows.
- A new theorem for UAV pairwise formation control is proposed based on an analysis of the conflict–collision relationship between multi-UAVs. Based on this, the task of multi-UAV synergetic formation control is broken down into multiple pairwise UAV synergetic formation control tasks using the dynamic pairing algorithm we designed, thus reducing the training difficulty for the Agent in the DRL model.
- A detailed deep reinforcement learning model of synergetic formation control for a UAV pair is proposed, including the reward function with collision-avoidance intensified, state transform, state–action space, etc.
- A general framework, P-DRL, is proposed to solve the problem of multiple UAV (10–20) dynamic formation control, which can be used for the task of simultaneous real-time dynamic multi-UAV formation control in complex environments with operational uncertainty and obstacles unknown.
This paper is structured as follows: Section 2 categorizes the advanced methods used for UAV formation tasks and their contributions, as well as the motivations for this paper. Section 3 introduces the formation control problem addressed in this study, the solving theorem, the basic control system of a single UAV, and the DRL model for UAV pair control. Section 4 provides the framework and P-DRL as an approach for UAV formation control. Section 5 conducts simulations of P-A3C, P-AC, and P-DDQN, constructed using the P-DRL framework. Section 6 presents the conclusions and discussion.
2. Research Basis
2.1. Related Work
Multi-UAV formation is essentially a control problem [8]. Unlike “stability” control, formation control belongs to the category of “synergetic” control, the former generally focusing on its own control system, while the latter focuses on the process of “synergetic decision-making” [12,13,14]. The process of UAV formation control is usually based on UAV dynamic models/systems as opposed to the design control algorithms used for different applications [15]. There have been various excellent works for UAV formation control theory, from the independent control method [16,17] to the “leader–follower” [18,19,20] and other heuristic control algorithms, as well as artificial intelligence (AI) control algorithms [21,22] in recent years. The existing research can be classified into two main categories from the perspective of UAV formation control algorithms: cybernetics and artificial intelligence.
The method based on cybernetics constructs the posture and dynamic model of the UAV and then controls the operation of the UAV through linear or nonlinear mapping between signals and displacement [23]. See, for example, classical proportional-integral-derivative (PID) control [2,15,24] backstepping control based on Lyapunov stability theory [25], and sliding mode control [26,27]. The formation result of this type of method widely depends on the accuracy of the parameters in the mathematical model and the ability of the UAV to adjust according to feedback, thus carrying out precise control of UAVs with good adaptability. In recent years, many improved theoretical models for drone formation control have achieved very good practical results, such as multi-level switching control [28], back-stepping [29], energetic reference generator [19], etc.
The method based on AI extracts key features from a UAV’s historical trajectory data and combines it with the UAV motion model, robust control [23], and the DRL method [30,31,32,33] to achieve UAV control. For example, operators can fit the UAV control signal and nonlinear control effect through a neural network, or learn from the control experience of UAV pilots/experts, train the AI model using input and feedback to control the UAVs [34], use a graph convolutional neural network (GCNN) to evaluate the operational uncertainty and make control decisions [27], and construct distributed control systems to train the control decision Agent [3,35], etc. These methods often have good robustness, fault tolerance, environment fitness, and the ability to extract key information when dealing with the control of nonlinear complex systems, which usually benefit from the use of adaptive deep reinforcement learning neural networks.
Although the above two categories of methods have their advantages in different aspects, there are still certain drawbacks when facing complex environments with dynamic, unknown conditions and operational interference. For example, the cybernetic model generally needs to be supported by the technology of trajectory planning and it is necessary to determine the four-dimensional trajectory (x, y, z-position, timestamp) of the UAV first, and then convert it into UAV control instructions through integration [36]. The implementation of this “two-stage” method is relatively cumbersome, since the process of solving the feasible 4D trajectory of the UAVs sometimes consumes a lot of computing resources. The AI-based UAV formation control algorithm usually directly controls the UAV using action allocations [37,38,39]. Its solution process is more direct but the application scenarios are limited. The input state in the training process grows exponentially with the number of UAVs and obstacles, making the convergence of the neural network difficult [3,14]. Therefore, AI control methods often struggle to extend to or improve on more complex or different scenarios due to the upper limitation of AI training abilities. Based on further reflection on the above difficulties, we made improvements and propose the P-DRL framework for multi-UAV formation control.
2.2. Motivation
Generally, for the formation control scenarios within unknown environments dealing with operational uncertainty, adopting a deep reinforcement learning architecture may be more advantageous compared to some deterministic control approaches. However, when using deep reinforcement learning for UAV formation control, two challenging problems must be considered:
- (1)
- Learning difficulty increases with the number of UAVs being controlled simultaneously.
For deep reinforcement learning methods to solve the UAV formation control problem, there is always a maximum number of UAVs that the Agent can control simultaneously. This phenomenon is mainly caused by the input dimension limit of the deep q-value/v-value network. For example, one quadcopter has three position parameters and four action variables, which are composed of a basic state matrix with seven dimensions. Therefore, training an Agent for 2–5 UAV control is achievable, but when the input dimensions are over 50 (these input parameters are completely independent in theory, such as the relationship between longitude and latitude and longitude and one of the rotor speeds), the training of the Agent will be difficult due to the exponential growth and the continuous search for space.
- (2)
- Training difficulty in improving the non-collision success rate.
Due to insufficient training and estimated errors in the q-value, the trained Agents may experience phenomena such as collisions between drones and obstacles, which should be avoided as much as possible. Thus, reward functions with a new structure should be designed to maximize conflict perception ability and ensure sufficient value iteration.
Therefore, the motivation to compress training input dimensions emerges. The P-DRL framework makes improvements from two main perspectives: (1) breaking down the multi-UAV formation control problem into multiple UAV pair formation control problems so we can train a DRL Agent to only focus on the synergetic control task of two UAVs, thereby resulting in less training difficulties. (2) A new DRL model for UAV pairwise formation control is constructed with better reward functions and interaction modes to improve collision avoidance capabilities.
From a macro perspective, the transformation from multi-UAVs formation control to UAV pairwise formation control enables the P-DRL framework to have better synergetic control capabilities. From a micro perspective, the pairwise UAV control DRL model has a smaller state–action space, allowing the trained Agents to achieve more effective training and better decision-making performance. These two perspectives are the fundamental reasons why the P-DRL framework can result in better formation control performance.
3. Problem Formation
3.1. Problem Definition
The problem addressed in this study is dynamic multiple UAVs formation control under operational uncertainty in unknown environments. To further clarify this problem, we describe the problem from four perspectives: objectives, decision variables, constraints, and assumptions.
- (1)
- Objectives: A group of UAVs (≥10) needs to arrange or maintain a specific configuration synergetically, where drones have a random initial state, which may be stationary or in motion.
- (2)
- Decision variables: The only decision variable is the rotor speed of the UAV. For example, a hexacopter with six propeller rotors has six decision variables, because it can theoretically control the speed of every single rotor. Similarly, a quadcopter (quadrotor UAV) has four decision variables. Drones achieve most postures such as climb, descent, and roll based on the adjustment of their rotor speed.
- (3)
- Constraints: Firstly, the maneuver of UAVs must meet their performance constraints. Secondly, UAVs cannot collide with each other during their formation process, and they cannot collide with other obstacles in the airspace.
- (4)
- Assumptions: Some communication factors such as signal transmission interference/delay are not considered, but some external interference like wind and inner control errors made by UAV systems need to be considered. All of the obstacles’ positions in the airspace are generated randomly, and the positions are unknown before the formation task begins. We further express the assumption as:
- Operational uncertainty: The next state of the UAV will not be formed completely according to the current state and control action, but it follows a normal distribution according to a specific variance, which is Pr[|, ] ≠ 1.
- Unknown environment: Obstacles in the operating environment cannot be predicted before the UAV approaches it/before the process of formation control, and they become knowable when the UAV approaches it in the process of formation control.
3.2. Pairwise Control Theorem
Since our approach is to break down the problem of multiple UAV formation control into multiple UAV pair formation control problems, it is necessary to demonstrate the feasibility of this mode. This means proving that conducting multiple UAV pair formation control can yield results equivalent to those obtained by directly conducting multiple UAVs formation control using the same assumptions and decision variables as Section 3.1.
- (1)
- Same objectives.
The formation objectives/results of the UAV formation control are equivalent regardless of the control algorithms used. A group of UAVs will arrange or maintain a specific configuration synergistically at the end if the approach is implemented successfully.
- (2)
- Same constraints.
There are three main constraints in the formation control model for multi-UAVs: (a) meet the performance of the UAV dynamic model; (b) avoid collision between any UAVs and obstacles in the environment; and (c) avoid collision between any UAVs. For constraint (a), it is easy to deduce that all UAVs in the fleet meet performance constraints and that any UAV pair in the UAV fleet meets performance constraints are sufficiently and with the necessary conditions in place. Similarly, if there is no collision with obstacles for the whole UAV fleet, then any UAV pair in the UAV fleet will naturally not collide with obstacles, and vice versa.
However, for constraint (c), the equivalence between a group of UAVs not colliding and multiple UAV pairs not colliding requires more discussion. The relationships between UAVs regarding conflicts/collisions are more complex than those between UAVs and obstacles. In brief, a UAV may have a conflict/collision trend with more than two surrounding UAVs at the same time, and whether the pairwise conflict relief control method can solve multiple conflict relief problems in a UAV fleet requires deduction.
For the equivalence proof of constraint (c), we need to clarify two definitions, which are conflict and collision. Conflict refers to the trend of collision between UAVs due to position, heading, and speed relationships [2,6]. Specifically, several UAVs will have a situation where horizontal positions and vertical height differences are less than a certain value in the future according to the current operation state. Collision refers to UAVs being in the same spatial position at a certain time and colliding with each other. Conflict occurs before a collision and there must be at least one conflict before a collision can happen. Therefore, if we want to avoid UAV collisions, we can realize this purpose by solving all of the UAV conflicts (a sufficient condition for collision avoidance).
We assume is the set of all operating UAVs, composed of n UAV elements , , …, . n∈ *, * is the set of natural numbers. For each UAV , = {, (t)}, where is the 3D position vector [x, y, z] of the UAV, where x, y is the lateral position and z is the height of the UAV, (t) represents the mapping from time t to 3D position vector P of by velocity . Define the safety interval between UAV as d, which means the interval between two UAVs should be larger than d to ensure safe operation. indicates a conflicting set, where UAVs in have conflicts with other UAVs in .
The mathematical description of conflicts in a UAV fleet can be represented as ①.
①: = {, ,…, }, n∈ *, ∃ ⊆ , || ≥ 3, ∀ = {, (t)}∈ , ∀ = {, (t)}∈ , i≠j; makes ∃t∈ (0, +∞), ← (t), ← (t), || − || ≤ d.
The mathematical description of conflicts between a UAV pair can be represented as ②.
②: ∃ = {, (t)}∈ , = {, (t)}∈ , i,j∈ *, i≠j; makes ∃t∈ (0, +∞), ← (t), ← (t), || − || ≤ d.
Prove Theorem 1 (① ⇒ ②).
The existence of conflicts in a UAV fleet is a sufficient condition for the existence of UAV pair conflicts.
Randomly select = {, (t)}∈ , = {, (t)}∈ .
According to the description of ①: For certain ∈ , ∃ ∈ , makes ← (t), ← (t), || − || ≤ d.
∵ || ≥ 3; ∴∃ ∈ , makes ← (t), ← (t), || − || ≤d, t∈ (0, +∞).
∵ ⊆ ; ∴ , , ∈ .
∴ When ① is established, which satisfies ∃ , , ∈ , i ≠ j ≠ k, makes ∃ t∈ (0, +∞), ← (t), ← (t), || − || ≤ d. And ∃ ∈ , makes ← (t), ← (t), || − || ≤d, t∈ (0, +∞), ② established.
∴ ① ⇒ ② is proven.
Now, we have the contrapositive of Theorem 1, recorded as Theorem 2:
Theorem 1 ( ⇒ ).
Non-conflict among all UAV pairs is a sufficient condition for non-conflict among all UAVs in the fleet, which is:
: ∀ = {, , …, }, n ∈ , ∃ ⊆ , ≥ 3, ∀ = {, (t)} ∈ , ∀
= {, (t)}∈ , i ≠ j, s.t. ∀ t ∈ (0, +∞),
← (t),
← (t), ||
–
|| > d.
: ∃
= {, (t)} ∈ , = {, (t)}∈ , i,j ∈{1, 2, …, n}, i ≠ j; s.t. ∀ t ∈ (0, +∞), ← (t), ← (t), ||
–|| > d.
∵ ① ⇒ ② has been proven, ⇒ is the contrapositive of ①
⇒ ②.
∴ ⇒ is proven.
The meaning of ⇒ (Theorem 2) is that if all conflicts between UAV pairs are resolved, it can be ensured that the UAV fleet (all of the drones) is also operating conflict-free. In summary, it can be proven that the pairwise conflict relief control method can indeed solve multiple conflict relief problems in a UAV fleet. Therefore, constraint (c) is equivalent for both pairwise formation control and directly conducting multi-UAV formation control.
3.3. Single UAV Control Model
The single UAV control model is a basic element in the multi-UAV formation process, as well as a basic unit in the deep reinforcement learning model of UAV pairwise formation control.
In this section, we use a type of quadrotor UAV as an example to build the UAV control model. The movement of the quadrotor UAV can be regarded as a combination of the translation of the UAV center and the rotation of the UAV body. The rotation matrix is:
where is the roll angle, is the pitch angle, and is the yaw angle of the UAV.
The control method for quadrotor UAVs involves adjusting the speed of the propeller rotors. By maneuvering between the different speeds of the propeller rotors, complex actions such as roll, yaw, climb, and descent can be realized. The lift generated by the propellers is:
where is the atmospheric density, is the i-th propeller rotor speed of the UAV, S is the propeller area of the UAV, is the lift coefficient of the propeller, and is the lift force of the UAV. = ·r/2, where r is the length of the UAV propeller; therefore, Equation (2) can be simplified as:
where b is a composite lift parameter constituted by ,S, . is the angular velocity (r/min, RPM) of the i-th propeller rotor, is a vector composed of the four angular velocities of the UAV propeller rotors, = [, , , . The balance equation of the UAV is as follows:
where m is the mass of the UAV, g is the acceleration of gravity, is the air resistance coefficient, is the acceleration on the x, y, z axes, and is the speed on the x, y, z axes of UAV.
Then, construct the rotation model of the UAV. Since the structure of the quadrotor UAV is almost symmetrical, the inertia matrix I of the UAV can be defined as diag (, , ), which reflects the difficulty of rotating the UAV along axes x, y, z. The rotation moment matrix of the UAV is:
where , , are the rolling moment, pitching moment, and yaw moment of the UAV, l is the distance from the UAV propeller center to the UAV geometric center, and is the inverse torque proportional coefficient of the rotor. Therefore, the rotational motion of the quadrotor UAV is:
where = + − − , is the moment inertia of the propeller around the axis of the body shaft, are the acceleration values of the roll angle, pitch angle, and yaw angle, and are the angular velocity values of the roll angle, pitch angle, and yaw angle.
Now, the UAV dynamic model is built and the four control variables are the different speeds of the UAV’s four propeller rotors. The state () after t s can be described as:
where = [, , , , , ] is the original state of the UAV and = [, , , , , ] is the new state at timestamp t of the UAV.
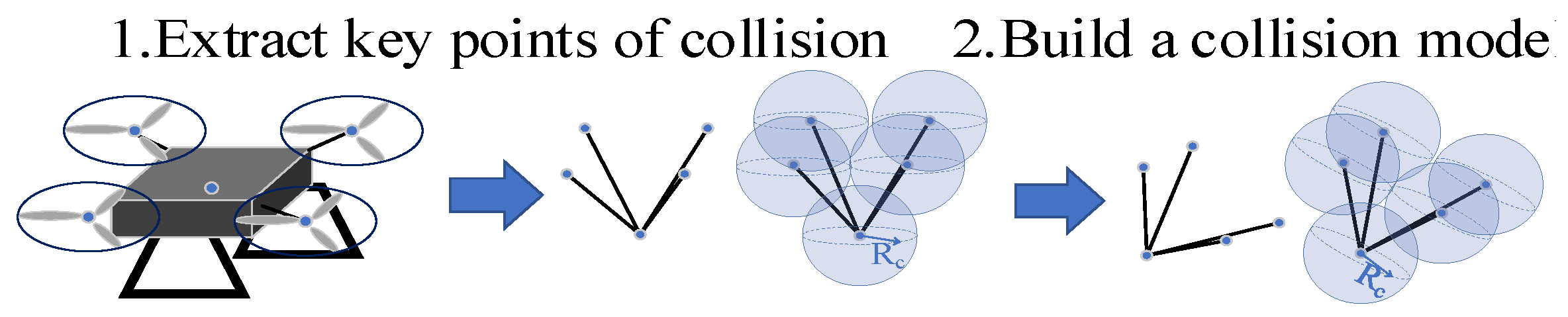
Finally, select the geometric center of the UAV and the centers of the four propellers as the collision points (Figure 1). Assuming that the geometric center of the UAV is also the Euler rotation center, the position of the collision points in the ground reference system [, , can be described as:
where [, , is the relative position of the key collision point to the geometric center of the UAV and [, , is the displacement of the UAV in the ground reference system.
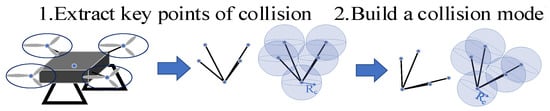
Figure 1.
The collision points of a quadrotor UAV.
3.4. DRL Model for UAV Pairwise Formation Control
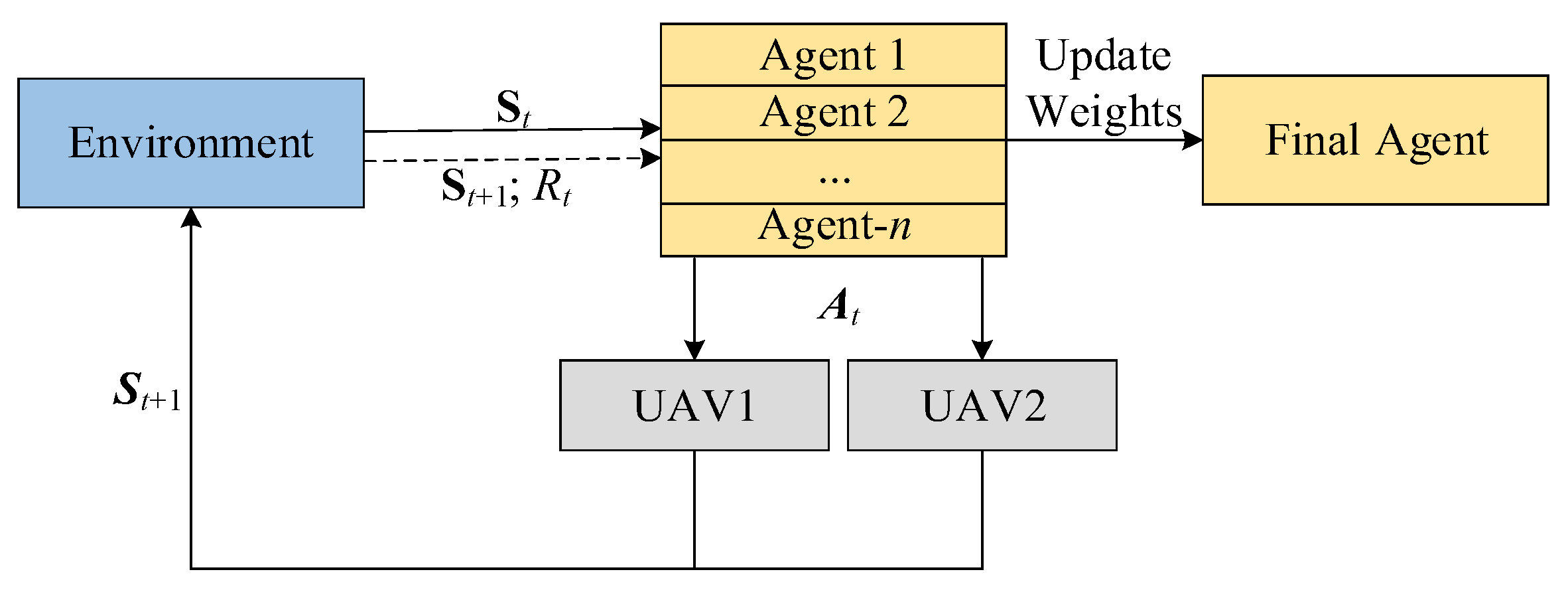
Construct the DRL model for UAV pairwise formation control based on the objectives, constraints, and UAV performance of this formation control problem (Section 3.1). It is worth noting that this DRL model is designed for the synergistic formation control of two UAVs, rather than the synergetic formation control of the UAV fleet directly, which is designed to reduce the training difficulty of the Agent. It is essential to integrate the dynamic pairing algorithm in Section 4.2 to realize the synergetic control of the UAV fleet. We use the classical structure of Environment–Agent to construct this DRL model.
3.4.1. Environment
- (a)
- State of the UAV pair.
A quadrotor UAV has the attributes of three position parameters (x, y, z), three rotation parameters (, , ), and four rotor speed parameters (, , , ). The state matrix , composed of two UAVs, has a total of 20 elements. Add the position parameters (, ), the height of the bottom surface , and the height of the top surface of the obstacle. Therefore, the state vector of a UAV pair can be described as:
The limitation of UAV performance can be described as:
where , are the minimum and maximum pitch angle of the UAV, and are the minimum and maximum roll angle of the UAV, means the maximum rotating speed of rotors, and is the state space of the UAV pair. These parameters are set to simulate the upper and lower limits of UAV performance and ensure it operates in a reasonable posture.
- (b)
- Action of the UAV pair.
The quadrotor UAV achieves roll, yaw, climb, and descend by controlling the speed of its four rotors. Therefore, the action of two UAVs at timestamp t can be defined as:
where is the adjustment of rotational speed for the j-th rotor in the i-th UAV, and is the 0–1 control variable for UAV hovering. When = 1, the i-th UAV hovers at the current position immediately and adjusts the speeds of the four rotors to balance the gravity. Due to the constraints of rotor acceleration and deceleration, choose the space of (adjustment of rotational speed, r/min, RPM) as:
The value of should also meet Equation (11), which means satisfying the performance constraints of the UAV, and the action space composed of is denoted as .
- (c)
- State transforming.
The state transforming function trans(.) is used to calculate the state of the UAV at timestamp t+1 after the UAV takes an action at state . The calculation process of the UAV’s position (x, y, z) and rotation (, , ) in this function as Equation (8), and the rotor speed parameters are calculated as:
In addition, the obstacle parameters (, , , , ) in are the closest obstacle parameters to any UAV in the UAV pair, which are derived directly from the Environment, as:
Then, a function of the UAV state transforming from timestamp t to t+1 is obtained, denoted as:
To further simulate the influence of the external environment, like wind, a random bias b needs to be added into , which is only effective for three position parameters (x, y, z), the final state of time t + 1 denoted as:
The expectation and variance of parameters in random bias b are denoted as: , , , .
3.4.2. Agent
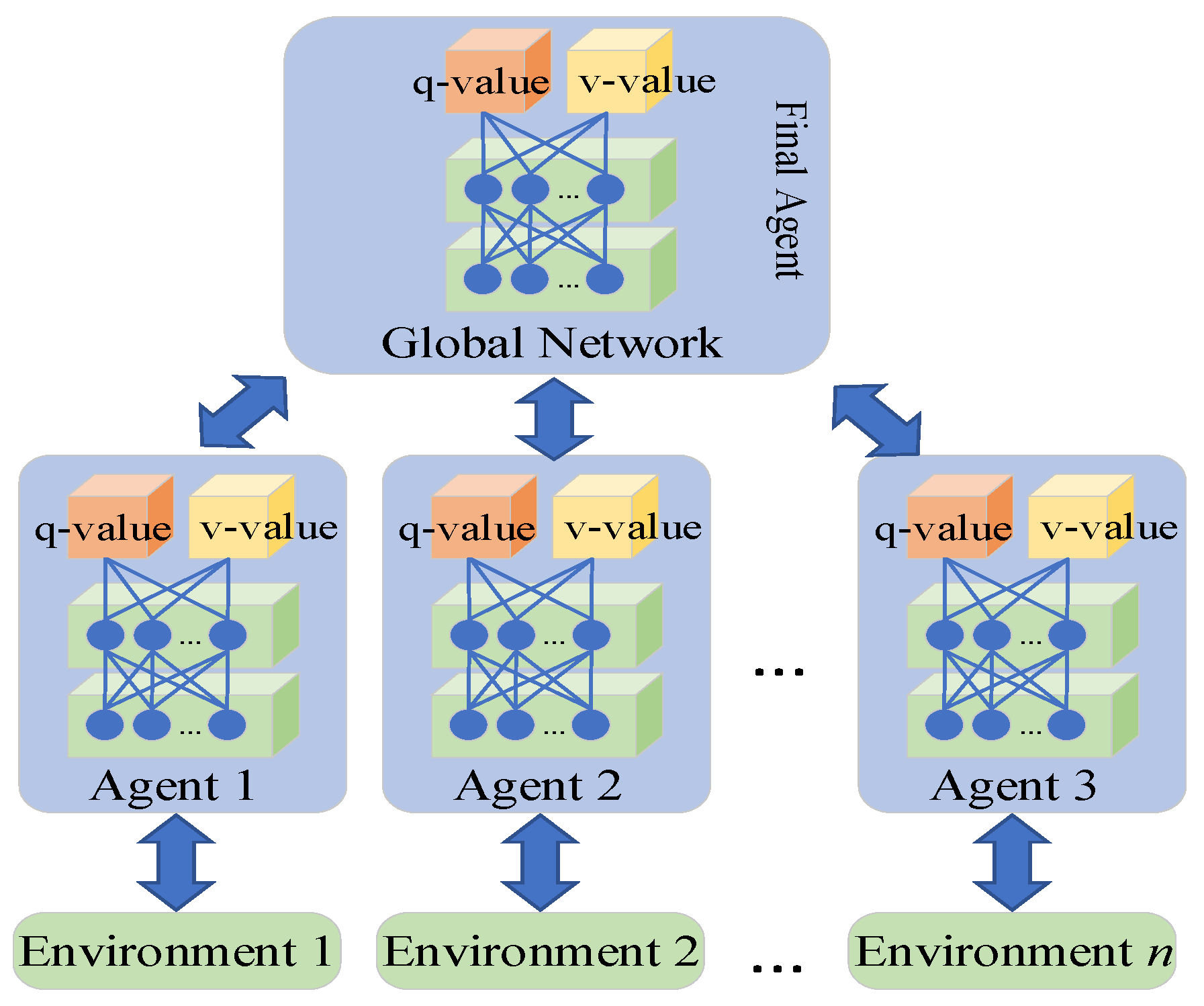
We use the A3C architecture to build the Agent as an example for implementing the P-DRL framework. There are two basic networks in each Agent: the Actor network and the Critic network. The same structure of Backpropagation (BP) neuron networks [40] is used for the Actor and Critic to evaluate the q-value and v-value, whose estimated values are denoted as (, ; W) and (; ), where W is the weight matrix of the Actor network and is the weight matrix of the Critic network. The input is the state of the UAV pair and the action in its action space, which are and .
The -greedy criterion is selected as the policy for the Agent to select the action at the state , policy () is denoted as:
where e is a random decimal between 0 and 1, which is obtained by the function random(.) and is a small positive constant.
3.4.3. Reward
Synergetic formation control of the UAV fleet needs to achieve the following goals: Firstly, the UAV must avoid obstacles and other UAVs. Secondly, the aircraft must reach the formation destination under this premise. Based on these drone formation control targets, the absolute value of the reward function can be designed according to the following principles: for every UAV pair composed of two UAVs, UAV safety reward ≈ Obstacle safety reward >> Formation reward. This enables the Agent to perform formation control while ensuring safe operation.
- (1)
- UAV safety reward.
Set the UAV safety reward at timestamp t as:
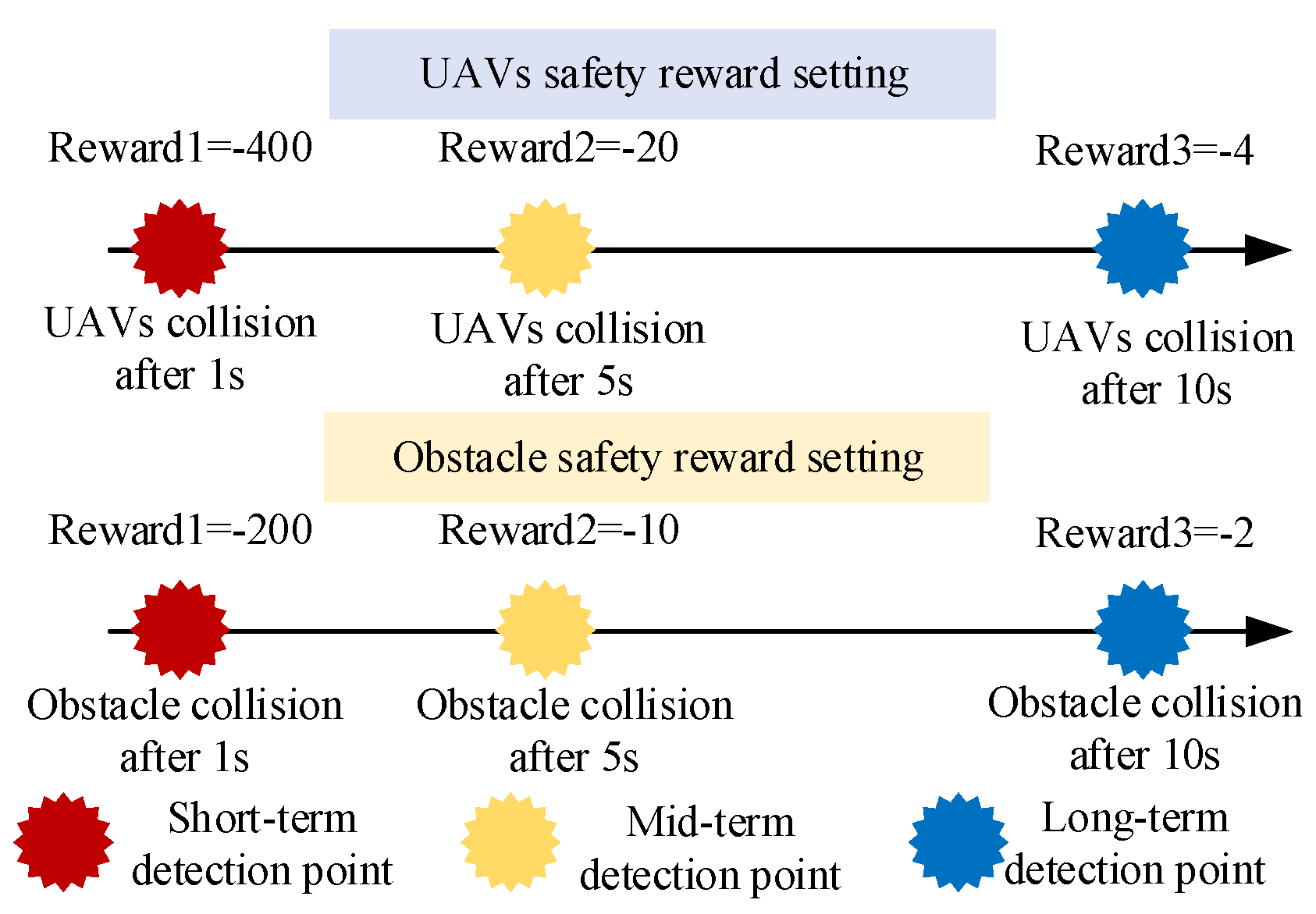
where [, , ] is the position of the i-th key collision point of UAV1 at timestamp t, and suffix j is for UAV2, for every single UAV, there are five key collision points, as seen in Figure 1. , , is the value of the reward, set = −400, = −20, = −4. , , are the prediction time spans according to the current state of the two UAVs. For example, it is assumed that = 1 s, = 5 s, = 10 s in this paper, which means the position of two UAVs after 1 s, 5 s, and 10 s will be calculated based on their current speed and attitude, then, it will receive its reward value according to whether there is a collision after 1 s, 5 s, and 10 s. d is the safety distance, which is used to judge whether UAVs collide, set d = 0.5 m.
- (2)
- Obstacle safety reward.
Set the Obstacle safety reward at timestamp t as follows:
where [, , ] is the position of the geometric center of the i-th UAV at timestamp k. [, ] is the position of the obstacle, and [, ] is the height of the bottom and top of the obstacle. is the radius of the obstacle. The values of , , , and , , are set in the same manner as in Equation (19) and summarized in Section 4.1.
- (3)
- Formation reward.
Set the Formation reward at timestamp t as follows:
where is the position of the i-th UAV at timestamp t. is the position of the i-th UAV at timestamp t+1, which is calculated by the transforming of the state and action . is the destination of the formation task. This mapping of the Formation reward can make the value of each UAV at a single timestamp falls within the interval −D to 0. Set the value of D = 10 in this paper.
Finally, the reward of the Environment–Agent interaction of two UAVs at timestamp t is:
There are some tips in reward shaping: Firstly, all of the rewards should be set as negative numbers to prevent the aircraft from circling in the airspace to get more rewards. Secondly, it is better to split the UAV safety reward and Obstacle safety reward into multiple rewards at different timestamps, which will speed up the convergence of the q-value and v-value, as well as play a role in conflict detection, as seen in Figure 2.
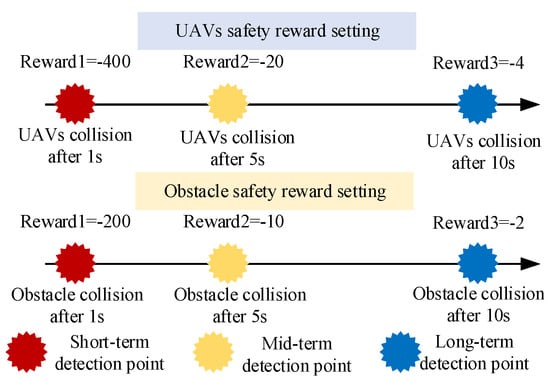
Figure 2.
Reward shaping with collision avoidance enhanced.
3.4.4. Interaction
This is similar to the architecture of most DRL models; for each timestamp t, the Agent selects the action based on the policy and the q/v-value of the state evaluated by the neural networks, then obtains the reward , and the state of UAV pair becomes . In the multi-agent learning model of A3C, it can be regarded that n Agents are performing the above steps and updating the weights of their common neural network, as seen in Figure 3 and Figure 4.
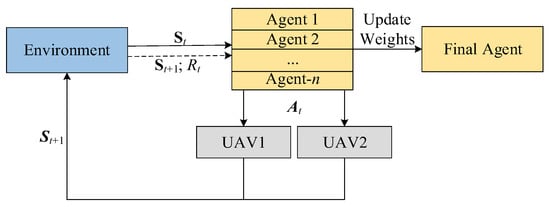
Figure 3.
Diagram of Environment–Agent interaction.
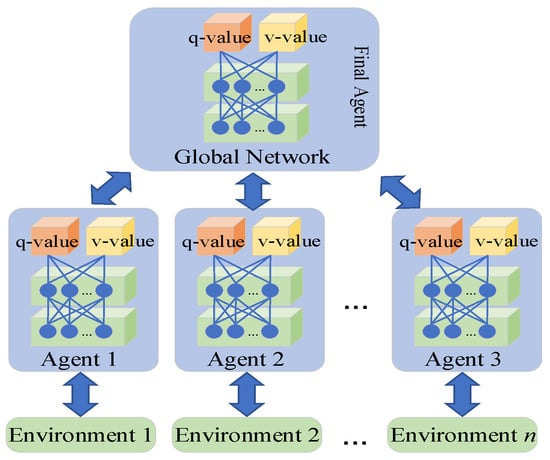
Figure 4.
Basic architecture of the A3C Agent.
As a result, the DRL model for UAV pairwise formation control can be represented as:
where (.) represents the mathematical expectations of the total reward under the policy , and T is the maximum timestamp in each round of formation control.
4. Approach
4.1. P-DRL Framework
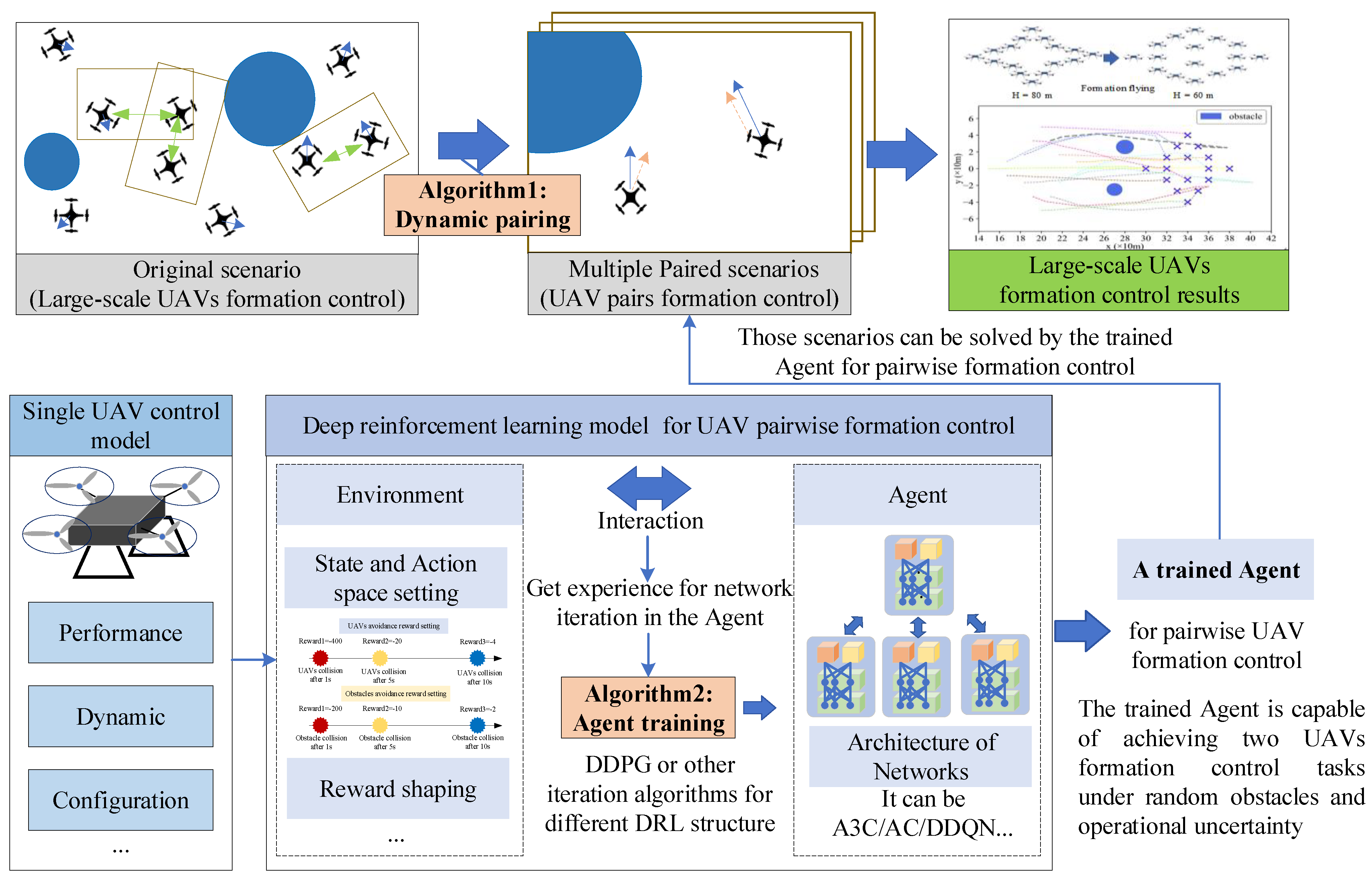
By integrating the dynamic pairing algorithm with the deep reinforcement learning method, we propose a real-time formation control framework for P-DRL, where the Agent in the DRL model can be many learning architectures of deep neuron networks, such as A3C, AC, DDQN, etc.
The main module in the framework and its functions are described below:
- Single UAV control model: this model is used to define the performance of UAVs, such as the maximum rotor speed, the range of rolling angle, the body configuration used for collision detection, and the state transforming function used in the DRL model.
- DRL model for pairwise formation control: this is the model used for training the Agent in the synergistic control of two UAVs, including the state, action space setting, and reward shaping in the Environment, the decision policy, the architecture of deep neuron networks in the Agent, and the Environment–Agent intersection mode.
- Algorithm 1—dynamic pairing: converts the formation control problem of a UAV fleet into a synergetic formation control problem involving multiple UAV pairs. This reduces the difficulty of Agent training and allows the control scenario to be solved by the Agent.
- Algorithm 2—Agent training: trains the Agent based on the reward returned by the Environment–Agent intersection.
- Implement: for every timestamp, the dynamic pairing algorithm chooses a UAV pair composed of two UAVs, then, the Agent allocates an action for each of them, loops until all of the UAVs have been paired, then turns to the next timestamp.
To simply describe this framework, we use the dynamic pairing algorithm to break down the original scenario into multiple paired scenarios, then we use the trained Agent to assign an action for the two UAVs, loop all the UAVs in the airspace, and iterate to the next timestamp. The Agent is trained based on the DRL model for UAV pairwise control, in which multiple DRL architectures such as AC, A3C, DDQN can be adopted. Therefore, we denote this framework as dynamic Pairing and Deep Reinforcement Learning (P-DRL), when the DRL uses the architecture of A3C, we denote the method as P-A3C. By analogy, formation control methods such as P-DDQN, P-AC can also be built based on this architecture, as seen in Figure 5.
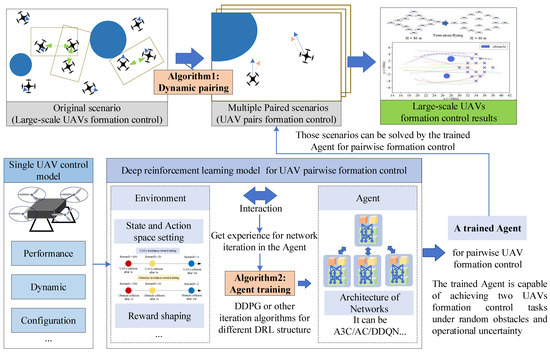
Figure 5.
Framework of dynamic pairing and deep reinforcement learning (P-DRL).
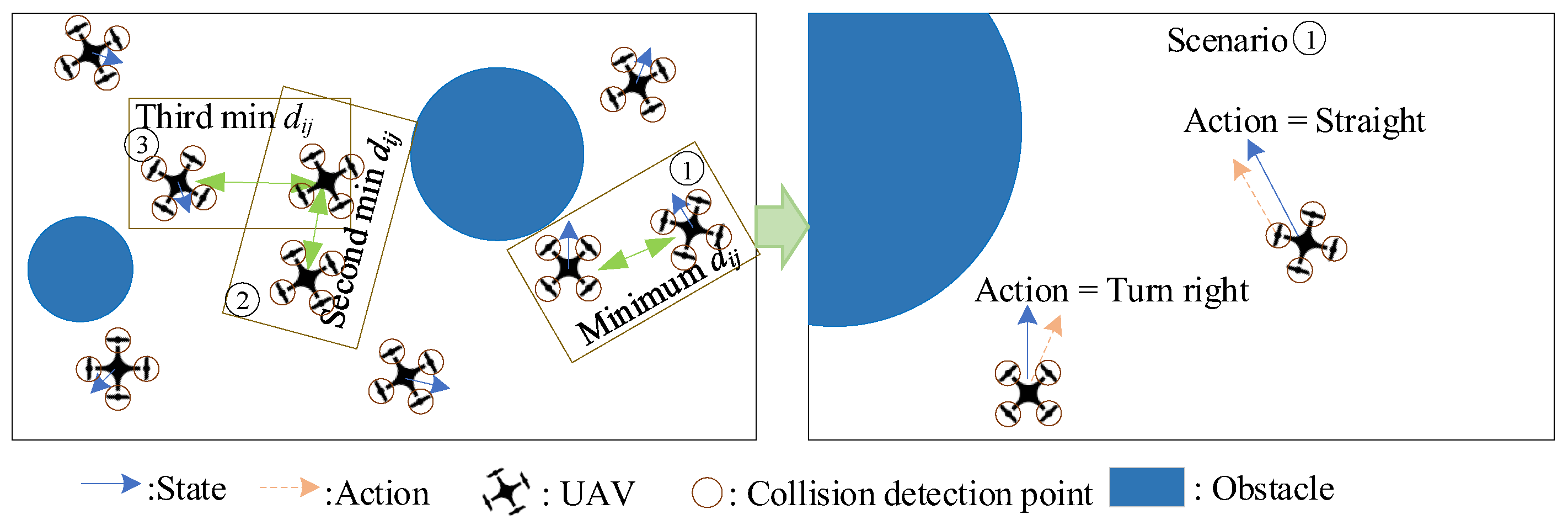
4.2. Dynamic Pairing
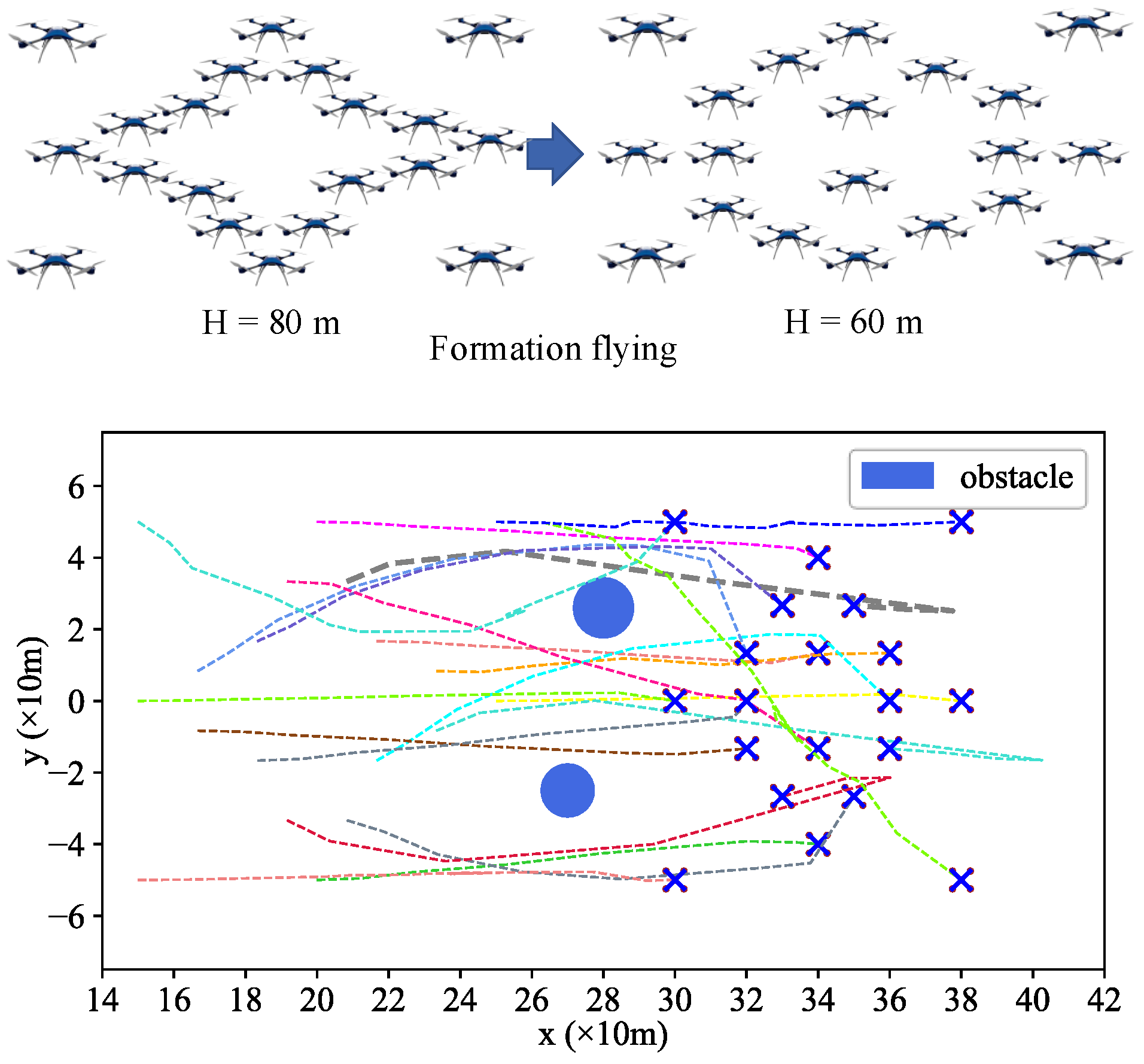
The core idea of dynamic pairing is to pair the UAV according to the severity of the conflict or potential conflict, The operational situation of UAVs varies over time, resulting in different UAV pairing results. This method simplifies the multi-UAV synergetic formation control problem to a two-UAV synergetic formation control problem, which can then be addressed by the trained agent, as seen in Figure 6.
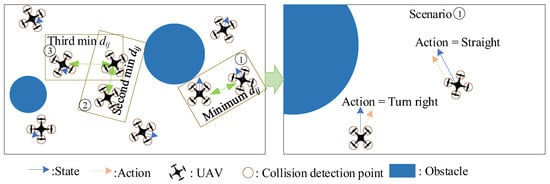
Figure 6.
The diagram of multi-UAVs formation control task simplified to multiple UAV pair formation control tasks.
A dynamic pairing algorithm is used to convert the synergetic formation control of n UAVs into multiple instance of two-UAV synergetic formation control. The main process is as follows:
Step 1: Build a set composed of UAVs waiting for formatting at timestamp t. Assuming there are n UAVs in the airspace (–). At timestamp t, initialize as:
Step 2: Build the distance matrix , as follows:
Step 3: Pick up the UAV pair (i,j) with the highest priority, as:
Step 4: For the UAV is in set , assign an action by the Agent, otherwise, skip it;
Step 5: Delete the UAV that has been assigned an action from , and return to step 3, until = ∅.
The pseudo-code of the dynamic pairing is shown below:
| Algorithm 1: Dynamic pairing algorithm for n UAVs. |
 |
This algorithm is designed based on the prioritization of conflict severity and pairwise action allocation. For the action assignment task at timestamp t, the number of UAVs is finite, so this pairing algorithm can traverse them. It is ensured that at least one UAV receives its action from the Agent in each dynamic pairing and action-allocating process. By repeatedly performing pairwise pairing and action allocation, the algorithm can traverse all of these UAVs at each timestamp t, finally completing the action assignment of multiple UAVs in the airspace.
It can be found that the algorithm complexity of this pairing method is polynomial, O(n−1), and the complexity for q-value and v-value evaluation by the trained Agent is also O(n), where n is the number of UAVs in the airspace. Therefore, the P-DRL-based method has a complexity of O(2n−1), which is perfect from the perspective of time complexity to realize real-time formation control in a complex environment.
4.3. Agent Training
This paper uses the A3C agent training architecture as an example to illustrate how to train an Agent using the constructed DRL model. For each instance of Environment–Agent interaction, the Actor network and the Critic network in the Agent will choose an action for two UAVs independently and assign the iteration parameters to the common network. For the Actor network, the Agent selects the action based on the value of (, ; W) and the strategy (). For the Critic network, the Agent selects the action based on the value of (; ), and executes the same processes as for the Actor.
Firstly, initialize the action value (q-value) evaluation neural network weight matrix W and the state value (v-value) evaluation neural network weight matrix . Initialize the learning rate , for the q-value and v-value network, and the discount rate .
Define the estimated value (, ; W) of the q-value by policy and weight W as:
Define the estimated value (; ) of the v-value by policy and weight as:
The Agent decides an action based on the value of (, ; W) or (; ) and the policy , then receives the reward feedback , and calculates the iteration error or .
Now, there are two weight matrices for the neural networks W and . Define the mapping , and the corresponding Fisher matrix of and are and , as follows:
Update W ←W + · (, ; W)· to decrease the value of [U − (, ; W)] · (| ; W), and update ← + · (; )· to decrease the value of [U − (; )]· (| ; ). The A3C training algorithm for synergetic control is Algorithm 2.
| Algorithm 2: Agent (A3C structure) training algorithm for UAV pairwise control. |
 |
4.4. Implement
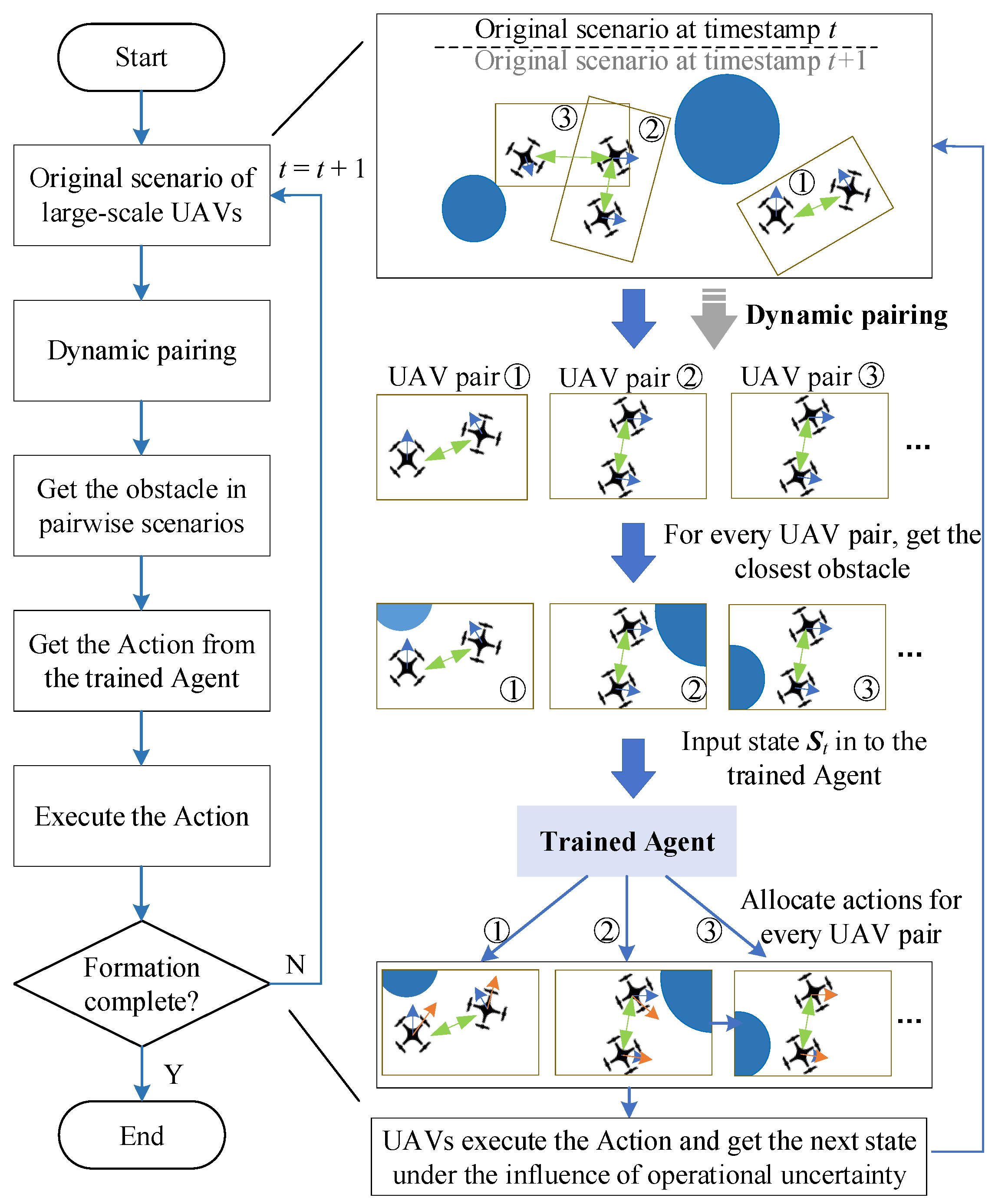
After the training process of the Agent is completed, we can use the Agent combined with the dynamic pairing algorithm. The implementation process of the P-DRL method can be demonstrated as seen in Figure 7.
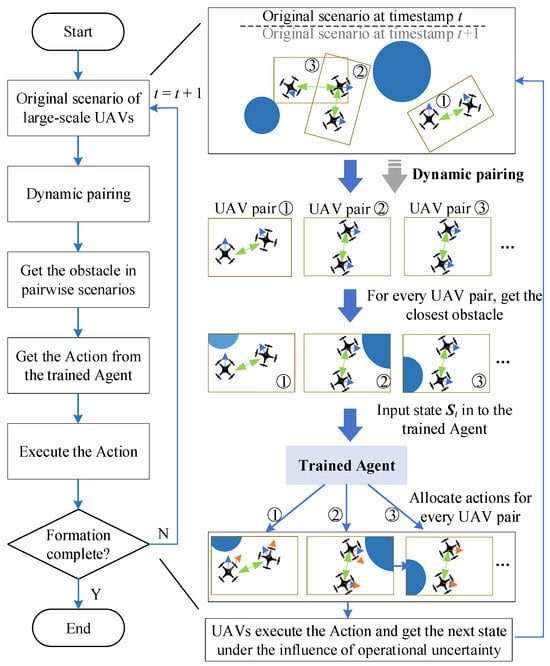
Figure 7.
Implementation of the method based on the P-DRL framework.
Step 1: Execute the process of dynamic pairing according to the situation of the UAV fleet at timestamp t. Then, we will obtain multiple UAV pairs using the pairing algorithm.
Step 2: For every UAV pair, obtain the obstacle which is closest to one of them, as:
Step 3: Then, we get the state of the UAV pair and the obstacle most related to their operation, as:
For every UAV pair, input this state vector into the trained Agent, then receive the action from the Agent, as seen in Equation (18).
Step 4: Every UAV executes the action from the Agent and receives a new state under the operational uncertainty.
Step 5: If the formation task has been completed, end this process, or else return to Step 1 with timestamp t + 1.
5. Simulation and Results
5.1. Background
We use the Da–Jiang Innovations (DJI) Phantom4-type UAV as our object for synergetic formation control experiments, and the key parameters are shown in Table 1. These parameters are set based on the official parameters of the drone manufacturer to ensure optimal simulation experiments [41].

Table 1.
Hyper-parameters of the UAV (Type: Phantom4).
The hyperparameter settings in the DRL model are summarized in Table 2.

Table 2.
Hyper-parameter settings in the DRL model.
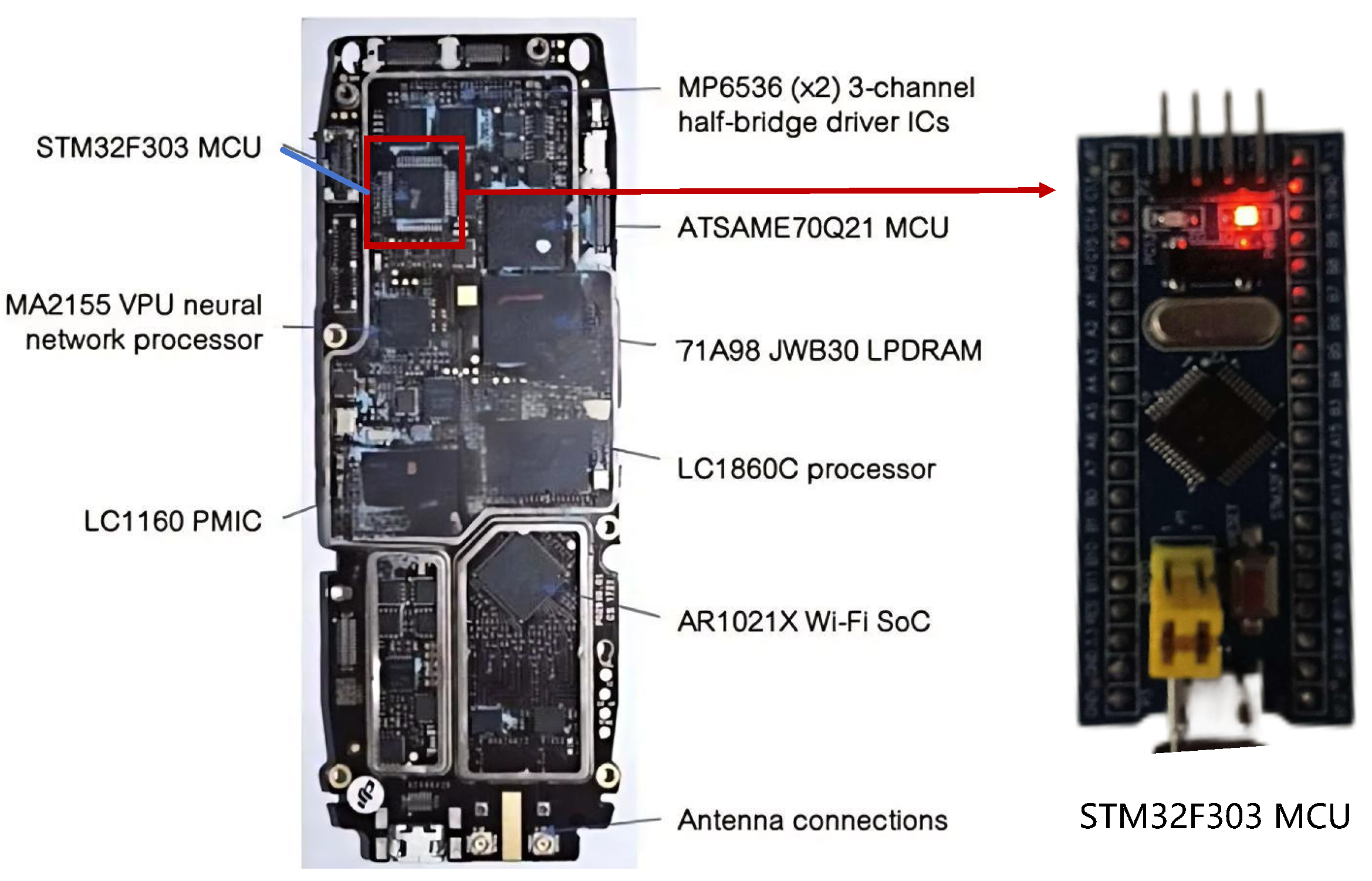
The simulations are based on a 64-bit operating system with 8 GB of processor RAM and i7-6700CPU. The simulation software is Spyder 5 with Python 3.8, and the hardware is a Microcontroller unit (MCU) of STM32F303 compiled using C language.
In the simulation experiments, we use the deep reinforcement learning architecture of A3C, Actor–Critic, and DDQN combined with the dynamic pairing algorithm, thus forming a P-DRL-based method (denoted as P-A3C, P-AC, P-DDQN) and we achieve synergetic formation control.
5.2. Simulations
5.2.1. Training the Agent
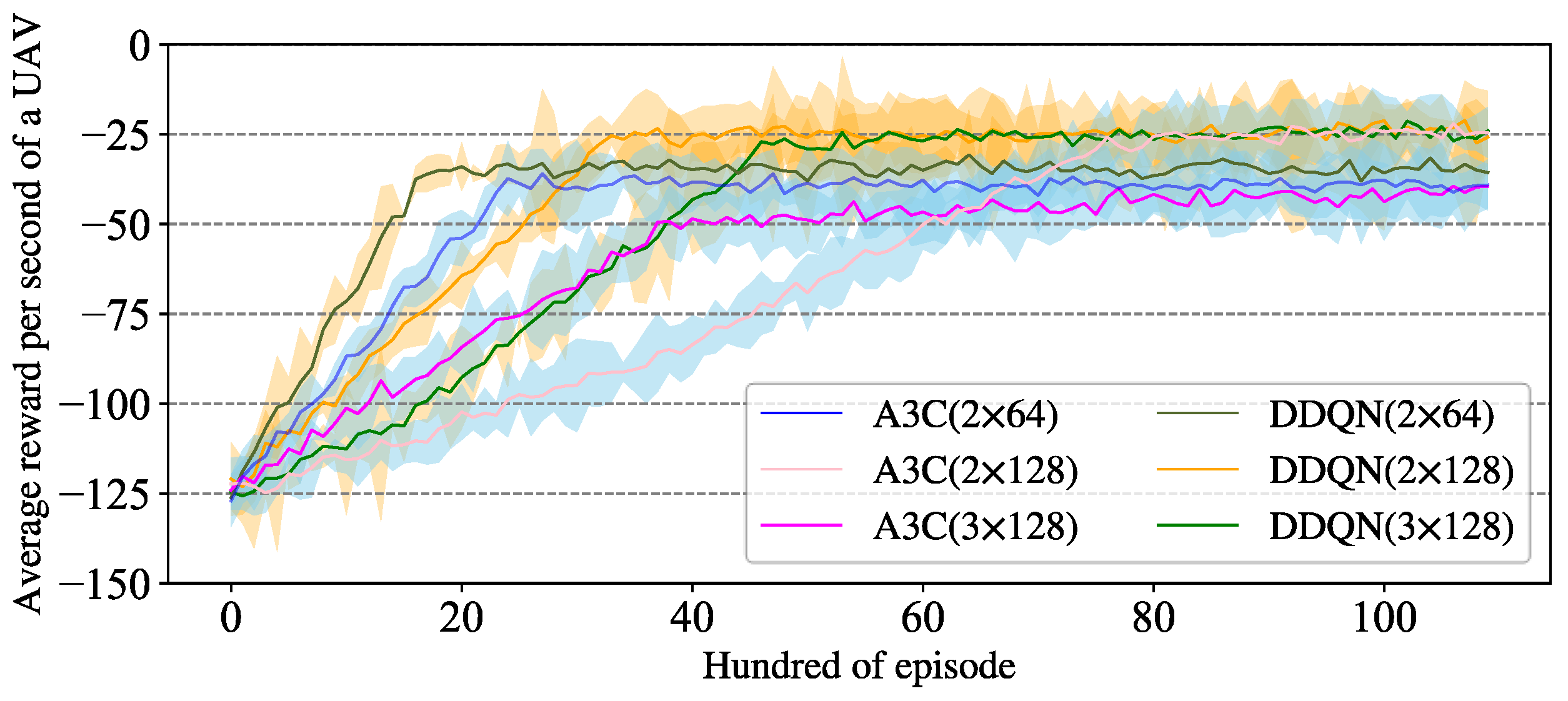
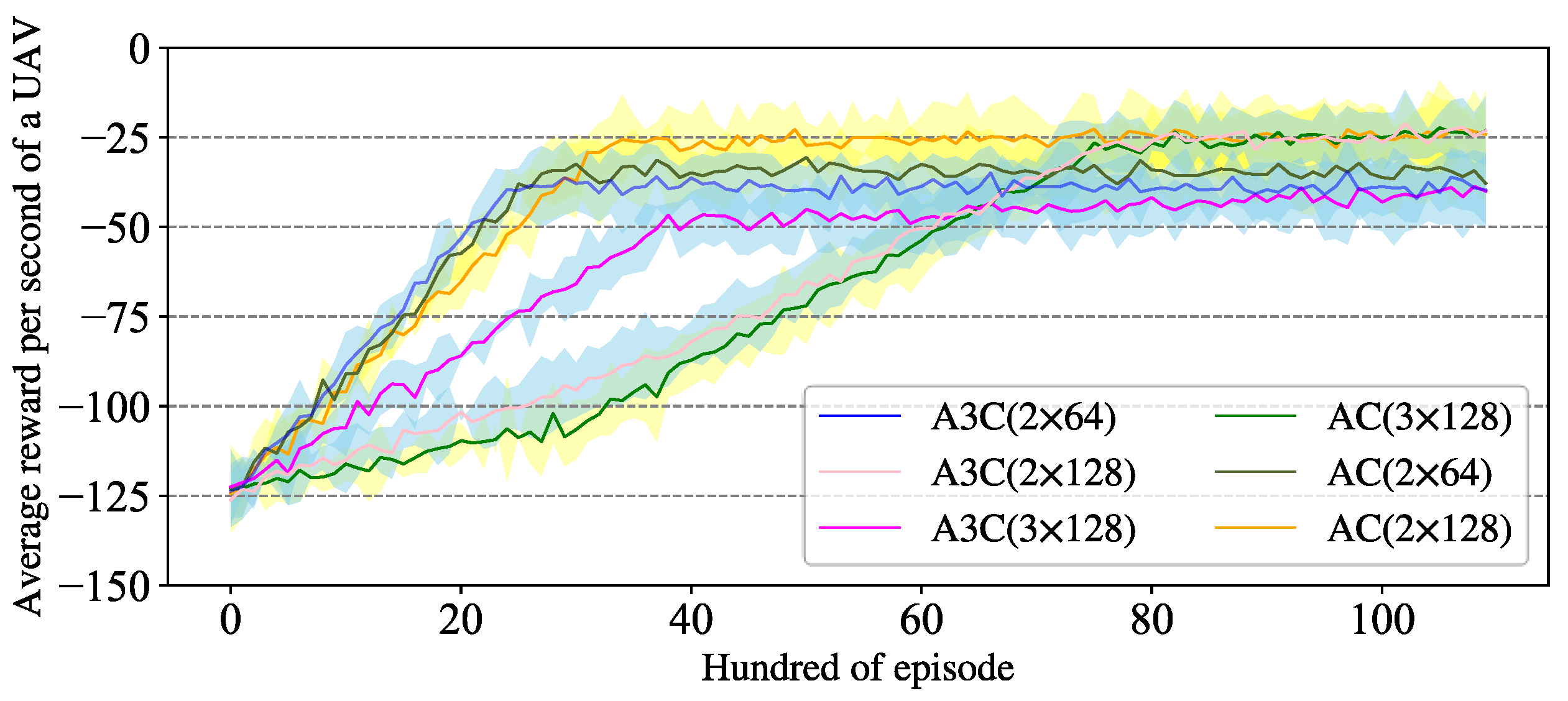
The architecture of the DRL model and the training algorithm have been described in Section 3.4 and Section 4.3. The P-DRL UAV formation control framework is a method that is compatible with multiple DRL models. In this paper, we choose three typical DRL models for experiments to demonstrate the excellent compatibility of the P-DRL model, and these models are A3C, DDQN, and AC. Taking A3C as an example, for both the Actor and Critic networks, we use the structure of two layers of BP neuron networks with 128 neurons per layer (denoted as 2 × 128), and 3 × 128 and 2 × 64 as the basic q-value and v-value estimation networks for ablation experiments. Double deep q-value network (DDQN) [42] and Actor-Critic [43] are used as extra experiments to demonstrate the universality of this control framework, where the Environment–Agent interaction mode, hyper-parameter settings, as well as the structure of the neuron networks are the same as A3C. The parameters in the reward function are set according to the principle of UAV safety reward ≈ Obstacle safety reward >> Formation reward, as described in Section 3.4.3. , , are set for collision detection over short-term, medium-term, and long-term periods. This approach enables the trained Agent to have more comprehensive conflict resolution capabilities. Also, the values of the learning rate and discount rate can be set as general deep reinforcement learning parameters. Then, we train an Agent using the DRL model of A3C, AC, and DDQN, as shown in Figure 8 and Figure 9.
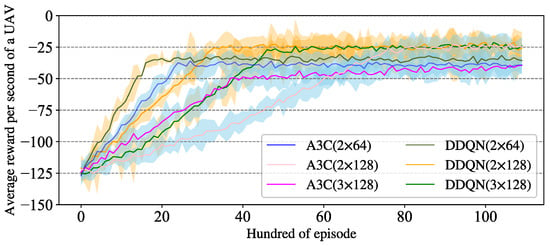
Figure 8.
The Agent training process of A3C and DDQN.
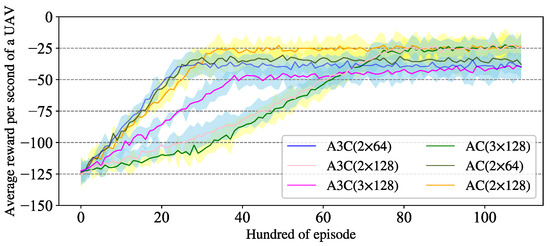
Figure 9.
The Agent training process of A3C and Actor-Critic.
The value of the average reward per second of a UAV reflects the synergetic control ability of the Agent. The training process shows that all of these methods have significant learning effects, but compared with the DDQN and Actor–Critic training algorithms, the Agent trained by the A3C algorithm has a more stable learning efficiency and better ultimate UAV pairwise synergetic formation control ability.
5.2.2. Formation Control
From the perspective of the UAV formation phase [44], UAV formation is mainly composed of four parts: formation shaping, keeping, reconfiguration, and dissolution.Formation shaping refers to the process from takeoff to achieving the predetermined spatial configuration, typically starting from a motionless state of the UAVs. Formation keeping mainly refers to the flying process of a UAV fleet in motion in a certain conformation in the airspace, which needs to counteract interference that will affect the formation [15], Formation reconfiguration refers to the process of changing the formation arrangement during the flying process. Formation dissolution is the process of the formation dissolving.
Generally, it is easier to execute formation-keeping and dissolution processes compared to shaping and reconfiguration. Therefore, choose the scenarios of shaping and reconfiguration to demonstrate the performance of the P-DRL-based method, in which UAVs should avoid multiple obstacles, counteract interference, and change the formation’s arrangements. The information on UAVs and obstacles in the scenarios is shown in Table 3.

Table 3.
Synergetic formation parameters for 20 UAVS.
- (1)
- Scenario 1: Formation Shaping Control
After training the Agent to complete the formation control tasks for two UAVs, the algorithm in Section 3.4.2 is used to convert the synergetic formation control of the UAV fleet into the synergetic formation control of multiple UAV pairs. Then, the Agent is used to solve the formation control task for the UAV pair at each timestamp and complete the formation control task of the UAV fleet by repeating the above process.
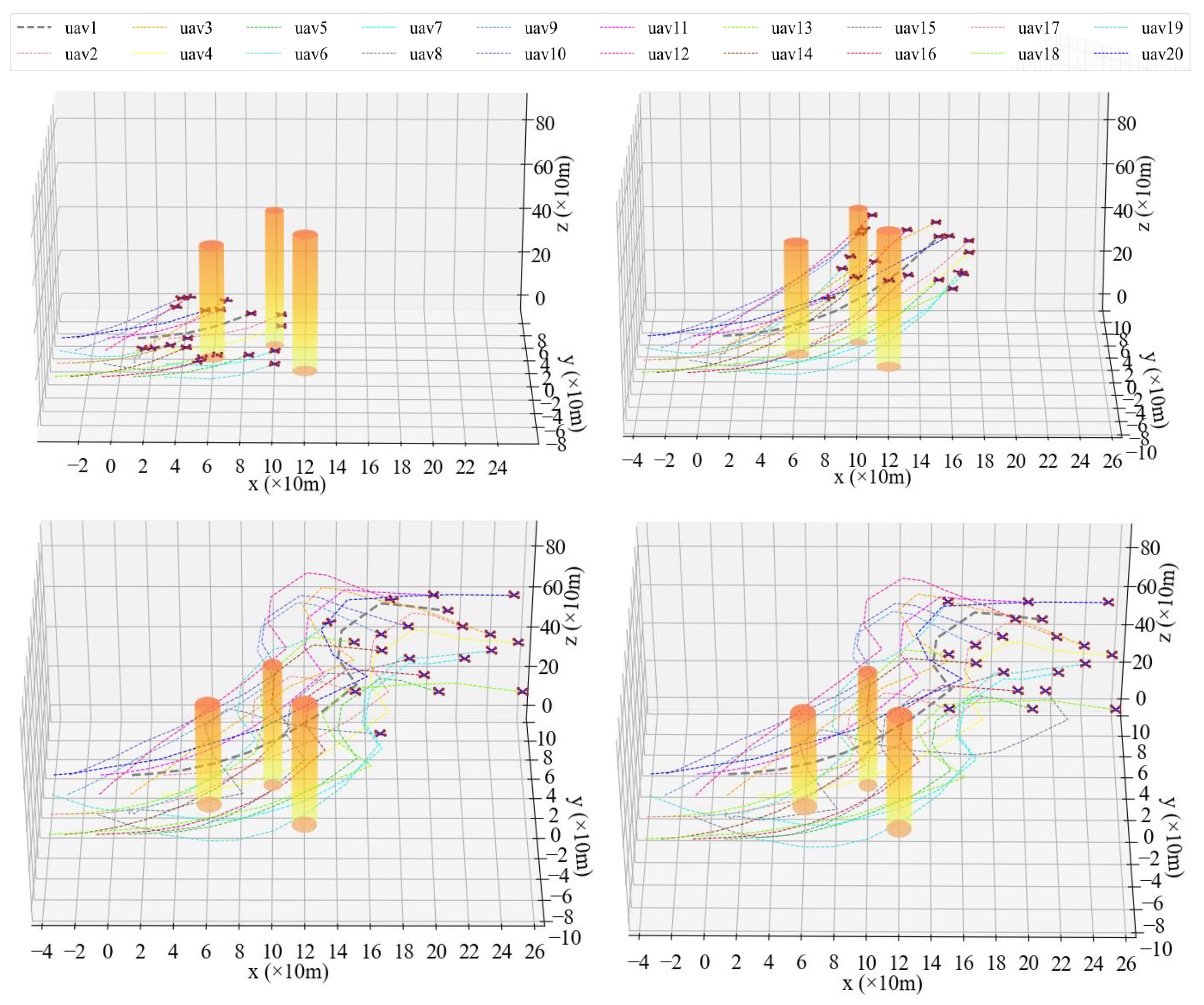
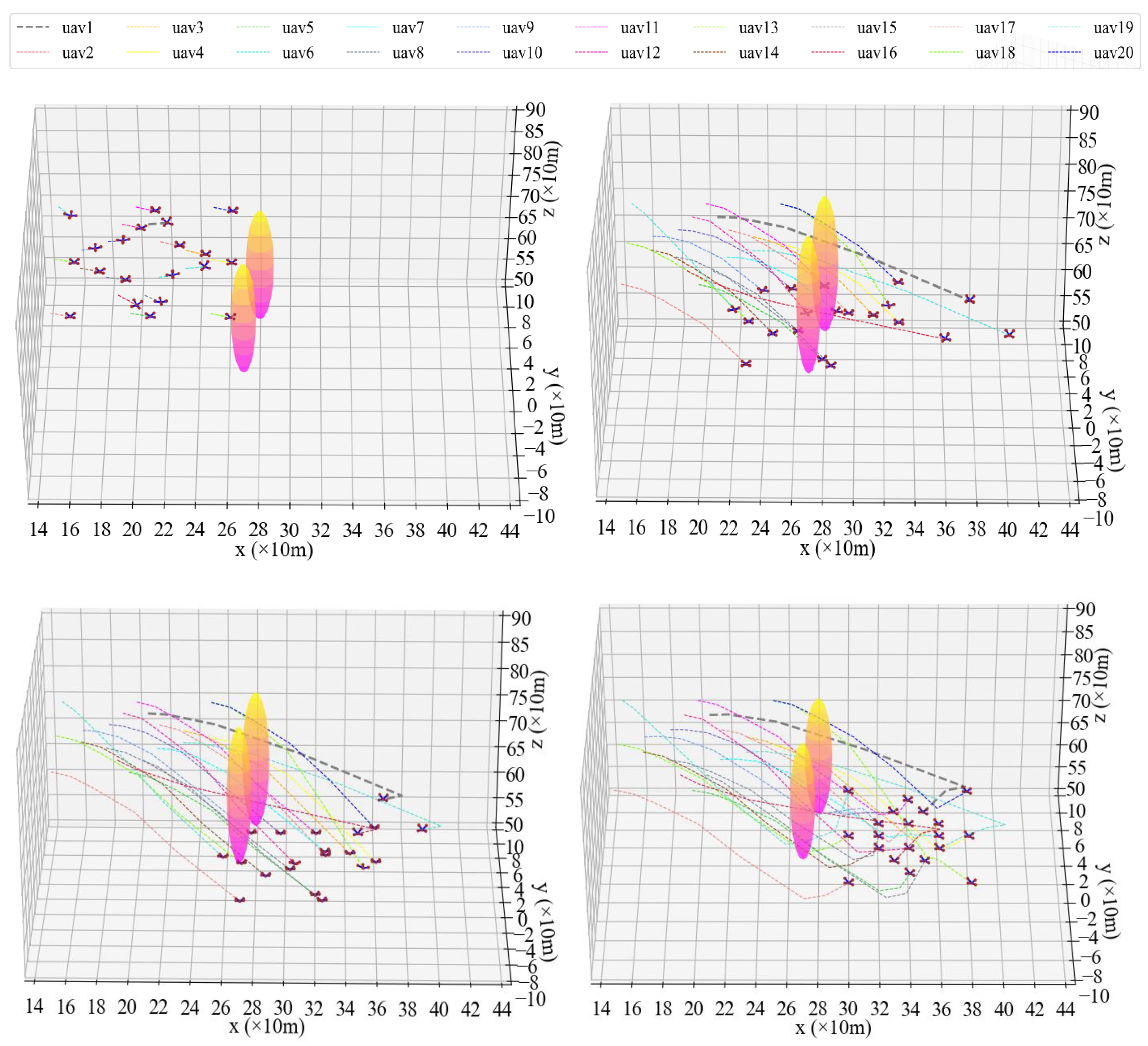
The process of taking 20 UAVs from a static state to formation arrangement based on the P-A3C method is shown in Figure 10 and Figure 11.
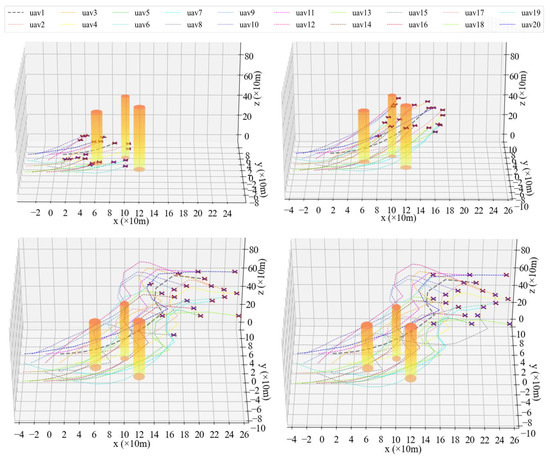
Figure 10.
3D diagram of UAV formation arrangement at different timestamps.
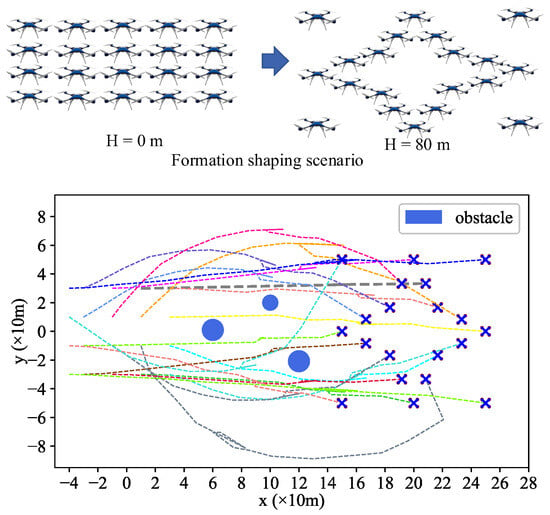
Figure 11.
2D diagram of UAVs’ formation shaping control.
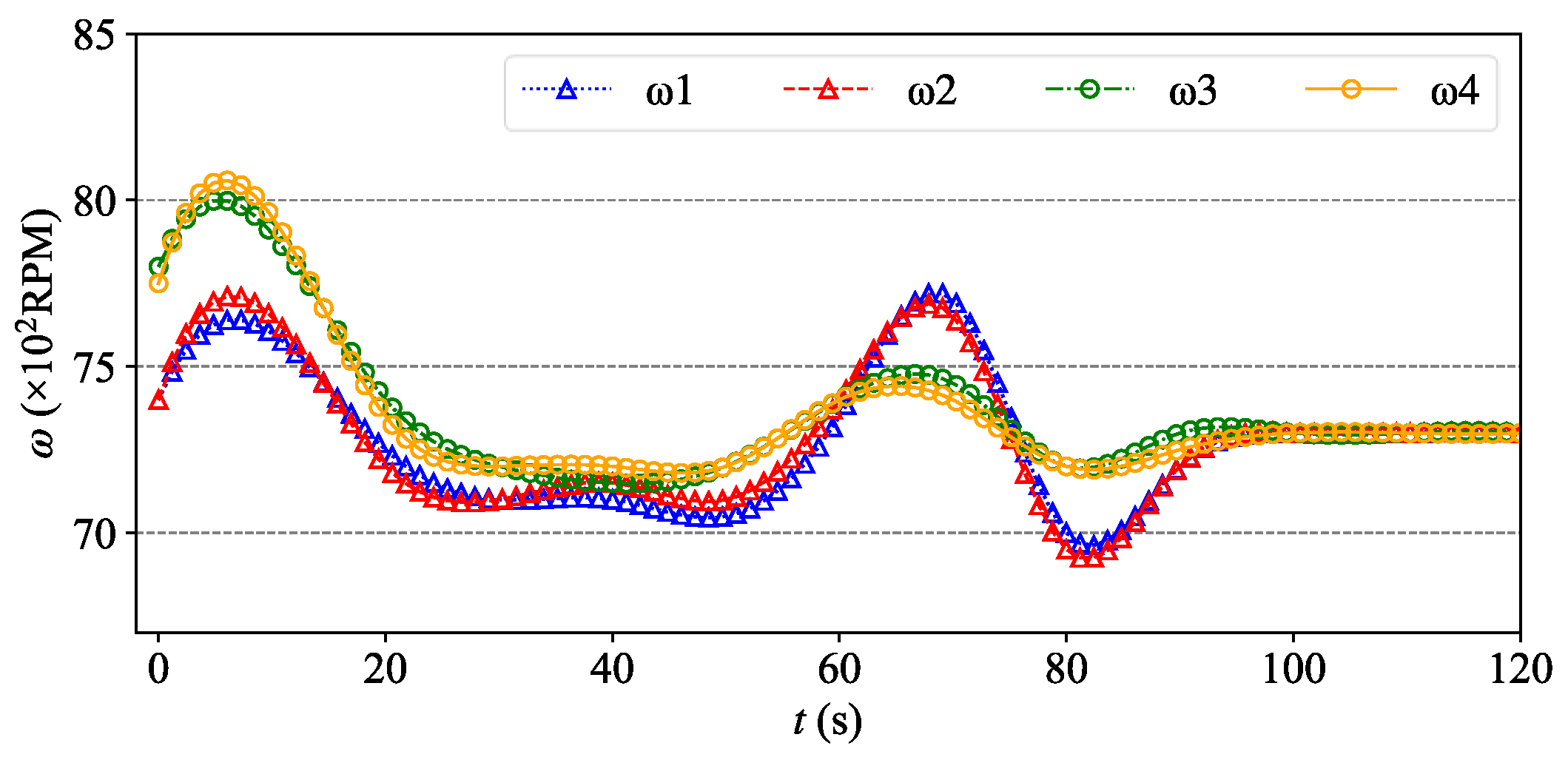
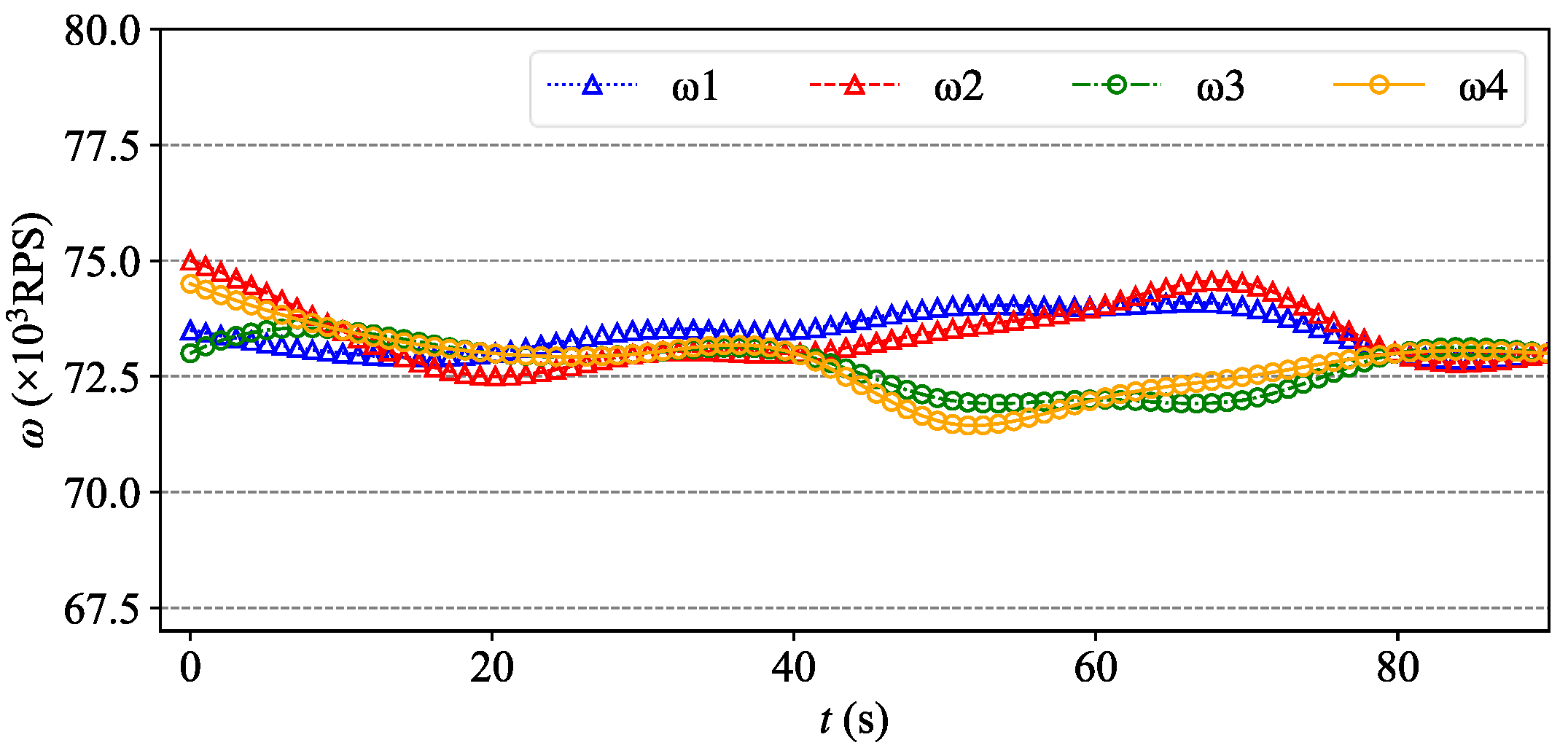
It can be seen from Figure 10 and Figure 11 that this synergetic formation control method for the UAV fleet achieved good results. The 20 UAVs avoided obstacles and avoided trajectory conflicts with other UAVs while reaching the formation destination at a relatively fast speed. In Figure 11, due to the requirement of adjusting altitude and avoiding surrounding drones, some repeated adjustments in a horizontal direction were made in the region of x = 80–160. Taking four propeller rotor speeds of UAV1 changing with time as an example (gray bold dotted line in Figure 10 and Figure 11), it can be seen in Figure 12 that the control of the UAV by the Agent is smooth and accurate, which conforms to the general aerodynamics.
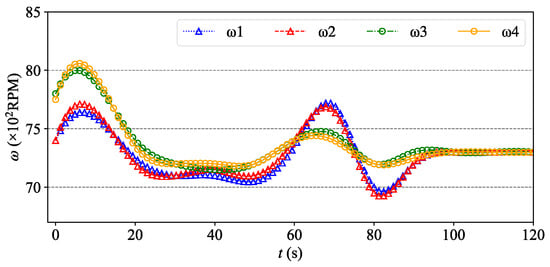
Figure 12.
Four propeller rotor speeds of UAV1 in the process of formation arrangement.
- (2)
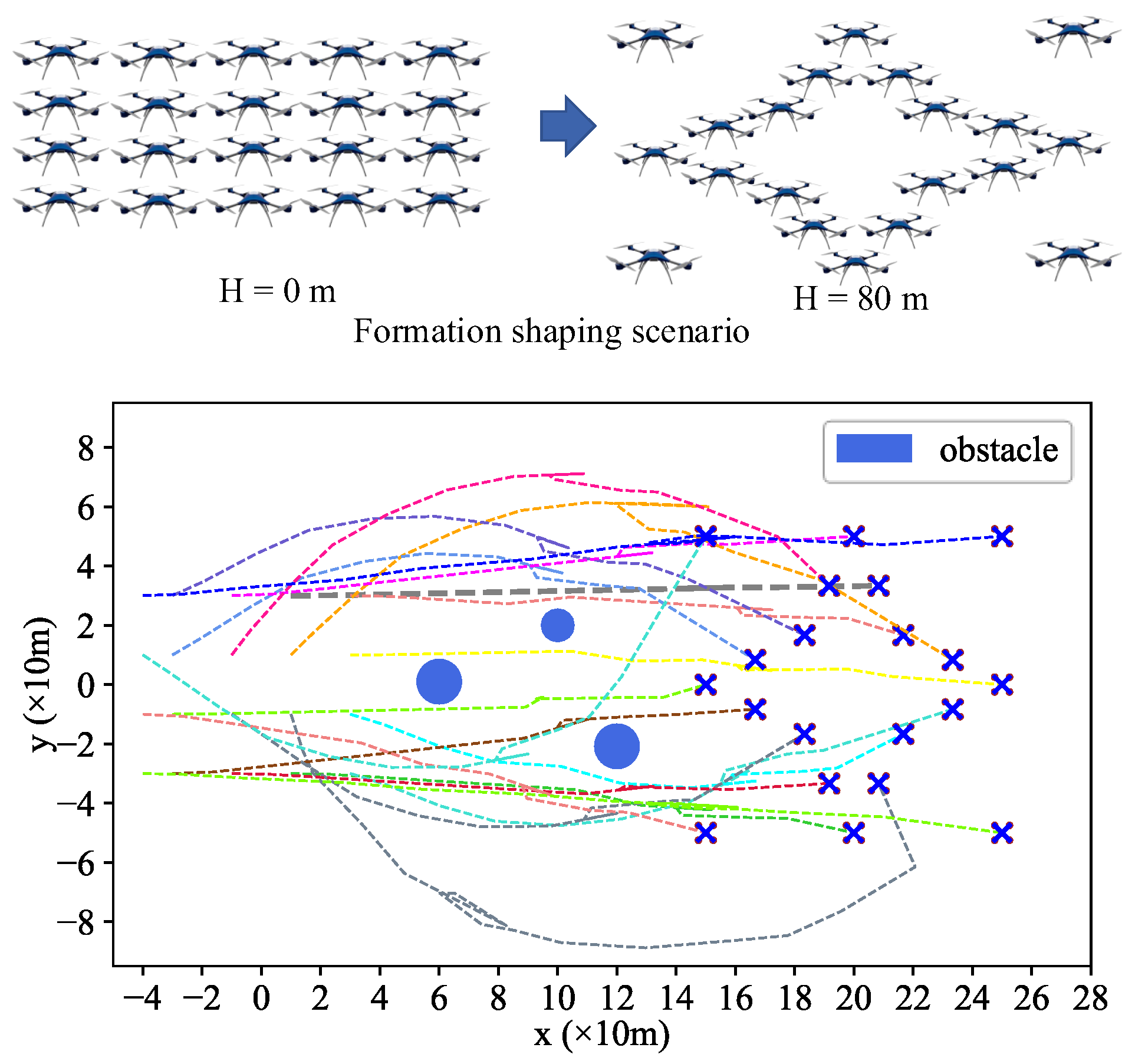
- Scenario 2: Formation Reconfiguration Control
Scenario 2 is an experiment starting from the formation arrangement results of Scenario 1. The 20 UAVs descended from a star formation and re-arranged into a diamond formation while avoiding collisions between UAVs and obstacles. The process of formation reconfiguration for 20 UAVs based on the P-A3C method is shown in Figure 13 and Figure 14.
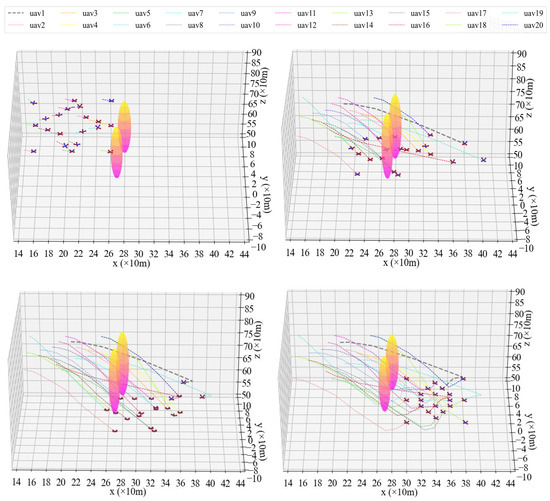
Figure 13.
3D Diagram of formation reconfiguration of UAVs at different timestamps.
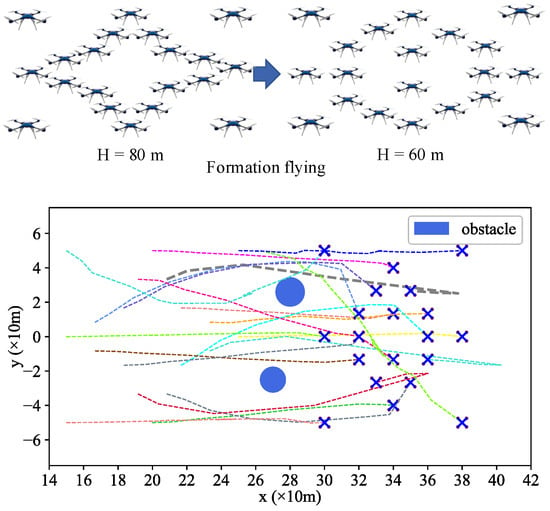
Figure 14.
2D diagram of formation reconfiguration control for UAVs.
It can be seen from Figure 13 and Figure 14 that these 20 UAVs can avoid obstacles and trajectory conflicts with others while reaching the new formation destination at a fast speed under the control of the Agent. In this simulation, we set an initial speed for the drones, therefore, the formation flying speed is relatively fast compared to Scenario 1. Four propeller rotor speeds for UAV1 (gray bold dotted line in Figure 13 and Figure 14) change with time, as shown in Figure 15.
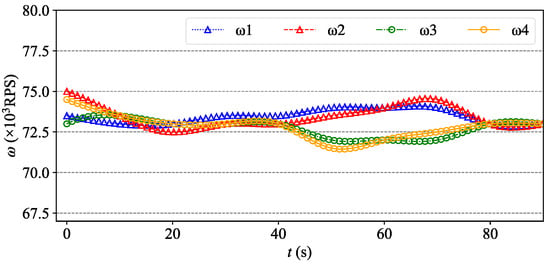
Figure 15.
Four propeller rotor speeds of UAV1 in the process of formation reconfiguration.
5.3. Performance Analysis
5.3.1. Success Rate of Non-Collision Formation Control
- (1)
- Success Rate sensitivity analysis by changing control frequency.
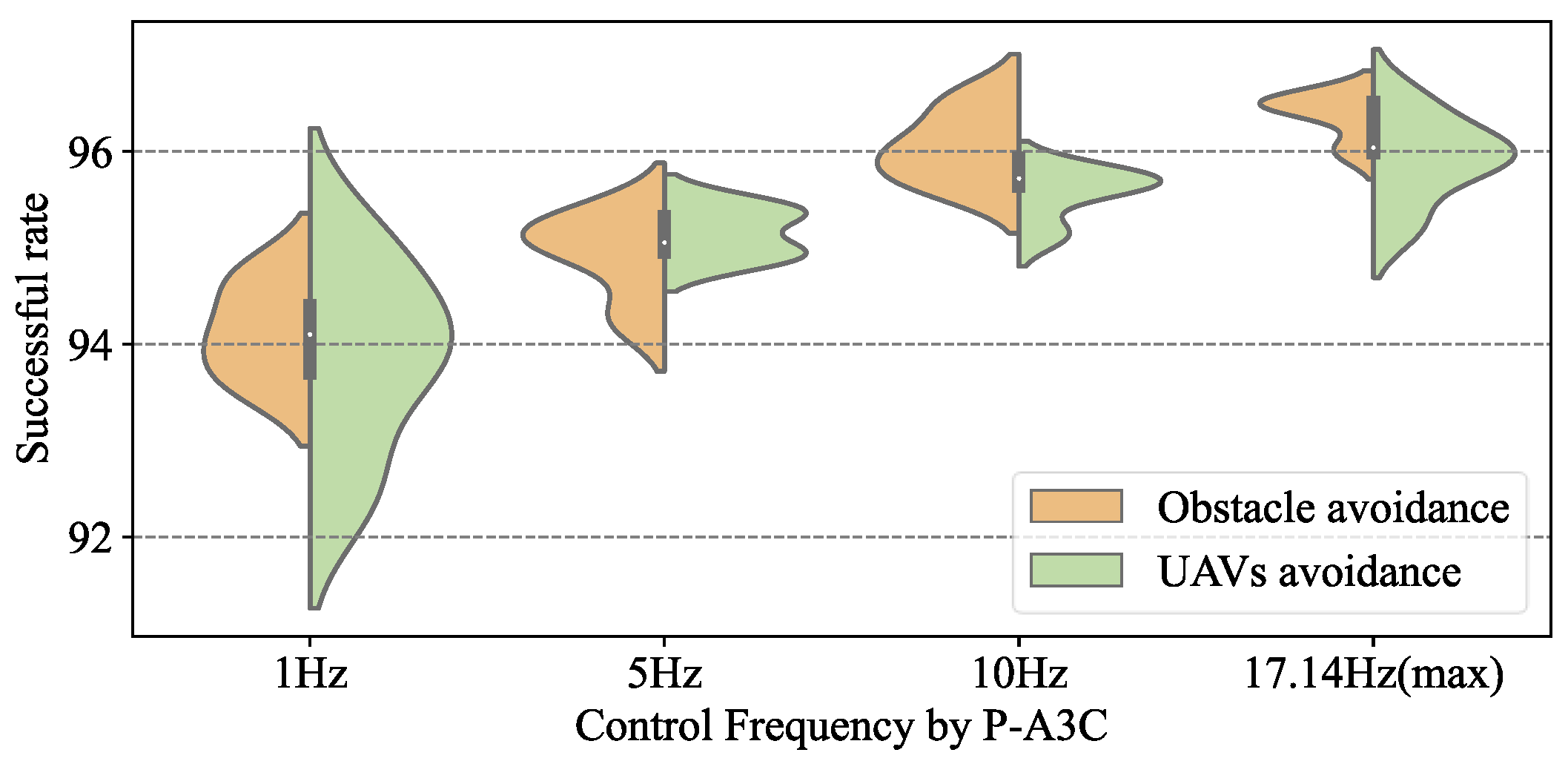
The P-A3C formation control framework can adapt to the multi-UAV formation tasks in the presence of multiple random obstacles, which means this method can be used in other scenarios without retraining the DRL model, even when the obstacles are unknown before the formation tasks and are controlled in real-time by the trained Agent. There are 49 other scenarios composed of 10–20 UAVs designed to test the success rate of non-collision synergetic formation control by P-A3C, P-DDQN, and P-AC. During this process, we attempted to change the control frequency of the Agent sending control commands to the UAVs. The non-collision success rate of P-A3C, P-DDQN, and P-AC changing with the control frequency are shown in Figure 16, Figure 17 and Figure 18.
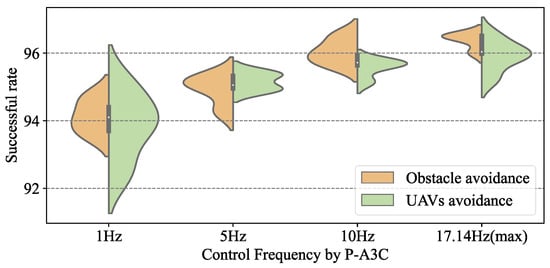
Figure 16.
Non-collision success rate of P-A3C changing with the control frequency.
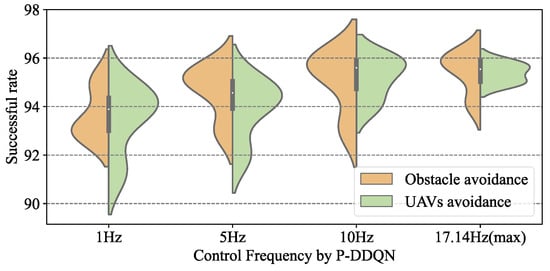
Figure 17.
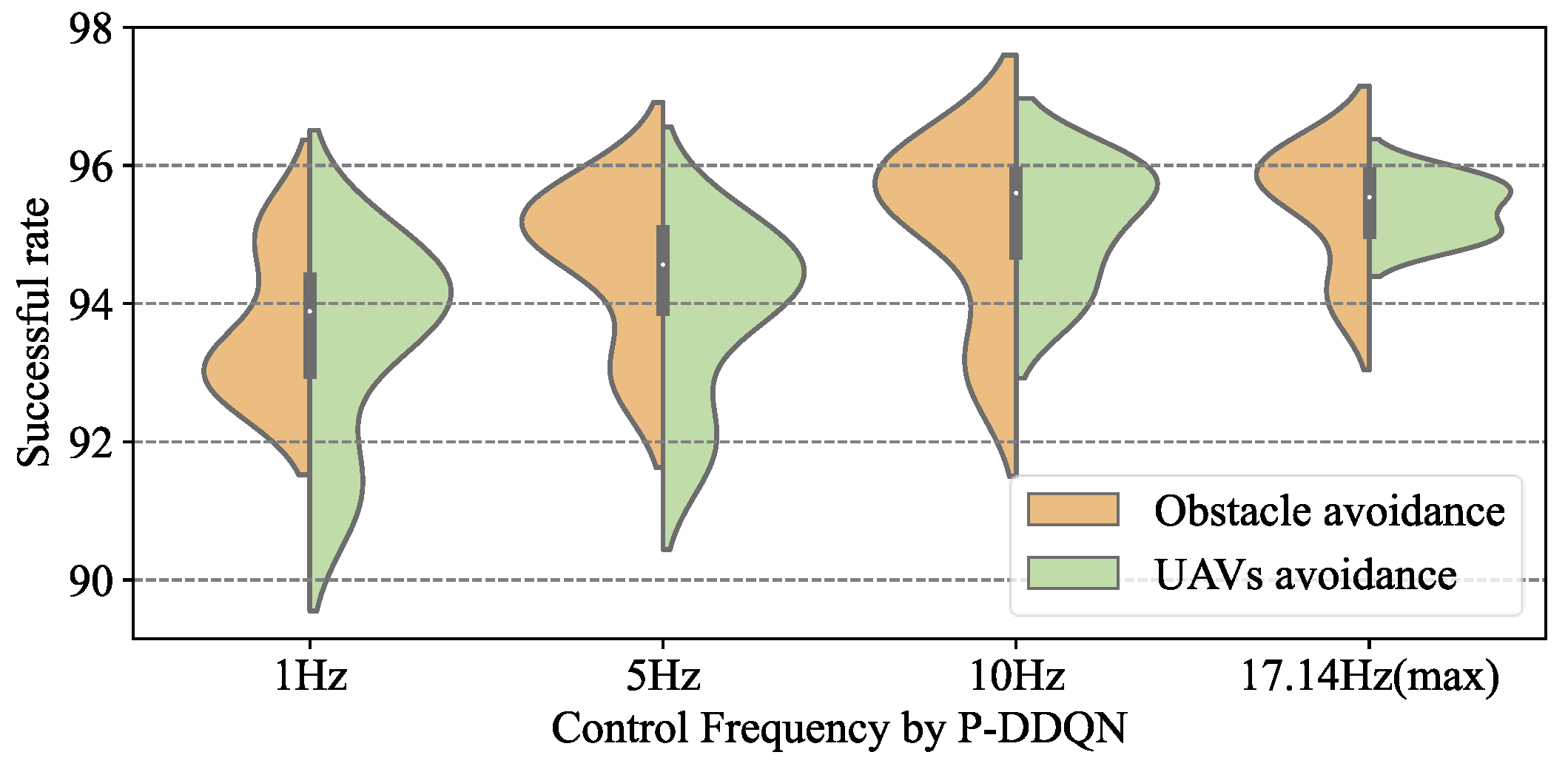
Non-collision successful rate of P-DDQN changing with the control frequency.
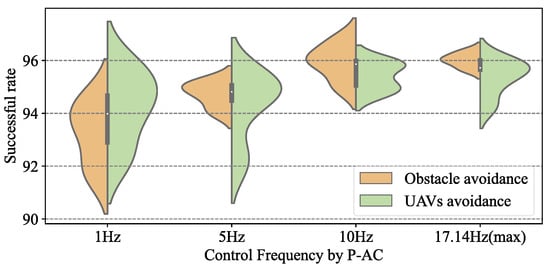
Figure 18.
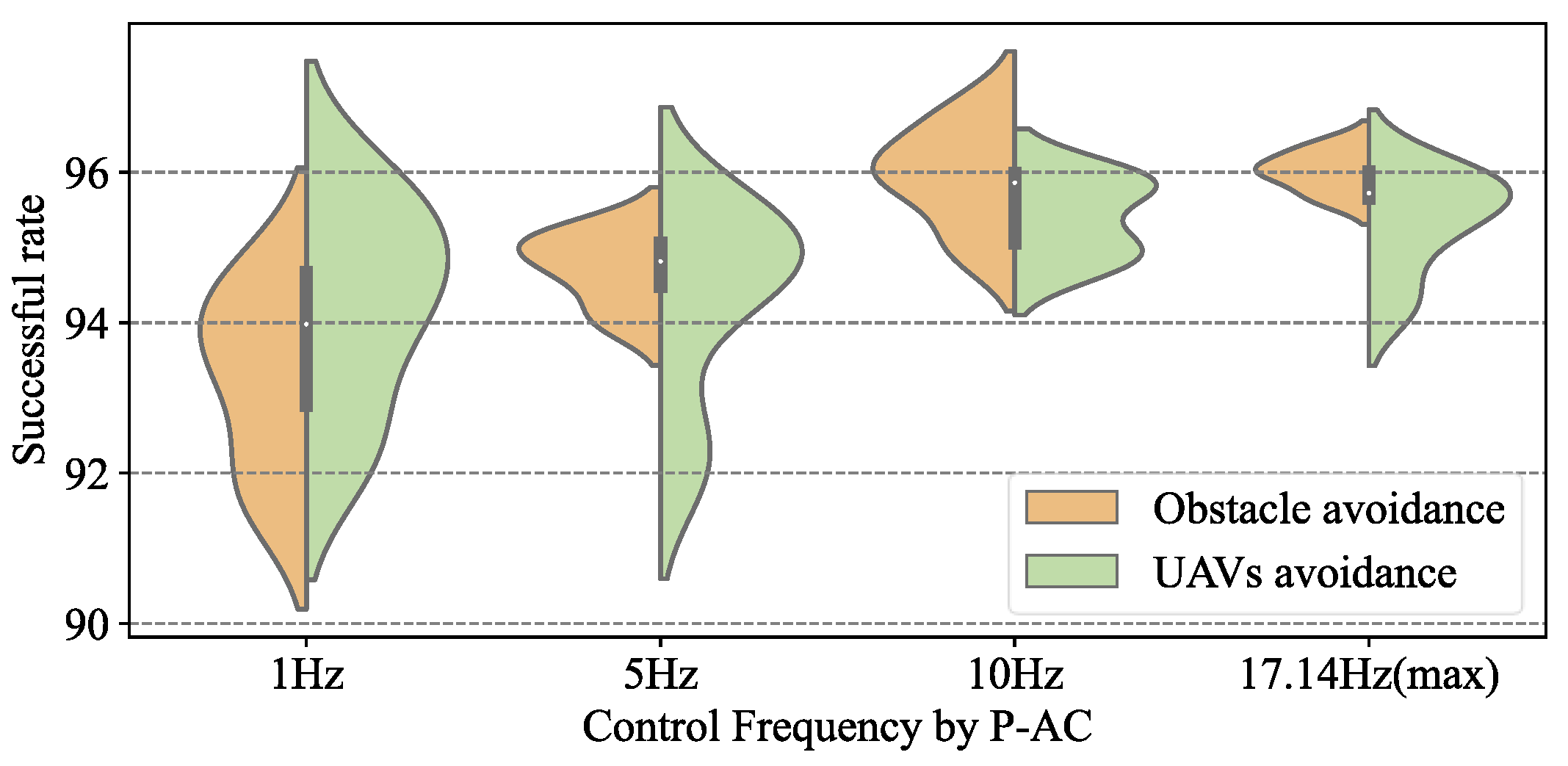
Non-collision success rate of P-AC changing with the control frequency.
Control frequency by the Agent represents the update frequency of the drone’s actions, for example, a control frequency of 1 Hz means the Agent controls the drones’ actions every second, and a control frequency of 10 Hz means the Agent controls the drones’ actions every 0.1 seconds. Due to the execution time requirement of the P-DRL formation control algorithm, the maximum control frequency is 17.14 Hz.
Firstly, Figure 16 reflects the excellent compatibility of the P-DRL formation control framework with multiple types of deep reinforcement learning methods. Although there were some differences in specific performance and stability, the A3C, DDQN, and AC deep reinforcement learning methods all performed well in this framework (A3C: 91.7–96.2%, DDQN: 90.0–96.2%, AC: 90.1–96.3%).
While continuously increasing the frequency of control decisions by the trained Agent, the success rate in the 50 c formation control scenarios shows a clear trend of “grow then stable”, which is a point worth paying attention to. In the P-DRL framework, increasing the control frequency of the Agent does not increase the success rate to 100%. The reason is that there is a performance limit on the UAV’s control. Sometimes even if the Agent makes the correct decision, it may still lead to collisions due to the high speed of the UAVs and the control lag. An obvious and effective solution is to limit the maximum operating speed of the UAV (such as setting = 5 m/s) to improve the success rate. Certainly, the experimental value of this measure is not significant and inefficient and time-consuming formation control can naturally improve its operational safety, rather than benefiting from the method improved.
- (2)
- Success rate with collision avoidance measure.
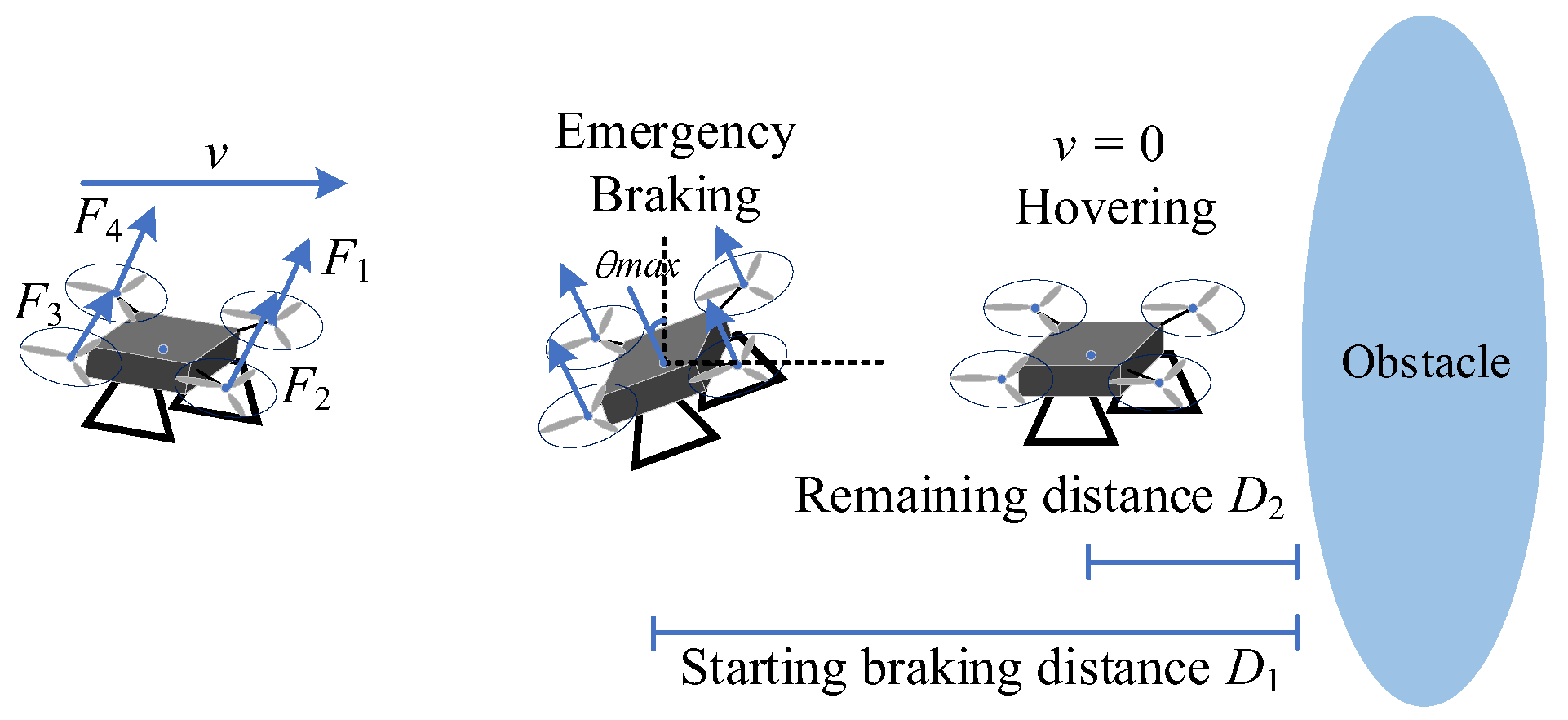
In this section, we introduce an emergency braking collision avoidance measure into the P-DRL formation control framework. Assuming that the surrounding sensors of the UAV detect that the distance from the obstacle to itself is less than = 0.5 m, then the UAV immediately brakes with maximum braking performance to ensure operational safety. In this experiment, emergency braking is not always safe. When the UAV flies towards an obstacle at high speed, emergency braking may fail, resulting in the UAV colliding with the obstacle. See the diagram of emergency braking in Figure 19.
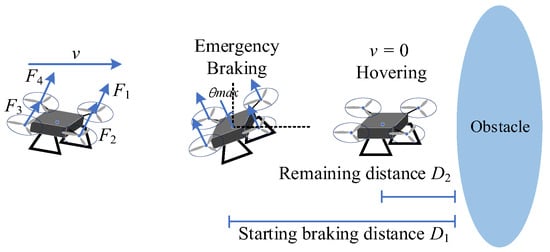
Figure 19.
Diagram of the emergency braking collision avoidance measure.
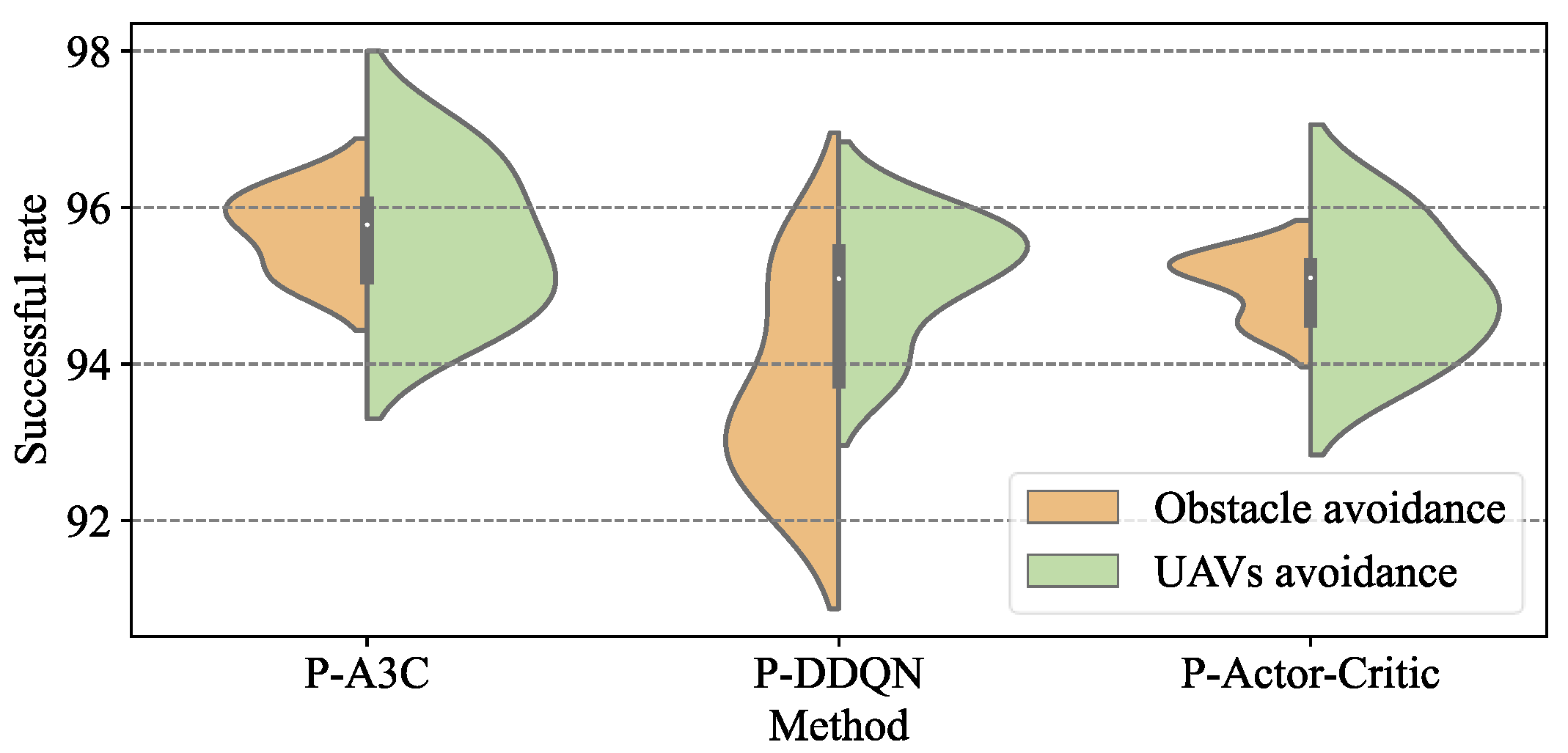
We set the control frequency of the Agent to 5 Hz and conducted UAV control experiments using the P-A3C, P-DDQN, and P-AC methods. The scenarios were the same as in Section 5.3.1, and the success rate distribution results are shown in Figure 20.
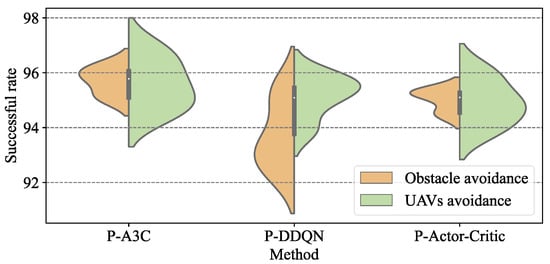
Figure 20.
Non-collision success rate with emergency braking.
Compared to the P-DRL formation control method without collision avoidance measures (P-A3C: 95.32%, P-DDQN: 94.51%, P-AC: 94.49%), the advantage of the P-DRL formation control method with avoidance measures in place is apparent (about P-A3C: 95.97%, P-DDQN: 94.98%, P-AC: 95.55%). Limiting the maximum operating speed of the UAV (such as setting = 5 m/s) is also an efficient measure to improve the non-collision success rate by sacrificing formation speed.
5.3.2. Average Formatting Speed of UAVs
The average formatting speed of UAVs reflects the efficiency of UAV formatting operations. The value of average formatting speed can be influenced by the radius of obstacles, and the performance of the UAVThe value of the average formation speed can be influenced by the radius of the obstacles and the performance of the UAV. Therefore, we use the same scenario as described in Section 5.2 to make a preliminary comparison. The results of the average formatting speed are 9.24 m/s for P-A3C, 9.01 m/s for P-DDQN, and 10.11 m/s for P-AC, as in Table 4.

Table 4.
Performance comparison of various methods based on the framework for P-DRL.
The average speed of UAVs controlled using P-A3C, P-DDQN, and P-Actor–Critic have no significant difference in this specific scenario. It can be speculated that when the structure and the reward of the DRL model are the same, the average speed of the UAVs controlled by the Agent will not change significantly.
5.3.3. Real-Time Performance
- (1)
- Only on software (without communication).
In this section, we only consider the P-DRL control framework operating in a computer software environment, which is implemented and executed using the Python programming language. The indicator of the trajectory output time is used to reflect the real-time performance of the UAV formation control methods. From the perspective of the simulation experiments, the faster the control algorithm outputs control actions, the faster the trajectory is at outputting control actions as well. Due to the running time of a single control action for drones being so short, we use the calculation time that completes the formation control and trajectory output of 20 UAVs as an indicator (120 times for control action output for every single UAV). Use the artificial potential field (APF) method [44,45] as a comparison, which is a common trajectory planning algorithm.
The trajectory output times in the software environment for 20 UAVs using different methods are shown in Table 4.
- (2)
- On software and hardware (with communication).
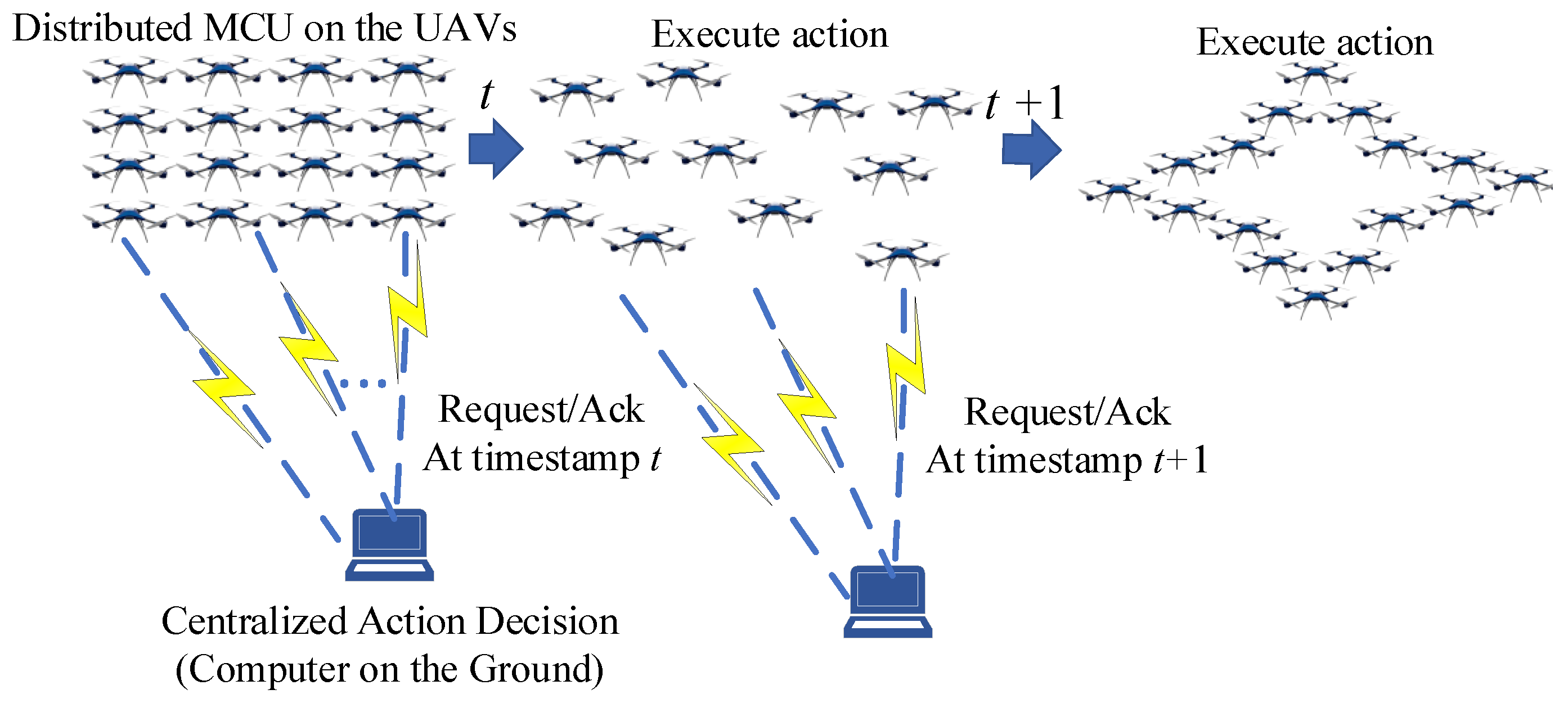
Next, we consider the deployment and operational mode of P-DRL in real multi-UAV systems. A typical mode involves achieving multi-UAV formation control through a ground computing center by building an air–ground communication link. In this mode, the UAV sends real-time operational information such as its position and attitude to the ground computing center through the air–ground communication link and requests action instructions from the ground center. Then, the ground responds and sends action instructions based on the information from multiple UAVs, as shown in Figure 21.
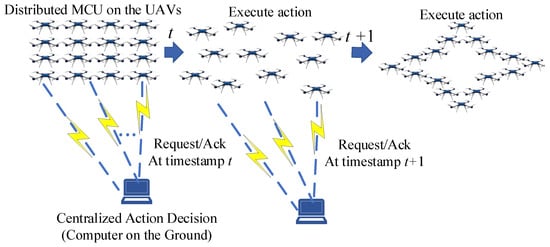
Figure 21.
A classic implementation diagram for P-DRL in the multi-UAV systems.
In this experiment, we used the control chip of a DJI Phantom 4 as an example. DJI Phantom 4 uses a STM32 Microcontroller Unit (MCU), which is relatively easy to purchase and obtain, as seen in Figure 22. Therefore, we can establish serial communication between PC and STM32 MCU to simulate the operation of P-DRL in real unmanned aerial vehicle systems.
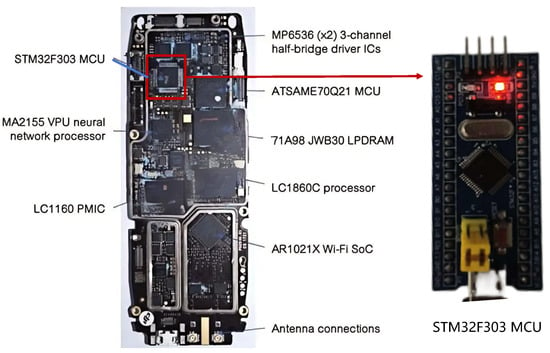
Figure 22.
STM32 microcontroller unit for DJI Phantom4 drones.
The trajectory output times for 20 UAVs in both software and hardware environments (with communication) using different methods are shown in Table 4. It can be seen that when using the P-DRL implementation method, as in Figure 21, the additional running time due to hardware information processing and communication is approximately 0.1 s. For the relevant code for the simulation in this paper, please refer to the link: https://github.com/jinlun8823/P-DRL_formation_control (accessed on 4 July 2024).
6. Discussion and Conclusions
The major contribution of this paper is a new UAV formation control framework that combines a DRL model with a heuristic algorithm, This framework transforms the synergetic formation control problem of the UAV fleet into synergetic formation control problems for multiple UAV pairs, thus limiting the number of UAVs that the Agent needs to control each time, making the training process for the Agent easier. The feasibility of the P-DRL framework has been demonstrated through theoretical analysis and simulations. We used A3C, AC, and DQN to demonstrate the feasibility of the P-DRL control framework. It can complete real-time synergetic formation control tasks for 10–20 aircrafts with nearly no collisions. Although this is a relatively large number compared to the current research, it is still not the upper limit of the number of UAVs that can be controlled simultaneously by this framework. Moreover, the time complexity of the P-DRL method for formation control is O(2n − 1), which is suitable for real-time formation control tasks of n(n≥ 10) UAVs in complex environments with random obstacles and operational uncertainty.
The P-DRL formation control framework has good environmental adaptability and real-time performance, but it still has deficiencies. For example, collision can still occur during the formation process. Therefore, finding a suitable collision avoidance control method as a supplement/safeguard to the P-DRL formation framework is very important. Meanwhile, although this paper proposes a simple experiment for deploying P-DRL in UAV systems, it only integrates part of the information exchange system. How to implement the P-DRL framework on existing UAV sensor system, collision avoidance system, and control system, as well as further improve its operational efficiency, success rate, and compatibility, are all important research directions for future studies.
Author Contributions
Conceptualization, J.Z.; methodology, J.Z. and H.Z.; software, M.H.; Validation, J.Z. and M.H.; formal analysis, F.W. and J.Y.; investigation, H.Z.; resources, M.H.; writing—original draft preparation, J.Z.; writing—review and editing, J.Z. and M.H.; visualization, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Foundation of China grant number 22&ZD169, the National Natural Science Foundation of China grant number U2333214.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The author would like to thank Shi Zongbei, Gang Zhong, and Hao Liu from Nanjing University of Aeronautics and Astronautics for their academic guidance and experimental resources.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, J.; Luo, C.; Luo, Y.; Li, K. Distributed UAV Swarm Formation and Collision Avoidance Strategies Over Fixed and Switching Topologies. IEEE Trans. Cybern. 2022, 52, 10969–10979. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Gou, J.; Ji, H.; Deng, J. Hierarchical Mission Replanning for Multiple UAV Formations Performing Tasks in Dynamic Situation. Comput. Commun. 2023, 200, 132–148. [Google Scholar] [CrossRef]
- Du, W.; Guo, T.; Chen, J.; Li, B.; Zhu, G.; Cao, X. Cooperative Pursuit of Unauthorized UAVs in Urban Airspace via Multi-agent Reinforcement Learning. Transp. Res. Part C Emerg. Technol. 2021, 128, 103122. [Google Scholar] [CrossRef]
- Meng, Q.; Qu, Q.; Chen, K.; Yi, T. Multi-UAV Path Planning Based on Cooperative Co-Evolutionary Algorithms with Adaptive Decision Variable Selection. Drones 2024, 8, 435. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Zhou, J.; Hua, M.; Zhong, G.; Liu, H. Adaptive Collision Avoidance for Multiple UAVs in Urban Environments. Drones 2023, 7, 2024050715. [Google Scholar] [CrossRef]
- Felix, B.; Stratis, K.; Madeline, C.; Roberto, P.; Mike, B. A Taxonomy of Validation Strategies to Ensure the Safe Operation of Highly Automated Vehicles. J. Intell. Transp. Syst. 2022, 26, 14–33. [Google Scholar] [CrossRef]
- Guanetti, J.; Kim, Y.; Borrelli, F. Control of Connected and Automated Vehicles: State of the Art and Future Challenges. Annu. Rev. Control 2018, 45, 18–40. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An Improved Artificial Potential Field Method for Path Planning and Formation Control of the Multi-UAV Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1129–1133. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Zhu, G.; Zhang, Y.; Wang, C.; Wang, Y.; Su, C.Y. Finite-Time Adaptive Quantized Control for Quadrotor Aerial Vehicle with Full States Constraints and Validation on QDrone Experimental Platform. Drones 2024, 8, 264. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, J.; Zheng, Z.; Yuan, J. Distributed Finite-Time ESO-Based Consensus Control for Multiple Fixed-Wing UAVs Subjected to External Disturbances. Drones 2024, 8, 260. [Google Scholar] [CrossRef]
- Patiño, D.; Mayya, S.; Calderon, J.; Daniilidis, K.; Saldaña, D. Learning to Navigate in Turbulent Flows with Aerial Robot Swarms: A Cooperative Deep Reinforcement Learning Approach. IEEE Robot. Autom. Lett. 2023, 8, 4219–4226. [Google Scholar] [CrossRef]
- Qi, Z.; Ziyang, Z.; Huajun, G.; Hongbo, C.; Rong, L.; Jicheng, L. UAV Formation Control based on Dueling Double DQN. J. Beijing Univ. Aeronaut. Astronaut. 2023, 49, 2137–2146. [Google Scholar] [CrossRef]
- La, H.M.; Lim, R.; Sheng, W. Multirobot Cooperative Learning for Predator Avoidance. IEEE Trans. Control Syst. Technol. 2015, 23, 52–63. [Google Scholar] [CrossRef]
- Xiang, X.; Yan, C.; Wang, C.; Yin, D. Coordination Control Method for Fixed-wing UAV Formation Through Deep Reinforcement Learning. Acta Aeronaut. Astronaut. Sin. 2021, 42, 524009. [Google Scholar] [CrossRef]
- Lombaerts, T.; Looye, G.; Chu, Q.; Mulder, J. Design and Simulation of Fault Tolerant Flight Control Based on a Physical Approach. Aerosp. Sci. Technol. 2012, 23, 151–171. [Google Scholar] [CrossRef]
- Liao, F.; Teo, R.; Wang, J.L.; Dong, X.; Lin, F.; Peng, K. Distributed Formation and Reconfiguration Control of VTOL UAVs. IEEE Trans. Control Syst. Technol. 2017, 25, 270–277. [Google Scholar] [CrossRef]
- Gu, Z.; Song, B.; Fan, Y.; Chen, X. Design and Verification of UAV Formation Controller based on Leader-Follower Method. In Proceedings of the 2022 7th International Conference on Automation, Control and Robotics Engineering (CACRE), Virutal, 15–16 July 2022; pp. 38–44. [Google Scholar] [CrossRef]
- Liu, C.; Wu, X.; Mao, B. Formation Tracking of Second-Order Multi-Agent Systems with Multiple Leaders Based on Sampled Data. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 331–335. [Google Scholar] [CrossRef]
- Bianchi, D.; Borri, A.; Cappuzzo, F.; Di Gennaro, S. Quadrotor Trajectory Control Based on Energy-Optimal Reference Generator. Drones 2024, 8, 29. [Google Scholar] [CrossRef]
- Liu, S.; Huang, F.; Yan, B.; Zhang, T.; Liu, R.; Liu, W. Optimal Design of Multimissile Formation Based on an Adaptive SA-PSO Algorithm. Aerospace 2022, 9, 21. [Google Scholar] [CrossRef]
- Kada, B.; Khalid, M.; Shaikh, M.S. Distributed cooperative control of autonomous multi-agent UAV systems using smooth control. J. Syst. Eng. Electron. 2020, 31, 1297–1307. [Google Scholar] [CrossRef]
- Kang, C.; Xu, J.; Bian, Y. Affine Formation Maneuver Control for Multi-Agent Based on Optimal Flight System. Appl. Sci. 2024, 14, 2292. [Google Scholar] [CrossRef]
- Brodecki, M.; Subbarao, K. Autonomous Formation Flight Control System Using In-Flight Sweet-Spot Estimation. J. Guid. Control Dyn. 2015, 38, 1083–1096. [Google Scholar] [CrossRef]
- Sun, G.; Zhou, R.; Xu, K.; Weng, Z.; Zhang, Y.; Dong, Z.; Wang, Y. Cooperative formation control of multiple aerial vehicles based on guidance route in a complex task environment. Chin. J. Aeronaut. 2020, 33, 701–720. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, H.H.T. Robust Nonlinear Close Formation Control of Multiple Fixed-Wing Aircraft. J. Guid. Control Dyn. 2021, 44, 572–586. [Google Scholar] [CrossRef]
- Dogan, A.; Venkataramanan, S. Nonlinear Control for Reconfiguration of Unmanned-Aerial-Vehicle Formation. J. Guid. Control Dyn. 2005, 28, 667–678. [Google Scholar] [CrossRef][Green Version]
- Yu, Y.; Guo, J.; Ahn, C.K.; Xiang, Z. Neural Adaptive Distributed Formation Control of Nonlinear Multi-UAVs with Unmodeled Dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 9555–9561. [Google Scholar] [CrossRef]
- Lin, Z.; Yan, B.; Zhang, T.; Li, S.; Meng, Z.; Liu, S. Multi-Level Switching Control Scheme for Folding Wing VTOL UAV Based on Dynamic Allocation. Drones 2024, 8, 303. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Zhang, P. Multi-UAV Formation Control Based on a Novel Back-Stepping Approach. IEEE Trans. Veh. Technol. 2020, 69, 2437–2448. [Google Scholar] [CrossRef]
- Hung, S.M.; Givigi, S.N. A Q-Learning Approach to Flocking with UAVs in a Stochastic Environment. IEEE Trans. Cybern. 2017, 47, 186–197. [Google Scholar] [CrossRef]
- Li, B.; Gan, Z.; Chen, D.; Sergey Aleksandrovich, D. UAV Maneuvering Target Tracking in Uncertain Environments Based on Deep Reinforcement Learning and Meta-Learning. Remote Sens. 2020, 12, 3789. [Google Scholar] [CrossRef]
- Li, R.; Zhang, L.; Han, L.; Wang, J. Multiple Vehicle Formation Control Based on Robust Adaptive Control Algorithm. IEEE Intell. Transp. Syst. Mag. 2017, 9, 41–51. [Google Scholar] [CrossRef]
- Xu, L.; Wang, T.; Cai, W.; Sun, C. UAV target following in complex occluded environments with adaptive multi-modal fusion. Appl. Intell. 2022, 53, 16998–17014. [Google Scholar] [CrossRef]
- Chen, H.; Duan, H. Multiple Unmanned Aerial Vehicle Autonomous Formation via Wolf Packs Mechanism. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 606–610. [Google Scholar] [CrossRef]
- Shi, G.; Hönig, W.; Shi, X.; Yue, Y.; Chung, S.J. Neural-Swarm2: Planning and Control of Heterogeneous Multirotor Swarms Using Learned Interactions. IEEE Trans. Robot. 2022, 38, 1063–1079. [Google Scholar] [CrossRef]
- Hu, H.; Wang, Q.l. Proximal Policy Optimization with an Integral Compensator for Quadrotor Control. Front. Inf. Technol. Electron. Eng. 2020, 21, 777–795. [Google Scholar] [CrossRef]
- Duan, H.; Luo, Q.; Shi, Y.; Ma, G. Hybrid Particle Swarm Optimization and Genetic Algorithm for Multi-UAV Formation Reconfiguration. IEEE Comput. Intell. Mag. 2013, 8, 16–27. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Shen, Y.; Zhang, X. Autonomous Navigation of UAVs in Large-Scale Complex Environments: A Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2019, 68, 2124–2136. [Google Scholar] [CrossRef]
- Xu, G.; Jiang, W.; Wang, Z.; Wang, Y. Autonomous Obstacle Avoidance and Target Tracking of UAV Based on Deep Reinforcement Learning. J. Intell. Robot. Syst. 2022, 104, 60. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; A Bradford Book: Cambridge, MA, USA, 2018. [Google Scholar]
- DJI. Parameters of DJI phantom4 pro. Available online: https://www.dji.com/cn/phantom-4-pro-v2/specs (accessed on 4 July 2024).
- Hasselt, H.v.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, AAAI’16, Phoenix, AZ, USA, 12–17 February 2016; pp. 2094–2100. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.M.O.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Szczepanski, R. Safe Artificial Potential Field - Novel Local Path Planning Algorithm Maintaining Safe Distance from Obstacles. IEEE Robot. Autom. Lett. 2023, 8, 4823–4830. [Google Scholar] [CrossRef]
- Ju, C.; Luo, Q.; Yan, X. Path Planning Using Artificial Potential Field Method And A-star Fusion Algorithm. In Proceedings of the 2020 Global Reliability and Prognostics and Health Management (PHM-Shanghai), Shanghai, China, 16–18 October 2020; pp. 1–7. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).