Selective Laser Sintering Induced Residual Stresses: Precision Measurement and Prediction
Abstract
:1. Introduction
2. Literature Review
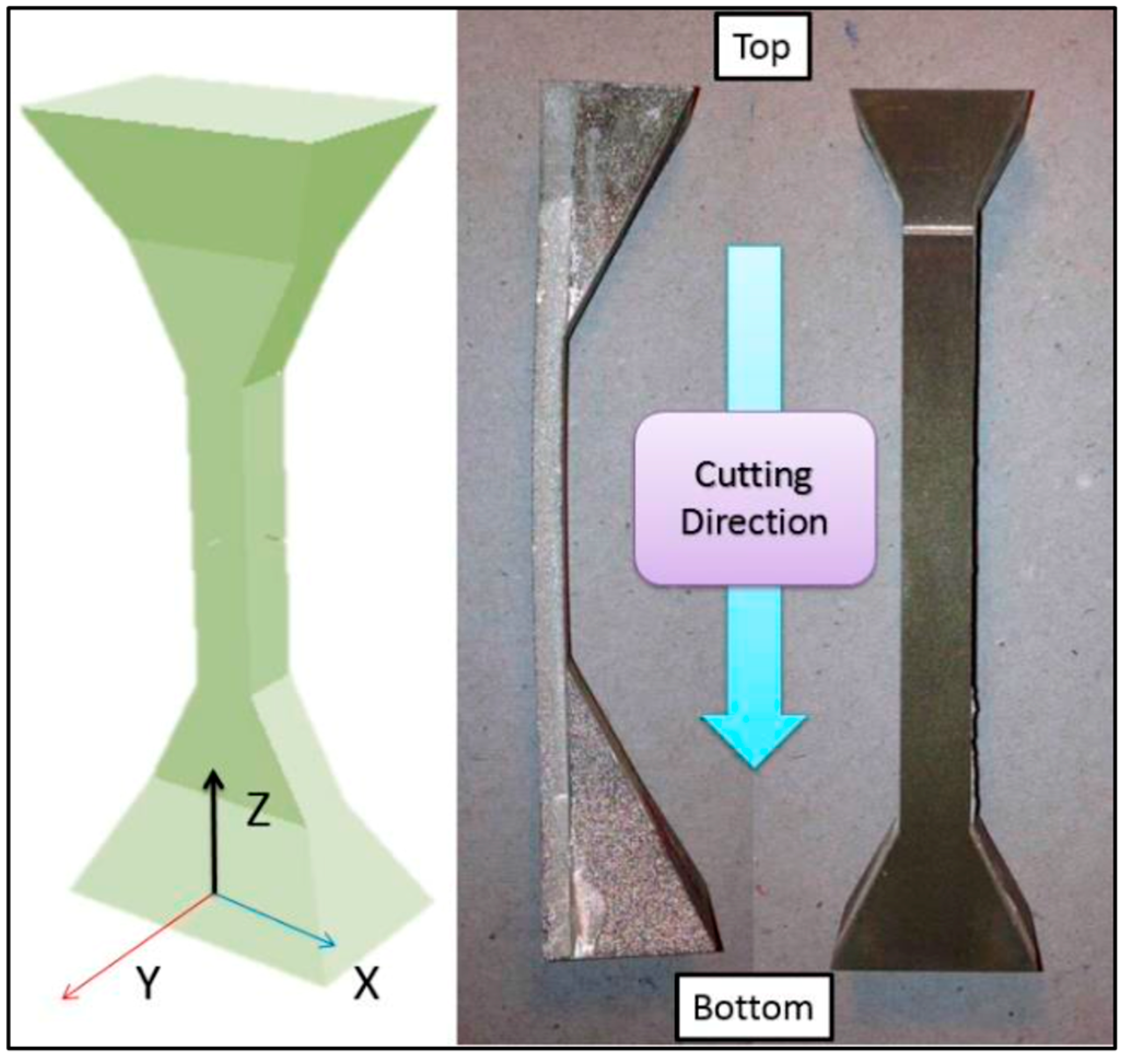
3. Materials and Methods
4. Residual Stresses Measurement
4.1. Non-Destructive Approach: Neutron Diffraction
4.2. Destructive Approach: The Contour Method
5. Prediction of Residual Stresses Using Finite Element Analysis
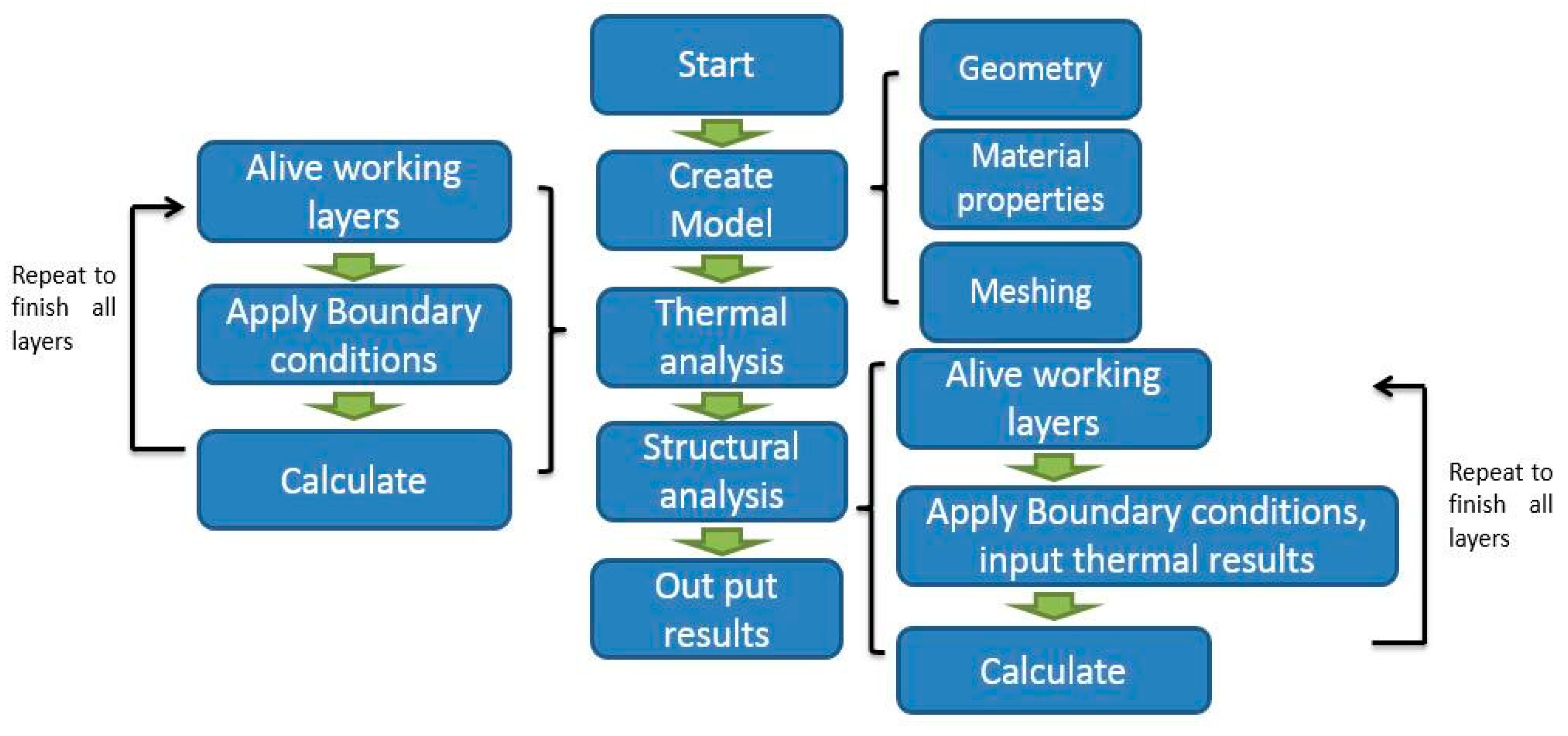
5.1. Modelling Approach
- Material is considered homogeneous with isotropic properties.
- New elements for adding material are considered as stress-free elements.
- Residual stresses are generated due to temperature change, and no phase change during the process is considered.
- Heat input is applied on the upper line/surface of each layer.
- Impact of heat input to the residual stresses;
- Importance of the base plate.
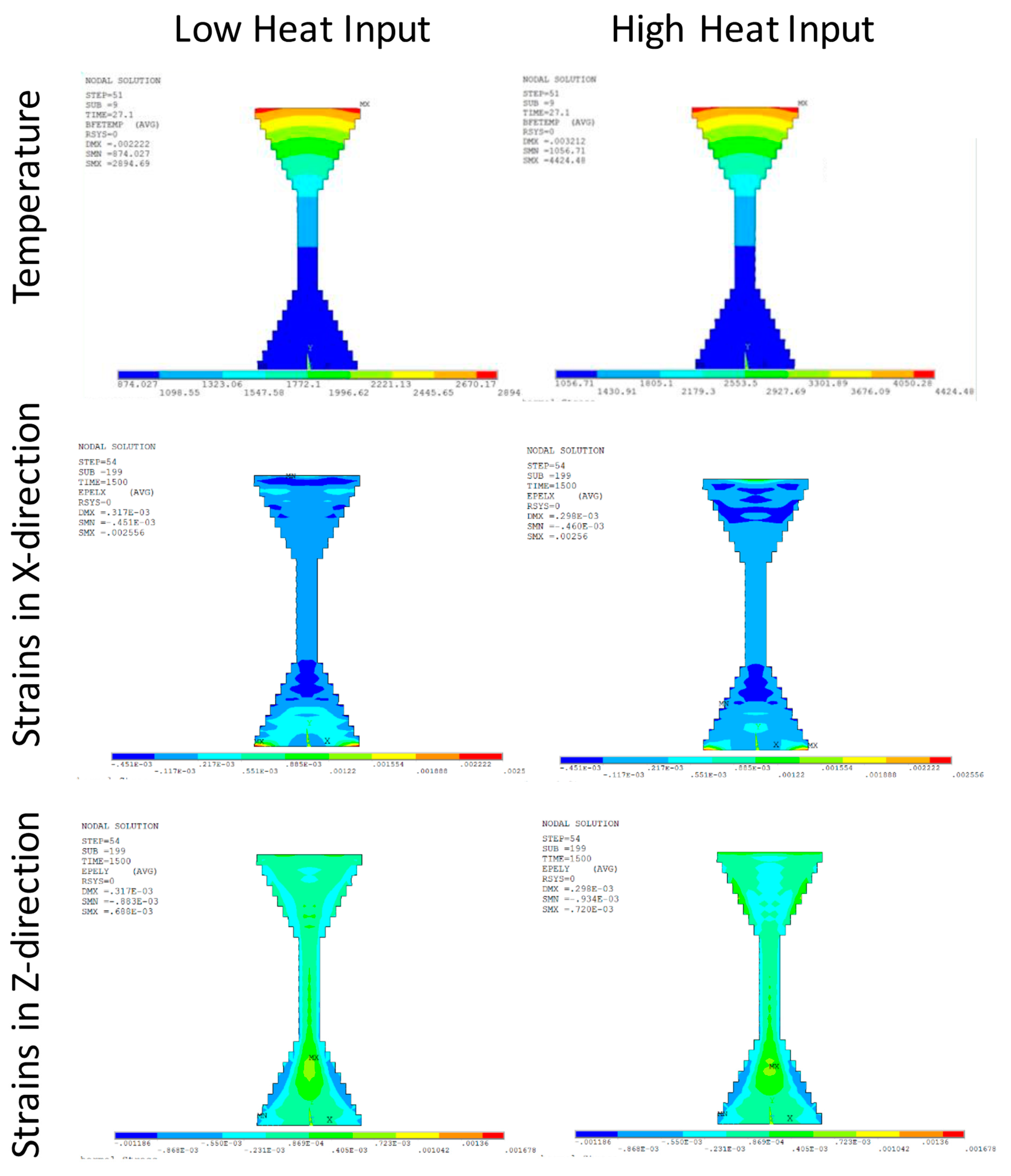
5.2. Heat Input Impact to Residual Stress
5.3. Base Plate Impact to Residual Stresses
6. Discussion
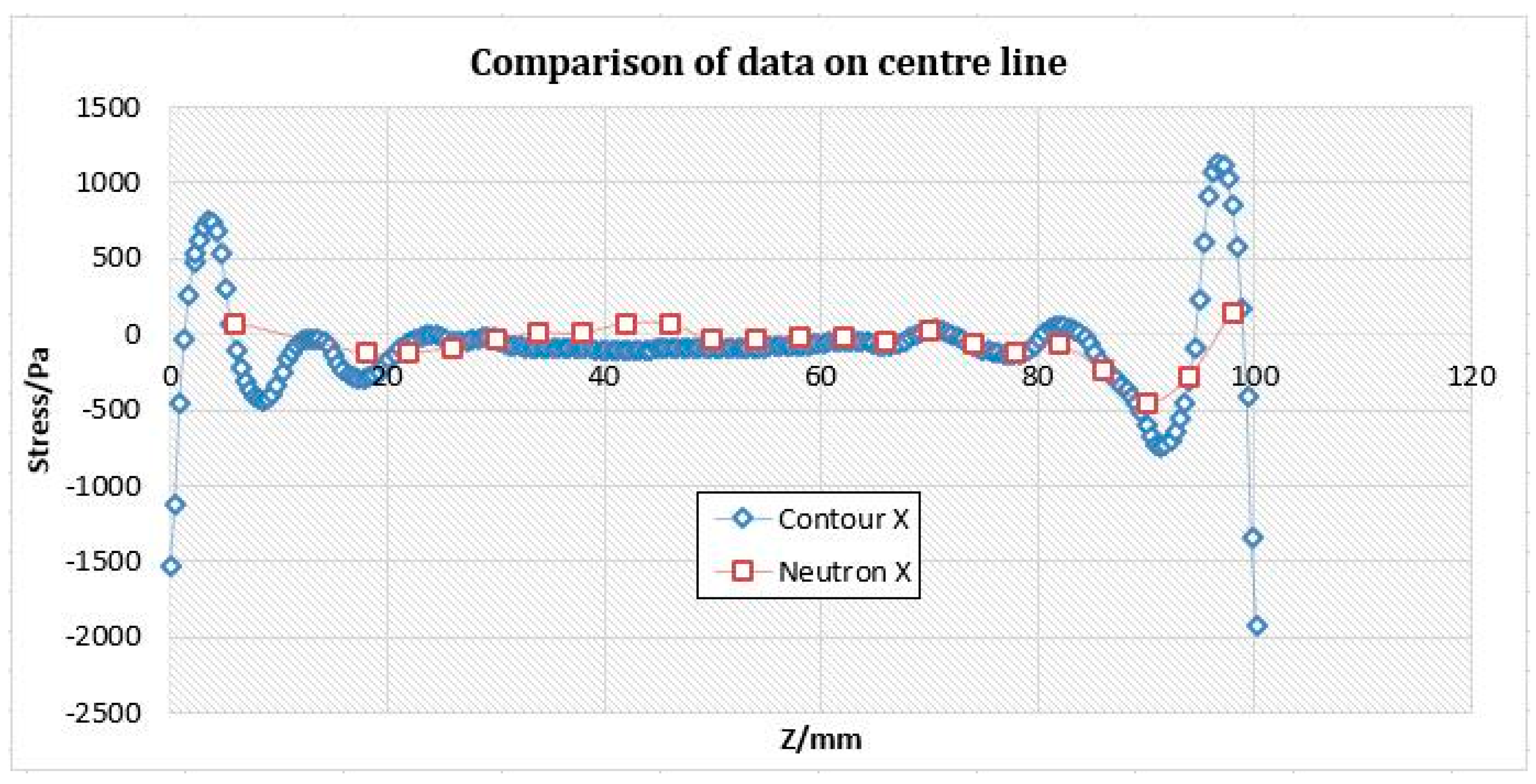
6.1. Comparison of Residual Stress Measurements
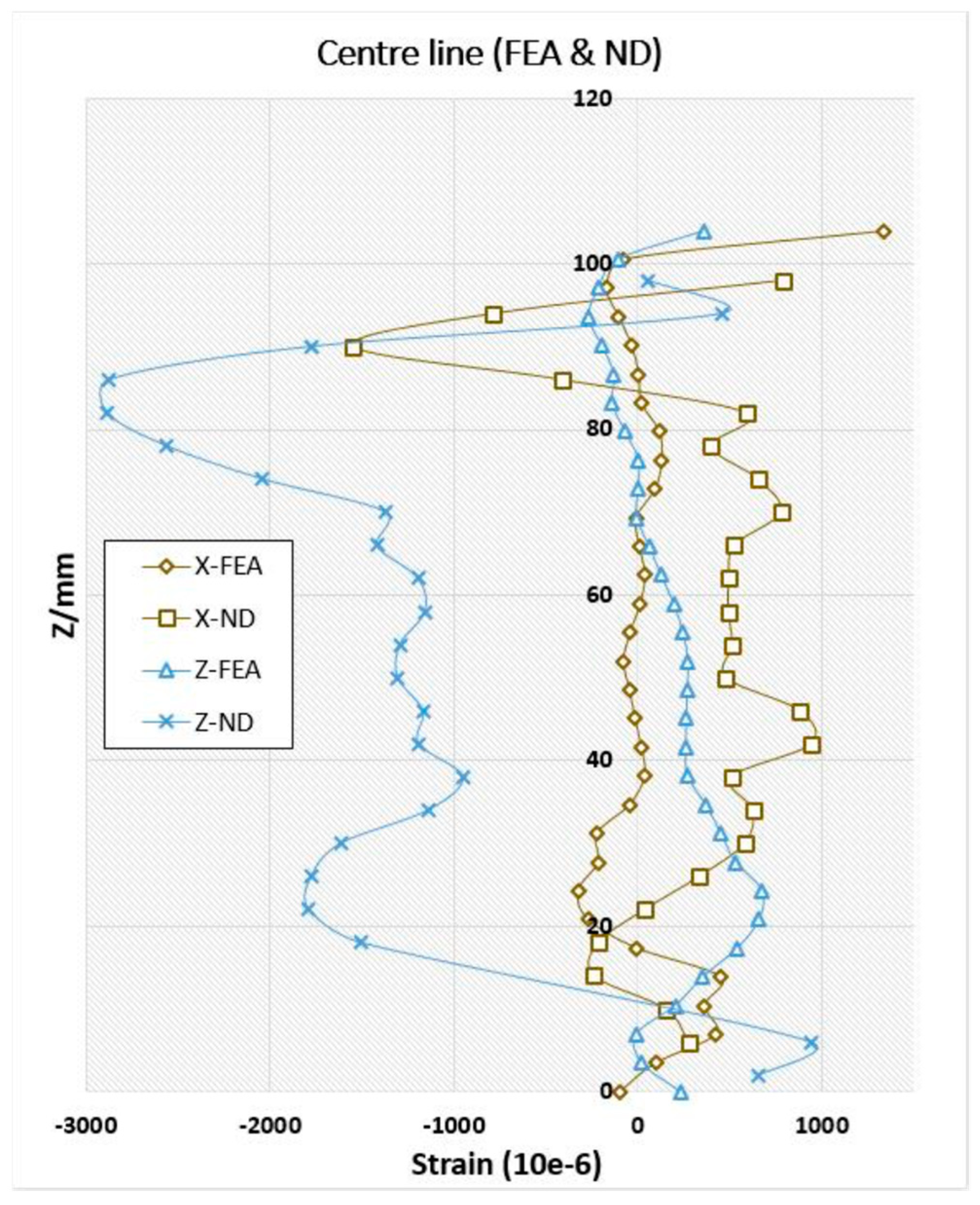
6.2. Validation of FEA Predictions with Neutron Diffraction Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salonitis, K. Design for additive manufacturing based on the axiomatic design method. Int. J. Adv. Manuf. Technol. 2016, 87, 989–996. [Google Scholar] [CrossRef]
- Bikas, H.; Lianos, A.K.; Stavropoulos, P. A design framework for additive manufacturing. Int. J. Adv. Manuf. Technol. 2019, 103, 3769–3783. [Google Scholar] [CrossRef] [Green Version]
- Sivarupan, T.; Balasubramani, N.; Saxena, P.; Nagarajan, D.; El Mansori, M.; Salonitis, K.; Jolly, M.; Dargusch, M.S. A review on the progress and challenges of binder jet 3D printing of sand moulds for advanced casting. Addit. Manuf. 2021, 40, 101889. [Google Scholar]
- Schoinochoritis, B.; Chantzis, D.; Salonitis, K. Simulation of metallic powder bed additive manufacturing processes with the finite element method: A critical review. Proc. IMechE Part B J. Eng. Manuf. 2017, 231, 96–117. [Google Scholar] [CrossRef]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modelling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2015, 83, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Salonitis, K.; D’Alvise, L.; Schoinochoritis, B.; Chantzis, D. Additive manufacturing and post-processing simulation: Laser cladding followed by high speed machining. Int. J. Adv. Manuf. Technol. 2016, 85, 2401–2411. [Google Scholar] [CrossRef]
- Dieter, G.E.; Bacon, D. Mechanical Metallurgy; McGraw-Hill: New York, NY, USA, 1986; Volume 3. [Google Scholar]
- Lyu, D.; Hu, W.; Ren, B.; Pan, X.; Wu, C. Numerical Prediction of Residual Deformation and Failure for Powder Bed Fusion Additive Manufacturing of Metal Parts. J. Mech. 2020, 36, 623–636. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H.K.D.H. Residual stress. Part 1—Measurement techniques. Mater. Sci. Technol. 2001, 17, 355–365. [Google Scholar] [CrossRef]
- Withers, P.J. Residual stress and its role in failure. Rep. Prog. Phys. 2007, 70, 2211–2264. [Google Scholar] [CrossRef] [Green Version]
- Duboeuf, F.; Lemaire, E.; Remouchamps, A.; Eekelen, T.V.; Chary, C.; François, M.; Vargalui, A.; Rodrigues, G. Integration of AM process in design cycle of metallic parts: Application to space components. In Proceedings of the 24th International Conference on Material Forming, Liège, Belgium, 14–16 April 2021. [Google Scholar] [CrossRef]
- Bartlett, J.L.; Li, X. An overview of residual stresses in metal powder bed fusion. Addit. Manuf. 2019, 27, 131–149. [Google Scholar] [CrossRef]
- Mercelis, P.; Kruth, J.-P. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R. Finite element simulation of the temperature and stress fields in single layers built without-support in selective laser melting. Mater. Des. 2013, 52, 638–647. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.F.; Fang, X.Y.; Guo, Y.B. Efficient predictive model of part distortion and residual stress in selective laser melting. Addit. Manuf. 2017, 17, 157–168. [Google Scholar] [CrossRef]
- Xie, D.; Lv, F.; Liang, H.; Shen, L.; Tian, Z.; Zhao, J.; Song, Y.; Shuai, C. Towards a comprehensive understanding of distortion in additive manufacturing based on assumption of constraining force. Virtual Phys. Prototyp. 2021, 16, 1–13. [Google Scholar] [CrossRef]
- Cheng, L.; To, A. Part-scale build orientation optimization for minimizing residual stress and support volume for metal additive manufacturing: Theory and experimental validation. Comput. Aided Des. 2019, 113, 1–23. [Google Scholar] [CrossRef]
- Vangi, D. Residual Stress Evaluation by the Hole-Drilling Method with Off-Center Hole: An Extension of the Integral Method. J. Eng. Mater. Technol. 1997, 119, 79–85. [Google Scholar] [CrossRef]
- Flaman, M.T.; Manning, B.H. Determination of residual-stress variation with depth by the hole-drilling method. Exp. Mech. 1985, 25, 205–207. [Google Scholar] [CrossRef]
- Pagliaro, P.; Prime, M.B.; Swenson, H.; Zuccarello, B. Measuring Multiple Residual-Stress Components using the Contour Method and Multiple Cuts. Exp. Mech. 2010, 50, 187–194. [Google Scholar] [CrossRef]
- Prime, M.B. Cross-sectional mapping of residual stresses by measuring the surface contour after a cut. J. Eng. Mater. Technol. 2001, 123, 162–168. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Hensel, J.; Köhler, M.; Dilger, K. Residual stress in wire and arc additively manufactured aluminum components. J. Manuf. Process. 2021, 65, 97–111. [Google Scholar] [CrossRef]
- Prime, M.B.; Sebring, R.J.; Edwards, J.M.; Hughes, D.J.; Webster, P.J. Laser surface-contouring and spline data-smoothing for residual stress measurement. Exp. Mech. 2004, 44, 176–184. [Google Scholar] [CrossRef]
- Zhang, Y.; Ganguly, S.; Edwards, L.; Fitzpatrick, M.E. Cross-sectional mapping of residual stresses in a VPPA weld using the contour method. Acta Mater. 2004, 52, 5225–5232. [Google Scholar] [CrossRef]
- Wu, A.S.; Brown, D.W.; Kumar, M.; Gallegos, G.F.; King, W.E. An Experimental Investigation into Additive Manufacturing-Induced Residual Stresses in 316L Stainless Steel. Metall. Mater. Trans. A 2014, 45, 6260–6270. [Google Scholar] [CrossRef]
- Allen, A.J.; Hutchings, M.T.; Windsor, C.G.; Andreani, C. Neutron diffraction methods for the study of residual stress fields. Adv. Phys. 1985, 34, 445–473. [Google Scholar] [CrossRef]
- Van Acker, K.; Root, J.; Van Houtte, P.; Aernoudt, E. Neutron diffraction measurement of the residual stress in the cementite and ferrite phases of cold-drawn steel wires. Acta Mater. 1996, 44, 4039–4049. [Google Scholar] [CrossRef]
- Anderoglu, O. Residual Stress Measurement Using X-ray Diffraction; Texas A&M University: College Station, TX, USA, 2005. [Google Scholar]
- Fitzpatrick, M.E.; Fry, A.T.; Holdway, P.; Kandil, F.A.; Shackleton, J.; Suominen, L. Determination of Residual Stresses by X-ray Diffraction, 2005. Available online: https://eprintspublications.npl.co.uk/2391/ (accessed on 10 August 2021).
- Prevey, P.S. X-ray diffraction residual stress techniques. ASM Int. ASM Handb. 1986, 10, 380–392. [Google Scholar]
- Oliver, E.C.; Mori, T.; Daymond, M.R.; Withers, P.J. Neutron diffraction study of stress-induced martensitic transformation and variant change in Fe–Pd. Acta Mater. 2003, 51, 6453–6464. [Google Scholar] [CrossRef]
- Paradowska, A.M.; Price, J.W.H.; Finlayson, T.R.; Lienert, U.; Ibrahim, R. Residual Stress Measurements of Welded Components Using Synchrotron and Neutron Diffraction; Argonne National Laboratory: Lemont, IL, USA, 2007.
- Goel, S.; Neikter, M.; Capek, J.; Polatidis, E.; Colliander, M.H.; Joshi, S.; Pederson, R. Residual stress determination by neutron diffraction in powder bed fusion-built Alloy 718: Influence of process parameters and post-treatment. Mater. Des. 2020, 195, 109045. [Google Scholar] [CrossRef]
- Pant, P.; Sjöström, S.; Simonsson, K.; Moverare, J.; Proper, S.; Hosseini, S.; Luzin, V.; Peng, R. A Simplified Layer-by-Layer Model for Prediction of Residual Stress Distribution in Additively Manufactured Parts. Metals 2021, 11, 861. [Google Scholar] [CrossRef]
- Carpenter, K.; Tabei, A. On residual stress development, prevention, and compensation in metal additive manufacturing. Materials 2020, 13, 255. [Google Scholar] [CrossRef] [Green Version]
- Webster, G.A.; Wimpory, R.C. Non-destructive measurement of residual stress by neutron diffraction. J. Mater. Process. Technol. 2001, 117, 395–399. [Google Scholar] [CrossRef]
- Ding, J.; Colegrove, P.; Mehnen, J.; Ganguly, S.; Sequeira Almeida, P.M.; Wang, F.; Williams, S. Thermo-mechanical analysis of Wire and Arc Additive Layer Manufacturing process on large multi-layer parts. Comput. Mater. Sci. 2011, 50, 3315–3322. [Google Scholar] [CrossRef] [Green Version]







| Element | Cr | Ni | Mo | Mn | Si |
|---|---|---|---|---|---|
| wt% | 16.0–18.0 | 10.0–14.0 | 2.0–3.0 | 2.0 max | 1.0 max |
| Element | P | S | C | Fe | |
| wt% | 0.04 max | 0.03 max | 0.03 max | Bal |
| Process Parameter | Units | Value |
|---|---|---|
| Laser power | W | 180 |
| Hatch spacing | μm | 70 |
| Laser beam diameter | μm | 60 |
| Powder layer thickness | μm | 40 |
| Laser scan speed | mm/s | 500 |
| Material Property | Temperature (°C) | Value |
|---|---|---|
| Thermal conductivity (W/mK) | 20 | 12.1 |
| 100 | 14.3 | |
| 500 | 21.4 | |
| Specific heat (J/kgK) | - | 449 |
| Elastic modules (GPa) | 20 | 195 |
| 200 | 187 | |
| 400 | 172 | |
| 600 | 157 | |
| Poisson ratio (-) | - | 0.27 |
| Density (kg/m3) | - | 7930 |
| Thermal expansion (1 °C−1 × 10−6) | 20 | 14.3 |
| 200 | 15.6 | |
| 400 | 16.9 | |
| 600 | 17.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Impey, S.; Saxena, P.; Salonitis, K. Selective Laser Sintering Induced Residual Stresses: Precision Measurement and Prediction. J. Manuf. Mater. Process. 2021, 5, 101. https://doi.org/10.3390/jmmp5030101
Impey S, Saxena P, Salonitis K. Selective Laser Sintering Induced Residual Stresses: Precision Measurement and Prediction. Journal of Manufacturing and Materials Processing. 2021; 5(3):101. https://doi.org/10.3390/jmmp5030101
Chicago/Turabian StyleImpey, Susan, Prateek Saxena, and Konstantinos Salonitis. 2021. "Selective Laser Sintering Induced Residual Stresses: Precision Measurement and Prediction" Journal of Manufacturing and Materials Processing 5, no. 3: 101. https://doi.org/10.3390/jmmp5030101
APA StyleImpey, S., Saxena, P., & Salonitis, K. (2021). Selective Laser Sintering Induced Residual Stresses: Precision Measurement and Prediction. Journal of Manufacturing and Materials Processing, 5(3), 101. https://doi.org/10.3390/jmmp5030101








