Digital Image Correlation for Elastic Strain Evaluation during Focused Ion Beam Ring-Core Milling
Abstract
:1. Introduction
2. FIB-DIC Technique
3. hDIC Technique
4. Case Study
4.1. Sample Preparation and Data Collection
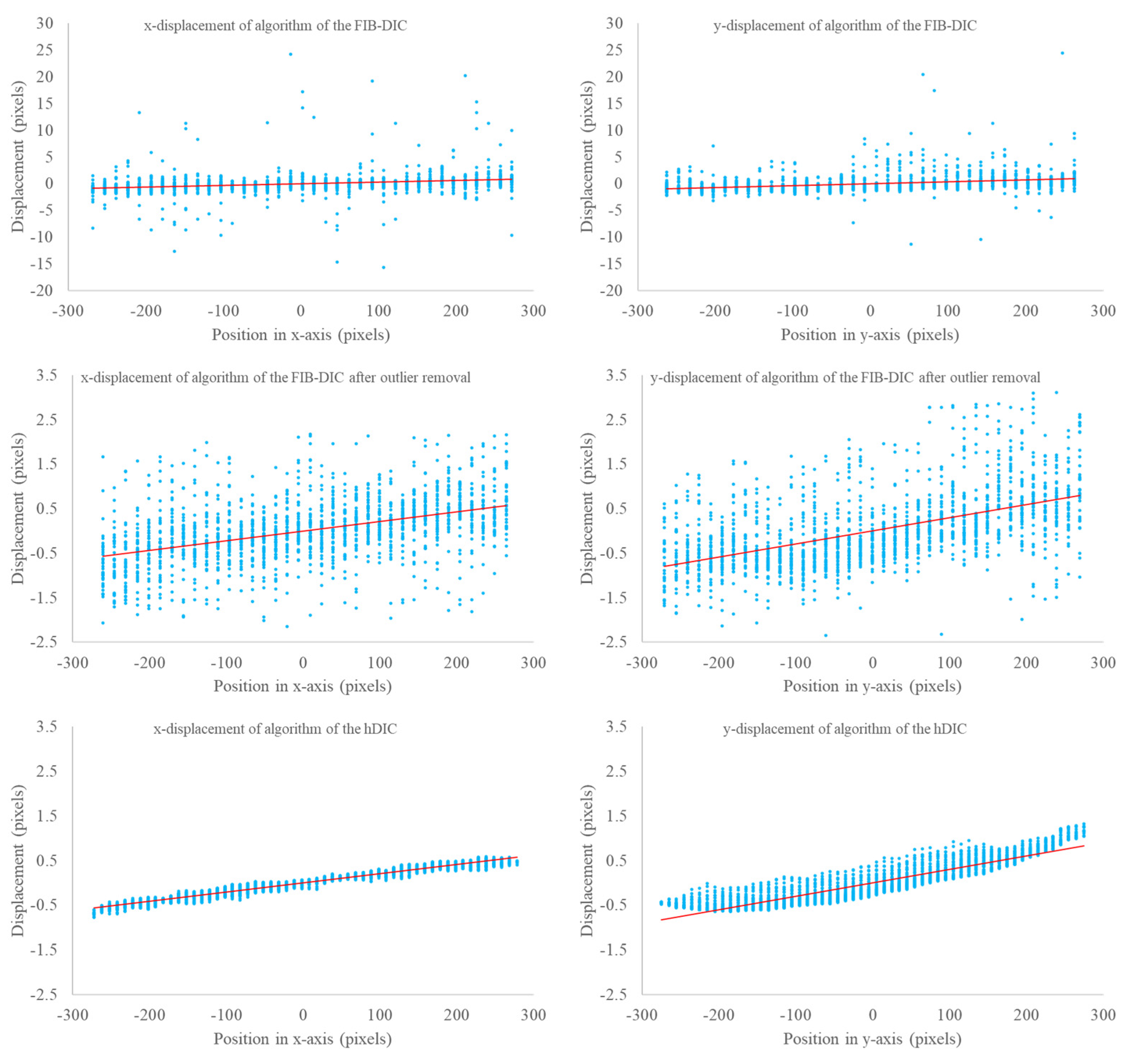
4.2. Utilizations of FIB-DIC and hDIC
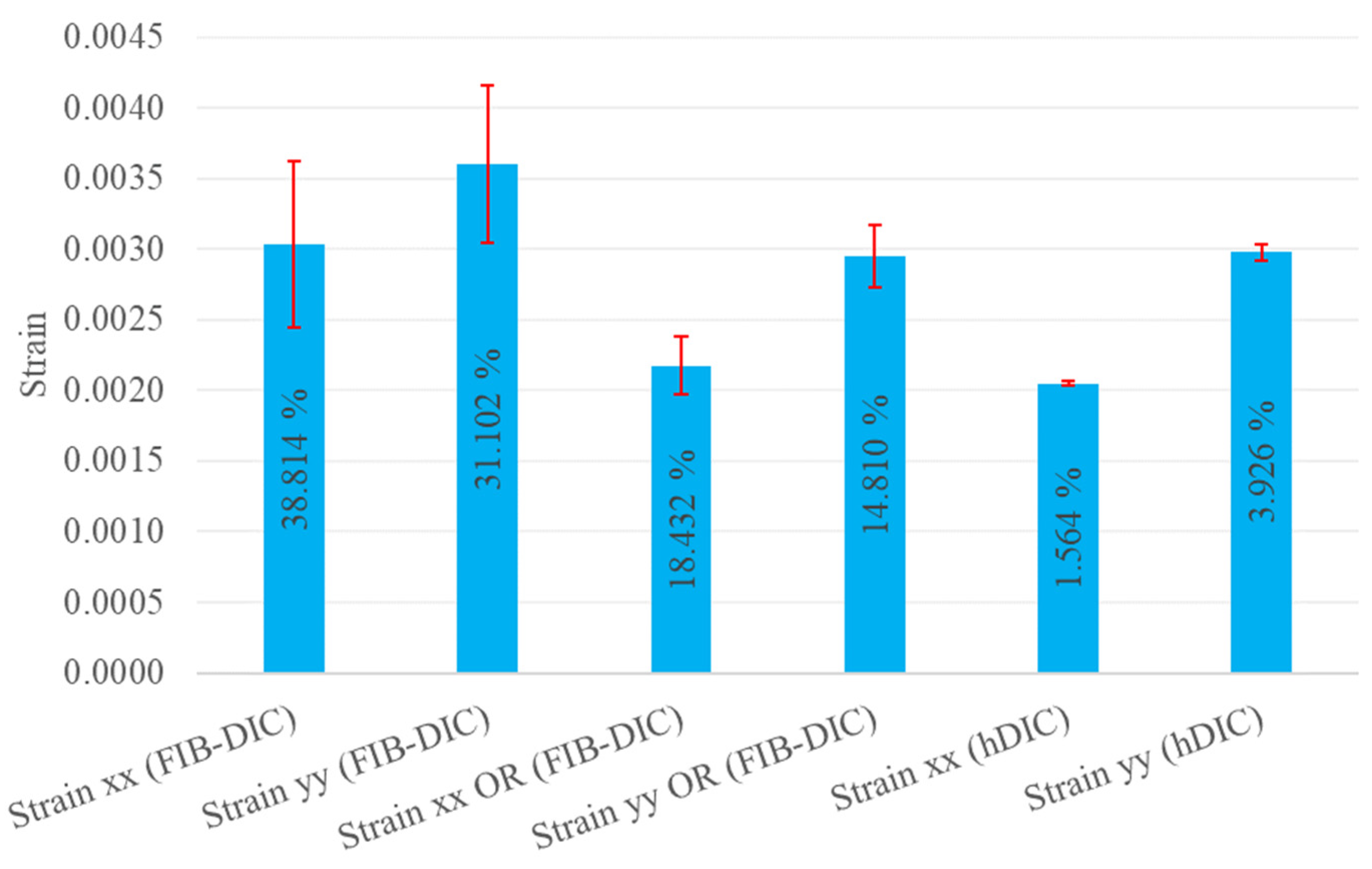
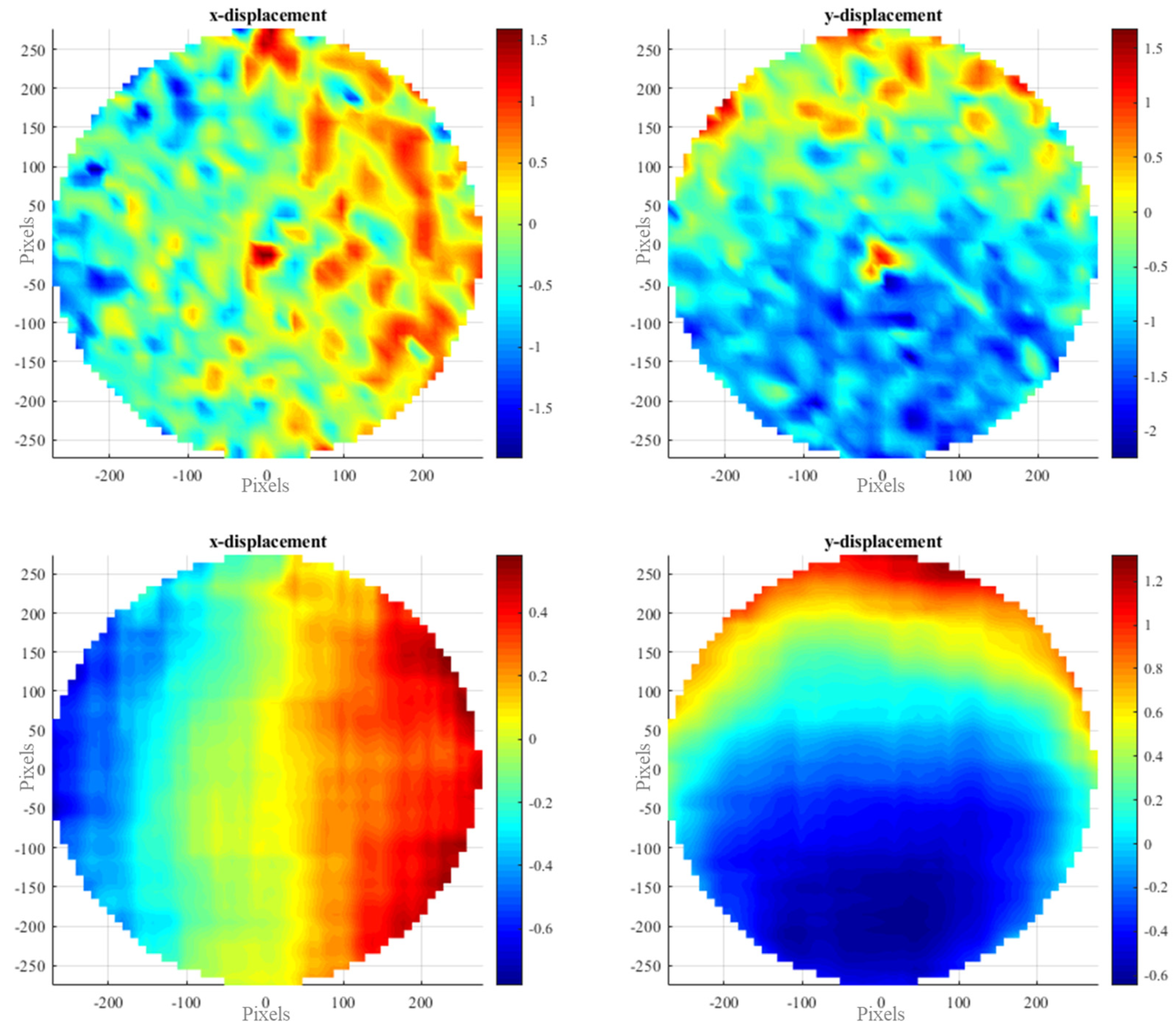
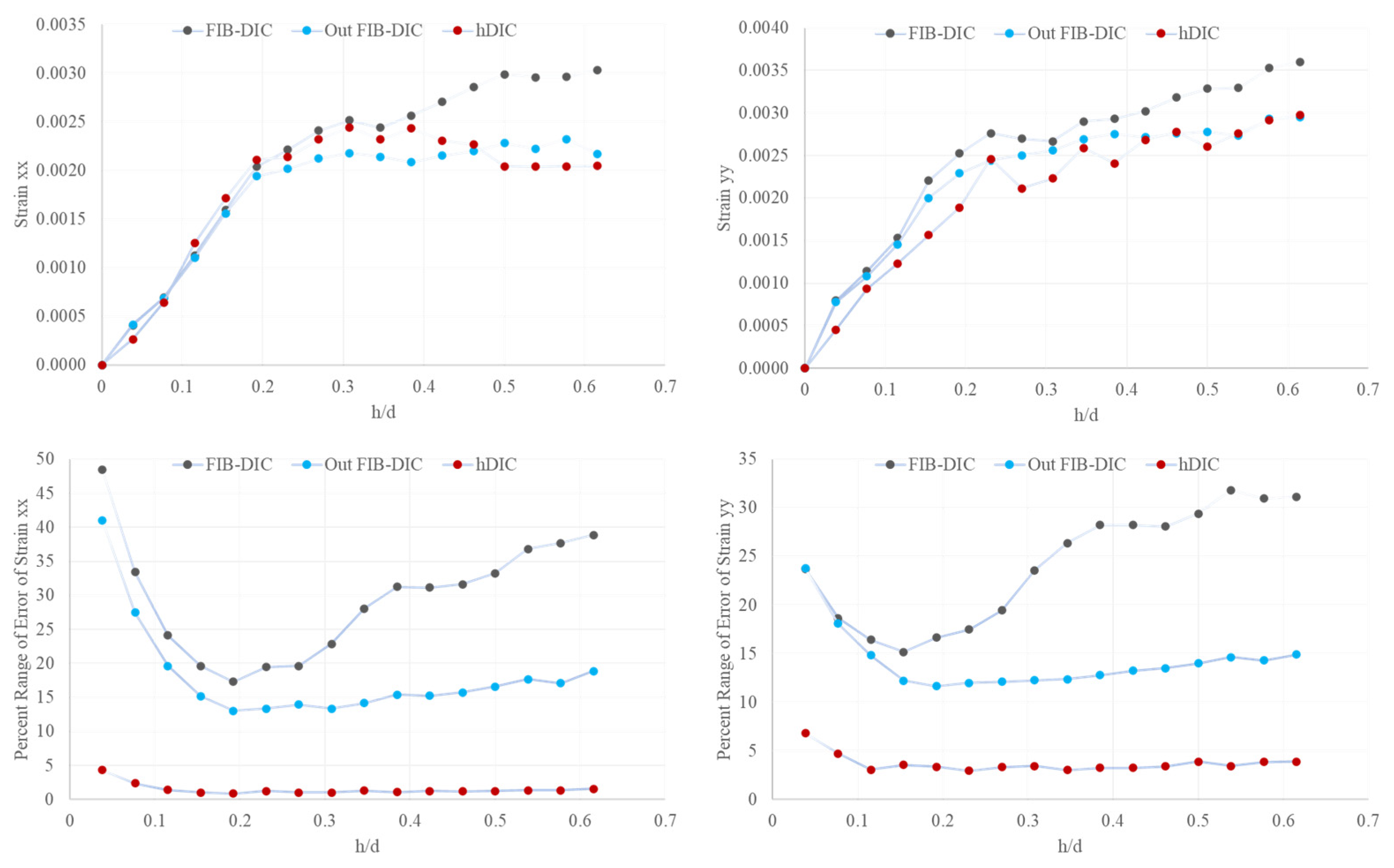
4.3. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pauleau, Y. Materials Surface Processing by Directed Energy Techniques. In Materials Surface Processing by Directed Energy Techniques; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–722. [Google Scholar] [CrossRef]
- Li, S.; Zhang, B.; Yang, L.; Zhang, J.; Wang, Y.; Kang, W. Study on Wear Properties of the Graphite-Sealing Surfaces in a Triple Eccentric Butterfly Valve Based on EDEM-Fluent Coupling. Machines 2023, 11, 463. [Google Scholar] [CrossRef]
- Wang, C.; Han, J.; Zhao, J.; Song, Y.; Man, J.; Zhu, H.; Sun, J.; Fang, L. Enhanced Wear Resistance of 316 L Stainless Steel with a Nanostructured Surface Layer Prepared by Ultrasonic Surface Rolling. Coatings 2019, 9, 276. [Google Scholar] [CrossRef]
- Chen, S.; Usta, A.D.; Eriten, M. Microstructure and Wear Resistance of Ti6Al4V Surfaces Processed by Pulsed Laser. Surf. Coat. Technol. 2017, 315, 220–231. [Google Scholar] [CrossRef]
- Dzionk, S.; Przybylski, W.; Ścibiorski, B. The Possibilities of Improving the Fatigue Durability of the Ship Propeller Shaft by Burnishing Process. Machines 2020, 8, 63. [Google Scholar] [CrossRef]
- Wen, Q.; Hu, J.; Yuan, Z. Sub-Fiber Scale Precision Dicing of Aramid Fiber-Reinforced Plastic Composites. Machines 2022, 10, 334. [Google Scholar] [CrossRef]
- Kahlin, M.; Ansell, H.; Basu, D.; Kerwin, A.; Newton, L.; Smith, B.; Moverare, J.J. Improved Fatigue Strength of Additively Manufactured Ti6Al4V by Surface Post Processing. Int. J. Fatigue 2020, 134, 105497. [Google Scholar] [CrossRef]
- Rogachev, S.O.; Bazhenov, V.E.; Komissarov, A.A.; Ten, D.V.; Li, A.V.; Andreev, V.A.; Statnik, E.S.; Sadykova, I.A.; Plegunova, S.V.; Yushchuk, V.V.; et al. High Strength and Ductility in a New Mg–Zn–Ga Biocompatible Alloy by Drawing and Rotary Forging. Results Mater. 2024, 21, 100524. [Google Scholar] [CrossRef]
- Au-Yeung, H.L.; Ataya, S.; Hassanin, H.; El-Sayed, M.A.; Ahmadein, M.; Alsaleh, N.A.; Ahmed, M.M.Z.; Essa, K. Non-Destructive Disassembly of Interference Fit under Wear Conditions for Sustainable Remanufacturing. Machines 2023, 11, 538. [Google Scholar] [CrossRef]
- Arackal Narayanan, J.; Kaji, F.; Zimny, M.; Toyserkani, E. Laser Directed Energy Deposition-Based Additive Manufacturing of Fe20Cr5.5AlY from Single Tracks to Bulk Structures: Statistical Analysis, Process Optimization, and Characterization. Machines 2023, 11, 58. [Google Scholar] [CrossRef]
- Kara, F.; Markopoulos, P.; Nas, E.; Kara, F. Optimization of EDM Machinability of Hastelloy C22 Super Alloys. Machines 2022, 10, 1131. [Google Scholar] [CrossRef]
- Schneller, W.; Leitner, M.; Pomberger, S.; Springer, S.; Beter, F.; Grün, F. Effect of Post Treatment on the Microstructure, Surface Roughness and Residual Stress Regarding the Fatigue Strength of Selectively Laser Melted AlSi10Mg Structures. J. Manuf. Mater. Process. 2019, 3, 89. [Google Scholar] [CrossRef]
- Ye, C.; Zhang, C.; Zhao, J.; Dong, Y. Effects of Post-Processing on the Surface Finish, Porosity, Residual Stresses, and Fatigue Performance of Additive Manufactured Metals: A Review. J. Mater. Eng. Perform. 2021, 30, 6407–6425. [Google Scholar] [CrossRef] [PubMed]
- Huchzermeyer, R.L. Measuring Mechanical Properties Using Digital Image Correlation: Extracting Tensile and Fracture Properties from a Single Sample. Doctoral Dissertation, Stellenbosch University, Stellenbosch, South Africa, 2017. [Google Scholar]
- Bárány, T.; Czigány, T.; Karger-Kocsis, J. Application of the Essential Work of Fracture (EWF) Concept for Polymers, Related Blends and Composites: A Review. Prog. Polym. Sci. 2010, 35, 1257–1287. [Google Scholar] [CrossRef]
- Abanto-Bueno, J.; Lambros, J. Investigation of Crack Growth in Functionally Graded Materials Using Digital Image Correlation. Eng. Fract. Mech. 2002, 69, 1695–1711. [Google Scholar] [CrossRef]
- Chen, J.; Chu, J.; Jiang, W.; Yao, B.; Zhou, F.; Wang, Z.; Zhao, P. Experimental and Numerical Simulation to Study the Reduction of Welding Residual Stress by Ultrasonic Impact Treatment. Materials 2020, 13, 837. [Google Scholar] [CrossRef] [PubMed]
- Johnson, E.M.; Watkins, T.R.; Schmidlin, J.E.; Dutler, S.A. A Benchmark Study on Casting Residual Stress. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2012, 43, 1487–1496. [Google Scholar] [CrossRef]
- Oberreiter, M.; Horvath, M.; Stoschka, M.; Fladischer, S. Effect of Surface Finishing State on Fatigue Strength of Cast Aluminium and Steel Alloys. Materials 2023, 16, 4755. [Google Scholar] [CrossRef] [PubMed]
- Petersen, L.; Lima, B.; Vinícius Puydinger, M.; Santos, M.A.; Keiler, A.; Ribeiro, A.; Cerdeira, A.; Pavanello, M.A.; Inkson, B.J.; Leclere, D.; et al. The Effect of Focused Ion Beam Machining on Residual Stress and Crack Morphologies in Alumina. J. Phys. Conf. Ser. 2006, 26, 219. [Google Scholar] [CrossRef]
- Chelladurai, S.J.S.; Murugan, K.; Ray, A.P.; Upadhyaya, M.; Narasimharaj, V.; Gnanasekaran, S. Optimization of Process Parameters Using Response Surface Methodology: A Review. Mater. Today Proc. 2021, 37, 1301–1304. [Google Scholar] [CrossRef]
- Mozetič, M. Surface Modification to Improve Properties of Materials. Materials 2019, 12, 441. [Google Scholar] [CrossRef]
- Dinsmore, D.L.; Alexander, P.A. A Critical Discussion of Deep and Surface Processing: What It Means, How It Is Measured, the Role of Context, and Model Specification. Educ. Psychol. Rev. 2012, 24, 499–567. [Google Scholar] [CrossRef]
- Alexander, M.; Thomas, M. Service Life Prediction and Performance Testing—Current Developments and Practical Applications. Cem. Concr. Res. 2015, 78, 155–164. [Google Scholar] [CrossRef]
- Lee, L.J.; Fu, K.E.; Yang, J.N. Prediction of Fatigue Damage and Life for Composite Laminates under Service Loading Spectra. Compos. Sci. Technol. 1996, 56, 635–648. [Google Scholar] [CrossRef]
- Kang, J.; Wilkinson, D.S.; Embury, J.D.; Jain, M. Microscopic Strain Mapping Using Scanning Electron Microscopy Topography Image Correlation at Large Strain. J. Strain Anal. Eng. Des. 2005, 40, 559–570. [Google Scholar] [CrossRef]
- Wang, X.; Pan, Z.; Fan, F.; Wang, J.; Liu, Y.; Mao, S.X.; Zhu, T.; Xia, S. Nanoscale Deformation Analysis With High-Resolution Transmission Electron Microscopy and Digital Image Correlation. J. Appl. Mech. 2015, 82, 121001. [Google Scholar] [CrossRef]
- Jiang, J.; Yang, J.; Zhang, T.; Zou, J.; Wang, Y.; Dunne, F.P.E.; Britton, T.B. Microstructurally Sensitive Crack Nucleation around Inclusions in Powder Metallurgy Nickel-Based Superalloys. Acta Mater. 2016, 117, 333–344. [Google Scholar] [CrossRef]
- Sun, C.; Standish, B.; Vuong, B.; Wen, X.-Y.; Yang, V. Digital Image Correlation—Based Optical Coherence Elastography. J. Biomed. Opt. 2013, 18, 121515. [Google Scholar] [CrossRef]
- Xu, Z.H.; Sutton, M.A.; Li, X. Mapping Nanoscale Wear Field by Combined Atomic Force Microscopy and Digital Image Correlation Techniques. Acta Mater. 2008, 56, 6304–6309. [Google Scholar] [CrossRef]
- Bruno, L. Full-Field Measurement with Nanometric Accuracy of 3D Superficial Displacements by Digital Profile Correlation: A Powerful Tool for Mechanics of Materials. Mater. Des. 2018, 159, 170–185. [Google Scholar] [CrossRef]
- Watkins, R.E.J.; Rockett, P.; Thoms, S.; Clampitt, R.; Syms, R. Focused Ion Beam Milling. Vacuum 1986, 36, 961–967. [Google Scholar] [CrossRef]
- Zhu, B.; Leung, N.; Kockelmann, W.; Kabra, S.; London, A.J.; Gorley, M.; Whiting, M.J.; Wang, Y.; Sui, T. Revealing the Residual Stress Distribution in Laser Welded Eurofer97 Steel by Neutron Diffraction and Bragg Edge Imaging. J. Mater. Sci. Technol. 2022, 114, 249–260. [Google Scholar] [CrossRef]
- Winiarski, B.; Withers, P.J. Micron-Scale Residual Stress Measurement Using Micro-Hole Drilling and Digital Image Correlation. Conf. Proc. Soc. Exp. Mech. Ser. 2012, 4, 189–198. [Google Scholar] [CrossRef]
- Blair, A.; Daynes, N.; Hamilton, D.; Horne, G.; Heard, P.J.; Hodgson, D.Z.L.; Scott, T.B.; Shterenlikht, A. Residual Stress Relaxation Measurements across Interfaces at Macro-and Micro-Scales Using Slitting and DIC. J. Phys. Conf. Ser. 2009, 181, 012078. [Google Scholar] [CrossRef]
- Lunt, A.J.G.; Korsunsky, A.M. A Review of Micro-Scale Focused Ion Beam Milling and Digital Image Correlation Analysis for Residual Stress Evaluation and Error Estimation. Surf. Coat. Technol. 2015, 283, 373–388. [Google Scholar] [CrossRef]
- Krottenthaler, M.; Schmid, C.; Schaufler, J.; Durst, K.; Göken, M. A Simple Method for Residual Stress Measurements in Thin Films by Means of Focused Ion Beam Milling and Digital Image Correlation. Surf. Coat. Technol. 2013, 215, 247–252. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Sebastiani, M.; Bemporad, E. Focused Ion Beam Ring Drilling for Residual Stress Evaluation. Mater. Lett. 2009, 63, 1961–1963. [Google Scholar] [CrossRef]
- Dong, W.; Liang, X.; Chen, Q.; Hinnebusch, S.; Zhou, Z.; To, A.C. A New Procedure for Implementing the Modified Inherent Strain Method with Improved Accuracy in Predicting Both Residual Stress and Deformation for Laser Powder Bed Fusion. Addit. Manuf. 2021, 102345. [Google Scholar] [CrossRef]
- Chen, W.; Xu, L.; Han, Y.; Zhao, L.; Jing, H. Control of Residual Stress in Metal Additive Manufacturing by Low-Temperature Solid-State Phase Transformation: An Experimental and Numerical Study. Addit. Manuf. 2021, 42, 102016. [Google Scholar] [CrossRef]
- Wang, Z.; Denlinger, E.; Michaleris, P.; Stoica, A.D.; Ma, D.; Beese, A.M. Residual Stress Mapping in Inconel 625 Fabricated through Additive Manufacturing: Method for Neutron Diffraction Measurements to Validate Thermomechanical Model Predictions. Mater. Des. 2017, 113, 169–177. [Google Scholar] [CrossRef]
- Foss, B.J.; Gray, S.; Hardy, M.C.; Stekovic, S.; McPhail, D.S.; Shollock, B.A. Analysis of Shot-Peening and Residual Stress Relaxation in the Nickel-Based Superalloy RR1000. Acta Mater. 2013, 61, 2548–2559. [Google Scholar] [CrossRef]
- Bragg, W.L. The Specular Reflection of X-rays. Nature 1912, 90, 410. [Google Scholar] [CrossRef]
- Withers, P.J. Synchrotron X-Ray Diffraction. In Practical Residual Stress Measurement Methods; Schajer, G.S., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; pp. 163–194. ISBN 9781118402832. [Google Scholar]
- Uzun, F.; Korsunsky, A.M. The Height Digital Image Correlation (HDIC) Technique For The Identification Of Triaxial Surface Deformations. Int. J. Mech. Sci. 2019, 159, 417–423. [Google Scholar] [CrossRef]
- Uzun, F.; Salimon, A.I.; Statnik, E.S.; Besnard, C.; Chen, J.; Moxham, T.; Salvati, E.; Wang, Z.; Korsunsky, A.M. Polar Transformation of 2D X-Ray Diffraction Patterns and the Experimental Validation of the HDIC Technique. Measurement 2019, 151, 107193. [Google Scholar] [CrossRef]
- Uzun, F.; Korsunsky, A.M. The Use of Surface Topography for the Identification of Discontinuous Displacements Due to Cracks. Metals 2020, 10, 1037. [Google Scholar] [CrossRef]
- Romano-Brandt, L.; Salvati, E.; Le Bourhis, E.; Moxham, T.; Dolbnya, I.P.; Korsunsky, A.M. Nano-Scale Residual Stress Depth Profiling in Cu/W Nano-Multilayers as a Function of Magnetron Sputtering Pressure. Surf. Coat. Technol. 2019, 381, 125142. [Google Scholar] [CrossRef]
- Schajer, G.S.; Winiarski, B.; Withers, P.J. Hole-Drilling Residual Stress Measurement with Artifact Correction Using Full-Field DIC. In Proceedings of the Experimental and Applied Mechanics, Volume 4; Ventura, C.E., Crone, W.C., Furlong, C., Eds.; Springer: New York, NY, USA, 2013; pp. 403–414. [Google Scholar]
- Cao, Y.; Xie, X.; Antonaglia, J.; Winiarski, B.; Wang, G.; Shin, Y.C.; Withers, P.J.; Dahmen, K.A.; Liaw, P.K. Laser Shock Peening on Zr-Based Bulk Metallic Glass and Its Effect on Plasticity: Experiment and Modeling. Sci. Rep. 2015, 5, 10789. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.J.; Yao, N.; He, M.Y.; Evans, A.G. A Method for in Situ Measurement of the Residual Stress in Thin Films by Using the Focused Ion Beam. Thin Solid. Films 2003, 443, 71–77. [Google Scholar] [CrossRef]
- Winiarski, B.; Gholinia, A.; Tian, J.; Yokoyama, Y.; Liaw, P.K.; Withers, P.J. Submicron-Scale Depth Profiling of Residual Stress in Amorphous Materials by Incremental Focused Ion Beam Slotting. Acta Mater. 2012, 60, 2337–2349. [Google Scholar] [CrossRef]
- Winiarski, B.; Langford, R.M.; Tian, J.; Yokoyama, Y.; Liaw, P.K.; Withers, P.J. Mapping Residual Stress Distributions at the Micron Scale in Amorphous Materials. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2010, 41, 1743–1751. [Google Scholar] [CrossRef]
- Mansilla, C.; Martínez-Martínez, D.; Ocelík, V.; De Hosson, J.T.M. On the Determination of Local Residual Stress Gradients by the Slit Milling Method. J. Mater. Sci. 2015, 50, 3646–3655. [Google Scholar] [CrossRef]
- Sebastiani, M.; Eberl, C.; Bemporad, E.; Korsunsky, A.M.; Nix, W.D.; Carassiti, F. Focused Ion Beam Four-Slot Milling for Poisson’s Ratio and Residual Stress Evaluation at the Micron Scale. Surf. Coat. Technol. 2014, 251, 151–161. [Google Scholar] [CrossRef]
- Sebastiani, M.; Eberl, C.; Bemporad, E.; Pharr, G.M. Depth-Resolved Residual Stress Analysis of Thin Coatings by a New FIB-DIC Method. Mater. Sci. Eng. A 2011, 528, 7901–7908. [Google Scholar] [CrossRef]
- Huang, H.; Dabiri, D.; Gharib, M. On Errors of Digital Particle Image Velocimetry. Meas. Sci. Technol. 1997, 8, 1427–1440. [Google Scholar] [CrossRef]
- Farebrother, R.W. Linear Least Squares Computations; Marcel Dekker, Inc.: New York, NY, USA, 1988; ISBN 0-82-477661-5. [Google Scholar]
- Russell, W.S. Polynomial Interpolation Schemes for Internal Derivative Distributions on Structured Grids. Appl. Numer. Math. 1995, 17, 129–171. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzun, F.; Korsunsky, A.M. Digital Image Correlation for Elastic Strain Evaluation during Focused Ion Beam Ring-Core Milling. J. Manuf. Mater. Process. 2024, 8, 144. https://doi.org/10.3390/jmmp8040144
Uzun F, Korsunsky AM. Digital Image Correlation for Elastic Strain Evaluation during Focused Ion Beam Ring-Core Milling. Journal of Manufacturing and Materials Processing. 2024; 8(4):144. https://doi.org/10.3390/jmmp8040144
Chicago/Turabian StyleUzun, Fatih, and Alexander M. Korsunsky. 2024. "Digital Image Correlation for Elastic Strain Evaluation during Focused Ion Beam Ring-Core Milling" Journal of Manufacturing and Materials Processing 8, no. 4: 144. https://doi.org/10.3390/jmmp8040144
APA StyleUzun, F., & Korsunsky, A. M. (2024). Digital Image Correlation for Elastic Strain Evaluation during Focused Ion Beam Ring-Core Milling. Journal of Manufacturing and Materials Processing, 8(4), 144. https://doi.org/10.3390/jmmp8040144






