Selective Sheet Extrusion: A Novel Manufacturing Process for Large-Format Material Extrusion
Abstract
1. Introduction
1.1. Large-Format Additive Manufacturing
1.2. Overcoming the Trade-Off between Resolution and Speed
2. Theoretical Analysis
2.1. Analytical Process
2.2. Results of Analysis
2.2.1. Predicted Increase in Speed
2.2.2. Predicted Increase in Material Efficiency
3. Experimental Validation
3.1. Selective Sheet Extrusion (SSE) System
3.2. Commercial Clay 3D Printer
3.3. Experimental Design
3.3.1. Three-Dimensional Model for Experimental Comparison
3.3.2. Predicted Print Times
3.4. Experimental Results
3.4.1. Actual Print Times
3.4.2. Comparison of Print Times
3.4.3. Photos of Printed Structures
4. Discussion
4.1. Analysis of Theoretical Results
4.2. Comparing Theoretical and Experimental Results
5. Conclusions
Future Work and Applications
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| LFAM | Large-Format Additive Manufacturing |
| CMU | Concrete Masonry Unit |
| DCMU | Digital Concrete Masonry Unit |
Appendix A. Theoretical Analysis–Calculations and Assumptions
Appendix A.1. Modeling the Performance of Single-Nozzle Solutions and SSE Systems
Appendix A.2. Comparison of SSE Systems to Single-Nozzle Systems
- The SSE system is rationalized to fit the generalized example being investigated. This means that the width of the teeth will match the features that need printing. Multiple potential tooth width settings are only considered in the first example (Appendix A.3) to facilitate a more comprehensive comparison. However, variable tooth widths across a single nozzle are not considered in any of these comparisons.
- The range of nozzle diameters investigated will always include an optimized nozzle diameter for both speed and material usage.
- The comparison will assume that all systems are printing continuously for simplicity.
- The comparison will assume that all generalized structures can be printed with single-nozzle systems, regardless of their nozzle diameter. Specifically, it is assumed that the nozzle can be moved along a path that accurately reproduces the desired structure with the extrusion profile assumed by Reference [14]’s model. As a result, the calculations of time to print are derived by calculating the material that will be printed and dividing by the flow rate.
- A description of a generalized geometry for that structure, specifying which features are required;
- Calculations of the material used to print the generalized geometry with both the SSE technology and single-nozzle systems of various nozzle diameters;
- Calculations of the effective material extrusion rate for both the SSE technology and single-nozzle systems of various nozzle diameters;
- Calculations of the time required to print the generalized geometry for each of the systems above;
- Table of results showing the calculated material usage and time required to print for the SSE system and single-nozzle systems, all normalized to the single-nozzle system with the diameter that prints at the fastest speed without wasting any material.
Appendix A.3. Application to a Large, Simple Structure Requiring No Internal Structuring and/or Very Low Resolution
Appendix A.3.1. Generalized Geometry
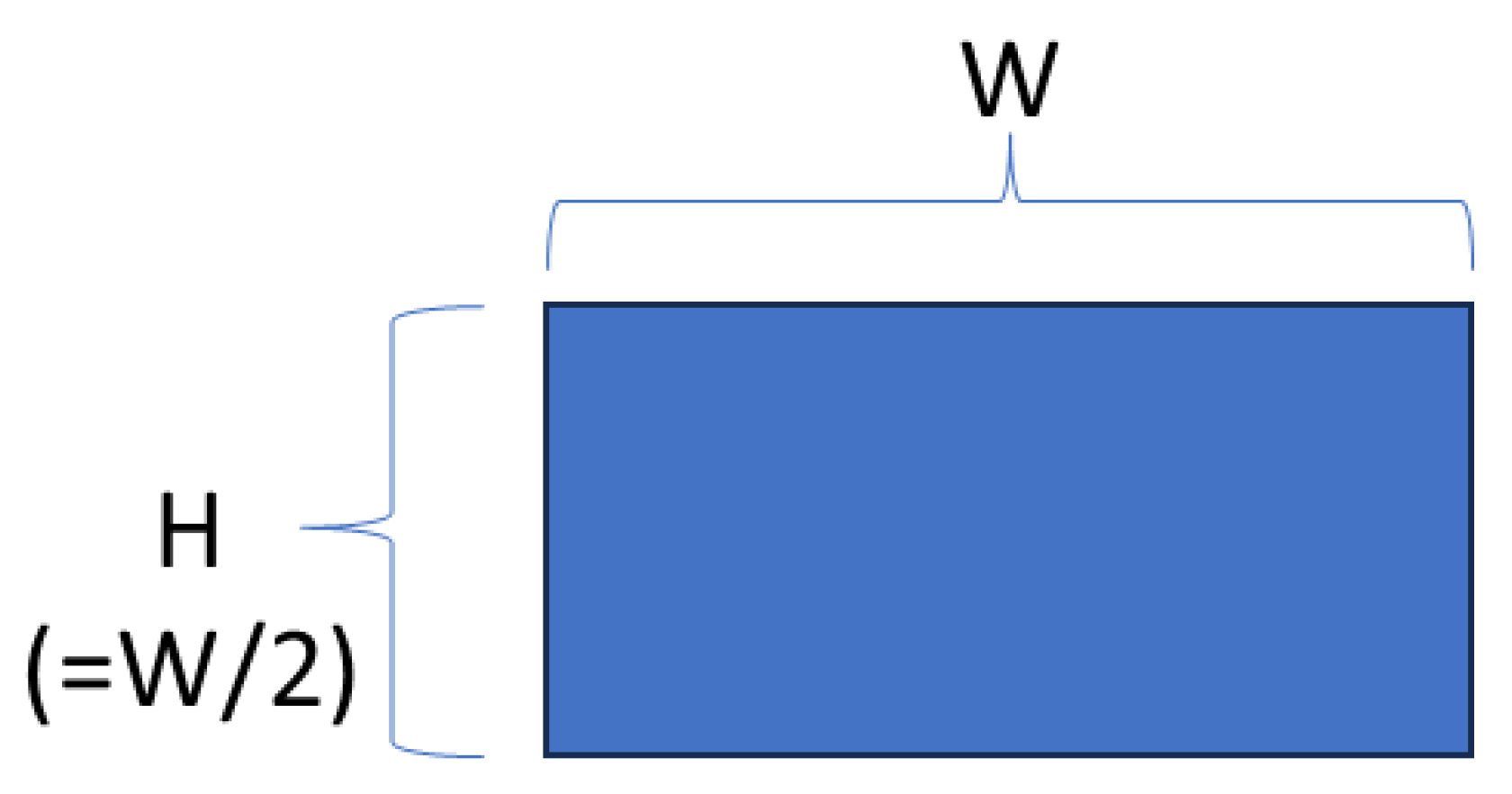
Appendix A.3.2. Material Used
Appendix A.3.3. Material Extrusion Rate
Appendix A.3.4. Time Required to Print Structure
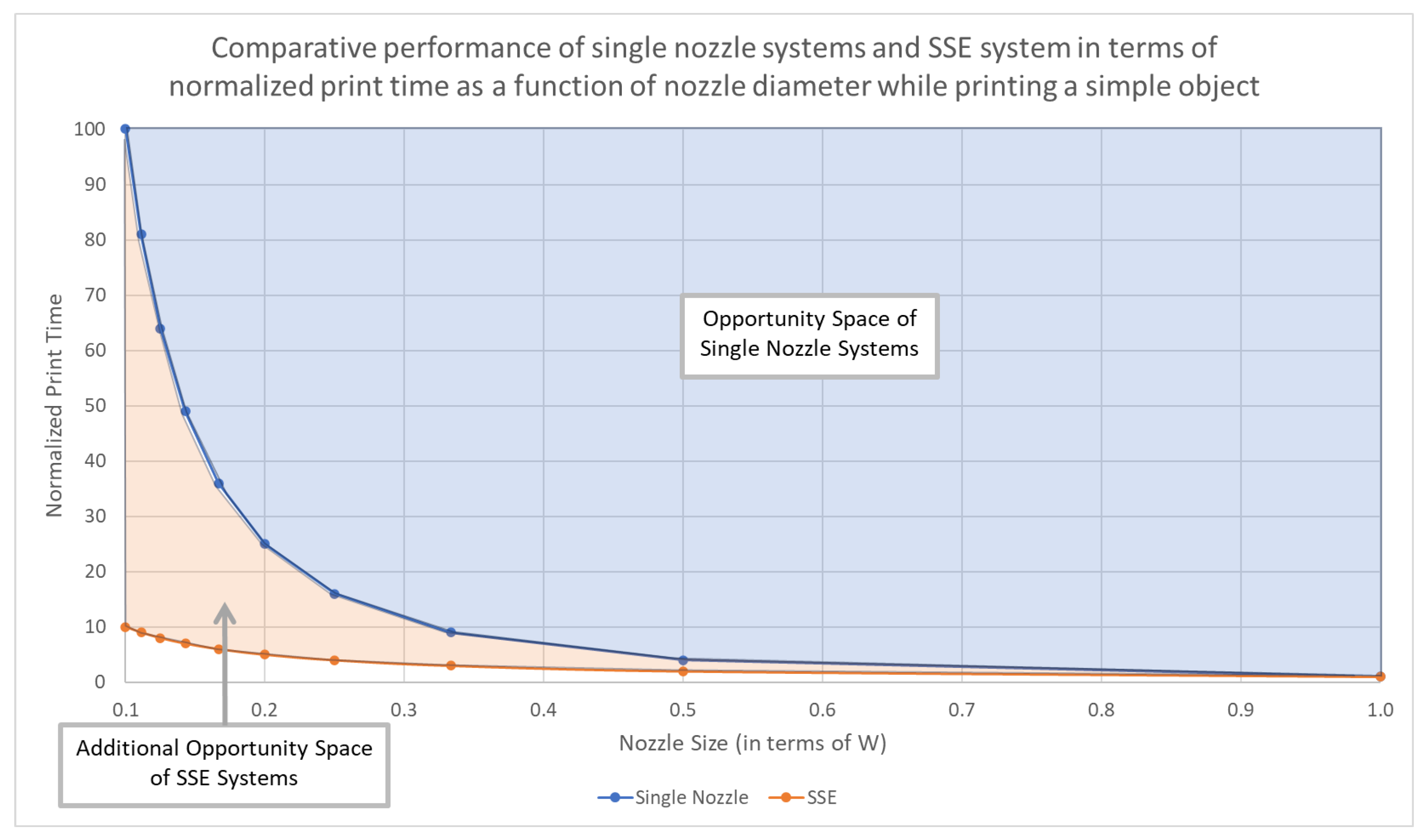
Appendix A.3.5. Table of Results
| Nozzle Diameter/Tooth Width | W | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Effective Nozzle Size ( and ) | 1.00 | 0.50 | 0.33 | 0.25 | 0.20 | 0.17 | 0.14 | 0.13 | 0.11 | 0.10 |
| Single-Nozzle Relative Time to Print | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| SSE System Relative Time to Print | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Appendix A.4. Application to a Generalized Wall Structure
Appendix A.4.1. Generalized Geometry
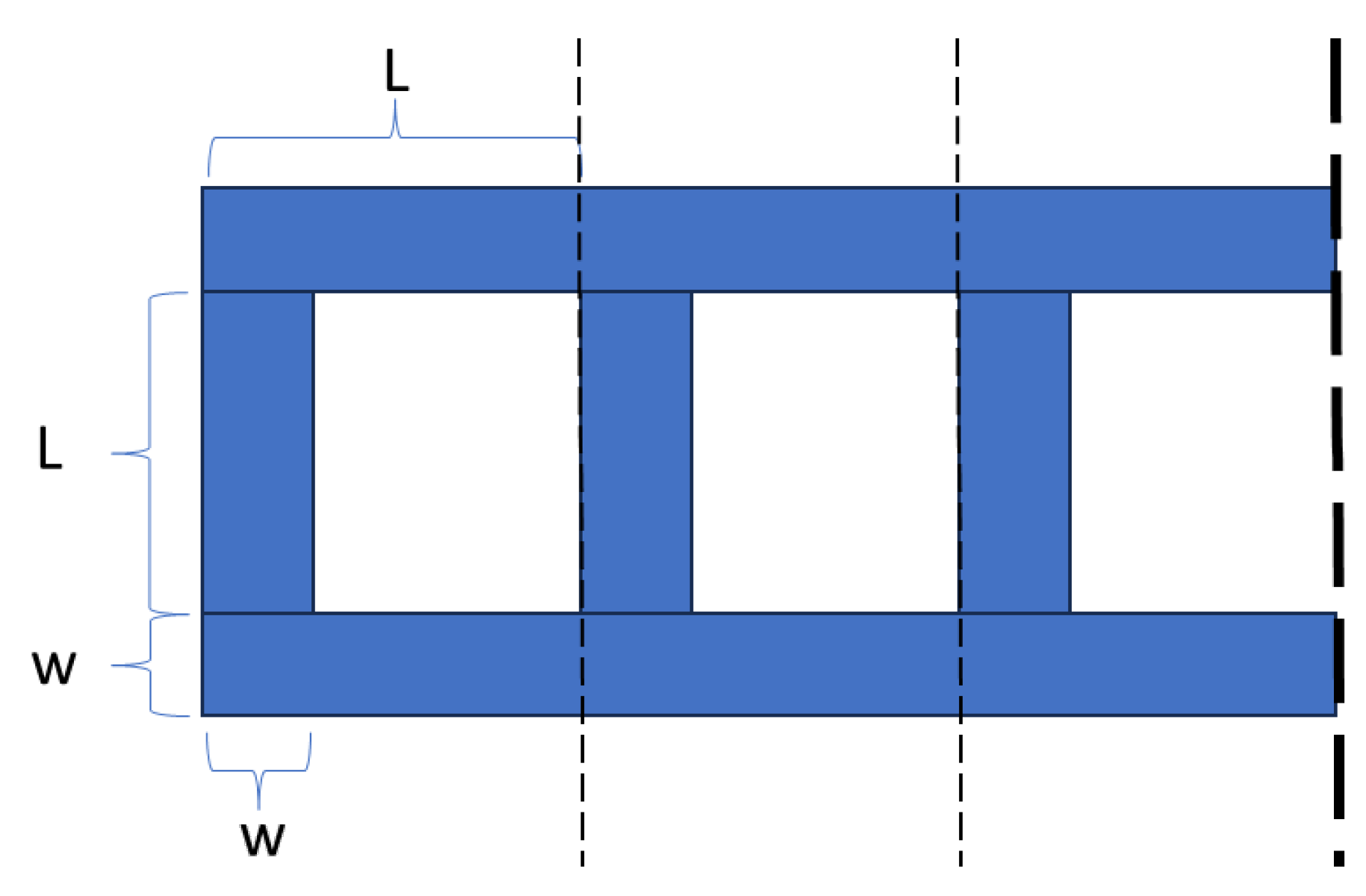
Appendix A.4.2. Material Used
Appendix A.4.3. Material Extrusion Rate
Appendix A.4.4. Time Required to Print Structure
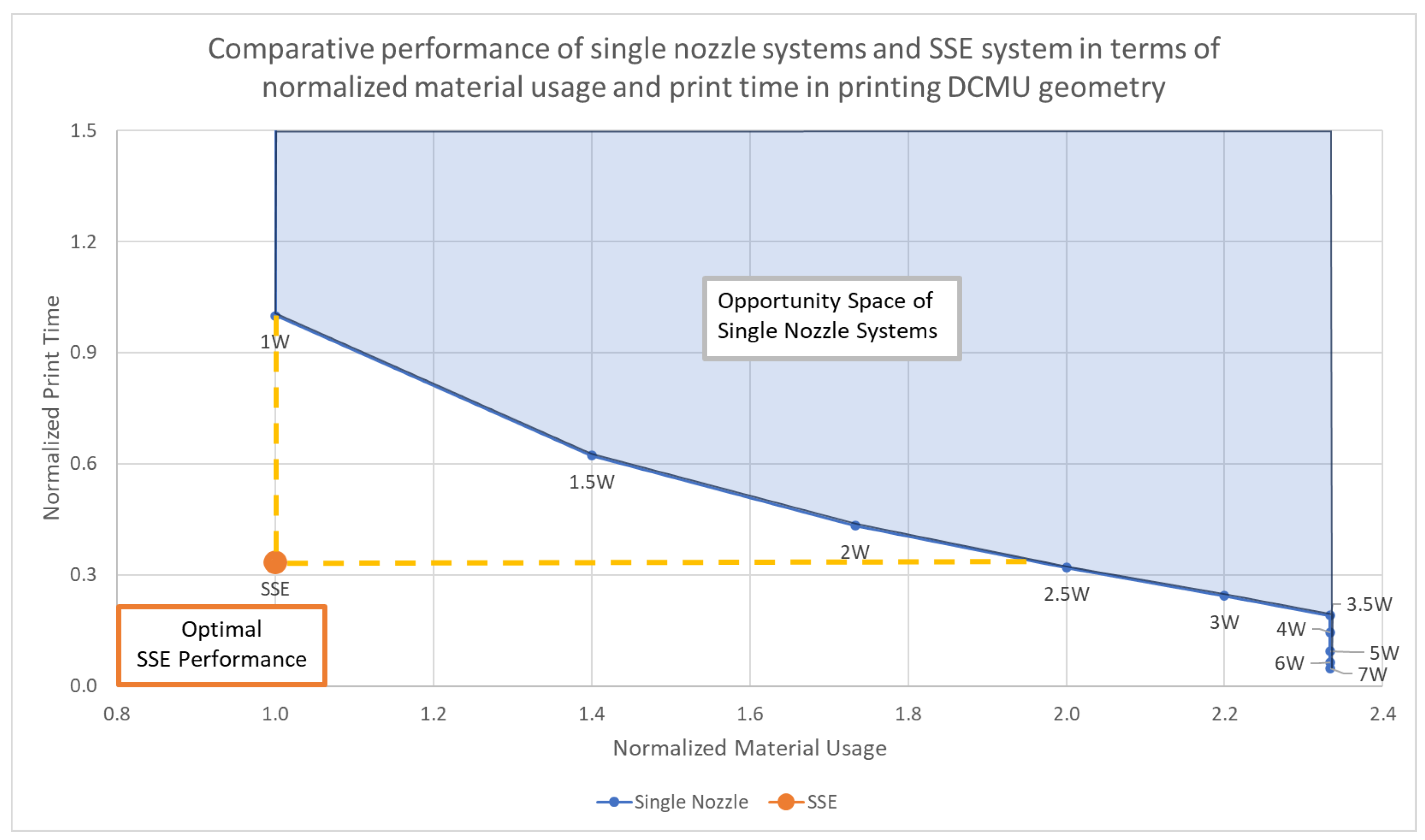
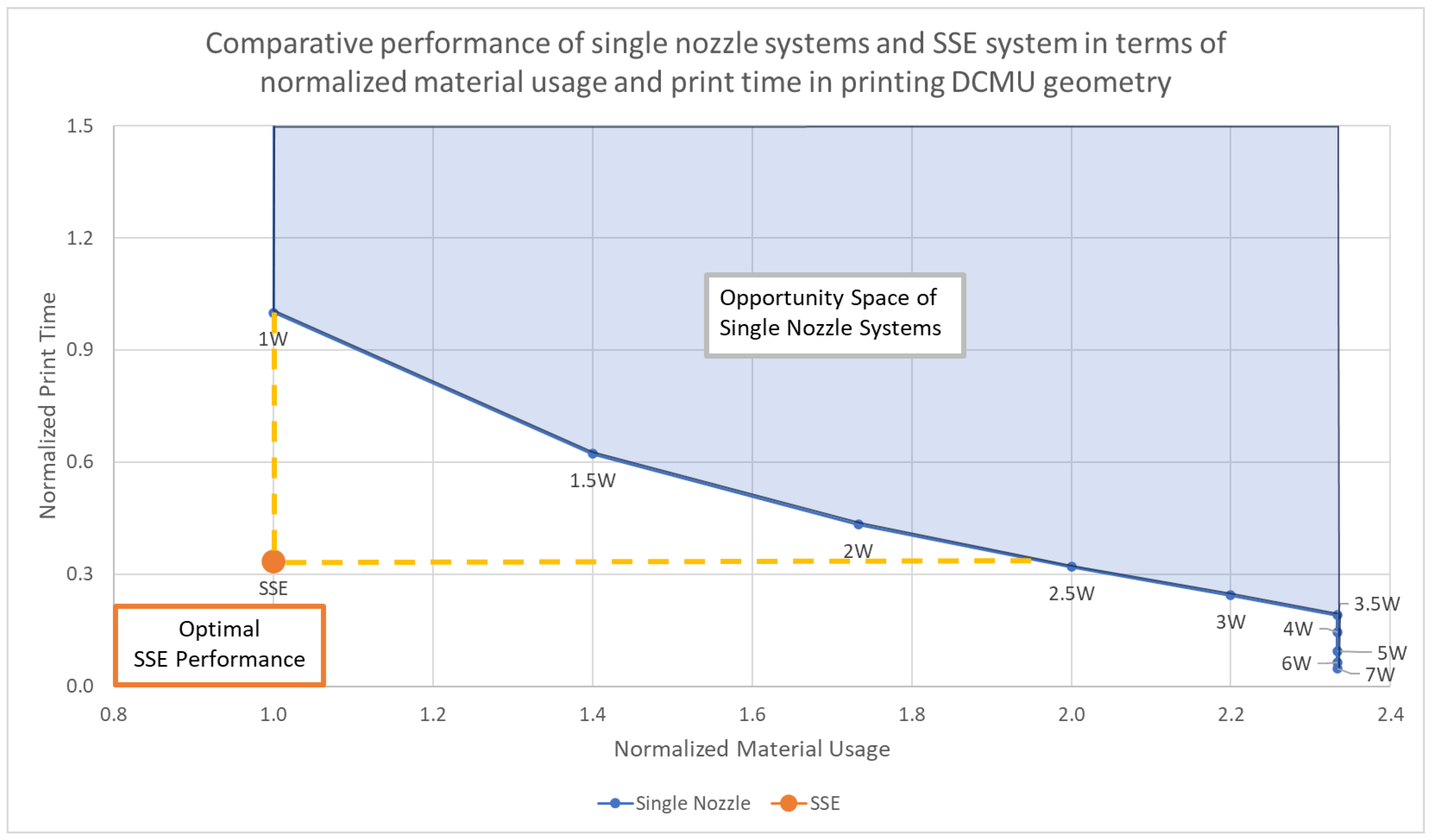
Appendix A.4.5. Table of Results
| Nozzle Diameter | 0.5w | 1w | 1.5w | 2w | 2.5w | 3w | 3.5w | 4w | 5w | 6w | 7w | SSE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Material Usage (norm) | 1.00 | 1.00 | 1.40 | 1.73 | 2.00 | 2.20 | 2.33 | 2.33 | 2.33 | 2.33 | 2.33 | 1 | |
| Normalized Print Time | 4.00 | 1.00 | 0.62 | 0.43 | 0.32 | 0.24 | 0.19 | 0.15 | 0.09 | 0.06 | 0.05 | 0.33 |
Appendix A.5. Application to a Generalized Conduit Structure
Appendix A.5.1. Generalized Geometry
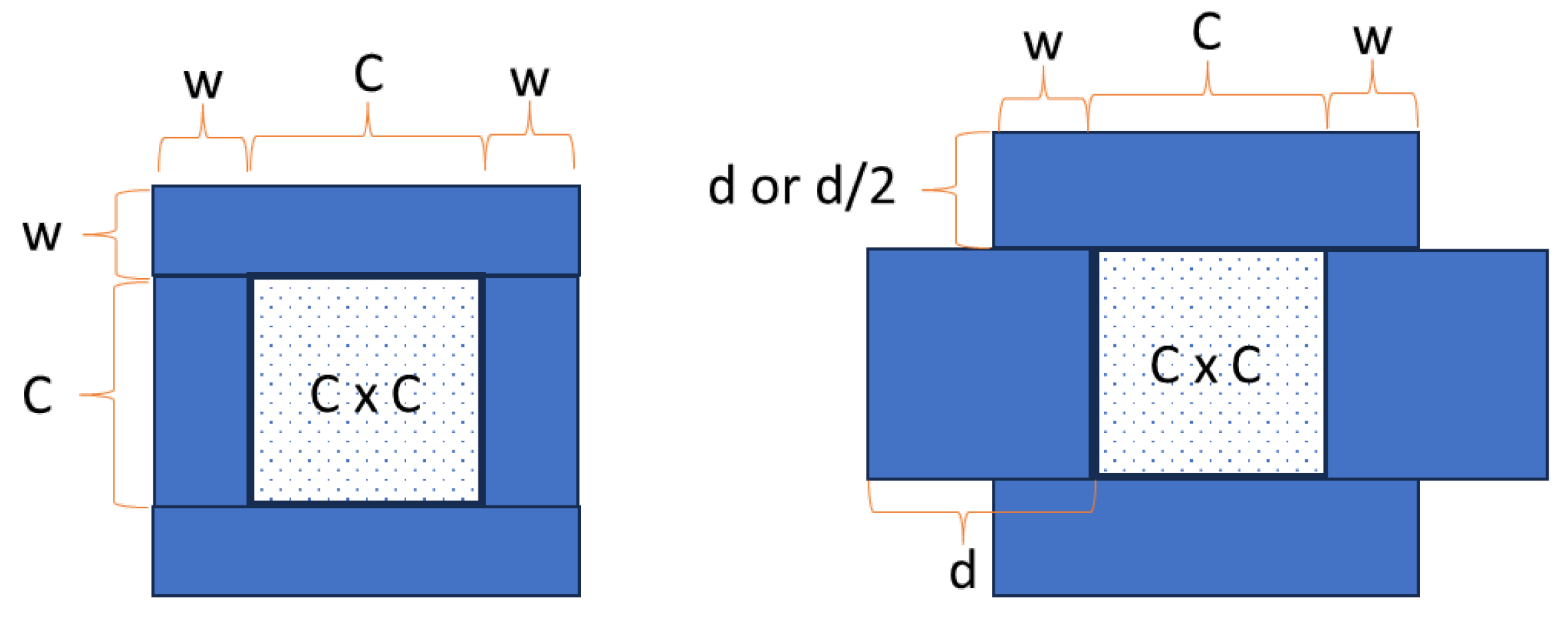
Appendix A.5.2. Material Used
Appendix A.5.3. Material Extrusion Rate
Appendix A.5.4. Time Required to Print Structure
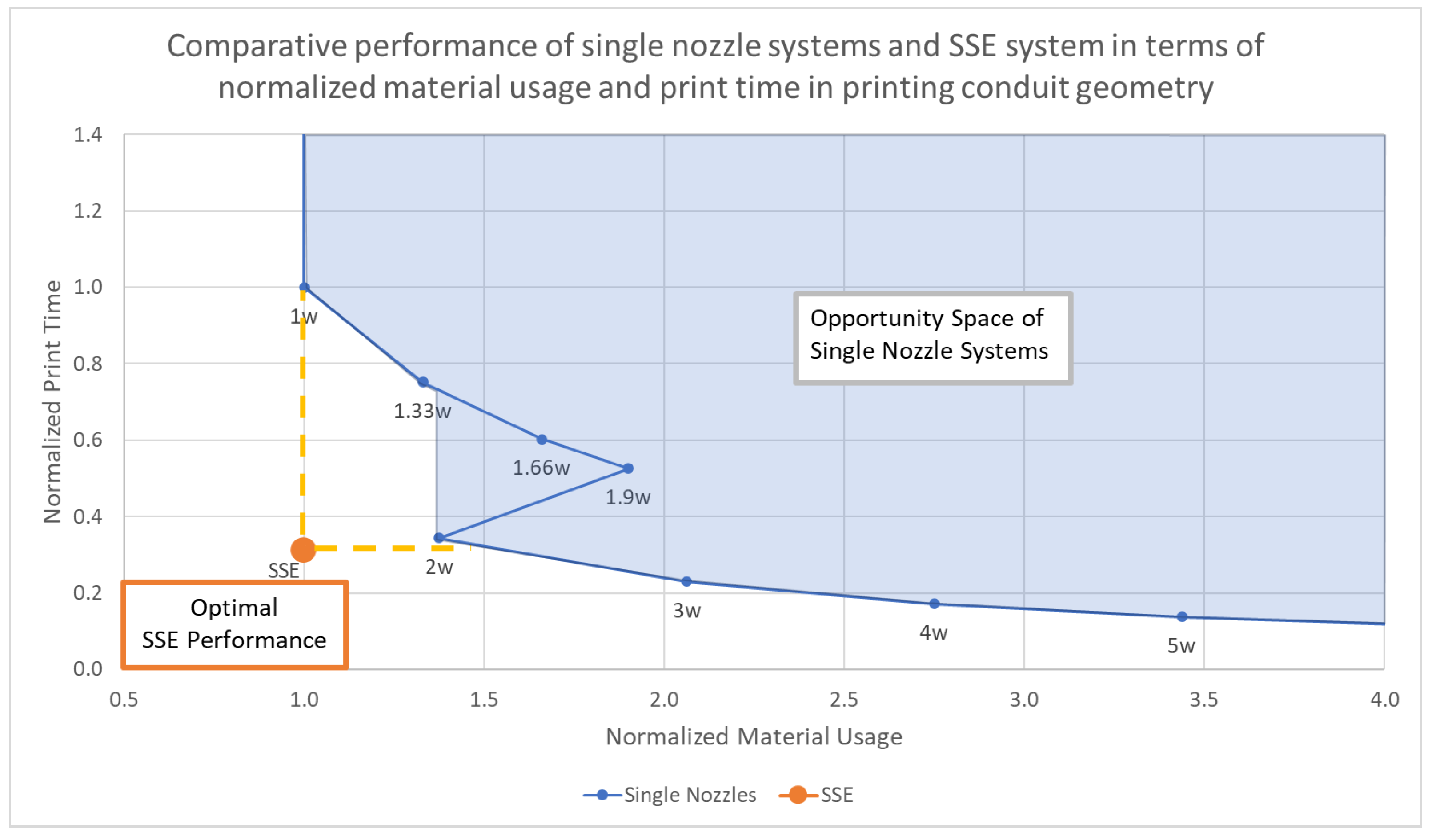
Appendix A.5.5. Table of Results
| Nozzle Diameter | 0.5w | 1w | 1.33w | 1.66w | 1.9w | 2w | 3w | 4w | 5w | 6w | SSE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Material Usage (norm) | 1.0 | 1.0 | 1.3 | 1.7 | 1.9 | 1.4 | 2.1 | 2.8 | 3.4 | 4.1 | 1.0 | |
| Normalized Print Time | 4.0 | 1.0 | 0.8 | 0.6 | 0.5 | 0.3 | 0.2 | 0.2 | 0.1 | 0.1 | 0.3 |
References
- Prashar, G.; Vasudev, H.; Bhuddhi, D. Additive manufacturing: Expanding 3D printing horizon in industry 4.0. Int. J. Interact. Des. Manuf. 2022, 17, 2221–2235. [Google Scholar] [CrossRef]
- Whitehead, J.; Lipson, H. Multi-Process Printing Method Combining Powder and Resin Based Additive Manufacturing. Addit. Manuf. Lett. 2022, 3, 100062. [Google Scholar] [CrossRef]
- Roach, D.J.; Hamel, C.M.; Dunn, C.K.; Johnson, M.V.; Kuang, X.; Qi, H.J. The m4 3D printer: A multi-material multi-method additive manufacturing platform for future 3D printed structures. Addit. Manuf. 2019, 29, 100819. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies: Rapid Prototyping to Direct Digital Manufacturing, 1st ed.; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Roberts, T. Additive Manufacturing Trend Report 2021; Technical Report; HUBS: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Schwaar, C. 3D-Printed Rockets Set to Blast Off. 2022. Available online: https://www.forbes.com/sites/carolynschwaar/2022/06/30/3d-printed-rockets-set-to-blast-off/?sh=5016bc0b2b6a (accessed on 6 June 2024).
- Hitchens, O. 3D-Printed Rocket Engines: The Technology Driving the Private Sector Space Race. 2021. Available online: https://www.space.com/3d-printed-rocket-engines-private-space-technology (accessed on 6 June 2024).
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Love, L.; Post, B.; Noakes, M.; Nycz, A.; Kunc, V. There’s Plenty of Room at the Top. Addit. Manuf. 2020, 39, 101727. [Google Scholar] [CrossRef]
- Buswell, R.A.; de Silva, W.R.L.; Jones, S.Z.; Dirrenberger, J. 3D printing using concrete extrusion: A roadmap for research. Cem. Concr. Res. 2018, 112, 37–49. [Google Scholar] [CrossRef]
- Kishore, V.; Ajinjeru, C.; Nycz, A.; Post, B.; Lindahl, J.; Kunc, V.; Duty, C. Infrared preheating to improve interlayer strength of big area additive manufacturing (BAAM) components. Addit. Manuf. 2017, 14, 7–12. [Google Scholar] [CrossRef]
- Borish, M.; Post, B.K.; Roschli, A.; Chesser, P.C.; Love, L.J. Real-Time Defect Correction in Large-Scale Polymer Additive Manufacturing via Thermal Imaging and Laser Profilometer. Procedia Manuf. 2020, 48, 625–633. [Google Scholar] [CrossRef]
- Roschli, A.; Gaul, K.T.; Boulger, A.M.; Post, B.K.; Chesser, P.C.; Love, L.J.; Blue, F.; Borish, M. Designing for Big Area Additive Manufacturing. Addit. Manuf. 2019, 25, 275–285. [Google Scholar] [CrossRef]
- Chesser, P.; Post, B.; Roschli, A.; Carnal, C.; Lind, R.; Borish, M.; Love, L. Extrusion control for high quality printing on Big Area Additive Manufacturing (BAAM) systems. Addit. Manuf. 2019, 28, 445–455. [Google Scholar] [CrossRef]
- Hirsch, P.; Scholz, S.; Borowitza, B.; Vyhnal, M.; Schlimper, R.; Zscheyge, M.; Kotera, O.; Stipkova, M.; Scholz, S. Processing and Analysis of Hybrid Fiber-Reinforced Polyamide Composite Structures Made by Fused Granular Fabrication and Automated Tape Laying. J. Manuf. Mater. Process. 2024, 8, 25. [Google Scholar] [CrossRef]
- Butt, J.; Bhaskar, R.; Mohaghegh, V. Investigating the Influence of Material Extrusion Rates and Line Widths on FFF-Printed Graphene-Enhanced PLA. J. Manuf. Mater. Process. 2022, 6, 57. [Google Scholar] [CrossRef]
- Lu, B.; Weng, Y.; Li, M.; Qian, Y.; Leong, K.F.; Tan, M.J.; Qian, S. A systematical review of 3D printable cementitious materials. Constr. Build. Mater. 2019, 207, 477–490. [Google Scholar] [CrossRef]
- Goh, G.D.; Wong, K.K.; Tan, N.; Seet, H.L.; Nai, M.L.S. Large-format additive manufacturing of polymers: A review of fabrication processes, materials, and design. Virtual Phys. Prototyp. 2024, 19, e2336160. [Google Scholar] [CrossRef]
- Singh, A.P.; Pervaiz, S. Current Status and Prospects of Multi-Jet Fusion (MJF) Based 3D Printing Technology. In Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition, Online, 1–5 November 2021. [Google Scholar]
- Shakor, P.; Chu, S.H.; Puzatova, A.; Dini, E. Review of binder jetting 3D printing in the construction industry. Prog. Addit. Manuf. 2022, 7, 643–669. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, D.; Chen, P.; Li, N.; Perrot, A. A Review of the Extruder System Design for Large-Scale Extrusion-Based 3D Concrete Printing. Materials 2023, 16, 2661. [Google Scholar] [CrossRef] [PubMed]
- Tagscherer, N.; Bär, A.M.; Zaremba, S.; Drechsler, K. Mechanical Analysis of Parameter Variations in Large-Scale Extrusion Additive Manufacturing of Thermoplastic Composites. J. Manuf. Mater. Process. 2022, 6, 36. [Google Scholar] [CrossRef]
- Vidakis, N.; Petousis, M.; David, C.N.; Sagris, D.; Mountakis, N.; Karapidakis, E. Mechanical Performance over Energy Expenditure in MEX 3D Printing of Polycarbonate: A Multiparametric Optimization with the Aid of Robust Experimental Design. J. Manuf. Mater. Process. 2023, 7, 38. [Google Scholar] [CrossRef]
- Yuan, P.F.; Zhan, Q.; Wu, H.; Beh, H.S.; Zhang, L. Real-time toolpath planning and extrusion control (RTPEC) method for variable-width 3D concrete printing. J. Build. Eng. 2022, 46, 103716. [Google Scholar] [CrossRef]
- Abilgaziyev, A.; Kulzhan, T.; Raissov, N.; Ali, M.H.; Match, W.L.; Mir-Nasiri, N. Design and development of multi-nozzle extrusion system for 3D printer. In Proceedings of the 2015 4th International Conference on Informatics, Electronics and Vision (ICIEV 2015), Fukuoka, Japan, 15–18 June 2015; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Mhatre, P.S. Process Planning for Concurrent Multi-Nozzle 3D Printing. Master’s Thesis, Rochester Institute of Technology, Rochester, NY, USA, 2019. [Google Scholar]
- Panda, B.; Paul, S.C.; Tan, M.J. Anisotropic mechanical performance of 3D printed fiber reinforced sustainable construction material. Mater. Lett. 2017, 209, 146–149. [Google Scholar] [CrossRef]
- Khoshnevis, B.; Dutton, R. Innovative Rapid Prototyping Process Makes Large Sized, Smooth Surfaced Complex Shapes in a Wide Variety of Materials. Mater. Technol. 1998, 13, 53–56. [Google Scholar] [CrossRef]
- Lao, W.; Li, M.; Tjahjowidodo, T. Variable-geometry nozzle for surface quality enhancement in 3D concrete printing. Addit. Manuf. 2021, 37, 101638. [Google Scholar] [CrossRef]
- COBOD. BOD2 Specifications; Technical Report; COBOD: København, Denmark, 2020. [Google Scholar]
- Soltan, D.G.; Li, V.C. A self-reinforced cementitious composite for building-scale 3D printing. Cem. Concr. Compos. 2018, 90, 1–13. [Google Scholar] [CrossRef]
- Parrott, B. Fast Layered Extrusion for Additive Manufacturing. U.S. Patent Application 20230031850A1, 2 February 2023. Available online: https://patents.google.com/patent/US20230031850A1/ (accessed on 6 June 2024).
- Parrott, B. Fast Layered Extrusion for Additive Manufacturing. U.S. Patent Application US20230031400A1, 2 February 2023. Available online: https://patents.google.com/patent/US20230031400A1/ (accessed on 6 June 2024).
- Parrott, B. Fast Layered Extrusion for Additive Manufacturing. U.S. Patent Application 20230030198A1, 2 February 2023. Available online: https://patents.google.com/patent/US20230030198A1/ (accessed on 6 June 2024).
- Spitaels, L.; Fuentes, E.N.; Rivière-Lorphèvre, E.; Arrazola, P.J.; Ducobu, F. A Systematic Method for Assessing the Machine Performance of Material Extrusion Printers. J. Manuf. Mater. Process. 2024, 8, 36. [Google Scholar] [CrossRef]
- Bici, A.; Yunitsyna, A. Analysis of 3D printing techniques for building construction: A review. Constr. Robot. 2023, 7, 107–123. [Google Scholar] [CrossRef]








| Description | Figure | Tooth Count 1 | Fill Factor | Relative Speed of SSE 2 |
|---|---|---|---|---|
| Simple Box | 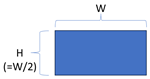 | 1 | 100% | 1 3 |
| DCMU | 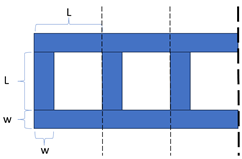 | 7 | 43% | 3 |
| Conduit | 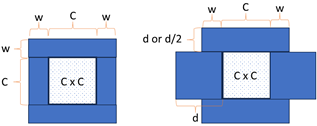 | 5 | 64% | 3.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parrott, B.; Coronado Preciado, A.; Feron, E. Selective Sheet Extrusion: A Novel Manufacturing Process for Large-Format Material Extrusion. J. Manuf. Mater. Process. 2024, 8, 145. https://doi.org/10.3390/jmmp8040145
Parrott B, Coronado Preciado A, Feron E. Selective Sheet Extrusion: A Novel Manufacturing Process for Large-Format Material Extrusion. Journal of Manufacturing and Materials Processing. 2024; 8(4):145. https://doi.org/10.3390/jmmp8040145
Chicago/Turabian StyleParrott, Brian, Angelica Coronado Preciado, and Eric Feron. 2024. "Selective Sheet Extrusion: A Novel Manufacturing Process for Large-Format Material Extrusion" Journal of Manufacturing and Materials Processing 8, no. 4: 145. https://doi.org/10.3390/jmmp8040145
APA StyleParrott, B., Coronado Preciado, A., & Feron, E. (2024). Selective Sheet Extrusion: A Novel Manufacturing Process for Large-Format Material Extrusion. Journal of Manufacturing and Materials Processing, 8(4), 145. https://doi.org/10.3390/jmmp8040145








