Design for Additive Manufacturing of Lattice Structures for Functional Integration of Thermal Management and Shock Absorption
Abstract
:1. Introduction
2. Materials and Methods
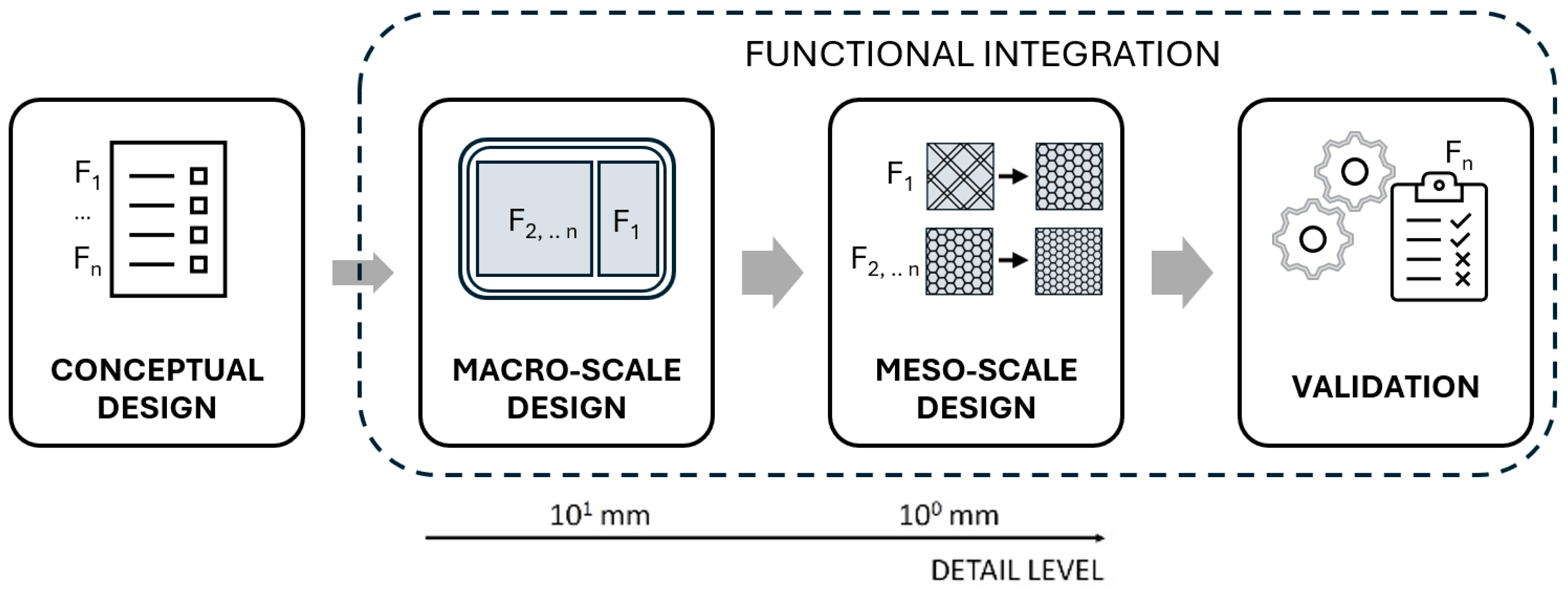
2.1. Conceptual Design
2.2. Embodiment Design
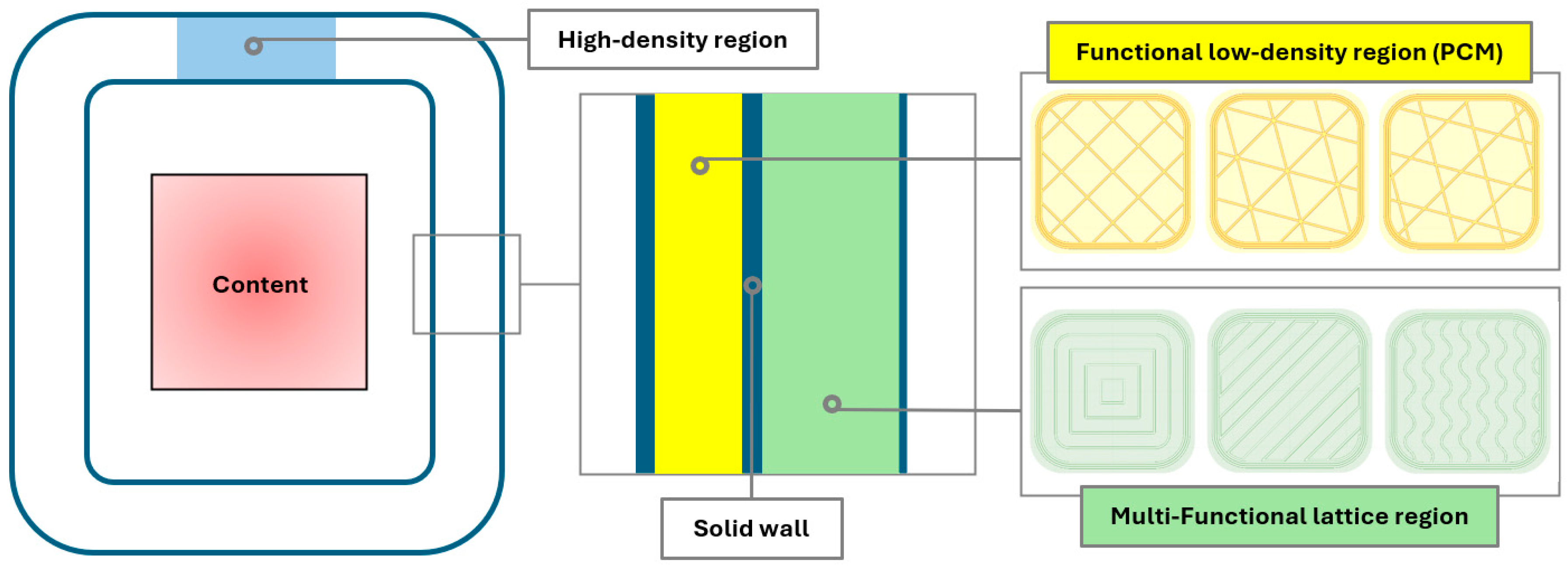
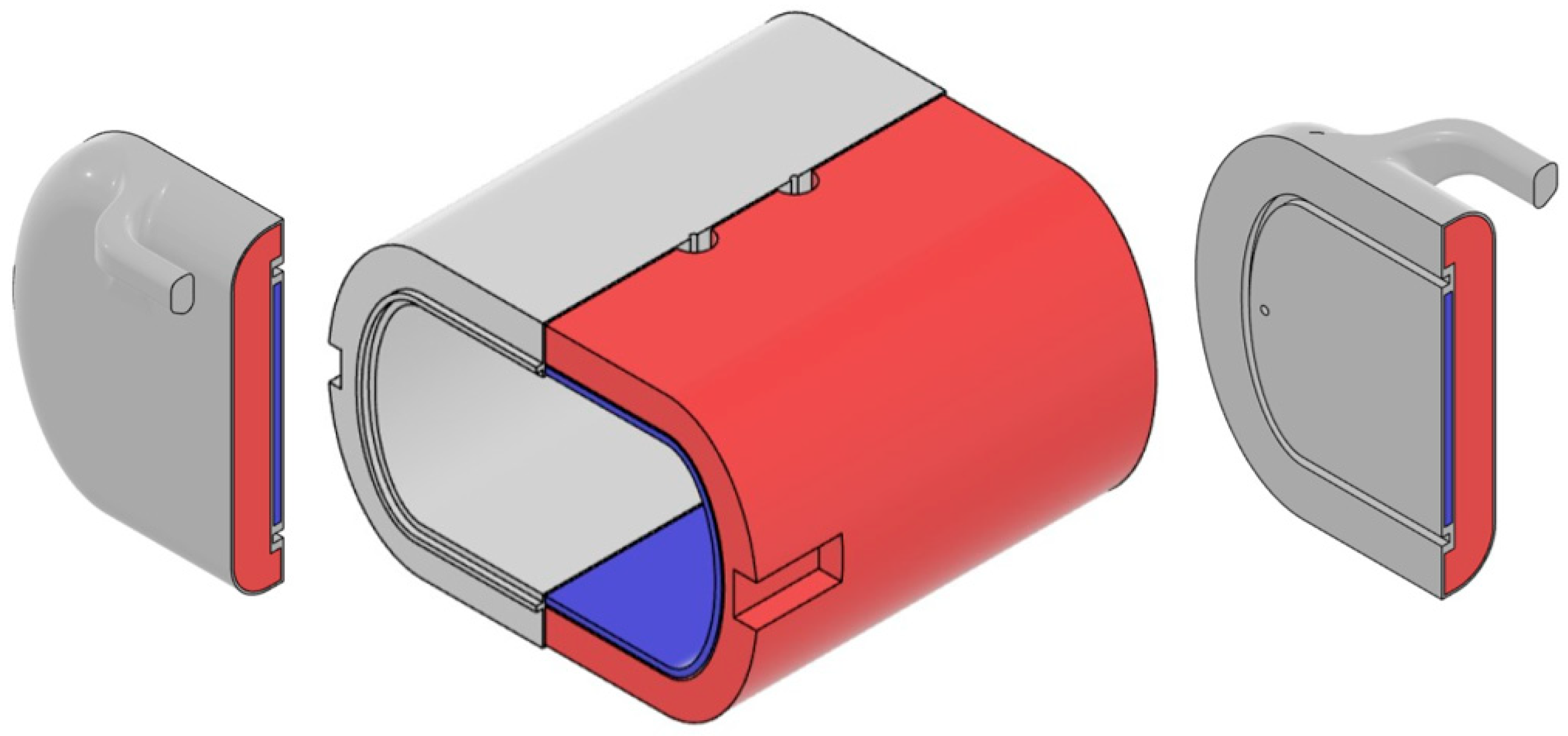
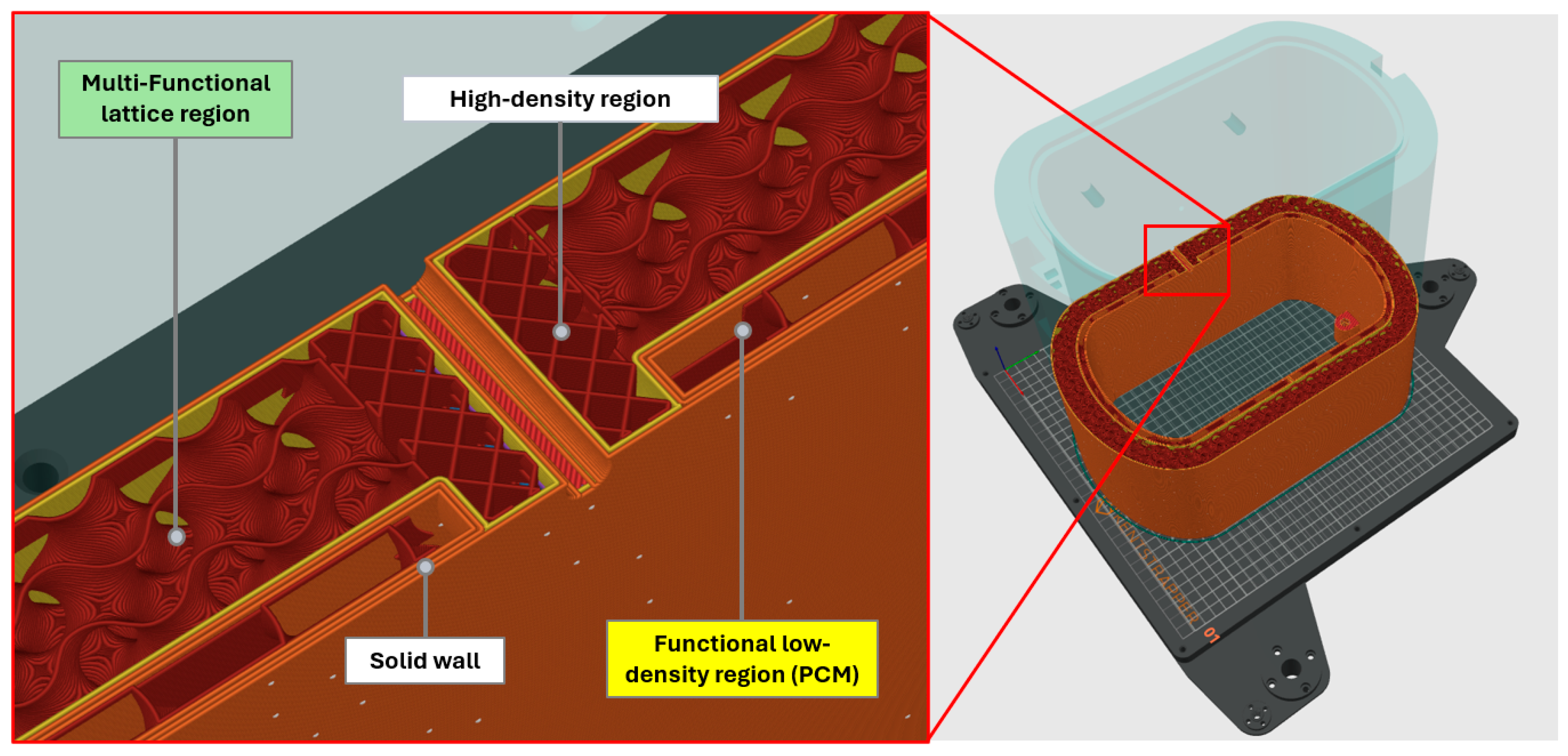
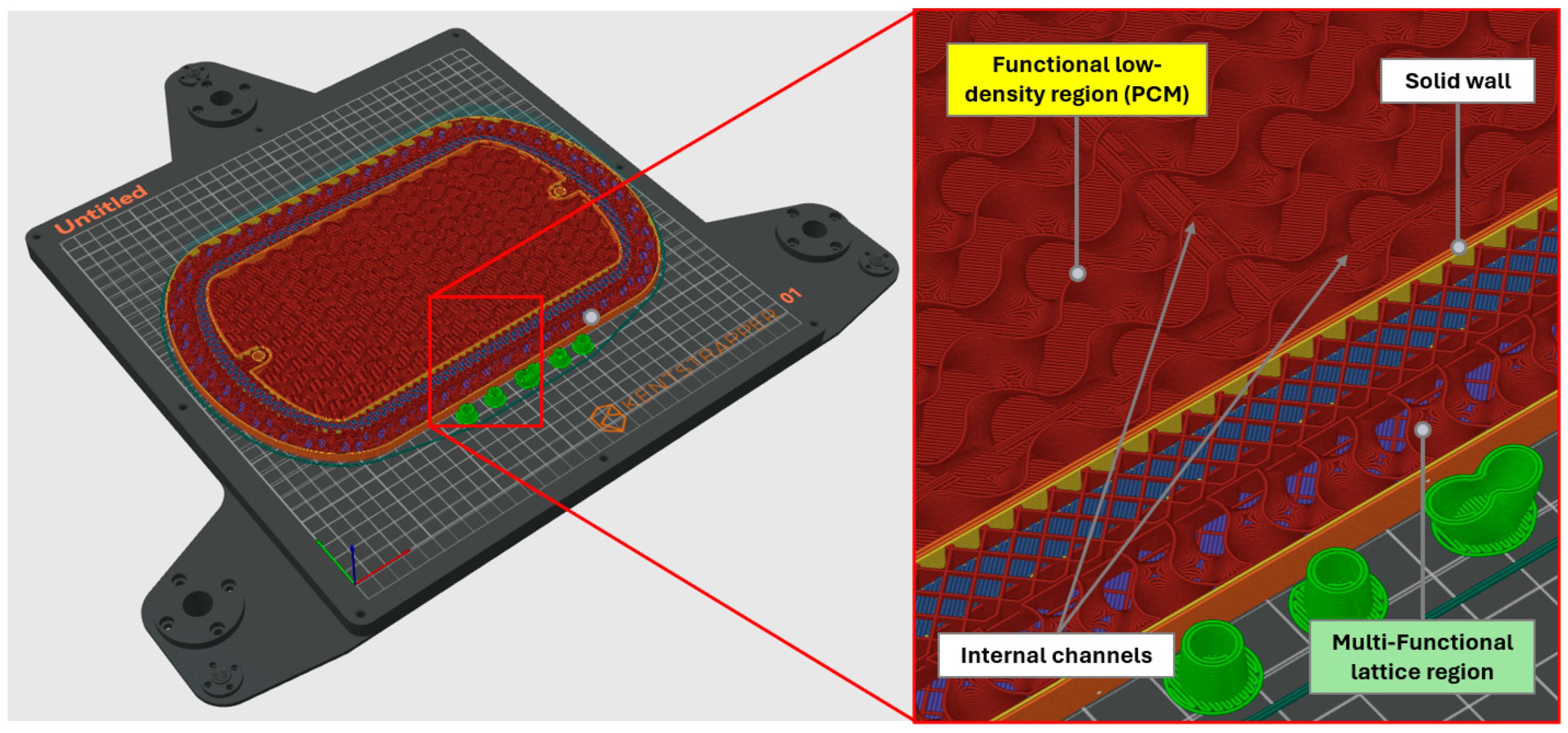
2.3. Functional Container Structure
- An outer layer with multifunctional lattice structures optimized for thermal insulation and impact energy absorption, as shown in the green region in Figure 2; the outer layer will be dimensioned at macroscale level and designed via thermal and mechanical simulations at mesoscale level;
- An inner layer with low-density infill regions to store the PCM, shown in the yellow region; it will be dimensioned at macroscale level and optimized for minimum material usage for structural integrity and manufacturability;
- Solid walls for structural containment of the layers and strength, shown in the blue region; they will be dimensioned for PCM waterproofness and lightweighting;
- High-density infill regions for mechanical performance of structural features, shown in the light blue region; they will be integrated only where necessary for enhanced lightweighting.
3. Theory and Calculations
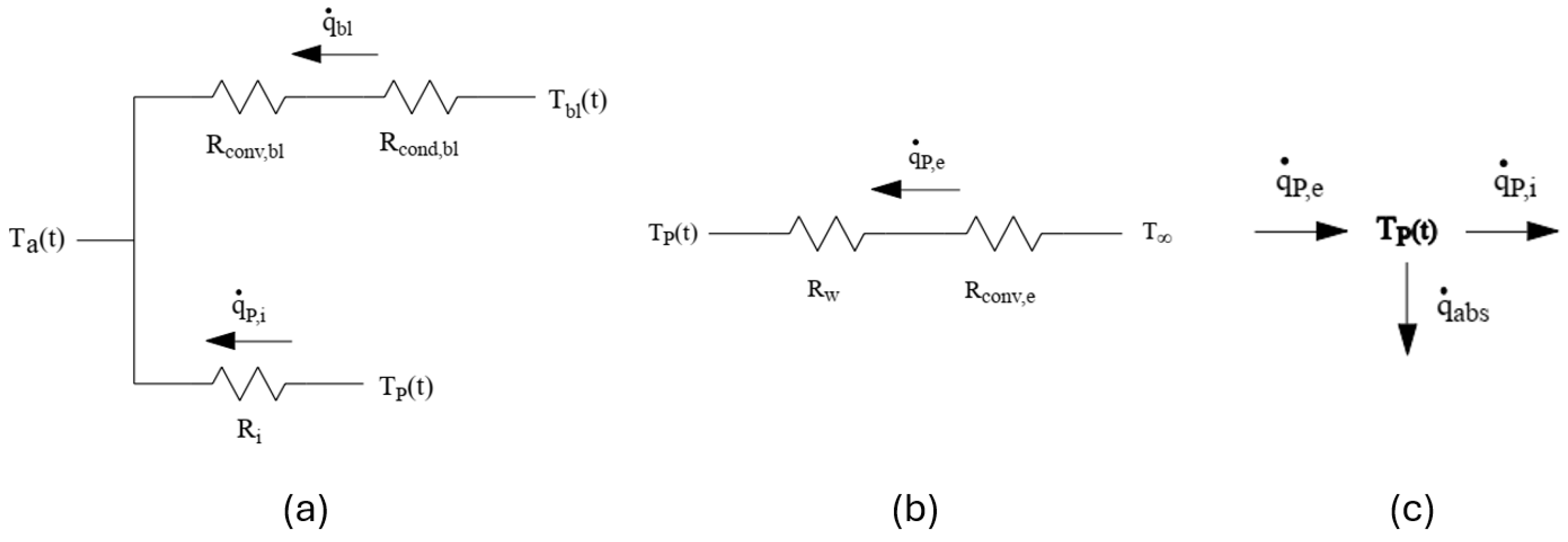
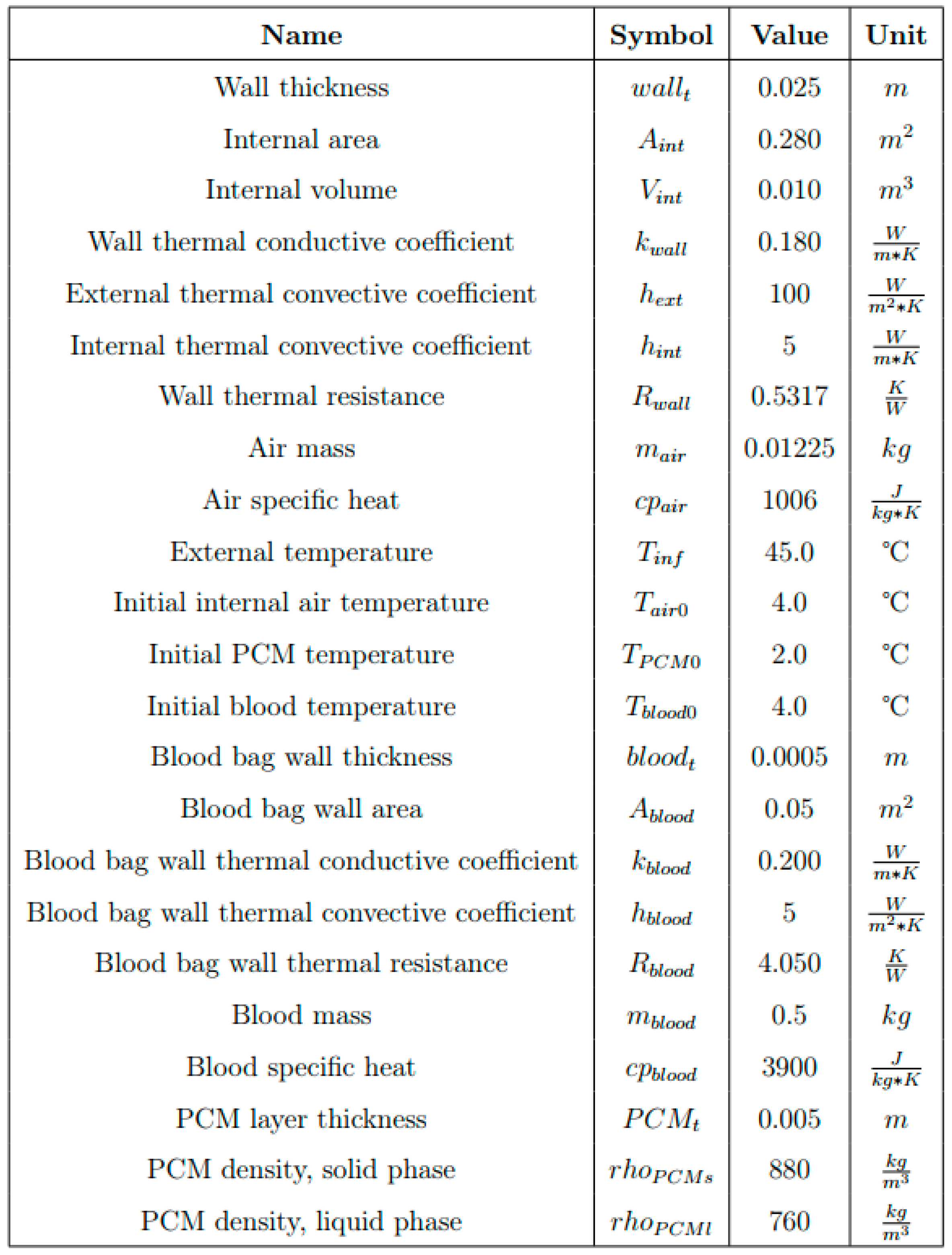
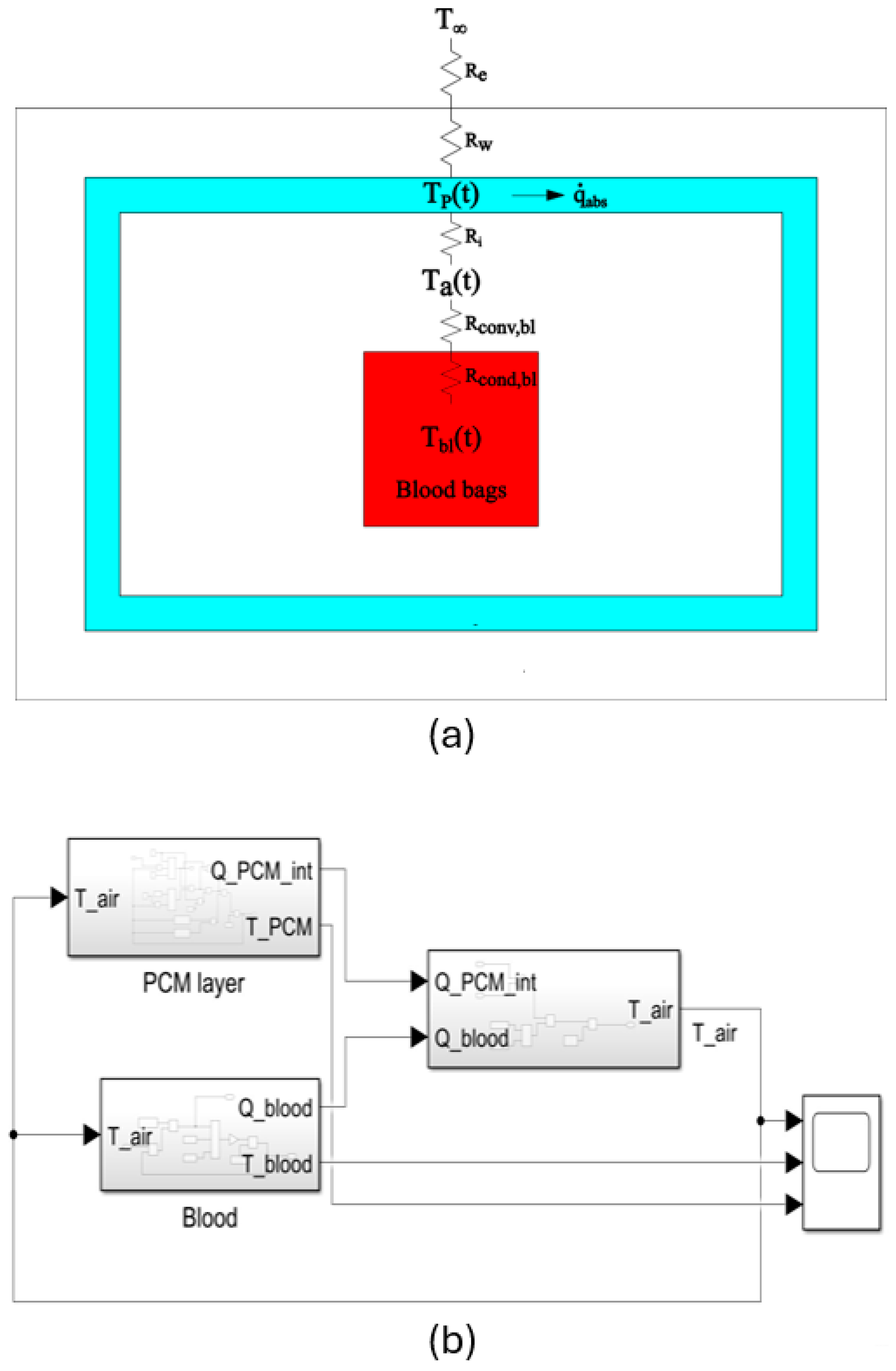
3.1. Overall Thermal Simulation
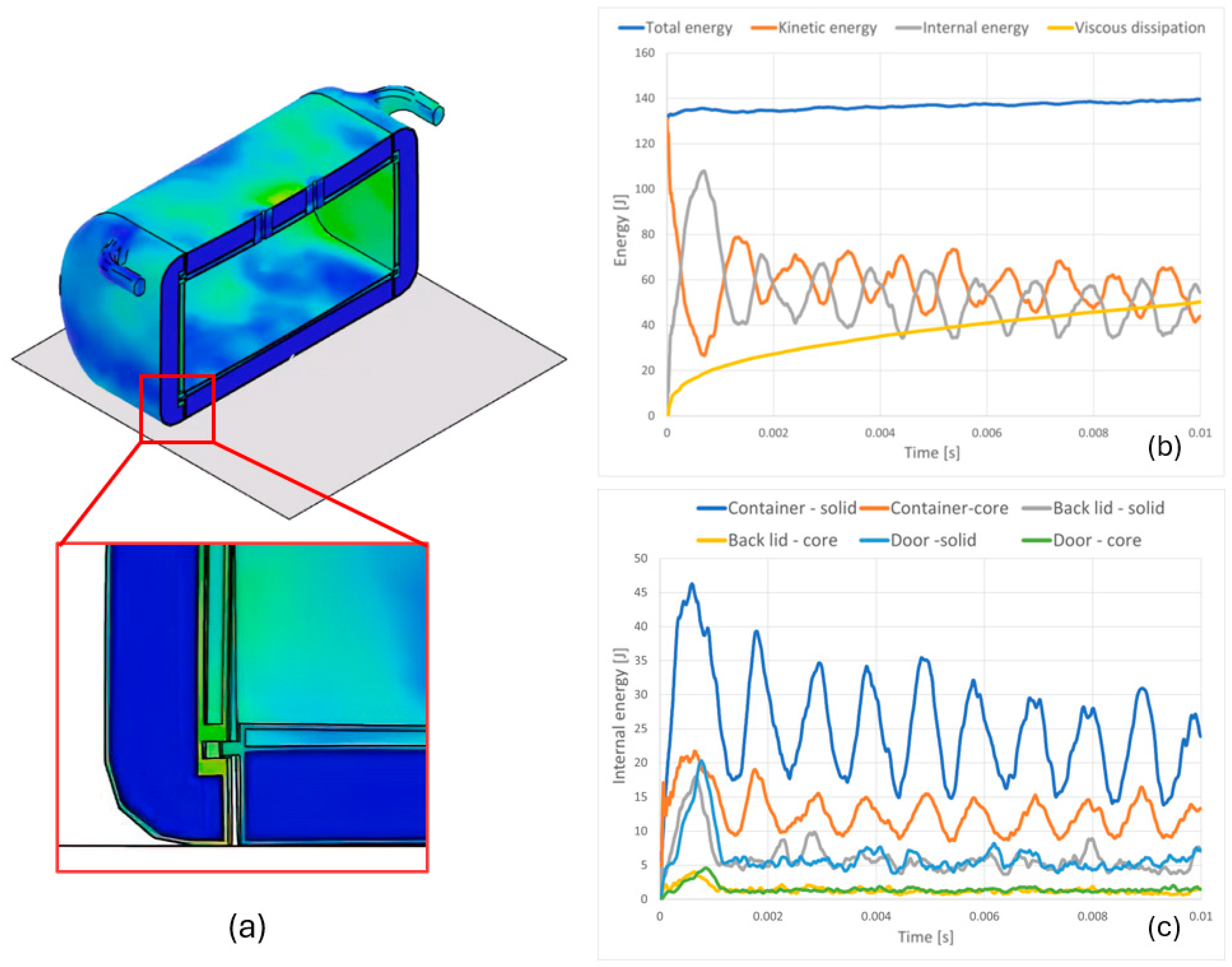
3.2. Overall Structural Simulation
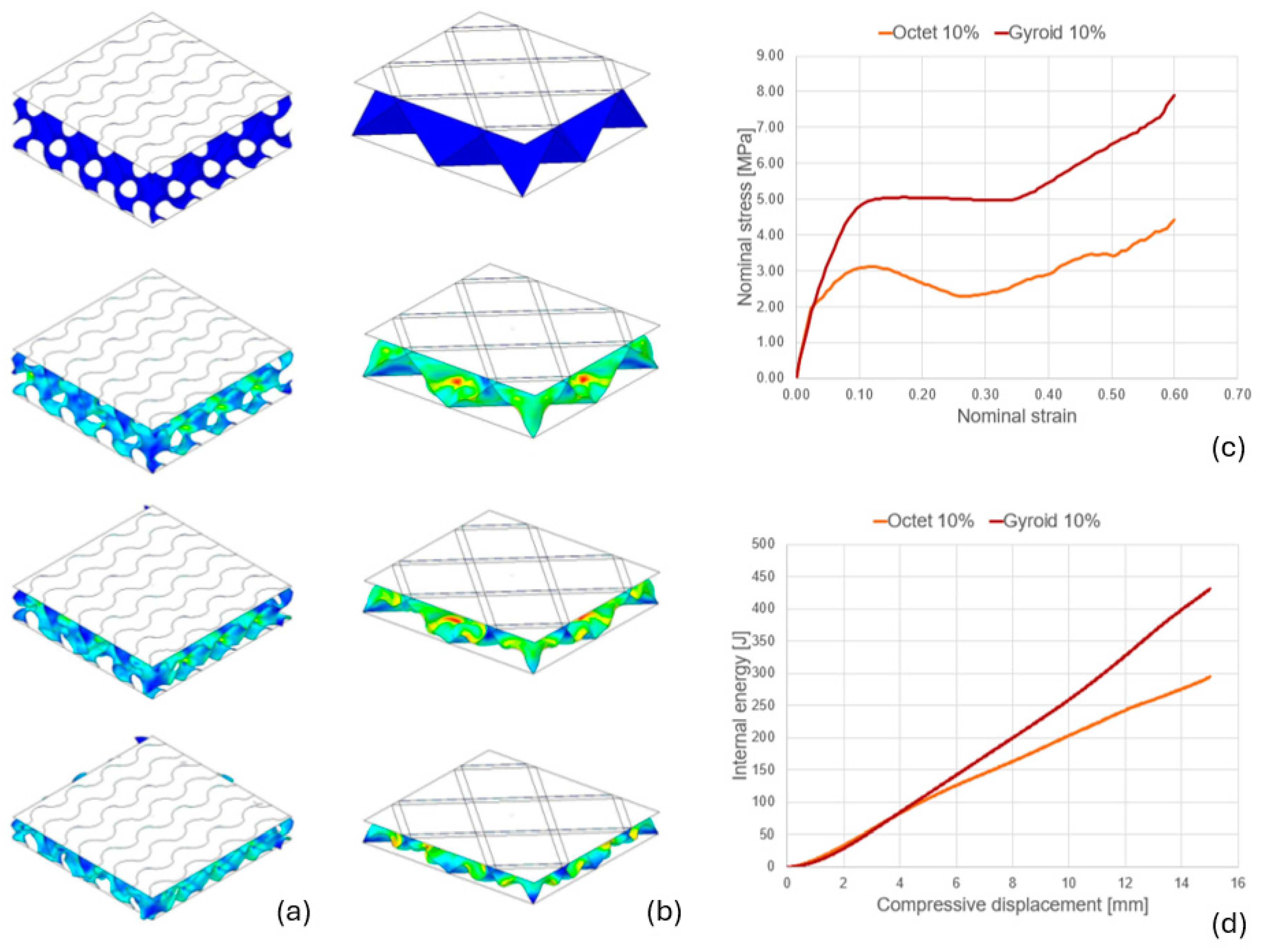
3.3. Mechanical Analysis of the Lattice Structures
- Quasi-static compression simulation of lattice structures with reduced relative density;
- Evaluation of the energy-absorption characteristics and the force-displacement curves;
- Calibration of the selected structure to create an equivalent material with the same behavior as the tested lattice.
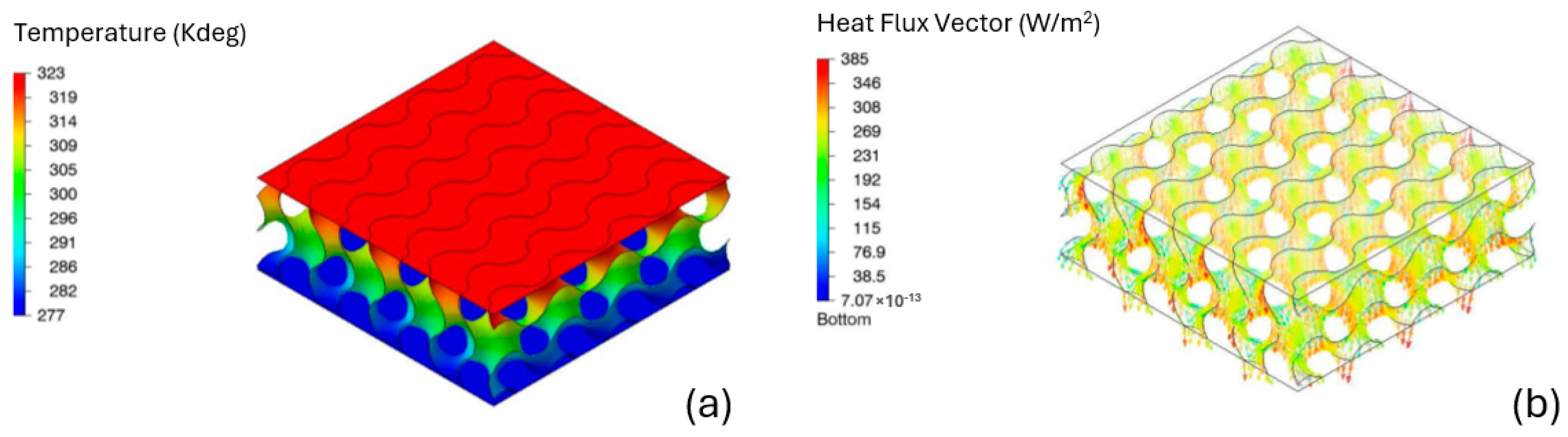
3.4. Thermal Analysis of the Lattice Structures
- Static simulation of heat conduction, considering the boundary temperatures at the walls and the thermal conductivity of the inner material;
- Steady-state analysis of the stable heat flux to calculate the final Qavg;
- The equivalent conductivity is finally determined from:
4. Case Study and Results
4.1. Conceptual Design
- Maintenance of the blood at 4 +/− 2 °C for 1 h;
- Crash protection to avoid any leakage of potentially hazardous material.
- Weight minimization for flight efficiency;
- Ease of use for operational efficiency.
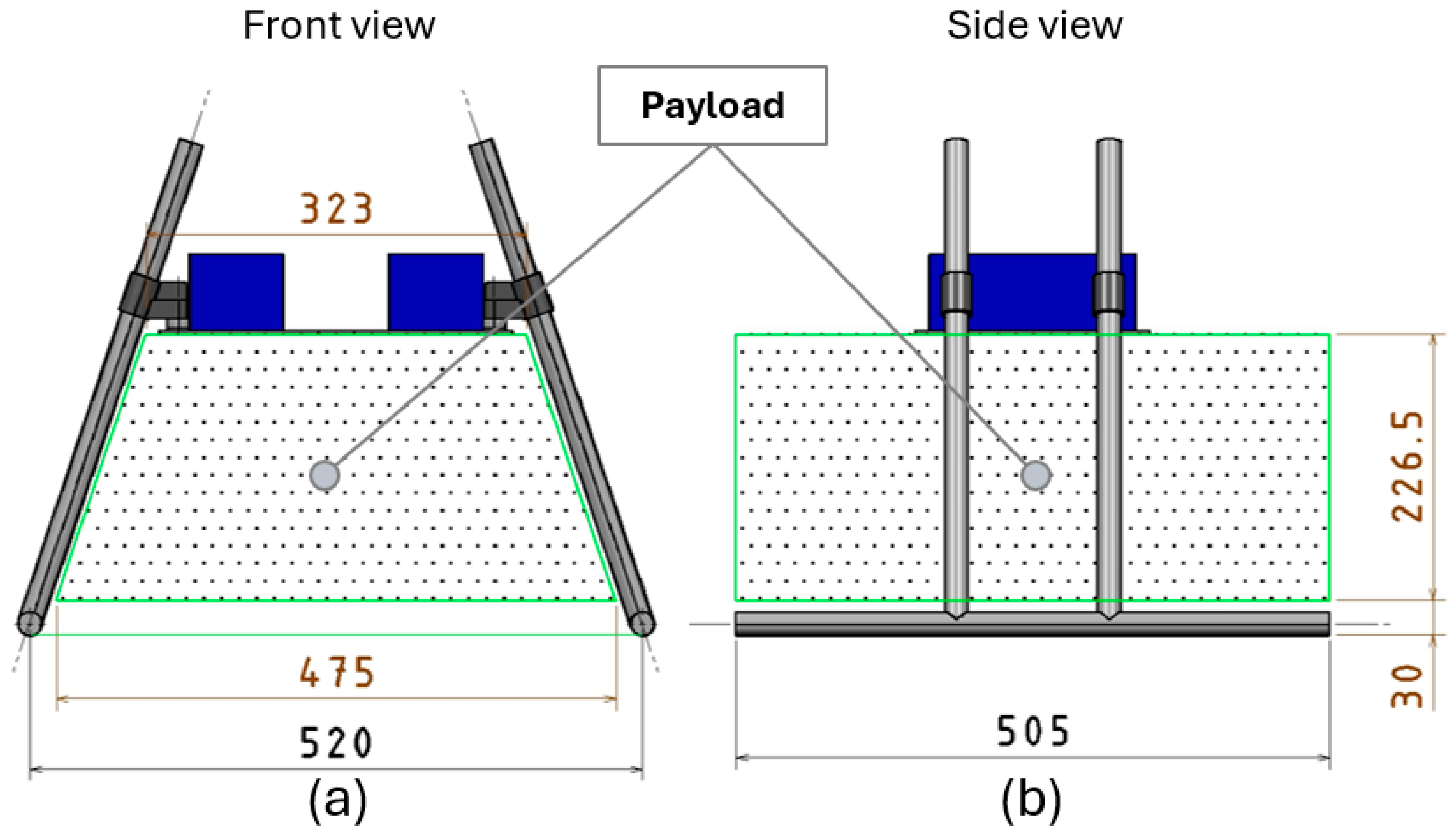
4.2. Macroscale Design
4.3. Mesoscale Design
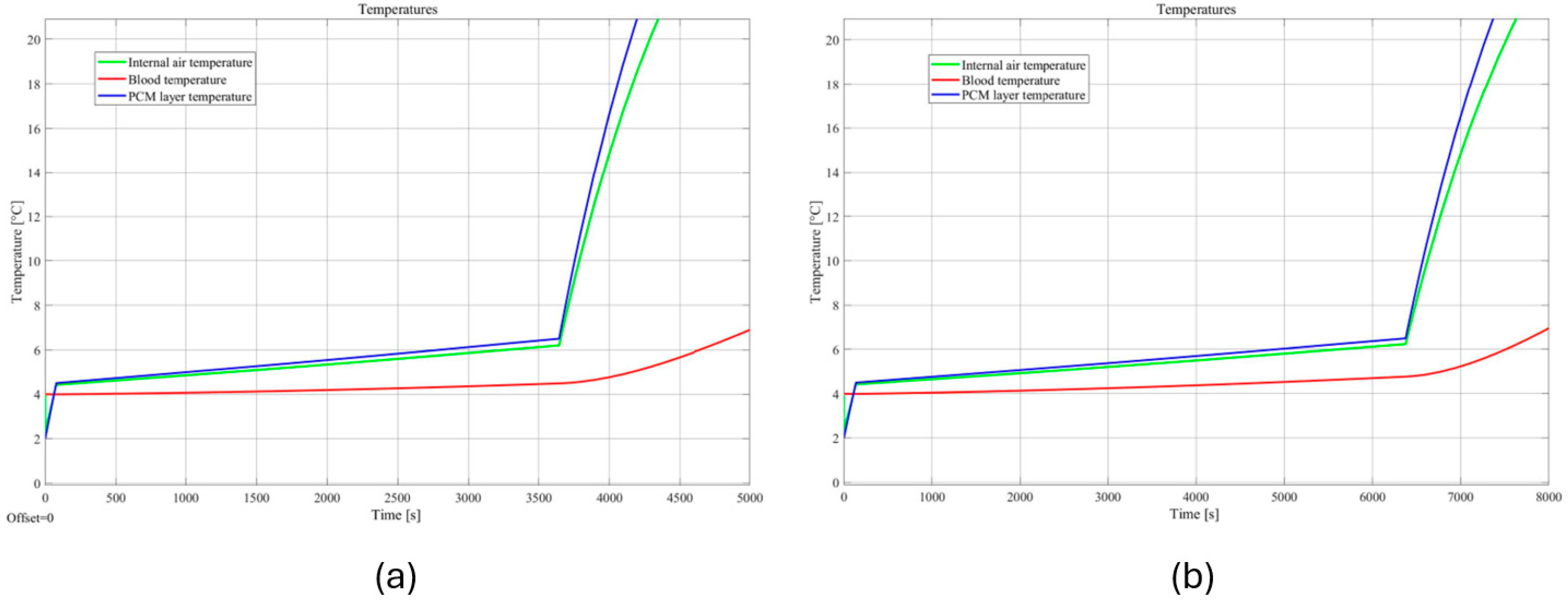
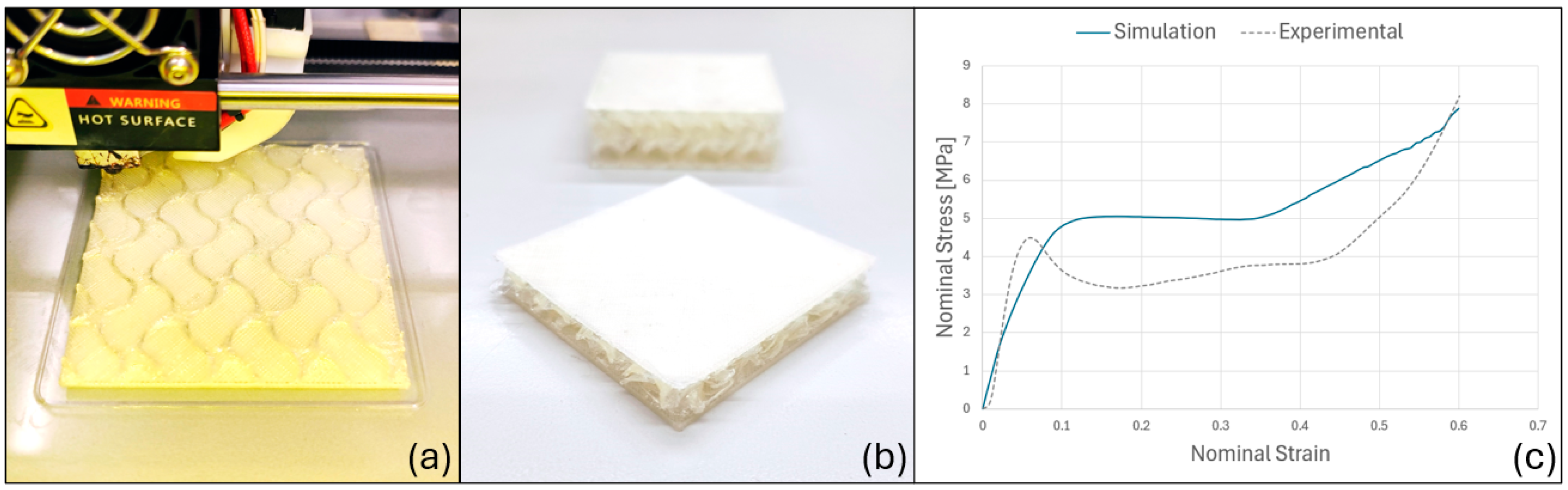
4.4. Validation
4.5. Real Flight Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Yang, S.; Zhao, Y.F. Additive manufacturing-enabled design theory and methodology: A critical review. Int. J. Adv. Manuf. Technol. 2015, 80, 327–342. [Google Scholar] [CrossRef]
- Thompson, M.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for additive manufacturing: Trends, opportunities, considerations, and constraints. CIRP Ann. Manuf. Technol. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Alfaify, A.; Saleh, M.; Abdullah, F.M.; Al-Ahmari, A.M. Design for additive manufacturing: A systematic review. Sustainability 2020, 12, 7936. [Google Scholar] [CrossRef]
- Vaneker, T.; Bernard, A.; Moroni, G.; Gibson, I.; Zhang, Y. Design for additive manufacturing: Framework and methodology. CIRP Ann. 2020, 69, 578–599. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Pradel, P.; Zhu, Z.; Bibb, R.; Moultrie, J. A framework for mapping design for additive manufacturing knowledge for industrial and product design. J. Eng. Des. 2018, 29, 291–326. [Google Scholar] [CrossRef]
- ISO 52910:2018; Additive Manufacturing—Design—Requirements, Guidelines and Recommendations. International Organization for Standardization: Geneva, Switzerland, 2018.
- Liu, J. Guidelines for AM part consolidation. Virtual Phys. Prototyp. 2016, 11, 133–141. [Google Scholar] [CrossRef]
- Plocher, J.; Panesar, A. Review on design and structural optimisation in additive manufacturing: Towards next-generation lightweight structures. Mater. Des. 2019, 183, 108164. [Google Scholar] [CrossRef]
- Durakovic, B. Design for additive manufacturing: Benefits, trends and challenges. Period. Eng. Nat. Sci. 2018, 6, 179–191. [Google Scholar] [CrossRef]
- Obi, M.U.; Pradel, P.; Sinclair, M.; Bibb, R. A bibliometric analysis of research in design for additive manufacturing. Rapid Prototyp. J. 2022, 28, 967–987. [Google Scholar] [CrossRef]
- Fuchs, D.; Bartz, R.; Kuschmitz, S.; Vietor, T. Necessary advances in computer-aided design to leverage on additive manufacturing design freedom. Int. J. Interact. Des. Manuf. 2022, 16, 1633–1651. [Google Scholar] [CrossRef]
- Grabowska, B.; Kasperski, J. The Thermal Conductivity of 3D Printed Plastic Insulation Materials—The Effect of Optimizing the Regular Structure of Closures. Materials 2020, 13, 4400. [Google Scholar] [CrossRef]
- Alqahtani, S.; Ali, H.M.; Farukh, F.; Silberschmidt, V.V.; Kandan, K. Thermal performance of additively manufactured polymer lattices. J. Build. Eng. 2021, 39, 102243. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Zhong, H.; Song, T.; Li, C.; Das, R.; Gu, J.; Qian, M. The Gibson-Ashby model for additively manufactured metal lattice materials: Its theoretical basis, limitations and new insights from remedies. Curr. Opin. Solid State Mater. Sci. 2023, 27, 101081. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, W.; Zhu, L.; Meng, F.; Liu, J.; Wen, G. Review on lattice structures for energy absorption properties. Compos. Struct. 2023, 304, 116397. [Google Scholar] [CrossRef]
- Lu, C.; Hsieh, M.; Huang, Z.; Zhang, C.; Lin, Y.; Shen, Q.; Chen, F.; Zhang, L. Architectural Design and Additive Manufacturing of Mechanical Metamaterials: A Review. Engineering 2022, 17, 44–63. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Li, D.; Zhao, Y.F. Design and optimization of solid lattice hybrid structures fabricated by additive manufacturing. Addit. Manuf. 2020, 33, 101116. [Google Scholar] [CrossRef]
- Tang, Y.; Zhao, Y.F. A survey of the design methods for additive manufacturing to improve functional performance. Rapid Prototyp. J. 2016, 22, 569–590. [Google Scholar] [CrossRef]
- Tamburrino, F.; Graziosi, S.; Bordegoni, M. The Design Process of Additively Manufactured Mesoscale Lattice Structures: A Review. ASME J. Comput. Inf. Sci. Eng. 2018, 18, 040801. [Google Scholar] [CrossRef]
- Cheng, L.; Bai, J.; To, A.C. Functionally graded lattice structure topology optimization for the design of additive manufactured components with stress constraints. Comput. Methods Appl. Mech. Eng. 2019, 344, 334–359. [Google Scholar] [CrossRef]
- Wang, C.; Gu, X.; Zhu, J.; Zhou, H.; Li, S.; Zhang, W. Concurrent design of hierarchical structures with three-dimensional parameterized lattice microstructures for additive manufacturing. Struct. Multidiscip. Optim. 2020, 61, 869–894. [Google Scholar] [CrossRef]
- Kim, J.E.; Park, K. Multiscale Topology Optimization Combining Density-Based Optimization and Lattice Enhancement for Additive Manufacturing. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 8, 1197–1208. [Google Scholar] [CrossRef]
- Li, S.; Xin, Y.; Yu, Y.; Wang, Y. Design for additive manufacturing from a force-flow perspective. Mater. Des. 2021, 204, 109664. [Google Scholar] [CrossRef]
- Pahl, G.; Beitz, W.; Feldhuesen, J.; Grote, K.H. Engineering Design: A Systematic Approach; Springer: London, UK, 2007; Volume 34. [Google Scholar] [CrossRef]
- VDI. VDI 2221. Systematic Approach to the Development and Design of Technical Systems and Products; VDI: Berlin, Germany, 1993. [Google Scholar]
- Tomiyama, T.; Gu, P.; Jin, Y.; Lutters, D.; Kind, C.; Kimura, F. Design methodologies: Industrial and educational applications. CIRP Ann.—Manuf. Technol. 2009, 58, 543–565. [Google Scholar] [CrossRef]
- Schmitt, P.; Zorn, S.; Gericke, K. Additive manufacturing research landscape: A literature review. Proc. Des. Soc. 2021, 1, 333–344. [Google Scholar] [CrossRef]
- Bourell, D.L.; Leu, M.C.; Rosen, D.W. Roadmap for Additive Manufacturing Identifying the Future of Freeform Processing; University of Texas for Freeform Fabrication Advanced Manufacturing Center: Austin, TX, USA, 2009. [Google Scholar]
- Kumke, M.; Watschke, H.; Vietor, T. A newmethodological framework for design for additive manufacturing. Virtual Phys. Prototyp. 2016, 11, 3–19. [Google Scholar] [CrossRef]
- Wiberg, A.; Persson, J.; Ölvander, J. Design for additive manufacturing—A review of available design methods and software. Rapid Prototyp. J. 2019, 25, 1080–1094. [Google Scholar] [CrossRef]
- Lopez, L.; Maury, H.; Pacheco, J. Design for additive manufacturing: A comprehensive review of the tendencies and limitations of methodologies. Rapid Prototyp. J. 2021, 27, 918–966. [Google Scholar] [CrossRef]
- Egan, P.F. Design for Additive Manufacturing: Recent Innovations and Future Directions. Designs 2023, 7, 83. [Google Scholar] [CrossRef]
- Alam, M.; Singh, H.; Limbachiya, M.C. Vacuum Insulation Panels (VIPs) for building construction industry—A review of the contemporary developments and future directions. Appl. Energy 2011, 88, 3592–3602. [Google Scholar] [CrossRef]
- Damiani, L.; Revetria, R.; Morra, E.; Giribone, P. A Smart Box for Blood Bags Transport: Simulation Model of the Cooling Autonomy Control System. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 249–255. [Google Scholar] [CrossRef]
- du Plessis, A.; Broeckhoven, C.; Yadroitsava, I.; Yadroitsev, I.; Hands, C.H.; Kunju, R.; Bhate, D. Beautiful and Functional: A Review of Biomimetic Design in Additive Manufacturing. Addit. Manuf. 2019, 27, 408–427. [Google Scholar] [CrossRef]
- Nath, S.D.; Nilufar, S. An overview of additive manufacturing of polymers and associated composites. Polymers 2020, 12, 2719. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.A.; Mobarak, M.H.; Rimon, M.I.H.; Al Mahmud, M.Z.; Ghosh, J.; Ahmed, M.M.S.; Hossain, N. Additive manufacturing in polymer research: Advances, synthesis, and applications. Polym. Test. 2024, 132, 108364. [Google Scholar] [CrossRef]
- Palanisamy, C.; Raman, R.; Dhanraj, P.K. Additive manufacturing: A review on mechanical properties of polyjet and FDM printed parts. Polym. Bull. 2022, 79, 7065–7116. [Google Scholar] [CrossRef]
- Saleh Alghamdi, S.; John, S.; Roy Choudhury, N.; Dutta, N.K. Additive Manufacturing of Polymer Materials: Progress, Promise and Challenges. Polymers 2021, 13, 753. [Google Scholar] [CrossRef]
- Shanmugam, V.; Babu, K.; Kannan, G.; Mensah, R.A.; Samantaray, S.K.; Das, O. The thermal properties of FDM printed polymeric materials: A review. Polym. Degrad. Stab. 2024, 228, 110902. [Google Scholar] [CrossRef]
- Gorguluarslan, R.M.; Gungor, O.U.; Yıldız, S.; Erem, E. Energy absorption behavior of stiffness optimized graded lattice structures fabricated by material extrusion. Meccanica 2021, 56, 2825–2841. [Google Scholar] [CrossRef]
- Chamini, R.; Shanqing, X.; Yvonne, D.; Darren, F.; Dong, R. Quasi-static and dynamic compression of additively manufactured functionally graded lattices: Experiments and simulations. Eng. Struct. 2023, 284, 115909. [Google Scholar] [CrossRef]
- Dalpadulo, E.; Vergnano, A.; Leali, F. Urban Air Mobility for Medical Delivery: An Innovative Approach to Healthcare Logistics. In Proceedings of the ADM 2024, Palermo, Italy, 11–13 September 2024. Lecture Notes in Mechanical Engineering, 2024. [Google Scholar]
- Orca Slicer—3D printing Slicer. Available online: https://orcaslicer.net/about/ (accessed on 1 December 2024).
- Jia, Z.; Liu, F.; Jiang, X.; Wang, L. Engineering lattice metamaterials for extreme property, programmability, and multifunctionality. J. Appl. Phys. 2020, 127, 150901. [Google Scholar] [CrossRef]
- Babatola, O.; Patil, G.; Hsieh, D.; Matlack, K.; Sinha, S. Independently Tunable Thermal Conductance and Phononic Band Gaps of 3D Lattice Materials. Adv. Eng. Mater. 2019, 22, 1901004. [Google Scholar] [CrossRef]
- Li, X.; Zhao, M.; Yu, X.; Chua, J.W.; Yang, Y.; Lim, K.M.; Zhai, W. Multifunctional and customizable lattice structures for simultaneous sound insulation and structural applications. Mater. Des. 2023, 234, 112354. [Google Scholar] [CrossRef]
- Ye, H.; Shen, W.; Wang, W.; Tao, R. A systematic design of multifunctional lattice structures with energy absorption and phononic bandgap by topology and parameter optimization. Int. J. Smart Nano Mater. 2023, 14, 265–285. [Google Scholar] [CrossRef]



| Material | Density ρ (kg/m3) | Specific Strength Ys (kN·m/kg) | Toughness G (kJ/m2) | Thermal Conductivity λ (W/m·°C) | Glass Temperature TG (°C) | Cost (EUR/kg) |
|---|---|---|---|---|---|---|
| PLA (tough) | 1.22–1.25 × 103 | 30.7–48.6 | 2.21–3.67 | 0.13–0.17 | 52–60 | 20 |
| PETG | 1.26–1.28 × 103 | 37.7–41.7 | 2.18–3.1 | 0.257–0.267 | 81–91 | 22.5 |
| ABS | 1.02–1.08 × 103 | 28.2–42.1 | 1.35–2.04 | 0.226–0.235 | 88–120 | 40 |
| PA | 1–1.02 × 103 | 34.4–43 | 8.01–10.7 | 0.218–0.306 | 40–43 | 45 |
| PEEK | 1.3–1.32 × 103 | 68.7–84 | 2.02–4.6 | 0.24–0.26 | 143–157 | 720 |
| PEI | 1.26–1.28 × 103 | 57.9–63.9 | 1.46–5 | 0.123–0.13 | 215–217 | 300 |
| Problem Definition | Conceptual Design | Embodiment Design |
|---|---|---|
| Thermal maintenance—insulation | Insulating materials and/or lattice structure. | Selection of polymers with low thermal conductivity. Design at mesoscale: lattice structure for improved thermal insulation. |
| Thermal maintenance—conditioning | Active cooling systems powered with electric energy or passive systems based on PCM walls of the container. | Design at macroscale: regions of lattice structure filled with PCM. |
| Crash protection | Robust structure made of a high-strength material or sacrificial impact attenuators or lattice structure. | Selection of polymers with high strength and toughness. Design at the macroscale for impact and at the mesoscale for lattice structure shock absorption. |
| Lightweighting | Cellular or porous structures from nature. | Optimization of the geometries of the lattice structures, with high-density and low-density regions. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalpadulo, E.; Pollon, M.; Vergnano, A.; Leali, F. Design for Additive Manufacturing of Lattice Structures for Functional Integration of Thermal Management and Shock Absorption. J. Manuf. Mater. Process. 2025, 9, 24. https://doi.org/10.3390/jmmp9010024
Dalpadulo E, Pollon M, Vergnano A, Leali F. Design for Additive Manufacturing of Lattice Structures for Functional Integration of Thermal Management and Shock Absorption. Journal of Manufacturing and Materials Processing. 2025; 9(1):24. https://doi.org/10.3390/jmmp9010024
Chicago/Turabian StyleDalpadulo, Enrico, Mattia Pollon, Alberto Vergnano, and Francesco Leali. 2025. "Design for Additive Manufacturing of Lattice Structures for Functional Integration of Thermal Management and Shock Absorption" Journal of Manufacturing and Materials Processing 9, no. 1: 24. https://doi.org/10.3390/jmmp9010024
APA StyleDalpadulo, E., Pollon, M., Vergnano, A., & Leali, F. (2025). Design for Additive Manufacturing of Lattice Structures for Functional Integration of Thermal Management and Shock Absorption. Journal of Manufacturing and Materials Processing, 9(1), 24. https://doi.org/10.3390/jmmp9010024







