Adaptive Aberration Correction for Laser Processes Improvement
Abstract
:1. Introduction
2. Adaptive Optical Technologies
2.1. Adaptive Optics: Key Developments and Their Impact
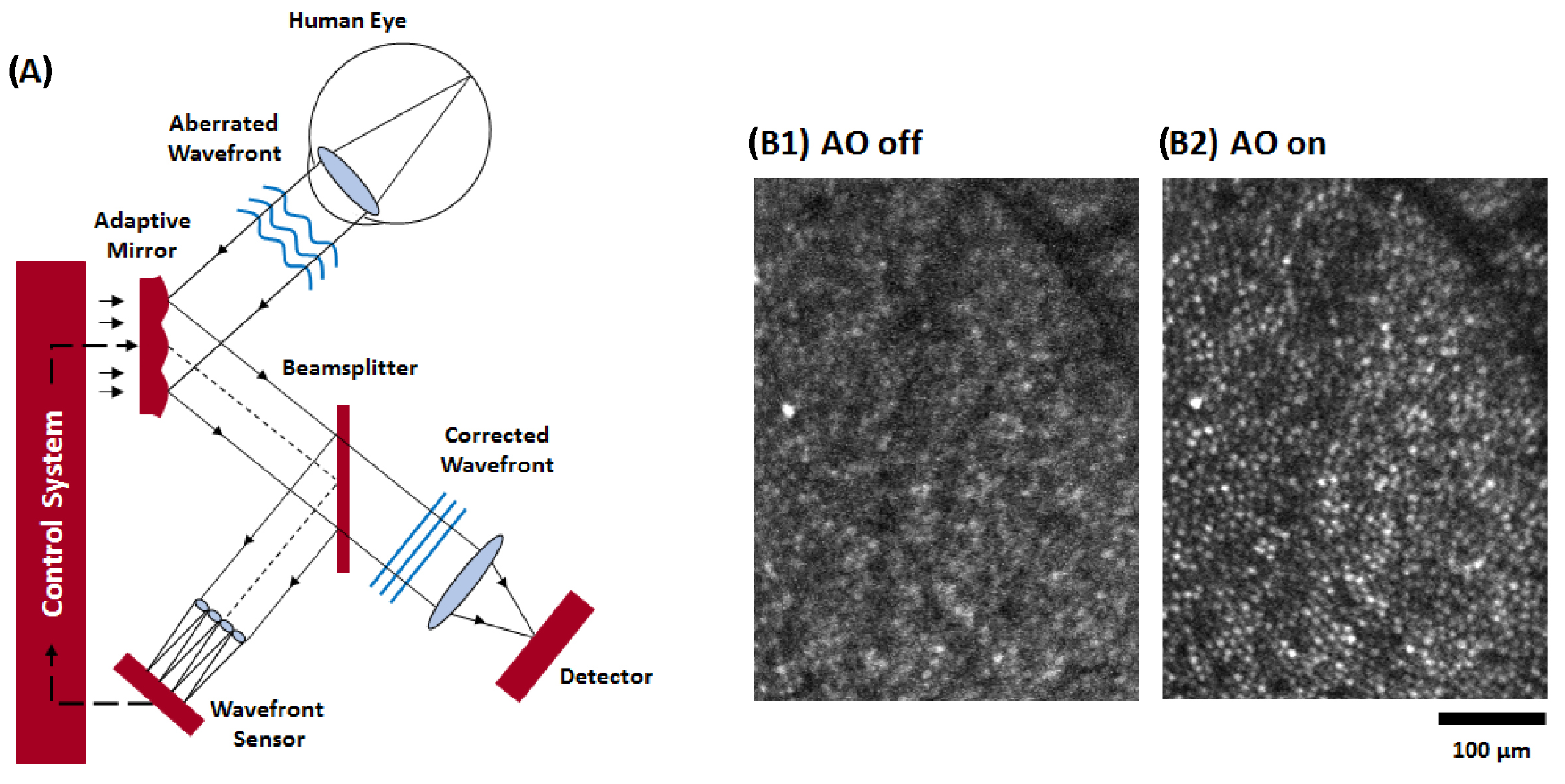
2.2. How Adaptive Optical Systems Work: Components and Principles
2.3. Adaptive Optics Systems: Common Architectures
- Wavefront sensors: These devices measure the aberrations in the incoming light wavefront. They can be either direct sensors or sensorless systems that infer distortions from image quality.
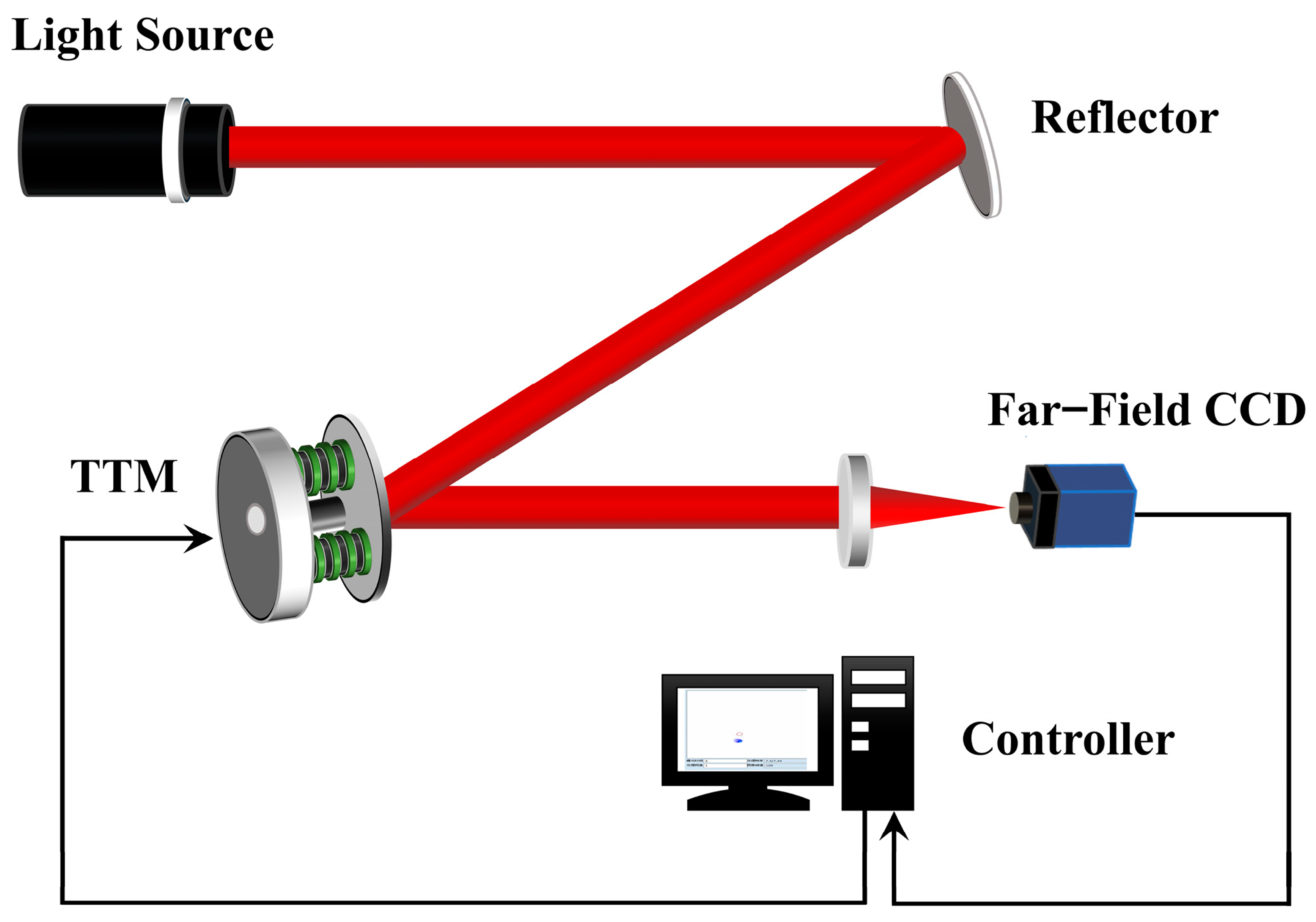
- Tip-tilt mirror (TTM): TTM corrects the tilts of the incoming wavefronts in two dimensions. It achieves this by making small rotations around two axes, effectively realigning the light path to reduce distortion. The TTM is typically placed in front of the wavefront sensor. This configuration allows for a closed system, where the sensor continuously measures wavefront distortions and sends corrective signals to the TTM [33] (Figure 7).The TTM is particularly effective at correcting low-order aberrations (such as tilt and defocus), which account for a significant portion of the distortion caused by atmospheric conditions. By addressing these errors first, higher-order aberrations can then be corrected using more complex deformable mirrors.
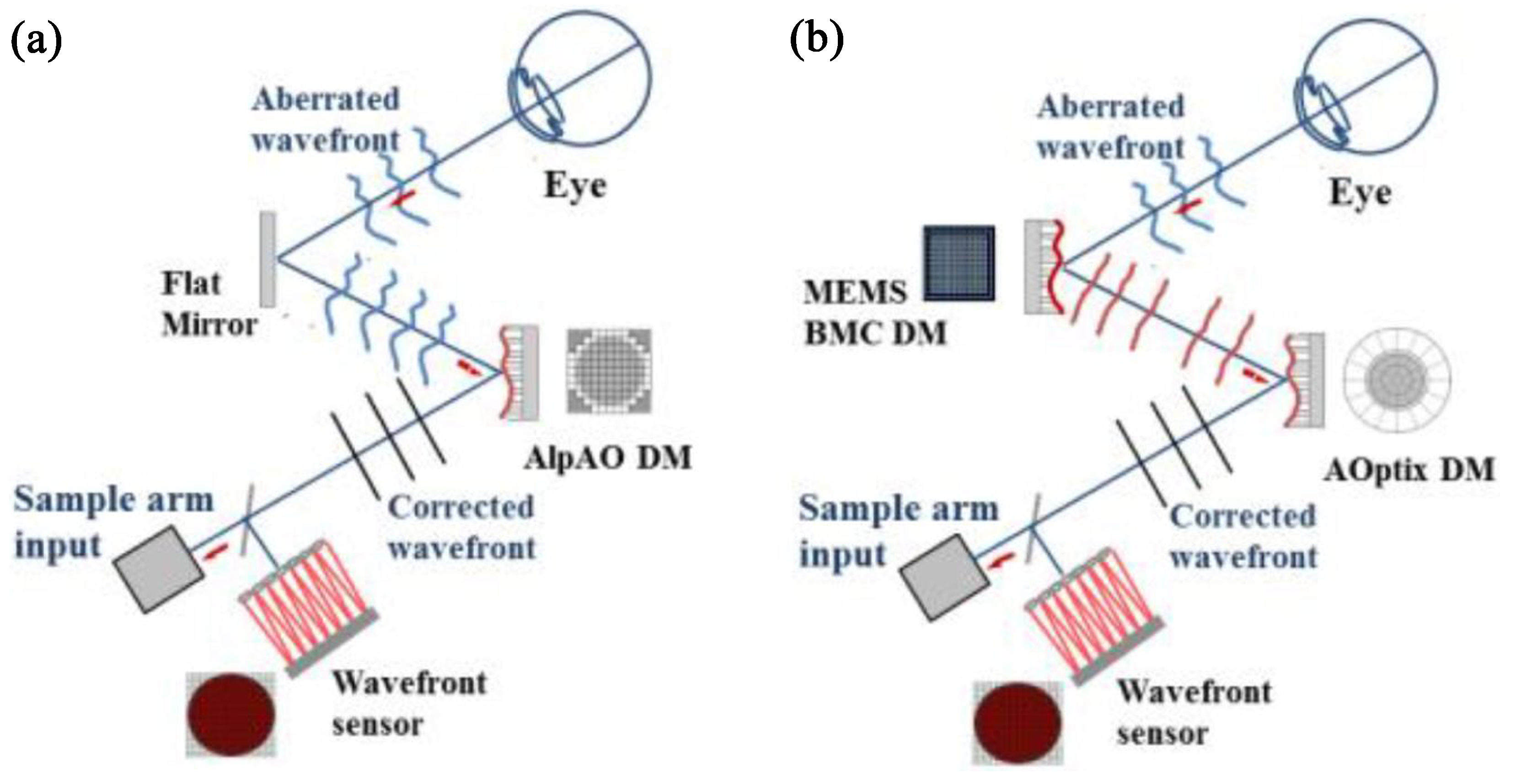
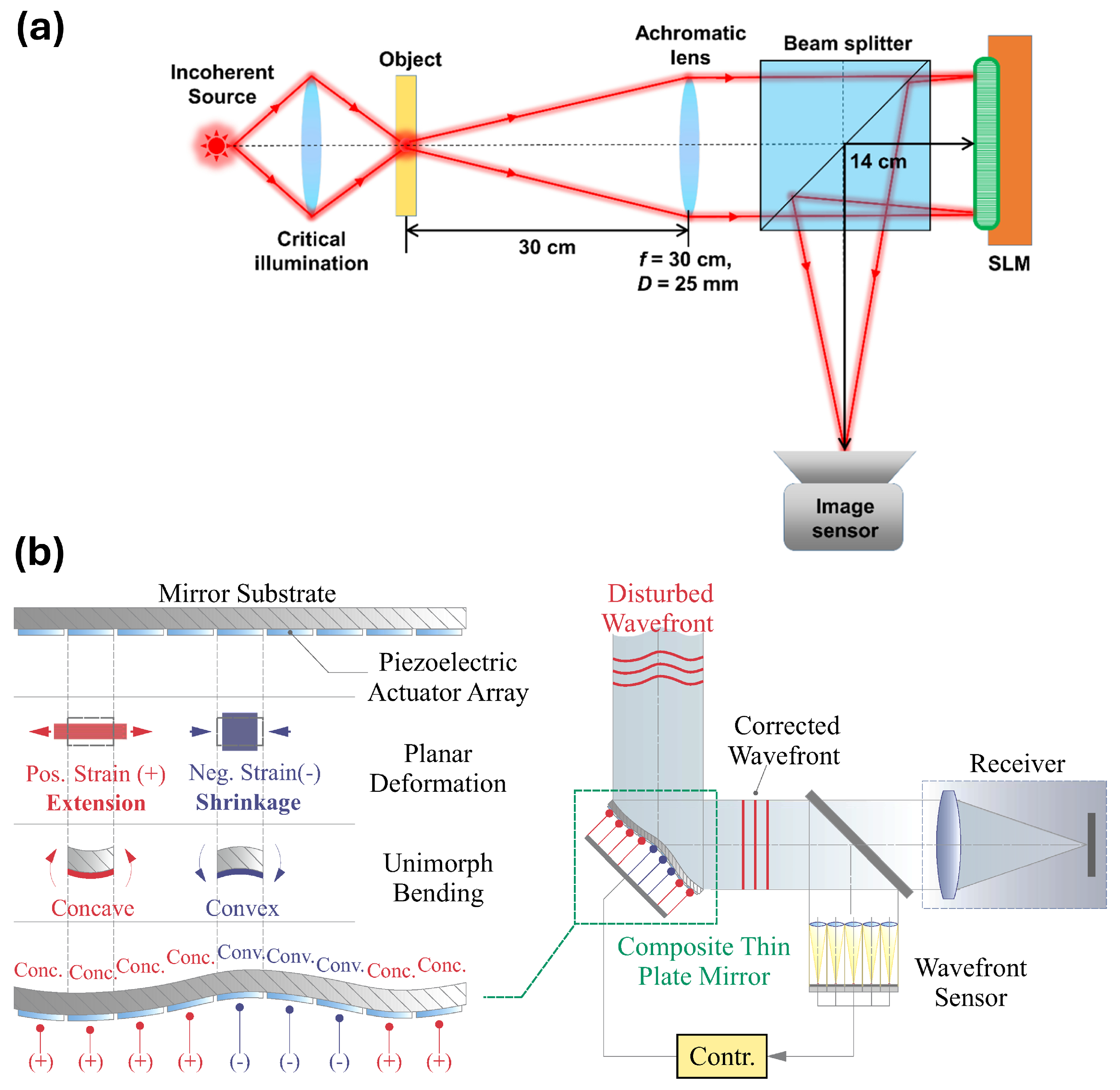
- Deformable Mirrors (DMs): DMs are critical components that adjust their shape in real-time to compensate for detected aberrations. They can have varying numbers of actuators, allowing for precise control over the wavefront correction [34]. Recent advancements include the development of liquid crystal spatial light modulators and MEMS-based deformable mirrors (Figure 8).These latter mirrors consist of a flexible membrane supported by an array of actuators that can adjust the mirror’s shape in real-time to correct for wavefront distortions caused by atmospheric turbulence or optical imperfections. For instance, an MEMS DM with 489 actuators has been shown to effectively generate individual Zernike polynomials, which are essential for correcting aberrations [35].
- Control Algorithms: Algorithms, such as hill-climbing or other feedback mechanisms, optimize the adjustments made by the DMs to enhance image quality.
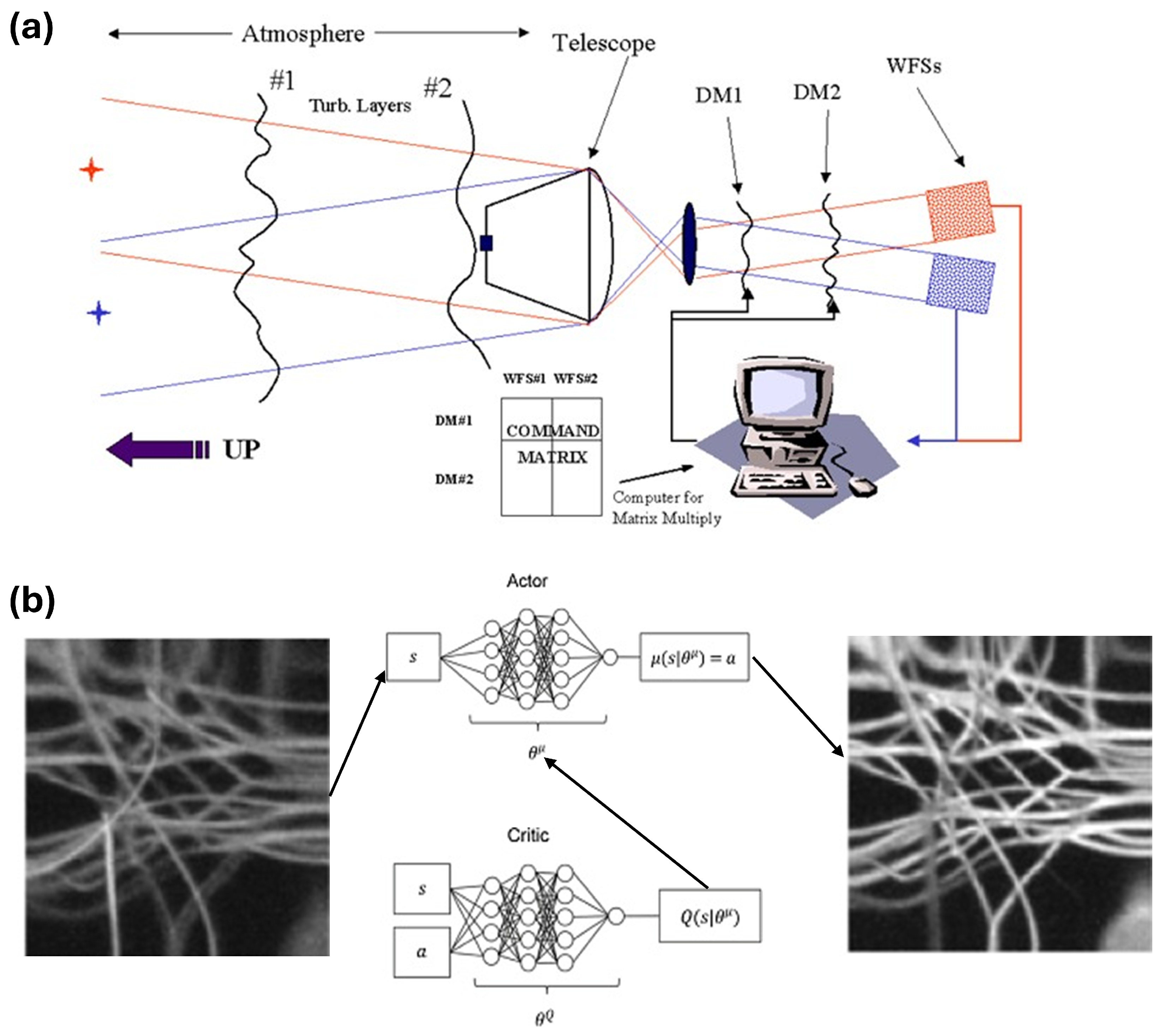
- Single-conjugate adaptive optics (SCAO), which is the simplest configuration, consisting of a single wavefront sensor and a single wavefront corrector. It measures wavefront distortions and applies corrections in a straightforward manner, typically using a deformable mirror placed in a pupil–conjugate plane to counteract atmospheric turbulence effects. It is commonly used in ground-based telescopes to enhance image quality by correcting for atmospheric disturbances (e.g., see Figure 2a and Figure 6b).
- Multi-Conjugate Adaptive Optics (MCAO) configuration employs multiple wavefront sensors and correctors located in different planes that are not mutually conjugate (Figure 9a). MCAO can better address aberrations originating from various directions [37]. While it offers superior performance, it significantly increases system complexity and cost, making it less common than SCAO.
- Sensorless adaptive optics (SAO) uses pre-existing knowledge about the expected image features to optimize corrections dynamically, which can be beneficial in certain imaging scenarios where sensor data are difficult to obtain. It usually considers iterative procedures that may involve the use of Deep Neural Networks (DNNs) [38] and Deep Reinforcement Learning (DRL) with policy gradients [39] (Figure 9b).
- Segmented mirror systems utilize an array of smaller mirrors that can be individually controlled to form a larger effective aperture. Each segment can be adjusted to correct for local aberrations, enhancing overall image quality. This configuration is often modeled using advanced optical design software to simulate and optimize performance.
3. Emerging Trends in Laser Material Processing: Opportunities and the Role of PSF and Zernike Polynomials
4. AO as a Transformative Technology When Integrated in a Wavefront Shaping System for a High-Power Laser Source
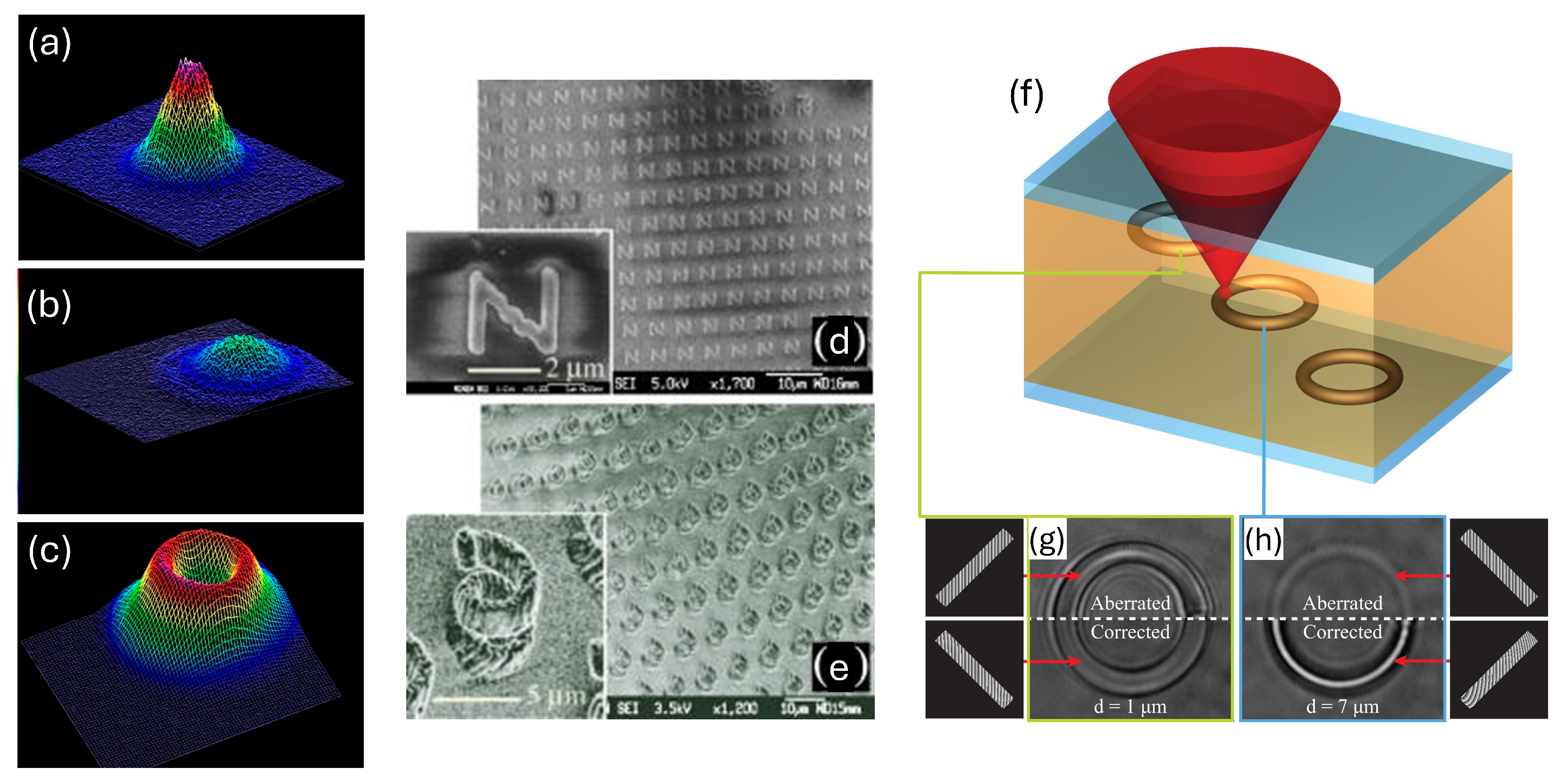
- Improved Beam Quality: Adaptive optics can modify the Gaussian beam shape typical of lasers into more suitable profiles for specific applications, such as a flat-top or ring-shaped intensity distribution. This modification can enhance the quality of laser marking and drilling processes by providing a more uniform energy distribution at the focus (Figure 11a–c).
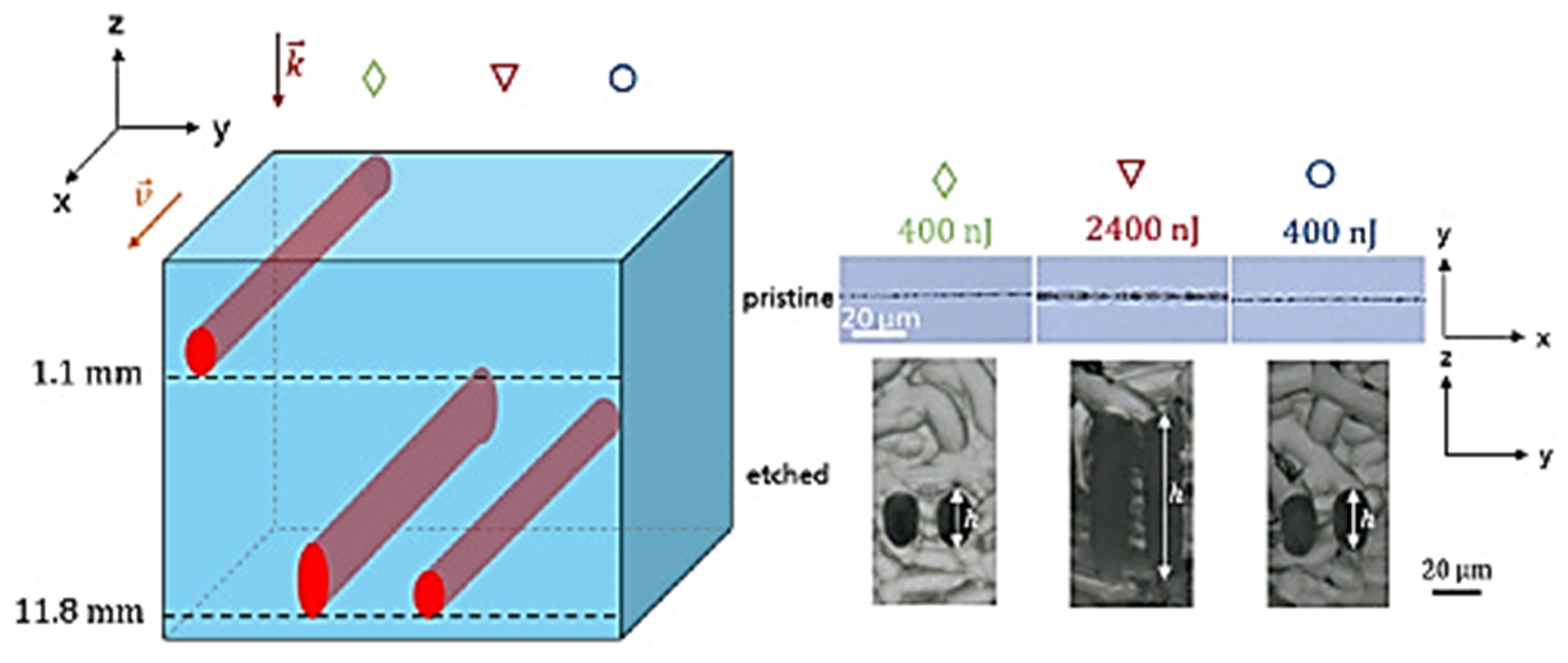
- Aberration Correction: When lasers are focused inside materials, aberrations can distort the beam, leading to inefficiencies in machining. Adaptive optics can correct these aberrations dynamically, ensuring that the laser maintains its diffraction-limited performance throughout the machining process. This is particularly beneficial for ultrafast laser applications where precision is critical.
- Parallel Processing: Adaptive optics can facilitate parallelization by generating multiple foci from a single laser beam, significantly reducing processing times for high-resolution tasks. This capability is especially advantageous for large-scale or complex three-dimensional fabrications (Figure 11d,e).
- Dynamic Control: The ability to adjust the beam shape and focus dynamically allows for complex structuring of materials during processing [56]. This flexibility enables manufacturers to tailor the laser’s properties in real-time, accommodating various fabrication tasks without needing to change equipment (Figure 11f–h).
- Enhanced Material Interaction: By controlling the intensity distribution at the focus, adaptive optics can optimize interactions with different materials, leading to improved outcomes in terms of precision and surface finish.
- Input beam characteristics: The input beam typically exhibits some level of distortion or non-uniformity in its wavefront. This could be due to imperfections in the laser source or optical components in the system.
- Role of DM: DM is strategically placed to manipulate the wavefront of the incoming beam. It consists of an array of actuators (often mechanical pistons) that can adjust the shape of the mirror’s surface. By altering this shape, the DM can compensate for wavefront aberrations present in [66].
- Wavefront correction: As the input beam interacts with the DM, it undergoes a transformation that aims to flatten or optimize its wavefront. The specific adjustments made by the DM are determined based on feedback from the Shack–Hartmann sensor, which measures the wavefront shape and identifies deviations from an ideal planar wavefront [57].
- Feedback loop: The Shack–Hartmann sensor captures the modified wavefront after it has been shaped by the DM. It analyzes the positions of focal spots created by an array of microlenses, allowing it to calculate parameters such as tip, tilt and curvature of the wavefront [67]. These data are then used to iteratively refine the DM’s adjustments, creating a closed feedback loop that continuously improves wavefront quality.
- Optimal wavefront shaping: The goal is to achieve a near-perfect wavefront before it reaches any subsequent optical components or processing stages in the laser micromachining setup. This ensures maximum efficiency and precision during laser ablation or machining processes, as a well-shaped beam can more effectively interact with materials [68].
5. Metasurfaces for Aberration Correction in Laser Scribing Processes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AO | Adaptive Optics |
| MTF | Modulation Transfer Function |
| OTF | Optical Transfer Function |
| PSD | Point Spread Function |
| LSA | Longitudinal Spherical Aberration |
| TSA | Transverse Spherical Aberration |
| DM | Deformable Mirror |
| SLM | Spatial Light Modulator |
Appendix A. Optical Imaging Processes and Aberration
Appendix A.1. Classification of Aberrations
- Lower-order aberrations (0, 1st and 2nd order);
- Higher-order aberrations (3rd, 4th, …order).
- Piston (), tip () and tilt () representing the reference surface;
- Defocus ();
- Astigmatism ().
- Spherical aberration, SA, (Primary SA , Secondary SA , …);
- Coma ();
- Distortion.
- Monochromatic aberrations: These depend on the geometry of the optical system and are therefore observed with both refracted and reflected light. Their name depends on the fact that they are present even when monochromatic light is used. These are divided into the following:
- Axial-type aberrationsThey occur when certain light rays incident on the optical system are too far from the optical axis and are affected by the spherical shape of lenses and mirrors (a condition in which the paraxial approximation is not valid). Spherical (or sphericity) aberration falls into this category.
- Extra-axial aberrationsThey occur with light from extended objects (i.e., all non-point objects) and from objects not arranged on the optical axis. The following aberrations fall into this category:
- -
- Coma;
- -
- Astigmatism;
- -
- Distortion;
- -
- Field curvature.
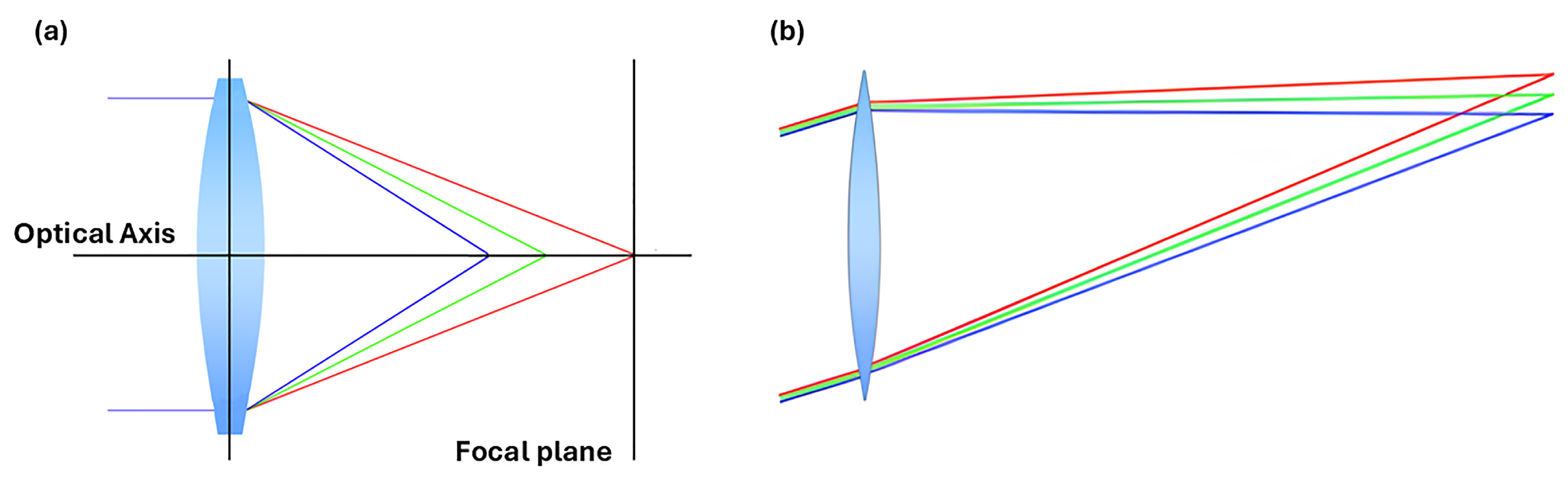
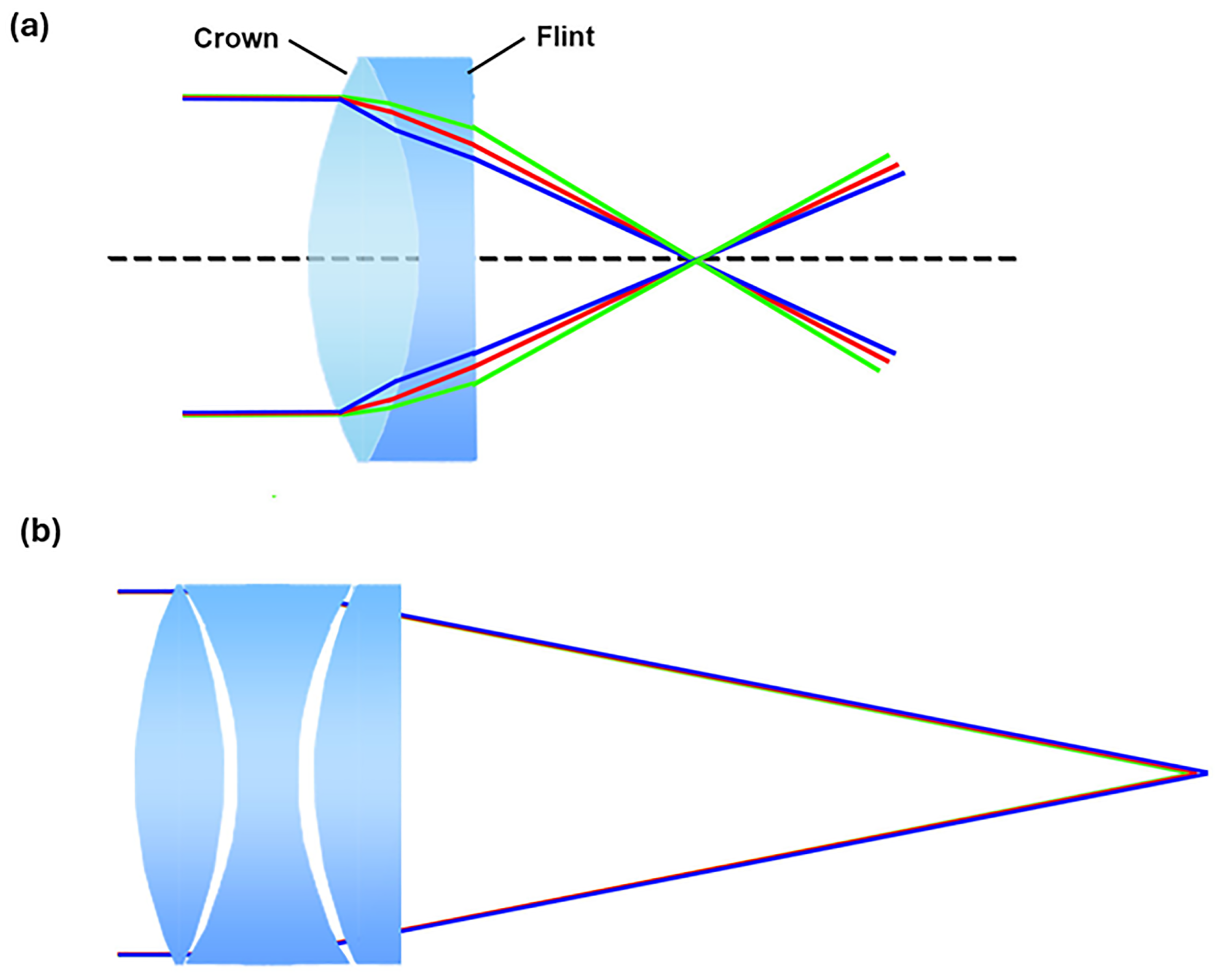
In high-power laser applications, the presence of axial- and extra-axial-type aberrations can alter the ideal diffraction-limited nature of a laser’s focal intensity distribution. This distortion can result in less-effective material modification during processes like cutting or engraving, where precise control over the laser focus is essential. Recently, by addressing both lower-order and higher-order aberrations through adaptive optics and precision optical design, manufacturers can enhance machining quality and efficiency, leading to better final product performance. - Chromatic aberrations: These depend on the dispersion of the optical system, i.e., changes in the refractive index of the lens materials as the wavelength changes. Due to dispersion, focusing will not occur at a single point. Chromatic aberration does not affect mirrors and does not occur in lenses when monochromatic light is used. Figure 2 shows examples of axial chromatic aberration (a) and lateral chromatic aberration (b), respectively.

Appendix A.1.1. Tilting and Defocus

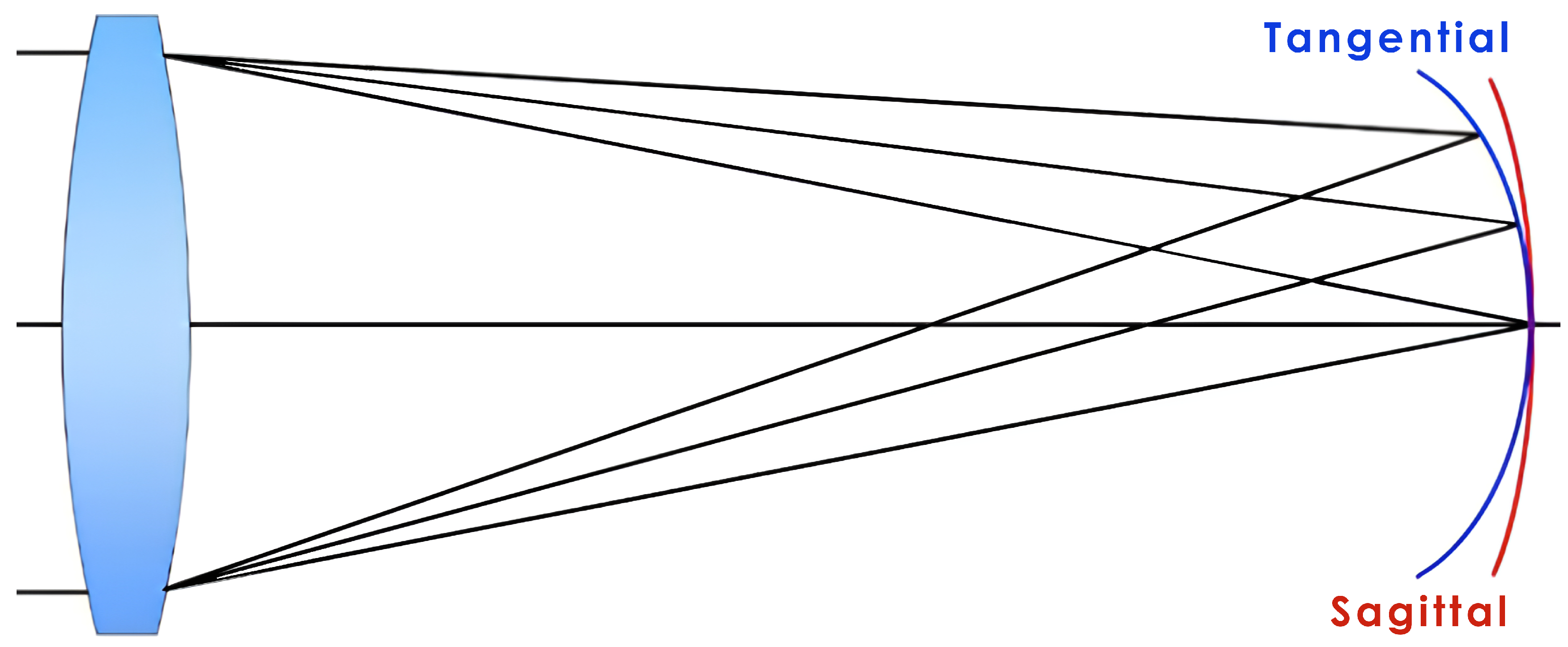
Appendix A.1.2. Astigmatism
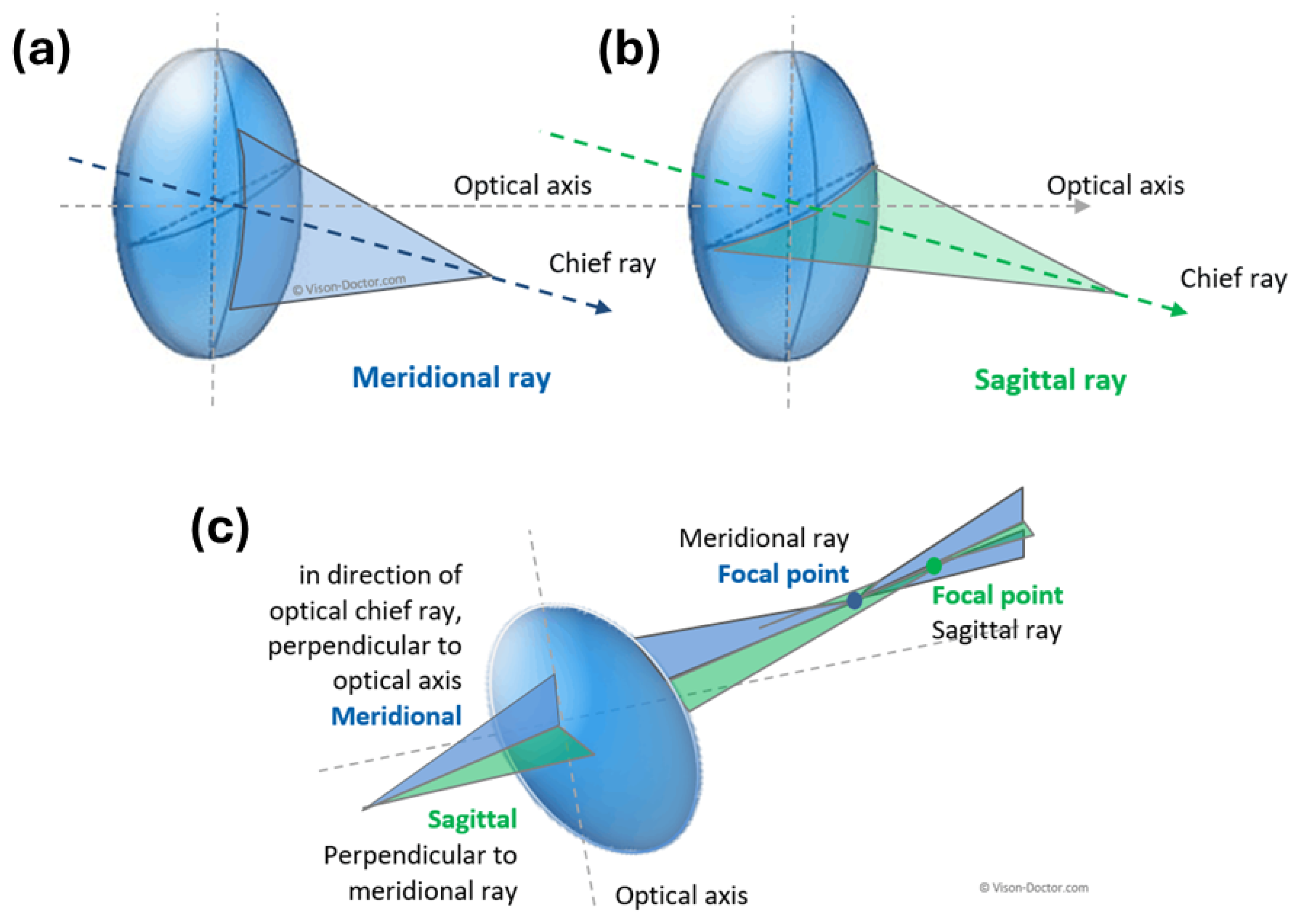

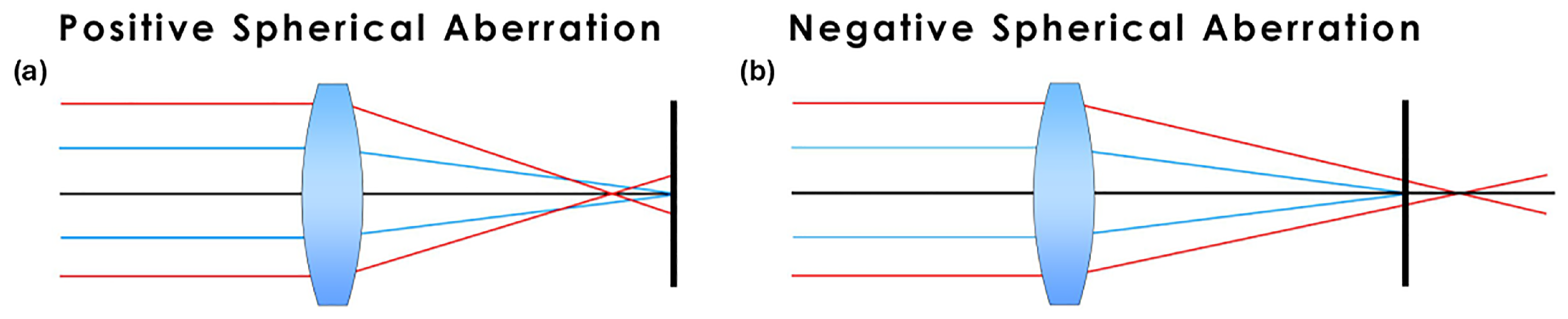
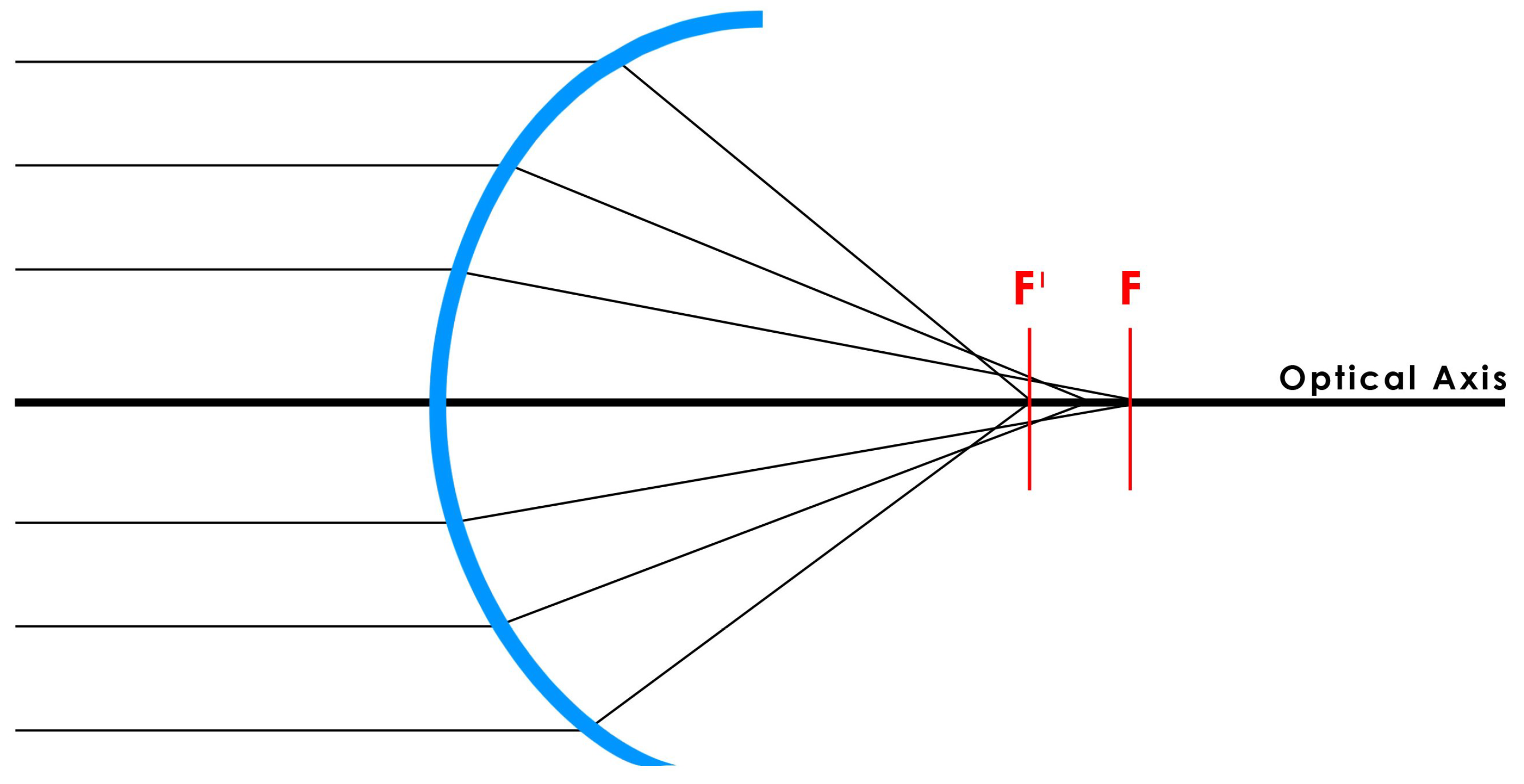
Appendix A.1.3. Spherical Aberration

Appendix A.1.4. Spherical Aberration of a Diopter and of a Thin Lens
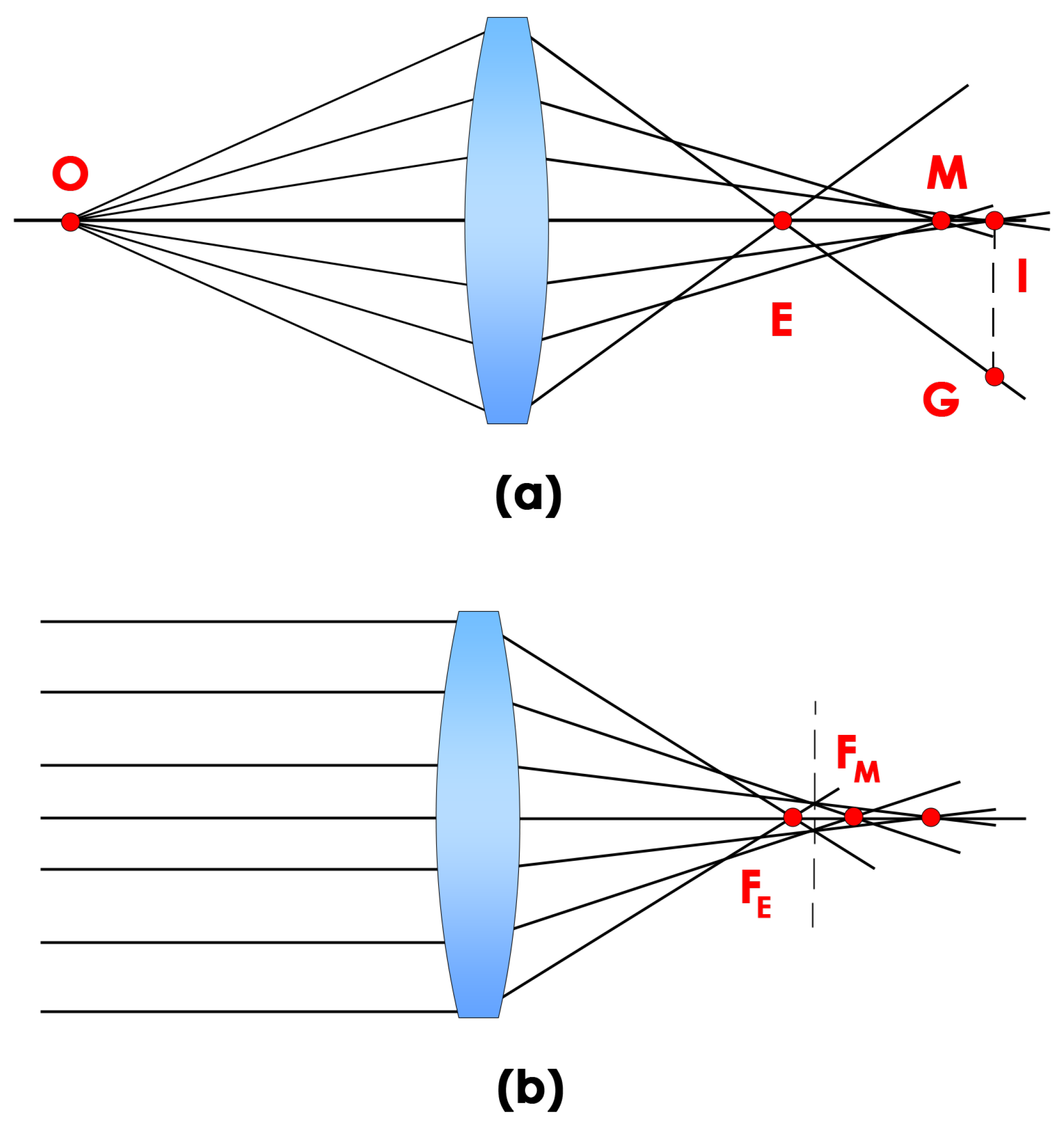


Appendix A.1.5. Aberration of Coma

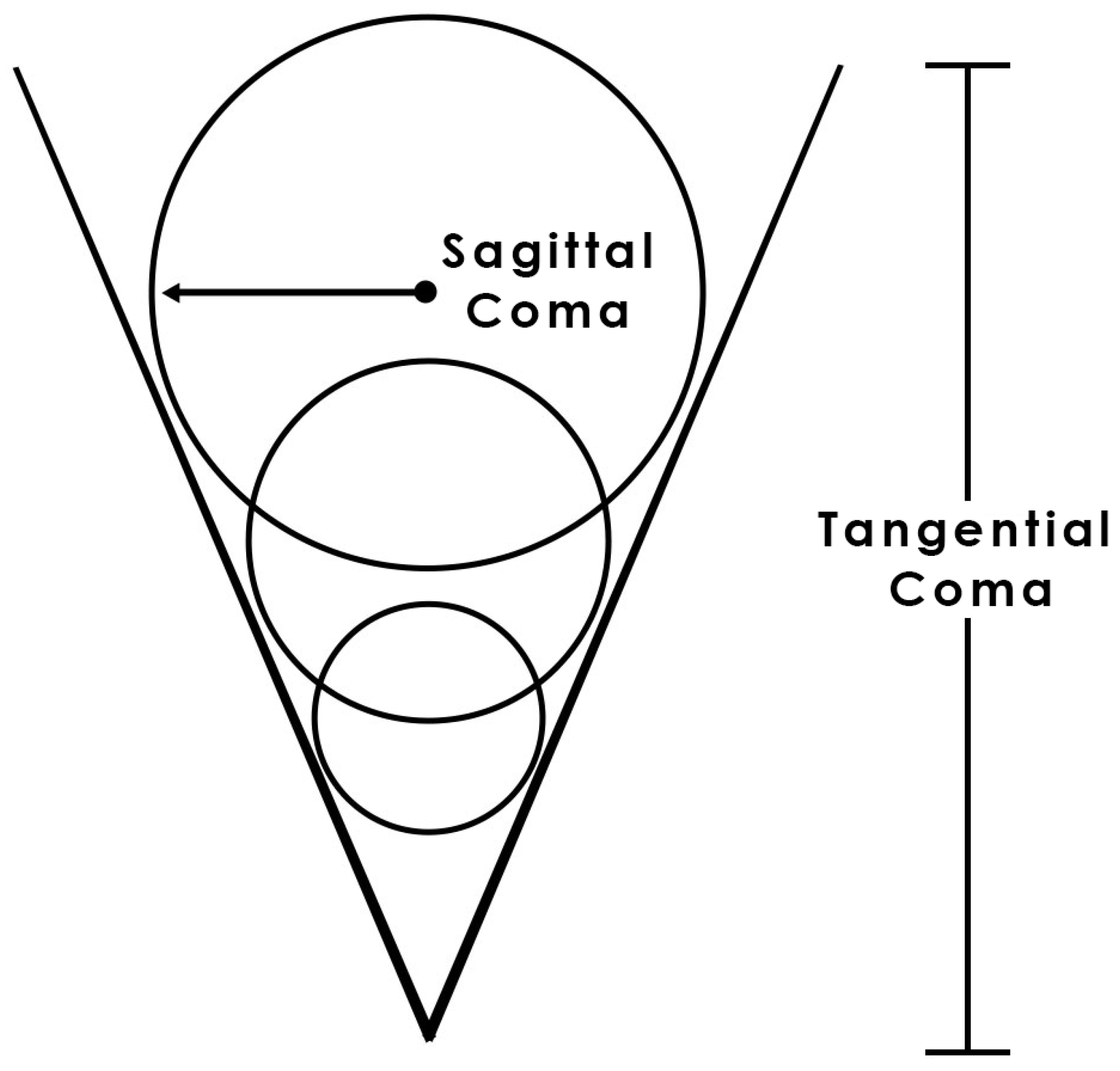
Appendix A.1.6. Distortion

Appendix A.1.7. Chromatic Aberration and Dispersion
Appendix A.1.8. Curvature of Field
References
- Salter, P.S.; Booth, M.J. Adaptive optics in laser processing. Light. Sci. Appl. 2019, 8, 110. [Google Scholar] [CrossRef] [PubMed]
- Park, K.; Yang, T.D.; Kim, H.J.; Kong, T.; Lee, J.M.; Choi, H.S.; Chun, H.J.; Kim, B.M.; Choi, Y. Inversion-free image recovery from strong aberration using a minimally sampled transmission matrix. Sci. Rep. 2019, 9, 1206. [Google Scholar] [CrossRef]
- Sawant, R.; Andrén, D.; Martins, R.J.; Khadir, S.; Verre, R.; Käll, M.; Genevet, P. Aberration-corrected large-scale hybrid metalenses. Optica 2021, 8, 1405. [Google Scholar] [CrossRef]
- Ho, A.H.; Kim, D.; Somekh, M.G. (Eds.) Handbook of Photonics for Biomedical Engineering; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Sirico, D.G.; Miccio, L.; Wang, Z.; Memmolo, P.; Xiao, W.; Che, L.; Xin, L.; Pan, F.; Ferraro, P. Compensation of aberrations in holographic microscopes: Main strategies and applications. Appl. Phys. B 2022, 128, 78. [Google Scholar] [CrossRef]
- Roorda, A. Adaptive optics for studying visual function: A comprehensive review. J. Vis. 2011, 11, 6. [Google Scholar] [CrossRef]
- Marcos, S.; Werner, J.S.; Burns, S.A.; Merigan, W.H.; Artal, P.; Atchison, D.A.; Hampson, K.M.; Legras, R.; Lundstrom, L.; Yoon, G.; et al. Vision science and adaptive optics, the state of the field. Vis. Res. 2017, 132, 3–33. [Google Scholar] [CrossRef]
- South, F.A.; Liu, Y.Z.; Bower, A.J.; Xu, Y.; Carney, P.S.; Boppart, S.A. Wavefront measurement using computational adaptive optics. J. Opt. Soc. Am. A 2018, 35, 466. [Google Scholar] [CrossRef]
- Baucom, D. The Adaptive Optics Revolution: A History (review). Technol. Cult. 2011, 52, 412–413. [Google Scholar] [CrossRef]
- Akyol, E.; Hagag, A.M.; Sivaprasad, S.; Lotery, A.J. Adaptive optics: Principles and applications in ophthalmology. Eye 2020, 35, 244–264. [Google Scholar] [CrossRef]
- Shemonski, N.D.; South, F.A.; Liu, Y.Z.; Adie, S.G.; Scott Carney, P.; Boppart, S.A. Computational high-resolution optical imaging of the living human retina. Nat. Photonics 2015, 9, 440–443. [Google Scholar] [CrossRef]
- Morgan, J.I.W.; Chui, T.Y.P.; Grieve, K. Twenty-five years of clinical applications using adaptive optics ophthalmoscopy [Invited]. Biomed. Opt. Express 2022, 14, 387. [Google Scholar] [CrossRef] [PubMed]
- Vacalebre, M.; Frison, R.; Corsaro, C.; Neri, F.; Conoci, S.; Anastasi, E.; Curatolo, M.C.; Fazio, E. Advanced Optical Wavefront Technologies to Improve Patient Quality of Vision and Meet Clinical Requests. Polymers 2022, 14, 5321. [Google Scholar] [CrossRef] [PubMed]
- Balas, M.; Ramalingam, V.; Pandya, B.; Abdelaal, A.; Shi, R.B. Adaptive optics imaging in ophthalmology: Redefining vision research and clinical practice. JFO Open Ophthalmol. 2024, 7, 100116. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, R.; Žurauskas, M.; Pande, P.; Bi, J.; Yuan, Q.; Wang, L.; Gao, Z.; Boppart, S.A. Automated fast computational adaptive optics for optical coherence tomography based on a stochastic parallel gradient descent algorithm. Opt. Express 2020, 28, 23306. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Crowell, J.A.; Kurokawa, K.; Bernucci, M.T.; Ji, Q.; Lassoued, A.; Jung, H.W.; Keller, M.J.; Marte, M.E.; Miller, D.T. Ultrafast adaptive optics for imaging the living human eye. Nat. Commun. 2024, 15, 10409. [Google Scholar] [CrossRef]
- Zawadzki, R.J.; Jones, S.M.; Balderas-Mata, S.E.; Maliszewska, S.M.; Olivier, S.S.; Werner, J.S. Performance of 97-elements ALPAO membrane magnetic deformable mirror in Adaptive Optics—Optical Coherence Tomography system for in vivo imaging of human retina. Photonics Lett. Pol. 2011, 3, 147–149. [Google Scholar] [CrossRef]
- Zawadzki, R.J.; Jones, S.M.; Pilli, S.; Balderas-Mata, S.; Kim, D.Y.; Olivier, S.S.; Werner, J.S. Integrated adaptive optics optical coherence tomography and adaptive optics scanning laser ophthalmoscope system for simultaneous cellular resolution in vivo retinal imaging. Biomed. Opt. Express 2011, 2, 1674. [Google Scholar] [CrossRef]
- Evans, J.W.; Zawadzki, R.J.; Jones, S.M.; Olivier, S.S.; Werner, J.S. Error budget analysis for an Adaptive Optics Optical Coherence Tomography System. Opt. Express 2009, 17, 13768. [Google Scholar] [CrossRef]
- Li, K.Y.; Mishra, S.; Tiruveedhula, P.; Roorda, A. Comparison of control algorithms for a MEMS-based adaptive optics scanning laser ophthalmoscope. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3848–3853. [Google Scholar] [CrossRef]
- South, F.A.; Kurokawa, K.; Liu, Z.; Liu, Y.Z.; Miller, D.T.; Boppart, S.A. Combined hardware and computational optical wavefront correction. Biomed. Opt. Express 2018, 9, 2562. [Google Scholar] [CrossRef]
- Booth, M.J. Adaptive optical microscopy: The ongoing quest for a perfect image. Light. Sci. Appl. 2014, 3, e165. [Google Scholar] [CrossRef]
- Zinchik, A. Application of spatial light modulators for generation of laser beams with a spiral phase distribution. Sci. Tech. J. Inf. Technol. Mech. Opt. 2015, 15, 817–824. [Google Scholar] [CrossRef]
- Weiner, A.M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 2000, 71, 1929–1960. [Google Scholar] [CrossRef]
- Jullien, A. Spatial light modulators. Photoniques 2020, 101, 59–64. [Google Scholar] [CrossRef]
- Hutterer, V.; Ramlau, R.; Shatokhina, I. Real-time adaptive optics with pyramid wavefront sensors: Part I. A theoretical analysis of the pyramid sensor model. Inverse Probl. 2019, 35, 045007. [Google Scholar] [CrossRef]
- Anand, V.; Khonina, S.; Kumar, R.; Dubey, N.; Reddy, A.N.K.; Rosen, J.; Juodkazis, S. Three-Dimensional Incoherent Imaging Using Spiral Rotating Point Spread Functions Created by Double-Helix Beams [Invited]. Nanoscale Res. Lett. 2022, 17, 37. [Google Scholar] [CrossRef]
- Wang, K.; Yu, Y.; Preumont, A. Shape Control of a Unimorph Deformable Mirror for Space Active Optics under Uncertainties. Micromachines 2023, 14, 1756. [Google Scholar] [CrossRef] [PubMed]
- Simmonds, R.D.; Salter, P.S.; Jesacher, A.; Booth, M.J. Three dimensional laser microfabrication in diamond using a dual adaptive optics system. Opt. Express 2011, 19, 24122. [Google Scholar] [CrossRef]
- Yu, Z.; Li, H.; Zhong, T.; Park, J.H.; Cheng, S.; Woo, C.M.; Zhao, Q.; Yao, J.; Zhou, Y.; Huang, X.; et al. Wavefront shaping: A versatile tool to conquer multiple scattering in multidisciplinary fields. Innovation 2022, 3, 100292. [Google Scholar] [CrossRef]
- Kuang, Z.; Liu, D.; Perrie, W.; Edwardson, S.; Sharp, M.; Fearon, E.; Dearden, G.; Watkins, K. Fast parallel diffractive multi-beam femtosecond laser surface micro-structuring. Appl. Surf. Sci. 2009, 255, 6582–6588. [Google Scholar] [CrossRef]
- Schmiedl, R. Adaptive Optics for CO2 Laser Material Processing. In Adaptive Optics for Industry and Medicine, Proceedings of the 2nd International Workshop, University of Durham, UK, 12–16 July 1999; World Scientific: Singapore, 1999; pp. 32–36. [Google Scholar] [CrossRef]
- Kong, L.; Yang, K.; Su, C.; Guo, S.; Wang, S.; Cheng, T.; Yang, P. Adaptive Optics Tip-Tilt Correction Based on Smith Predictor and Filter-Optimized Linear Active Disturbance Rejection Control Method. Sensors 2023, 23, 6724. [Google Scholar] [CrossRef]
- Yang, H.; Tang, L.; Yan, Z.; Chen, P.; Yang, W.; Li, X.; Ge, Y. Wavefront Correction for Extended Sources Imaging Based on a 97-Element MEMS Deformable Mirror. Micromachines 2024, 16, 50. [Google Scholar] [CrossRef] [PubMed]
- Helmbrecht, M.A.; Besse, M.; Kempf, C.J.; He, M. Speed enhancements for a 489-actuator, piston-tip-tilt segment, MEMS DM system. In Proceedings of the Advanced Wavefront Control: Methods, Devices, and Applications VIII, San Diego, CA, USA, 1–5 August 2010; Dayton, D.C., Rhoadarmer, T.A., Sanchez, D.J., Eds.; SPIE: Bremerhaven, Germany, 2010; Volume 7816, p. 78160F. [Google Scholar] [CrossRef]
- Iyer, R.R.; Liu, Y.Z.; Boppart, S.A. Automated sensorless single-shot closed-loop adaptive optics microscopy with feedback from computational adaptive optics. Opt. Express 2019, 27, 12998. [Google Scholar] [CrossRef]
- Rigaut, F.J.; Ellerbroek, B.L.; Flicker, R. Principles, limitations, and performance of multiconjugate adaptive optics. In Proceedings of the Adaptive Optical Systems Technology, Munich, Germany, 27 March–1 April 2000; Wizinowich, P.L., Ed.; SPIE: Bremerhaven, Germany, 2000; Volume 4007, pp. 1022–1031. [Google Scholar] [CrossRef]
- Polans, J.; Cunefare, D.; Cole, E.; Keller, B.; Mettu, P.S.; Cousins, S.W.; Allingham, M.J.; Izatt, J.A.; Farsiu, S. Enhanced visualization of peripheral retinal vasculature with wavefront sensorless adaptive optics optical coherence tomography angiography in diabetic patients. Opt. Lett. 2016, 42, 17. [Google Scholar] [CrossRef]
- Durech, E.; Newberry, W.; Franke, J.; Sarunic, M.V. Wavefront sensor-less adaptive optics using deep reinforcement learning. Biomed. Opt. Express 2021, 12, 5423. [Google Scholar] [CrossRef]
- Rimmele, T.R.; Marino, J. Solar Adaptive Optics. Living Rev. Sol. Phys. 2011, 8, 2. [Google Scholar] [CrossRef] [PubMed]
- Stuart, B.C.; Feit, M.D.; Herman, S.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Nanosecond-to-femtosecond laser-induced breakdown in dielectrics. Phys. Rev. B 1996, 53, 1749–1761. [Google Scholar] [CrossRef]
- Schaffer, C.B.; Brodeur, A.; Mazur, E. Laser-induced breakdown and damage in bulk transparent materials induced by tightly focused femtosecond laser pulses. Meas. Sci. Technol. 2001, 12, 1784–1794. [Google Scholar] [CrossRef]
- Tan, D.; Sharafudeen, K.N.; Yue, Y.; Qiu, J. Femtosecond laser induced phenomena in transparent solid materials: Fundamentals and applications. Prog. Mater. Sci. 2016, 76, 154–228. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Taylor, R.; Simova, E.; Rajeev, P.; Rayner, D.; Bhardwaj, V.; Corkum, P. Fabrication of microchannels in glass using focused femtosecond laser radiation and selective chemical etching. Appl. Phys. A 2006, 84, 47–61. [Google Scholar] [CrossRef]
- Bisch, N.; Guan, J.; Booth, M.J.; Salter, P.S. Adaptive optics aberration correction for deep direct laser written waveguides in the heating regime. Appl. Phys. A 2019, 125, 364. [Google Scholar] [CrossRef]
- Kratz, M.; Rückle, L.; Kalupka, C.; Reininghaus, M.; Haefner, C.L. Dynamic correction of optical aberrations for height-independent selective laser induced etching processing strategies. Opt. Express 2023, 31, 26104. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, S.; Hayasaki, Y. Femtosecond laser processing with adaptive optics based on convolutional neural network. Opt. Lasers Eng. 2021, 141, 106563. [Google Scholar] [CrossRef]
- Gatinel, D.; Rampat, R.; Malet, J.; Dumas, L. Wavefront sensing, novel lower degree/higher degree polynomial decomposition and its recent clinical applications: A review. Indian J. Ophthalmol. 2020, 68, 2670. [Google Scholar] [CrossRef]
- Dumas, L.; Gatinel, D.; Malet, J. A New Decomposition Basis for The Classification of Aberrations of The Human Eye. ESAIM: Proc. Surv. 2018, 62, 43–55. [Google Scholar] [CrossRef]
- Malinauskas, M.; Žukauskas, A.; Hasegawa, S.; Hayasaki, Y.; Mizeikis, V.; Buividas, R.; Juodkazis, S. Ultrafast laser processing of materials: From science to industry. Light. Sci. Appl. 2016, 5, e16133. [Google Scholar] [CrossRef] [PubMed]
- Weber, R.; Graf, T. The challenges of productive materials processing with ultrafast lasers. Adv. Opt. Technol. 2021, 10, 239–245. [Google Scholar] [CrossRef]
- Sugioka, K.; Cheng, Y. Ultrafast lasers—Reliable tools for advanced materials processing. Light. Sci. Appl. 2014, 3, e149. [Google Scholar] [CrossRef]
- Feng, J.; Wang, J.; Liu, H.; Sun, Y.; Fu, X.; Ji, S.; Liao, Y.; Tian, Y. A Review of an Investigation of the Ultrafast Laser Processing of Brittle and Hard Materials. Materials 2024, 17, 3657. [Google Scholar] [CrossRef]
- Beck, R.J. Adaptive Optics for Laser Processing. Ph.D. Thesis, Heriot-Watt University, Edinburgh, Scotland, 2011. [Google Scholar]
- Parry, J.; Beck, R.; Weston, N.; Shephard, J.; Hand, D. Application of adaptive optics to laser micromachining. In Proceedings of the International Congress on Applications of Lasers & Electro-Optics. Laser Institute of America, Anaheim, CA, USA, 26–30 September 2010; pp. 767–776. [Google Scholar] [CrossRef]
- Schmidt, M.; Cvecek, K.; Duflou, J.; Vollertsen, F.; Arnold, C.; Matthews, M. Dynamic beam shaping—Improving laser materials processing via feature synchronous energy coupling. CIRP Ann. 2024, 73, 533–559. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, L.; Zhang, Q.; Yang, L.; Tang, M.; Xiao, F.; Wang, X.; Shen, S.; Zhang, L.; Guo, Y. Femtosecond laser processing with aberration correction based on Shack-Hartmann wavefront sensor. Opt. Lasers Eng. 2025, 184, 108693. [Google Scholar] [CrossRef]
- Salter, P.S.; Booth, M.J. Focussing over the edge: Adaptive subsurface laser fabrication up to the sample face. Opt. Express 2012, 20, 19978. [Google Scholar] [CrossRef] [PubMed]
- Stallinga, S. Axial birefringence in high-numerical-aperture optical systems and the light distribution close to focus. J. Opt. Soc. Am. A 2001, 18, 2846. [Google Scholar] [CrossRef]
- Zhou, G.; Jesacher, A.; Booth, M.; Wilson, T.; Ródenas, A.; Jaque, D.; Gu, M. Axial birefringence induced focus splitting in lithium niobate. Opt. Express 2009, 17, 17970. [Google Scholar] [CrossRef] [PubMed]
- Karpinski, P.; Shvedov, V.; Krolikowski, W.; Hnatovsky, C. Laser-writing inside uniaxially birefringent crystals: Fine morphology of ultrashort pulse-induced changes in lithium niobate. Opt. Express 2016, 24, 7456. [Google Scholar] [CrossRef] [PubMed]
- Metel, A.; Stebulyanin, M.; Fedorov, S.; Okunkova, A. Power Density Distribution for Laser Additive Manufacturing (SLM): Potential, Fundamentals and Advanced Applications. Technologies 2018, 7, 5. [Google Scholar] [CrossRef]
- Kato, J.i.; Takeyasu, N.; Adachi, Y.; Sun, H.B.; Kawata, S. Multiple-spot parallel processing for laser micronanofabrication. Appl. Phys. Lett. 2005, 86, 044102. [Google Scholar] [CrossRef]
- Cumming, B.P.; Debbarma, S.; Luther-Davis, B.; Gu, M. Simultaneous compensation for aberration and axial elongation in three-dimensional laser nanofabrication by a high numerical-aperture objective. Opt. Express 2013, 21, 19135. [Google Scholar] [CrossRef]
- Li, S.; Zhou, L.; Cui, C.; Wang, K.; Yan, X.; Wang, Y.; Ding, L.; Wang, Y.; Lu, Z. Wavefront Shaping by a Small-Aperture Deformable Mirror in the Front Stage for High-Power Laser Systems. Appl. Sci. 2017, 7, 379. [Google Scholar] [CrossRef]
- Campbell, S.; Triphan, S.M.F.; El-Agmy, R.; Greenaway, A.H.; Reid, D.T. Direct optimization of femtosecond laser ablation using adaptive wavefront shaping. J. Opt. A Pure Appl. Opt. 2007, 9, 1100–1104. [Google Scholar] [CrossRef]
- Lin, V.; Wei, H.C.; Hsieh, H.T.; Su, G.D.J. An Optical Wavefront Sensor Based on a Double Layer Microlens Array. Sensors 2011, 11, 10293–10307. [Google Scholar] [CrossRef]
- Wei, X.; Jing, J.C.; Shen, Y.; Wang, L.V. Harnessing a multi-dimensional fibre laser using genetic wavefront shaping. Light. Sci. Appl. 2020, 9, 149. [Google Scholar] [CrossRef] [PubMed]
- Williams, W.H.; Auerbach, J.M.; Henesian, M.A.; Lawson, J.K.; Hunt, J.T.; Sacks, R.A.; Widmayer, C.C. Modeling characterization of the National Ignition Facility focal spot. In Proceedings of the High-Power Lasers, San Jose, CA, USA, 24–30 January 1998; Basu, S., Ed.; SPIE: Bremerhaven, Germany, 1998; Volume 3264, p. 93. [Google Scholar] [CrossRef]
- Haber, A.; Polo, A.; Smith, C.S.; Pereira, S.F.; Urbach, P.; Verhaegen, M. Iterative learning control of a membrane deformable mirror for optimal wavefront correction. Appl. Opt. 2013, 52, 2363. [Google Scholar] [CrossRef]
- Jia, X.; Fu, Y.; Li, K.; Wang, C.; Li, Z.; Wang, C.; Duan, J. Burst Ultrafast Laser Welding of Quartz Glass. Materials 2025, 18, 1169. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Xia, C.; Kuebler, S.M.; Golvari, P.; Sun, M.; Zhang, M.; Yu, X. Generation of Bessel-beam arrays for parallel fabrication in two-photon polymerization. J. Laser Appl. 2021, 33, 012040. [Google Scholar] [CrossRef]
- Balage, P.; Guilberteau, T.; Lafargue, M.; Bonamis, G.; Hönninger, C.; Lopez, J.; Manek-Hönninger, I. Bessel Beam Dielectrics Cutting with Femtosecond Laser in GHz-Burst Mode. Micromachines 2023, 14, 1650. [Google Scholar] [CrossRef]
- Guilberteau, T.; Balage, P.; Lafargue, M.; Lopez, J.; Gemini, L.; Manek-Hönninger, I. Bessel Beam Femtosecond Laser Interaction with Fused Silica Before and After Chemical Etching: Comparison of Single Pulse, MHz-Burst, and GHz-Burst. Micromachines 2024, 15, 1313. [Google Scholar] [CrossRef]
- Helmy, A.K.; El-Taweel, G.S. Image segmentation scheme based on SOM-PCNN in frequency domain. Appl. Soft Comput. 2016, 40, 405–415. [Google Scholar] [CrossRef]
- Xu, X.; Liang, T.; Wang, G.; Wang, M.; Wang, X. Self-Adaptive PCNN Based on the ACO Algorithm and its Application on Medical Image Segmentation. Intell. Autom. Soft Comput. 2016, 23, 303–310. [Google Scholar] [CrossRef]
- Suárez Gómez, S.L.; García Riesgo, F.; González Gutiérrez, C.; Rodríguez Ramos, L.F.; Santos, J.D. Defocused Image Deep Learning Designed for Wavefront Reconstruction in Tomographic Pupil Image Sensors. Mathematics 2020, 9, 15. [Google Scholar] [CrossRef]
- Nazir, S.; Vaquero, L.; Mucientes, M.; Brea, V.M.; Coltuc, D. Depth Estimation and Image Restoration by Deep Learning From Defocused Images. IEEE Trans. Comput. Imaging 2023, 9, 607–619. [Google Scholar] [CrossRef]
- Li, A.; Singh, S.; Sievenpiper, D. Metasurfaces and their applications. Nanophotonics 2018, 7, 989–1011. [Google Scholar] [CrossRef]
- Yang, Y.; Seong, J.; Choi, M.; Park, J.; Kim, G.; Kim, H.; Jeong, J.; Jung, C.; Kim, J.; Jeon, G.; et al. Integrated metasurfaces for re-envisioning a near-future disruptive optical platform. Light. Sci. Appl. 2023, 12, 152. [Google Scholar] [CrossRef] [PubMed]
- Caputo, R.; Ferraro, A. Metasurfaces: Theoretical Basis and Application Overview. In Hybrid Flatland Metastructures; AIP Publishing LLC: Melville, NY, USA, 2021; pp. 1–20. [Google Scholar] [CrossRef]
- Chen, M.K.; Wu, Y.; Feng, L.; Fan, Q.; Lu, M.; Xu, T.; Tsai, D.P. Principles, Functions, and Applications of Optical Meta-Lens. Adv. Opt. Mater. 2021, 9, 2001414. [Google Scholar] [CrossRef]
- Jung, J.; Kim, H.; Shin, J. Three-dimensionally reconfigurable focusing of laser by mechanically tunable metalens doublet with built-in holograms for alignment. Nanophotonics 2023, 12, 1373–1385. [Google Scholar] [CrossRef] [PubMed]
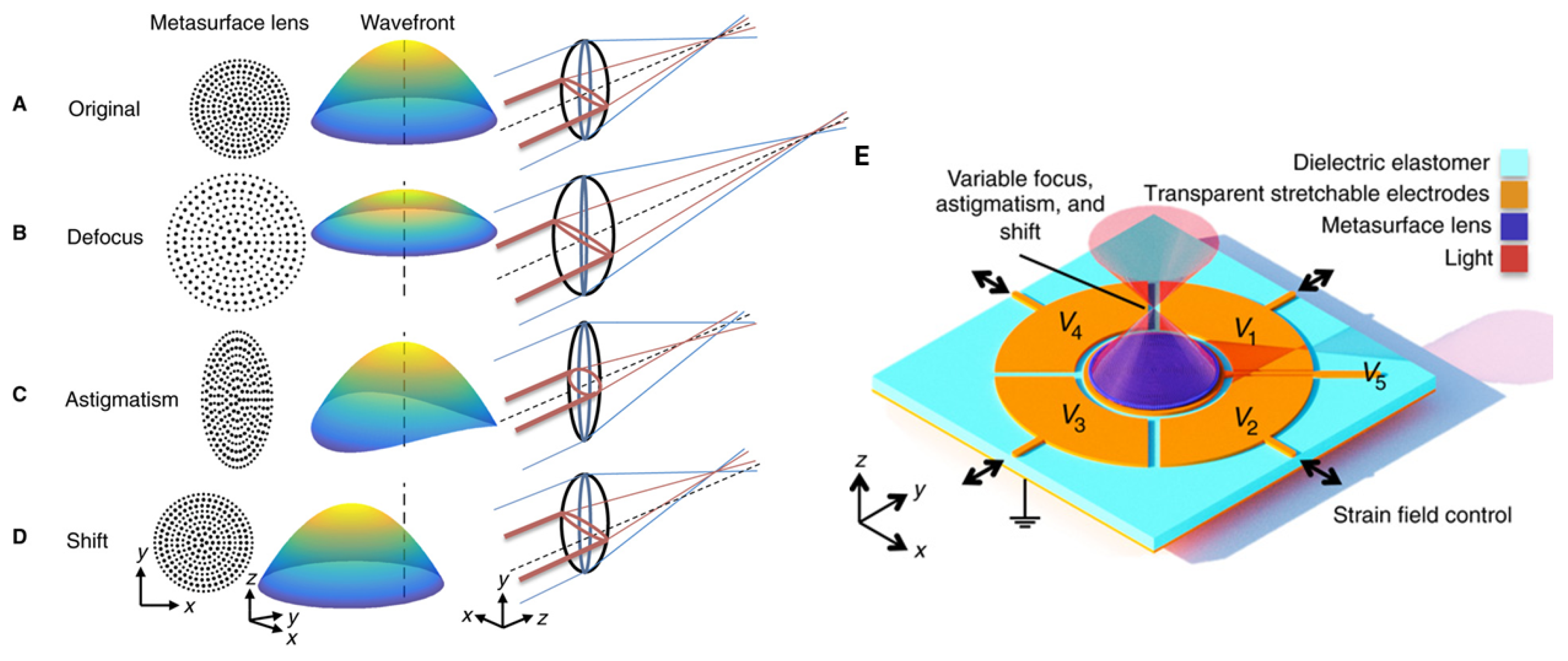
- She, A.; Zhang, S.; Shian, S.; Clarke, D.R.; Capasso, F. Adaptive metalenses with simultaneous electrical control of focal length, astigmatism, and shift. Sci. Adv. 2018, 4, eaap9957. [Google Scholar] [CrossRef]
- Li, X.; Cai, X.; Liu, C.; Kim, Y.; Badloe, T.; Liu, H.; Rho, J.; Xiao, S. Cascaded metasurfaces enabling adaptive aberration corrections for focus scanning. Opto-Electron. Adv. 2024, 7, 240085. [Google Scholar] [CrossRef]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Faraon, A. Conformal optical metasurfaces. U.S. Patent 20160320531A1, 12 June 2016. [Google Scholar]
- Chen, R.; Chang, S.; Lei, S. An Exploratory Study of Laser Scribing Quality through Cross-Section Scribing Profiles. Micromachines 2023, 14, 2020. [Google Scholar] [CrossRef]
- Shitrit, N. Surface-emitting lasers meet metasurfaces. Light. Sci. Appl. 2024, 13, 37. [Google Scholar] [CrossRef]
- Hudec, R.; Spurny, M.; Krizek, M.; Pata, P.; Slosiar, R.; Rerabek, M.; Klima, M. Detection of GRBs and OTs by All-Sky Optical and SID Monitors. Adv. Astron. 2010, 2010, 428943. [Google Scholar] [CrossRef]
- Luo, J.; Nie, Y.; Ren, W.; Cao, X.; Yang, M.H. Correcting Optical Aberration via Depth-Aware Point Spread Functions. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 5541–5555. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, Y.; Feng, P.; Qiao, X.; Ordones, S.; Su, R.; Wang, X. Distortion measurement of a lithography projection lens based on multichannel grating lateral shearing interferometry. Appl. Opt. 2024, 63, 2056. [Google Scholar] [CrossRef] [PubMed]
- Cunha, M.O.T.; Padua, S.; Walborn, S.; Monken, C. Quantum Erasure. Am. Sci. 2003, 91, 336. [Google Scholar] [CrossRef]
- van den Bos, A. Rayleigh wave-front criterion: Comment. J. Opt. Soc. Am. A 1999, 16, 2307. [Google Scholar] [CrossRef]
- Chen, L.; Singer, B.; Guirao, A.; Porter, J.; Williams, D.R. Image Metrics for Predicting Subjective Image Quality. Optom. Vis. Sci. 2005, 82, 358–369. [Google Scholar] [CrossRef]
- Hecht, E. Optics, 5th ed.; global edition ed.; Pearson Education, Inc.: Boston, MA, USA, 2017. [Google Scholar]
- Rojo, P.; Royo, S.; Ramírez, J.; Madariaga, I. Numerical implementation of generalized Coddington equations for ophthalmic lens design. J. Mod. Opt. 2014, 61, 204–214. [Google Scholar] [CrossRef]
- Liu, T.; Thibos, L.N. Compensation of corneal oblique astigmatism by internal optics: A theoretical analysis. Ophthalmic Physiol. Opt. 2017, 37, 305–316. [Google Scholar] [CrossRef]
- Welford, W.T. Aberrations of Optical Systems; Routledge: England, UK, 2017. [Google Scholar] [CrossRef]
- Freeman, M.; Hull, C. Optics; Butterworth-Heinemann: Oxford, UK, 2003; p. 576. [Google Scholar]
- Liu, T.; Thibos, L.N. Variation of axial and oblique astigmatism with accommodation across the visual field. J. Vis. 2017, 17, 24. [Google Scholar] [CrossRef]
- Pedrotti, F.; Pedrotti, L.; Pedrotti, L. Introduction to Optics, 3rd ed.; Addison-Wesley: Boston, MA, USA, 2006. [Google Scholar]
- Geary, J. Introduction to Lens Design: With Practical ZEMAX Examples; Willmann-Bell: Richmond, VA, USA, 2002. [Google Scholar]
- Kato, N.; Ikeda, S.; Hirakawa, M.; Ito, H. Correlation of the Abbe Number, the Refractive Index, and Glass Transition Temperature to the Degree of Polymerization of Norbornane in Polycarbonate Polymers. Polymers 2020, 12, 2484. [Google Scholar] [CrossRef]
- Zhao, H.; Mainster, M.A. The effect of chromatic dispersion on pseudophakic optical performance. Br. J. Ophthalmol. 2007, 91, 1225–1229. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corsaro, C.; Pelleriti, P.; Crupi, V.; Cosio, D.; Neri, F.; Fazio, E. Adaptive Aberration Correction for Laser Processes Improvement. J. Manuf. Mater. Process. 2025, 9, 105. https://doi.org/10.3390/jmmp9040105
Corsaro C, Pelleriti P, Crupi V, Cosio D, Neri F, Fazio E. Adaptive Aberration Correction for Laser Processes Improvement. Journal of Manufacturing and Materials Processing. 2025; 9(4):105. https://doi.org/10.3390/jmmp9040105
Chicago/Turabian StyleCorsaro, Carmelo, Priscilla Pelleriti, Vincenza Crupi, Daniele Cosio, Fortunato Neri, and Enza Fazio. 2025. "Adaptive Aberration Correction for Laser Processes Improvement" Journal of Manufacturing and Materials Processing 9, no. 4: 105. https://doi.org/10.3390/jmmp9040105
APA StyleCorsaro, C., Pelleriti, P., Crupi, V., Cosio, D., Neri, F., & Fazio, E. (2025). Adaptive Aberration Correction for Laser Processes Improvement. Journal of Manufacturing and Materials Processing, 9(4), 105. https://doi.org/10.3390/jmmp9040105









