Neural Network Optimization of Mechanical Properties of ABS-like Photopolymer Utilizing Stereolithography (SLA) 3D Printing
Abstract
:1. Introduction
2. Materials and Methods
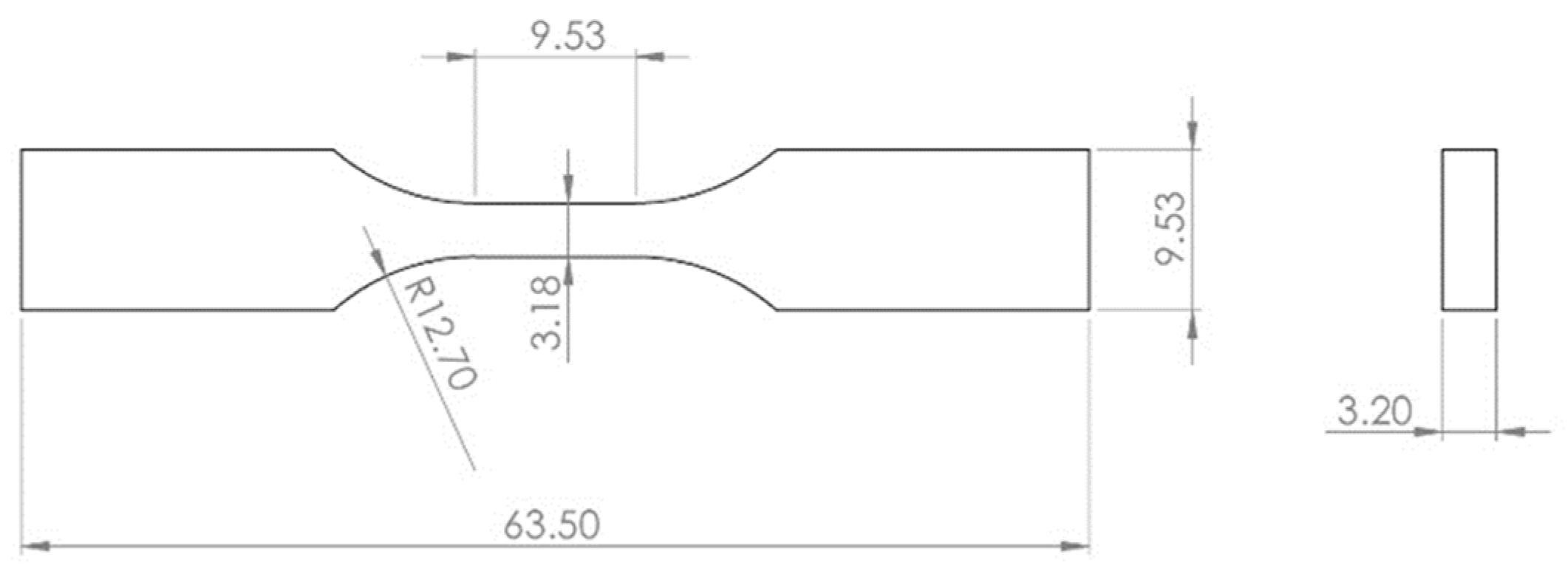
2.1. Test Specimens
2.2. Shore D Hardness Test
2.3. Tensile Test
2.4. Surface Roughness
3. Neural Networks Modeling
3.1. Tensile Strength and Yield Stress Modeling
3.2. Shore-D Hardness
3.3. Roughness Modelling
4. Optimization of ABS-like Photopolymer Printed Parts
5. Results and Discussion
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mukhtarkhanov, M.; Perveen, A.; Talamona, D. Application of Stereolithography Based 3D Printing Technology in Investment Casting. Micromachines 2020, 11, 946. [Google Scholar] [CrossRef] [PubMed]
- Salih, R.M.; Kadauw, A.; Zeidler, H.; Aliyev, R. Investigation of LCD 3D Printing of Carbon Fiber Composites by Utilising Central Composite Design. J. Manuf. Mater. Process. 2023, 7, 58. [Google Scholar] [CrossRef]
- Rojek, I.; Mikołajewski, D.; Dostatni, E.; Macko, M. AI-Optimized Technological Aspects of the Material Used in 3D Printing Processes for Selected Medical Applications. Materials 2020, 13, 5437. [Google Scholar] [CrossRef]
- Yadav, D.; Chhabra, D.; Garg, R.K.; Ahlawat, A. Optimization of FDM 3D printing process parameters for multi-material using artificial neural network. Mater. Today 2020, 21, 1583–1591. [Google Scholar] [CrossRef]
- Loy, J.; Novak, J.I.; Scerri, M. Developing transition research for disruptive technology: 3D printing innovation. In Advanced Perspectives on Global Industry Transitions and Business Opportunities; IGI Global: Hershey, PA, USA, 2021; Chapter 1. [Google Scholar] [CrossRef]
- Dzogbewu, T.C.; Amoah, N.; Fianko, S.K.; Afrifa, S.; De Beer, D. Additive manufacturing towards product production: A bibliometric analysis. Manuf. Rev. 2022, 9, 1–21. [Google Scholar] [CrossRef]
- Ukobitz, D.V.; Faullant, R. The relative impact of isomorphic pressures on the adoption of radical technology: Evidence from 3D printing. Technovation 2022, 113, 102418. [Google Scholar] [CrossRef]
- Bozkurt, Y.; Karayel, E. 3D printing technology; methods, biomedical applications, future opportunities and trends. J. Mater. Res. Technol. 2021, 14, 1430–1450. [Google Scholar] [CrossRef]
- Jandyal, A.; Chaturvedi, I.; Wazir, I.; Raina, A. 3D printing—A review of processes, materials and applications in industry 4.0. Sustain. Oper. 2022, 3, 33–42. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. Part B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Chen, C.T.; Gu, G.X. Generative Deep Neural Networks for Inverse Materials Design Using Backpropagation and Active Learning. Adv. Sci. 2020, 7, 1902607. [Google Scholar] [CrossRef]
- Hopkins, M.; Gunbay, S.; Hayes, C.; Moritz, V.F.; Fuenmayor, E.; Lyons, J.G.; Devine, D.M. Stereolithography SLA utilised to print injection mould tooling in order to evaluate thermal and mechanical properties of commercial polypropylene. Procedia Manuf. 2021, 55, 205–212. [Google Scholar] [CrossRef]
- Zhou, L.; Miller, J.; Vezza, J.; Mayster, M.; Raffay, M.; Justice, Q.; Al Tamimi, Z.; Hansotte, G.; Sunkara, L.D.; Bernat, J. Additive Manufacturing: A Comprehensive Review. Sensors 2024, 24, 2668. [Google Scholar] [CrossRef]
- Miller, Z.; Stidham, B.; Fairbanks, T.; Maldonado, C. The Use of Stereolithography (SLA) Additive Manufacturing in Space-Based Instrumentation. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Chohan, J.S.; Mittal, N.; Kumar, R.; Singh, S.; Sharma, S.; Singh, J.; Rao, K.V.; Mia, M.; Pimenov, D.Y.; Dwivedi, S.P. Mechanical Strength Enhancement of 3D Printed Acrylonitrile Butadiene Styrene Polymer Components Using Neural Network Optimization Algorithm. Polymers 2020, 12, 2250. [Google Scholar] [CrossRef]
- Zeng, Y.-S.; Hsueh, M.-H.; Hsiao, T.-C. Effect of ultraviolet post-curing, laser power, and layer thickness on the mechanical properties of acrylate used in stereolithography 3D printing. Mater. Res. Express 2023, 10, 025303. [Google Scholar] [CrossRef]
- Kazemi, M.; Rahimi, A. Stereolithography process optimization for tensile strength improvement of products. Rapid Prototyp. J. 2018, 24, 688–697. [Google Scholar] [CrossRef]
- Li, Y.; Teng, Z. Effect of printing orientation on mechanical properties of SLA 3D-printed photopolymer. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 1531–1545. [Google Scholar] [CrossRef]
- Wang, E.; Yang, F.; Shen, X.; Li, Z.; Yang, X.; Zhang, X.; Peng, W. Investigation and Optimization of the Impact of Printing Orientation on Mechanical Properties of Resin Sample in the Low-Force Stereolithography Additive Manufacturing. Materials 2022, 15, 6743. [Google Scholar] [CrossRef] [PubMed]
- Ciccone, F.; Bacciaglia, A.; Ceruti, A. Optimization with artificial intelligence in additive manufacturing: A systematic review. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 303. [Google Scholar] [CrossRef]
- Bolat, Ç.; Cebi, A.; Çoban, S.; Ergene, B. Estimation of friction and wear properties of additively manufactured recycled-ABS parts using artificial neural network approach: Effects of layer thickness, infill rate, and building direction. Int. Polym. Process. 2024, 39, 293–307. [Google Scholar] [CrossRef]
- Marković, M.-P.; Cingesar, I.K.; Vrsaljko, D. Maximizing Mechanical Performance of 3D Printed Parts Through Process Parameter Optimization. 3D Print. Addit. Manuf. 2023, 11, e2062–e2074. [Google Scholar] [CrossRef]
- Palacio, A.; Baniasadi, M.; Kardel, K. Investigating Mechanical Properties of Fabricated Carbon-Fiber-Reinforced Composites via LCD Additive Manufacturing. Polymers 2023, 15, 4556. [Google Scholar] [CrossRef]
- Castañares, M.; Antonio, J.; Rodriguez, T. Manufacturing Parameters Characterisation of a 3D Printer. Bachelor’s Thesis, Escola d’Enginyeria de Barcelona Est (EEBE), Barcelona, Spain, 2017. [Google Scholar]
- Hosford, W.F. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2005; Chapter 3; pp. 39–52. [Google Scholar] [CrossRef]
- Schmidleithner, C.; Kalaskar, D.M. Stereolithography. In 3D Printing; InTech: London, UK, 2018. [Google Scholar] [CrossRef]
- Hu, G.; Cao, Z.; Hopkins, M.; Hayes, C.; Daly, M.; Zhou, H.; Devine, D.M. Optimizing the hardness of SLA printed objects by using the neural network and genetic algorithm. Procedia Manuf. 2019, 38, 117–124. [Google Scholar] [CrossRef]
- Pérez, P.; Trier, A.; Reyes, J. Prediction of PM2.5 concentrations several hours in advance using neural networks in Santiago, Chile. Atmos. Environ. 2000, 34, 1189–1196. [Google Scholar] [CrossRef]
- Mahmood, M.A.; Visan, A.I.; Ristoscu, C.; Mihailescu, I.N. Artificial Neural Network Algorithms for 3D Printing. Materials 2021, 14, 163. [Google Scholar] [CrossRef]
- Zhang, Y.; Tiňo, P.; Leonardis, A. A survey on neural network interpretability. IEEE Trans. Emerg. 2021, 5, 726–742. [Google Scholar] [CrossRef]
- Agron, D.J.; Nwakanma, C.I.; Lee, J.; Kim, D. Smart Monitoring for SLA-type 3D Printer using Artificial Neural Network. 2020. Available online: https://api.semanticscholar.org/CorpusID:221147445 (accessed on 1 January 2020).
- Khammas, A.; AL-Khafaji, M. Neural Network Modeling of Oxidation Kinetics in Air of Steel T21 Alloy Coated by Simultaneous Germanium-Doped Aluminizing-Siliconzing Process. Eng. Technol. 2013, 31, 632–645. [Google Scholar]
- AL-Khafaji, M.M.; Alwan, H.L.; Albaghdadi, B.M. Roughness Assessment for Machined Surfaces in Turning Operation Using Neural Network. Eng. Technol. 2014, 32 Pt A, 1331–1344. [Google Scholar]
- Dabrowski, J.J.; Zhang, Y.F.; Rahman, A. ForecastNet: A time-variant deep feed-forward neural network architecture for multi-step-ahead time-series forecasting. In Neural Information Processing: 27th International Conference, ICONIP 2020, Bangkok, Thailand, 23–27 November 2020, Proceedings, Part III 27; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Sharkawy, A.N. Principle of neural network and its main types. J. Adv. Appl. Comput. Math. 2020, 7, 8–19. [Google Scholar] [CrossRef]




| No of Levels | Levels Value | |
|---|---|---|
| Orientation | 2 | Edge and Flat |
| Lifting speed | 3 | 70, 100, and 130 mm/h |
| Lifting distance | 3 | 4, 5, and 6 mm |
| Exposure time | 3 | 3, 5, and 7 s |
| Run Order | Orientation | Lifting Speed mm/h | Lifting Distance mm | Exposure Time s | Run Order | Orientation | Lifting Speed mm/h | Lifting Distance mm | Exposure Time s |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Edge | 100 | 6 | 7 | 28 | Flat | 100 | 4 | 3 |
| 2 | Flat | 100 | 5 | 5 | 29 | Edge | 100 | 4 | 7 |
| 3 | Edge | 100 | 6 | 5 | 30 | Flat | 130 | 5 | 5 |
| 4 | Flat | 100 | 6 | 3 | 31 | Flat | 70 | 6 | 7 |
| 5 | Edge | 130 | 5 | 7 | 32 | Flat | 100 | 6 | 5 |
| 6 | Flat | 130 | 6 | 5 | 33 | Edge | 70 | 5 | 5 |
| 7 | Flat | 70 | 5 | 3 | 34 | Flat | 70 | 4 | 3 |
| 8 | Flat | 70 | 4 | 5 | 35 | Edge | 130 | 5 | 5 |
| 9 | Edge | 70 | 5 | 3 | 36 | Flat | 100 | 5 | 7 |
| 10 | Edge | 130 | 6 | 7 | 37 | Flat | 130 | 4 | 5 |
| 11 | Edge | 70 | 6 | 7 | 38 | Edge | 100 | 4 | 5 |
| 12 | Edge | 130 | 6 | 5 | 39 | Edge | 100 | 4 | 3 |
| 13 | Flat | 100 | 4 | 5 | 40 | Edge | 70 | 6 | 5 |
| 14 | Flat | 70 | 4 | 7 | 41 | Flat | 130 | 5 | 7 |
| 15 | Flat | 70 | 6 | 5 | 42 | Edge | 70 | 4 | 7 |
| 16 | Flat | 130 | 4 | 7 | 43 | Edge | 130 | 4 | 3 |
| 17 | Edge | 70 | 4 | 5 | 44 | Edge | 130 | 5 | 3 |
| 18 | Edge | 130 | 6 | 3 | 45 | Flat | 130 | 5 | 3 |
| 19 | Edge | 70 | 4 | 3 | 46 | Edge | 70 | 6 | 3 |
| 20 | Flat | 130 | 6 | 3 | 47 | Edge | 70 | 5 | 7 |
| 21 | Flat | 100 | 5 | 3 | 48 | Flat | 130 | 4 | 3 |
| 22 | Flat | 70 | 5 | 5 | 49 | Edge | 100 | 5 | 5 |
| 23 | Edge | 130 | 4 | 5 | 50 | Edge | 100 | 5 | 3 |
| 24 | Flat | 70 | 5 | 7 | 51 | Flat | 70 | 6 | 3 |
| 25 | Flat | 130 | 6 | 7 | 52 | Flat | 100 | 4 | 7 |
| 26 | Edge | 100 | 6 | 3 | 53 | Edge | 130 | 4 | 7 |
| 27 | Flat | 100 | 6 | 7 | 54 | Edge | 100 | 5 | 7 |
| RunOrder | Tensile Test Results (Mpa) | Shore D HD | Ra μm | ||
|---|---|---|---|---|---|
| Max Stress | Yield Stress | Young Modulus | |||
| 1 | 30.760 | 19.118 | 349.194 | 76.333 | 1.195 |
| 2 | 29.137 | 26.591 | 278.470 | 75.667 | 0.677 |
| 3 | 31.618 | 20.711 | 135.568 | 67.667 | 1.013 |
| 4 | 21.053 | 18.027 | 234.751 | 75.583 | 0.215 |
| 5 | 28.154 | 15.654 | 326.249 | 74.583 | 1.435 |
| 6 | 29.394 | 21.625 | 328.434 | 74.917 | 0.665 |
| 7 | 24.380 | 18.595 | 293.159 | 74.583 | 0.081 |
| 8 | 27.793 | 22.207 | 335.891 | 79.500 | 0.078 |
| 9 | 30.247 | 24.432 | 316.107 | 64.083 | 1.585 |
| 10 | 30.325 | 1.232 | 304.325 | 70.167 | 1.285 |
| 11 | 36.698 | 24.254 | 428.677 | 75.833 | 1.289 |
| 12 | 30.223 | 13.393 | 429.108 | 69.083 | 1.485 |
| 13 | 30.369 | 23.256 | 367.418 | 84.083 | 0.067 |
| 14 | 30.528 | 21.826 | 351.453 | 84.000 | 0.613 |
| 15 | 24.100 | 21.308 | 314.815 | 78.667 | 0.684 |
| 16 | 28.056 | 21.051 | 366.289 | 82.667 | 0.077 |
| 17 | 29.148 | 20.299 | 390.395 | 67.333 | 0.772 |
| 18 | 20.119 | 15.619 | 227.371 | 66.250 | 1.386 |
| 19 | 6.031 | 4.951 | 68.796 | 66.417 | 1.481 |
| 20 | 23.029 | 19.260 | 274.188 | 80.750 | 0.101 |
| 21 | 29.913 | 17.533 | 340.266 | 80.833 | 0.579 |
| 22 | 30.417 | 23.541 | 349.021 | 82.083 | 0.671 |
| 23 | 26.582 | 20.200 | 318.094 | 78.083 | 1.466 |
| 24 | 29.878 | 22.016 | 391.153 | 81.250 | 0.601 |
| 25 | 26.804 | 21.031 | 352.556 | 83.333 | 0.065 |
| 26 | 21.169 | 15.846 | 236.090 | 67.917 | 1.105 |
| 27 | 28.982 | 22.420 | 371.249 | 81.583 | 0.056 |
| 28 | 19.228 | 16.180 | 244.032 | 80.583 | 0.721 |
| 29 | 24.265 | 15.607 | 293.110 | 77.917 | 1.494 |
| 30 | 24.791 | 21.459 | 274.197 | 81.833 | 0.098 |
| 31 | 30.014 | 23.186 | 346.043 | 82.500 | 0.641 |
| 32 | 24.860 | 20.950 | 346.128 | 80.333 | 0.113 |
| 33 | 28.787 | 12.375 | 379.223 | 77.083 | 1.182 |
| 34 | 25.868 | 18.838 | 347.764 | 81.583 | 0.652 |
| 35 | 28.681 | 21.692 | 327.757 | 77.917 | 1.267 |
| 36 | 33.749 | 21.454 | 434.659 | 81.417 | 0.223 |
| 37 | 40.947 | 34.958 | 495.827 | 82.417 | 0.092 |
| 38 | 37.529 | 19.451 | 485.563 | 72.500 | 1.158 |
| 39 | 34.406 | 19.698 | 428.315 | 66.750 | 0.904 |
| 40 | 36.269 | 18.653 | 495.339 | 77.333 | 1.307 |
| 41 | 40.398 | 21.053 | 488.564 | 81.000 | 0.786 |
| 42 | 44.279 | 18.905 | 597.916 | 78.500 | 1.704 |
| 43 | 34.652 | 20.737 | 481.976 | 78.833 | 1.185 |
| 44 | 33.265 | 0.204 | 390.274 | 76.250 | 0.944 |
| 45 | 31.863 | 10.755 | 463.426 | 77.583 | 0.843 |
| 46 | 30.374 | 23.594 | 330.477 | 65.917 | 0.960 |
| 47 | 39.503 | 18.396 | 489.172 | 70.917 | 1.514 |
| 48 | 34.894 | 18.621 | 404.614 | 77.250 | 0.104 |
| 49 | 39.241 | 23.070 | 456.214 | 64.083 | 1.256 |
| 50 | 33.401 | 22.539 | 349.113 | 71.333 | 0.415 |
| 51 | 30.980 | 22.261 | 327.935 | 78.417 | 0.601 |
| 52 | 41.825 | 23.860 | 466.392 | 74.833 | 0.181 |
| 53 | 45.006 | 20.457 | 505.391 | 77.417 | 1.404 |
| 54 | 45.288 | 21.542 | 532.454 | 68.250 | 1.215 |
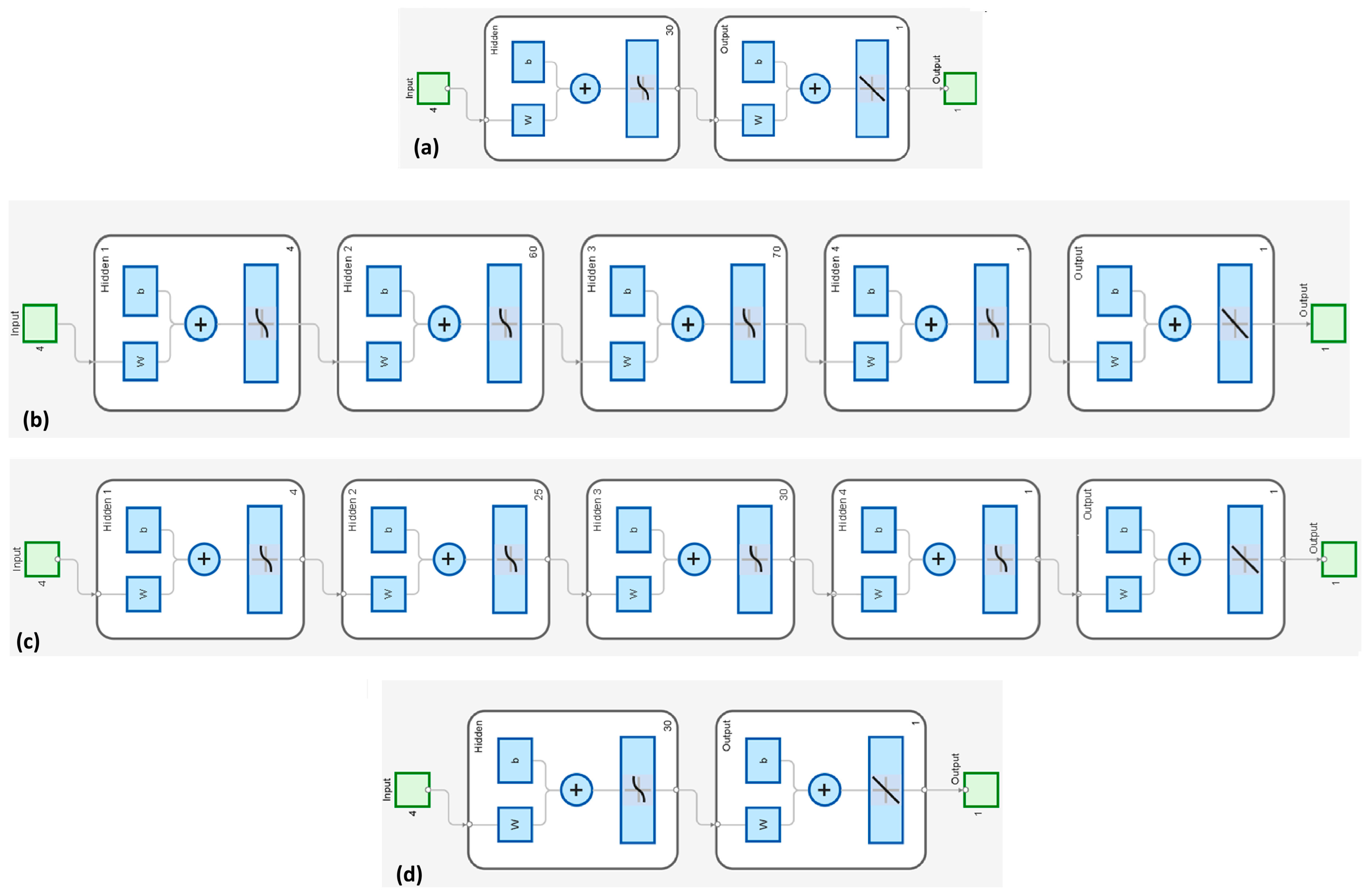
| Layer No. | Layer Size (Neurons) | Layer Transfer Function (Activation Function) |
|---|---|---|
| 1 | 4 | tansig |
| 2 | 60 | tansig |
| 3 | 70 | tansig |
| 4 | 1 | tansig |
| 5 | 1 | purelin |
| Layer No. | Layer Size (Neurons) | Layer Transfer Function (Activation Function) |
|---|---|---|
| 1 | 4 | tansig |
| 2 | 25 | tansig |
| 3 | 30 | tansig |
| 4 | 1 | tansig |
| 5 | 1 | purelin |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadauw, A.A.A. Neural Network Optimization of Mechanical Properties of ABS-like Photopolymer Utilizing Stereolithography (SLA) 3D Printing. J. Manuf. Mater. Process. 2025, 9, 116. https://doi.org/10.3390/jmmp9040116
Kadauw AAA. Neural Network Optimization of Mechanical Properties of ABS-like Photopolymer Utilizing Stereolithography (SLA) 3D Printing. Journal of Manufacturing and Materials Processing. 2025; 9(4):116. https://doi.org/10.3390/jmmp9040116
Chicago/Turabian StyleKadauw, Abdulkader Ali Abdulkader. 2025. "Neural Network Optimization of Mechanical Properties of ABS-like Photopolymer Utilizing Stereolithography (SLA) 3D Printing" Journal of Manufacturing and Materials Processing 9, no. 4: 116. https://doi.org/10.3390/jmmp9040116
APA StyleKadauw, A. A. A. (2025). Neural Network Optimization of Mechanical Properties of ABS-like Photopolymer Utilizing Stereolithography (SLA) 3D Printing. Journal of Manufacturing and Materials Processing, 9(4), 116. https://doi.org/10.3390/jmmp9040116








