Design and Manufacture of a Flexible Adaptive Fixture for Precision Grinding of Thin-Walled Bearing Rings
Abstract
1. Introduction
2. Adaptive Flexible Fixture Design
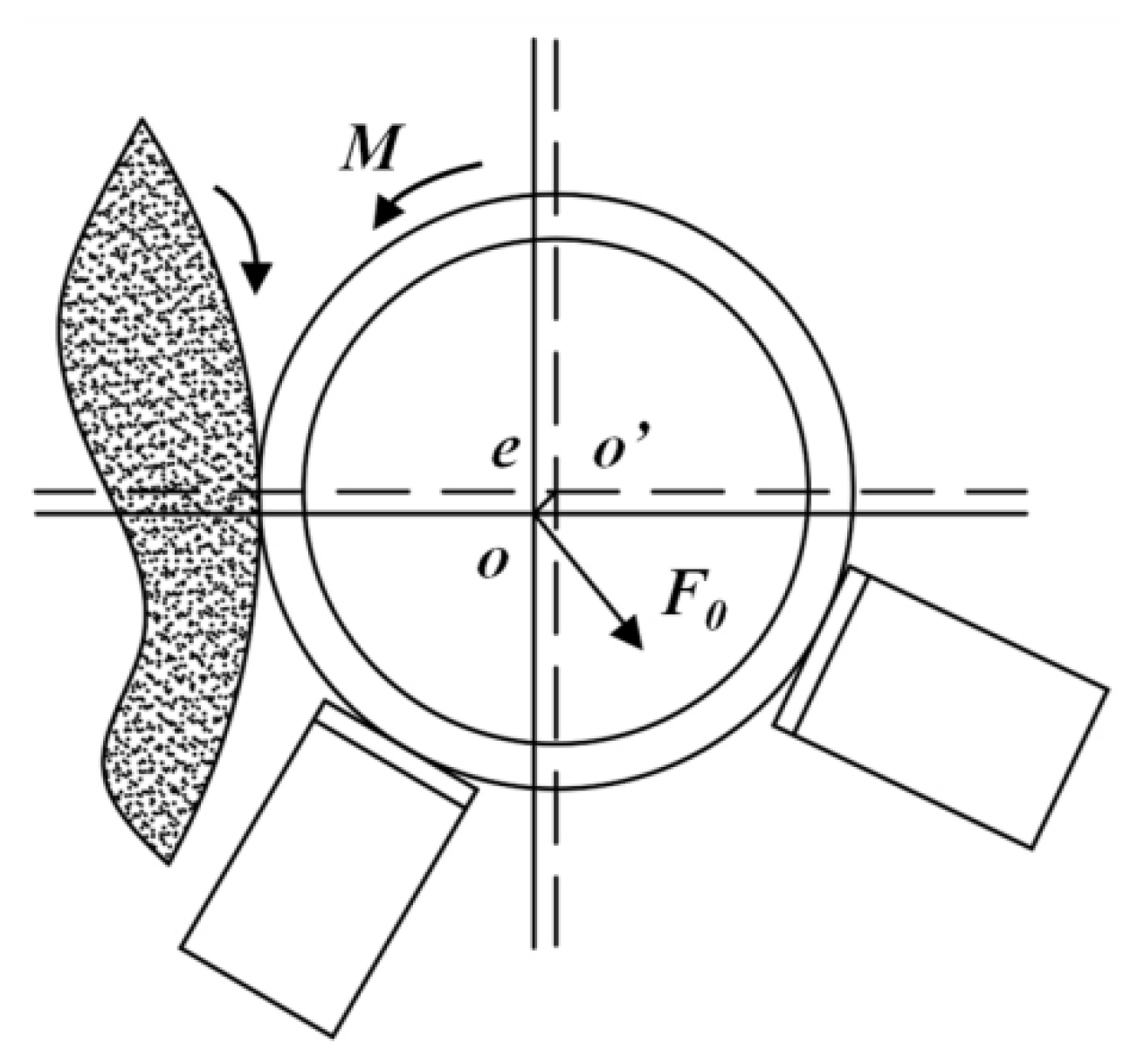
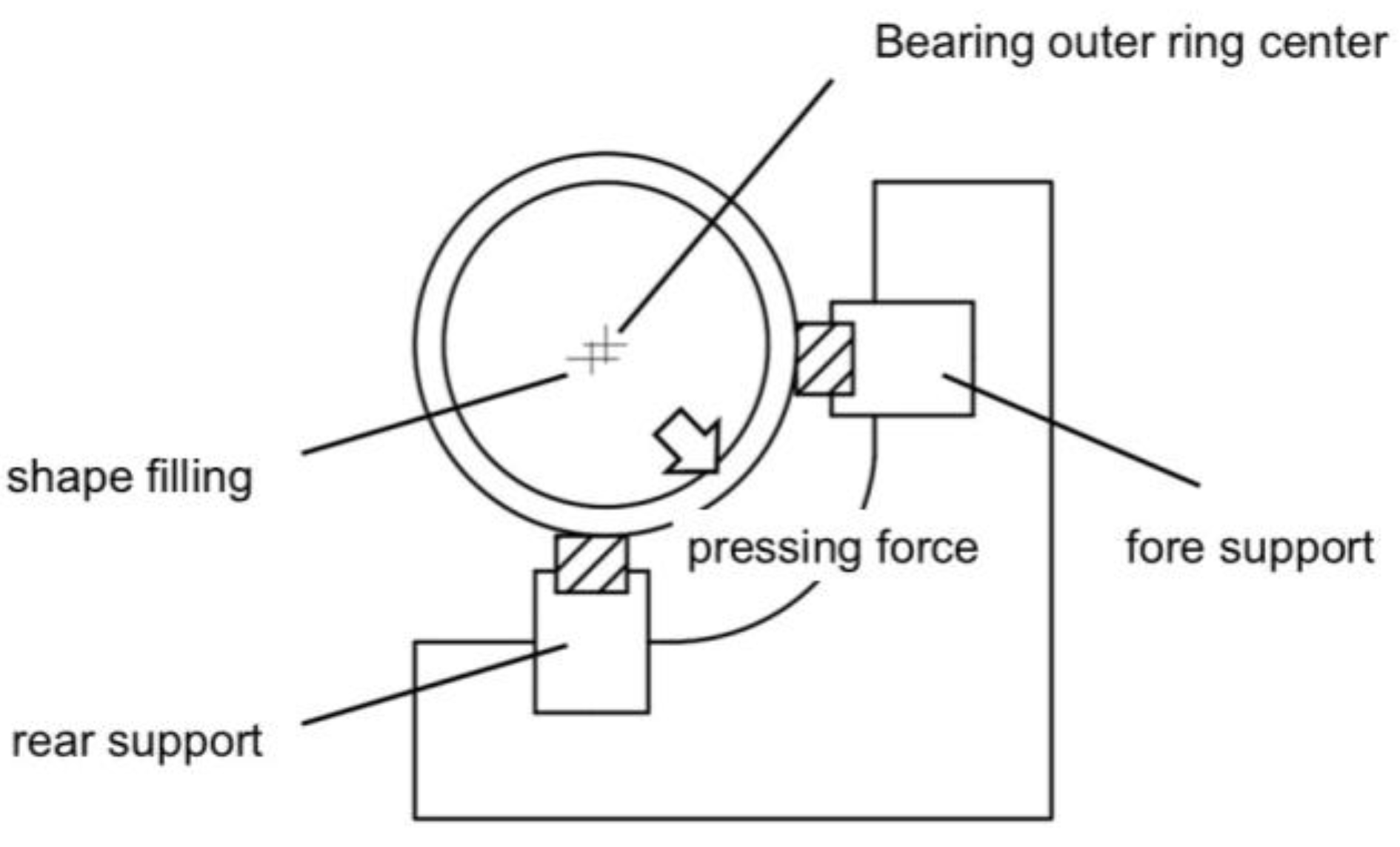
2.1. Grinding Fixture Principle and Defect Analysis
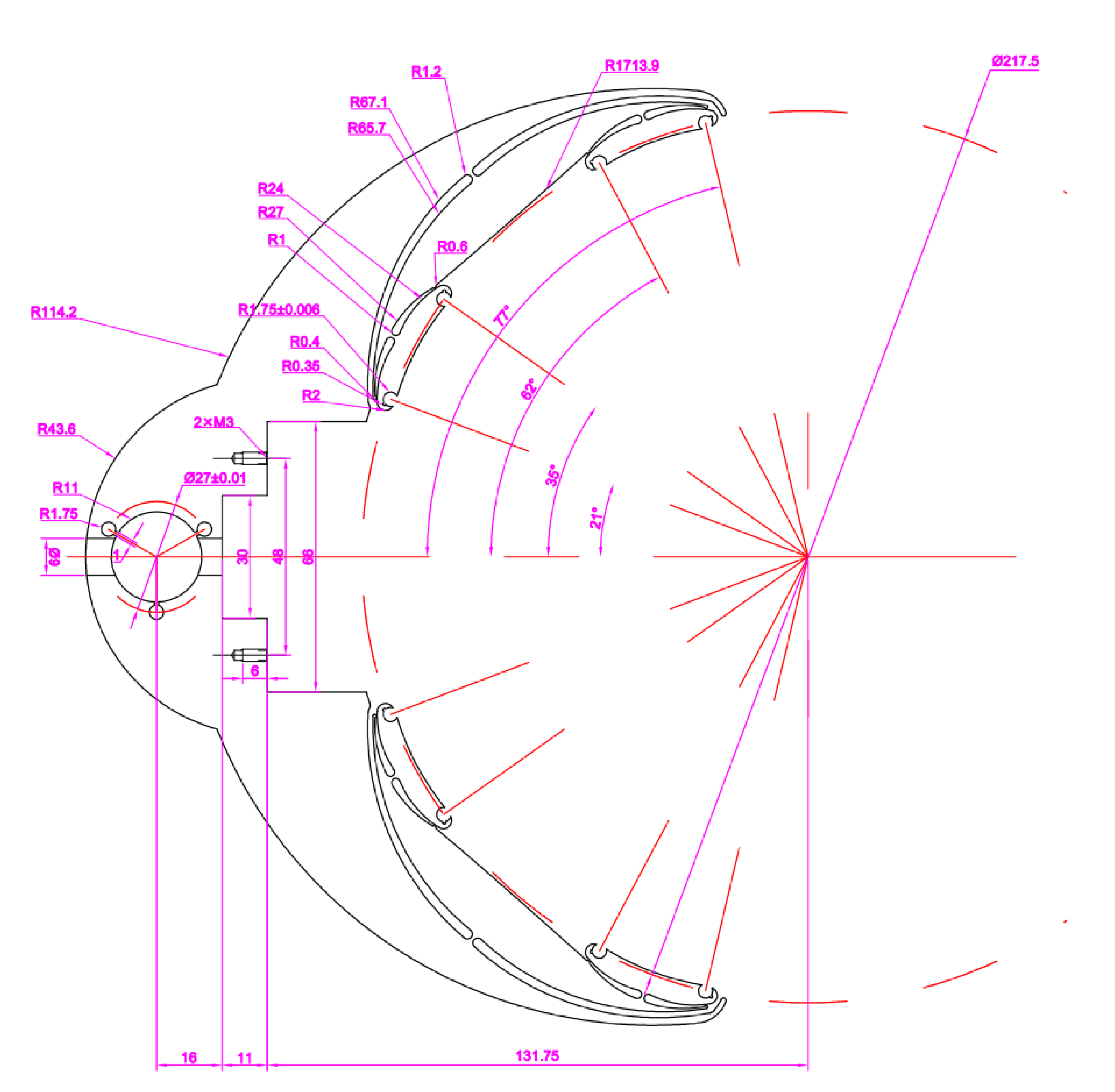
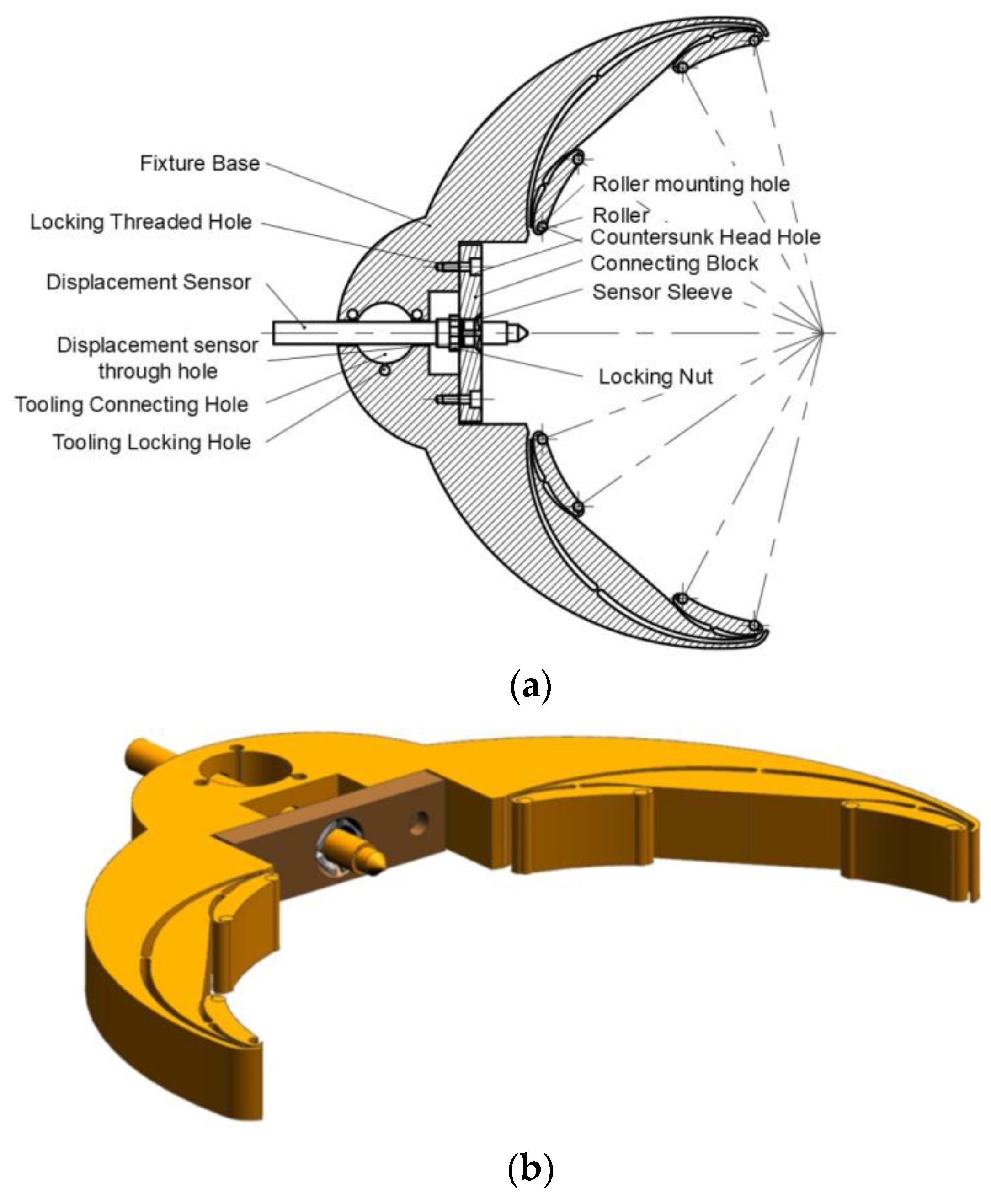
2.2. Adaptive Flexible Grinding Fixture Design
3. Modal and Stress Displacement Simulation of Adaptive Flexible Fixtures
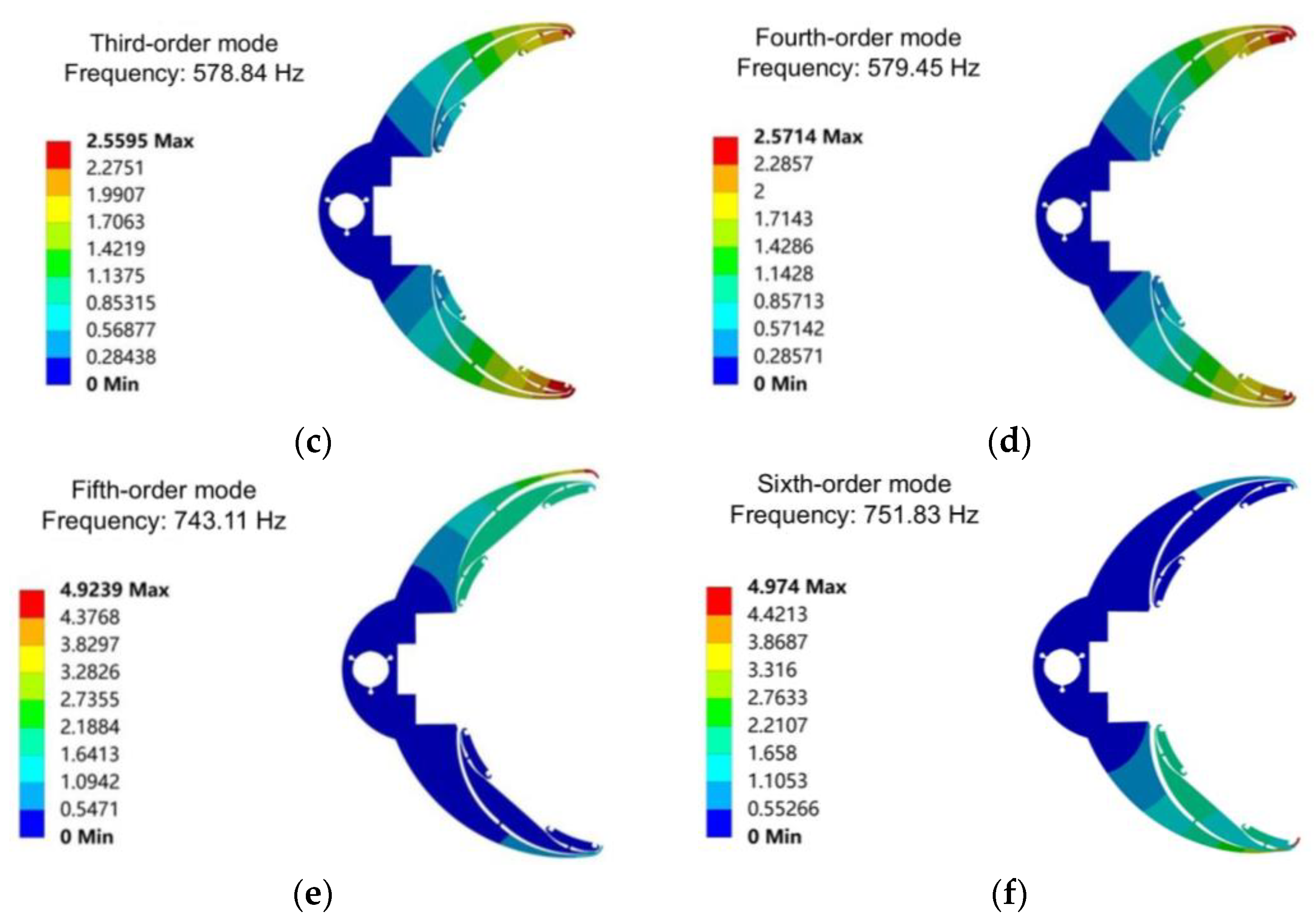
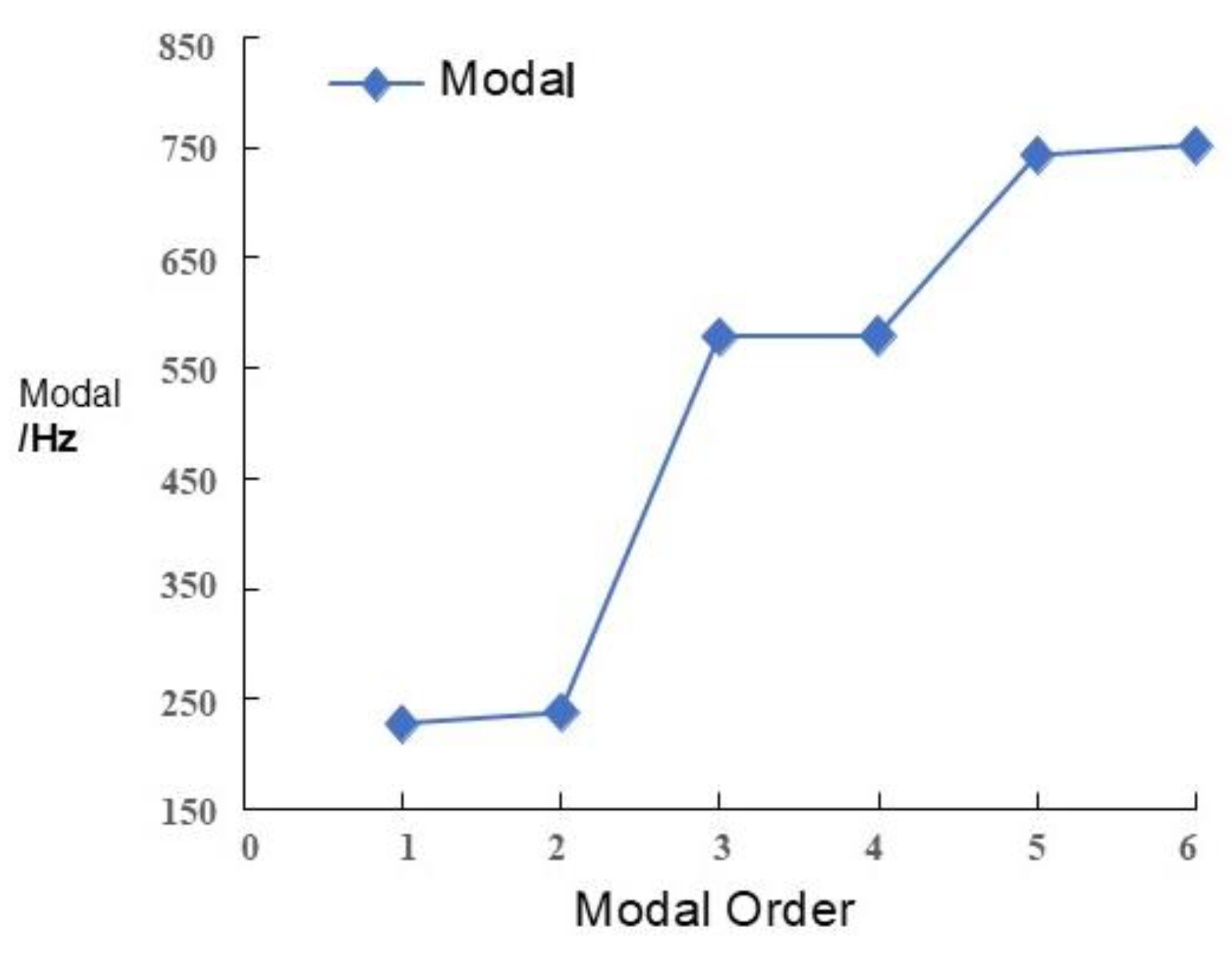
3.1. Modal Analysis
3.2. Stress-Displacement Analysis
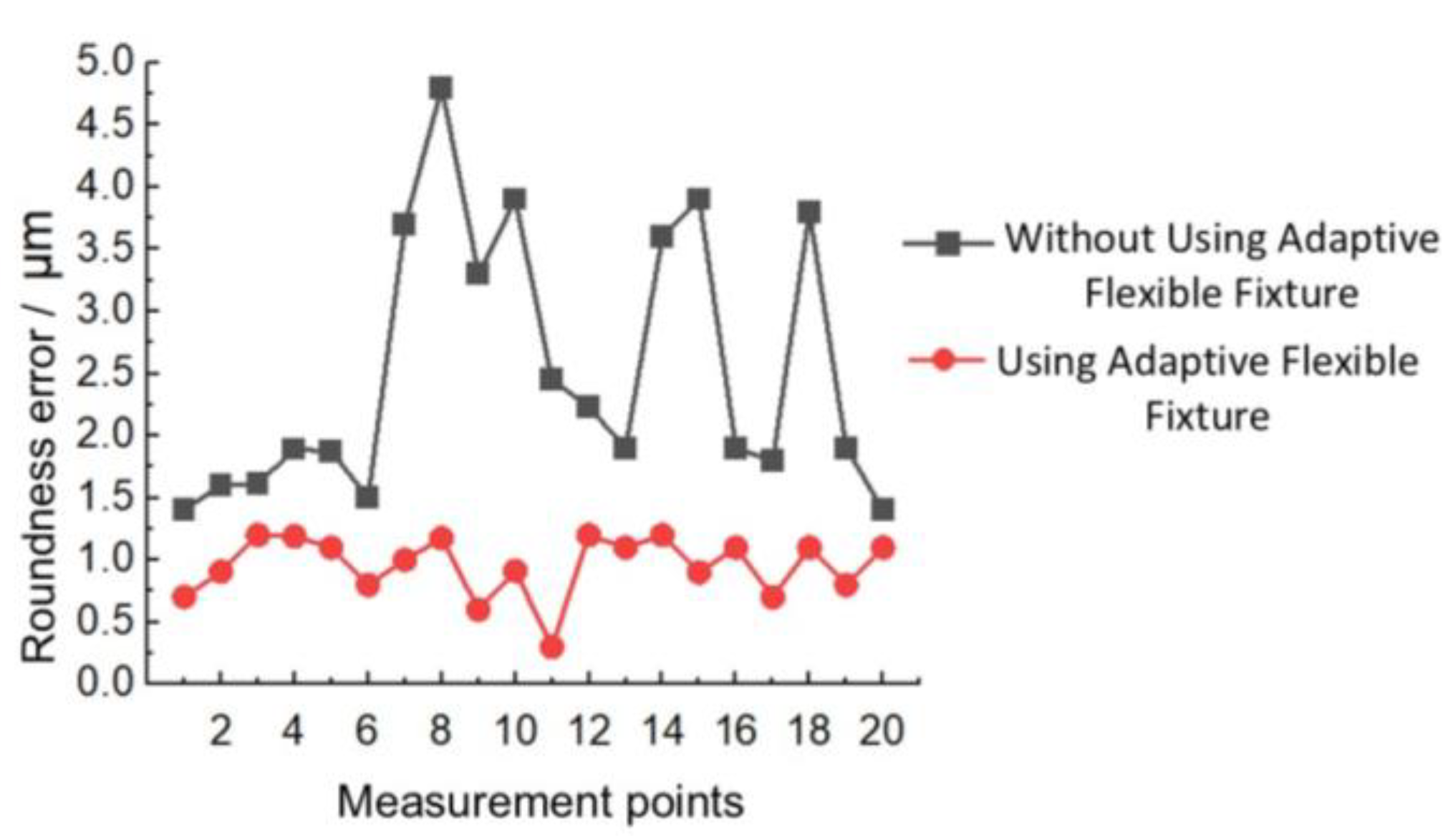
4. Adaptive Flexible Fixture Manufacturing and Roundness Error Analysis in Grinding Machining
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Song, H.; Gao, H.; Wu, Q.; Zhang, Y. Effects of segmented thermal-vibration stress relief process on residual stresses, mechanical properties and microstructures of large 2219 Al alloy rings. J. Alloys Compd. 2021, 886, 161269. [Google Scholar] [CrossRef]
- Gašpar, T.; Kovač, I.; Ude, A. Optimal layout and reconfiguration of a fixturing system constructed from passive Stewart platforms. J. Manuf. Syst. 2021, 60, 226–238. [Google Scholar] [CrossRef]
- Krishnakumar, K.; Melkote, S.N. Machining fixture layout optimization using the genetic algorithm. Int. J. Mach. Tools Manuf. 2000, 40, 579–598. [Google Scholar] [CrossRef]
- Liu, H.; Wang, C.; Li, T.; Bo, Q.; Liu, K.; Wang, Y. Fixturing technology and system for thin-walled parts machining: A review. Front. Mech. Eng. 2023, 17, 55. [Google Scholar] [CrossRef]
- Gonzalo, O.; Seara, J.M.; Gurudeva, E.; Izpizua, A.; Esparta, M.; Zamakona, I.; Uterga, N.; Aranburu, A.; Thoelen, J. A method to minimize the workpiece deformation using a concept of intelligent fixture. Robot. Comput.-Integr. Manuf. 2017, 48, 209–218. [Google Scholar] [CrossRef]
- Wu, N.; Chan, K.C.; Leong, S. Static interactions of surface contacts in a fixture–workpiece system. J. Comput. Appl. Technol. 2014, 10, 133–151. [Google Scholar]
- Patalas, A.; Regus, M.; Peta, K. Studies of thin-walled parts deformation by gripping force during turning process on an example of bearing ring. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 244, p. 02010. [Google Scholar] [CrossRef]
- Chen, B.; Zha, J.; Cai, Z.; Wu, M. Predictive modelling of surface roughness in precision grinding based on hybrid algorithm. CIRP J. Manuf. Sci. Technol. 2025, 59, 1–17. [Google Scholar] [CrossRef]
- Chai, S.; Ouyang, L.; Bi, Q.; Yu, J.; Zhang, Y. An adaptive fixture for suppress vibrations and measuring workpiece deformation of thin-walled casings. Procedia CIRP 2021, 101, 322–325. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Hao, X.; Gao, J.X.; Maropoulos, P.G. Responsive fixture design using dynamic product inspection and monitoring technologies for the precision machining of large-scale aerospace parts. CIRP Ann. 2015, 64, 173–176. [Google Scholar] [CrossRef]
- Hao, Q.; Yang, Q. A self-adaptive auxiliary fixture for deformation control in blade machining. Int. J. Adv. Manuf. Technol. 2020, 111, 1415–1423. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, F.; Zhang, J.; Huang, K.; Xu, Z.; Liu, X.; Ma, Y.; Feng, P.; Feng, F. An adaptive clamp system for deformation control of aerospace thin-walled parts. J. Manuf. Process. 2023, 107, 115–125. [Google Scholar] [CrossRef]
- Gandhi, M.V.; Thompson, B.S.; Maas, D.J. Adaptable Fixture Design: An Analytical Experimental Study of Fluidized-Bed Fixturing. J. Mech. Des. ASME Digit. Collect. 1986, 108, 15–21. [Google Scholar] [CrossRef]
- Wang, T.; Zha, J.; Jia, Q.; Chen, Y. Application of low-melting alloy in the fixture for machining aeronautical thin-walled component. Int. J. Adv. Manuf. Technol. 2016, 87, 2797–2807. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, Y.; Lu, W.; Gao, S.; Liu, L.; Liu, X. Characteristics of shear stress based on magnetorheological fluid flexible fixture during milling of the thin-walled part. Int. J. Adv. Manuf. Technol. 2020, 108, 2607–2619. [Google Scholar]
- Merlo, A.; Ricciardi, D.; Salvi, E.; Fantinati, D.; Iorio, E. Novel Adaptive Fixturing for Thin Walled Aerospace Parts. IOP Conf. Ser. Mater. Sci. Eng. 2011, 26, 012020. [Google Scholar] [CrossRef]
- Papastathis, T.N.; Ratchev, S.M.; Popov, A.A. Dynamics model of active fixturing systems for thin-walled parts under moving loads. Int. J. Adv. Manuf. Technol. 2012, 62, 1233–1247. [Google Scholar] [CrossRef]
- Bakker, O.J.; Popov, A.A.; Salvi, E.; Merlo, A.; Ratchev, S.M. Model-Based Control of An Active Fixture for Advanced Aerospace Components. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 35–51. [Google Scholar] [CrossRef]
- Kashyap, S.; DeVries, W.R. Finite element analysis and optimization in fixture design. Struct. Optim. 1999, 18, 193–201. [Google Scholar] [CrossRef]
- Ivanov, V.; Mital, D.; Karpus, V.; Dehtiarov, I.; Zajac, J.; Pavlenko, I.; Hatala, M. Numerical simulation of the system “fixture–workpiece” for lever machining. Int. J. Adv. Manuf. Technol. 2017, 91, 79–90. [Google Scholar] [CrossRef]
- Calabrese, M.; Primo, T.; Del Prete, A. Optimization of Machining Fixture for Aeronautical Thin-walled Components. Procedia CIRP 2017, 60, 32–37. [Google Scholar] [CrossRef]
- Andrews, A.; Abraham, P.; Rex, F.M.T. An Integrated Approach for Fixture Layout Design and Clamping Force Optimization. J. Sci. Ind. Res. 2022, 81, 1204–1216. [Google Scholar]
- Chen, C.; Zhang, P.; Xue, C. Test verification of emergency separation fuse pins for aircraft engines. J. Phys. Conf. Ser. 2022, 2368, 012036. [Google Scholar] [CrossRef]
- Hamedi, M. Optimizing workholding efficiency through fixture function simulation. Int. J. Prod. Res. 2005, 43, 2775–2788. [Google Scholar] [CrossRef]
- Kaya, N. Machining fixture locating and clamping position optimization using genetic algorithms. Comput. Ind. 2006, 57, 112–120. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Z.; Yang, Y.; Qing, S.; Liu, C.; Gao, F. Multi-objective optimization of fixture locating layout for sheet metal part using Kriging, M.O.B.A. Procedia CIRP 2022, 112, 418–423. [Google Scholar] [CrossRef]
- Sikström, F.; Ericsson, M.; Christiansson, A.K.; Niklasson, K. Tools for Simulation Based Fixture Design to Reduce Deformation in Advanced Fusion Welding. In Intelligent Robotics and Applications; Xiong, C., Liu, H., Huang, Y., Xiong, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 398–407. [Google Scholar]
- Yu, K.; Wang, X. Modeling and optimization of welding fixtures for a high-speed train aluminum alloy sidewall based on the response surface method. Int. J. Adv. Manuf. Technol. 2022, 119, 315–327. [Google Scholar] [CrossRef]
- Siebenaler, S.P.; Melkote, S.N. Prediction of workpiece deformation in a fixture system using the finite element method. Int. J. Mach. Tools Manuf. 2006, 46, 51–58. [Google Scholar] [CrossRef]
- Hashimoto, F.; Gallego, I.; Oliveira, J.F.G.; Barrenetxea, D.; Takahashi, M.; Sakakibara, K.; Stålfelt, H.-O.; Staadt, G.; Ogawa, K. Advances in centerless grinding technology. CIRP Ann. 2012, 61, 747–770. [Google Scholar] [CrossRef]
- Gaygol, S.; Wani, K. Modal analysis of plate to analyze the effect of mass stiffeners using the Chladni plate approach. Mater. Today Proc. 2023, 72, 1314–1321. [Google Scholar] [CrossRef]





| Material | Densities/ (g·cm−3) | Elastic Modulus/ (GPa) | Poisson’s Ratio | Temperature/ (°C) |
|---|---|---|---|---|
| stainless steel | 7.93 | 200 | 0.29 | 20 |
| Parts | Densities/ (g·cm−3) | Elastic Modulus/(GPa) | Poisson’s Ratio | Temperature/(°C) |
|---|---|---|---|---|
| Fixture (Stainless steel) | 7.93 | 200 | 0.29 | 20 |
| Rolling (Tungsten steel) | 15.63 | 530 | 0.31 | 20 |
| Workpiece (bearing steel) | 7.812 | 201 | 0.27 | 20 |
| Number | Grinding Force/N | Workpiece Speed/(rad·s−1) | Friction Coefficient |
|---|---|---|---|
| 1 | 5 | 1.05 | 0.01 |
| 2 | 5 | 2.09 | 0.02 |
| 3 | 5 | 3.14 | 0.03 |
| 4 | 10 | 1.05 | 0.02 |
| 5 | 10 | 2.09 | 0.03 |
| 6 | 10 | 3.14 | 0.01 |
| 7 | 15 | 1.05 | 0.03 |
| 8 | 15 | 2.09 | 0.01 |
| 9 | 15 | 3.14 | 0.02 |
| Number | Total Displacement/ μm | X-Direction Displacement/ μm | Stresses/ Mpa |
|---|---|---|---|
| 1 | 1.003 | 0.25437 | 0.20583 |
| 2 | 1.0027 | 0.2541 | 0.20587 |
| 3 | 1.0023 | 0.25364 | 0.20593 |
| 4 | 2.0061 | 0.50883 | 0.41165 |
| 5 | 2.0058 | 0.50856 | 0.41168 |
| 6 | 2.0054 | 0.5081 | 0.41174 |
| 7 | 3.0091 | 0.76329 | 0.61747 |
| 8 | 3.0089 | 0.76302 | 0.6175 |
| 9 | 3.0084 | 0.76256 | 0.61756 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; He, Y.; Zha, J.; Chen, B.; Shi, C.; Wu, M. Design and Manufacture of a Flexible Adaptive Fixture for Precision Grinding of Thin-Walled Bearing Rings. J. Manuf. Mater. Process. 2025, 9, 139. https://doi.org/10.3390/jmmp9050139
Shi Y, He Y, Zha J, Chen B, Shi C, Wu M. Design and Manufacture of a Flexible Adaptive Fixture for Precision Grinding of Thin-Walled Bearing Rings. Journal of Manufacturing and Materials Processing. 2025; 9(5):139. https://doi.org/10.3390/jmmp9050139
Chicago/Turabian StyleShi, Yao, Yu He, Jun Zha, Bohao Chen, Chaoyu Shi, and Ming Wu. 2025. "Design and Manufacture of a Flexible Adaptive Fixture for Precision Grinding of Thin-Walled Bearing Rings" Journal of Manufacturing and Materials Processing 9, no. 5: 139. https://doi.org/10.3390/jmmp9050139
APA StyleShi, Y., He, Y., Zha, J., Chen, B., Shi, C., & Wu, M. (2025). Design and Manufacture of a Flexible Adaptive Fixture for Precision Grinding of Thin-Walled Bearing Rings. Journal of Manufacturing and Materials Processing, 9(5), 139. https://doi.org/10.3390/jmmp9050139






