Comprehensive Composite Mould Filling Pattern Dataset for Process Modelling and Prediction
Abstract
1. Introduction
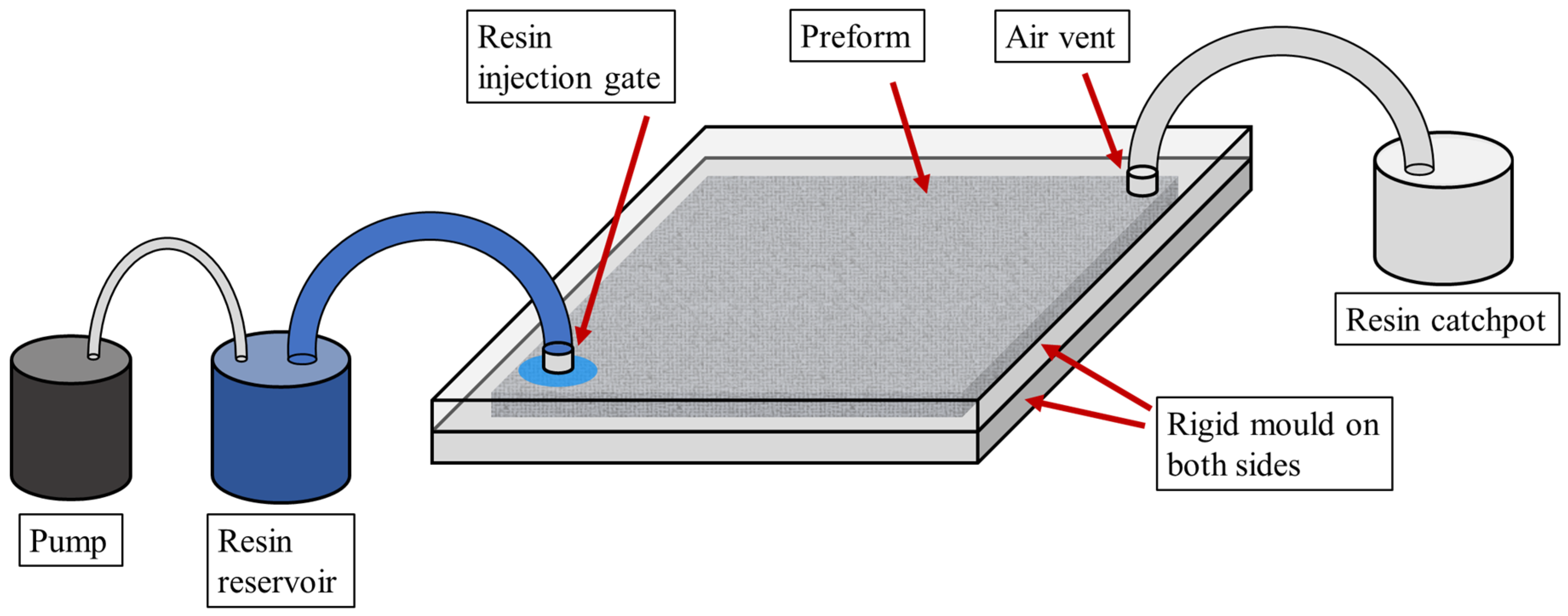
2. Problem Statement
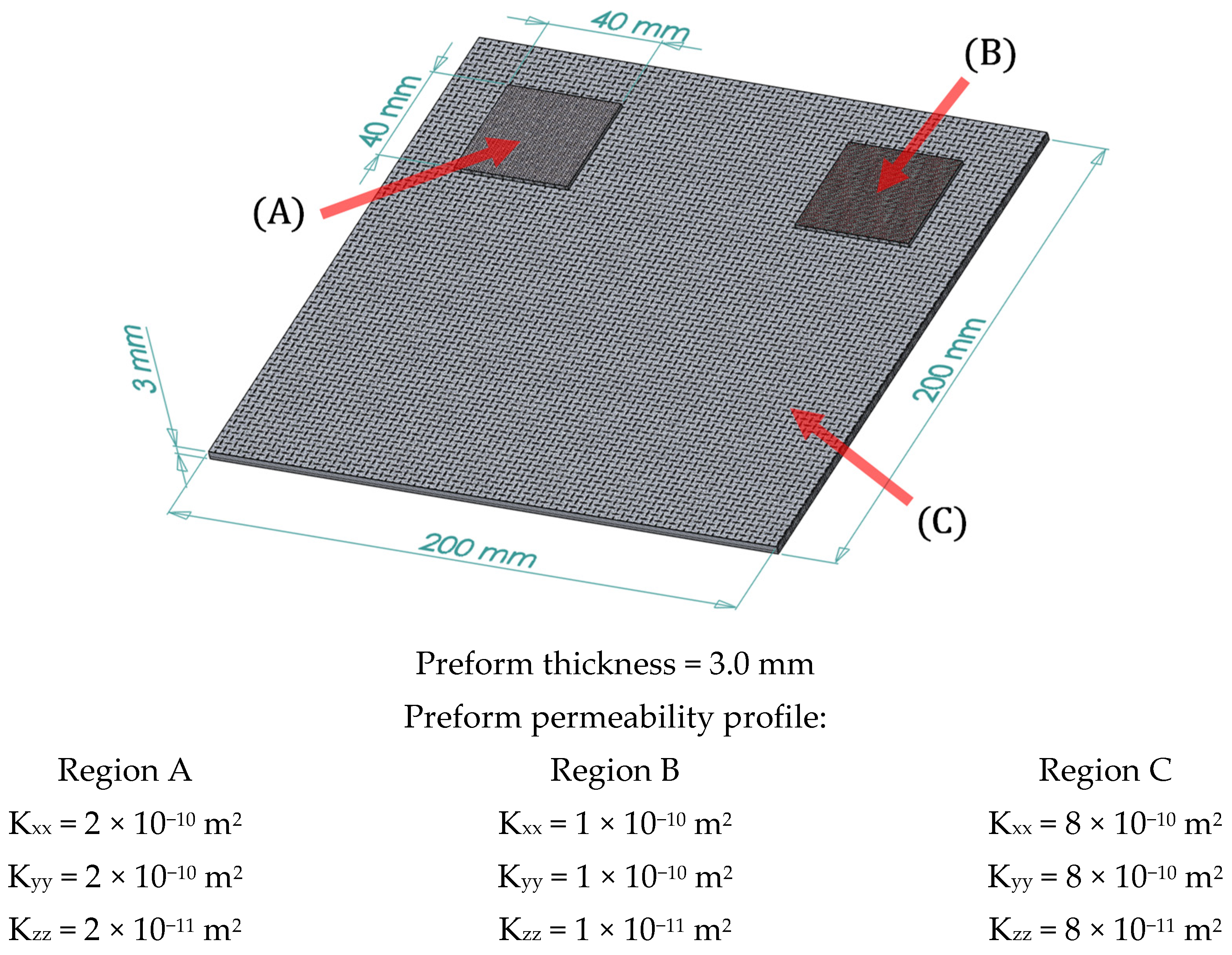
3. Problem Framework
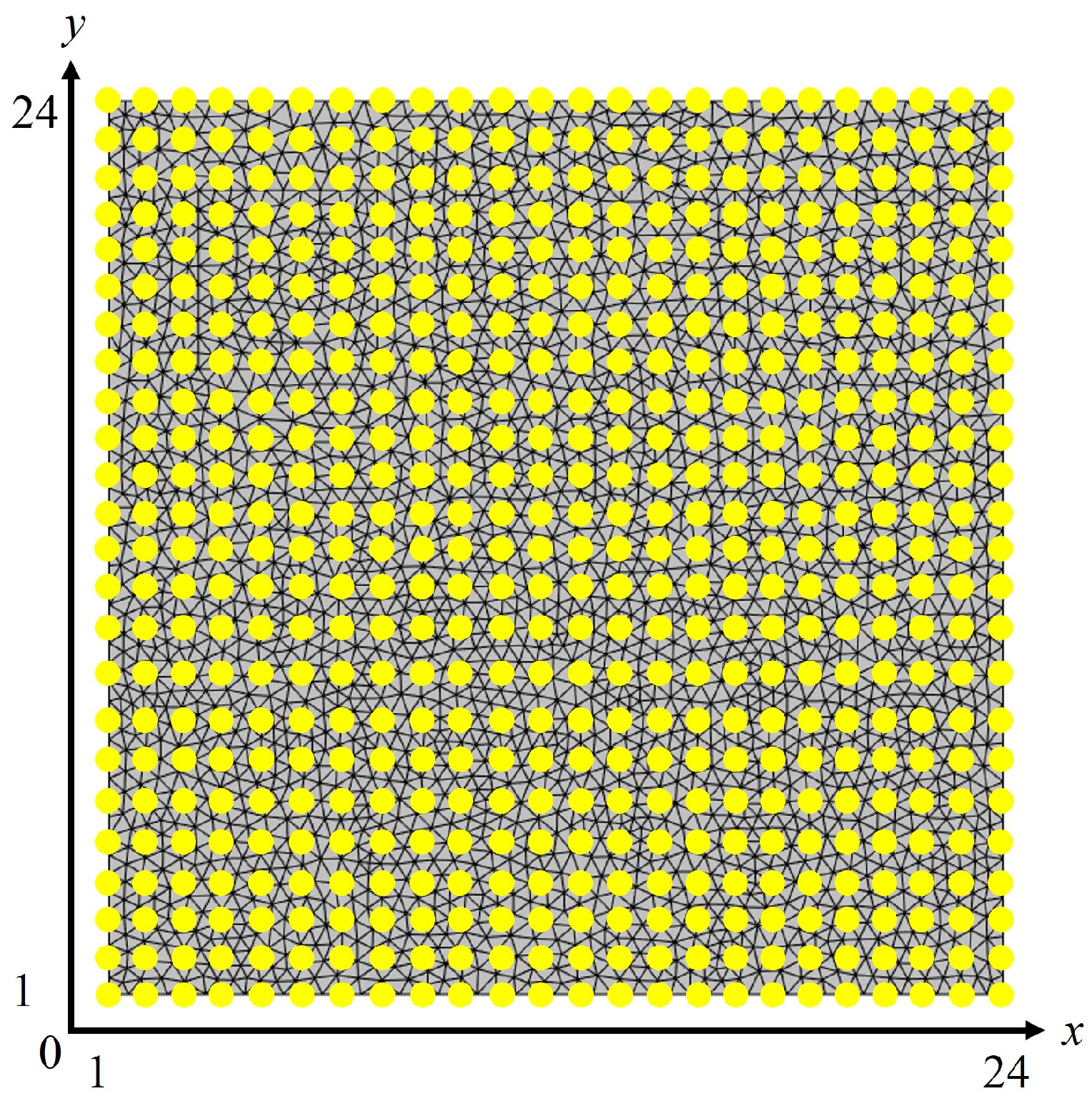
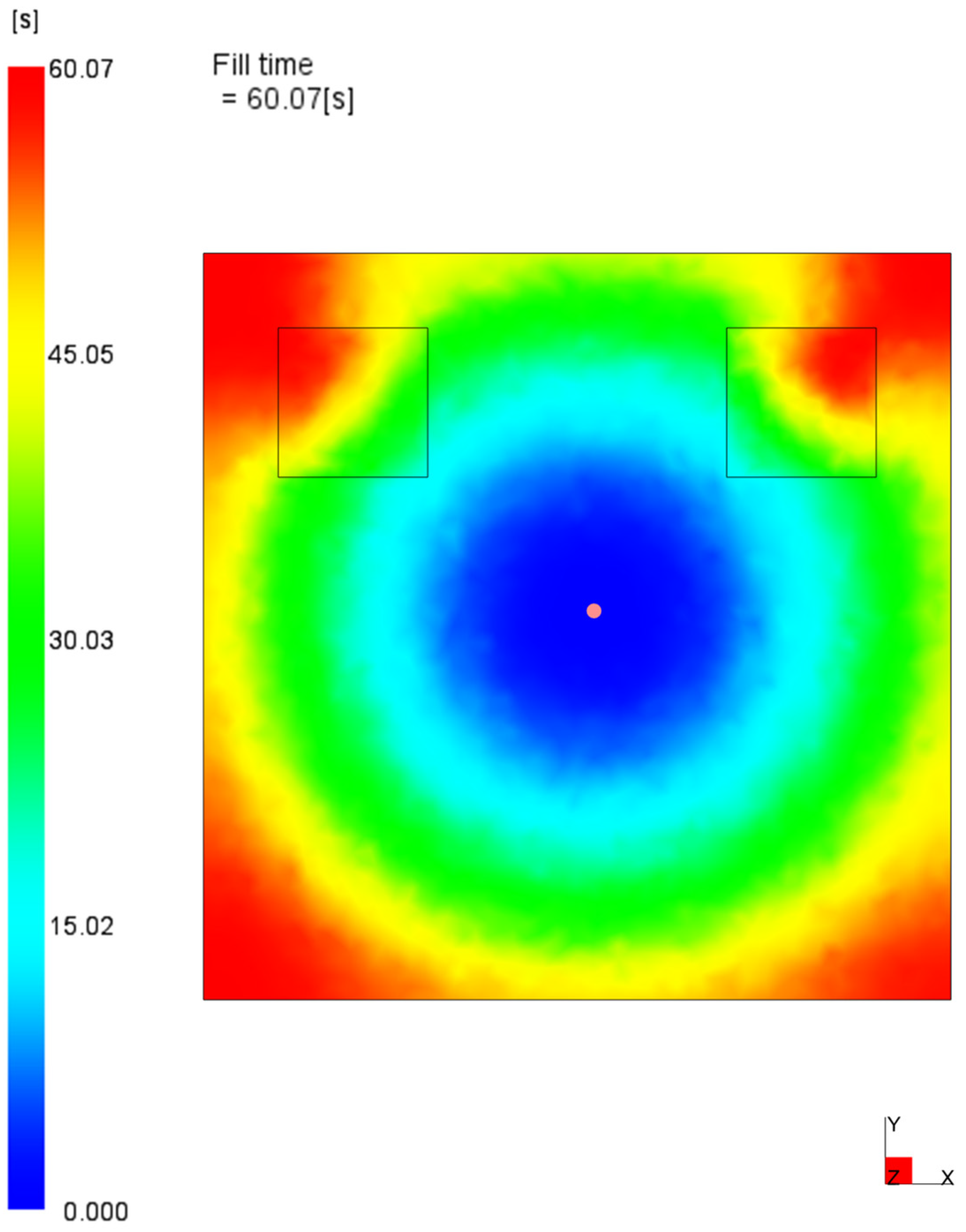
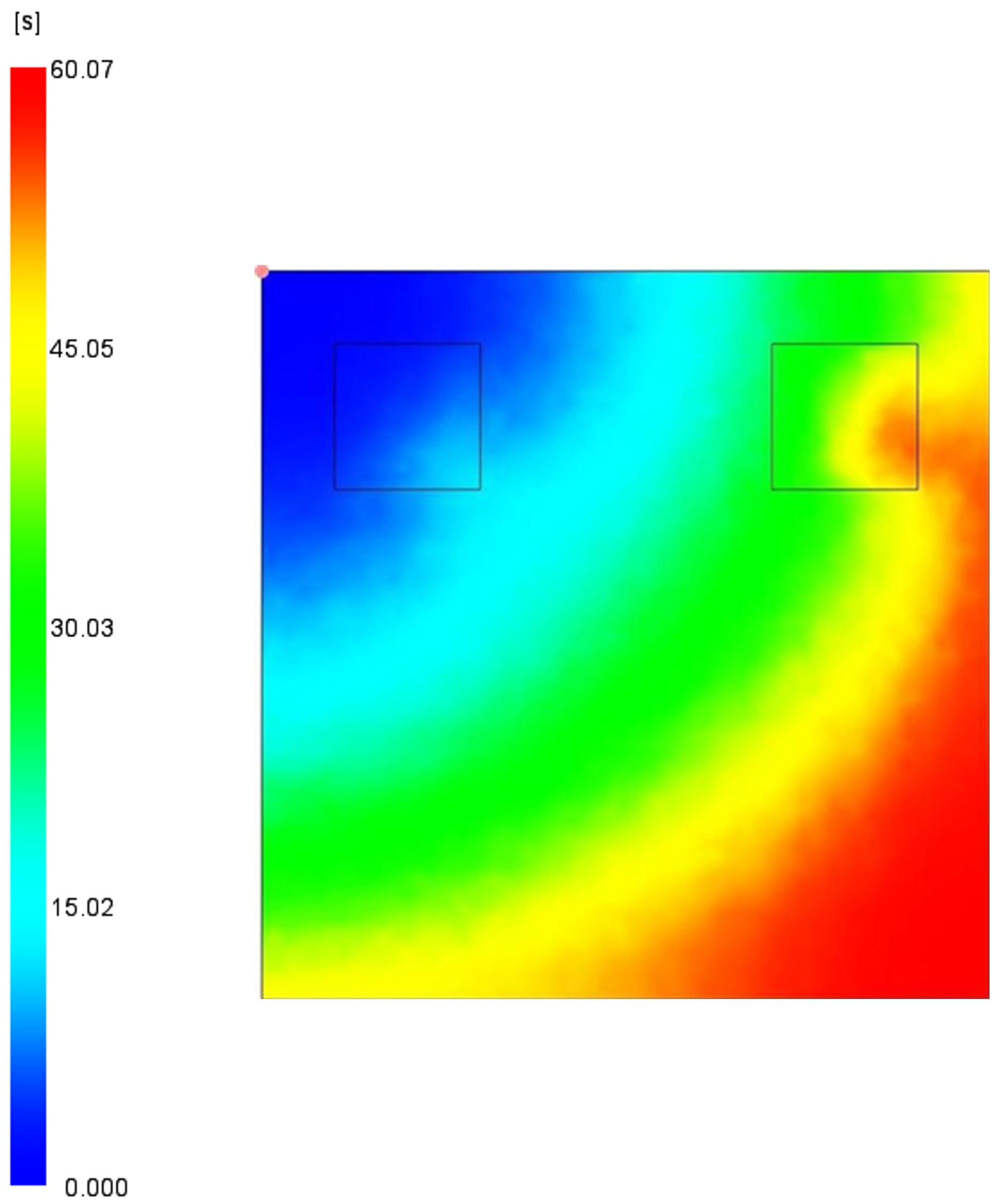
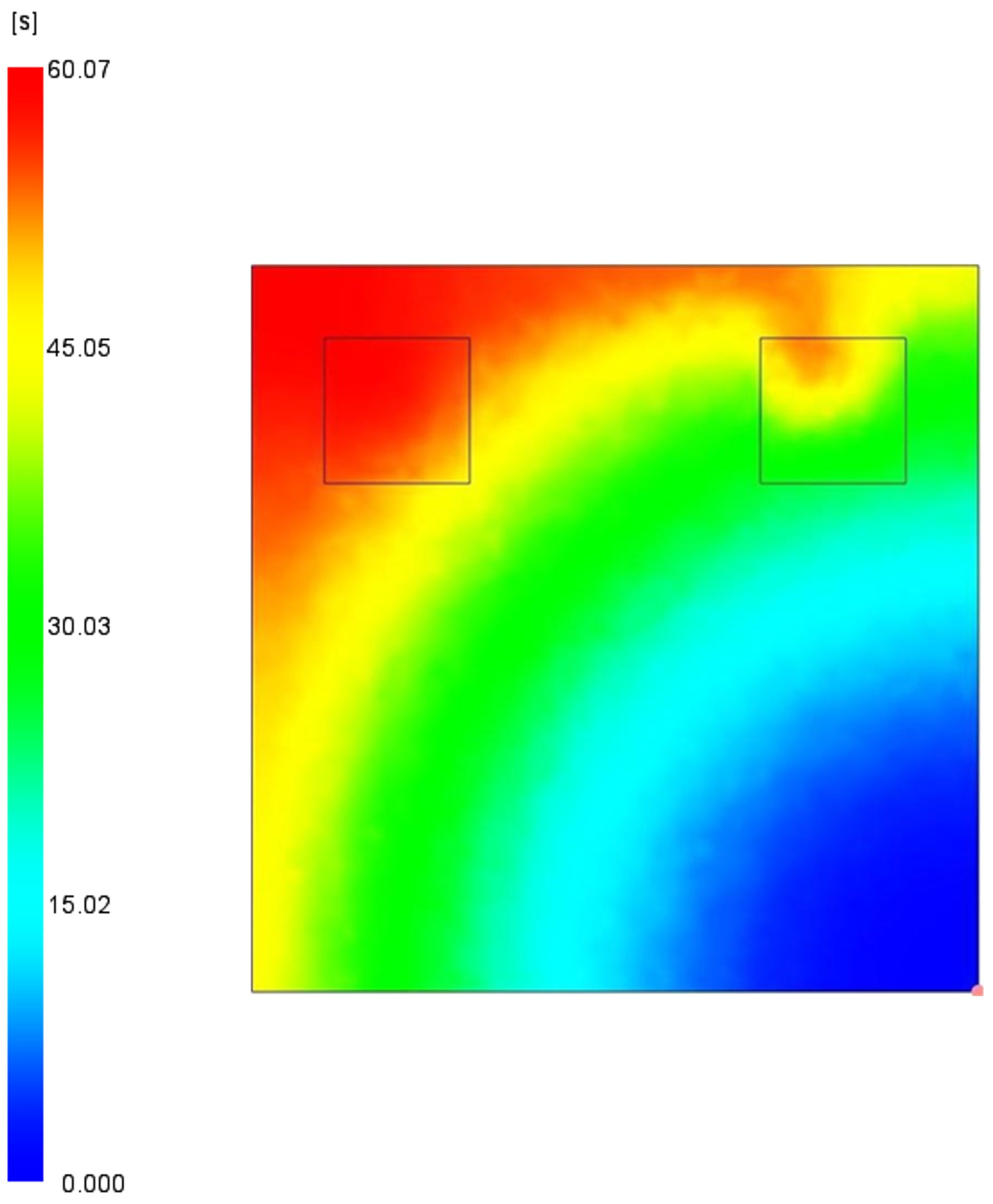
4. Data Generation Methodology
5. Discussions and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chai, B.X.; Eisenbart, B.; Nikzad, M.; Fox, B.; Wang, Y.; Bwar, K.H.; Zhang, K. Review of Approaches to Minimise the Cost of Simulation-Based Optimisation for Liquid Composite Moulding Processes. Materials 2023, 16, 7580. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Xie, J.; Chen, L. A hybrid optimization algorithm for gate locations in the liquid composite molding process. Text. Res. J. 2022, 92, 4912–4920. [Google Scholar] [CrossRef]
- Capricho, J.C.; Subhani, K.; Chai, B.X.; Bryant, G.; Salim, N.; Juodkazis, S.; Fox, B.L.; Hameed, N. Porous macroradical epoxy-based supercapacitors. Polymer 2022, 259, 125356. [Google Scholar] [CrossRef]
- Zade, A.; Kuppusamy, R. A review on numerical optimization in liquid composite moulding processes. Mater. Today Proc. 2019, 19, 329–332. [Google Scholar] [CrossRef]
- Facciotto, S.; Simacek, P.; Advani, S.G.; Middendorf, P. Modeling of anisotropic dual scale flow in RTM using the finite elements method. Compos. Part B Eng. 2021, 214, 108735. [Google Scholar] [CrossRef]
- Mendikute, J.; Plazaola, J.; Baskaran, M.; Zugasti, E.; Aretxabaleta, L.; Aurrekoetxea, J. Impregnation quality diagnosis in Resin Transfer Moulding by machine learning. Compos. Part B Eng. 2021, 221, 108973. [Google Scholar] [CrossRef]
- May, D.; Aktas, A.; Advani, S.G.; Berg, D.C.; Endruweit, A.; Fauster, E.; Lomov, S.V.; Long, A.; Mitschang, P.; Abaimov, S.; et al. In-plane permeability characterization of engineering textiles based on radial flow experiments: A benchmark exercise. Compos. Part A Appl. Sci. Manuf. 2019, 121, 100–114. [Google Scholar] [CrossRef]
- Han, W.S.; Jung, Y.; Kim, S. Numerical simulation of RTM process using the extended finite element method combined with the level set method. J. Reinf. Plast. Compos. 2013, 32, 308–317. [Google Scholar] [CrossRef]
- Chai, B.X.; Eisenbart, B.; Nikzad, M.; Fox, B.; Blythe, A.; Blanchard, P.; Dahl, J. A novel heuristic optimisation framework for radial injection configuration for the resin transfer moulding process. Compos. Part A Appl. Sci. Manuf. 2023, 165, 107352. [Google Scholar] [CrossRef]
- Blythe, A.; Fox, B.; Nikzad, M.; Eisenbart, B.; Chai, B.X.; Blanchard, P.; Dahl, J. Evaluation of the Failure Mechanism in Polyamide Nanofibre Veil Toughened Hybrid Carbon/Glass Fibre Composites. Materials 2022, 15, 8877. [Google Scholar] [CrossRef]
- Vernet, N.; Ruiz, E.; Advani, S.; Alms, J.B.; Aubert, M.; Barburski, M.; Barari, B.; Beraud, J.M.; Berg, D.C.; Correia, N.; et al. Experimental determination of the permeability of engineering textiles: Benchmark II. Compos. Part A Appl. Sci. Manuf. 2014, 61, 172–184. [Google Scholar] [CrossRef]
- Okabe, T.; Oya, Y.; Yamamoto, G.; Sato, J.; Matsumiya, T.; Matsuzaki, R.; Yashiro, S.; Obayashi, S. Multi-objective optimization for resin transfer molding process. Compos. Part A Appl. Sci. Manuf. 2017, 92, 1–9. [Google Scholar] [CrossRef]
- Hanna, J.M.; Aguado, J.V.; Comas-Cardona, S.; Le Guennec, Y.; Borzacchiello, D. A self-supervised learning framework based on physics-informed and convolutional neural networks to identify local anisotropic permeability tensor from textiles 2D images for filling pattern prediction. Compos. Part A Appl. Sci. Manuf. 2024, 179, 108019. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Liang, R.; Wang, B. Robust design of composites manufacturing processes with process simulation and optimisation methods. Int. J. Prod. Res. 2008, 46, 2087–2104. [Google Scholar] [CrossRef]
- Seyednourani, M.; Yildiz, M.; Sas, H.S. A two-stage optimization methodology for gate and vent locations and distribution media layout for liquid composite molding process. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106522. [Google Scholar] [CrossRef]
- Gu, G.X.; Chen, C.T.; Richmond, D.J.; Buehler, M.J. Bioinspired hierarchical composite design using machine learning: Simulation, additive manufacturing, and experiment. Mater. Horiz. 2018, 5, 939–945. [Google Scholar] [CrossRef]
- Huang, J.P.; Zhilyaev, I.; Snezhina, N.; Shevtsov, S. Evaluation of the vacuum infusion process objectives at the early stages of computer simulation. In Proceedings of the 10th International Conference on Mathematical Modeling in Physical Sciences, Virtual, 6–9 September 2021. [Google Scholar]
- Bodaghi, M.; Simacek, P.; Advani, S.G.; Correia, N.C. A model for fibre washout during high injection pressure resin transfer moulding. J. Reinf. Plast. Compos. 2018, 37, 865–876. [Google Scholar] [CrossRef]
- Rautela, M.; Huber, A.; Senthilnath, J.; Gopalakrishnan, S. Inverse characterization of composites using guided waves and convolutional neural networks with dual-branch feature fusion. Mech. Adv. Mater. Struct. 2022, 29, 6595–6611. [Google Scholar] [CrossRef]
- Achim, V.; Ruiz, E. Guiding selection for reduced process development time in RTM. Int. J. Mater. Form. 2010, 3, 1277–1286. [Google Scholar] [CrossRef]
- Caglar, B.; Broggi, G.; Ali, M.A.; Orgéas, L.; Michaud, V. Deep learning accelerated prediction of the permeability of fibrous microstructures. Compos. Part A Appl. Sci. Manuf. 2022, 158, 106973. [Google Scholar] [CrossRef]
- Chen, C.T.; Gu, G. Generative Deep Neural Networks for Inverse Materials Design Using Backpropagation and Active Learning. Adv. Sci. 2020, 7, 1902607. [Google Scholar] [CrossRef] [PubMed]
- Sacco, C.; Baz Radwan, A.; Anderson, A.; Harik, R.; Gregory, E. Machine learning in composites manufacturing: A case study of Automated Fiber Placement inspection. Compos. Struct. 2020, 250, 112514. [Google Scholar] [CrossRef]
- Ali, M.A.; Guan, Q.; Umer, R.; Cantwell, W.J.; Zhang, T. Deep learning based semantic segmentation of µCT images for creating digital material twins of fibrous reinforcements. Compos. Part A Appl. Sci. Manuf. 2020, 139, 106131. [Google Scholar] [CrossRef]
- Cassola, S.; Duhovic, M.; Schmidt, T.; May, D. Machine learning for polymer composites process simulation—A review. Compos. Part B Eng. 2022, 246, 110208. [Google Scholar] [CrossRef]
- Chai, B.X.; Eisenbart, B.; Nikzad, M.; Fox, B.; Blythe, A.; Bwar, K.H.; Wang, J.; Du, Y.; Shevtsov, S. Application of KNN and ANN Metamodeling for RTM Filling Process Prediction. Materials 2023, 16, 6115. [Google Scholar] [CrossRef]
- Ejaz, F.; Hwang, L.K.; Son, J.; Kim, J.S.; Lee, D.S.; Kwon, B. Convolutional neural networks for approximating electrical and thermal conductivities of Cu-CNT composites. Sci. Rep. 2022, 12, 13614. [Google Scholar] [CrossRef] [PubMed]
- Kokalis, C.-C.A.; Tasakos, T.; Kontargyri, V.T.; Siolas, G.; Gonos, I.F. Hydrophobicity classification of composite insulators based on convolutional neural networks. Eng. Appl. Artif. Intell. 2020, 91, 103613. [Google Scholar] [CrossRef]
- Shen, C.; Sheng, Q.; Zhao, H. Predicting effective thermal conductivity of fibrous and particulate composite materials using convolutional neural network. Mech. Mater. 2023, 186, 104804. [Google Scholar] [CrossRef]
- Luo, J.; Liang, Z.; Zhang, C.; Wang, B. Optimum tooling design for resin transfer molding with virtual manufacturing and artificial intelligence. Compos. Part A Appl. Sci. Manuf. 2001, 32, 877–888. [Google Scholar] [CrossRef]
- Wang, J.; Ren, Y.; Li, J.; Deng, K. The Footprint of Factorization Models and Their Applications in Collaborative Filtering. ACM Trans. Inf. Syst. 2021, 40, 1–32. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, S.; Rong, Q.; Bao, H. Predicting the effective thermal conductivities of composite materials and porous media by machine learning methods. Int. J. Heat Mass Transf. 2018, 127, 908–916. [Google Scholar] [CrossRef]
- Chen, C.T.; Gu, G. Machine learning for composite materials. MRS Commun. 2019, 9, 556–566. [Google Scholar] [CrossRef]
- Wu, J.; Xu, X.; Liu, C.; Deng, C.; Shao, X. Lamb wave-based damage detection of composite structures using deep convolutional neural network and continuous wavelet transform. Compos. Struct. 2021, 276, 114590. [Google Scholar] [CrossRef]
- Torres, M. Parameters’ monitoring and in-situ instrumentation for resin transfer moulding: A review. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105500. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. Part B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Tabian, I.; Fu, H.; Sharif Khodaei, Z. A Convolutional Neural Network for Impact Detection and Characterization of Complex Composite Structures. Sensors 2019, 19, 4933. [Google Scholar] [CrossRef]
- Mezeix, L.; Rivas, A.S.; Relandeau, A.; Bouvet, C. A New Method to Predict Damage to Composite Structures Using Convolutional Neural Networks. Materials 2023, 16, 7213. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharyya, S.; Maulik, U. Quantum Inspired Meta-Heuristics for Image Analysis; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Dalmont: Paris, France, 1856. [Google Scholar]
- Dammann, C.; Mahnken, R. Simulation of a resin transfer molding process using a phase field approach within the theory of porous media. Compos. Part A Appl. Sci. Manuf. 2019, 120, 147–160. [Google Scholar] [CrossRef]
- Park, C.H.; Lee, W.I. Modeling void formation and unsaturated flow in liquid composite molding processes: A survey and review. J. Reinf. Plast. Compos. 2011, 30, 957–977. [Google Scholar] [CrossRef]
- Mathur, R.; Advani, S.; Fink, B.K. A real-coded hybrid genetic algorithm to determine optimal resin injection locations in the resin transfer molding process. Comput. Model. Eng. Sci. 2003, 4, 587–601. [Google Scholar]
- Crawford, B.; Rashif, K.M.S.; Rashidi, A.; Sadiq, R.; Milani, A.S. A Bayesian belief approach to quality control of resin transfer molding process. Int. J. Adv. Manuf. Technol. 2020, 109, 1953–1968. [Google Scholar] [CrossRef]
- Yu, Y.X. Theoretical insights into surface-phase transition and ion competition during alkali ion intercalation on the Cu4Se4 nanosheet. Phys. Chem. Chem. Phys. 2024, 26, 323–335. [Google Scholar] [CrossRef] [PubMed]
- Bodaghi, M.; Simacek, P.; Correia, N.; Advani, S.G. Experimental parametric study of flow-induced fiber washout during high-injection-pressure resin transfer molding. Polym. Compos. 2019, 41, 1053–1065. [Google Scholar] [CrossRef]
- Wang, M.; Hang, X. Finite Element Analysis of Residual Stress Distribution Patterns of Prestressed Composites Considering Interphases. Materials 2023, 16, 1345. [Google Scholar] [CrossRef] [PubMed]
- Sandberg, M.; Hattel, J.H.; Spangenberg, J. Simulation of liquid composite moulding using a finite volume scheme and the level-set method. Int. J. Multiph. Flow 2019, 118, 183–192. [Google Scholar] [CrossRef]
- Phunpeng, V.; Saensuriwong, K.; Kerdphol, T.; Uangpairoj, P. The Flexural Strength Prediction of Carbon Fiber/Epoxy Composite Using Artificial Neural Network Approach. Materials 2023, 16, 5301. [Google Scholar] [CrossRef]
- Zhilyaev, I.; Chigrinets, E.; Shevtsov, S.; Chotchaeva, S.; Snezhina, N. ANN-based estimation of the defect severity in the drilling of GFRP/Ti multilayered composite structure. J. Compos. Sci. 2022, 6, 370. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, B.X.; Wang, J.; Dang, T.K.M.; Nikzad, M.; Eisenbart, B.; Fox, B. Comprehensive Composite Mould Filling Pattern Dataset for Process Modelling and Prediction. J. Compos. Sci. 2024, 8, 153. https://doi.org/10.3390/jcs8040153
Chai BX, Wang J, Dang TKM, Nikzad M, Eisenbart B, Fox B. Comprehensive Composite Mould Filling Pattern Dataset for Process Modelling and Prediction. Journal of Composites Science. 2024; 8(4):153. https://doi.org/10.3390/jcs8040153
Chicago/Turabian StyleChai, Boon Xian, Jinze Wang, Thanh Kim Mai Dang, Mostafa Nikzad, Boris Eisenbart, and Bronwyn Fox. 2024. "Comprehensive Composite Mould Filling Pattern Dataset for Process Modelling and Prediction" Journal of Composites Science 8, no. 4: 153. https://doi.org/10.3390/jcs8040153
APA StyleChai, B. X., Wang, J., Dang, T. K. M., Nikzad, M., Eisenbart, B., & Fox, B. (2024). Comprehensive Composite Mould Filling Pattern Dataset for Process Modelling and Prediction. Journal of Composites Science, 8(4), 153. https://doi.org/10.3390/jcs8040153






