A Numerical Tool for Assessing Random Vibration-Based Fatigue Damage Diagnosability in Thermoplastic Coupons

Abstract

A numerical tool is developed to simulate the random vibration-response-only-based fatigue delamination diagnosability in thermoplastic coupons. That is the ability to both detect damage and identify its current severity, aiming to establish a virtual framework for optimizing diagnosability methods. The numerical tool employs the FE method. It comprises two modules: a fatigue delamination module and a random vibration module. The first module implements a fatigue crack growth model based on the cohesive zone modeling method to predict delamination accumulation, while the second module uses an experimentally verified FE model of the delaminated coupon to predict its random vibration response. Delamination accumulation is evident in the ‘predicted’ FE-based power spectral densities. The model’s capability to diagnose delamination is demonstrated using seven different damage metrics based on simulated random vibration responses, enabling damage detection and severity assessment (increasing trend guides to distinguishing each fatigue state from its counterparts). Comparisons with their experimentally obtained counterparts are also used in the assessment. The procedure clearly suggests that the proposed numerical tool may be reliably used for virtually assessing the efficacy of random vibration-based fatigue damage diagnosability for any given structure and also to aid the user in selecting the method’s parameters for virtual diagnosability optimization.

1. Introduction

Since the launch of the Boeing 787 Dreamliner, in which composites account for nearly 50% of its structural weight, and the Airbus A350 XWB, where composites make up about 52% of its structural weight, Carbon Fiber Reinforced Plastics (CFRP) have become a dominant material in the aeronautical industry [1]. While thermosets are primarily used in aircraft structures, thermoplastics are gaining popularity due to their advantages, particularly in terms of dynamic behavior, recyclability, and weldability.

Fatigue behavior remains a critical design factor for composite aircraft structures due to its stochastic nature, which is further enhanced by the inherent anisotropy of CFRPs. To date, CFRP structures have primarily been designed based on experimental data, as reliable predictive models are still lacking.

Improving safety has become a paramount concern for aircraft manufacturers and operators, particularly in light of recent incidents and accidents that have resulted in the grounding of hundreds of aircraft for extended periods. Structural Health Monitoring (SHM) offers a valuable solution by providing reliable diagnostic and prognostic tools that can help prevent critical structural failures [2,3]. Additionally, SHM has the potential to enhance the efficiency and effectiveness of maintenance procedures, ultimately contributing to improved operational safety and reduced downtime.

SHM of composite structures has undergone rapid advancements over the past decade [3,4]. Traditionally, offline experimental techniques have been used to detect the initiation of damage, track its progression, and, in some cases, predict the residual fatigue life and strength of structures [5]. Common methods include X-rays [6,7], acoustic emission [8,9,10], optical and surface observation [11,12], and post-damage analysis through Scanning Electron Microscopy (SEM) [13,14]. In contrast, a promising family of online SHM methods relies on vibration-data-driven methods. These offer two key advantages [15]: Continuous, real-time information on the structure’s health state without disrupting normal operation and operating via sensors that are not necessarily in the neighborhood of the damage location. This renders vibration-based methods especially useful for the real-time monitoring of complex composite structures.

Vibration-based SHM has been widely used across various engineering sectors, though predominantly in beam-like structures. Most studies have employed experimental approaches [16,17,18,19,20,21,22,23,24,25,26,27], with fewer studies utilizing a combined experimental–numerical approach [28,29,30,31,32,33,34,35,36], an experimental–analytical approach [37], or a purely numerical approach [38,39,40,41,42,43]. Certain studies [44,45,46] employed the wavelet transform, while others [47,48,49] utilized artificial neural networks. The majority of the published works focus on damage detection, with only a small subset [24,27] addressing fatigue damage of composite materials. All experimental–numerical approaches and purely numerical approaches have exploited experimental data to predict damage accumulation or fatigue life of the structures, while only the work of Sartorato et al. [39] employed numerical analyses to support the design of a piezoelectric-based SHM system for metallic materials. Additionally, some important studies [19,50,51] examined the non-linearities, which are inserted in the problem of vibration–fatigue damage.

The goal of this study is the development of an integrated fatigue damage–random vibration numerical tool for the parametric simulation of random vibration-based progressive fatigue damage detectability for thermoplastic coupons. The implementation of the numerical tool requires no experimental data, with the exception of the fatigue model. Following its validation against mechanical fatigue and random vibration tests, the numerical models are used to assess the effects of specific parameters on fatigue damage diagnosability.

The study’s innovative aspects may be summarized as follows:

• Development of a numerical methodology of random vibration-response-only-based fatigue damage diagnosability for thermoplastic coupons;
• Development of an efficient simulation process for random vibration experiments;
• Examination of progressive fatigue damage through numerical random vibration responses in the frequency domain;
• Employment of several damage metrics for fatigue damage diagnosability in thermoplastic coupons using numerical random vibration response data;
• Generation of an integrated numerical model/tool, which can be used to support random vibration-response-only-based SHM systems for composite structures.

2. Conceptual Framework

The concept of detecting damage in materials and structures by exploiting random vibration response is based on the premise that damage alters their characteristics (stiffness and damping), thus their dynamical behavior, which subsequently leads to changes in their vibration response characteristics [52]. Yet, as damage characteristics can also be affected by other factors, such as operational and environmental conditions, care should be exercised to distinguish between actual damage and other external influences [53,54,55,56,57,58].

Especially, detecting fatigue damage from random vibration responses and modal characteristics, such as frequency, damping ratio, spectral distance, PSD estimates, etc., requires the ability to deeply understand the initial propagation, constant evolution, and the critical damage modes before failure, with the aim of understanding the vibration behavior and the correlation of it with fatigue damage. The proposed fatigue degradation model is based on the loading envelope approach proposed by [59] in which the cyclic loading is simulated by a linear force incremental to the maximum value of applied force. The implementation of the model was undertaken on an element basis and was based on a modified Paris’ law. For more details, Section 3 of this present paper, as [59,60,61], describes the fatigue delamination growth model.

The implementation of the random vibration model also needs a comprehensive understanding of the exact and with which tendency the modal characteristics are influenced by progressive fatigue damage. The random vibration simulation process lies in the modal superposition method to characterize the linear dynamic behavior of the structure [62].

3. The Numerical Tool for Fatigue Damage Diagnosability

Both the Fatigue Delamination Module (FDM) and the Random Vibration Module (RVM) were developed in LS-Dyna. These are two distinct models functioning dependently on each other. The FDM has been described in detail in [61], so only a brief overview of it is presently provided for the sake of presentation completeness.

3.1. The Fatigue Delamination Module (FDM)

The FDM was based on the fatigue crack growth model developed in [60] for simulating interfacial fracture in co-consolidated thermoplastic joints. The model utilizes the cohesive zone modeling method and incorporates a modified Paris’ law, expressed as:

$${\displaystyle \frac{da}{dN}}=c{\left(G_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^m$$

(1)

where ${\displaystyle \frac{da}{dN}}$ is the fatigue crack growth rate, $c$ and $m$ are the modified Paris’ law parameters for each simulated FS, and $G_{\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the maximum energy release rate for the affected element at a given FS. The instantaneous energy release rate $G_{\mathrm{i}}$ for each cohesive element is consistently set to $G_{\mathrm{m}\mathrm{a}\mathrm{x}}$, reflecting the maximum energy release rate of the actual loading spectrum due to the use of the load envelope technique. The intermediate mixed-mode parameters $c$ and $m$ are derived using the prediction model of Russel and Street [63], which requires only pure mode I and mode II fatigue experimental data as inputs.

Numerical fatigue degradation was implemented using the method of cumulative static and fatigue element damage parameters, described by:

$$d_{\mathrm{t}\mathrm{o}\mathrm{t}}=d_s+d_f$$

(2)

where $d_{\mathrm{t}\mathrm{o}\mathrm{t}}$ is the total damage variable (ranging from 0 for undamaged to 1 for failed), while $d_s$ and $d_f$ are the static and fatigue contributing damage variables, respectively. The stress state σ for each element in the fatigue-activated zone is then degraded using:

$$\sigma =\left(1-d_{\mathrm{t}\mathrm{o}\mathrm{t}}\right){\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(3)

where ${\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum traction of the affected element.

In this study, the modified Paris’ law was applied, accounting solely for $G_{\mathrm{m}\mathrm{a}\mathrm{x}}$. The fatigue crack growth model was fully validated using the same experimental parameters, such as stress ratio and maximum load percentage, for the same interfaces as detailed in [60].

Fatigue loading was implemented using the loading envelope technique [59], where the actual sinusoidal spectrum was approximated by a constant force corresponding to the maximum fatigue load value, as illustrated in Figure 1.

During each numerical iteration, the rate of fatigue crack growth was calculated using Equation (1), which operates in a singular direction. This resulted in the establishment of an equivalent rate of damage development uniformly across all axes, disregarding the orthotropic nature of thermoplastics and the complexity of three-dimensional interfaces. To address this limitation, a specific length measurement was assigned to each element, guiding the progression of damage by considering input from the cohesive integration points. This measurement is particularly significant in cases where there is considerable variation in element aspect ratios and irregularities within the interfaces. The calculation of the fatigue damage rate, $df$, requires the characteristic element length, $l_e$, as described in detail in [29]. $l_e$ was computed for each iteration through an internal loop, which determined the minimum distance from the midpoint of a non-failed element to the midpoint of neighboring elements. Following this, the elements’ data, including $G_I$ and $G_{II}$, were calculated, and a check for fatigue module activation was performed. If either $G_I$ or $G_{II}$ exceeded the threshold value $G_{th}$, the fatigue module was activated; otherwise, static degradation was applied. The value of $G_{th}$ was based on literature. The stress $\sigma$ of the cohesive element is governed by the mixed-mode stress, which combines the contributions from both normal and tangential stress components, according to LS-Dyna’s MAT_138 formulation [35]. Therefore, cohesive elements subjected to fatigue damage are fully governed by mixed-mode stress $\left(\sigma \right)$ for their response, degradation, and failure. The iterative numerical procedure for the fatigue crack growth model is illustrated in Figure 2.

The pure mode I and mode II modified Paris’ laws used in the study are:

$${\left({\displaystyle \frac{d\alpha }{dN}}\right)}_t=0.0027G_{I,max}^{4.23}$$

(4)

$${\left({\displaystyle \frac{d\alpha }{dN}}\right)}_{II}=0.00040G_{II,max}^{5.31}$$

(5)

where ${\left({\displaystyle \frac{da}{dN}}\right)}_I$, ${\left({\displaystyle \frac{da}{dN}}\right)}_{II}$ and $G_{I,\mathrm{m}\mathrm{a}\mathrm{x}}$, $G_{II,\mathrm{m}\mathrm{a}\mathrm{x}}$ are the fatigue crack growth rates and the maximum energy release rates per cycle for mode I and mode II, respectively. More details on the derivation of Equations (1) and (2) can be found in [60].

3.2. The Random Vibration Module (RVM)

The RVM was developed using LS-Dyna’s graphical interface pre-processor LS-PrePost 4.8. The damping ratio was determined using:

$$\xi ={\displaystyle \frac{\mathrm{\Delta }f}{2f_n}}$$

(6)

where $f_n$ is the first natural frequency and $\mathrm{\Delta }f$ is the bandwidth of the half-power points [40]. To prevent hourglass-induced instabilities, a conversion of the excitation amplitude was necessary.

The applied excitation was calculated using [64]:

$$\left[\mathrm{d}\mathrm{B}\right]=20 \times {\log }_{10}\left({\displaystyle \frac{P}{2 \times {10}^5}}\right)$$

(7)

where $P$ is the pressure of white noise in Pascal and $2 \times {10}^5$ is reference sound pressure in Pascal.

Respectively, the numerical results were converted from [mm/s] to [dB] using [65]:

$$v_{\mathrm{d}\mathrm{B}}=20 \times {\log }_{10}\left(v_{\mathrm{m}\mathrm{m}/\mathrm{s}} \times {10}^6\right)$$

(8)

where $v_{\mathrm{d}\mathrm{B}}$ is the resulting velocity in dB and $v_{\mathrm{m}\mathrm{m}/\mathrm{s}}$ is the resulting velocity in mm/s.

With the aim of calibrating the model parameters, and checking how basic parameters (such as boundary conditions, measurement points, and mesh density—more details in Section 4.5) influence the coupon’s behavior, Frequency Response Functions (FRF) analyses were implemented. The geometry (see below—Section 4.4 and the material model (orthotropic elastic—see below

Table 1. Orthotropic elastic properties of the thermoplastic lamina [61].

Property	Value
Density (ton/mm3)	1.75 × 10−9
Elastic modulus—a direction (MPa)	95,000
Elastic modulus—b direction (MPa)	8500
Elastic modulus—c direction (MPa)	8500
Shear modulus—ab direction (MPa)	4300
Shear modulus—bc direction (MPa)	3571
Shear modulus—ac direction (MPa)	4300
Poisson’s ratio—νba	0.027
Poisson’s ratio—νca	0.024
Poisson’s ratio—νcb	0.172

) were the same as described in the RVM model.

The FE modeling procedure for the damaged coupon is outlined in the flowchart of Figure 3. This process combined the RVM with the FDM. For each FS, the FDM was executed to predict the delamination state, which corresponds to deleted cohesive elements representing the interfaces among layers. All cohesive elements were exported to a dynain.ASCII file, from which the deleted cohesive elements were isolated into a new keyfile (set.k). The set.k file was then imported into the initial FE model, and by reversing the deleted elements, duplicated cohesive layers (both healthy and damaged) were created. Finally, the deleted cohesive elements saved in the set.k file were removed, and the remaining duplicate nodes were merged. This procedure effectively “inserts” the delaminated (deleted) cohesive elements into the cohesive layers.

An important clarification should be given at this point: the coupons that were submitted to T-T fatigue had transverse and off-axis cracks, except for delamination, which surely contributed to the final failure. The initiation and propagation of fatigue damage, which was validated from C-Scan images, showed that delamination was the main cause of failure [61]—so, as with the FDM, the RVM also considers only the delamination as damage mode.

4. Numerical Tool Assessment and Experimental Verification

In [27], the concept of using random vibration response to detect fatigue damage in thermoplastic coupons was experimentally demonstrated. The objective of this present work was the numerical development of [27] that comprehensively examines the influence of testing parameters on the method’s efficiency and virtually optimizes the process for structural parts. A key difference to be kept in mind is that while in the experimental procedure, all damage modes may be present, the numerical tool presently included only delamination damage. Thus, the assessment was based on the premise that delamination is the predominant damage mode in coupons subjected to tension-tension fatigue—which was validated by C-Scan images [61]. The numerical tool assessment was the application of the above two modules into a thermoplastic coupon, which was experimentally validated at various stages. The FDM was validated by C-Scan images [61], and the RVM was validated by the experimental PSD Welch estimates [27,66]. Any deviation between the numerical and experimental results is justified below.

4.1. Material and Coupons

The coupons employed in the study were fabricated from T700 carbon fiber reinforced low-melt semi-crystalline PAEK (polyaryletherketone) matrix prepregs (Toray Cetex^® TC1225) [67,68,69]. The fiber volume fraction was 66%, and each ply was 0.14 mm thick. The lay-up was quasi-isotropic, with the sequence [−45°/0°/45°/90°] 2s. The dimensions of the coupons were $250 \mathrm{m}\mathrm{m}\times 25 \mathrm{m}\mathrm{m}\times 2.24 \mathrm{m}\mathrm{m}$. Tabs made of the same material, measuring $50 \mathrm{m}\mathrm{m}\times 25 \mathrm{m}\mathrm{m}\times 2.24 \mathrm{m}\mathrm{m}$, were bonded to the coupons. In total, 23 coupons were subjected to mechanical loads and excitation. The properties of the material are provided in Table 1 [61] and the dimensions od the coupon are illustrated in Figure 4.

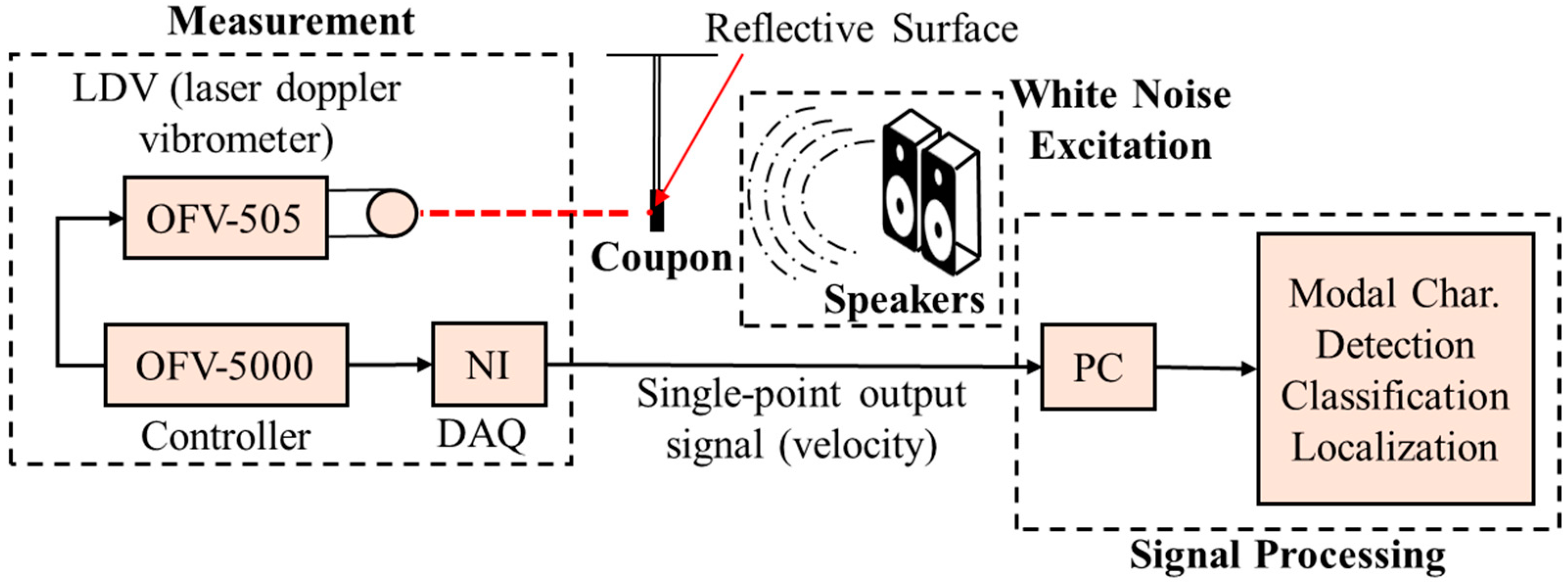
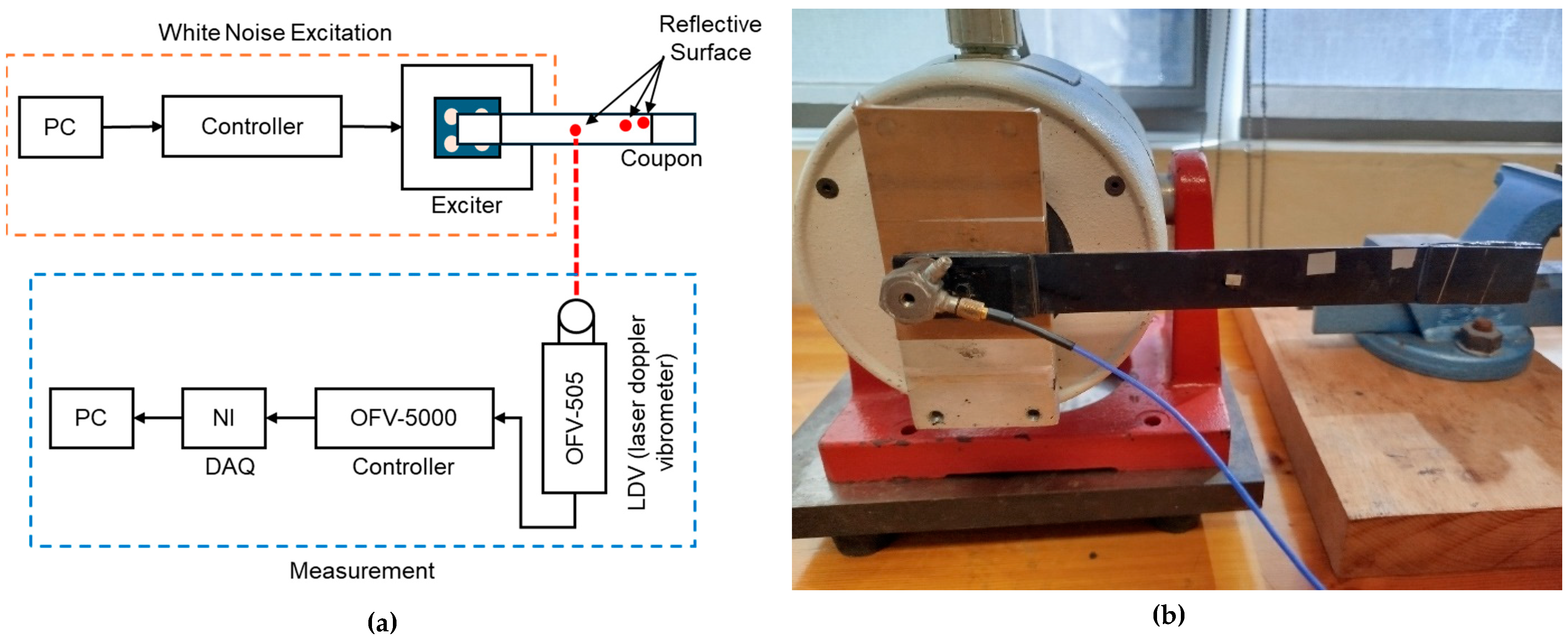
4.2. Brief Overview of the Experimental Procedure

The random vibration test setup is illustrated in Figure 5, while Figure 6 provides a sketch of the testing and data acquisition processes. The test setup consisted of a Laser Doppler Vibrometer (LDV) OFV-505 (Polytec GmbH, Karlsruhe, Germany), its OFV-5000 controller (Polytec GmbH, Karlsruhe, Germany), an NI-9230 acquisition card (National Instruments, Austin, TX, USA), and a PC. The applied excitation was a MATLAB (R2024a)-generated band-limited (within the 0–6.4 kHz range) white noise. The coupons were supported via elastic cords to simulate free-free boundary conditions. Vibration velocity measurements were taken using the laser vibrometer, which was focused on a reflective surface positioned at the center of the upper face of each coupon. The random vibration test was implemented every 10,000 fatigue cycles for all coupons.

Non-parametric signal analysis was performed, based on which Welch-based Power Spectral Density (PSD) estimates were obtained for the Healthy State (HS) and various Fatigue States (FSs). The signal characteristics and the Welch estimation parameters are summarized in

Table 2. Signal characteristics and Welch PSD estimation details for random vibration testing [27].

Random Vibration Test with Acoustic Excitation
Signal Characteristics		Welch Parameters
$\mathrm{Sampling}\mathrm{frequency}{f}_s$	12,800 Hz	Segment length	25,600 samples
Signal duration	60 s	Overlap	90%
Signal bandwidth	0–6400 Hz	$\mathrm{Frequency}\mathrm{resolution}\delta f$	1 Hz

. Progressive fatigue damage detection was conducted on a population of 13 coupons, with one representative sample selected for model comparison and validation. The results across the coupons were grossly consistent, with random deviations attributed to the stochastic nature of fatigue damage accumulation. This variability is discussed by the authors in references [66,70]. The PSD Welch estimates for Coupon #3 under HS and various FSs (70 PSD estimates under the HS and 35 under each FS) are presented in Figure 7. A clear and consistent effect of fatigue damage was observed on the PSD Welch estimates in that certain resonant frequencies (in particular, those in the 3–3.6 kHz range) shifted from higher to lower frequencies as the damage progressed.

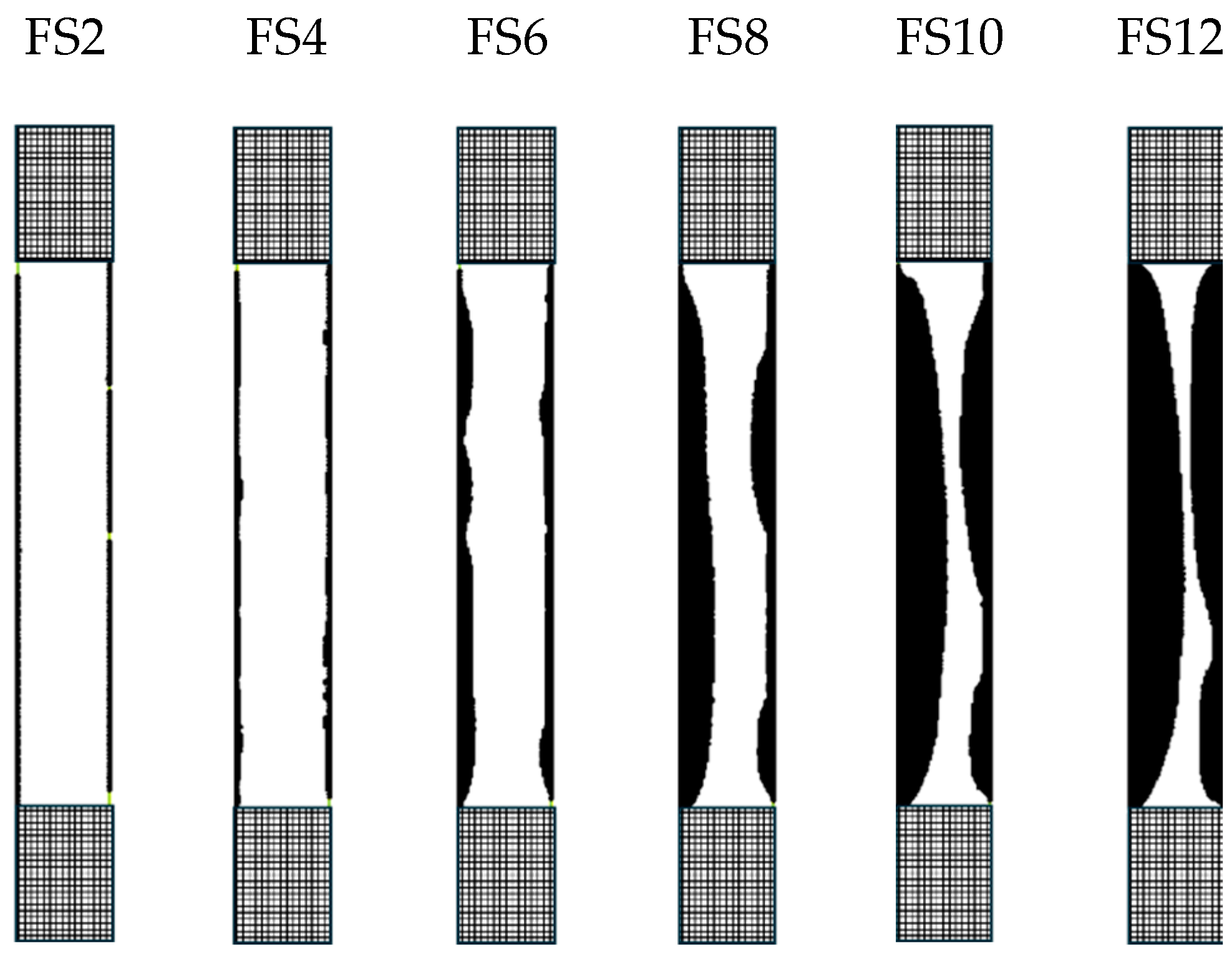
4.3. FDM Results

Figure 8 illustrates a typical fatigue delamination propagation pattern predicted by the FDM (Section 3.1) for a thermoplastic coupon. Delamination was initiated at the free edges of the coupon, driven by high through-the-thickness normal and intralaminar shear stresses, and propagated towards the center of the coupon. The propagation pattern was not fully symmetric, which is attributed to the nature of fatigue—repeated loading in specific directions can create progressive damage in certain ply orientations before others, as the material model used here [60,61] is sensitive to element orientation, which can create directional differences in damage evolution. The consecutive Fatigue States (FS) corresponded to the successive fatigue cycles—each FS corresponded to 20,000 cycles. The significance of the fatigue delamination pattern lies in its ability to accurately model delamination growth and capture the characteristics of thermoplastic coupon’s fatigue behavior.

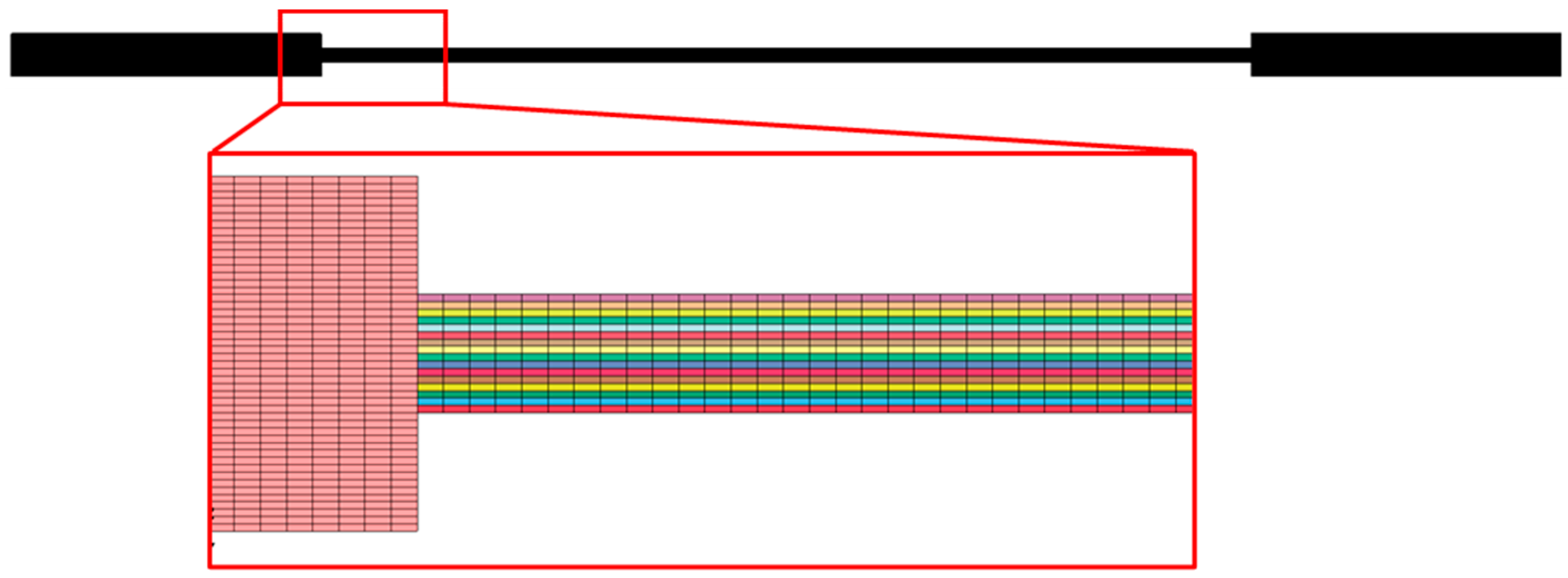
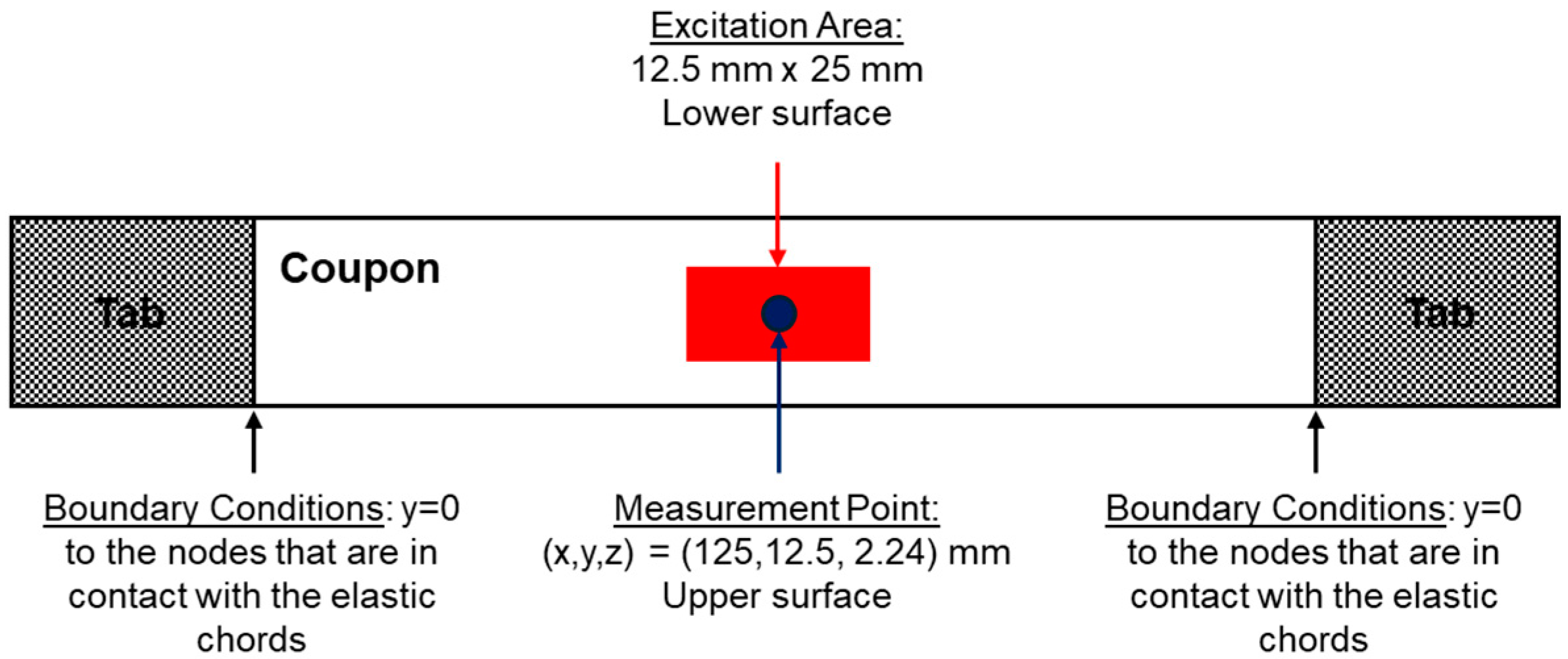
4.4. RVM Modeling

A typical FE mesh of the coupon is shown in Figure 9. The coupon’s damping ratio was calculated as 0.01 from Equation (6). The thermoplastic plies were modeled using solid 8-noded elements with a constant stress formulation (ELFORM 1). The orthotropic elastic material properties used for the elements are listed in Table 1. As boundary conditions, only the nodes that were in contact with the elastic cords were restricted to the y-axis. Velocity was measured at the middle and upper face nodes.

Figure 10 shows the applied white noise excitation in the time and frequency (spectral) domains. Figure 11 shows the applied boundary conditions and the measurement location in the coupon.

4.5. RVM Results

4.5.1. Calibration of the RVM

A stepwise validation and calibration process was employed for the RVM. The modeling parameters that were calibrated included the mesh density, the boundary conditions, the measurement point, and the excitation area. To achieve this, in-house experimental results from [27] and laboratory-scale experimental results of a simplified test were utilized.

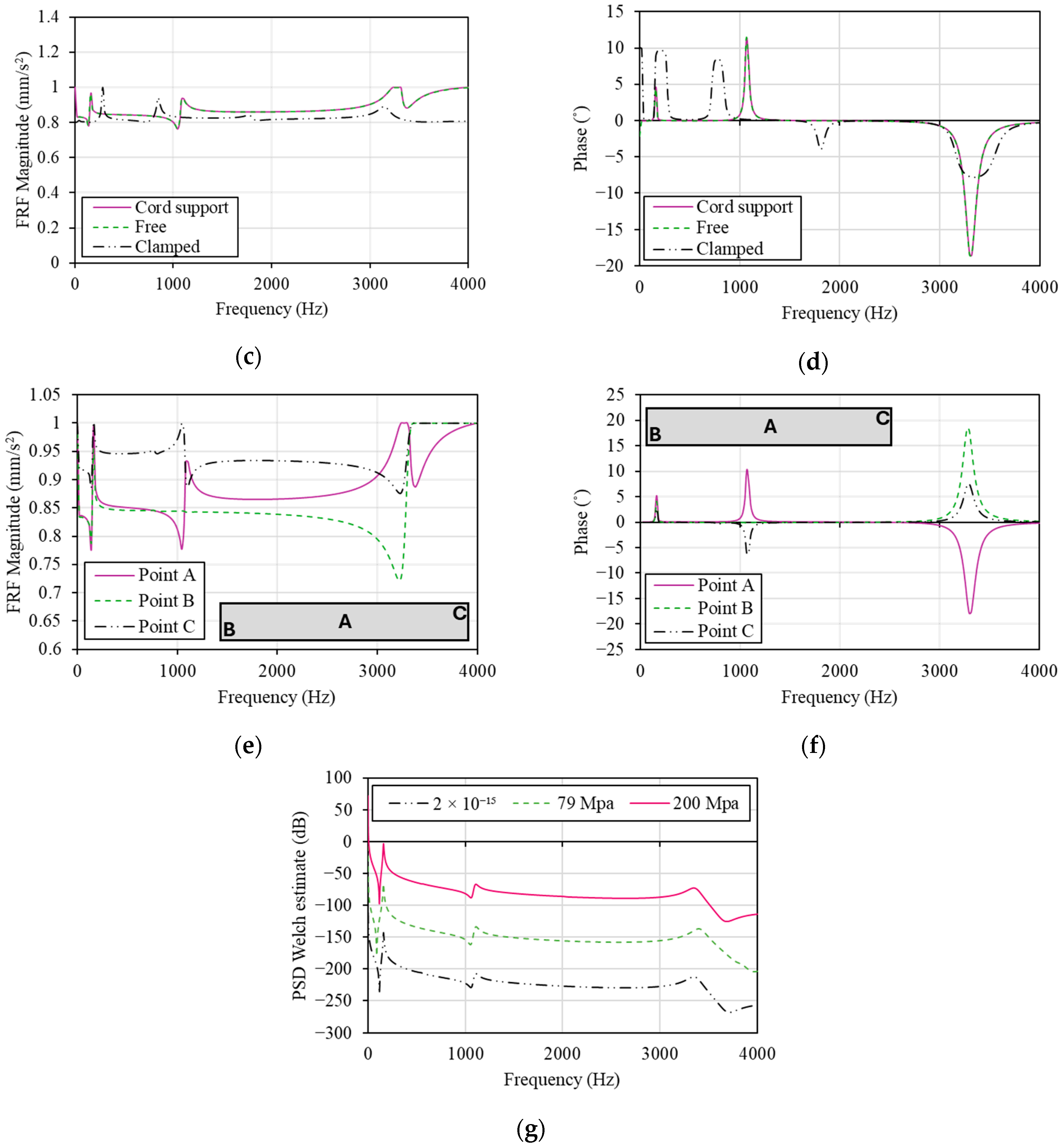
4.5.2. Parametric Frequency Response Function (FRF) Analysis

As a first step, parametric FRF analysis of the healthy coupon was conducted and the FRF amplitude and phase considering the above parameters were compared. The parameters used are listed in

Table 3. Parameter values used in the calibration of the RVM.

Parameter	Values
Measurement location	Center, Upper right corner, Lower left corner
Mesh density	235,000 elements, 432,000 elements, 2,080,000 elements
Boundary conditions	Cord-support, Free, Clamped
Excitation intensity	2 × 10−15 MPa, 79 MPa, 200 MPa

.

The FRF amplitude and phase for varying mesh densities, measurement locations, boundary conditions, and excitation intensities are compared in Figure 12.

As the mesh density increased, the computed results progressively converged, although the differences between the FE meshes remained minor. Final convergence was achieved with the mesh of 432,000 elements, which was then applied consistently in all subsequent analyses. The comparison between free–free and elastic cord support boundary conditions revealed only minor differences in FRF characteristics, and the elastic cord support was ultimately selected to align with the experimental setup, while fixed boundary conditions affected the dynamic behavior of the coupon. Meanwhile, the location of the measurement point and excitation intensity (expectedly) influenced the magnitude intensity; yet the resonant frequencies (spectral peaks) remained unaffected. The dynamics remained approximately linear under different excitation intensities, as the shape did not change, and the measurement point and the boundary conditions could be replicated in the FEM successfully.

To ensure consistency with the experimental procedure, the measurement point was positioned at the center of the coupon, corresponding to the setup used in the experiment.

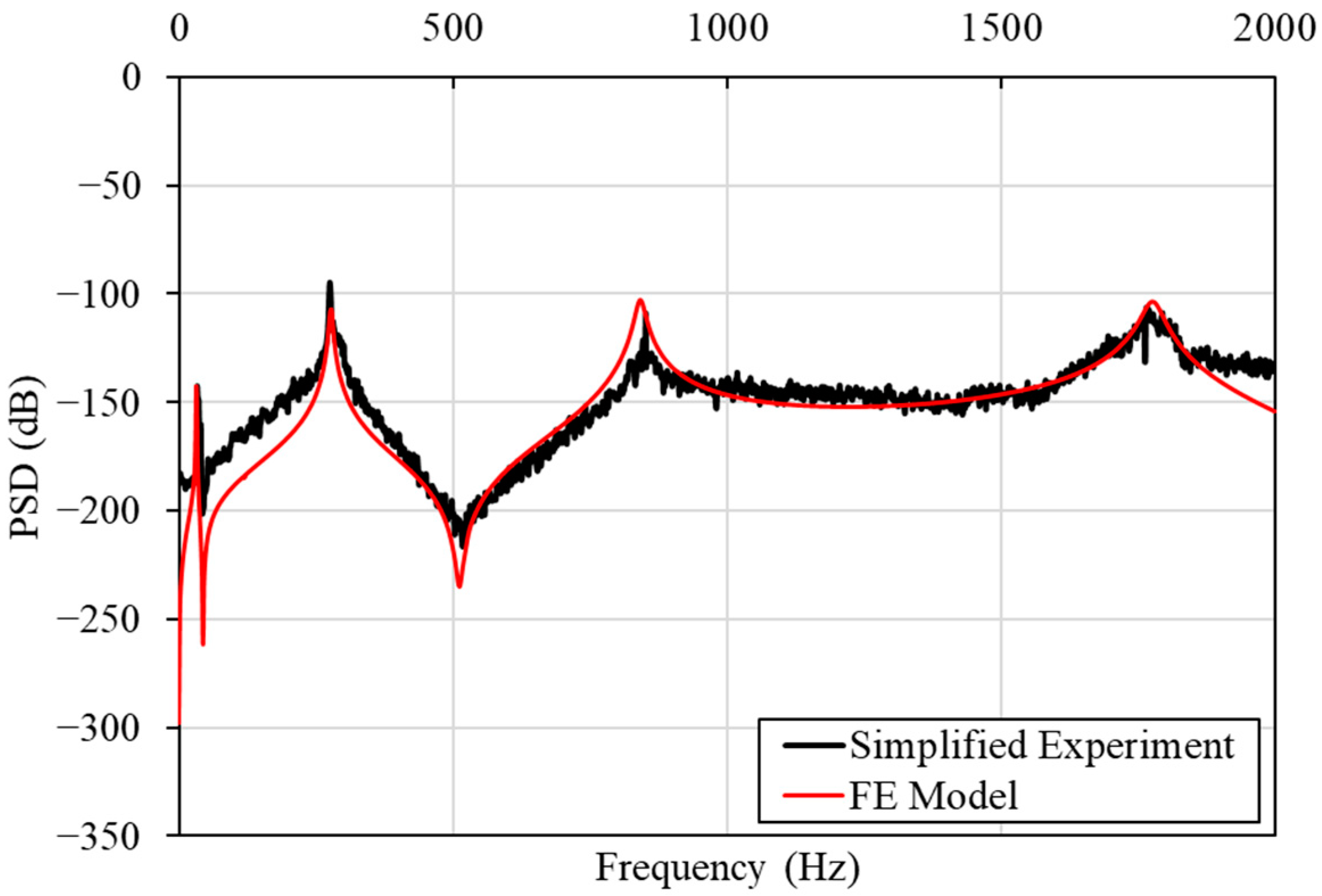
4.5.3. Validation of the RVM (Healthy State)

Given the complexity of the random vibration response that the RVM aims to simulate, validating its accuracy is crucial. To this end, different comparison cases against experimental results were considered, reflecting different vibration scenarios for both healthy and damaged coupons. The validation had two primary objectives: (a) To confirm the model’s capacity to accurately represent the random vibration behavior of the thermoplastic coupons and (b) to assess the model’s ability to capture the effect of damage on the coupon’s vibration behavior.

For the healthy state, two validation cases involving different random vibration-based excitation and support conditions were considered.

In the first case, the random vibration test performed in [27] was considered. Figure 12 compares the numerical-based and experimental PSD estimates. A satisfactory agreement of the intensity of the response amplitude was evident. Furthermore, the model captured three of the resonant frequencies indicated by the peaks in the PSD Welch estimate. The additional peaks in the experimental PSD Welch estimate may be attributed to various factors and uncertainty, including unmodelled phenomena, complicated excitation due to reflections of the white noise acoustic excitation in the room during the experiments, inherent instrumentation effects, and noise in the measurement devices, and so on.

To ensure that the deviation observed in Figure 13 was indeed due to the experimental parameters and conditions of the random vibration tests, and not because the FE model contained misleading information, a second validation case using a simplified random vibration test was considered. This simplified test was conducted on a cantilever coupon. In this case, white noise was generated by an electromechanical exciter (LDS Model V406 with its controller, LDS COMET USB COM-200) and applied to the fixed end (tab) of the coupon. A laser vibrometer was used to measure the velocity at 3 points (the midpoint and 2 points near the right tab) on the upper surface of the coupon. A key difference from the previous experiment is that non-acoustic excitation was used, and the tests were conducted in a significantly larger room. A schematic illustration of the simplified random vibration test and a photograph of the test rig are provided in Figure 14. The excitation signal was recorded and applied with the same intensity as the FE model. The electromechanical exciter stimulated frequencies ranging from 0 to 2 kHz, with direct contact between the exciter and the coupon. Regarding the FE model, the modeling process remained consistent with the previous setup, using the same mesh (432,000 elements), the same thermoplastic coupon, and geometry (Figure 4). The only differences were the location of the excitation point (on the tab), the intensity of the excitation (−100 dB), the boundary conditions (clamped on the left tab), and the measurement points. This simplified setup helped isolate and eliminate factors, such as acoustic reflections, ensuring a more controlled and accurate validation of the FE model’s performance.

The signal characteristics and the Welch PSD estimation details for the simplified random vibration tests are summarized in

Table 4. Signal characteristics and Welch PSD estimation details for simplified random vibration testing.

Simplified Random Vibration Test
Signal Characteristics		Welch Parameters
$\mathrm{Sampling}\mathrm{frequency}{f}_s$	2000 Hz	Segment length	4000 samples
Signal duration	10 s	Overlap	90%
Signal bandwidth	0–2000 Hz	$\mathrm{Frequency}\mathrm{resolution}\delta f$	1 Hz

. The signal bandwidth was shorter than in the random vibration tests excited by white noise, as the goal was the examination of lower-frequency bandwidth.

Figure 15 presents the comparison between the FEM-based analytical PSD and its Welch-based estimate obtained from the experimental procedure. Evidently, the resonant frequencies, as well as the overall PSD, were quite accurately captured by the FE model. This validated the FE model’s capability to properly represent the coupon dynamics.

4.6. Numerical Fatigue Damage Identifiability Assessment

As already mentioned, the damage identifiability assessment of the numerical tool was also based on the experimental procedure and the database of our recent work [27] which employed various Fatigue States (FSs) and a more complex acoustic excitation. The complexity of the acoustic excitation, which was not only spatially dependent but also included reflections from the surrounding lab walls, implies that some discrepancies between the experimental and simulated results were expected. Yet, viewed in a positive light, this was intended to provide a sense of the robustness of the assessment results when such discrepancies—that are difficult to model precisely—are present. The assessment results are then presented in Section “Assessment Results with Experimental Validation”.

Assessment Results with Experimental Validation

In Figure 16, the FEM-based analytical PSDs are compared to their experimental Welch-based counterparts for the thermoplastic coupon (Coupon #3) under different Fatigue States (FSs). Even from the early beginning (FS2), the dynamic behavior of the coupon was captured from the FEM-based spectrum, which confirmed the usefulness of the proposed numerical tool. As expected, in the Fatigue State 10 (FS10), the effects of damage on the PSDs were intense.

As demonstrated in the present section, the RVM’s ability to properly model progressive fatigue damage was shown through its effects on the PSD and, in particular, shifts in the resonant frequencies. These are more evident in Figure 17, where the FEM-based spectrums for six FSs are depicted, clearly highlighting the model’s ability to model the effects of fatigue damage accumulation on the dynamics.

The model successfully predicted the decrease in resonant frequencies caused by fatigue damage accumulation. Consistent with the experimental results, the decrease was more pronounced at higher frequencies.

Damage diagnosability is based on dynamics-based Damage Metrics (DMs) that characterize the ‘distance’ of the Healthy State from any Fatigue State (FS) within a proper dynamical feature-based space. Specifically, in this present work, seven Damage Metrics were employed based on the numerical vibration PSD spectrum: Three (Metrics 1 to 3) previously used in [39], and four (Metrics 4 to 7) presently introduced. The DMs were dimensionless, except for DM5. These metrics are defined as follows:

DM 1:

$${\displaystyle \frac{\log \left(S_{{FS}_i}\left(f_i\right)-S_H\left(f_i\right)\right)}{\log \left(S_H\left(f_i\right)\right)}}\times 100\mathrm{\%}\left[{\displaystyle \frac{\mathrm{dB}}{\mathrm{dB}}}\right]$$

(9)

DM 2:

$${\displaystyle \frac{{\sum }_{i=1}^n\left|S_{{FS}_i}\left(f_i\right)-S_H\left(f_i\right)\right|}{{\sum }_{i=1}^n\left|S_{{FS}_i}\left(f_i\right)\right|}}\left[{\displaystyle \frac{\mathrm{dB}}{\mathrm{dB}}}\right]$$

(10)

DM 3:

$$\sum _{i=1}^n{\displaystyle \frac{1}{f_c}}{\displaystyle \frac{{\sum }_{j=1}^i\left|S_{{FS}_i}\left(f_j\right)-S_H\left(f_j\right)\right|}{{\sum }_{i=1}^j\left|S_H\left(f_j\right)\right|}}\left[{\displaystyle \frac{\mathrm{dB}}{\mathrm{dB}}}\right]$$

(11)

DM 4:

$$\sum _{i=1}^n\left(\left|S_{{FS}_i}\right|-\left|S_H\right|\right)\left[\mathrm{dB}\right]$$

(12)

DM 5:

$${\displaystyle \frac{\left|S_H-S_{{FS}_i}\right|}{S_{{FS}_i}}}\times 100\mathrm{\%}\left[{\displaystyle \frac{\mathrm{dB}}{\mathrm{dB}}}\right]$$

(13)

DM 6:

$$\cos \left(S_H,S_{{FS}_i}\right)={\displaystyle \frac{\sum _{i=1}^n{S}_H·S_{{FS}_i}}{‖S_H‖‖S_{{FS}_i}‖}}\left[{\displaystyle \frac{\mathrm{dB}}{\mathrm{dB}}}\right]$$

(14)

DM 7:

$$d\left(S_H,S_{{FS}_i}\right)={\displaystyle \frac{\sqrt{{\left(S_H-S_{{FS}_i}\right)}^T{C}^{-1}\left(S_H-S_{{FS}_i}\right)}}{\max \left(\sqrt{{\left(S_H-S_{{FS}_i}\right)}^T{C}^{-1}\left(S_H-S_{{FS}_i}\right)}\right)}}\left[{\displaystyle \frac{\mathrm{dB}}{\mathrm{dB}}}\right]$$

(15)

where

• $S_{{FS}_i}$: FEM-based analytical PSD for the $i-th$FS;
• $S_H$: FEM-based analytical PSD for the Healthy State;
• $\left|S_{{FS}_i}\right|$: absolute of the FEM-based analytical PSD for the $i-th$FS;
• $\left|S_H\right|$: absolute value of the FEM-based analytical PSD for the Healthy State,
• $f_i$: a specific frequency;
• $f_c$: the upper (max) frequency within the range of interest;
• $\cos \left(S_H,S_{{FS}_i}\right)$: cosine of the angle between the two FEM-based analytical PSDs;
• $‖S_{{FS}_i}‖$: $l_2$ norm of the FEM-based analytical PSD;
• $d$: normalized Mahalanobis distance between two health states;
• $S_H-S_{{FS}_i}$: difference between two FEM-based analytical PSDs;
• $C$: estimated covariance matrix of the two FEM-based analytical PSDs (Healthy and corresponding Fatigue State); and
• $C^{-1}$: inverse of the estimated covariance matrix of the two FEM-based analytical PSDs (Healthy and corresponding Fatigue State).

The values of the Damage Metrics (DM) computed from the FEM-based analytical PSDs for six Fatigue States (FSs) are compared to those of the Healthy State (HS), as well as to their experimentally obtained counterparts, in Figure 18. The DMs for all FSs exhibited considerable differences from the Healthy State, with noticeable deviations starting from FS2, clearly indicating the onset of fatigue damage. DM1, DM2, DM3, and DM5 showed a consistent increase across the FSs, suggesting their suitability not only for detecting damage but also for classifying its severity (extent). In contrast, DM4 displayed random variation, making it unsuitable for damage classification. Numerical-based damage metrics tended to have better behavior, due to a clear mode of damage and the separation of each Fatigue State from one another.

5. Concluding Remarks

In this work, we developed an integrated numerical model to simulate random-vibration fatigue damage detectability in thermoplastics. The model comprised two key modules: a fatigue damage simulation module and a random vibration simulation module. This numerical approach digitally replicates a previously established experimental process. Based on the numerical results, the following conclusions can be drawn:

• The Fatigue Delamination Module (FDM) accurately simulates the fatigue delamination initiation and propagation. Furthermore, FDM captures the fatigue behavior of thermoplastic coupons, proving how severe delamination is for the coupon;
• The Random Vibration Model (RVM) accurately simulates the vibration response of both healthy and damaged composite coupons under various excitation conditions. This was validated in two different cases using in-house experimental data. Additionally, the RVM demonstrated similar sensitivity to damage as observed in the experiments, showing a shift in the natural frequencies to the left;
• A parametric study using the FRF model revealed that the Finite Element (FE) mesh density had a minimal effect, while the measurement location, boundary conditions, and excitation intensity significantly influenced the FRF amplitude’s intensity;
• All damage metrics, using the FEM-based Power Spectral Density (PSD) spectrums, achieved highly effective damage detectability, reaching 100% performance. Frequency-related damage metrics also showed a monotonic increase, making them suitable for damage classification;
• The proposed numerical tool supports the design and optimization of a random vibration-based Structural Health Monitoring (SHM) system for composite structures through the following steps:
  • Predicting fatigue damage progression and residual strength as functions of the number of cycles.
  • Simulating the random vibration response of the healthy structure.
  • Introducing fatigue damage into the RVM and simulating the random vibration response of the damaged structure.
  • Maximizing detection efficiency by comparing the FEM-based PSD spectrums of the healthy and damaged states.