Implementation of Composite Materials for an Industrial Vehicle Component: A Design Approach
Abstract
1. Introduction
2. Materials and Methods
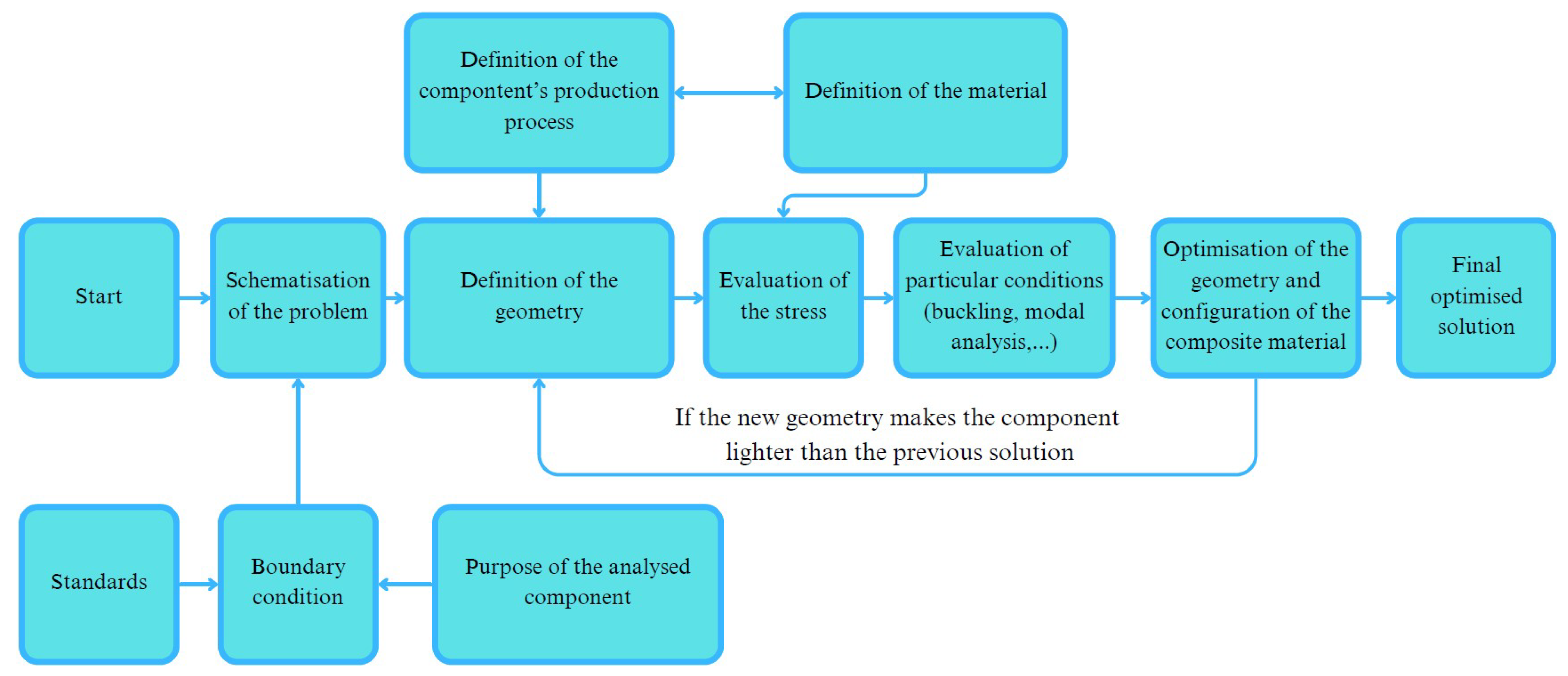
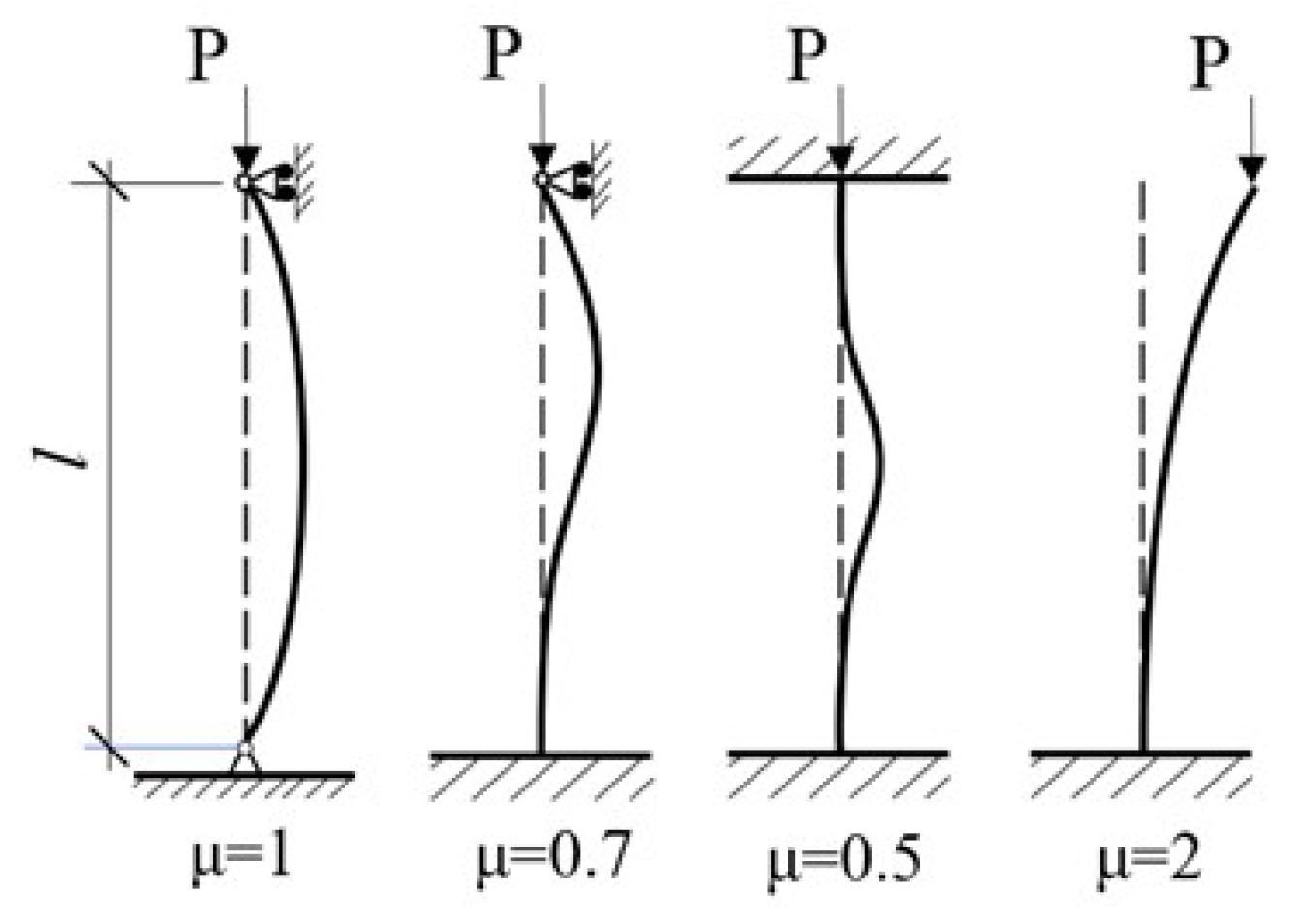
2.1. Theoretical Background of the Design Approach
2.2. Methods and Criteria Adopted
2.3. Choice of the Materials
2.4. Optimization of the Geometry
- Minimizing the weight;
- Maximizing the mechanical properties;
- Minimizing the cost of the component.
3. Implementation of the Design Approach: The Front Underrun Protection Device
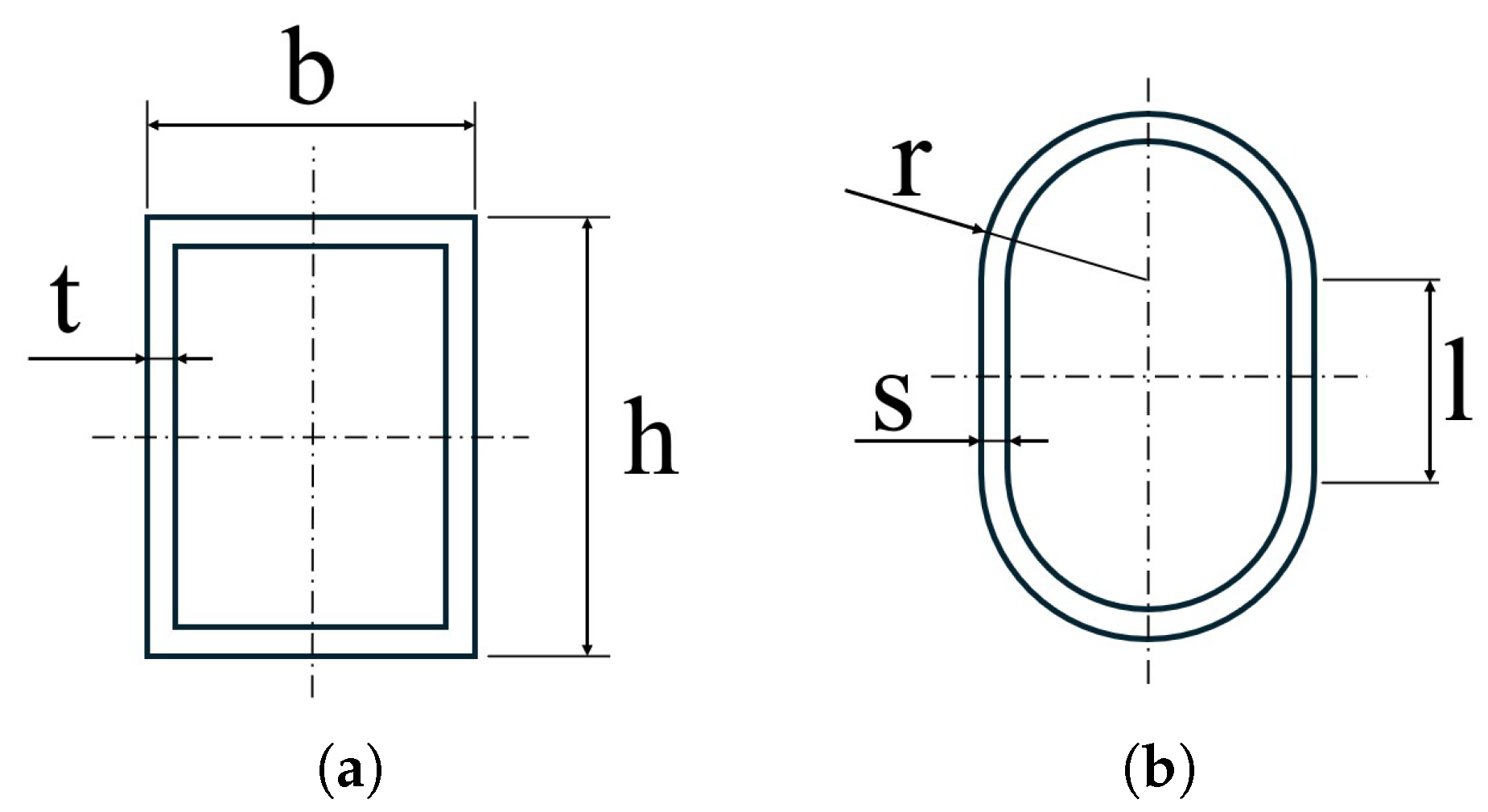
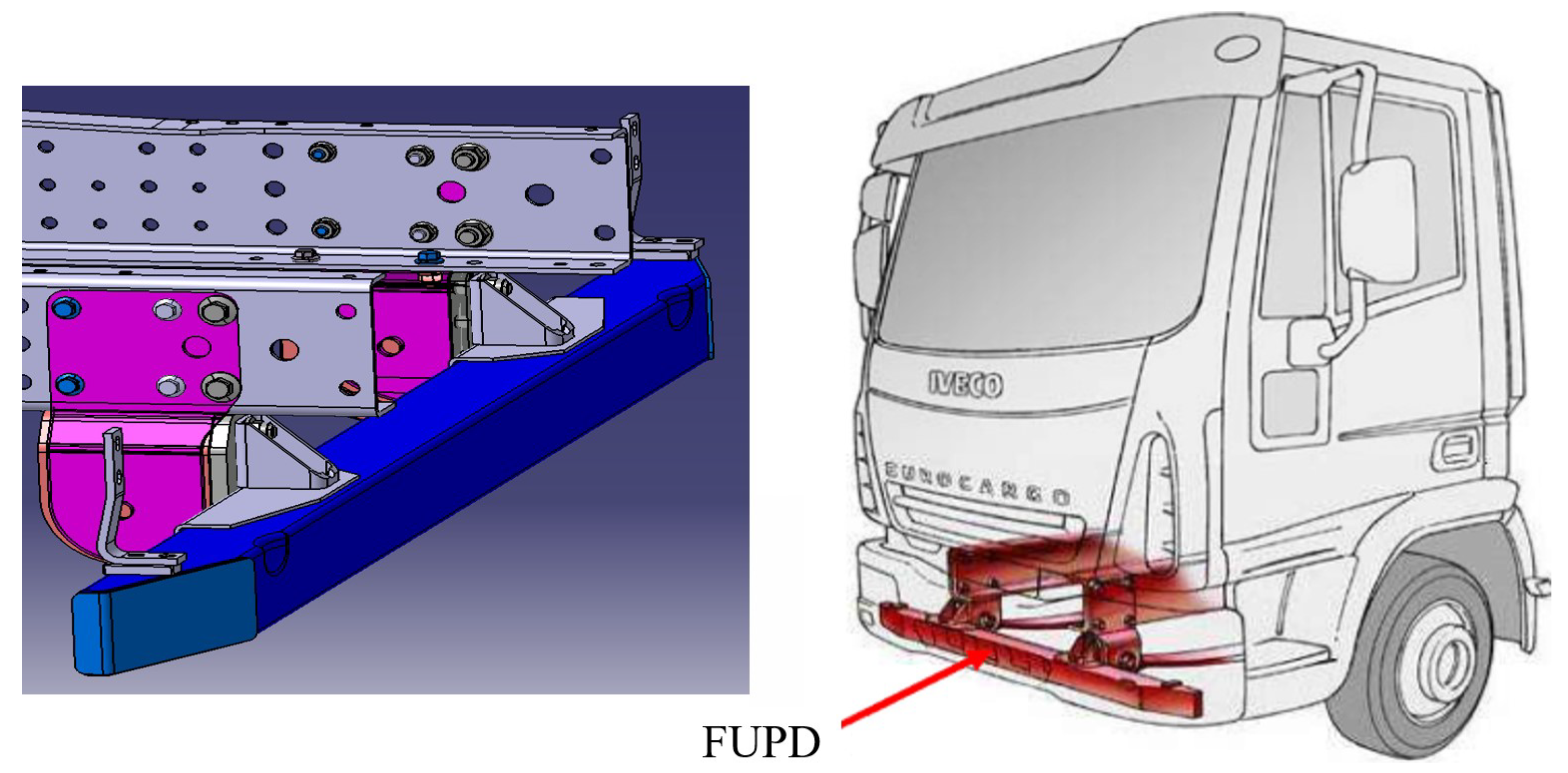
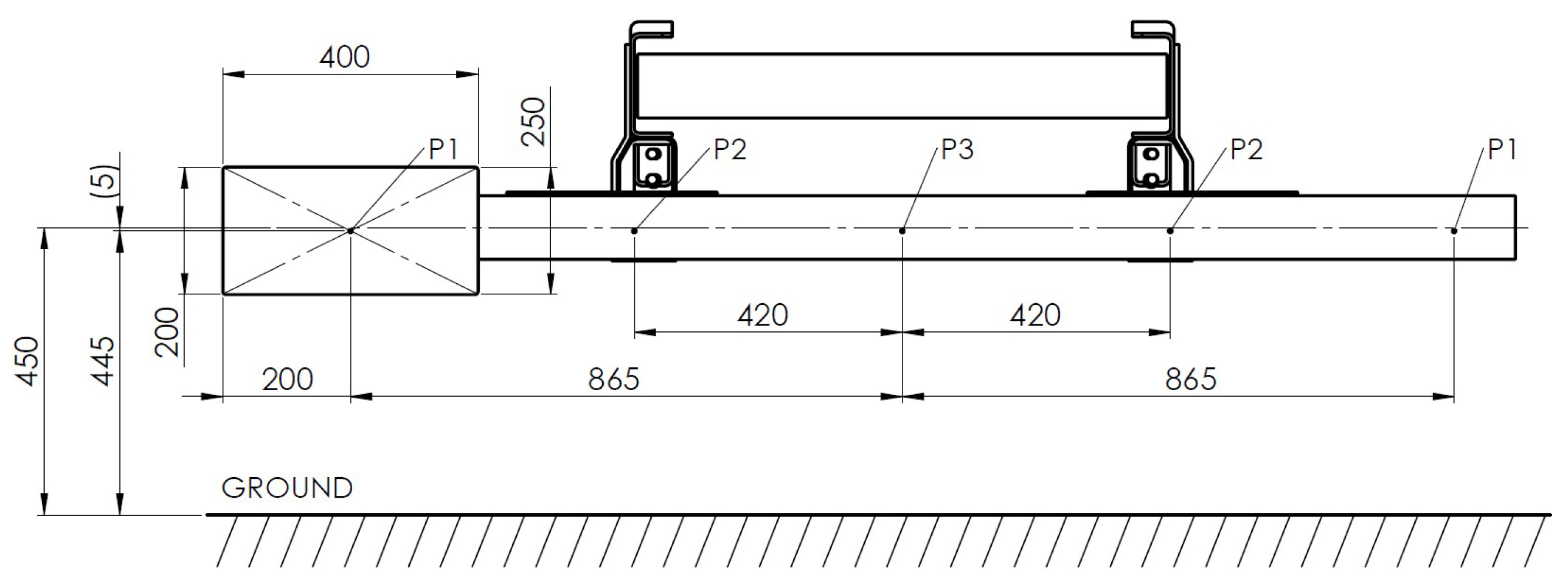
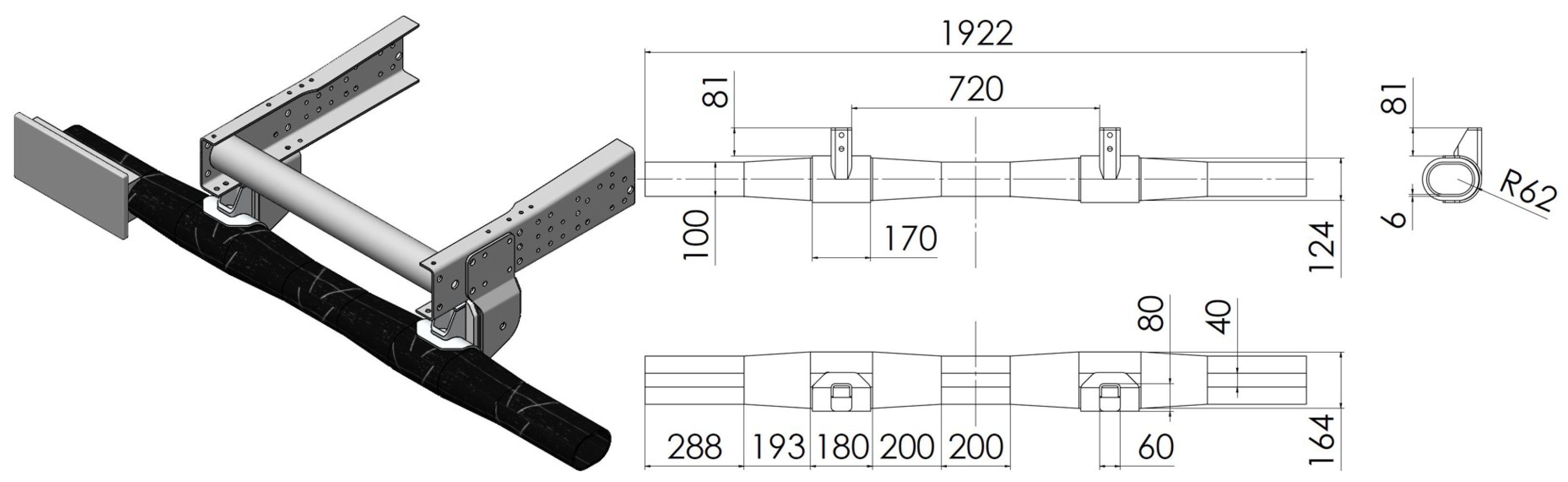
3.1. Description of the Component
- Be compliant with the United Nations Economic Commission for Europe (UN/ECE) standard n.93 [35];
- Exhibit natural frequencies higher than the characteristic internal and external excitation frequencies of the vehicle;
- Prevent buckling of the structure.
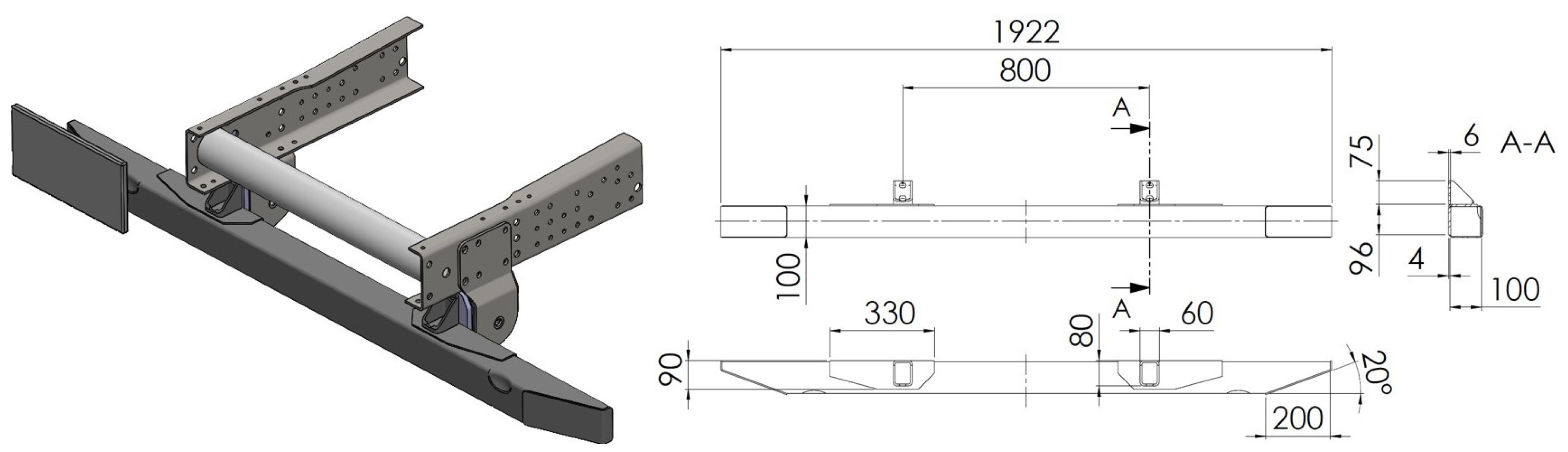
3.2. Traditional Solution
3.3. GFRP Innovative Solution
3.4. CFRP Innovative Solution
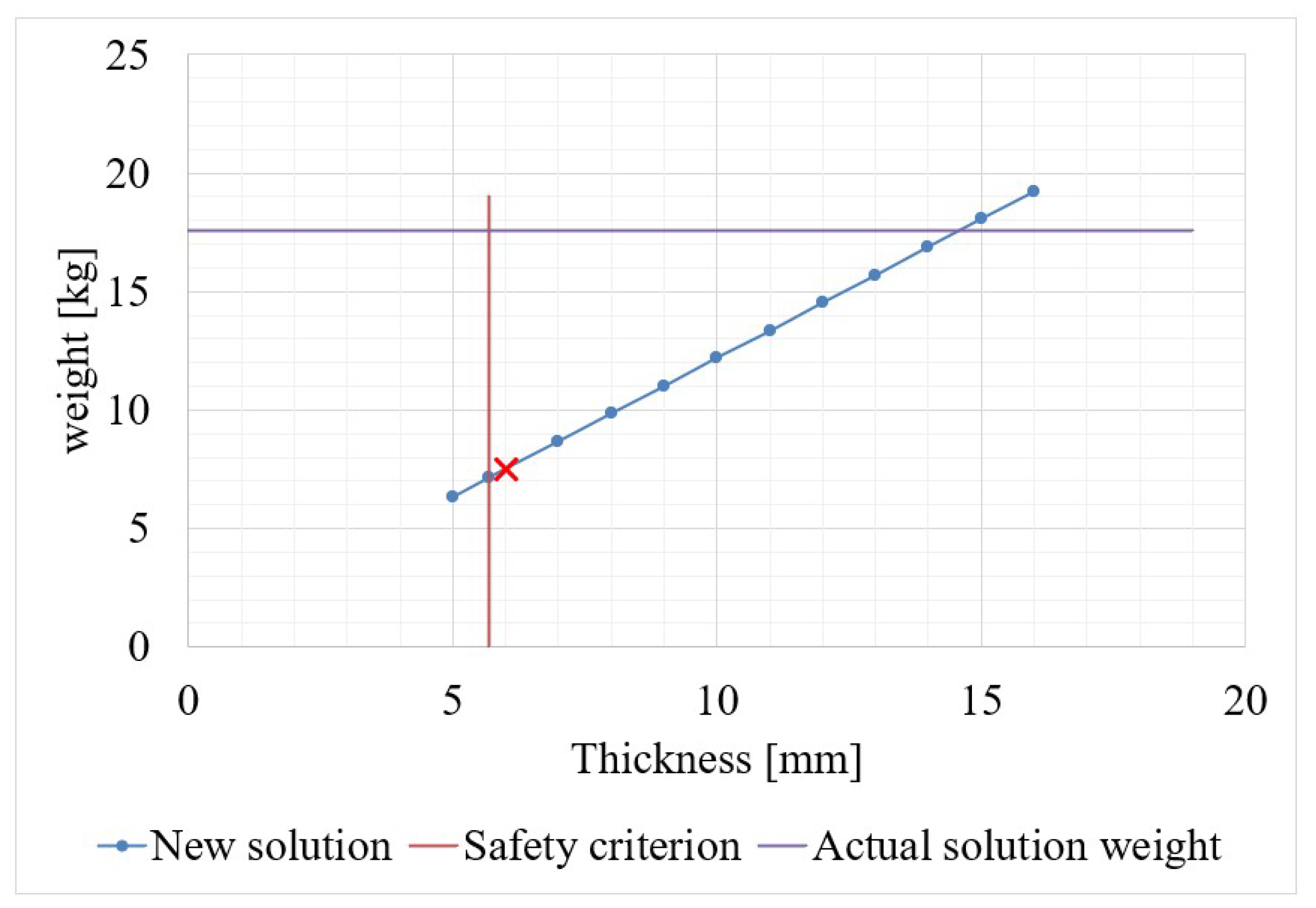
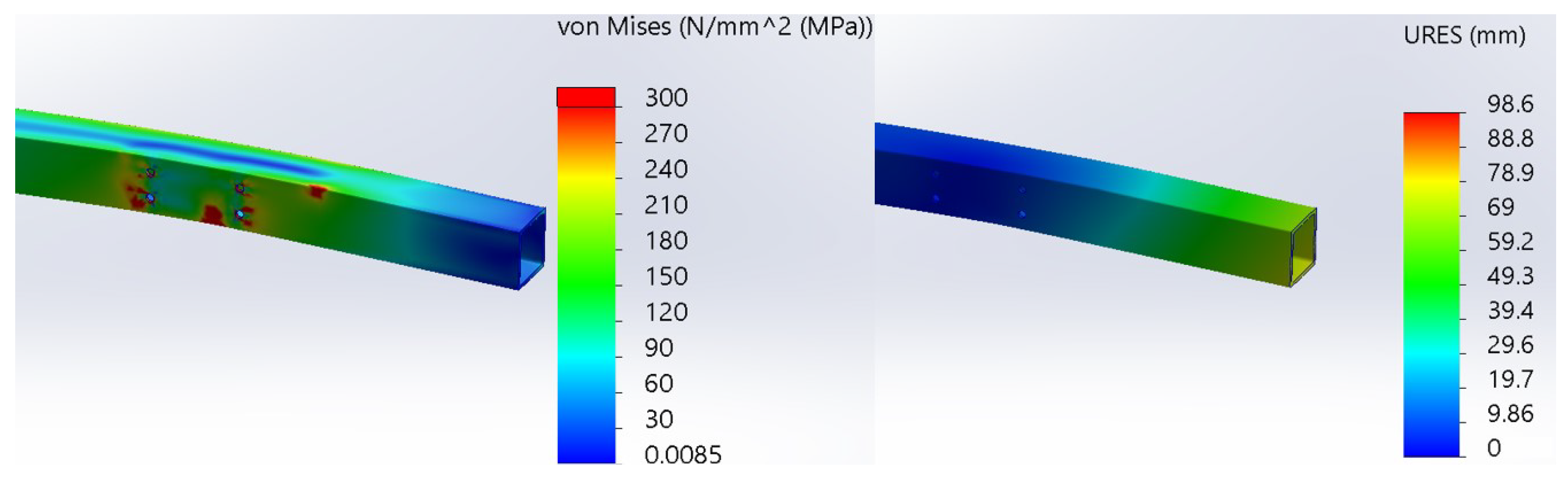
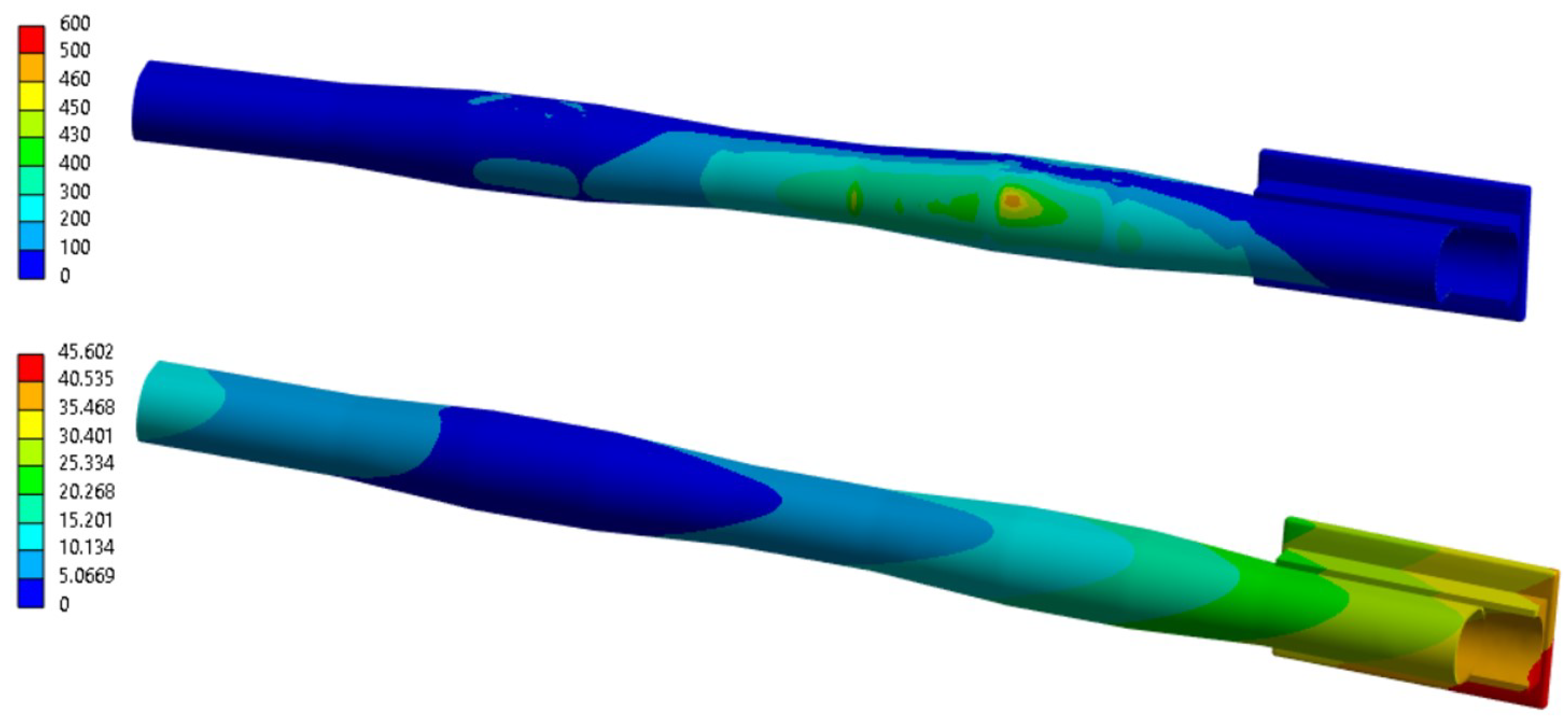
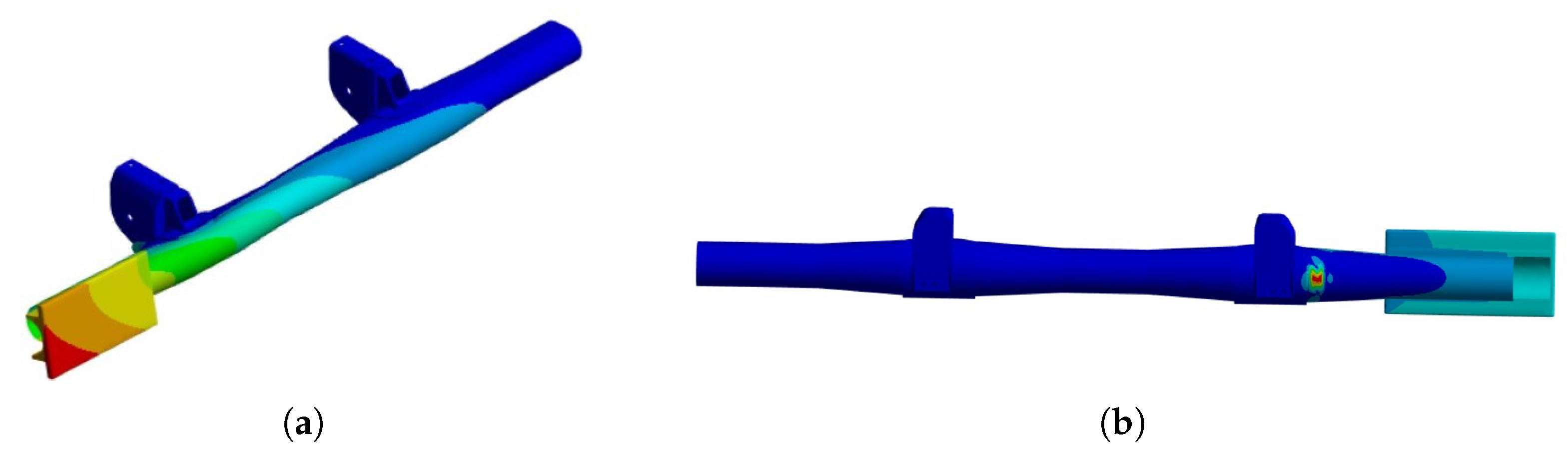
4. Discussion of the Results
5. Conclusions
- The GFRP configuration, when compared to the CFRP one, exhibits higher displacement under load due to its lower stiffness;
- However, the glass fibre solution requires a lower economic investment (+23.8% compared to the original configuration) than the CFRP (+530.1%);
- The carbon fibre solution offers instead greater long-term economic savings (equal to 512.94 EUR) by the end of the vehicle’s useful life than the glass fibre one (equal to EUR 270.41). This is achieved due to a weight reduction of 55% (compared to the original configuration) for the CFRP solution, while a minor weight reduction of 18% for the GFRP configuration was evaluated.
- This method is costlier than alternatives due to the necessity of experimental equipment and prototypes;
- Nevertheless, it does not necessitate expensive optimization tools;
- The selection is dependent upon the requirements of the end user: if optimization is necessary for a singular component, the presented methodology may serve as a viable solution, yielding more dependable outcomes. However, when this method is consistently implemented, the cost of this design strategy is not justified.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| FUPD | front underrun protection device |
| GFRP | glass-fibre-reinforced polymer |
| CFRP | carbon-fibre-reinforced polymer |
| FEM | finite element method |
| LD | linear dichroism |
References
- Njuguna, J. (Ed.) Lightweight Composite Structures in Transport: Design, Manufacturing, Analysis and Performance; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar] [CrossRef]
- Solazzi, L. Feasibility study of hydraulic cylinder subject to high pressure made of aluminum alloy and composite material. Compos. Struct. 2019, 209, 739–746. [Google Scholar] [CrossRef]
- Bonanno, A.; Crupi, V.; Epasto, G.; Guglielmino, E.; Palomba, G. Aluminum honeycomb sandwich for protective structures of earth moving machines. Procedia Struct. Integr. 2018, 8, 332–344. [Google Scholar] [CrossRef]
- Solazzi, L.; Danzi, N. Jib crane lightweighting through composite material and prestressing technique. Compos. Struct. 2024, 343, 118283. [Google Scholar] [CrossRef]
- Suvorov, V.; Vasilyev, R.; Melnikov, B.; Kuznetsov, I.; Bahrami, M.R. Weight Reduction of a Ship Crane Truss Structure Made of Composites. Appl. Sci. 2023, 13, 8916. [Google Scholar] [CrossRef]
- Faruk, O.; Tjong, J.; Sain, M. (Eds.) Lightweight and Sustainable Materials for Automotive Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Mallick, P.K. (Ed.) Materials, Design and Manufacturing for Lightweight Vehicles; Woodhead Publishing: Sawston, UK, 2020. [Google Scholar]
- Braga, D.F.; Tavares, S.M.O.; Da Silva, L.F.; Moreira, P.M.G.P.; De Castro, P.M. Advanced design for lightweight structures: Review and prospects. Prog. Aerosp. Sci. 2014, 6, 29–39. [Google Scholar] [CrossRef]
- Potes, F.C.; Silva, J.M.; Gamboa, P.V. Development and characterization of a natural lightweight composite solution for aircraft structural applications. Compos. Struct. 2016, 136, 430–440. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Dib, A.; Babamohammadi, S.; Campigli, S.; Benedetti, D.; Agnelli, J. Mechanical analysis of a carbon fiber composite woven composite laminate for ultra-light applications in aeronautics. Compos. Part C Open Access 2024, 14, 100447. [Google Scholar] [CrossRef]
- Saeedi, A.; Motavalli, M.; Shahverdi, M. Recent advancements in the applications of fiber-reinforced polymer structures in railway industry—A review. Polym. Compos. 2024, 45, 77–97. [Google Scholar] [CrossRef]
- Dragatogiannis, D.A.; Zaverdinos, G.; Galanis, A. Structural Analysis of Deck Reinforcement on Composite Yacht for Crane Installation. J. Mar. Sci. Eng. 2024, 12, 934. [Google Scholar] [CrossRef]
- Rahman, M.H.; Ma, S.; Mahfuz, H. Finite element simulation of composite ship structures under extreme wave and slamming loads. In Proceedings of the 2013 Grand Challenges on Modeling and Simulation Conference, Vista, CA, USA, 7–10 July 2013. [Google Scholar]
- Gardie, E.; Paramasivam, V.; Dubale, H.; Chekol, E.T.; Selvaraj, K. Numerical analysis of reinforced carbon fiber composite material for lightweight automotive wheel application. Mater. Today Proc. 2021, 46, 7369–7374. [Google Scholar] [CrossRef]
- Ciampaglia, A.; Santini, A.; Belingardi, G. Design and analysis of automotive lightweight materials suspension based on finite element analysis. Proc. Inst. Mech. Eng. Part C 2020, 235, 1501–1511. [Google Scholar] [CrossRef]
- Collotta, M.; Solazzi, L. New design concept of a tank made of plastic material for firefighting vehicle. Int. J. Automot. Mech. Eng. 2017, 14, 4603–4615. [Google Scholar] [CrossRef]
- Solazzi, L.; Danzi, N.; Pasinetti, M. Development and Design of an Innovative and Lightweight Reconnaissance Rover Using Composite Materials. J. Multiscale Model. 2024, 15, 2441003. [Google Scholar] [CrossRef]
- Solazzi, L.; Bertoli, D.; Ghidini, L. Static and dynamic study of the industrial vehicle transmission adopting composite materials. Compos. Struct. 2023, 316, 117042. [Google Scholar] [CrossRef]
- Carpinteri, A. Scienza Delle Costruzioni 1; Società Editrice Esculapio: Bologna, Italy, 2023. [Google Scholar]
- Jerath, S. Structural Stability Theory and Practice: Buckling of Columns, Beams, Plates, and Shells; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- da Silva, L.S.; Simoes, R.; Gervasio, H. Design of Steel Structures: Eurocode 3: Design of Steel Structures-General Rules and Rules for Buildings, 1st ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2013. [Google Scholar]
- Vasiliev, V.V.; Morozov, E.V. Advanced Mechanics of Composite Materials and Structures; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Ashby, M.F.; Cebon, D. Materials selection in mechanical design. MRS Bull. 2005, 30, 995. [Google Scholar] [CrossRef]
- Christensen, R.M. Mechanics of Composite Materials; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Naik, N.K.; Kumar, R.S. Compressive strength of unidirectional composites: Evaluation and comparison of prediction models. Compos. Struct. 1999, 46, 299–308. [Google Scholar] [CrossRef]
- Xu, Y.L.; Reifsnider, K.L. Micromechanical modeling of composite compressive strength. J. Compos. Mater. 1993, 27, 572–588. [Google Scholar] [CrossRef]
- Fleck, N.A.; Budiansky, B. Compressive failure of fibre composites due to microbuckling. In Inelastic Deformation of Composite Materials: IUTAM Symposium, Troy, New York, 29 May–1 June 1990; Springer: New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Solazzi, L.; Vaccari, M. Reliability design of a pressure vessel made of composite materials. Compos. Struct. 2022, 279, 114726. [Google Scholar] [CrossRef]
- Solazzi, L. Reliability evaluation of critical local buckling load on the thin walled cylindrical shell made of composite material. Compos. Struct. 2022, 284, 115163. [Google Scholar] [CrossRef]
- Stojcevski, F.; Hilditch, T.; Henderson, L.C. A modern account of Iosipescu testing. Compos. Part A Appl. Sci. Manuf. 2018, 107, 545–554. [Google Scholar] [CrossRef]
- Komartin, R.S.; Balanuca, B.; Necolau, M.I.; Cojocaru, A.; Stan, R. Composite materials from renewable resources as sustainable corrosion protection coatings. Polymers 2021, 13, 3792. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zheng, Y. Constructing multi-protective functional polyurethane composite coating via internal-external dual modification: Achieving superhydrophobicity, enhanced barrier, corrosion inhibition, and UV aging resistance properties. Prog. Org. Coat. 2024, 194, 108540. [Google Scholar] [CrossRef]
- Nikbakt, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures Part I: Laminated composites. Compos. Struct. 2018, 195, 158–185. [Google Scholar] [CrossRef]
- Solazzi, L. Applied research for weight reduction of an industrial trailer. Fme Trans. 2012, 40, 57–62. [Google Scholar]
- European Union. Regulation No 93 of the Economic Commission for Europe of the United Nations (UN/ECE), Uniform Provisions Concerning the Approval of: I. Front underrun protective devices (FUPDs)—II. Vehicles with regard to the Installation of an FUPD of an Approved Type—III. Vehicles with Regard to Their Front Underrun Protection (FUP); European Union: Brussels, Belgium, 17 July 2010. [Google Scholar]
- Lombaert, G.; Degrande, G. The experimental validation of a numerical model for the prediction of the vibrations in the free field produced by road traffic. J. Sound Vib. 2003, 262, 309–331. [Google Scholar] [CrossRef]
- Zhang, Y.-L.; Lin, H.-B.; Zhu, Z.-C. Numerical study on the forward and inverse problems of the mobile pump truck frame. Sci. Rep. 2024, 14, 20329. [Google Scholar] [CrossRef]
- Gould, P.L.; Feng, Y. Introduction to Linear Elasticity; Springer: New York, NY, USA, 1994; Volume 2. [Google Scholar]
- Visconti, I.C.; Caprino, G.; Langella, A. Materiali Compositi: Tecnologie, Progettazione, Applicazioni; U. Hoepli: Milano, Italy, 2009. [Google Scholar]
- Balasubramanian, M. Composite Materials and Processing; CRC Press: Boca Raton, FL, USA, 2014; Volume 711. [Google Scholar]
- Ochola, R.; Marcus, K.; Nurick, G.; Franz, T. Mechanical behaviour of glass and carbon fibre reinforced composites at varying strain rates. Compos. Struct. 2004, 63, 455–467. [Google Scholar] [CrossRef]
- David Müzel, S.; Bonhin, E.P.; Guimarães, N.M.; Guidi, E.S. Application of the finite element method in the analysis of composite materials: A review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef]
- High-Strength Aluminum Powder Metallurgy Alloys. Properties and Selection: Nonferrous Alloys and Special-Purpose Materials. 1990. Available online: https://www.tagmaindia.org/public/Doc/asm-handbook-volume-2.pdf (accessed on 26 April 2024).
- Toray Composite Materials America Inc. M50J High Modulus Carbon Fiber. Available online: https://cdn.thomasnet.com/ccp/30164375/140079.pdf (accessed on 26 April 2024).
- Mates Italiana, Product Data Sheet: SX10. Available online: https://fileserver.mates.it/Prodotti/2_Matrici/TDS/Resine/Mates/SX10_DS.pdf (accessed on 26 April 2024).
- Solazzi, L.; Buffoli, A. Fatigue design of hydraulic cylinder made of composite material. Compos. Struct. 2021, 277, 114647. [Google Scholar] [CrossRef]
- Konchakova, N.; Mueller, R.; Barth, F.J. Modelling of damage evolution in adhesive metal-composite structures for various joint designs. Mech. Control 2011, 30, 213–220. [Google Scholar]
- Meszler, D.; Delgado, O.; Rodríguez, F.; Muncrief, R. European Heavy-Duty Vehicles: Cost-Effectiveness of Fuel-Efficiency Technologies for Long-Haul Tractor-Trailers in the 2025–2030 Timeframe; International Council on Clean Transportation: Washington, DC, USA, 2018. [Google Scholar]
- Ministero Delle Infrastrutture e dei Trasporti. Costo Chilometrico Medio Relativo al Consumo di Gasolio Delle Imprese di Autotrasporto per Conto Terzi. Available online: http://www.mit.gov.it/sites/default/files/media/documentazione/2016-03/costo%20chilometrico%20medio%20consumo%20gasolio%20FEBBRAIO%202010.pdf (accessed on 19 March 2024).
- Kim, H.C.; Wallington, T.J. Life cycle assessment of vehicle lightweighting: A physics-based model to estimate use-phase fuel consumption of electrified vehicles. Environ. Sci. Technol. 2016, 50, 11226–11233. [Google Scholar] [CrossRef]
- Agenzia per la Protezione dell’Ambiente e dei Servizi Tecnici. Analisi dei Fattori di Emissione di CO2 dal Settore dei Trasporti. Available online: https://www.isprambiente.gov.it/contentfiles/00003900/3906-rapporti-03-28.pdf (accessed on 19 March 2024).















| Ultimate Tensile Strength Rm [MPa] | Yield Strength [MPa] | Young’s Modulus E [Mpa] | Density [kg/m3] | Poisson’s Coefficient ν |
|---|---|---|---|---|
| 620 | 460 | 210,000 | 7860 | 0.29 |
| Mechanical Property | Symbol | Value | UOF |
|---|---|---|---|
| Bending elasticity modulus | 29 | GPa | |
| Longitudinal tensile elasticity modulus | 29 | GPa | |
| Transversal tensile elasticity modulus | 7 | GPa | |
| Shear elasticity modulus | 3 | GPa | |
| Longitudinal tensile strength | 240 | MPa | |
| Transversal tensile strength | 50 | MPa | |
| Longitudinal bending strength | 240 | MPa | |
| Transversal bending strength | 100 | MPa | |
| Density | 1.92 | kg/dm3 | |
| Glass fibre percentage | 58 | % |
| FOS | Rated Load [daN] | Actual Load [daN] | Deviation [%] | |
|---|---|---|---|---|
| FEM values | 0.446 | 6000 | 2676.44 | |
| Experimental test values | 0.449 | 6000 | 2811.16 | ref. |
| Ultimate Tensile Strength Rm [MPa] | Yield Strength [MPa] | Young’s Module E [Mpa] | Density [kg/m3] | Poisson’s Coefficient ν |
|---|---|---|---|---|
| 570 | 505 | 72,000 | 2.81 | 0.33 |
| Carbon Fibre | Epoxy Resin | |||
|---|---|---|---|---|
| Property | Symbol | Value | Symbol | Value |
| Density | 1880 kg/m3 | 1200 kg/m3 | ||
| Young’s modulus | 475 GPa | 3.3 GPa | ||
| Tensile strength | 4120 MPa | 65 MPa | ||
| Compressive strength | - | 120 MPa | ||
| Poisson ratio | 0.28 | 0.34 | ||
| Mechanical Property | Symbol | Value | U.O.M. |
|---|---|---|---|
| Longitudinal tensile elasticity modulus | 286 | GPa | |
| Transversal tensile elasticity modulus | 8.16 | GPa | |
| Shear elasticity modulus | 3 | GPa | |
| Longitudinal tensile strength | 2472 | MPa | |
| Transversal tensile strength | 45 | MPa | |
| Longitudinal compression strength | 880 | GPa | |
| Transversal compression strength | 99.2 | MPa | |
| Shear strength | S | 59 | MPa |
| Density | 1608 | [kg/m3] | |
| Poisson ratio | 0.3 | ||
| Carbon fibre percentage | 60 | % |
| Steel S460Q | Glass Fibre Reinforced Polymer | Carbon Fibre Reinforced Polymer | ||||
|---|---|---|---|---|---|---|
| Weight [kg] | Cost [EUR] | Weight [kg] | Cost [EUR] | Weight [kg] | Cost [EUR] | |
| Brackets | 4.38 (S460Q) | 14.76 | 4.59 (Al 7075-T6) | 23.3 | 2.22 (Al 7075-T6) | 10.71 |
| FUPD | 17.58 | 59.50 | 12.36 | 57.9 | 7.51 | 450.6 |
| links | - | - | 1.13 | 10.74 | 0.02 | 6.6 |
| Total | 21.96 | 74.26 | 18.08 | 91.94 | 9.75 | 467.91 |
| Percentage change | - | - | −17.7% | +23.8% | −55.6% | +530.1% |
| Property | Value CFRP | Value GFRP | U.O.M. |
|---|---|---|---|
| Standard consumption [49] | 0.21 | 0.21 | L/km |
| Annual mileage [48] | 135,000 | 135,000 | km/year |
| Fuel consumption | 28,350 | 28,350 | L/year |
| Fuel consumption variation index for Internal Combustion Engine Vehicles (ICEVs) [50] | 0.000025 | 0.000025 | L/(km kg) |
| Mass decrease with respect to the standard solution | 12.21 | 3.88 | kg |
| Optimized consumption | 0.000305 | 0.000097 | L/km |
| Fuel consumption (optimised semi-trailer) | 28,308.79 | 28,336.91 | L/year |
| Fuel consumption decrease (with respect to the standard solution) | 41.21 | 13.09 | L/year |
| CO2 emissions per kilogram of diesel [51] | 3.17 | 3.17 | kgCO2/kgdiesel |
| Density of diesel (at 15 °C) | 820 | 820 | kg/m3 |
| CO2 emissions per litre of diesel | 2.60 | 2.60 | kgCO2/ldiesel |
| Reduction in CO2 emissions (with respect to the standard solution) | 107.12 | 34.04 | kgCO2/year |
| Current diesel price | 2 | 2 | EUR/L |
| Economic saving (with respect to the standard solution) | 82.42 | 26.19 | EUR/year |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomasi, I.; Grandi, S.; Solazzi, L. Implementation of Composite Materials for an Industrial Vehicle Component: A Design Approach. J. Compos. Sci. 2025, 9, 168. https://doi.org/10.3390/jcs9040168
Tomasi I, Grandi S, Solazzi L. Implementation of Composite Materials for an Industrial Vehicle Component: A Design Approach. Journal of Composites Science. 2025; 9(4):168. https://doi.org/10.3390/jcs9040168
Chicago/Turabian StyleTomasi, Ivan, Stefano Grandi, and Luigi Solazzi. 2025. "Implementation of Composite Materials for an Industrial Vehicle Component: A Design Approach" Journal of Composites Science 9, no. 4: 168. https://doi.org/10.3390/jcs9040168
APA StyleTomasi, I., Grandi, S., & Solazzi, L. (2025). Implementation of Composite Materials for an Industrial Vehicle Component: A Design Approach. Journal of Composites Science, 9(4), 168. https://doi.org/10.3390/jcs9040168










