Fracture Behavior of Additively Manufactured Carbon Fiber Reinforced Acrylonitrile-Styrene-Acrylate Containing Cracks and Notches

Abstract

Within the context of the increasing use of additive manufacturing techniques and the corresponding need to understand the behavior of 3D-printed materials, this paper analyzes the fracture behavior of additively manufactured carbon fiber reinforced (10 wt.%) acrylonitrile-styrene-acrylate (ASA) with three different raster orientations (90/0, 45/−45, 30/−60). The analyzed material (ASA-CF10) combines the remarkable resistance to weathering agents typical of ASA with the enhanced mechanical properties resulting from the inclusion of carbon fiber reinforcement. The analysis is performed on single-edge-notched bending (SENB) specimens containing different types of defects, from cracks to U-notches with notch radii of 0.5 mm, 1 mm and 2 mm. When compared to non-reinforced ASA, the fracture resistance is noticeably higher (nearly double) for the reinforced material in all raster orientations. The notch effect, defined as the increase in the fracture resistance when the notch radius increases, is analyzed through the Theory of Critical Distances (TCD), and it is mostly higher in the reinforced material than in the pristine polymer. These observations are supported by Scanning Electron Microscopy analyses.

1. Introduction

Additive manufacturing is an extensively used technology that is capable of generating intricate geometries through a relatively simple process. Among its different technologies, Fused Filament Fabrication (FFF) is of particular interest due to its versatility and simplicity. It consists of extruding a heated plastic filament through a nozzle, which is deposited layer by layer to build a predefined digital model. FFF requires materials with a low coefficient of thermal expansion and an adequate fluid index, together with sufficiently high mechanical properties [1]. This technology has been the subject of extensive research aimed at optimizing the properties of the resulting materials, covering everything from the definition of printing parameters to the application of potential post-treatments on the printed parts (e.g., [2,3]).

Focusing on polymers and polymer-matrix composites, the most typical materials used in FFF are acrylonitrile–butadiene–styrene (ABS) and polylactic acid (PLA), whose fracture behavior has been analyzed by the authors in [4,5]. Generally, FFF polymers have poor mechanical performance when compared to other structural materials, so they have often been combined with reinforcements (e.g., graphene, nanotubes, particles, fibers) [6,7] to generate improved mechanical properties. In this sense, research on the fracture behavior of FFF polymers and polymer–matrix composites has been abundant in recent years (e.g., [8,9,10,11,12,13,14,15,16,17,18]).

Within this frame of reference, ASA terpolymer arises as a promising alternative. It presents a core–shell structure similar to that of ABS, but where acrylate rubber replaces butadiene rubber, thus mitigating the consequences of butadiene ageing [19].

There are several works analyzing the tensile properties of additively manufactured ASA (e.g., [20,21]), generally revealing modest performance, with reported moderate tensile strengths which are generally below 30 MPa. Regarding fracture behavior, the data available in literature are scarcer (e.g., [22]). Indeed, so far, the only work analyzing the notch effect (on fracture resistance) developed by ASA has been recently published by the authors [23], revealing both moderate fracture toughness and low notch effect. However, the notch effect may be crucial from a structural integrity point of view, as there are materials for which introducing a small radius in the defect tip may generate noteworthy rises in the fracture resistance (e.g., [24]).

With the aim of overcoming the modest mechanical properties of FFF ASA material, one of the most promising lightweight alternatives is the addition of carbon fiber (CF), which provides additional strength, ability to withstand high temperatures and chemical resistance. CF is non-toxic, has a low density, is highly resistant to wear and is non-corrosive and recyclable, with an exceptional strength-to-weight ratio. Overall, it has exceptional thermal, mechanical and electrical properties. CF is produced by carbonization of source materials such as synthetic polymers (such as polyacrylonitrile, tar resin or rayon yarn) through oxidation and thermal treatments at high temperatures, with a fine control of final properties. CF-reinforced polymer matrix composites are widely used in different applications for their excellent mechanical, thermal, electrical, structural and tribological properties [25,26]. Concerning carbon reinforced ASA (ASA-CF), few studies have been reported so far in the literature. Sanchez et al. [27] implemented ASA in a large format additive manufacturing (LFAM) device, focusing on the development and characterization of ASA and carbon fiber for LFAM. The 20% weight ASA-CF composite showed a 350% increase in flexural Young’s modulus compared to raw ASA and a 500% improvement in thermal conductivity. Song et al. [28] analyzed ASA-CF composites that were manufactured by injection molding. The effects of CF on the morphology, mechanical and rheological properties of ASA composites were investigated.

With all this, once the importance and potential of FFF technology, ASA polymer and CF reinforcement has been described, together with the lack of knowledge regarding the fracture behavior of FFF ASA-CF material, this work analyzes the fracture behavior of (FFF) carbon fiber reinforced (10 wt.%) ASA SENB specimens containing U-notches of different notch radii (ρ), thus making it possible to analyze both the fracture behavior and the notch effect in this particular material. This carbon fiber content (10 wt.%) was selected for being a generally commercially available option and for offering a particularly interesting combination of enhanced mechanical properties (when compared to pure ASA) and printability. The analysis covers three different raster orientations (RO). The theoretical framework used to analyze the notch effect is the Theory of Critical Distances (TCD) [24].

2. Materials and Methods

The material used in this research was provided by 3DJake (Paldau, Austria) as ASA-matrix commercial filaments with a carbon fiber content of 10 wt.% (here, referred to as ASA-CF10). The samples were fabricated by FFF with the following parameters: layer height: 0.2 mm; line width: 0.42 mm; infill degree: 100%; printing temperature: 250 °C; bed temperature: 90 °C; printing speed: 40 mm/s. These parameters fall within the recommended ranges provided by the filament manufacturer and are the same as those used in [23] for the pristine ASA material, allowing for a direct comparison between the results. In this regard, it is important to note that the objective of this work is not the optimization of the printing parameters, but rather the analysis of the notch effect of the materials obtained using commercially recommended printing parameters.

The experimental program covered 72 fracture tests and 9 tensile tests, all printed in the flat position. Figure 1 shows a schematic of both types of specimens, including the nominal dimensions. The fracture specimens covered notch radii of 0 mm (crack-like defects), 0.50 mm, 1 mm and 2 mm, and three different raster orientations (0/90, 45/−45 and 30/−60).

Each combination of notch radius and raster orientation was tested 6 times with the aim of capturing the characteristic scatter of fracture processes. In the case of the tensile tests, where scatter is much lower, three specimens were tested per combination. The notches of the SENB specimens were machined, except for those with a notch radius of 0 mm (i.e., crack-like defects), which were produced by sawing with a razor blade. This avoids introducing additional anisotropy around the notch tip. All tests were performed at room temperature with an applied loading rate of 1 mm/min. Tensile tests followed ASTM D638 [29] and were performed in a 5 kN capacity universal servo-hydraulic testing machine (Servosis, Madrid, Spain), whereas fracture tests followed ASTM D6068 [30], provided that the material response did not meet the linear-elastic criteria established in ASTM D5045 [31], and were performed in universal electro-mechanical machine (Zwick-Roell, Ulm, Germany) with a load capacity of 2.5 kN (see Figure 2).

The fracture resistance of the different SENB specimens was measured through the apparent fracture toughness (${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$), defined as the fracture resistance developed by the material in the presence of a notch and quantified by using the formulation provided by ASTM D6068 for cracked conditions. In the case of cracks, ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$ coincides with the material fracture toughness (K_mat). Critical conditions were evaluated at the maximum load of the corresponding load-displacement curve, assuming that there is no stable crack propagation before final fracture (this was confirmed in the fracture surfaces, see Section 3, where there was no trace of any stable propagation).

Once ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$ results were derived for all the specimens, they were analyzed by using the TCD [24]. This theory embraces different methodologies that are characterized by the use of a material length parameter denominated the critical distance (L), which in fracture analyses follows Equation (1):

$$\mathrm{L}={\displaystyle \frac{1}{\mathsf{\pi }}}{\left({\displaystyle \frac{{\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}}{{\mathsf{\sigma }}_0}}\right)}^2$$

(1)

σ₀ is the material inherent strength. In those materials with linear-elastic behavior at both the micro and the macro scales, σ₀ coincides with the material tensile strength (σ_u), whereas in materials with non-linear behavior (such as ASA and ASA-CF), σ₀ requires calibration. The reader is referred to [24] for further details on the TCD. Here, suffice it to say that one of the main approaches of the TCD is the Line Method (LM), which states that that fracture occurs when the average stress along a distance of 2L (measured from the defect tip) equals the inherent strength (σ₀) (see Figure 3):

$${\displaystyle \frac{1}{2\mathrm{L}}}{\int }_0^{2\mathrm{L}}\mathsf{\sigma }\left(\mathrm{r}\right)\mathrm{d}\mathrm{r}={\mathsf{\sigma }}_0$$

(2)

Finally, the combination of the LM with the Creager–Paris stress field at the notch tip [25] provides a simple equation that allows the apparent fracture toughness ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$ to be estimated [24]:

$${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}={\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}\sqrt{1+{\displaystyle \frac{\mathsf{\rho }}{4\mathrm{L}}}}$$

(3)

This equation may be used, together with the least squares criterion, to provide the best fit of the experimental results, with L being the fitting parameter and providing reliable estimations of this material parameter [4,23,24]. Besides, its application is circumscribed to slender U-notches, in agreement with the validity range of the Creager–Paris stress distribution. Nonetheless, the authors have applied this to analogous geometries to those analyzed in this research (i.e., SENB U-notched specimens with notch radii up to 2.0 mm) obtaining reasonably accurate results (e.g., [4,5,23,32]).

Here, it is important to note that there are other significant methodologies which are capable of addressing the analysis of the notch effect. Some examples are linear-elastic notch fracture mechanics (e.g., [33]), the Average Strain Energy Density (ASED) criterion (e.g., [34]) or progressive damage models (e.g., [35,36]).

3. Results and Discussion

3.1. Tensile Tests

The relevant tensile properties of the ASA-CF10 material, for each RO, are shown in

Table 1. Tensile properties for ASA-CF10 in each raster orientation (average and standard deviation). E: Young’s modulus; σ_t: tensile strength at break; ɛ_u: Strain under maximum load. Values for ASA material also included for comparison. L values from the fit of Equation (3).

Material	RO	E (MPa)	σt (MPa)	ɛu (%)	L (mm)
ASA-CF10	0/90	4002 ± 236	37.5 ± 0.4	1.8 ± 0.2	2.45
	45/−45	2797 ± 174	30.5 ± 1.8	2.0 ± 0.1	0.61
	30/−60	3496 ± 457	39.6 ± 6.2	1.9 ± 0.1	0.78
ASA [23]	0/90	1050 ± 66	19.4 ± 1.0	2.8 ± 0.2	1.68
	45/−45	1053 ± 22	18.5 ± 0.7	4.5 ± 0.2	1.29
	30/−60	990 ± 28	16.5 ± 0.1	2.8 ± 0.1	1.50

. Additionally, Figure 4 shows some examples of the obtained tensile curves, also including the curves obtained for the original ASA material [23]. The maximum strengths are achieved in raster orientations 0/90 and 30/−60, which also present the highest elastic moduli. These results are very different from those obtained for the pristine ASA material [23], where raster orientation 30/−60 presented the lowest tensile properties. In any case, ASA-CF10 material, for the three raster orientations, presents elastic moduli which are more than two times larger (almost four times larger for raster orientation 0/90) than those measured on ASA, and the tensile strength is also doubled (approximately). On the contrary, the strain under maximum load decreases significantly to values around 2% (from values in ASA between 2.8% and 4.5%). Qualitatively, it is worth mentioning that the tensile strength for the three raster orientations in ASA-CF10 material is located at break, with no further material capacity to develop additional strains, whereas in the ASA material the tensile strength was achieved at yield (i.e., the first point on the stress–strain curve at which an increase in strain occurs without an increase in stress [29]), developing (after yielding) non-linear decreasing stress–strain behavior up to the final failure.

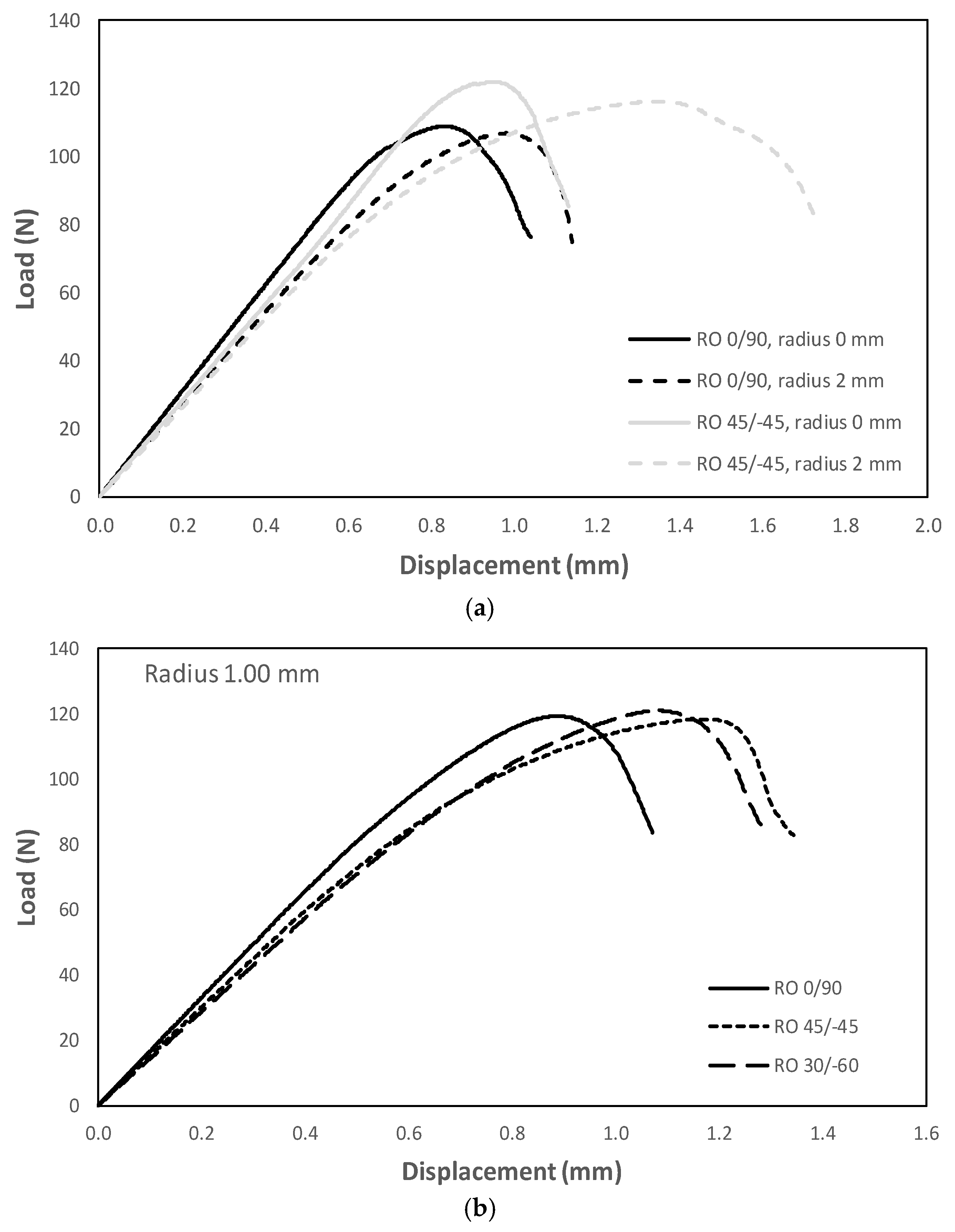
3.2. Fracture Tests

Fracture tests on ASA-CF10 SENB specimens were performed following ASTM D6068 standard [30], given that the obtained load–displacement curves did not meet the (linear-elastic) requirements of ASTM 5045 [31]. This is the same situation experienced for the ASA material [23]. The load–displacement curves have an initial linear-elastic behavior followed by a loss of linearity up to the maximum load of the curve, which is finally followed by a decreasing load–displacement relation. The details of the tests are openly available at [37]. Considering that no stable crack propagation was detected before the final rupture of the specimens, a critical value of the J integral at maximum load (P_crit) was calculated as follows [30]:

$${\mathrm{J}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}={\displaystyle \frac{\mathsf{\eta }\times {\mathrm{U}}^{\mathrm{N}}}{\mathrm{B}\times (\mathrm{W}-{\mathrm{a}}_0)}}$$

(4)

with U^N being the area below the load–displacements curve up to the maximum load (see Figure 5), η being a coefficient equal to 2 for SENB specimens, B being the thickness of the specimen, W being the width of the specimen and a₀ being the defect length. The results obtained from Equation (4) were subsequently converted into stress intensity factor units as follows:

$${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}=\sqrt{{\displaystyle \frac{{\mathrm{J}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}\times \mathrm{E}}{1-{\mathsf{\upsilon }}^2}}}$$

(5)

with υ being the Poisson’s ratio and E being the Young’s modulus. Figure 5 shows examples of the obtained load–displacement curves, while

Table A1. Raster orientation (RO) 0/90. Actual geometrical measurements and experimental apparent fracture toughness results (individual tests together with the average and standard deviation for the different combinations of raster orientation and notch radius). RO: raster orientation; ρ: notch radius; W: specimen width; B: specimen thickness; S: specimen span; a₀: crack length; ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$: apparent fracture toughness; ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t},\mathrm{a}\mathrm{v}\mathrm{g}}^{\mathrm{N}}$: average value of apparent fracture toughness; Std. Dev.: standard deviation of ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$.

RO	Test nº	ρ (mm)	W (mm)	B (mm)	S (mm)	a0 (mm)	Pmax (N)	${\mathbf{K}}_{\mathbf{m}\mathbf{a}\mathbf{t}}^{\mathbf{N}}$ (MPam1/2)	${\mathbf{K}}_{\mathbf{m}\mathbf{a}\mathbf{t},\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathbf{N}}$ (MPam1/2)	Std. Dev. (MPam1/2)
0/90	1	0.00	10.04	4.94	40.00	5.37	104.9	4.72	4.47	0.17
	2	0.00	10.11	4.97	40.00	5.77	86.1	4.47
	3	0.00	10.02	4.93	40.00	5.15	108.9	4.39
	4	0.00	10.15	5.00	40.00	5.62	101.7	4.26
	5	0.00	10.12	4.93	40.00	5.00 *	127.0	4.56
	6	0.00	10.14	4.95	40.00	4.63	-	-
	1	0.65	10.03	4.97	40.00	5.43	100.9	4.47	4.53	0.12
	2	0.65	10.10	5.05	40.00	5.55	99.6	4.50
	3	0.64	10.10	4.90	40.00	5.50	97.9	4.36
	4	0.65	10.11	4.97	40.00	5.50	101.6	4.55
	5	0.65	10.03	4.98	40.00	5.43	105.6	4.72
	6	0.66	10.20	4.98	40.00	5.64	105.5	4.61
	1	1.08	10.26	4.95	40.00	5.14	116.2	4.68	4.69	0.15
	2	1.09	10.12	4.98	40.00	5.32	119.4	4.76
	3	1.07	10.19	4.95	40.00	5.26	108.7	4.60
	4	1.07	10.24	4.99	40.00	5.30	112.7	4.57
	5	1.00	10.09	5.00	40.00	5.17	111.6	4.57
	6	1.06	10.24	4.92	40.00	5.43	120.2	4.97
	1	2.08	10.05	4.99	40.00	5.62	135.3	4.98	4.92	0.09
	2	2.14	10.25	4.98	40.00	5.75	103.4	4.98
	3	2.14	10.05	4.91	40.00	5.63	104.2	4.94
	4	2.14	10.03	4.94	40.00	5.59	102.0	4.84
	5	2.12	10.08	4.97	40.00	5.68	103.6	4.79
	6	2.10	10.20	4.97	40.00	5.72	107.8	5.00
45/−45	1	0.00	10.19	4.96	40.00	5.55	97.45	4.050	4.05	0.20
	2	0.00	10.31	4.9	40.00	5.44	110.12	4.104
	3	0.00	9.99	4.78	40.00	5.12	120.51	4.000
	4	0.00	10.12	4.94	40.00	5.16	114.78	3.694
	5	0.00	10.24	4.83	40.00	5.33	121.88	4.157
	6	0.00	10.24	4.87	40.00	4.80 *	150.37	4.274
	1	0.66	9.97	4.83	40.00	5.48	99.95	4.314	4.43	0.12
	2	0.66	10.19	4.92	40.00	5.60	108.37	4.490
	3	0.65	10.15	4.95	40.00	5.51	113.48	4.539
	4	0.64	10.32	4.9	40.00	5.72	108.05	4.536
	5	0.67	10.03	4.84	40.00	5.56	108.07	4.451
	6	0.64	10.06	4.87	40.00	5.47	108.15	4.239
	1	1.11	10.24	5.03	40.00	5.21	128.33	4.815	4.77	0.16
	2	1.15	10.21	4.96	40.00	5.37	129.45	5.016
	3	1.12	9.97	4.82	40.00	5.03	118.33	4.787
	4	1.12	10.22	5.03	40.00	5.41	116.22	4.640
	5	1.13	10.07	4.88	40.00	5.23	117.03	4.548
	6	1.13	10.23	4.93	40.00	5.42	123.25	4.793
	1	2.06	10.14	4.9	40.00	5.71	113.27	5.657	5.47	0.18
	2	2.07	10.15	4.91	40.00	5.66	116.17	5.301
	3	2.09	10.04	4.85	40.00	5.50	121.61	5.651
	4	2.07	9.99	4.68	40.00	5.81	92.42	5.472
	5	2.09	10.17	3.57	40.00	5.73	81.98	5.551
	6	2.08	10.24	4.77	40.00	5.77	107.59	5.211
30/−60	1	0.00	10.11	4.91	40.00	5.32	119.75	4.82	4.46	0.36
	2	0.00	10.22	4.87	40.00	5.69	107.36	4.59
	3	0.00	10.23	4.87	40.00	5.24	128.85	4.83
	4	0.00	10.01	4.9	40.00	4.94 *	135.00	4.40
	5	0.00	9.97	4.87	40.00	5.72	83.67	3.90
	6	0.00	10.13	4.89	40.00	5.11	112.86	4.22
	1	0.70	10.09	4.94	40.00	5.29	114.4	4.79	4.61	0.26
	2	0.64	10.17	4.89	40.00	5.40	106.5	4.59
	3	0.66	10.30	4.90	40.00	5.59	111.7	4.75
	4	0.64	9.99	4.86	40.00	5.39	96.3	4.31
	5	0.65	10.23	4.92	40.00	5.55	112.3	4.92
	6	0.66	9.99	4.89	40.00	5.20	99.6	4.30
	1	1.10	10.04	4.97	40.00	5.16	120.92	4.98	5.07	0.20
	2	1.10	10.19	4.90	40.00	5.40	122.94	5.18
	3	1.07	10.24	4.88	40.00	5.57	121.02	5.13
	4	1.11	10.14	4.91	40.00	5.11	122.12	4.84
	5	1.15	10.07	4.88	40.00	5.09	120.72	4.91
	6	1.13	10.16	4.91	40.00	5.41	125.41	5.38
	1	2.07	10.30	4.91	40.00	5.81	119.34	5.84	5.80	0.29
	2	2.12	10.05	4.90	40.00	5.59	109.84	5.73
	3	2.08	10.20	4.92	40.00	5.70	116.76	6.28
	4	2.09	10.13	4.92	40.00	5.62	112.43	5.39
	5	2.09	10.18	4.91	40.00	5.68	113.68	5.76
	6	2.10	10.35	4.92	40.00	5.85	117.07	5.83

* Specimens where a₀/W is (slightly) out of range following [30] (0.50 ≤ a₀/W ≤ 0.65).

(see Appendix A) gathers the individual results of the different tests. It can be observed (Figure 5a) how the notch effect is very moderate for raster orientation 0/90 (i.e., similar area below the curve for the crack and the 2 mm notch radius), and much more evident for raster orientation 45/−45, where the area below the curve (thus, ${\mathrm{J}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$ and ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$) significantly increases when increasing the notch radius. Moreover, Figure 5b shows that, for a given notch radius (1 mm), the area below the curve up to the maximum load is lower for raster orientation 0/90 and higher for raster orientations 45/−45 and 30/−60.

Figure 6 shows the results of the fracture tests, also including the best-fit (Equation (3), least squares methodology) providing the values of L for each raster orientation included in Table 1. Raster orientation 0/90 and 30/−60 have the highest values of K_mat, but when a finite notch radius appears on the notch tip, raster orientation 30/−60, with a larger notch effect (smaller L), quickly develops higher values of ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$. Raster orientation 45/-45 develops the largest notch effect (smallest L) and provides higher values of ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$ than raster orientation 0/90 for notch radii above 1 mm (always lower than those provided by raster orientation 30/−60 for the range of notch radii considered here). Thus, raster orientation 30/−60 shows the best fracture behavior across the entire range of notch radii analyzed in this work, developing a significant notch effect. Raster orientation 45/−45 has the lowest fracture resistance under cracked conditions, but since it develops the largest notch effect, its fracture resistance in notched conditions becomes higher than that observed in raster orientation 0/90. The latter, whose fracture resistance in cracked conditions is practically equal to that of raster orientation 30/−60, develops a significantly smaller notch effect than the other two cases and, therefore, becomes the least resistant raster orientation for notch radii greater than 1 mm.

When comparing ASA and ASA-CF10, the latter presents K_mat values in cracked conditions of 4.47, 4.05 and 4.46 MPam^1/2 for raster orientations of 0/90, 45/−45 and 30/−60, respectively, whereas such values in ASA were noticeably lower: 2.47, 2.90 and 2.72 MPam^1/2 (i.e., the increase ranges between 80.9% in raster orientation 0/90 and 41.0% in raster orientation 45/−45).

Regarding the notch effect, L in ASA-CF10 is around one half of that measured in ASA [23] for raster orientation 45/−45 and raster orientation 30/−60, and around twice that for raster orientation 0/90, so the sensitivity to the notch effect in these two materials depends very much on the raster orientation being considered.

3.3. SEM Analysis

Figure 7 shows SEM images of the fracture surfaces of specimens with raster orientation 0/90 and 30/−60 (the latter being very similar to raster orientation 45/−45). The orientation of the different filaments is indicated in the different images. They all show the defect front (crack or notch) in the lower part of the corresponding image. In both cases, the fracture mechanisms are very similar when comparing cracked and notched specimens, but in raster orientation 30/−60 (as in raster orientation 45/−45) the length of the fibers remaining above the fracture surface generally seems larger in the notched case. This may suggest a larger bridging effect, enhancing ${\mathrm{K}}_{\mathrm{m}\mathrm{a}\mathrm{t}}^{\mathrm{N}}$. This was not observed in raster orientation 0/90, so the notch effect is more moderate, and it is solely generated by the stress relaxation caused by the notch. As shown by the authors in previous works (e.g., [32,38,39]), the generation of a large notch effect requires that fracture mechanisms evolve with increasing notch radius, such that as the notch radius increases, more non-linear or complex (e.g., plasticity, bridging) fracture micromechanisms appear. In contrast, in materials where the increase in the notch radius is not accompanied by an evolution in the fracture micromechanisms, the notch effect is caused solely by the stress relaxation and is much more moderate (e.g., [40]).

Macroscopically, the fracture planes were always perpendicular to the longitudinal direction of the specimens (i.e., perpendicular to the principal bending stresses), see Figure 7, whereas in [23] the ASA material had fracture planes clearly following one of the printing directions.

4. Conclusions

This paper analyzes the fracture behavior of FFF carbon reinforced (10 wt.%) ASA (referred to ASA-CF10) when containing cracks and notches with notch radii up to 2 mm. This kind of analysis is essential to understand the possible structural applications of additively manufactured printed parts made of this particular material and also to understand the effect of raster orientation and fiber content in the resulting mechanical behavior. The obtained results have been compared to those previously obtained in the pristine (non-reinforced) ASA. The main conclusions are as follows:

• ASA-CF10 material presents, for the three raster orientations analyzed here (0/90, 45/−45 and 30/−60), noticeably higher values of fracture toughness and apparent fracture toughness than the pristine ASA.
• Regarding the notch effect, this is generally higher (lower L) in ASA-CF10 than in ASA.
• Raster orientation 30/−60 provides the best fracture behavior of the three raster orientations (90/0, 45/−45, 30/−60), with a similar fracture toughness (cracked conditions) to raster orientation 0/90, but developing a much higher notch effect.
• SEM observations justify the results obtained in this research.

Future research could address certain issues not covered (or not sufficiently clarified) by this work, including the effect of different amounts of carbon fiber, the optimization of printing parameters and their effect on the mechanical performance of this particular material (ASA-CF10), or the implications of the raster orientation (and other variables) in the fracture mechanisms and the resulting notch effect, among others.