A Unified Size-Dependent Theory for Analyzing the Free Vibration Behavior of an FG Microplate Under Fully Simply Supported Conditions and Magneto-Electro-Thermo-Mechanical Loads Considering Couple Stress and Thickness Stretching Effects
Abstract
1. Introduction
2. Formulations
2.1. The Unified Kinematics Model and Relevant Equations
2.2. Generalized Constitutive Equations
2.3. Strong Form
3. Applications
4. Numerical Examples
4.1. Validation and Comparison
- (a)
- Open-circuit surface conditions
- (b)
- Closed-circuit surface conditions
4.1.1. FG Piezoelectric Microplates
4.1.2. FG-MEE Macroscale Plates
4.2. Parametric Studies
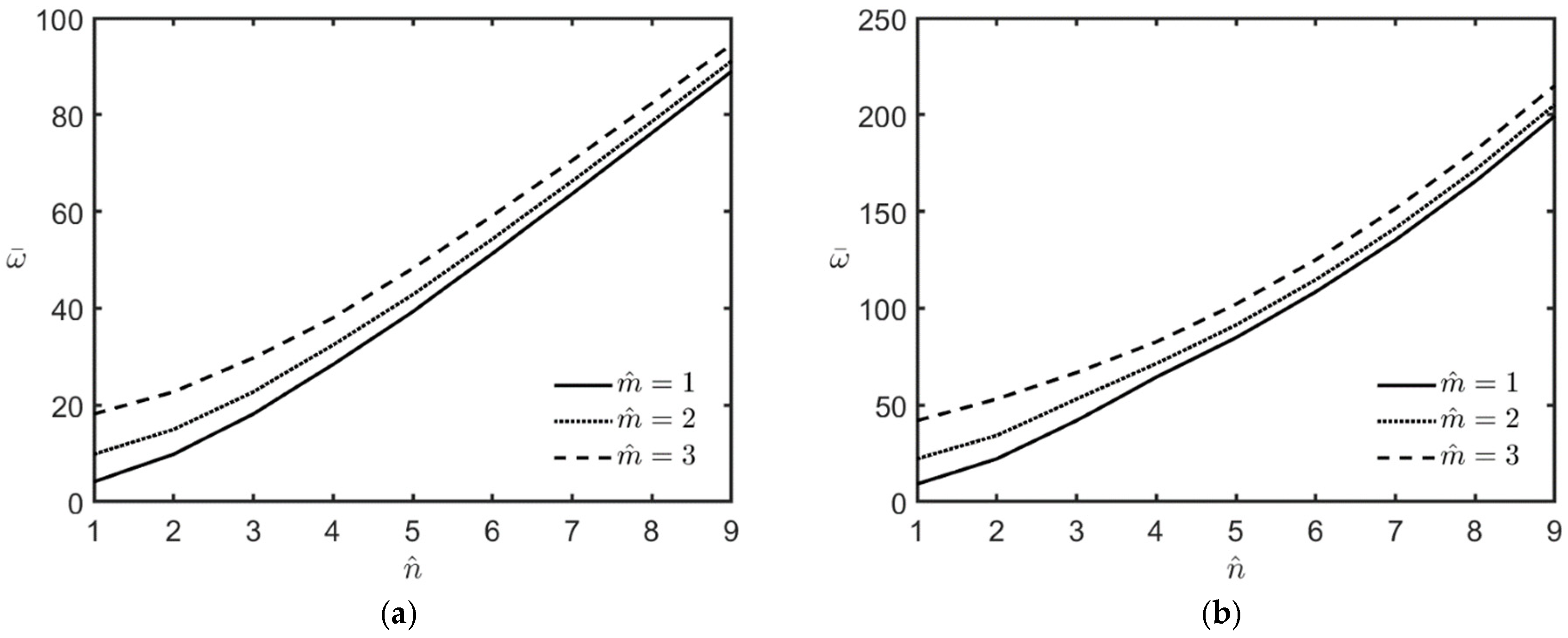
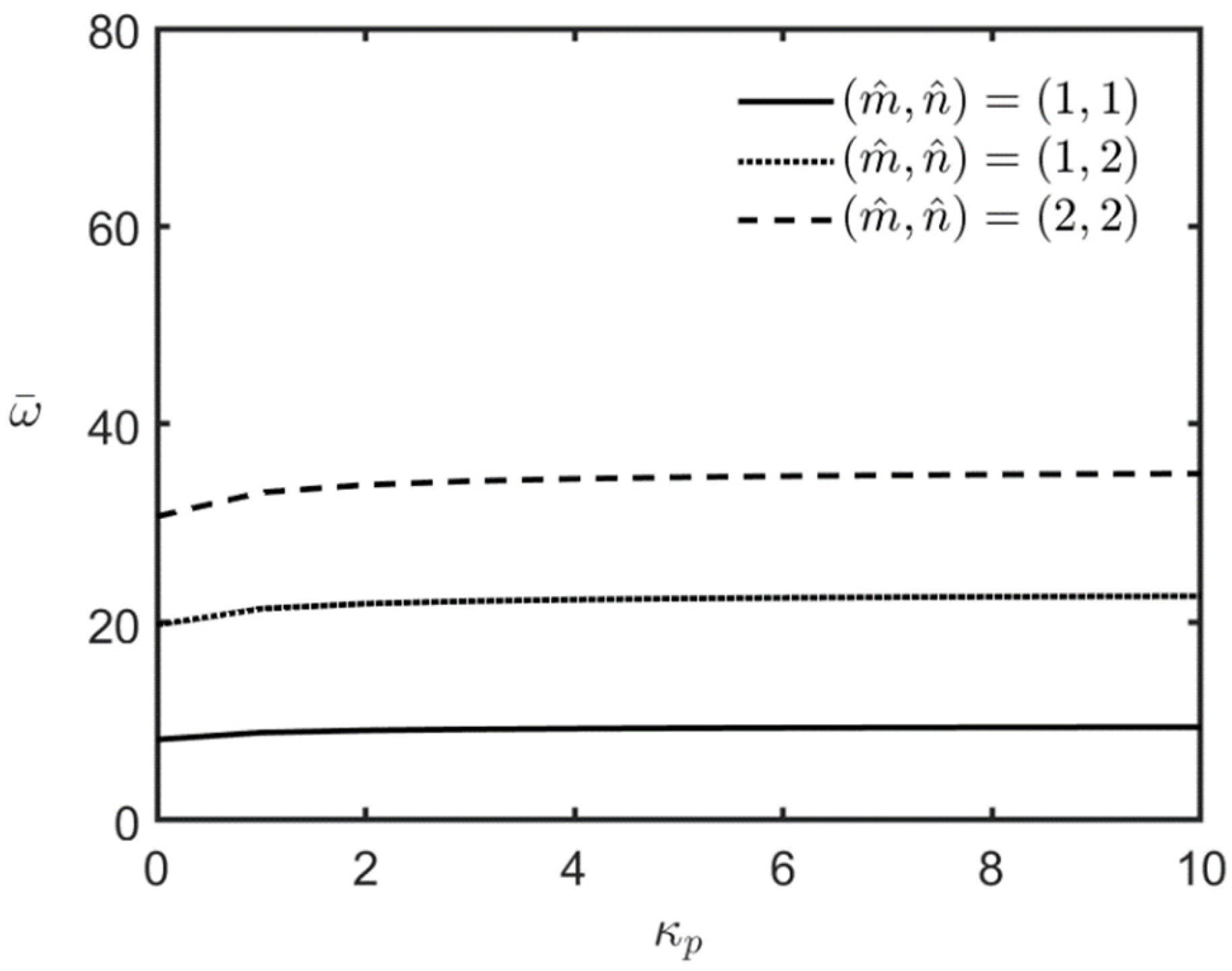
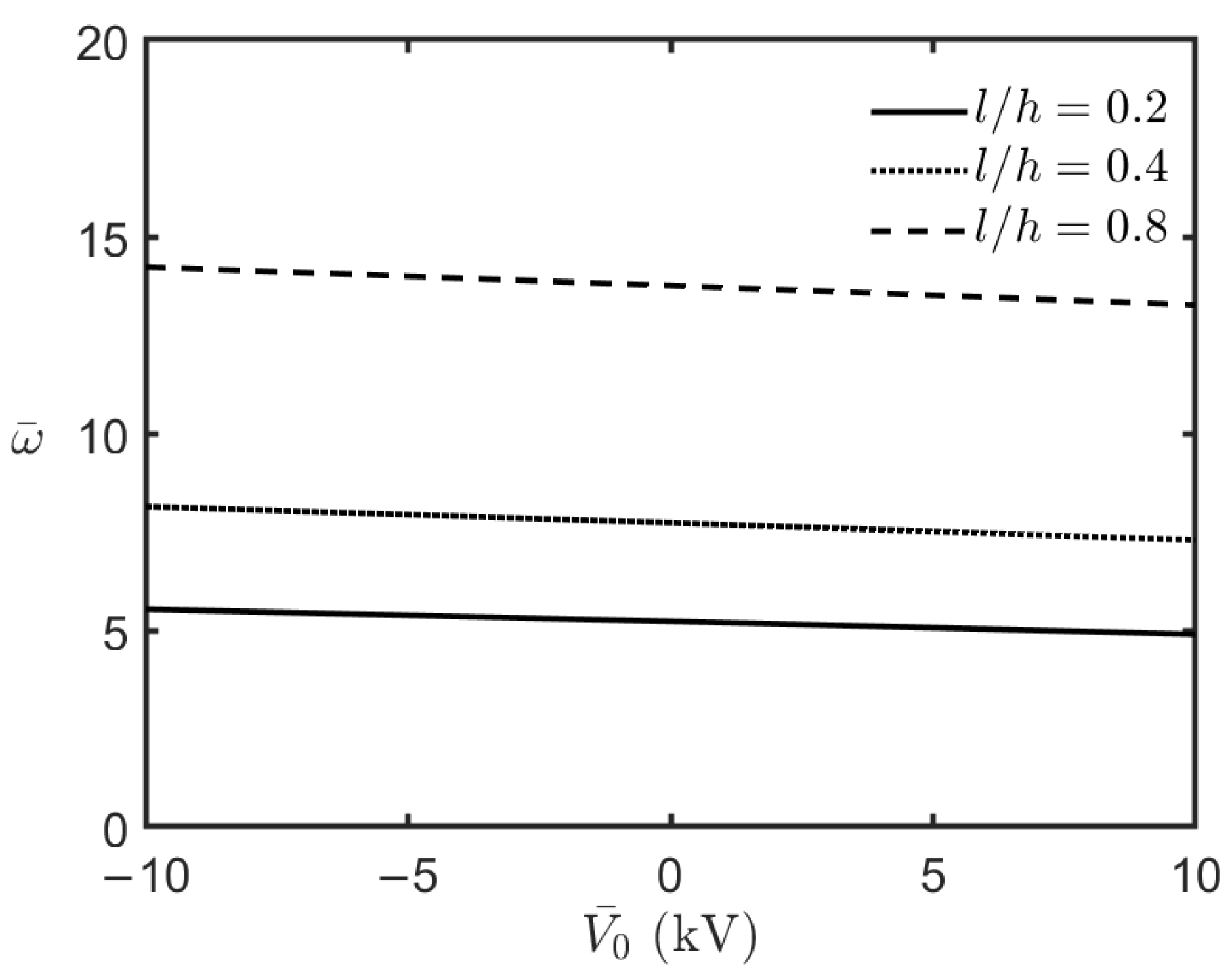
4.2.1. Unloaded FG-MEE Microplates Under Open-Circuit Surface Conditions
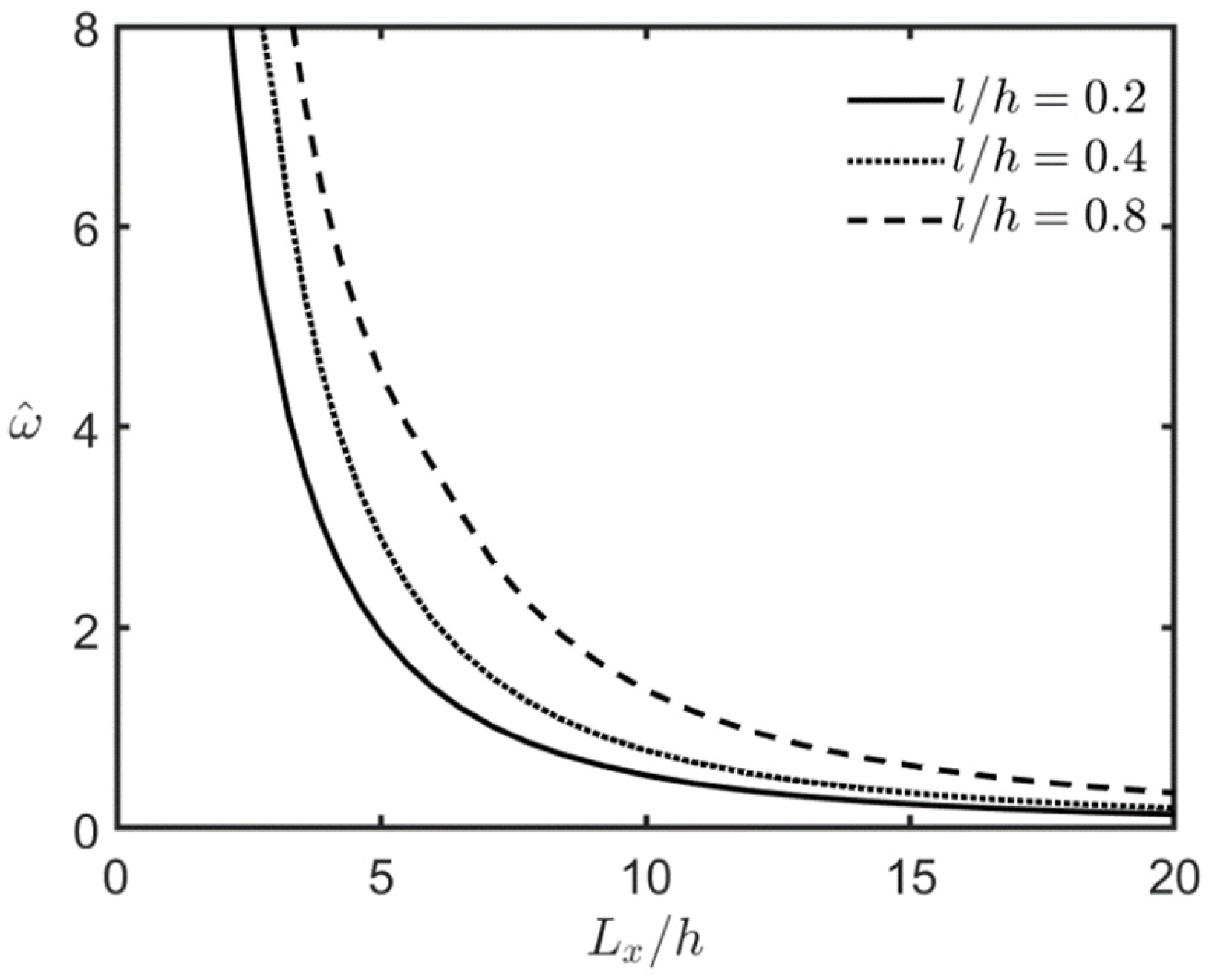
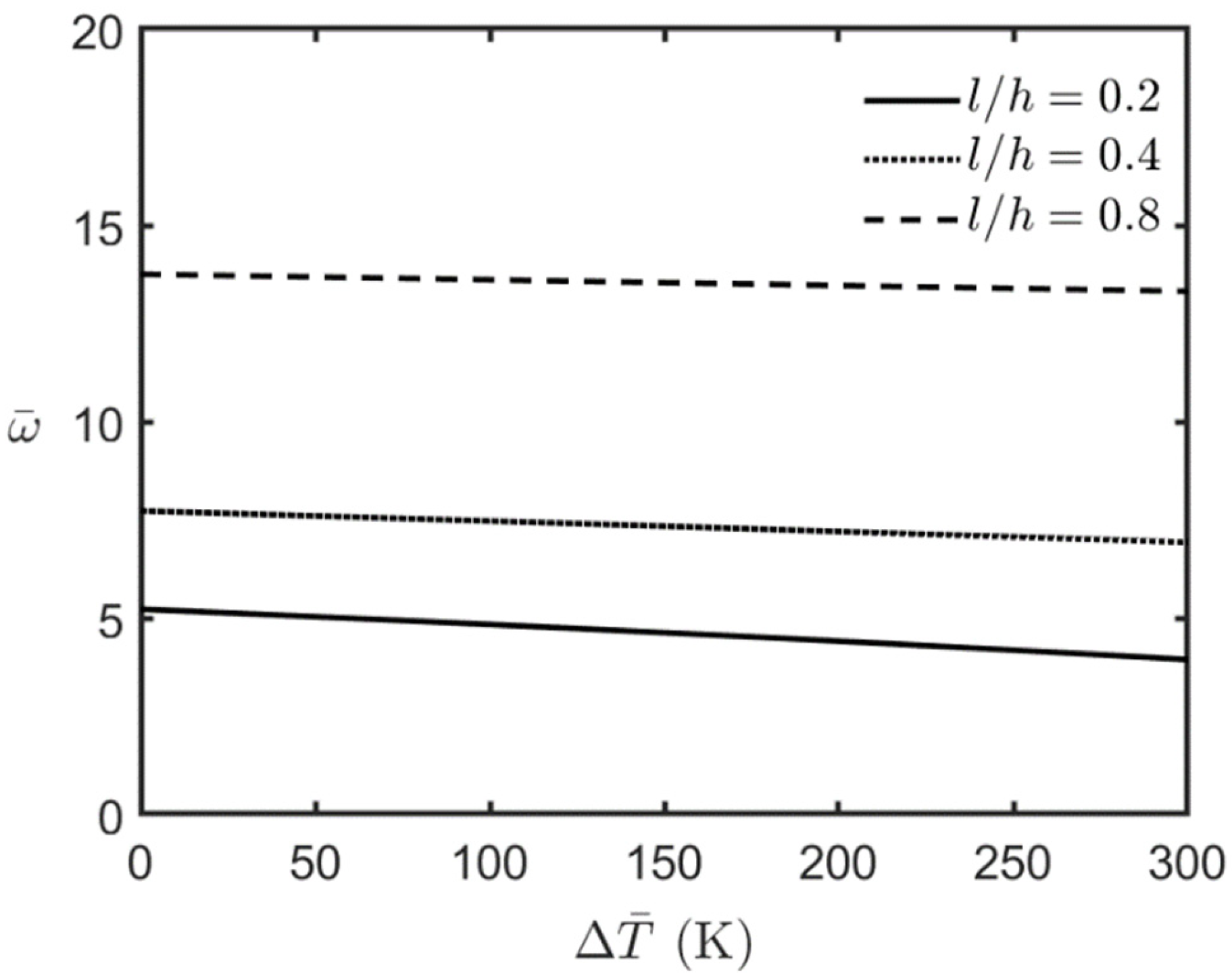
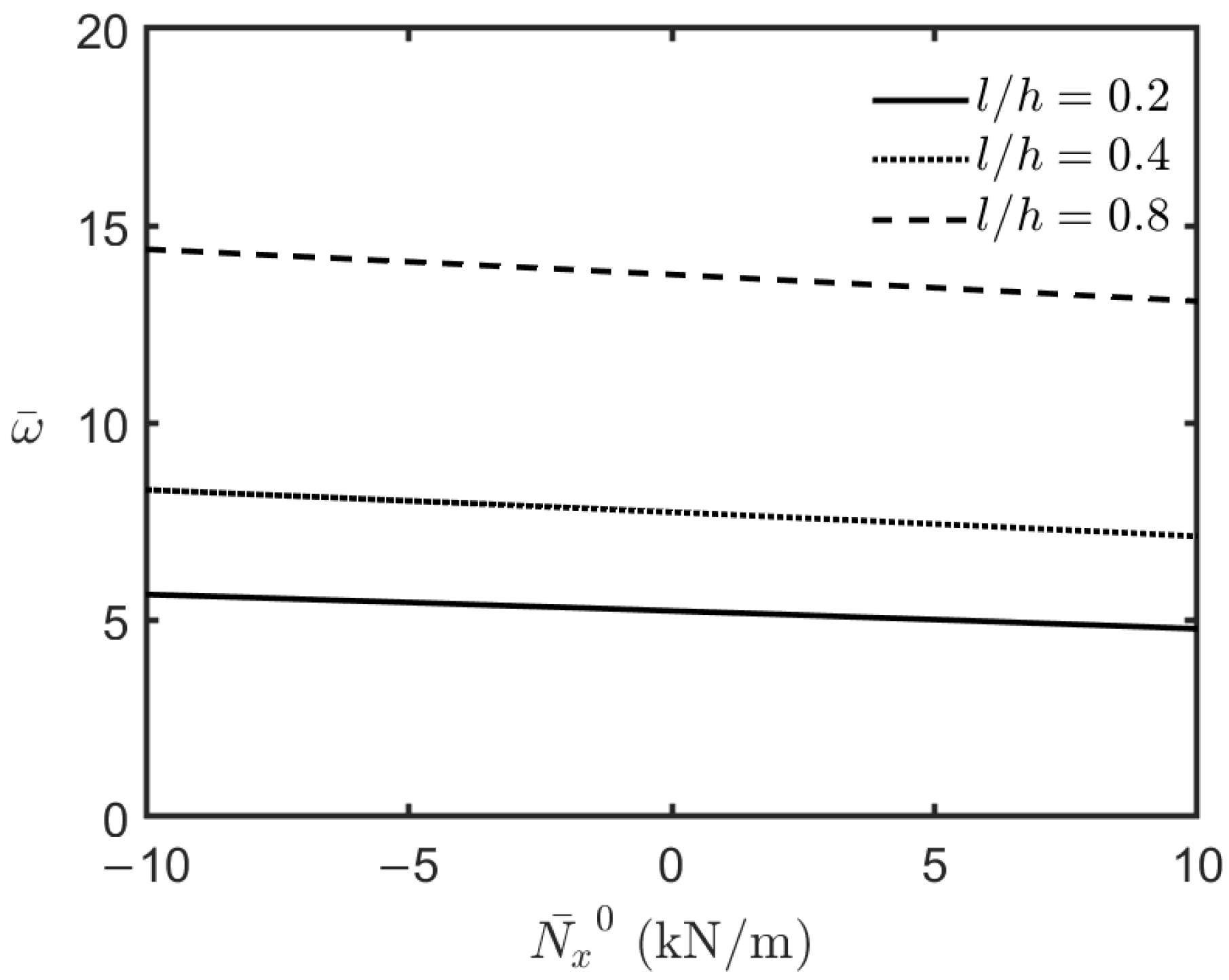
4.2.2. Loaded FG-MEE Microplates Under Closed-Circuit Surface Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCM | Classical continuum mechanics |
| CCST | Consistent couple stress theory |
| CPT | Classical plate theory |
| SDSDT | Size-dependent shear deformation theory |
| SDT | Shear deformation theory |
| FG | Functionally graded |
| HOCM | Higher-order continuum mechanics |
| MCST | Modified couple stress theory |
| MEE | Magneto-electro-elastic |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
Appendix A. The Generalized Force/Moment Resultants–Generalized Displacement Components Relationships
Appendix B. The Detailed Expressions of Generalized Initial In-Plane Force Resultants
Appendix C. The Detailed Expressions of Kij and Ik
Appendix D. The Detailed Expressions of kij, mij, and
References
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Koizumi, A. Recent progress of functionally graded materials in Japan. Cream. Eng. Sci. Proc. 1992, 13, 333–347. [Google Scholar]
- Ding, S.; Wu, C.P. Optimization of material composition to minimize the thermal stresses induced in FGM plates with temperature-dependent material properties. Int. J. Mech. Mater. Des. 2018, 14, 527–549. [Google Scholar] [CrossRef]
- Wu, C.P.; Li, K.W. Multi-objective optimization of functionally graded beams using a genetic algorithm with non-dominated sorting. J. Compos. Sci. 2021, 5, 92. [Google Scholar] [CrossRef]
- Bargatin, I.; Kozinsky, I.; Roukes, M. Efficient electrothermal actuation of multiple modes of high-frequency nanoelectromechanical resonators. Appl. Phys. Lett. 2007, 9, 093116. [Google Scholar] [CrossRef]
- Jalili, N.; Laxminarayana, K. A review of atomic force microscopy imaging systems: Application to molecular metrology and biological sciences. Mechatronics 2004, 14, 907–945. [Google Scholar] [CrossRef]
- Muller, E.; Drasar, C.; Schilz, J.; Kaysser, W.A. Functionally graded materials for sensors and energy applications. Mater. Sci. Eng. A 2003, 362, 17–39. [Google Scholar] [CrossRef]
- Kumar, S.; Murthy Reddy, K.V.V.S.; Kumar, A.; Rohini Devi, G. Development and characterization of polymer-ceramic continuous fiber reinforced functionally graded composites for aerospace application. Aerosp. Sci. Technol. 2013, 26, 185–191. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P.; Nguyen, T.K.; Kim, S.E. A review of continuum mechanics models for size-dependent analysis of beams and plates. Compos. Struct. 2017, 177, 196–219. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Khater, M.E.; Emam, S.A. A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Appl. Math. Modell. 2016, 40, 4109–4128. [Google Scholar] [CrossRef]
- Shariati, M.; Shishesaz, M.; Sahbafar, H.; Pourabdy, M.; Hosseini, M. A review on stress-driven nonlocal elasticity theory. J. Comput. Appl. Mech. 2021, 52, 535–552. [Google Scholar]
- Wu, C.P.; Yu, J.J. A review of mechanical analyses of rectangular nanobeams and single-, double-, and multi-walled carbon nanotubes using Eringen’s nonlocal elasticity theory. Arch. Appl. Mech. 2019, 89, 1761–1792. [Google Scholar] [CrossRef]
- Wu, C.P.; Hu, H.X. A review of dynamic analyses of single- and multi-layered graphene sheets/nanoplates using various nonlocal continuum mechanics-based plate theories. Acta Mech. 2021, 232, 4497–4531. [Google Scholar] [CrossRef]
- Kong, S. A review on the size-dependent models of micro-beam and micro-plate based on the modified couple stress theory. Arch. Comput. Methods Eng. 2022, 29, 1–31. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Nguyen, T.N.; Abdel-Wahab, M.; Bordas, S.P.A.; Nguyen-Xuan, H.; Vo, T.P. A refined quasi-3D isogeometric analysis for functionally graded microplates based on the modified couple stress theory. Comput. Methods Appl. Mech. Eng. 2017, 313, 904–940. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Couple stress theory for solids. Int. J. Solids Struct. 2011, 48, 2496–2510. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R. Size-dependent piezoelectricity. Int. J. Solids Struct. 2013, 50, 2781–2791. [Google Scholar] [CrossRef]
- Wu, C.P.; Hu, H.X. A unified size-dependent plate theory for static bending and free vibration analyses of micro- and nano-scale plates based on the consistent couple stress theory. Mech. Mater. 2021, 162, 104085. [Google Scholar] [CrossRef]
- Wu, C.P.; Lin, E.L. Free vibration analysis of porous functionally graded piezoelectric microplates resting on an elastic medium subjected to electric voltages. Arch. Mech. 2022, 74, 463–511. [Google Scholar]
- Thai, S.; Thai, H.T.; Vo, T.P.; Patel, V.I. Size-dependent behavior of functionally graded microplates based on the modified strain gradient elasticity theory and isogeometric analysis. Comput. Struct. 2017, 190, 219–241. [Google Scholar] [CrossRef]
- Thai, C.H.; Hung, P.T.; Nguyen-Xuan, H.; Phung-Van, P. A size-dependent mesh-free approach for magneto-electro-elastic functionally graded nanoplates based on nonlocal strain gradient theory. Eng. Struct. 2023, 292, 116521. [Google Scholar] [CrossRef]
- Le, T.M.; Vo, D.; Rungamornrat, J.; Bui, T.Q. Strain-gradient theory for shear deformation free-form microshells: Governing equations of motion and general boundary conditions. Int. J. Solids Struct. 2022, 248, 111579. [Google Scholar] [CrossRef]
- Carrera, E.; Zozulya, V.V. Carrera unified formulation (CUF) for the micropolar plates and shells. I. Higher Order theory. Mech. Adv. Mater. Struct. 2022, 29, 773–795. [Google Scholar] [CrossRef]
- Carrera, E.; Zozulya, V.V. Carrera unified formulation (CUF) for the micropolar plates and shells. II. Complete Linear expansion case. Mech. Adv. Mater. Struct. 2022, 29, 796–815. [Google Scholar] [CrossRef]
- Zozulya, V.V. Higher order theory of micropolar plates and shells. ZAMM J. Appl. Math. Mech. 2018, 98, 886–918. [Google Scholar] [CrossRef]
- Hassanpour, S.; Heppler, G.R. Micropolar elasticity theory: A survey of linear isotropic equations, representative notations, and experimental investigations. Math. Mech. Solids 2015, 22, 224–242. [Google Scholar] [CrossRef]
- Gul, U.; Aydogdu, M. Structural modelling of nanorods and nanobeams using doublet mechanics theory. Int. J. Mech. Mater. Des. 2018, 14, 195–212. [Google Scholar] [CrossRef]
- Karamanli, A. Structural behaviours of zigzag and armchair nanobeams using finite element doublet mechanics. Eur. J. Mech. A/Solids 2021, 89, 104287. [Google Scholar] [CrossRef]
- Trinh, L.C.; Nguyen, H.X.; Vo, T.P.; Nguyen, T.K. Size-dependent behaviour of functionally graded microbeams using various shear deformation theories based on the modified couple stress theory. Compos. Struct. 2016, 154, 556–572. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Q. Nonlinear dynamics of two-directional functionally graded microbeam with geometrical imperfection using unified shear deformable beam theory. Appl. Math. Model. 2021, 98, 783–800. [Google Scholar] [CrossRef]
- Simsek, M.; Reddy, J.N. A unified higher order beam theory for buckling of a functionally graded microbeam embedded in elastic medium using modified couple stress theory. Compos. Struct. 2013, 101, 47–58. [Google Scholar] [CrossRef]
- Li, Z.; Wang, H.; Zheng, S. Bending and free vibration of functionally graded piezoelectric microbeams based on the modified couple stress theory. Ann. Solid Struct. Mech. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Lou, J.; He, L.; Du, J. A unified higher order plate theory for functionally graded microplates based on the modified couple stress theory. Compos. Struct. 2015, 133, 1036–1047. [Google Scholar] [CrossRef]
- Tran, V.T.; Nguyen, T.K.; Nguyen, P.T.T.; Vo, T.P. Stochastic vibration and buckling analysis of functionally graded microplates with a unified higher-order shear deformation theory. Thin-Walled Struct. 2022, 177, 109473. [Google Scholar] [CrossRef]
- Wu, C.P.; Huang, Z. A unified consistent couple stress beam theory for functionally graded microscale beams. Steel Compos. Struct. 2024, 51, 103–116. [Google Scholar]
- Serpilli, M.; Rizzoni, R.; Ramos, R.R.; Lebon, F. A size-dependent model of strain gradient elastic laminated micro-beams with a weak adhesive layer. ZAMM J. Appl. Math. Mech. 2024, 105, e202400609. [Google Scholar] [CrossRef]
- Jedrysiak, J. On the tolerance modelling of thermoelasticity problems for transversally graded laminates. Arch. Civ. Mech. Eng. 2011, 11, 61–74. [Google Scholar] [CrossRef]
- Jedrysiak, J.; Kazmierczak-Sobinska, M. Dynamics of one-directional functionally graded plates with different sizes of microstructure: Theoretical tolerance modelling. Materials 2025, 18, 328. [Google Scholar] [CrossRef]
- Kazmierczak, M.; Jedrysiak, J. Tolerance modelling of vibrations of thin functionally graded plates. Thin-Walled Struct. 2011, 49, 1295–1303. [Google Scholar] [CrossRef]
- Jedrysiak, J. Free vibrations of thin functionally graded plates with microstructure. Eng. Struct. 2014, 75, 99–112. [Google Scholar] [CrossRef]
- Jedrysiak, J. Tolerance modelling of free vibrations of medium thickness functionally graded plates. Compos. Struct. 2018, 202, 1253–1262. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Tolerance and asymptotic modelling of dynamic problems for thin microstructured transversally graded shells. Compos. Struct. 2017, 162, 365–373. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. A new asymptotic-tolerance model of dynamic and stability problems for longitudinally graded cylindrical shells. Compos. Struct. 2018, 202, 473–481. [Google Scholar] [CrossRef]
- Kazmierczak, M.; Jedrysiak, J. A new combined asymptotic-tolerance model of vibrations of thin transversally graded plates. Eng. Struct. 2013, 46, 322–331. [Google Scholar] [CrossRef]
- Vinyas, M. Computational analysis of smart magneto-electro-elastic materials and structures: Review and classification. Arch. Comput. Methods Eng. 2021, 28, 1205–1248. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Zhao, Y.F.; Wang, X.; Chen, M.; Schmidt, R. Static and dynamic analysis of functionally graded magneto-electro-elastic plates and shells. Compos. Struct. 2022, 281, 114950. [Google Scholar] [CrossRef]
- Garcia Lage, R.; Mota Soares, C.M.; Mota Soares, C.A.; Reddy, J.N. Layerwise partial mixed finite element analysis of magneto-electro-elastic plates. Comput. Struct. 2004, 82, 1293–1301. [Google Scholar] [CrossRef]
- Pan, E.; Han, F. Exact solution for functionally graded and layered magneto-electro-elastic plates. Int. J. Eng. Sci. 2005, 43, 321–339. [Google Scholar] [CrossRef]
- Ghadiri, M.; Safarpour, H. Free vibration analysis of embedded magneto-electro-thermo-elastic cylindrical nanoshell based on the modified couple stress theory. Appl. Phys. A 2016, 122, 833. [Google Scholar] [CrossRef]
- Qu, Y.L.; Li, P.; Zhang, G.Y.; Jin, F.; Gao, X.L. A microstructure-dependent anisotropic magneto-electro-elastic Mindlin plate model based on an extended modified couple stress theory. Acta Mech. 2020, 231, 4323–4350. [Google Scholar] [CrossRef]
- Guo, J.; Chen, J.; Pan, E. Static deformation of anisotropic layered magnetoelectroelastic plates based on modified couple stress theory. Compos. Part B Eng. 2016, 107, 84–96. [Google Scholar] [CrossRef]
- Zhong, Z.; Yu, T. Vibration of a simply supported functionally graded piezoelectric rectangular plate. Smart Mater. Struct. 2016, 15, 1404–1412. [Google Scholar] [CrossRef]
- Chen, J.; Chen, H.; Pan, E.; Heyliger, P.R. Modal analysis of magneto-electro-elastic plates using the state-vector approach. J. Sound Vibr. 2007, 304, 722–734. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.A. A Hermite-family C1 finite layer method for the three-dimensional free vibration analysis of exponentially graded piezoelectric microplates based on the consistent couple stress theory. Int. J. Struct. Stab. Dyn. 2023, 23, 2350044. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.C. A modified Pagano method for the 3D dynamic responses of functionally graded magneto-electro-elastic plates. Compos. Struct. 2009, 90, 363–372. [Google Scholar] [CrossRef]
- Tsai, Y.H.; Wu, C.P. Dynamic responses of functionally graded magneto-electro-elastic shells with open-circuit surface conditions. Int. J. Eng. Sci. 2008, 46, 843–857. [Google Scholar] [CrossRef]
- Ramirez, F.; Heyliger, P.R.; Pan, E. Discrete layer solution to free vibrations of functionally graded magneto-electro-elastic plates. Mech. Adv. Mater. Struct. 2006, 13, 249–266. [Google Scholar] [CrossRef]


| Material Properties | PZT-4 [52] | BaTiO3 [53] | CoFe2O4 [53] |
|---|---|---|---|
| 139 | 166.0 | 286.0 | |
| 77.8 | 77.0 | 173.0 | |
| 74.3 | 78.0 | 170.5 | |
| 115 | 162.0 | 269.5 | |
| 25.6 | 43.0 | 45.3 | |
| 30.6 | 44.5 | 56.5 | |
| −5.2 | −4.4 | 0.0 | |
| 15.1 | 18.6 | 0.0 | |
| 12.7 | 11.6 | 0.0 | |
| 0.0 | 0.0 | 580.3 | |
| 0.0 | 0.0 | 699.7 | |
| 0.0 | 0.0 | 550.0 | |
| 6.46 × 10−9 | 11.2 × 10−9 | 0.08 × 10−9 | |
| 5.62 × 10−9 | 12.6 × 10−9 | 0.093 × 10−9 | |
| 0.0 | 5.0 × 10−6 | −590.0 × 10−6 | |
| 0.0 | 10.0 × 10−6 | 157.0 × 10−6 | |
| NA | 15.7 × 10−6 | 10 × 10−6 | |
| NA | 6.4 × 10−6 | 10 × 10−6 | |
| 0.0 | 0.0 | 0.0 | |
| 7500 | 5800.0 | 5300.0 | |
| l for the CCST (m) | 8.8 × 10−6 | 8.8 × 10−6 | 8.8 × 10−6 |
| for the MCST (m) | 17.6 × 10−6 | 17.6 × 10−6 | 17.6 × 10−6 |
| Surface Conditions | 2D and 3D Size-Dependent Theories Based on the CCST | |||||||
|---|---|---|---|---|---|---|---|---|
| (1, 1) | (1, 2) | (1, 3) | (2, 2) | |||||
| Open-circuit | 0.5 | 5 | 1 | CPT | 0.28716 | 0.68609 | 1.02396 | 0.90005 |
| First-order SDT | 0.24919 | 0.53777 | 0.93294 | 0.78305 | ||||
| Reddy’s refined SDT | 0.25378 | 0.57257 | 1.02396 | 0.85218 | ||||
| Sinusoidal SDT | 0.25428 | 0.57416 | 1.02396 | 0.85510 | ||||
| Exponential SDT | 0.25515 | 0.57665 | 1.02396 | 0.85940 | ||||
| Hyperbolic SDT | 0.25375 | 0.57248 | 1.02396 | 0.85199 | ||||
| 3D CCST [54] | 0.25922 | 0.58043 | 1.02476 | 0.85664 | ||||
| Open-circuit | 0.5 | 5 | 10 | CPT | 0.26847 | 0.64749 | 1.02396 | 0.90005 |
| First-order SDT | 0.23724 | 0.51880 | 0.90777 | 0.75996 | ||||
| Reddy’s refined SDT | 0.24438 | 0.55881 | 1.01260 | 0.83852 | ||||
| Sinusoidal SDT | 0.24467 | 0.55973 | 1.01381 | 0.84039 | ||||
| Exponential SDT | 0.24525 | 0.56146 | 1.01411 | 0.84359 | ||||
| Hyperbolic SDT | 0.24437 | 0.55876 | 1.01244 | 0.83842 | ||||
| 3D CCST [54] | 0.24681 | 0.55954 | 0.99989 | 0.83247 | ||||
| Open-circuit | 0.5 | 10 | 10 | CPT | 0.06840 | 0.16938 | 0.33352 | 0.26847 |
| First-order SDT | 0.06580 | 0.15542 | 0.28852 | 0.23724 | ||||
| Reddy’s refined SDT | 0.06499 | 0.15721 | 0.30019 | 0.24438 | ||||
| Sinusoidal SDT | 0.06506 | 0.15739 | 0.30057 | 0.24467 | ||||
| Exponential SDT | 0.06520 | 0.15774 | 0.30132 | 0.24525 | ||||
| Hyperbolic SDT | 0.06498 | 0.15720 | 0.30018 | 0.24437 | ||||
| 3D CCST [54] | 0.06588 | 0.15909 | 0.30276 | 0.24681 | ||||
| Open-circuit | 1 | 10 | 10 | CPT | 0.10503 | 0.26009 | 0.51198 | 0.41227 |
| First-order SDT | 0.09903 | 0.22931 | 0.41720 | 0.34536 | ||||
| Reddy’s refined SDT | 0.10219 | 0.24859 | 0.47793 | 0.38813 | ||||
| Sinusoidal SDT | 0.10224 | 0.24873 | 0.47833 | 0.38841 | ||||
| Exponential SDT | 0.10234 | 0.24907 | 0.47926 | 0.38908 | ||||
| Hyperbolic SDT | 0.10218 | 0.24858 | 0.47792 | 0.38812 | ||||
| 3D CCST [54] | 0.10423 | 0.24862 | 0.46589 | 0.38193 | ||||
| Surface Conditions | 2D and 3D Size-Dependent Theories Based on the CCST | |||||||
|---|---|---|---|---|---|---|---|---|
| (1, 1) | (1, 2) | (1, 3) | (2, 2) | |||||
| Closed-circuit | 0.5 | 5 | 1 | CPT | 0.28449 | 0.68043 | 1.02396 | 0.90005 |
| First-order SDT | 0.24181 | 0.50913 | 0.85945 | 0.72805 | ||||
| Reddy’s refined SDT | 0.23337 | 0.52092 | 0.92233 | 0.76963 | ||||
| Sinusoidal SDT | 0.23405 | 0.52302 | 0.92721 | 0.77338 | ||||
| Exponential SDT | 0.23560 | 0.52702 | 0.93528 | 0.77983 | ||||
| Hyperbolic SDT | 0.23335 | 0.52082 | 0.92205 | 0.76943 | ||||
| 3D CCST [54] | 0.24803 | 0.54884 | 0.96382 | 0.80666 | ||||
| Closed-circuit | 0.5 | 5 | 10 | CPT | 0.26695 | 0.64416 | 1.02396 | 0.90005 |
| First-order SDT | 0.23260 | 0.49907 | 0.85288 | 0.71996 | ||||
| Reddy’s refined SDT | 0.23018 | 0.52034 | 0.93044 | 0.77407 | ||||
| Sinusoidal SDT | 0.23070 | 0.52197 | 0.93454 | 0.77712 | ||||
| Exponential SDT | 0.23191 | 0.52527 | 0.94176 | 0.78274 | ||||
| Hyperbolic SDT | 0.23016 | 0.52028 | 0.93022 | 0.77393 | ||||
| 3D CCST [54] | 0.22395 | 0.50170 | 0.89103 | 0.74291 | ||||
| Closed-circuit | 0.5 | 10 | 10 | CPT | 0.06800 | 0.16840 | 0.33167 | 0.26695 |
| First-order SDT | 0.06518 | 0.15318 | 0.28192 | 0.23260 | ||||
| Reddy’s refined SDT | 0.06165 | 0.14859 | 0.28214 | 0.23018 | ||||
| Sinusoidal SDT | 0.06177 | 0.14890 | 0.28282 | 0.23070 | ||||
| Exponential SDT | 0.06206 | 0.14964 | 0.28436 | 0.23191 | ||||
| Hyperbolic SDT | 0.06165 | 0.14858 | 0.28212 | 0.23016 | ||||
| 3D CCST [54] | 0.06054 | 0.14514 | 0.27393 | 0.22395 | ||||
| Closed-circuit | 1 | 10 | 10 | CPT | 0.10476 | 0.25945 | 0.51099 | 0.41129 |
| First-order SDT | 0.09850 | 0.22703 | 0.40979 | 0.34030 | ||||
| Reddy’s refined SDT | 0.09987 | 0.24188 | 0.46179 | 0.37605 | ||||
| Sinusoidal SDT | 0.09995 | 0.24210 | 0.46236 | 0.37646 | ||||
| Exponential SDT | 0.10016 | 0.24273 | 0.46394 | 0.37763 | ||||
| Hyperbolic SDT | 0.09987 | 0.24188 | 0.46179 | 0.37605 | ||||
| 3D CCST [54] | 0.09646 | 0.22651 | 0.41729 | 0.34410 | ||||
| Surface Conditions | Theories | Lowest | Second Lowest | ||
|---|---|---|---|---|---|
| Open-circuit | 10 | 1 | CPT | 12.1415 | 28.8462 |
| First-order SDT | 10.9389 | 28.8444 | |||
| Reddy’s refined SDT | 9.5951 | 28.8444 | |||
| Sinusoidal SDT | 9.6308 | 28.8444 | |||
| Exponential SDT | 9.7097 | 28.8444 | |||
| Hyperbolic SDT | 9.5941 | 28.8444 | |||
| State space sols [55] | 9.5543 | 28.8389 | |||
| Asymptotic sols [56] | 9.5545 | 28.8389 | |||
| Discrete sols [57] | 9.525 | 28.762 | |||
| Open-circuit | 10 | 3 | CPT | 13.3624 | 30.4768 |
| First-order SDT | 11.8391 | 30.4757 | |||
| Reddy’s refined SDT | 9.9926 | 30.4757 | |||
| Sinusoidal SDT | 10.0351 | 30.4757 | |||
| Exponential SDT | 10.1411 | 30.4757 | |||
| Hyperbolic SDT | 9.9920 | 30.4757 | |||
| State space sols [55] | 9.7730 | 30.0246 | |||
| Asymptotic sols [56] | 9.7730 | 30.0246 | |||
| Discrete sols [57] | 9.747 | 29.975 | |||
| Closed-circuit | 10 | 1 | CPT | 12.0904 | 28.8462 |
| First-order SDT | 10.8868 | 28.8444 | |||
| Reddy’s refined SDT | 9.3344 | 28.8444 | |||
| Sinusoidal SDT | 9.3720 | 28.8444 | |||
| Exponential SDT | 9.4627 | 28.8444 | |||
| Hyperbolic SDT | 9.3338 | 28.8444 | |||
| State space sols [55] | 9.5289 | 28.8390 | |||
| Closed-circuit | 10 | 3 | CPT | 13.3030 | 30.4768 |
| First-order SDT | 11.8082 | 30.4757 | |||
| Reddy’s refined SDT | 9.8945 | 30.4757 | |||
| Sinusoidal SDT | 9.9400 | 30.4757 | |||
| Exponential SDT | 10.0527 | 30.4757 | |||
| Hyperbolic SDT | 9.8939 | 30.4757 | |||
| State space sols [55] | 9.7667 | 30.0246 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-P.; Hsu, C.-D. A Unified Size-Dependent Theory for Analyzing the Free Vibration Behavior of an FG Microplate Under Fully Simply Supported Conditions and Magneto-Electro-Thermo-Mechanical Loads Considering Couple Stress and Thickness Stretching Effects. J. Compos. Sci. 2025, 9, 201. https://doi.org/10.3390/jcs9050201
Wu C-P, Hsu C-D. A Unified Size-Dependent Theory for Analyzing the Free Vibration Behavior of an FG Microplate Under Fully Simply Supported Conditions and Magneto-Electro-Thermo-Mechanical Loads Considering Couple Stress and Thickness Stretching Effects. Journal of Composites Science. 2025; 9(5):201. https://doi.org/10.3390/jcs9050201
Chicago/Turabian StyleWu, Chih-Ping, and Cheng-Dao Hsu. 2025. "A Unified Size-Dependent Theory for Analyzing the Free Vibration Behavior of an FG Microplate Under Fully Simply Supported Conditions and Magneto-Electro-Thermo-Mechanical Loads Considering Couple Stress and Thickness Stretching Effects" Journal of Composites Science 9, no. 5: 201. https://doi.org/10.3390/jcs9050201
APA StyleWu, C.-P., & Hsu, C.-D. (2025). A Unified Size-Dependent Theory for Analyzing the Free Vibration Behavior of an FG Microplate Under Fully Simply Supported Conditions and Magneto-Electro-Thermo-Mechanical Loads Considering Couple Stress and Thickness Stretching Effects. Journal of Composites Science, 9(5), 201. https://doi.org/10.3390/jcs9050201








