Microscopic-Phenomenological Model of Glass Transition and Temperature Dependence of Viscosity—Part I: Foundations of the Model

Abstract

The glass transition is described as a time- and history-independent singular event, which takes place in an interval dependent on the distribution width of molecular vibration amplitudes. The intrinsic glass transition is not seen as a relaxation phenomenon, but is characterized by a fixed volumetric state at the glass temperature Tg₀. The relaxation behavior of the transport properties depends on the distance to Tg₀. Free volume is redefined and its generation is the result of the fluctuating transfer of thermal energy into condensed matter and the resulting combined interactions between the vibration elements. This creates vacancies between the elements which are larger than the cross-section of an adjacent element or parts thereof. Possible shifts of molecules or molecular parts through such apertures depend on the size and axis orientation and do not require further energetic activation. After a displacement, additional volume is created by delays in occupying abandoned positions and restoring the energetic equilibrium. The different possibilities of axis orientation in space result in the different diffusive behavior of simple molecules and chain molecules, silicate network formers, and associated liquids. Glass transformation takes place at a critical volume Vg₀ when the cross-section of apertures becomes smaller than the cross-section of the smallest molecular parts. The glass transition temperature Tg₀ is assigned to Vg₀ and is therefore independent of molecular relaxation processes. Tg₀ is well above the Kauzmann and Vogel temperatures, usually just a few degrees below the conventionally measured glass temperature Tg_(qT). The specific volume at the two temperatures mentioned above cannot be achieved by a glass with an unordered structure but only with aligned molecular axes, i.e. in a crystalline state. Simple liquids consisting of non-spherical molecules additionally alter their behavior above Vg₀ at Vg_l where the biggest gaps are as small as the largest molecular diameter. Tg_l is located in the region of the crystalline melting point T_m. Both regions, above and below T_m, belong to different physical states and have to be treated separately. In the region close to Vg₀ respectively Tg₀, the distribution of vibration amplitudes has to be taken into account. The limiting volume Vg₀ and the formation of apertures larger than the cross-section of the vibrating elements or parts thereof, in conjunction with the distribution width of molecular vibrations as Vg₀ is approached, and the spatial orientation of the molecular axes is key to understanding the glass transition.

1. Introduction

Transport properties are one of the key properties for characterizing internal processes in liquids. Molecular kinetic processes during the transition from liquid to glass have a strong influence on many critical processes in nature and technology, such as volcanism or the physical aging of polymers.

The definition of the upper limit from the liquid to the gaseous state does not cause any problems, however the relations of the liquid state to the vitreous state are not unambiguously clear. These relations are of worldwide interest and are considered to be an unresolved problem of solid state physics [1,2,3].

Since the beginning of the last century, a connection between the liquid and the glassy state has been discussed in such a way that glasses were considered to be “frozen” liquids with long term viscous properties. The glass transition is usually interpreted as a loss of thermal equilibrium due to different time scales used in experimental studies and the molecular relaxation time. According to these ideas, there is no definite glass temperature, but only a glass transition or transformation temperature Tg(qT), which depends on respective cooling/heating rates qT = (±)dT/dt. However, for a cooling rate moving towards 0 the idea of a thermodynamically based glass temperature which corresponds to a phase transition of the 1st or 2nd order has been discussed.

Therefore, a challenging question arises as to whether transport properties such as viscosity in the normal liquid range have something to do with the glass state, or in other words: does a function describing the dependence of viscosity on temperature require a limit value parameter above the absolute zero point?

The idea that the presence of “free volume” between molecules was the reason for the mobility of liquids emerged in 1870 with van der Waals’ dissertation and experienced a renaissance in the 1950s. However, there is currently no agreement on the type, scope, and distribution of this free volume. In particular, there is no generally accepted theory on the generation of additional empty space, as even for crystalline solid bodies the occupied space is larger than the corresponding sum of the molecular volumes. Thus it is not surprising that still in recent years the main work dealing with glass transition concentrates on temperature dependence and not on dependence on specific volume and thermal expansion.

In 1980, the author developed an equation based on the assumption that relative changes of viscosity (or other transport properties) are proportional to the relative change of free volume [4]. Due to the (erroneous) simple substitution of V by T, a power equation with three material-dependent parameters was developed, which provided very good results in the calculation of viscosity values for polymers and inorganic glasses as well as in super-cooled simple molecular liquids in the range outside the glass transition interval. In addition, one of the parameters was almost perfectly consistent with the Tg values from the literature. In the case of simple molecular liquids in the normal liquid regime, however, large deviations can be observed, which presumably are attributed to the increasing influence of vapor pressure and the resulting internal structural changes. As will be shown later, volume ratios play a central role in this scenario, but the quantitative relations during the passage of a vibrating element through apertures between surrounding elements are temperature-dependent, according to the model presented.

Starting with the development of mode coupling models (MC) published in 1984 [5,6,7], which led to a power law equation similar to the author’s from 1980, additional to Tg a second dynamic transition above Tg was supposed. As will be shown, the temperature parameter Tc of the MC power law equation may have a volume-dependent origin and may be replaced by the value Vg_l presented in this study.

There are a lot of competing theoretical models on this topic (e.g., configurational entropy model of Adam and Gibbs [8], energy landscape approach [9,10], random first order transition theory [11], entropic barrier hopping, frustration limited domains, shovel model) (s. Cummins et al. 1997 [12] and Dyre 2006 [13]), bond orientational two-order-parameter model (Tanaka 2012 [14]), jamming scenarios (Liu and Nagel 1998/2010 [15,16]). To date, however, no consistent theory has prevailed without contradiction. There are even reflections negating any transition but assuming a continuous process down to absolute zero (Kivelson et al. 1996 [17] and Hecksher et al. 2008 [18], Elmatad et al. 2008 [19], Pogna et al. 2015 [20]). Still today [21] it is common (in the author’s view one of the main inadequate treatments leading to possible erroneous models) to treat low-viscosity regimes above the melting point of the crystalline phase Tm and the high-viscous states in the supercooled region below Tm as continuum, despite the fact that already by 1958 [22] pre-crystallizing had been discussed to be the cause of changes in viscosity behavior. Furthermore, the new model will show that molecular shape and the possibilities of rotation lead to a modified behavior at the characteristic volume vg_l.

It is well known that self-diffusion as a basic transport phenomenon in the normal liquid state above Tm is subject to the same temperature and pressure dependence as viscosity. As self-diffusion is independent from external influences it is generally best suited to show temperature and pressure dependence. From a microscopic point of view, the conditions of self-diffusion are best illustrated by the new model.

Based on the theoretically established and experimentally confirmed equivalence between diffusion and viscosity dependence in the liquid range above Tg_l and due to the rich data material, the subsequent verification of the new model concept was mainly performed using viscosity data. However, this does not mean that the equalization is completely beyond doubt, because the process of self-diffusion is a microscopic one, whereas viscosity has some macroscopic aspects.

Martinez-Garcia et al. [23] stress that the transfer of the results to further transport phenomena should be very likely. This author agrees with a majority of researchers in recent years that the dielectric coefficient has the same temperature dependence as viscosity. This may well be the case but, due to different molecular processes—molecular shifts in viscosity and self-diffusion compared to intramolecular deformations in dielectric measurements—there are doubts about the admissibility of a joint treatment. Of course, volumetric relationships play a role in both cases, but the orientation of the molecular axes in space should have a different influence on the measurements. Higher pressures in particular should have different effects on intra- and intermolecular processes. The results of the dielectric measurements, which are said to be more accurate than viscosity measurements but decouple slightly from the latter when approaching Tg₀ [2,24], are therefore not included in the study.

It is, according to the author’s understanding, imperative and of fundamental importance for the precise prediction of liquid characteristics to involve the glass transition into the theory of the liquid state.

Pioneer studies and comprehensive surveys on the subject are presented, for example Kauzmann, 1946 [25], Tool, 1947 [26], Fox and Flory, 1950/1954 [27,28], Ritland, 1953 [29], Rost 1955 [30], Williams et al., 1955 [31], Cohen and Turnbull, 1961 [32], Kovacs, 1963 [33], Barlow et al., 1965 [34], Koppelmann, 1965 [35], Rötger, 1968 [36], Plazek et al., 1966/1968/1994/1999 [37,38,39,40], Davis and Matheson, 1966 [41], Breuer and Rehage, 1967 [42], Kanig, 1969 [43], Goldstein, 1969 [9], Donth, 1981 [44], McKenna and Angell, 1991 [45], Brüning and Samwer, 1992 [46], Böhmer et al., 1993 [47], Angell, 1995 [48], Ediger et al., 1996 [49], Colucci et al., 1997 [50], Rössler et. al., 1998 [51], Ngai, 2000 [52], Tarjus and Kivelson, 2000 [53], Berthier and Garrahan, 2003 [54], Yue et al., 2004 [55], Tanaka, 2005 [56], Dyre, 2006 [13], Ojovan, 2008 [57], Hutchinson, 2009 [58], Liu and Nagel, 2010 [15], Tarjus, 2010 [59], Berthier and Piroli, 2011 [60], Chen et al., 2012 [2], Stillinger and Debenedetti, 2013 [61], Biroli and Garrahan, 2013 [62], Langer, 2013 [63], Miracle and Senkov, 2016 [64], Schmelzer and Tropin, 2018 [65], and Zheng et al., 2019 [66].

2. Liquid Structure and Glass Formation

Common Sights of Internal Molecular Mobility in Liquids

The liquid as well as the gaseous state is generally considered a disordered state. According to the more widely known theories regarding the liquid state molecules have to surmount potential barriers by adjoining molecules when flowing. Surmounting is done in activated discrete jumps. Batschinski, 1913 [67] seems to be the first to neglect energetics and develop a simple equation based on the idea of free volume that allows liquids to flow. Ideas regarding the free volume’s redistribution free of additional activating energy were also put forward by Hirschfelder et al., 1935 [68], 1954 [69], however, they could not be established. Fox and Flory, 1950 [27], Cohen and Turnbull, 1961 [32], as well as Grest and Cohen, 1981 [70], turned again to the idea of a free volume, whereby Cohen and Turnbull underlined, however, with reference to the diffusion theory in Glasstone, Laidler, and Eyring, 1941 [71], that part of the molecules of a liquid were in an activated state (“5–10%”). They stated that molecules move with gas kinetic velocity and are temporarily captivated in a “cage” formed by adjoining molecules. Due to occasional variations in density, a hole opens up on a cage that is large enough to allow a substantial displacement of the molecule contained in it. A diffusive movement then only occurs when another molecule has reached the newly formed empty space before the first molecule returns to its original position. They underlined also that this diffusion in their understanding is not based on activation in the normal sense but is rather the result of a redistribution of the free volume within the liquid. In 1967 Chen and Turnbull [72] reiterated, in accordance with the model introduced here, that “η depends primarily on configuration rather than temperature per se.”

3. Foundations of the New Microscopic Phenomenological Model

3.1. Origin of Internal Fluctuations of Free Volume and Implications Thereupon

In condensed matter the vibrating elements—molecules, atoms, ions, chain segments—in the matrix are positioned such that the intermolecular attractive and repulsive forces are in equilibrium. This basic principle should be temperature-independent. An input of temperature energy leads to increasing vibration amplitudes. If the distances between the centers of the molecules remained unchanged, the repulsive forces become larger. According to Le Chatelier’s principle, therefore, the distances between the elements must increase in order to maintain the equilibrium of the forces. This is considered the normal thermal expansion of solids and liquids.

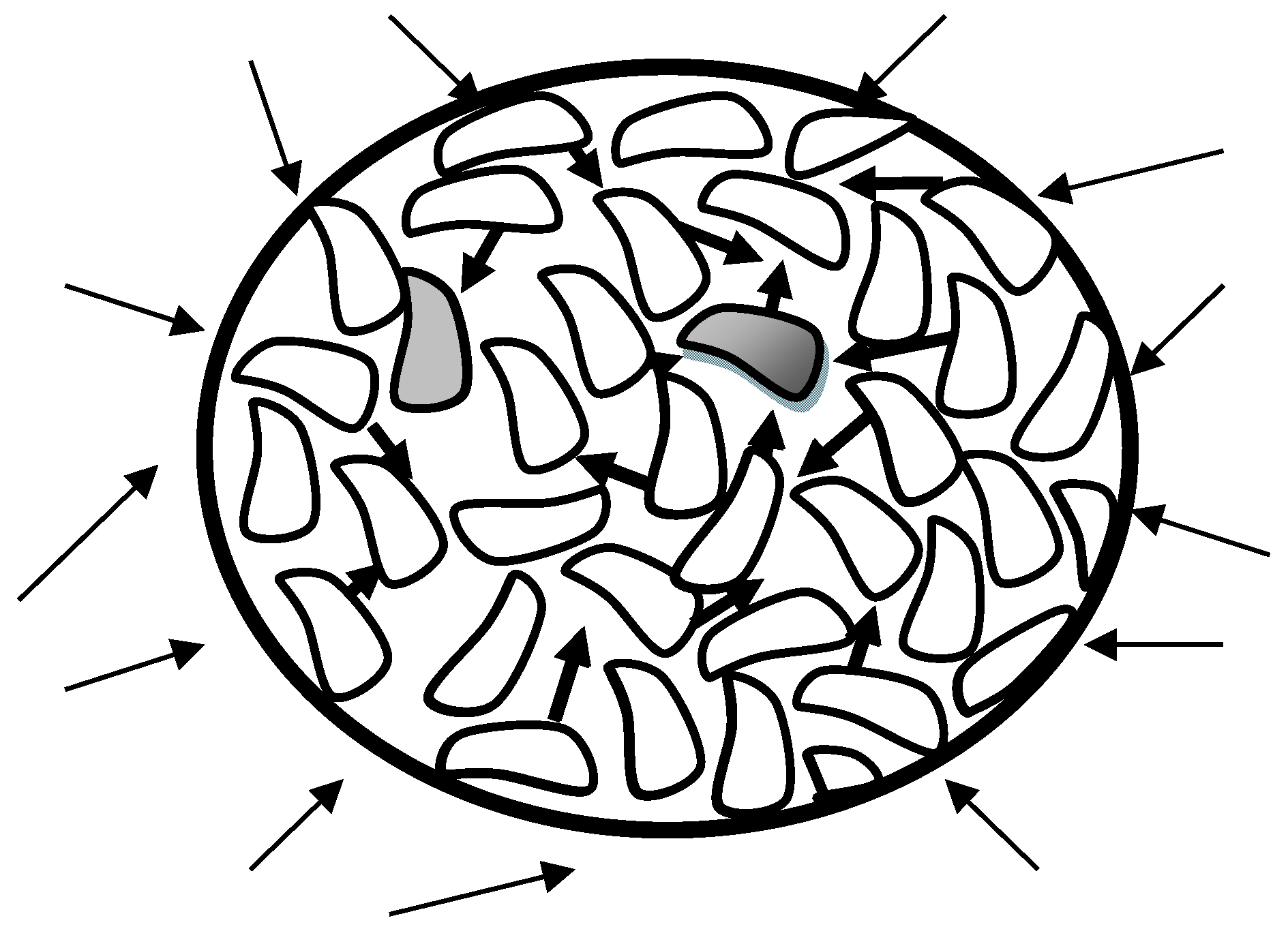
The transfer of thermal energy into the molecular matrix cannot be uniform but fluctuates in time and space. In succession the elements of the liquid matrix vibrate around temporally and locally fluctuating centers and, in immediate consequence, the equilibrium of attractive and repulsive forces become disturbed (see Figure 1). As every movement of an element out of its equilibrium position causes a spontaneous evasive movement of the neighbors, the whole matrix is influenced.

As mentioned above, it is the general and undisputed physical view that the molecules in a matrix of condensed matter attempt to reach the most energetically favorable equilibrium position. In the case of spherical molecules, this state, and the optimum distance between the molecular centers, should always be present. In the case of non-spherical particles, on the other hand, axis alignment determines the distance between the molecular centers. In a liquid, molecular axes are not evenly arranged in space and, due to the undirected repulsion forces of neighboring molecules, tend to rotate in all directions of space. Due to local mutual hindrances by adjacent molecular fields, however, it should hardly be possible to rotate in a single operation. Free rotations would require the displacements of neighboring molecules. Assuming that the principle of minimum constraint remains valid even with a kT-excited molecular matrix, this is considered improbable.

Molecules try to position their center of mass in positions of equilibrium, which are characterized by the potential minima, but this is prevented by irregularly aligned axes. The smallest distances between the molecules are achieved with uniformly arranged axes, meaning—contrary to the impetus of entropy—in the crystalline state. This energetically preferred state is aimed for at all temperatures by partial revolutions, but temporarily formed structures with aligned axes cannot be consistent at high kT levels. When approaching Tm from higher temperatures, more and more clusters withstand the destructive forces of high-energy neighbors and finally crystallites are formed that solidify the entire matrix. Therefore, the rotational possibilities of the vibrating molecules are crucial for each transition scenario.

From the above situation, it follows that when Tm is approached, the number of particles per unit volume decreases as short-lived clusters of aligned molecules are formed resulting in a decrease in the number of translations per unit time and, in immediate succession, in viscosity. The real behavior of almost all investigated substances seems to confirm this model concept, as the numerical study in part II will show.

Vibrational amplitudes are distributed around a mean value and as long as the spatial changes consist only of a normal volume increase of the thermal expansion, interpenetrations of the molecular components are not possible because of the size of the cavities being too small. A critical event is created by the random occurrence of combined actions of a certain number of elements, then evasive movements can intensify and create temporary free spaces and openings. The number and size of such short-lived apertures depend on the temperature and are distributed around an average value.

If the gaps are larger than the cross-section of an adjacent element, a shift of this element in principle, wholly or partly with a molecular part, is possible. A further prerequisite that such a change of position can actually occur is the corresponding spatial direction of the adjacent vibration amplitude. Due to their axis-independent orientation, spherical elements should not be subject to any spatial influence, but since the forms of real molecules are only exceptionally perfectly spherical, the projection of the molecular form directed to the aperture is decisive, as shown in Figure 1.

The above picture may appear trivial prima facie, but it is to emphasize the importance of axis orientation, a factor only rarely taken into consideration [41], as crucial for the physics of glass transitions. Above a characteristic temperature Tg_g the respective gaps of some cavities are large enough for the (partial) occupation by neighboring molecules, if their vibration directions permit it. In the case of a (partial) occupation, the occupying molecule itself leaves behind an empty position, which can only be occupied again with a time delay until the size and direction of the vibration amplitude of an adjacent molecule is suitable. If reoccupation at the second position coincides with the release in the first position, the volume changes are compensated for one another. However, since the abandoned sites cannot be immediately reoccupied, the system reacts by restoring the equilibrium molecular distances and creating additional volume.

In contrast to the conventional idea of the requirement of activation energy during transport processes, the new model concept assumes that the fluctuating input of thermal energy into the liquid matrix causes only inharmonic oscillations and, as a consequence, leads to the occurrence of cavities between the elements. This is not to say, however, that the energetic conditions have no influence on the displacement of vibrating elements. Using the common corpuscular-atomistic view within the oscillating matrix, mutual penetrations are unthinkable because of the too small vibration amplitudes, as stated above. If there are adjacent openings of the order of magnitude of the cross-section of the vibrating elements, displacements are possible in principle. However, such displacements—percolations—can only occur against the field forces of the adjacent elements acting in the openings. Since the field forces depend on the distance between the cavity boundaries and the center of mass of a passing element, it follows that the smaller the difference between the cross-sections, the higher the required shear forces acting on the passing element must be.

The size of the apertures decreases with falling temperature and at the same time the required shear forces increase, thus as a direct consequence the value of the time constant τ for the adjustment of the internal structural equilibrium and that of the coefficients for self-diffusion, viscosity, and other transport variables increases.

From the above consideration it can also be derived that the higher the required thrust to pass a gap, the higher the “cooperativity” of the vibrating elements must be. Cooperativity is not a specific physical quantity, but the random interaction of several elements oscillating in the same direction and thus causing a higher shear force.

At the beginning of the work it was mentioned that the new model was based on the theory of free volume. This statement has to be modified insofar as to say it is not the size of the cavities but the width of the apertures that is decisive. Behind a narrow opening there may well be a larger cavity, but this has little or no effect on the energetic conditions during the molecular passage. However, the question arises as to whether there is a fixed relationship, independent of temperature, between generated free volume and the number and width of apertures. Since both repulsive and attractive forces can act, these quantitative relationships are complicated and require further theoretical clarification. Qualitatively, however, the result is a closed picture that clearly illustrates the glass transition.

The fact that self-diffusion depends on the proportion of molecular size to kT may be shown by the following simple (fictive) experiment: (Figure 2).

Seven spheres, six white and one black, were placed in a circle on a vibrating support. The black sphere was situated in the center, encircled by the other spheres. The spheres were surrounded by a circular limitation at a certain distance from the outer virtually enveloping sphere ring. The question arises as to which diameter the limitation must take on so that the black sphere moves out of its central position. If the distance is less than a certain fraction of the sphere diameter the black sphere will indeed move around its central position but cannot leave it. If, however, the limitation distance is larger the black sphere will leave its central position the faster the larger the limitation diameter is. In this experiment, the limitation symbolizes the average vibratory amplitude of the molecules, and thus kT, and η corresponds to the average shifting velocity. The vibration intensity and frequency concerning the minimum distance of the limitation should have no influence during this experiment. “Tg”, the limiting temperature between the solid and the liquid state, is reached when the limitation distance has such a value that the black sphere moves out of the central position. The experiment yields the free volume fraction in a simple way without considering energy foundations.

Figure 2 shows some simple shifting possibilities in reference to the dependence of the relation between the radii of the vibrating spheres and the diameter of the outer limitation:

The experiment addresses one of the unsolved, and probably unsolvable [73], problems in physics and mathematics. It is well known that the tightest packing of spheres will become 1−1/6 π2^0.5 ≈ 74% when the spheres are arranged by hand in hexagonal packing. On the other hand, when the spheres are poured into a container and are compacted by mechanical vibrations the packing density reaches at maximum about 63% [74], meaning that there is no moment where the spheres are packed in the tightest way possible. If one refers this result to the problem of glass formation one may suppose that the situation depicted in Figure 2c would become very interesting ifnon-spherical molecular adequate bodies with varying elasticity modules were used instead of hard spheres. This might perhaps explain the influence of the molecular rotation possibilities and answer the question asked above. Suitable computer simulations should not imply too big a problem.

There is no doubt that viscosity is associated with molecular changes in position within space, as the equivalence to self-diffusion shows. As the number of position changes is strongly temperature-dependent, and since each position change leads to apertures between the elements, viscosity could also be calculated in direct dependence on temperature.

This opens up a challenging question: why look for a relationship with an entity that itself depends on temperature rather than approaching this in a more direct manner? If there is a simple proportionality between temperature and the number and size of apertures without an additional singularity and without further temperature-dependent processes that take place simultaneously, the answer should be: the introduction of volume is unnecessary. However, the fact is that such a simple proportionality does not exist in reality. Already the simultaneous temperature-dependent development of vapor pressure which influences the distribution of internal energy raises questions about simple proportionality. Looking back to the model it should be evident that, at least, there are two different processes increasing volume with temperature, at first the normal thermal expansion as common also for crystalline matter and, in the case of liquids, the generation of additional volume by the aforementioned process (see Figure 3). Both partial volumes do not necessarily exhibit the same temperature dependence. Consequently, the situation could be formulated in such a way that the energetic framework conditions are hidden in the development of the volume (and vapor pressure) and do not necessarily have to be considered additionally for later derivative relationships. Therefore, the introduction of volume into an equation describing the dependency of transport properties on temperature seems very reasonable, and the definition of free volume is of great importance, not least with regard to the influence of pressure, the third main variable of the two-phase system. From a practical point of view, however, it is probably possible to work with a temperature function when the vapor pressure is very low, such as with supercooled liquids. This will be shown in part II of the work with viscosity values on silicate glasses and further substances in the supercooled range.

3.2. Defining the Boundary Line between Liquid and Glass

3.2.1. Definitions of Free Volume

At first glance, the term “free volume” appears to be quite plausible. However, in literature the definitions of “free volume” are very different. Definitions and correlations can be found that are either based on the basic molecular volume ΣV_M, the liquid volume Vl₀ extrapolated to 0 K (Doolittle [75]), or the crystalline state. In the diagram above (Figure 3) V_TK is shown as a definition that defines the volume at the Kauzmann temperature T_K, the temperature at which the extrapolated curve of the equilibrium density of the liquid intersects with that of the crystalline state. As this volume, according to the new model, cannot be reached by a glass consisting of non-spherical elements but only in an ordered crystalline state, this definition is regarded as irrelevant as is the reference to Vk₀. The definition Vf_hs which is based on the molecular basic volume ΣV_M (van der Waals volume, hard sphere volume) may not be used for defining free volume as it implies the configurative volume V_conf. The configurative empty space V_conf as the difference between the zero point volume Vg₀₀ and the molecular volume ΣV_M is determined by the molecule shape and cannot be reduced further. Even at higher temperatures, it has to be assumed that, due to the too small dimension size, that molecule associated space cannot simply be used by neighbor molecules for position changes. The free volume according to Vf_SW [76] should have no direct relation to molecular transport. Figure 4 demonstrates some possibilities to define the free volume.

According to Figure 3, the specific volume is therefore composed as follows:

V_(T) = ΣV_M + V_conf + V_vib(T) + V_gen(T)

(1)

This definition does not take into account the influence of the pressure, which should also have a large or very small influence on the temperature-independent partial volumes.

How free volume should be defined depends on whether or not one considers the vibratory expansion at Tg, V_vib(g) as free volume useable for transport processes and whether one considers a basic volume necessary.

Three differently defined “free” volumes will be discussed below (Figure 4). One case implies different viscosity behavior at the limits of the liquid state.

3.2.2. Pre-Crystallizing and Supercooling

As already known from the 1965 work of Barlow, Lamb, and Matheson [34] the viscosity behavior of some simple liquids at the region of the melting point of the crystalline phase changes without visible crystallization and barely perceptible variances in density. Deduced from the course of viscosity temperature dependence of simple liquids in both regions, above and below Tm, a crossover of different molecular transport mechanisms in two temperature regimes was concluded.

In his early 1980/1981 studies [4,77], the author depicted the viscosities of o-terphenyl, the salt blend potassium nitrate/calcium nitrate 60/40, glycerol, and those of the glass standard DGG-1of the German glass society as log(η) = f(log(1 − Tg/T)) and demonstrated the different behavior, too. Both o-terphenyl and the salt blend potassium nitrate/calcium nitrate 60/40 showed a distinct kink at a certain temperature, which was interpreted as a change in packing density in connection with pre-crystallization appearing in the vicinity of the melting point.

Since the molecular spacing is closer to energetic equilibrium when the molecular axes are oriented uniformly (crystalline state) than when the axes point in all spatial directions (glassy state), the system prefers the crystalline state and attempts to achieve it by partial rotations. This should principally be valid for all temperature ranges. Because of the temporally and spatially fluctuating input of thermal energy into the system, at higher temperatures however, axis alignment is disturbed and prevented.

This structural change cannot remain without having an effect on the transport properties of the molecules. As the temperature gradually decreases, these areas increase and form nuclei to which further molecules attach quickly, which eventually leads to an immediate crystalline solidification. If, on the other hand, cooling takes place very quickly, enlargement of the pre-crystalline zones is impeded and no nuclei can be formed or at least no crystallization can take place. Similar considerations are taken up again in the 2004 work of Blazhnov et al. [78], although the role of nuclei seems somewhat over-emphasized and the negation of influence on viscosity may be questioned. Dyre [79] assumes “fairly large and well-defined crystallites” which are deformed and hardly detectable by standard X-ray or neutron scattering. Semmelhack and Esquinazi [80] investigated “metastable ordered structures” and “unstable crystalline structures” in OTP. Baran et al., 2014 [81] measured OTP with FT-IR and discovered that below 1.2 Tg crystal nuclei appear which are absent above that temperature.

Therefore, one can begin from the premise that with simple liquids approaching Tm, a pre-crystalline state will successively be generated and that, considered physical, there are two different substances above and below the onset of cluster generation.

A coherent equation of the viscosity behavior encompassing both regions with common parameters should therefore be inadmissible. This does not mean that no composite equation can be developed to describe the whole range, although it should be strongly assumed that the properties in the supercooled region are dependent on the measuring and cooling conditions.

4. Glass Transition/Transformation Range

4.1. Time Dependence of Properties Approaching the Glass Transition Regime

One of the big problems of determining the behavior of properties approaching the glass transition regime is time dependence.

The usual methods of measuring the glass (transition, transformation) temperature, dilatometric or calorimetric measurements with a constant rate of change in temperature qT = ±dT/dt, do not give the molecular elements sufficient time to preserve the equilibrium density when the temperature falls below a certain value dependent on qT. The temperature range in which this time dependence is clearly perceivable is defined as the transformation or glass transition range, with the deviation from equilibrium density described as “beginning freezing”. It has to be pointed out, however, that the width of the “transformation range” is variable depending on qT and can be moved on the temperature axis. This is also true for the hysteresis range used for definition purposes by Mazurin and Rekhson [82]. Theoretically, there is no upper limit since the thermodynamic equilibrium is fundamentally disturbed when the rate of temperature alteration is higher than the respective relaxation time τ of the inner structure. The fictive temperature Tf, i.e., the temperature that the system would have in equilibrium with the current density, deviates increasingly from the current temperature the faster the cooling rate or the higher the relaxation time of the inner structure respectively the higher the viscosity is. In the presented model concept, the volume deviation from the equilibrium density is not interpreted as a beginning freezing. As long as the actual temperature remains above the true glass temperature Tg₀ during the cooling processthe system tries to achieve the equilibrium density and will finally reach this after sufficient waiting time (annealing). Therefore, the “glass transformation”, in that inadequate sense, is not a special property of supercooled liquids but in general a property of any liquid which is being cooled from any high temperature. In a nutshell, starting at a very high temperature with a fast cooling rate the fictive temperature Tf, and thus density, may deviate from the equilibrium density even above Tm. In this case, a stable glass with a large free volume below Tg₀ should be present, which does not react to annealing with respect to its viscous behavior. Figure 5 shows the time-dependent development of the specific volume at constant cooling rate.

Within the range close to Tg₀ many properties depend not only on temperature but also on time, a fact emphasized by Williams, Landel, and Ferry [31] who established for this range their well-known time-temperature superposition principle. In order to use the WLF equation it is not necessary to know Tg₀ but instead one may use an arbitrary temperature parameter in the transition range within wide bounds. This underlines the above assessment that the deviation from equilibrium density is only indirectly related to glass formation.

The existence of a limit temperature Tg₀ is still the most controversial question within glass science today. The existing uncertainty is caused, among other things, by the functional course of the time-dependent measured Tg values, which until the beginning of the millennium was regarded as linear in relation to the logarithm of the cooling rate qT, Tg(qT) = a + b * log(qT). Although Brüning and Samwer [46] discovered a flattening of the curve at very low cooling rates in 1992 on the basis of DSC measurements, the theoretical significance of this was apparently widely overlooked. A second uncertainty comes from the numerical success of the VFT equation, the most commonly used viscosity equation, which yields a limiting temperature well below the glass transition region.

Only below Tg₀, the temperature at which the apertures produced are smaller than the smallest cross-section of the elements and V < Vg₀, should a material be termed “glass”, either as an ideal glass or as a real glass, which still contains some free volume, as it is the only experimentally attainable state. An ideal glass does not contain free volume available for transport processes and, therefore, it should be a stable matter.

An important question arises as to what happens when the temperature of the out-of-equilibrium-liquid falls below Tg₀. In this case we then have a real glass and a scenario in which small vibratory amplitudes are coupled with an excessive empty space.

The topic of excess free volume is of great practical importance, for example, for the ageing of polymers. This has been studied in the context of the fictive temperature concept by many researchers (for example [26,83,84,85,86]) and falls outside the scope of this work, but the model presented here can also contribute to a changed perspective. The basic principle should be that an ideal glass, i.e., a glass without free volume, should not be subject to viscosity-related physical ageing. This again underlines the importance of the knowledge of Tg₀ for glass science.

A further question arises with regard to the classification of glass transformation in the thermodynamic sense. Undoubtedly, the assumption of a singular glass transition temperature influences the thermodynamic evaluation, but if one follows the discussions on this subject (see e.g., Zanotto and Mauro, 2017 [87], Nemilov, 2018 [88]), this is a difficult question that should be dealt with by physicists. From a chemical engineering point of view, the glass state could be considered stable and the supercooled liquid state unstable. These evaluations refer to the existing real possibilities of state changes. Within the supercooled liquid, existing pre-crystalline structures can lead to crystallization over time since molecular rotations and clustering are possible. In contrast, the glass structure below Tg₀ cannot change even after an extremely long waiting period due to a lack of space and associated lack of rotation possibilities. Whether this statement applies in the above-mentioned case of an excessively large “frozen” free volume does not yet seem to have been conclusively clarified.

On the other hand, since undirected molecular axes prevent the molecular centers from positioning themselves on the equilibrium position, there should be an “adaptive force”, but this cannot be effective. From the author’s point of view, a certain arbitrariness remains, since many substances can crystallize in more than one form with different densities and they are all defined as stable in the thermodynamic sense.

In his 1991 work, Angell [89] emphasized the thermodynamic importance of T₀ in the VFT equation by comparing the ratios of Tg/T₀ and Tg/T_k, which were the same for some substances where entropy was calculated below Tg. However, this assessment does not call into question the fact that the glass transition at Tg₀ may intervene and the alignment of the molecular axes becomes impossible. In an interesting work of Yamamuro et al. [90] the heat capacity of toluene and ethylbenzene was measured in an adiabatic calorimeter and the configurational entropy was calculated in a convincing manner. The configuration entropy decreased steadily with decreasing temperature and at Tg (117 resp. 115 K) reached a constant value in the glassy state in a sharp bend. The same was observed with 3-bromopentane, 1-butene, o-terphenyl, and the glass-forming plastic crystal cyanoadamantane. Nevertheless, this assessment of Angell seems to have a physical significance with spherical molecules, as previously stated. Tg₀ (derived from Vg₀) and T_k possibly could be the same if the alignment of the axes in the liquid and the crystalline state are identical.

In two more recent papers [87,91], it was stated that the ultimate fate of glasses is the crystalline state. However, this scenario does not seem very likely, given the increasing mutual obstruction and the lack of usable free volume (see also [66]). Spherical molecules such as noble gases are an exception due to their uniform axes, as already mentioned.

In this context, the conditions of physical vacuum deposition (PVD) [92,93,94] must also be addressed. During this process, monomolecular layers are successively deposited from the gas phase onto a substrate that has a temperature below the conventional glass temperature Tg_{(DSC qT=10min/K)}.

Depending on the substrate temperature, denser or less dense glasses are obtained than those with conventional cooling. The process is used, among other things, to “get deeper into the glass state and to achieve more stable glasses”. This phrase is based on the idea that suitable measures can be taken to approach the Kauzmann temperature T_k or at least the Vogel temperature (T₀ in the VFT viscosity equation) or the temperature T₂ of the ADM theory [8]. As already mentioned, this is not possible in space with irregularly aligned molecular axes, but the path below Tg₀ may only be possible with at least partly parallel aligned axes. If the intersection point at T₂ or T_k exists, then this implies that the vibrating elements have to be arranged in a spatial alignment of the molecular axes at decreasing temperatures, which would then be identical to the crystalline state at their intersection point.

A glass should have a completely disordered state. Each partial order come up closer to the crystalline state and thus to higher densities. However, such a partial order is to be expected with the PVD, because there is a high probability that the molecules, already affected by gravity, will not be arranged perpendicular to the substrate. Compared to the glasses obtained conventionally from liquid by cooling there should be a lack of one spatial component in the precipitated glasses. PVD-glasses, one could call them 2D-glasses, should correspond to an intermediate stage between the completely amorphous and the crystalline state. Therefore, PVD results cannot easily be compared with conventionally obtained results.

4.2. Influence of Axis Orientation in Space

The definition of axis orientation is not as simple as it seems on first glance. Molecular elements have interior grades of freedom which may lead to the deformation of molecular shape, particularly those with chain-like molecules. In such cases a cross-area may involve a larger part of a molecule, for example when a short-chained substance has the ability to build up cyclic structures when flowing. Nevertheless, the general fact remains that also with deformed molecules smaller and larger cross-areas exist and, therefore, the term “axis” may be used also in such cases.

The temperature-dependent generation of empty spaces and time-dependent axis orientation are in principle two different processes. In the very high temperature range vibration amplitudes are large and the free spaces generated by combined actions are big enough to become occupied by all neighboring elements independently of their axis orientation in space, only governed by the appropriate direction of modes. That range should be the normal low-viscosity region. When the temperature decreases to Tg_l all apertures become smaller than the largest molecular diameter of the vibrating molecules. This means axis orientation in space starts to have an influence on translational possibilities. The number of position changes decreases more than would be possible without any alignment restrictions, as translations only happen when the axis of an element is aligned in space such that the geometrical projection onto the gap is smaller than its diameter. Lowering the temperature further finally leads to a situation where the broadest apertures of the void distribution only allow vibrating elements to translate when their cross-sections, totally or partially, are smaller than the diameter of that aperture and, additionally, are pointed to the gap. The limit volume of the liquid state is reached in this situation and can be termed Vg₀. Since at Tg₀ about half of the distribution width of the vibration amplitudes corresponds to V > Vg₀, some cavities are still present at Tg₀ (but cannot contribute to flowability, as explained later). Only when the temperature is lowered further to Tg_g, are all apertures smaller than the smallest molecular cross-section thus making passage impossible. The disordered solid state should then be reached. Figure 6 shows the relationships outlined above:

In practice, the ideal glass state without any usable free volume cannot be reached by normal cooling as the waiting times for the molecular rearrangement are too long.

Certainly, there exists empty space in between the molecules also below Tg₀, but that volume (configurative empty space V_conf) cannot be filled with adjoining molecules or parts of them due to the dimensions of these areas being too small.

Undoubtedly, changes in position below Vg_0, respectively Tg_0, are much less frequent than above, since three states must occur simultaneously:

• a gap must be wider than the cross-section of the smallest dimensional portion of a neighboring molecule,
• the alignment in space of the molecular axis of an adjoining molecule must be pointed to the gap,
• and, last but not least, the direction of the mode of that vibrating molecule must be strictly directed to that aperture.

Therefore, this influence causes transport properties to adopt a new quality and the interesting question arises as to whether there are differences between the various classes of material. Another question is whether the molecular clusters that form in the region of the crystalline melting point, which are considered to be causal for the altered viscosity behavior are related to the possibilities of axis alignment. It should be clear that chain molecules are not able to shift entirely, whereas non-spherical simple molecules have more than one possibility to move through a neighboring opening. As the numerical analysis of simple molecular liquids with data above T_m shows, Tg_l corresponds to the temperature at which the viscosity appears to diverge. In reality this is not the case as fluidity persists until Tg₀ is reached. This partition between two viscosity regimes has also been addressed by mode coupling models, such as “dynamic cross-over”. In fact, the characteristic temperature Tc of these models corresponds approximately to Tg_l (deducted from Vg_l). On the other hand, however, only side-groups or segments of chain molecules can shift through an adjacent aperture so that the viscous behavior corresponds to the simple molecules below Vg_l. Therefore, with chain molecules Vg_l does not intervene and only Vg₀ controls viscosity. This statement was convincingly verified with viscosity data of polystyrene and polybutene whereby viscosities at a T/Tg-relations of 1.08 were included into the regression analysis without any kink in the viscosity curve becoming apparent.

Assuming that there is only one driving force that causes molecules to adopt their equilibrium positions, the spatial arrangement of spherical molecules at the glass transition should not deviate from their arrangement in densely packed crystal. If this assessment is correct, glass formed at a temperature Tx below Tm should have the same density and structure as the crystal at Tx formed at Tm. In the case of spherical molecules, therefore, no distinction should be possible between glass and crystal. Some preliminary tests confirm this important statement using the example of noble gases (argon: V_cryst. 0.619 g cm⁻³—from viscosity calculations with NIST data Vg_l = Vg₀ 0.616−0.622 g cm⁻³; krypton: V_cryst. 0.334 g cm⁻³, Vg₀ 0.34−0.35 g cm⁻³; xenon: V_cryst. 0.274 g cm⁻³, Vg₀ 0.27 g cm⁻³; neon: V_cryst. 0.66 g cm⁻³, Vg₀ 0.72−0.74 g cm⁻³).

For non-spherical molecules, however, the difference between Tg₀ and Tg_l is probably related to the ratio A_Molmax to A_Molmin (Figure 6).

4.3. Influence of Mode Distribution Approaching Tg₀

Two very fundamental questions remain: which influences cause the fixing of a liquid structure when the cooling rate goes towards 0, and does viscosity really get to infinity when approaching Tg₀, as Figure 4a,b implies? Which role does mode distribution play in this scenario?

This necessitates the examination of the influence of the vibration amplitudes in the transformation interval, as follows.

The vibrations of the vibrating elements are undoubtedly distributed around a mean value corresponding to the respective temperature. The width of the vibration amplitudes is limited and corresponds to a defined range of specific volumes V_i. Vg₀ represents the specific volume below which the apertures between molecules are smaller than the smallest molecular axis cross-sections. If, when approaching Vg₀, the lowest V_i values within a distribution are smaller than Vg₀, the result is a state in which both liquid and glassy solid matter is present. This condition is basically present in the glass transition interval between Tg_g and Tg_liq. The relations in the transition interval are depicted in Figure 7.

In the glass transition range the above relations are strongly time-dependent. Below Tg_liq more and more solid glassy matter is formed and it is assumed that there exists a suspension-like state. Decreasing the temperature further should create a state where the solid predominates and starts building a fixed structure with enclosed liquid droplets. When this status is reached, the reduction of the cooling rate can no longer influence the viscosity. That state should not be able to relax furthermore and qT should not have any influence. That limiting qT should be denoted qT_min (see also: Zondervan et al., 2008 [95]). Of course, when qT < qT_min the included liquid droplets further on become smaller and smaller and can continue to relax, but this can no longer affect the entire system. Therefore, the viscosity should reach its maximum equilibrium value according to the relaxation time present at this point. In a paper from 2002 Krüger et al. [96] the authors, based on time domain Brillouin spectroscopy and hypersonic experiments, stated a cut off of the α-relaxation at a temperature T_gs and strongly hinted at the existence of an “isostructural” phase transition, however the transition mechanism was not elucidated. There is a certain probability that T_gs is identical to the Tg_g of this work and the measurable α-relaxation ends because the state “liquid droplets in a solid matrix” is reached.

5. Identifying Tg₀ from Measurements

The determination of Tg₀ from the Tg_(qT) values measured at a higher rate of temperature change is one of the key tasks of the problems associated with glass transition. There is a wealth of published work on both the theoretical basis and the detailed definition of the measured Tg values. An evaluation of the different measuring methods and definitions cannot be made by the author due to a lack of own experience and is also not the goal of this work. As an important result, however, it can be seen from the literature and it should be stressed that the Tg_(qT) values, even at the same cooling or heating rate, can be quite different.

Dilatometric and calorimetric measuring methods are common. Hutchinson [58] gives a very good overview and analysis. Obviously, there are experimental difficulties in achieving Tg_(qT) values. Dilatometry problems occur due to the deformability of the melt and as regards calorimetry mainly the problem of thermal lag in the samples causes difficulties. The calibration of the instruments also seems to be a source of uncertainty.

From the principle of physical simplicity, dilatometry should be the preferred method, but due to experimental manageability and the small sample quantities required DSC measurements have established themselves in practice. However, DSC measurements are not handled uniformly and the definition of the Tg value found in the literature varies. If the rate of temperature change is equal to or less than the reciprocal value of the structural equilibrium constant τ, no deviation from the equilibrium density or enthalpy of the liquid should be obtained above Tg₀. At Tg₀, within an interval corresponding to the distribution width of the molecular vibrations, the equilibrium line is turned into the glass state.

The measurements can be carried out at equal or different heating or cooling rates, and thus the beginning and ending of the transition interval and the position of Tg in the interval can be defined diversely. There should be no question that the relationship between the heating rate and structural relaxation constant τ, i.e., the distance to thermal equilibrium, determines the course of the examined property within the transition interval. The tangential inclination of the liquid side of the DSC transition step should be further on a function of the volume viscosity. The latter is very different for different substances at the same distance to Tg₀, since it is very likely that the molecular packing density also determines this inclination and, subsequently, determines the position of the intersection of the two tangents. Regardless of the fundamental issues, this further restricts the physical significance of Tg_(qT>0).

Furthermore, it is very questionable that rate dependence can be calculated with one and the same equation for measurements with different definitions of Tg_(qT). In the best case scenario only the parameters of the equation are different, but it is quite likely that the general dependency is distinct. Therefore the determination of Tg₀ from the Tg_(qT) data represents a major challenge.

Incidentally, the detected time dependence is not limited to Tg only. DSC measurements of crystalline matter show a temporal dependence of the same order for the start of crystallization [97] (Figure 3b there).

As the molecular vibrations are not uniform but distributed around a center value, the glass transition should not take place as singularity but in an interval. This should be valid independently from the preset cooling or heating rate, even for qT→0 (resp. qT_min, see later).

From dilatometric measurements the earliest stage of the onset of the glass transformation Tg_g may be taken as the temperature at which an initial alteration of the expansion coefficient in the glassy state starts. This should be independent of the amount of incorporated free volume, i.e., apply to all practical glasses, however at high rates of temperature change volume changes are difficult to detect.

The fact that in spite of different temperature changing rates the coefficients of volume expansion retain a constant value at a given characteristic temperature for the glass has been proven by studies of Bero and Plazek [98] on an epoxy resin. The phenomenon can, however, already be seen in former volume curves, e.g., by Ritland [29] for a BSC glass, Rötger [99] for the glass “Jena Normal 16 III”, deBolt et al. [100] for B₂O₃, and Chen and Turnbull [73] for a gold-germanium-silicon-alloy.

Evaluations undertaken from the glass side are appropriate in measuring Tg₀, as has also been confirmed by dielectric studies. For toluene, Döß et al. [101] have demonstrated that the dielectric constant independently from the used measuring frequencies always show a sharp kink at T = 117 K, the same value as measured by DSC (as depicted in Figure 1 of that paper and [90]) and the calculated Tg₀ value from viscosity measurements. Another impressive confirmation may be drawn from Figure 3 for a basaltic melt in Yue et al. [55].

If Tg is defined thermo-analytically (DTA, DSC), then Tg_g is the temperature at which the basis line turns upward for the first time during the heating process. Although the heating method with heating rates greater than qTmin basically assumes a state outside the thermal equilibrium, the excess free volume does not prevent the generation of further vacancies. Exemplary measurement results are given for instance in Figure 3 for CH₃COO(Li_0.86 Na_0.14) (Tg_g approximately 360K) and in Figure 6 for GeO₂ (Tg_g approximately 740 K) in the study by Brüning and Crowell [102].

In the literature one often finds representations of Tg_(qT) as a straight line plotted over log (qT), and indeed with the usual qT values, this relationship seems to be valid with many substances from different material classes.

Tg(qT) = Tg_(qT=1) + u * ln(│qT│)

(2)

Exemplary results are shown by the dilatometric studies of Bero and Plazek [98] and the work of Brüning and Crowell [102] using the DSC results of LiNaAcetate and GeO2, as well as by Greiner and Schwarzl [103] and Hadač et al. [104] for polystyrene.

Such plots give the impression that there is no Tg₀. However, the equation per se does not rule out that there is a cooling rate qT_min, and that falling below this rate has an effect on the overall system. In the frame of the new model there should be definitely a lower bound of Tg_(qT) and a qT_min where the limit state is reached at which the transition from the status “solid particles in liquid medium” to “droplets in solid medium” takes place (see section “Influence of mode distribution approaching Tg₀”).

The surprising idea that a certain qT_min should exist was stated by Bero and Plazek [98] in their work of 1991:

“The data indicate that upon sufficiently slow cooling (ca. 2 °C per century) a sharp transition should be observed which could be thermodynamic in nature, since Tg would be independent of rate at all slower rates.”

These authors state furthermore:

“If the data correctly indicate bona fide evidence for a Tg-related thermodynamic transition, it does not seem likely that it is the T_∞ suggested by a free volume analysis, or the T₂ of Gibbs, Adams, and Dimarzio, since the observed constant temperature of 118 is but 14 °C below the Tg obtained at a rate of cooling of 0.9 °C/min. The values of T_∞ and T₂ are usually thought to be some 30 to 60 °C below the nominal Tg obtained at about a 1 °C/min rate of cooling.”

The dilatometric results of an epoxy resin examined by Bero and Plazek [98] listed in

Table 1. Dilatometric results for Epon 1001f-DDS.

qT (K/min)	Tgi (K)
0.9	131.7
0.25	130.5
0.05	128.9
0.003	126.1

are very interesting because they were obtained at very low cooling rates. Therefore, they should be analyzed in more detail.

Depending on the cooling rate qT_i, the following Tg_i values were measured:

The first deviation from the expansion coefficient of the glass was detected above Tg_g = 118 K.

Using Equation (2) the following equation parameters are obtained: Tg_(qT=1K/min) = 131.83 K; u = 0.9847. See Table 1.

If Table 1 is extended with Tg_g and the standard deviation is determined as a function of an arbitrarily assumed effective minimum cooling rate at 118 K, the following regression results are obtained (

Table 2. Evolution of standard deviation for Epon 1001f-DDS with arbitrarily chosen qT_min at 118 K.

qTmin (K/min)	σ(Tg) (K)	qTmin (K/min)	σ(Tg) (K)	qTmin (K/min)	σ(Tg) (K)	qTmin (K/min)	σ(Tg) (K)
1 × 10−9	0.86	1 × 10−6	0.054	7.95 × 10−7	0.0278	5 × 10−7	0.091
1 × 10−8	0.64	9 × 10−7	0.038	7.5 × 10−7	0.0297	1 × 10−5	0.607
1 × 10−7	0.35	8 × 10−7	0.028	7 × 10−7	0.037

):

Figure 8 shows the steep but finite increase in the gradient of Tg(qT) at very slow temperature changes.

An interesting result offers the comparison of the qT_min parameter for EP with the stated values of Bero and Plazek: 2 K/century = 3.8 × 10⁻⁸ K/min versus 7.9 × 10⁻⁷ K/min. Bero and Plazek gave no derivation for the stated value but it can be supposed that it is surely not pure invention. In any case, it is a remarkable agreement.

According to the new model presuming a fixed Tg₀, the function must be curved in a semilogarithmic plot. Furthermore, there must be a qT_min at which a further slowing down of the cooling rate has no effect anymore, because the state “liquid droplets in solid environment” is reached.

Figure 9 shows the basic conditions.

In 1991 Brüning and Samwer [46] carried out DSC measurements on metallic glasses, B₂O₃, and polymers with very slow rates of temperature change and suspected a temperature T_g⁰ as “lower limit of Tg” due to the deflection of the function Tg = f(ln(qT)). They measured Tg as the onset of the ΔCp peak on heating at the point of intersection between the linearly extrapolated curve below the transition with the steepest tangent of the rise in ΔCp, making the important remark that “it is apparent that the extension of the measurements to low heating rates is necessary to observe the deviation from a straight line in the semilogarithmic plot.”

They gave an equation for the dependence of Tg from qT:

Tg(qT) = Tg⁰ + A/ln(B/qT)

(3)

whereby Tg(qT) is defined as the onset of the Tg step.

The theoretical consequences of the experimental findings of Brüning and Samwer concerning the fundamental questions of the glass transition do not seem to have been considered further in the subsequent period, or only very rarely. In 2015 Schawe [105] published a paper containing measurements on polystyrene with very slow and very fast qT values using a new type of DSC equipment. Tg was defined by the equal area method [106,107] as a mid-step value and the VFT form was used for calculating qT dependence. The experiments confirm the logical consequence of the presented model that there must be a lower limit of Tg, here denoted as Tg₀.

Table 3. Measured Tg(qT) values.

Rate	B2O3 [46]	Pd40Ni59P19Si1 [46]	PMMA [46]		Polystyrene [107]
qT (K/min)	Tg(qT)	Tg(qT)	qT (K/min)	Tg(qT)	qT (K/s)	Tg(qT)	qT (K/s)	Tg(qT)	qT (K/s)	Tg(qT)	qT (K/s)	Tg(qT)	qT (K/s)	Tg(qT)	qT (K/s)	Tg(qT)
0.1	538.6	554.6	0.1	378.1	0.0033	368.8	0.5	374.2	5	478.3	100	381.5	700	386.8	3000	390
0.2	540	555.7	0.2	377.8	0.008	369.2	0.5	375	10	377.3	100	382.3	700	387.5	3000	390.5
0.5	544.5	560.0	0.5	378.5	0.016	370.6	0.65	374	10	378.6	100	382.5	800	385.4	3000	391
1.0	547.4	561.9	1.0	378.5	0.033	370.7	0.83	373.8	10	379.3	200	383.2	800	387	4000	391.3
2.0	553.8	565.1	2.0	380.3	0.05	371.5	0.83	374.5	20	379	200	384	800	388	4000	391.5
5.0	555.8	567.5	5.0	381.1	0.08	372	1	375.5	20	379.8	200	385	1000	387	5000	392
10.0	566.8	571.8	5.0	381.8	0.1	372	1	375.2	20	381	200	385.8	1000	388
20.0	571.2	576.7	10	382.5	0.1	373	2	375.8	50	380	500	384	1000	388
50.0	574.9	581.2	10	383.2	0.17	372.5	2	376.9	50	380.8	500	386	2000	389
100.0	589.7	586.9	20	385.1	0.2	373.6	2	378.5	50	382	500	387	2000	390
200.0	602.5	595.0	20	385.8	0.33	373	5	377.6	50	382.6	700	385.5	2000	390.5
			50	386.0
			100	388.0

shows the used substances, qT and Tg_(qT), whereby the data are extracted from the graphic of Figure 5 by Brüning and Samwer and from Figure 6 by Schawe.

To determine whether there is a functional relationship, regression analyses were performed with the following equations which are listed in

Table 4. Equations used.

Equations	Name	Formula
1	Brüning–Samwer	Tg(qT) = T0 + a/ln(B/qT)
2	Yue-invers [55]	Tg(qT) = Tg/((−ln(x) − a)/b)k
3	GS-1 a	Tg(qT) = Tg0 + (qT/qTmin)b
4	GS-2 a	Tg(qT) = Tg0/(1 − (qT * qTmin)b)
5	Bartenew–Ritland	Tg(qT) = 1/(a − b * ln(qT))
6	lin-log (Equation (2))	Tg(qT) = Tg(qT=1) + u * ln(qT)

^a This work. Equations GS-1 and GS-2 were developed with the goal of keeping Tg constant below qT_min as required by the model. Mathematical functions were sought that led to this result.

.

The results for B2O3 are given in

Table 5. Regression results for B₂O₃.

	Results for
	B2O3 (All Data)						B2O3 (Without qT = 50 K/s)
Equation	σ (K)	R2	Tg0/T0 (K)	a, (qTmin)	b/B/u	k	σ (K)	R2	Tg0/T0 (K)	a, (qTmin)	b/B/u	k
Yue-invers	2.52	0.990	496.4	−7.0917	30.65	0.0680	1.86	0.995	499.7	−7.596	25.028	0.0783
Brüning–Samwer	2.46	0.989	492.5	601.42	49,719.5		1.67	0.995	483.3	760.94	120,613
GS-1	2.60	0.988	525.8	1.58 × 10−6	0.2314		1.65	0.995	522.2	2.186 × 10−7	0.2122
GS-2	2.56	0.988	523.6	1.91 × 10−7	0.2016		1.65	0.995	519.3	8.697 × 10−8	0.1812
Bartenew–Ritland	2.75	0.948	-	0.0018	2.5 × 10−5		4.68	0.958		0.0018	2.63 × 10−5
lin-log (Equation (2))	5.82	0.930	(550.0)	-	7.822		6.37	0.945	(550.4)	8.209

Red characters prob(t) fails.

.

The calculated Tg₀ values of equations GS-1 and GS-2 are nearly similar to the values found with viscosity [108], where it can be assumed that the water content of the measured samples is low (<0.1%) but not identical.

The equations Brüning and Samwer and Yue-invers do not reach a constant value even at a qT of 10⁻⁴⁰ K/min, whereas with equation GS-1 the Tg value decreases by a maximum of 1 K when qT values below qT_min are chosen. Interestingly qT_min again has an order of magnitude of around 10⁻⁷ K/min.

Figure 10 shows the predicted course of the functions Tg = f(qT) for very low cooling rates.

The results for two metallic alloys are listed in

Table 6. Regression results for Pd₄₀Ni₄₀P₁₉Si₁ and La₅₅Al₂₅Ni₂₀.

	Pd40Ni40P19Si1						La55Al25Ni20 (Without Highest qT)
Equations	σ (K)	R2	Tg0/T0 (K)	a, (qTmin)	b/B	k	σ (K)	R2	Tg0/T0 (K)	a, (qTmin)	b/B	k
Yue-invers	0.72	0.998	591.2	−7.3620	2.3605	0.0451	1.24	0.992	356.2	−9.74	18.02	0.1143
Brüning–Samwer	0.81	0.997	522.5	451.65	106,262		1.13	0.992	308.2	1214.0	135,785
GS-1	0.98	0.996	545.4	1.90 × 10−6	0.2103		1.14	0.992	347.4	1.59 × 10−12	0.1305
GS-2	0.95	0.996	544.4	1.22 × 10−8	0.1919		1.14	0.992	343.9	2.82 × 10−10	0.1037
Bartenew–Ritland	2.6	0.964	-	0.0018	1.6 × 10−5		1.51	0.984		0.0026	3.45 × 10−5

Red characters prob(t) fails.

below.

The predicted course of Tg(qT) for Pd₄₀Ni₄₀P₁₉Si₁ with the above tabulated equations is shown in Figure 11.

Additionally, with the metal alloy Pd₄₀Ni₄₀P₁₉Si₁, equations GS-1 and GS-2 again give a qT_min of the order 10⁻⁷ K/min.

The results for two measured polymers are listed in

Table 7. Regression results for the high polymers PMMA and PS.

	Results for
	PMMA						Polystyrene (Mw 270,000; Mn 95,000 g/mol)
Equation	σ (K)	R2	Tg0/T0 (K)	a, (qTmin)	b/B/u	k	σ (K)	R2	Tg0/T0 (K)	a, (qTmin)	b/B/u	k
GS-1	0.74	0.961	373. 5	1.17 × 10−4	0.1979		0.78	0.987	358.7	1.4 × 10−13	0.083
GS-2	0.74	0.960	373.3	3.32 × 10−10	0.1885		0.78	0.987	357.5	1.6 × 10−20	0.074
Brüning–Samwer	0.77	0.958	364. 2	192.56	292,795		0.78	0.987	338.8	974.2	2.8 × 1013
Yue-invers	0.83	0.955	373.6	−7.814	14.60	0.026	0.78	0.987	340.6	−19.93	86.17	0.057
Bartenew–Ritland	1.0	0.920	-	0.00263	1.068 × 10−5		1.14	0.972	-	0.0027	1.2 × 10−5
lin-log	0.71	0.947	(379.9)	-	1.549		1.22	0.968	(368.8)	-	1.687

Red characters prob(t) fails.

.

The data scatter with PMMA seems to be too strong for a reliable regression analysis. Nevertheless, the result for equation GS-1 yields the expected Tg₀. The predicted course calculated with the equations is shown in Figure 12.

The results of Schawe for PS are depicted in Figure 13.

As mentioned, Schawe uses a different definition for the measured Tg(qT) values. Therefore it is questionable if the same equations can be applied. The qualitative picture shown in Figure 13 offers a rather similar behavior in respect to the other investigated materials, however the constant value for Tg with equations GS-1 and GS-2 is achieved at somewhat lower cooling rates. The calculated Tg₀ values are very plausible and match well the viscosity-based values, where equation GS-1 may be preferable because of its simple mathematical structure.

The calculations are strongly influenced by the data scatter and more data with slower cooling rates are urgently needed for a final decision, both on the extension to very slow cooling rates and on the number of substances. This also applies to dilatometric or volumetric data, which are of interest by the principle of thermo-physical simplicity.

Nevertheless, the equations providing a constant Tg value at not too low qT values are a strong confirmation of the presented physical model predicting a lower limit of Tg(qT) at qT_min.

6. Location of Tg₀ in the Transition Interval

Another interesting question refers to the limits and mean values of mode distribution in the transition interval. In the study of Holubová et al. [109] the step scan-DSC technique was applied. The authors point out that the ascertained Tg values are independent from the thermal history and the rate of temperature change. The transformation intervals were determined for various substances with Tg values in between 23 °C and 507 °C. The authors concluded from the gathered data that the glass transition cannot be seen as a pure kinetic process. They propose to define the inflection point determined by the step scan-DSC technique as clear material specific glass temperature.

It should be noted, however, that the step scan technique has its limitations when approaching Tg₀, since the waiting times increase exponentially and are difficult to maintain experimentally.

If one presupposes that real matters show vibration distributions around a medium value, the Cp step, as set out above, has to cover a temperature interval even when the cooling rate decreases towards 0. Consequently, the selection of the inflection point within the interval seems to be absolutely reasonable. At normal DSC measurements this inflection point is, however, not visible as it is covered up by the time-dependent enthalpy modifications. In this case, it remains reasonable to define the first deviation from the basis line as Tg_g.

In a study from 2003 by Holubová et al. [110] the inflection point T_i was fixed at 0.632 of the entire interval width. In a later study (Chromčíková et al. [110]) the position of the inflection point was stated as 0.5−RT_i/ΔH. If one considers the vibration distributions to be deemed qualitatively possible for the limit temperatures of both states, and if one supposes that the distribution width is in proportion to the respective temperature, it may be suggested that the inflection point is situated in the lower interval region close to the center value in accordance with the above-mentioned study. In the second part of this thesis it will be shown that the best results of the calculation of viscosity when approaching the glass transition interval are obtained when Ω = e^−Ω = 0.56714 is selected as the inflection point. By choosing Ω, the viscosity reaches its maximum value and dη/dT becomes 0.

Finally, it should be pointed out that the width of the transition interval can differ greatly across the different substance classes. If one puts the distribution of the vibration amplitudes in proportion with the width of the density fluctuation, the relation between the limiting and the main temperatures is well clarified as shown in Figure 14.

From Figure 14 a feature of highly practical importance may be deduced. The width of the transformation interval depends strongly on Tg₀ itself, roughly as a rule of thumb about 0.1 Tg₀, but there are large deviations (for example anorthite 0.09, B₂O₃ 0.1, SiO₂ 0.18, GeO₂ 0.18, Ca 0.39 0.06, 6-Phenylether 0.06, see part II), presumably caused by different packing densities. Specifically in the case of silicate glasses softening may start at more than 100 K lower than the conventional measured Tg_(qT=10K/min). In many studies this effect has been disregarded when a statement was given that a material was probed below Tg. To avoid relaxation processes from liquid fractions, an investigation of glasses should always performed below Tg₀ or even better below Tg_g. An equal disregard frequently appears with investigations of the liquid state, for example with measurements of viscosity covering as well the regime above Tg_liq as the range near Tg₀.

7. Conclusions

The most important foundations of the new model are:

• the generation of apertures of a sufficient size by combinative mode amplification allowing molecular shifts,
• the limiting of volume Vg₀ and following thereupon a defined time- and history-independent, material-specific glass temperature Tg₀ for all substances,
• the independence of Tg₀ from qT
• the strong influence of the orientation of molecular axes and thereupon following variable possibilities for molecules to move through neighboring apertures,
• the existence of a material-specific intermediate limiting volume Vg_l for simple non-spherical molecules, below which molecular translation possibilities adopt a new quality,
• the importance of mode distribution approaching Vg₀,
• a finite maximum value for equilibrium viscosity at Tg_g,
• different viscosity behavior below and above the melting point of the crystalline phase,
• the dependence of the molecular transport processes on thermal expansion and size and the number of generated apertures.

In the author’s opinion, the model presented here provides a consistent microscopic view of the glass transition and molecular processes within liquids. It considers the principle of thermophysical simplicity and can be verified by experiments.

8. Prospects

In part II of this work the experimental validation of the new model has been performed by multiple regression analysis with new viscosity equations which are based on the premises set out above. The new equations are in no case significantly worse and in the very most cases superior to the well-known equations of Vogel–Fulcher–Tamman (VFT), Doolittle, MCT, Bässler–Avramov, MYEGA, and to new proposed scaling procedures based on equations containing both volume and temperature first developed by Andrade 1934.

Part II deals with a few exceptions only with conditions in the supercooled region, but the basic equation developed by the author as early as 1980 is also applicable to the normal liquid region up to the critical point and at higher exterior pressures with pressure-dependent terms without changing the basic parameters. (A working paper 2017 has been deposited at doi:10.13140/RG.2.2.21857.61286).