Analytical Model of Deformation of a Functionally Graded Ceramic Coating under Local Load
Abstract
1. Introduction
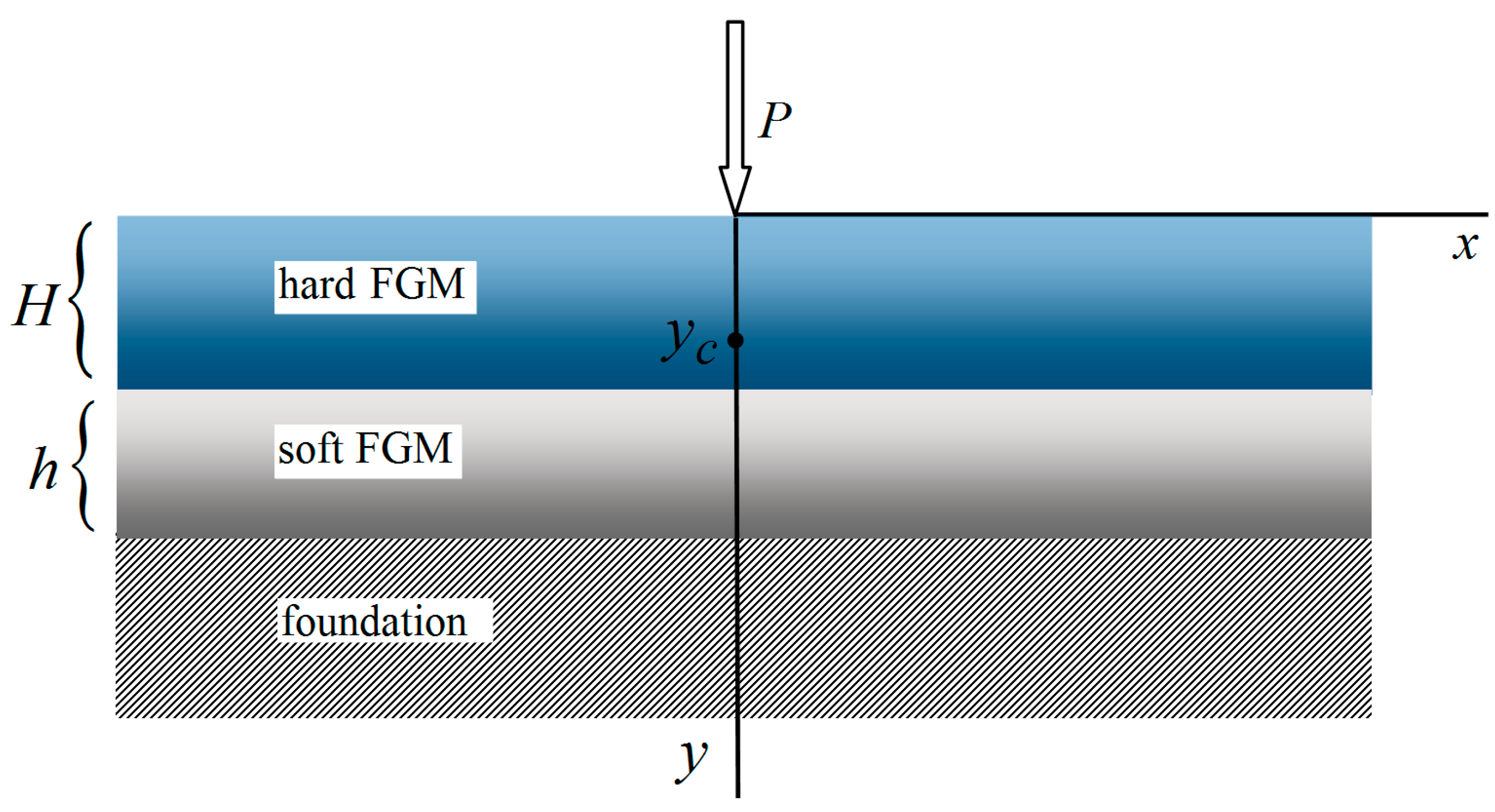
2. Materials and Methods
3. Results and Analysis
3.1. Analytical Solution
3.2. Approximation of Functional-Gradient Properties
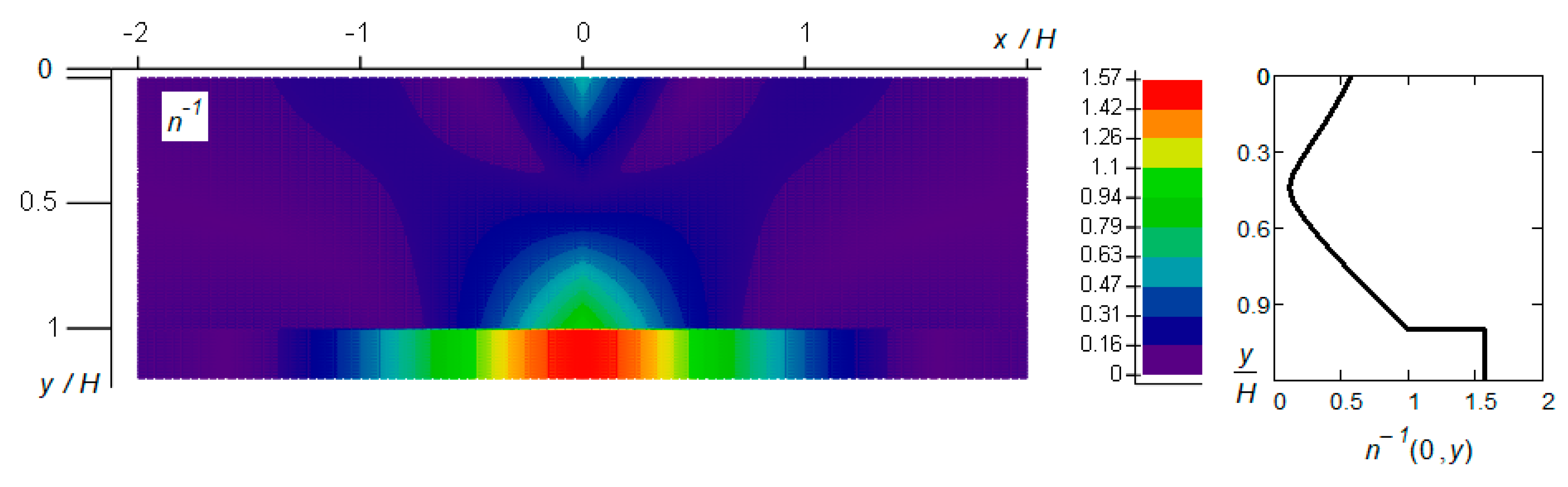
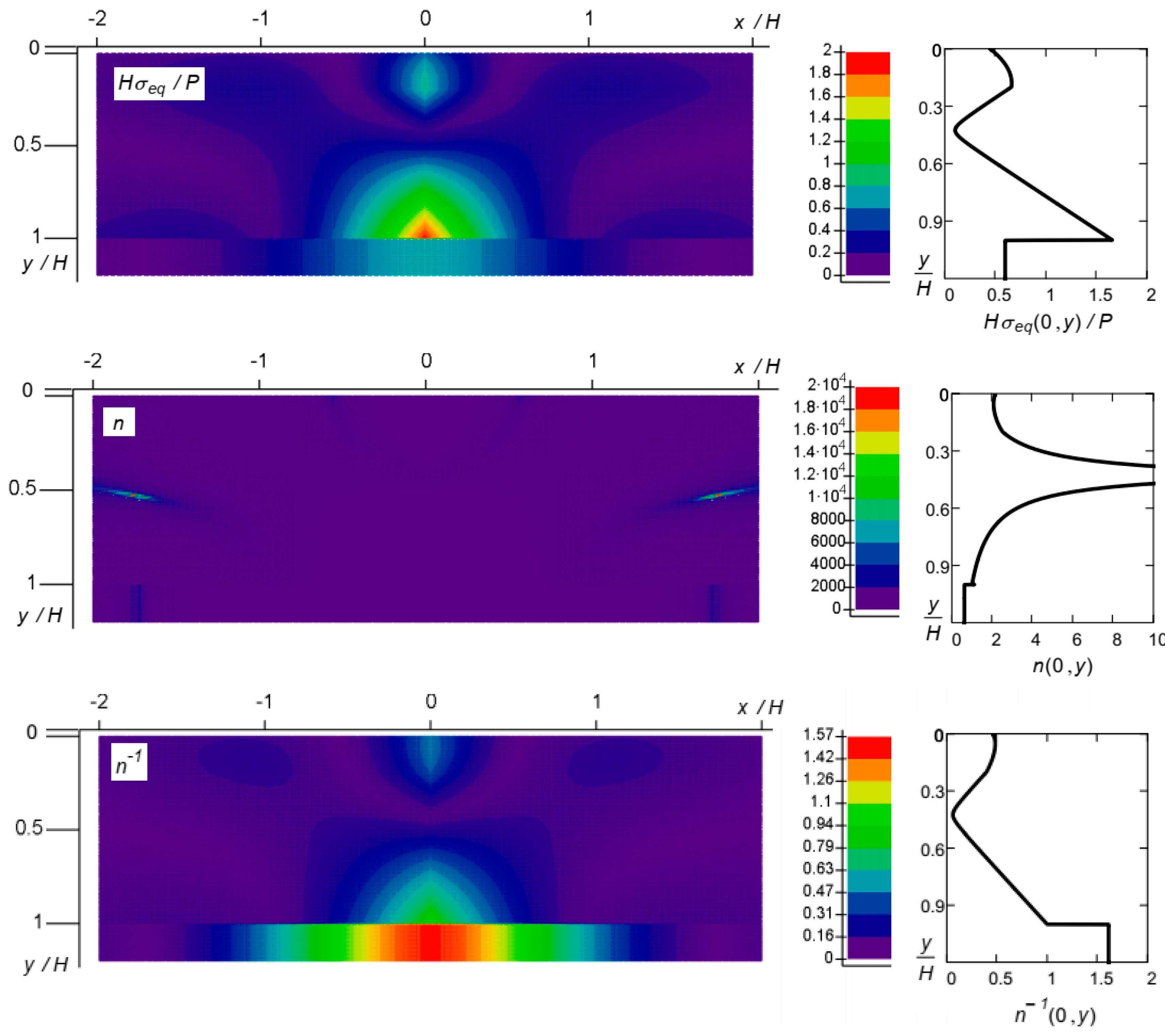
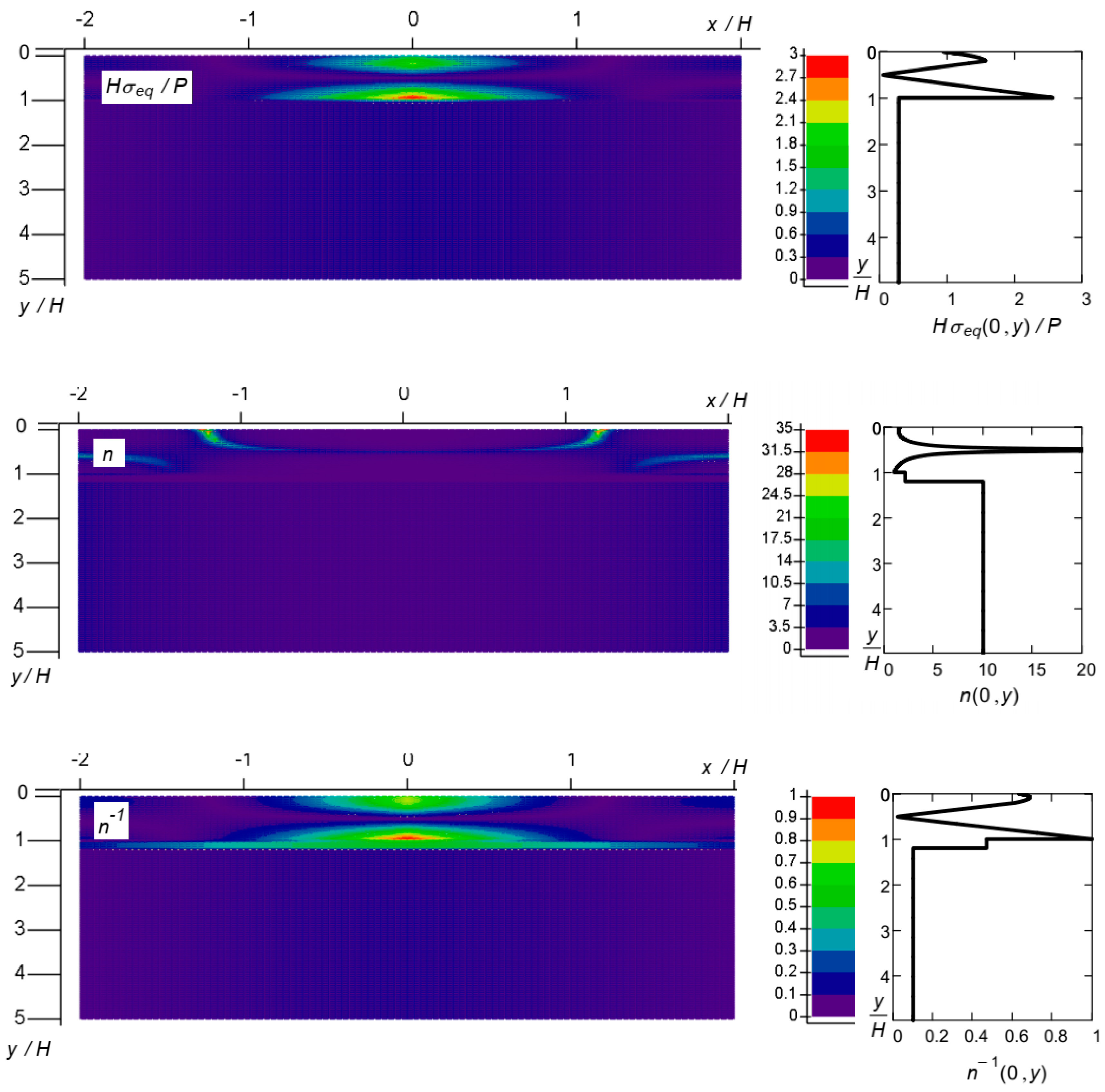
3.3. Calculation Examples
3.3.1. Example 1
3.3.2. Example 2
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fayomi, O.S.; Akande, I.G.; Okokpujie, I.P.; Fakehinde, O.B.; Abioye, A.A. Composite Coating and its Industrial Applications: The Impact and Trends. Procedia Manuf. 2019, 35, 1013–1017. [Google Scholar] [CrossRef]
- Ramírez, C.; Belmonte, M.; Miranzo, P.; Osendi, M.I. Applications of Ceramic/Graphene Composites and Hybrids. Materials 2021, 14, 2071. [Google Scholar] [CrossRef] [PubMed]
- Dutkiewicz, M.; Dalyak, T.; Shatskyi, I.; Venhrynyuk, T.; Velychkovych, A. Stress Analysis in Damaged Pipeline with Composite Coating. Appl. Sci. 2021, 11, 10676. [Google Scholar] [CrossRef]
- Devarajan, D.K.; Rangasamy, B.; Amirtharaj Mosas, K.K. State-of-the-Art Developments in Advanced Hard Ceramic Coatings Using PVD Techniques for High-Temperature Tribological Applications. Ceramics 2023, 6, 301–329. [Google Scholar] [CrossRef]
- Rajiv, A.; Natalia, S.; Mrityunjay, S. Wettability and interfacial phenomena in the liquid-phase bonding of refractory diboride ceramics: Recent developments. Int. J. Appl. Ceram. Technol. 2022, 19, 1029–1049. [Google Scholar] [CrossRef]
- Semmler, C.; Gyoktepeliler-Akin, E.; Killinger, A. Plasma sprayed ceramic coatings for the thermal protection of carbon fiber reinforced plastics (CFRP): Thermal and mechanical properties of YSZ, aluminum titanate, cordierite and mullite coatings. Surf. Coat. Technol. 2023, 462, 129509. [Google Scholar] [CrossRef]
- Ropyak, L.; Shihab, T.; Velychkovych, A.; Bilinskyi, V.; Malinin, V.; Romaniv, M. Optimization of Plasma Electrolytic Oxidation Technological Parameters of Deformed Aluminum Alloy D16T in Flowing Electrolyte. Ceramics 2023, 6, 146–167. [Google Scholar] [CrossRef]
- Umashanker, L.; Bharathesh, T.P.; Roopashree, C.; Saravanan, R. A review on ceramic coatings for low carbon steel methods materials and applications. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1189, 012015. [Google Scholar] [CrossRef]
- Aimovi-Pavlovi, Z.; Prsti, A.; Andri, L.; Miloevi, V.; Milievi, S. Ceramic Coating for Cast House Application; InTech: Rijeka, Croatia, 2012; pp. 261–286. [Google Scholar] [CrossRef]
- Liutyi, R.; Petryk, I.; Mogylatenko, V.; Popovych, V.; Shatska, H. Research Thermal Fields in the Crystallization Process of Steel Cast Parts. Adv. Mater. Sci. Eng. 2022, 2022, 7331866. [Google Scholar] [CrossRef]
- Paione, C.M.; Baino, F. Non-Oxide Ceramics for Bone Implant Application: State-of-the-Art Overview with an Emphasis on the Acetabular Cup of Hip Joint Prosthesis. Ceramics 2023, 6, 994–1016. [Google Scholar] [CrossRef]
- Sartori, M.; Maglio, M.; Tschon, M.; Nicoli Aldini, N.; Visani, A.; Fini, M. Functionalization of Ceramic Coatings for Enhancing Integration in Osteoporotic Bone: A Systematic Review. Coatings 2019, 9, 312. [Google Scholar] [CrossRef]
- Guillon, O. Ceramic materials for energy conversion and storage: A perspective. Int. J. Ceram. Eng. Sci. 2021, 3, 100–104. [Google Scholar] [CrossRef]
- Pal, S.; Taurino, A.; Catalano, M.; Licciulli, A. Block Copolymer and Cellulose Templated Mesoporous TiO2-SiO2 Nanocomposite as Superior Photocatalyst. Catalysts 2022, 12, 770. [Google Scholar] [CrossRef]
- Li, L.; Reynaud, P.; Fantozzi, G. Cyclic-Dependent Damage Evolution in Self-Healing Woven SiC/[Si-B-C] Ceramic-Matrix Composites at Elevated Temperatures. Materials 2020, 13, 1478. [Google Scholar] [CrossRef] [PubMed]
- Fang, G.; Gao, X.; Song, Y. A Review on Ceramic Matrix Composites and Environmental Barrier Coatings for Aero-Engine: Material Development and Failure Analysis. Coatings 2023, 13, 357. [Google Scholar] [CrossRef]
- Mehboob, G.; Liu, M.-J.; Xu, T.; Hussain, S.; Mehboob, G.; Tahir, A. A review on failure mechanism of thermal barrier coatings and strategies to extend their lifetime. Ceram. Int. 2020, 46, 8497–8521. [Google Scholar] [CrossRef]
- Bembenek, M.; Mandziy, T.; Ivasenko, I.; Berehulyak, O.; Vorobel, R.; Slobodyan, Z.; Ropyak, L. Multiclass Level-Set Segmentation of Rust and Coating Damages in Images of Metal Structures. Sensors 2022, 22, 7600. [Google Scholar] [CrossRef]
- Sathish, M.; Radhika, N.; Saleh, B. A critical review on functionally graded coatings: Methods, properties, and challenges. Compos. Part B Eng. 2021, 225, 109278. [Google Scholar] [CrossRef]
- Duryahina, Z.A.; Kovbasyuk, T.M.; Bespalov, S.A.; Pidkova, V.Y. Micromechanical and Electrophysical Properties of Al2O3 Nanostructured Dielectric Coatings on Plane Heating Elements. Mater. Sci. 2016, 52, 50–55. [Google Scholar] [CrossRef]
- Petrova, V.; Schmauder, S.; Georgiadis, A. Thermal Fracture of Functionally Graded Coatings with Systems of Cracks: Application of a Model Based on the Rule of Mixtures. Ceramics 2023, 6, 255–264. [Google Scholar] [CrossRef]
- Han, D.; Fan, H.; Yan, C.; Wang, T.; Yang, Y.; Ali, S.; Wang, G. Heat Conduction and Cracking of Functionally Graded Materials Using an FDEM-Based Thermo-Mechanical Coupling Model. Appl. Sci. 2022, 12, 12279. [Google Scholar] [CrossRef]
- Bhandari, M.; Purohit, K. Dynamic fracture analysis of functionally graded material structures—A critical review. Compos. Part C Open Access 2022, 7, 100227. [Google Scholar] [CrossRef]
- Nakajima, R.; Katori, H.; Ito, K.; Arai, M.; Suidzu, T. Numerical simulation on internal stress evolution based on formation of thermally grown oxide in thermal barrier coatings. Eng. Res. Express 2020, 2, 025037. [Google Scholar] [CrossRef]
- Tian, C.; Duan, P. Finite Element Analysis of the Nanomechanics of Hard Coatings on a Soft Polymer Substrate by a Spherical Indenter. Adv. Polym. Technol. 2020, 2020, 6903196. [Google Scholar] [CrossRef]
- Baldissera, P.; Delprete, C. Finite Element Thermo-Structural Methodology for Investigating Diesel Engine Pistons with Thermal Barrier Coating. SAE Int. J. Engines 2019, 12, 69–78. [Google Scholar] [CrossRef]
- Beake, B.D. Nano- and Micro-Scale Impact Testing of Hard Coatings: A Review. Coatings 2022, 12, 793. [Google Scholar] [CrossRef]
- Skordaris, G.; Bouzakis, K.; Charalampous, P. A critical review of FEM models to simulate the nano-impact test on PVD coatings. MATEC Web Conf. 2018, 188, 04017. [Google Scholar] [CrossRef][Green Version]
- Luo, Y.; Ning, C.; Dong, Y.; Xiao, C.; Wang, X.; Peng, H.; Cai, Z. Impact Abrasive Wear Resistance of CrN and CrAlN Coatings. Coatings 2022, 12, 427. [Google Scholar] [CrossRef]
- Prysyazhnyuk, P.; Ivanov, O.; Matvienkiv, O.; Marynenko, S.; Korol, O.; Koval, I. Impact and abrasion wear resistance of the hardfacings based on high-manganese steel reinforced with multicomponent carbides of Ti-Nb-Mo-V-C system. Procedia Struct. Integr. 2022, 36, 130–136. [Google Scholar] [CrossRef]
- Tkadletz, M.; Schalk, N.; Daniel, R.; Keckes, J.; Czettl, C.; Mitterer, C. Advanced characterization methods for wear resistant hard coatings: A review on recent progress. Surf. Coat. Technol. 2016, 285, 31–46. [Google Scholar] [CrossRef]
- Shatskii, I.P. Tension of a plate containing a rectilinear cut with hinged rims. J. Appl. Mech. Tech. Phys. 1989, 30, 828–830. [Google Scholar] [CrossRef]
- Shatskii, I.P. The interaction of collinear cuts with hinged rims in a plate under tension. J. Sov. Math. 1993, 67, 3355–3358. [Google Scholar] [CrossRef]
- Shatskii, I.P. A periodic system of parallel slits with contacting edges in a distended plate. J. Math. Sci. 1995, 76, 2370–2373. [Google Scholar] [CrossRef]
- Mohammadi, S.; Yousefi, M.; Khazaei, M. A review on composite patch repairs and the most important parameters affecting its efficiency and durability. J. Reinf. Plast. Compos. 2020, 40, 3–15. [Google Scholar] [CrossRef]
- Shatskyi, I.P.; Makoviichuk, M.V.; Shcherbii, A.B. Equilibrium of Cracked Shell with Flexible Coating. In Shell Structures: Theory and Applications; CRC Press: Leiden, The Netherlands, 2018; Volume 4, pp. 165–168. [Google Scholar]
- Shatskyi, I.P.; Makoviichuk, M.V.; Shcherbii, A.B. Influence of flexible coating on the limit equilibrium of a spherical shell with meridional crack. Mater. Sci. 2020, 55, 484–491. [Google Scholar] [CrossRef]
- Nassar, M.; Mohamed, S.; Matbuly, M.; Bichir, S. Analytical Solution Of Cracked Shell Resting On Elastic Foundation. Acta Mech. Solida Sin. 1996, 9, 306–319. [Google Scholar]
- Shats’kyi, I.P.; Makoviichuk, M.V. Contact interaction of the crack edges in the case of bending of a plate with elastic support. Mater. Sci. 2003, 39, 371–376. [Google Scholar] [CrossRef]
- Sylovanyuk, V.P.; Yukhim, R.Y. Material strengthening by crack and cavity healing. Strength Mater. 2011, 43, 33–41. [Google Scholar] [CrossRef]
- Shatskyi, I.; Kurtash, I. Strength of plate with the filled crack under multiparameter loading. Procedia Struct. Integr. 2018, 13, 1482–1487. [Google Scholar] [CrossRef]
- Panasyuk, V.V.; Sylovanyuk, V.P.; Marukha, V.I. Injection Technologies for the Repair of Damaged Concrete Structures; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Shats’kyi, I.P. Limiting equilibrium of a plate with partially healed crack. Mater. Sci. 2015, 51, 322–330. [Google Scholar] [CrossRef]
- Kulchytsky-Zhyhailo, R.; Bajkowski, A.S. Three-dimensional analytical elasticity solution for loaded functionally graded coated half-space. Mech. Res. Commun. 2015, 65, 43–50. [Google Scholar] [CrossRef]
- Yilmaz, K.B.; Çömez, I.; Güler, M.A.; Yildirim, B. Sliding frictional contact analysis of a monoclinic coating/isotropic substrate system. Mech. Mater. 2019, 137, 103132. [Google Scholar] [CrossRef]
- Balci, M.N.; Dag, S. Dynamic frictional contact problems involving elastic coatings. Tribol. Int. 2018, 124, 70–92. [Google Scholar] [CrossRef]
- Jahedi, R.; Adibnazari, S.; Farrahi, G.H. Performance Analysis of Functionally Graded Coatings in Contact with Cylindrical Rollers. Adv. Mech. Eng. 2015, 7, 456848. [Google Scholar] [CrossRef]
- Liu, T.-J. Axisymmetric Indentation Response of Functionally Graded Material Coating; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Simchen, F.; Sieber, M.; Kopp, A.; Lampke, T. Introduction to Plasma Electrolytic Oxidation—An Overview of the Process and Applications. Coatings 2020, 10, 628. [Google Scholar] [CrossRef]
- Student, M.M.; Ivasenko, I.B.; Posuvailo, V.M.; Veselivs’ka, H.H.; Pokhmurs’kyi, A.Y.; Sirak, Y.Y.; Yus’kiv, V.M. Influence of the Porosity of a Plasma-Electrolytic Coating on the Corrosion Resistance of D16 Alloy. Mater. Sci. 2019, 54, 899–906. [Google Scholar] [CrossRef]
- Ivasenko, I.; Posuvailo, V.; Veselivska, H.; Vynar, V. Porosity Segmentation and Analysis of Oxide Ceramic Coatings of D16T Alloy. In Proceedings of the 2020 IEEE 15th International Conference on Computer Sciences and Information Technologies (CSIT), Zbarazh, Ukraine, 23–26 September 2020; Volume 2, pp. 50–53. [Google Scholar] [CrossRef]
- Sikdar, S.; Menezes, P.V.; Maccione, R.; Jacob, T.; Menezes, P.L. Plasma Electrolytic Oxidation (PEO) Process–Processing, Properties, and Applications. Nanomaterials 2021, 11, 1375. [Google Scholar] [CrossRef]
- Ragalevičius, R.; Stalnionis, G.; Niaura, G.; Jagminas, A. Micro-Arc oxidation of Ti in a solution of sulfuric acid and Ti+3 salt. Appl. Surf. Sci. 2008, 254, 1608–1613. [Google Scholar] [CrossRef]
- Hartjen, P.; Hoffmann, A.; Henningsen, A.; Barbeck, M.; Kopp, A.; Kluwe, L.; Precht, C.; Quatela, O.; Gaudin, R.; Heiland, M.; et al. Plasma Electrolytic Oxidation of Titanium Implant Surfaces: Microgroove-Structures Improve Cellular Adhesion and Viability. Vivo 2018, 32, 241–247. [Google Scholar] [CrossRef]
- Pokhmurskii, V.; Nykyforchyn, H.; Student, M.; Klapkiv, M.; Pokhmurska, H.; Wielage, B.; Grund, T.; Wank, A. Plasma electrolytic oxidation of arc-sprayed aluminum coatings. J. Therm. Spray Technol. 2007, 16, 998–1004. [Google Scholar] [CrossRef]
- Posuvailo, V.M.; Klapkiv, M.D.; Student, M.M.; Sirak, Y.Y.; Pokhmurska, H.V. Gibbs energy calculation of electrolytic plasma channel with inclusions of copper and copper oxide with Al-base. IOP Conf. Ser. Mater. Sci. Eng. 2017, 181, 012045. [Google Scholar] [CrossRef]
- Tokovyy, Y.; Ma, C.-C. The Direct Integration Method for Elastic Analysis of Nonhomogeneous Solids; Cambridge Scholars Publishing: Newcastle, UK, 2021; p. 342. ISBN 10-1-5275-6149-6. [Google Scholar]
- Tokovyy, Y.V. Solutions of Axisymmetric Problems of Elasticity and Thermoelasticity for an Inhomogeneous Space and a Half Space. J. Math. Sci. 2019, 240, 86–97. [Google Scholar] [CrossRef]
- Tokovyy, Y.; Chyzh, A.; Ma, C.C. An analytical solution to the axisymmetric thermoelasticity problem for a cylinder with arbitrarily varying thermomechanical properties. Acta Mech. 2019, 230, 1469–1485. [Google Scholar] [CrossRef]
- Shatskyi, I.P.; Ropyak, L.Y.; Makoviichuk, M.V. Strength optimization of a two-layer coating for the particular local loading conditions. Strength Mater. 2016, 48, 726–730. [Google Scholar] [CrossRef]
- Ropyak, L.Y.; Shatskyi, I.P.; Makoviichuk, M.V. Analysis of interaction of thin coating with an abrasive using one-dimensional model. Metallofiz. Noveishie Tekhnol. 2019, 41, 647–654. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]


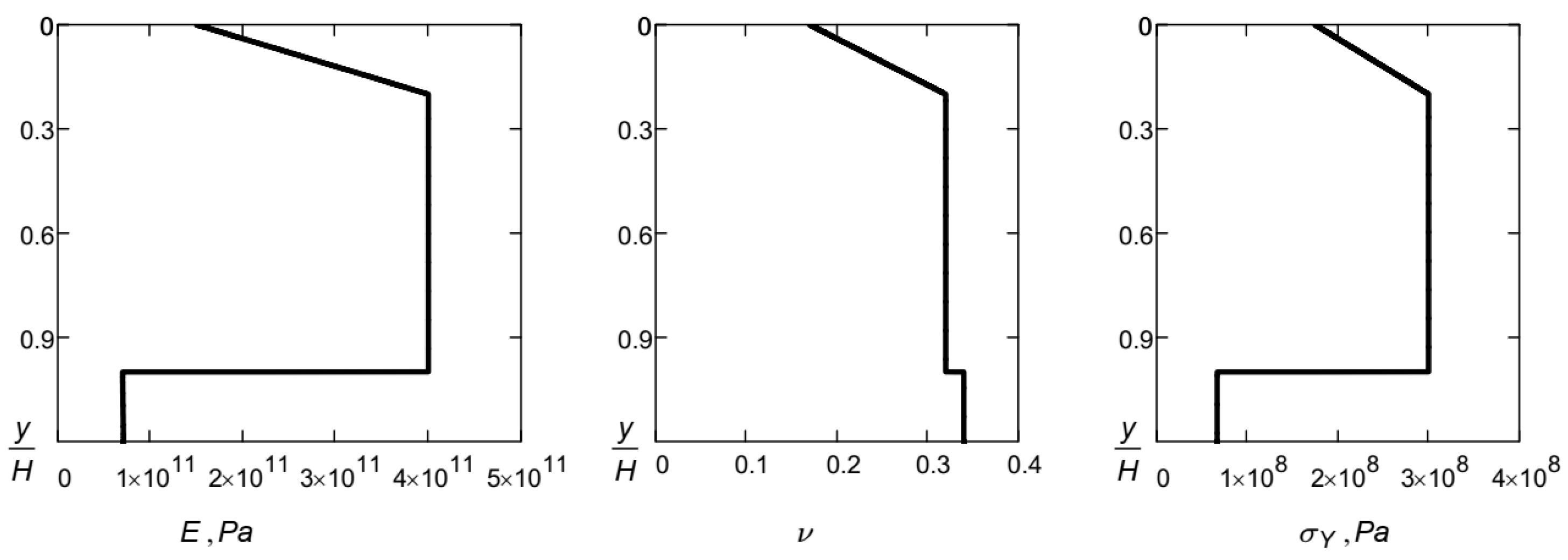
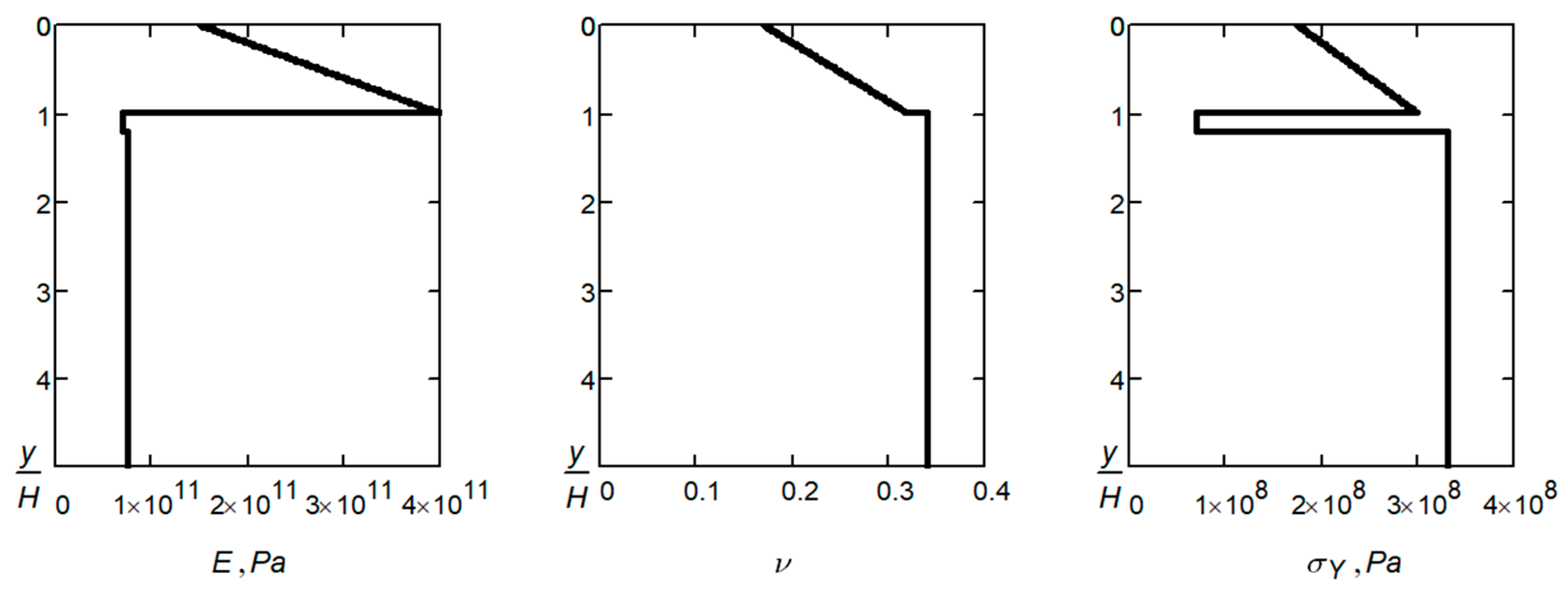


| Material | Layer Boundary Coordinate y, μm | , GPa | , MPa | |
|---|---|---|---|---|
| Al2O3 | 0 | 150 | 0.17 | 175 |
| 250 – 0 | 400 | 0.32 | 300 | |
| Al | 250 + 0 | 75 | 0.34 | 67 |
| 300 | 75 | 0.34 | 67 |
| Material | Layer Boundary Coordinate y, μm | E, GPa | ν | σY, MPa |
|---|---|---|---|---|
| Al2O3 | 0 | 150 | 0.17 | 175 |
| 50 | 400 | 0.32 | 300 | |
| 250 − 0 | 400 | 0.32 | 300 | |
| Al | 250 + 0 | 75 | 0.34 | 67 |
| 300 | 75 | 0.34 | 67 |
| Material | Layer Boundary Coordinate y, μm | , GPa | , MPa | |
|---|---|---|---|---|
| Al2O3 | 0 | 150 | 0.17 | 175 |
| 250 − 0 | 400 | 0.32 | 300 | |
| Al | 250 + 0 | 70 | 0.34 | 70 |
| 300 – 0 | 70 | 0.34 | 70 | |
| D16T | 300 + 0 | 75 | 0.34 | 330 |
| 1250 | 75 | 0.34 | 330 |
| Material | Layer Boundary Coordinate y, μm | E, GPa | σY, MPa | |
|---|---|---|---|---|
| Al2O3 | 0 | 150 | 0.17 | 175 |
| 50 | 400 | 0.32 | 300 | |
| 250 − 0 | 400 | 0.32 | 300 | |
| Al | 250 + 0 | 70 | 0.34 | 70 |
| 300 – 0 | 70 | 0.34 | 70 | |
| D16T | 300 + 0 | 75 | 0.34 | 330 |
| 1250 | 75 | 0.34 | 330 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shatskyi, I.; Makoviichuk, M.; Ropyak, L.; Velychkovych, A. Analytical Model of Deformation of a Functionally Graded Ceramic Coating under Local Load. Ceramics 2023, 6, 1879-1893. https://doi.org/10.3390/ceramics6030115
Shatskyi I, Makoviichuk M, Ropyak L, Velychkovych A. Analytical Model of Deformation of a Functionally Graded Ceramic Coating under Local Load. Ceramics. 2023; 6(3):1879-1893. https://doi.org/10.3390/ceramics6030115
Chicago/Turabian StyleShatskyi, Ivan, Mykola Makoviichuk, Liubomyr Ropyak, and Andrii Velychkovych. 2023. "Analytical Model of Deformation of a Functionally Graded Ceramic Coating under Local Load" Ceramics 6, no. 3: 1879-1893. https://doi.org/10.3390/ceramics6030115
APA StyleShatskyi, I., Makoviichuk, M., Ropyak, L., & Velychkovych, A. (2023). Analytical Model of Deformation of a Functionally Graded Ceramic Coating under Local Load. Ceramics, 6(3), 1879-1893. https://doi.org/10.3390/ceramics6030115








