Rare-Earth Doped Gd3−xRExFe5O12 (RE = Y, Nd, Sm, and Dy) Garnet: Structural, Magnetic, Magnetocaloric, and DFT Study
Abstract
:1. Introduction
2. Experimental Details
2.1. Synthesis
2.2. Characterization
2.3. Density Functional Theory
3. Results and Discussion
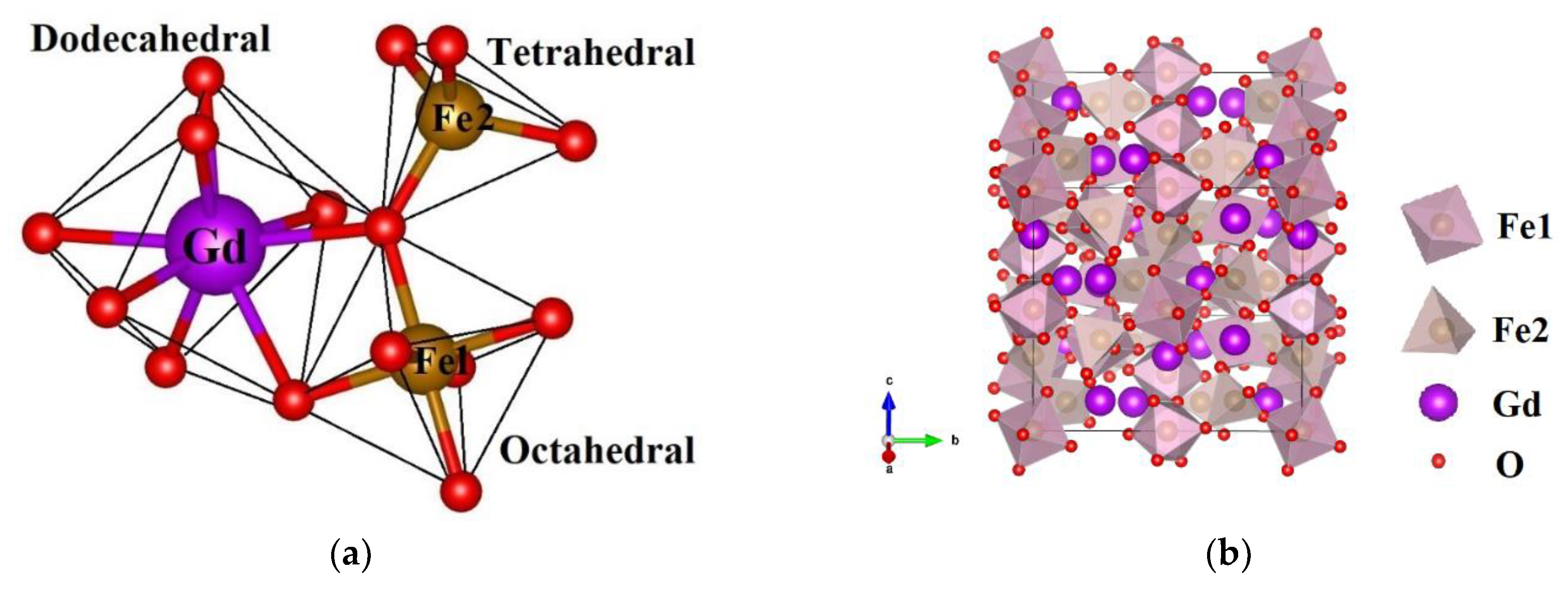
3.1. Structural Properties
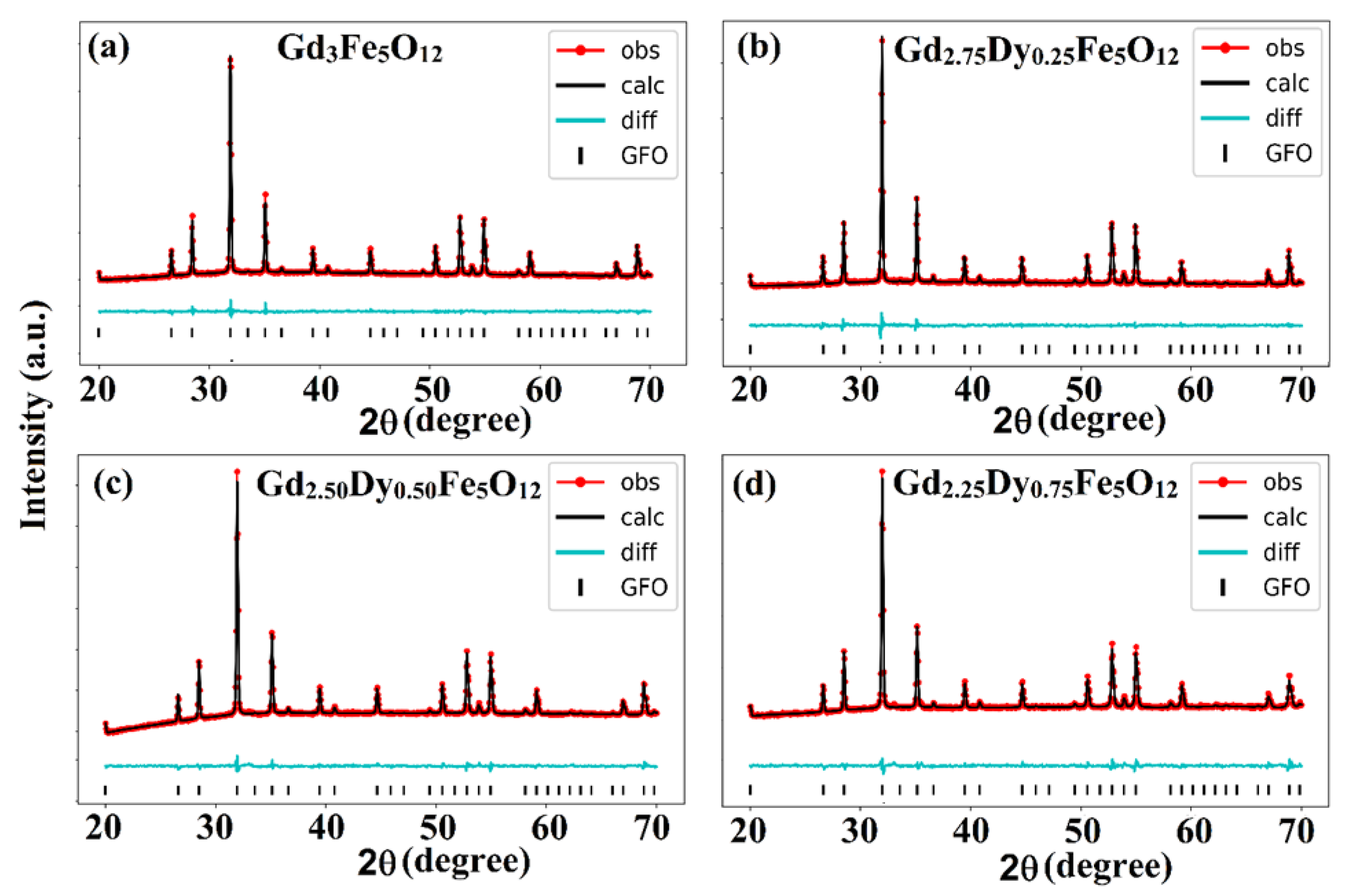
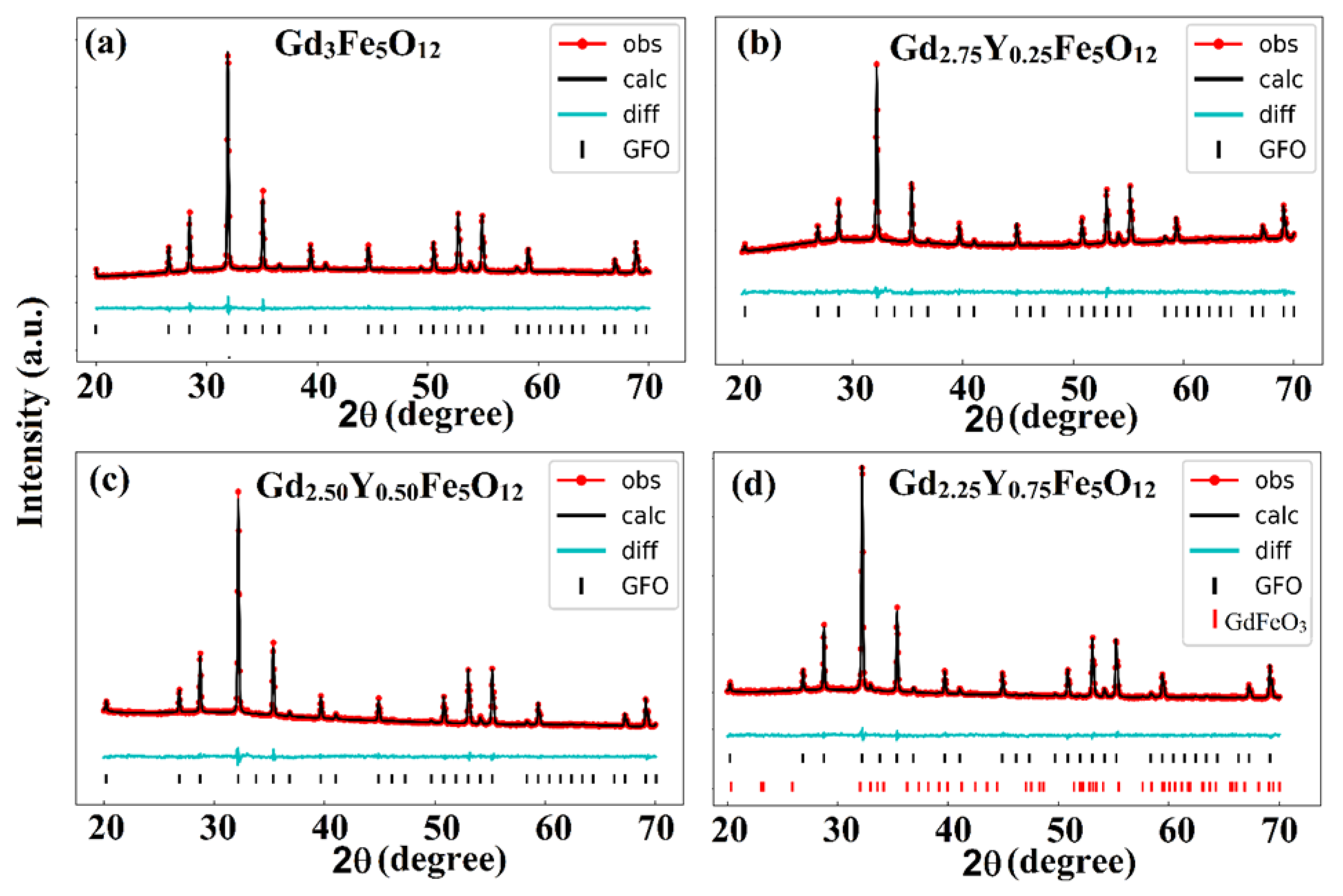
3.1.1. Phase Analysis
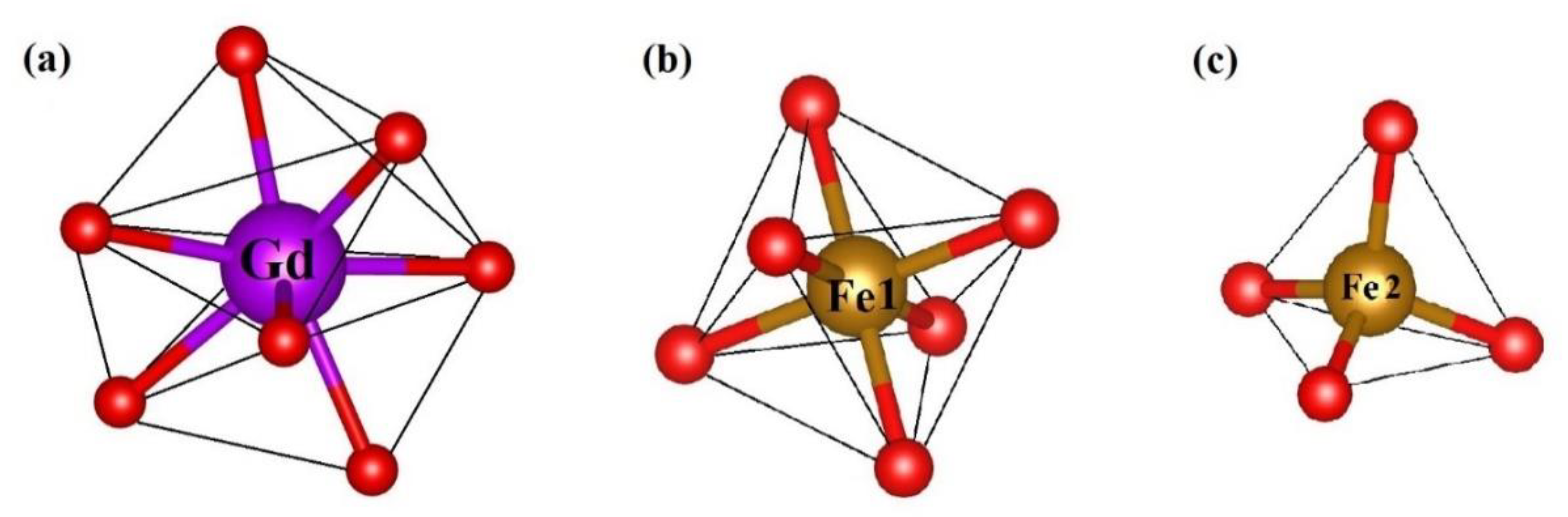
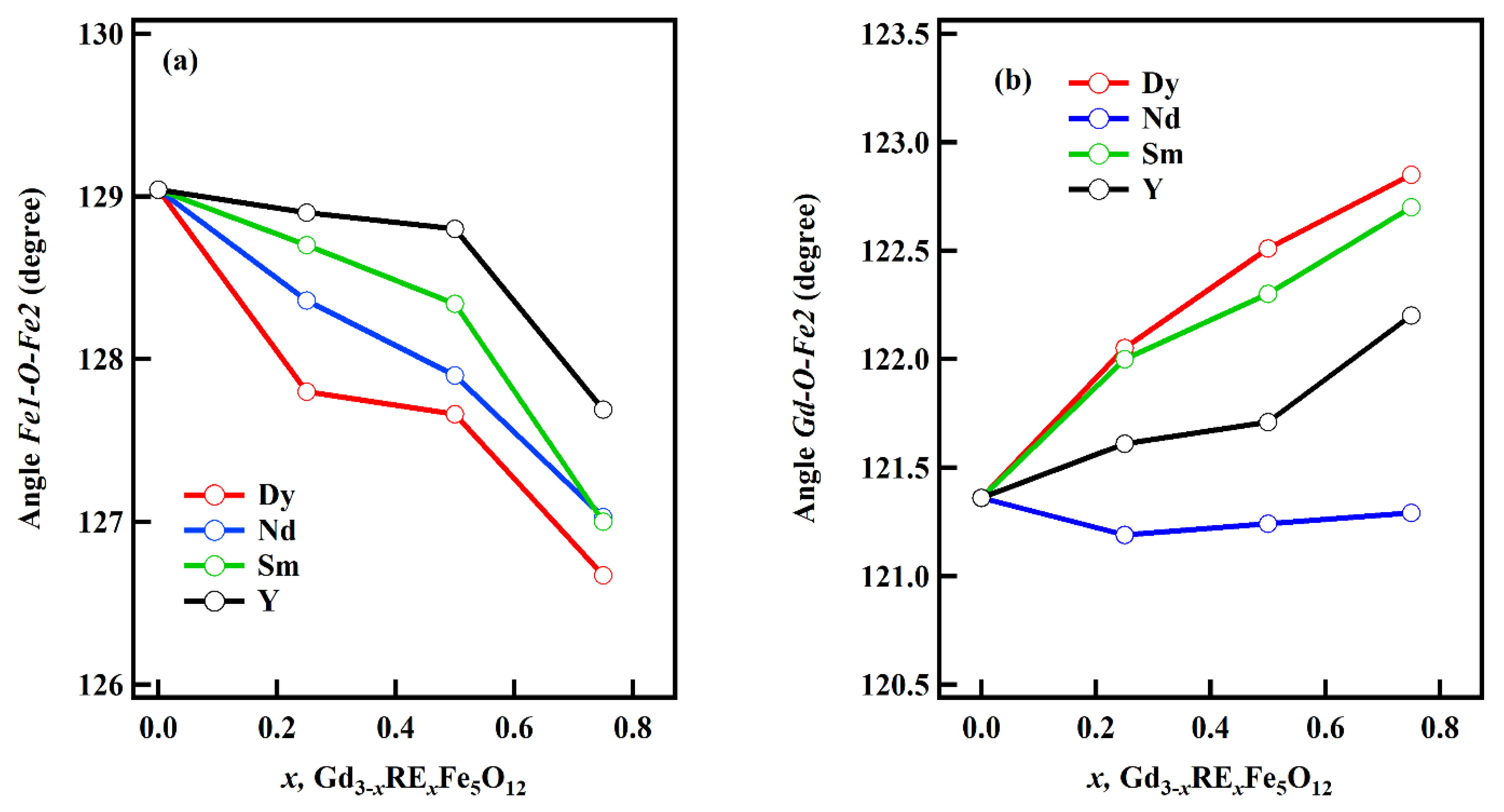
3.1.2. Bond Angle and Bond Length
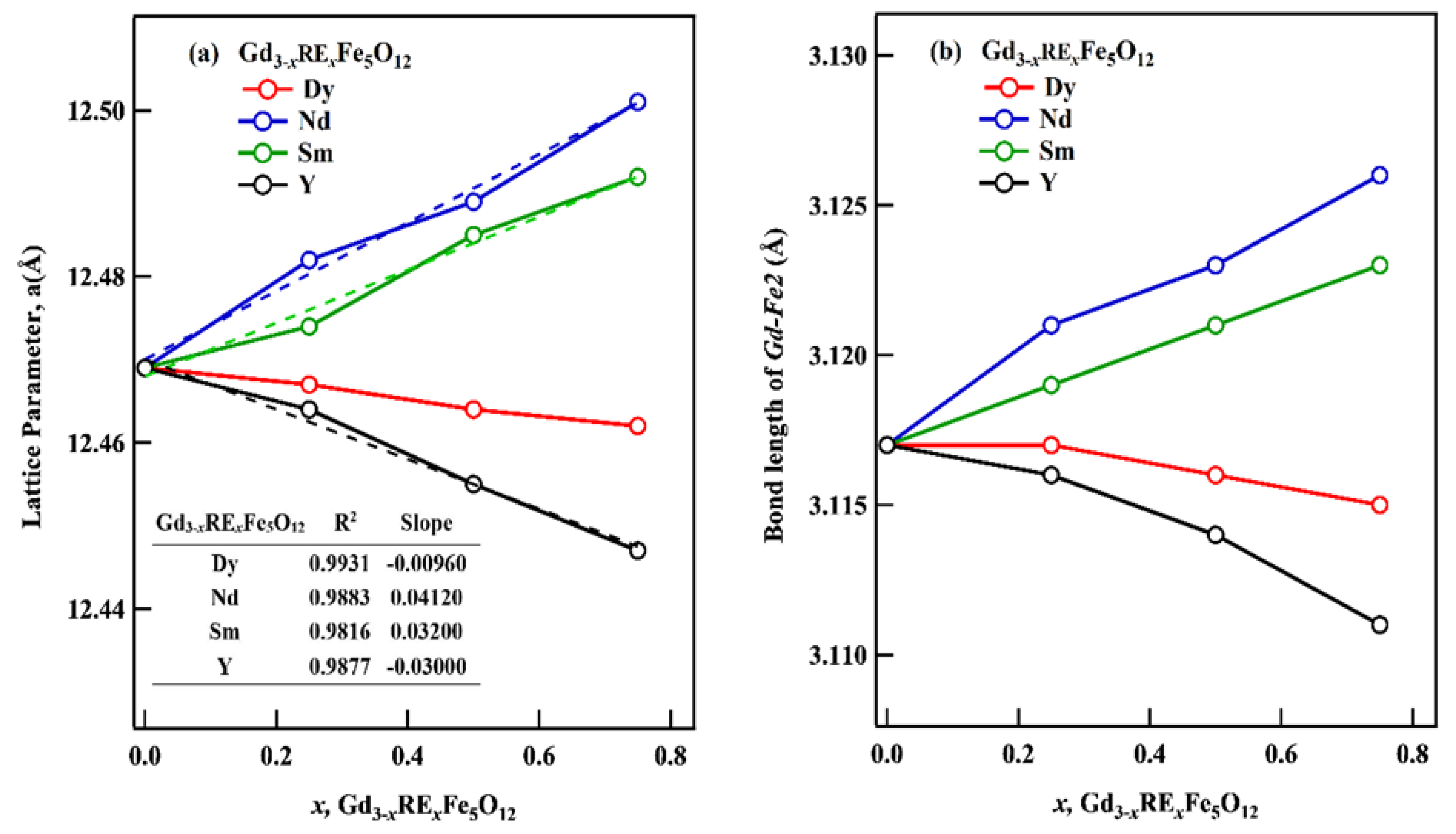
3.2. Structural Parameters
3.3. Crystallite Size and Density
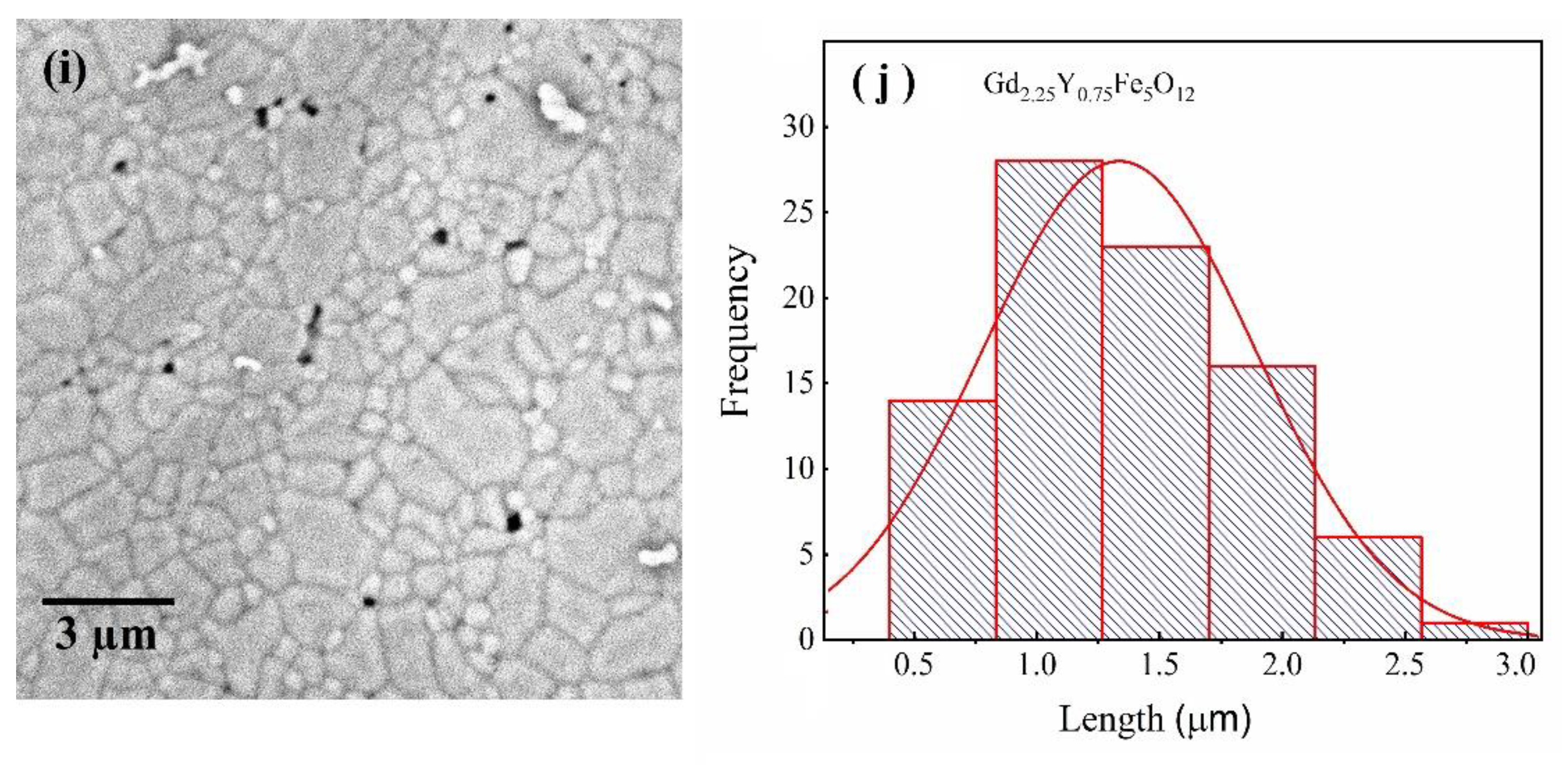
3.4. Microstructural Analysis
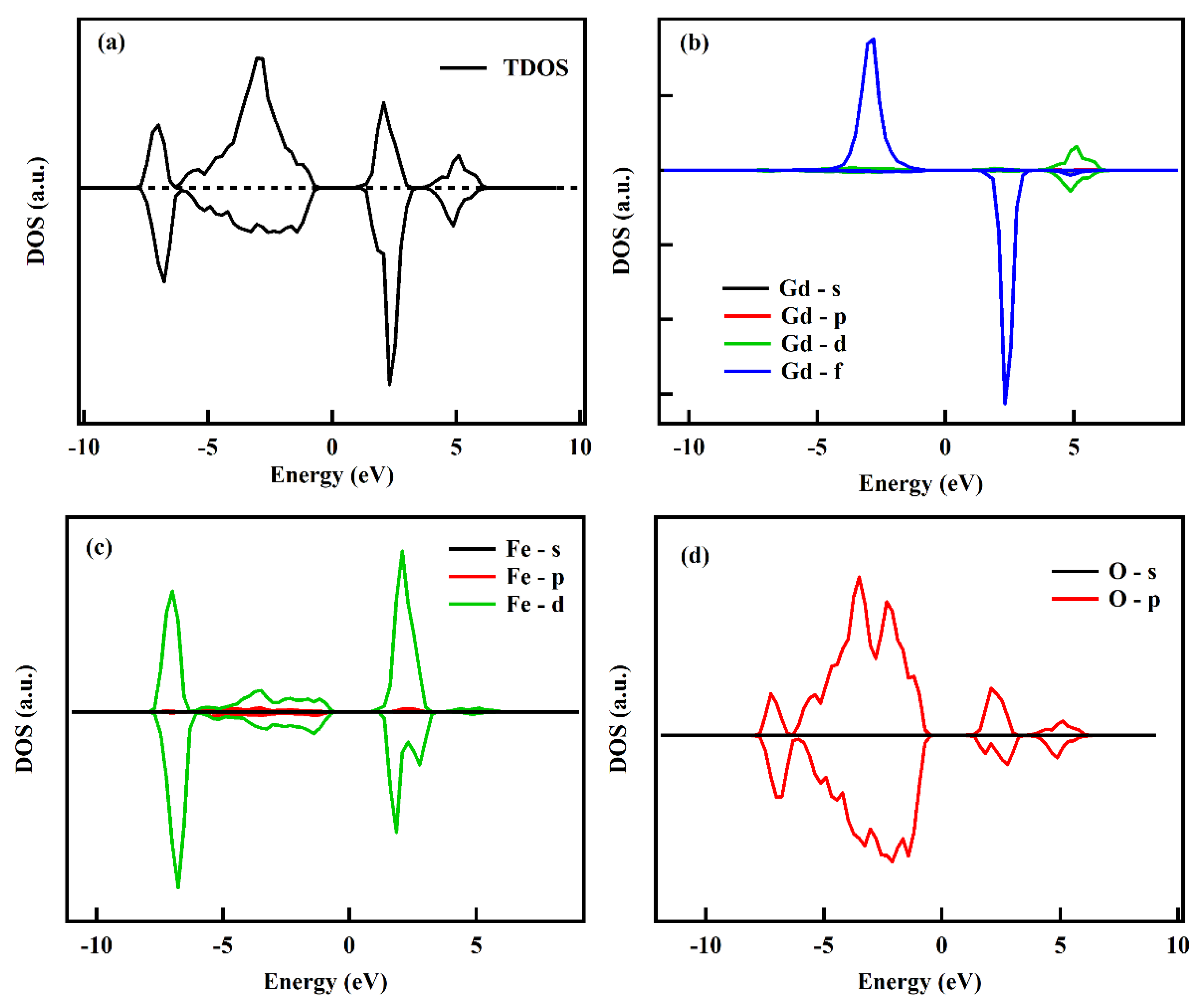
3.5. Theoretical Study
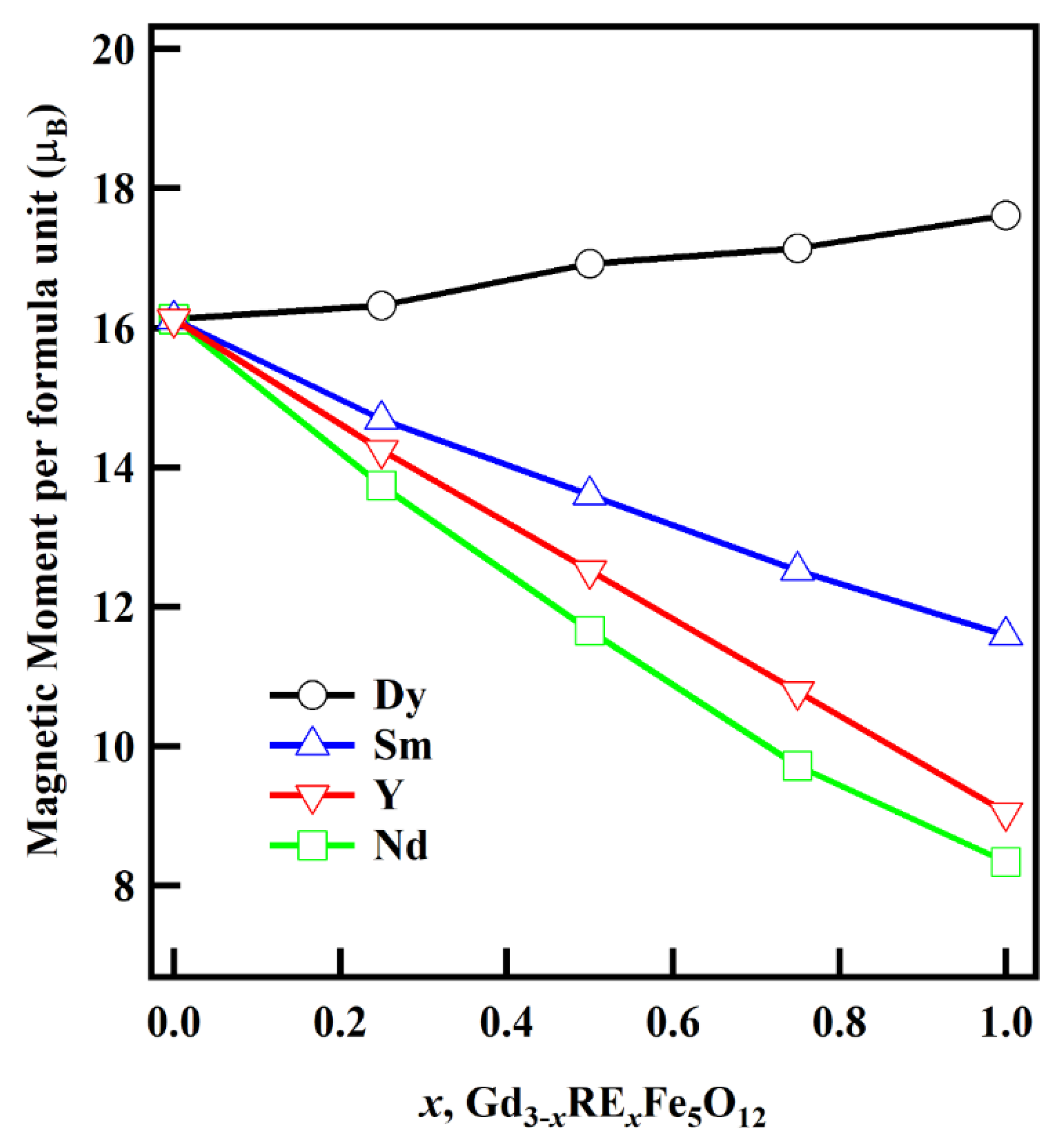
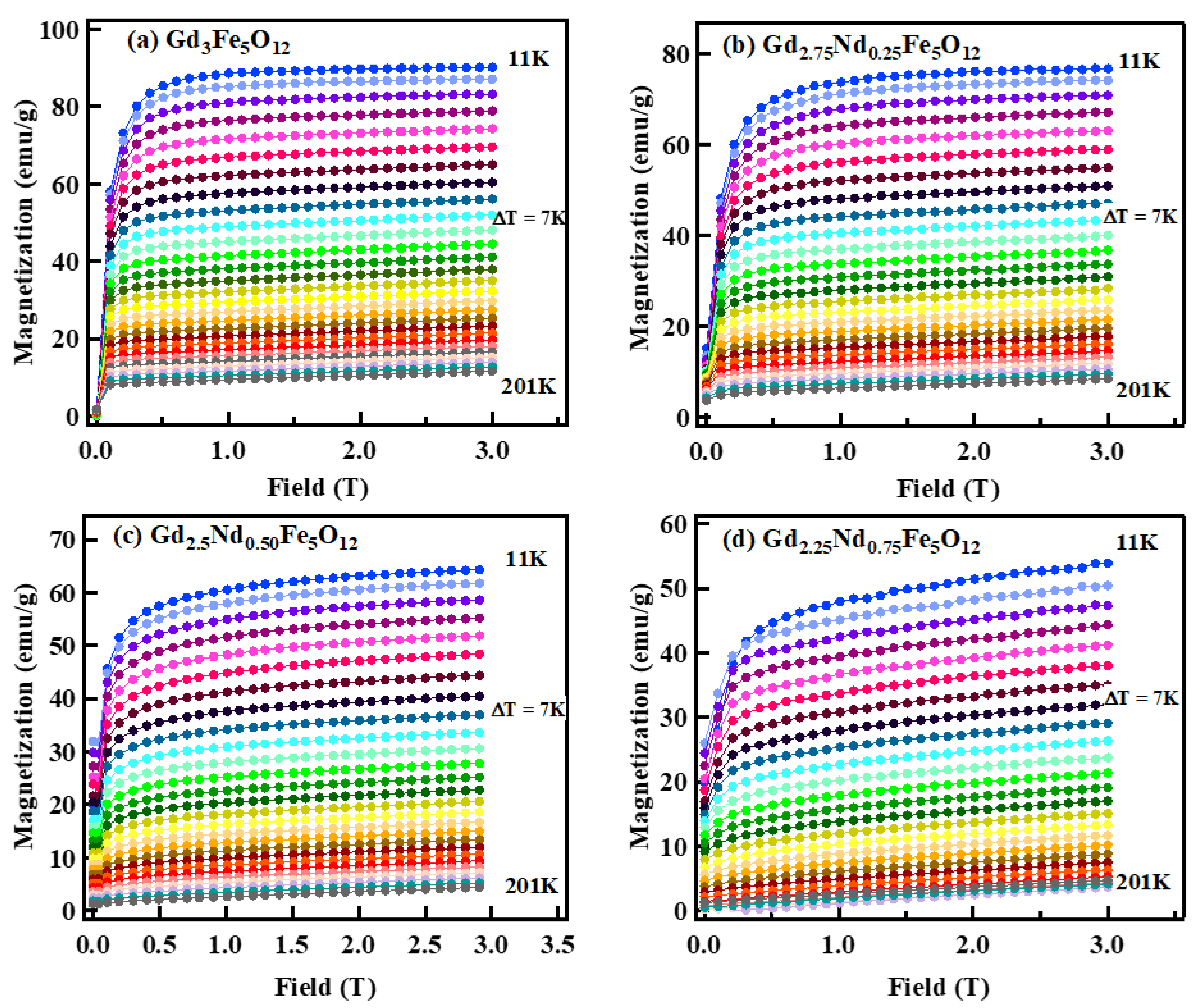
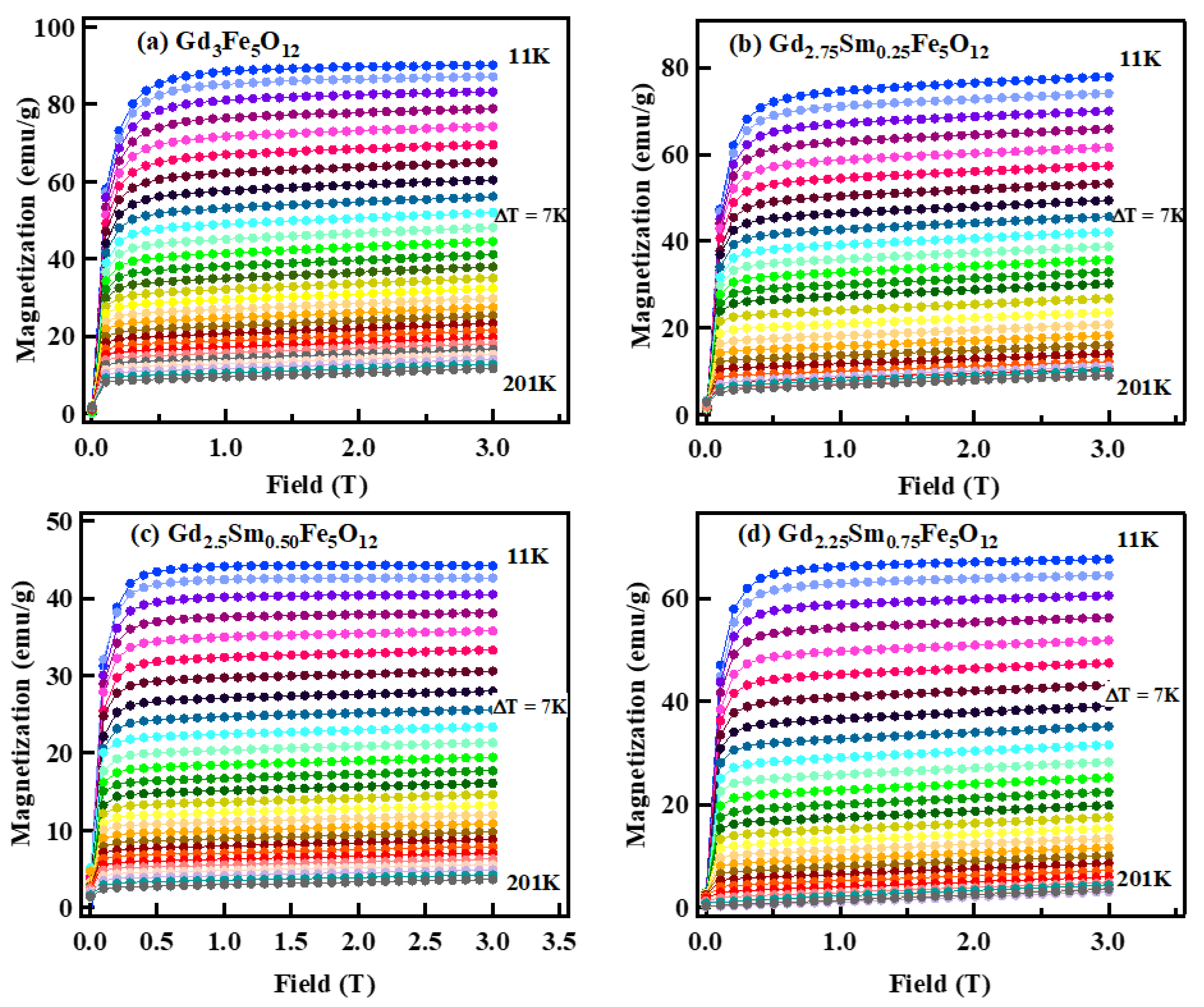
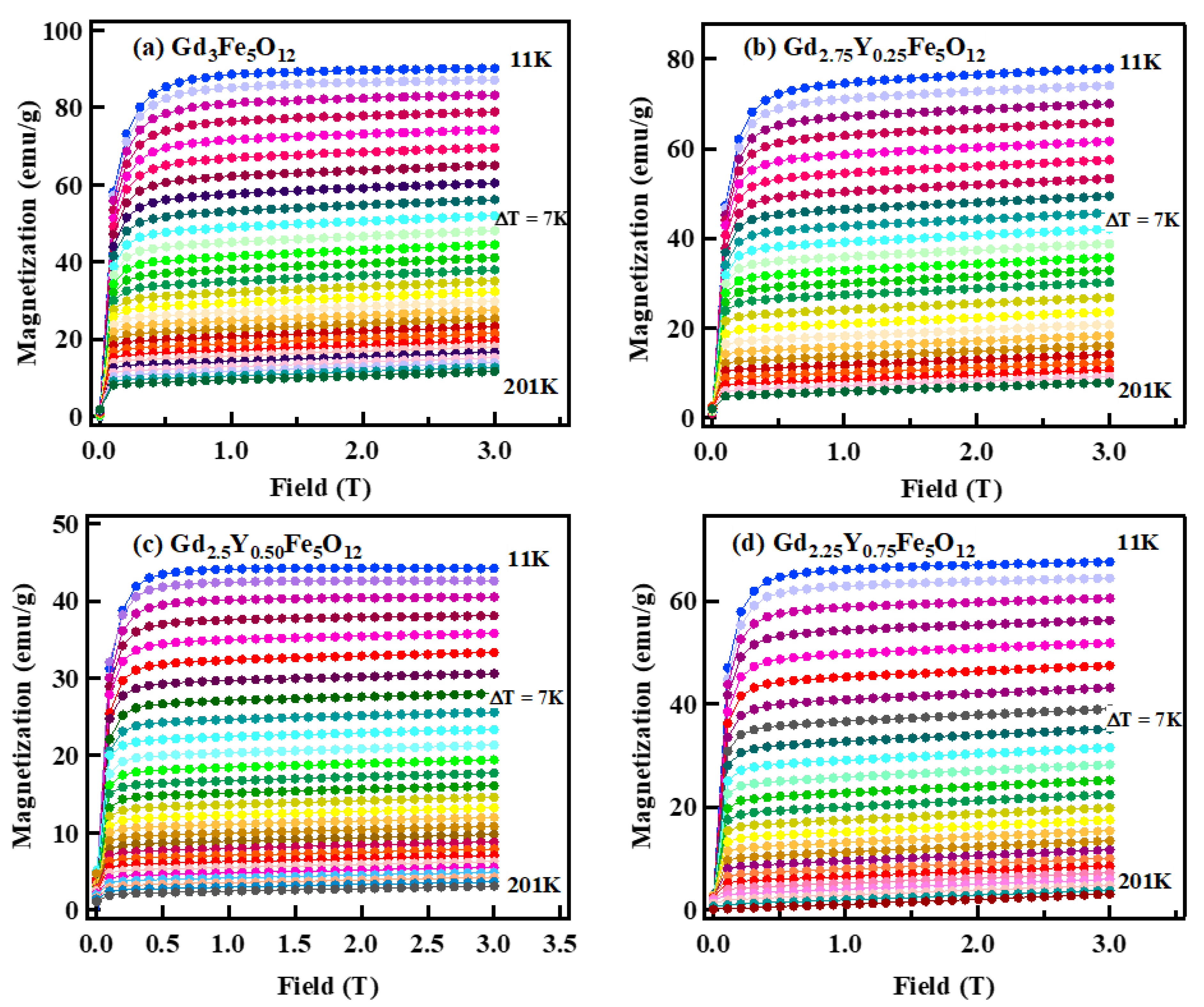
3.6. Magnetic Properties
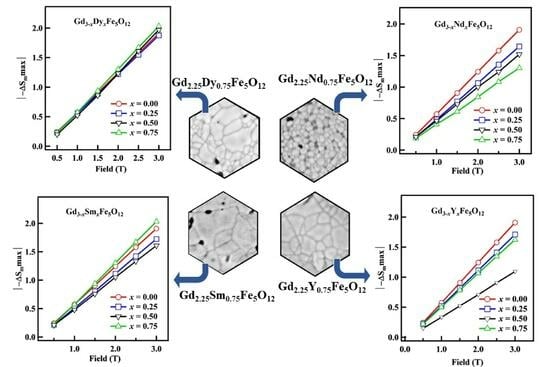
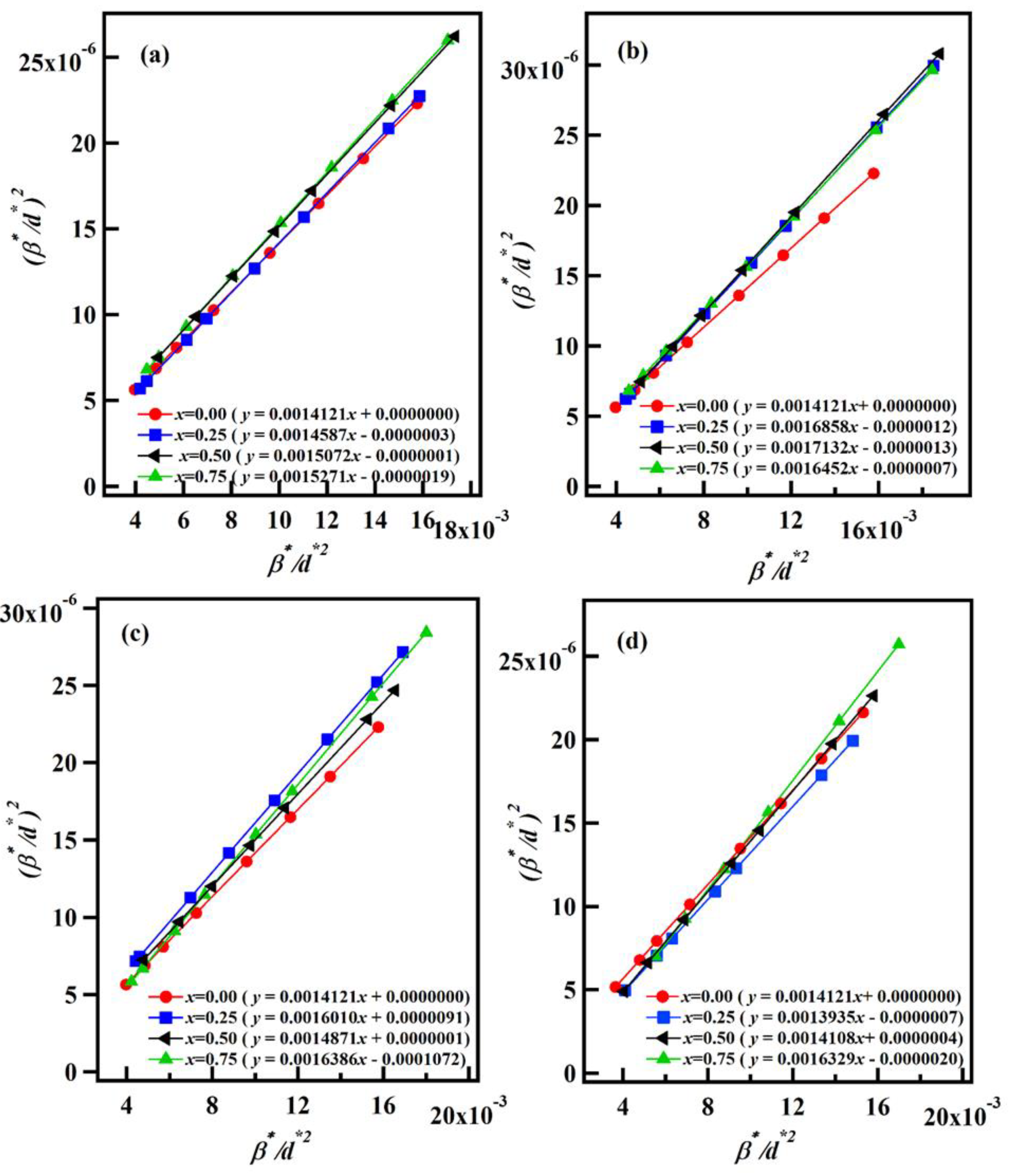
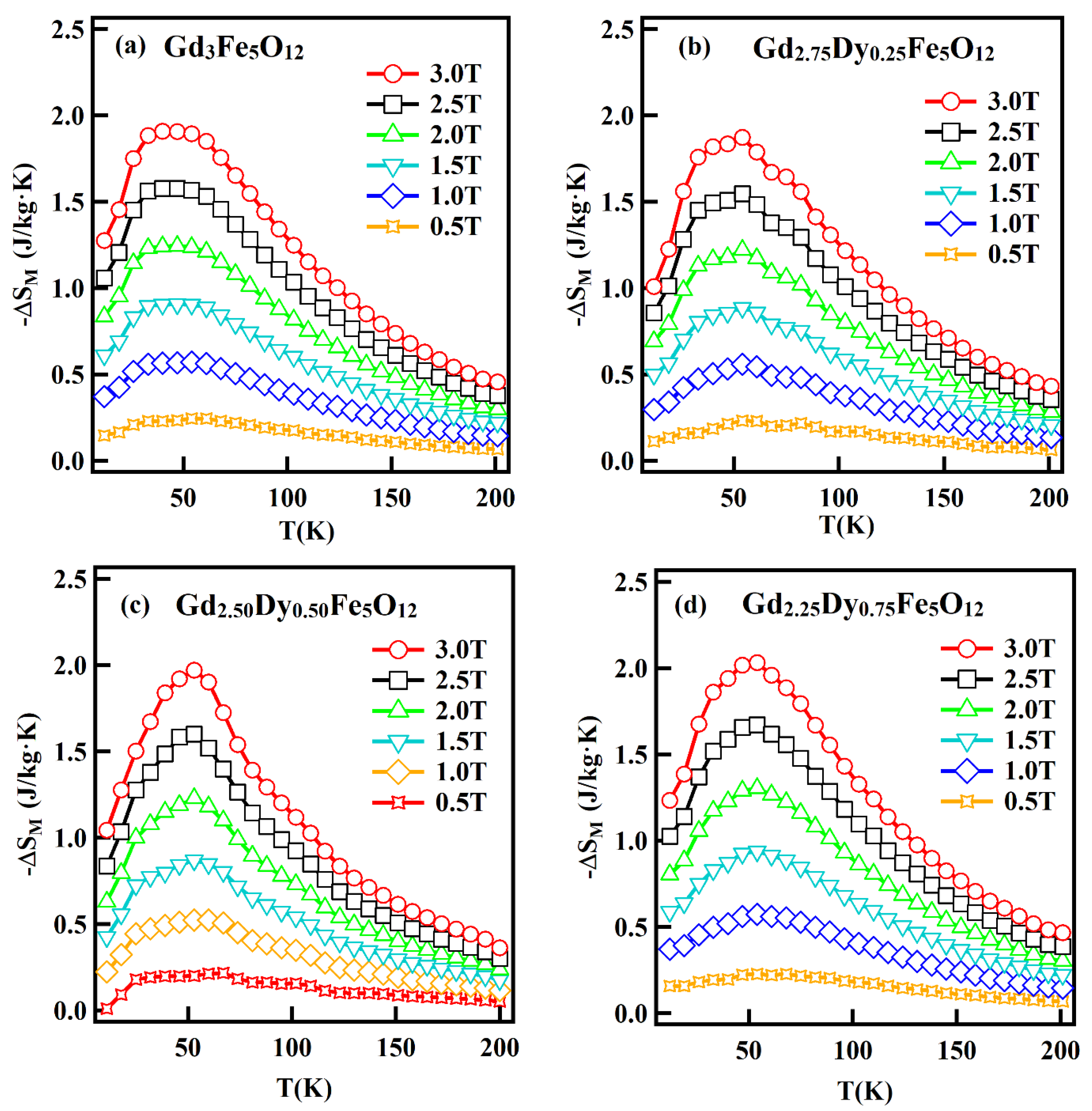
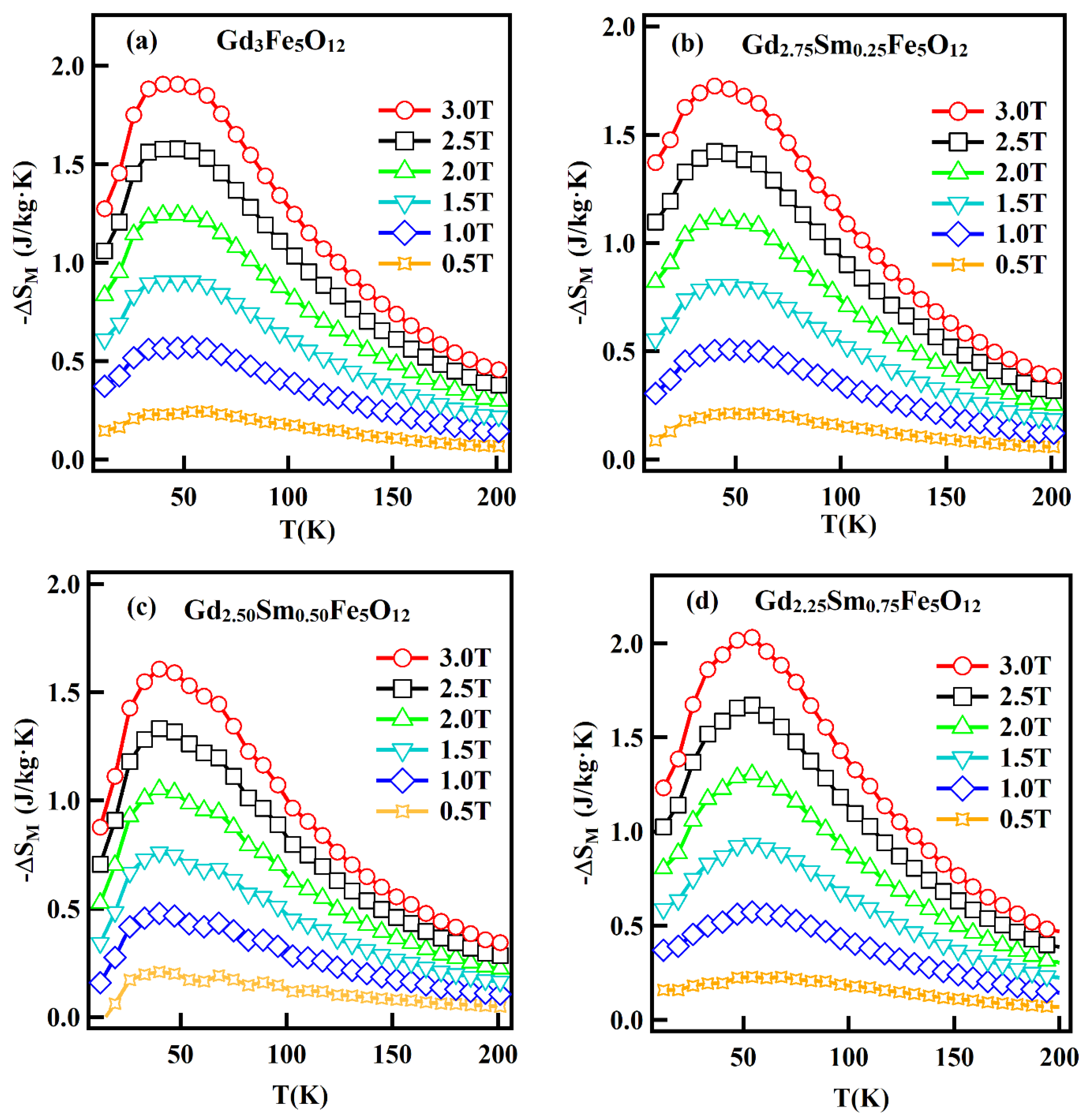
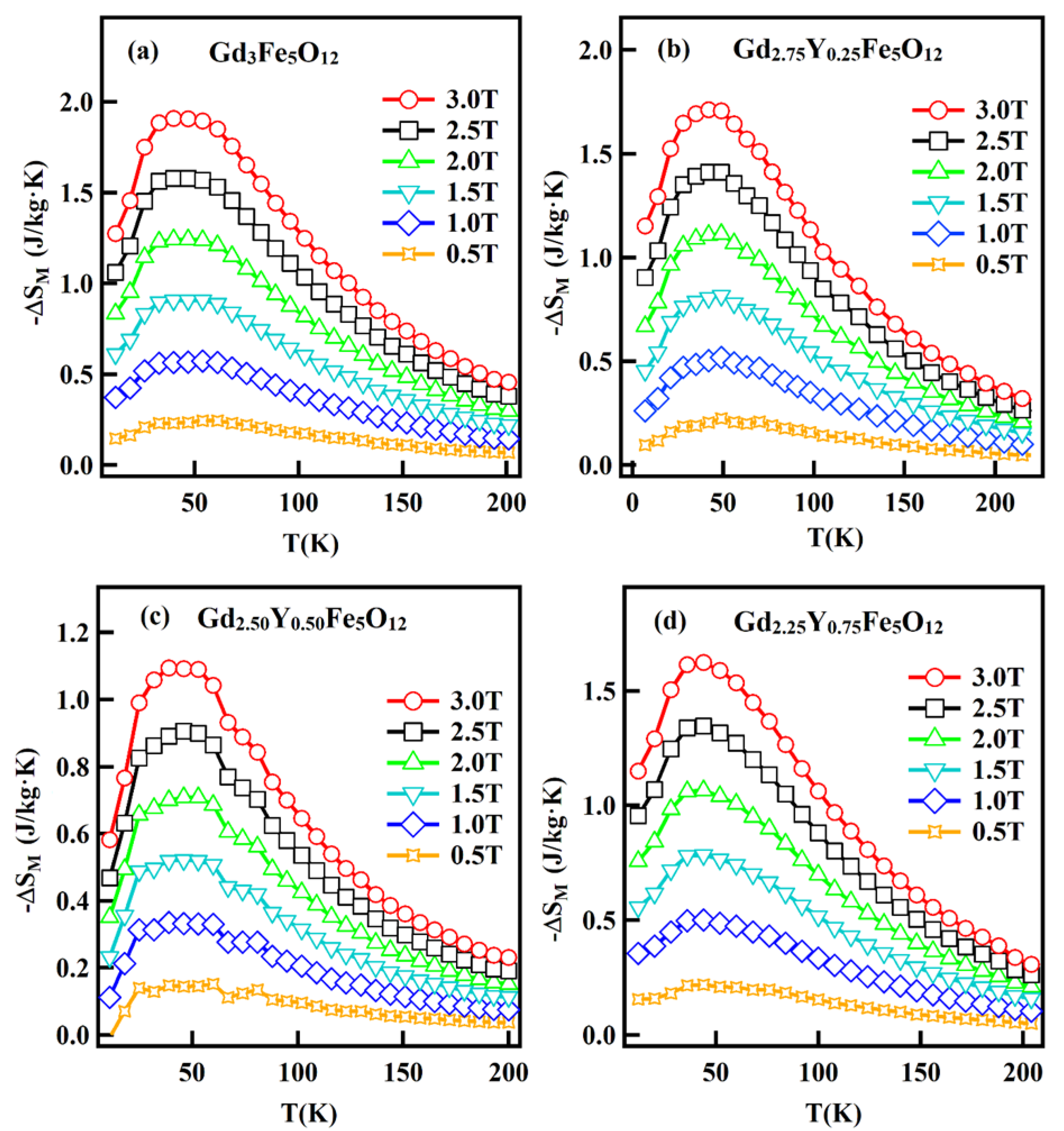
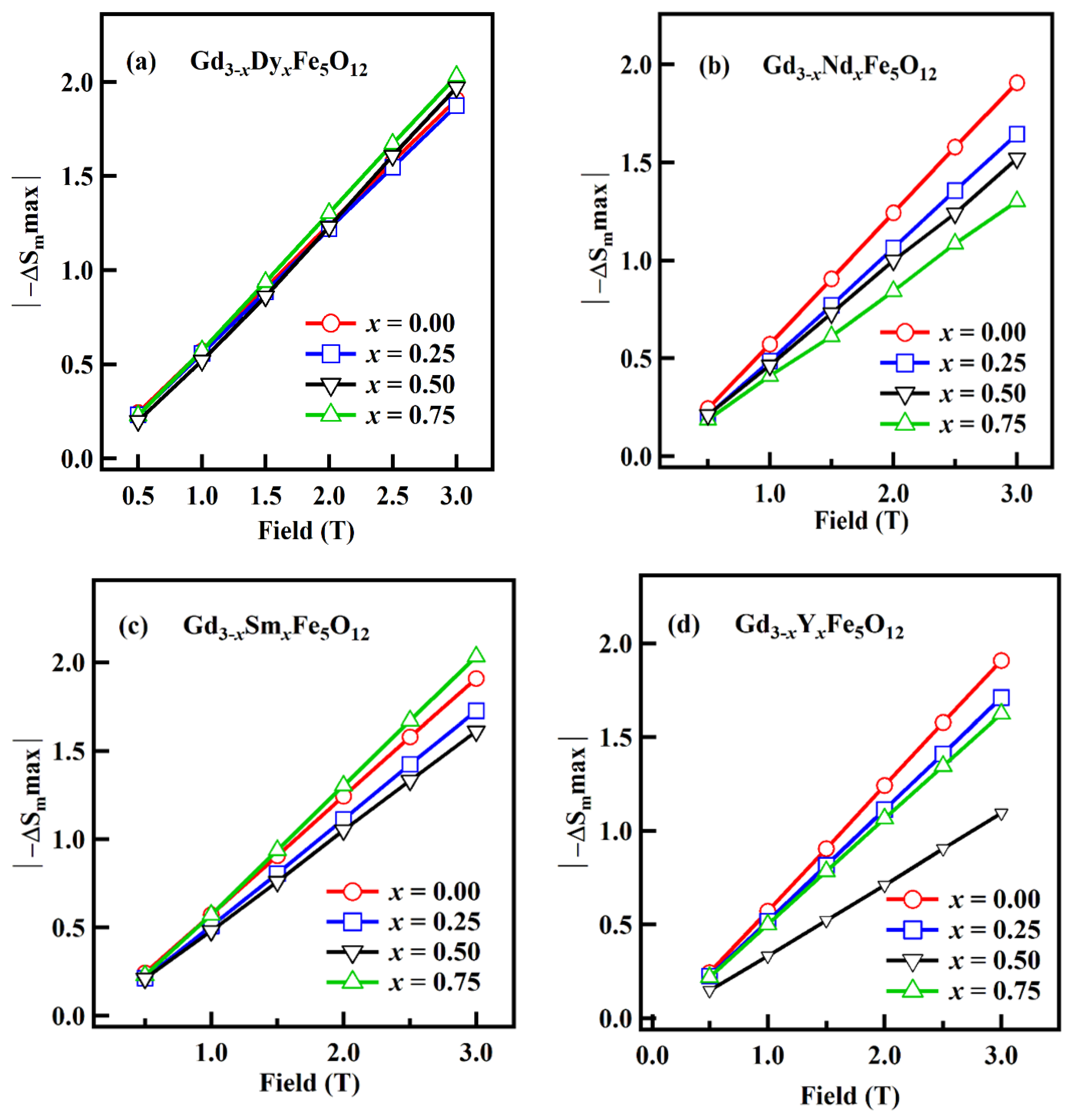
3.7. Magnetocaloric Study
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phan, M.H.; Yu, S.C. Review of the magnetocaloric effect in manganites materials. J. Magn. Magn. Mater. 2007, 308, 325. [Google Scholar] [CrossRef]
- Neupane, D.; Hulsebosch, L.; Ali, K.S.; Bhattarai, R.; Shen, X.; Pathak, A.K.; Mishra, S.R. Enhanced Magnetocaloric Effect in Aluminum doped Gd3Fe5−xAlxO12 Garnet: Structural, Magnetic, and Mössbauer Study. Materialia 2021, 21, 101301. [Google Scholar] [CrossRef]
- Phan, M.H.; Morales, M.B.; Chinnasamy, C.N.; Latha, B.; Harris, V.G.; Srikanth, H. Magnetocaloric effect in bulk and nanostructured Gd3Fe5O12 materials. J. Phys. D Appl. Phys. 2009, 42, 115007. [Google Scholar] [CrossRef]
- Petrov, D.N.; Koshkid’Ko, Y.S.; Ćwik, J.; Nenkov, K. Large magnetocaloric effect in LiLnP4O12 (Ln = Gd, Tb, Dy) single crystals. J. Phys. D Appl. Phys. 2020, 53, 495005. [Google Scholar] [CrossRef]
- Lassri, H.; Hlil, E.K.; Prasad, S.; Krishnan, R. Magnetic and electronic properties of nanocrystalline Gd3Fe5O12 garnet. J. Solid State Chem. 2011, 184, 3216–3220. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, S.; Zheng, M.; Chen, H.; Wu, A. Synthesis and magnetic properties of nanocrystalline Gd3Fe5O12 and GdFeO3 powders prepared by sol–gel auto-combustion method. Mater. Res. Bull. 2018, 104, 92–96. [Google Scholar] [CrossRef]
- Zhang, G. Preparation and Characterization of New Magneto-Optical Crystals for Optical Communication. Ph.D. Thesis, NUS Singapore, Singapore, 2005. Available online: http://scholarbank.nus.edu.sg/handle/10635/14540 (accessed on 10 September 2020).
- Fu, Q.; Xu, Q.; Zhao, Z.; Liu, X.; Huang, Y.; Hu, X.; Zhuang, N.; Chen, J. New magneto-optical film of Ce, Ga: GIG with high performance. J. Am. Ceram. Soc. 2016, 99, 234–240. [Google Scholar] [CrossRef]
- Bahadur, D. Current trends in applications of magnetic ceramic materials. Bull. Mater. Sci. 1992, 15, 431–439. [Google Scholar] [CrossRef]
- Schreier, M.; Chiba, T.; Niedermayr, A.; Lotze, J.; Huebl, H.; Geprägs, S.; Takahashi, S.; Bauer, G.E.; Gross, R.; Goennenwein, S.T. Current-induced spin torque resonance of a magnetic insulator. Phys. Rev. B 2015, 92, 144411. [Google Scholar] [CrossRef]
- Chaturvedi, A. Novel Magnetic Materials for Sensing and Cooling Applications. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2011. [Google Scholar]
- Opuchovic, O.; Beganskiene, A.; Kareiva, A. Sol–gel derived Tb3Fe5O12 and Y3Fe5O12 garnets: Synthesis, phase purity, micro-structure and improved design of morphology. J. Alloys Compd. 2015, 647, 189–197. [Google Scholar] [CrossRef]
- Uemura, M.; Yamagishi, T.; Ebisu, S.; Chikazawa, S.; Nagata, S. A double peak of the coercive force near the compensation temperature in the rare earth iron garnets. Philos. Mag. 2008, 88, 209–228. [Google Scholar] [CrossRef]
- Serier-Brault, H.; Thibault, L.; Legrain, M.; Deniard, P.; Rocquefelte, X.; Leone, P.; Perillon, J.L.; Le Bris, S.; Waku, J.; Jobic, S. Thermochromism in yttrium iron garnet compounds. Inorg. Chem. 2014, 53, 12378–12383. [Google Scholar] [CrossRef] [PubMed]
- Gilleo, M.A. Ferromagnetic insulators: Garnets. Handb. Ferromagn. Mater. 1980, 2, 1–53. [Google Scholar]
- Kalashnikova, A.M.; Pavlov, V.V.; Kimel, A.V.; Kirilyuk, A.; Rasing, T.; Pisarev, R.V. Magneto-optical study of holmium iron garnet Ho3Fe5O12. Low Temp. Phys. 2012, 38, 863–869. [Google Scholar] [CrossRef]
- Bsoul, I.; Olayaan, R.; Lataifeh, M.; Mohaidat, Q.I.; Mahmood, S.H. Structural and magnetic properties of Er3Fe5−xGaxO12 garnets. Mater. Res. Express 2019, 6, 076114. [Google Scholar] [CrossRef]
- Nguyet, D.T.T.; Duong, N.P.; Satoh, T.; Hien, T.D.; Anh, L.N.; Loan, T.T. Crystallization and magnetic characterizations of DyIG and HoIG nanopowders fabricated using citrate sol–gel. J. Sci. Adv. Mater. Devices 2016, 1, 193–199. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, L.; Wang, S.; Hou, C. Nd3−xAExFe5O12: Hydrothermal synthesis, structure and magnetic properties. Chem. Res. Chin. Univ. 2017, 33, 869–875. [Google Scholar] [CrossRef]
- Li, C.; Qiu, Y.; Barasa, G.O.; Yuan, S. Spin reorientation, normal and inverse magnetocaloric effects in heavy rare-earth iron garnets. Ceram. Int. 2020, 46, 18758–18762. [Google Scholar] [CrossRef]
- Aparnadevi, N.; Kumar, K.S.; Manikandan, M.; Kumar, B.S.; Punitha, J.S.; Venkateswaran, C. Structural properties, optical, electrical and magnetic behavior of bismuth doped Gd3Fe5O12 prototype garnet. J. Mater. Sci. Mater. Electron. 2020, 31, 2081–2088. [Google Scholar] [CrossRef]
- Li, C.; Barasa, G.O.; Qiu, Y.; Yuan, S. Magnetocaloric effect and sign reversal of magnetic entropy change across the spin reorientation temperature in R3Fe5O12 (R = Gd, Dy). J. Alloys Compd. 2020, 820, 153138. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A Cryst. Phys. Diffr. Theor. Gen. Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Hutchison, W.D.; Stewart, G.A.; Cadogan, J.M.; Princep, A.; Stewart, R.; Ryan, D.H. Magnetic ground state of Dy3+ in DyNiAl4. AIP Adv. 2017, 7, 055702. [Google Scholar] [CrossRef]
- Przeniosło, R.; Sosnowska, I.; Fischer, P. Magnetic moment ordering of Nd3+ ions in NdFeO3. J. Magn. Magn. Mater. 1995, 140, 2153–2154. [Google Scholar] [CrossRef]
- Cevallos, F.A.; Guo, S.; Cava, R.J. Magnetic properties of lithium-containing rare earth garnets Li3RE3Te2O12 (RE = Y, Pr, Nd, Sm-Lu). Mater. Res. Express 2018, 5, 126106. [Google Scholar] [CrossRef]
- Alves, T.E.P.; Pessoni, H.V.S.; Franco, A., Jr. The effect of Y3+ substitution on the structural, optical band-gap, and magnetic properties of cobalt ferrite nanoparticles. Phys. Chem. Chem. Phys. 2017, 19, 16395–16405. [Google Scholar] [CrossRef] [PubMed]
- Geller, S.; Remeika, J.P.; Sherwood, R.C.; Williams, H.J.; Espinosa, G.P. Magnetic study of the heavier rare-earth iron garnets. Phys. Rev. 1965, 137, A1034. [Google Scholar] [CrossRef]
- Lataifeh, M.S.; Al-Sharif, A. Magnetization measurements on some rare-earth iron garnets. Appl. Phys. A 1995, 61, 415–418. [Google Scholar] [CrossRef]
- Lataifeh, M.S.; McCausland, M.H. On the molecular field seen by Gd3+ in iron garnets. Mu’tah Lil-Buhooth Wa Al-Dirasat 1994, 9, 23–30. [Google Scholar]
- Prasad, D.H.; Jung, H.Y.; Jung, H.G.; Kim, B.K.; Lee, H.W.; Lee, J.H. Single step synthesis of nano-sized NiO–Ce0.75Zr0.25O2 composite powders by glycine nitrate process. Mater. Lett. 2008, 62, 587–590. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Rietveld, H.M. The Rietveld method. Phys. Scr. 2014, 89, 09800. [Google Scholar] [CrossRef]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Vegard, L. Die konstitution der mischkristalle und die raumfüllung der atome. Z. Für Phys. 1921, 5, 17–26. [Google Scholar] [CrossRef]
- Geller, S.; Gilleo, M.A. The crystal structure and ferrimagnetism of yttrium-iron garnet, Y3Fe2(FeO4)3. J. Phys. Chem. Solids 1957, 3, 30–36. [Google Scholar] [CrossRef]
- Coronado, E.; Tsukerblat, B.S.; Georges, R. Exchange Interactions I: Mechanisms. In Molecular Magnetism: From Molecular Assemblies to the Devices; Springer: Dordrecht, The Netherlands, 1996; pp. 65–84. [Google Scholar]
- Néel, L.; Pauthenet, R.; Dreyfus, B. Chapter VII—The rare earth garnets. In Progress in Low Temperature Physics; Elsevier: Amsterdam, The Netherlands, 1964; Volume 4. [Google Scholar]
- Kramers, H.A. L’interaction entre les atomes magnétogènes dans un cristal paramagnétique. Physica 1934, 1, 182–192. [Google Scholar] [CrossRef]
- Rovani, P.R.; Ferreira, A.S.; Pereira, A.S.; de Lima, J.C. Effect of pressure on nanostructured Gd3Fe5O12. J. Appl. Phys. 2017, 122, 035904. [Google Scholar] [CrossRef]
- Weil, L.; Bertaut, F.; Bochirol, L. Propriétés magnétiques et structure de la phase quadratique du ferrite de cuivre. J. Phys. Radium 1950, 11, 208–212. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Ali, K.; Umer, A.; Ahmad, T.; Khan, M.A. Structural elucidation, and morphological and magnetic behavior evaluations, of low-temperature sintered, Ce-doped, nanostructured garnet ferrites. Mater. Res. Bull. 2018, 101, 48–55. [Google Scholar] [CrossRef]
- Sickafus, K.E.; Hughes, R. Spinel compounds: Structure and property relations. J. Am. Ceram. Soc. 1999, 82, 3277–3278. [Google Scholar]
- Akhtar, M.N.; Khan, S.N.; Ahmad, H.; Nazir, M.S.; Khan, M.A. Structural elucidation and magnetic behaviour evaluation of gallium substituted garnet ferrites. Ceram. Int. 2018, 44, 22504–22511. [Google Scholar] [CrossRef]
- Halder, N.C.; Wagner, C.N.J. Separation of particle size and lattice strain in integral breadth measurements. Acta Crystallogr. 1996, 20, 312–313. [Google Scholar] [CrossRef]
- Cureton, W.F.; Palomares, R.I.; Walters, J.; Tracy, C.L.; Chen, C.H.; Ewing, R.C.; Lang, M.; Baldinozzi, G.; Lian, J.; Trautmann, C. Grain size effects on irradiated CeO2, ThO2, and UO2. Acta Mater. 2018, 160, 47–56. [Google Scholar] [CrossRef]
- Dipesh, D.N.; Wang, L.; Adhikari, H.; Alam, J.; Mishra, S.R. Influence of Al3+ doping on structural and magnetic properties of CoFe2−xAlxO4 Ferrite nanoparticles. J. Alloys Compd. 2016, 688, 413–421. [Google Scholar] [CrossRef]
- Zulueta, Y.A.; Dawson, J.A.; Mune, P.D.; Froeyen, M.; Nguyen, M.T. Oxygen vacancy generation in rare-earth-doped SrTiO3. Phys. Status Solidi (B) 2016, 253, 2197–2203. [Google Scholar] [CrossRef]
- Poudel, T.P.; Rai, B.K.; Yoon, S.; Guragain, D.; Neupane, D.; Mishra, S.R. The effect of gadolinium substitution in inverse spinel nickel ferrite: Structural, Magnetic, and Mössbauer study. J. Alloys Compd. 2019, 802, 609–619. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, Y.; Zhou, L.; Wei, J.; Wu, J.; Yao, D. Effect of Gd and La doping on the structure, optical and magnetic properties of NiZnCo ferrites. Ceram. Int. 2019, 45, 6236–6242. [Google Scholar] [CrossRef]
- Odo, E.A. Morphology and Elemental Study of Silicon Nanoparticles Produced Using a Vibratory Disc Mill. Nanosci. Nanotechnol. 2015, 5, 57–63. [Google Scholar]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Harmon, B.N.; Antropov, V.P.; Liechtenstein, A.I.; Solovyev, I.V.; Anisimov, V.I. Calculation of magneto-optical properties for 4f systems: LSDA + Hubbard U results. J. Phys. Chem. Solids 1995, 56, 1521–1524. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, J.; Yao, F.; Zhang, W.; Liu, X.; Meng, J.; Zhang, H. Insight into the mechanism of the ionic conductivity for Ln-doped ceria (Ln = La, Pr, Nd, Pm, Sm, Gd, Tb, Dy, Ho, Er, and Tm) through first-principles calculation. Inorg. Chem. 2018, 57, 12690–12696. [Google Scholar] [CrossRef] [PubMed]
- Wurmehl, S.; Fecher, G.H.; Kandpal, H.C.; Ksenofontov, V.; Felser, C.; Lin, H.J.; Morais, J. Geometric, electronic, and magnetic structure of Co2 FeSi: Curie temperature and magnetic moment measurements and calculations. Phys. Rev. B 2005, 72, 184434. [Google Scholar] [CrossRef]
- Taneja, S.P. On the Magnetic Properties of Dy3+ Ion in Dysprosium Ethylsulfate Single Crystal. Phys. Status Solidi (B) 1969, 36, 525–529. [Google Scholar] [CrossRef]
- Sugiyama, J.; Miwa, K.; Nozaki, H.; Kaneko, Y.; Hitti, B.; Arseneau, D.; Morris, G.D.; Ansaldo, E.J.; Brewer, J.H. Magnetic moment of rare-earth elements in R2Fe14B estimated with μ+ SR. Phys. Rev. Mater. 2019, 3, 064402. [Google Scholar] [CrossRef]
- Liu, C.; Kan, X.; Liu, X.; Zhang, Z.; Hu, J. Magnetic compensation and critical behavior in spinel Co2TiO4. Phys. Chem. Chem. Phys. 2020, 22, 20929–20940. [Google Scholar] [CrossRef]
- Ivanov, S.A.; Tellgren, R.; Porcher, F.; Andre, G.; Ericsson, T.; Nordblad, P.; Sadovskaya, N.; Kaleva, G.; Baldini, M.; Mathieu, R. Structural and magnetic properties of nickel antimony ferrospinels. Mater. Chem. Phys. 2015, 158, 127–137. [Google Scholar] [CrossRef]
- Mahmood, S.H.; Bsoul, I.; Hawamdeh, K. Effect of Al-substitution on Structural and Magnetic Properties of Er3Fe5−xAlxO12 Garnets. Mater. Res. Found. 2020, 83, 21–40. [Google Scholar]
- Lahoubi, M.; Guillot, M.; Marchand, A.; Tcheou, F.; Roudault, E. Double umbrella structure in terbium iron garnet. IEEE Trans. Magn. 1984, 20, 1518–1520. [Google Scholar] [CrossRef]
- Fadly, M.; Feldmann, P.; Le Gall, H.; Guillot, M.; Makram, H. Magnetooptical coefficients of Ho3+ ions induced by electric and magnetic dipole transitions in single crystal HoIG. IEEE Trans. Magn. 1978, 14, 448–450. [Google Scholar] [CrossRef]
- Rudolf, P.; Sette, F.; Tjeng, L.H.; Meigs, G.; Chen, C.T. Magnetic moments in a gadolinium iron garnet studied by soft-X-ray magnetic circular dichroism. J. Magn. Magn. Mater. 1992, 109, 109–112. [Google Scholar] [CrossRef]
- Geller, S. Magnetic behavior of substituted ferrimagnetic garnets. J. Appl. Phys. 1966, 37, 1408–1415. [Google Scholar] [CrossRef]
- Levy, P.M. Rare-earth-iron exchange interaction in the garnets. I. Hamiltonian for anisotropic exchange interaction. Phys. Rev. 1964, 135, A155. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- Gavrilova, T.P.; Gilmutdinov, I.F.; Deeva, J.A.; Chupakhina, T.I.; Lyadov, N.M.; Faizrakhmanov, I.A.; Milovich, F.O.; Kabirov, Y.V.; Eremina, R.M. Magnetic and magnetocaloric properties of (1 − x) La0.7Sr0.3MnO3/xNaF composites. J. Magn. Magn. Mater. 2018, 467, 49–57. [Google Scholar] [CrossRef]
- Rogers, P.D.; Choi, Y.J.; Standard, E.; Kang, T.D.; Ahn, K.H.; Dubroka, A.; Marsik, P.; Wang, C.; Bernhard, C.; Park, S.; et al. Optical Identification of Hybrid Magnetic and Electric Excitations in Dy3Fe5O12 Garnet. arXiv 2011, arXiv:1101.2675. [Google Scholar]
- Provenzano, V.; Li, J.; King, T.; Canavan, E.; Shirron, P.; DiPirro, M.; Shull, R.D. Enhanced magnetocaloric effects in R3(Ga1−xFex)5O12 (R = Gd, Dy, Ho; 0 < x < 1) nanocomposites. J. Magn. Magn. Mater. 2003, 266, 185–193. [Google Scholar]
- McMichael, R.D.; Ritter, J.J.; Shull, R.D. Enhanced magnetocaloric effect in Gd3Ga5−xFexO12. J. Appl. Phys. 1993, 73, 6946–6948. [Google Scholar] [CrossRef]
- Hamilton, A.S.; Lampronti, G.I.; Rowley, S.E.; Dutton, S.E. Enhancement of the magnetocaloric effect driven by changes in the crystal structure of Al-doped GGG, Gd3Ga5−xAlxO12 (0 ≤ x ≤ 5). J. Phys. Condens. Matter 2014, 26, 116001. [Google Scholar] [CrossRef]
- Mukherjee, P.; Dutton, S.E. Enhanced magnetocaloric effect from Cr substitution in Ising lanthanide gallium garnets Ln3CrGa4O12 (Ln = Tb, Dy, Ho). Adv. Funct. Mater. 2017, 27, 1701950. [Google Scholar] [CrossRef]




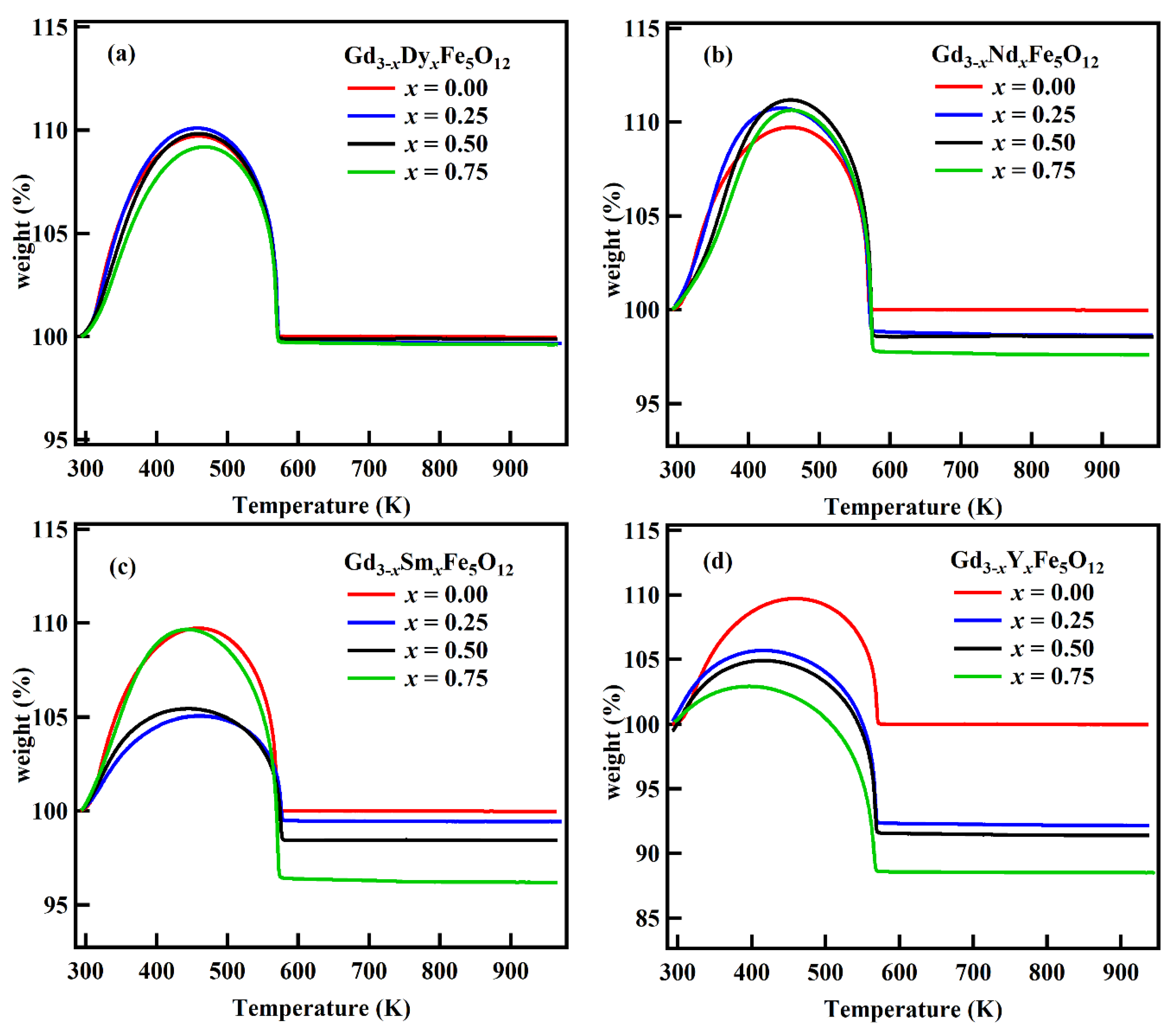

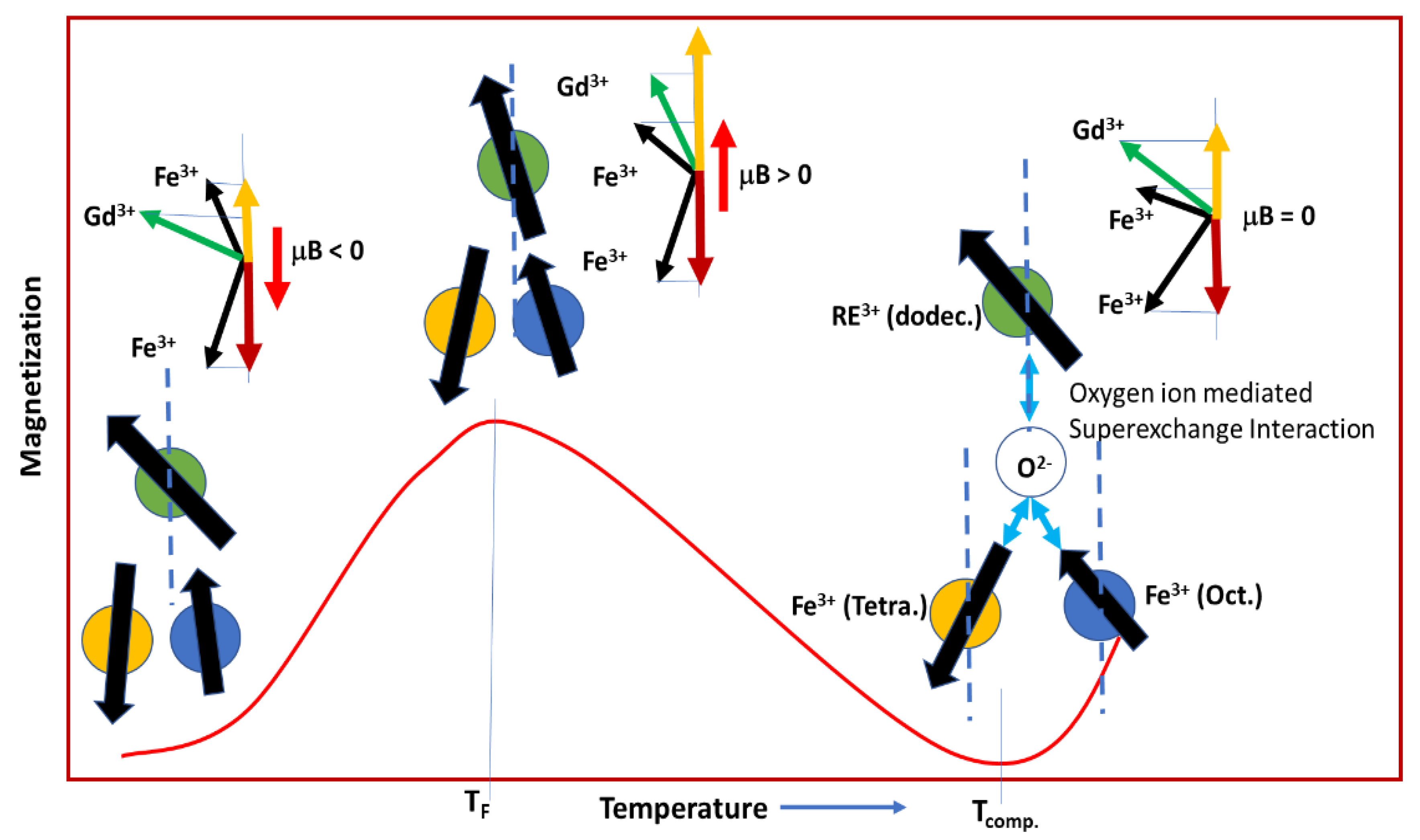
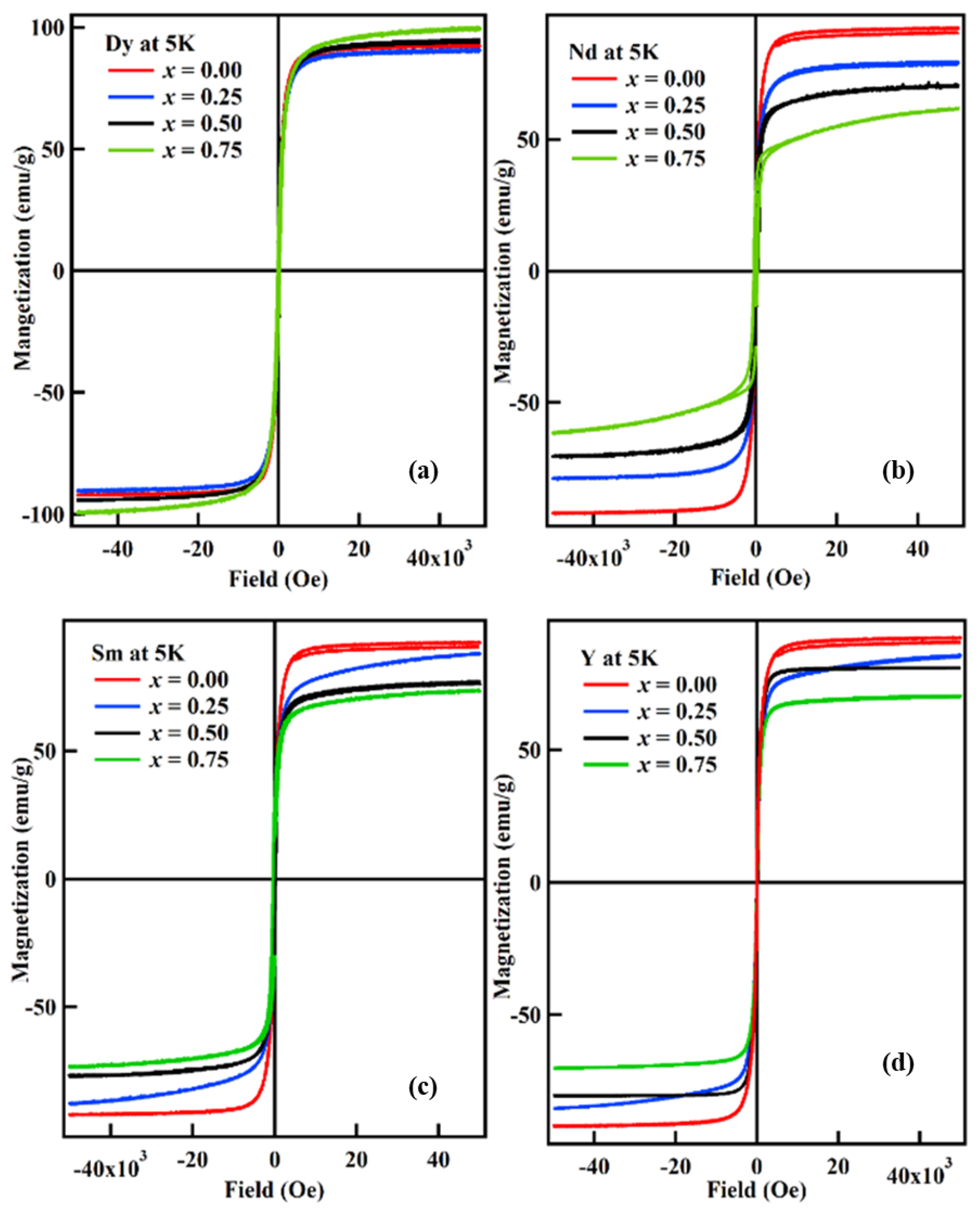

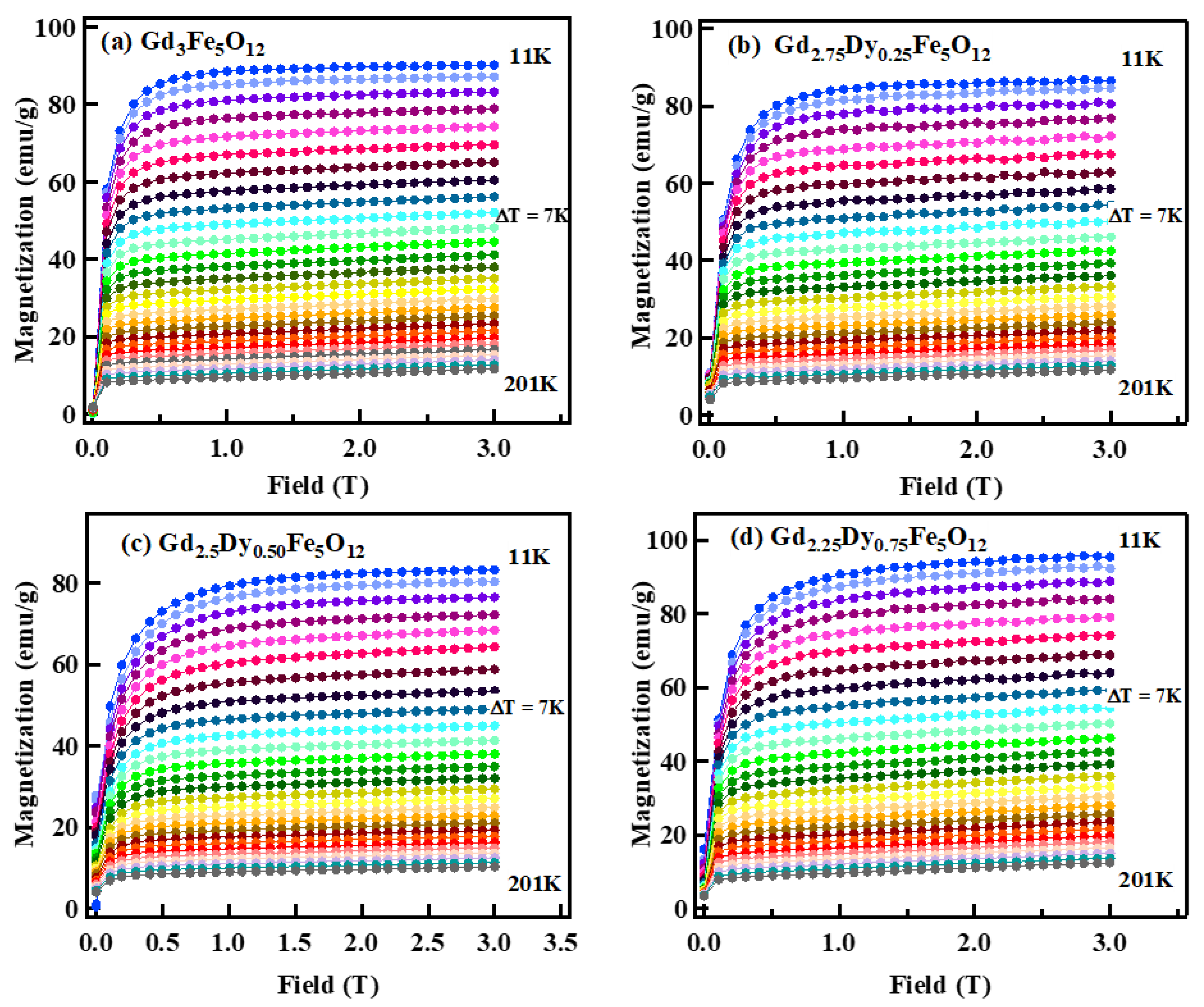


| Gd3−xRExFe5O12 | Gd(NO3)3. 6H2O | Fe(NO3)3. 9H2O | Dy(NO3)3. H2O | Nd(NO3)3. 6H2O | Sm(NO3)3. 6H2O | Y(NO3)3. 5H2O | Glycine | |
|---|---|---|---|---|---|---|---|---|
| RE3+ | x | |||||||
| Weight in gm. | ||||||||
| Dy | 0.00 | 0.718 | 1.071 | 0.000 | - | - | - | 0.318 |
| 0.25 | 0.657 | 1.069 | 0.046 | - | - | - | 0.318 | |
| 0.50 | 0.596 | 1.068 | 0.092 | - | - | - | 0.317 | |
| 0.75 | 0.536 | 1.066 | 0.138 | - | - | - | 0.317 | |
| Nd | 0.00 | 0.718 | 1.071 | - | 0.000 | - | - | 0.318 |
| 0.25 | 0.661 | 1.075 | - | 0.058 | - | - | 0.319 | |
| 0.50 | 0.602 | 1.078 | - | 0.117 | - | - | 0.321 | |
| 0.75 | 0.544 | 1.082 | - | 0.176 | - | - | 0.321 | |
| Sm | 0.00 | 0.718 | 1.071 | - | - | 0.000 | - | 0.318 |
| 0.25 | 0.659 | 1.073 | - | - | 0.059 | - | 0.319 | |
| 0.50 | 0.601 | 1.075 | - | - | 0.118 | - | 0.319 | |
| 0.75 | 0.541 | 1.077 | - | - | 0.177 | - | 0.321 | |
| Y | 0.00 | 0.718 | 1.071 | - | - | - | 0.000 | 0.318 |
| 0.25 | 0.671 | 1.091 | - | - | - | 0.049 | 0.324 | |
| 0.50 | 0.621 | 1.111 | - | - | - | 0.100 | 0.33 | |
| 0.75 | 0.569 | 1.132 | - | - | - | 0.153 | 0.336 | |
| Gd3−xRExFe5O12 | a (Å) | V (Å3) | O(x) | O(y) | O(z) | Density | Rwp (%) | χ2 | |
|---|---|---|---|---|---|---|---|---|---|
| x | (g/cm3) | ||||||||
| Dy | 0.00 | 12.4693(11) | 1938.629(5) | −0.0296 | 0.0538 | 0.1467 | 6.487 | 1.194 | 1.64 |
| 0.25 | 12.4676(14) | 1937.697(6) | −0.0283 | 0.0562 | 0.1492 | 6.489 | 1.622 | 2.82 | |
| 0.50 | 12.4647(12) | 1936.299(5) | −0.0297 | 0.0563 | 0.1470 | 6.485 | 1.351 | 2.55 | |
| 0.75 | 12.4616(13) | 1935.367(18) | −0.0279 | 0.0561 | 0.1496 | 6.497 | 1.515 | 4.21 | |
| Nd | 0.00 | 12.4693(11) | 1938.629(5) | −0.0296 | 0.0538 | 0.1467 | 6.487 | 1.194 | 1.64 |
| 0.25 | 12.482213) | 1944.699(6) | −0.0292 | 0.0524 | 0.1483 | 6.419 | 1.269 | 1.88 | |
| 0.50 | 12.4899(12) | 1948.422(5) | −0.0306 | 0.0545 | 0.1472 | 6.430 | 1.207 | 1.80 | |
| 0.75 | 12.5018(13) | 1953.594(6) | −0.0273 | 0.0567 | 0.1449 | 6.346 | 1.575 | 2.67 | |
| Sm | 0.00 | 12.4693(11) | 1938.629(5) | −0.0296 | 0.0538 | 0.1467 | 6.487 | 1.194 | 1.64 |
| 0.25 | 12.4746(13) | 1940.963(6) | −0.0282 | 0.0558 | 0.1481 | 6.474 | 1.249 | 1.97 | |
| 0.50 | 12.4848(14) | 1946.077(7) | −0.0298 | 0.0554 | 0.1461 | 6.423 | 1.586 | 3.50 | |
| 0.75 | 12.4925(19) | 1949.377(9) | −0.0307 | 0.0573 | 0.1492 | 6.480 | 1.982 | 4.38 | |
| Y | 0.00 | 12.4693(11) | 1938.629(5) | −0.0296 | 0.0538 | 0.1467 | 6.487 | 1.194 | 1.64 |
| 0.25 | 12.4648(13) | 1936.298(6) | −0.0284 | 0.0558 | 0.1460 | 6.392 | 1.406 | 1.72 | |
| 0.50 | 12.4550(11) | 1932.136(5) | −0.0295 | 0.0537 | 0.1481 | 6.235 | 1.458 | 2.24 | |
| 0.75 | 12.4466(32) | 1928.386(2) | −0.026 | 0.0580 | 0.1460 | 6.100 | 1.256 | 1.64 | |
| (A) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Gd3−xRExFe5O12 | Bond Angle (°) | ||||||||||
| Gd–O–Fe2(tetra) | Gd–O–Fe2(tetra) | Gd–O–Fe1(Octa) | Gd–O–Fe1(Octa) | Fe1–O–Fe2 | |||||||
| x | Theory | Expt. | Theory | Expt. | Theory | Expt. | Theory | Expt. | Theory | Expt. | |
| Dy3+ | 0.00 | 93.37 | 92.36 | 122.95 | 121.36 | 101.54 | 101.78 | 104.17 | 104.43 | 126.19 | 129.04 |
| 0.25 | 93.19 | 93.10 | 123.3 | 122.05 | 102.02 | 101.94 | 103.99 | 104.12 | 125.86 | 127.82 | |
| 0.50 | 93.18 | 91.87 | 123.11 | 122.51 | 101.52 | 102.46 | 103.99 | 103.66 | 125.92 | 127.66 | |
| 0.75 | 93.08 | 93.23 | 122.04 | 122.85 | 101.43 | 102.55 | 103.65 | 104.15 | 126.6 | 126.67 | |
| Nd3+ | 0.00 | 93.37 | 92.36 | 122.95 | 121.36 | 101.54 | 101.78 | 104.17 | 104.43 | 126.19 | 129.04 |
| 0.25 | 93.38 | 93.36 | 122.72 | 121.19 | 101.71 | 100.82 | 103.95 | 104.73 | 127.26 | 128.36 | |
| 0.50 | 93.55 | 92.28 | 121.62 | 121.24 | 100.35 | 101.66 | 102.56 | 103.73 | 128.73 | 127.92 | |
| 0.75 | 93.41 | 91.21 | 122.03 | 121.29 | 100.88 | 101.66 | 102.67 | 104.88 | 128.2 | 127.03 | |
| Sm3+ | 0.00 | 93.37 | 92.36 | 122.95 | 121.36 | 101.54 | 101.78 | 104.17 | 104.43 | 126.19 | 129.04 |
| 0.25 | 93.46 | 92.60 | 123.42 | 122.10 | 101.02 | 102.21 | 103.89 | 104.32 | 127.44 | 128.75 | |
| 0.50 | 93.21 | 91.71 | 122.11 | 122.32 | 100.84 | 102.48 | 103.36 | 104.04 | 128.13 | 128.34 | |
| 0.75 | 93.37 | 92.43 | 122.04 | 122.71 | 100.79 | 101.71 | 103.47 | 102.72 | 128.16 | 127.92 | |
| Y3+ | 0.00 | 93.37 | 92.36 | 122.95 | 121.36 | 101.54 | 101.78 | 104.17 | 104.43 | 126.19 | 129.04 |
| 0.25 | 93.22 | 91.72 | 123.52 | 121.61 | 101.02 | 101.83 | 104.25 | 104.51 | 127.44 | 128.93 | |
| 0.50 | 93.53 | 92.95 | 123.56 | 121.71 | 100.86 | 101.25 | 103.83 | 104.33 | 127.64 | 128.82 | |
| 0.75 | 93.63 | 93.06 | 123.58 | 122.21 | 100.85 | 101.34 | 103.88 | 103.92 | 127.53 | 127.69 | |
| (B) | |||||||||||
| Gd3−xRExFe5O12 | Bond Lengths (Å) | ||||||||||
| Gd–Fe2(Tetra) | Gd–Fe1(Octa) | Fe2(Tetra)–O | Fe1–Fe2 | Fe1(Octa)–O | |||||||
| x | Theory | Expt. | Theory | Expt. | Theory | Expt. | Theory | Expt. | Theory | Expt. | |
| Dy3+ | 0.00 | 3.117 | 3.117 | 3.485 | 3.485 | 1.878 | 1.876 | 3.484 | 3.485 | 2.029 | 1.984 |
| 0.25 | 3.111 | 3.117 | 3.482 | 3.485 | 1.875 | 1.877 | 3.467 | 3.485 | 2.043 | 1.993 | |
| 0.50 | 3.104 | 3.116 | 3.456 | 3.483 | 1.867 | 1.884 | 3.462 | 3.4838 | 2.028 | 1.997 | |
| 0.75 | 3.102 | 3.115 | 3.456 | 3.483 | 1.864 | 1.875 | 3.454 | 3.483 | 2.015 | 2.022 | |
| Nd3+ | 0.00 | 3.117 | 3.117 | 3.485 | 3.485 | 1.878 | 1.876 | 3.484 | 3.485 | 2.029 | 1.984 |
| 0.25 | 3.112 | 3.121 | 3.473 | 3.4888 | 1.876 | 1.872 | 3.469 | 3.4888 | 2.002 | 1.997 | |
| 0.50 | 3.121 | 3.123 | 3.466 | 3.4911 | 1.863 | 1.871 | 3.474 | 3.4911 | 1.996 | 1.998 | |
| 0.75 | 3.11 | 3.126 | 3.472 | 3.4944 | 1.863 | 1.889 | 3.464 | 3.4944 | 2.043 | 1.928 | |
| Sm3+ | 0.00 | 3.117 | 3.117 | 3.485 | 3.485 | 1.878 | 1.876 | 3.484 | 3.485 | 2.029 | 1.984 |
| 0.25 | 3.113 | 3.119 | 3.462 | 3.4868 | 1.865 | 1.886 | 3.465 | 3.4868 | 1.997 | 2.007 | |
| 0.50 | 3.114 | 3.121 | 3.469 | 3.4896 | 1.865 | 1.891 | 3.471 | 3.4896 | 2.003 | 1.986 | |
| 0.75 | 3.115 | 3.123 | 3.472 | 3.4918 | 1.865 | 1.867 | 3.472 | 3.4918 | 1.995 | 2.034 | |
| Y3+ | 0.00 | 3.117 | 3.117 | 3.485 | 3.485 | 1.878 | 1.876 | 3.484 | 3.485 | 2.029 | 1.984 |
| 0.25 | 3.111 | 3.116 | 3.467 | 3.4846 | 1.866 | 1.87 | 3.466 | 3.4846 | 1.999 | 1.981 | |
| 0.50 | 3.113 | 3.114 | 3.463 | 3.4813 | 1.865 | 1.864 | 3.475 | 3.4813 | 1.995 | 1.996 | |
| 0.75 | 3.108 | 3.111 | 3.463 | 3.4789 | 1.864 | 1.863 | 3.477 | 3.4789 | 1.998 | 2.012 | |
| Gd3−xRExFe5O12 | Gd | RE | Fe2(tetra.) | Fe1(Octa.) | Chemical Formula | |
|---|---|---|---|---|---|---|
| RE | x | |||||
| Dy3+ | 0.00 | 1.0052 | - | 0.9982 | 1.0093 | Gd3.02Fe2.99Fe2.02O12 |
| 0.25 | 0.9264 | 0.0899 | 0.9923 | 1.0587 | Gd2.78Dy0.27Fe2.98Fe2.12O12 | |
| 0.50 | 0.8288 | 0.1492 | 1.0006 | 1.0067 | Gd2.49Dy0.45Fe3.00Fe2.01O12 | |
| 0.75 | 0.7784 | 0.2181 | 1.0033 | 1.0108 | Gd2.34Dy0.65Fe3.01Fe2.02O12 | |
| Nd3+ | 0.00 | 1.0052 | - | 0.9982 | 1.0093 | Gd3.02Fe2.99Fe2.02O12 |
| 0.25 | 0.9245 | 0.0806 | 0.9900 | 0.9917 | Gd2.77Nd0.24Fe2.97Fe1.98O12 | |
| 0.50 | 0.849 | 0.1649 | 0.9985 | 1.0022 | Gd2.55Nd0.49Fe3.00Fe2.00O12 | |
| 0.75 | 0.7438 | 0.2526 | 1.0022 | 1.0111 | Gd2.23Nd0.76Fe3.01Fe2.02O12 | |
| Sm3+ | 0.00 | 1.0052 | - | 0.9982 | 1.0093 | Gd3.02Fe2.99Fe2.02O12 |
| 0.25 | 0.9111 | 0.0829 | 1.011 | 1.0186 | Gd2.73Sm0.25Fe3.03Fe2.04O12 | |
| 0.50 | 0.8215 | 0.1604 | 0.9946 | 1.0073 | Gd2.47Sm0.48Fe2.98Fe2.01O12 | |
| 0.75 | 0.7688 | 0.2269 | 1.0576 | 1.049 | Gd2.31Sm0.68Fe3.17Fe2.10O12 | |
| Y3+ | 0.00 | 1.0052 | - | 0.9982 | 1.0093 | Gd3.02Fe2.99Fe2.02O12 |
| 0.25 | 0.9020 | 0.0873 | 1.0512 | 1.0705 | Gd2.71Y0.26Fe3.15Fe2.01O12 | |
| 0.50 | 0.8171 | 0.1682 | 0.9917 | 0.9977 | Gd2.45Y0.51Fe2.98Fe2.00O12 | |
| 0.75 | 0.7890 | 0.2156 | 1.0220 | 0.9900 | Gd2.37Y0.65Fe3.07Fe1.98O12 | |
| Site Radii | Bond Length | Shared Edges | Unshared Edges | Tolerance Factor | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RE | x | u | rA (Å) | rB (Å) | RA (Å) | RB (Å) | dAE (Å) | dBE (Å) | dBEU (Å) | t |
| Dy3+ | 0.00 | 0.382 | 1.542 | 1.704 | 2.862 | 3.026 | 4.673 | 4.143 | 4.412 | 0.669 |
| 0.25 | 0.381 | 1.509 | 1.721 | 2.829 | 3.043 | 4.620 | 4.195 | 4.410 | 0.658 | |
| 0.50 | 0.382 | 1.536 | 1.705 | 2.856 | 3.028 | 4.664 | 4.149 | 4.410 | 0.668 | |
| 0.75 | 0.381 | 1.503 | 1.723 | 2.823 | 3.045 | 4.611 | 4.201 | 4.408 | 0.656 | |
| Nd3+ | 0.00 | 0.382 | 1.542 | 1.704 | 2.862 | 3.026 | 4.673 | 4.143 | 4.412 | 0.669 |
| 0.25 | 0.382 | 1.528 | 1.716 | 2.848 | 3.038 | 4.651 | 4.175 | 4.416 | 0.663 | |
| 0.50 | 0.382 | 1.527 | 1.720 | 2.847 | 3.042 | 4.649 | 4.182 | 4.418 | 0.662 | |
| 0.75 | 0.385 | 1.617 | 1.672 | 2.937 | 2.998 | 4.796 | 4.043 | 4.427 | 0.694 | |
| Sm3+ | 0.00 | 0.382 | 1.542 | 1.704 | 2.862 | 3.026 | 4.673 | 4.143 | 4.412 | 0.669 |
| 0.25 | 0.382 | 1.531 | 1.712 | 2.851 | 3.034 | 4.656 | 4.164 | 4.413 | 0.665 | |
| 0.50 | 0.383 | 1.559 | 1.700 | 2.878 | 3.023 | 4.701 | 4.127 | 4.418 | 0.674 | |
| 0.75 | 0.380 | 1.491 | 1.741 | 2.811 | 3.063 | 4.591 | 4.242 | 4.418 | 0.649 | |
| Y3+ | 0.00 | 0.382 | 1.542 | 1.704 | 2.862 | 3.026 | 4.673 | 4.143 | 4.412 | 0.669 |
| 0.25 | 0.383 | 1.569 | 1.686 | 2.889 | 3.010 | 4.717 | 4.096 | 4.412 | 0.679 | |
| 0.50 | 0.382 | 1.515 | 1.714 | 2.835 | 3.036 | 4.629 | 4.177 | 4.406 | 0.661 | |
| 0.75 | 0.381 | 1.497 | 1.721 | 2.817 | 3.043 | 4.601 | 4.201 | 4.403 | 0.655 | |
| Gd3−xRExFe5O12 | Average Crystallite Size (nm) | Grain Size from SEM (nm) | Strain from HWL Method | X-ray Density, ρ (g/cm3) | |
|---|---|---|---|---|---|
| RE | x | HWL Method | ×10−4 | ||
| Dy3+ | 0.00 | 70.82 | 1000 | 3.7 | 6.46 |
| 0.25 | 68.55 | 12.5 | 6.47 | ||
| 0.50 | 66.34 | 5.6 | 6.48 | ||
| 0.75 | 65.48 | 1000 | 2.8 | 6.49 | |
| Nd3+ | 0.00 | 70.82 | 1000 | 3.7 | 6.46 |
| 0.25 | 59.32 | 22.3 | 6.42 | ||
| 0.50 | 58.68 | 23.1 | 6.39 | ||
| 0.75 | 60.78 | 500 | 16.8 | 6.34 | |
| Sm3+ | 0.00 | 70.82 | 1000 | 3.7 | 6.46 |
| 0.25 | 62.46 | 6.0 | 6.44 | ||
| 0.50 | 67.24 | 7.1 | 6.41 | ||
| 0.75 | 61.03 | 1500 | 7.1 | 6.39 | |
| Y3+ | 0.00 | 70.82 | 1000 | 3.7 | 6.46 |
| 0.25 | 70.81 | 17.6 | 6.35 | ||
| 0.50 | 70.88 | 12.7 | 6.25 | ||
| 0.75 | 74.70 | 1000 | 13.4 | 6.14 | |
| Ions | Orbital Moment (μL) | Spin Moment (μS) | Total Moment (μT) |
|---|---|---|---|
| Dy3+ | 4.07 | 4.98 | 9.05 |
| Nd3+ | −4.43 | 2.89 | −1.54 |
| Sm3+ | −2.43 | 4.98 | 2.55 |
| Y3+ | 0.00 | 0.00 | 0.00 |
| Gd3+ | 0.00 | 6.99 | 6.99 |
| Fe3+ (Tetra) | 0.00 | −4.06 | −4.06 |
| Fe3+ (Octa) | 0.00 | 4.16 | 4.16 |
| O2− | 0.00 | 0.00 | 0.00 |
| Compounds | Tcomp (K) | TC (K) | Reference |
|---|---|---|---|
| Er3Fe5O12 | 87 | [63] | |
| Er3Fe4.2Al0.8O12 | 139 | [63] | |
| Tb3Fe5O12 | 244 | [64] | |
| Ho3Fe5O12 | 137 | [65] | |
| Gd3Fe5O12 | 288 | [66] | |
| Gd3Fe5O12 | 280 | 570 | Present work |
| Gd2.25Dy0.75Fe5O12 | 287 | 572 | Present work |
| Gd2.25Nd0.75Fe5O12 | 263 | 574 | Present work |
| Gd2.25Sm0.75Fe5O12 | 260 | 572 | Present work |
| Gd2.25Y0.75Fe5O12 | 238 | 567 | Present work |
| Gd3−xRExFe5O12 | Ms (emu/g) | Bohr Magneton | (α)Y-K (Degrees) | |
|---|---|---|---|---|
| x | (µB) | |||
| 0.00 | 92.3 | 2.40 | - | |
| Dy3+ | 0.25 | 90.1 | 2.35 | 12.70 |
| 0.50 | 94.8 | 2.47 | 40.08 | |
| 0.75 | 99.3 | 2.59 | 55.34 | |
| Nd3+ | 0.25 | 79.4 | 2.08 | 21.11 |
| 0.50 | 70.6 | 1.84 | 48.13 | |
| 0.75 | 61.7 | 1.62 | 64.83 | |
| Sm3+ | 0.25 | 88.0 | 2.29 | 14.89 |
| 0.50 | 76.8 | 2.01 | 46.07 | |
| 0.75 | 73.6 | 1.91 | 62.15 | |
| Y3+ | 0.25 | 85.6 | 2.22 | 17.23 |
| 0.50 | 81.0 | 2.11 | 44.81 | |
| 0.75 | 70.5 | 1.84 | 62.74 | |
| Compound | Tpeak | ΔSMmax | H (T) | RCP | R | Reference |
|---|---|---|---|---|---|---|
| Ho3Fe5O12 | 34 | 4.72 | 5 | 136 | [16] | |
| Er3Fe5O12 | 24 | 4.94 | 5 | 103 | [16] | |
| Gd3Fe5O12 | 40 | 1.99 | 3 | 193 | [22] | |
| Dy3Fe5O12 | 58 | 2.03 | 3 | 165 | [18] | |
| Gd3Ga2.5Fe2.5O12 | 12 | ~1.70 | 1 | [72] | ||
| Gd2.25Dy0.75Ga2.5Fe2.5O12 | 10 | ~1.55 | 1 | [18] | ||
| Gd3Fe5O12 (bulk) | 40 | 0.45 | 1 | [73] | ||
| Gd3Fe5O12 (50 nm) | 25 | 1.49 | 3 | [28] | ||
| Gd3Fe5O12 | 40 | 1.91 | 3 | 219 | 1.10 | Present work |
| Gd2.25Dy0.75Fe5O12 | 54 | 2.04 | 3 | 234 | 1.13 | Present work |
| Gd2.25Nd0.75Fe5O12 | 40 | 1.25 | 3 | 140 | 1.14 | Present work |
| Gd2.25Sm0.75Fe5O12 | 54 | 2.03 | 3 | 234 | 1.13 | Present work |
| Gd2.25Y0.75Fe5O12 | 44 | 1.62 | 3 | 180 | 1.12 | Present work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neupane, D.; Kramer, N.; Bhattarai, R.; Hanley, C.; Pathak, A.K.; Shen, X.; Karna, S.; Mishra, S.R. Rare-Earth Doped Gd3−xRExFe5O12 (RE = Y, Nd, Sm, and Dy) Garnet: Structural, Magnetic, Magnetocaloric, and DFT Study. Ceramics 2023, 6, 1937-1976. https://doi.org/10.3390/ceramics6040120
Neupane D, Kramer N, Bhattarai R, Hanley C, Pathak AK, Shen X, Karna S, Mishra SR. Rare-Earth Doped Gd3−xRExFe5O12 (RE = Y, Nd, Sm, and Dy) Garnet: Structural, Magnetic, Magnetocaloric, and DFT Study. Ceramics. 2023; 6(4):1937-1976. https://doi.org/10.3390/ceramics6040120
Chicago/Turabian StyleNeupane, Dipesh, Noah Kramer, Romakanta Bhattarai, Christopher Hanley, Arjun K. Pathak, Xiao Shen, Sunil Karna, and Sanjay R. Mishra. 2023. "Rare-Earth Doped Gd3−xRExFe5O12 (RE = Y, Nd, Sm, and Dy) Garnet: Structural, Magnetic, Magnetocaloric, and DFT Study" Ceramics 6, no. 4: 1937-1976. https://doi.org/10.3390/ceramics6040120
APA StyleNeupane, D., Kramer, N., Bhattarai, R., Hanley, C., Pathak, A. K., Shen, X., Karna, S., & Mishra, S. R. (2023). Rare-Earth Doped Gd3−xRExFe5O12 (RE = Y, Nd, Sm, and Dy) Garnet: Structural, Magnetic, Magnetocaloric, and DFT Study. Ceramics, 6(4), 1937-1976. https://doi.org/10.3390/ceramics6040120