Dynamic Extrusion Control in Spot Deposition Modeling for Porous 3D Clay Structures
Abstract
:1. Introduction
2. Materials and Methods
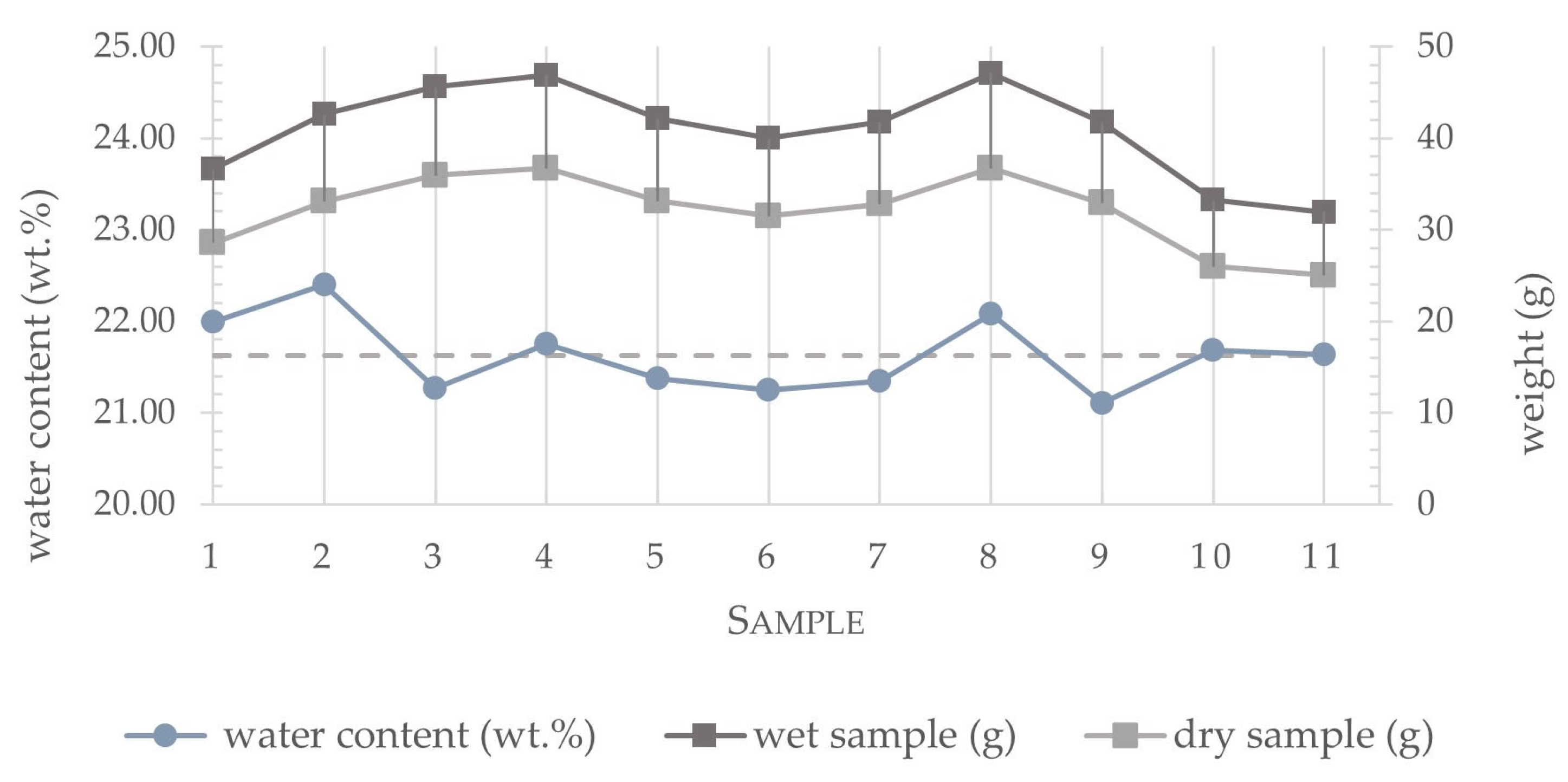
2.1. Clay Paste
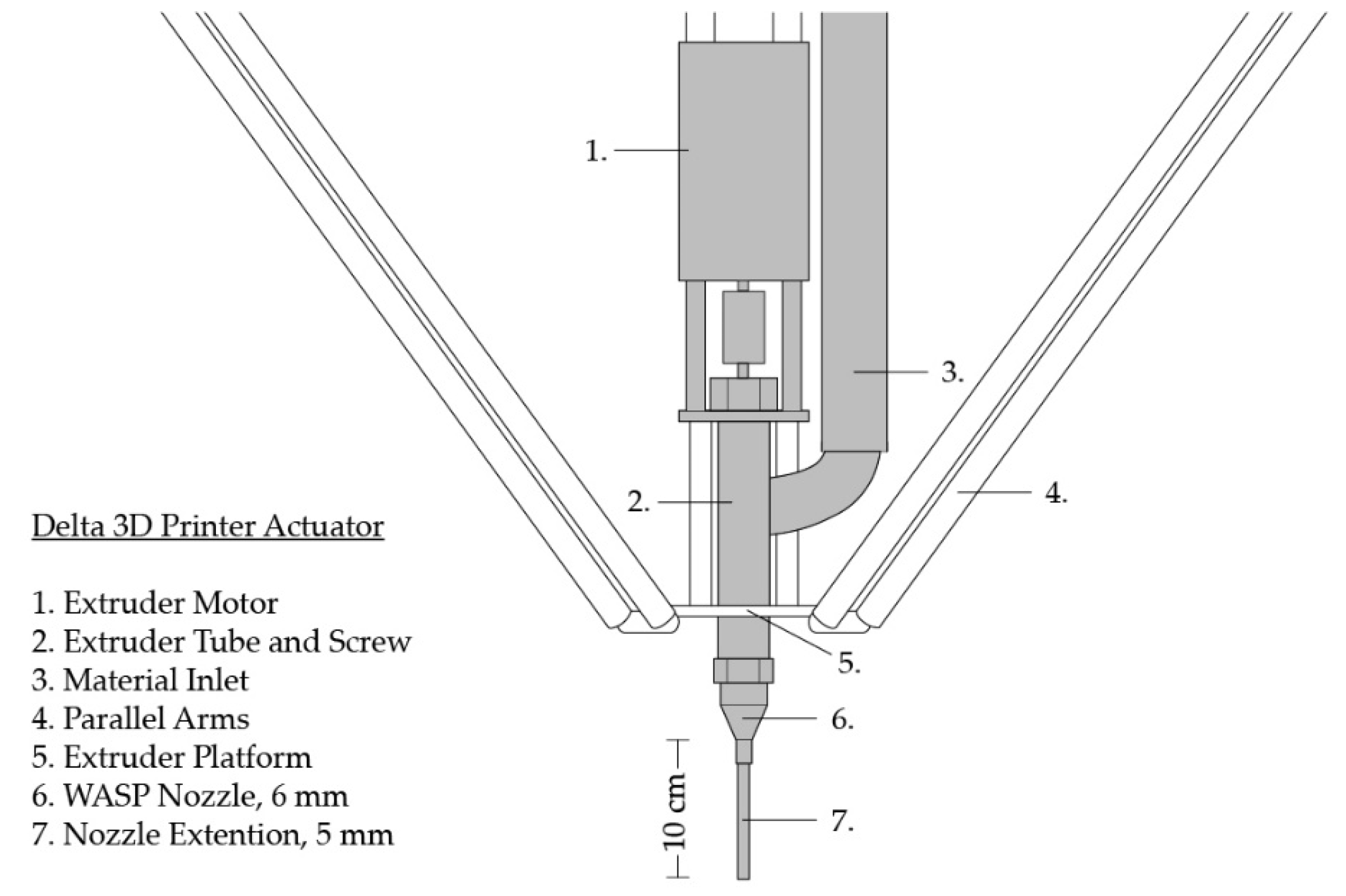
2.2. Liquid Deposition Modeling System
2.3. Parametric Modeling and G-Code
- The type of movement that uses the letter address G, e.g., G00 and G01 are the commands for linear movements (without and with extrusion).
- The velocity variable F controls the speed of movement towards the set goal/ coordinate/ point and is set in mm/min.
- The variables X, Y and Z describe the absolute or relative coordinates for the geometrical target point of the movement set in mm.
- The variable E sets the number of rotations of the extruder motor. The WASP 3D clay printer is pre-calibrated by the manufacturer, and an extrusion value corresponding to the distance between two consecutive points (path length) will produce a sufficient volume of material to cover the traveled distance. For example, an extrusion value of 10, corresponding to a rotation of the motor of 45°, will produce material that can horizontally cover 10 mm. By multiplying the path length using an extrusion factor, the volume of extruded material can be digitally increased or decreased, without modifying the pressure in the clay tank, leading to an object with dynamic extrusion.
2.4. Spot Deposition
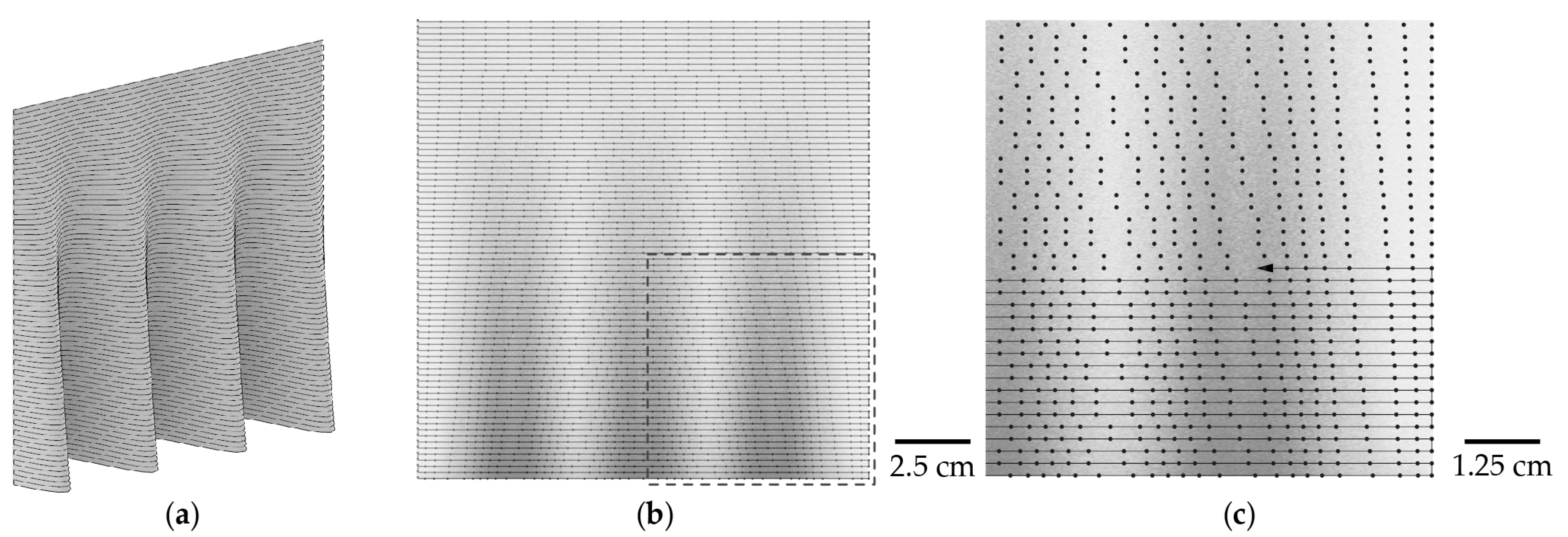
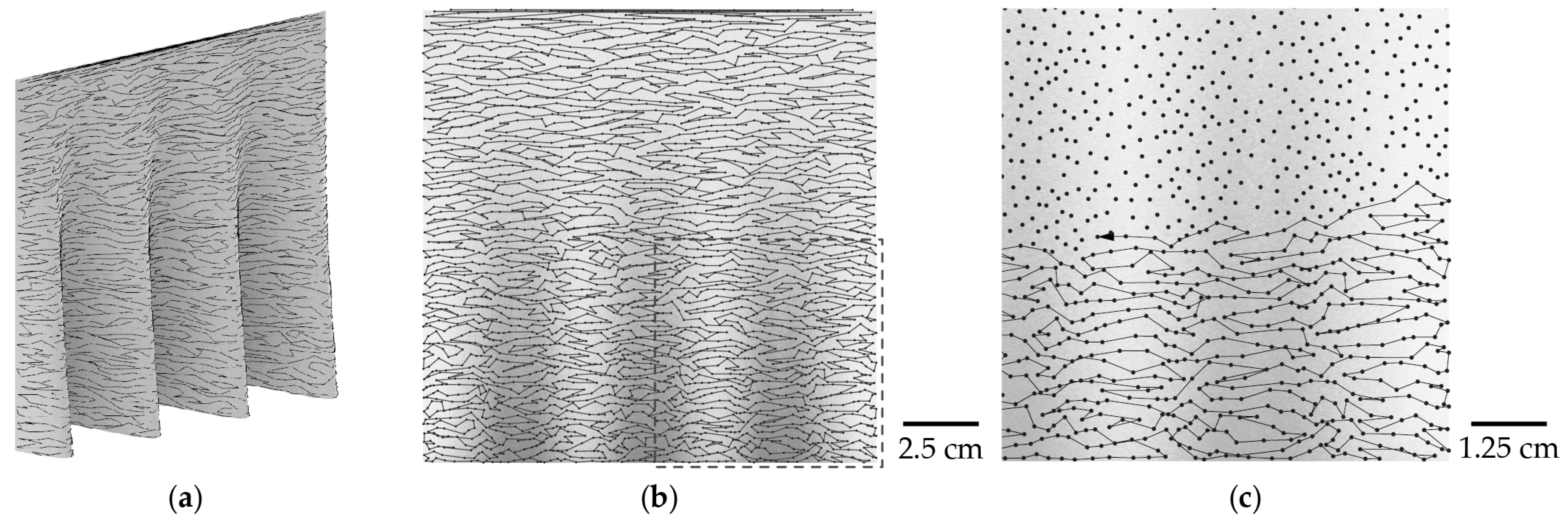
2.5. Evaluation of Vertical Face Porosity
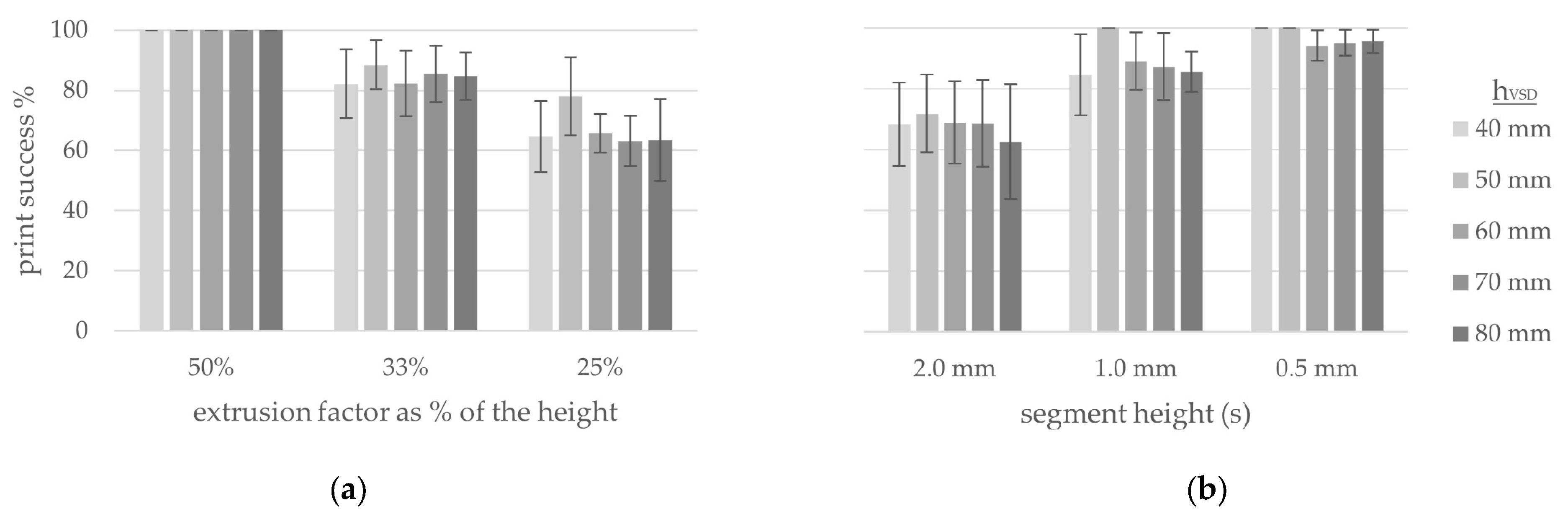
3. Horizontal Spot Deposition and Extrusion Control
4. 3D Lattice Structures out of Bent Vertical Extrusions
4.1. Bending of the Vertical Spot Depositions (vSDs)
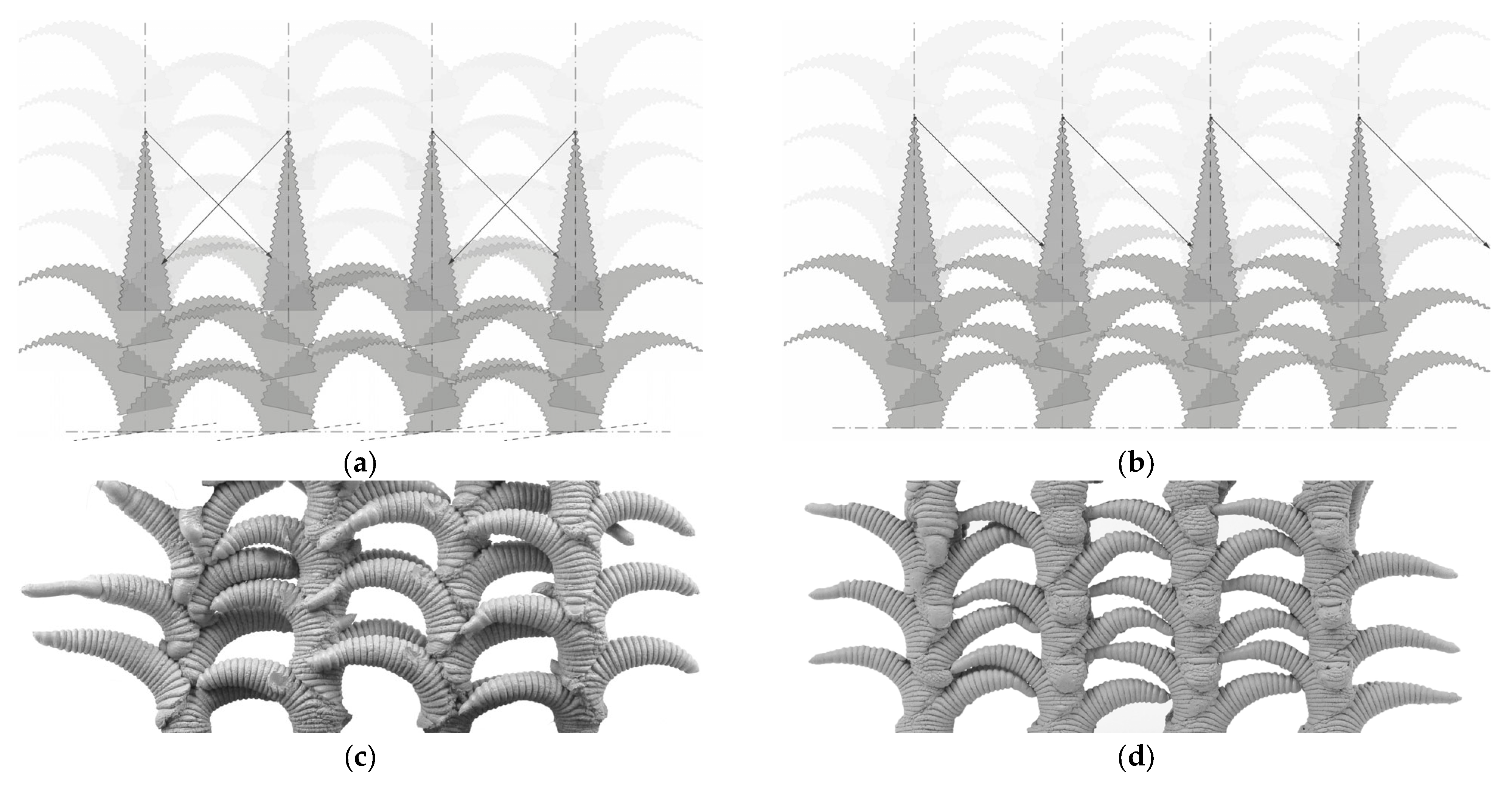
4.2. Interlocking Patterns
4.3. Closed One-Shelled Lattice Structures
4.4. Opened One-Shelled Lattice Structures
4.5. Opened Two-Shelled Linear Lattice Structures
4.6. Opened Two-Shelled Curved Lattice Structures
5. Discussion
6. Conclusions
- Three-dimensional lattice structures out of clay paste with face porosity in the range of 25–35% can be fabricated using material plasticity and viscosity in combination with dynamic extrusion and deformations through travel path.
- vSDs and pre-compression of the deposited clay material can allow for the creation of non-massive structures with less height discrepancies during material buildup and drying that enables new structural possibilities.
- vSDs and extrusion control allow the harnessing of the plastic behavior of clay paste for the creation of complex surfaces without volumetric modeling, without much computing capacity and without digital feedback loops.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters | Visual Evaluation | ||||||
|---|---|---|---|---|---|---|---|
| Test No. | Speed (mm/s) | Layer h (mm) | Resolution (mm) | Clean Nozzle Separation | Displacement | Spot Merging | Collapse |
| 1 | 20 | 2 | 2 | false | 0 | 1 | false |
| 2 | 20 | 2 | 4 | false | 1 | 1 | false |
| 3 | 20 | 2 | 7.5 | true | 0.5 | 0.5 | false |
| 4 | 20 | 2 | 10 | true | 0.25 | 0.25 | false |
| 5 | 20 | 4 | 4 | false | 0.75 | 1 | false |
| 6 | 20 | 6 | 2 | false | 0 | 1 | true |
| 7 | 20 | 4 | 7.5 | true | 1 | 0.5 | false |
References
- Torta, S.; Torta, J. (Eds.) An Overview of 3D Printing. In 3D Printing; De Gruyter: Berlin, Germany, 2019; pp. 1–220. ISBN 9781683922452. [Google Scholar]
- Kuipers, T.; Doubrovski, E.L.; Wu, J.; Wang, C.C. A Framework for Adaptive Width Control of Dense Contour-Parallel Toolpaths in Fused Deposition Modeling. Comput.-Aided Des. 2020, 128, 102907. [Google Scholar] [CrossRef]
- Forman, J.; Dogan, M.D.; Forsythe, H.; Ishii, H. DefeXtiles. In Proceedings of the UIST ‘20: The 33rd Annual ACM Symposium on User Interface Software and Technology, Virtual Event, 20–23 October 2020; Iqbal, S., Ed.; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1222–1233. ISBN 9781450375146. [Google Scholar]
- Klug, C. Data Transmission and Complex Mechanisms of Action. In Hybride Denkwerkzeuge—Hybrid Tools for Thought; Groninger, H., Hensel, S., Klug, C., Eds.; RWTH Aachen University: Aachen, Germany, 2023; pp. 175–179. [Google Scholar]
- Mohite, A.; Kotnik, T. Speed of Deposition: Vehicle for structural and aesthetic expression in CAM. In Proceedings of the International Conference on Education and Research in Computer Aided Architectural Design in Europe: Architecture in the Age of the 4th Industrial Revolution, Porto, Portugal, 11–13 September 2019. [Google Scholar]
- Cerato, A.B.; Lutenegger, A.J. Shrinkage of Clays. In Unsaturated Soils 2006, Proceedings of the Fourth International Conference on Unsaturated Soils, Carefree, AZ, USA, 2–6 April 2006; Miller, G.A., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2010; ISBN 9781628705881. [Google Scholar]
- Gürsoy, B. From Control to Uncertainty in 3D Printing with Clay. In Computing for a Better Tomorrow, Proceedings of the 36th International Conference on Education and Research in Computer Aided Architectural Design in Europe (eCAADe 2018), Łódź, Poland, 19–21 September 2018, 1st ed.; Faculty if Civil Engineering, Architecture and Environmental Engineering, Lodz University of Technology: Łódź, Poland, 2018; ISBN 9789491207167. [Google Scholar]
- de Rycke, K.; Gengnagel, C.; Baverel, O.; Burry, J.; Mueller, C.; Nguyen, M.M.; Rahm, P.; Thomsen, M.R. (Eds.) Humanizing Digital Reality: Design Modelling Symposium Paris 2017, 1st ed.; Springer: Singapore, 2018; ISBN 9789811066115. [Google Scholar]
- Clarke-Hicks, J.; Ochoa, I.; Correa, D. Harnessing plastic deformation in porous 3D printed ceramic light screens. Archit. Struct. Constr. 2023, 3, 193–204. [Google Scholar] [CrossRef]
- Rosenwasser, D.; Mantell, S.; Sabin, J. Clay Non-Wovens: Robotic Fabrication and Digital Ceramics. In Disciplines & Disruption, Proceedings of the 37th Annual Conference of the Association for Computer Aided Design in Architecture, Cambridge, MA, USA, 2–4 November 2017; ACADIA Publishing, Co.: Lafayette, LA, USA, 2017. [Google Scholar]
- Farahbakhsh, M.; Rybkowski, Z.K.; Zakira, U.; Kalantar, N.; Onifade, I. Impact of robotic 3D printing process parameters on interlayer bond strength. Autom. Constr. 2022, 142, 104478. [Google Scholar] [CrossRef]
- Elsayed, H.; Rebesan, P.; Giacomello, G.; Pasetto, M.; Gardin, C.; Ferroni, L.; Zavan, B.; Biasetto, L. Direct ink writing of porous titanium (Ti6Al4V) lattice structures. Mater. Sci. Eng. C Mater. Biol. Appl. 2019, 103, 109794. [Google Scholar] [CrossRef] [PubMed]
- Coffigniez, M.; Gremillard, L.; Balvay, S.; Lachambre, J.; Adrien, J.; Boulnat, X. Direct-ink writing of strong and biocompatible titanium scaffolds with bimodal interconnected porosity. Addit. Manuf. 2021, 39, 101859. [Google Scholar] [CrossRef]
- AlOthman, S.; Im Hyeonji, C.; Jung, F.; Bechthold, M. Spatial Print Trajectory: Controlling Material Behavior with Print Speed, Feed Rate, and Complex Print Path. In Robotic Fabrication in Architecture, Art and Design 2018; Willmann, J., Ed.; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Claire Im, H.; AlOthman, S.; García del Castillo, J.L. Responsive Spatial Print. Clay 3D printing of spatial lattices using real-time model recalibration. In ACADIA 2018: Re/Calibration: On Imprecision and Infidelity, Proceedings of the 38th Annual Conference of the Association for Computer Aided Design in Architecture (ACADIA), Mexico City, Mexico, 18–20 October 2018; Anzalone, P., Del Signore, M., Wit, A.J., Eds.; ACADIA Publishing: Lafayette, LA, USA, 2018; pp. 286–293. [Google Scholar]
- Feucht, T.; Lange, J.; Erven, M.; Costanzi, C.B.; Knaack, U.; Waldschmitt, B. Additive manufacturing by means of parametric robot programming. Constr. Robot. 2020, 4, 31–48. [Google Scholar] [CrossRef]
- Laghi, V.; Palermo, M.; Gasparini, G.; Trombetti, T. Manufacturing the first stainless steel djagrid column. In Print Architecture! Tessmann, O., Knaack, U., Borg Costanzi, C., Rosendahl, P., Wibranek, B., Eds.; AADR (Spurbuchverlag): Baunach, Germany, 2022; pp. 72–75. ISBN 978-3-88778-619-9. [Google Scholar]
- Dörfler, K.; Willmann, J.; Piskorec, L.; Ernst, S.; Helm, V.; Gramazio, F.; Kohler, M. Remote Material Deposition. In What’s the Matter?, Proceedings of the Materiality and Materialism at the Age of Computation, International Conference, Barcelona, Spain, 4–6 September 2014; Voyatzaki, M., Ed.; European Network of Heads of Schools of Architecture: Thessaloniki, Greece, 2014; pp. 361–377. [Google Scholar]
- Jenny, D.; Mayer, H.; Aejmelaeus-Lindström, P.; Gramazio, F.; Kohler, M. A Pedagogy of Digital Materiality: Integrated Design and Robotic Fabrication Projects of the Master of Advanced Studies in Architecture and Digital Fabrication. Archit. Struct. Constr. 2022, 2, 649–660. [Google Scholar] [CrossRef]
- Ming, C.; Mirjan, A.; Medina Ibáñez, J.; Gramazio, F.; Kohler, M. Impact Printing. 3D Print. Addit. Manuf. 2022, 9, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Bechthold, M.; Kane, A.; King, N. (Eds.) Ceramic Material Systems: In Architecture and Interior Design; Birkhäuser: Basel, Switzerland; Berlin, Germany; Boston, MA, USA, 2015; ISBN 9783038210245. [Google Scholar]
- Sibelco Deutschland GmbH. AteliermasseWeiß2505: Technical Data. Available online: https://www.eurokeramiki.gr/images/uploads/file/AteliermasseWeiß2505.pdf (accessed on 27 July 2023).
- Moretti, F. WASP Launches the New Professional Clay Extruder. WASP. 22 May 2016. Available online: https://www.3dwasp.com/en/wasp-launches-the-new-professional-clay-extruder/ (accessed on 25 September 2023).
- Cuevas, D.G.; Pugliese, G. Advanced 3D Printing with Grasshopper®: Clay and FDM.; Independently Published; Amazon Distribution GmbH: Leipzig, Germany, 2020; ISBN 9798635379011. [Google Scholar]
- Fraguada, L.E.; Jokic, S.; Laarman, J.; Markopoulou, A.; Novikov, P. Anti-Gravity Additive Manufacturing. In Fabricate: Negotiating Design & Making, 2nd ed.; Gramazio, F., Kohler, M., Langenburg, S., Eds.; UCL Press: London, UK, 2014; pp. 192–197. ISBN 9781787352148. [Google Scholar]
- Lewis, J.A.; Gratson, G.M. Direct writing in three dimensions. Mater. Today 2004, 7, 32–39. [Google Scholar] [CrossRef]
- Lawson, S.; Li, X.; Thakkar, H.; Rownaghi, A.A.; Rezaei, F. Recent Advances in 3D Printing of Structured Materials for Adsorption and Catalysis Applications. Chem. Rev. 2021, 121, 6246–6291. [Google Scholar] [CrossRef] [PubMed]
- de Witte, D. Evolution. In Clay Printing: The Fourth Generation Brickwork; de Witte, D., Ed.; Springer Vieweg: Wiesbaden, Germany, 2022; pp. 199–204. ISBN 978-3-658-37160-9. [Google Scholar]
- Klug, C.; Schmitz, T.H. Examining the Interactions of Design Parameters in the LDM of Clay as the Basis for New Design Paradigms. Ceramics 2022, 5, 131–147. [Google Scholar] [CrossRef]
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1990; ISBN 978-0-387-94676-4. [Google Scholar]













| Chemical Analysis | SiO2 | TiO2 | Al2O3 | Fe2O3 | CaO | MgO | K2O | Na2O |
| 75.0% | 1.4% | 19.5% | 0.80% | 0.20% | 0.30% | 2.30% | 0.20% | |
| Moisture | 16.8wt.% | |||||||
| Cylinder | hL * | DVSD * | α° * | lAP * | Print Time |
|---|---|---|---|---|---|
| a | 20 mm | 15 mm | 35° | 0.0 mm | 63 min |
| b | 20 mm | 15 mm | 35° | 0.0 mm | 68 min |
| c | 17.4 mm | 15 mm | 35° | 20.0 mm | 60 min |
| hvSD | Segment (s) | Decreasing f * | Speed | hL | DVSD | lbend | α° | β1 | β2 | lAP | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Upper limit | 60 mm | 2 mm | 20 to 1 | 2000 mm/sec | 20 mm | 52.5 mm | 80.0 mm | 45° | 19.5° | 14.9° | 60.0 mm |
| Lower limit | 12.5 mm | 30.0 mm | 60.0 mm | 89° | 4.9° | 4.6° | 0.0 mm | ||||
| Mean | 17.4 mm | 39.4 mm | 73.7 mm | 57.3° | 11.2° | 8.2° | 19.3 mm |
| hL | DVSD | lbend | α° | β1 | β2 | lAP |
|---|---|---|---|---|---|---|
| 12.5 mm | 45 mm | 80 mm | 45° | 8° | 8° | 60 mm |
| Structure | Area of the Vertical Face (cm2) | Achieved Height (mm) | Porosity Normal to the Surface of Vertical Face | Height Deviation from Dig. Model (mm) | Pore Width × Height (mm) |
|---|---|---|---|---|---|
| Spatial Print Trajectory [12] | 330 | 220 | 25% | 60 | 15 × 30 |
| two-shelled lattice with horizontal overlap | 360 | 240 | 35% | 2.5 | 25 × 30 |
| two-shelled lattice with vertical overlap | 300 | 200 | 34% | 10 | 25 × 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabakova, V.; Klug, C.; Schmitz, T.H. Dynamic Extrusion Control in Spot Deposition Modeling for Porous 3D Clay Structures. Ceramics 2023, 6, 2018-2035. https://doi.org/10.3390/ceramics6040124
Tabakova V, Klug C, Schmitz TH. Dynamic Extrusion Control in Spot Deposition Modeling for Porous 3D Clay Structures. Ceramics. 2023; 6(4):2018-2035. https://doi.org/10.3390/ceramics6040124
Chicago/Turabian StyleTabakova, Vesela, Christina Klug, and Thomas H. Schmitz. 2023. "Dynamic Extrusion Control in Spot Deposition Modeling for Porous 3D Clay Structures" Ceramics 6, no. 4: 2018-2035. https://doi.org/10.3390/ceramics6040124
APA StyleTabakova, V., Klug, C., & Schmitz, T. H. (2023). Dynamic Extrusion Control in Spot Deposition Modeling for Porous 3D Clay Structures. Ceramics, 6(4), 2018-2035. https://doi.org/10.3390/ceramics6040124






