Computational Investigation of the Influencing Parameters on the Solidification of Thermoplastic Beryllium Oxide Slurry in a Cylindrical Shell
Abstract
:1. Introduction
2. Materials
2.1. Characteristics of Beryllium Oxide Powder and Thermoplastic Slurry
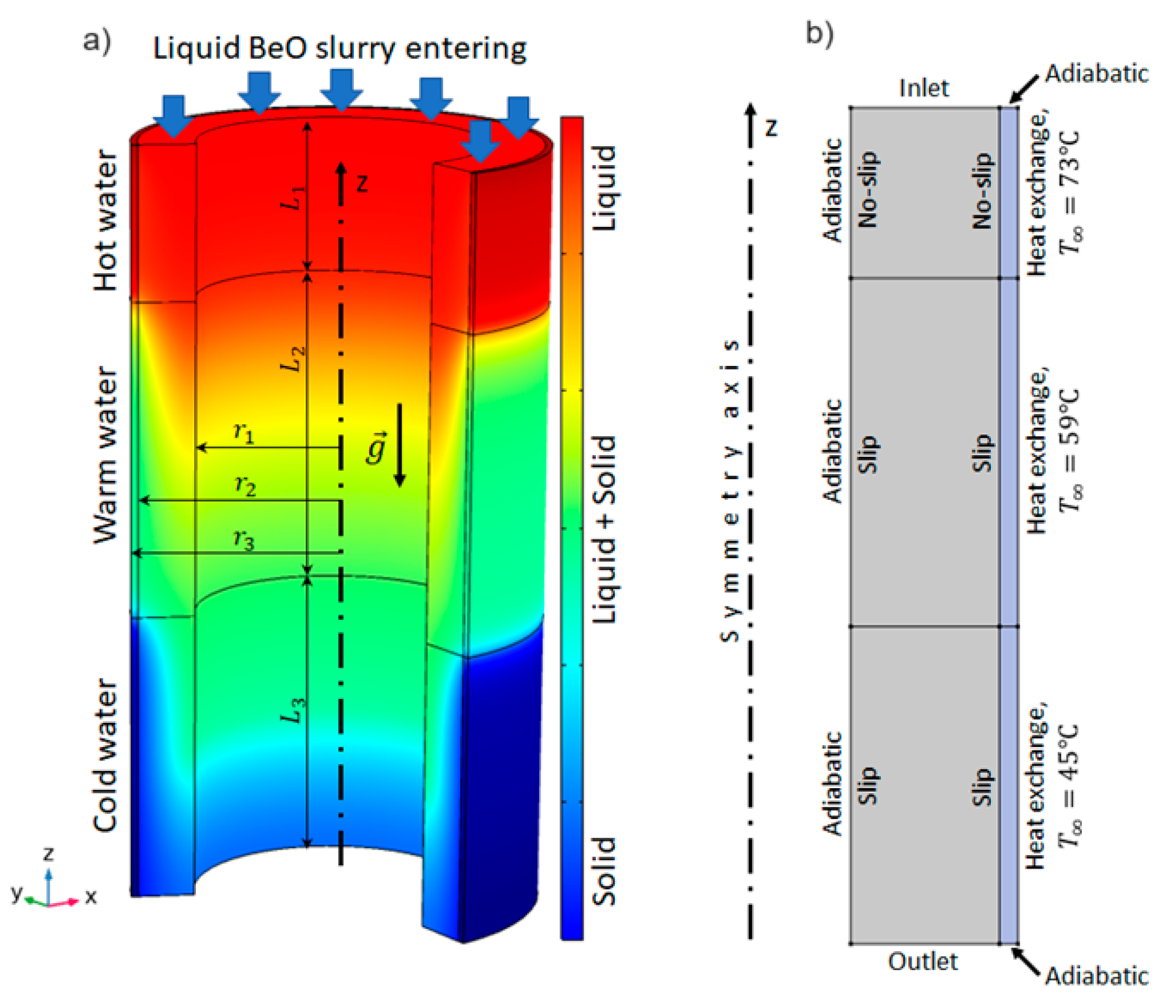
2.2. Experimental Studies of the Casting Process
3. Mathematical Model
- Laminar due to the low casting velocity;
- Steady state;
- Weakly compressible;
- Axisymmetric.
3.1. Fluid Flow Equations
3.2. Energy Equation for BeO Slurry
3.3. Energy Equation for the Crystallizer
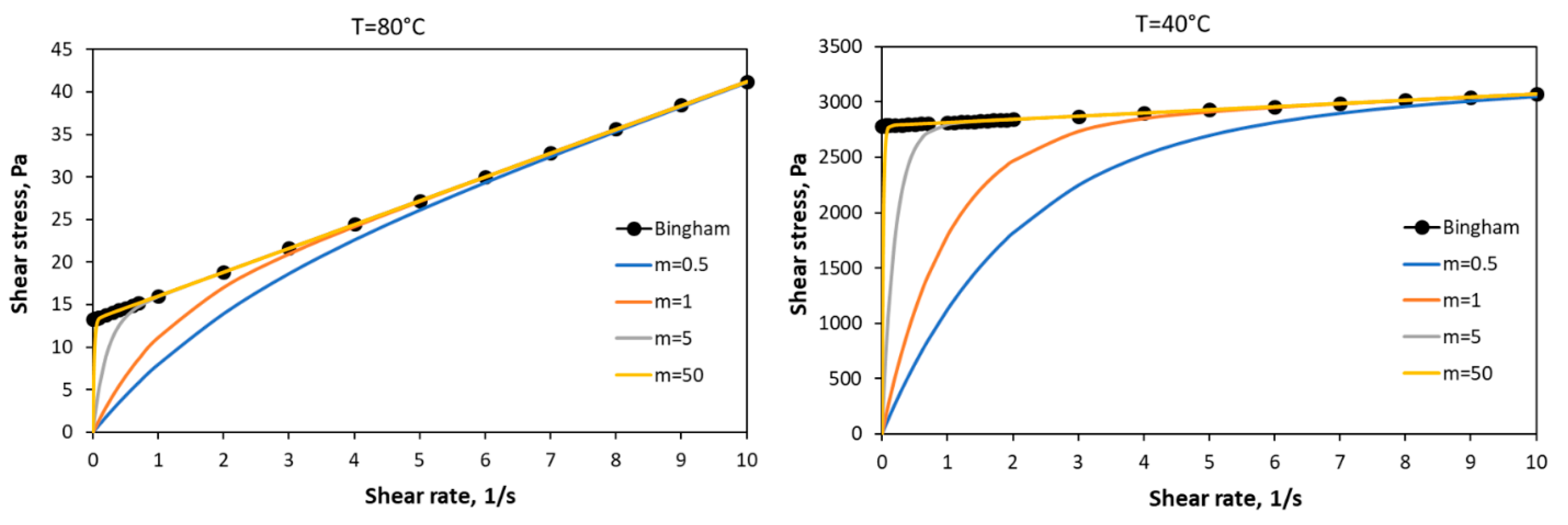
3.4. Bingham–Papanastasiou Model
3.5. Boundary Conditions
4. Numerical Simulation Procedure and Model Validation
4.1. Rheology Model Validation
4.2. CFD Model Validation
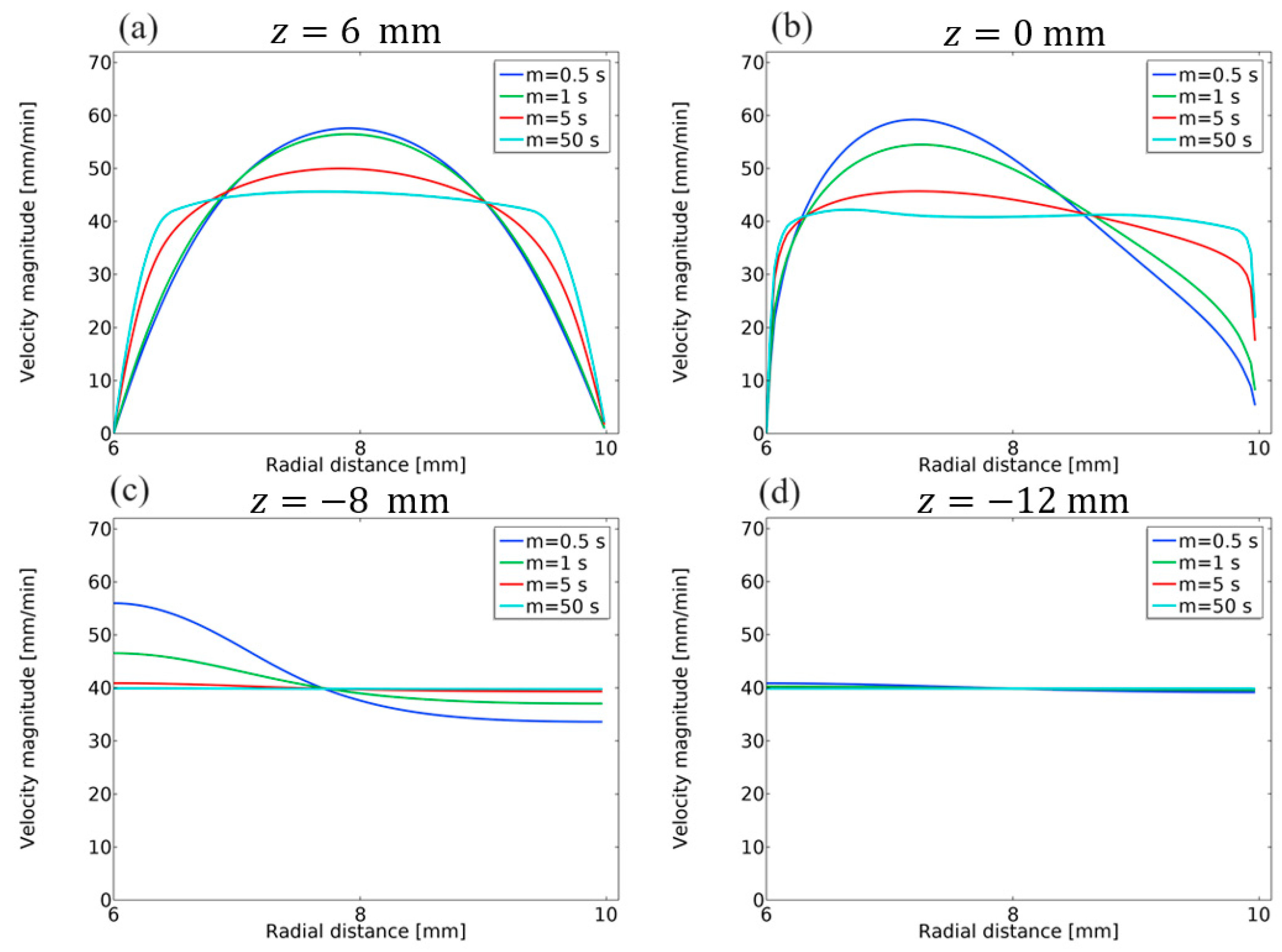
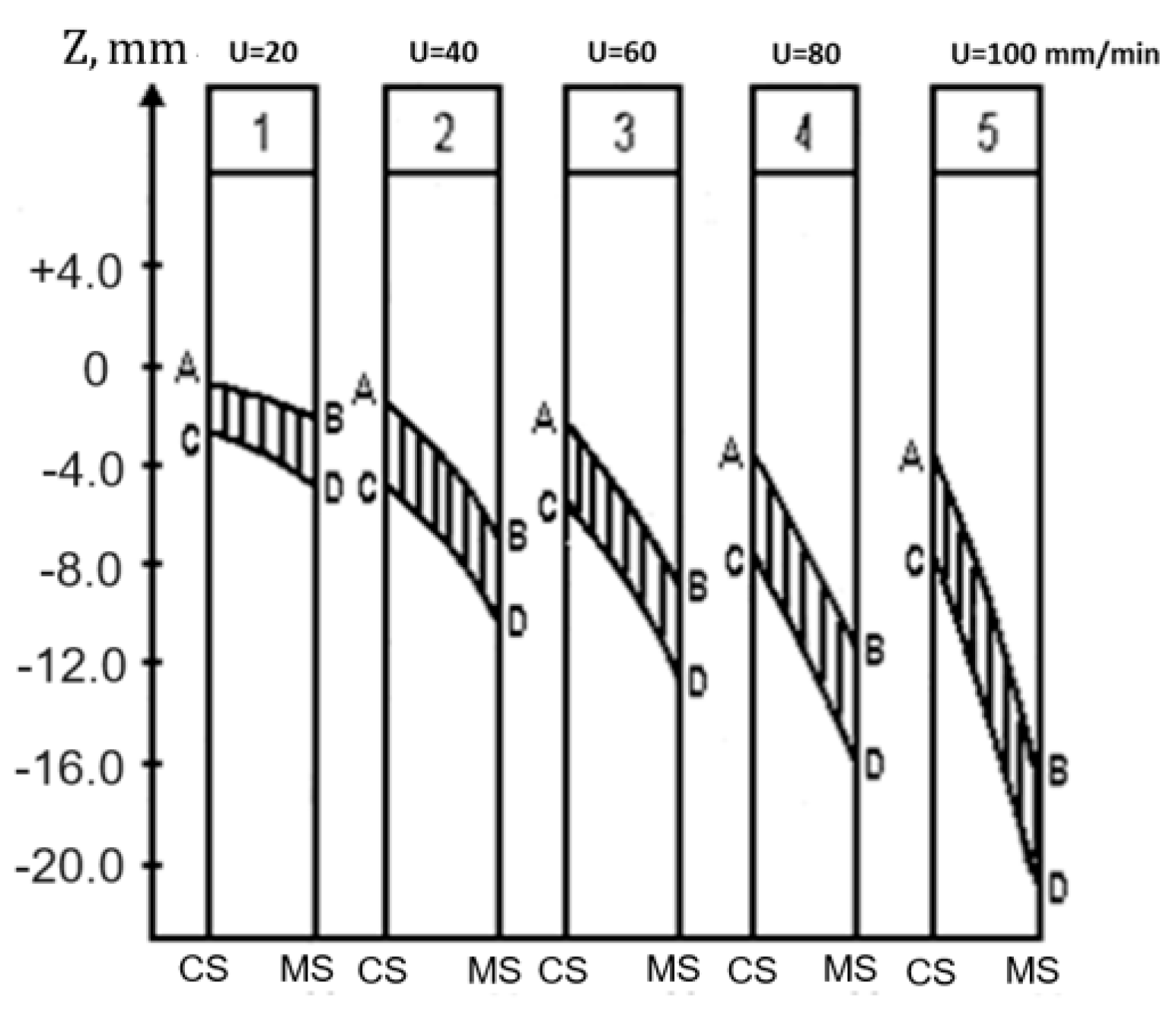
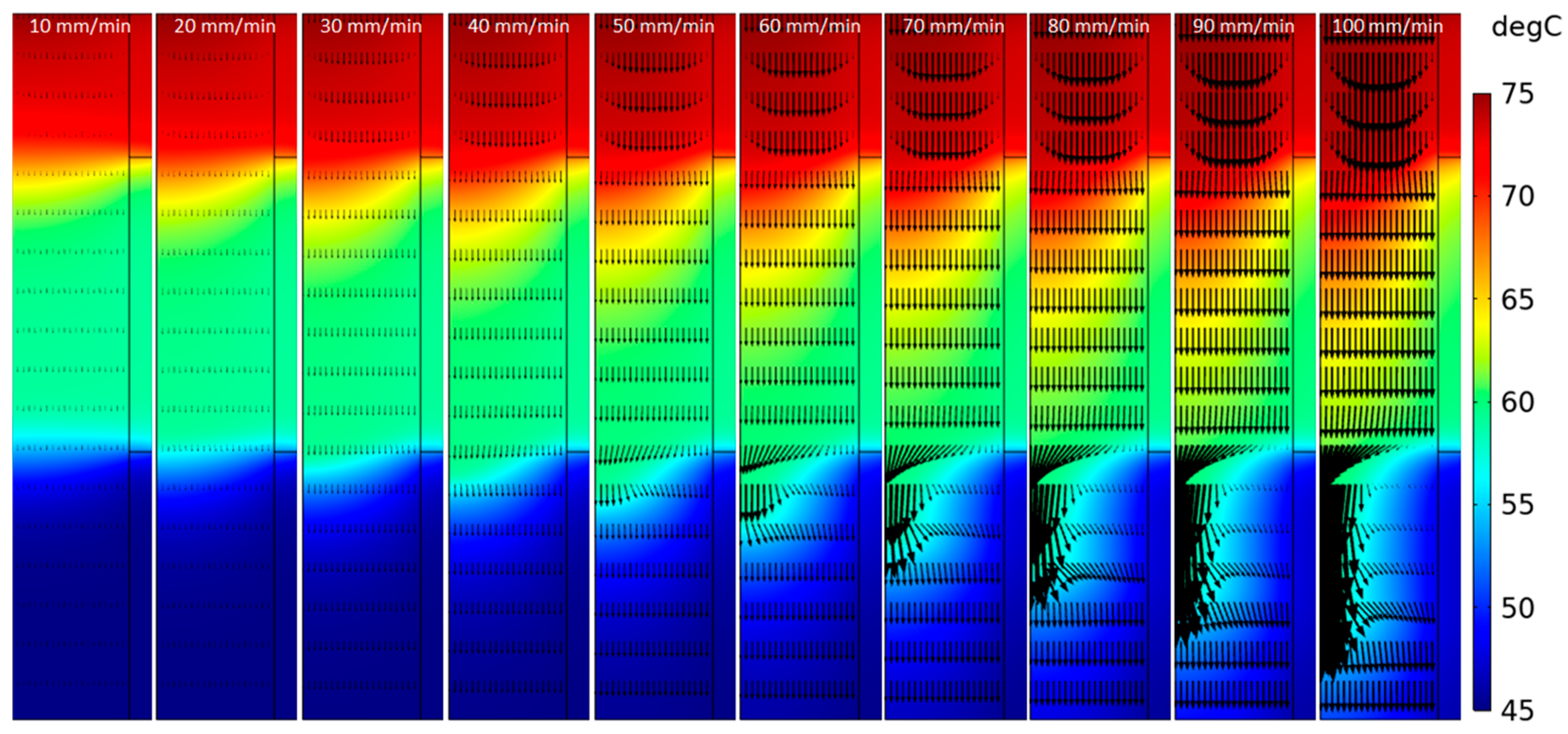
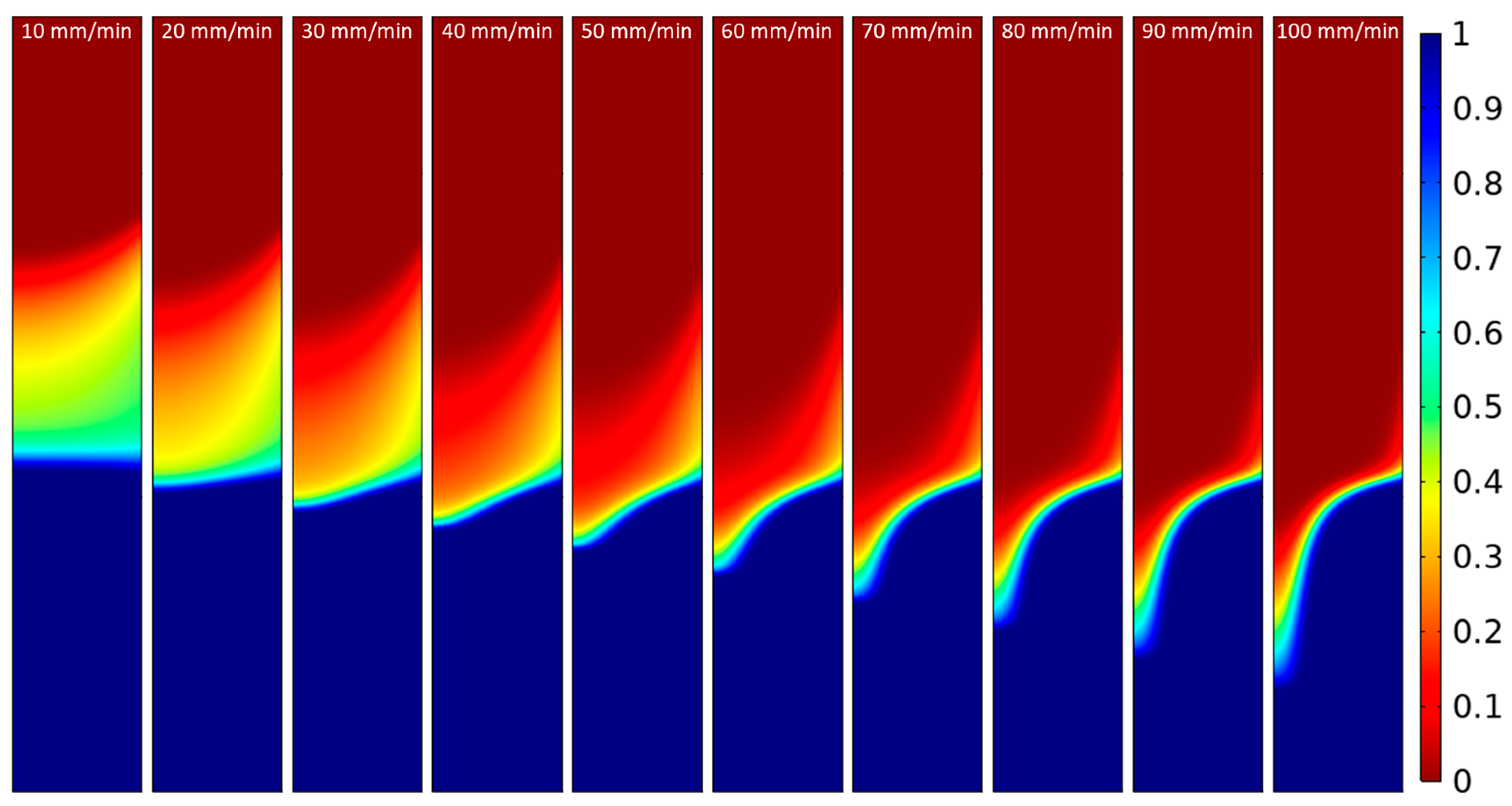
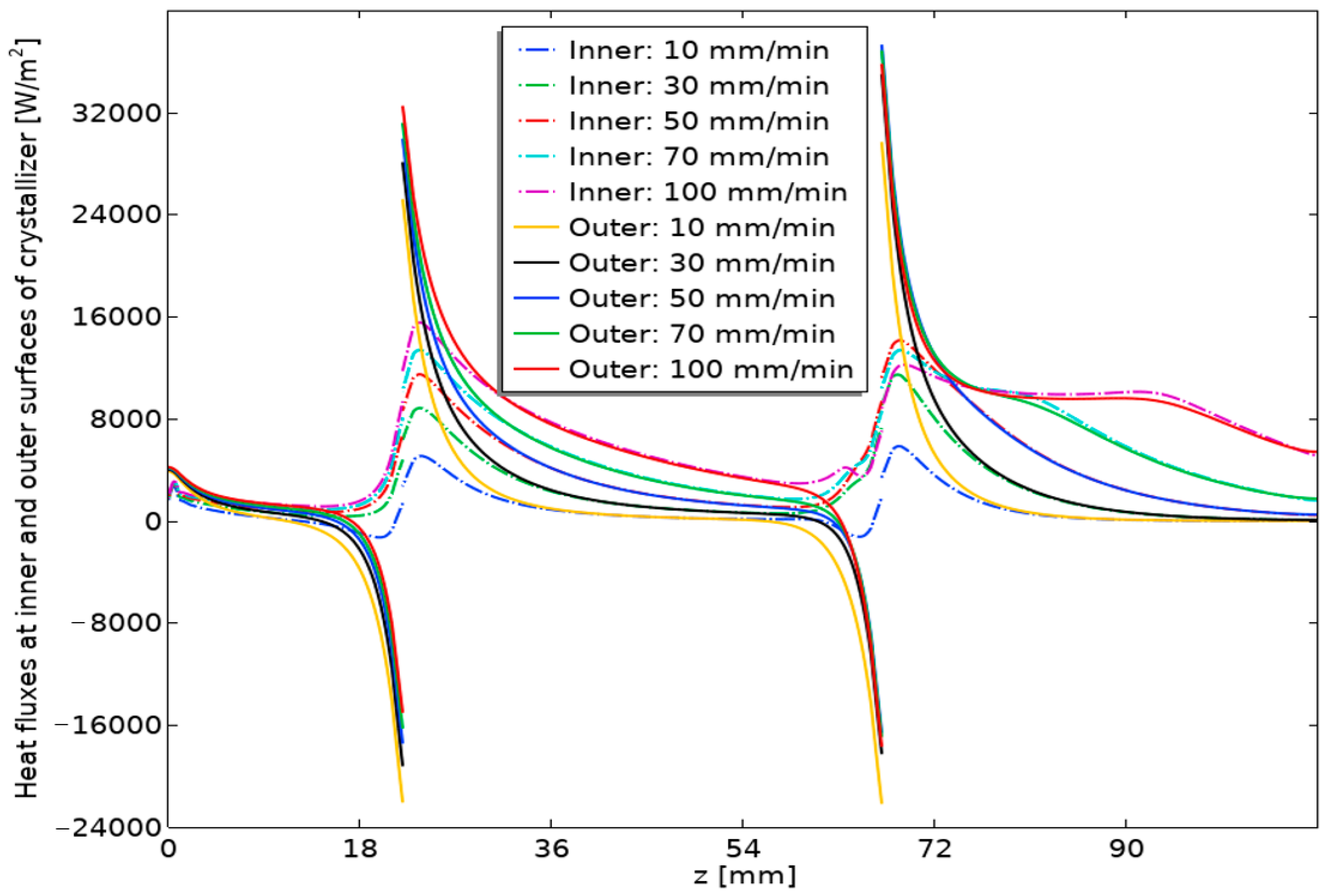
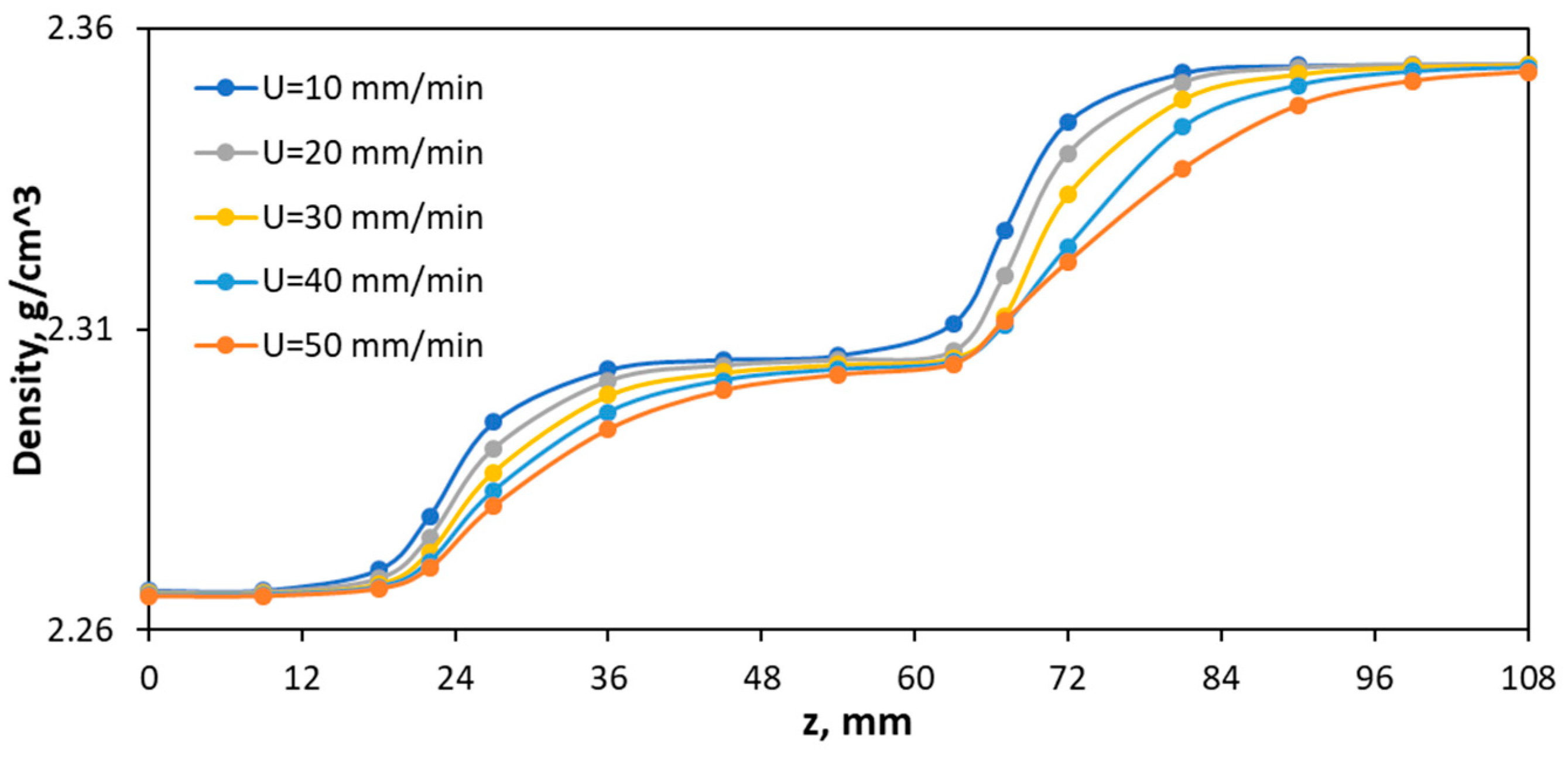
5. Discussion of Calculated Data
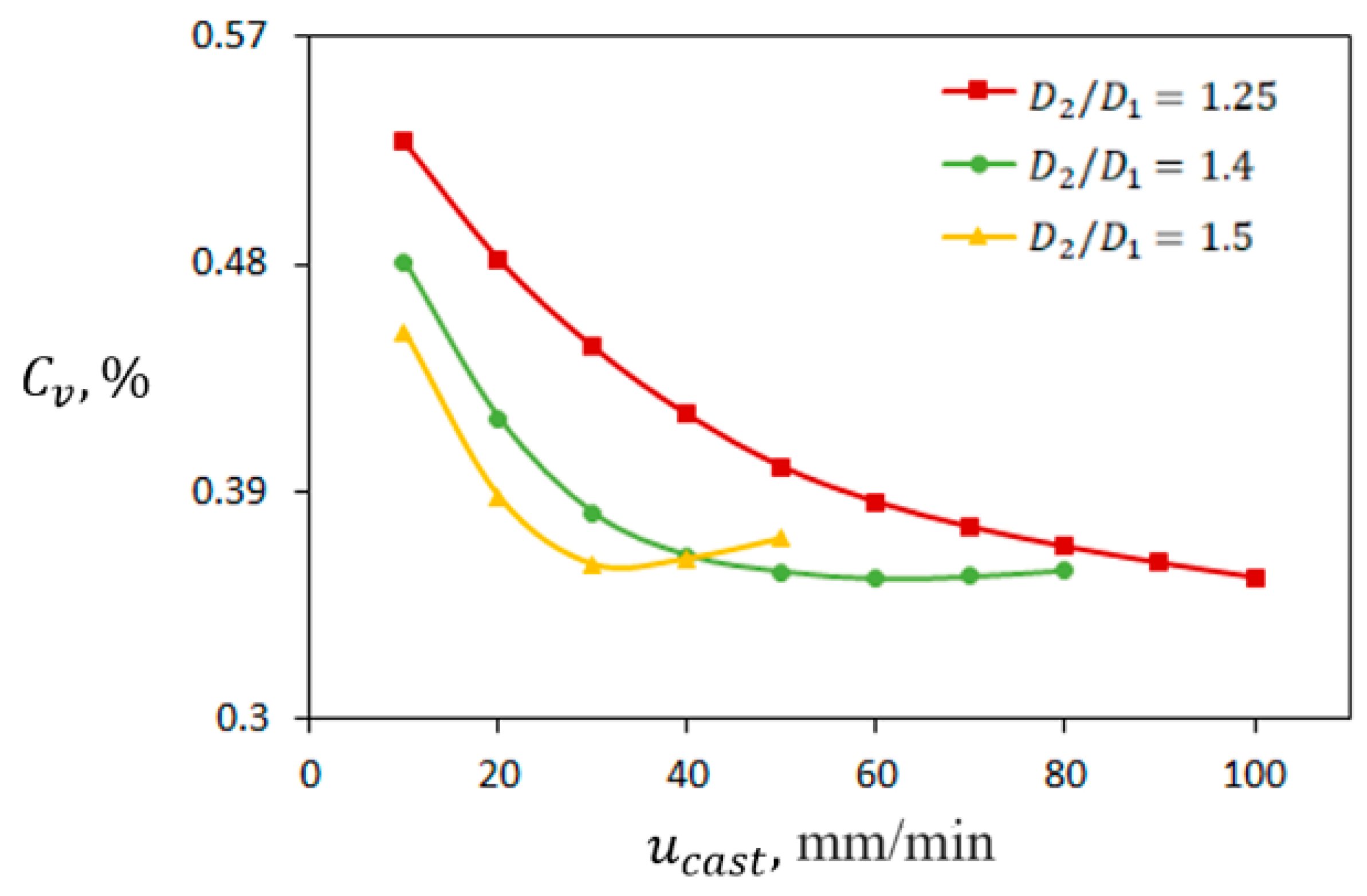
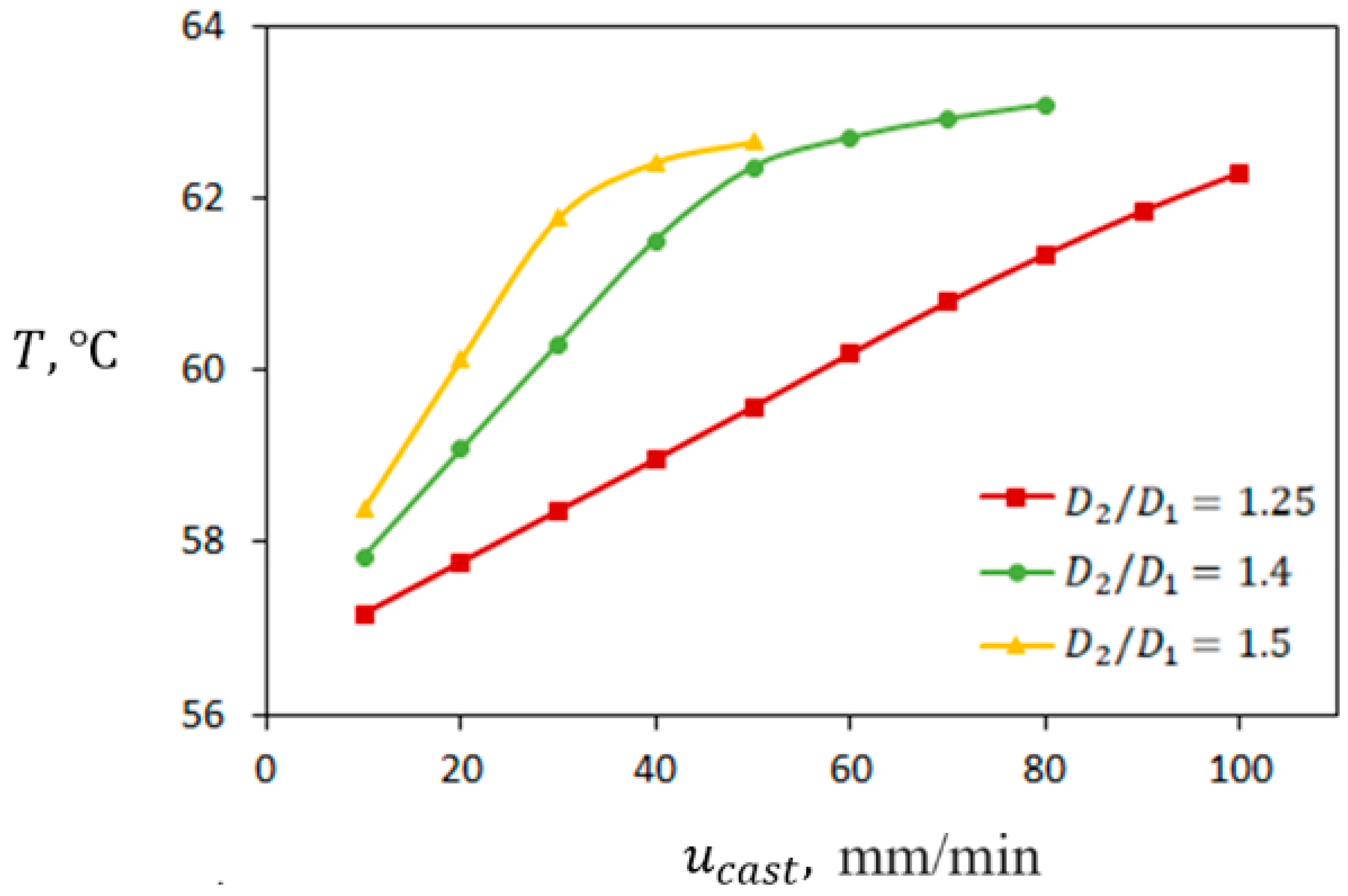
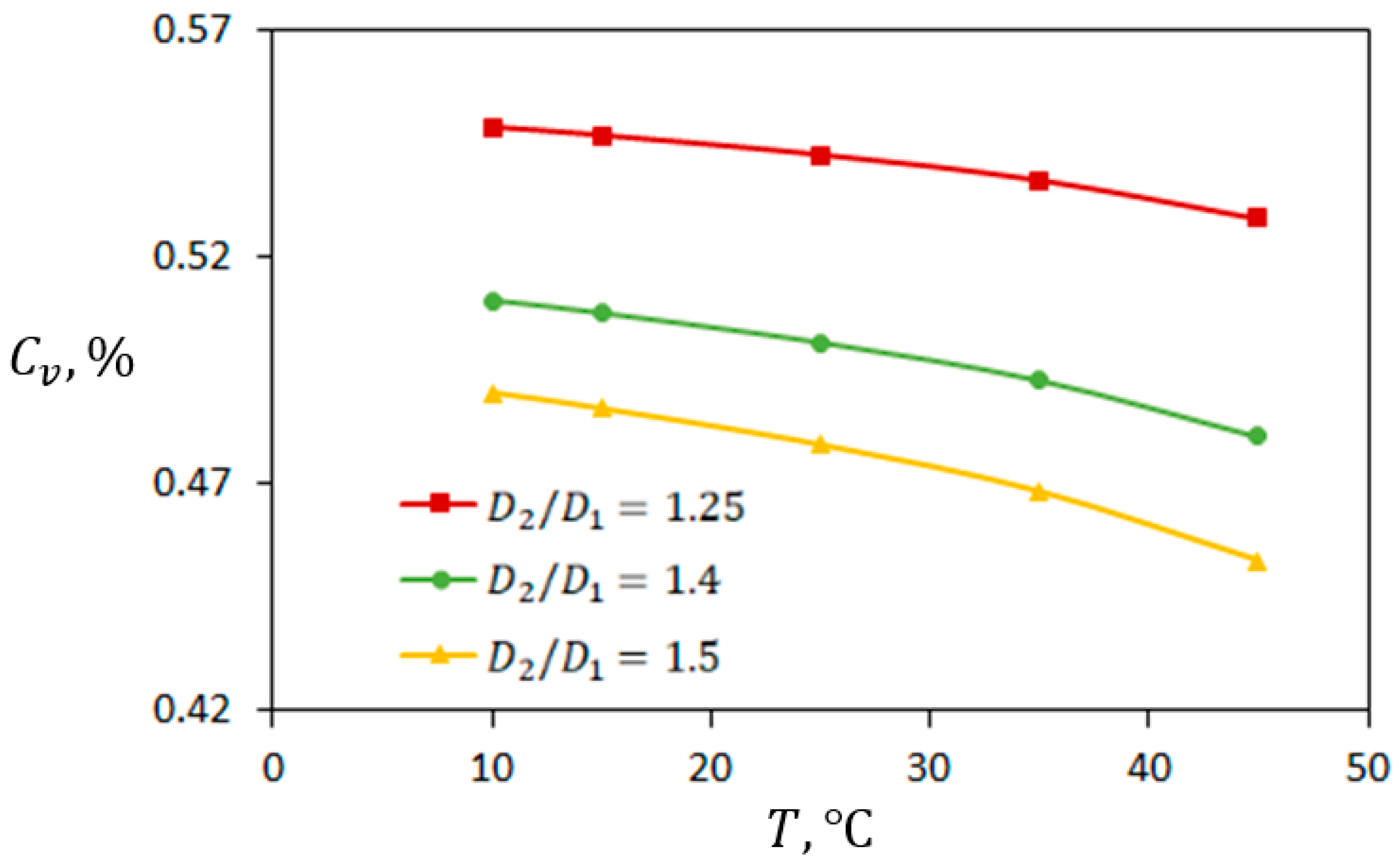
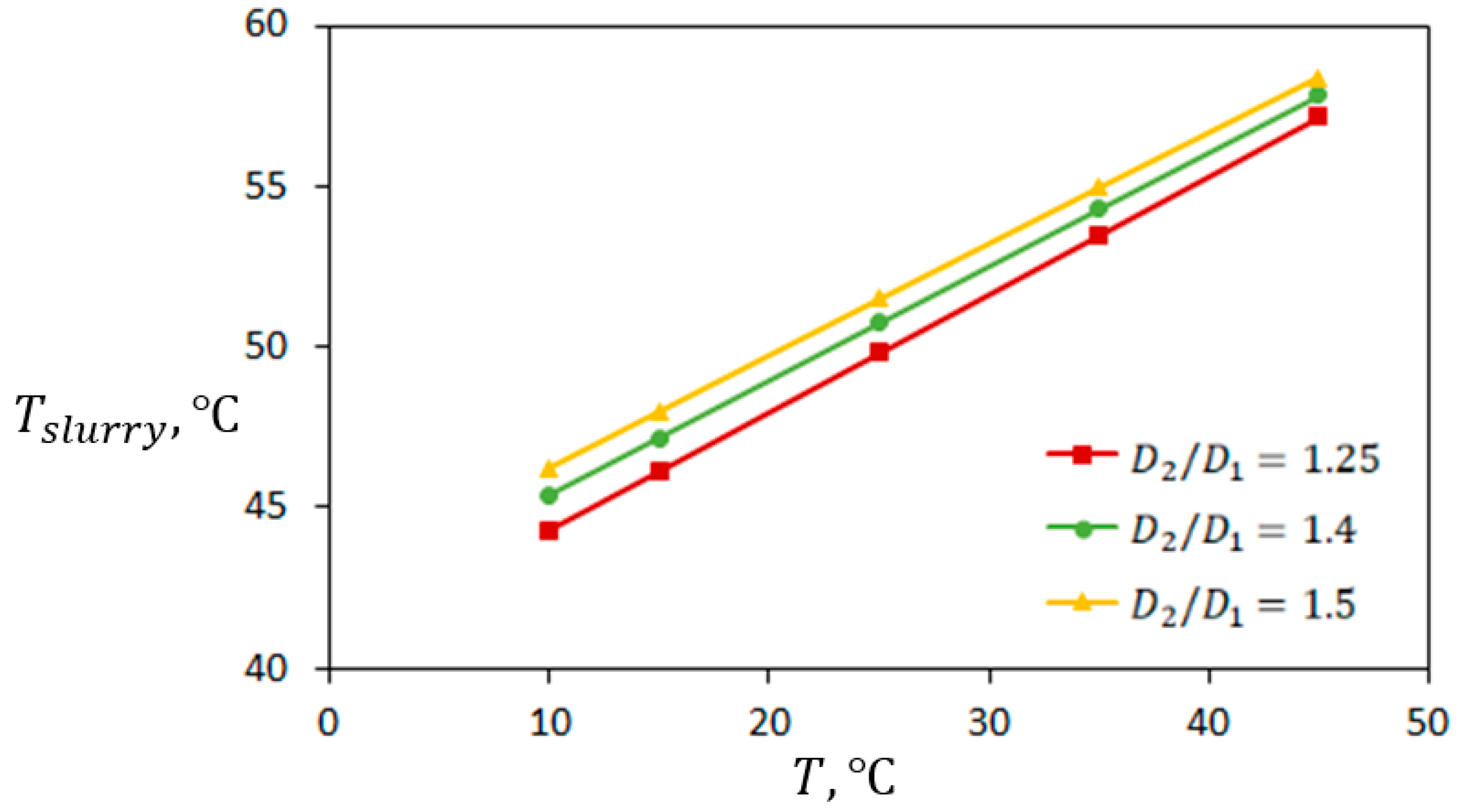
5.1. The Effect of Casting Velocity
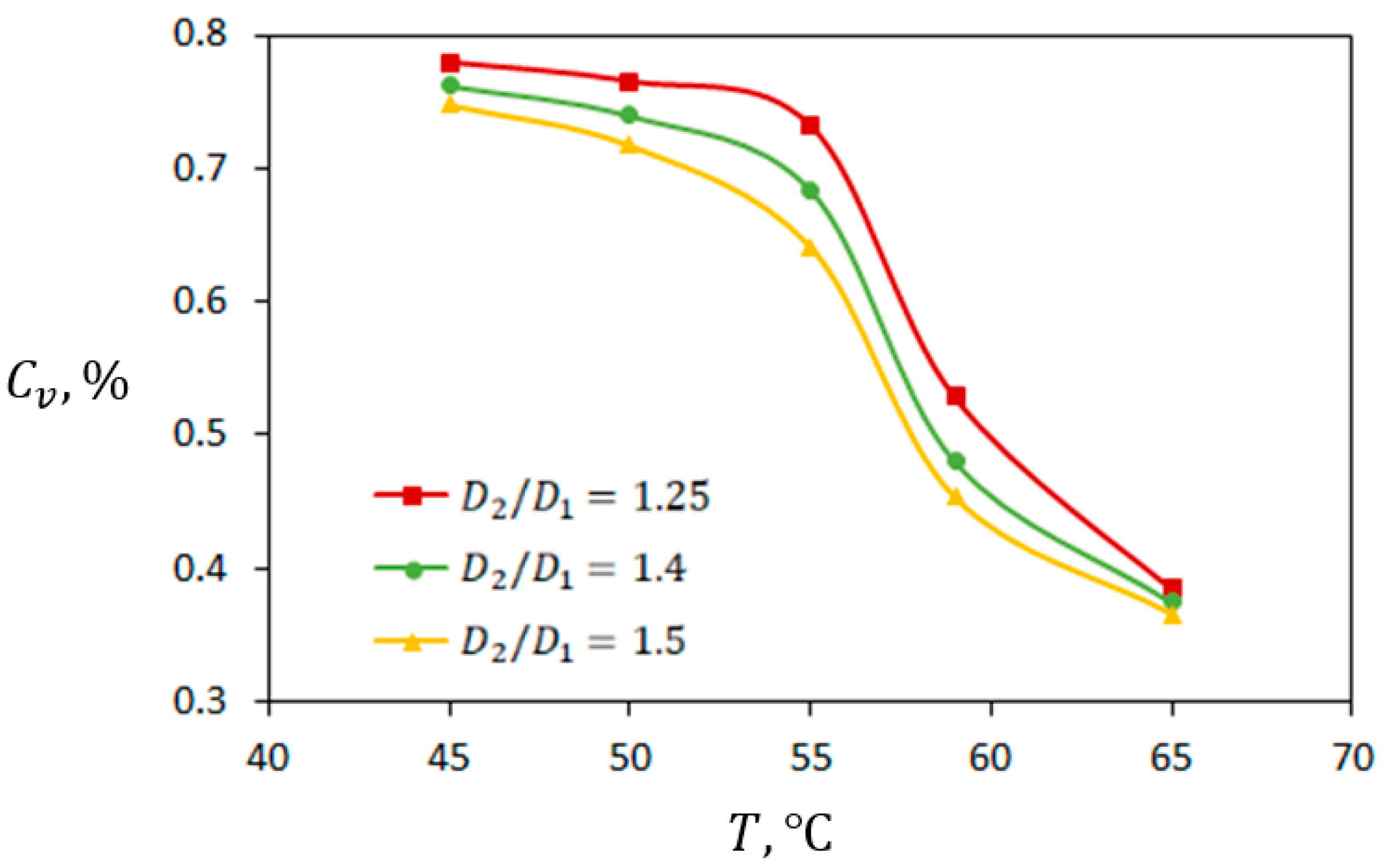
5.2. The Effect of Temperature of Warm Water
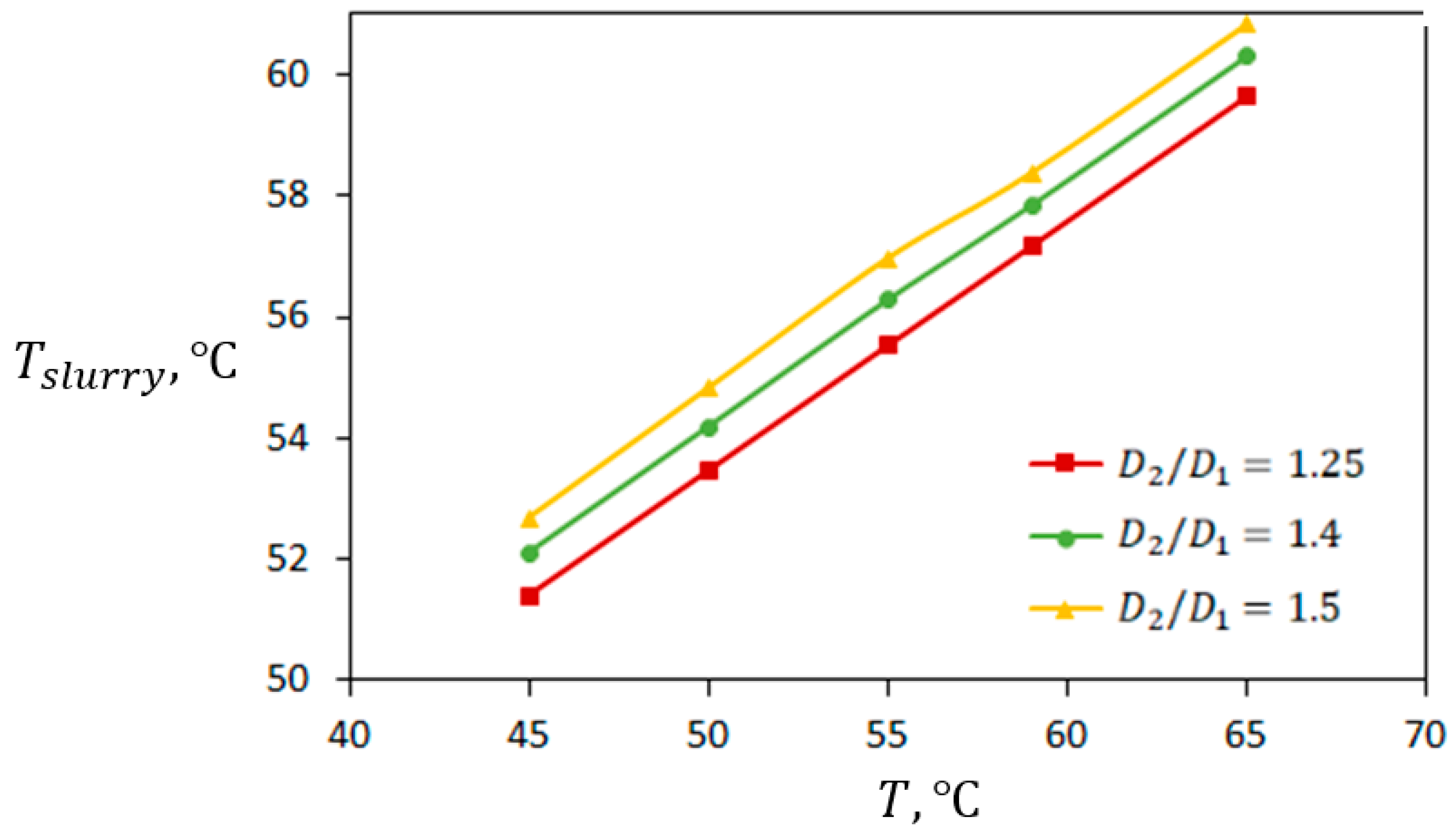
5.3. The Effect of Temperature of Cold Water
6. Conclusions
- -
- Experimentally determined intervals of phase transitions at different casting speeds of beryllium ceramics are compared with phase transitions obtained using the Bingham–Papanastasiou model.
- -
- Parametric studies have been carried out on the changes in the hardening degree and the temperature of a suspension in three hot, warm, and cold circuits, depending on casting speed and cylinder dimensions.
- -
- Casting velocities up to 30 mm/min will be optimal since further increasing their values does not change the average temperature of the BeO slurry.
- -
- Maintaining the temperature of the warm water zone up to is an optimal condition because its further increase leads to sharp decrease in the solid fraction after cooling.
- -
- The solid fraction of BeO slurry is less sensitive to the temperature of cold water.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, J.; Zhou, W.; Zhou, W.; Li, S.; Shen, P.; Ren, S.; Hu, A. Modified Embedded Atom Method Potential for Modeling the Thermodynamic Properties of High Thermal Conductivity Beryllium Oxide. ACS Omega 2019, 4, 6339–6346. [Google Scholar] [CrossRef] [PubMed]
- Walsh, K.A. Beryllium Chemistry and Processing; ASM International: Materials Park, OH, USA, 2009. [Google Scholar] [CrossRef]
- Kiiko, V.S.; Vaispapir, V.Y. Thermal Conductivity and Prospects for Application of BeO Ceramic in Electronics. Glass Ceram. 2015, 71, 387–391. [Google Scholar] [CrossRef]
- Sardarian, M.; Mirzaee, O.; Habibolahzadeh, A. Mold filling simulation of low pressure injection molding (LPIM) of alumina: Effect of temperature and pressure. Ceram. Int. 2017, 43, 28–34. [Google Scholar] [CrossRef]
- Zhapbasbayev, U.; Ramazanova, G.; Kenzhaliev, B.; Sattinova, Z.; Shakhov, S. Experimental and calculated data of the beryllium oxide slurry solidification. Appl. Therm. Eng. 2016, 96, 593–599. [Google Scholar] [CrossRef]
- Sattinova, Z.K.; Bekenov, T.N.; Assilbekov, B.K.; Ramazanova, G.I.; Zhapbasbayev, U.K.; Nussupbek, Z.T. Mathematical modeling of the rheological behavior of thermoplastic slurry in the molding process of beryllium ceramics. Ceram. Int. 2022, 48, 31102–31110. [Google Scholar] [CrossRef]
- Agranat, B.A.; Gudovich, A.P. Ultrasound Powder Metallurgy; Metallurgy: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Shakhov, S.A.; Bitsoev, G.D. Application of Ultrasound in the Manufacture of High Thermal Conductivity Ceramic Articles; Ust’-Kamenogorsk, Kazakhstan, 1999. (In Russian) [Google Scholar]
- Miyamoto, K.; Miyamoto, H.; Takahashi, Y.; Taguchi, H. Preparation of Al2O3 ceramics by low pressure injection molding method. Bull. Inst. Chem. Res. 1986, 64, 287–291. [Google Scholar]
- Dobrovolsky, A.G. Slip Casting; Metallurgy: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Weiß, M.; Maurath, J.; Willenbacher, N.; Koos, E. Shrinkage and dimensional accuracy of porous ceramics derived from capillary suspensions. J. Eur. Ceram. Soc. 2019, 39, 1887–1892. [Google Scholar] [CrossRef]
- Shakhov, S.A.; Gagarin, A.E. Rheological characteristics of thermoplastic disperse systems treated with ultrasound. Glass Ceram. 2008, 65, 122–124. [Google Scholar] [CrossRef]
- Ruan, Z.-H.; Gao, X.-Y.; Yuan, Y.; Tan, H.-P. Determining the heat transfer coefficient during the continuous casting process using stochastic particle swarm optimization. Case Stud. Therm. Eng. 2021, 28, 101439. [Google Scholar] [CrossRef]
- Papanastasiou, T.C.; Boudouvis, A.G. Flows of viscoplastic materials: Models and computations. Comput. Struct. 1997, 64, 677–694. [Google Scholar] [CrossRef]
- Jabbari, M.; Bulatova, R.; Tok, A.I.Y.; Bahl, C.R.H.; Mitsoulis, E.; Hattel, J.H. Ceramic tape casting: A review of current methods and trends with emphasis on rheological behaviour and flow analysis. Mater. Sci. Eng. B 2016, 212, 39–61. [Google Scholar] [CrossRef]
- Mehmood, A.; Khan, W.A.; Mahmood, R.; Rehman, K.U. Finite Element Analysis on Bingham–Papanastasiou Viscoplastic Flow in a Channel with Circular/Square Obstacles: A Comparative Benchmarking. Processes 2020, 8, 779. [Google Scholar] [CrossRef]
- Kiiko, V.S.; Vaispapir, V.Y. The fabrication technological abilities and the properties of the ceramic products on base of the mixture of low- and high-fired BeO-powders. Novye Ogneupory (New Refract.) 2016, 8, 55–58. (In Russian) [Google Scholar]
- Balkevich, V.L.; Mosin, Y.M. Rheological Properties of Ceramic Mass; Moscow Institute of Chemical Technology named after, D.I. Mendeleev: Moscow, Russia, 1983. (In Russian) [Google Scholar]
- Ammosova, S.; Cano Cano, L.; Schuschnigg, S.; Kukla, C.; Mönkkönen, K.; Suvanto, M.; Gonzalez-Gutierrez, J. Effect of metal particle size and powder volume fraction on the filling performance of powder injection moulded parts with a microtextured surface. Precis. Eng. 2021, 72, 604–612. [Google Scholar] [CrossRef]
- Dvinskikh, Y.V.; Popil’skii, R.Y.; Kostin, L.I.; Kulagin, V.V. The thermophysical properties of thermoplastic cast slips of some highly refractory oxides. Refractories 1979, 20, 1573–9139. [Google Scholar] [CrossRef]
- Bradshaw, P.; Cebeci, T. Physical and Computational Aspects of Convective Heat Transfer; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar] [CrossRef]
- Voller, V.R.; Cross, M.; Markatos, N.C. An Entalpy Method for Convection/Diffusion Phase Change. Int. J. Numer. Methods Eng. 1987, 24, 271–284. [Google Scholar] [CrossRef]
- Brent, A.D.; Voller, V.R.; Reid, K.J. Enthalpy-porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal. Numer. Heat Transf. 1988, 13, 297–318. [Google Scholar] [CrossRef]
- Viswanath, R.; Jaluria, Y. A comparison of different solution methodologies for melting and solidification problems in enclosures. Numer. Heat Transf. Part B Fundam. 1993, 24, 77–105. [Google Scholar] [CrossRef]
- Vogel, J.; Felbinger, J.; Johnson, M. Natural convection in high temperature flat plate latent heat thermal energy storage systems. Appl. Energy 2016, 184, 184–196. [Google Scholar] [CrossRef]
- Fadl, M.; Eames, P.C. Numerical investigation of the influence of mushy zone parameter Amush on heat transfer characteristics in vertically and horizontally oriented thermal energy storage systems. Appl. Therm. Eng. 2019, 151, 90–99. [Google Scholar] [CrossRef]
- Chakraborty, P.R. Enthalpy porosity model for melting and solidification of pure-substances with large difference in phase specific heats. Int. Commun. Heat Mass Transf. 2017, 81, 183–189. [Google Scholar] [CrossRef]
- Yamamoto, T.S.; Komarov, V. Influence of ultrasound irradiation on transient solidification characteristics in DC casting process: Numerical simulation and experimental verification. J. Mater. Process. Technol. 2021, 294, 117116. [Google Scholar] [CrossRef]
- Mehalaine, K.; Lafri, D. Improving the energy release of a latent heat storage with multiple phase change materials loading and partition shaping. Appl. Therm. Eng. 2023, 230, 120679. [Google Scholar] [CrossRef]
- Rubinetti, D.; Weiss, D.A.; Chaudhuri, A.; Kraniotis, D. Convective Melting Modeling Approach for Phase Change Materials with Variable Boundary Heating. In Proceedings of the 59th Conference on Simulation and Modelling, Oslo Metropolitan University, Oslo, Norway, 26–28 September 2018; Linköping Electronic Conference Proceedings. Volume 153, pp. 103–110. [Google Scholar] [CrossRef]
- Atal, A.; Wang, Y.; Harsha, M.; Sengupta, S. Effect of porosity of conducting matrix on a phase change energy storage device. Int. J. Heat Mass Transf. 2016, 93, 9–16. [Google Scholar] [CrossRef]
- Mohamed Moussa, E.I.; Karkri, M. A numerical investigation of the effects of metal foam characteristics and heating/cooling conditions on the phase change kinetic of phase change materials embedded in metal foam. J. Energy Storage 2019, 26, 100985. [Google Scholar] [CrossRef]
- Soto, H.P.; Martins-Costa, M.L.; Fonseca, C.; Frey, S. A numerical investigation of inertia flows of Bingham-Papanastasiou fluids by an extra stress-pressure-velocity galerkin least-squares method. J. Braz. Soc. Mech. Sci. Eng. 2010, 32, 450–460. [Google Scholar] [CrossRef]
- Lampaert, S.G.E.; van Ostayen, R.A.J. Experimental results on a hydrostatic bearing lubricated with a magnetorheological fluid. Curr. Appl. Phys. 2019, 19, 1441–1448. [Google Scholar] [CrossRef]
- Jeong, J.; Chuta, E.; Ramézani, H.; Guillot, S. Rheological properties for fresh cement paste from colloidal suspension to the three-element Kelvin–Voigt model. Rheol. Acta 2020, 59, 47–61. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Memon, A.A.; Memon, M.A.; Bhatti, K.; Khan, I.; Alshammari, N.; Al-Johani, A.S.; Hamadneh, N.N.; Andualem, M. Thermal decomposition of propylene oxide with different activation energy and Reynolds number in a multicomponent tubular reactor containing a cooling jacket. Sci. Rep. 2022, 12, 4169. [Google Scholar] [CrossRef] [PubMed]
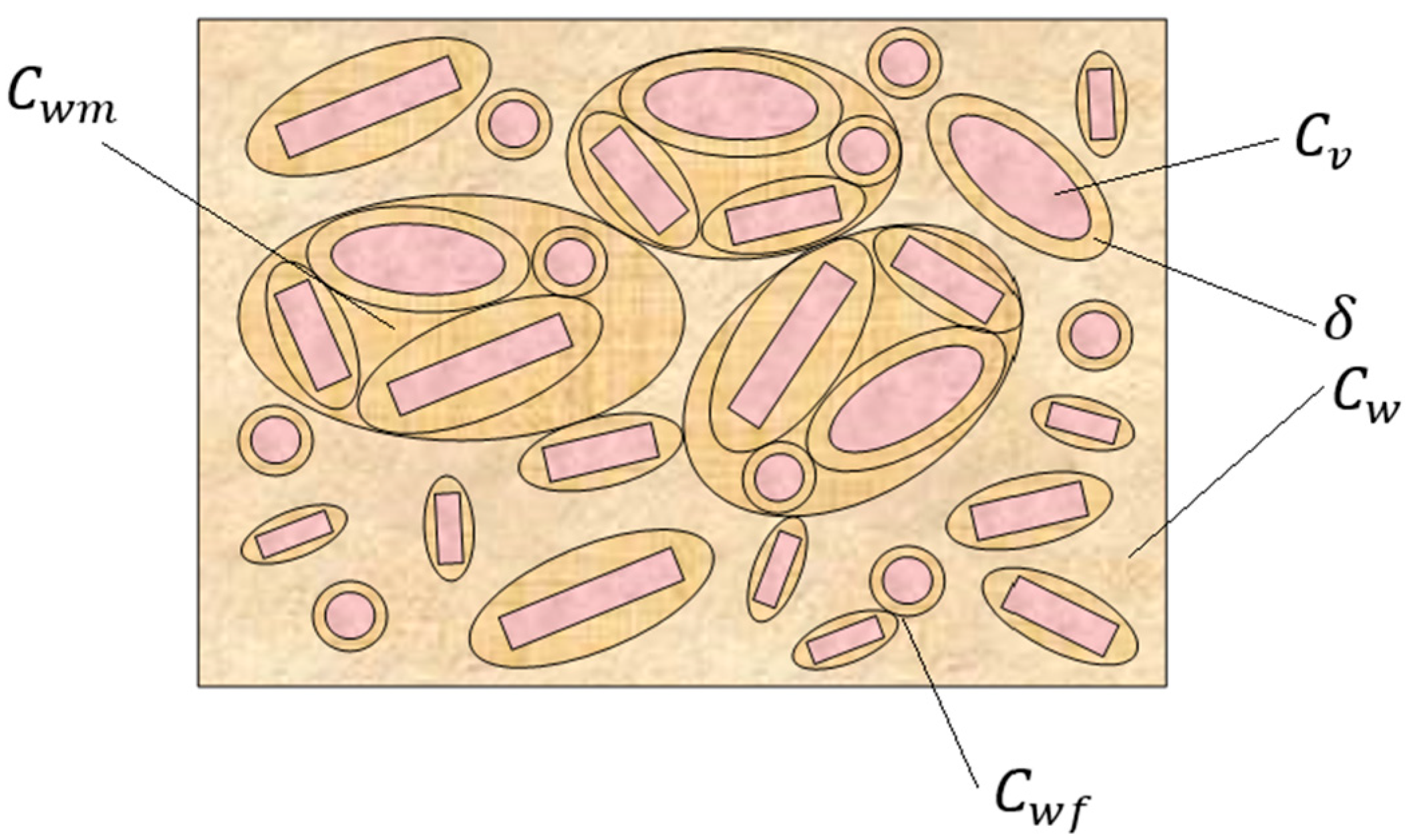
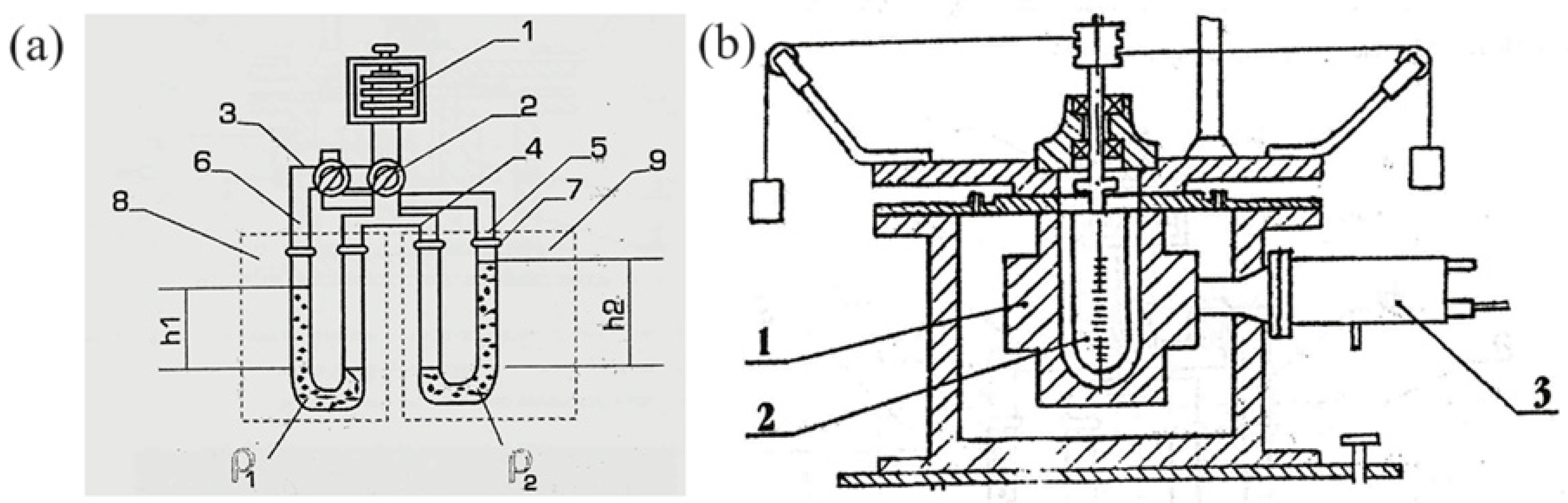
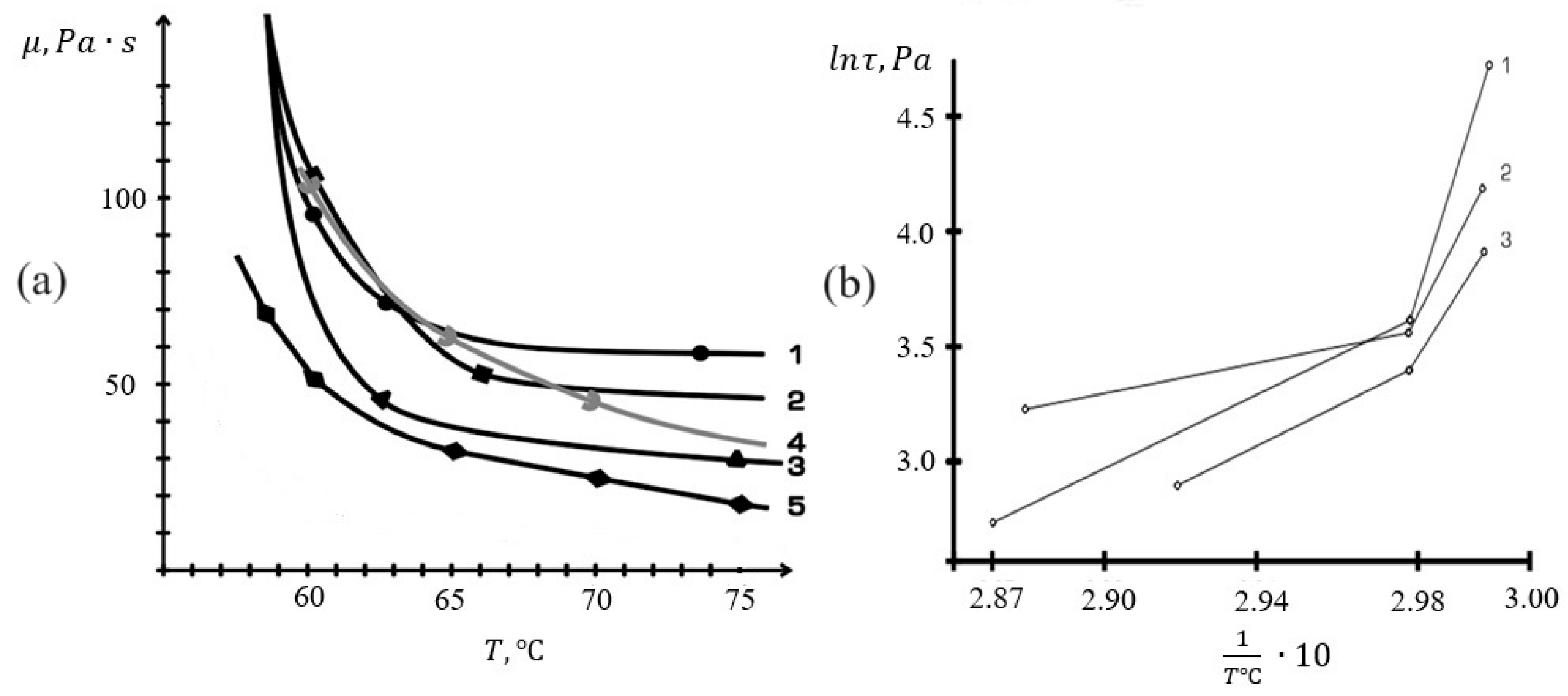
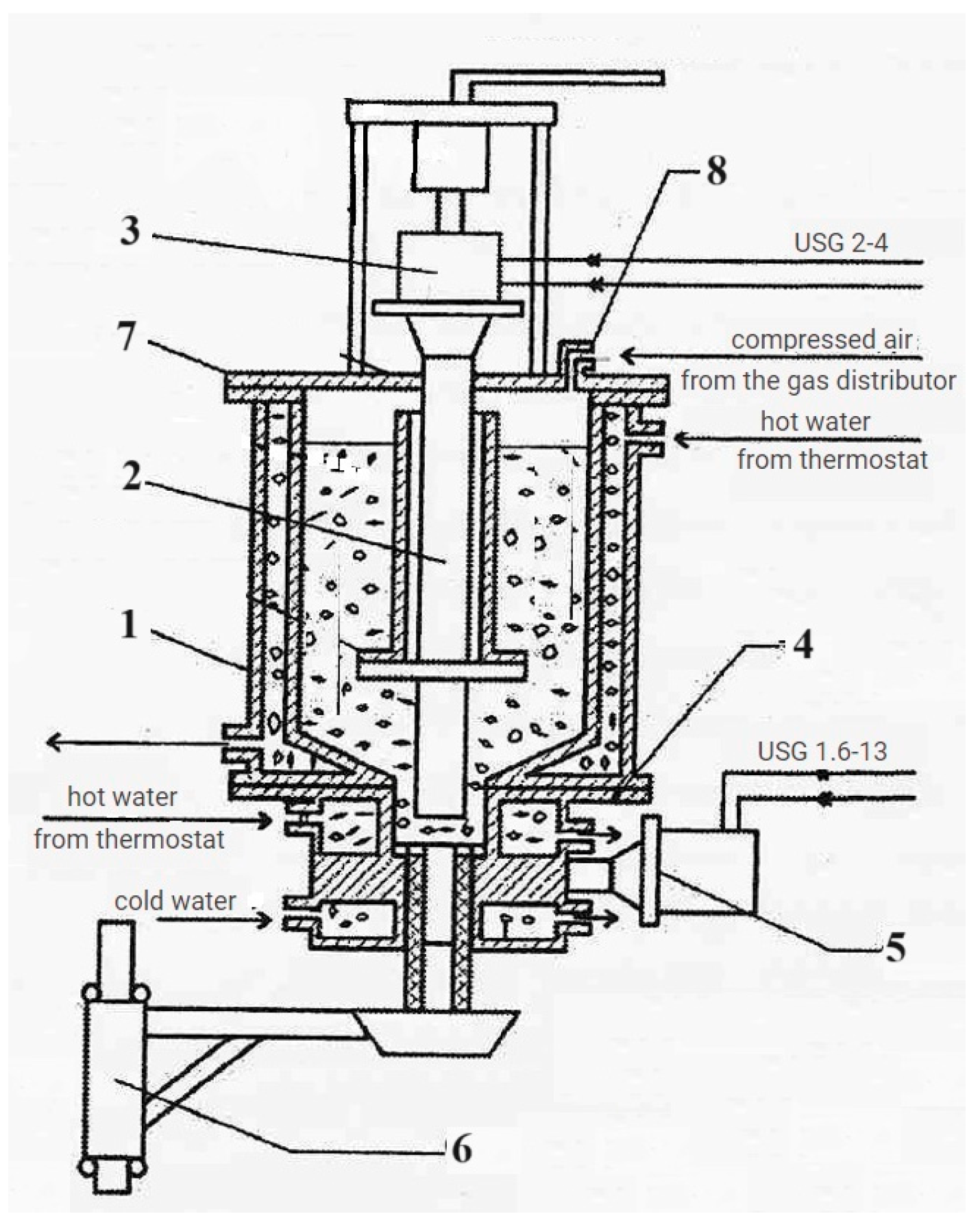

| Powder, Grade | Apparent Density, | |||
|---|---|---|---|---|
| 1.4–4.2 | 2570 ± 30 | 2.30 | 0.72 |
| Component | Chemical Structure | ||||
|---|---|---|---|---|---|
| Paraffin B2 | 52–56 | 0.918 | 0.784 | 0.781 | |
| Oleic Acid | 16 | 0.937 | 0.886 | 0.888 | |
| Beeswax | 61–63 | 0.942 | 0.835 | 0.827 | |
| BeO | 11.7 | 0.657 | 0.723 | 0.908 | 0.092 | 0.251 |
| 10.7 | 0.679 | 0.728 | 0.932 | 0.068 | 0.253 | |
| 10.0 | 0.695 | 0.734 | 0.946 | 0.054 | 0.251 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sattinova, Z.; Assilbekov, B.; Bekenov, T.; Ramazanova, G. Computational Investigation of the Influencing Parameters on the Solidification of Thermoplastic Beryllium Oxide Slurry in a Cylindrical Shell. Ceramics 2024, 7, 906-925. https://doi.org/10.3390/ceramics7030059
Sattinova Z, Assilbekov B, Bekenov T, Ramazanova G. Computational Investigation of the Influencing Parameters on the Solidification of Thermoplastic Beryllium Oxide Slurry in a Cylindrical Shell. Ceramics. 2024; 7(3):906-925. https://doi.org/10.3390/ceramics7030059
Chicago/Turabian StyleSattinova, Zamira, Bakytzhan Assilbekov, Tassybek Bekenov, and Gaukhar Ramazanova. 2024. "Computational Investigation of the Influencing Parameters on the Solidification of Thermoplastic Beryllium Oxide Slurry in a Cylindrical Shell" Ceramics 7, no. 3: 906-925. https://doi.org/10.3390/ceramics7030059
APA StyleSattinova, Z., Assilbekov, B., Bekenov, T., & Ramazanova, G. (2024). Computational Investigation of the Influencing Parameters on the Solidification of Thermoplastic Beryllium Oxide Slurry in a Cylindrical Shell. Ceramics, 7(3), 906-925. https://doi.org/10.3390/ceramics7030059





