Density Functional Theory Study of Pressure-Dependent Structural and Electronic Properties of Cubic Zirconium Dioxide
Abstract
:1. Introduction
2. Materials and Methods
3. Results
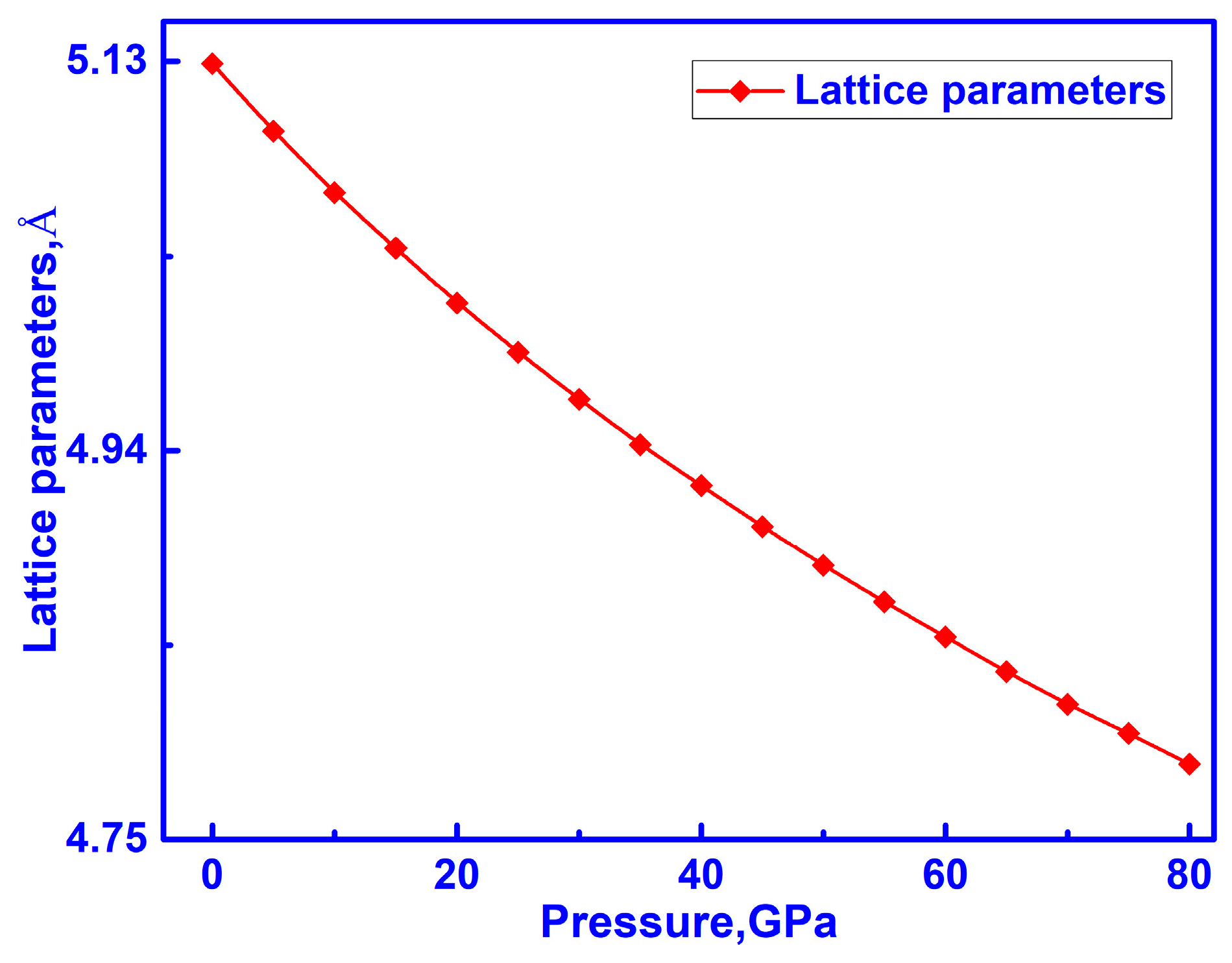
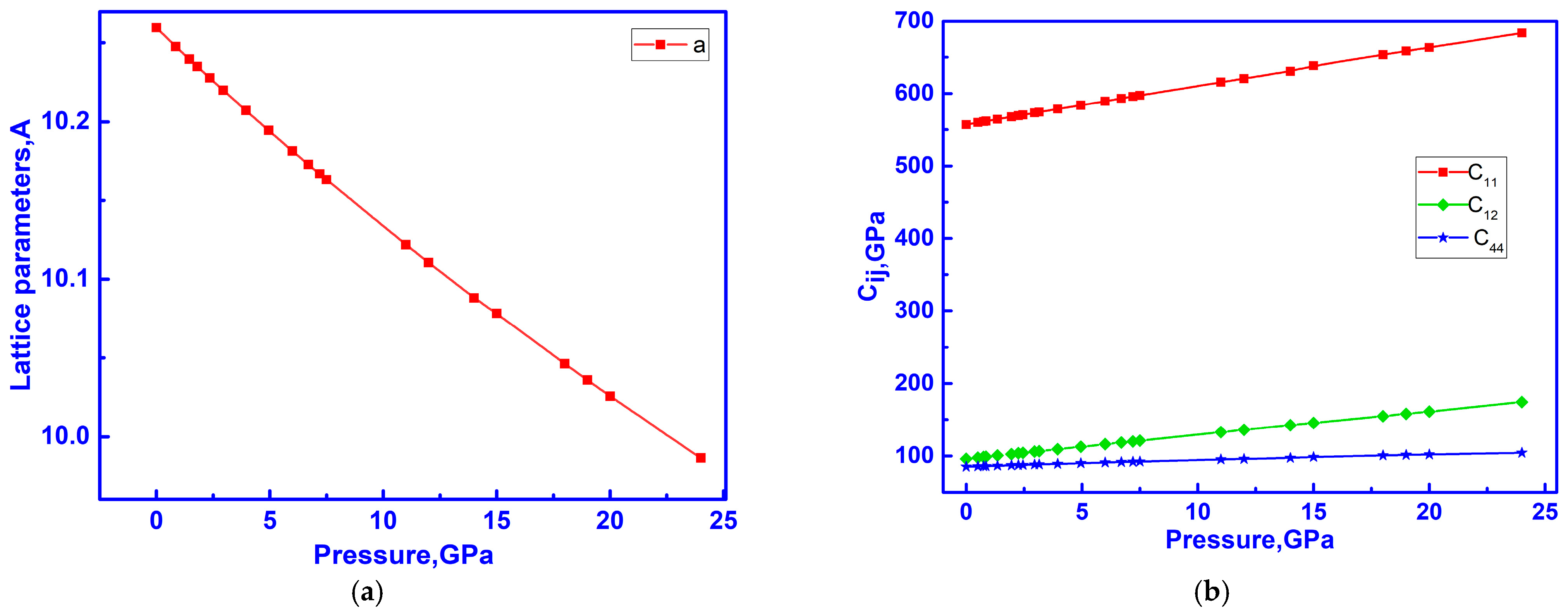
3.1. Structure of C-ZrO2
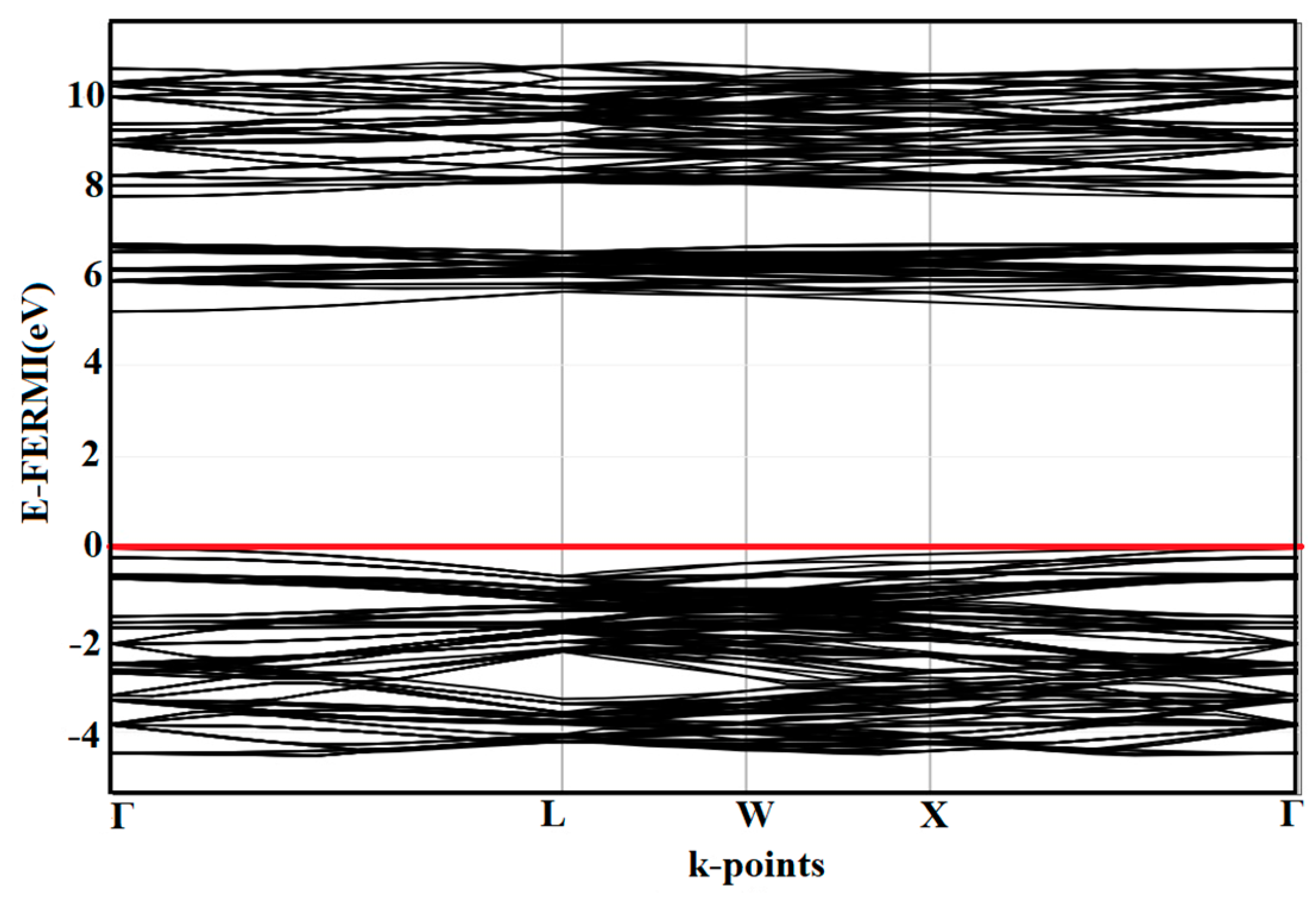
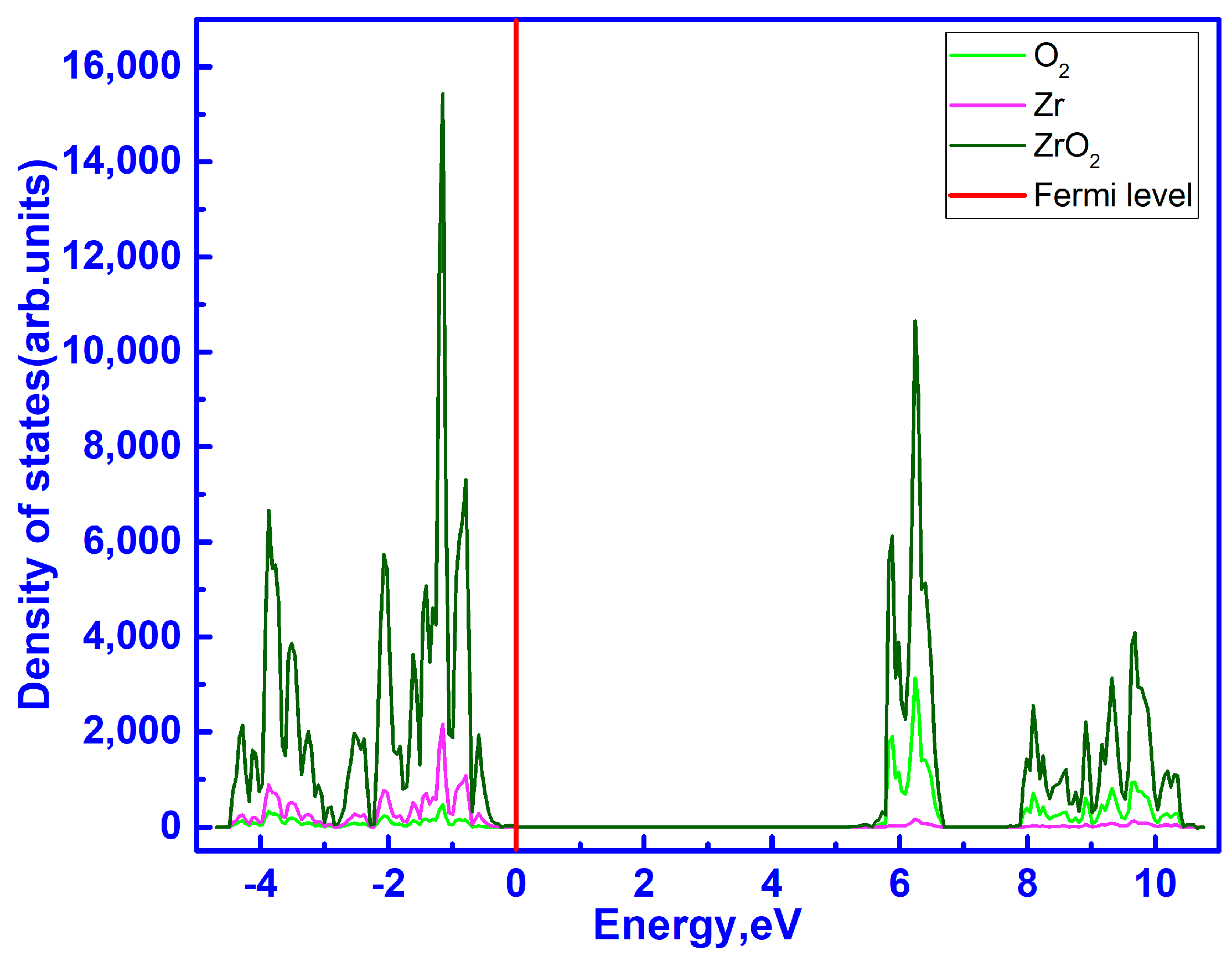
3.2. Band Structure of C-ZrO2
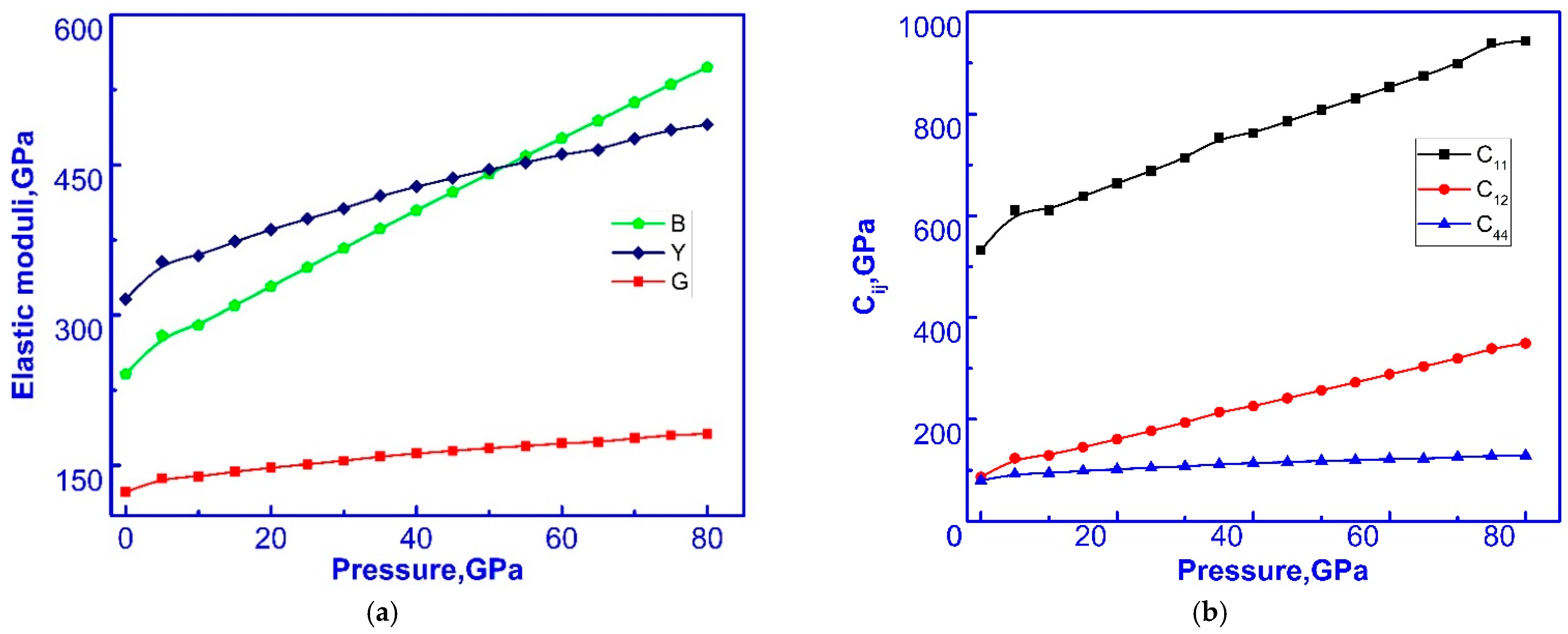
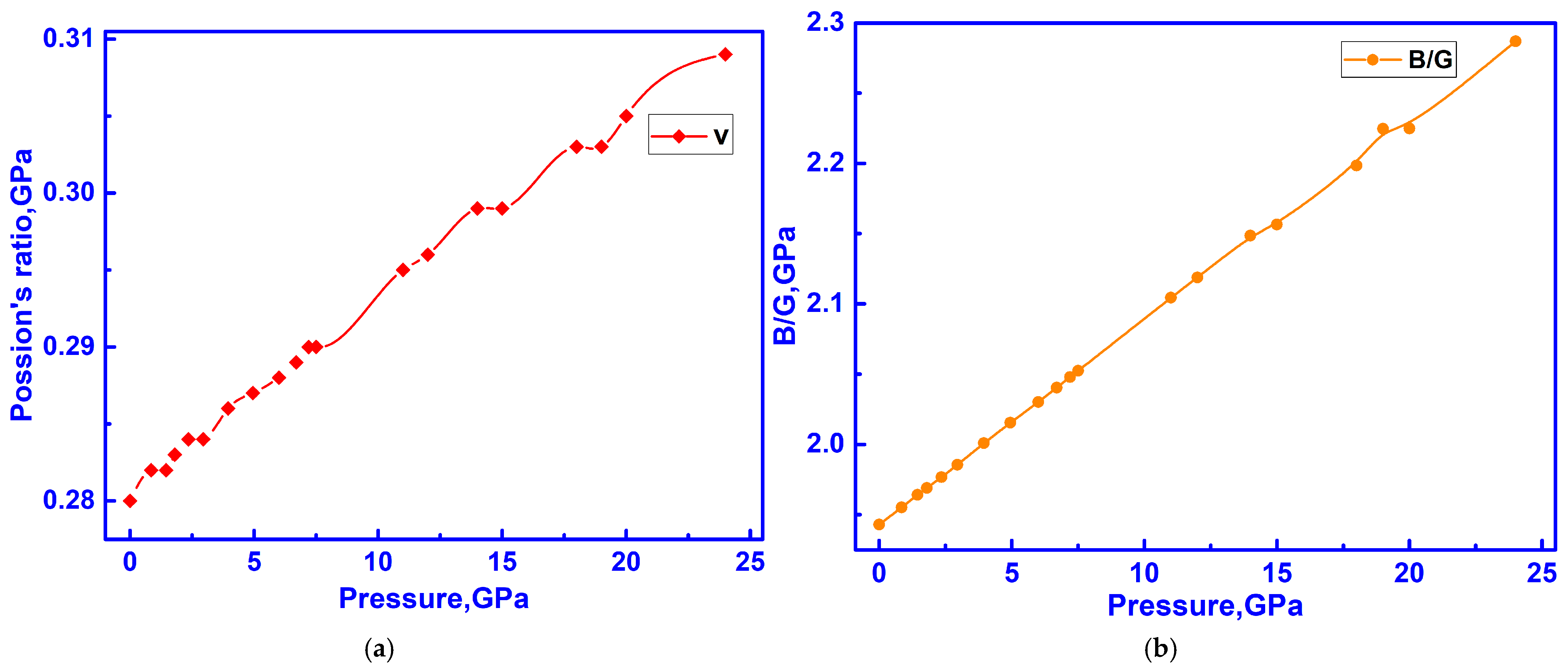
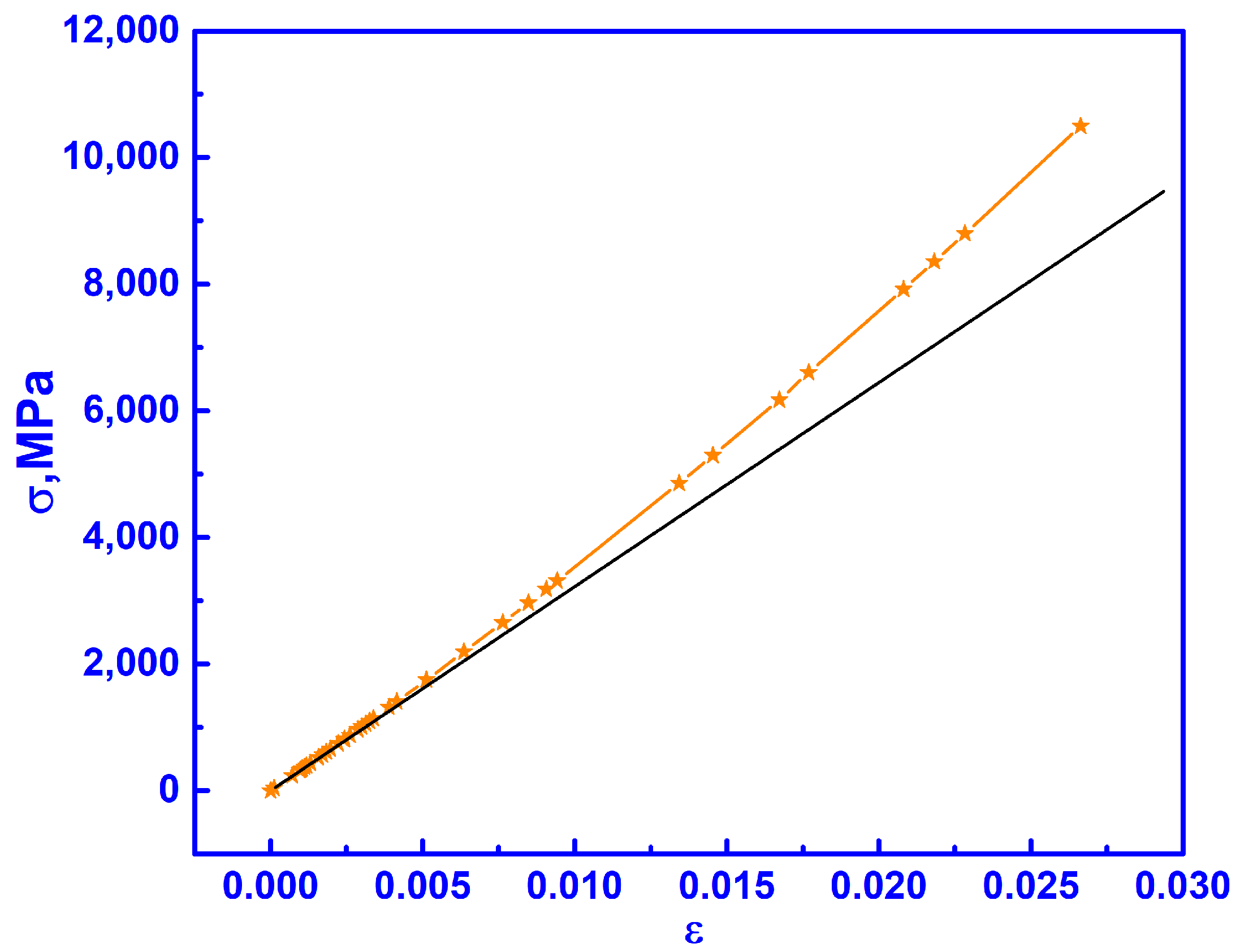
3.3. Elastic Properties of C-ZrO2
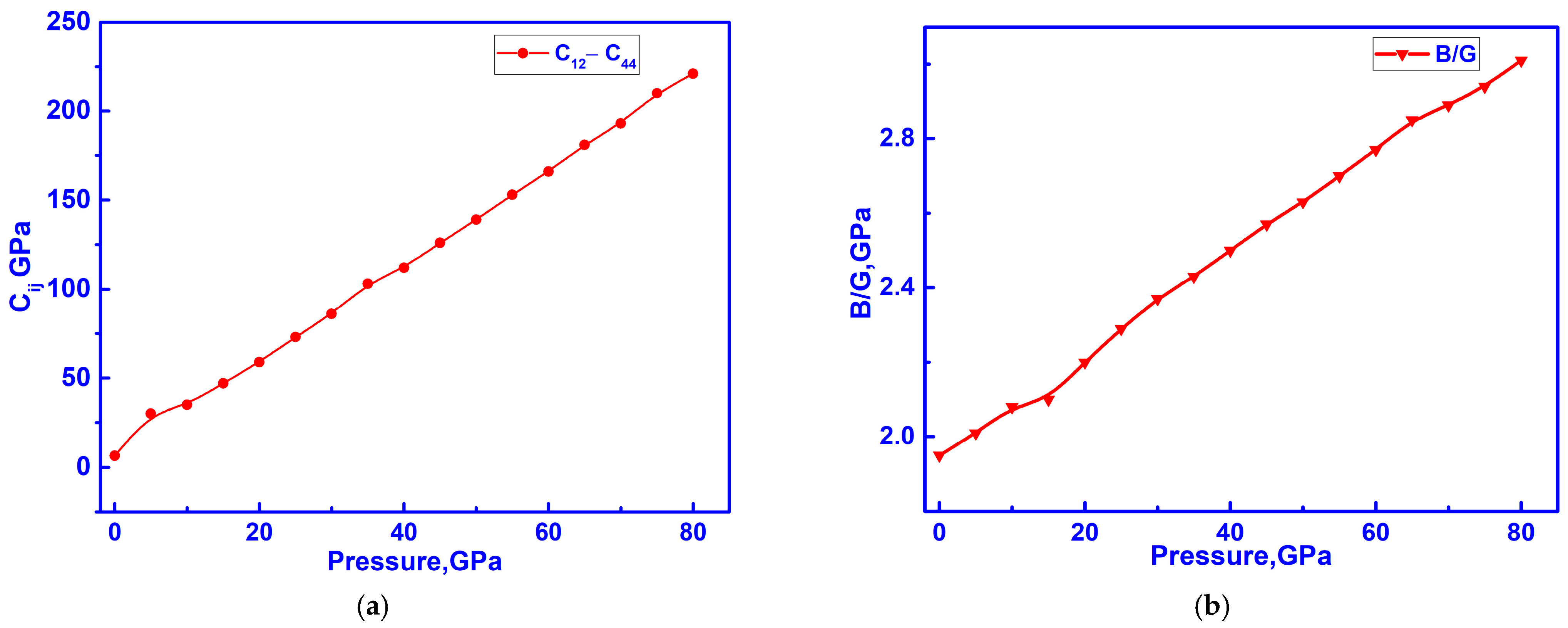
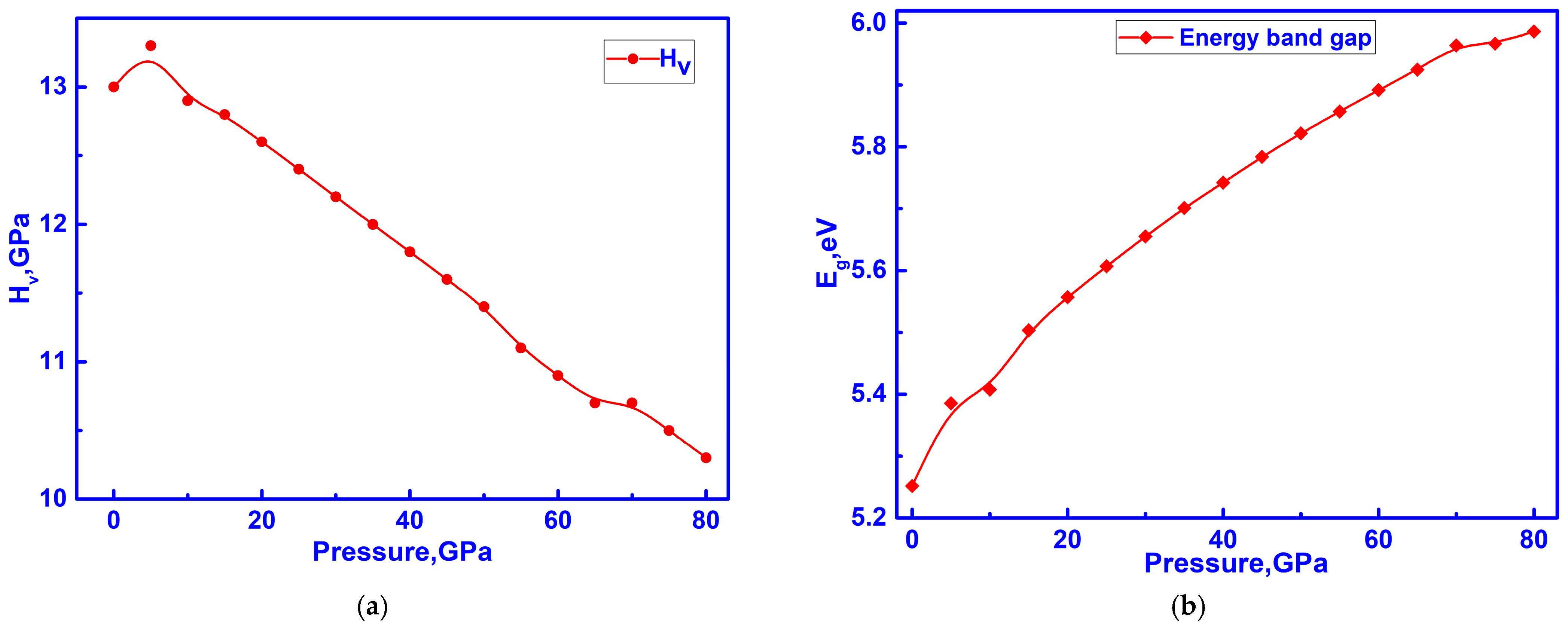
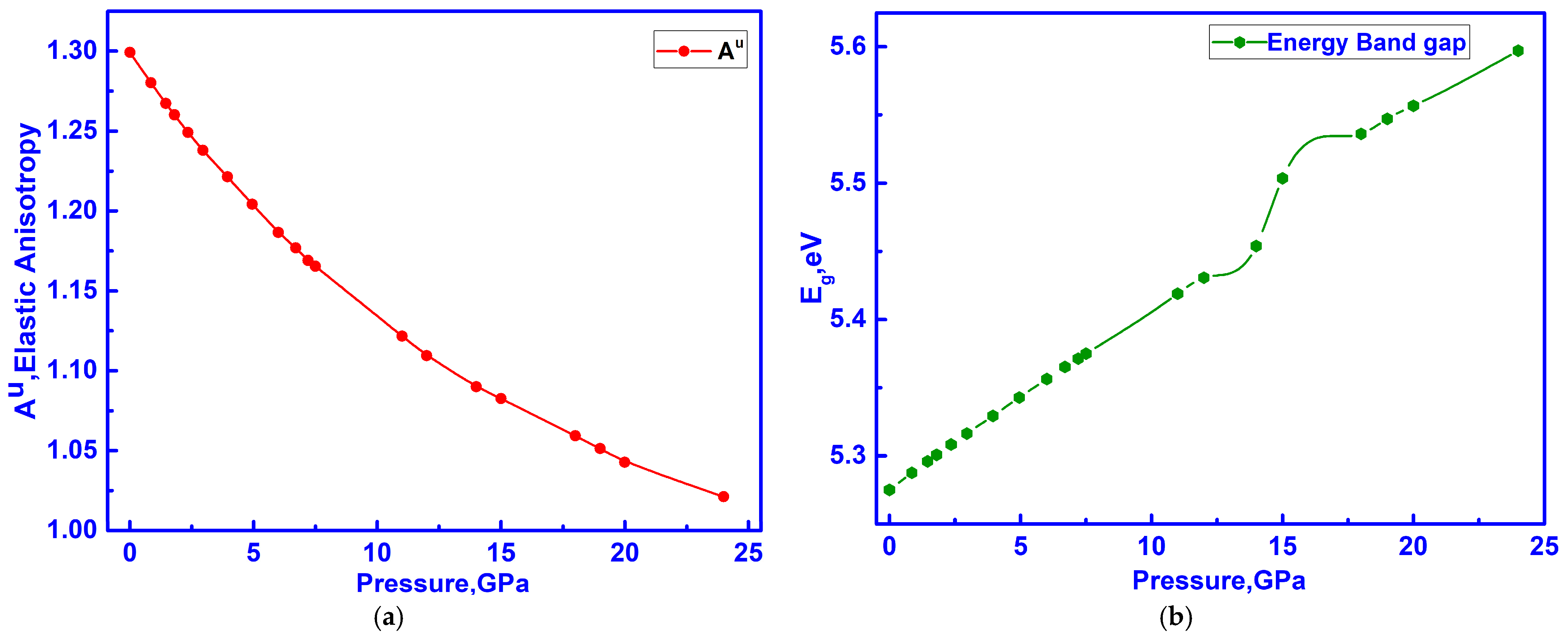
3.4. Hidden Anomalies in the Elastic and Electronic Properties of C-ZrO2 Under Low Pressure
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Muñoz, M.C.; Gallego, S.; Beltrán, J.I.; Cerdá, J. Adhesion at metal–ZrO2 interfaces. Surf. Sci. Rep. 2006, 61, 303–344. [Google Scholar] [CrossRef]
- Kisi, E.H.; Howard, C.J. Crystal structures of zirconia phases and their inter-relation. Key Eng. Mater. 1998, 153, 1–36. [Google Scholar] [CrossRef]
- Luthardt, R.G.; Sandkuhl, O.; Herold, V. Reliability and properties of ground Y-TZP-zirconia ceramics. J. Dent. Res. 2002, 81, 487–491. [Google Scholar] [CrossRef]
- Jin, L.; Yu, Q.; Rauf, A.; Zhou, C. Elastic, electronic and thermal properties of YSZ from first principles. Solid State Sci. 2012, 14, 106. [Google Scholar] [CrossRef]
- Garzon, F.H.; Mukundan, R.; Lujan, R.; Brosha, E.L. Solid state ionic devices for combustion gas sensing. Solid State Ion. 2004, 175, 487. [Google Scholar] [CrossRef]
- Fleischhauer, F.; Bermejo, R.; Danzer, R.; Mai, A.; Graule, T.; Kuebler, J. High temperature mechanical properties of zirconia tapes used for electrolyte supported solid oxide fuel cells. J. Power Sources 2015, 273, 237. [Google Scholar] [CrossRef]
- Messaddeq, S.H.; Pulcinelli, S.H.; Santilli, C.V.; Guastaldi, A.C.; Messaddeq, Y. Microstructure and corrosion resistance of inorganic–organic (ZrO2–PMMA) hybrid coating on stainless steel. J. Non-Cryst. Solids 1999, 247, 164. [Google Scholar] [CrossRef]
- Ananchenko, D.V.; Nikiforov, S.V.; Sobyanin, K.V.; Konev, S.F.; Dauletbekova, A.K.; Akhmetova-Abdik, G.; Akilbekov, A.T.; Popov, A.I. Paramagnetic Defects and Thermoluminescence in Irradiated Nanostructured Monoclinic Zirconium Dioxide. Materials 2022, 15, 8624. [Google Scholar] [CrossRef]
- Ali, I.; Imanova, G.T.; Garibov, A.A.; Agayev, T.N.; Jabarov, S.H.; Almalki, A.S.; Alsubaie, A. Gamma rays mediated water splitting on nano-ZrO2 surface: Kinetics of molecular hydrogen formation. Radiat. Phys. Chem. 2021, 183, 109431. [Google Scholar] [CrossRef]
- Qi, S.; Porotnikova, N.M.; Ananyev, M.V.; Kuzmin, A.V.; Eremin, V.A.; Pankratov, A.A.; Molchanova, N.G.; Reznitskikh, O.G.; Farlenkov, A.S.; Vovkotrub, E.G.; et al. High-temperature glassy-ceramic sealants SiO2-Al2O3-BaO-MgO and SiO2-Al2O3-ZrO2-CaO-Na2O for solid oxide electrochemical devices. Trans. Nonferr. Met. Soc. China 2016, 26, 2916–2924. [Google Scholar] [CrossRef]
- Farlenkov, A.S.; Ananyev, M.V.; Eremin, V.A.; Porotnikova, N.M.; Kurumchin, E.K.; Melekh, B.T. Oxygen isotope exchange in doped calcium and barium zirconates. Solid State Ion. 2016, 290, 108–115. [Google Scholar] [CrossRef]
- Dauletbekova, A.; Zvonarev, S.; Nikiforov, S.; Akilbekov, A.; Shtang, T.; Karavannova, N.; Akylbekova, A.; Ishchenko, A.; Akhmetova-Abdik, G.; Baymukhanov, Z.; et al. Luminescence Properties of ZrO2: Ti Ceramics Irradiated with Electrons and High-Energy Xe Ions. Materials 2024, 17, 1307. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Konuhova, M.; Borgekov, D.B. Study of irradiation temperature effect on radiation-induced polymorphic transformation mechanisms in ZrO2 ceramics. Opt. Mater. 2024, 156, 115994. [Google Scholar] [CrossRef]
- Imanova, G.T.; Agayev, T.N.; Jabarov, S.H. Investigation of structural and optical properties of zirconia dioxide nanoparticles by radiation and thermal methods. Mod. Phys. Lett. B 2021, 35, 2150050. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Konuhova, M.; Shlimas, D.I.; Borgekov, D.B.; Zdorovets, M.V.; Shakirziyanov, R.I.; Popov, A.I. Study of the Effect of Nanostructured Grains on the Radiation Resistance of Zirconium Dioxide Ceramics During Gas Swelling under High-dose Irradiation with Helium Ions. ES Mater. Manuf. 2024, 24, 1165. [Google Scholar] [CrossRef]
- Kadyrzhanov, K.K.; Kozlovskiy, A.A.; Konuhova, M.; Popov, A.I.; Shlimas, D.D.; Borgekov, D.B. Determination of gamma radiation shielding efficiency by radiation-resistant composite ZrO2-Al2O3-TiO2-WO3-Nb2O5 ceramics. Opt. Mater. 2024, 154, 115752. [Google Scholar] [CrossRef]
- Abyshev, B.K.; Giniyatova, S.G.; Kozlovskiy, A.L. Effect of irradiation temperature on the mobility of structural and vacancy defects in the damaged layer of Li2ZrO3 ceramics. Opt. Mater. X 2024, 24, 100376. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Alin, M.; Borgekov, D.B. Study of Polymorphic Transformation Processes and Their Influence in Polycrystalline ZrO2 Ceramics upon Irradiation with Heavy Ions. Ceramics 2023, 6, 686–706. [Google Scholar] [CrossRef]
- Teufer, G. The crystal structure of tetragonal ZrO2. Acta Crystallogr. 1962, 15, 1187. [Google Scholar] [CrossRef]
- Suchanek, W.; Yoshimura, M. Processing and properties of hydroxyapatite-based biomaterials for use as hard tissue replacement implants. J. Mater. Res. 1998, 13, 94–117. [Google Scholar] [CrossRef]
- Harmsworth, P.; Stevens, R. Phase composition and properties of plasma-sprayed zirconia thermal barrier coatings. J. Mater. Sci. 1992, 27, 611–615. [Google Scholar] [CrossRef]
- McCullough, J.T.; Trueblood, K. The crystal structure of baddeleyite (monoclinic ZrO2). Acta Crystallogr. 1959, 12, 507–511. [Google Scholar] [CrossRef]
- Bandura, A.V.; Evarestov, R.A. Ab initio structure modeling of ZrO2 nanosheets and single-wall nanotubes. Comput. Mater. Sci. 2012, 65, 395–405. [Google Scholar] [CrossRef]
- Howard, C.J.; Hill, R.J.; Reichert, B.E. Structures of the polymorphs of the high-temperature superconductor YBa₂Cu₃O₇−x. Acta Crystallogr. B 1988, 44, 116–120. [Google Scholar] [CrossRef]
- Garvie, R.C.; Hannink, R.H.; Pascoe, R.T. Ceramic steel? Nature 1975, 258, 703. [Google Scholar] [CrossRef]
- Roth, W.L. Crystal Structure and Chemical Bonding in Inorganic Chemistry; Rooymans, C.J., Rabenau, A., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1975; pp. 85–102. [Google Scholar]
- Proffen, T.; Neder, R.B.; Frey, F.; Assmus, W. Defect structure and diffuse scattering of zirconia single crystals doped with 7 mol% CaO. Acta Crystallogr. B 1993, 49, 599. [Google Scholar] [CrossRef]
- Hevorkian, E.; Jozwik, J.; Rucki, M.; Kolodnitskyi, V.; Morozova, O.; Dziedzic, K. Reproducibility of properties of zirconia-based composites. In Proceedings of the 2024 11th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Lublin, Poland, 3–5 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 484–489. [Google Scholar]
- Sun, N.; Zhu, T.; Zeng, Y.; Wang, Y.; Wang, H.; Li, Y.; Sang, S.; Xie, Z.; Cao, H. Achieving excellent toughness and wear resistance in WC-ZrO2-Al2O₃ ceramics by combining laminated structure and two-step oscillatory pressure sintering. SSRN 2024, 5027477. [Google Scholar] [CrossRef]
- Wu, H.; Duan, Y.; Liu, K.; Lv, D.; Qin, L.; Shi, L.; Tang, G. First-principles study of phase transition and band structure of ZrO2 under pressure. J. Alloys Compd. 2015, 645, 352–357. [Google Scholar] [CrossRef]
- Eklund, K.; Alajoki, J.; Karttunen, A.J. Elastic properties of binary d-metal oxides studied by hybrid density functional methods. Cryst. Growth Des. 2023, 23, 3427–3436. [Google Scholar] [CrossRef]
- Mirgorodsky, A.P.; Quintard, P.E. Lattice-dynamic treatment of vibrational and elastic properties of cotunnite-type ZrO2 and HfO2: Comparison with ambient pressure polymorphs. J. Am. Ceram. Soc. 1999, 82, 3121–3124. [Google Scholar] [CrossRef]
- Muhammad, I.D.; Awang, M. Modelling the interatomic potential of cubic zirconia. Appl. Mech. Mater. 2013, 446–447, 151–157. [Google Scholar] [CrossRef]
- French, R.H.; Glass, S.J.; Ohuchi, F.S.; Xu, Y.-N.; Ching, W.Y. Experimental and theoretical determination of the electronic structure and optical properties of three phases of ZrO2. Phys. Rev. B 1994, 49, 5133–5142. [Google Scholar] [CrossRef]
- Erba, A.; Desmarais, J.K.; Casassa, S.; Civalleri, B.; Donà, L.; Bush, I.J.; Searle, B.; Maschio, L.; Edith-Daga, L.; Cossard, A.; et al. CRYSTAL23: A program for computational solid-state physics and chemistry. J. Chem. Theory Comput. 2023, 19, 6891–6932. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200. [Google Scholar] [CrossRef]
- Ziesche, P.; Eschrig, H. (Eds.) Electronic Structure of Solids’ 91: Proceedings of the 75. WE-Heraeus-Seminar and 21st Annual International Symposium on Electronic Structure of Solids Held in Gaussig (Germany), March 11–15, 1991; De Gruyter Akademie Forschung: Berlin, Germany, 1991; Volume 17. [Google Scholar]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Eglitis, R.I.; Popov, A.I.; Jia, R.; Kruchinin, S.P.; Derkaoui, I.; Kabatas, M.A. B3LYP and B3PW computations of BaSnO3 and BaZrO3 perovskite (001) surfaces. Low Temp. Phys. 2024, 50, 905–910. [Google Scholar] [CrossRef]
- Kaptagay, G.A.; Satanova, B.M.; Abuova, A.U.; Konuhova, M.; Zakiyeva, Z.Y.; Tolegen, U.Z.; Koilyk, N.O.; Abuova, F.U. Effect of rhodium doping for photocatalytic activity of barium titanate. Opt. Mater. X 2025, 25, 100382. [Google Scholar] [CrossRef]
- Rusevich, L.L.; Brik, M.G.; Gryaznov, D.; Srivastava, A.M.; Chervyakov, I.; Zvejnieks, G.; Bocharov, D.; Kotomin, E.A. First-Principles Linear Combination of Atomic Orbitals Calculations of K2SiF6 Crystal: Structural, Electronic, Elastic, Vibrational and Dielectric Properties. Materials 2024, 17, 4865. [Google Scholar] [CrossRef] [PubMed]
- Piasecki, M.; Myronchuk, G.L.; Zamurueva, O.V.; Khyzhun, O.Y.; Parasyuk, O.V.; Fedorchuk, A.O.; Albassam, A.; El-Naggar, A.M.; Kityk, I.V. Huge operation by energy gap of novel narrow band gap Tl1−xIn1−xBxSe2 (B = Si, Ge): DFT, X-ray emission and photoconductivity studies. Mater. Res. Express 2016, 3, 025902. [Google Scholar] [CrossRef]
- Lisovski, O.; Chesnokov, A.; Piskunov, S.; Bocharov, D.; Zhukovskii, Y.F.; Wessel, M.; Spohr, E. Ab initio calculations of doped TiO2 anatase (101) nanotubes for photocatalytical water splitting applications. Mat. Sci. Semicon. Proc. 2016, 42, 138–141. [Google Scholar] [CrossRef]
- Rudysh, M.Y.; Brik, M.G.; Stadnyk, V.Y.; Brezvin, R.S.; Shchepanskyi, P.A.; Fedorchuk, A.; Khyzhun, O.Y.; Kityk, I.V.; Piasecki, M. Ab initio calculations of the electronic structure and specific optical features of β-LiNH4SO4 single crystals. Phys. B Condens. Matter 2018, 528, 37–46. [Google Scholar] [CrossRef]
- Ma, C.G.; Brik, M.G. Hybrid density-functional calculations of structural, elastic and electronic properties for a series of cubic perovskites CsMF3 (M= Ca, Cd, Hg, and Pb). Comput. Mater. Sci. 2012, 58, 101–112. [Google Scholar] [CrossRef]
- Rudysh, M.Y.; Brik, M.G.; Khyzhun, O.Y.; Fedorchuk, A.O.; Kityk, I.V.; Shchepanskyi, P.A.; Stadnyk, V.Y.; Lakshminarayana, G.; Brezvin, R.S.; Bak, Z.; et al. Ionicity and birefringence of α-LiNH4SO4 crystals: Ab initio DFT study, X-ray spectroscopy measurements. RSC Adv. 2017, 7, 6889–6901. [Google Scholar] [CrossRef]
- Buryi, M.; Babin, V.; Děcká, K.; Ridzoňová, K.; Neykova, N.; Hájek, F.; Velkov, Z.; Remeš, Z.; Tomala, R.; Socha, P. Charge trapping and luminescence of the mixed size CsPbBr3 particles grown in one batch. Opt. Mater. 2024, 151, 115279. [Google Scholar] [CrossRef]
- Parasyuk, O.V.; Babizhetskyy, V.S.; Khyzhun, O.Y.; Levytskyy, V.O.; Kityk, I.V.; Myronchuk, G.L.; Tsisar, O.V.; Piskach, L.V.; Jedryka, J.; Maciag, A.; et al. Novel Quaternary TlGaSn2Se6 Single Crystal as Promising Material for Laser Operated Infrared Nonlinear Optical Modulators. Crystals 2017, 7, 341. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef]
- Perger, W.F.; Criswell, C.; Civalleri, B.; Dovesi, R. Ab-initio calculation of elastic constants of crystalline systems with the CRYSTAL code. Comput. Phys. Commun. 2009, 180, 1753–1759. [Google Scholar] [CrossRef]
- Erba, A.; Mahmoud, A.; Orlando, R.; Dovesi, R. Elastic properties of six silicate garnet end-members from accurate ab initio simulations. Phys. Chem. Miner. 2014, 41, 151–160. [Google Scholar] [CrossRef]
- Kishore, N.; Nagarajan, V.; Chandiramouli, R. First-principles studies on mechanical properties and band structures of TMO2 (TM = Zr or Hf) nanostructures under high pressure. Phys. B Condens. Matter 2019, 559, 1–7. [Google Scholar] [CrossRef]
- Terki, R.; Feraoun, H.; Bertrand, G.; Aourag, H. First principles calculations of structural, elastic and electronic properties of XO2 (X=Zr, Hf and Th) in fluorite phase. Comput. Mater. Sci. 2005, 33, 44–52. [Google Scholar] [CrossRef]
- Jamal, M.; Asadabadi, S.J.; Ahmad, I.; Aliabad, H.R. Elastic constants of cubic crystals. Comput. Mater. Sci. 2014, 95, 592–599. [Google Scholar] [CrossRef]
- Yang, J.; Shahid, M.; Wan, C.; Jing, F.; Pan, W. Anisotropy in elasticity, sound velocities and minimum thermal conductivity of zirconia from first-principles calculations. J. Eur. Ceram. Soc. 2017, 37, 689–695. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.-X.; Duan, L.; Fan, J.-B.; Ni, L.; Ji, V. A comparison study of the structural and mechanical properties of cubic, tetragonal, monoclinic, and three orthorhombic phases of ZrO2. J. Alloy. Compd. 2018, 749, 283–292. [Google Scholar] [CrossRef]
- Khitrova, V.I.; Klechkovskaya, V.V. Electron-diffraction investigation of phase transformation and crystal structure of thin layers of cubic zirconium oxide. Kristallografiya 1985, 30, 126–130. [Google Scholar]
- Soo, Y.L.; Chen, P.J.; Huang, S.H.; Shiu, T.J.; Tsai, T.Y.; Chow, Y.H.; Lin, Y.C.; Weng, S.C.; Chang, S.L.; Wang, G.; et al. Local Structures Surrounding Zr in Nanostructurally Stabilized Cubic Zirconia: Structural Origin of Phase Stability. J. Appl. Phys. 2008, 104, 113535. [Google Scholar] [CrossRef]
- Wang, C. Multiscale Modeling and Simulation of Nanocrystalline Zirconium Oxide. Ph.D. Thesis, University of Nebraska, Lincoln, Nebraska, 2009. [Google Scholar]
- Chang, Y.; Wang, H.; Zhu, Q.; Luo, P.; Dong, S. Theoretical calculation and analysis of ZrO2 spherical nanometer powders. J. Adv. Ceram. 2013, 2, 21–25. [Google Scholar] [CrossRef]
- Suciu, C.; Gagea, L.; Hoffmann, A.C.; Mocean, M. Sol-gel production of zirconia nanoparticles with a new organic precursor. Chem. Eng. Sci. 2006, 61, 7831–7835. [Google Scholar] [CrossRef]
- Nematov, D.D.; Burhonzoda, A.S.; Kholmurodov, K.T.; Lyubchyk, A.I.; Lyubchyk, S.I. A detailed comparative analysis of the structural stability and electron-phonon properties of ZrO2: Mechanisms of water adsorption on t-ZrO2 (101) and t-YSZ (101) surfaces. Nanomaterials 2023, 13, 2657. [Google Scholar] [CrossRef] [PubMed]
- Erba, A.; Mahmoud, A.; Belmonte, D.; Dovesi, R. High pressure elastic properties of minerals from ab initio simulations: The case of pyrope, grossular and andradite silicate garnets. J. Chem. Phys. 2014, 140, 124703. [Google Scholar] [CrossRef] [PubMed]
- Nazir, M.A.; Mahmood, T.; Zafar, A.A.; Akhtar, N.; Hussain, T.; Saeed, M.A.; Aleem, F.-E.; Saeed, A.; Raza, J.; Cao, C. Electronic, optical, and elastic properties of cubic zirconia (c-ZrO2) under pressure: A DFT study. Phys. B Condens. Matter 2021, 604, 412462. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Kishore, N.; Nagarajan, V.; Chandiramouli, R. Mechanical properties and band structure of CdSe and CdTe nanostructures at high pressure - a first-principles study. Process. Appl. Ceram. 2019, 13, 124–131. [Google Scholar] [CrossRef]
- Kong, Y.; Duan, Y.; Ma, L.; Li, R. Phase stability, elastic anisotropy and electronic structure of cubic MAl2(M = Mg, Ca, Sr and Ba) Laves phases from first-principles calculations. Mater. Res. Express 2016, 3, 106505. [Google Scholar] [CrossRef]
- Kishore, N.; Nagarajan, V.; Chandiramouli, R. Mechanical and electronic properties under high pressure on ternary AlGaN and InGaN compounds—a first-principles perspective. Mater. Res. Express 2018, 6, 015052. [Google Scholar] [CrossRef]
- Zhao, X.-S.; Shang, S.-L.; Liu, Z.-K.; Shen, J.-Y. Elastic properties of cubic, tetragonal and monoclinic ZrO2 from first-principles calculations. J. Nucl. Mater. 2011, 415, 13–17. [Google Scholar] [CrossRef]
- Morita, K.; Sekino, T.; Niihara, K. Fracture strength and toughness of nanocrystalline cubic zirconia prepared by HIPing. J. Eur. Ceram. Soc. 2006, 26, 1521–1525. [Google Scholar] [CrossRef]
- Promakhov, V.V.; Buyakova, S.P. Structural and mechanical behavior of ultrafine-grained ZrO2-based ceramics under shock-wave loading. Powder Metall. Struct. Mater. 2019, 5, 23–31. [Google Scholar]
- Vasileva, A.M.; Kulkov, S.E. Mechanical and structural properties of ZrO2–MgO composites with different porosity levels. J. Mech. Behav. Mater. 2017, 26, 121–126. [Google Scholar]
- Ullah, Z.; Sattar, F.; Kim, H.J.; Jang, S.; Mary, Y.S.; Zhan, X.; Kwon, H.W. Computational study of toxic gas removal. J. Mol. Liq. 2022, 365, 120213. [Google Scholar] [CrossRef]
- Hichem, N.; Hadjer, Z.; Fateh, S.; Feriel, L.; Wang, Z. The potential exposure and hazards of zirconia nanoparticles: A review. Ecotoxicol. Environ. Contam. 2022, 17, 1–21. [Google Scholar] [CrossRef]
- Lyashenko, E.N.; Uzbekova, L.D.; Polovinkina, V.V.; Dorofeeva, A.K.; Ibragimov, S.-U.S.-U.; Tatamov, A.A.; Avkaeva, A.G.; Mikhailova, A.A.; Tuaeva, I.S.; Esiev, R.K.; et al. Study of the Embryonic Toxicity of TiO2 and ZrO2 Nanoparticles. Micromachines 2023, 14, 363. [Google Scholar] [CrossRef] [PubMed]
- Chitoria, A.K.; Mir, A.; Shah, M.A. A review of ZrO2 nanoparticles applications and recent advancements. Ceram. Int. 2023, 49, 32343–32358. [Google Scholar] [CrossRef]
- Ramanavicius, S.; Jagminas, A.; Ramanavicius, A. Gas sensors based on titanium oxides. Coatings 2022, 12, 699. [Google Scholar] [CrossRef]
- Usseinov, A.B.; Akilbekov, A.T.; Kotomin, E.A.; Karipbayev, Z.T. The first principles calculations of CO2 adsorption on (1010) ZnO surface. AIP Conf. Proc. 2019, 2174, 020181. [Google Scholar]



| Parameters | Functional | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| c-ZrO2 | B3LYP | B3PW | PBE | PBE SOL | LDA | HSE06 | SCAN | Others | Experiment |
| a = b = c | 5.107 | 5.075 | 5.104 | 5.056 | 5.020 | 5.067 | 5.076 | 5.11 [59] 3.58 [33] | 5.11 [60] 3.6012 [61] |
| V, Ả3 | 33.31 | 32.68 | 33.24 | 32.32 | 31.63 | 32.53 | 32.69 | 32.5850 [62] | 32.723 [61] |
| ρ, g/cm3 | 6.075 | 6.192 | 6.088 | 6.263 | 6.398 | 6.220 | 6.190 | 6.081 [63] | 6.151 [63] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salikhodzha, Z.M.; Bairbayeva, G.B.; Kassymkhanova, R.N.; Konuhova, M.; Zhangylyssov, K.B.; Popova, E.; Popov, A.I. Density Functional Theory Study of Pressure-Dependent Structural and Electronic Properties of Cubic Zirconium Dioxide. Ceramics 2025, 8, 41. https://doi.org/10.3390/ceramics8020041
Salikhodzha ZM, Bairbayeva GB, Kassymkhanova RN, Konuhova M, Zhangylyssov KB, Popova E, Popov AI. Density Functional Theory Study of Pressure-Dependent Structural and Electronic Properties of Cubic Zirconium Dioxide. Ceramics. 2025; 8(2):41. https://doi.org/10.3390/ceramics8020041
Chicago/Turabian StyleSalikhodzha, Zhussupbek M., Guldari B. Bairbayeva, Raigul N. Kassymkhanova, Marina Konuhova, Keleshek B. Zhangylyssov, Elena Popova, and Anatoli I. Popov. 2025. "Density Functional Theory Study of Pressure-Dependent Structural and Electronic Properties of Cubic Zirconium Dioxide" Ceramics 8, no. 2: 41. https://doi.org/10.3390/ceramics8020041
APA StyleSalikhodzha, Z. M., Bairbayeva, G. B., Kassymkhanova, R. N., Konuhova, M., Zhangylyssov, K. B., Popova, E., & Popov, A. I. (2025). Density Functional Theory Study of Pressure-Dependent Structural and Electronic Properties of Cubic Zirconium Dioxide. Ceramics, 8(2), 41. https://doi.org/10.3390/ceramics8020041







