Determination of Firebrand Characteristics Using Thermal Videos
Abstract
1. Introduction
2. Materials and Methods
2.1. Development of GUI
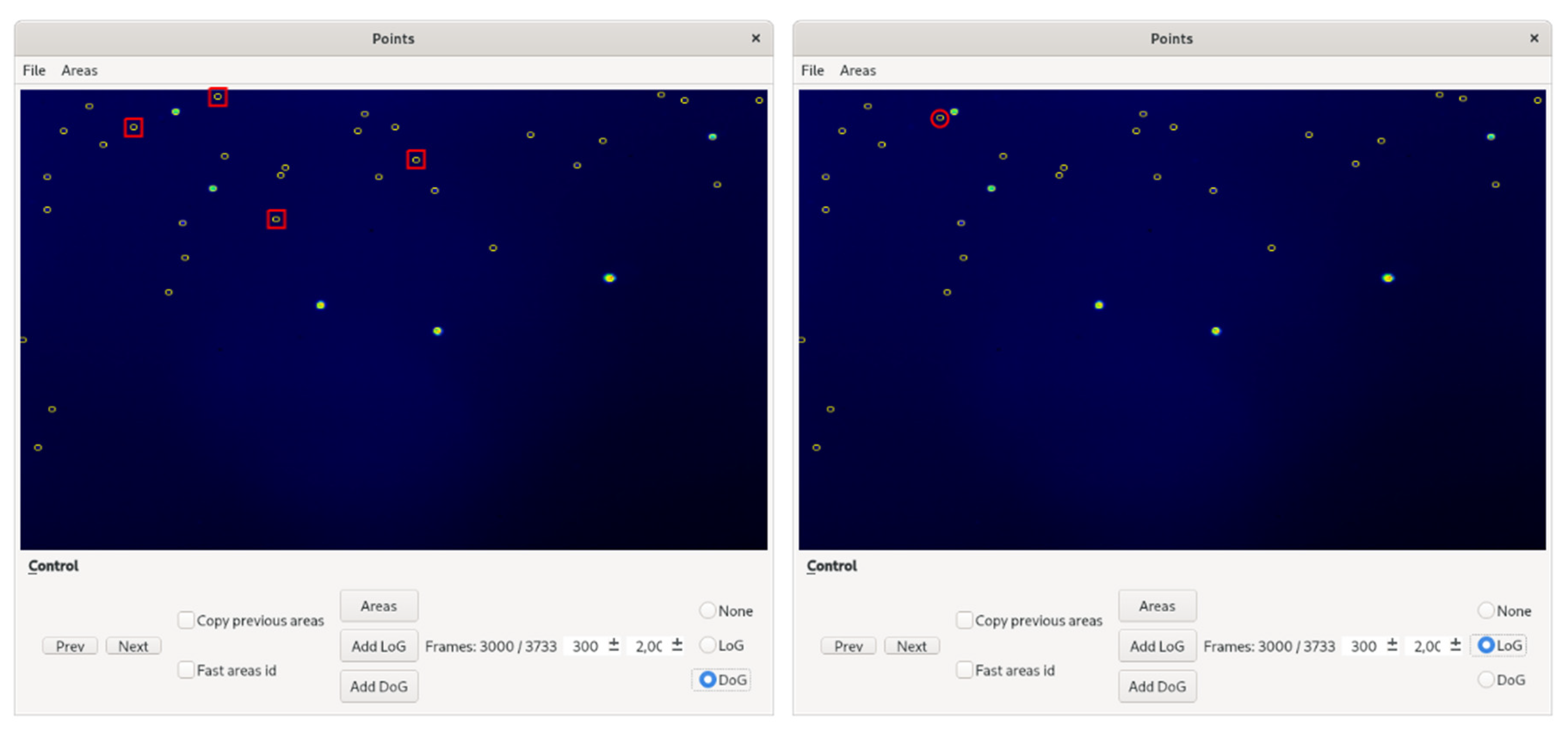
2.2. Testing Algorithms
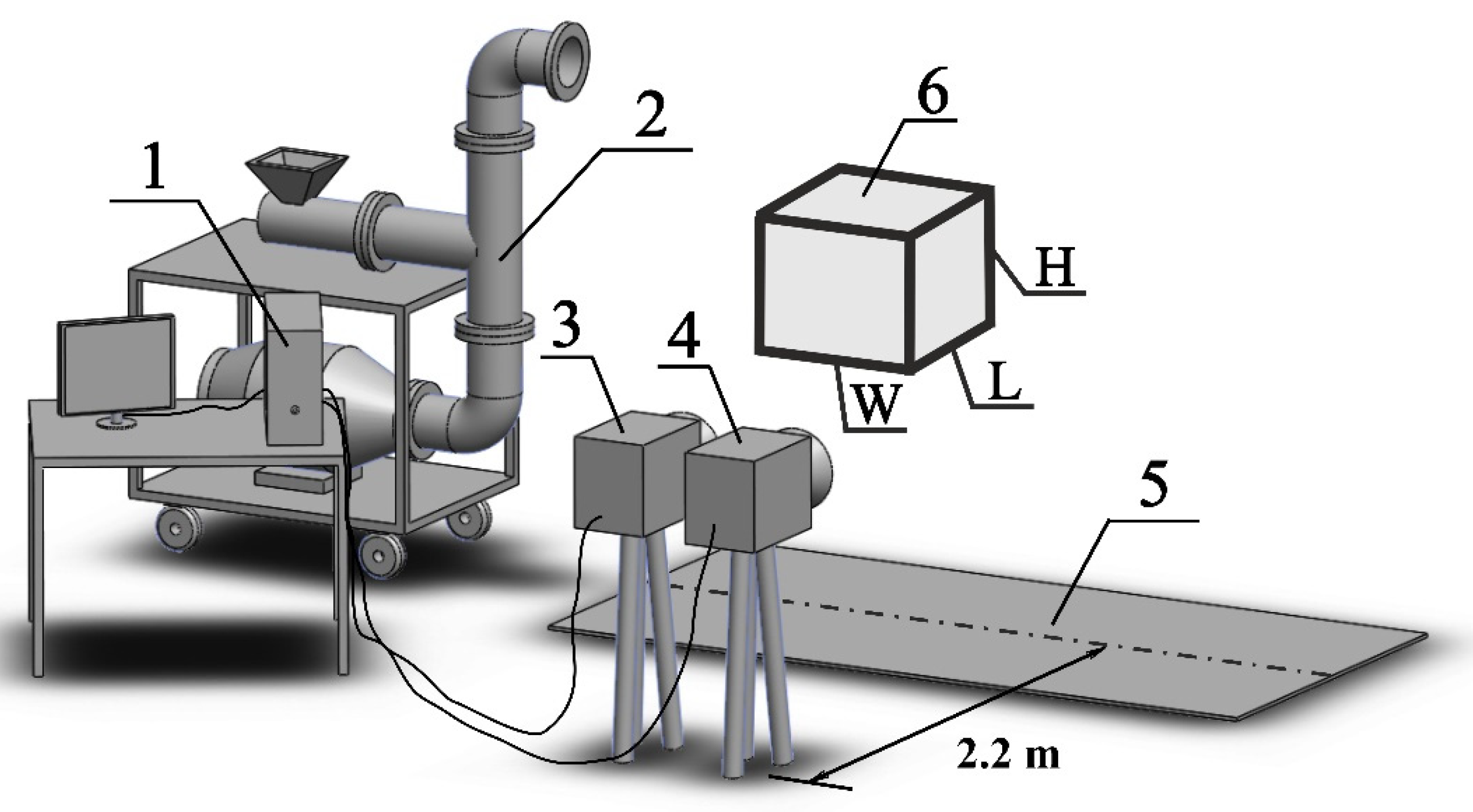
2.3. Laboratory Experiments
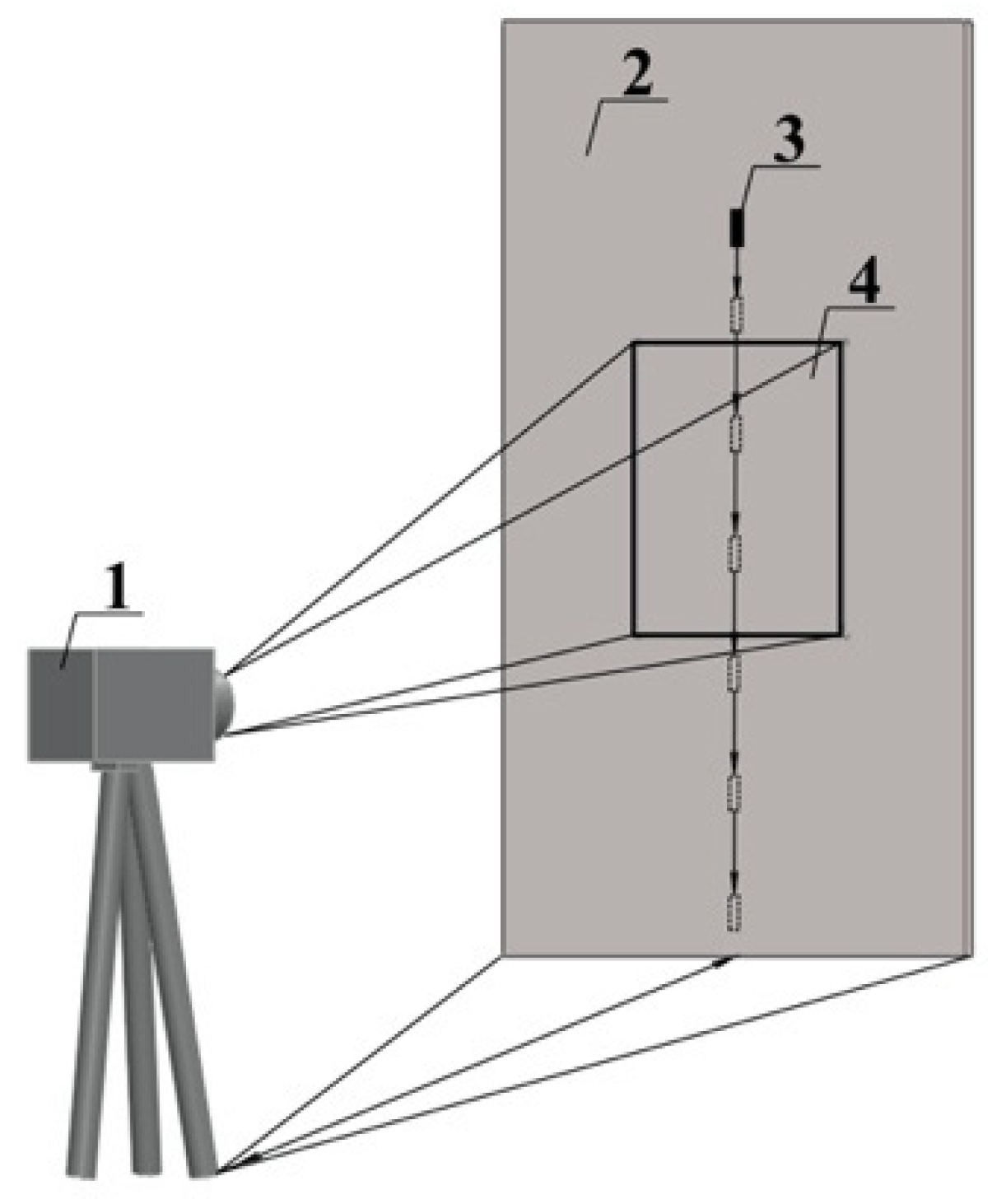
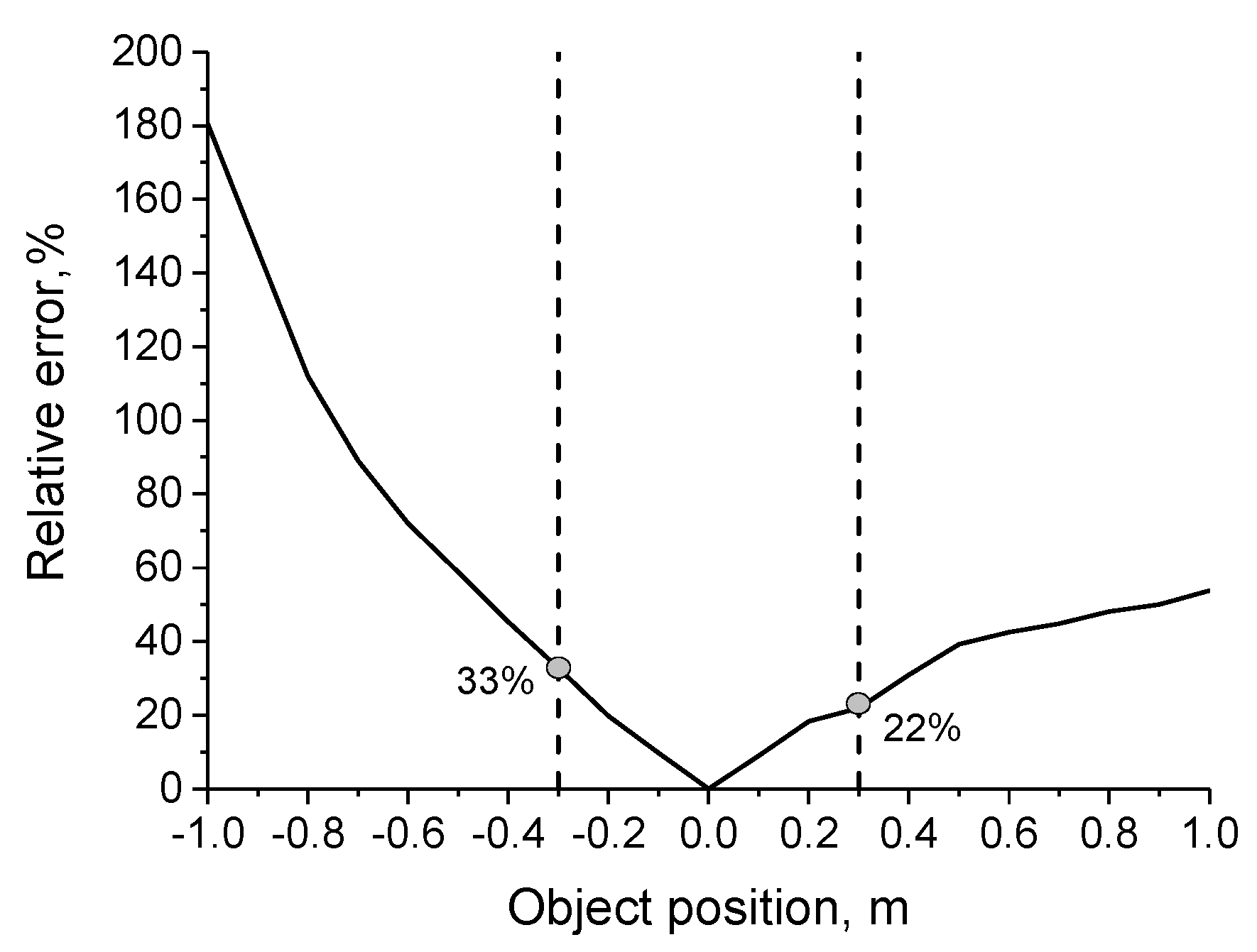
2.4. Particle Area and Temperature Measurements
3. Results and Discussion
3.1. Graphical User Interface (GUI) and Video Annotation
3.2. Laboratory Experiments
3.3. Annotated Video Database
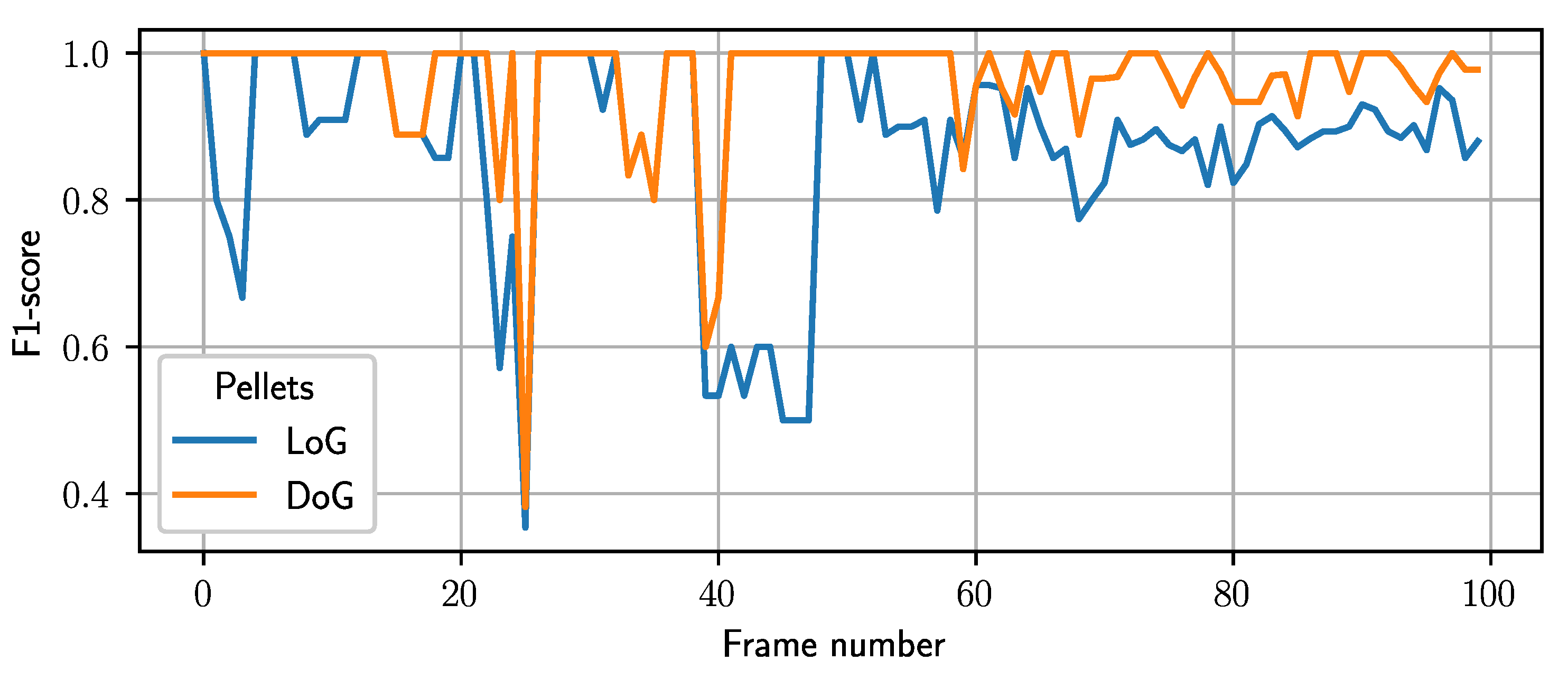
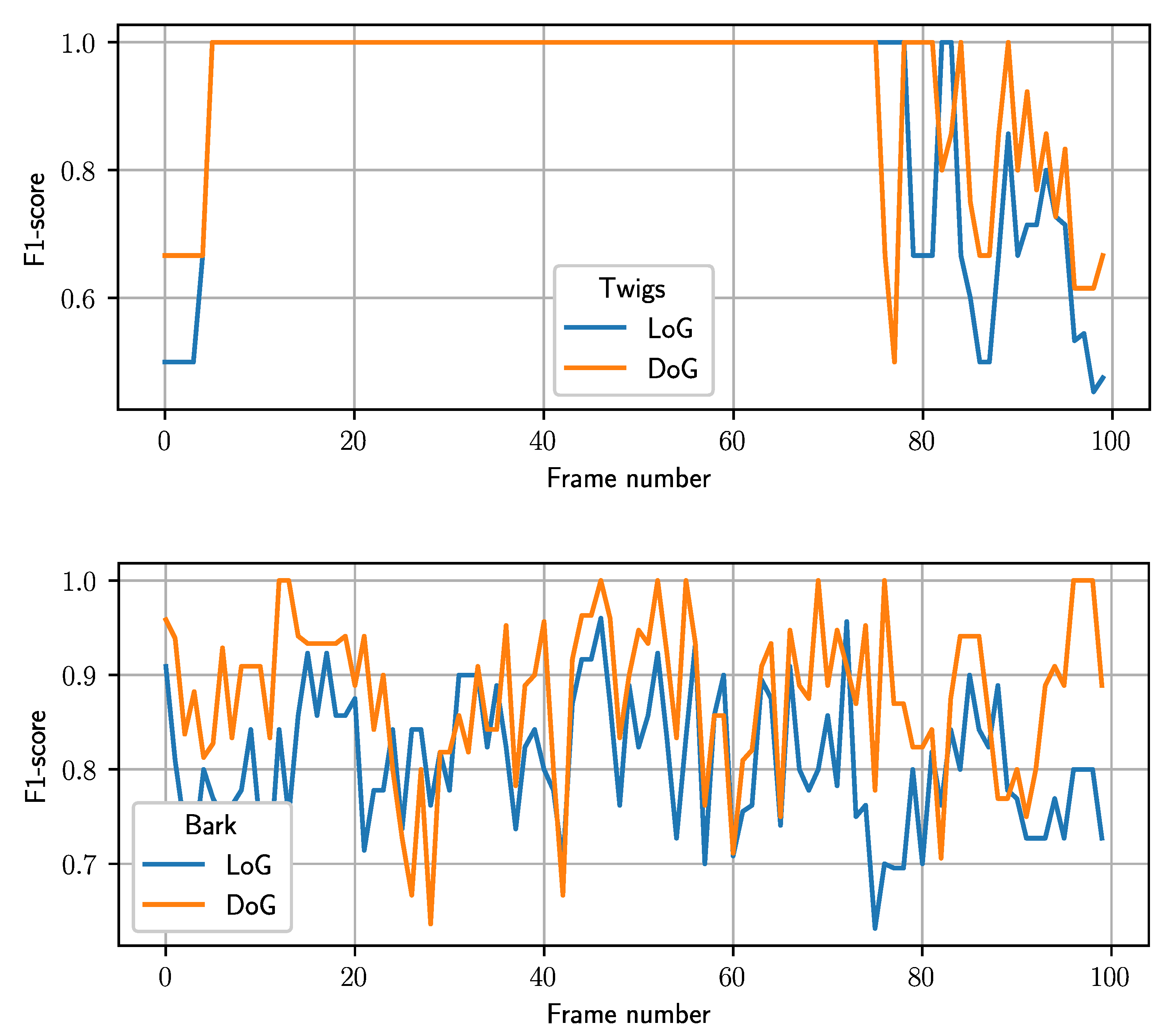
3.4. Detector Testing
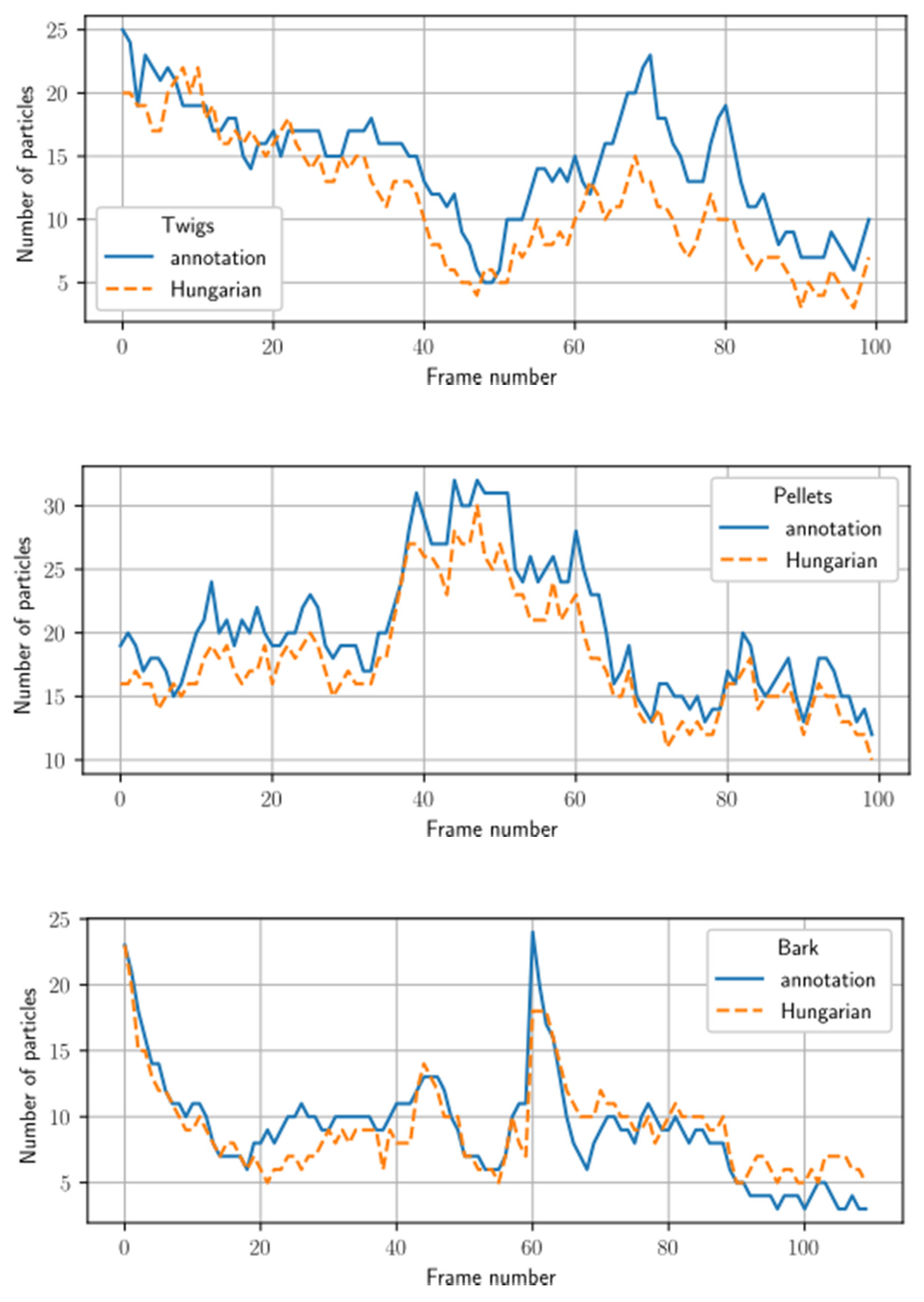
3.5. Tracker Testing Results
3.6. Software Application and Future Research
3.7. Limitations of the Current Study
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Valkó, O.; Török, P.; Deák, B.; Tóthmérész, B. Review: Prospects and limitations of prescribed burning as a management tool in European grasslands. Basic Appl. Ecol. 2014, 15, 26–33. [Google Scholar] [CrossRef]
- Corona, P.; Ascoli, D.; Barbati, A.; Bovio, G.; Colangelo, G.; Elia, M.; Garfì, V.; Iovino, F.; Lafortezza, R.; Leone, V.; et al. Integrated forest management to prevent wildfires under mediterranean environments. Ann. Silvic. Res. 2015, 39, 1–22. [Google Scholar]
- Dupéy, L.N.; Smith, J.W. An Integrative Review of Empirical Research on Perceptions and Behaviors Related to Prescribed Burning and Wildfire in the United States. Environ. Manag. 2018, 61, 1002–1018. [Google Scholar] [CrossRef] [PubMed]
- Leavesley, A.; Wouters, M.; Thornton, R. Prescribed Burning in Australasia: The Science Practice and Politics of Burning the Bush; Australasian Fire and Emergency Service Authorities Council Limited: Melbourne, Australia, 2020. [Google Scholar]
- Morgan, G.W.; Tolhurst, K.G.; Poynter, M.W.; Cooper, N.; McGuffog, T.; Ryan, R.; Wouters, M.A.; Stephens, N.; Black, P.; Sheehan, D.; et al. Prescribed burning in south-eastern Australia: History and future directions. Aust. For. 2020, 83, 4–28. [Google Scholar] [CrossRef]
- Black, A.E.; Hayes, P.; Strickland, R. Organizational Learning from Prescribed Fire Escapes: A Review of Developments over the Last 10 Years in the USA and Australia. Curr. For. Rep. 2020, 6, 41–59. [Google Scholar] [CrossRef]
- Cruz, M.G.; Sullivan, A.L.; Gould, J.S.; Sims, N.C.; Bannister, A.J.; Hollis, J.J.; Hurley, R.J. Anatomy of a catastrophic wildfire: The Black Saturday Kilmore East fire in Victoria, Australia. For. Ecol. Manag. 2012, 284, 269–285. [Google Scholar] [CrossRef]
- Tarifa, C.S.; Notario, P.P.D.; Moreno, F.G. On the flight paths and lifetimes of burning particles of wood. Symp. Combust. 1965, 10, 1021–1037. [Google Scholar] [CrossRef]
- Albini, F.A. Spot Fire Distance from Burning Trees—A Predictive Model; No. General Technical Report INT-GTR-56; USDA Forest Service: Ogden, UT, USA, 1979.
- Albini, F.A. Transport of firebrands by line thermalst. Combust. Sci. Technol. 1983, 32, 277–288. [Google Scholar] [CrossRef]
- Tse, S.D.; Fernandez-Pello, A.C. On the flight paths of metal particles and embers generated by power lines in high winds—A potential source of wildland fires. Fire Saf. J. 1998, 30, 333–356. [Google Scholar] [CrossRef]
- Manzello, S.L.; Suzuki, S. Exposing Decking Assemblies to Continuous Wind-Driven Firebrand Showers. Fire Saf. Sci. 2014, 11, 1339–1352. [Google Scholar] [CrossRef][Green Version]
- Suzuki, S.; Manzello, S.L. Characteristics of Firebrands Collected from Actual Urban Fires. Fire Technol. 2018, 54, 1533–1546. [Google Scholar] [CrossRef] [PubMed]
- Halofsky, J.E.; Peterson, D.L.; Harvey, B.J. Changing wildfire, changing forests: The effects of climate change on fire regimes and vegetation in the Pacific Northwest, USA. Fire Ecol. 2020, 16, 4. [Google Scholar] [CrossRef]
- Radeloff, V.C.; Helmers, D.P.; Kramer, H.A.; Mockrin, M.H.; Alexandre, P.M.; Bar-Massada, A.; Butsic, V.; Hawbaker, T.J.; Martinuzzi, S.; Syphard, A.D.; et al. Rapid growth of the US wildland-urban interface raises wildfire risk. Proc. Natl. Acad. Sci. USA 2018, 115, 3314. [Google Scholar] [CrossRef] [PubMed]
- El Houssami, M.; Mueller, E.; Filkov, A.; Thomas, J.C.; Skowronski, N.; Gallagher, M.R.; Clark, K.; Kremens, R.; Simeoni, A. Experimental Procedures Characterising Firebrand Generation in Wildland Fires. Fire Technol. 2016, 52, 731–751. [Google Scholar] [CrossRef]
- Filkov, A.; Prohanov, S.; Mueller, E.; Kasymov, D.; Martynov, P.; Houssami, M.E.; Thomas, J.; Skowronski, N.; Butler, B.; Gallagher, M.; et al. Investigation of firebrand production during prescribed fires conducted in a pine forest. Proc. Combust. Inst. 2017, 36, 3263–3270. [Google Scholar] [CrossRef]
- Thomas, J.C.; Mueller, E.V.; Santamaria, S.; Gallagher, M.; El Houssami, M.; Filkov, A.; Clark, K.; Skowronski, N.; Hadden, R.M.; Mell, W.; et al. Investigation of firebrand generation from an experimental fire: Development of a reliable data collection methodology. Fire Saf. J. 2017, 91, 864–871. [Google Scholar] [CrossRef]
- Caton-Kerr, S.E.; Tohidi, A.; Gollner, M.J. Firebrand Generation from Thermally-Degraded Cylindrical Wooden Dowels. Front. Mech. Eng. 2019, 5, 32. [Google Scholar] [CrossRef]
- Hedayati, F.; Bahrani, B.; Zhou, A.; Quarles, S.L.; Gorham, D.J. A Framework to Facilitate Firebrand Characterization. Front. Mech. Eng. 2019, 5, 43. [Google Scholar] [CrossRef]
- Liu, K.; Liu, D. Particle tracking velocimetry and flame front detection techniques on commercial aircraft debris striking events. J. Vis. 2019, 22, 783–794. [Google Scholar] [CrossRef]
- Liu, Y.; Urban, J.L.; Xu, C.; Fernandez-Pello, C. Temperature and Motion Tracking of Metal Spark Sprays. Fire Technol. 2019, 55, 2143–2169. [Google Scholar] [CrossRef]
- Bouvet, N.; Link, E.D.; Fink, S.A. Development of a New Approach to Characterize Firebrand Showers during Wildland-Urban Interface (WUI) Fires: A Step towards High-Fidelity Measurements in Three Dimensions; No. Technical Note; NIST: Gaithersburg, MD, USA, 2020.
- Filkov, A.; Prohanov, S. Particle Tracking and Detection Software for Firebrands Characterization in Wildland Fires. Fire Technol. 2019, 55, 817–836. [Google Scholar] [CrossRef]
- Guttag, J.V. Introduction to Computation and Programming Using Python; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Hand, D.; Christen, P. A note on using the F-measure for evaluating record linkage algorithms. Stat. Comput. 2018, 28, 539–547. [Google Scholar] [CrossRef]
- Knuth, D.E. The Art of Computer Programming, 3rd ed.; Fundamental Algorithms; Addison Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1997; Volume 1. [Google Scholar]
- Munkres, J. Algorithms for the Assignment and Transportation Problems. J. Soc. Ind. Appl. Math. 1957, 5, 32–38. [Google Scholar] [CrossRef]
- Bernardin, K.; Stiefelhagen, R. Evaluating Multiple Object Tracking Performance: The CLEAR MOT Metrics. EURASIP J. Image Video Process. 2008, 2008, 246309. [Google Scholar] [CrossRef]
- Kasymov, D.P.P.V.V.; Filkov, A.I.; Agafontsev, A.M.; Reyno, V.V.; Gordeev, E.V. Generator of Flaming and Glowing Firebrands; FIPS: Moscow, Russia, 2017; p. 183063. [Google Scholar]
- Introducing JSON. Available online: https://www.json.org/ (accessed on 31 August 2020).
- Hua, W.; Mu, D.; Zheng, Z.; Guo, D. Online multi-person tracking assist by high-performance detection. J. Supercomput. 2017, 76, 4076–4094. [Google Scholar] [CrossRef]
- Rahul, M.V.; Ambareesh, R.; Shobha, G. Siamese Network for Underwater Multiple Object Tracking. In Proceedings of the 9th International Conference on Machine Learning and Computing, Singapore, 24–26 February 2017; pp. 511–516. [Google Scholar]




| Cylinder | Sphere | ||||||
|---|---|---|---|---|---|---|---|
| Frequency (Hz) | 190 | 63 | 30 | 190 | 63 | 30 | |
| Mean relative error (%) | 3 m (1.8 × 1.8 mm pixel size) | 3.8 | 4.1 | 4.7 | 3.7 | 4.2 | 4.3 |
| 6 m (3.6 × 3.6 mm pixel size) | 4.9 | 6.9 | 7.8 | 4.9 | 5.3 | 5.6 | |
| File # | Fuel Type | Test Type | Total Number of Firebrands, Pieces | Mean Firebrands Per Frame, Pieces |
|---|---|---|---|---|
| 1 | Pellets | Calibration | 227 | 13 |
| 2 | Pellets | Calibration | 694 | 21 |
| 3 | Pellets | Blind comparison | 238 | 14 |
| 4 | Twigs | Calibration | 51 | 5 |
| 5 | Twigs | Calibration | 210 | 19 |
| 6 | Twigs | Blind comparison | 152 | 15 |
| 7 | Bark | Calibration | 108 | 19 |
| 8 | Bark | Blind comparison | 67 | 22 |
| Firebrands | Average F1 Score (%) | |
|---|---|---|
| Calibration Test | Blind Test | |
| Pellets | 86 | 74 |
| Twigs | 79 | 44 |
| Bark | 83 | 78 |
| Firebrand Type | Algorithm of Tracker | MOTP (%) | MOTA (%) | ||
|---|---|---|---|---|---|
| Calibration Test | Blind Test | Calibration Test | Blind Test | ||
| Pellets | Nearest neighbor | 86 | 86 | 52 | 46 |
| Hungarian algorithm | 86 | 86 | 66 | 64 | |
| Twigs | Nearest neighbor | 90 | 88 | 35 | 33 |
| Hungarian algorithm | 89 | 88 | 45 | 42 | |
| Bark | Nearest neighbor | 85 | 89 | 62 | 41 |
| Hungarian algorithm | 85 | 89 | 73 | 58 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prohanov, S.; Filkov, A.; Kasymov, D.; Agafontsev, M.; Reyno, V. Determination of Firebrand Characteristics Using Thermal Videos. Fire 2020, 3, 68. https://doi.org/10.3390/fire3040068
Prohanov S, Filkov A, Kasymov D, Agafontsev M, Reyno V. Determination of Firebrand Characteristics Using Thermal Videos. Fire. 2020; 3(4):68. https://doi.org/10.3390/fire3040068
Chicago/Turabian StyleProhanov, Sergey, Alexander Filkov, Denis Kasymov, Mikhail Agafontsev, and Vladimir Reyno. 2020. "Determination of Firebrand Characteristics Using Thermal Videos" Fire 3, no. 4: 68. https://doi.org/10.3390/fire3040068
APA StyleProhanov, S., Filkov, A., Kasymov, D., Agafontsev, M., & Reyno, V. (2020). Determination of Firebrand Characteristics Using Thermal Videos. Fire, 3(4), 68. https://doi.org/10.3390/fire3040068






