Evacuation Path Planning Based on the Hybrid Improved Sparrow Search Optimization Algorithm
Abstract
:1. Introduction
2. Introduction of the Basic Sparrow Algorithm
3. The Proposed Sparrow Optimization Algorithm
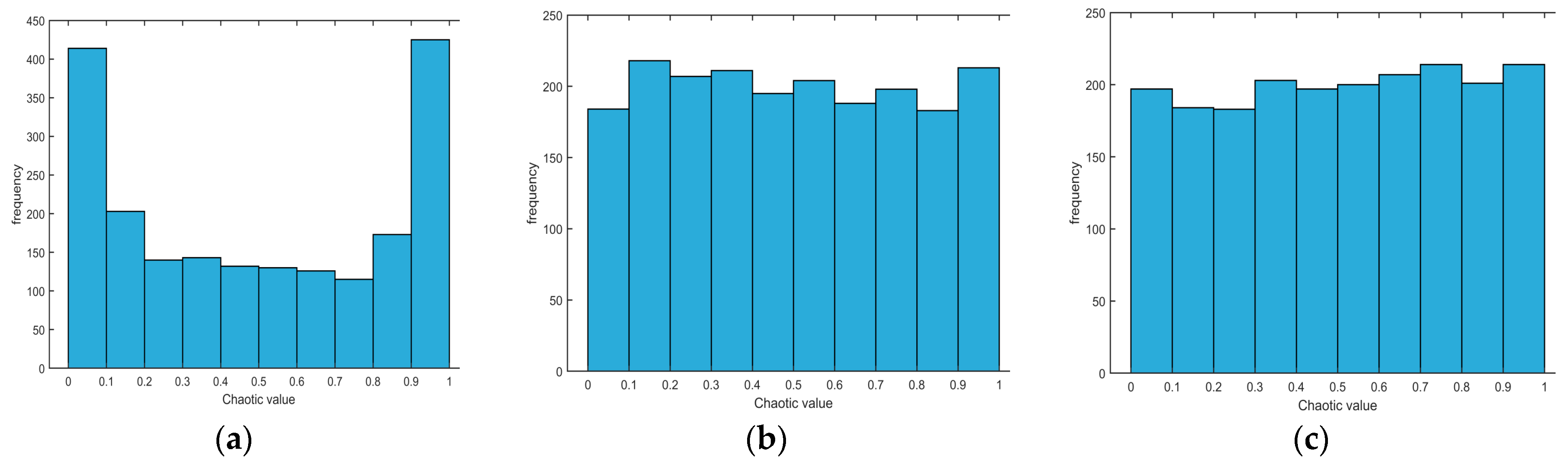
3.1. Optimization of Initial Sparrow Population Diversity—Logistic-Tent Chaos Mapping
3.2. Optimization of the Producers’ Location—The Adaptive Convergence Factor
3.3. Optimization of the Scroungers’ Location—The Lévy Flight Mechanism
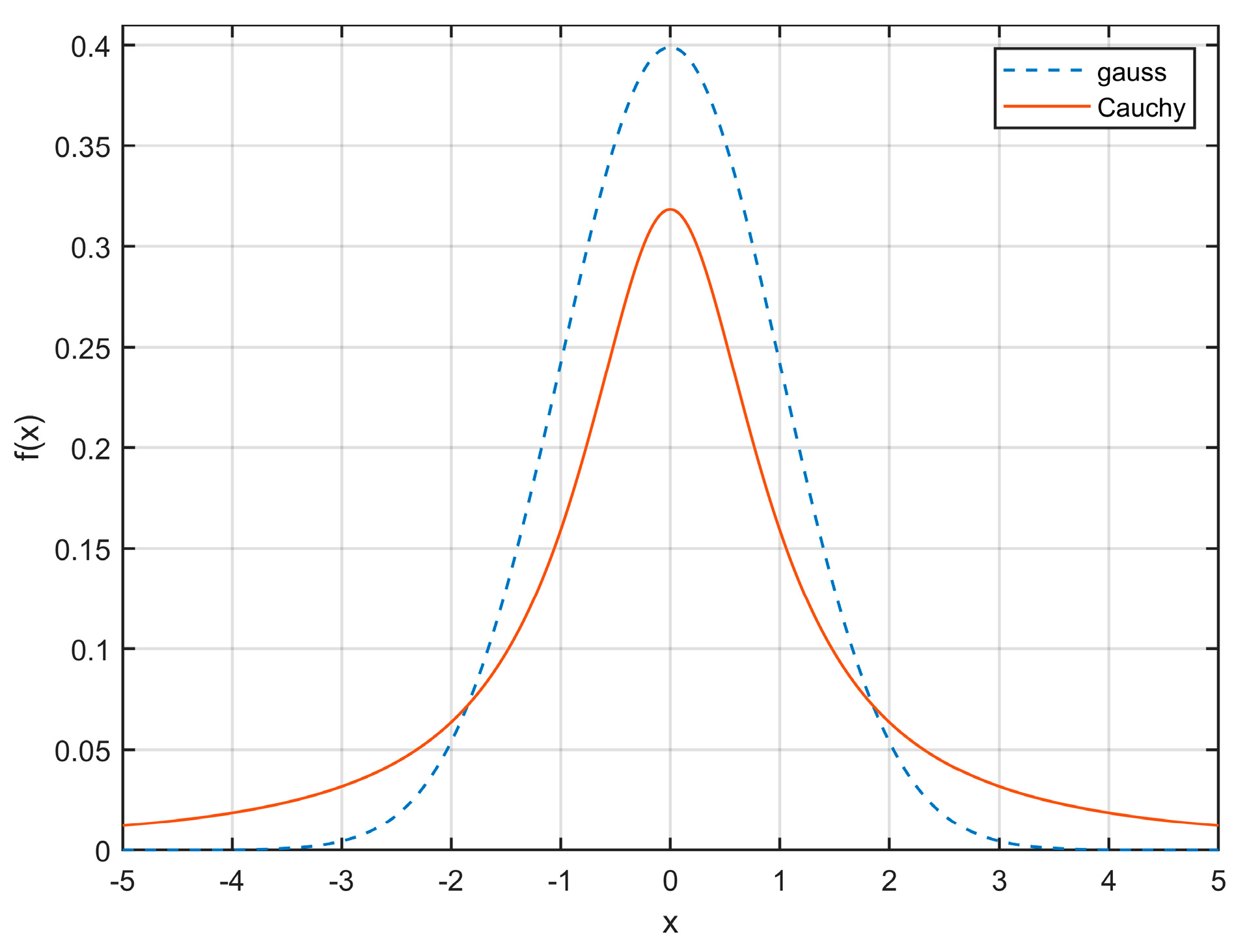
3.4. Jumping out of the Local Optima—The Mutation Factor
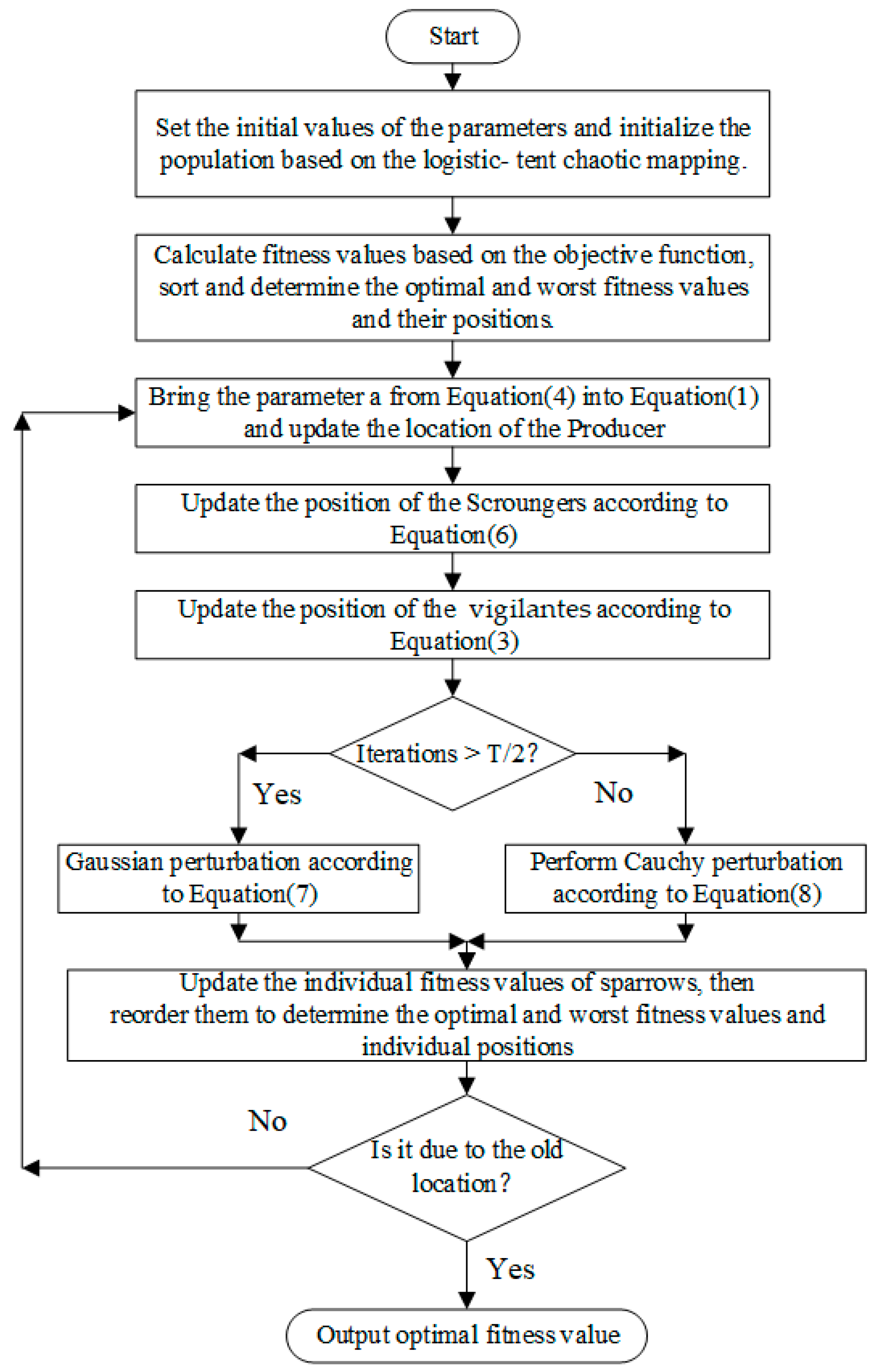
3.5. The Process of the Optimization Sparrow Algorithm
4. Simulation Experiments and Analysis
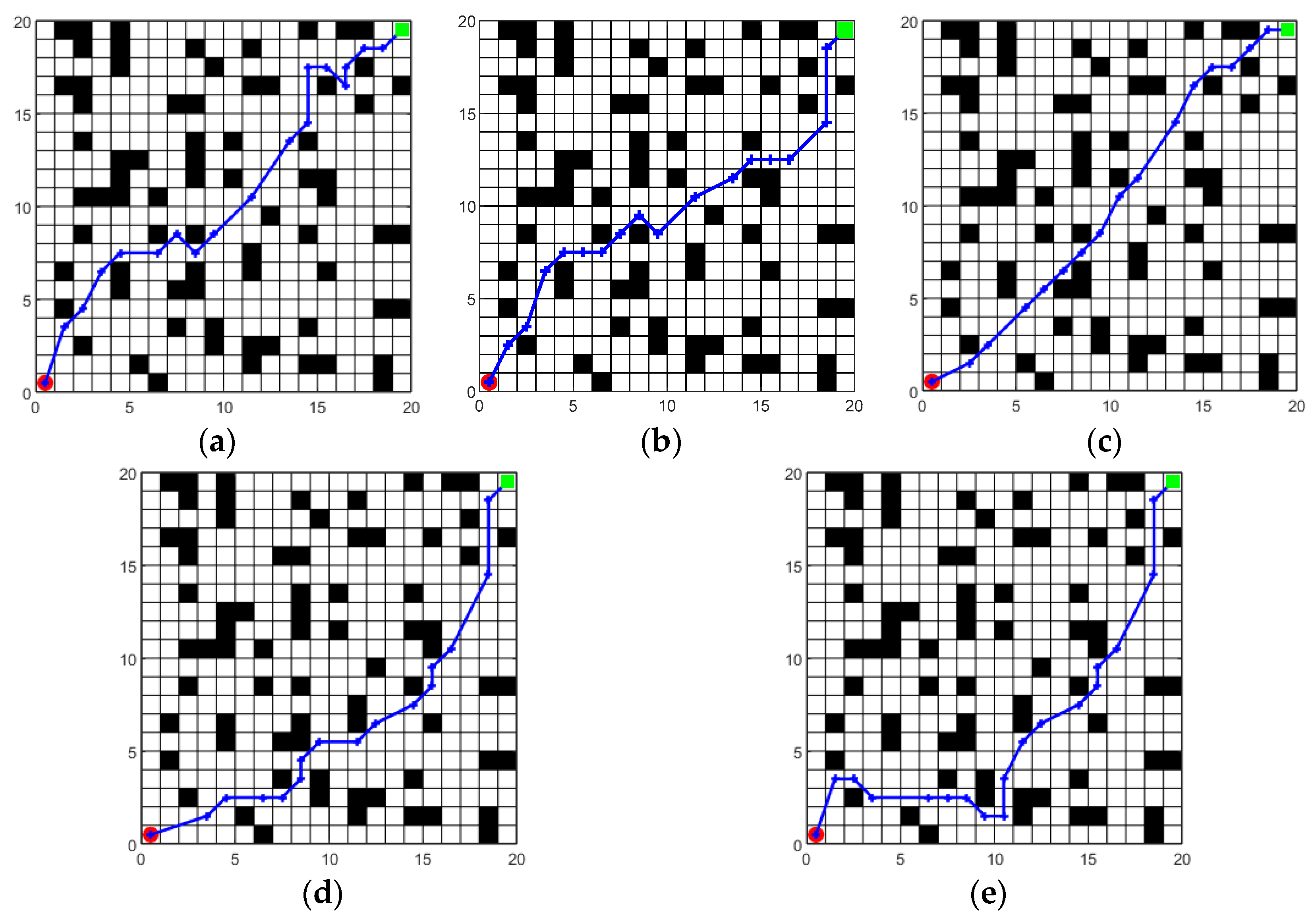
4.1. Path Planning Simulation Using the Hybrid Optimization Sparrow Algorithm
4.2. Qualitative Analysis of Path Planning
4.3. Quantitative Analysis of Path Planning Results
4.3.1. The Length of Optimal
- (1)
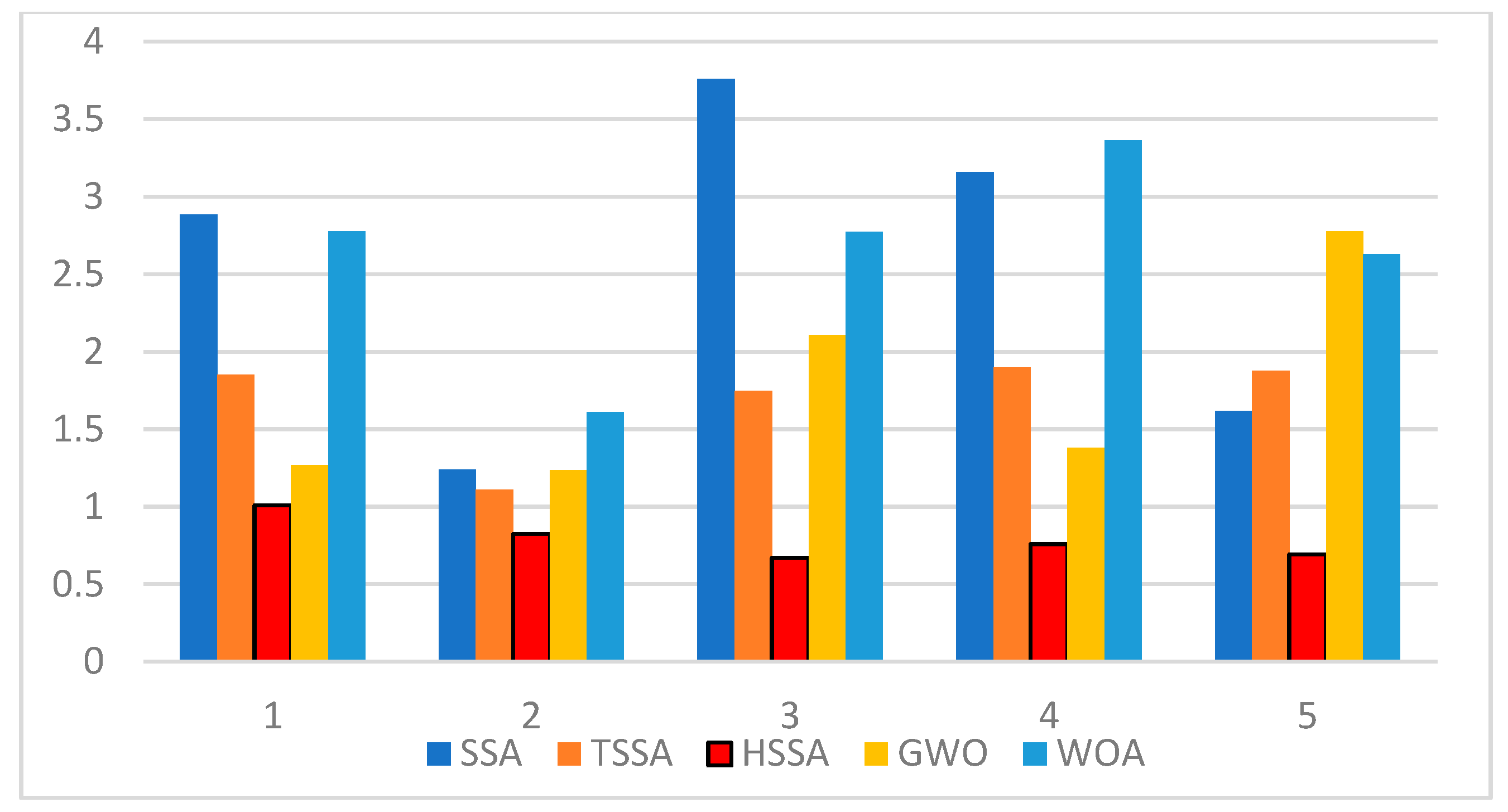
- In Figure 7a, compared with the lengths of the optimal paths planned by the SSA algorithm for five different maps, the lengths of the optimal paths planned with the HSSA algorithm are shortened by 22.52%, 18.26%, 20.43%, 10.97%, and 22.02%, respectively. In Figure 7b, the lengths of the average paths planned by the HSSA are decreased by 29.24%, 19.50%, 27.14%, 19.16%, and 26.34%, respectively, compared with the SSA algorithm. Meanwhile, the standard deviations of the optimal path lengths are also significantly smaller than those of the SSA algorithm.
- (2)
- In Figure 7a, compared with the lengths of the optimal paths planned by the TSSA algorithm for five different maps, the lengths of the optimal paths planned with the HSSA algorithm are shortened by 3.53%, 10.58%, 7.89%, 5.28%, and 10.05%, respectively. In Figure 7b, the lengths of the average paths planned by the HSSA are decreased by 15.81%, 13.62%, 13.11%, 10.70%, and 15.02%, respectively, compared with the TSSA algorithm. The corresponding standard deviation of the optimal path lengths planned by the HSSA algorithm is also smaller than that of the TSSA algorithm, indicating that the performance of the HSSA algorithm is stronger than the performances of the SSA and TSSA algorithms.
- (3)
- In Figure 7a, compared with the lengths of the optimal paths planned by the GWO algorithm for five different maps, the lengths of the optimal paths planned with the HSSA algorithm are shortened by 5.58%, 7.62%, 6.80%, 5.28%, and 7.38%, respectively. In Figure 7b, the average lengths of the optimal paths planned by the HSSA algorithm are decreased by 7.55%, 8.74%, 11.63%, 8.69%, and 14.90%, respectively, compared with the GWO algorithm. As shown in Figure 8, the standard deviations of the optimal path lengths planned by the HSSA algorithm are decreased by 20.40%, 30.36%, 68.20%, 44.99%, and 70.74%. The minimums of the optimal path lengths, the averages of the optimal path lengths, and the standard deviations of the optimal path lengths could prove that the stability and searching ability of the HSSA algorithm is much stronger than that of the GWO algorithm on the five maps.
- (4)
- Comparing with the WOA algorithm, the lengths of the optimal paths planned by the HSSA algorithm are shortened by 15.22%, 9.49%, 18.42%, 1.77%, and 17.81%, respectively, and the average lengths of the optimal paths are decreased by 17.68%, 13.33%, 27.47%, 13.39%, and 25.08%, separately. Meanwhile, with regard to the path planning in map 4, although the length of the optimal path planned by the HSSA algorithm is just a little smaller than that of the WOA algorithm, the average lengths and the standard deviations of the optimal paths also could prove the stronger stability and searching ability of the HSSA algorithm than that of the WOA algorithm on this map.
4.3.2. The Time Cost of the Optimal Path
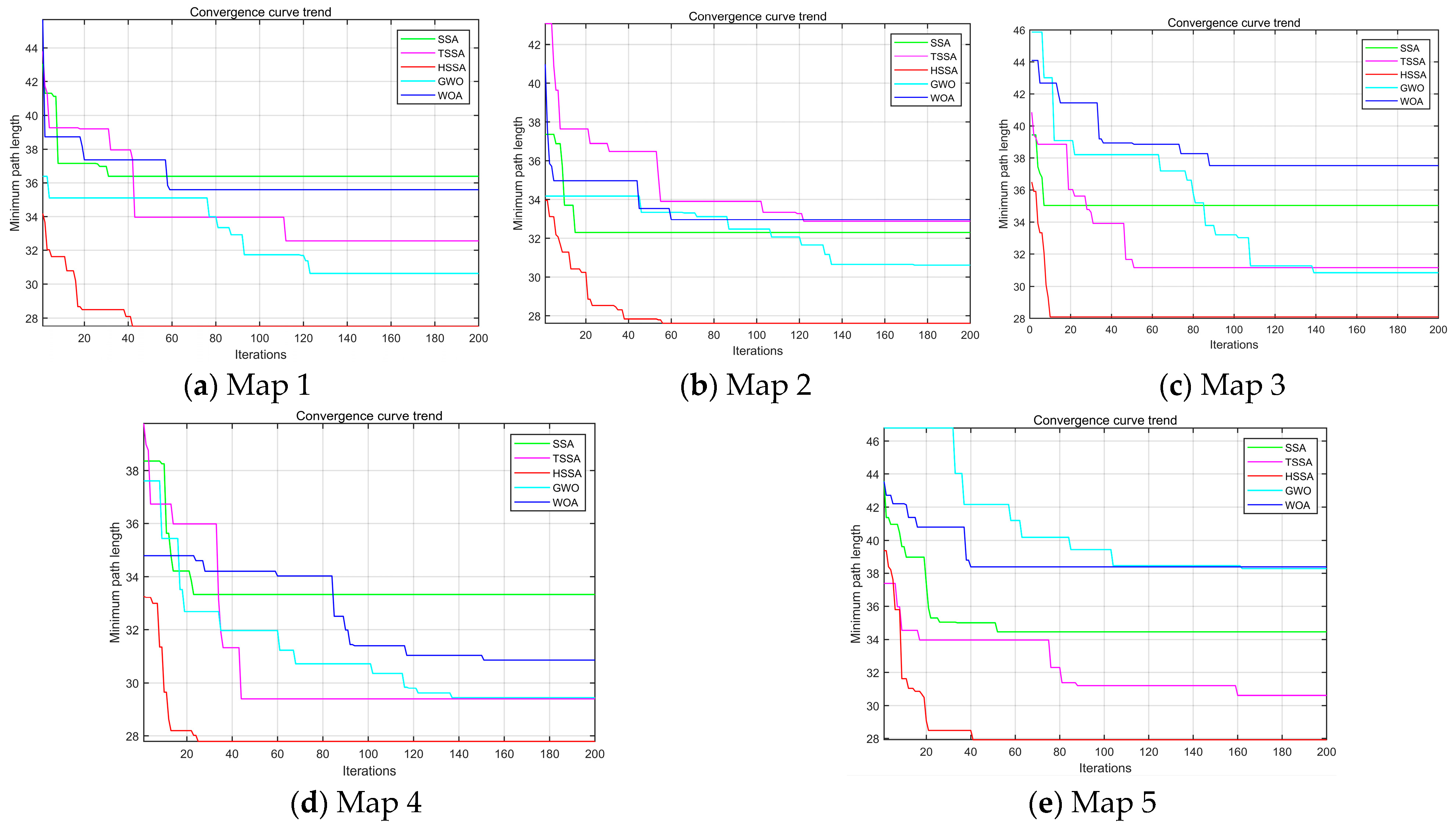
4.3.3. The Convergence of Different Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Haghani, M.; Sarvi, M. Crowd behaviour and motion: Empirical methods. Transp. Res. Part B Methodol. 2018, 107, 253–294. [Google Scholar] [CrossRef]
- Fridolf, K.; Nilsson, D.; Frantzich, H. Fire evacuation in underground transportation systems: A review of accidents and empirical research. Fire Technol. 2013, 49, 451–475. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Y.; Qu, D.; Chen, X.; Li, Y. Multi-Objective Optimization of Evacuation Route for Heterogeneous Passengers in the Metro Station Considering Node Efficiency. IEEE Trans. Intell. Transp. Syst. 2023, 99, 1–14. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Venkat, I.; Subramanian, K.G.; Khader, A.T.; Wilde, P.D. Intelligent evacuation management systems: A review. ACM Trans. Intell. Syst. Technol. (TIST) 2016, 7, 1–27. [Google Scholar] [CrossRef]
- Sharbini, H.; Sallehuddin, R.; Haron, H. Crowd evacuation simulation model with soft computing optimization techniques: A systematic literature review. J. Manag. Anal. 2021, 8, 443–485. [Google Scholar] [CrossRef]
- Guan, W.; Hou, S.; Yu, G.; Gong, H.; Guan, S.; Zhao, J. Dynamic Evacuation Path Planning for Multi-Exit Building Fire: Bi-Objective Model and Algorithm. Fire Technol. 2023, 59, 2853–2876. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, H.; Wang, Z.; Li, Q.; Dou, Z.; Xie, W.; Zhang, Z.; Wang, R.; Nie, W. Optimal Evacuation Route Planning of Urban Personnel at Different Risk Levels of Flood Disasters Based on the Improved 3D Dijkstra’s Algorithm. Sustainability 2022, 14, 10250. [Google Scholar] [CrossRef]
- Liu, L.; Wang, B.; Xu, H. Research on path-planning algorithm integrating optimization A-star algorithm and artificial potential field method. Electronics 2022, 11, 3660. [Google Scholar] [CrossRef]
- Zhang, R.; Sun, W.; Tsai, S.-B. Simulation of Sports Venue Based on Ant Colony Algorithm and Artificial Intelligence. Wirel. Commun. Mob. Comput. 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Asghari, K.; Masdari, M.; Gharehchopogh, F.S.; Saneifard, R. A chaotic and hybrid gray wolf-whale algorithm for solving continuous optimization problems. Prog. Artif. Intell. 2021, 10, 349–374. [Google Scholar] [CrossRef]
- Peng, Y.; Li, S.-W.; Hu, Z.-Z. A self-learning dynamic path planning method for evacuation in large public buildings based on neural networks. Neurocomputing 2019, 365, 71–85. [Google Scholar] [CrossRef]
- Zhou, Z.-X.; Nakanishi, W.; Asakura, Y. Data-driven framework for the adaptive exit selection problem in pedestrian flow: Visual information based heuristics approach. Phys. A Stat. Mech. Its Appl. 2021, 583, 126289. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, H.; Gao, K.; Zhang, L. Improved multi-agent reinforcement learning for path planning-based crowd simulation. IEEE Access 2019, 7, 73841–73855. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Song, J.; Jin, L.; Xie, Y.; Wei, C. Optimized XGBoost based sparrow search algorithm for short-term load forecasting. In Proceedings of the 2021 IEEE International Conference on Computer Science, Artificial Intelligence and Electronic Engineering (CSAIEE), Beijing, China, 20–22 August 2021. [Google Scholar]
- Liu, T.; Yuan, Z.; Wu, L.; Badami, B. An optimal brain tumor detection by convolutional neural network and enhanced sparrow search algorithm. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2021, 235, 459–469. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Z.; Wu, L.; Badami, B. Optimal brain tumor diagnosis based on deep learning and balanced sparrow search algorithm. Int. J. Imaging Syst. Technol. 2021, 31, 1921–1935. [Google Scholar] [CrossRef]
- Kathiroli, P.; Selvadurai, K. Energy efficient cluster head selection using improved Sparrow Search Algorithm in Wireless Sensor Networks. J. King Saud Univ. -Comput. Inf. Sci. 2022, 34, 8564–8575. [Google Scholar] [CrossRef]
- Cao, L.; Yue, Y.; Zhang, Y. A data collection strategy for heterogeneous wireless sensor networks based on energy efficiency and collaborative optimization. Comput. Intell. Neurosci. 2021, 2021, 9808449. [Google Scholar] [CrossRef]
- Lv, J.; Sun, W.; Wang, H.; Zhang, F. Coordinated approach fusing RCMDE and sparrow search algorithm-based SVM for fault diagnosis of rolling bearings. Sensors 2021, 21, 5297. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; He, R.; Yang, K. A bioinspired path planning approach for mobile robots based on improved sparrow search algorithm. Adv. Manuf. 2022, 10, 114–130. [Google Scholar] [CrossRef]
- Jiang, Z.; Ge, J.; Xu, Q.; Yang, T. Fast Trajectory Optimization for Gliding Reentry Vehicle Based on Improved Sparrow Search Algorithm. J. Phys. Conf. Ser. 2021, 1986, 012114. [Google Scholar] [CrossRef]
- Liu, G.; Shu, C.; Liang, Z.; Peng, B.; Cheng, L. A modified sparrow search algorithm with application in 3d route planning for UAV. Sensors 2021, 21, 1224. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Elaziz, M.A.; Lu, S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018, 108, 1–27. [Google Scholar] [CrossRef]
- Teng, Z.-J.; Lv, J.-L.; Guo, L.-W. An improved hybrid grey wolf optimization algorithm. Soft Comput. 2019, 23, 6617–6631. [Google Scholar] [CrossRef]
- Shan, L.; Qiang, H.; Li, J.; Wang, Z. Chaotic optimization algorithm based on Tent map. Control. Decis. 2005, 20, 179–182. [Google Scholar]
- Reynolds, A. Liberating Lévy walk research from the shackles of optimal foraging. Phys. Life Rev. 2015, 14, 59–83. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]



| Map | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Algorithm | ||||||
| SSA | Minimum (s) | 0.2154 | 0.2326 | 0.2182 | 0.2004 | 0.2304 |
| Average (s) | 0.3144 | 0.3696 | 0.3966 | 0.3532 | 0.4045 | |
| Standard deviation | 0.0954 | 0.1052 | 0.1174 | 0.1374 | 0.1882 | |
| TSSA | Minimum (s) | 0.6281 | 0.4056 | 0.9589 | 0.2528 | 0.5586 |
| Average (s) | 0.9297 | 0.8297 | 1.2329 | 0.7021 | 0.9218 | |
| Standard deviation | 0.2382 | 0.2441 | 0.2578 | 0.2499 | 0.2976 | |
| HSSA | Minimum (s) | 0.3581 | 0.2331 | 0.2920 | 0.2818 | 0.3266 |
| Average (s) | 0.5547 | 0.4323 | 0.4534 | 0.4035 | 0.5202 | |
| Standard deviation | 0.0974 | 0.1215 | 0.1158 | 0.0795 | 0.1160 | |
| GWO | Minimum (s) | 0.2453 | 0.2413 | 0.2729 | 0.2845 | 0.2587 |
| Average (s) | 0.4747 | 0.4585 | 0.4078 | 0.4552 | 0.4419 | |
| Standard deviation | 0.1711 | 0.1862 | 0.0789 | 0.1496 | 0.0852 | |
| WOA | Minimum (s) | 0.3827 | 0.3432 | 0.3397 | 0.2689 | 0.3402 |
| Average (s) | 0.5937 | 0.4830 | 0.4712 | 0.4044 | 0.4089 | |
| Standard deviation | 0.1575 | 0.1342 | 0.1092 | 0.1167 | 0.0614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Zhang, Y.; Zhao, Y. Evacuation Path Planning Based on the Hybrid Improved Sparrow Search Optimization Algorithm. Fire 2023, 6, 380. https://doi.org/10.3390/fire6100380
Wei X, Zhang Y, Zhao Y. Evacuation Path Planning Based on the Hybrid Improved Sparrow Search Optimization Algorithm. Fire. 2023; 6(10):380. https://doi.org/10.3390/fire6100380
Chicago/Turabian StyleWei, Xiaoge, Yuming Zhang, and Yinlong Zhao. 2023. "Evacuation Path Planning Based on the Hybrid Improved Sparrow Search Optimization Algorithm" Fire 6, no. 10: 380. https://doi.org/10.3390/fire6100380
APA StyleWei, X., Zhang, Y., & Zhao, Y. (2023). Evacuation Path Planning Based on the Hybrid Improved Sparrow Search Optimization Algorithm. Fire, 6(10), 380. https://doi.org/10.3390/fire6100380









