Comparative Assessment of Wildland Fire Rate of Spread Models: Effects of Wind Velocity
Abstract
1. Introduction
2. Materials and Methods
2.1. Semi-Empirical, Laboratory-Developed ROS Models
2.2. Empirical, Laboratory-Developed ROS Models
2.3. Wind Correction Empirical Sub-Models
2.4. Empirical, Field-Based Models and Wind Adjustment Factor
2.5. Laboratory Experimental Data
3. Results
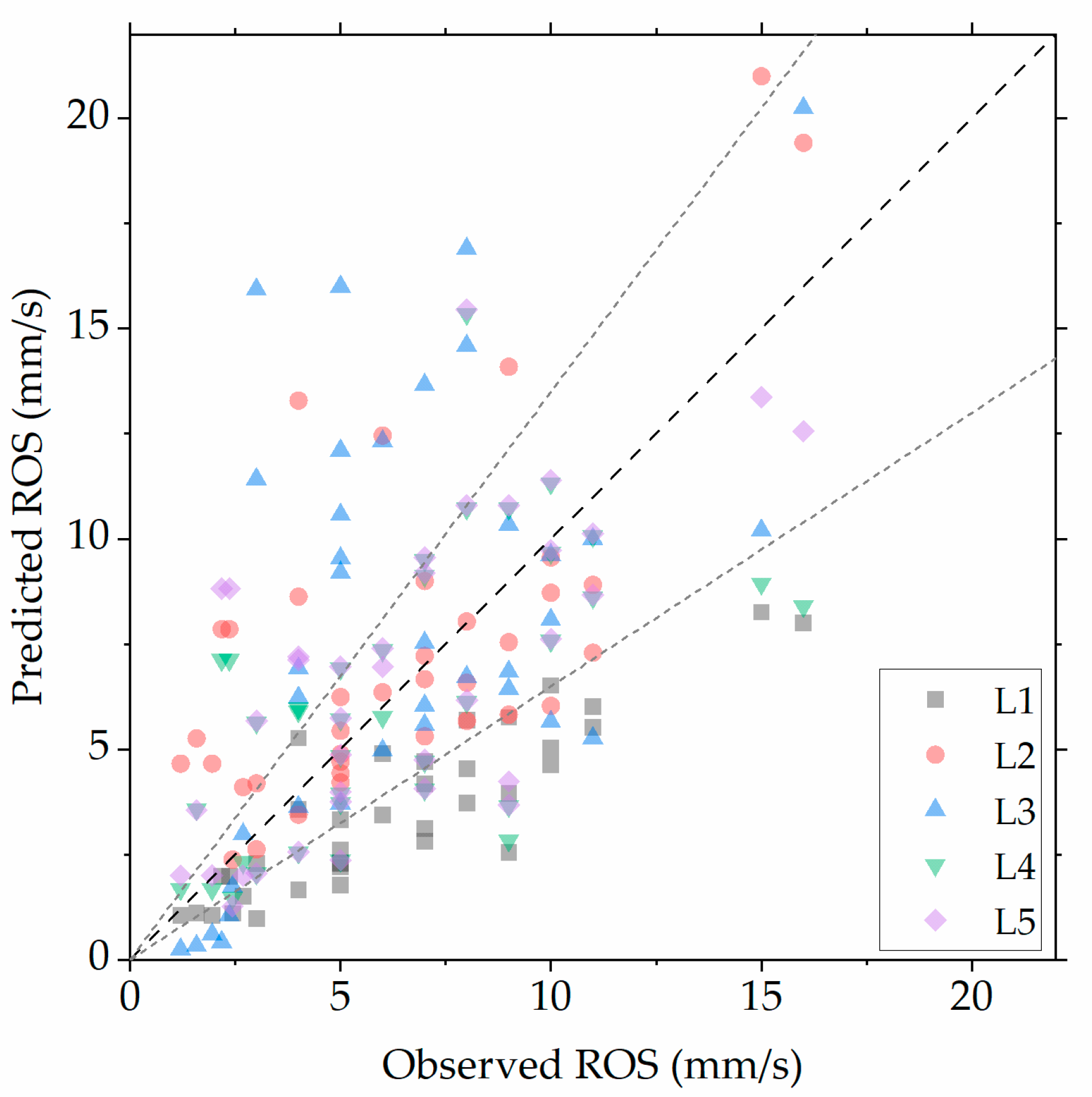
3.1. Laboratory-Developed Models in Quiescent Conditions
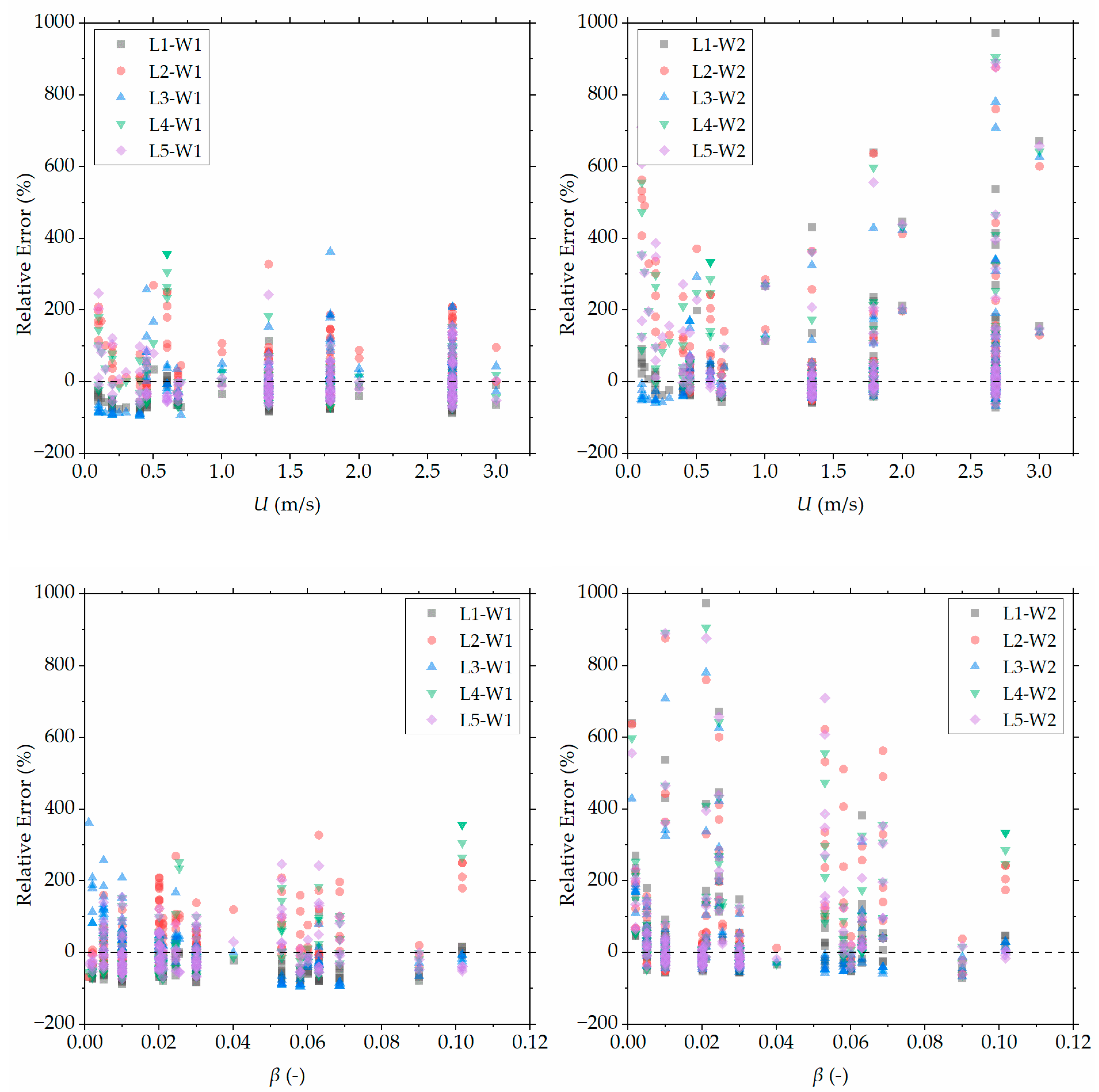
3.2. Laboratory-Developed Models, Combined with Wind-Correction Sub-Models, against External Wind Conditions
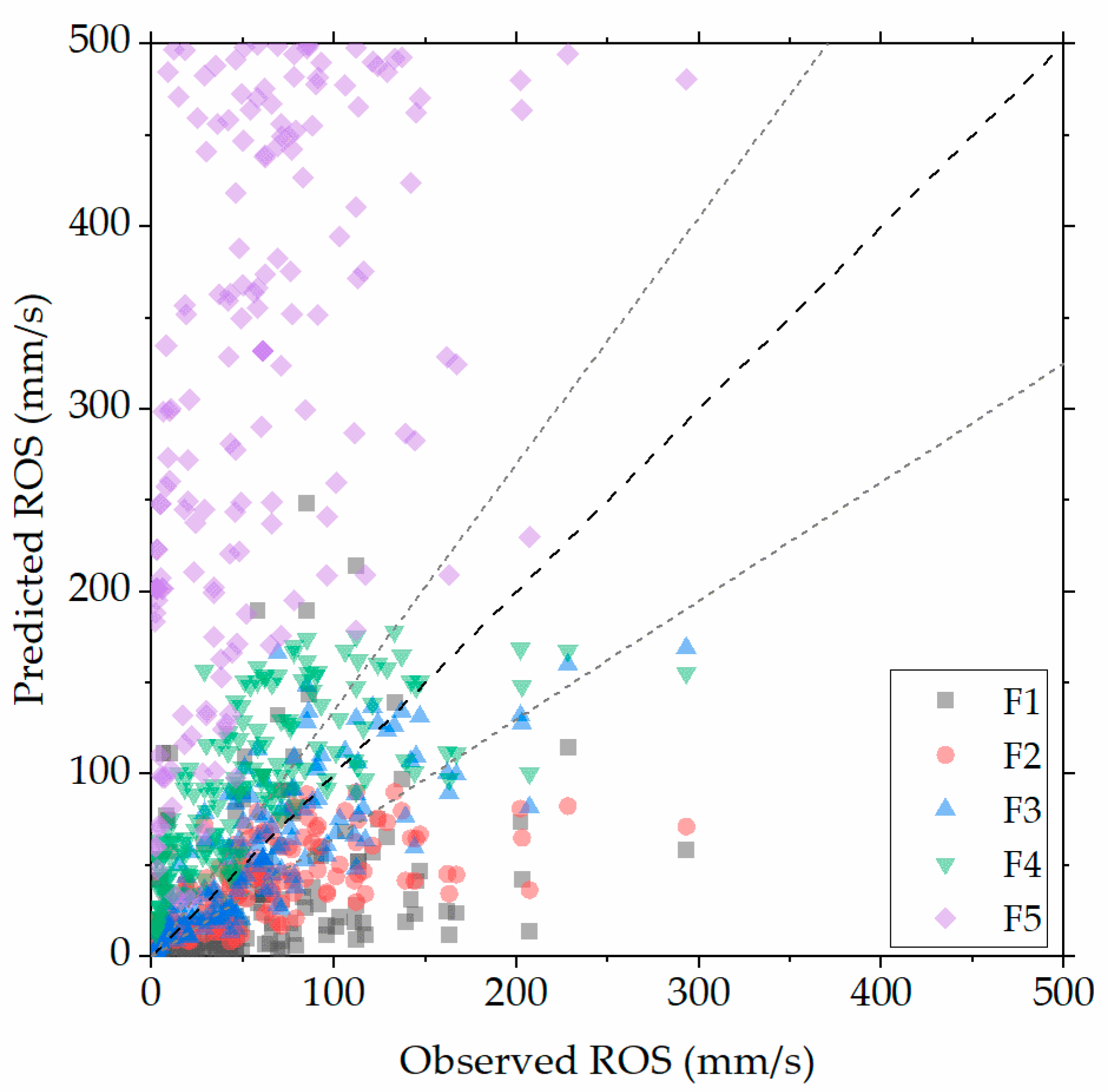
3.3. Field-Developed Models against External Wind Conditions
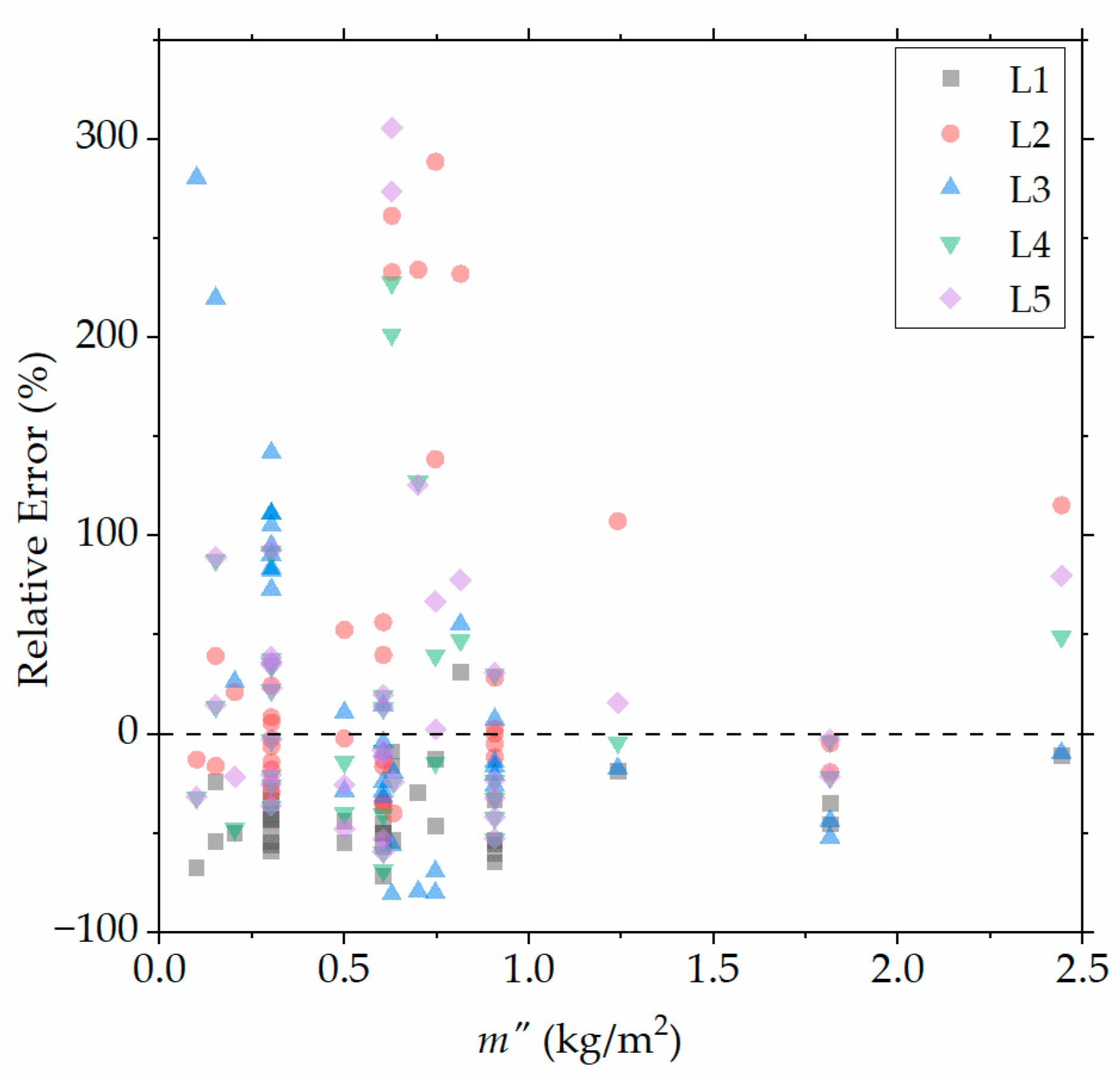
3.4. Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Units | Description |
| A, B, …, F | - | Empirically fitted constants or functions |
| a, b, c | - | Fuel parameters, used in model F5 |
| FC | % | Surface fuel cover |
| fil | - | Ignition line length factor, used in sub-model W2 |
| Hf | m | Flame height |
| h | kJ/kg | Fuel lower calorific value |
| hv | kJ/kg | Fuel’s pyrolysis gas lower calorific value |
| IB | kW/m | Byram’s fireline intensity |
| IP | kW/m2 | Propagation heat flux |
| IR | kW/m2 | Reaction intensity |
| ISI | - | Initial Spread Index, used in model F5 |
| k | - | Moisture damping constant, used in model L3 |
| Lig | kJ/m3 | Heat per unit volume required for ignition |
| M* | - | Fuel moisture content—FMC (dry basis) |
| Mc | - | Characteristic moisture, used in model L2 |
| Mx | - | Moisture of extinction, used in model L1 |
| kg/s·m | Rate of fuel added to combustion zone | |
| mn″ | kg/m2 | Net fuel load |
| md″ | kg/m2 | Dry fuel load |
| nx | - | Extinction index |
| - | Extinction adjustment factor | |
| n | - | Total number of experiments |
| Pf | - | Probability function for fire extinction |
| Qp | kJ/kg | Heat of pyrolysis |
| Qw | kJ/kg | Required heat to evaporate the fuel’s moisture |
| R0 | m/s* | “Base” ROS in quiescent and horizontal conditions |
| R | m/s* | Rate of spread |
| Rexp | m/s* | Experimentally measured rate of spread |
| Rpred | m/s* | Predicted rate of spread |
| Ru | - | Wind correction factor, used in sub-model W2 |
| Se | - | Effective mineral content |
| St | - | Total mineral content |
| s | m2/kg | Fuel particle specific surface |
| Ta | °C | Ambient temperature |
| U | m/s* | Wind velocity |
| Uz | m/s* | Wind velocity measured at height z |
| m/s* | Wind velocity at mid-flame height | |
| W | m | Fuel bed width |
| z | ft* | Wind velocity measuring height |
| β | - | Fuel bed packing ratio |
| Γ′ | min−1 | Potential reaction velocity |
| δ | m | Fuel bed height |
| ε | - | Effective heating number |
| ηΜ | - | Moisture damping coefficient |
| ηS | - | Mineral damping coefficient |
| ξ | - | Propagating heat flux ratio |
| ρb | kg/m3 | Fuel bed density |
| ρp | kg/m3 | Fuel particle density |
| σ | m−1 | Surface area-to-volume (SAV) ratio |
| Φw | - | Wind correction factor, used in sub-model W1 |
| * Properties may, in certain cases, be expressed in different units (see text). Numerical subscripts (in Table 1, Table A1, Table A2 and Table A6) indicate different constant or function. | ||
Appendix A. Detailed Forms of Equation Functions
| Function | Units |
|---|---|
| (kJ/min·m2) | |
| (min−1) | |
| (kg/m2) | |
| (kJ/m3) | |
| σ | (cm−1) |
| Function | Units |
|---|---|
| (kJ/m3) | |
| (kJ/min·m2) | |
| (min−1) | |
| (kW/m2) | |
| σ | (cm−1) |
| Function | Units |
| Function | Units |
| Function | Units |
| Uz | (km/h) |
Appendix B. Values of Empirical Parameters
| Model | Parameter | Value | Model | Parameter | Value |
| L4, L5 | A4 | 0.2859 | F1 | A8 | 40.982 |
| A5 | 0.1557 | B8 | 1.399 | ||
| B4,5 | −0.7734 | C8 | 1.201 | ||
| C4,5 | 0.9440 | D8 | 1.699 | ||
| D5 | 0.8173 | F2, F3 | A9 | 5.6715 | |
| W2 | A7 | 2.143 × 10−5 | B9 | 0.9102 | |
| B7 | 1.710 | C9 | 0.2227 | ||
| C7 | −1.169 | D9 | 0.0762 | ||
| D7 | −1.166 | A10 | 3.8320 | ||
| F5 | α | 45 | B10 | 1.0927 | |
| b | 0.0305 | C10 | −0.2098 | ||
| c | 2 | D10 | 0.0721 | ||
| A12 | 0.208 | E9,10 | 9 | ||
| B12 | 0.05039 | F9,10 | 0.00316 | ||
| C12 | 91.9 | F4 | A11 | 0.773 | |
| D12 | −0.1386 | B11 | 0.707 | ||
| E12 | 4.93 × 10−7 | C11 | −0.039 | ||
| F12 | 5.31 | D11 | 0.188 |
References
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 1: Physical and quasi-physical models. Int. J. Wildland Fire 2009, 18, 349–368. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 2: Empirical and quasi-empirical models. Int. J. Wildland Fire 2009, 18, 369–386. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 3: Simulation and mathematical analogue models. Int. J. Wildland Fire 2009, 18, 387–403. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. Uncertainty associated with model predictions of surface and crown fire rates of spread. Environ. Modell. Softw. 2013, 47, 16–28. [Google Scholar] [CrossRef]
- Viegas, D.X. On the existence of a steady state regime for slope and wind driven fires. Int. J. Wildland Fire 2004, 13, 101–117. [Google Scholar] [CrossRef]
- Weise, D.R.; Biging, G.S. A Qualitative comparison of fire spread models incorporating wind and slope effects. Forest Sci. 1997, 43, 170–180. [Google Scholar] [CrossRef]
- Weise, D.R.; Koo, E.; Zhou, X.; Mahalingam, S.; Morandini, F.; Balbi, J.H. Fire spread in chaparral-a comparison of laboratory data and model prediction in burning live fuels. Int. J. Wildland Fire 2016, 25, 980–994. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E.; Sullivan, A.L.; Gould, J.S.; Kilinc, M. Assessing improvements in models used to operationally predict wildland fire rate spread. Environ. Modell. Softw. 2018, 105, 54–63. [Google Scholar] [CrossRef]
- Kolaitis, D.I.; Pallikarakis, C.N.; Founti, M.A. Effects of wind velocity on prediction of wildland fire rate of spread models: A comparative assessment using surface fuel fire tests. In Proceedings of the IX International Conference on Forest Fire Research, Coimbra, Portugal, 14–18 November 2022. [Google Scholar]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Res. Pap. INT-115; USDA Forest Service, Intermountain Forest and Range Experiment Station: Fort Collins, CO, USA, 1972. [Google Scholar]
- Wilson, R.A. Reexamination of Rothermel’s Fire Spread Equations in No-Wind and No-Slope Conditions; Res. Pap. INT-434; USDA Forest Service, Intermountain Research Station: Fort Collins, CO, USA, 1990. [Google Scholar]
- Catchpole, W.R.; Catchpole, E.A.; Butler, B.W.; Rothermel, R.C.; Morris, G.A.; Latham, D.J. Rate of spread of free-burning fires in woody fuels in a wind tunnel. Combust. Sci. Technol. 1998, 131, 1–37. [Google Scholar] [CrossRef]
- Rossa, C.G.; Fernandes, P.M. Empirical modeling of fire spread rate in no-wind and no-slope conditions. Forest Sci. 2018, 64, 358–370. [Google Scholar] [CrossRef]
- Rossa, C.G.; Fernandes, P.M. An empirical model for the effect of wind on fire spread. Fire 2018, 1, 31. [Google Scholar] [CrossRef]
- Burrows, N.; Gill, M.; Sharples, J. Development and validation of a model for predicting fire behaviour in spinifex grasslands of Arid Australia. Int. J. Wildland Fire 2019, 27, 271–279. [Google Scholar] [CrossRef]
- Anderson, W.R.; Cruz, M.G.; Fernandes, P.M.; McCaw, L.; Vega, J.A.; Bradstock, R.A.; Fogarty, L.; Gould, J.; McCarthy, G.; Marsden-Smedley, J.B.; et al. A generic, empirical-based model for predicting rate of fire spread in shrublands. Int. J. Wildland Fire 2015, 24, 443–460. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Botelho, H.S.; Rego, F.C.; Loureiro, C. Empirical modelling of surface fire behavior in maritime pine stand. Int. J. Wildland Fire 2009, 18, 698–710. [Google Scholar] [CrossRef]
- Forest Canada Fire Danger Group. Development and Structure of the Canadian Forest Fire Behavior Prediction System; Information Report St-X-3; Forestry Canada, Science and Sustainable Development Directorate: Ottawa, Canada, 1992. [Google Scholar]
- Frandsen, W.H. Fire spread through porous fuels from conservation of energy. Combust. Flame 1971, 16, 9–16. [Google Scholar] [CrossRef]
- Byram, G.M. Combustion of Forest Fuels; McGraw-Hill: New York, NY, USA, 1959; pp. 61–89. [Google Scholar]
- Rossa, C.G.; Fernandes, P.M. Fuel-related fire-behaviour relationships for mixed live and dead fuels burned in the laboratory. Can. J. Forest. Res. 2017, 47, 883–889. [Google Scholar] [CrossRef]
- Albini, F.A.; Baughman, R.G. Estimating Windspeeds for Predicting Wildland Fire Behavior; Res. Pap. INT-221; USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1979. [Google Scholar]
- Andrews, P.L. Modeling Wind Adjustment Factor and Midflame Wind Speed for Surface Fire Spread Model; Gen. Tech. Rep; RMRS-GTR-266; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2012. [Google Scholar]
- Baughman, R.G.; Albini, F.A. Estimating Midflame Windspeed; Northern Forest Fire Laboratory: Missoula, MT, USA, 1980; pp. 88–92. [Google Scholar]
- Mendez-Lopez, J.M.; Ventura, J.M.; Amaral, J.M.P. Flame characteristics, temperature-time curves, and rate of spread in fires propagating in a bed of Pinus Pinaster needles. Int. J. Wildland Fire 2003, 12, 67–84. [Google Scholar] [CrossRef]
- Lozano, J.; Tachajapong, W.; Pan, H.; Swanson, A.; Kelley, C.; Princevac, M.; Mahalingam, S. Experimental investigation of the velocity field in a controlled wind-aided propagating fire using particle image velocimetry. In Proceedings of the Fire Safety Science-Proceedings of the 9th International Symposium, University of Karlsruhe, Karlsruhe, Germany, 21–26 September 2008; pp. 255–266. [Google Scholar]
- Anderson, W.R.; Catchpole, E.A.; Butler, B.W. Convective heat transfer in fire spread through fine fuel beds. Int. J. Wildland Fire 2010, 19, 284–298. [Google Scholar] [CrossRef]
- Korobenichev, O.; Tereshchenko, A.; Paletsky, A.; Shmakov, A.; Gonchikzhapov, M.; Chernov, A.; Kataeva, L.; Maslennikov, D.; Liu, N. The velocity and structure of the flame front at spread of fire across thepne needle bed depending on the wind velocity. In Proceedings of the 10th Asia-Oceania Symposium on Fire Science and Technology, Tsukuba, Japan, 5–7 October 2014; pp. 771–779. [Google Scholar]
- Korobeinichev, O.; Kumaran, S.M.; Shanmugasundaram, D.; Raghavan, V.; Trubachev, S.A.; Paletsky, A.A.; Shmakov, A.G.; Glaznev, R.K.; Chernov, A.A.; Tereshchenko, A.G. Experimental and numerical study of flame spread over bed of pine needles. Fire Technol. 2022, 58, 1227–1264. [Google Scholar] [CrossRef]
- Morandini, F.; Perez-Ramirez, Y.; Tihay, V.; Santoni, P.; Barboni, T. Radiant, convective and heat release characterization of vegetation fire. Int. J. Therm. Sci. 2013, 70, 83–91. [Google Scholar] [CrossRef]
- Tihay, V.; Morandini, F.; Santoni, P.A.; Perez-Ramirez, Y.; Barboni, T. Combustion of forest litters under slope condition: Burning rate, heat release rate, convective and radiant fractions for different loads. Combust. Flame 2014, 161, 3237–3248. [Google Scholar] [CrossRef]
- Finney, M.A.; McAllister, S.S.; Grumstrup, T.P.; Forthofer, J.M. Wildland Fire Behavior: Dynamics, Principles and Processes; CSIRO Publishing: Melbourne, Australia, 2021; pp. 15–45. [Google Scholar]
- Morvan, D.; Frangieh, N. Wildland fires behaviour: Wind effect versus Byram’s convective number and consequences upon the regime of propagation. Int. J. Wildland Fire 2018, 27, 636–641. [Google Scholar] [CrossRef]
- Cheney, N.P.; Gould, J.S.; Catchpole, W.R. The influence of fuel, weather and fire shape variables on fire-spread in grasslands. Int. J. Wildland Fire 1993, 3, 698–710. [Google Scholar] [CrossRef]
- Cheney, N.P.; Gould, J.S. Fire growth in grassland fuels. Int. J. Wildland Fire 1995, 5, 237–247. [Google Scholar] [CrossRef]

| Model Type | Model | General Form | Ref. |
|---|---|---|---|
| ROS models developed using laboratory tests | L1 | [10] | |
| L2 | [11] | ||
| L3 | [12] | ||
| L4 | [13] | ||
| L5 | [13] | ||
| “Wind correction” sub-models | W1 | [10] | |
| W2 | [14] | ||
| ROS models developed using field tests | F1 | [15] | |
| F2 | [16] | ||
| F3 | [16] | ||
| F4 | [17] | ||
| F5 | [18] |
| Ref. | Fire Tests | No-Wind/Wind Tests | Fuel Type |
|---|---|---|---|
| [25] | 9 | 2/7 | Pine needles (Pinus Pinaster) |
| [26] | 6 | 0/6 | Bamboo sticks |
| [27] | 163 | 30/133 | Pine needles (Pinus Ponderosa)/Excelsior |
| [28] | 7 | 1/6 | Pine needles (Pinus Sibirica) |
| [29] | 18 | 4/14 | Pine needles (Pinus Sibirica) |
| Model | RMSE | MAPE (%) | MBE |
|---|---|---|---|
| L1 | 3.5 | 42.8 | −2.8 |
| L2 | 3.2 | 59.3 | 1.0 |
| L3 | 4.7 | 71.6 | 1.5 |
| L4 | 3.1 | 45.8 | −0.2 |
| L5 | 2.9 | 50.9 | 0.3 |
| Models | RMSE | MAPE (%) | MBE |
|---|---|---|---|
| L1-W1 | 40.1 | 46.5 | −25.3 |
| L2-W1 | 51.5 | 59.2 | 14.8 |
| L3-W1 | 91.8 | 49.3 | 30.8 |
| L4-W1 | 40.2 | 52.0 | −6.7 |
| L5-W1 | 42.1 | 43.1 | 1.2 |
| L1-W2 | 143.8 | 78.0 | 34.4 |
| L2-W2 | 127.8 | 105.3 | 35.2 |
| L3-W2 | 101.0 | 67.1 | 26.8 |
| L4-W2 | 131.3 | 94.9 | 33.7 |
| L5-W2 | 124.5 | 90.1 | 33.0 |
| Model | RMSE | MAPE (%) | MBE |
|---|---|---|---|
| F1 | 59.2 | 119.0 | −24.0 |
| F2 | 44.4 | 67.5 | −21.2 |
| F3 | 30.7 | 63.1 | −3.9 |
| F4 | 51.5 | 231.3 | 35.2 |
| F5 | 280.0 | 1278.3 | 251.6 |
| Parameter | Model | −25% Change | Assumed Value | +25% Change |
|---|---|---|---|---|
| h | L1 | 4.42 (25.9%) | 3.51 | 2.67 (−23.8%) |
| St | L1 | 3.46 (−1.5%) | 3.51 | 3.56 (1.5%) |
| Se | L1 | 3.31 (−5.6%) | 3.51 | 3.65 (4.2%) |
| Mx | L1 | 3.80 (8.3%) | 3.51 | 3.31 (−5.7%) |
| hv | L2 | 2.82 (−13.0%) | 3.24 | 4.70 (45.3%) |
| fil | W2 (L5-W2) | 85.70 (−31.2%) | 124.50 | 165.84 (33.2%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolaitis, D.I.; Pallikarakis, C.; Founti, M.A. Comparative Assessment of Wildland Fire Rate of Spread Models: Effects of Wind Velocity. Fire 2023, 6, 188. https://doi.org/10.3390/fire6050188
Kolaitis DI, Pallikarakis C, Founti MA. Comparative Assessment of Wildland Fire Rate of Spread Models: Effects of Wind Velocity. Fire. 2023; 6(5):188. https://doi.org/10.3390/fire6050188
Chicago/Turabian StyleKolaitis, Dionysios I., Christos Pallikarakis, and Maria A. Founti. 2023. "Comparative Assessment of Wildland Fire Rate of Spread Models: Effects of Wind Velocity" Fire 6, no. 5: 188. https://doi.org/10.3390/fire6050188
APA StyleKolaitis, D. I., Pallikarakis, C., & Founti, M. A. (2023). Comparative Assessment of Wildland Fire Rate of Spread Models: Effects of Wind Velocity. Fire, 6(5), 188. https://doi.org/10.3390/fire6050188










