Impact of Pipe Diameter on the Discharge Process of Halon1301 in a Fire Extinguishing System with Horizontal Straight Pipe
Abstract
:1. Introduction
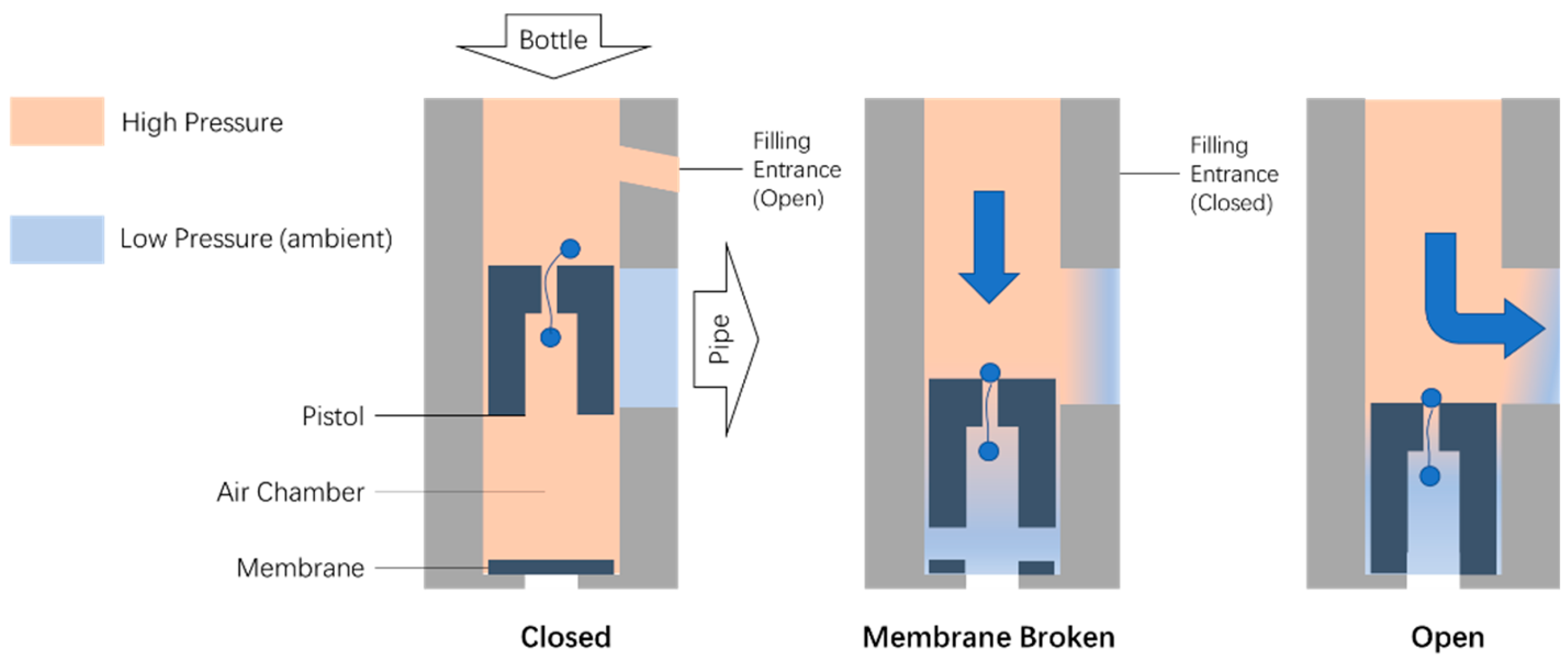
2. Materials and Methods
3. Results and Discussion
3.1. Discharge Time
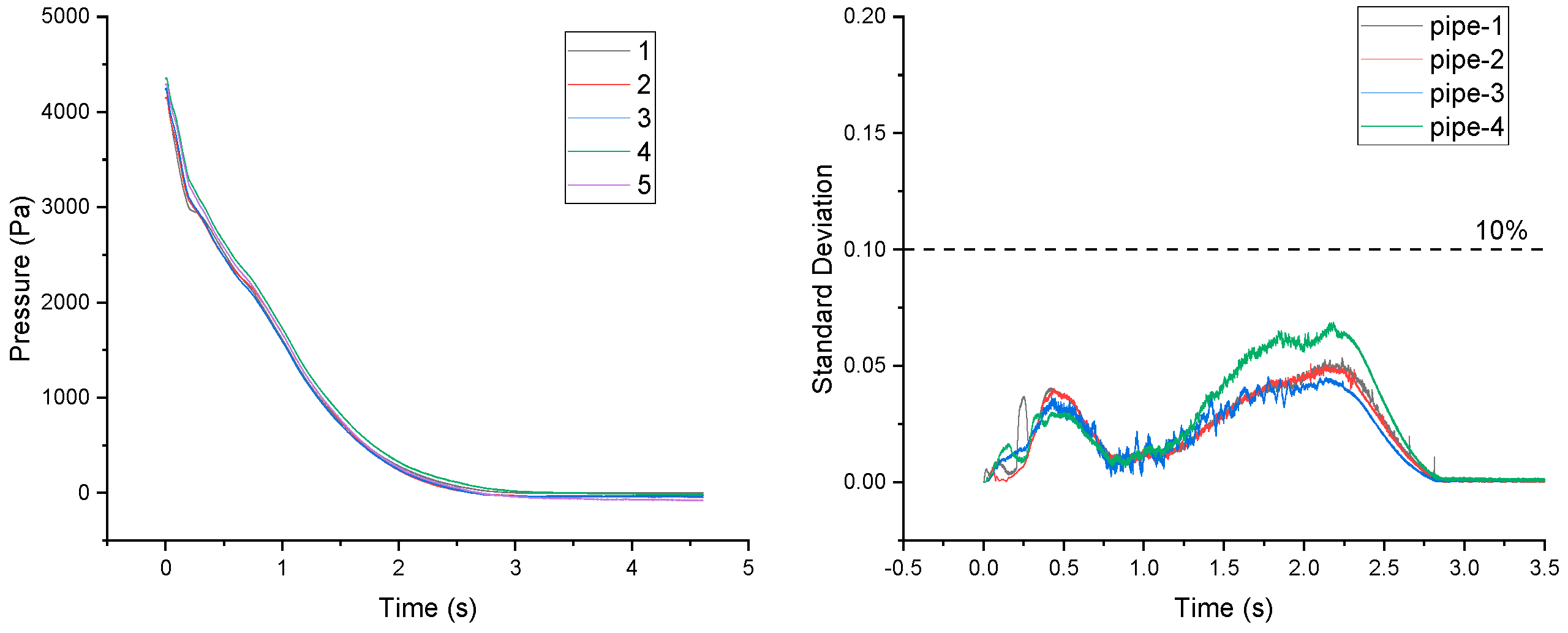
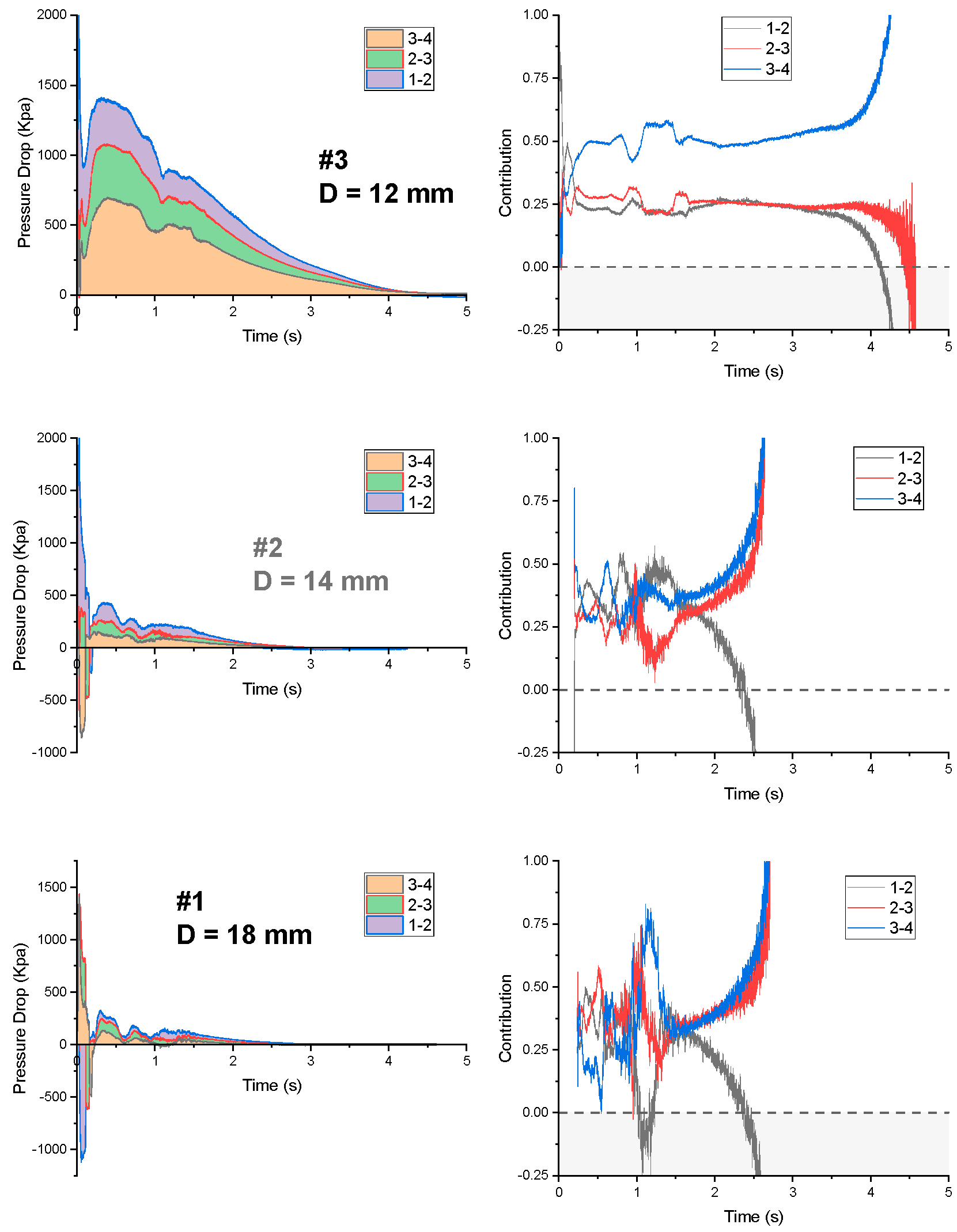
3.2. Pressure Distribution
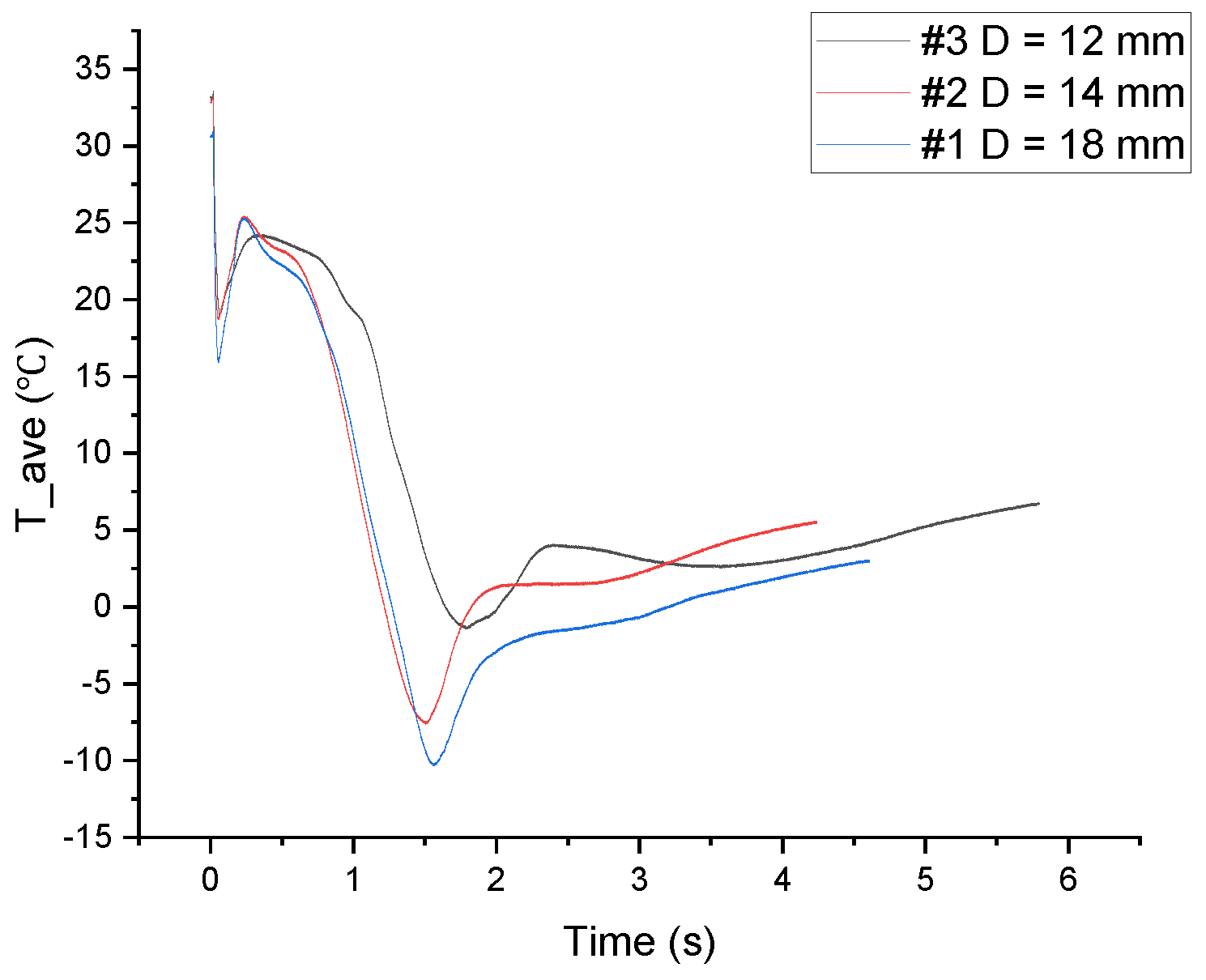
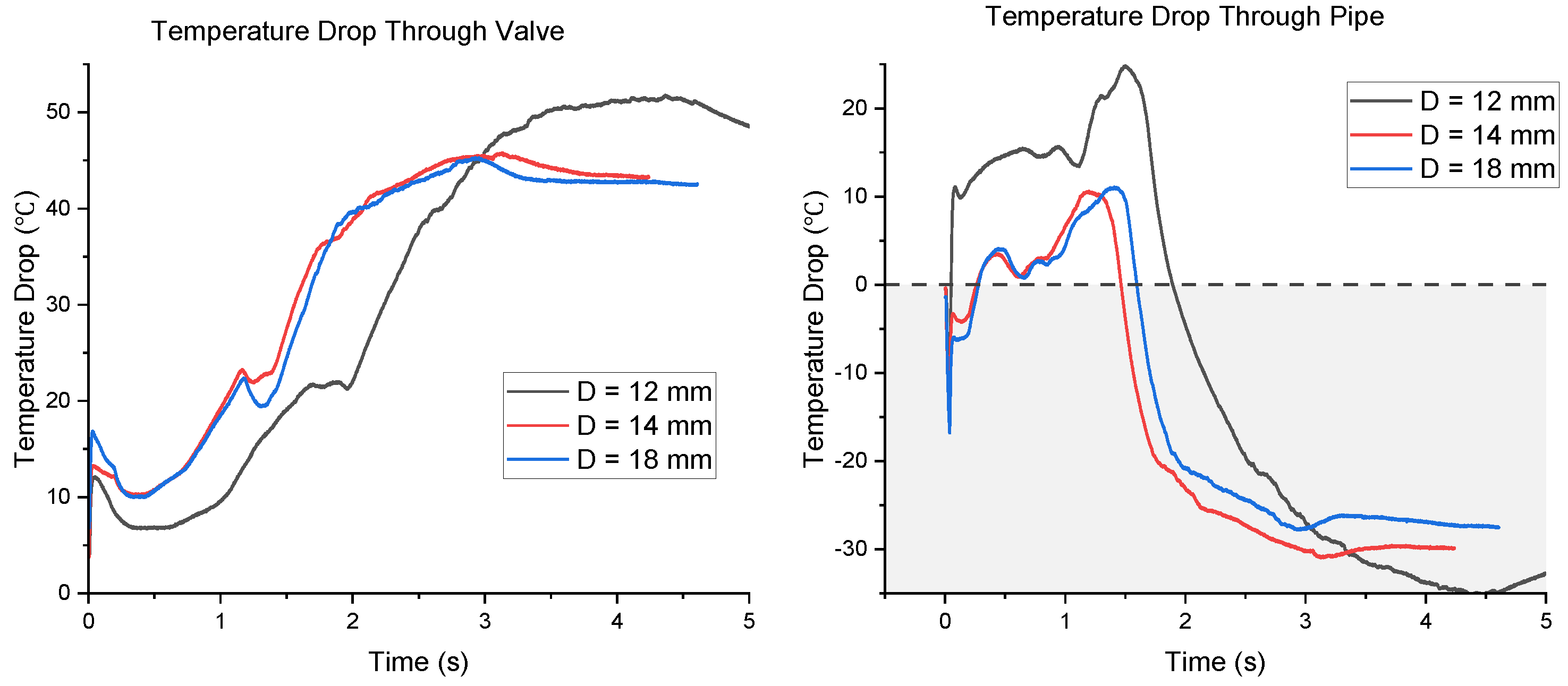
3.3. Pipe Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hariram, S.; Philipp, P.; Dummeyer, D. Fire protection: Engines and Auxiliary power units. Aero Q. 2010, 10, 15. [Google Scholar]
- Hariram, S.S. Fire Protection on Airplanes; SAE: Warrendale, PA, USA, 2005. [Google Scholar]
- Lee, J. Simulation method for the fire suppression process inside the engine core and APU compartments. In Proceedings of the Fourth Triennial International Aircraft Fire and Cabin Safety Research Conference, Lisabon, Portugal, 21–23 May 2004. [Google Scholar]
- DElliott, G.; Garrison, P.W.; Klein, G.A.; Moran, K.M.; Zydowicz, M.P. Flow of Nitrogen-Pressurized Halon 1301 in Fire Extinguishing Systems; JPL Publication: Pasadena, CA, USA, 1984; Volume 84, p. 62. [Google Scholar]
- Ni, X.; Chen, Y.; Huang, Q.; Zhao, C.; Li, S.; Huang, J.; Wang, J. An Experimental Study on the Transportation Characteristics of Perfluoro(2-methyl-3-pentanone) in a Straight Pipe. Fire 2023, 6, 156. [Google Scholar] [CrossRef]
- Jiang, Y.; Hua, M.; Yan, P.; Zhang, H.; Li, Q.; Pan, X. The transport and diffusion characteristics of superheated fire extinguish agent released via different nozzles in a confined space. Saf. Sci. 2020, 129, 104787. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, Y.; Li, H.; Dai, C.; Lu, S.; Zhang, H. ‘Simulation study of filling conditions for aircraft fire suppression systems’. In Proceedings of the IET Conference Proceedings, Nanchang, China, 17–20 August 2022; pp. 1172–1178. [Google Scholar]
- Robinson, D.B.; Peng, D.Y. A New Two-Constant Equation of State Industrial and Engineering Chemistry: Fundamentals. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar]
- Huber, M.L.; Ely, J.F. A predictive extended corresponding states model for pure and mixed refrigerants including an equation of state for R134a. Int. J. Refrig. 1994, 17, 18–31. [Google Scholar] [CrossRef]
- Yang, J.C.; Huber, M.L.; Boyer, C.I. Model for Calculating Alternative Agent/Nitrogen Thermodynamic Properties; NIST: Gaithersburg, MD, USA, 1995. [Google Scholar]
- Duan, Q.; Xiao, H.; Gao, W.; Shen, X.; Wang, Q.; Sun, J. Experimental investigation on shock waves generated by pressurized gas release through a tube. J. Loss Prev. Process. Ind. 2015, 36, 39–44. [Google Scholar] [CrossRef]
- Li, Q.; Ge, H.; Pan, R.; Zhang, Z.; Chen, R. Numerical Study on Flow and Release Characteristics of Gas Extinguishing Agent under Different Filling Pressure and Amount Conditions. Processes 2021, 9, 1683. [Google Scholar] [CrossRef]
- Jin, J.; Pan, R.; Chen, R.; Xu, X.; Li, Q. Flow and Diffusion Characteristics of Typical Halon Extinguishing Agent Substitute under Different Release Pressures. Processes 2020, 8, 1684. [Google Scholar] [CrossRef]
- Tuzla, K.; Palmer, T.; Chen, J.C.; Sundaram, R.K.; Yeung, W.S. Development of Computer Program for Fire Supressant Fluid Flow; Lehigh University & Duke Engineering and Services, Inc.: Bethlehem, PA, USA, 2000. [Google Scholar]
- Liu, R.; Yuan, C.; Ma, W.; Liu, S.; Lu, S.; Zhang, H.; Gong, J. Simulation Study on Aircraft Fire Extinguishing Pipeline with Different Filling Conditions and Pipeline Characteristics. Fire 2022, 5, 86. [Google Scholar] [CrossRef]
- Amatriain, A.; Parra, I.; Rubio, G. Study of bubble growth in a multicomponent mixture at high pressure. In Proceedings of the 4th World Congress on Momentum, Heat and Mass Transfer, Roma, Italy, 10–12 April 2019. [Google Scholar]
- Li, Q.; Li, Z.; Chen, R.; Zhang, Z.; Ge, H.; Zhou, X.; Pan, R. Numerical Study on Effects of Pipeline Geometric Parameters on Release Characteristics of Gas Extinguishing Agent. Symmetry 2021, 13, 1766. [Google Scholar] [CrossRef]
- Li, Q.; He, X.; Chen, Y.; Lin, J.; Zhang, Y.; Chen, R.; Zhou, X. Numerical Study on Effects of Geometric Parameters on the Release Characteristics of Straight Sudden Expansion Gas Extinguishing Nozzles. Symmetry 2021, 13, 2440. [Google Scholar] [CrossRef]
- Blander, M. Bubble nucleation in liquids. Adv. Colloid Interface Sci. 1979, 10, 1–32. [Google Scholar] [CrossRef]
- Forest, T.W.; Ward, C.A. Homogeneous nucleation of bubbles in solutions at pressures above the vapor pressure of the pure liquid. J. Chem. Phys. 1978, 69, 2221–2230. [Google Scholar] [CrossRef]
- Wallis, G. Critical two-phase flow. Int. J. Multiph. Flow 1980, 6, 97–112. [Google Scholar] [CrossRef]
- Bartak, J. A study of the rapid depressurization of hot water and the dynamics of vapour bubble generation in superheated water. Int. J. Multiph. Flow 1990, 16, 789–798. [Google Scholar]
- Brockett, G.; Curet, H.; Heiselmann, H.W. Experimental Investigations of Reactor System Blowdown; Technical Report; Idaho Nuclear Corp.: Idaho Falls, ID, USA, 1970. [Google Scholar]
- Liao, Y.; Lucas, D. A review on numerical modelling of flashing flow with application to nuclear safety analysis. Appl. Therm. Eng. 2021, 182, 116002. [Google Scholar]
- Amatriain, A.; Rubio, G.; Parra, I.; Valero, E.; Andreu, D.; Martín, P.M. Mathematical modeling of nitrogen-pressurized Halon flow in fire extinguishing systems. Fire Saf. J. 2021, 122, 103356. [Google Scholar] [CrossRef]
- Chen, M.; Xie, Y.; Wu, H.; Shi, S.; Yu, J. Modeling solubility of nitrogen in clean fire extinguishing agent by Peng-Robinson equation of state and a correlation of Henry’s law constants. Appl. Therm. Eng. 2017, 110, 457–468. [Google Scholar] [CrossRef] [Green Version]
- Ockendon, H.; Ockendon, J.R. Waves and Compressible Flow; Springer: New York, NY, USA, 2016; pp. 23–25. [Google Scholar]
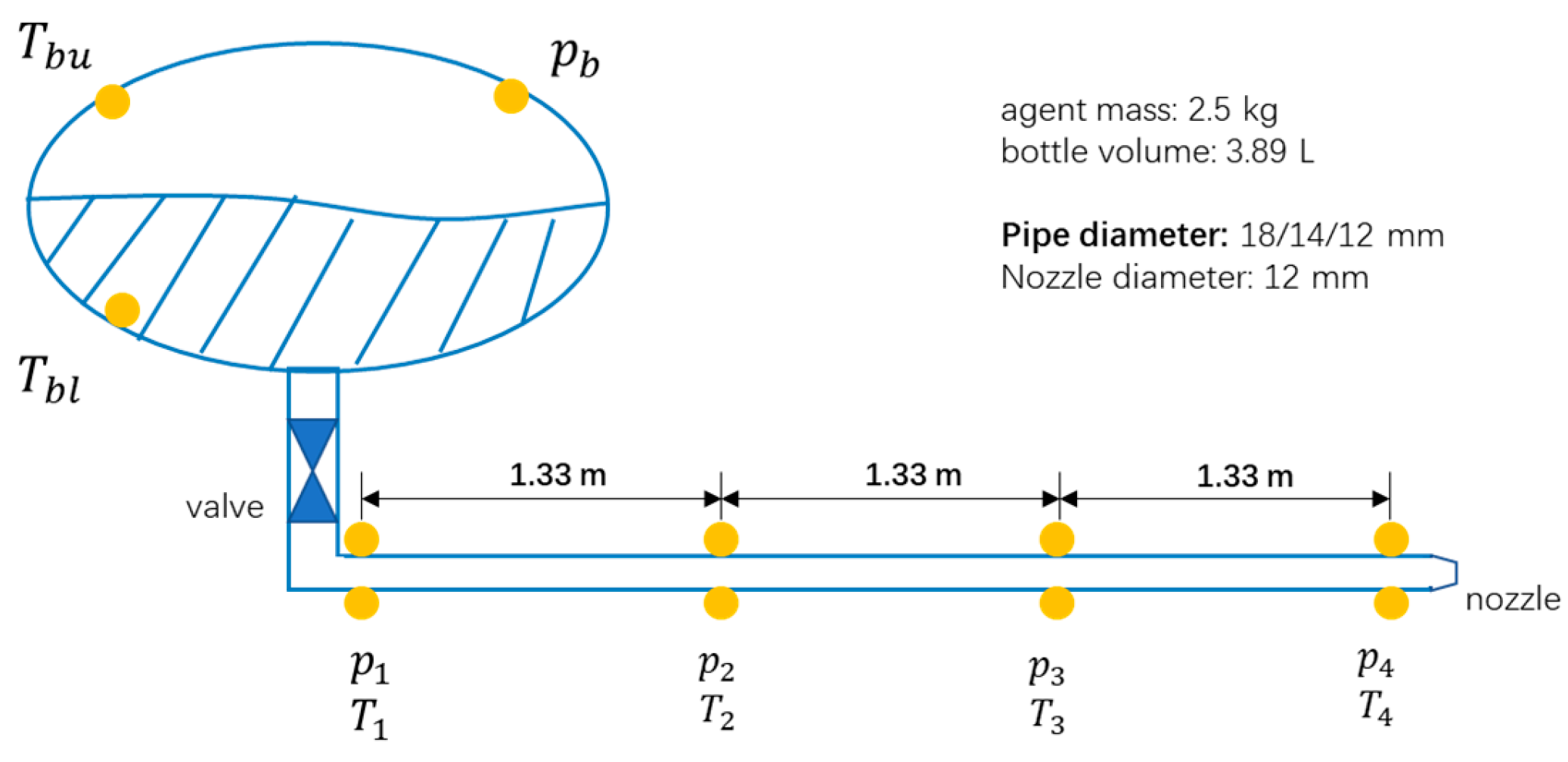
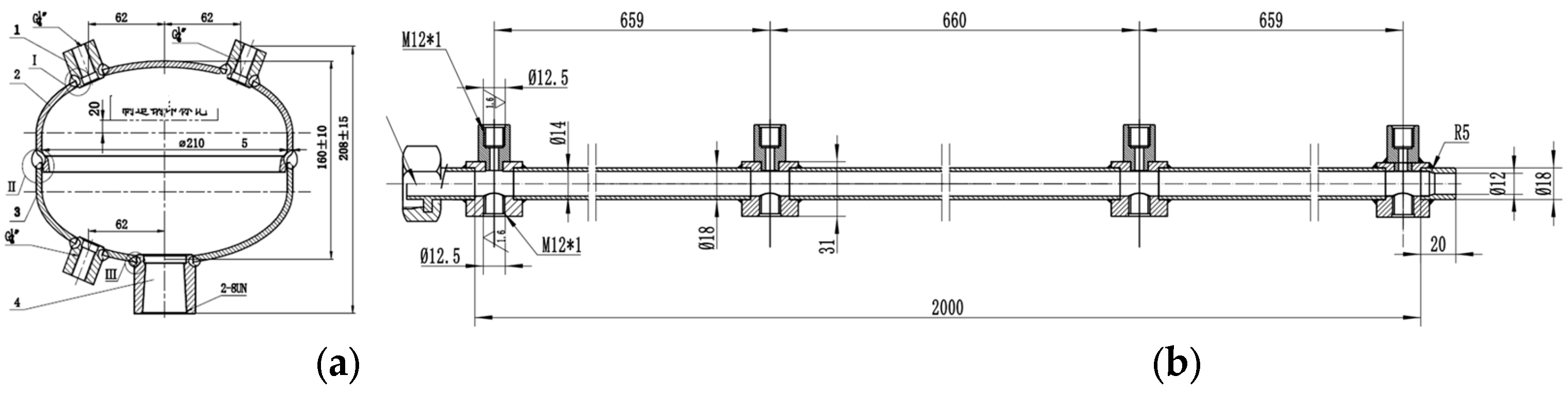

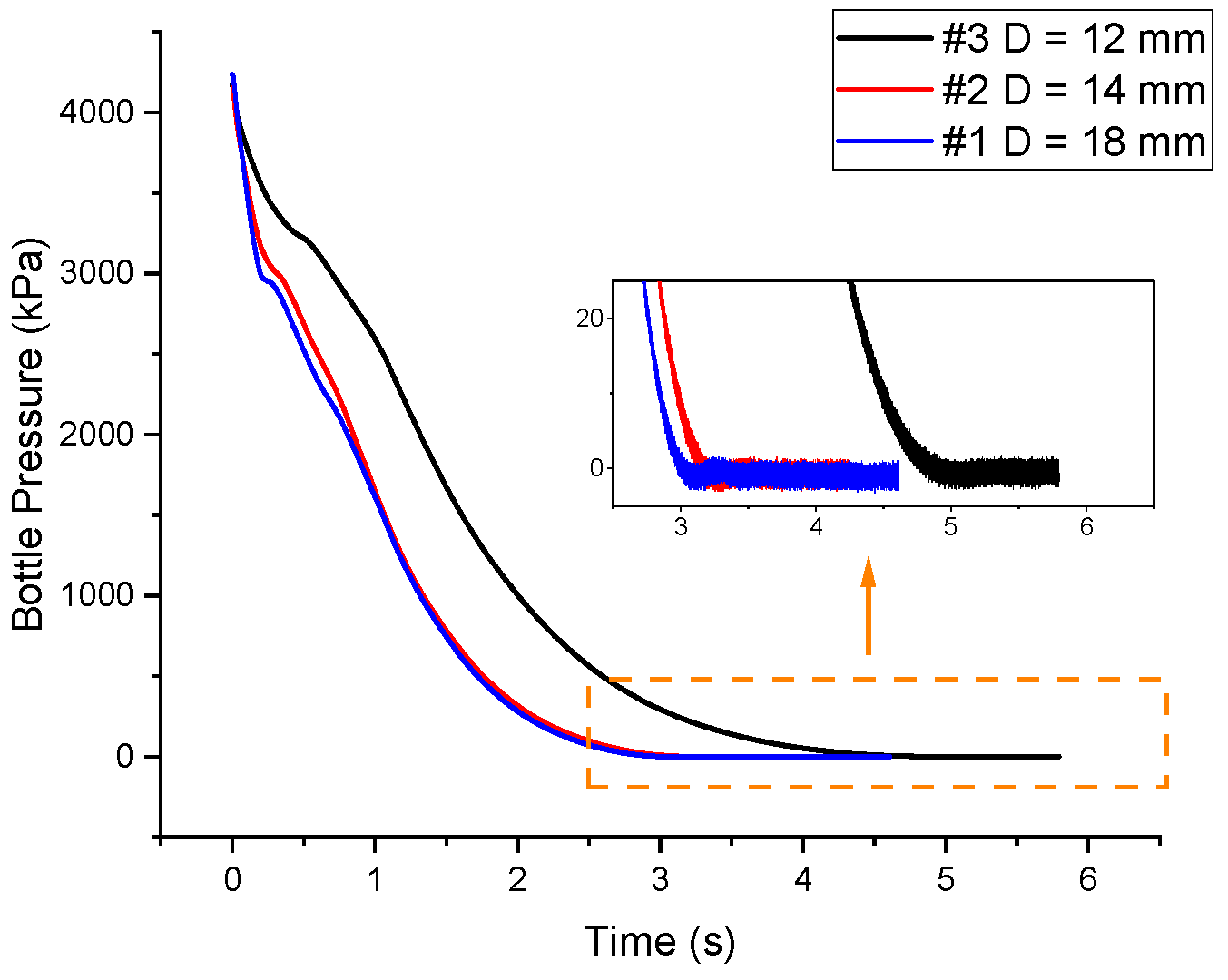
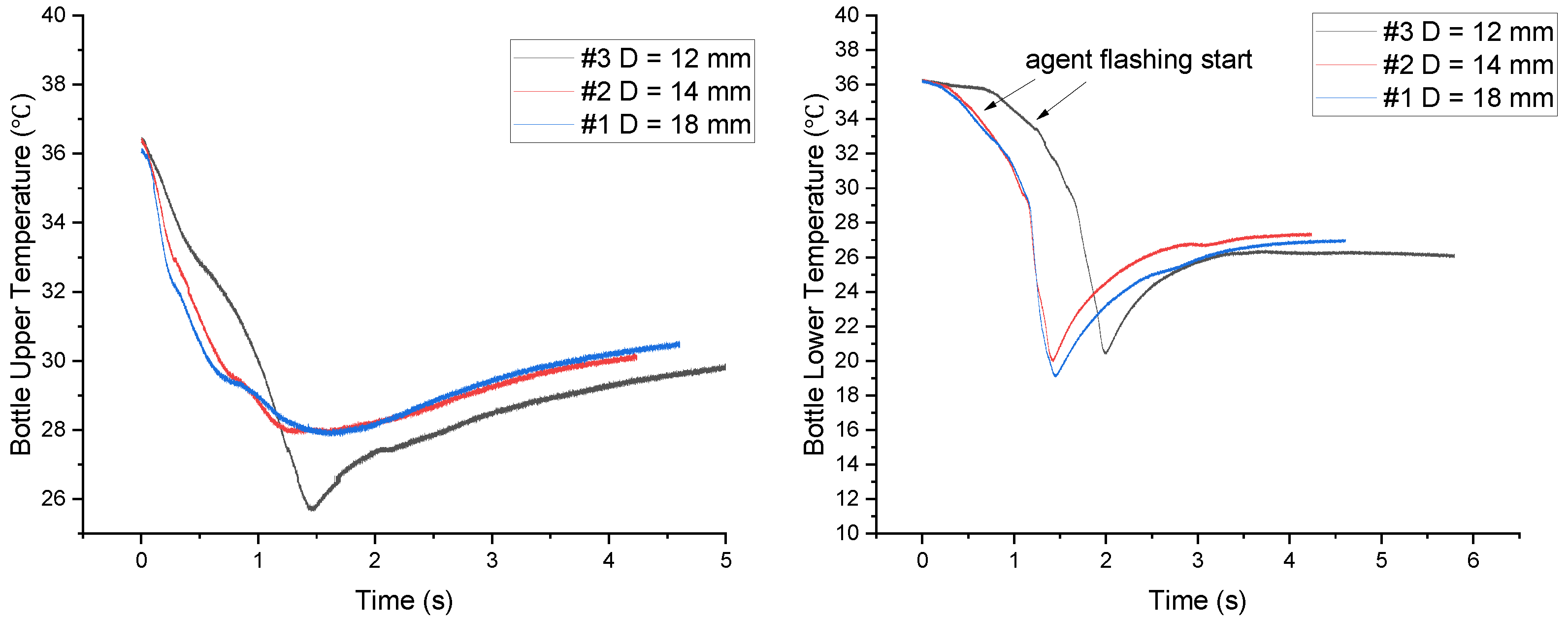
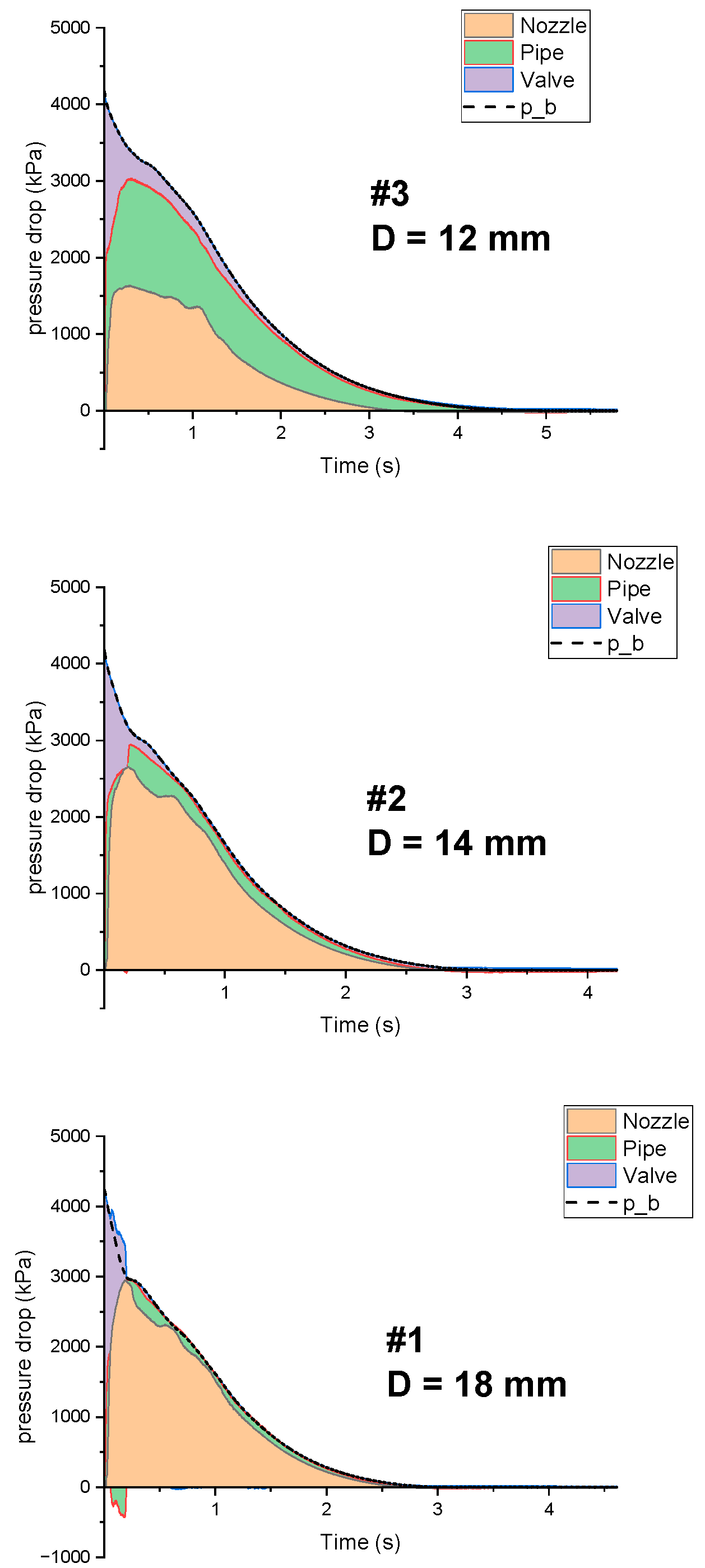
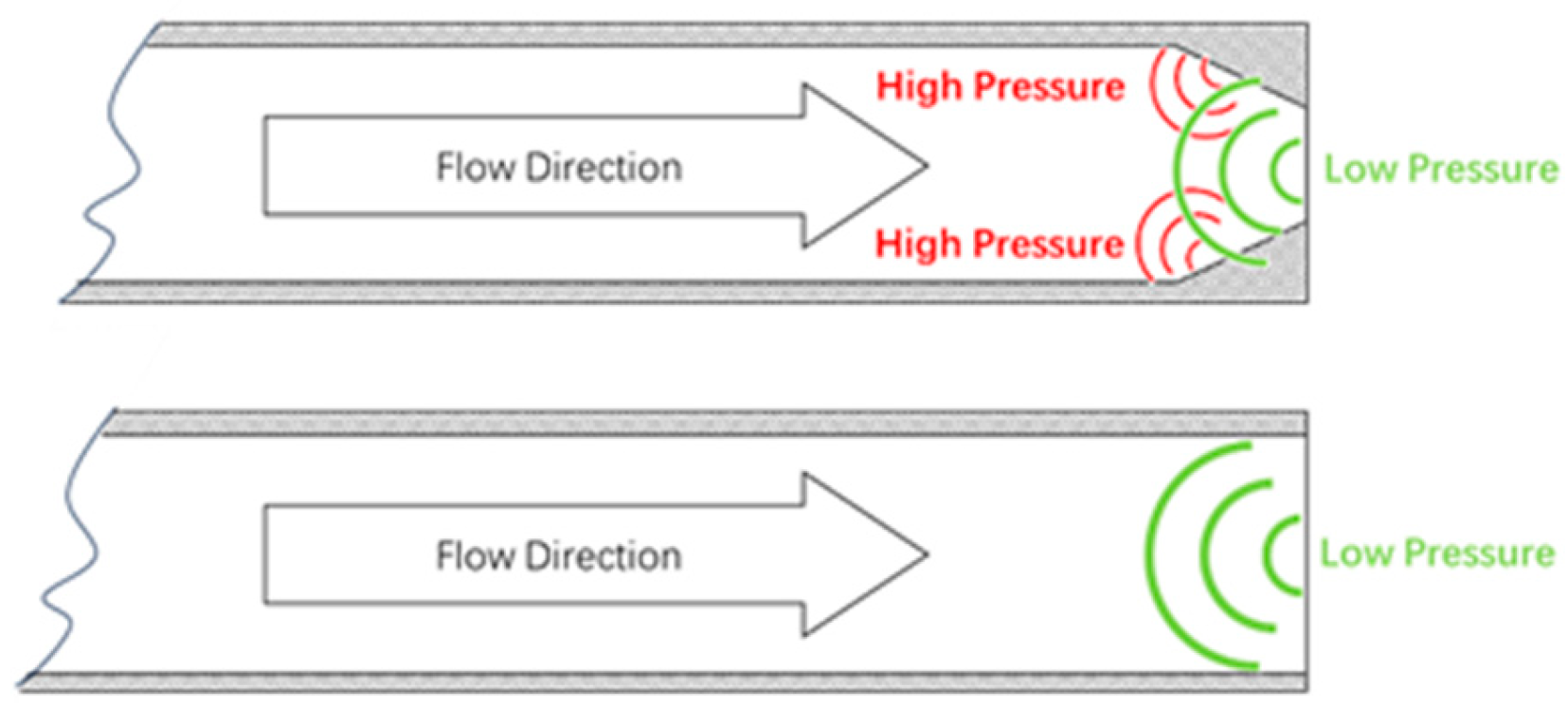
| Experiment | Pipe Diameter (mm) | Nozzle Diameter (mm) | Pipe Length (m) | Initial Pressure (KPa) | Halon Mass (kg) |
|---|---|---|---|---|---|
| #1 | 18 | 12 | 4 | 4300 | 2.5 |
| #2 | 14 | 12 | 4 | 4300 | 2.5 |
| #3 | 12 | 12 | 4 | 4300 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhao, C.; Huang, Q.; Li, S.; Huang, J.; Ni, X.; Wang, J. Impact of Pipe Diameter on the Discharge Process of Halon1301 in a Fire Extinguishing System with Horizontal Straight Pipe. Fire 2023, 6, 287. https://doi.org/10.3390/fire6080287
Chen Y, Zhao C, Huang Q, Li S, Huang J, Ni X, Wang J. Impact of Pipe Diameter on the Discharge Process of Halon1301 in a Fire Extinguishing System with Horizontal Straight Pipe. Fire. 2023; 6(8):287. https://doi.org/10.3390/fire6080287
Chicago/Turabian StyleChen, Ye, Chenxi Zhao, Qiurui Huang, Songyang Li, Jiahui Huang, Xiaomin Ni, and Jian Wang. 2023. "Impact of Pipe Diameter on the Discharge Process of Halon1301 in a Fire Extinguishing System with Horizontal Straight Pipe" Fire 6, no. 8: 287. https://doi.org/10.3390/fire6080287
APA StyleChen, Y., Zhao, C., Huang, Q., Li, S., Huang, J., Ni, X., & Wang, J. (2023). Impact of Pipe Diameter on the Discharge Process of Halon1301 in a Fire Extinguishing System with Horizontal Straight Pipe. Fire, 6(8), 287. https://doi.org/10.3390/fire6080287






