Forest Fire Risk Prediction Based on Stacking Ensemble Learning for Yunnan Province of China
Abstract
:1. Introduction
- (1)
- The assessment of forest fire risk associated with the weather involves intricate formulas and rules to categorize meteorological fire risk levels. The forest fire weather index (FWI) system, a widely employed system, relies solely on meteorological factors [6]. However, the existing simplistic weather index falls short of meeting practical requirements.
- (2)
- Multicriteria decision-making approaches [7], which have the capability to take into account various factors and objectives during the planning process, are particularly valuable when dealing with complex wildfire risk scenarios. This method is recognized as a crucial component in the wildfire risk assessment framework established by the U.S. Forest Service [8]. However, it relies on subjective expert ratings, lacking objectivity.
- (3)
- (4)
- The relationship between different combustibles and meteorological factors is established by combustion experiments to predict forest fire risk [12]. This method requires a large number of field experiments, and the physical parameters are very labor intensive to prepare and only applicable to a small area.
2. Materials and Methods
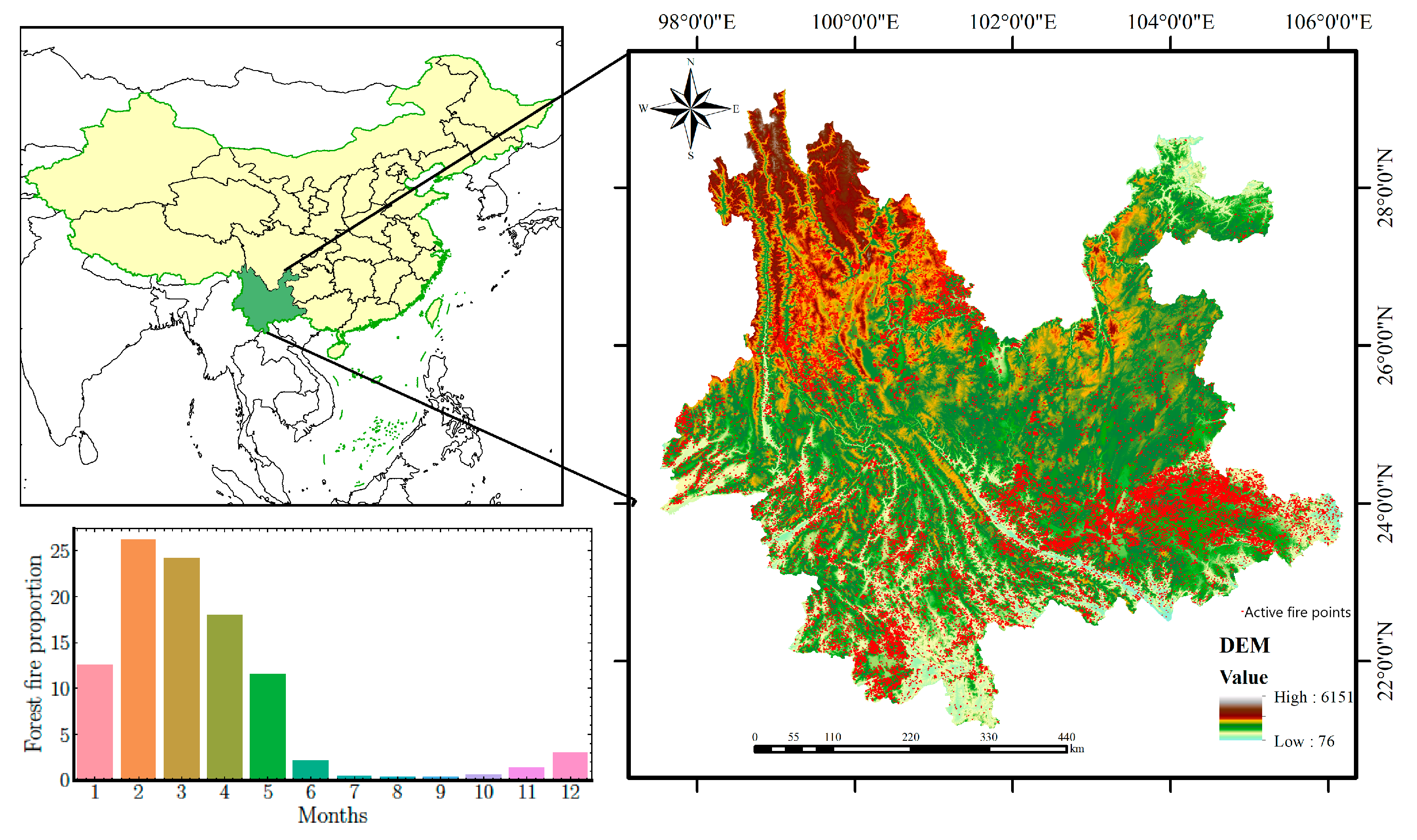
2.1. Study Area
2.2. Data Resources
2.2.1. Fire Point Inventory
2.2.2. Forest Fires Risk Influencing Factors
2.2.3. Spatial Interpolation of Meteorological Data
2.2.4. Data Preprocessing
2.3. Methodology
2.3.1. Selecting the Forest Fire Influencing Factors
2.3.2. Modeling the Forest Fire Risk Using the Stacking Ensemble Technique
| Algorithm 1: Stacking fusion model. | |
| Input: Four models in the first layer: { = RF, = XGBoost, = LightGBM, = MLP} = LightGBM} | |
| Output: The prediction results on the testing data. | |
| //Training the first layer model | |
| 1: | : |
| 2: | ; |
| 3: | ://k-fold cross validation |
| 4: | ; |
| 5: | ); |
| 6: | ); |
| 7: | ; |
| 8: | End For |
| 9: | End For |
| //Training the second layer model | |
| 10: | ; |
| 11: | according to the row to get the testing data of second layer: ; |
| 12: | ; |
| 13: | ; |
2.3.3. Ranking Feature Importance Based on SHAP Interpretation Framework
2.3.4. Evaluating the Forest Fire Risk Prediction Models
2.3.5. Producing and Validating the Forest Fire Susceptibility Maps
3. Results
3.1. Forest Fire Influencing Factor Selection
3.2. Model Comparison and Validation
3.3. Forest Fire Susceptibility Map
3.4. Feature Importance
4. Discussion
4.1. Predictive Model Comparison
4.2. Impact Factor Analysis
4.3. Limitations and Prospects
5. Conclusions
- We devised a stacking fusion model by amalgamating four disparate machine learning methods (RF, XGBoost, LightGBM, and MLP) for forest fire risk prediction. Although currently limited by the specific sampling dataset used in this study, the model showed promising results in generating daily forest fire sensitivity maps.
- Through multiple covariance tests and Pearson coefficient analyses involving meteorological, topographic, vegetation, and human activity data, we identified 16 significant factors influencing forest fire risk.
- Model performance was meticulously evaluated using various metrics, including accuracy, AUC, and fire density. The results demonstrated that the stacking fusion model exhibited remarkable accuracy with an AUC of 0.970 on the test set, significantly surpassing the performance of individual machine learning models, which had AUC values ranging from 0.935 to 0.953. Furthermore, the stacking fusion model effectively captured the maximum fire density in extremely high susceptibility areas, demonstrating enhanced generalization capabilities. This research expands the application of stacking ensemble learning for predicting forest fire risk.
- To address the interpretability challenges arising from the intricate internal structure of stacking fusion models, we employed the SHAP framework for an interpretable analysis of the model’s prediction results, yielding a feature importance ranking.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnstone, J.F.; Allen, C.D.; Franklin, J.F.; Frelich, L.E.; Harvey, B.J.; Higuera, P.E.; Mack, M.C.; Meentemeyer, R.K.; Metz, M.R.; Perry, G.L. Changing disturbance regimes, ecological memory, and forest resilience. Front. Ecol. Environ. 2016, 14, 369–378. [Google Scholar] [CrossRef]
- Kirchmeier-Young, M.C.; Gillett, N.P.; Zwiers, F.W.; Cannon, A.J.; Anslow, F. Attribution of the influence of human-induced climate change on an extreme fire season. Earth’s Future 2019, 7, 2–10. [Google Scholar] [CrossRef]
- Hasan, S.S.; Zhang, Y.; Chu, X.; Teng, Y. The role of big data in China’s sustainable forest management. For. Econ. Rev. 2019, 1, 96–105. [Google Scholar] [CrossRef]
- Vigna, I.; Besana, A.; Comino, E.; Pezzoli, A. Application of the socio-ecological system framework to forest fire risk management: A systematic literature review. Sustainability 2021, 13, 2121. [Google Scholar] [CrossRef]
- Chicas, S.D.; Østergaard Nielsen, J. Who are the actors and what are the factors that are used in models to map forest fire susceptibility? A systematic review. Nat. Hazards 2022, 114, 2417–2434. [Google Scholar] [CrossRef]
- Ntinopoulos, N.; Spiliotopoulos, M.; Vasiliades, L.; Mylopoulos, N. Contribution to the Study of Forest Fires in Semi-Arid Regions with the Use of Canadian Fire Weather Index Application in Greece. Climate 2022, 10, 143. [Google Scholar] [CrossRef]
- Nuthammachot, N.; Stratoulias, D. Multi-criteria decision analysis for forest fire risk assessment by coupling AHP and GIS: Method and case study. Environ. Dev. Sustain. 2021, 23, 17443–17458. [Google Scholar] [CrossRef]
- Scott, J.H.; Thompson, M.P.; Calkin, D.E. A Wildfire Risk Assessment Framework for Land and Resource Management; General Technical Report; USDA Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2013; Volume 10. [Google Scholar]
- De Santana, R.O.; Delgado, R.C.; Schiavetti, A. Modeling susceptibility to forest fires in the Central Corridor of the Atlantic Forest using the frequency ratio method. J. Environ. Manag. 2021, 296, 113343. [Google Scholar] [CrossRef]
- Salavati, G.; Saniei, E.; Ghaderpour, E.; Hassan, Q.K. Wildfire risk forecasting using weights of evidence and statistical index models. Sustainability 2022, 14, 3881. [Google Scholar] [CrossRef]
- Abedi Gheshlaghi, H.; Feizizadeh, B.; Blaschke, T. GIS-based forest fire risk mapping using the analytical network process and fuzzy logic. J. Environ. Plan. Manag. 2020, 63, 481–499. [Google Scholar] [CrossRef]
- Bakhshaii, A.; Johnson, E.A. A review of a new generation of wildfire–atmosphere modeling. Can. J. For. Res. 2019, 49, 565–574. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M.D. A review of machine learning applications in wildfire science and management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Pan, J.; Wang, W.; Li, J. Building probabilistic models of fire occurrence and fire risk zoning using logistic regression in Shanxi Province, China. Nat. Hazards 2016, 81, 1879–1899. [Google Scholar] [CrossRef]
- Rodrigues, M.; de la Riva, J.; Fotheringham, S. Modeling the spatial variation of the explanatory factors of human-caused wildfires in Spain using geographically weighted logistic regression. Appl. Geogr. 2014, 48, 52–63. [Google Scholar] [CrossRef]
- Shao, Y.; Feng, Z.; Sun, L.; Yang, X.; Li, Y.; Xu, B.; Chen, Y. Mapping China’s forest fire risks with machine learning. Forests 2022, 13, 856. [Google Scholar] [CrossRef]
- Milanović, S.; Marković, N.; Pamučar, D.; Gigović, L.; Kostić, P.; Milanović, S.D. Forest fire probability mapping in eastern Serbia: Logistic regression versus random forest method. Forests 2020, 12, 5. [Google Scholar] [CrossRef]
- Xie, L.; Zhang, R.; Zhan, J.; Li, S.; Shama, A.; Zhan, R.; Wang, T.; Lv, J.; Bao, X.; Wu, R. Wildfire risk assessment in Liangshan Prefecture, China based on an integration machine learning algorithm. Remote Sens. 2022, 14, 4592. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, F.; Lin, H.; Xu, S. A Forest Fire Susceptibility Modeling Approach Based on Light Gradient Boosting Machine Algorithm. Remote Sens. 2022, 14, 4362. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, Z.; Feng, Z.; Sun, L.; Yang, X.; Zheng, J.; Ma, T. Assessment of China’s forest fire occurrence with deep learning, geographic information and multisource data. J. For. Res. 2023, 34, 963–976. [Google Scholar] [CrossRef]
- Naderpour, M.; Rizeei, H.M.; Ramezani, F. Forest fire risk prediction: A spatial deep neural network-based framework. Remote Sens. 2021, 13, 2513. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
- Costache, R.; Tin, T.T.; Arabameri, A.; Crăciun, A.; Costache, I.; Islam, A.R.M.T.; Sahana, M.; Pham, B.T. Stacking state-of-the-art ensemble for flash-flood potential assessment. Geocarto Int. 2022, 37, 13812–13838. [Google Scholar] [CrossRef]
- Cui, S.; Yin, Y.; Wang, D.; Li, Z.; Wang, Y. A stacking-based ensemble learning method for earthquake casualty prediction. Appl. Soft Comput. 2021, 101, 107038. [Google Scholar] [CrossRef]
- Xie, Y.; Peng, M. Forest fire forecasting using ensemble learning approaches. Neural Comput. Appl. 2019, 31, 4541–4550. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, M.; Liu, K. Wildfire susceptibility assessment in Southern China: A comparison of multiple methods. Int. J. Disaster Risk Sci. 2017, 8, 164–181. [Google Scholar] [CrossRef]
- Sun, H.; Wang, J.; Xiong, J.; Bian, J.; Jin, H.; Cheng, W.; Li, A. Vegetation change and its response to climate change in Yunnan Province, China. Adv. Meteorol. 2021, 2021, 8857589. [Google Scholar] [CrossRef]
- Han, J.; Shen, Z.; Ying, L.; Li, G.; Chen, A. Early post-fire regeneration of a fire-prone subtropical mixed Yunnan pine forest in Southwest China: Effects of pre-fire vegetation, fire severity and topographic factors. For. Ecol. Manag. 2015, 356, 31–40. [Google Scholar] [CrossRef]
- Ye, J.; Wu, M.; Deng, Z.; Xu, S.; Zhou, R.; Clarke, K.C. Modeling the spatial patterns of human wildfire ignition in Yunnan province, China. Appl. Geogr. 2017, 89, 150–162. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Yao, J.; Zhai, H.; Tang, X.; Gao, X.; Yang, X. Amazon fire monitoring and analysis based on multi-source remote sensing data. IOP Conf. Ser. Earth Environ. Sci. 2020, 474, 042025. [Google Scholar] [CrossRef]
- Santos, F.L.; Libonati, R.; Peres, L.F.; Pereira, A.A.; Narcizo, L.C.; Rodrigues, J.A.; Oom, D.; Pereira, J.M.; Schroeder, W.; Setzer, A.W. Assessing VIIRS capabilities to improve burned area mapping over the Brazilian Cerrado. Int. J. Remote Sens. 2020, 41, 8300–8327. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, J.; Jian, H.; Fan, X.; Yan, F. Fire diurnal cycle derived from a combination of the Himawari-8 and VIIRS satellites to improve fire emission assessments in southeast Australia. Remote Sens. 2021, 13, 2852. [Google Scholar] [CrossRef]
- Ma, C.; Yang, J.; Chen, F.; Ma, Y.; Liu, J.; Li, X.; Duan, J.; Guo, R. Assessing heavy industrial heat source distribution in China using real-time VIIRS active fire/hotspot data. Sustainability 2018, 10, 4419. [Google Scholar] [CrossRef]
- Shangqi, D.; Haidong, C.; Xingke, G.; Shuangde, H.; Tao, W.; Debin, X.; Baoyu, X. Analysis of topographic features based on Yunnan fire. IOP Conf. Ser. Earth Environ. Sci. 2021, 658, 012015. [Google Scholar] [CrossRef]
- Pimont, F.; Dupuy, J.-L.; Linn, R. Coupled slope and wind effects on fire spread with influences of fire size: A numerical study using FIRETEC. Int. J. Wildland Fire 2012, 21, 828–842. [Google Scholar] [CrossRef]
- Viegas, D.X. On the existence of a steady state regime for slope and wind driven fires. Int. J. Wildland Fire 2004, 13, 101–117. [Google Scholar] [CrossRef]
- Li, W.; Xu, Q.; Yi, J.; Liu, J. Predictive model of spatial scale of forest fire driving factors: A case study of Yunnan Province, China. Sci. Rep. 2022, 12, 19029. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Fan, Z.; Niu, S.; Zheng, J. The influence of precipitation and consecutive dry days on burned areas in Yunnan Province, Southwestern China. Adv. Meteorol. 2014, 2014, 748923. [Google Scholar] [CrossRef]
- Stocks, B.J.; Lawson, B.; Alexander, M.; Wagner, C.V.; McAlpine, R.; Lynham, T.; Dube, D. The Canadian forest fire danger rating system: An overview. For. Chron. 1989, 65, 450–457. [Google Scholar] [CrossRef]
- Wotton, B.M. Interpreting and using outputs from the Canadian Forest Fire Danger Rating System in research applications. Environ. Ecol. S tat. 2009, 16, 107–131. [Google Scholar] [CrossRef]
- Turner, J.A.; Lawson, B.D. Weather in the Canadian Forest Fire Danger Rating System: A User Guide to National Standards and Practices; Information Report BC-X-177; Fisheries and Environment Canada, Canadian Forest Service, Pacific Forest Research Centre: Victoria, BC, Canada, 1978; 40p. [Google Scholar]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Coogan, S.C.; Robinne, F.-N.; Jain, P.; Flannigan, M.D. Scientists’ warning on wildfire—A Canadian perspective. Can. J. For. Res. 2019, 49, 1015–1023. [Google Scholar] [CrossRef]
- Pereira, M.; Malamud, B.; Trigo, R.; Alves, P. The history and characteristics of the 1980–2005 Portuguese rural fire database. Nat. Hazards Earth Syst. Sci. 2011, 11, 3343–3358. [Google Scholar] [CrossRef]
- Salinero, E.C. Wildland Fire Danger Estimation and Mapping: The Role of Remote Sensing Data; World Scientific: Singapore, 2003; Volume 4. [Google Scholar]
- Gigović, L.; Pourghasemi, H.R.; Drobnjak, S.; Bai, S. Testing a new ensemble model based on SVM and random forest in forest fire susceptibility assessment and its mapping in Serbia’s Tara National Park. Forests 2019, 10, 408. [Google Scholar] [CrossRef]
- Ikechukwu, M.N.; Ebinne, E.; Idorenyin, U.; Raphael, N.I. Accuracy assessment and comparative analysis of IDW, spline and kriging in spatial interpolation of landform (topography): An experimental study. J. Geogr. Inf. Syst. 2017, 9, 354–371. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, T. Long-Term Spatial and Temporal Variation of Near Surface Air Temperature in Southwest China during 1969–2018. Front. Earth Sci. 2021, 9, 753757. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; McVicar, T.R.; Van Niel, T.; Yang, Q.; Li, R. Introduction of the professional interpolation software for meteorology data-ANUSPLIN. Meteorologicalmonthly 2008, 34, 92–100. [Google Scholar]
- Zhang, G.; Wang, M.; Liu, K. Forest fire susceptibility modeling using a convolutional neural network for Yunnan province of China. Int. J. Disaster Risk Sci. 2019, 10, 386–403. [Google Scholar] [CrossRef]
- Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–4. [Google Scholar]
- Colkesen, I.; Sahin, E.K.; Kavzoglu, T. Susceptibility mapping of shallow landslides using kernel-based Gaussian process, support vector machines and logistic regression. J. Afr. Earth Sci. 2016, 118, 53–64. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Hughes, M.J.; Kennedy, R.E. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wang, S. Artificial neural network. In Interdisciplinary Computing in Java Programming; Springer: Boston, MA, USA, 2003. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems 25, Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Kumar, I.E.; Venkatasubramanian, S.; Scheidegger, C.; Friedler, S. Problems with Shapley-value-based explanations as feature importance measures. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5491–5500. [Google Scholar]
- Jaafari, A.; Termeh, S.V.R.; Bui, D.T. Genetic and firefly metaheuristic algorithms for an optimized neuro-fuzzy prediction modeling of wildfire probability. J. Environ. Manag. 2019, 243, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef]
- Bui, Q.-T. Metaheuristic algorithms in optimizing neural network: A comparative study for forest fire susceptibility mapping in Dak Nong, Vietnam. Geomat. Nat. Hazards Risk 2019, 10, 136–150. [Google Scholar] [CrossRef]
- Menahem, E.; Rokach, L.; Elovici, Y. Troika–an improved stacking schema for classification tasks. Inf. Sci. 2009, 179, 4097–4122. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on typical tabular data? In Proceedings of the Advances in Neural Information Processing Systems 35, New Orleans, LA, USA, 28 November–9 December 2022; pp. 507–520. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Chuvieco, E.; Cocero, D.; Riano, D.; Martin, P.; Martınez-Vega, J.; De La Riva, J.; Pérez, F. Combining NDVI and surface temperature for the estimation of live fuel moisture content in forest fire danger rating. Remote Sens. Environ. 2004, 92, 322–331. [Google Scholar] [CrossRef]
- Kim, S.J.; Lim, C.-H.; Kim, G.S.; Lee, J.; Geiger, T.; Rahmati, O.; Son, Y.; Lee, W.-K. Multi-temporal analysis of forest fire probability using socio-economic and environmental variables. Remote Sens. 2019, 11, 86. [Google Scholar] [CrossRef]
- Bjånes, A.; De La Fuente, R.; Mena, P. A deep learning ensemble model for wildfire susceptibility mapping. Ecol. Inform. 2021, 65, 101397. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C. Comparison of free high resolution digital elevation data sets (ASTER GDEM2, SRTM v2. 1/v4. 1) and validation against accurate heights from the Australian National Gravity Database. Aust. J. Earth Sci. 2014, 61, 213–226. [Google Scholar] [CrossRef]
- Yang, C.; Liu, L.-L.; Huang, F.; Huang, L.; Wang, X.-M. Machine learning-based landslide susceptibility assessment with optimized ratio of landslide to non-landslide samples. Gondwana Res. 2023, 123, 198–216. [Google Scholar] [CrossRef]
- Lin, X.; Li, Z.; Chen, W.; Sun, X.; Gao, D. Forest Fire Prediction Based on Long-and Short-Term Time-Series Network. Forests 2023, 14, 778. [Google Scholar] [CrossRef]










| Influencing Factors | Variable | Unit | Symbol | Source |
|---|---|---|---|---|
| Topography | Altitude | m | Altitude | Geospatial Data Cloud https://www.gscloud.cn (accessed on 20 July 2023) |
| Slope | degree | Slope | ||
| Aspect | degree | Aspect | ||
| Meteorology | Average daily air temperature | °C | Ate | China Meteorological Data Network https://data.cma.cn (accessed on 20 July 2023) |
| Maximum daily air temperature | °C | Mte | ||
| Average daily relative humidity | ratio | Arh | ||
| 24-h cumulative precipitation | mm | Pre | ||
| Hours of sunshine | h | Suh | ||
| Maximum daily wind speed | m/s | Mws | ||
| Fine fuel moisture content | - | FFMC | Forest Fire Weather Index (FWI) | |
| Duff moisture content | - | DMC | ||
| Drought code | - | DC | ||
| Vegetation | Vegetation normalized index | ratio | NDVI | Resource and Environment Science and Data Center https://www.resdc.cn (accessed on 20 July 2023) |
| Vegetation type | class | VT | Global Land Cover with Fine Classification System at 30 m in 2020 https://zenodo.org/record/4280923 (accessed on 20 July 2023) | |
| Human activity | Population rate | persons/km2 | Pop | Resource and Environment Science and Data Center https://www.resdc.cn (accessed on 20 July 2023) |
| Distance to roads | class | Road | ||
| Distance to rivers | class | River |
| Model | Hyperparameters |
|---|---|
| RF | n_estimators = 580; max_depth = 17; max_features = 15; max_features = “sqrt” |
| XGBoost | n_estimators = 960; max_depth = 10; colsample_bytree = 0.6; learning_rate = 0.16; gamma = 0.17; reg_lambda = 0.77 |
| LightGBM | n_estimators = 530; max_depth = 18; min_child_samples = 22; colsample_bytree = 0.52, num_leaves = 960; reg_lambda = 0.7 |
| MLP | solver = ‘adam’; activation = ‘relu’; hidden_layer_sizes = (215, 215) |
| No. | Feature | VIF | TOL |
|---|---|---|---|
| 1 | Altitude | 2.43 | 0.41 |
| 2 | Slope | 1.09 | 0.92 |
| 3 | Aspect | 3.41 | 0.29 |
| 4 | Hours of sunshine | 3.61 | 0.28 |
| 5 | Maximum daily air temperature | 2.43 | 0.41 |
| 6 | Average daily relative humidity | 4.12 | 0.24 |
| 7 | 24 h cumulative precipitation | 2.93 | 0.34 |
| 8 | Maximum daily wind speed | 2.26 | 0.44 |
| 9 | Fine fuel moisture content | 5.00 | 0.20 |
| 10 | Duff moisture content | 3.91 | 0.26 |
| 11 | Drought code | 3.47 | 0.29 |
| 12 | Population rate | 1.32 | 0.76 |
| 13 | Distance to roads | 1.51 | 0.66 |
| 14 | Distance to rivers | 1.41 | 0.71 |
| 15 | NDVI | 1.31 | 0.77 |
| 16 | Vegetation type | 3.63 | 0.28 |
| Indicators | RF | XGBoost | LightGBM | MLP | Stacking |
|---|---|---|---|---|---|
| Accuracy | 0.873 | 0.886 | 0.879 | 0.866 | 0.906 |
| Precision | 0.879 | 0.888 | 0.882 | 0.872 | 0.908 |
| Recall | 0.873 | 0.886 | 0.879 | 0.866 | 0.906 |
| F1-score | 0.880 | 0.890 | 0.884 | 0.874 | 0.909 |
| AUC | 0.942 | 0.953 | 0.946 | 0.935 | 0.970 |
| Model | Extremely Low | Low | Medium | High | Extremely High |
|---|---|---|---|---|---|
| RF | 0.05 | 0.36 | 0.87 | 1.55 | 2.09 |
| XGBoost | 0.04 | 0.34 | 0.79 | 1.48 | 2.29 |
| LightGBM | 0.04 | 0.33 | 0.85 | 1.64 | 2.32 |
| MLP | 0.09 | 0.88 | 1.18 | 1.82 | 2.10 |
| Stacking | 0.04 | 0.30 | 0.40 | 1.26 | 2.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, G.; Wang, K.; Wang, Z.; Chen, Y. Forest Fire Risk Prediction Based on Stacking Ensemble Learning for Yunnan Province of China. Fire 2024, 7, 13. https://doi.org/10.3390/fire7010013
Li Y, Li G, Wang K, Wang Z, Chen Y. Forest Fire Risk Prediction Based on Stacking Ensemble Learning for Yunnan Province of China. Fire. 2024; 7(1):13. https://doi.org/10.3390/fire7010013
Chicago/Turabian StyleLi, Yanzhi, Guohui Li, Kaifeng Wang, Zumin Wang, and Yanqiu Chen. 2024. "Forest Fire Risk Prediction Based on Stacking Ensemble Learning for Yunnan Province of China" Fire 7, no. 1: 13. https://doi.org/10.3390/fire7010013
APA StyleLi, Y., Li, G., Wang, K., Wang, Z., & Chen, Y. (2024). Forest Fire Risk Prediction Based on Stacking Ensemble Learning for Yunnan Province of China. Fire, 7(1), 13. https://doi.org/10.3390/fire7010013





