A Numerical Analysis of Premixed Hydrogen–Methane Flame with Three Different Header Types of Combustor
Abstract
1. Introduction
2. Simulation Methods
2.1. Governing Equation
2.2. Design Parameters
2.3. Simulation Models
3. Results and Discussion
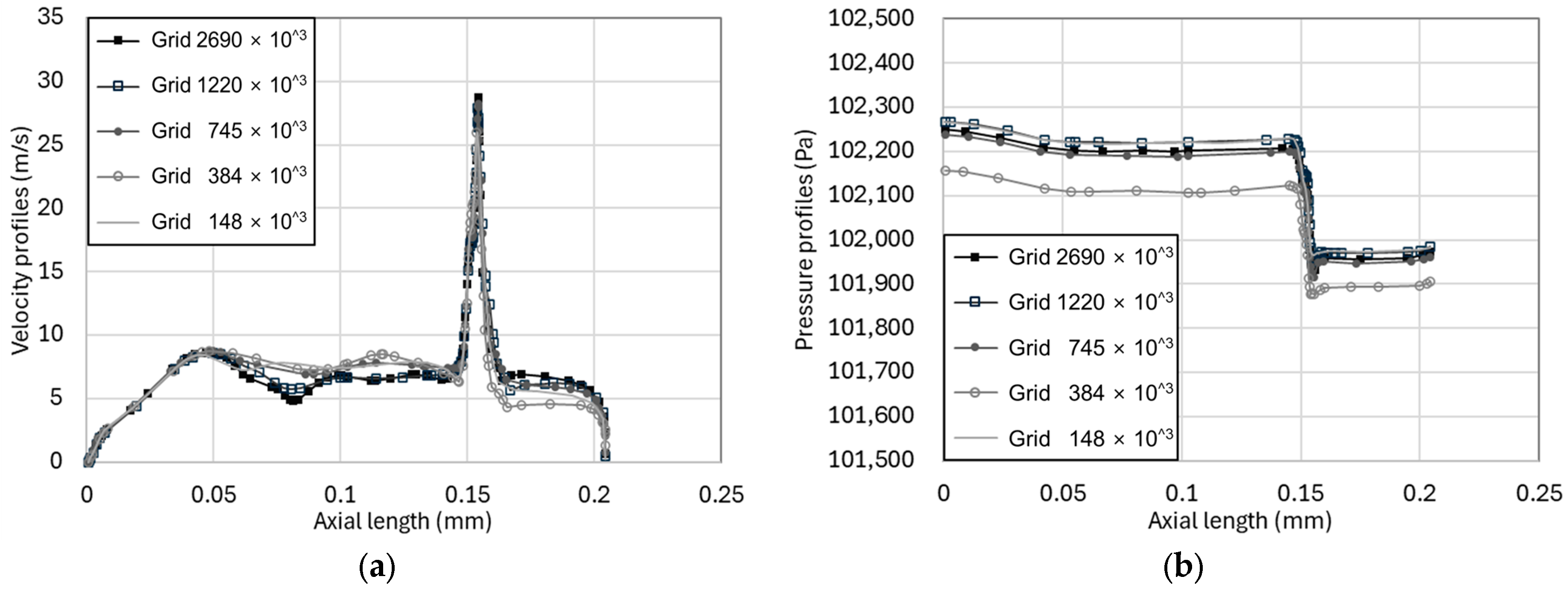
3.1. Mesh Validation
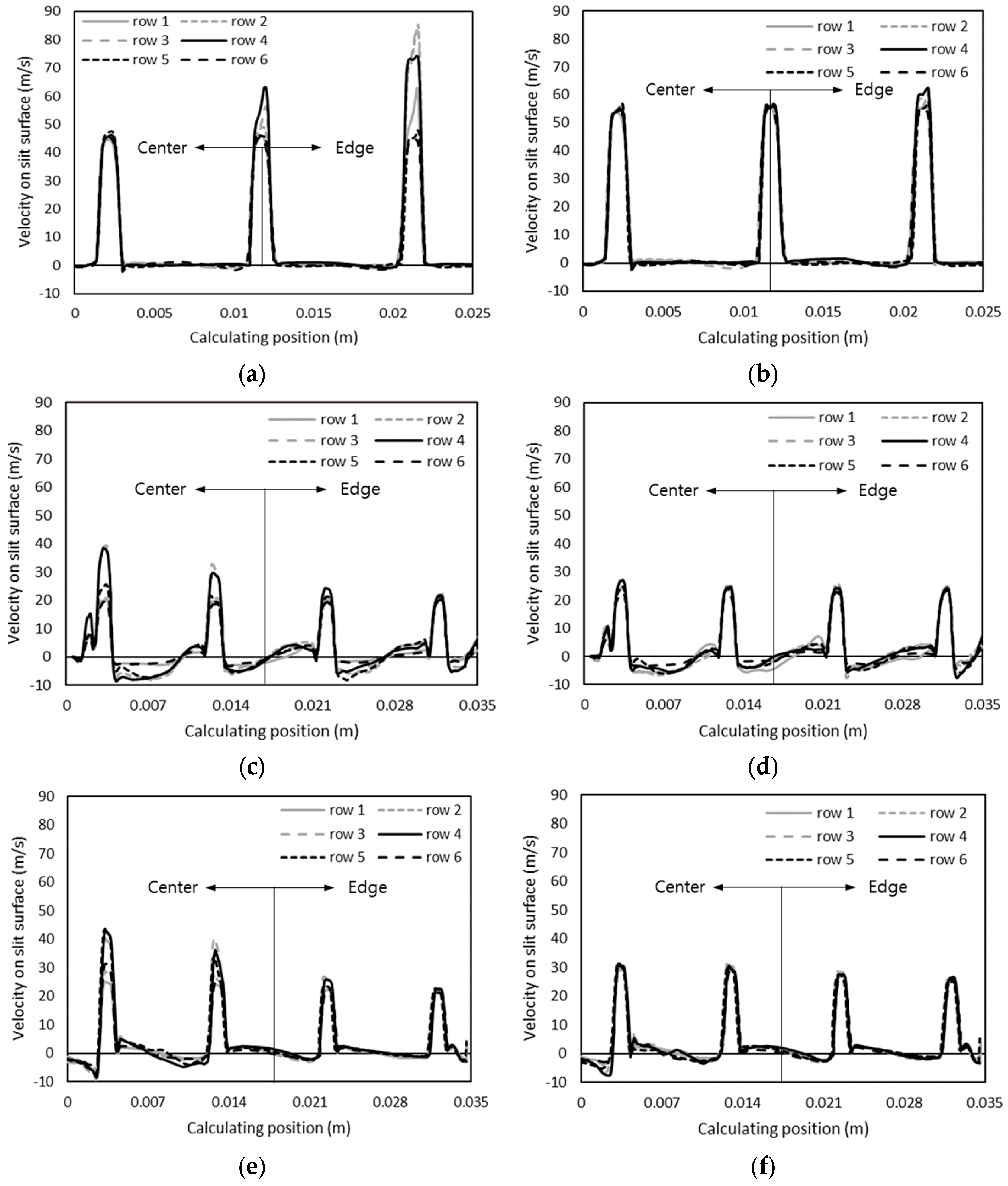
3.2. Internal Flow Characteristics
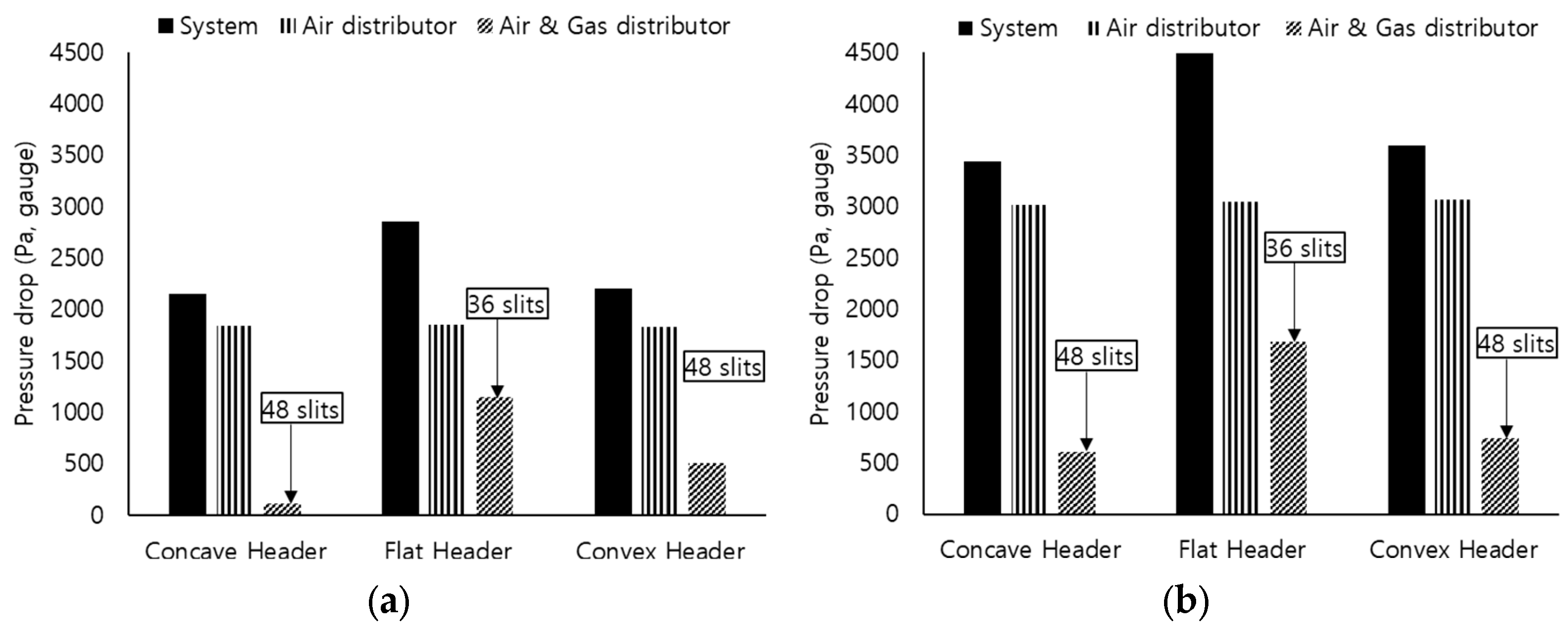
3.3. Pressure Drop across Distribution Plates
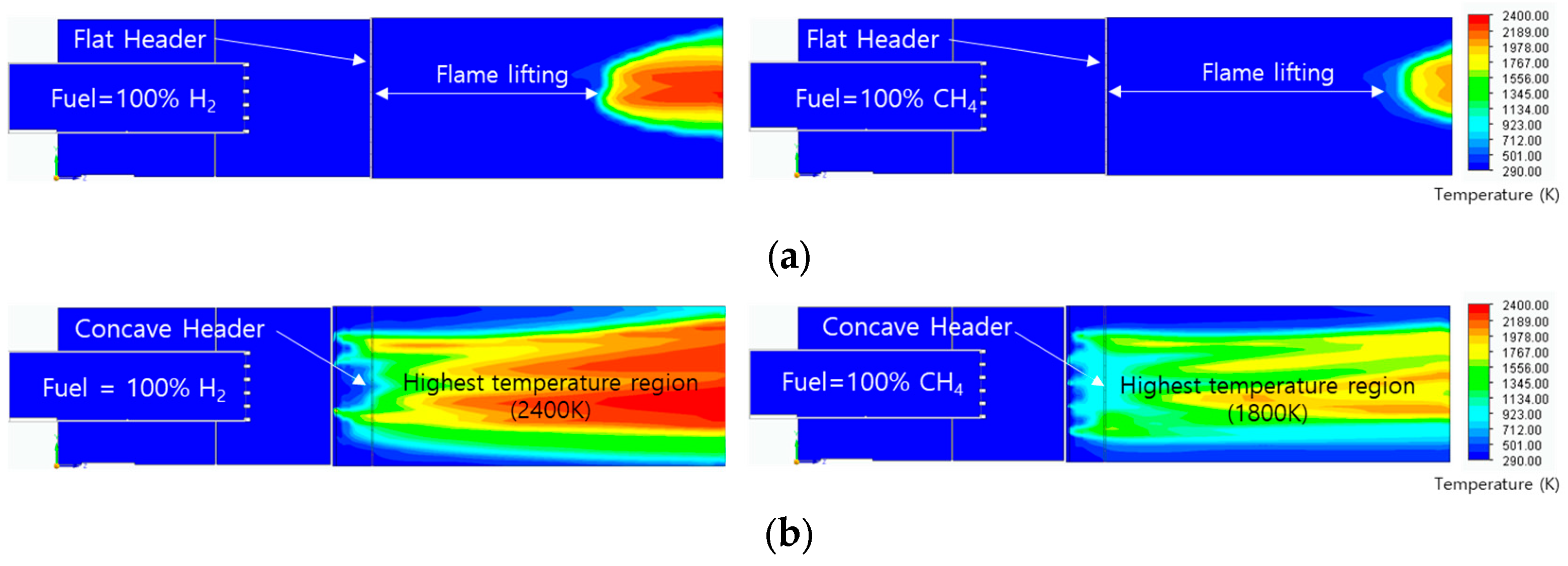
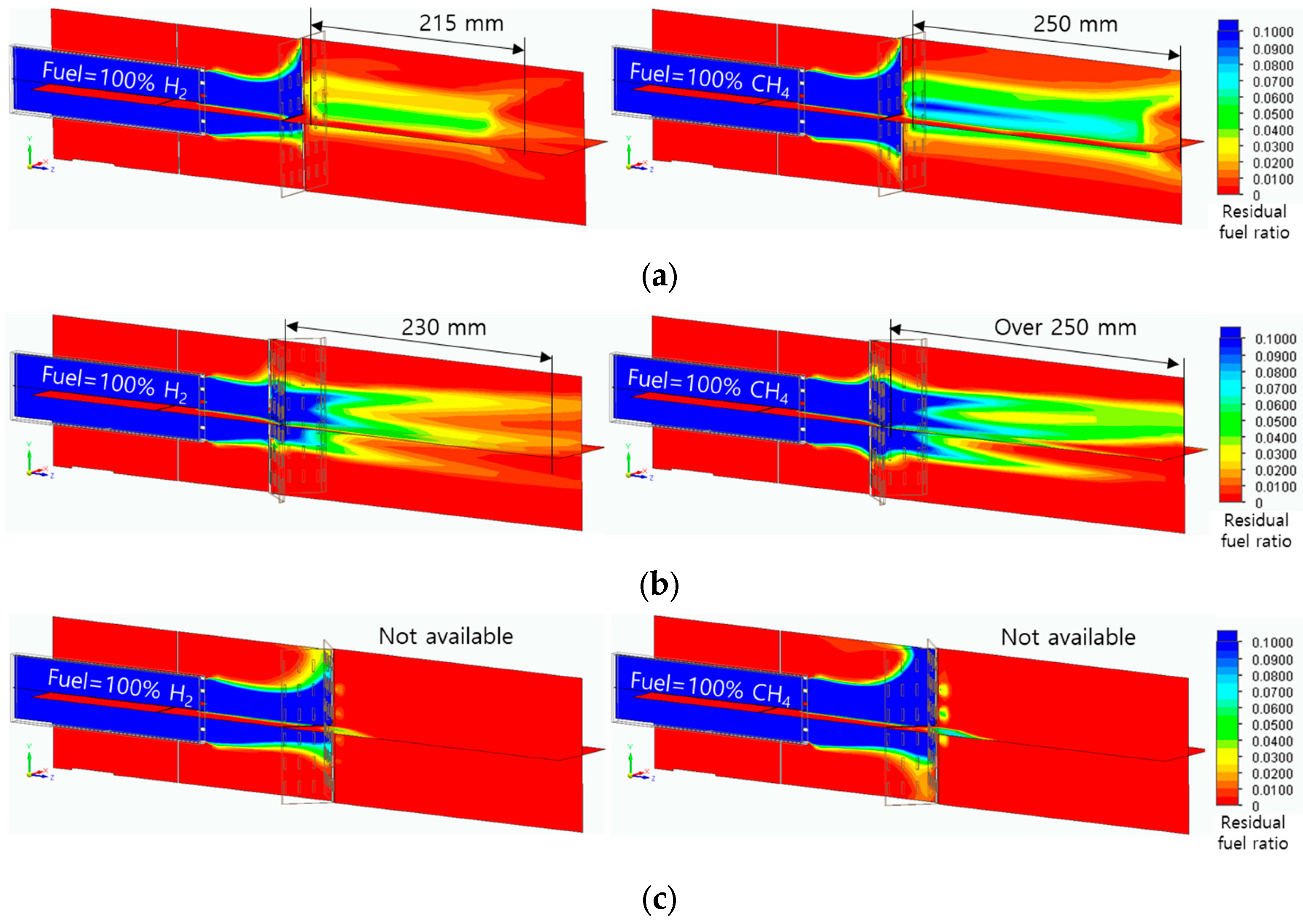
3.4. Flame Shape with Temperature and Residual Fuel Ratio
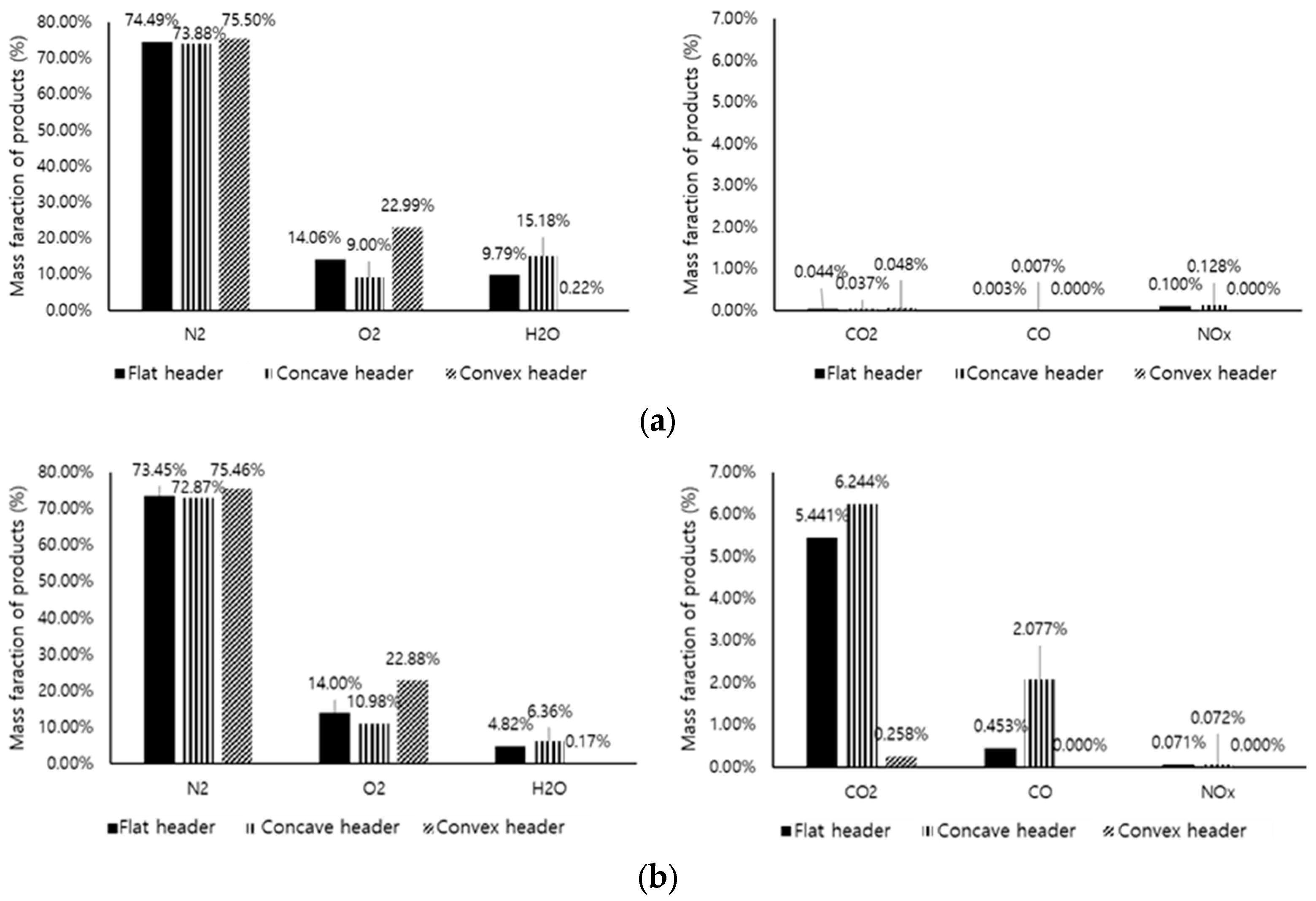
3.5. Exhaust Gas Composition
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Fluid velocity, m/s | |
| Fluid density, kg/m3 | |
| Viscous shear stress tensor, N/m2 | |
| Mass-distributed external force per unit mass, N/kg | |
| Dynamic viscosity coefficient, N∙s/m2 | |
| Turbulent eddy viscosity coefficient, N∙s/m2 | |
| Turbulent kinetic energy, kg m2/s2 | |
| Turbulent dissipation, kg m2/s2 | |
| Turbulent viscosity factor | |
| Turbulence generation due to buoyancy forces, N | |
| Molecular matrices of diffusion | |
| Turbulent matrices of diffusion | |
| Rate of production or consumption, kg/s | |
| Combustion products, mol | |
| Reaction rate, mol/m3∙s | |
| Mass fraction of residual fuel | |
| Mass fraction of oxidizing agent | |
| Molar mass of fuel, kg | |
| Molar mass of oxidizing agent, kg | |
| Ignition temperature, °C | |
| R | One-way reaction rate, mol/m3∙s |
References
- Kadowaki, S.; Hasegawa, T. Numerical simulation of dynamics of premixed flames: Flame instability and vortex–flame interaction. Prog. Energy Combust. Sci. 2005, 31, 193–241. [Google Scholar] [CrossRef]
- Sarli, V.D.; Benedetto, A.D. Laminar burning velocity of hydrogen–methane/air premixed flames. Int. J. Hydrogen Energy 2007, 32, 637–646. [Google Scholar] [CrossRef]
- Xiao, H.; Duan, Q.; Sun, J. Premixed flame propagation in hydrogen explosions. Renew. Sustain. Energy Rev. 2018, 81, 1988–2001. [Google Scholar] [CrossRef]
- Giannakopoulos, G.K.; Gatzoulis, A.; Frouzakis, C.E.; Matalon, M.; Tomboulides, A.G. Consistent definitions of “Flame Displacement Speed” and “Markstein Length” for premixed flame propagation. Combust. Flame 2015, 162, 1249–1264. [Google Scholar] [CrossRef]
- Takeno, K.; Kido, H.; Takeda, H.; Yamamoto, S.; Shentsov, V.; Makarov, D.; Molkov, V. Flame stabilisation mechanism for under-expanded hydrogen jets. J. Fire 2024, 7, 48–59. [Google Scholar] [CrossRef]
- Chakraborty, N.; Dopazo, C. Timescales associated with the evolution of reactive scalar gradient in premixed turbulent combustion: A direct numerical simulation analysis. J. Fire 2024, 7, 73–92. [Google Scholar] [CrossRef]
- Zhang, C.; Shen, X.; Wen, J.X.; Xiu, G. The behavior of methane/hydrogen/air premixed flame in a closed channel with inhibition. J. Fuel 2020, 265, 116810. [Google Scholar] [CrossRef]
- Halter, F.; Chauveau, C.; Gokalp, I. Characterization of the effects of hydrogen addition in premixed methane/air flames. Int. J. Hydrogen Energy 2007, 32, 2585–2592. [Google Scholar] [CrossRef]
- Okafor, C.E.; Hayakawa, A.; Nagano, Y.; Kitagawa, T. Effects of hydrogen concentration on premixed laminar flames of hydrogen-methane-air. Int. J. Hydrogen Energy 2014, 39, 2409–2417. [Google Scholar] [CrossRef]
- Funke, H.H.W.; Beckmann, N.; Abanteriba, S. An overview on dry low NOx micromix combustor development for hydrogen-rich gas turbine applications. Int. J. Hydrogen Energy 2019, 44, 6978–6990. [Google Scholar] [CrossRef]
- Cao, Z.; Lyu, Y.; Peng, J.; Qiu, P.; Liu, L.; Yang, C.; Yu, Y.; Chang, G.; Yan, B.; Sun, S.; et al. Experimental study of flame evolution, frequency and oscillation characteristics of steam diluted micro-mixing hydrogen flame. J. Fuel 2021, 301, 121078. [Google Scholar] [CrossRef]
- You, C.; Lee, H.; Hwang, S. Low NOX combustion characteristics by hydrogen micro jet flame in cross flow. J. Mech. Sci. Technol. 2023, 37, 445–455. [Google Scholar] [CrossRef]
- An, Q.; Kheirkhah, S.; Bergthorson, J.; Yun, S.; Hwang, J.; Lee, W.J.; Kim, M.K.; Cho, J.H.; Kim, H.S.; Vena, P. Flame stabilization mechanisms and shape transitions in a 3D printed, hydrogen enriched, methane/air low-swirl burner. Int. J. Hydrogen Energy 2021, 46, 14764–14779. [Google Scholar] [CrossRef]
- Schefer, R.W. Hydrogen enrichment for improved lean flame stability. Int. J. Hydrogen Energy 2003, 28, 1131–1141. [Google Scholar] [CrossRef]
- Esfahani, J.A.; Fanaee, S.A. Analytical modeling of hydrogen–air mixture in a catalytic microchannel. J. Thermophys. Heat Transf. 2015, 29, 274–280. [Google Scholar] [CrossRef]
- Edalati-nejad, A.; Fanaee, S.A.; Ghodrat, M.; Khadem, J. Investigation of unsteady premixed micro/macro counterflow flames for lean to rich methane/air mixture. J. Energy Resour. Technol. 2021, 143, 052302. [Google Scholar] [CrossRef]
- Edalati-nejad, A.; Fanaee, S.A.; Ghodrat, M. Numerical investigation of methane-air counterflow premixed flame into a newly designed plus-shaped chamber with platinum and rhodium catalysts coated walls. Combust. Sci. Technol. 2023, 195, 2598–2613. [Google Scholar] [CrossRef]
- Pourali, M.; Esfahani, J.A.; Fanaee, S.A.; Kim, K.C. Developing mathematical modeling of the heat and mass transfer in a planar micro-combustor with detailed reaction mechanisms. J. Therm. Anal. Calorim. 2021, 143, 2679–2694. [Google Scholar] [CrossRef]
- Bidabadi, M.; Montazerinejad, S.; Fanaee, S.A. The influence of radiation on the flame propagation through micro organic dust particles with non-unity Lewis number. J. Energy Inst. 2014, 87, 354–366. [Google Scholar] [CrossRef]
- Fanaee, S.A.; Esfahani, J.A. The analytical modeling of propane-oxygen mixture at catalytic micro-channel. Heat Mass Transf. 2014, 50, 1365–1373. [Google Scholar] [CrossRef]
- Somers, L.M.T.; Goey, L.P.H. A numerical study of a premixed flame on a slit burner. Combust. Sci. Technol. 1995, 108, 121–132. [Google Scholar] [CrossRef]
- Guo, L.; Zhai, M.; Shen, Q.; Qi, H.; Dong, P.; Zhu, J. Methane-air partially premixed flame behaviors in a micro plate slit. Chem. Eng. Process. Process Intensif. 2020, 158, 108200. [Google Scholar] [CrossRef]
- Liu, T.; Yang, L.; Qin, L.; Jiang, X.; Li, J. Models of the time-averaged heat release rate of the two-dimensional laminar premixed slit flame subjected to the transverse disturbance. Aerosp. Sci. Technol. 2023, 132, 108072. [Google Scholar] [CrossRef]
- Raghavan, K.A.S.; Rao, S.S.; Raju, V.R.K. Numerical investigation of the effect of slit-width on the combustion characteristics of a micro-combustor with a centrally slotted bluff body. Int. J. Hydrogen Energy 2023, 48, 5696–5707. [Google Scholar] [CrossRef]
- Chen, P.; Luo, G.; Sun, Y.; Lv, Q. Impacts of plate slits on flame acceleration of premixed methane/air in a closed tube. J. Energy Inst. 2018, 91, 563–572. [Google Scholar] [CrossRef]
- Tyagi, A.; Boxx, I.; Peluso, S.; O’Connor, J. The role of flow interaction in flame–flame interaction events in a dual burner experiment. Proc. Combust. Inst. 2019, 37, 2485–2491. [Google Scholar] [CrossRef]
- Mentor Graphics Corporation, FloEFD Technical Reference Software Version 17. 2018. Available online: https://www.smart-fem.de/media/floefd/TechnicalReferenceV17.pdf (accessed on 20 August 2024).
- Zeldovich, Y.B.; Barenblatt, G.I.; Librovich, V.B.; Makhviladze, G.M. The Mathematical Theory of Combustion and Explosions; Springer: New York, NY, USA, 1985. [Google Scholar]
- Siriganano, W.; Merzhabov, A.; De Luca, L. Advances in Combustion Science in Honor of Ya. B. Zeldovich; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 1996. [Google Scholar]

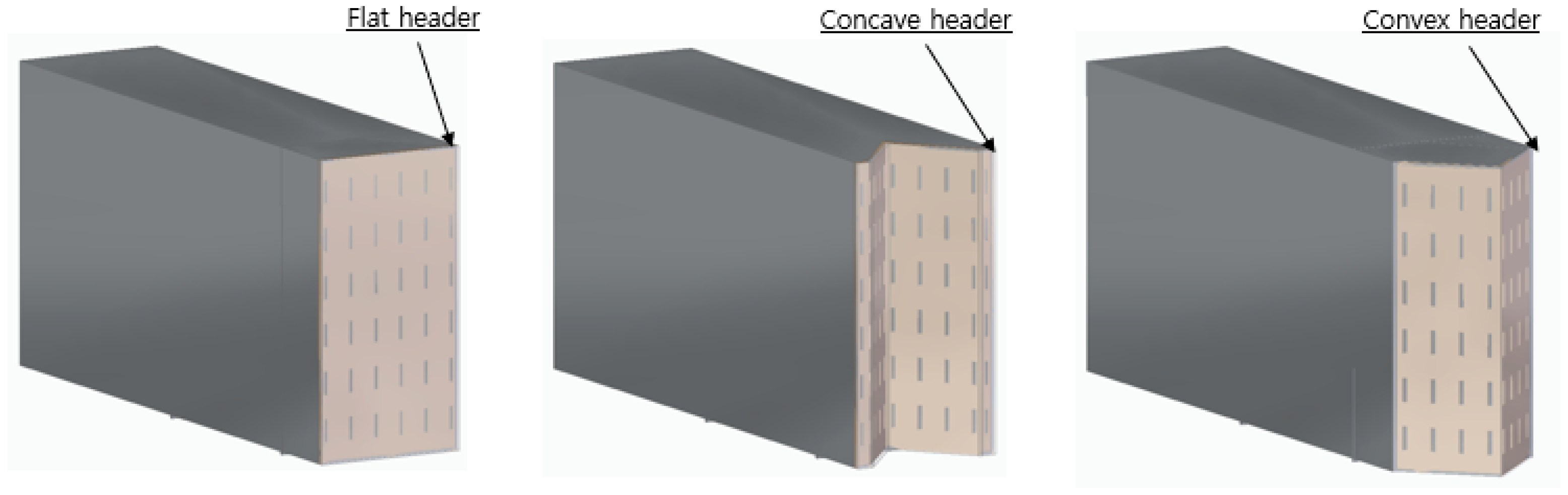



| Design Parameter | CH4 | H2 |
|---|---|---|
| Required heat input | 40,000 kcal/h | 40,000 kcal/h |
| Fuel flow rate | 4.5 Nm3/h | 13.8 Nm3/h |
| Higher calorific value | 8698 kcal/Nm3 | 2796 kcal/Nm3 |
| Fuel inlet temperature | 15 °C | 15 °C |
| Combustion air flow rate | 55.0 Nm3/h | 42.8 Nm3/h |
| Mixture flow rate | 59.5 Nm3/h | 56.6 Nm3/h |
| Excess air ratio | 1.3 | 1.3 |
| Reynolds number | 4905 | 4665 |
| Total Number of Cells | Number of Fluid Cells | Number of Solid Cells |
|---|---|---|
| 147,953 | 83,237 | 64,716 |
| 384,030 | 214,906 | 169,124 |
| 745,486 | 425,719 | 319,767 |
| 1,220,378 | 765,356 | 455,022 |
| 2,691,036 | 1,800,925 | 890,111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Sohn, C.B.; Jeong, Y.S.; Kim, Y.B. A Numerical Analysis of Premixed Hydrogen–Methane Flame with Three Different Header Types of Combustor. Fire 2024, 7, 361. https://doi.org/10.3390/fire7100361
Lee J, Sohn CB, Jeong YS, Kim YB. A Numerical Analysis of Premixed Hydrogen–Methane Flame with Three Different Header Types of Combustor. Fire. 2024; 7(10):361. https://doi.org/10.3390/fire7100361
Chicago/Turabian StyleLee, Jaeyoung, Chang Bum Sohn, Young Sik Jeong, and Young Bae Kim. 2024. "A Numerical Analysis of Premixed Hydrogen–Methane Flame with Three Different Header Types of Combustor" Fire 7, no. 10: 361. https://doi.org/10.3390/fire7100361
APA StyleLee, J., Sohn, C. B., Jeong, Y. S., & Kim, Y. B. (2024). A Numerical Analysis of Premixed Hydrogen–Methane Flame with Three Different Header Types of Combustor. Fire, 7(10), 361. https://doi.org/10.3390/fire7100361






