Site Quality Models and Fuel Load Dynamic Equation Systems Disaggregated by Size Fractions and Vegetative States in Gorse and High Heath Shrublands in Galicia (NW Spain)
Abstract
1. Introduction
2. Material and Methods
2.1. Study Area, Shrub Communities and Inventory Plots
2.2. Biomass Sampling
2.3. Laboratory Work
2.4. Development of Total Fuel Load Growth Curves
2.5. Compatible System for the Shrub Fuel Complex
2.6. Assessing the Effect of Topographic and Climatic Variables on Site Quality
3. Results
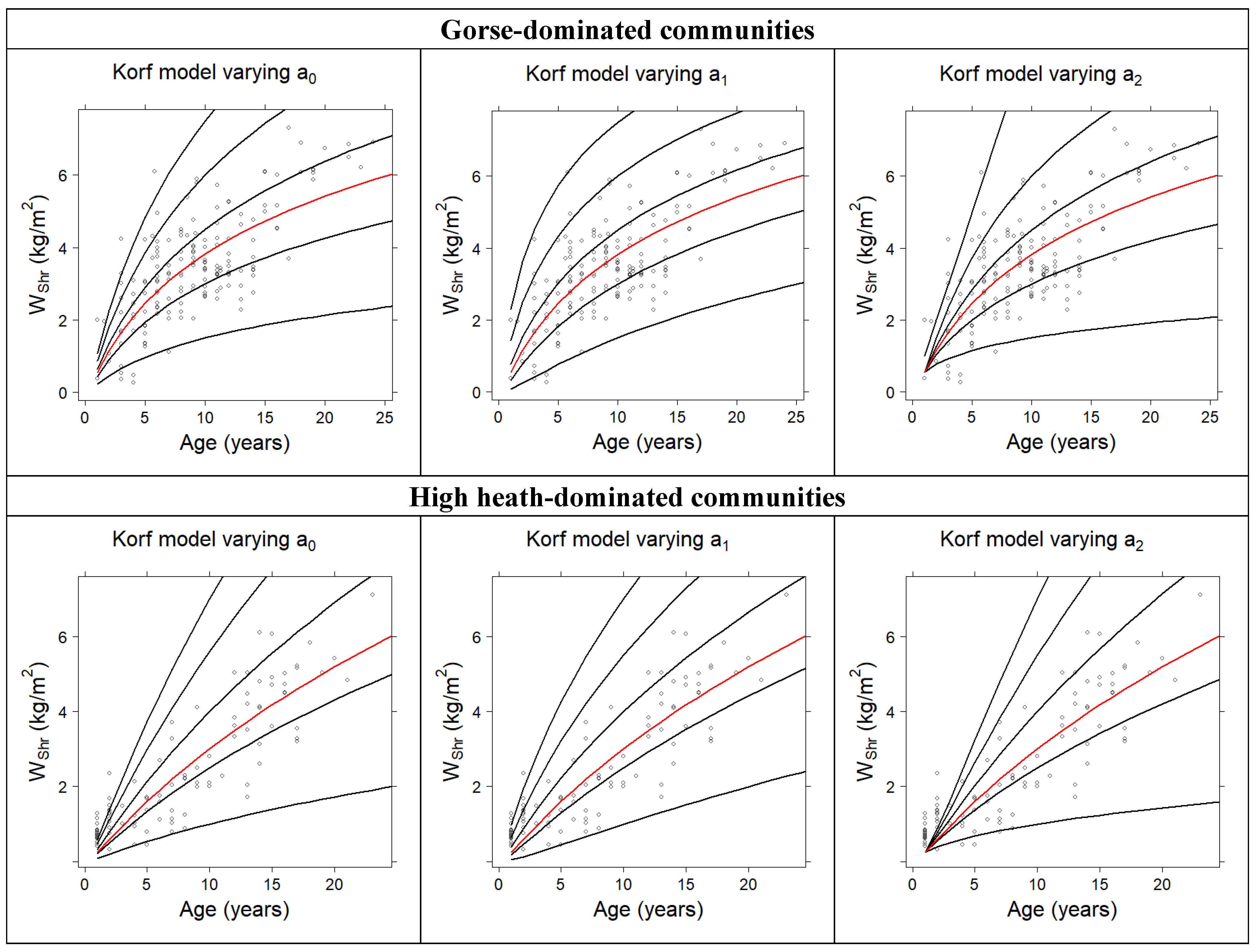
3.1. Development of Total Fuel Load Growth Curves
3.2. Effect of Topographic and Climatic Variables on Site Quality
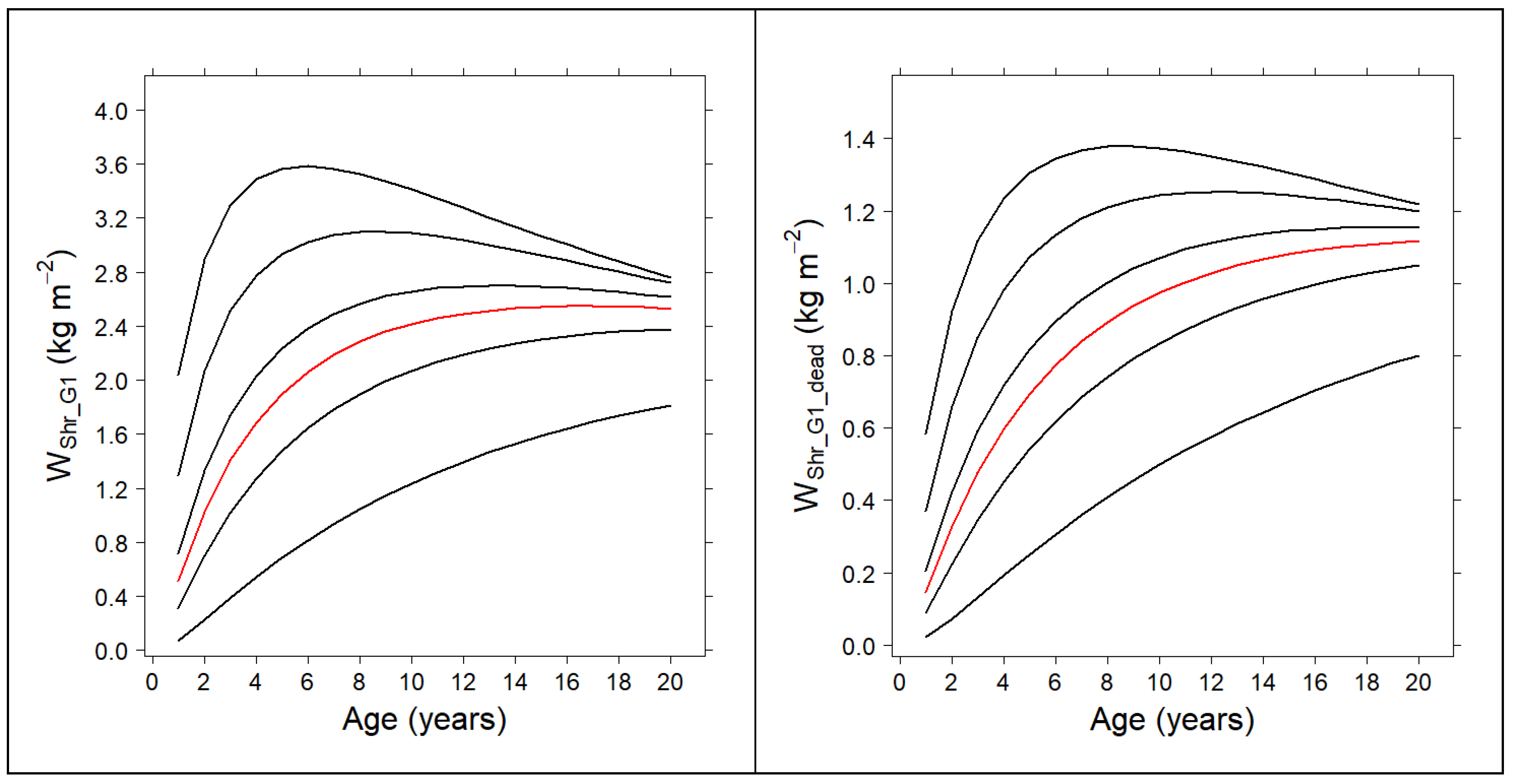
3.3. Compatible System for the Shrub Fuel Complex
4. Discussion
4.1. Effect of Topographic and Climatic Variables on Site Quality
4.2. Biomass Accumulation and Mean Annual Increment (MAI)
4.3. Fine Ratio
4.4. Dead Ratio
4.5. Implications for Fuel Hazard Management
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pasalodos-Tato, M.; Ruiz-Peinado, R.; del Río, M.; Montero, G. Shrub biomass accumulation and growth rate models to quantify carbon stocks and fluxes for the Mediterranean region. Eur. J. For. Res. 2015, 134, 537–553. [Google Scholar] [CrossRef]
- Lombardo, E.; Bancheva, S.; Domina, G.; Venturella, G. Distribution, ecological role and symbioses of selected shrubby species in the Mediterranean Basin: A review. Plant Biosyst. 2020, 154, 438–454. [Google Scholar] [CrossRef]
- Madrigal-González, J.; Fernández-Santos, B.; Silla, F.; García Rodríguez, J.A. Shrub diversity in Mediterranean shrublands: Rescuer or victim of productivity? J. Veg. Sci. 2023, 34, e13169. [Google Scholar] [CrossRef]
- Moreira, F.; Viedma, O.; Arianoutsou, M.; Curt, T.; Koutsias, N.; Rigolot, E.; Barbati, A.; Corona, P.; Vaz, P.; Xanthopoulos, G.; et al. Landscape–wildfire interactions in southern Europe: Implications for landscape management. J. Environ. Manag. 2011, 92, 2389–2402. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, P.M.; Loureiro, C.; Guiomar, N.; Pezzatti, G.B.; Manso, F.; Lopes, L. The dynamics and drivers of fuel and fire in the Portuguese public forest. J. Environ. Manag. 2014, 146, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Archer, S.R.; Andersen, E.M.; Predick, K.I.; Schwinning, S.; Steidl, R.J.; Woods, S.R. Woody Plant Encroachment: Causes and Consequences. In Rangeland Systems; Briske, D.D., Ed.; Springer Series on Environmental Management; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Vega, J.A.; Arellano-Pérez, S.; Álvarez-González, J.G.; Fernández, C.; Jiménez, E.; Fernández-Alonso, J.M.; Vega-Nieva, D.; Briones-Herrera, C.; Alonso-Rego, C.; Fontúrbel, T.; et al. Modelling aboveground biomass and fuel load components at stand level in shrub communities in NW Spain. For. Ecol. Manag. 2022, 505, 119926. [Google Scholar] [CrossRef]
- Kukavskaya, E.A.; Buryak, L.V.; Shvetsov, E.G.; Conard, S.G.; Kalenskaya, O.P. The impact of increasing fire frequency on forest transformations in southern Siberia. For. Ecol. Manag. 2016, 382, 225–235. [Google Scholar] [CrossRef]
- Coop, J.D.; Parks, S.A.; Stevens-Rumann, C.S.; Crausbay, S.D.; Higuera, P.D.; Hurteau, M.D.; Tepley, A.; Whitman, E.; Assal, T.; Collins, B.M.; et al. Wildfire-Driven Forest Conversion in Western North American Landscapes. BioScience 2020, 70, 659–667. [Google Scholar] [CrossRef]
- Lloret, F.; Pausas, J.G.; Vila, M. Responses of Mediterranean plant species to different fire frequencies in Garraf Natural Park (Catalonia, Spain): Field observations and modelling predictions. Plant Ecol. 2003, 167, 223–235. [Google Scholar] [CrossRef]
- Fernández-García, V.; Marcos, E.; Fulé, P.Z.; Reyes, O.; Santana, V.M.; Calvo, L. Fire regimes shape diversity and traits of vegetation under different climatic conditions. Sci. Total Environ. 2020, 716, 137137. [Google Scholar] [CrossRef]
- Baeza, M.J.; Raventós, J.; Escarré, A.; Vallejo, V.R. Fire risk and vegetation structural dynamics in Mediterranean shrubland. Plant Ecol. 2006, 187, 189–201. [Google Scholar] [CrossRef]
- Valdecantos, A.; Baeza, M.J.; Vallejo, V.R. Vegetation management for promoting ecosystem resilience in fire-prone Mediterranean shrublands. Restor. Ecol. 2009, 17, 414–421. [Google Scholar] [CrossRef]
- Keeley, J.E.; Pausas, J.G.; Rundel, P.W.; Bond, W.J.; Bradstock, R.A. Fire as an evolutionary pressure shaping plant traits. Trends Plant Sci. 2011, 16, 406–411. [Google Scholar] [CrossRef]
- Keeley, J.E.; Bond, W.J.; Bradstock, R.A.; Pausas, J.G.; Rundel, P.W. Fire in Mediterranean Ecosystems: Ecology, Evolution and Management; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Pausas, J.G.; Schwilk, D. Fire and plant evolution. New Phytol. 2012, 193, 301–303. [Google Scholar] [CrossRef] [PubMed]
- Chandler, C.; Cheney, P.; Thomas, P.; Trabaud, L.; Williams, D. Fire in Forestry. Vol. 1. Forest Fire Behavior and Effects; John Wiley & Sons, Inc.: New York, NY, USA, 1983. [Google Scholar]
- Pyne, S.J.; Andrews, P.L.; Laven, R.D. Introduction to Wildland Fire, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1996. [Google Scholar]
- Scott, A.C.; Bowman, D.M.J.S.; Bond, W.J.; Pyne, S.J.; Alexander, M.E. Fire on Earth: An Introduction; Wiley-Blackwell: Hoboken, NJ, USA, 2014. [Google Scholar]
- Krawchuk, M.; Moritz, M. Constraints on global fire activity vary across a resource gradient. Ecology 2011, 92, 121–132. [Google Scholar] [CrossRef]
- Pausas, J.G.; Ribeiro, E. The global fire–productivity relationship. Glob. Ecol. Biogeogr. 2013, 22, 728–736. [Google Scholar] [CrossRef]
- Pausas, J.G.; Keeley, J.E. A burning story: The role of fire in the history of life. Bioscience 2009, 59, 593–601. [Google Scholar] [CrossRef]
- Fontaine, J.B.; Westcott, V.C.; Enright, N.J.; Lade, J.C.; Miller, B.P. Fire behaviour in south-western Australian shrublands: Evaluating the influence of fuel age and fire weather. Int. J. Wildland Fire 2012, 21, 385–395. [Google Scholar] [CrossRef]
- Clarke, P.J.; Knox, K.J.; Wills, K.E.; Campbell, M. Landscape patterns of woody plant response to crown fire: Disturbance and productivity influence sprouting ability. J. Ecol. 2005, 93, 544–555. [Google Scholar] [CrossRef]
- Pausas, J.G.; Keeley, J.E.; Schwilk, D.W. Flammability as an ecological and evolutionary driver. J. Ecol. 2017, 105, 289–297. [Google Scholar] [CrossRef]
- Tiribelli, F.; Kitzberger, T.; Morales, J.M. Changes in vegetation structure and fuel characteristics along post-fire succession promote alternative stable states and positive fire–vegetation feedbacks. J. Veg. Sci. 2018, 29, 147–156. [Google Scholar] [CrossRef]
- Wei, P.; Lamont, B.; He, T.; Xue, W.; Wang, P.C.; Song, W.; Zhang, R.; Keyhani, A.B.; Zhao, S.; Lu, W.; et al. Vegetation-fire feedbacks increase subtropical wildfire risk in scrubland and reduce it in forests. J. Environ. Manag. 2024, 351, 119726. [Google Scholar] [CrossRef] [PubMed]
- Duff, T.J.; Keane, R.E.; Penman, T.D.; Tolhurst, K.G. Revisiting wildland fire fuel quantification methods: The challenge of understanding a dynamic, biotic entity. Forests 2017, 8, 351. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Botelho, H.S. A review of prescribed burning effectiveness in fire hazard reduction. Int. J. Wildland Fire 2003, 12, 117–128. [Google Scholar] [CrossRef]
- Thompson, M.P.; Vaillant, N.M.; Haas, J.R.; Gebert, K.M.; Stockmann, K.D. Quantifying the potential impacts of fuel treatments on wildfire suppression costs. J. For. 2013, 111, 49–58. [Google Scholar] [CrossRef]
- Baeza, M.J.; De Luís, M.; Raventós, J.; Escarré, A. Factors influencing fire behaviour in shrublands of different stand ages and the implications for using prescribed burning to reduce wildfire risk. J. Environ. Manag. 2002, 65, 199–208. [Google Scholar] [CrossRef]
- De Cáceres, M.; Casals, P.; Gabriel, E.; Castro, X. Scaling-up individual-level allometric equations to predict stand-level fuel loading in Mediterranean shrublands. Ann. For. Sci. 2019, 76, 87. [Google Scholar] [CrossRef]
- Rego, F.C.; Morgan, P.; Fernandes, P.; Hoffman, C. Fuel dynamics and management. In 2021 Fire Science: From Chemistry to Landscape Management; Rego, F.C., Morgan, P., Hoffman, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 363–420. [Google Scholar]
- Plucinski, M.P.; Gill, A.M.; Bradstock, R.A. Fuel dynamics in shrub dominated landscapes. Proc. R. Soc. Qld. 2009, 115, 145–151. [Google Scholar] [CrossRef]
- Dalgleish, S.A.; Van Etten, E.J.; Stock, W.D.; Knuckey, C. Fuel dynamics and vegetation recovery after fire in a semiarid Australian shrubland. Int. J. Wildland Fire 2015, 24, 613–623. [Google Scholar] [CrossRef]
- Li, Z.; Shi, H.; Vogelmann, J.E.; Hawbaker, T.J.; Peterson, B. Assessment of fire fuel load dynamics in shrubland ecosystems in the western United States using MODIS products. Remote Sens. 2020, 12, 1911. [Google Scholar] [CrossRef]
- Davies, G.M.; Gray, A.; Hamilton, A.; Legg, C.J. The future of fire management in the British uplands. Int. J. Biodiver. Sci. Manag. 2008, 4, 127–147. [Google Scholar] [CrossRef] [PubMed]
- Estornell, J.; Ruiz, L.A.; Velázquez-Martí, B.; Fernández-Sarría, A. Estimation of shrub biomass by airborne LiDAR data in small forest stands. For. Ecol. Manag. 2011, 262, 1697–1703. [Google Scholar] [CrossRef]
- Botequim, B.; Zubizarreta-Gerendiain, A.; Garcia-Gonzalo, J.; Silva, A.; Marques, S.; Fernandes, P.M.; Pereira, J.M.C.; Tomé, M. A model of shrub biomass accumulation as a tool to support management of portuguese forests. IForest 2014, 8, 114–125. [Google Scholar] [CrossRef]
- Alonso-Rego, C.; Arellano-Pérez, S.; Cabo, C.; Ordoñez, C.; Álvarez-González, J.G.; Díaz-Varela, R.A.; Ruiz-González, A.D. Estimating fuel loads and structural characteristics of shrub communities by using terrestrial laser scanning. Remote Sens. 2020, 12, 3704. [Google Scholar] [CrossRef]
- Alonso-Rego, C.; Arellano-Pérez, S.; Guerra-Hernández, J.; Molina-Valero, J.A.; Martínez-Calvo, A.; Pérez-Cruzado, C.; Castedo-Dorado, F.; González-Ferreiro, E.; Álvarez-González, J.G.; Ruiz-González, A.D. Estimating stand and fire-related surface and canopy fuel variables in pine stands using low-density airborne and single-scan terrestrial laser scanning data. Remote Sens. 2021, 13, 5170. [Google Scholar] [CrossRef]
- Fernández-Alonso, J.M.; Llorens, R.; Sobrino, J.A.; Ruiz-González, A.D.; Alvarez-González, J.G.; Vega, J.A.; Fernández, C. Exploring the Potential of Lidar and Sentinel-2 Data to Model the Post-Fire Structural Characteristics of Gorse Shrublands in NW Spain. Remote Sens. 2022, 14, 6063. [Google Scholar] [CrossRef]
- Hartley, R.J.; Davidson, S.J.; Watt, M.S.; Massam, P.D.; Aguilar-Arguello, S.; Melnik, K.O.; Pearce, H.G.; Clifford, V.R. A mixed methods approach for fuel characterisation in gorse (Ulex europaeus L.) scrub from high-density UAV laser scanning point clouds and semantic segmentation of UAV imagery. Remote Sens. 2022, 14, 4775. [Google Scholar] [CrossRef]
- Clutter, J.L.; Forston, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management. A Quantitative Approach; Krieger Publishing Company: New York, NY, USA, 1992. [Google Scholar]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; Cab International: Wallingford, UK, 1994. [Google Scholar]
- Fernandes, P.; Ruivo, L.; Gonçalves, P.; Rego, F.; Silveira, S. Dinâmica da combustibilidade nas comunidades vegetais da Reserva Natural da Serra da Malcata. In Proceedings of the Actas do Congresso Ibérico de Fogos Florestais, Castelo Branco, Portugal, 17–19 December 2000; Volume 17, p. 19. [Google Scholar]
- Pearce, H.G.; Anderson, W.R.; Fogarty, L.G.; Todoroki, C.L.; Anderson, S.A.J. Linear mixed-effects models for estimating biomass and fuel loads in shrublands. Can. J. For. Res. 2010, 40, 2015–2026. [Google Scholar] [CrossRef]
- Carswell, F.; Mason, N.; Holdaway, R.; Burrows, L.; Payton, I.; Sutherland, A.; Price, R.; Pearce, G.; Corich-Hermans, O.; Williams, P. Indirect Estimation of Gorse and Broom ‘Non-Forest Land’ to ‘Forest Land’ Transition; Technical Paper 2019/17; Ministry for Primary Industries New Zealand Government: Wellington, New Zealand, 2013. [Google Scholar]
- Westcott, V.C.; Enright, N.J.; Miller, B.P.; Fontaine, J.B.; Lade, J.C.; Lamont, B.B. Biomass and litter accumulation patterns in species-rich shrublands for fire hazard assessment. Int. J. Wildland Fire 2014, 23, 860. [Google Scholar] [CrossRef]
- Montero, G.; López-Leiva, C.; Ruiz-Peinado, R.; López-Senespleda, E.; Onrubia, R.; Pasalodos, M. Producción de Biomasa y Fijación de Carbono por los Matorrales Españoles y por el Horizonte Orgánico Superficial de los Suelos Forestales; Minsterio de Agruicultura Pesca y Alimentacion: Madrid, Spain, 2021. [Google Scholar]
- Marsden-Smedley, J.B.; Catchpole, W.R. Fire behaviour modelling in Tasmanian buttongrass moorlands. I. Fuel characteristics. Int. J. Wildland Fire 1995, 5, 203–214. [Google Scholar] [CrossRef]
- Pimont, F.; Dupuy, J.L.; Rigolot, E. A simple model for shrub-strata-fuel dynamics in Quercus coccifera L. communities. Ann. For. Sci. 2018, 75, 44. [Google Scholar] [CrossRef]
- Rothermel, R.C.; Philpot, C.W. Predicting changes in chaparral flammability. J. For. 1973, 71, 640–643. [Google Scholar]
- Fernandes, P.; Rego, F.C. Changes in fuel structure and fire behaviour with heathland aging in Northern Portugal. In Proceedings of the 13th Fire and Forest Meteorology Conference, Lorne, Australia, 27–31 October 1996; pp. 433–436. [Google Scholar]
- Fernandes, P.M.; Ribeiro, L.; Botelho, H.; Rodrigues, A. Short-term recovery of Erica australis shrubland in NE Portugal after prescribed burning. In Proceedings of the III International Conference on Forest Fire Research and 14th Conference on Fire and Forest Meteorology, Luso, Portugal, 16–20 November 1998. [Google Scholar]
- Egunjobi, J.K. Ecosystem processes in a stand of Ulex europaeus L. I. Dry matter production, litterfall and efficiency of solar energy utilization. J. Ecol. 1971, 59, 31–38. [Google Scholar] [CrossRef]
- Radcliffe, J.E. Gorse-a resource for goats? N. Z. J. Exp. Agric. 1986, 14, 399–410. [Google Scholar] [CrossRef]
- Marino, E.; Guijarro, M.; Hernando, C.; Madrigal, J.; Díez, C. Fire hazard after prescribed burning in a gorse shrubland: Implications for fuel management. J. Environ. Manag. 2011, 92, 1003–1011. [Google Scholar] [CrossRef] [PubMed]
- Madrigal, J.; Marino, E.; Guijarro, M.; Hernando, C.; Díez, C. Evaluation of the flammability of gorse (Ulex europaeus L.) managed by prescribed burning. Ann. For. Sci. 2012, 69, 387–397. [Google Scholar] [CrossRef]
- Dent, J.M.; Buckley, H.L.; Lustig, A.; Curran, T.J. Flame temperatures saturate with increasing dead material in Ulex europaeus, but flame duration, fuel consumption and overall flammability continue to increase. Fire 2019, 2, 6. [Google Scholar] [CrossRef]
- Boissard, C.; Cao, X.L.; Juan, C.Y.; Hewitt, C.N.; Gallagher, M. Seasonal variations in VOC emission rates from gorse (Ulex europaeus). Atmos. Environ. 2001, 35, 917–927. [Google Scholar] [CrossRef]
- Galappaththi, H.S.D.; de Silva, W.P.P.; Clavijo Mccormick, A. A mini-review on the impact of common gorse in its introduced ranges. Trop. Ecol. 2023, 64, 1–25. [Google Scholar] [CrossRef]
- Vega, J.A.; Cuiñas, P.; Fonturbel, T.; Perez-Gorostiaga, P.; Fernandez, C. Predicting fire behaviour in Galician (NW Spain) shrubland fuel complexes. In Proceedings of the 3rd International Conference on Forest Fire Research & 14th Fire and Forest Meteorology, Luso, Portugal, 16–20 November 1998; pp. 713–728. [Google Scholar]
- Vega, J.A.; Jiménez, E.; Dupuy, J.L.; Linn, R.R. Effects of flame interaction on the rate of spread of heading and suppression fires in shrubland experimental fires. Int. J. Wildland Fire 2012, 21, 950–960. [Google Scholar] [CrossRef]
- Anderson, S.A.; Anderson, W.R. Ignition and fire spread thresholds in gorse (Ulex europaeus). Int. J. Wildland Fire 2010, 19, 589–598. [Google Scholar] [CrossRef]
- Elvira, L.M.; Hernando, C. Inflamabilidad y Energía de las Especies de Sotobosque: Estudio Piloto con Aplicación a los Incendios Forestales; Monografia 68; INIA: Madrid, Spain, 1989. [Google Scholar]
- Viana, H.; Vega-Nieva, D.J.; Torres, L.O.; Lousada, J.; Aranha, J. Fuel characterization and biomass combustion properties of selected native woody shrub species from central Portugal and NW Spain. Fuel 2012, 102, 737–745. [Google Scholar] [CrossRef]
- Arellano-Pérez, S.; Vega, J.A.; Ruiz-González, A.D.; Arellano, A.; Álvarez-González, J.G.; Vega-Nieva, D.; Pérez, E. Foto-Guía de Combustibles Forestales de Galicia y Comportamiento del Fuego Asociado; Andavira: Santiago de Compostela, Spain, 2017; 244p. [Google Scholar]
- Fernández-Guisuraga, J.M.; Suárez-Seoane, S.; García-Llamas, P.; Calvo, L. Vegetation structure parameters determine high burn severity likelihood in different ecosystem types: A case study in a burned Mediterranean landscape. J. Environ. Manag. 2021, 288, 112462. [Google Scholar] [CrossRef]
- MARM, Ministerio de Medio Ambiente, Medio Rural y Marino. Cuarto Inventario Forestal Nacional; MARM: Madrid, Spain, 2011. [Google Scholar]
- Xunta de Galicia. Plan de Prevención e Defensa Contra os Incendios Forestais en Galicia (PLADIGA); Consellería de Medio Rural: Santiago de Compostela, Spain, 2020. [Google Scholar]
- Ojeda, F. 4030 Brezales Secos Europeos En: VV. AA.; Bases Ecológicas Preliminares para la Conservación de los Tipos de Hábitat de Interés Comunitario en España; Ministerio de Medio Ambiente y Medio Rural y Marino: Madrid, Spain, 2009. [Google Scholar]
- MARM. Mapa Forestal de España. Galicia. Escala 1:25.000; Ministerio de Medio Ambiente y Medio Rural y Marino: Madrid, Spain, 2011. [Google Scholar]
- Brown, J.K.; Oberhau, R.D.; Johnston, C.M. Handbook for Inventorying Surface Fuels and Biomass in the Interior West; USDA Forest Service General Technical Reports INT-GTR-129; USDA: Washington, DC, USA, 1982; 48p.
- Fosberg, M.A.; Lancaster, J.W.; Schroeder, M.J. Fuel moisture response—Drying relationships under standard and field conditions. For. Sci. 1970, 16, 21–128. [Google Scholar]
- Burgan, R.E.; Rothermel, R.C. BEHAVE: Fire Behaviour Prediction and Fuel Modeling System—FUEL Subsystem; USDA Forest Service General Technical Reports INT-167; USDA: Washington, DC, USA, 1984.
- Finney, M.A. FARSITE: Fire Area Simulator–Model Development and Evaluation; Research Paper RMRS-RP-4 Revised; USDA Forest Service Rocky Mountain Research Station: Ogden, UT, USA, 1998.
- Scott, J.H.; Burgan, R.E. Standard Fire Behavior Fuel Models: A Comprehensive Set for Use with Rothermel’s Surface Fire Spread Model; General Technical Report RMRS-GTR-153; USDA Forest Service Rocky Mountain Research Station: Ogden, UT, USA, 2005.
- Vega, J.A.; Álvarez-González, J.G.; Arellano-Pérez, S.; Fernández, C.; Cuiñas, P.; Jiménez, E.; Fernández-Alonso, J.M.; Fontúrbel, T.; Alonso-Rego, C.; Ruiz-González, A.D. Developing customized fuel models for shrub and bracken communities in Galicia (NW Spain). J. Environ. Manag. 2024, 351, 119831. [Google Scholar] [CrossRef]
- Bennet, F.A.; McGee, C.E.; Clutter, J.L. Yield of Old-Field Slash Pine Plantations; Paper 107; USDA Forest Service Southeastern Forest Experiment Station: Asheville, NC, USA, 1959.
- Newberry, J.D.; Pienaar, L.V. Dominant Height Growth Models and Site Index Curves for Site-Prepared Slash Pine Plantations in the Lower Coastal Plain of Georgia and North Florida; Research Paper 4; Plantation Management Research Cooperation: Athens, GA, USA, 1978. [Google Scholar]
- Kiviste, A.; Álvarez-González, J.G.; Rojo, A.; Ruiz, A.D. Funciones de Crecimiento de Aplicación en el Ámbito Forestal, Monografía INIA: Forestal nº 4; Ministerio de Ciencia y Tecnología: Madrid, Spain, 2002. [Google Scholar]
- Borders, T.H.; Bailey, R.L.; Ware, K.D. Slash pine site index from a polymorphic model by joining (splining) nonpolynomial segments with an algebraic difference method. For. Sci. 1984, 30, 411–423. [Google Scholar]
- Parresol, B.R.; Vissage, J.S. White Pine Site Index for Southern Forest Survey; Research Paper SRS-10; USDA Forest Service Southern Research Station: Asheville, NC, USA, 1998. [Google Scholar]
- Álvarez-González, J.G.; Ruiz-González, A.D.; Rodríguez-Soalleiro, R.; Barrio-Anta, M. Ecoregional site index models for Pinus pinaster in Galicia (northwestern Spain). Ann. For. Sci. 2005, 62, 115–127. [Google Scholar] [CrossRef]
- Cieszewski, C.J.; Bailey, R.L. Generalized algebraic difference approach: Theory based derivation of dynamic equations with polymorphism and variable asymptotes. For. Sci. 2000, 46, 116–126. [Google Scholar]
- Cieszewski, C.J. Comparing fixed-and variable-base-age site equations having single versus multiple asymptotes. For. Sci. 2002, 48, 7–23. [Google Scholar]
- Peschel, W. Die Mathematische Methoden zur Herleitung der Wachstumgesetze von Baum und Bestan un die Ergebnisse ihrer Anwendung. Tharandter Forstl. Jahrburch 1938, 89, 169–247. [Google Scholar]
- Ludqvist, B. On the height growth in cultivated stands of pine and spruce in Northern Sweden. Medd. Fran Statens Skogforsk. Band 1957, 47, 1–64. [Google Scholar]
- Bertalanffy, L. A quantitative theory of organic growth (inquires on growth laws II). Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Myers, R.H. Classical and Modern Regression with Applications, 2nd ed.; Duxbury Press: Belmont, CA, USA, 1990. [Google Scholar]
- White, H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 1980, 48, 817–838. [Google Scholar] [CrossRef]
- Cailliez, F. Estimación del Volumen Forestal y Predicción del Rendimiento; FAO: Rome, Italy, 1980. [Google Scholar]
- Harvey, A.C. Estimating regression models with multiplicative heteroscedasticity. Econometrica 1976, 44, 461–465. [Google Scholar] [CrossRef]
- SAS Institute Inc. SAS/ETS© 9.1 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2004. [Google Scholar]
- Gonzalo, J. Diagnosis Fitoclimática de la España Peninsular: Actualización y Análisis Geoestadístico Aplicado. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2008. [Google Scholar]
- González-Rodríguez, M.A.; Diéguez-Aranda, U. Exploring the use of learning techniques for relating the site index of radiata pine stands with climate, soil and physiography. For. Ecol. Manag. 2020, 458, 117803. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Arellano-Pérez, S.; González-Ferreiro, E.; Pascual, A.; Altelarrea, V.S.; Ruiz-González, A.D.; Álvarez-González, J.G. Developing a site index model for P. pinaster stands in NW Spain by combining bi-temporal ALS data and environmental data. For. Ecol. Manag. 2021, 481, 118690. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Milborrow, S.; Hastei, T.; Tibshirani, R.; Miller, A.; Lumley, T.; Earth: Multivariate Adaptive Regression Splines. R Package Version 5.1.1. 2019. Available online: https://CRAN.R-project.org/package=earth (accessed on 14 December 2023).
- R Core Team. R: A Language and Environment for Statistical Computing, Version 3.6.1; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Weiskittel, A.; Hann, D.W.; Kershaw, J.; Vanclay, J.K. Forest Growth and Yield Modelling; Wiley-Blackwell: Oxford, UK, 2011. [Google Scholar]
- Deeming, J.; Burgan, R.; Cohen, J. The National Fire-Danger Rating System-1978; U.S. Department of Agriculture Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1978.
- Van Wagner, C.E. The Development and Structure of the Canadian Forest Fire Weather Index System; Ont. FTR-35; Canadian Forest Service, Petawawa National Forestry Institute: Chalk River, ON, Canada, 1987. [Google Scholar]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; General Technical Report INT-GTR-115; USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1972.
- Santana, V.M.; Marrs, R.H. Flammability properties of British heathland and moorland vegetation: Models for predicting fire ignition. J. Environ. Manag. 2014, 139, 88–96. [Google Scholar] [CrossRef]
- Plucinski, M.P.; Anderson, W.R.; Bradstock, R.A.; Gill, A.M. The initiation of fire spread in shrubland fuels recreated in the laboratory. Int. J. Wildland Fire 2010, 19, 512–520. [Google Scholar] [CrossRef]
- Schwilk, D.W. Flammability is a niche construction trait: Canopy architecture affects fire intensity. Am. Nat. 2003, 162, 725–733. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Z.; Li, Y.; He, J.; Wu, X. Dynamic growth models for Caragana korshinskii shrub biomass in China. J. Environ. Manag. 2020, 269, 110675. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Xu, H.; Wang, B.; Wang, X. Dynamic Model for Caragana korshinskii Shrub Aboveground Biomass Based on Theoretical and Allometric Growth Equations. Forests 2022, 13, 1444. [Google Scholar] [CrossRef]
- Richardson, R.G.; Hill, R.L. The biology of Australian weeds. 34. Ulex europaeus L. Plant Prot. Q. 1998, 13, 46–58. [Google Scholar]
- Clements, D.R.; Peterson, D.J.; Prasad, R. The biology of Canadian weeds: 112–Ulex europaeus L. Can. J. Plant Sci. 2001, 81, 325–337. [Google Scholar] [CrossRef]
- Ruiz de la Torre, J. Flora Mayor. D.G. Biodiversidad; Ministerio de Medio Ambiente: Madrid, Spain, 2006. [Google Scholar]
- Rivas-Martinez, S.; Izco, J.; Díaz-González, T.; Penas, A.; Costa, J.C.; Amigo, J.; Herrero, L.; Giménez de Azcarate, J.; Del Rio, S. The Galician-Portuguese biogeographic sector. An initial advance. Int. J. Geobot. Res. 2014, 4, 65–81. [Google Scholar]
- Christina, M.; Limbada, F.; Atlan, A. Climatic niche shift of an invasive shrub (Ulex europaeus): A global scale comparison in native and introduced regions. J. Plant Ecol. 2020, 13, 42–50. [Google Scholar] [CrossRef]
- Gränzig, T.; Clasen, A.; Fassnacht, F.E.; Cord, A.; Förster, M. Combining remote sensing, habitat suitability models and cellular automata to model the spread of the invasive shrub Ulex europaeus. Biol. Invasions 2023, 25, 3711–3736. [Google Scholar] [CrossRef]
- Rivas Martinez, S. Brezales y jarales de Europa occidental (Revision fitosociologica de las clases Calluno-Ulicetea y Cisto-Lavanduletea). Lazaroa 1979, 1, 5–127. [Google Scholar]
- Zielke, K.; Boateng, J.; Caldicott, N.; Williams, H. Broom and Gorse: A Forestry Perspective Problem Analysis; British Columbia Ministry of Forests: Queen Charlotte, BC, Canada, 1992. [Google Scholar]
- Correia, A.C.; Costa e Silva, F.; Correia, A.V.; Hussain, M.Z.; Rodrigues, A.D.; David, J.S.; Pereira, J.S. Carbon sink strength of a Mediterranean cork oak understorey: How do semi-deciduous and evergreen shrubs face summer drought? J. Veg. Sci. 2014, 25, 411–426. [Google Scholar] [CrossRef]
- Martinez-Cortizas, A. Estimación del balance hídrico de los suelos gallegos con escasa reserva. An. Edafol. Agrobiol. 1986, 45, 901–916. [Google Scholar]
- Martinez-Cortizas, A.; Castillo-Rodríguez, F.; Pérez-Alberti, A. Factores que influyen en la precipitación y el balance de agua en Galicia. Boletín Asoc. Geógrafos Españoles 1994, 18, 79–96. [Google Scholar]
- Maturano-Ruiz, A.; Ruiz-Yanetti, S.; Manrique-Alba, À.; Moutahir, H.; Chirino, E.; Vilagrosa, A.; Bellot, J.F. The main factors that drive plant dieback under extreme drought differ among Mediterranean shrubland plant biotypes. J. Veg. Sci. 2023, 34, e13187. [Google Scholar] [CrossRef]
- Rodríguez-Ramírez, N.; Santonja, M.; Baldy, V.; Ballini, C.; Montès, N. Shrub species richness decreases negative impacts of drought in a Mediterranean ecosystem. J. Veg. Sci. 2017, 28, 985–996. [Google Scholar] [CrossRef]
- Marteau, A.; Fourmaux, M.; Mevy, J.P. The Role of Gorse (Ulex parviflorus Pourr. Scrubs) in a Mediterranean shrubland undergoing climate change: Approach by hyperspectral measurements. Plants 2023, 12, 879. [Google Scholar] [CrossRef] [PubMed]
- Delerue, F.; González, M.; Michalet, R.; Pellerin, S.; Augusto, L. Weak evidence of regeneration habitat but strong evidence of regeneration niche for a leguminous shrub. PLoS ONE 2015, 10, e0130886. [Google Scholar] [CrossRef] [PubMed]
- Burroughs, W.J. Frost damage during the winter of 1981/82. Weather 1982, 37, 346–352. [Google Scholar] [CrossRef]
- Hernández-Lambraño, R.E.; González-Moreno, P.; Sánchez-Agudo, J.Á. Towards the top: Niche expansion of Taraxacum officinale and Ulex europaeus in mountain regions of South America. Austral Ecol. 2017, 42, 577–589. [Google Scholar] [CrossRef]
- Cruz, A.; Pérez, B.; Quintana, J.R.; Moreno, J.M. Resprouting in the Mediterranean-type shrub Erica australis affected by soil resource availability. J. Veg. Sci. 2002, 13, 641–650. [Google Scholar]
- Ramírez, D.A.; Parra, A.; Resco de Dios, V.; Moreno, J.M. Differences in morpho physiological leaf traits reflect the response of growth to drought in a seeder but not in a resprouter Mediterranean species. Funct. Plant Biol. 2012, 39, 332–341. [Google Scholar] [CrossRef]
- Parra, A.; Moreno, J.M. Post-fire environments are favourable for plant functioning of seeder and resprouter Mediterranean shrubs, even under drought. New Phytol. 2017, 214, 1118–1131. [Google Scholar] [CrossRef] [PubMed]
- Parra, A.; Moreno, J.M. Drought differentially affects the post-fire dynamics of seeders and resprouters in a Mediterranean shrubland. Sci. Total Environ. 2018, 626, 1219–1229. [Google Scholar] [CrossRef] [PubMed]
- Peñuelas, J.; Prieto, P.; Beier, C.; Cesaraccio, C.; De Angelis, P.; de Dato, G.; Emmett, B.A.; Estiarte, M.; Garadnai, J.; Gorissen, A.; et al. Response of plant species richness and primary productivity in shrublands along a north–south gradient in Europe to seven years of experimental warming and drought: Reductions in primary productivity in the heat and drought year of 2003. Glob. Chang. Biol. 2007, 13, 2563–2581. [Google Scholar] [CrossRef]
- Calvo, L.; Tárrega, R.; Luis, E. Secondary succession after perturbations in a shrubland community. Acta Oecologica 2002, 23, 393–404. [Google Scholar] [CrossRef]
- Calvo, L.; Tárrega, R.; Luis, E. The dynamics of mediterranean shrub species over 12 years following perturbations. Plant Ecol. 2002, 160, 25–42. [Google Scholar] [CrossRef]
- Calvo, L.; Tárrega, R.; Luis, E.D.; Valbuena, L.; Marcos, E. Recovery after experimental cutting and burning in three shrub communities with different dominant species. Plant Ecol. 2005, 180, 175–185. [Google Scholar] [CrossRef]
- Paula, S.; Ojeda, F. Resistance of three co-occurring resprouter Erica species to highly frequent disturbance. Plant Ecol. 2006, 183, 329–336. [Google Scholar] [CrossRef]
- Fernández, C.; Vega, J.A.; Fontúrbel, T. Shrub resprouting response after fuel reduction treatments: Comparison of prescribed burning, clearing and mastication. J. Environ. Manag. 2013, 117, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Fernández, C.; Vega, J.A.; Fontúrbel, T. Does shrub recovery differ after prescribed burning, clearing and mastication in a Spanish heathland? Plant Ecol. 2015, 216, 429–437. [Google Scholar] [CrossRef]
- Paula, S.; Ojeda, F. Belowground starch consumption after recurrent severe disturbance in three resprouter species of the genus Erica. Botany 2009, 87, 253–259. [Google Scholar] [CrossRef]
- Ojeda, F.; Arroyo, J.; Marañón, T. Ecological distribution of four co-occurring Mediterranean heath species. Ecography 2000, 23, 148–159. [Google Scholar] [CrossRef]
- Fernandez, C.; Vega, J.A.; Fontúrbel, T. Does fire severity influence shrub resprouting after spring prescribed burning? Acta Oecologica 2013, 48, 30–36. [Google Scholar] [CrossRef]
- Cruz, R.; Lago, A.; Lage, A.; Rial, M.E.; Díaz-Fierros, F.; Salsón, S. Evolución reciente del clima de Galicia. tendencias observadas en variables meteorológicas. In Análisis de Evidencias e Impactos del Cambio Climático en Galicia; Pérez Muñuzuri, V., Fernández Cañamero, M., Gómez Gesteira, J.M., Eds.; Xunta de Galicia: Santiago, Spain, 2009; pp. 19–58. [Google Scholar]
- Vega, J.A.; Fernández, C.; Jiménez, E.; Ruiz, A.D. Evidencias de cambio climático en Galicia a través de la tendencia de los índices de peligro de incendios forestales. In Análisis de Evidencias e Impactos del Cambio Climático en Galicia; Pérez Muñuzuri, V., Fernández Cañamero, M., Gómez Gesteira, J.M., Eds.; Xunta de Galicia: Santiago, Spain, 2009; pp. 173–194. [Google Scholar]
- Kaal, J.; Costa-Casais, M.; Ferro-Vázquez, C.; Pontevedra-Pombal, X.; Martínez-Cortizas, A. Soil formation of “Atlantic rankers” from NW Spain—A high resolution aluminium and iron fractionation study. Pedosphere 2008, 18, 441–453. [Google Scholar] [CrossRef]
- Kaal, J.; Criado-Boado, F.; Costa-Casais, M.; López-Sáez, J.A.; López-Merino, L.; Mighall, T.; Carrión, Y.; Silva Sánchez, N.; Martínez Cortizas, A. Prehistoric land use at an archaeological hot-spot (the rock art park of Campo Lameiro, NW Spain) inferred from charcoal, synanthropic pollen and non-pollen palynomorph proxies. J. Archaeol. Sci. 2013, 40, 1518–1527. [Google Scholar] [CrossRef]
- Fábregas, R.; Fernández, C.; Ramil, P. La adopción de la economía productora en el noroeste ibérico. In O Neolítico Atlántico e as Orixes do Megalistismo Universidade de Santiago; Rodríguez Casal, A., Ed.; Consello da Cultura Galega: Santiago, Spain, 1997. [Google Scholar]
- Guitián Rivera, L. Los incendios forestales a través de la historia: Pervivencias y cambios en el uso del fuego en el noroeste peninsular. In Incendios Históricos; Araque Jiménez, E., Ed.; Una Aproximación Multidisciplinar; Universidad Internacional de Andalucía: Seville, Spain, 1999; pp. 149–162. [Google Scholar]
- Balboa López, X. El fuego en la historia de los montes gallegos: De las rozas al incendio forestal. In Incendios Históricos; Araque, E., Ed.; Una Aproximación Multidisciplinar; Universidad Internacional de Andalucía: Seville, Spain, 1999; pp. 255–277. [Google Scholar]
- Davies, G.M.; Hamilton, A.; Smith, A.; Legg, C.J. Using visual obstruction to estimate heathland fuel load and structure. Int. J. Wildland Fire 2008, 17, 380–389. [Google Scholar] [CrossRef]
- Harris, M.P.K.; Allen, K.A.; McAllister, H.A.; Eyre, G.; Le Duc, M.G.; Marrs, R.H. Factors affecting moorland plant communities and component species in relation to prescribed burning. J. Appl. Ecol. 2011, 48, 1411–1421. [Google Scholar] [CrossRef]
- Ramil Rego, P.; Rodríguez Guitián, M.A.; López Castro, H.; Ferreiro da Costa, J.; Muñoz Sobrino, C. Loss of European dry heaths in NW Spain: A case study. Diversity 2013, 5, 557–580. [Google Scholar] [CrossRef]
- Forgeard, F. Étude expérimentale du rôle de la structure et de la biomasse végétale sur le comportement du feu dans les landes de Bretagne. Acta Oecologica 1989, 10, 273–294. [Google Scholar]
- Atlan, A.; Udo, N.; Hornoy, B.; Darrot, C. Evolution of the uses of gorse in native and invaded regions: What are the impacts on its dynamics and management? La Terre Et La Vie-Rev. D’écologie 2015, 70, 191–206. [Google Scholar] [CrossRef]
- Hornoy, B.; Tarayre, M.; Herve, M.; Gigord, L.; Atlan, A. Invasive plants and enemy release: Evolution of trait means and trait correlations in Ulex europaeus. PLoS ONE 2011, 6, e26275. [Google Scholar] [CrossRef]
- Blossey, B.; Notzold, R. Evolution of increased competitive ability in invasive nonindigenous plants: A hypothesis. J. Ecol. 1995, 83, 887–889. [Google Scholar] [CrossRef]
- Joshi, J.; Vrieling, K. The enemy release and EICA hypothesis revisited: Incorporating the fundamental difference between specialist and generalist herbivores. Ecol. Lett. 2005, 8, 704–714. [Google Scholar] [CrossRef]
- De Luis, M.; Raventós, J.; González-Hidalgo, J.C. Post-fire vegetation succession in Mediterranean gorse shrublands. Acta Oecologica 2006, 30, 54–61. [Google Scholar] [CrossRef]
- Reyes, O.; Casal, M.; Rego, F.C. Resprouting ability of six Atlantic shrub species. Folia Geobot. 2009, 44, 19–29. [Google Scholar] [CrossRef]
- Baeza, M.J.; Santana, V.M. Biological significance of dead biomass retention trait in Mediterranean Basin species: An analysis between different successional niches and regeneration strategies as functional groups. Plant Biol. 2015, 17, 1196–1202. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Abascal, I.; Luis, E.; Tárrega, R.; Marcos, E. Trends in post-fire biomass recovery in an Erica australis heathland. In Fire and Biological Processes; Trabaud, L., Prodon, P., Eds.; Bachuys Publishers: Leiden, The Netherlands, 2002; pp. 33–42. [Google Scholar]
- Rey Castelao, O. Montes y Política Forestal en la Galicia del Antiguo Régimen; Monografías de la Universidad de Santiago de Compostela: Santiago de Compostela, Spain, 1995. [Google Scholar]
- Moreira, B.; Castellanos, M.C.; Pausas, J.G. Genetic component of flammability variation in a Mediterranean shrub. Mol. Ecol. 2014, 23, 1213–1223. [Google Scholar] [CrossRef] [PubMed]
- Pausas, J.G.; Alessio, G.A.; Moreira, B.; Corcobado, G. Fires enhance flammability in Ulex parviflorus. New Phytol. 2012, 193, 18–23. [Google Scholar] [CrossRef]
- Anderson, W.R.; Cruz, M.G.; Fernandes, P.M.; McCaw, L.; Vega, J.A.; Bradstock, R.A.; Fogarty, L.; Gould, J.; McCarthy, G.; Marsden-Smedley, J.B.; et al. A generic, empirical-based model for predicting rate of fire spread in shrublands. Int. J. Wildland Fire 2015, 24, 443–460. [Google Scholar] [CrossRef]
- Baeza, M.J.; Santana, V.M.; Pausas, J.G.; Vallejo, V.R. Successional trends in standing dead biomass in Mediterranean basin species. J. Veg. Sci. 2011, 22, 467–474. [Google Scholar] [CrossRef]


| Variable | Statistic | Ue | Ea |
|---|---|---|---|
| n | 165 | 102 | |
| Mean | 123.56 | 107.28 | |
| (cm) | Std. dev. | 67.43 | 69.72 |
| CovShr | Mean | 8589 | 89.75 |
| (%) | Std. dev. | 22.53 | 17.49 |
| t | Mean | 9.36 | 8.00 |
| (years) | Std. dev. | 4.69 | 5.98 |
| WShr | Mean | 3.49 | 2.40 |
| (kg m−2) | Std. dev. | 1.46 | 1.68 |
| WShr_G23 | Mean | 1.33 | 0.91 |
| (kg m−2) | Std. dev. | 1.06 | 1.11 |
| WShr_G1 | Mean | 2.16 | 1.49 |
| (kg m−2) | Std. dev. | 0.71 | 0.74 |
| WShr_G1_dead | Mean | 0.85 | 0.41 |
| (kg m−2) | Std. dev. | 0.36 | 0.27 |
| WShr_G1_live | Mean | 1.31 | 1.08 |
| (kg m−2) | Std. dev. | 0.47 | 0.52 |
| Species | Elevation | Slope | P | Ps | T | Twm | Tcm | P/T | Rd | Rds | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| U. europaeus | 572a | 11a | 1560a | 137a | 11.8a | 18.3a | 6.5a | 132.5a | 2.5a | 10.7a | 4.8a |
| n = 156 | (242) | (7) | (239) | (19) | (1.2) | (1.0) | (1.5) | (20.0) | (0.4) | (2.2) | (1.7) |
| range | 30–1113 | 0–35 | 1036–1975 | 92–186 | 8.6–14.6 | 15.5–20.7 | 3–9.5 | 89.3–181.7 | 1.6–3.8 | 9.6–11.9 | 3.9–5.9 |
| E. australis | 1005b | 18b | 1449b | 144b | 10.0b | 17.9b | 3.5b | 150.0b | 2.7b | 9.8b | 4.8a |
| n = 102 | (281) | (9) | (277) | (28) | (1.3) | (1.3) | (1.4) | (43.9) | (0.7) | (2.1) | (1.7) |
| range | 497–1710 | 2–43 | 873–2004 | 91–211 | 6.1–12.3 | 14.4–20.8 | −0.6–6.2 | 71.0–272.5 | 1.5–4.1 | 8.6–10.7 | 3.9–5.9 |
| Gorse-Dominated Communities | |||||
|---|---|---|---|---|---|
| Model | a0 | a1 | a2 | ME | RMSE (kg m−2) |
| Hossfeld | 1.3634 | 0.3704 | --- | 0.4792 | 1.0624 |
| Korf | 3.0581 | −3.6646 | 0.3291 | 0.5083 | 1.0323 |
| Bertalanffy–Richards | 8.1410 | 0.0522 | 0.8504 | 0.5073 | 1.0333 |
| High Heath-Dominated Communities | |||||
| Model | a0 | a1 | a2 | ME | RMSE (kg m−2) |
| Hossfeld | 2.8215 | 0.2965 | --- | 0.7321 | 0.8801 |
| Korf | 5.1644 | −6.5425 | 0.2070 | 0.7538 | 0.8436 |
| Bertalanffy–Richards | 9.6599 | 0.0498 | 1.2765 | 0.7529 | 0.8453 |
| Gorse-Dominated Communities | ||
|---|---|---|
| Model | ME | RMSE (kg m−2) |
| 0.6934 | 0.3949 | |
| 0.8630 | 0.3949 | |
| 0.5699 | 0.2382 | |
| 0.4803 | 0.3426 | |
| High Heath-Dominated Communities | ||
| Model | ME | RMSE (kg m−2) |
| 0.8590 | 0.2792 | |
| 0.9377 | 0.2792 | |
| 0.7291 | 0.1436 | |
| 0.7715 | 0.2505 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vega, J.A.; Álvarez-González, J.G.; Arellano-Pérez, S.; Fernández, C.; Ruiz-González, A.D. Site Quality Models and Fuel Load Dynamic Equation Systems Disaggregated by Size Fractions and Vegetative States in Gorse and High Heath Shrublands in Galicia (NW Spain). Fire 2024, 7, 126. https://doi.org/10.3390/fire7040126
Vega JA, Álvarez-González JG, Arellano-Pérez S, Fernández C, Ruiz-González AD. Site Quality Models and Fuel Load Dynamic Equation Systems Disaggregated by Size Fractions and Vegetative States in Gorse and High Heath Shrublands in Galicia (NW Spain). Fire. 2024; 7(4):126. https://doi.org/10.3390/fire7040126
Chicago/Turabian StyleVega, José A., Juan Gabriel Álvarez-González, Stéfano Arellano-Pérez, Cristina Fernández, and Ana Daría Ruiz-González. 2024. "Site Quality Models and Fuel Load Dynamic Equation Systems Disaggregated by Size Fractions and Vegetative States in Gorse and High Heath Shrublands in Galicia (NW Spain)" Fire 7, no. 4: 126. https://doi.org/10.3390/fire7040126
APA StyleVega, J. A., Álvarez-González, J. G., Arellano-Pérez, S., Fernández, C., & Ruiz-González, A. D. (2024). Site Quality Models and Fuel Load Dynamic Equation Systems Disaggregated by Size Fractions and Vegetative States in Gorse and High Heath Shrublands in Galicia (NW Spain). Fire, 7(4), 126. https://doi.org/10.3390/fire7040126






