Study on Response Time Hysteresis Model of Smoke Detectors in Aircraft Cargo Compartment
Abstract
:1. Introduction
2. Hysteresis of Smoke Detectors
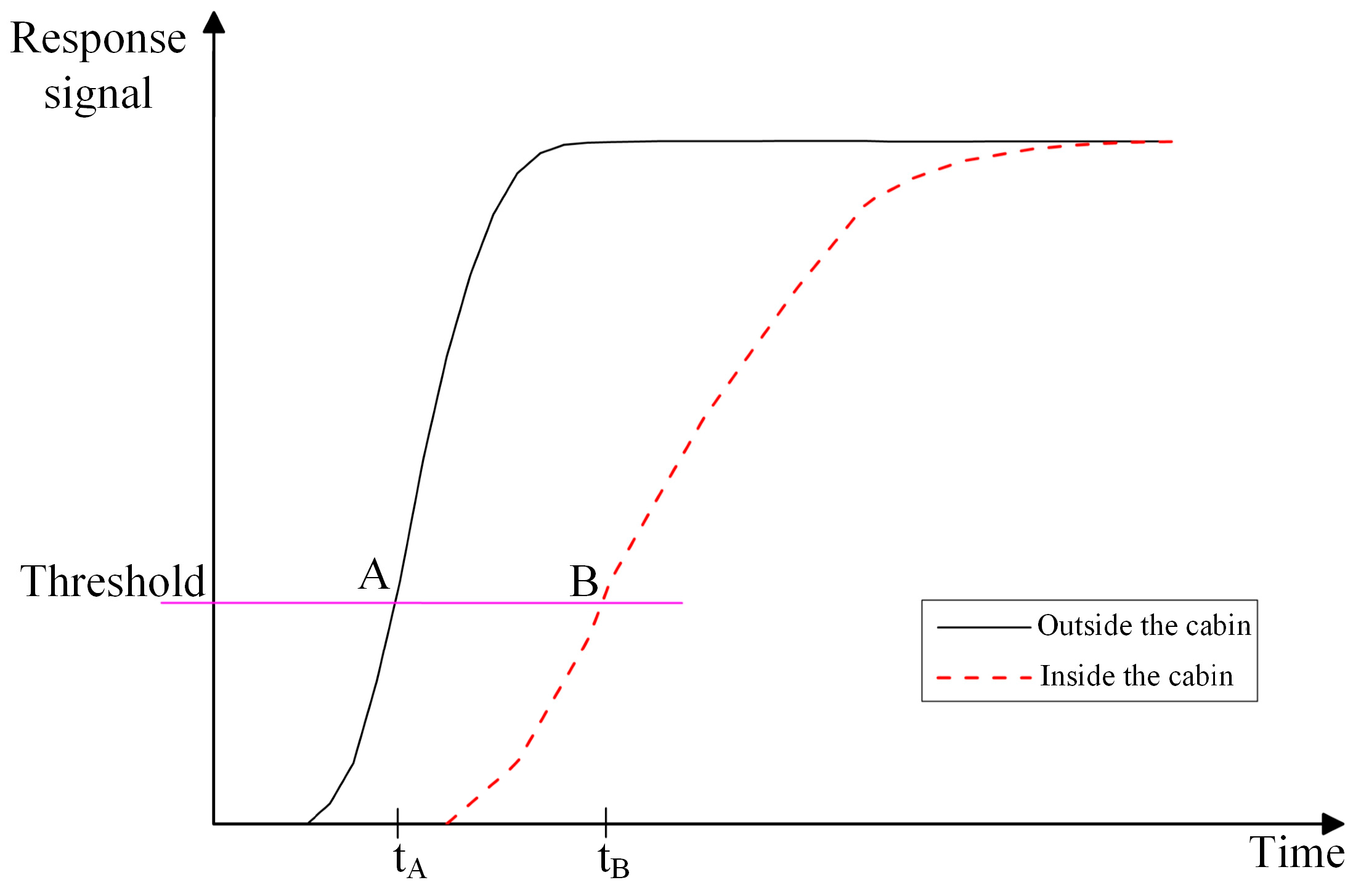
2.1. Hysteresis Effect
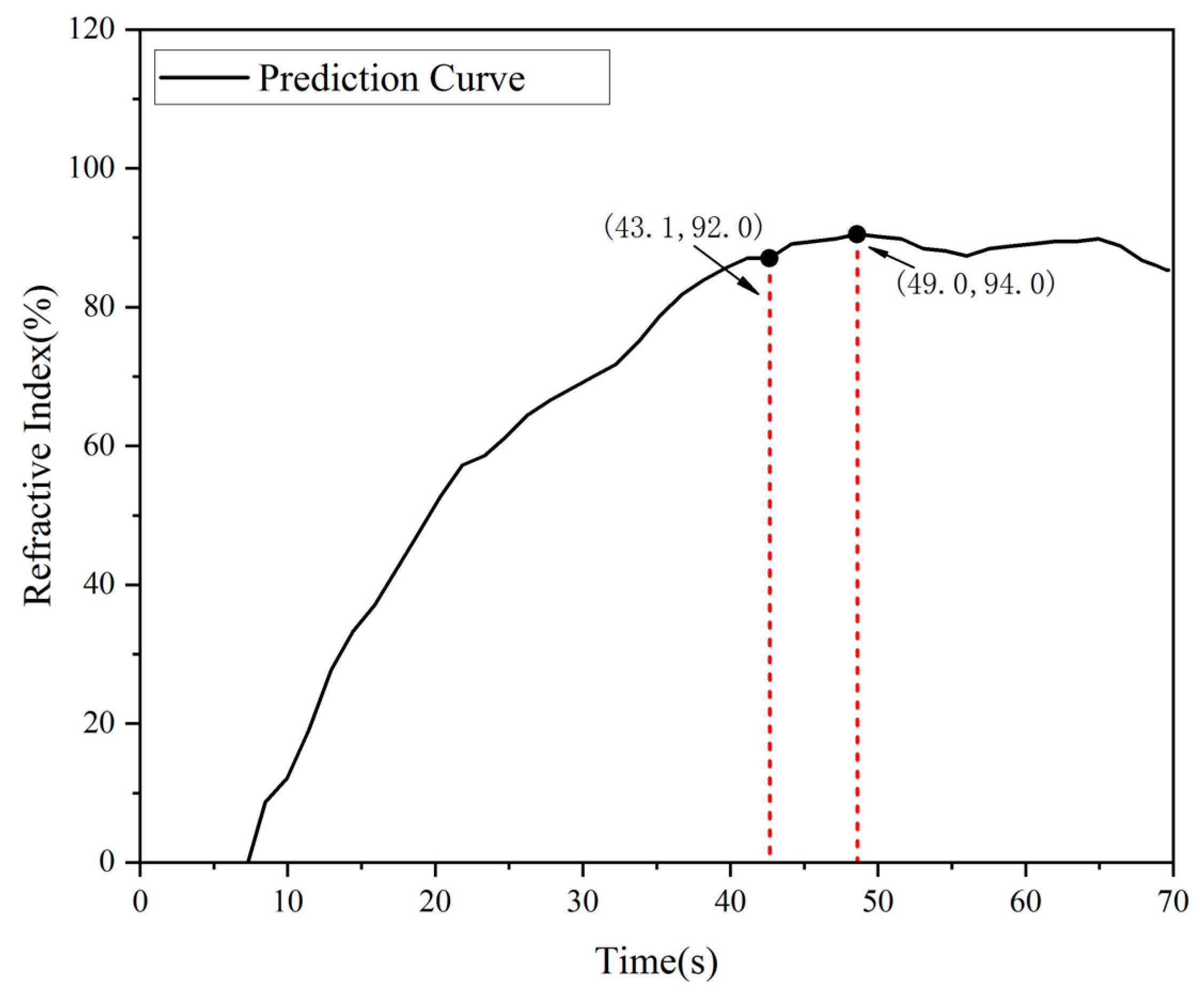
2.2. Hysteresis Model
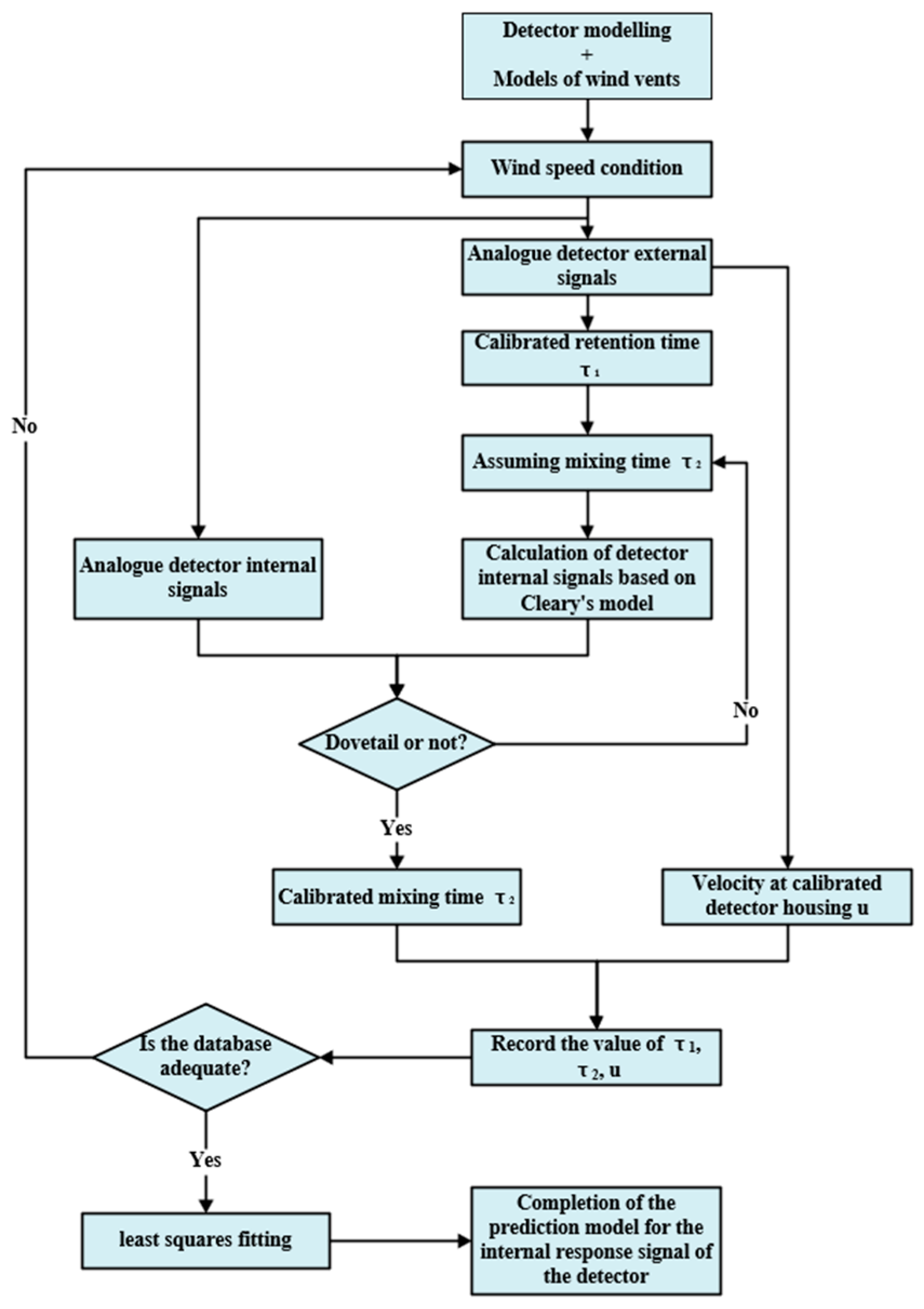
2.3. Calibration Process of Model Parameters
- (a)
- The stationary segment of the u(t) curve can be calculated as the average value of the time, and u can be calibrated.
- (b)
- Let and be the jumping times of FDS simulation curves of and , respectively, and calibrate them according to .
- (c)
- Equation (1) is written as Euler iterative formula 4, the initial value is taken, and , , and are calculated according to the obtained by Equation (4).
- (d)
- Use the dichotomy to adjust so that the calculated curve of is in good agreement with the FDS simulation curve, and can be calibrated.
- (e)
- By changing the air velocity of the tuyere, multiple groups (u, and ) values in the wind speed section can be obtained, and then the fitting of and can be carried out to determine the characteristic parameters of the detector hysteresis model.
3. Calculation of the Parameters of the Response Time Hysteresis Model for Smoke Detector
3.1. Simulation Model
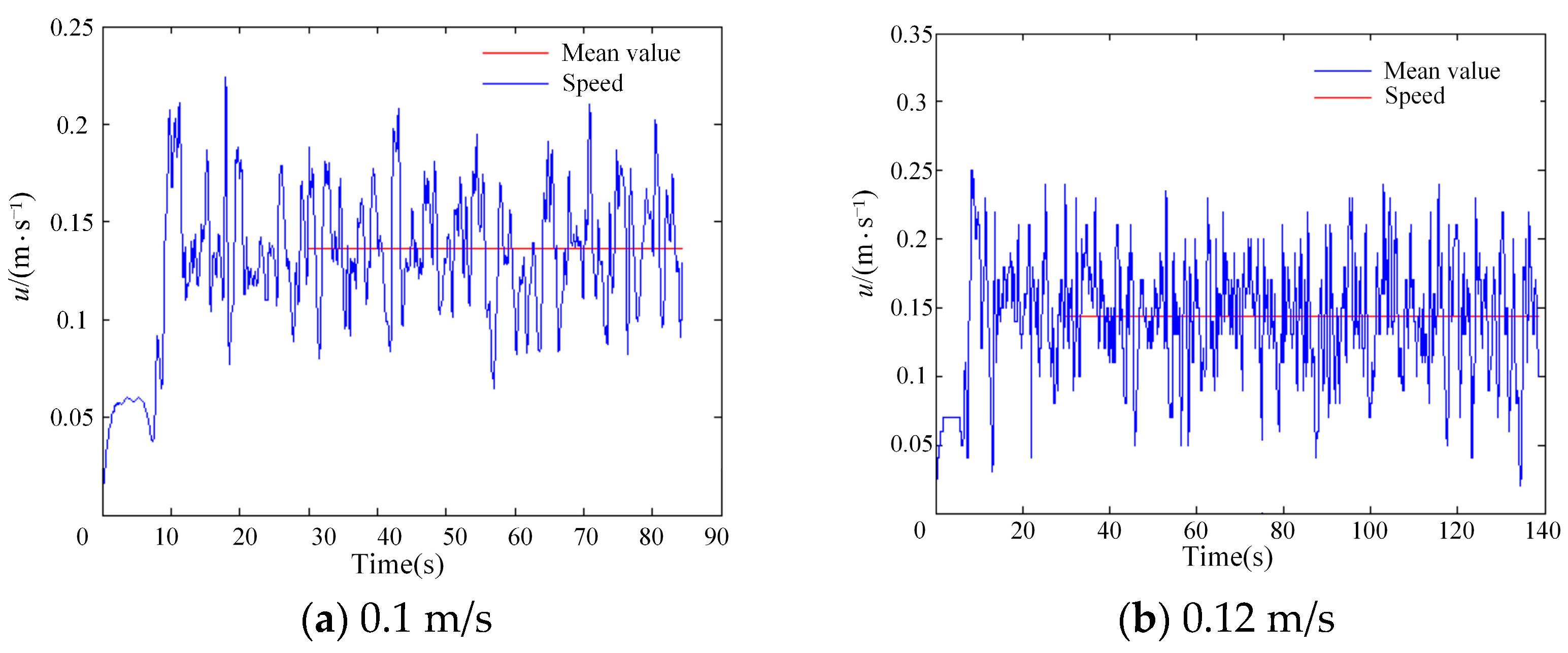
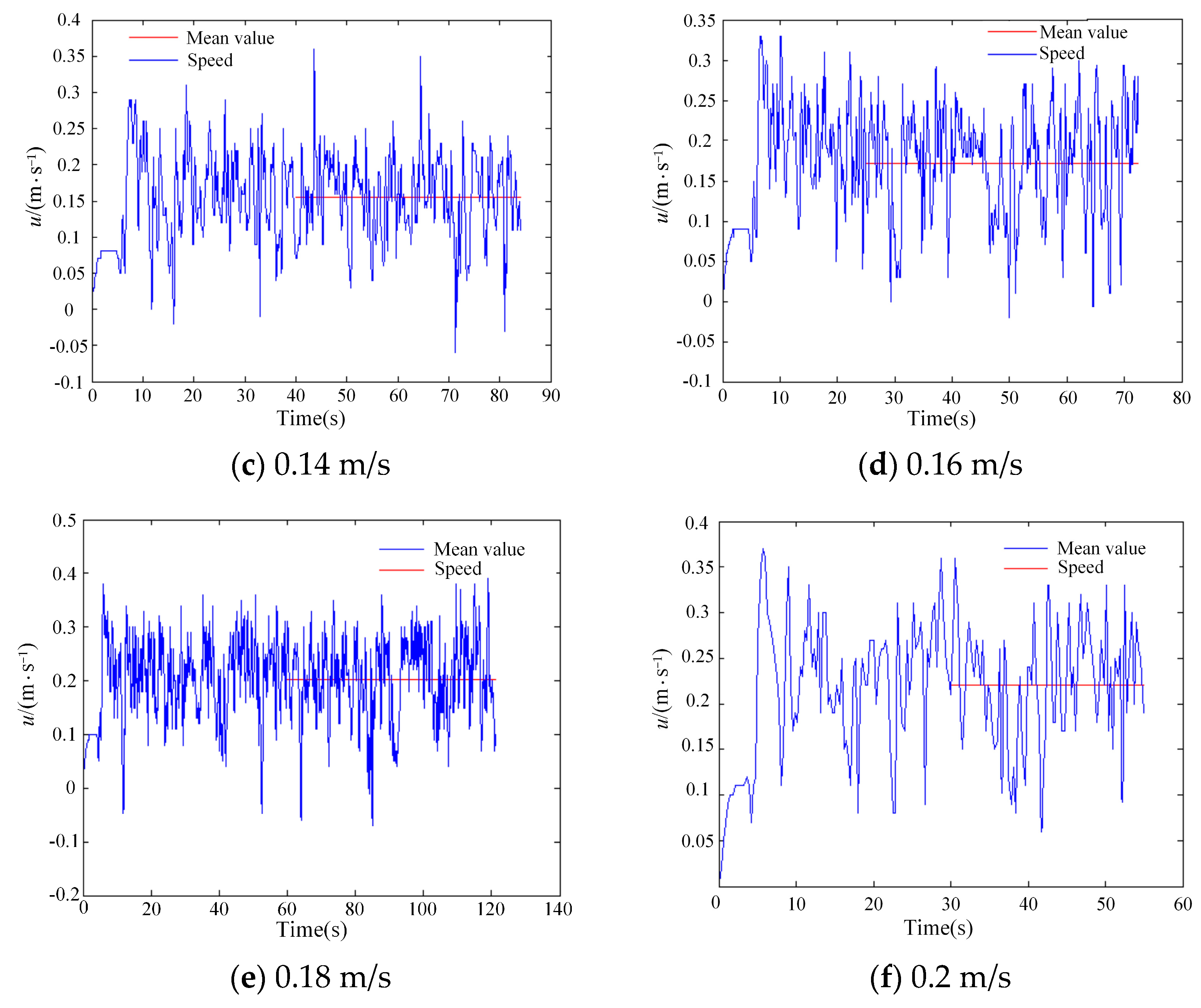
3.2. Numerical Simulation
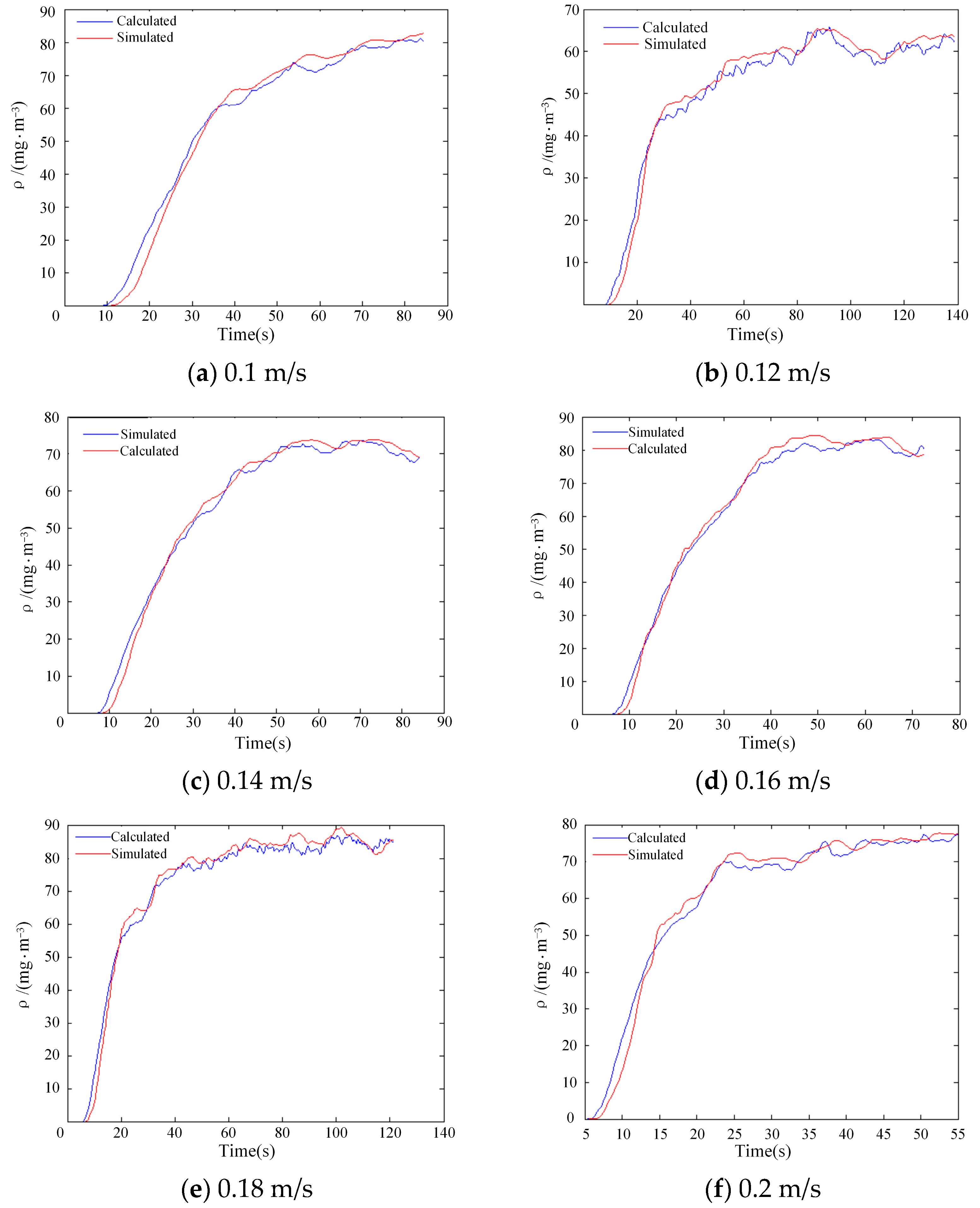
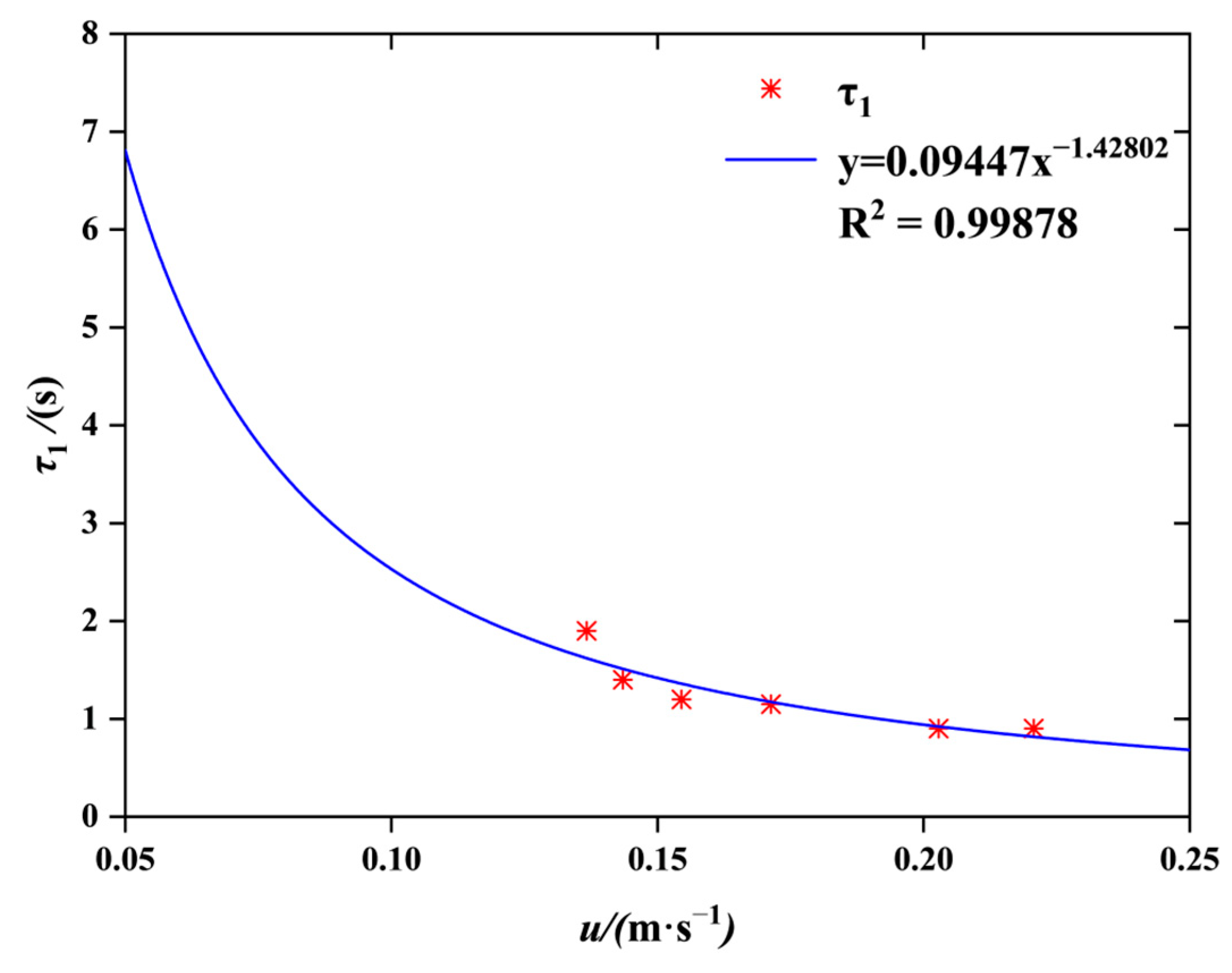
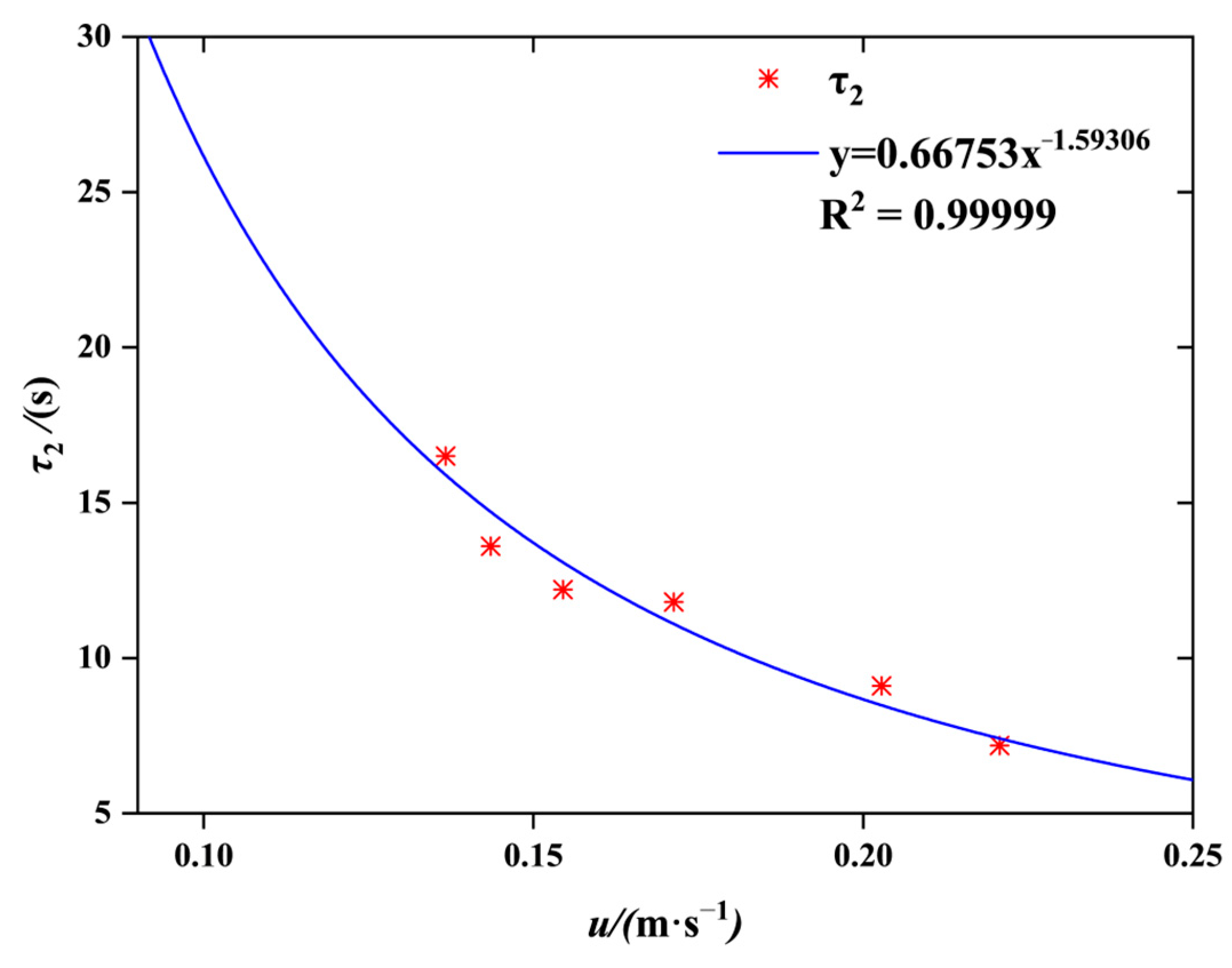
3.3. Parameter Fitting
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- HB7098-1994; Aviation Industry Standards of the People’s Republic of China. China Aviation Industry Corporation 301 Research Institute: Beijing, China, 1994.
- Han, L.; Lin, G.; Fang, J.; Wang, J.; Zhang, Y. Effect of optical labyrinth on the response performance of aircraft cargo hold smoke detectors. Fire Sci. 2016, 25, 208–212. [Google Scholar]
- Wang, J.; Lu, K.; Lu, S.; Zhang, H. Experimental study on ceiling temperature profile of sidewall fires at reduced pressure in an aircraft cargo compartment. Exp. Therm. Fluid Sci. 2017, 82, 326–332. [Google Scholar] [CrossRef]
- Li, C.; Xu, W.; Jin, Y.; Wang, C.; Liu, Q.; Zhang, H. Numerical investigations on combustion characteristics of full-size cabin fire with typical material pyrolysis and burnout under different fire source positions. Case Stud. Therm. Eng. 2024, 54, 104075. [Google Scholar] [CrossRef]
- Keller, A.; Loepfe, M.; Nebiker, P.; Pleisch, R.; Burtscher, H. On-line determination of the optical properties of particles produced by test fires. Fire Saf. J. 2006, 41, 266–273. [Google Scholar] [CrossRef]
- Kruell, W.; Schultze, T.; Willms, I.; Freiling, A. Developments in non-fire sensitivity testing of optical smoke detectors-proposal for a new test method. Fire Saf. Sci 2011, 10, 543–554. [Google Scholar] [CrossRef]
- Zhou, Y.; Shi, L.; Li, C.; Zhang, H.; Zheng, R. Scattering Characteristics of Fire Smoke and Dust Aerosol in Aircraft Cargo Compartment. Fire Technol. 2023, 59, 2543–2565. [Google Scholar] [CrossRef]
- Zheng, R.; Lu, S.; Shi, Z.; Li, C.; Jia, H.; Wang, S. Research on the aerosol identification method for the fire smoke detection in aircraft cargo compartment. Fire Saf. J. 2022, 130, 103574. [Google Scholar] [CrossRef]
- Chen, X.; Shao, Z.; Yang, J. Comparison between actual and simulated smoke for smoke detection certification in aircraft cargo compartments using the CFD method. Fire Technol. 2020, 56, 469–488. [Google Scholar] [CrossRef]
- Chen, X.; Yan, X.; Yang, J. Closed-Loop Control Strategy for Simulated Smoke Concentration in Aircraft Cargo Compartment Mock-Up. Fire Technol. 2023, 59, 2263–2297. [Google Scholar] [CrossRef]
- Papa, R.; Andrade, C.R.; Zaparoli, E.L.; de C. Santos, L.C. CFD analysis of smoke transport inside an aircraft cargo compartment. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 327–334. [Google Scholar] [CrossRef]
- Blake, D.; Suo-Anttila, J. Aircraft cargo compartment fire detection and smoke transport modeling. Fire Saf. J. 2008, 43, 576–582. [Google Scholar] [CrossRef]
- Oztekin, E.S.; Blake, D.; Lyon, R.E. Fire induced flow behavior in a ventilated aircraft cargo compartment. In Proceedings of the 13th International Conference and Exhibition on Fire and Materials, San Francisco, CA, USA, 28–30 January 2013; pp. 28–30. [Google Scholar]
- Oztekin, E.S. Heat and mass transfer due to a small-fire in an aircraft cargo compartment. Int. J. Heat Mass Transf. 2014, 73, 562–573. [Google Scholar] [CrossRef]
- Suo-Anttila, J.; Gill, W.; Luketa-Hanlin, A.; Gallegos, C. Cargo Compartment Smoke Transport Computational Fluid Dynamic Code Validation; US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2007.
- Lu, K.H.; Mao, S.H.; Wang, J.; Lu, S. Numerical simulation of the ventilation effect on fire characteristics and detections in an aircraft cargo compartment. Appl. Therm. Eng. 2017, 124, 1441–1446. [Google Scholar] [CrossRef]
- Zhang, P.; Meng, M.; Wang, J. Optimised arrangement technology and platform development for aircraft cargo hold smoke detection system. Fire Sci. 2016, 25, 228–232. [Google Scholar]
- Heskestad, G. Generalized characterization of smoke entry and response for products of combustion detectors. In Proceeding of the Fire Detection for Life Safety Symposium, Washington, DC, USA, 31 March–1 April 1975; National Academy of Science: Washington, DC, USA, 1977; pp. 93–127. [Google Scholar]
- Brozovsky, E.L. A first approximation method for smoke detector placement based on design fire size, critical velocity, and detector aerosol entry lag time. Fire Technol. Fourth Quart. 1995, 31, 336–353. [Google Scholar] [CrossRef]
- UL217; Standard for Safety for Single and Multiple Station Smoke Alarms. Underwriters Laboratories Inc.: Northbrook, IL, USA, 2006.
- Cleary, T.; Chernovsky, A.; Grosshandler, W.L.; Anderson, M.D. Particulate entry lags in spot-type smoke detectors. In Proceeding of the 6th International Symposium of IAFSS Poitiers, Poitiers, France, 5–9 July 1999; pp. 779–790. [Google Scholar]



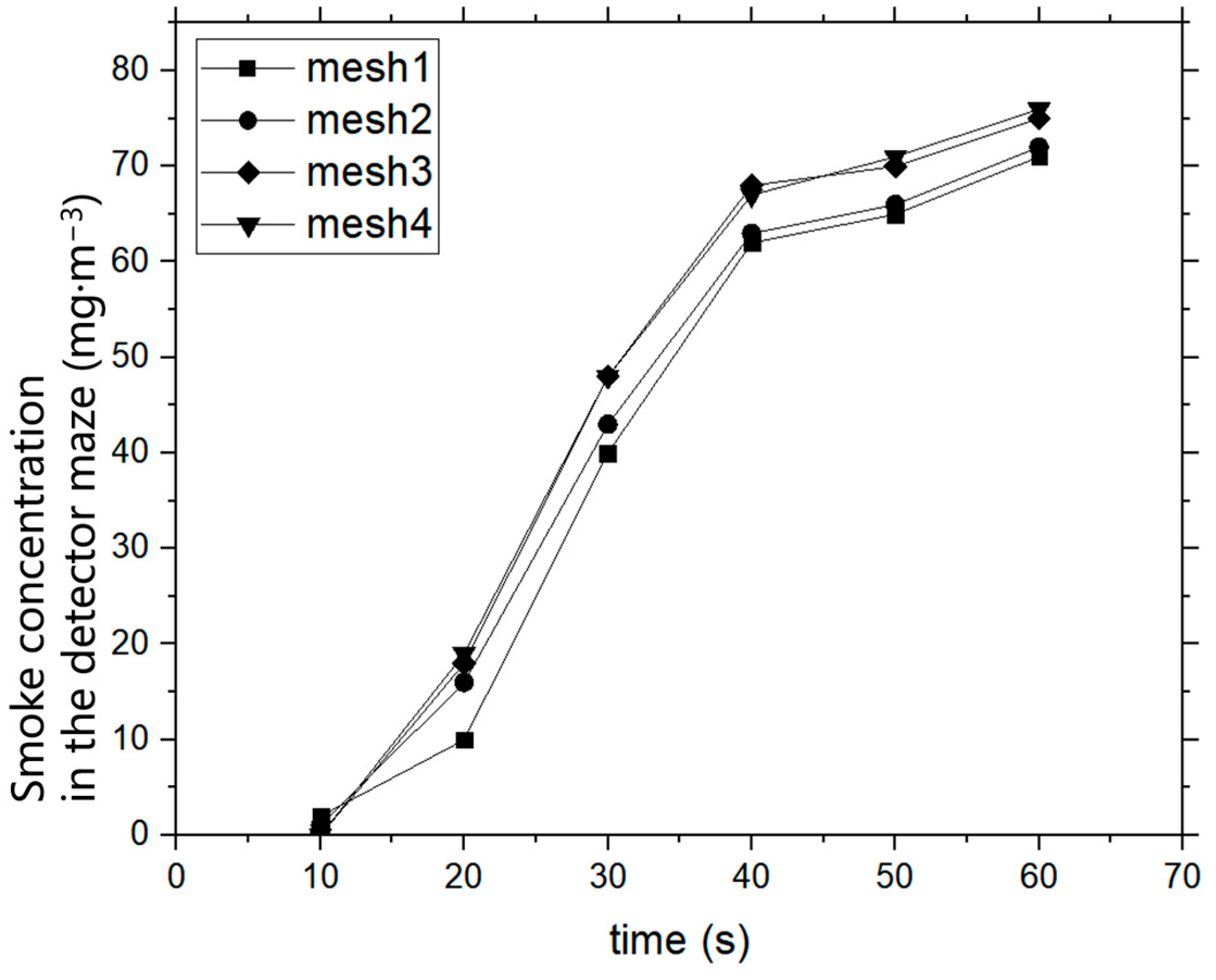




| Grid Size | Inside the Detector | Detector and Surrounding | The Rest of the Space |
|---|---|---|---|
| Mesh1 | 2 | 10 | 40 |
| Mesh2 | 1.5 | 7 | 30 |
| Mesh3 | 1 | 5 | 20 |
| Mesh4 | 0.5 | 3 | 10 |
| Vel. (m/s) | u (m/s) | /s | /s | /s | /s | R |
|---|---|---|---|---|---|---|
| 0.20 | 0.2207 | 5.4 | 6.3 | 0.9 | 7.18 | 0.9841 |
| 0.18 | 0.2028 | 6 | 6.9 | 0.9 | 9.1 | 0.9821 |
| 0.16 | 0.1713 | 6.6 | 7.6 | 1.0 | 11.5 | 0.9919 |
| 0.14 | 0.1545 | 7.4 | 8.6 | 1.2 | 12.2 | 0.9905 |
| 0.12 | 0.1435 | 8.4 | 9.8 | 1.4 | 13.6 | 0.9794 |
| 0.10 | 0.1367 | 9.3 | 11.2 | 1.9 | 16.5 | 0.9852 |
| Serial Number | Wind Velocity (m/s) | Cargo Tank Pressure (atm) | Air Leakage Flow Rate (m3/min) | Temperature (°C) | Alarm Time (s) |
|---|---|---|---|---|---|
| 1 | 0.10 | 1.01 | 1.26 | 25.1 | 48.9 |
| 2 | 0.12 | 1.00 | 1.33 | 25.0 | 48.4 |
| 3 | 0.14 | 1.02 | 1.41 | 25.2 | 45.1 |
| 4 | 0.16 | 0.98 | 1.48 | 24.9 | 45.5 |
| 5 | 0.18 | 0.98 | 1.54 | 24.8 | 44.4 |
| 6 | 0.20 | 1.01 | 1.60 | 24.9 | 43.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Ruan, C.; Wang, S.; Lu, S.; Zhang, H.; Wang, M. Study on Response Time Hysteresis Model of Smoke Detectors in Aircraft Cargo Compartment. Fire 2024, 7, 317. https://doi.org/10.3390/fire7090317
Cui H, Ruan C, Wang S, Lu S, Zhang H, Wang M. Study on Response Time Hysteresis Model of Smoke Detectors in Aircraft Cargo Compartment. Fire. 2024; 7(9):317. https://doi.org/10.3390/fire7090317
Chicago/Turabian StyleCui, Hongwei, Chenran Ruan, Shengdong Wang, Song Lu, Heping Zhang, and Minqiang Wang. 2024. "Study on Response Time Hysteresis Model of Smoke Detectors in Aircraft Cargo Compartment" Fire 7, no. 9: 317. https://doi.org/10.3390/fire7090317
APA StyleCui, H., Ruan, C., Wang, S., Lu, S., Zhang, H., & Wang, M. (2024). Study on Response Time Hysteresis Model of Smoke Detectors in Aircraft Cargo Compartment. Fire, 7(9), 317. https://doi.org/10.3390/fire7090317






